Crosstalk and Competition in Signaling Networks

Abstract

Signaling networks have evolved to transduce external and internal information into critical cellular decisions such as growth, differentiation, and apoptosis. These networks form highly interconnected systems within cells due to network crosstalk, where an enzyme from one canonical pathway acts on targets from other pathways. It is currently unclear what types of effects these interconnections can have on the response of networks to incoming signals. In this work, we employ mathematical models to characterize the influence that multiple substrates have on one another. These models build off of the atomistic motif of a kinase/phosphatase pair acting on a single substrate. We find that the ultrasensitive, switch-like response these motifs can exhibit becomes transitive: if one substrate saturates the enzymes and responds ultrasensitively, then all substrates will do so regardless of their degree of saturation. We also demonstrate that the phosphatases themselves can induce crosstalk even when the kinases are independent. These findings have strong implications for how we understand and classify crosstalk, as well as for the rational development of kinase inhibitors aimed at pharmaceutically modulating network behavior.

Introduction

Signal propagation through a network of interacting proteins is central to a cell’s ability to process and respond to stimuli. In most cases, these interactions involve an enzyme (e.g., a kinase) that covalently modifies a substrate and changes its functionality (i.e., activates/deactivates it as an enzyme, or causes translocation to a different compartment). To regulate the signal, another enzyme (e.g., a phosphatase) reverses the modification, restoring the original functionality of the substrate in question. The net activity of these enzymes alters the functional state of the proteins in the network in response to inputs, and the overall state of the network ultimately determines the cellular response.

Intracellular signaling networks are extremely complex in metazoans, which makes it difficult to understand their behavior (1,2). A major source of this complexity is network crosstalk, i.e., the sharing of input signals between multiple canonical pathways (3–7). For example, kinases can often transmit signals to a large number of different targets: Akt can act on at least 18 substrates, and the receptor tyrosine kinases in the EGF/ErbB family can interact with >20 substrates (8,9). Because eukaryotic genomes contain fewer distinct phosphatases than distinct kinases, phosphatases are generally considered more promiscuous, and even with adaptor proteins targeting their activity, they often act on multiple substrates (10). Although it is clear that crosstalk is widespread in mammalian signaling networks, we currently do not have a clear conceptual picture of how this highly interconnected architecture might influence the response of a network to incoming signals.

In this work, we seek to understand how the competition and promiscuity induced by crosstalk ultimately influence network behavior. In classic crosstalk, a kinase is shared between two pathways and can transfer signals from one pathway to another (3,5,7,11); for instance, mitogen-activated protein kinase (MAPK) networks often use the same enzymes in multiple cascades (12). Most previous computational studies on this subject have focused on characterizing the spatial or temporal mechanisms for the insulation of MAPK signaling cascades despite the potential for crosstalk (13–15). It has been demonstrated, however, that competition among targets of the same kinase can have profound effects on substrate phosphorylation (16). Here, we extend these previous findings to characterize in detail how crosstalk can actively couple the response of multiple proteins to incoming signals. We developed models that consider a set of general motifs, with the goal of understanding how features such as substrate saturation and phosphatase architecture can influence substrate response.

Our models build off a simple futile cycle in which one enzyme modifies a single substrate and another enzyme removes the modification, which we represent as a kinase and phosphatase pair interacting with a target protein (see Fig. 1 A). As first shown by Goldbeter and Koshland (18) over 30 years ago, the fraction of modified substrate for this cycle can be expressed as a function of three parameters:

$$K_K=\frac{K_{m,K}}{{\left[S\right]}_0},K_P=\frac{K_{m,P}}{{\left[S\right]}_0},r=\frac{V_{\mathit{max},K}}{V_{\mathit{max},P}}$$ (1)

where [S]₀ is the total amount of substrate, K_m,K and K_m,P are the Michaelis constants for the two enzymes, K_K and K_P represent the inverse of the degree of saturation of the enzymes, and r is the ratio of their maximum velocities. Detailed definitions of these constants in terms of the underlying rates of the enzymatic reactions can be found in the context of Eq. 2 below. One can easily solve the underlying system of differential equations (see Fig. 1 A) at steady state, providing a relationship between overall substrate phosphorylation and the parameters listed in Eq. 1 (see Eq. 3 below, with α_K,1 = α_P,1 = 1). Because protein levels tend to change slowly (17), we expect that saturation (and thus K_K and K_P) will remain constant on short timescales during the response to signal. On the other hand, r changes with the concentration of active kinase and phosphatase. Incoming signals generally modulate active K or P concentration, thus making r the dominant response parameter. When the substrate does not saturate the enzymes, phosphorylation of the substrate increases hyperbolically with r. However, when the substrate saturates both enzymes, the loop displays a switch-like behavior in r, referred to as 0^th order ultrasensitivity (Fig. 1 B). In this case, at values of r < 1 the fraction of phosphorylated substrate is very low, and at r > 1 the system switches to a highly phosphorylated state (18). The ultrasensitive response of a substrate at saturating concentrations has been observed experimentally in a number of systems (16,19–23).

Figure 1.

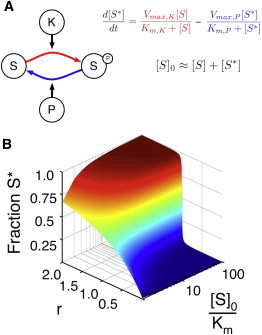
The Goldbeter-Koshland loop. (A) A pair of enzymes (say, a kinase K and a phosphatase P) acts on a single substrate. The associated equations show the change in S^∗ concentration as the difference between the production of S^∗ by the kinase (in red) and the production of S by the phosphatase (in blue). Here we assume that the concentration of free S and S^∗ is far greater than the concentrations of bound S in either form, which is necessary to obtain the standard Michaelis-Menten forms for the enzymatic reaction velocities (18). (B) The fraction of phosphorylated S (z axis) is a function of r and [S]₀. The total concentration of [S] is normalized by its K_m (which is identical for both the kinase and phosphatase) and is plotted on a log scale.

We expanded this model to include competing substrates at either or both enzymes to characterize the influence of multiple targets on signaling (Fig. 2, A–C). All three of the motifs we consider are found in well-known signaling systems, such as the Fus3/Cdk1 network in yeast and other eukaryotes (Fig. 2 D). We found that shared signaling enzymes can couple the responses of different substrates. For instance, when there is more than one substrate of the same kinase and phosphatase (see Fig. 2 A), if one substrate is at sufficient concentration to elicit an ultrasensitive response, then all substrates that share the pair enzymes in the cycle will exhibit ultrasensitivity without necessarily saturating the enzyme themselves. We have shown that in systems in which two substrates share a phosphatase (see Fig. 2 C), one substrate saturating the phosphatase can cause the other substrate to ultrasensitively respond to signals from the first kinase. This indicates a novel potential for phosphatases to be involved in network crosstalk.

Figure 2.

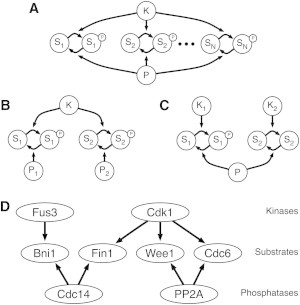
Crosstalk schematic. (A) A pair of enzymes (a kinase K and phosphatase P) acting on N substrates; we term this the 1K1P loop. (B) A kinase that has two substrates, each with its own independent phosphatase (P₁ and P₂); we term this the 1K2P loop. (C) Two independent kinases (K₁ and K₂) acting on two substrates that share a single phosphatase P; we term this the 2K1P loop. (D) A section of the yeast Cdk1 signaling network, including each of these three motifs (16,44–49). Although the interactions shown are specific to yeast, there are human homologs for each of the proteins listed. The full network in this case contains a number of downstream feedback mechanisms that are omitted for clarity. These mechanisms may be abrogated by mutations so that the local influence of competition can be studied experimentally (16). The competition between Wee1 and Cdc6 is an example of the 1K1P loop, whereas Wee1 and Fin1 form a 1K2P loop, and Fin1 and Bni1 form a 2K1P loop.

Kinases are becoming increasingly popular drug targets in the treatment of cancer and other diseases (24). We considered how such inhibitors might influence the behavior of these various crosstalk architectures, and found that these inhibitors can have important consequences that would be difficult to predict in the absence of a detailed understanding of network topology and enzyme saturation.

Overall, our work demonstrates that enzymes with multiple targets can couple signal responses, and that systems considered in a cellular context may exhibit behaviors vastly different from those considered in isolated models. These results have implications for how we understand the role of crosstalk in signaling, and how we can potentially control the propagation of the effects of enzymatic inhibitors through highly connected networks.

Materials and Methods

The behaviors of each model are described by sets of ordinary differential equations (ODEs), which are written explicitly for each system in section 1 of the Supporting Material. The systems of ODEs were numerically integrated using the CVODE package from SUNDIALS (25). We employed the dense linear solver with the backward differentiation formula and a Newton iteration methodology available in that package for all of the dynamics discussed in this work. The values of the parameters used in each case are included in the Supporting Material.

Steady-state measurements were obtained by allowing the system to run until the level of each species of the system stabilized. The actual times at which the measurements were made were chosen heuristically by visual inspection of the trajectories themselves. The surfaces obtained in Figs. 3 and 4 were confirmed analytically by solving for S₁^∗ in the same manner as described by Goldbeter and Koshland (18). The analytical results are derived in sections 2–4 of the Supporting Material.

Figure 3.

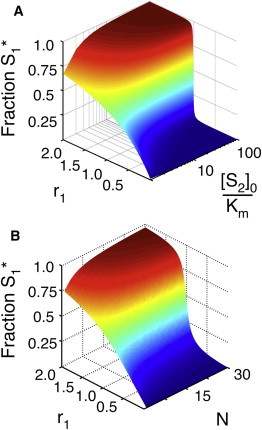
Results for the 1K1P loop. (A) The fraction of phosphorylated S₁ (z axis) as a function of r₁ and [S₂]₀. Note that for the purpose of display, we have set r₁ = r₂ in this case. The total concentration of [S₂] is normalized by its K_m (which is identical for both the kinase and phosphatase) and is plotted on a log scale. (B) The fraction of phosphorylated S₁ as a function of r₁ and the number of additional substrates in the loop (N, see Fig. 2A). All substrates are below saturating concentrations ([S_i]₀ = 0.1 × K_m). As in A, for the purpose of display, the r and K_m parameters have been set to be equal for all substrates. Note that in both panels A and B, the fraction S₁^∗ responds to r₁ with increasing ultrasensitivity as the total saturation of the enzymes (represented by [S₂]₀/K_m or N, respectively) increases.

Figure 4.

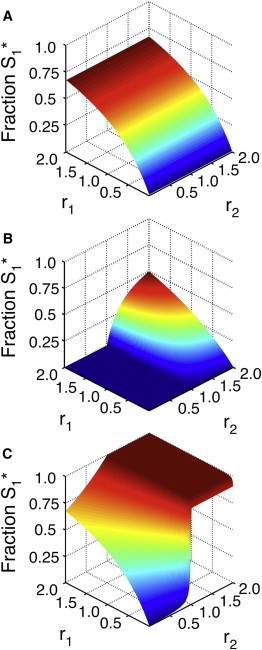
Influence of phosphatase architecture on network response. (A) The fraction of phosphorylated S₁ as a function of r₁ and r₂ when [S₂]₀ ≪ K_m for both the 1K2P and 2K1P loops. In this case, [S₁]₀ = 0.1 × K_m. Note that r₂ has little effect on the response of the S₁ loop. (B) The fraction of phosphorylated S₁ as a function of r₁ and r₂ for a 1K2P loop with [S₂]₀ = 20 × K_m. As in A, S₁ = 0.1 × K_m. If S₂ saturates the enzymes, it becomes a gatekeeper; when r₂ < 1 (i.e., when the S₂ loop is switched to the unphosphorylated state), the S₁ loop essentially cannot respond to incoming signals. When r₂ > 1, however, S₁^∗ responds hyperbolically in both r₁ and r₂. (C) The fraction of phosphorylated S₁ as a function of r₁ and r₂ for a 2K1P loop. As in B, [S₁]₀ = 0.1 × K_m and [S₂]₀ = 20 × K_m. Saturating concentrations of S₂ generally increase phosphorylation in this case. Note that even when r₁ ≪ 1, S₁ shows an ultrasensitive response to r₂ (and thus K₂) despite receiving only basal levels of signal from its own kinase. This indicates the potential for significant phosphatase crosstalk in signaling networks.

Results

1-Kinase/1-phosphatase loop with two substrates

We first considered a signaling motif in which a kinase (K) and phosphatase (P) act on multiple substrates, which we term the 1-kinase/1-phosphatase (1K1P) loop. An example of this can be found in yeast, where the proteins Wee1 and Cdc6 compete for both the kinase Cdk1 and phosphatase PP2A (Fig. 2 D). In the simplest case, we included two substrates of the kinase and phosphatase, S₁ and S₂, each of which can exist in an unphosphorylated and phosphorylated (e.g., S₁^∗) form (see Fig. 2 A, N = 2). The set of enzymatic reactions is as follows:

$$\begin{array}{l}{S}_1+K\underset{k_{-,K,1}}{\overset{k_{+,K,1}}{\rightleftharpoons }}K{S}_1\stackrel{k_{cat,K,1}}{\rightharpoonup }{S}_1^{\ast }+K\\ S_2+K\underset{k_{-,K,2}}{\overset{k_{+,K,2}}{\rightleftharpoons }}K{S}_2\stackrel{k_{cat,K,2}}{\rightharpoonup }{S}_2^{\ast }+K\\ S_1^{\ast }+P\underset{k_{-,P,1}}{\overset{k_{+,P,1}}{\rightleftharpoons }}P{S}_1^{\ast }\stackrel{k_{cat,P,1}}{\rightharpoonup }{S}_1+P\\ S_2^{\ast }+P\underset{k_{-,P,2}}{\overset{k_{+,P,2}}{\rightleftharpoons }}P{S}_2^{\ast }\stackrel{k_{cat,P,1}}{\rightharpoonup }{S}_2+P\end{array}$$ (2)

Each of the above reactions involves three elementary rates: the rate of complex formation (k₊), the rate of complex dissociation (k₋), and the enzyme catalytic rate (k_cat). From these rates we can obtain the Michaelis constant for both enzymes: K_m,K,i = (k_-,K,i +k_cat,K,i)/k_+,K,i and K_m,P,i = (k_-,P,i +k_cat,P,i)/k_+,P,i._. Additionally, we can define the maximum velocity of each enzymatic reaction as V_max,K,i = [K]₀ k_cat,K,i and V_max,P,i = [P]₀ k_cat,P,i. Each kinase and phosphatase molecule can only bind and act on one substrate at any given moment, and as such, S₂ acts as a competitive inhibitor of the kinase and phosphatase reactions with S₁. This results in a set of inhibitory constants, α_K,1 = 1 + [S₂]/K_m,K,2 and α_P,1 = 1 + [S₂^∗]/K_m,P,2, that capture the effects of S₂ on the S₁ kinase and phosphatase reactions, respectively. S₁ inhibition of the S₂ reactions generates similar constants, α_K,2 and α_P,2 (see the Supporting Material). The fact that multiple targets constitute competitive inhibitors of each other has been observed experimentally for both kinases and phosphatases (16,26,27). These α terms are identical to what one would obtain for a generic competitive inhibitor, α = 1 + [I]/K_I (28). Where the activity of a generic inhibitor against its target enzyme depends solely on its concentration, a competitive substrate will inhibit either the kinase or the phosphatase based on the concentrations of its unphosphorylated and phosphorylated forms, respectively. Because these concentrations are controlled by incoming signals, mutual inhibition has the potential to couple substrate responses.

The chemical reactions in Eq. 2 can be readily used to define a system of ODEs in which the binding, dissociation, and catalysis steps are treated explicitly (see the Supporting Material). We numerically integrated these equations and calculated the fraction S₁^∗ ≡ [S₁^∗]/[S₁]₀ at steady state at various concentrations of S₂ for a case in which S₁ does not saturate the enzymes. In this work, we consider a case in which the saturation of all enzymes by any given substrate is equal; we leave the case of differential saturation among enzymes (12) to future studies. The response of the system is controlled by two r values, r₁ and r₂, which are the ratios of the maximum velocities of the enzymes with respect to either substrate. The results of these calculations are summarized in Fig. 3 A. As expected, when there is no S₂ present to compete with S₁ for the enzymes, S₁^∗ increases as a rectangular hyperbola in r₁. When S₂ saturates the enzymes, however, we find that S₁ displays an ultrasensitive response in r₁ in a fashion similar to the ultrasensitive response obtained by increasing S₁ concentration in Fig. 1 B.

These findings can be understood by treating the 1K1P loop analytically. In the limit in which the total concentration of the substrates is much larger than the total concentration of either enzyme (i.e., [S_i]₀ ≈ [S_i] + [S₁^∗]), we can calculate the fraction S₁^∗ as

$$S_1^{\ast }=\frac{\left(r_1-1\right)-\left({\alpha }_{K,1}{K}_{K,1}+{\alpha }_{P,1}{r}_1{K}_{P,1}\right)+\sqrt{{\left(\left(r_1-1\right)-\left({\alpha }_{K,1}{K}_{K,1}+r_1{\alpha }_{P,1}{K}_{P,1}\right)\right)}^2+4\left(r_1-1\right)r_1{\alpha }_{P,1}{K}_{P,1}}}{2\left(r_1-1\right)}$$ (3)

which is identical to the original result of Goldbeter and Koshland (18) except for the α inhibition terms (see the Supporting Material for details about the solution). Note that S₁^∗ depends on [S₁]₀ through the K terms as well as [S₂] and [S₂^∗] through the α terms. The equation for S₂^∗ is identical to Eq. 3 with a change of indices. This result is a generalization of previous findings on multiple substrates in a Goldbeter-Koshland loop, allowing for both kinase saturation and saturation of a shared phosphatase (16). When [S₁]₀ ≪ K_m, as in Fig. 3 A, α_K,2 ≈ 1 and α_P,2 ≈ 1. In this case, S₂ will behave as an isolated Goldbeter-Koshland loop and as such will display an ultrasensitive response in r₂ when [S₂]₀ ≫ K_m. Because incoming signals vary r by changing the relative concentrations of active enzymes, r₁ ∝ r₂ (for purposes of display in Fig. 3 A, we assumed r₁ = r₂). When r₂ < 1, S₂ will be largely unphosphorylated and will inhibit the kinase’s action on S₁, causing S₁ to be primarily in its unphosphorylated state. Similarly, when r₂ > 1, S₂ will be mostly phosphorylated and will inhibit the S₁ dephosphorylation reaction by saturating the phosphatase. In combination, this coupling transfers the ultrasensitive response of S₂ to the S₁ curve. We have proven mathematically that an increase in S₂ ultrasensitivity (i.e., increasing S₂ concentration) always increases the ultrasensitivity of the response of S₁ in r₂ regardless of the values of the kinetic parameters (see the Supporting Material). The general behavior observed in Fig. 3 A is thus a qualitative feature of all 1K1P loops.

It has been shown experimentally that the competition between multiple phosphorylation sites on the protein Wee1 contributes to the ultrasensitivity of Wee1’s response to incoming signals (16). Although multisite phosphorylation can have a number of influences on such systems (e.g., by introducing thresholds or bistability (2,29,30)), these findings are consistent with the predictions made by Eq. 3.

1K1P with many substrates

We further developed the 1K1P loop to include N > 2 substrates of the kinase and phosphatase (see Fig. 2 A). As described above, we numerically integrated the resulting ODEs and calculated the fraction S₁ at steady state in a case in which we include a varying number of substrates, each of which does not saturate the enzymes. The results of these calculations are summarized in Fig. 3 B. As expected, S₁^∗ increases as a rectangular hyperbola in r₁ in the absence of other substrates. As new unsaturating substrates are added to the system, we see that S₁^∗ starts to show an ultrasensitive response in r₁, even though none of the substrates are at a concentration that would produce such a response on their own.

Once again, these results can be understood by treating the loop analytically. In this case, the collection of substrates act as competitive inhibitors of the S₁ loop. As such, the inhibitory constants must now account for all competing substrates and can be expressed as ${\alpha }_{K,1}=1+{\sum }_{i=2}^N\left[S_i\right]/K_{m,K,i}$ and ${\alpha }_{P,1}=1+{\sum }_{i=2}^N\left[S_i^{\ast }\right]/K_{m,P,i}$ (see the Supporting Material for the derivation). Considering the case in which N > 2 reveals that saturation of the enzymes can be the combined result of many substrates, rather than one substrate saturating the enzymes on its own. When the kinase is saturated by any subset of its targets, S₁’s kinase reaction is inhibited, and a similar inhibition occurs with the phosphatase. Thus, given enough substrates, the entire system can show ultrasensitivity in r₁ even when none of the substrates individually saturate the enzymes.

As mentioned in the Introduction, kinases often have multiple targets within cells; for instance, Cdk1 has hundreds of substrates in yeast (2,31,32), and the ErbB receptor tyrosine kinases in humans have between 20 and 40 potential targets. In the latter case, the K_D values measured by Kaushansky et al. (33) indicate that the 1 μM K_M value used in generating Fig. 3 is a reasonable estimate. The collective-saturation mechanism described above may thus represent a common scenario for generating ultrasensitivity in substrate response.

1-Kinase/2-phosphatase loop

Most of our empirical understanding of crosstalk comes from studies that focused on the motif of a kinase with more than one substrate (34). Because the specific phosphatases that act on any given set of targets are often not known, it is not clear that all kinase crosstalk will follow the 1K1P pattern discussed above (Fig. 2 A). For instance, Fin1 and Wee1 share the same kinase (Cdk1) but have separate phosphatases (Cdc14 and PP2A, respectively; Fig. 2 D). Also, because kinases often have a very large number of targets, systems in which substrates share the same kinase but possess separate phosphatases may be widespread (8,9,31,32). As such, we considered the behavior of the 1-kinase/2-phosphatase (1K2P) loop as diagramed in Fig. 2 B. In this case, because the phosphatases are independent, we can separate the r parameters (i.e., r₂ 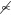r₁). At low substrate concentrations, S₁ responds hyperbolically in r₁ and is insensitive to r₂ (Fig. 4 A). When [S₂]₀ ≫ K_m and r₂ < 1, S₁ phosphorylation is greatly reduced (Fig. 4 B). In fact, one observes very little S₁ phosphorylation until r₂ > 1. In contrast to the 1K1P loop, the response of S₁ to r₂ thus exhibits a threshold: when r₂ < 1, S₁ essentially cannot respond to signals. At values of r₂ > 1, however, S₁ responds hyperbolically to both r₁ and r₂.

The fraction S₁^∗ for the 1K2P loop also follows Eq. 3, but with α_P,1 = 1 because the phosphatases are independent. The presence of S₂ in the system thus generally decreases the phosphorylation level of S₁ (compare Fig. 4, A and B). The thresholding behavior seen in Fig. 4 B occurs because the concentration of the inhibitor (i.e., unphosphorylated S₂) responds ultrasensitively to r₂. If r₂ < 1, the inhibitor concentration is high, and no phosphorylation of S₁ can take place. At r₂ > 1, the inhibitor is largely removed from the system, allowing S₁ to respond to incoming signals. However, it is only in the limit r₂ → ∞ (i.e., α_K,1 → 1) that S₁ will behave as an isolated futile cycle. As with the 1K1P loop, we have shown mathematically that addition of S₂ always decreases S₁^∗ regardless of the values of the parameters in the limit S₁^∗ ≪ K_m (see the Supporting Material). This indicates that the gatekeeper function played by S₂ is a robust feature of 1K2P loops.

Kim and Ferrell (16) showed experimentally that adding Fin1 and Cdc6 to Xenopus cell extracts increases the active kinase concentration (i.e., r) required to induce a Wee1 response. Although the experiment in this case involves both a 1K1P and a 1K2P loop (Fig. 2 D), these findings are consistent with our prediction that competitive substrates tend to decrease the phosphorylation levels of other targets when the phosphatase is not shared.

2-Kinase/1-phosphatase loop

The human genome encodes ∼150 catalytically active phosphatases and phosphatase domains, and almost 500 kinases (35,36). As such, phosphatases are generally considered promiscuous; although adaptor proteins help increase phosphatase specificity, these complexes still can target multiple substrates (10). Because of this promiscuity, it is reasonable to imagine that motifs in which two substrates share a single phosphatase but are phosphorylated by independent kinases are relatively common arrangements in signaling networks. There are certainly examples of such situations: for instance, Fin1 and Bni1 in yeast share a phosphatase (Cdc14) but have different kinases (Cdk1 and Fus3, respectively; Fig. 2 D). We used the 2-kinase/1-phosphatase (2K1P) loop as modeled in Fig. 2 C to characterize the behavior of such systems. As with the 1K2P loop, the distinct kinases in the 2K1P system allow the separation of r parameters so that r₁ 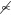r₂.

At low substrate concentrations, this is essentially the case. As anticipated, S₁ responds hyperbolically in r₁ and is insensitive to r₂ (see Fig. 4 A). The situation is very different when [S₂]₀ ≫ K_m. We see the expected hyperbolic S₁ response in r₁ when r₂ is nearly zero (i.e., when the S₂ loop has not received an activation signal); however, as r₂ increases, the fraction of phosphorylated S₁ molecules increases until it reaches nearly one at r₂ > 1 (Fig. 4 C). When r₁ is close to zero, S₁ responds ultrasensitively to r₂. This indicates that a signal that switches S₂ to its phosphorylated state can cause a similar switch in S₁ even if very little signal is received via K₁.

As with the 1K1P loop, this behavior can be explained in terms of the inhibition of one loop by another. In this case, the fraction S₁^∗ can be defined as in Eq. 3 with α_K,1 =1 to account for the independence of the kinases. Adding S₂ to the system thus generally increases phosphorylation of S₁ (compare Fig. 4, A and C). Because phosphorylated S₂ acts as a phosphatase inhibitor, an incoming signal that increases r₂ to values greater than one introduces high concentrations of the inhibitor in a switch-like manner, inducing a response in S₁. We have shown mathematically that this increase in phosphorylation in response to S₂ competition will always occur regardless of parameters in the limit S₁^∗ ≪ K_m (see the Supporting Material).

Phosphatase tunneling

In the models described above, we focused on crosstalk occurring between substrates on the same level of signaling; the only relationship between the substrates is the shared enzymes. Signaling networks, however, often contain cascades in which a set of proteins activate each other in sequence (37). Although the sharing of phosphatases between different levels of a cascade has been documented (6), the phosphatase architecture in these cases is often poorly understood. Indeed, anonymous and independent phosphatases are often added to mathematical models of MAPK cascades to fill in these gaps (21,38–40). Given this ambiguity, we constructed models of cascades in which each kinase has an independent phosphatase, in addition to a case in which a single phosphatase acts on all of the proteins in the cascade (Fig. 5, A and B).

Figure 5.

Influence of phosphatase tunneling on cascade signals. (A) A kinase cascade with N members. The kinase K provides the input signal, and each substrate S_i acts as the kinase for substrate S_i+1. In this model, there are N independent phosphatases (P_i). This expands upon systems previously described by Goldbeter and Koshland (18). (B) A kinase cascade similar to that in panel A, but with a single shared phosphatase P. (C) Fractional phosphorylation of the final substrate in the cascade as a function of r for cascades with two to five substrates. In this case, r is defined as the V_max of the input kinase (K in A and B) divided by the V_max of the phosphatase for the first substrate in the cascade (P₁ in A, and P in B). The dashed lines represent cascades with N phosphatases and the solid lines represent cascades with a single shared phosphatase. Note that the responses of cascades become exponentially more sensitive to r with increasing depth N. Cascades with a single shared phosphatase are considerably more sensitive to r compared with those with independent phosphatases. (D) In this case, we define a parameter, r_1/2, as the value of r in panel C at which the response of a cascade is half-maximal. For any given number of substrates, N, the r_1/2 ratio is the r_1/2 of the independent case divided by the r_1/2 of the shared case (i.e., the r_1/2 of the dashed curve in C divided by the r_1/2 for the solid curve). For N = 2, the independent case requires ∼5 times as much input signal to achieve a half-maximal response; for N = 3, 4, and 5, the independent case requires ∼13 times as much input signal.

Each type of cascade was modeled with depth N = 2, 3, 4, or 5 substrates present in saturating (10 × K_m) or unsaturating (0.1 × K_m) concentrations. The input parameter r was defined as the ratio of the maximum velocities of the initial kinase (K) to the phosphatase acting on S₁ (P₁ or P for the independent and shared cases, respectively), and the models were analyzed for the fraction of the final substrate phosphorylated (S_N^∗) at steady state.

For both classes of cascade, we found that the response of the final substrate becomes exponentially more sensitive to input signals with increasing cascade depth. The N = 5 case generally reaches its r_1/2 (the r-value at which half of S_N is phosphorylated) with 9 orders of magnitude less input than N = 2 (see Fig. 5 C). This increase in sensitivity is an expected outcome of amplification in signaling cascades (18,41). Additionally, models with a single, shared phosphatase show a higher degree in input sensitivity in r compared with models with independent phosphatases, but only when the substrates are present at saturating concentrations.

To quantify the changes in input sensitivity for saturating conditions, we took the ratio of the r_1/2-values for the two types of cascade at a given value of N (see Fig. 5 D). In the most basic cascade, with N = 2, the r_1/2 for the single phosphatase model is ∼5 times less than that for the multiple phosphatase model. This ratio increases and plateaus for cascades with depth N ≥ 3; in these cases, the single phosphatase models require ∼13 times less signal. This occurs because the signal is able to tunnel through the shared phosphatase when the substrates are at saturating concentrations. Activation of the upstream kinases not only activates the rest of the cascade but also produces phosphorylated substrate molecules that act as phosphatase inhibitors. This reduces the effective concentration of free phosphatase available for downstream substrates, amplifying the apparent signal strength.

Kinase inhibitors

As mentioned above, there is a growing interest in developing small molecules that target and inhibit kinases as potential therapeutics for a variety of diseases (24). It is unclear, however, what kind of effects these inhibitors will have in loops with significant kinase or phosphatase crosstalk; in these cases, kinase inhibitors not only influence their targets’ activity but also the concentration of other inhibitors (namely, S₂ and S₂^∗) in the system. We considered the impact of two separate types of inhibitors on the loops described above. Type 1 inhibitors, which are currently by far the most commonly used in practice (24), target the ATP-binding site of a specific kinase and disrupt its activity toward all of its targets. Type 2 inhibitors, on the other hand, target and disrupt a specific kinase–target interaction, leaving the kinase free to act on a subset of its other targets. Although the latter is not currently common, peptide inhibitors have been successfully used in this manner (27), and there is increasing interest in developing the capacity to inhibit specific protein-protein interactions within cells (42).

We modeled the potential effects of these inhibitors by including explicit inhibitor molecules in our loops, with I₁ and I₂ representing type 1 and type 2 inhibitors, respectively. We first considered a 1K1P loop with S₂ at saturating concentrations and in the active state (r₁ = r₂ = 1.5; see Fig. 2 A). As one would expect, adding I₁ significantly decreases S₁^∗, because a generic inhibitor for the kinase will clearly reduce overall phosphorylation of all targets (Fig. 6 A). However, even an inhibitor that is specific to S₂ decreases the phosphorylation of S₁ (Fig. 6 A). The specific inhibitor in this case decreases the concentration of S₂^∗, reducing competition for the phosphatase and thus decreasing S₁^∗.The effect of I₂ is not as dramatic as that of I₁ for the 1K1P loop, but this nonetheless represents a potentially unintended consequence of a (putatively) specific inhibitor.

Figure 6.

Effect of kinase inhibitors in the presence of crosstalk. (A) A 1K1P loop with two substrates in the presence of one of two kinase inhibitors: I₁, which prevents reactions with all targets of the kinase (red), or I₂, which specifically disrupts K-S₂ interactions (blue). We plot the fraction of phosphorylated S₁ against the ratio of [I₁] or [I₂] to [K]. In this case, [S₁]₀ = 0.1 × K_m, [S₂]₀ = 20 × K_m and r₁ = r₂ = 1.5. Note that using either inhibitor causes a decrease in the fraction S₁^∗, although the effect is less pronounced with the S₂-specific inhibitor. In the latter scenario, I₂ reduces the [S₂^∗], which is itself a phosphatase inhibitor for S₁^∗. The net effect of I₂ is thus to decrease S₁ phosphorylation. (B) A 1K2P loop with the same kinase inhibitors as in panel A. The fraction of phosphorylated S₁ is plotted against the ratio of [I₁] or [I₂] to [K]. In this case, [S₁]₀ = 0.1 × K_m, [S₂]₀ = 20 × K_m, r₁ = 0.5 and r₂ = 1.5. Although the general inhibitor still reduces S₁^∗, the specific inhibitor increases S₁^∗. This is because decreasing the concentration of S₂^∗ reduces competition for the shared kinase. (C) A 2K1P loop in the presence of both I₁ and I₂. Note that because the kinases are independent in this case, the effects of both inhibitors are identical. The fraction of phosphorylated S₁ is plotted against the ratio of the concentrations of [I₂] to [K]. In this case, [S₁]₀ = 0.1 × K_m, [S₂]₀ = 20 × K_m, r₁ = 0.01 and r₂ = 1.5. Both inhibitors decrease S₁^∗, as the reduction in phosphorylated S₂ due to the inhibitors reduces S₂^∗’s inhibition of the S₁ phosphatase reaction.

In the 1K2P case, we find exactly the opposite behavior: whereas I₁ decreases S₁^∗ as expected, I₂ increases the phosphorylation of the first substrate (Fig. 6 B). This is because the inhibitor reduces S₂ interactions with the kinase, alleviating competition. In this case, the response of the system is perhaps more intuitive: because S₂ is a competitive inhibitor of S₁ phosphorylation, inhibiting its phosphorylation in a specific way increases the capacity of S₁ to respond to signals.

In the 2K1P loop, if the two types of inhibitors are aimed at the second kinase (K₂), they have the same net effect. Because K₂ cannot act on S₁ in this model, there is no difference between an inhibitor that simply targets K₂ and one that specifically targets the K₂-S₂ interaction. When the second loop is activated by a signal and the first loop is not, the K₂ inhibitor completely abolishes S₁ phosphorylation (Fig. 6 C). Although the source of this behavior is clear from Fig. 4 C, the effect is nonetheless striking. In the absence of knowledge about the shared phosphatase (or the phenomenology of the 2K1P loop), a response like the one shown in Fig. 4 C might lead to the erroneous conclusion that K₂ acts directly on S₁, or that the inhibitor in this case is nonspecific.

Discussion

The 1K1P and 1K2P loops discussed above (Fig. 2, A and B) represent two variations on the classic crosstalk motif, i.e., a kinase that has multiple downstream targets in different pathways. In the traditional view, the coupling between the substrates in these two loops is understood as simply arising from the fact that they will all respond to some of the same upstream signals (34). Our work reveals that a shared enzyme not only modifies each target but also can strongly couple the response of one target to that of another through competitive inhibition at the shared enzyme. For instance, if the targets in question share the same phosphatase, we find that 0^th-order ultrasensitivity becomes transitive; all of the targets in this case will respond in a switch-like manner to incoming signals (Fig. 3 A). We also find that in situations where there are a large number of substrates (Fig. 3 B), the system can respond ultrasensitively even if none of the targets is at a high enough concentration to elicit such a response on its own (Fig. 3 B). It has been shown that some kinases do in fact act on many targets (e.g., Akt, the EGF receptors, and Cdk1 (8, 9, 31, 32)), indicating that this collective saturation may represent a common mechanism for inducing ultrasensitivity without having to express any given protein target at saturating levels.

We find that the alternative variation on traditional kinase crosstalk, the 1K2P loop (Fig. 2 B), displays a completely different set of behaviors from those observed when the phosphatase is shared. In this case, the saturating substrate acts as a type of gatekeeper for the other substrates in the loop. Below the signal threshold at which this saturating substrate switches into the phosphorylated state, other substrates will simply be unable to respond to incoming signals, whereas above this threshold the unsaturating targets will respond in a hyperbolic manner (Fig. 4 B). Although direct experimental tests are currently lacking, our predictions for both 1K1P and 1K2P loops are consistent with available data (16). Overall, these findings indicate that when a particular kinase has multiple targets in multiple pathways, it is difficult to reason in general about the behavior of the system in the absence of detailed information regarding phosphatase architecture and relative saturation levels (Figs. 3 and 4).

To date, nearly all experimental characterizations of crosstalk have focused on kinases, and, to our knowledge, the potential for phosphatases to couple signaling responses on their own has not been previously considered (34). Our analysis of the 2K1P loop (Fig. 2 C) demonstrates that such coupling is readily achieved. Indeed, a shared phosphatase can elicit an ultrasensitive response of a target to signals from kinases that do not directly act on the target in question (Fig. 4 C). Furthermore, phosphatase architecture plays a role in the sensitivity of a signaling cascade. We found that cascades in which every substrate shares a common phosphatase are more responsive to input signals than cascades with independent phosphatases when the substrates are at saturating levels. Given that phosphatases are generally considered more promiscuous than kinases, this indicates that phosphatase crosstalk may be widespread in biological networks. Because the specific phosphatases that act on many targets in signaling networks are often not known (38–40), it is currently unclear to what extent phosphatase crosstalk can influence global network behavior.

Given the widespread crosstalk present in mammalian signaling networks, our work highlights the inherent difficulty of predicting a priori the effects that kinase inhibitors will have on cells. These effects ultimately will depend not only on the kinase connectivity of the network but also on the degree of saturation in the targets and the phosphatase architecture. In many cases, both of these facts are unknown—even if the intracellular concentrations of the target proteins are known, the K_m-values for kinases and (especially) phosphatases are not known, and for many signaling pathways the relevant phosphatases have not yet been identified. Understanding these details will be a crucial component of any attempt to rationally design a kinase inhibition strategy that can elicit some desired effect on some set of targets without inducing unintended decreases (or increases) in the phosphorylation levels of other proteins in the network (Fig. 6).

Ultimately, our work indicates that studies on signaling and regulatory networks need to be increasingly mindful of the highly interconnected and interdependent structure of the networks themselves. This is especially true of phosphatases. To understand the real consequences of rampant kinase crosstalk, we clearly must obtain more reliable information about which phosphatases act on which targets, what adaptor domains they employ, etc. The findings described above also highlight the fact that individual elements of signaling networks can exhibit responses that are sensitive to the context in which the element is found. Care must be taken to ensure that this dependence on network architecture informs our interpretation and understanding of how networks function and interact with each other.