Gene Regulation by Riboswitches with and without Negative Feedback Loop

Abstract

Riboswitches, structured elements in the untranslated regions of messenger RNAs, regulate gene expression by binding specific metabolites. We introduce a kinetic network model that describes the functions of riboswitches at the systems level. Using experimental data for flavin mononucleotide riboswitch as a guide, we show that efficient function, implying a large dynamic range without compromising the requirement to suppress transcription, is determined by a balance between the transcription speed, the folding and unfolding rates of the aptamer, and the binding rates of the metabolite. We also investigated the effect of negative feedback accounting for binding to metabolites, which are themselves the products of genes that are being regulated. For a range of transcription rates negative feedback suppresses gene expression by nearly 10-fold. Negative feedback speeds the gene expression response time, and suppresses the change of steady-state protein concentration by half relative to that without feedback, when there is a modest spike in DNA concentration. A dynamic phase diagram expressed in terms of transcription speed, folding rates, and metabolite binding rates predicts different scenarios in riboswitch-mediated transcription regulation.

Introduction

Riboswitches are cis-acting RNA elements located in the untranslated region of mRNAs that regulate associated gene expression by sensing and binding target cellular metabolites (1–3). In bacteria, binding of metabolites to the conserved aptamer domain allosterically alters the folding patterns of the downstream expression platform, whose conformation controls transcription termination or translation initiation (2,4,5). The target metabolites are usually the products or their derivatives of the downstream gene that riboswitches control. Hence, metabolite binding to riboswitches serves as a feedback signal to control RNA transcription or translation initiation. The feedback through metabolite binding is naturally designed to be a fundamental network motif for riboswitches. For example, tandem riboswitches respond to multiple metabolites to control a single gene with greater regulatory complexity (6,7), whereas single glmS riboswitch has been shown to respond to multiple signals using both negative and positive feedback (8). Understanding the various in vivo riboswitch functions requires a theoretical framework that takes into account the interplay between speed of RNA transcription, folding kinetics of the nascent RNA transcript, and kinetics of metabolite binding to the nascent RNA transcript, and the role of feedback arising from interactions between synthesized metabolities and the transcript. The effects of speed of RNA transcription and metabolite binding kinetics have been examined in vitro in an insightful study involving the flavin mononucleotide (FMN) riboswitches (9). They argued that FMN riboswitch is kinetically driven implying that the riboswitch does not reach thermodynamic equilibrium with FMN before a decision between continued transcription and transcription termination needs to be made.

The regulatory roles played by riboswitches have also inspired the design of novel RNA-based gene-control elements that respond to small molecules (10,11). Several models have been proposed to describe how riboswitches function and meet their regulatory demands (12,13). However, they focused solely on the transcription process without accounting for the feedback effect from the metabolite produced by the gene encoding the riboswitch. Here, we introduce a general kinetic network model that can be used to describe both in vivo and in vitro functions of riboswitches. Our coarse-grained kinetic network model, which takes into account the interplay of cotranscriptional folding, speed of transcription, and kinetics of metabolite binding, also models effects of a negative feedback loop so that predictions for in vivo functions of riboswitches can be made. As an illustration of the theory, we first consider the dependence of metabolite concentration on the regulation of in vitro transcription termination of FMN riboswitches without a feedback loop, which enables us to obtain the range of folding rates and transcription rates that produce results consistent with experiments (9). We then include the negative feedback loop in the network to study how riboswitches regulate gene expression at the systems level.

Methods

General kinetic model

The riboswitch is transcribed from the leader, the nonprotein-coding region, of the associated gene (Fig. 1). We simplify the multiple complex in vitro biochemical steps in the function of the off riboswitch, involving transcription, cotranscriptional RNA folding, and metabolite binding, to a few key kinetic steps (Fig. 1). Without feedback, the first stage is the transcription of the aptamer domain (B). The antiterminator sequence is transcribed $\left(B_2\right)$ in the second step. At each stage, the aptamer domain of the RNA transcript can either cotranscriptionally fold or unfold. Only when the aptamer domain is folded ($B^{\ast }$, $B_2^{\ast }$) can the RNA transcript bind the metabolite (M). At the second stage, when the aptamer domain is unfolded, the RNA transcript is in an alternative folding pattern with the formation of the antiterminator stem $\left(B_2\right)$. The final stage of the transcription occurs when the terminator sequence is transcribed $\left(R_i\right)$. If the terminator sequence is transcribed following $B_2$, the antiterminator structure prevents the formation of a terminator stem and the transcription proceeds until the downstream coding region is fully transcribed $\left(R_f\right)$. If the terminator sequence is transcribed following $B_2^{\ast }$ or $B_2^{\ast }M$, the absence of antiterminator allows the terminator to form, which subsequently leads to the dissociation of RNA transcript ($B_{2t}^{\ast }$ and $B_{2t}^{\ast }M$) from the DNA template and terminates the transcription. The feedback effect involved with translation and metabolite synthesis will be discussed in later sections.

Figure 1.

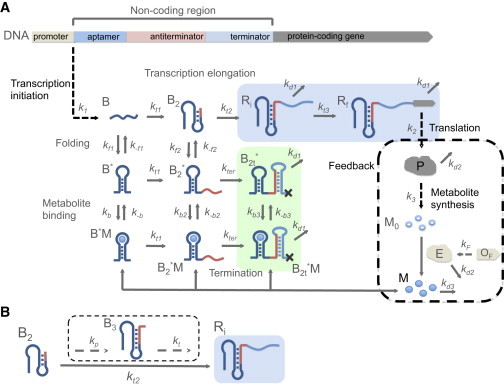
(A) Kinetic network model for RNA transcription mediated by riboswitches. The leader, upstream of the protein-coding gene, consists of sequences that can be transcribed to the aptamer domain (B), antiterminator $\left(B_2\right)$ and terminator region $\left(R_i\right)$ of the riboswitch. After transcription initiation, elongation, folding of RNA transcript, and metabolite binding are simplified to several key steps. Starting from the transcript B, where the aptamer sequence is transcribed, transcription can continue to $B_2$ (antiterminator sequence transcribed) at a transcription rate constant $k_{t1}$. Further elongation through the terminator sequence with transcription rate constant $k_{t2}$ results in the synthesis of full RNA without termination. $R_i$ is the transcript with the sequence of the protein-coding region starting to be transcribed, and eventually grows to $R_f$, the full protein-coding region transcribed, with a rate of $k_{t3}$. Besides transcription elongation, each of the transcript states, B and $B_2$, can form states with aptamer domain folded ($B^{\ast }$ and $B_2^{\ast }$) with a folding rate of $k_{f1}$ and $k_{f2}$, respectively. The aptamer folded states can bind metabolite (M) leading to the bound states ($B^{\ast }M$ and $B_2^{\ast }M$) with association rate constant $k_b$. The transcripts in state $B_2^{\ast }$ and $B_2^{\ast }M$ can continue elongating until the terminator sequence is transcribed with their expression platform forming a transcription terminator stem and dissociate from the DNA template terminating transcription, with a rate of $k_{ter}$ ($B_{2t}^{\ast }$ and $B_{2t}^{\ast }M$). The fraction of transcription termination, $f_{ter}$, is determined from the amount of the terminated transcripts (in green block) versus nonterminated transcripts (in blue block). In the presence of a negative feedback loop (steps included by the box in dashes) additional biochemical steps have to be included. In this case after RNA is fully synthesized, it can produce protein P at a rate $k_2$ or get degraded with a rate $k_{d1}$. The fate of P is either degradation (rate $k_{d2}$) or production of an inactive metabolite $M_0$, which is activated by the enzyme (E) encoded by the gene $O_F$. The activated enzyme can bind to the folded aptamer and can abort transcription. (B) Simplification of the step from $B_2$ to $R_i$ for FMN riboswitch. In the application to FMN riboswitch, $B_2$ represents the transcript out of the RNA polymerase at the second pause site (9). The step $B_2\to R_i$ is a simplification of the potential multiple chemical process, including pausing and emerging of the antiterminator sequence $\left(B_2\to B_3\right)$, and transcription to the terminator sequence $\left(B_3\to R_i\right)$. The rate $k_{t2}$ is approximated as the pausing rate $k_p$, because pausing is likely to be the rate-limiting step in the transcription process.

To assess how the metabolite concentration, $\left[M\right]$, regulates transcription termination, we computed the fraction of terminated transcript, $f_{ter}$, given an initial concentration of RNA transcript with aptamer sequence transcribed (B). Some of the rate constants can be estimated from the in vitro experiments (9) for FMN riboswitches, which we use to illustrate the efficacy of the theory. The experimental values of the FMN association rate constant $k_b$ for the FMN aptamer is $\sim 0.1$ μM⁻¹s⁻¹, and the dissociation rate constant $k_{-b}$ is $\sim {10}^{-3}$ s⁻¹, giving the equilibrium $K_D\equiv k_{-b}/k_b=10$ nM. RNA polymerases (RNAP) pause at certain transcription sites during transcription. There are two pause sites for the FMN riboswitch, one after the aptamer domain sequence with a lifetime of the paused complex being ∼10 s, and the other at the end of the antiterminator sequence with a lifetime ∼1 min. To approximately account for the pause times in our simplified model, we observe that $B_2$ represents the transcript of the FMN riboswitch with part of the antiterminator out of RNAP, when RNAP pauses at the second pause site. Even with only part of the antiterminator sequence, the transcript still has high probability of forming alternate folding patterns (9), similar to a full antiterminator sequence. Hence, we set the effective transcription rates $k_{t1}=0.1$ s⁻¹ and $k_{t2}=0.016$ s⁻¹, which reflects the pause times for the FMN riboswtich (see Fig. 1 B for additional explanation of this approximation).

Extraction of minimal set of parameters from in vitro transcription experiments

To make testable predictions using our model, we need estimates of the cotranscriptional folding and unfolding rates of the aptamer B as well as $B_2$, the aptamer with the antiterminator sequence. The kinetic model described mathematically in the Supporting Material can be used to extract parameters that most closely fit the measured dependence on $\left[M\right]$ for the FMN riboswitch (9). When the aptamer sequence is transcribed, the transcript favors the aptamer folded state, and when the antiterminator sequence is transcribed, the folding pattern changes in favor of forming the antiterminator stem with disruption of the aptamer folded structure (9). Thus, there are restraints on the folding rates, $k_{f1}>k_{-f1}$ and $k_{f2}<k_{-f2}$. We also assume the same association (dissociation) rate constant for metabolite binding to $B^{\ast }$, $B_2^{\ast }$, and $B_{2t}^{\ast }$ because there is little change in the results when the values of $k_{b2}$ and $k_{b3}$ are drastically altered. In addition, because we only allow the folded states of the aptamer to bind M the effective $K_D$ is a convolution of the folding rates and the binding rate. Thus, even though $k_b$ is the same the decrease in the folding rate as the transcript length increases effectively decreases $K_D$. The values of the transitions rates that reproduce the measured $f_{ter}$ (blue squares in Fig. 2) are listed in Table 1. The folding rates $k_{f1}$ and $k_{f2}$ are within an order of magnitude of the theoretical prediction based on, $k_f\sim k_0{e}^{-\sqrt{N}}$, $k_0\sim {10}^6$ s⁻¹, where N is the number of nucleotides (14,15). Moreover, the rate $k_{f1}$ we obtained is in the same order of magnitude of the folding rate of other riboswitch aptamer with similar lengths observed in experiments (16). Thus, for the purposes of quantitatively describing the in vitro experiments we need only two kinetic rates ($k_{-f1}$ and $k_{-f2}$).

Figure 2.

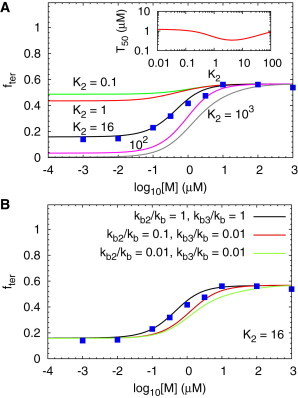
Dependence of transcription termination on metabolite concentration without feedback. (A) Fraction of terminated RNA transcripts, $f_{ter}$, as a function of the logarithm of the metabolite concentration for different values of $K_2\equiv k_{-f2}/k_{f2}$ with $k_{b2}=k_{b3}=k_b$. Parameters that reproduce the in vitro experimental $f_{ter}$ are listed in Table 1. The inset in (A) shows the half-response metabolite concentration, $T_{50}$, as a function of K₂. (B) Sensitivity of $f_{ter}$ to different values of $k_{b2}$ and $k_{b3}$. Except for modest changes in $T_{50}$ there is little change in $f_{ter}$ when the binding rates are drastically altered. The blue points in (A) and (B) are data from experiments on FMN riboswitch (9).

Table 1.

Kinetic parameters for model in Fig. 1 without feedback

kf1∗	k−f1	kf2	k−f2	kt1†	kt2†	kb†§	k−b†
0.1	0.04	2.5 × 10−3	0.04	0.1	0.016	0.1	10−3

^∗In unit of s⁻¹ for all rates except k_b.

^†Values from experimental data (9).

^§In unit of μM⁻¹s⁻¹.

The folding rate of the aptamer is comparable to $k_{t1}$ (Fig. 1). The transition rate $\left(k_{-f2}\right)$ from $B_2^{\ast }$ (Fig. 1) to $B_2$ is 2–3 times the rate of transcription elongation to the stage where the terminator sequence is transcribed $\left(k_{t2}\right)$. Because the results are not sensitive to $k_{-f1}$, if the other rates are fixed, we choose $k_{-f1}\sim k_{-f2}$ because both involve unfolding of the folded aptamer structure. With this assumption, the parameter set that emerges when our model is used to quantitatively describe (see Fig. 2) the in vitro kinetic experiments is unique. In addition, under these conditions, the regulation of transcription termination works when $\left[M\right]$ is in large excess over RNA transcript, when ${\left[M\right]}_0/{\left[B\right]}_0>10$. With $\left[M\right]=1$ $\mu M$ for metabolite concentration and $k_b=0.1$ $\mu M^{-1}{s}^{-1}$, the binding time is ∼10 s, which is of the same order of magnitude as the transcription elongation rate and the folding rate of the antiterminator stem. Consequently, the metabolite binding is unlikely to reach equilibrium before formation of the antiterminator stem. Large excess of metabolite, exceeding the equilibrium $K_D$ (∼10 nM) for FMN binding to $B_2^{\ast }$, over RNA transcript is needed for the metabolites to bind the riboswitches with sufficient speed to regulate transcription under the conditions explored in experiments (9).

Results

Dependence of $f_{ter}$ on $K_2$

We investigated how $f_{ter}$ depends on variations in the transition rates around the parameter set listed in Table 1. Fig. 2 shows that the fraction of terminated transcripts converges to the same value in the limit of high metabolite concentration, independent of $K_2\equiv k_{-f2}/k_{f2}$, while keeping the other parameters fixed. At high $\left[M\right]$, $B^{\ast }$ and $B_2^{\ast }$ are always metabolite bound, which results in very low $\left[B_2^{\ast }\right]$. Hence, varying $k_{-f2}$ does not affect $f_{ter}$ at high $\left[M\right]$. In the limit of low $\left[M\right]$, $f_{ter}$ decreases as $K_2$ increases because $k_{-f2}$ exceeds the effective binding rate $k_b\left[M\right]$ so that $B_2$ is preferentially populated.

The effective metabolite concentration $T_{50}$, at which

$$\frac{f_{ter}\left(T_{50}\right)-f_{ter}^L}{f_{ter}^H-f_{ter}^L}=0.5,$$ (1)

where $f_{ter}^H\left(f_{ter}^L\right)$ is the value of $f_{ter}$ at high (low) $\left[M\right]$, does not change much as $K_2$ is varied (see the inset in Fig. 2). Even when $K_2$ is small $T_{50}/K_D>1$ implying the concentration of $\left[M\right]$ is in excess of the equilibrium $K_D$ to effect binding to $B_2^{\ast }$. Because the population of $B_2$ is favored as $K_2$ increases, it follows that $f_{ter}$ decreases at all concentrations of the metabolite as $K_2$ is changed from a low to a high value (Fig. 2). In addition, the transcription rate from $B_2$ (or $B_2^{\ast }$) to the next stage where terminator sequence forms $\left(k_{t2}\right)$ is about one order of magnitude larger than $k_{f2}$, which means that at low or normal metabolite concentration, transitions between $B_2$ and $B_2^{\ast }$ states do not reach equilibrium before the terminator sequence is transcribed—a result that also follows from the inequality $T_{50}>K_D$. Finally, the dissociation rate constant is much smaller than $k_{t2}$, which indicates that once the metabolite is bound, the bound state remains stable through transcription termination. Hence, the riboswitch is in the kinetically driven regime with the parameters used here—a conclusion that was reached in the previous study (9).

Dynamic range and thermodynamic control

Thermodynamic equilibrium between $B_2$ and $B_2^{\ast }$ can be reached only if the transcription speed is much slower than the transition rates between different folding patterns and the association rate with metabolites (Fig. 1). We varied the transcription speed to probe how the riboswitch can be driven from kinetic to thermodynamic control, which can be experimentally realized by increasing the pausing time, achievable by adding transcription factors, such as NusA. The dependence of $f_{ter}$ on $\left[M\right]$ at various ${\gamma }_2\equiv k_{t2}/k_{f2}$ values shows that, in the limit of low metabolite concentration, $f_{ter}$ is roughly equal to the fraction of folded aptamer $f_{B_2^{\ast }}\simeq k_{f2}/\left(k_{f2}+k_{-f2}\right)\sim 0.06$. At high metabolite concentrations, almost all riboswitches are metabolite bound, and transcription is terminated with high probability (Fig. 3 A). As ${\gamma }_2$ increases, the system transitions to a kinetically driven regime and the probability that the transcription is terminated at high $\left[M\right]$ decreases, whereas the fraction of terminated transcript at low $\left[M\right]$ increases.

Figure 3.

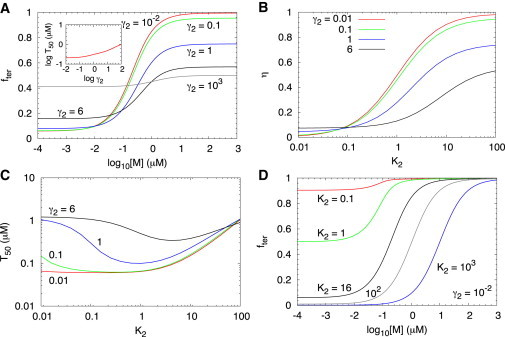
Speed of transcription and gene expression. (A) Fraction of terminated RNA transcripts, $f_{ter}$, as a function of the logarithm of metabolite concentration for different values of ${\gamma }_2\equiv k_{t2}/k_{f2}$. The parameters that reproduce the experimental $f_{ter}$ results in ${\gamma }_2=6$. The inset shows log $\left(T_{50}\right)$ as a function of log $\left({\gamma }_2\right)$. (B) The dynamic range $\eta \equiv f_{ter}^H-f_{ter}^L$, where $f_{ter}^H$$\left(f_{ter}^L\right)$ is the value of $f_{ter}$ at high (low) metabolite concentration, as a function of K₂. (C) Variation of T₅₀ as a function of K₂. (D) Fraction of terminated RNA transcripts as a function of the logarithm of metabolite concentration for different values of K₂ with ${\gamma }_2={10}^{-2}$. Other parameters used are listed in Table 1.

Interestingly, at high $\left[M\right]$ we find that $f_{ter}$ decreases as ${\gamma }_2$ increases because in this limit the folded $B_2^{\ast }$ has insufficient time to make a transition to $B_2$. As a result the population of $B_2$ decreases at high ${\gamma }_2$, resulting in a reduction in $f_{ter}$ (Fig. 3 A). Surprisingly, the exact opposite result is obtained at low $\left[M\right]$ as ${\gamma }_2$ is varied. At low $\left[M\right]$ and small ${\gamma }_2$ the binding rate $k_b\left[M\right]$ is small enough that the transition to $B_2$ occurs with high probability resulting in a decrease in $f_{ter}$. As ${\gamma }_2$ increases, the flux from $B_2^{\ast }$ to $B_2$ decreases and the pathway to $B_2^{\ast }$ from $B^{\ast }$ becomes relevant leading to an increase in $f_{ter}$ at low $\left[M\right]$ (Fig. 3 A). Thus, at high ${\gamma }_2$ and low $\left[M\right]$ the extent of transcription termination is controlled by $K_1\equiv k_{-f1}/k_{f1}$ and ${\gamma }_1\equiv k_{t1}/k_{f1}$. The value of $T_{50}$ increases substantially relative to $K_D$ as ${\gamma }_2$ increases (see the inset in Fig. 3 A). Even when ${\gamma }_2$ is very small $T_{50}$ exceeds $K_D$ implying that it is difficult to drive the FMN riboswitch to thermodynamic control under the conditions used in experiments (9).

Fig. 3 B shows the dynamic range $\eta \equiv f_{ter}^H-f_{ter}^L$ as a function of $K_2$ for different values of ${\gamma }_2$. The riboswitch functions with maximal dynamic range when the system is nearly under thermodynamic control corresponding to small $K_2$ values. The range of $T_{50}$ is between 0.1 $\mu M$ $\left(\approx 100K_D\right)$ and 1 $\mu M$ $\left(\approx 1000K_D\right)$ for ${\gamma }_2>1$ (Fig. 3 C). When the unfolding rate of the aptamer folded structure $\left(B_2^{\ast }\right)$ is comparable to the speed of transcription to the terminator sequence, $K_2\sim {\gamma }_2$, $T_{50}$ has the smallest value. The minimum $T_{50}$ decreases as ${\gamma }_2$ decreases, and $T_{50}$ becomes less dependent on $K_2$ when $K_2<1$. When ${\gamma }_2\ll 1$, as shown in Fig. 3 D, the probability of transcription termination approaches unity in the limit of high metabolite concentration at all values of $K_2$. On the other hand, in the limit of low metabolite concentration ($k_b\left[M\right]$ is small), $f_{ter}$ increases and $T_{50}$ decreases as $K_2$ decreases. The results in Fig. 3 show that the efficiency of the riboswitch function is determined by a compromise between the need to maximize η (${\gamma }_2$ should be small) and the ability to terminate transcription (${\gamma }_2$ should be large).

Effect of aptamer folding rates on $f_{ter}$

In the kinetically driven regime $\left({\gamma }_2>1\right)$, the probability of transcription termination depends on the fraction of the aptamer formed state before transcription of the antiterminator sequence. This fraction can be changed by altering $k_{f1}$, or equivalently the ratio $K_1\equiv k_{-f1}/k_{f1}$, or by varying the transcription speed from the aptamer domain sequence to antiterminator sequence, $k_{t1}$. When $K_1\gg 1$, most of the riboswitches do not form stable folded aptamer domain $B^{\ast }$ (Fig. 1), resulting in a very small fraction of transcription termination and low response to changes in the metabolite concentration. As the transition rate from the unfolded state (B) to the folded aptamer state $\left(B^{\ast }\right)$ increases relative to the reverse transition rate, the fraction of terminated transcripts and dynamic range increases (Fig. 4 A). In the limit of high $\left[M\right]$, the probability of transcription termination approaches 1 when $K_1\ll 1$, whereas in the low $\left[M\right]$ limit, almost all the riboswitches are aptamer folded but without metabolite bound $\left(B^{\ast }\right)$ before transcription to antiterminator sequence. Just as in Fig. 2, $T_{50}$ is not sensitive to changes in $K_1$ (see inset in Fig. 4 A).

Figure 4.

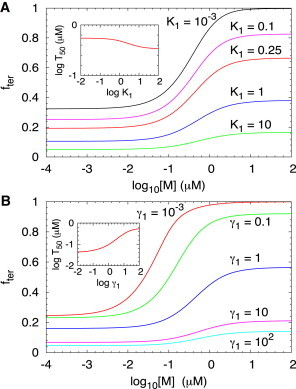
Aptamer folding rates and $f_{ter}$. (A) Fraction of terminated RNA transcripts as a function of log $\left(\left[M\right]\right)$ for different values of $K_1\equiv k_{-f1}/k_{f1}$ using the parameters listed in Table 1 except for $k_{-f1}$. (B) Fraction of terminated RNA transcripts as a function of log $\left(\left[M\right]\right)$ for different values of ${\gamma }_1\equiv k_{t1}/k_{f1}$. Inset shows the dependence of $T_{50}$ on ${\mathit{\gamma }}_1$.

Fig. 4 B shows the concentration dependence of the fraction of terminated transcripts for different transcription rates to the antiterminator sequence, or the ratio ${\gamma }_1\equiv k_{t1}/k_{f1}$. When the transcription rate is much faster than the folding rate, the riboswitch does not have enough time to form the aptamer folded structure, which results in a low fraction of terminated transcripts and low response to metabolite concentration change. When the transcription rate is much slower than the folding rate, the folded and unfolded states of the aptamer are able to reach equilibrium before transcription to antiterminator sequence. In the high metabolite concentration limit, the riboswitch is always metabolite bound resulting in transcription termination. At low $\left[M\right]$, the riboswitch does not bind the metabolite. The fraction of aptamer formed state without bound metabolite is $k_{f1}/\left(k_{f1}+k_{-f1}\right)\approx f_{ter}$ before transcription to the antiterminator sequence. There is substantial variation in $T_{50}$ as ${\gamma }_1$ changes as the inset in Fig. 4 B shows. Thus, besides the speed of transcription and the binding rates, the folding rates of the aptamers have considerable influence on $f_{ter}$ (compare insets in Fig. 3 A and Fig. 4 B).

Transcription with negative feedback loop

Most riboswitches regulate gene expression of the downstream platform that encodes for proteins involved in the production of the specific metabolite that itself binds to the riboswitch (Fig. 1). Therefore, sensing and binding of its own metabolite by the riboswitch acts as a feedback to control gene expression. For riboswitches that suppress gene expression by binding to metabolites with high selectivity (for example, guanine riboswitches or FMN riboswitches) such feedback loop is an example of negative autoregulation, which has been widely studied in gene regulation networks associated with transcription factors (17). We include the role negative feedback plays in regulating transcription termination by generalizing the in vitro kinetic model considered in the previous section. Our minimal model, illustrated in Fig. 1 and described in detail in the Supporting Material, provides a framework for interpreting future in vivo experiments.

We consider transcription and translation in a cell and take into account RNA degradation and cell expansion. The transcription process is similar to that described without a feedback loop, except now we include the effect of cell expansion and RNA degradation. We assume that the cell grows at a rate of $\mu =5\times {10}^{-4}$ s⁻¹, resulting in a typical doubling time of $\text{ln}2/\mu \sim 20$ minutes for an Escherichia coli cell, and that the degradation rate of the fully transcribed RNA or terminated RNA transcript is $k_{d1}$. The values of $k_{d1}$, and other parameters in the feedback loop are in Table 2. The fully transcribed RNA serves as a template for the translation of the protein (P) that synthesizes metabolite $M_0$, which is then converted to an active form M by the enzyme E encoded by the gene $O_F$ (Fig. 1). The species M, with a degradation rate of $k_{d3}$, is the target metabolite that binds to the riboswitch.

Table 2.

Additional kinetic parameters for model in Fig. 1 with negative feedback

kt3∗	K1	k2†	k3‡	kd1§	kd2¶	kd3ǁ	μ
0.01	0.016	0.3	0.064	2.3 × 10−3	2.7 × 10−4	4.5 × 10−3	5 × 10−4

^∗In unit of s⁻¹ for all rates.

^†Ref. (26).

^‡Ref. (27).

^§Ref. (28).

^¶Ref. (29).

^ǁSee the Supporting Material.

In the case of FMN riboswitches, $M_0$ represents riboflavin, the eventual product encoded by the gene ribD $\left(O_R\right)$, which is subsequently converted to FMN by flavokinase (E), synthesized by the gene ribC $\left(O_F\right)$. The degradation rate $k_{d3}$ takes into account the effect of conversion from FMN to FAD (flavin adenine dinucleotide) by FAD synthetase in vivo (see the Supporting Material for more details). However, we neglect the potential binding of FAD to the riboswitch because there is a 60-fold difference (or potentially even larger factor in the absence of FMN) in the binding of FMN and FAD to the FMN riboswitch (18). In the model with negative feedback the extent of regulation by riboswitches is expressed in terms of the production of the protein P (Fig. 1).

We assume that the activated level of the operon, $O_R$, for transcription initiation of the riboswitch is a constant, and set $\left[DNA\right]=\left[O_R\right]=2.5$ nM, which is equivalent to one DNA molecule in an E. coli cell, and assume that the aptamer sequence, B, is produced with an effective rate constant $k_1=0.016$ s¹, taking into account the transcription initiation rate ($\sim 50$ s between initiation events (19,20)) and the typical transcription speed, $\sim 10-35$ nucleotides/s (21). With these parameters fixed, which are used for illustrative purposes only, we can study the effect of feedback by varying the effective rate $k_F$, at which E is produced from O_F. We set $\left[O_F\right]=\left[O_R\right]$. If E is produced at a rate similar to that of protein P, without feedback, then $k_F\sim 1$ s⁻¹, which we set as a reference rate $k_{F0}$ (see the Supporting Material for details). At this rate, the steady-state level of enzyme E is ∼10³ copies per cell. The variation of rate $k_F$ can result from delays or speed up in the process of the transcription from $O_F$ or translation of E, or even deficiency in $O_F$.

Dependence of $\left[P\right]$ on enzyme production and metabolite binding rates

We assess the extent of regulation due to feedback by the changes in the protein level expression, $\left[P\right]$, as the parameters in the network are varied. The results in Fig. 5 A show that when $k_F/k_{F0}$ is low, very few active metabolites are formed to suppress protein expression. Consequently, the expression level of protein does not change at low $k_F/k_{F0}$ at all values of ${\gamma }_2$ (Fig. 5 A). This finding explains the observation that deficiency in ribC ($O_F$ in Fig. 1), the gene that encodes for flavokinase (E in Fig. 1), causes accumulation of riboflavin ($M_0$ in Fig. 1) without converting it to FMN, and thus cannot suppress the synthesis of riboflavin (22,23). When $k_F$ increases to about ${10}^{-3}{k}_{F0}$, the expression of the protein starts to be suppressed. There is a substantial suppression of protein concentration (Fig. 5 A) at all ${\gamma }_2$ values when $k_F/k_{F0}>{10}^{-2}$. As $k_F$ exceeds $0.1k_{F0}$, the suppression begins to saturate (Fig. 5 A) because most of $M_0$ produced are converted to M, and the $\left[P\right]$ level is essentially determined by the production of ${\left[M\right]}_0$, which is independent of $k_F$. Thus, at all ${\gamma }_2$ values, $\left[P\right]$ level varies between two steady-state values as $k_F$ is changed.

Figure 5.

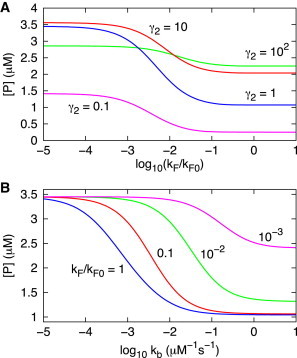
Effect of negative feedback. (A) Protein (P in Fig. 1) concentration at different ${\gamma }_2$ values as a function of the logarithm of $k_F$, the production rate constant of enzyme E that produces the metabolite M, relative to $k_{F0}=1$ s⁻¹. The parameters are given in Table 1 and Table 2 except $k_{t2}$. (B) The extent of regulation expressed in terms of protein level as a function of the logarithm of association rate constant k_b for metabolite binding. The parameters are listed in Table 1 and Table 2 except $k_b$ and $k_{-b}$. $K_D$ is fixed at 10 nM.

In contrast to the results in Fig. 5 A, the extent of regulation ($\left[P\right]$ levels) varies greatly with the binding rate constant of metabolites while keeping $K_D$ fixed at 10 nM (Fig. 5 B). Changes in $\left[P\right]$ as $k_b$ is varied, which affect synthesis of $M_0$ (Fig. 1), depend on $k_F/k_{F0}$. When $k_F\ge k_{F0}$, most of the aptamer folded structures are metabolite bound at the experimental value of $k_b=0.1$ μM⁻¹s⁻¹, and hence the level of protein expression is suppressed. Therefore, with ∼10³ copies of enzyme E in a cell, the production of $\left[P\right]$ decreases substantially even if the binding rate constant is small. Binding occurs because the concentration of active metabolites (∼25 μM) is far larger than RNA transcripts (∼10 nM), resulting in a high effective binding rate $k_b\left[M\right]$. The ability to suppress protein production decreases if the binding rate constant is smaller than the experimental value by more than one order of magnitude, or when the value of $k_F$ decreases. Not surprisingly, when $k_F$ is very low, the dependence of binding rate on expression of P decreases. As a consequence the changes in P production decrease greatly as $k_F/k_{F0}$ decreases (Fig. 5 B). Thus, only over a small range of $k_b$ and $k_F/k_{F0}$ does the riboswitch function with sufficient dynamic range.

Interplay between cotranscriptional folding and transcription speed

The dependence of transcription rate on the extent of regulation, shown in Fig. 6, exhibits three distinct functional modality depending on the value of $k_{t2}$ relative to $k_{-f2}$. First, consider the case with $k_F=0$ (black line in Fig. 6 A). If $k_{t2}\gg k_{-f2}$, the fraction of fully transcribed RNA (Fig. 6 A), $f_{tra}=1-f_{ter}$, becomes

$$f_{tra}\equiv \frac{\left[RNA\right]}{{\left[RNA\right]}_0}\simeq \frac{K_1\left(1+\frac{k_{t1}+\mu }{k_{-f1}}\right)}{1+K_1\left(1+\frac{k_{t1}+\mu }{k_{-f1}}\right)},$$ (2)

where ${\left[RNA\right]}_0$ is the sum of concentration of the fully transcribed and terminated RNA transcripts, and $K_1\equiv k_{-f1}/k_{f1}$. In this limit, $f_{tra}$ depends predominantly on the folding transition rate before the antiterminator sequence $\left(B_2\right)$ is transcribed (Fig. 1). Hence, $f_{tra}$ is a function of $k_{t1}$, $k_{-f1}$, and the rate of cell expansion. When $k_{t2}/k_{-f2}$ decreases, cotranscriptional folding results in the formation of the antiterminator stem, which prevents transcription termination. If $k_{t2}\ll k_{-f2}$ and $\mu \ll k_{-f2}$, then

$$f_{tra}\simeq \frac{K_2}{K_2+1}=\frac{k_{-f2}}{k_{f2}+k_{-f2}},$$ (3)

where $K_2\equiv k_{-f2}/k_{f2}$. In this limit, $B_2$ and $B_2^{\ast }$ (Fig. 1) are in equilibrium. These results are the same as those in the limit of low metabolite concentration without the feedback loop (Fig. 3 A).

Figure 6.

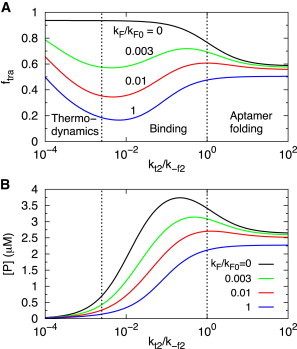
Role of $k_{t2}$ on negative feedback. (A) The fraction of fully transcribed RNA, $f_{tra}=1-f_{ter}$, as a function of $k_{t2}/k_{-f2}$. The numbers give values of $k_F/k_{F0}$ with $k_{F0}=1$ s⁻¹. The dependence of $f_{tra}$ on $k_{t2}/k_{-f2}$ shows three regimes: thermodynamic controlled regime for low $k_{t2}$ ($k_{t2}/k_{-f2}<0.025$, or $k_{t2}<0.1k_{-b}$), aptamer folding dominated regime for high $k_{t2}$$\left(k_{t2}>k_{-f2}\right)$, and intermediate regime with significant metabolite binding. (B) The P concentration as a function of $k_{t2}/k_{-f2}$ at different $k_F/k_{F0}$ values (as described in (A)).

For finite $k_F$, when $k_{t2}$ is fast relative to $k_{-f2}$ the expression level of protein P is nearly independent of $k_{t2}$ (Fig. 6 B). In this regime transcription termination and hence the extent of completed transcription is determined by the folding rates of the aptamer, which is not greatly affected by negative feedback. When the transcription speed decreases, the expression of protein P increases for small $k_F$ (Fig. 6 B). The expression level of P reaches a peak when $k_{t2}/k_{-f2}\sim 0.1-1$, and it disappears when $k_F/k_{F0}\ge 1$ because the metabolite binding becomes significant enough to stabilize the folded aptamer structure and offset the effect of formation of the antiterminator stem. This is illustrated in Fig. 6 A, which shows that $f_{tra}$ decreases significantly when $k_{t2}$ goes below $0.1k_{-f2}$ and reaches a minimum at $k_{t2}/k_{-f2}\sim 0.01$. The dependence of $\left[P\right]$ on $k_{t2}/k_{-f2}$ is maximal when $k_{t2}/k_{-f2}\sim 0.01-0.1$. When the transcription rate decreases further ($k_{t2}\le 0.1k_{-b}$, or $k_{t2}/k_{-f2}\le 2.5\times {10}^{-3}$ as shown by the left dashed line in Fig. 6 A), the fraction of fully transcribed RNA increases sharply because the transcription rate is slow enough for the dissociation of metabolites from riboswitches to occur significantly. The system can establish thermodynamic equilibrium, which increases the favorability of the formation of antiterminator stem when $k_{t2}$ decreases resulting in decreasing effective binding rate $k_b\left[M\right]$. However, the overall expression level of protein P becomes very low because slow transcription results in a decrease in P production. In addition, there is also significant probability of RNA degradation, which also results in a decrease in P expression. Therefore, the extent of regulation due to the negative feedback of metabolite binding has a maximal effect when $k_{t2}/k_{-f2}\sim 0.01$ where the protein expression is suppressed by metabolite binding by as large as 85%.

Dynamic phase diagram: competition between folding, transcription, and binding rates

To have a more complete picture on how the interplay between folding of RNA transcripts, transcription, and metabolite binding regulate the expression of P, we study the dependence of $\left[P\right]$ on the transcription rates and the effective binding rate $k_b\left[M\right]$. The dynamic phase diagram in Fig. 7 is calculated by varying both $k_{t1}$, $\left(k_{t2}\right)$, and $k_b$ with $K_D=10$ nM. In the first stage of transcription elongation, i.e., after the aptamer sequence is transcribed, the formation of the aptamer structure is the key step in regulating transcription termination. Thus, the folding rate $k_{f1}$ and the effective metabolite binding rate are the key rates in competition with $k_{t1}$ for regulation of $\left[P\right]$. Fig. 7 A shows three regimes for the dependence of $\left[P\right]$ on $k_{t1}$ and $k_b\left[M\right]$. In regime I, $k_{t1}>k_{f1}$, the folding rate is slow relative to transcription to the next stage (Fig. 1). Thus, the aptamer structure does not have enough time to form. The dominant flux is from B to $B_2$, which leads to high probability of fully transcribed RNA downstream because of the low transition rate from $B_2$ to $B_2^{\ast }$. The metabolite binding has little effect on protein expression in this regime, particularly for large $k_{t1}/k_{f1}$, and hence the protein is highly expressed. In regime II, $k_b\left[M\right]<k_{t1}<k_{f1}$, the aptamer has enough time to fold but the metabolite binding is slow. The dominant flux is $B\to B^{\ast }\to B_2^{\ast }$, leading to formation of antitermination stem $\left(B_2^{\ast }\to B_2\right)$ or transcription termination $\left(B_2^{\ast }\to B_{2t}^{\ast }\right)$. The expression level of protein is thus mainly determined by $k_{-f2}$ and $k_{t2}$, and the protein production is partially suppressed in this regime. In regime III, $k_{t1}<k_{f1}$ and $k_{t1}<k_b\left[M\right]$, the aptamer has sufficient time to both fold and bind metabolite, the dominant pathway is $B\to B^{\ast }\to B^{\ast }M\to B_2^{\ast }M$, leading to transcription termination. The protein production is highly suppressed in this regime. The results using parameters from Table 1 and Table 2 ($k_{t1}=k_{f1}$ and $k_b\left[M\right]/k_{f1}\sim 25$) fall on the interface of regime I and regime III, as shown by the arrow in Fig. 7 A. The metabolite binding does not reach thermodynamic equilibrium due to a low dissociation constant. However, the effective binding rate is high because the steady-state concentration of metabolites (∼25 μM) is in large excess over RNA transcripts. Thus, the riboswitch is kinetically driven under this condition even when feedback is included.

Figure 7.

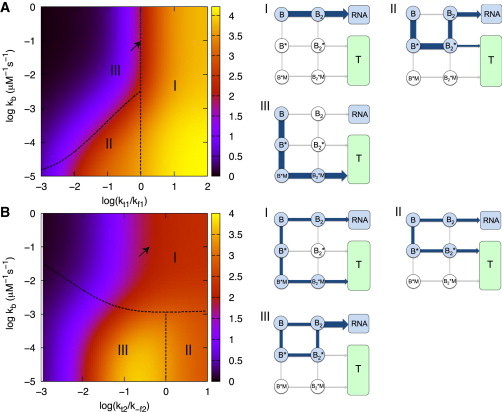
Dependence of protein production on the network parameters with feedback. (A) Protein levels as functions of $k_{t1}/k_{f1}$ and $k_b$ with negative feedback using parameters in Table 1 and Table 2. The scale for the $\left[P\right]$ production is shown in the color spectrum. The dependence of $\left[P\right]$ on $k_{t1}$ and $k_b$ is categorized into three regimes (see text for details). Points on the dashed line separating regime II and regime III satisfy $k_b\left[M\right]=k_{t1}$. The major pathway in the transcription process in each regime is shown on the right. The arrow indicates the data point resulting from using the value of $k_{t1}$ and $k_b$ in Table 1. (B) Expression level of proteins as functions of $k_{t2}/k_{-f2}$ and $k_b$ with negative feedback using the parameters in Table 1 and Table 2. The dependence of $\left[P\right]$ on $k_{t2}$ and $k_b\left[M\right]$ is categorized into three regimes. Points on the dashed line separating regime I and regime II/III satisfy $k_b\left[M\right]=k_{-f2}$. The corresponding major transcription pathways are shown on the right. The data point corresponding to the arrow results from using the value of $k_{t2}$ and $k_b$ in Table 1.

With $k_{t1}$ comparable to $k_{f1}$, at the second stage of transcription elongation the key step against transcription termination is the formation of the antiterminator stem $\left(B_2^{\ast }\to B_2\right)$. Fig. 7 B also shows three regimes for the dependence of $\left[P\right]$ on $k_{t2}$ and $k_b\left[M\right]$ relative to $k_{-f2}$, and the associated most probable pathways are displayed on the right. In regime I, $k_b\left[M\right]>k_{-f2}$, the effective binding rate competes favorably with $B_2^{\ast }\to B_2$ transition so that $B_2$, if populated, is not likely to form the antiterminator stem. However, in this regime, the effective binding rate is also likely to be larger than $k_{t1}$, resulting in most of the metabolite binding occurring at the first stage of transcription. Protein production is partially suppressed with the flux toward transcription termination flowing through $B^{\ast }M\to B_2^{\ast }M\to T$ (terminated transcript). In regime II, $k_b\left[M\right]<k_{-f2}<k_{t2}$, both the metabolite binding and $B_2^{\ast }\to B_2$ transition are too slow to occur. The protein production level is mainly determined by $k_{t1}$ and $k_{f1}$. The major pathways are $B\to B_2\to RNA$ and $B\to B^{\ast }\to B_2^{\ast }\to T$, leading to partial protein suppression. In regime III, $k_b\left[M\right]<k_{-f2}$ and $k_{t2}<k_{-f2}$, metabolite binding is too slow to occur, but the riboswitch has enough time to form the antiterminator stem before the terminator sequence is transcribed. The major flux from $B_2^{\ast }$ flows to $B_2$, leading to fully transcribed RNA, and proteins are highly expressed. We note that using the parameters from Table 1 and Table 2 ($k_{t2}/k_{-f2}=0.4$ and $k_{b}M/k_{-f2}\sim 60$), the result falls in regime I with partial protein suppression. Among the three regimes, regime I has efficient negative feedback, whereas the slow metabolite binding in regime II and regime III make results resemble those without feedback. The dynamic phase diagrams predict results with limiting cases of various parameters, whose values may be within range in vivo and most certainly in vitro.

Role of feedback in response to DNA bursts

To assess how feedback affects the response to a sudden burst in DNA concentration we calculated the time dependent changes in the protein concentration,

$$\frac{\Delta P\left(t\right)}{\Delta P_{st}}=\frac{P_{{\left[DNA\right]}_f}\left(t\right)-P_{{\left[DNA\right]}_i}\left(t\right)}{P_{{\left[DNA\right]}_f}^{st}-P_{{\left[DNA\right]}_i}^{st}},$$ (4)

when the DNA concentration is switched from ${\left[DNA\right]}_i$ to ${\left[DNA\right]}_f$. In Eq. 4 st stands for steady state. Fig. 8 A shows the response time, defined as the time needed to reach halfway to the new steady-state level (dashed line in Fig. 8 A), for ${\left[DNA\right]}_f$ = 3.75 nM and ${\left[DNA\right]}_i$ = 2.5 nM using folding and unfolding rates one order of magnitude larger than those in Table 1. Small transient fluctuations in DNA concentration could arise from environmental stresses, and hence it is interesting to examine the response of the network to such changes. The values of the folding rates from Table 1 result in little difference in response time between cases with negative feedback and without feedback. However, with larger folding rates, the response time for the systems with negative feedback is significantly shorter than without feedback (Fig. 8 A). The fractional change of the fully transcribed RNA, $\Delta F\left(t\right)\equiv f_{tra}\left({\left[DNA\right]}_f,t\right)-f_{tra}\left({\left[DNA\right]}_i,t\right)$ (Fig. 8 B), shows a slight increase with overshoot initially before settling into a steady-state level lower than the original one in the case of negative feedback (blue line in Fig. 8 B). For the case without feedback, the fraction of fully transcribed RNA decreases initially before reaching the expected steady-state level (red line in Fig. 8 B).

Figure 8.

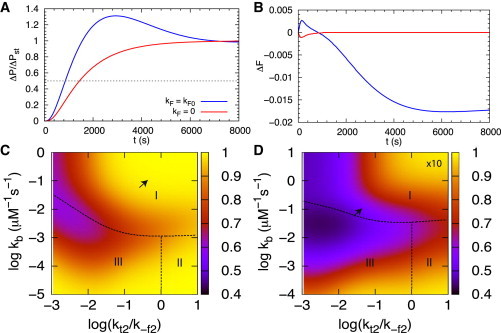
Role of feedback to a spike in the DNA concentration. (A) Response of protein level $\left(\Delta P\right)$ relative to the change of steady-state level $\left(\Delta P_{st}\right)$ when the DNA level increases by 50%. The response time is 850 s with negative feedback (blue line) and 1450 s without feedback (red line). The values of folding and unfolding rates used are 10-fold larger than those given in Table 1. (B) Response of the fraction of fully transcribed RNA, $\Delta F$, when the DNA level increases by 50%. The fraction of fully transcribed RNA increases initially with negative feedback (blue line) and decreases initially without feedback (red line) before settling to a new steady state. (C) Fractional change in protein steady-state level relative to that in DNA concentration, $\delta P_{st}/\delta D$, in response to a 50% rise in DNA level, as a function of $k_{t2}/k_{-f2}$ and $k_b$ for the riboswitch network with negative feedback using parameters in Table 1. Points on the dashed line separating regime I and regime II/III satisfy $k_b\left[M\right]=k_{-f2}$. (D) Same as (C) with the overall folding and unfolding rates being 10-fold greater than those in Table 1. The arrow indicates the data point when $k_{t2}$ and $k_b$ are at the values from Table 1.

With negative feedback and 10-fold increase in overall folding and unfolding rates, the fractional increase in the protein steady-state level, $\delta P_{st}\equiv \left(P_{{\left[DNA\right]}_f}^{st}-P_{{\left[DNA\right]}_i}^{st}\right)/P_{{\left[DNA\right]}_i}^{st}$, in response to the increase in DNA level, $\delta D=\left({\left[DNA\right]}_f-{\left[DNA\right]}_i\right)/{\left[DNA\right]}_i$, is reduced by more than half of that in the case without feedback for a certain range of parameters, as shown in Fig. 8, C and D. Without feedback, $\delta P_{st}=\delta D$. Negative feedback noticeably reduces the variations of expression in protein due to DNA level change. Substantial reduction occurs when the effective binding rate is comparable to $k_{-f2}$ and when $k_{t2}\le k_{-f2}$ (the interface between regime I and regime III in Fig. 8 D).

Discussion

Transcription, regulated by metabolite binding to riboswitches, depends on interplay of a number of timescales that are intrinsic to the cotranscriptional folding of the riboswitch as well as those determined by cellular conditions. For a riboswitch to function with a large dynamic range, transcription levels should change significantly as the metabolite concentration increases from a low to high value. In the high concentration limit, RNA transcript in the aptamer folded state binds a metabolite. Low dissociation rate constant results in the formation of a terminator stem, which subsequently terminates transcription. In the low concentration limit, the aptamer folded state is mostly unbound and can remain folded until transcription termination or can fold to the antiterminator state leading to the transcription of the full RNA. The levels of transcription termination are thus controlled by the transition rates between the aptamer folded and unfolded states.

For in vitro description the efficiency of riboswitch is determined by two conflicting requirements. If η, the dynamic range, is to be maximized, then ${\gamma }_2$ has to be sufficiently low. However, at low ${\gamma }_2$ and realistic values of the metabolite concentration, $f_{ter}\approx 1$, implies the switching function (needed to abort transcription) cannot be achieved. Thus, ${\gamma }_2$ has to have an optimal range $\left({\gamma }_2\sim \left(1-10\right)\right)$ for the riboswitch to have sufficient dynamic range without compromising the ability to switch from an on to off state.

In the presence of a negative feedback loop the concentration of target metabolites is also regulated by gene expression. Under nominal operating conditions $\left(k_{t2}/k_{-f2}\sim 0.01-0.1\right)$ binding of target metabolites, products of the downstream gene that riboswitches regulate, significantly suppresses the expression of proteins. Negative feedback suppresses the protein level by about half relative to the case without feedback. In vivo, the presence of RNA binding proteins, such as NusA, may increase the pausing times, thus effectively reducing the transcription rates. Thus, the repression of the protein level by the riboswitch through metabolite binding may be up to 10-fold. Faster RNA folding and unfolding rates than those we obtained may also increase the suppression by negative feedback and broaden the range of transcription rates over which maximal suppression occurs. These predictions are amenable to experimental test.

In response to changes in the active operon level, the negative feedback speeds up the response time of expression and modestly reduces the percentage change in the protein level relative to change in the operon level. The steady-state level of expression for autoregulation varies as a square root of the DNA concentration. Adaptive biological systems may minimize the variation in gene expression to keep the systems functioning normally even when the environments change drastically. One may need to consider more complex networks than the single autoregulation in the transcription network to find near perfect adaptation to the environmental change (24).

Riboswitches provide novel ways to engineer biological circuits to control gene expression by binding small molecules. As found in tandem riboswitches (6,7), multiple riboswitches can be engineered to control a single gene with greater regulatory complexity or increase in the dynamic range of gene control. Synthetic riboswitches have been successfully used to control the chemotaxis of bacteria (25). Our study provides a physical basis for not only analyzing future experiments but also in anticipating their outcomes.