A Novel Methodology for Assessing the Bounded-Input Bounded-Output Instability in QT Interval Dynamics: Application to Clinical ECG With Ventricular Tachycardia

Abstract

The goal of this paper is to present a new methodology for assessing the bounded-input bounded-output (BIBO) stability in QT interval (QTI) dynamics from clinical ECG. The ECG recordings were collected from 15 patients who experienced ventricular tachycardia (VT). Ten-minute-long ECG recordings extracted immediately before the onset of a chosen VT, one per patient, were assembled into a VT group, while the control group comprised 10-min-long ECGs extracted 1 h before VT onset and at least 1 h after any prior arrhythmic event. Each 10-min recording was subdivided into 1-min ECG recordings (minECGs). The QTI dynamics of each minECG was defined as a function of several prior QTIs and RR intervals; the BIBO stability of this function was then assessed in the z-domain. The number of minECGs with unstable QTI dynamics (N_us) and the frequency of premature activations (PA), f_PA, were counted for each ECG recording and were compared between the VT and control groups. The results show that the present methodology successfully captured the instability in QTI dynamics leading to VT onset in the studied population. Significantly larger N_us was found in the VT group compared against the control and a positive correlation between N_us and f_PA was identified in both groups.

I. Introduction

UNSTABLE dynamics of cardiac repolarization plays an important role in the mechanisms of arrhythmia. It has been widely reported that unstable dynamics of action potential duration (APD), the latter a measure of cardiac repolarization at the cellular level, is responsible for wave breakup and the initiation of arrhythymia [1]–[3]. At the organ level, the QT interval (QTI) in the ECG is a global manifestation of the ventricular repolarization. Unstable QTI dynamics in an ECG recording has been linked to arrhythmia susceptibility in patients with different cardiac diseases, such as long QT syndrome [4]–[6], acute myocardial infarction [7]–[9], and dilated cardiomyopathy [10].

APD has been studied as a function of its preceding diastolic interval (DI), a relationship known as APD restitution. The slope of APD restitution has been used as an indicator of the instability in APD dynamics. It is known that given a large (>1) APD restitution slope, a small perturbation in DI (a bounded input) causes diverging oscillations in APD (an unbounded output) [11]. In other words, the slope of the APD restitution curve is considered to determine the bounded-input bounded-output (BIBO) stability of APD dynamics. If a system is BIBO-stable, then the output will be bounded for every bounded input to the system; otherwise, the system is considered BIBO-unstable [12].

The contribution of APD restitution to arrhythmogenesis has been extensively studied over the past decade. It has been widely reported that unstable APD dynamics causes the failure of activation [11], increases the gradient in APD distribution [2], [13], initiates ventricular tachycardia (VT) [2], [14], [15], and causes the transition from VT to ventricular fibrillation (VF) [1], [3]. However, studies have reported that APD restitution slope is not always a predictor of arrhythmia occurrence [16], [17]. This failure has been attributed to the presence of short-term memory, i.e., the dependence of APD on activation history prior to the preceding DI [17], [18]. In restitution studies, a constant pacing train is usually applied so that the response to the initial conditions (the activation history prior to constant pacing) dies out during the pacing, thus eliminating the contribution of short-term memory to APD dynamics. However, research has demonstrated that the presence of short-term memory can either enhance or suppress APD instability [18], [19]. In case when the contribution of short-term memory cannot be eliminated by the pacing protocol, APD restitution slope is not a reliable measure of BIBO stability in APD dynamics, and thus cannot be used to predict the onset of arrhythmia.

Based on the concept of APD restitution, QTI restitution, which is the dependence of QTI on the preceding TQ interval (TQI), has been studied using clinical ECG recordings. Increased QTI restitution slope revealing BIBO-unstable QTI dynamics has been reported in diseased human hearts [20], [21]. Similar to APD restitution, QTI restitution is usually assessed under invasive constant pacing protocols that eliminate short-term memory. However, the heart rhythm preceding arrhythmia onset is typically nonconstant, and thus the contribution of short-term memory to QTI dynamics and arrhythmia initiation cannot be ignored. Currently, there is no reliable way to detect BIBO instability in QTI dynamics from the clinical ECG recording without pacing to eliminate short-term memory.

We have developed a methodology to assess BIBO instability in QTI dynamics from the clinical ECG recordings without the need of pacing to eliminate short-term memory, applied this methodology to patients with cardiac disease, and successfully identified enhanced QTI instability before the onset of VT [22]. However, the engineering details of the methodology have not been comprehensively described. The goal of this paper is to present in detail the algorithm for assessing the level of BIBO stability in QTI dynamics without the need to eliminate the contribution of short-term memory. Furthermore, we present conceptual as well as implementation advancements in the algorithm. We illustrate the various aspects of the performance of the developed methodology by examining the results of the application of the algorithm to ECG recordings collected from patients who had experienced VT.

II. Methods

The new methodology for assessing the level of BIBO stability in QTI dynamics consists of two parts. First, the dependence of each QTI on several prior QTIs and RRIs is represented as an autoregressive model with exogenous input (ARX). Second, the BIBO stability of the ARX model is determined in the z-domain. The details of ECG data collection and annotation, ARX modeling of QTI dynamics, BIBO stability analysis in the z-domain, and data analysis are presented in the following sections.

A. ECG Recordings

ECG recordings from 15 patients were provided by the Johns Hopkins Hospital. All ECGs were recorded with specialized intensive care unit MARS telemetry system (GE Medical Systems, Milwaukee, WI); this system continuously records up to 28 h of multilead ECG, sampled at 125 Hz [23]. VT was identified in the ECG of each of these patients. The clinical demographics of the studied population, such as age, gender, diagnosis, beta-blocker usage, and antiarrhythmic drug therapy are presented in Table I.

TABLE 1.

Clinical Demographic of the Studied Population

Age	67.1±12.7
Gender (male)	60%
Diagnosis
Heart Failure	20%
Arrhythmia	60%
Acute Myocardial infarction (AMI)	100%
Comorbidities
Diabetes Mellitus	26.7%
Hypertension	53.3%
Beta blocker	46.7%
Antiarrhythmic drug	73.3%

From each patient's multilead recordings, the recording with the best SNR was chosen for analysis to reduce the need of additional filtering. Cardiac events such as VT or VF were identified from these ECGs by the cardiologist. From the ECG recording of each patient, a 10-min-long ECG trace was extracted immediately before the onset of a chosen VT, one per patient, and was used to construct the VT group. A control group was assembled in the same way, except that 10-min ECG traces, again one per patient, were extracted 1 h before the onset of the chosen VT, and at least 1 h after any prior arrhythmia event. The choice of 1 h before VT onset is supported by the findings of several clinical studies, which identified abnormal QTI dynamics and increased PA frequency as VT precursors minutes before the onset [24]–[26]. Within each group, each 10-min recording was then divided into ten 1-min ECG recordings (minECGs).

In this study, noise filtering was not needed in most of the cases due to the good quality of the ECG recordings. However, in cases where noise was present in the signal, a wavelet-based denoising filter developed by Donoho et al. [27] was applied; the performance of this filter is illustrated in Fig. 1. Within each minECG, the beginning of the Q wave Q_begin, the peak of the R wave R_peak, and the end of T wave T_end were annotated to obtain QTI, TQI, and RR intervals (RRI), as illustrated in Fig. 1. Q_begin and R_peak were annotated following the detection of the QRS complex, using the method by Pan et al. [28]. T_end was annotated as in Zhou et al. [29].

Fig. 1.

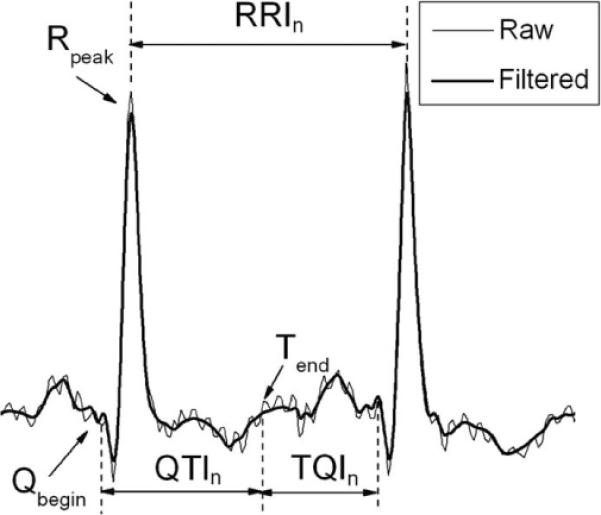
ECG recording before and after denoising, and annotation of Q_begin, R_peak, T_end, QTI, and RRI.

B. ARX Modeling of QTI Dynamics

We used an established approach, ARX [30], to model the QTI dynamics in each minECG:

$${\mathrm{QTI}}_n=\sum _{i=1}^M{a}_i\times {\mathrm{QTI}}_{n-i}+\sum _{i=1}^M{b}_i\times {\mathrm{RRI}}_{n-i}$$ (1)

where n is the beat number in the minECG; QTI and RRI are two discrete-time signals of the same length (the number of beats in the minECG); QTI_n , QTI_n−i , and RRI_n−i are the values of the signal for beat n or n−i, respectively; a_i and b_i (i = 1, … , M) are the weights (constants) with which each preceding QTI and RRI, respectively, contributes to QTI_n . M is the extent of the activation history (short-term memory) to be included in the ARX model. Notice that in this study, which differs from a QTI restitution study, we used RRI instead of TQI, because TQI is affected by the preceding QTI, and thus is not an independent exogenous input. Clearly, (1) incorporates both restitution (dependence on the preceding RRI, RRI_n−1) and the contribution of activation history to QTI (dependence on the rest of the input variables).

The parameters of the ARX model were evaluated with Steiglitz-McBride iteration based on the entire QTI and RRI datasets for each minECG. The Steiglitz-McBride iteration identifies an unknown system based on both input and output sequences that describe the system's behavior. Using the RRI dataset as an input, the output of each ARX model was computed and compared with the QTI dataset to evaluate the accuracy of the model in predicting QTI dynamics. For each ARX model (i.e., each minECG), the value of M was determined by increasing it from 1, in steps of 1, and examining, at each step, whether an accurate prediction of the QTI dynamics of the minECG was achieved for that extent of the activation history. The value of M at which the prediction reached a predetermined accuracy was denoted as M_max. The predetermined accuracy in this study was that the mean square error between the predicted and the measured QTI was smaller than 5 m·s². In addition to that, each ARX model was also validated with residual analysis.

C. Assessment of the Level of BIBO Stability in QTI Dynamics

The level of BIBO stability of each ARX model was assessed in the z-domain. To do so, the ARX model was first transformed from the time domain into the z-domain, where z is a complex number [12].

In the z-domain, the original function (1) becomes the transfer function H(z) [12]

$$H\left(z\right)=\frac{\mathrm{QTI}\left(z\right)}{\mathrm{RRI}\left(z\right)}=g\frac{(z-{\beta }_1)\cdots (z-{\beta }_i)\cdots (z-{\beta }_M)}{(z-{\alpha }_1)\cdots (z-{\alpha }_i)\cdots (z-{\alpha }_M)}$$ (2)

where α_i, β_i (i = 1, …, M), and g are coefficients (constants) derived from the weights a_i, and b_i (i = 1, …, M), while M is the number of components in H(z), which is the extent of the activation history M in the ARX model. QTI(z) and RRI(z) are the z-transforms of QTI and RRI. In (2), when z is set equal to any of the α_i (i = 1, …, M), one obtains a pole of the system; when z is set equal to any of the β_i (i = 1, …, M), one obtains a zero of the system; the system has M pole-and-zero pairs. A pole is canceled if it is equal to a zero. In this study, we assume that a pole is practically canceled by a zero if the difference between a pole and a zero is smaller than 0.05. According to the stability analysis theory [12], the system represented by the ARX (1) has BIBO-unstable dynamics if any pole falls outside of the unit circle |z| = 1, i.e., the magnitude of the pole, |pole|, is >1.

D. Data Analysis

The stability of QTI dynamics in each minECG (i.e., of each ARX) was assessed as described earlier. A minECG was tagged as stable if stable QTI dynamics was identified for all M values, otherwise the minECG was tagged as unstable. High-order (large M) ARX models with pole-zero cancellation were excluded from stability analysis in this study. A pole-zero cancellation suggests that a lower order (smaller M) model can be used to describe QTI dynamics. The increased M value in the high-order ARX resulted in extra poles and zeros into (2). These extra poles and zeros represent noise in the data but not the actual system. The noise can be caused by low sampling frequency (125 Hz) or other artifacts in the ECG recording, such as motion artifacts, poor lead-to-skin contact, or electromagnetic noise.

For each patient, the numbers of unstable minECGs in the VT and in the control groups were determined (denoted as N_us). It is well known that a PA could initiate unstable APD dynamics [11] depending on the restitution slope, which is an expanding oscillation of APD around a fixed point in the APD restitution curve. Therefore, we also calculated the frequency of premature activation (PA) for each 10-min ECG in each group and termed it as f_PA. We also calculated another index of QTI dynamics used in the literature, the QT variability index (QTVI) [10]. In the cases where the analyzed variables followed a normal distribution, paired t-test was used for comparisons between groups. Otherwise, Wilcoxon rank-sum test was used to compare the medians of the variables between groups. To ascertain whether f_PA is related to QTI instability, the correlation coefficient between f_PA and N_us was calculated in both the VT group and the control group. The significance level of all these tests was 0.05.

III. Results

A. ARX Modeling of QTI Dynamics

The statistical summary of QTI, TQI, and RRI of both the VT and the control groups can be found in Table II. For each minECG an ARX model was constructed. Using the RRI of the minECG as input, the output of the model was computed, as shown in Fig. 2. Fig. 2(a) demonstrates that an accurate prediction of QTI dynamics was achieved for M_max = 46. The dependence of the prediction error on M is presented in Fig. 2(b) for the same minECG. The mean value of M_max of the VT group was 37.8 ± 8.8, which was significantly (p < 0.01) different from that of the control group (32.1 ± 8.16).

TABLE II.

Statistical Summary of RRI, QTI, and TQI

	VT	Control	p
RRI (ms)	659±150	705±157	<0.01
QTI (ms)	401±84	429±65	<0.01
TQI (ms)	258±130	276±141	<0.01

Fig. 2.

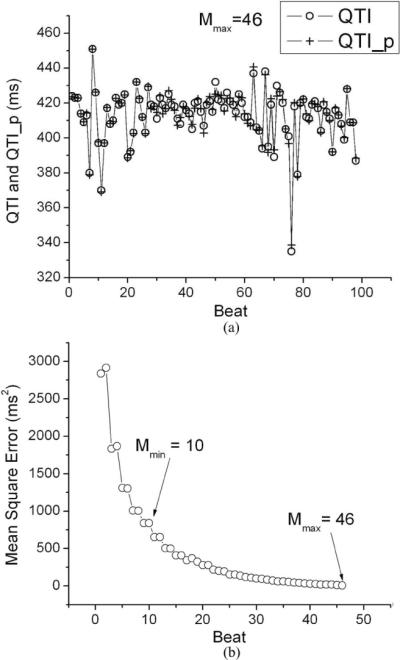
(a) Predicted QTI (QTI_p) dynamics of a minECG, compared to the QTI dynamics extracted from the same minECG for M_max = 46. (b) Dependence of prediction accuracy (mean square error) on the value of M. M_min is the M at which unstable QTI dynamics was first identified.

B. Instability Analysis

Example pole-zero plots resulting from the same minECG as in Fig. 2 at M = 10 and M = 46 are illustrated in Fig. 3. The QTI dynamics of this minECG was unstable [see Fig. 3(a)], evidenced by several pairs of not-canceled-poles that are located outside of the unit circle. Fig. 3(b) shows that although M = 10 does not result in a good QTI dynamics prediction [large mean square error in Fig. 2(b)], it nonetheless captures the instability in QTI dynamics accurately, as is evident by the presence of the two not-canceled-poles (marked with arrows) outside of the unit circle. As M is increased to 46, the locations of the two poles in Fig. 3(b) remain the same as those in Fig. 3(a) (marked with arrows), with new not-canceled-poles appearing at M = 46. This result indicates that although accurate prediction of QTI dynamics requires a higher value of M (M_max), instability in QTI dynamics is first captured at a much smaller M, i.e., a shorter activation history is needed for accurate prediction of the instability in QTI dynamics than for the accurate prediction of QTI dynamics. The minimum M at which QTI instability is detected is termed M_min. The mean M_min for the VT group was 7.0 ± 5.4, which was not significantly (p = 0.75) different from that of the control group (7.4 ± 5.5). Note that minECGs with stable QTI dynamics were excluded from the calculation of the mean M_min. This finding indicates that, for each patient, instability in QTI dynamics away from an arrhythmia event was determined by a similar number of preceding beats (i.e., extent of activation history) as before the onset of VT.

Fig. 3.

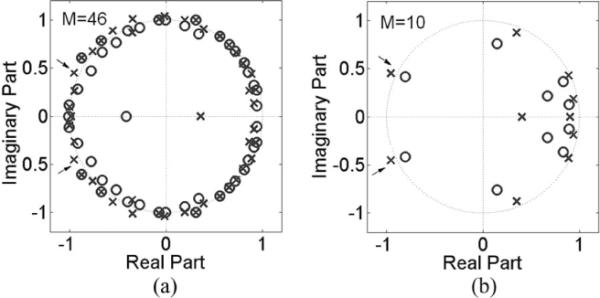
Pole-zero plot of a minECG for different values of M: (a) M_max = 46; (b) M_min = 10.

C. N_us, f_PA, and QTVI

In the VT group, the median of N_us was significantly larger (p < 0.02) than that in the control group, as illustrated in Fig. 4(a). This indicates that more minECGs became unstable before VT onset as compared with those in control. We also found that the median of f_PA of the VT group was significantly (p < 0.03) higher than that of the control group, as illustrated in Fig. 4(b). This indicates that more PAs took place before VT onset. The correlation coefficient between N_us and f_PA was found to be 0.85 (p < 0.01) in the VT group and 0.69 (p < 0.05) in the control group, indicating dependency between N_us and f_PA in the studied population. Finally, the difference in the median of QTVI was insignificant between the two groups (p = 0.38).

Fig. 4.

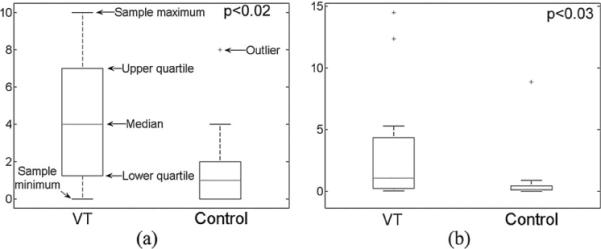
Comparisons of the median of (a) N_us and (b) f_PA.

IV. Discussion

This study presents a novel methodology for assessing the level of BIBO stability in QTI dynamics from the clinical ECG recording. The results of this study show that the methodology is capable of capturing the BIBO-unstable QTI dynamics preceding VT onset. The results also revealed that VT onset and unstable QTI dynamics were correlated with the frequency of PAs. This finding is consistent with a previous study which reported that QTI dispersion was correlated with the frequency of ectopic beats in patients with acute myocardial infarction [31].

In the following discussion, we compare the present methodology with other approaches that have been applied in the study of repolarization dynamics, and discuss the possible clinical applications of the new methodology.

A. ARX Versus Restitution

In this study, we used an ARX model to describe the relationship between a given QTI and several prior QTIs and RRIs in the ECG; restitution relates the given QTI to its preceding TQI only. Without loss of generality, QTI restitution at a given TQI can be expressed as:

$${\mathrm{QTI}}_n=d\times {\mathrm{TQ}}_{n-1}=d\times ({\mathrm{RRI}}_{n-1}-{\mathrm{QTI}}_{n-1})$$ (3)

where d is the slope (a constant) of the QTI restitution curve at the given TQI. The transfer function of (3) in the z-domain is

$$H\left(z\right)=\frac{\mathrm{QTI}\left(z\right)}{\mathrm{RRI}\left(z\right)}=\frac{d}{z+d}.$$ (4)

It is evident that (3) is a reduced version of (1) (i.e., the restitution is a reduced version of ARX) with a₁ = −d, b₁ = d, and all other parameters equal to 0. In this reduced case, all activation history except the preceding beat is ignored. It is clear that when activation history cannot be ignored (a_i ≠ 0, β_i ≠ 0, i = 1, …, M), restitution (3) and (4) is not an accurate means of describing QTI dynamics. This limitation can be further illustrated in Fig. 5, which presents the QTI restitution curve constructed from a minECG belonging to the VT group; the minECG was tagged as unstable using the present methodology. From Fig. 5, we can see that, due to the large scatter in the data points, the goodness of the curve fit is unacceptable (R² < 0.5). It has been reported in both animal and clinical studies that the outlier points in the restitution plot indicate increased arrhythmogenic risk [32], [33], and thus should not be ignored. The present algorithm includes these outlier points into the assessment of QTI instability, and thus constitutes a more comprehensive methodology, compared with restitution, to study the mechanisms of arrhythmia initiation.

Fig. 5.

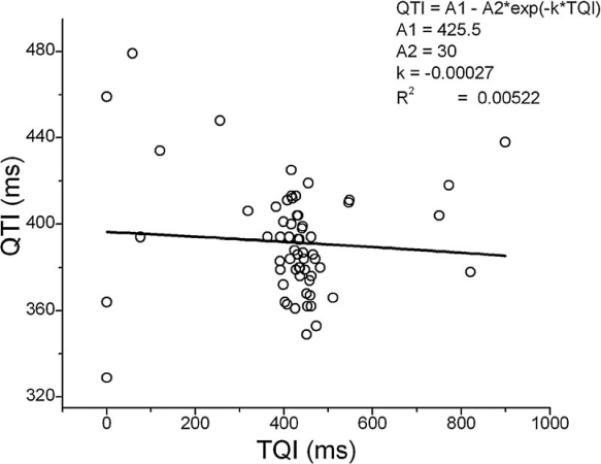
Example of a QTI restitution relationship constructed from a minECG.

From (4), it is evident that the reduced ARX model has only one pole, d. If the magnitude of d is larger than 1, which means either d > 1 or d < −1, the ARX model is BIBO-unstable. In restitution analysis, a large restitution slope (>1) has been traditionally used as the instability criterion, while the effect of a negative restitution slope on APD or QTI dynamics has not been extensively studied [34], [35], although there are ample experimental observations of it [30], [36]. In the present study, we provide a general way to perform stability analysis of QTI dynamics, which in the reduced case of (4) also allows us to explore QTI dynamics under the conditions of negative restitution slope. The latter is presented graphically in Fig. 6. Following a perturbation in TQI (a bounded input), values of d < −1 resulted in unstable QTI dynamics in Fig. 6(a), while in Fig. 6(b) a less negative value of d (0 > d > −1) resulted in a stable QTI dynamics.

Fig. 6.

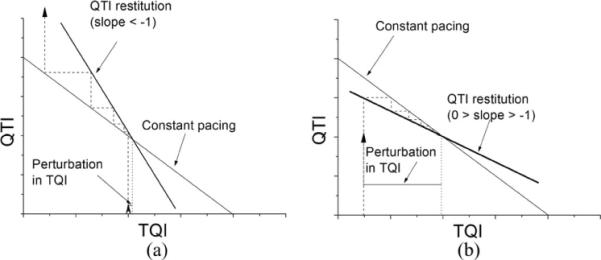
(a) QTI restitution slope d < −1. A small perturbation of TQI initiated diverging QTI dynamics. (b) 0 > d > −1. A large perturbation of TQI initiated converging QTI dynamics.

B. Comparison of the Present Methodology to QTVI

QTVI has been a valuable technique in arrhythmia risk stratification. QTVI characterizes in a statistical manner, the relationship between QTI and RRI dynamics in the ECG recording, and provides an overall estimation of QTI variability, normalized by the magnitude of RRI variability. Elevated QTVI, which has been reported in diseased hearts, indicates QTI dynamics that is out of proportion to RRI dynamics [10], [37]. Although QTVI has been used as an index of repolarization lability [38], [39], it is not a BIBO stability index, and thus is different from the present approach. In addition to this fundamental difference between QTVI and the present approach, as we have mentioned in [22], ectopic beats are typically excluded from QTVI analysis, reflecting QTI dynamics under sinus rhythm only. However, ectopic beats could uncover arrhythmogenic unstable repolarization dynamics in the heart, much like the way a sudden short DI unmasks instability in APD when restitution is steep [1], [11]; the present methodology captures this instability. It is clear that QTVI and the present algorithm reveal different aspects of repolarization dynamics in the heart.

C. Extent of Short-Term Memory

The results of this study provided new information regarding the extent of activation history that contributes to arrhythmogenesis. While ARX modeling has been used previously to assess the contributions of short-term memory and restitution to APD dynamics [30], [40], the extent of the activation history was fixed at four beats; the studies concluded that APD dynamics cannot be fully explained with restitution and the chosen (four beat) activation history. It has also been reported that the extent of activation history affecting QTI could be as long as 150 beats when only prior RRIs were considered [41], [42]. The present algorithm uses M prior beats as activation history, where M is dynamically calculated, and could have a different value for each minECG. We found that to accurately reproduce QTI dynamics, M_max number of prior QTIs and RRIs need to be incorporated in the ARX model (mean M_max < 38), while the extent of activation history that contributes to QTI instability is much shorter (mean M_min < 8). These new findings shed light on the contribution of short-term memory to arrhythmogenesis.

D. Clinical Significance

The presented methodology could have important clinical applications. Our results presented in this paper, as well as in the findings reported in a previous paper [22], demonstrate that that the present methodology can be applied in the clinic to monitor the development of QTI instability and the development of arrhythmia risk. It also has the potential to be used for risk stratification purposes.

It is important to underscore that the present methodology for representing the ECG signal as an ARX uses different extents of activation history depending on the specific application of the methodology. If the goal of an application is to achieve an accurate (mean square error <5 ms² in this study) prediction of QTI dynamics, then the largest number of beats, M_max, needs to be included in the ARX model. Alternatively, if the goal of an application is to determine whether QTI dynamics is BIBO-stable or not, then using M_min number of beats in the ARX model is sufficient for this purpose, and this saves computational time. Again, M_min represents the number of beats (out of the entire activation history, M_max) that are the major determinants of the BIBO stability in QTI dynamics.

E. Limitations

In this study, ectopic beats were not excluded from the analysis, and were treated in the same way as a sinus beat. It is necessary to keep PA in the study. The ARX modeling and stability analysis of QTI dynamics are based on the response of the model to perturbations in RRI, which is PA. Excluding PA will make it impossible to identify the ARX model correctly. However, the QRS width caused by an ectopic beat is typically different from that of a sinus beat. Sinus beats and ectopic beats also cause different T-wave morphologies. Therefore, the estimation of QTI stability in an ECG recording with a large number of ectopic beats might be less accurate than in a recording without ectopic beats.

We used an ARX model to describe the relationship between QTI and RRI dynamics. A limitation of this model is that ECG artifacts, such as motion artifacts, poor lead-to-skin contact, or electromagnetic noise, were included in the model. Another model, the autoregressive moving average model with exogenous inputs (ARMAX), is capable of decoupling the system dynamics from the artifacts. However, we found that the parameter estimation of an ARMAX model usually required a larger dataset size, and could not be applied to a number of minECGs in this study.

Finally, short-term memory was represented here by a series of preceding QTIs and RRIs. This representation ignores the fact that the same QTIs may be associated with different T-wave shapes. Further studies need to be conducted to ascertain whether this limitation might have any impact on the results of this study.

Biographies

Xiaozhong Chen received the M.S. degree in electrical engineering from the China University of Mining Technology (CUMT), Beijing, China, in 1998, and the Ph.D. degree in biomedical engineering from the University of Alabama at Birmingham, Birmingham, USA, in 2006.

He is currently a Postdoctoral Fellow in the Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD. His research interests include arrhythmia risk stratification algorithm and cardiac electrophysiology.

Natalia A. Trayanova (SM'91) is a Professor in the Department of Biomedical Engineering and the Institute for Computational Medicine at Johns Hopkins University, Baltimore, MD, and is the inaugural Murray B. Sachs Chair in Biomedical Engineering. She has published extensively and has presented at a large number of international meetings. She is on the Editorial Board of the journals Heart Rhythm and American Journal of Physiology (Heart and Circulatory System), and is an Area Editor of IEEE Reviews in Biomedical Engineering. She was the Vice-Chair in 2007 and the Chair in 2009 of the Gordon Research Conference on Cardiac Arrhythmia Mechanisms. She is the Editor of the book Cardiac Defibrillation - Mechanisms, Challenges and Implications (InTech Publishing, 2011).

Dr. Trayanova is the recipient of numerous awards, among which Excellence in Research and Scholarship Award (2005) and Outstanding Researcher Award (2002), and Fulbright Distinguished Research Award (2002). She is a Fellow of the Heart Rhythm Society, American Heart Association, and American Institute for Medical and Biological Engineering. She is an Associate Editor of Frontiers in Computational Physiology and Medicine, and served as an Associate Editor of the IEEE Transactions of Biomedical Engineering in the period 1997–2005.