Modeling Regulatory Networks to Understand Plant Development: Small Is Beautiful

Abstract

We now have unprecedented capability to generate large data sets on the myriad genes and molecular players that regulate plant development. Networks of interactions between systems components can be derived from that data in various ways and can be used to develop mathematical models of various degrees of sophistication. Here, we discuss why, in many cases, it is productive to focus on small networks. We provide a brief and accessible introduction to relevant mathematical and computational approaches to model regulatory networks and discuss examples of small network models that have helped generate new insights into plant biology (where small is beautiful), such as in circadian rhythms, hormone signaling, and tissue patterning. We conclude by outlining some of the key technical and modeling challenges for the future.

INTRODUCTION: ANALYZING GENE REGULATORY NETWORKS TO UNDERSTAND BIOLOGICAL COMPLEXITY

Plants are complex organisms that can adapt their morphology to suit environmental conditions. As for other organisms, their development is a continuous and dynamical process, in which large numbers of components interact at various scales, from genes and molecules to cells and tissues. Until recently, plant scientists would study only a handful of these components at a time, and to make sense of their behavior, they would typically assume only a simple chain of cause and effect. In many cases, however, this will provide only a partial representation of the underlying complexity. In the last 15 years, the analysis of plant systems (among others) has moved progressively toward monitoring these elements in large numbers. This has been fueled in large part by the advent of -omics technologies, allowing one to follow thousands of genes or proteins simultaneously. In turn, this has forced biologists to envisage new ways of elucidating the underlying biological mechanisms.

Systems biology offers a powerful framework to analyze large, complex data sets, whereby the organism (or part thereof) is viewed as a set of entities interacting according to a particular set of rules, so that the properties of the organism emerge from these interactions. This vision holds at all scales and in particular at the genomic scale, with gene regulatory and signaling networks processing multiple cell-autonomous and non-cell-autonomous inputs to generate emergent cellular behaviors. These will give rise to emergent behaviors at the tissue scale. One of the key challenges then is to assemble the pertinent gene regulatory and signaling networks and to understand how they process signals to generate appropriate responses.

The availability of large-scale data sets, however, has not eliminated the need for complementary smaller scale analyses. Studies of whole-genome gene networks have led to the suggestion that these are composed of smaller and topologically distinct subnetworks (Milo et al., 2002) that can be studied separately from the rest of the network. On the other hand, even with the traditional reductionist approach, one rapidly finds that systems approaches are also required to deal with processes involving just a few genes/proteins that have been identified, for example, through classical genetics. Indeed, many of the success stories in systems biology derive from such smaller scale studies, building up understanding of a process by working outwards from a key molecule of interest. Examples of small-scale network studies have flourished in recent years. The aims of this review are to illustrate the importance of studying these networks in plants, to provide biologists an overview of mathematical approaches used for modeling them, and to illustrate how systems analysis of small networks can be used to generate biological knowledge, focusing more specifically on recent studies of gene regulatory and signaling networks involved in plant growth and development.

DYNAMICAL MODELING OF GENE REGULATORY NETWORKS

Before focusing on small networks, it is necessary to introduce mathematical concepts and definitions of dynamical models, which allow addressing how a network behaves over time under various conditions. Simple intuition about a complex system can indeed often be misleading, and models are essential to facilitate our understanding and clarify our assumptions. Here, a model can be defined as a mathematical representation of a system, which can be used to test hypotheses, make predictions, and carry out in silico experiments (“What happens if…?”). Models are always simplifications and, thus, invariably are incorrect. Ideally, they should be improved in an iterative loop in association with experimental work, a point that we will discuss further below. When considering genes and signals within a complex network, there are methods to infer their topology. This has been the subject of other reviews (for example, see De Smet and Marchal, 2010; Bassel et al., 2012; Kholodenko et al., 2012) and will not be discussed here.

What Do We Study with Dynamical Modeling?

Dynamical models predict how interactions between network components can lead to changes in the state of a system. The most basic process is for a system component to respond positively or negatively to some stimulus. However, developmental processes often require more complex responses, such as a switch between different cell fates, this being a common characteristic of developmental systems (for example, see Middleton et al., 2009). There are many examples of biological switches for which mathematical modeling has made a crucial contribution, including the lactose operon-inducible system (Santillán and Mackey, 2008) and the lysis-lysogeny decision by phage lambda (Shea and Ackers, 1985; Santillán and Mackey, 2004). In plants, it has recently been shown that a spatially distributed switch regulates root epidermis patterning (see below and Figure 4; Savage et al., 2008). Another typical complex dynamical behavior is an oscillator, such as the cell cycle (Sha et al., 2003) and the circadian rhythm (discussed below; Locke et al., 2006). More complex still is the coordination of these ingredients to make an organism, which for plants involves graded responses to stimuli and cell fate decisions (switches), coupled to regulation of the cell cycle (oscillators) and cell growth. Note that there need not be a correlation between complex behavior and the complexity of a network; it is possible for quite simple networks to behave in a highly complex manner, while extremely complex networks can behave, due to their specify topology, in a regular and tightly controlled way (Csete and Doyle, 2004; Marr et al., 2007).

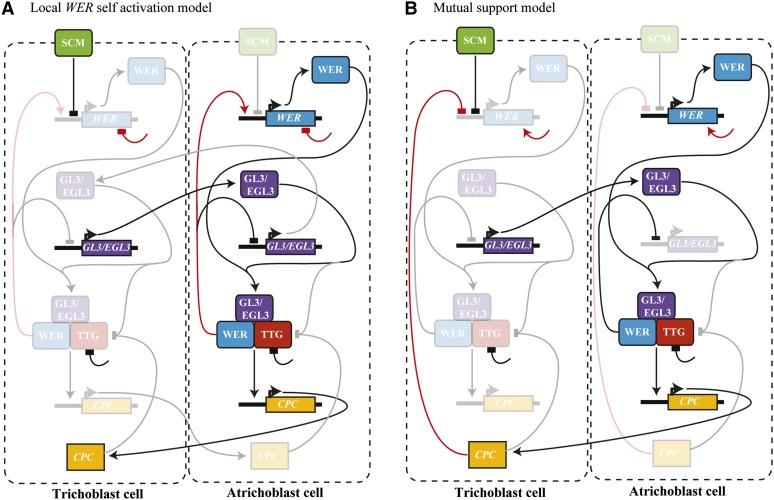
Figure 4.

Intercellular Signaling and Its Impact on Network Dynamics.

Two competing models for root epidermal patterning considered in Savage et al. (2008): (A) The WER self-activation model and (B) The mutual support mechanism. Interactions and components that are not active in a cell appear faded. Key differences between the two models appear in red.

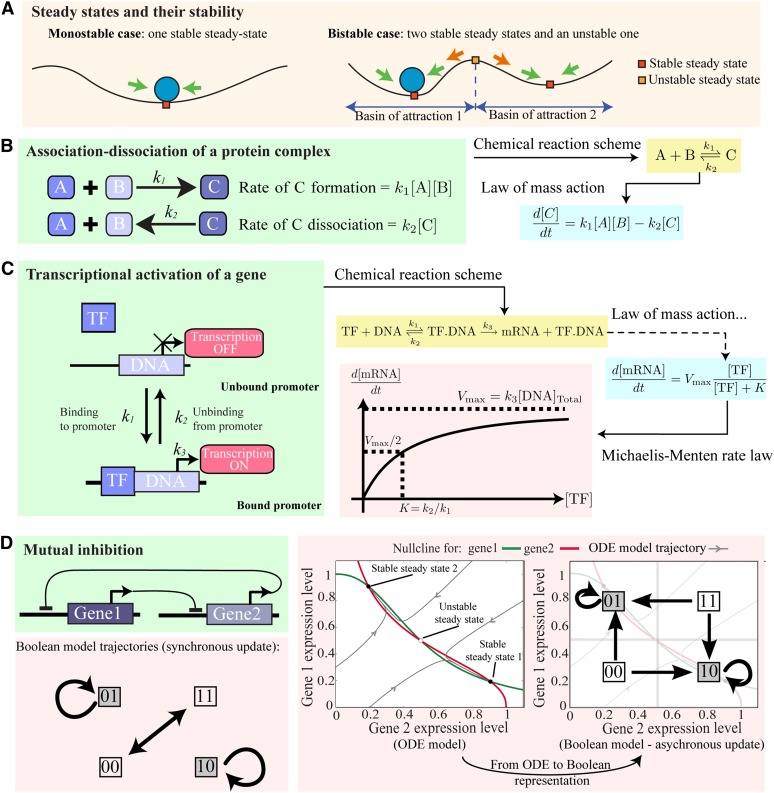
Given a dynamical model (of whatever size or complexity), it is of crucial interest to learn as much as possible about the model steady states (where all components of the network, for example, concentrations of various proteins or mRNAs, are in equilibrium so that they do not change in time) and their stability (whether or not the system moves toward the steady state when given a small perturbation away from it) as determinants of system dynamics. These ideas can be visualized in terms of how a ball might move if placed on a smooth landscape (illustrated in Figure 1A). If carefully balanced at the peak of a hill, the ball will stay there for all time. Thus, this position can be thought of as a steady state of the system. However, if given a small perturbation away from the peak, it will move down the hill and not return. Thus, this particular steady state is unstable. The bottom of a valley is also a steady state of the system. However, in this case, if given a small push away, the ball will roll back. In this case, we can say the steady state is stable. Analogously, in a model of a gene network, the system should return to a stable steady state if given a small perturbation away from it. This is particularly significant since biological systems are continually subjected to both internal and external perturbations. Thus, stable steady states (as opposed to unstable ones) are the only type of steady state to be attained in practice. Other more complex long-term behavior can be observed in dynamical models, such as sustained oscillations (also known as a limit cycle). Both stable steady states and stable limit cycles are examples of attractors. Attractors can be understood, more generally, as a set of states toward which a system will evolve over time. Each attractor can be reached by a certain set of initial states, called its basin of attraction (Figure 1A). In the case where the system can have two stable steady states (e.g., two distinct valleys, in the case of Figure 1A), it is referred to as bistable. The properties of the system (e.g., the number, type, and stability of attractors) can depend crucially on the parameter values of the model. If changing a particular parameter value results in a change in one of these properties, then we call this change a bifurcation. Although initially not termed mathematically, it was suggested quite long ago (Waddington, 1940; Delbrück, 1949) that cell types correspond to attractors and that developmental processes correspond to different populations of cells entering one attraction basin or another (so the system has multiple steady states). This biological interpretation of the dynamics of regulatory networks is a key concept, independent of the mathematical formalism used to specify a particular model. The study of these various system properties (steady states, limit cycles, etc.) is often referred to as mathematical analysis in the literature.

Figure 1.

Introduction to Dynamical Models of Small Networks.

(A) Cartoon illustrating key properties of a dynamical model.

(B) Mass action model for the association and dissociation of two proteins. These can be written in terms of a chemical reaction scheme. The law of mass action dictates how the rate of formation and dissociation depend on the concentration of the reactants. From this an ODE can be formulated.

(C) A Michaelis-Menten model of gene expression. The model can be formulated by applying the law of mass action to the chemical reaction scheme depicted. TF, transcription factor.

(D) The mutual inhibition feedback loop. Both Boolean- and ODE-based models (right panel) are bistable (for certain parameter values) and have analogous steady states. However, in the Boolean model, transitions between the states depend on which update method is used (cf. right panel and bottom panel).

Mathematical Frameworks to Build Dynamical Models

The systems mentioned above, along with their associated behaviors, are usually described in terms of dynamical models. Here, we introduce the mathematical frameworks that can be used to build them. The state S of the model at time t is just the set of all the variables “x₁, x₂, …, x_N” at time t:

which can be considered as a point in the (N-dimensional) state space of the system. In principle, the variables are measurable quantities, such as mRNA, protein, or hormone concentrations (although these may be difficult, if not impossible, to obtain in practice using current experimental techniques). We would like to be able to understand the past and present and predict the future, based upon the interactions between the system components. If the state is changing with time t, then the model is dynamical, and the time-varying components of the state are the variables x₁(t), x₂(t), . . . , x_N(t). The form of model we shall study is:

where f is a function encoding our understanding of how the system components affect one another, and p₁, p₂,…, p_M are model parameters. Equation 2 simply states that the future state of the system is some function of its past state (i.e., that the future is predictable). A trajectory of the system is then the set of future states given a particular initial state. The parameters are numerical values that encode information about the system and do not vary in time, such as the degradation rate of an mRNA. A particular choice of parameter values can be thought of as a point in parameter space. The components [x_i(t)] and interactions (encoded in f) can be inferred from a wide range of data sources, such as genetic and RNA interference screens, mRNA profiling, protein–protein interaction screens, and analysis of transcription factor binding. Each has strengths and limitations, and integration of multiple data sources is important for reliably inferring the interactions in a network (see Bassel et al., 2012 in this issue).

In gene-regulatory networks, where the state variables typically correspond to mRNAs, proteins, and other molecules, each variable should be represented by a discrete quantity, an integer (e.g., the number of molecules), and changes in state are discrete events (namely, the creation or degradation of a molecule). If the amount of each component is sufficiently large, then its state can be approximated by a continuous variable that changes in time (e.g., concentration). This leads naturally to the use of ordinary differential equations (ODEs), defined by the rates of change of the system components, interpreted (in words) as:

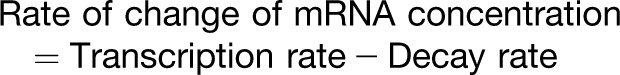The use of ODEs is not computationally demanding and is very common within the plant systems biology literature. Another type of model often used is based on Boolean networks, in which the state variables are either OFF (0) or ON (1), rather than numbers of molecules or concentrations. These are two types of models that represent the most common frameworks, and we describe them in greater detail below (the interested reader should see also the Conclusion and Future Challenges section for a discussion on stochastic models).

ODEs

If we represent the network state S(t) as a continuous variable, then it has a well-defined rate of change. An ODE model gives the rates of change of the variables x_i(t) as functions of the state at that time:

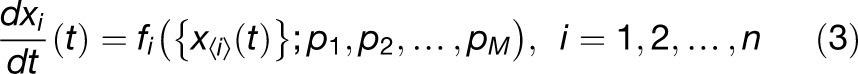where {x_<i>(t)} is the set of variables that affect x_i(t), and we write dx_i(t)/dt to denote its rate of change. The functions f_i encode the interactions between components (e.g., chemical reactions, transcriptional regulation, etc.) and are in general hard to determine. In practice, however, models are often based on a small set of standard forms for f_i (see later for examples), derived from the laws of physics and chemistry. For chemical reactions, an important concept for formulating f_i is the law of mass action, which states that the rate of a chemical reaction is proportional to the product of the concentrations of the reactants. A simple example of this is illustrated in Figure 1B, showing how an ODE model for the binding and unbinding of two proteins can be formulated. Given a set of reactions, it is relatively straightforward to write down the corresponding ODEs. For processes such as transcriptional regulation, commonly used forms can be derived by considering the binding and unbinding of transcription factors to DNA. For example, Figure 1C illustrates an activating transcription factor binding to DNA to give a complex that leads to the production of mRNA. By assuming transcription factor binding and unbinding is relatively fast compared with transcription, one can obtain the following expression for the rate of mRNA production:

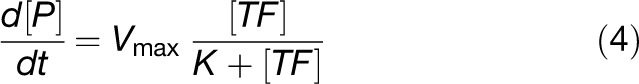where [P] is the product (mRNA) concentration, [TF] is the transcription factor concentration, and V_max and K are parameters derived from the rates of transcription factor binding and unbinding, and mRNA formation. This is similar to the Michaelis-Menten equation for enzyme substrate reactions (Alon, 2006) and is a natural form to use for transcriptional activation by a single TF. Functions representing transcriptional repression can be derived in similar way, as can Hill functions (increasing and decreasing) in the case where binding to DNA is cooperative. More difficult is the problem of how to combine multiple transcriptional regulators (e.g., an activator and a repressor). Three main approaches have been considered in the literature: phenomenological, extensions to the above Michaelis-Menten quasi–steady state approach, and a thermodynamic approach (Shea and Ackers, 1985). However, in many cases, these all lead to the same or similar mathematical expressions (Bintu et al., 2005a, 2005b).

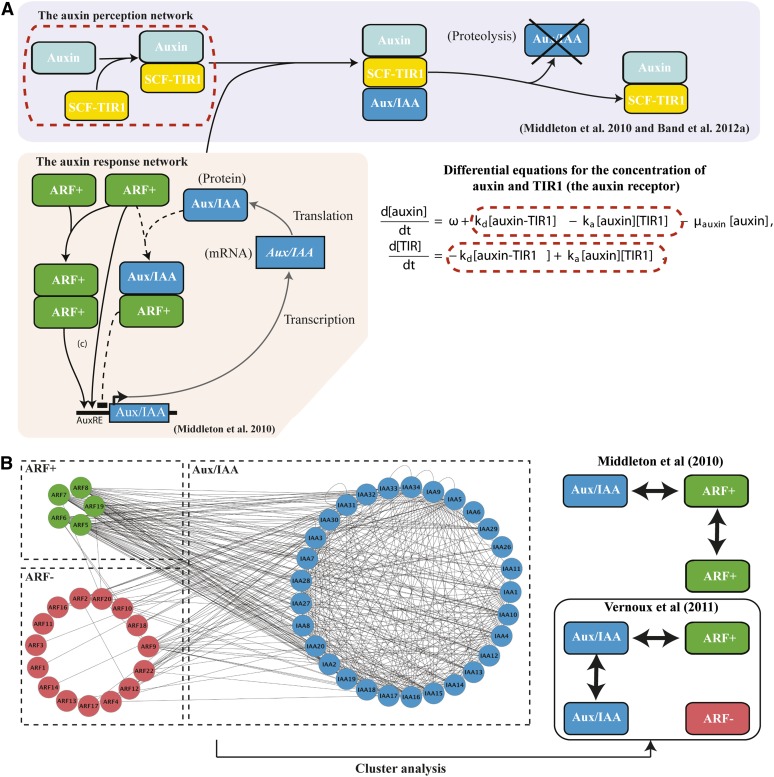
What we have now are ODE models for gene regulatory networks whose variables are mRNA and protein concentrations, with rates of change given in terms of mass action, functions representing transcriptional activation and repression, linear decay, and translation. Model parameters include thresholds for transcriptional regulation; effective cooperativities; half-lives; relative contributions of multiple transcriptional regulators; transfer rates (e.g., cytosol to cell surface); transformation rates (e.g., cleavage, phosphorylation); and binding. To illustrate this further, below we discuss the construction of an ODE model for the auxin signaling and response network (Figure 2A).

Figure 2.

Ingredients for a Small Network Model.

(A) Modularity of hormone signaling in plants. The Aux/IAA negative feedback model (Middleton et al., 2010) was formulated using the law of mass action (see Figures 1B and 1C); illustrative equations are provided. AuxRE, auxin response elements (ARF binding sites).

(B) Top-down approach to small network generation. Cluster analysis performed on the ARF-Aux/IAA interactome. From this the interactions between repressor and activator ARFs and Aux/IAA were identified (Vernoux et al., 2011; compare with Middleton et al., 2010).

Boolean Networks

In the case of Boolean networks, variables now represent the state of a gene and can either be 0 or 1. The rules governing how the current state relates to the next one are encoded according to Boolean logic and are intended to reflect the topology of the gene or signaling network. In these Boolean rules, the activation of a component (e.g., a gene) is represented by an instantaneous switch from 0 to 1. Furthermore, one can choose whether to update components simultaneously (synchronous update; Kauffman, 1993) or to update one component at a time (asynchronous update, for which there are different approaches, see below; Thomas and D’Ari, 1990). In the synchronous case, the next state is entirely determined by the previous one, so that one can write, as before:

Here, S(t) is a Boolean vector, a list of 0s and 1s representing the state of each gene in the network. Once the system is at an attractor, the system will cycle between different states, so that S₁→S₂ = f(S₁)→ … → S_n = f(S_n−1)→S₁ = f(S_n) in some repetitive fashion. Steady states correspond to cycles of length 1, whereas for oscillations the cycle will consist of two states or more.

In general, both the transient dynamics (i.e., how it changes over time before it settles to an attractor) and oscillations are different depending whether the updates are synchronous or asynchronous (and also which rule is chosen for the asynchronous case; see below). However, steady states are identical for both types of update. It follows that the simpler synchronous update schemes are often used if one wishes to study only the steady states of the system, whereas asynchronous is better suited to study the dynamics of the system. For an asynchronous update, the choice of which gene is updated at each time step can be made in several ways, which may be defined as follows: (1) globally, for instance, by specifying an order in which genes are updated, (2) based on a specific delay for each gene, which is compared with a global clock and reset after a change of state, or (3) as a stochastic event: At each time step, one gene is chosen randomly and updated (Li et al., 2006). In fact, more general random update functions can be used (Shmulevich et al. 2002). Cases 2 and 3 above require some numeric parameters to specify the model. More generally, Boolean models may require (1) no quantitative parameters at all, all regulatory functions being specified using logical gates (e.g., AND, NOT, OR); (2) time delay parameters for asynchronous updates (as in points 2 and 3 above); and (3) weights for each input of regulatory function, together with a threshold (with which the weighted sum of inputs is compared; this approach being inspired by neural network models).

Example: The Mutual Inhibition Feedback Loop

To illustrate the main ideas mentioned above, we now consider a well-known example, with two genes inhibiting each other; this sometimes is called a toggle switch or a mutual inhibition feedback loop (Figure 1D; Cherry and Adler, 2000; Gardner et al., 2000). Models of this network can be formulated using either Boolean or ODE-based approaches. In the case of an ODE model, the variables are the expression level of the two genes (namely, gene 1 and gene 2). Since there are only two variables, we visualize the dynamics of the system by plotting the expression level of gene 1 against the expression level of gene 2 (instead of their levels against time). Example trajectories of the model are illustrated (Figure 1D). We also plot nullclines; these indicate when the rate of change of just one gene is zero; steady states are at the intersections of the two nullclines (i.e., so that the rate of change for both genes is zero). We see from Figure 1D that the system is bistable: There are two stable steady states (where one of the genes is expressed at a high level and the other is expressed at a low level) and an unstable one (where the two genes are expressed at a comparable level). We also note that the (stable) steady state to which the system evolves depends crucially on the initial starting point (i.e., in which basin of attraction we start the system). In the Boolean case (it being much simpler), we can write the model in terms of the regulatory rules, namely, gene₁(t+1) = NOT[gene₂(t)] and gene₂(t+1) = NOT[gene₁(t)]. However, we must choose an update method (see above). For a synchronous update, the behavior of the network is summarized in Table 1, and a schematic representation is provided in Figure 1D (where arrows indicate transitions between states). The stable steady states are analogous to the ones from the ODE model, these being (in terms of a Boolean vector) 01 and 10 (i.e., one gene is “on” and the other one gene is “off”). However, a key difference with the ODE-based model is that if we started at 00 or 11, the system would cycle between them; 01 and 10 can only be attained if we start the system at that state. Thus, synchronous update is not required or helpful if one wishes to study how the network behaves over time but does give information on the steady states of the system.

Table 1. Summary of Transitions between Different States for a Boolean Model of the Mutual Inhibition Feedback Loop (Illustrated in Figure 1D) for Synchronous Update.

(Gene1,Gene2)t	(Gene1,Gene2)t+1
00	11
01	01
10	10
11	00

The case of asynchronous update is also illustrated in Figure 1D. States 01 and 10 are again stable steady states of the system. However, we now find that if started at 00 or 11, the system will tend to either 01 or 10. Hence, 11 and 00 are in the basins of attraction of 01 and 10 (Figure 1D). However, the manner in which this network changes over time (i.e., its dynamics) will depend on which particular asynchronous update method is used. Thus, unlike ODE-based models, there is a degree of ambiguity associated with the transients of Boolean networks. However, additional parameters specifying the response time of both genes may help reduce this ambiguity and give more biological meaning to the transients of the model.

Parameters and Parameterization of Models

We have seen that both Boolean and ODE-based models contain parameters. The behavior of both types of model can depend strongly on their parameter values. In many cases, estimates for these parameters are not yet available. For some problems, however, even qualitative predictions can give new biological insight. In this case, one can simulate the model for different parameter values (i.e., explore the parameter space and identify each of the various behaviors that it can generate). The predictive capabilities of the model will thus depend on how much of the parameter space can be explored, and the different behaviors can be treated as different predictions that subsequently can be tested experimentally. This includes situations, for example, where one demonstrates the existence of sustained oscillations or bistability for biologically plausible parameters (François and Hakim, 2005; Middleton et al., 2010; Muraro et al., 2011).

In some situations, however, it can be more important that a model generates quantitative predictions. This may be the case, for example, when one is interested in the sensitivity of the network outputs to some stimulus. In this case, parameter estimates can be obtained by fitting quantitative data to the relevant model outputs. For example, this was recently done with a model of gibberellin (GA) signaling network (Middleton et al., 2012) and with the auxin signal transduction pathway (Band et al., 2012c) in conjunction with the novel auxin reporter, DII-Venus (Brunoud et al., 2012). These are both discussed further below.

A detailed discussion of parameter estimation is beyond the scope of this review (reviewed in Ashyraliyev et al., 2009). For our purposes, however, it is important to note that larger models typically have more parameters and that the more parameters to be estimated, the more difficult it becomes to generate an accurate model. Even for small network models, however, it is often the case that estimates for model parameters are not in fact well constrained by the data. In other words, it is possible that from two equally good model fits one obtains two different parameter sets with significantly different estimates for the individual parameters (this being referred to as sloppiness in the fitting problem; Gutenkunst et al., 2007). However, even if this is the case, one can still use the different parameter sets to identify qualitatively distinct model behaviors. These in turn can be treated as predictions to be tested for experimentally (see below for a further discussion of model-experiment loop). Thus, in summary, it is not always necessary for good parameter estimates to be available for a model to be predictive or insightful.

SMALL-SCALE NETWORKS

Why Using Small Scale Networks Makes Sense

Small-scale networks are often generated via bottom-up approaches of network discovery, where one starts with a gene, protein, or signaling molecule of interest and works outwards, finding other components it interacts with. From these small networks, relatively simple models can be generated (see the next section for examples) for which it is often possible to identify all the possible behaviors of the network for plausible parameter values (see above). The usefulness of such a model (and indeed of any model) is apparent if there is a discrepancy between what is predicted by the model and what is observed experimentally, this suggesting that it might be necessary to include novel components in the model. In this way, dynamical models can help in predicting candidate components or interactions whose existence has then to be determined through experimentation. This is discussed further below.

One limitation of the above strategy is that it relies heavily on our ability to explore all the possible behaviors of a particular model. As noted above, experience with even simple networks shows their behavior can often be highly counterintuitive and strongly depend on system parameters. For larger networks, such a comprehensive analysis of the dynamics can be even more difficult; increasing the number of model components and parameters can lead to an explosion in the combinatorial complexity of the problem. Thus, for systems with more than a handful of variables, we rely mostly on computer simulation to understand their dynamics and hence can rarely be sure that we have fully explored all the possible system behaviors. This can significantly impair our ability to make robust or predictive models for larger-scale networks. Thus, there are two main conceptual difficulties with large-scale networks: our inability to parameterize them and our inability, except in special cases, to fully classify their behavior.

One way to overcome the above is in fact to rely on the analysis of small networks and furthermore to consider them as modules of a much larger and complex network. In this way, the dynamics of each module can be studied individually (see below for examples). In particular, there is an increasing body of evidence that biological systems are modular in their organization (Hartwell et al., 1999; Milo et al., 2002; Spirin and Mirny, 2003; Stuart et al., 2003; Gavin et al., 2006; Alon, 2007; Peregrín-Alvarez et al., 2009). The isolation of modules can be based upon a bottom-up approach (described above) or by a top-down approach, identifying modules based on the connectivity in large-scale networks. One notable example of this is through the identification of network motifs, these being small networks (for which there are only a few nodes) with a statistically significant topology. Nevertheless, we would like to stress that the extent to which we can study the dynamics of large-scale networks by dividing them into smaller-scale ones (i.e., modules) remains to be fully understood. We discuss this further in the Conclusion and Future Challenges section.

How to Build and Analyze Small Networks

As we have now discussed, small-scale networks are appealing because we can build models that are simple enough to analyze and retain enough mechanistic detail to be insightful for the biology. Hence, whereas large network models typically involve phenomenological descriptions for the least known interactions, it is often possible to build small network models using only the laws of physics and chemistry. There is no definitive recipe to build a good model. However, one should keep in mind that dialogue between experimentalist and modeler is essential to the success of a modeling approach. While there has been much in the systems biology literature about the experiment-model cycle, it is often not emphasized that this cycle can extend over long period of times and that there are many stages of modeling. Models of small-scale networks are typically based on known interactions. For particularly well-characterized pathways, a model is initially expected to capture the known experimental observations (at least qualitatively). In the second stage of modeling, various perturbations of the model (e.g., hormonal, chemical, or genetic) should be simulated. At this stage, model outputs can be considered to be predictions that must be validated experimentally. Often, it is only if new data sets have been generated (based on the model predictions) that new insight can be obtained. As mentioned in the previous section, the most useful scenario is when there is in fact a discrepancy between a prediction and the resulting experimental observation, as it can point to the existence of missing components, which subsequently can be identified through further numerical and wet-lab investigations. This type of multidisciplinary exchange has, for instance, led to the discovery of novel feedback loops involved in the circadian clock of Arabidopsis thaliana, an illustrative example that will be discussed further below (Locke et al., 2005a, 2005b, 2006; Zeilinger et al., 2006). While such exemplar studies exist, it is more often the case that model-based investigations will stop at the first stage, this being when existing experimental observations can be accounted for by the model and new model predictions have been generated but remain to be validated. This can lead to the perception that dynamical models have trouble predicting novel components or providing new insight. However, we argue that this is merely because subsequent rounds of the model-experiment loop have not yet been performed.

The modeler-experimentalist dialogue is also crucial in deciding how much detail is available to include in the model and, hence, which framework (e.g., Boolean or ODE-based) should be used. This can reflect a number of important factors, including how well characterized the network is experimentally (i.e., the level of mechanistic detail available), the biological question to be answered, and whether quantitative time-resolved data on the various network components is available.

Since Boolean networks explicitly assume that genes (and other network components) are either on or off, they typically require far less mechanistic detail to develop and, hence, often contain fewer parameters than their ODE-based counterparts. Thus, one can quickly characterize the overall behavior of the system. Boolean networks are most likely relevant in situations where the system has multiple steady states. For example, this can be the case in developmental processes involving cell differentiation, where the different steady states correspond to the different cell fates (these being characterized by the expression of specific genes). We discuss this further below with examples in root epidermis and flower patterning (Mendoza et al., 1999; Espinosa-Soto et al., 2004; Savage et al., 2008).

Because of the intrinsic state representation used in Boolean networks, it can sometimes be difficult to relate their outputs to the real dynamic behavior of the system. ODE-based approaches may therefore be more desirable, particularly if the system outputs of interest are intrinsically continuous. As an example of an ODE-based model, Figure 2A shows the network diagram and some of the corresponding equations for a model of auxin signal transduction (Middleton et al., 2010). The equations for auxin and its binding to its F-box coreceptor TRANSPORT INHIBITOR RESISTANT1 (TIR1) are shown in Figure 2A. These are based on the law of mass action (Figure 1D). The auxin signaling pathway is one of the best characterized in plants, extensive knowledge of which has been produced using biochemical, genetic, and genomic approaches (see overview in Del Bianco and Kepinski, 2011). Taking this information into account, the model includes various reactions between auxin and the proteins known to mediate transcriptional responses to auxin (a single auxin response factor [ARF], an auxin/indole-3-acetic acid [Aux/IAA], and the coreceptor TIR1 that controls degradation of the Aux/IAA in response to auxin; Chapman and Estelle, 2009) and translation and decay rates of the mRNAs. In the model, transcription of the Aux/IAA is positively regulated by ARFs (although in reality there are also repressor ARFs), and this interaction is antagonized by Aux/IAA proteins. This antagonism establishes a negative feedback loop in the network. The model equations are derived using the law of mass action together with an Aux/IAA transcription rate that is a complex function of ARF, ARF dimers, and ARF-Aux/IAA.

It should be noted that while it is not always possible to have such a precise mechanistic description of the system, one could instead use more phenomenological approaches by introducing quantitative concepts. Examples of these include growth rates (Kennaway et al., 2011), a function describing the size of a stem cell population (Geier et al., 2008), or the gradient of an unknown diffusing signal (Jönsson et al., 2005; Kennaway et al., 2011). These help avoid having to include specific molecular details.

Because ODE-based models can capture a high degree of biological detail, they can easily become large and overly complicated. Thus, one key aspect of ODE-based model development is that of simplification. One common approach is to retain the quantitative effects of certain molecular players or processes, without including them explicitly in the model so there are fewer variables or parameters. Probably the best example of this is the quasi–steady state assumption. This assumes that some subset of reactions or processes occur on a much faster timescale than others (i.e., there is a separation of timescales), which allows the elimination of certain variables from the dynamic model (Murray, 2002). For instance, the auxin signaling model by Vernoux et al. (2011) reduces the binding of TIR1 receptors with auxin and Aux/IAA to a simple Michaelis-Menten term in the equations (Figure 2A) by assuming this processes is fast when compared with changes in gene expression. This type of reduction is also often used to eliminate the variables describing dimers from a system, assuming protein–protein binding is much faster than the processes such as transcription or translation (for example, see Savage et al., 2008; van Mourik et al., 2010; Band et al., 2012c). However, it is worth stressing that the quasi–steady state assumption can lead to the wrong dynamics if this assumption is not valid (i.e., if there is not a clear separation of timescales). Its validity thus needs a careful evaluation, again requiring the experimentalist-modeler dialogue.

The choice of network components to be modeled can also allow for simplifications. Organisms such as Arabidopsis typically have large gene families in their genome (such as the 29 Aux/IAAs and 23 ARFs; Chapman and Estelle, 2009), and it is common for modelers to try and reduce this complexity by lumping whole gene families together so that they are represented by a single variable (for example, see Middleton et al., 2010; van Mourik et al., 2010). This is a reasonable first step and is most likely a valid one provided the individual family members all have similar behavior. However, it is often the case that individual gene family members have rather distinct functions (for example, see Bridge et al., 2012) or that subsets of genes can be grouped together in a more systematic way (for example, using clustering-based approaches; Vernoux et al., 2011). Furthermore, it may be possible to isolate network components according to where (i.e., in which tissue) and when (i.e., during a developmental process) they are active. Examples of this type of approach include the study of isolated modules from the auxin signaling pathway, like the pairs Aux/IAA14-ARF7, ARF19, or Aux/IAA12-ARF5, which have been shown to be active in a specific temporal sequence (De Smet et al., 2010).

USING SMALL-SCALE NETWORK MODELING TO UNRAVEL THE BIOLOGICAL LOGIC UNDERLYING PLANT DEVELOPMENT

Cell-Autonomous Small-Scale Networks

In systems biology, mathematical or computational models are often used to ascertain whether a particular set of proposed interactions (e.g., a gene network) can explain the biological observations. A way to start addressing this is simply to analyze a model’s behavior (using some of the techniques outlined above). In particular, the model itself may behave in an unintuitive or unexpected way, and through this process one can obtain a clearer interpretation of a specific data set and hence gain a better understanding of the real system.

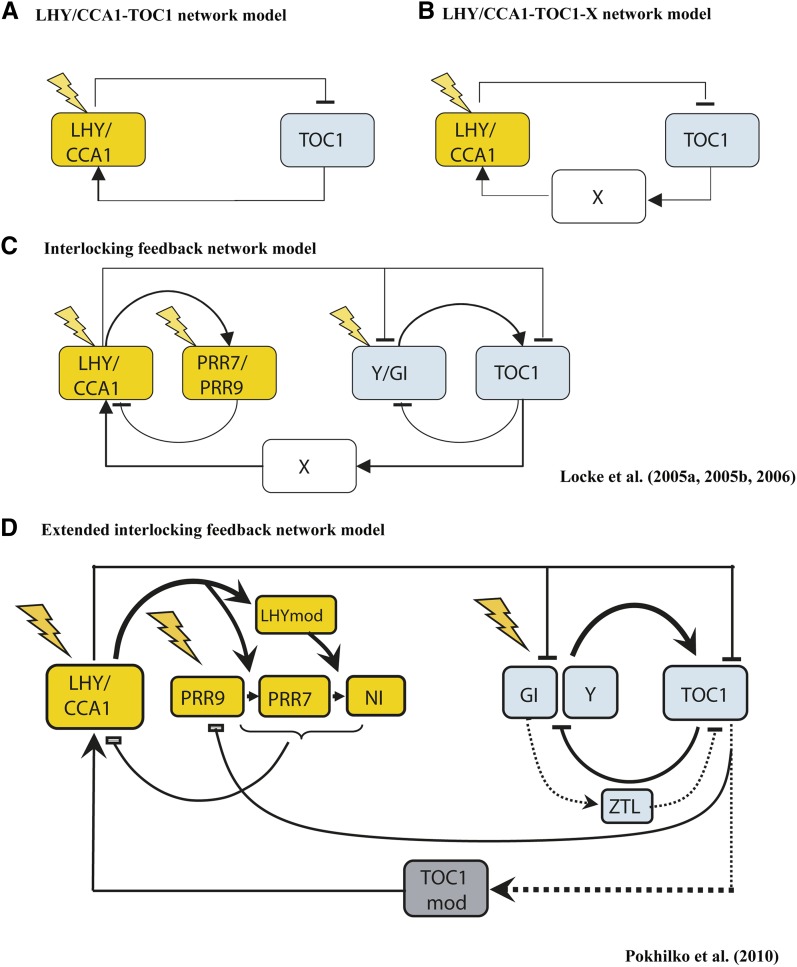
An excellent example of the use of small-scale models to enhance biological understanding can be found in the work of Millar and coworkers on the plant circadian rhythm, already mentioned earlier (Locke et al., 2005a, 2005b, 2006). A number of articles (for an overview, see Dalchau, 2012) show how an iterative cycle of model refinement, validation, and comparison to new data has led to the discovery of new network components and a clearer understanding of how the interlocking feedback loops regulate the rhythm. The first four stages of model development are illustrated in Figure 3. This process started with a single oscillator model (Figure 3A) involving only LATE ELONGATED HYPOCOTYL/CIRCADIAN CLOCK ASSOCIATED1 (LHY/CCA1) and TIMING OF CAB1 (TOC1) (Locke et al., 2005a). Comparisons between this model and (what was then) already published data showed that, while the model could correctly reproduce the phases of LHY and TOC1 oscillations, it failed to account for a number of experimental observations (Locke et al., 2005b). This indicated that additional components might be missing from the model and led the authors to consider other possible interactions. The most promising of these involved an additional step in the feedback loop whereby TOC1 activated LHY via a putative gene X (Figure 3B). This new model could account for the published experimental observations. We note that this point in the authors’ studies reflects perhaps the first stage in the model-experiment loop discussed above. However, the authors went further to compare the model behavior and novel data generated from cca1 lhy double mutants. Again, the model failed to account for the new experimental observations. The above process was therefore repeated again and a new component proposed (initially referred to as gene Y), this forming a second loop in the network (Figure 3C). The gene GIGANTEA (GI) was initially proposed to be a candidate for gene Y (Locke et al., 2005b, 2006). More recently, further interplay between model and experiment has indicated that GI only fulfills part of this function (Pokhilko et al., 2010). Furthermore, the component originally proposed to be gene X could rather be the posttranscriptional modification of TOC1 protein or its interaction with other complexes. Collectively, these studies have led to a data-consistent view that circadian rhythms are driven by at least two oscillators (morning and evening). These are coupled intracellularly and involve nontranscriptional regulations (Pokhilko et al., 2010) (Figure 3D). Another level of complexity was recently explored by Guerriero et al. (2012). Here, the authors investigated how stochasticity (caused by there being small numbers of molecules) can affect the behavior of the system. It was found that their stochastic model can provide a better agreement with experiments than the previous ODE-based models. In particular, an observed dampening of oscillations in constant light could be explained by noise-induced desynchronization in a cell population, and a more realistic entrainment to light under changes of photoperiod was also achieved.

Figure 3.

Unraveling the Circadian Clock.

(A) The initial model for the circadian clock involved interaction between TOC1 and LHY /CCA1.

(B) To account for discrepancies between the model and data, an additional component in the network was proposed (gene X), which mediates LHY/TOC1 activation.

(C) Further comparison between new experimental data and the model indicated that the circadian clock involves two interlocking feedback loops, this comprising the original loop and feedback between putative gene Y and TOC1.

(D) While GI was proposed as a candidate for Y, even further experimental validation revealed that this only fulfils part of the role. Furthermore, gene X has subsequently been proposed to reflect TOC1 modification or protein binding.

Small-scale network analysis has also been instrumental in advancing our knowledge on how plant cells process hormonal signals. In Li et al. (2006), the authors considered the role of abscisic acid signaling in the control of stomatal closure. After collecting biochemical, genetic, and pharmacological data, the authors built an interaction network involving more than 40 elements to model abscisic acid–dependent stomatal closure. In the absence of quantitative information on the pathway, such as the relative timings of the activity of these elements, they chose a Boolean model with asynchronous update (see above) based on randomly chosen relative timings. Simulations with 10,000 random initial states were performed, from which probabilities of stomatal closure at a given time were estimated. Similar simulations were also performed in situations mimicking known mutations. From these, the authors predicted the most crucial elements of the network, in terms of the effect that the removal of an element (i.e., an in silico mutation) has on the typical time to reach steady state or on the sensitivity of the network’s response. These predictions were consistent with experimental observations on the mutants from the literature, thus confirming the predictive value of the model.

Several groups have also independently built models of auxin signaling and response. Middleton et al. (2010) developed the first such model; above we described how it was built (Figure 2A). The model can generate qualitative predictions about how this network might respond to changes in exogenous auxin and help explain why the transcriptional response of Aux/IAA genes to auxin treatment can vary from family member to family member (Abel et al., 1995). In particular, the data of Abel et al. (1995) indicate that, depending on the family member, an Aux/IAA gene will make one of three distinct types of response to treatment with exogenous auxin. First, over relatively short treatments (namely 8 h), Aux/IAA transcript levels can rise gradually and reach a steady state level. Second, transcript levels rise to reach a peak and then decrease to an upregulated steady state level. In this case, we say the system overshoots the steady state. Third, expression levels peak as before but now decrease back to their initial untreated levels. The model can account for the first two types of behavior, which reflect different parameter regimes of the model. However, the third type of Aux/IAA transcription behavior in response to auxin could not be observed in the model. This indicates that (in this case) additional regulatory mechanisms must be at work. Biologically, such parameter regimes could result from interactions of different Aux/IAAs and ARFs, for which a significant diversity of biochemical properties (i.e., association and dissociation rates) are expected. Notably, Aux/IAA proteins can have quite distinct half-lives and binding affinities (Dreher et al., 2006; Calderón Villalobos et al., 2012). It is important to note that these changes in Aux/IAA mRNA are observed in the model even though intracellular auxin levels are predicted to rapidly increase and reach equilibrium. In other words, just because the gene expression levels are changing in time, it does not mean that auxin levels are. Furthermore, it was also found that the network could generate oscillations in Aux/IAA mRNA levels, even though free auxin levels are predicted to be more or less constant. Interestingly, oscillations of the DR5 auxin-inducible reporter have been observed in the root basal meristem and are thought to regulate the initiation of lateral roots (De Smet et al., 2007). Although it was proposed that the DR5 oscillations might be under the control of an auxin-independent clock mechanism (Moreno-Risueno et al., 2010), these simulations also open the possibility that they might result in part from the Aux/IAA feedback loop itself.

Vernoux et al. (2011) explored this pathway further by first obtaining a near-complete Aux/IAA-ARF interactome (there are 29 Aux/IAAs and 23 ARFs). In particular, unlike Middleton et al. (2010), the authors included repressor ARFs in their model. Using a graph clustering technique (illustrated in Figure 2B), they show that the Aux/IAA, activator ARF, and repressor ARF correspond to three classes having a specific structure of interaction profiles: Aux/IAA interact with themselves and with activator ARF; activator ARF interacts with Aux/IAA; and repressor ARFs have very limited interactions. This analysis of the topology of the Aux/IAA-ARF network can be viewed as a top-down approach for generating a small network. The authors incorporated this information into their ODE model. In particular, it should be noted that the repressor ARF do not interact with the other proteins (as suggested by the interactome; Figure 2B) but rather compete with the activator ARF for the ARF binding sites in the promoter of the auxin-inducible gene. In contrast with the model of Middleton et al. (2010), the model by Vernoux et al. (2011) can only reproduce the first type of behavior described above, an Aux/IAA transcriptional response rising gradually to steady state with no overshoot. However, as already noted, a key difference between the models is that the latter implicitly assumes that the auxin perception pathway is quasi-steady, which could explain the discrepancy. The work of Vernoux et al. (2011) is discussed further below.

The GA signaling network is similar to that of auxin, in that bioactive GAs act by targeting the degradation of a repressor protein (namely, members of the DELLA family). DELLA proteins mediate the transcriptional regulation of genes encoding GA biosynthesis enzymes (GA20-oxidase and GA3-oxidase) and the GA receptors (GA INSENSITIVE DWARF1 (GID1); among others). This naturally leads to a rather complex gene network, comprising several negative feedback loops. In Middleton et al. (2012), the authors took the approach of parameterizing the model using both published and new data sets. In particular, they used quantitative time-course data on almost every aspect of the network, including the signal transduction pathway (whereby GA binds to its receptor, GID1), the biosynthesis pathway (GA precursors are converted into the bioactive form via multiple enzyme-substrate reactions), and transcriptional responses to GA treatment. By doing so, they were able to constrain the model parameters according to the data. This can be thought of as a form of model calibration: It can ensure that the model can quantitatively reproduce the behavior of the system that has already been observed experimentally. However, as noted before, the fitting process does not necessarily lead to a unique estimate for a parameter. In the case of the GA-signaling network, Middleton et al. found that the parameter sets obtained from each of their best fits generated similar qualitative predictions. In this way, the authors were able to explore how the different feedback loops modulated the sensitivity of a cell to changes in GA.

Small-Scale Networks Underlying Cell Autonomous Tissue Patterning

The models discussed above are all single-cell ones, in that spatial aspects are ignored. Nevertheless, in certain circumstances, single cell models can also be used to bring insight to the spatial patterns observed.

The first scenario is where the model has multiple stable steady states corresponding to different cell fates. This has been applied to the regulation of flower morphogenesis in Arabidopsis (Mendoza et al., 1998, 1999; Espinosa-Soto et al., 2004; Alvarez-Buylla et al., 2008; Sánchez-Corrales et al., 2010). Here, Boolean network–based models were developed based on published data. In the models, good agreement was obtained between the steady states of the models and the experimentally observed gene expression patterns (this being the case for both wild-type and mutant plants). In doing so, they were led to hypothesize new regulations, which thus improved the knowledge of this system. Since a Boolean approach was used, a relatively high number of genes (around 15) could be studied. However, more recently, an ODE-based model (van Mourik et al., 2010) of floral specification has been developed. The model reproduced known mutant behaviors for several mutations but also predicted new phenotypic effects of mutations yet to be tested.

Along similar ideas, La Rota et al. (2011) collected data on the genes known to be important for floral development, including known interactions and experimentally observed expression patterns. These data were used to build a model for the specification of sepal polarity, where cells differentiate into abaxial and adaxial tissue types. Starting with 48 genes, they were able to reduce the system to 21 variables. Using a Boolean model, they were able to estimate the parameter values for which the steady states of their model were in good agreement with gene expression patterns in emerging sepals. This estimation led to the prediction of three novel pathways involving HOMEODOMAIN LEUCINE ZIPPER II, ARGONAUTE, and cytokinin-related genes, which can serve as a guide for future experimental investigations.

Another type of scenario where single-cell models can be used in the study of spatial patterning is where the expression patterns of particular network components are hard-coded into the model (rather than being emergent properties of it). This can be achieved by choosing model parameters to depend on space. An example of this can be found in Vernoux et al. (2011), already discussed above. Here, the authors used in situ hybridization to show a differential expression pattern of the ARF genes between the center and the periphery of the shoot apical meristem (SAM). Parameters representing ARF production were chosen to capture this observation in the model, namely, by considering low and high production of ARFs as representative of the SAM center and periphery, respectively. Mathematical analysis and numerical simulations indicated that differential expression of activator and repressor ARFs cause variations in the sensitivity of a cell’s transcriptional responses to auxin. In particular, it was found that there is low sensitivity to auxin in the center, while a high sensitivity is expected at the periphery. Their results further suggested that in these two domains, the coexpression of activator and repressor ARFs provide cells with the ability to buffer gene expression against fluctuations in auxin. This view was confirmed after comparing the spatio-temporal patterns of the DII-Venus auxin sensor (Brunoud et al., 2012) in the SAM with that of the DR5 auxin-inducible reporter (which gives information on the transcriptional response to auxin; Sabatini et al., 1999). This indicated that the ARF prepattern might explain (at least in part) why auxin can only induce organ formation at the periphery of the SAM. Another example of using small scale networks to understand cell-autonomous patterning is provided by Band et al. (2012b), wherein the GA signaling network model of Middleton et al. (2012) was embedded in a multicellular model of the root. This allowed the authors to explore how the various components are affected as the cells in the root elongate and hormone concentration levels dilute; this is discussed further by Band et al. (2012a).

Small-Scale Networks to Understand Intercellular Signaling and Signal Distribution in Tissues

In the previous section, we discussed how gene network models can be used to explore tissue patterning problems, even if the spatial aspect of the problem is not explicitly included in the model. This type of approach is particularly relevant when intercellular communication does not greatly affect the behavior of the networks (so that, in effect, cells respond autonomously). However, intercellular communication can be essential in plant patterning and can sometimes strongly influence the behavior of a given network. We discuss examples of this below.

In Savage et al. (2008), the authors used a Boolean framework to explore the regulatory mechanisms underlying trichoblast and atrichoblast patterning in Arabidopsis root epidermis. To do this, they developed two competing network models in which CAPRICE (CPC), WEREWOLF (WER), and GLABRA3 (GL3) interact to regulate the patterning process. The first proposed mechanism involves a self-activation feedback loop for activation of WER, whereas the second corresponds to a mutual support mechanism where CPC inhibits WER and only intercellular movement of CPC can relieve this inhibition. Since intercellular communication was a crucial aspect of the biology, both network models were embedded in a multicellular geometry. These two networks and how their behaviors are impacted by the inclusion of intercellular communication are illustrated in Figure 4. From their simulations, the authors were able to design an experiment that could distinguish between the two mechanisms. Based on this, they were able to rule out the existence of WER self-activation in favor of the mutual support mechanism.

Another example can be found in the study of the maintenance of the stem cell niche in the SAM. A negative feedback loop between the WUSCHEL (WUS) transcription factor and the CLAVATA3 (CLV3) peptide regulates the size of the stem cell niche. Several groups have described the dynamics of this system by means of ODE-based models, both in wild-type and mutant plants. In the first such model, Jönsson et al. (2005) showed that a simple ODE-based model was able to robustly reproduce the sharp WUS expression domain. Here, the authors included a purely hypothetical repressing signal diffusing from the L1 layer, and a reaction-diffusion mechanism could activate the WUS gene. Models of this process have since increased in sophistication as new biological data have become available. In particular, the interplay between experimental approaches and modeling has provided strong support for the idea that cytokinin signaling is crucial for the positioning and regulation of the size of the WUS and CLV3 domains in the SAM (Gordon et al., 2009; Hohm et al., 2010; Yadav et al., 2011; Chickarmane et al., 2012). Here, cytokinin signaling is involved in the activation of WUS expression (Gordon et al., 2009). Furthermore, movement of WUS and repression of cytokinin biosynthesis by WUS could establish a cytokinin gradient that in turn determines the position of WUS domain (Yadav et al., 2011). The repressing signal diffusing from the L1 predicted by Jönsson et al. (2005) would thus rather be a gradient of an activator resulting from WUS movement.

Auxin also functions as a key intercellular signal and is actively transported between cells. Modeling has been used mainly to explore possible mechanisms explaining the dynamic properties of polar auxin transport in tissues. This has been covered in several reviews already (Garnett et al., 2010; Santos et al., 2010), and we will not discuss it here in detail. One of the major limitations in testing the predictions of the auxin transport models has been the absence of reliable tools to follow the spatio-temporal dynamics of auxin distribution in tissues. Recently, Band et al. (2012c) were able combine the use of a novel auxin sensor, DII-Venus, with a mathematical model to quantify auxin levels in tissues. DII-Venus is composed of the auxin binding domain of the Aux/IAA28 protein fused to a fast-maturing variant of yellow fluorescent protein, Venus. To quantify this, the authors simplified the model by Middleton et al. (2010), taking into account the fact that the protein is expressed under a constitutively active promoter and not acting as a repressor of gene transcription. Excellent agreement between the model and high-resolution, time-resolved, auxin dose–response data were obtained. Using the model, the authors were able to infer relative levels of endogenous auxin from the level of DII florescence. The authors next applied this model to study the role of auxin in gravitropism. Here, auxin is thought to be redistributed to the lower half of the root. By taking this into account, the authors were able to infer from the dynamics that roots use a tipping point mechanism that operates to reverse the asymmetric auxin flow at the midpoint of root bending (Band et al., 2012a). It is likely that this combination of modeling and experimental approaches can be extended to study auxin transport in other organs and will provide further key insight into the mechanisms regulating auxin distribution during developmental processes.

CONCLUSIONS AND FUTURE CHALLENGES

We discussed why, in many cases, it is productive to focus on small networks and outlined a number of examples where this approach has given significant biological insight (where small is beautiful). However, these successes inevitably lead to a drive to include further complexity in the modeling framework, the number of system components, both in terms of genes, proteins, and their interactions, but also in different cell types and spatial contexts.

Moving beyond deterministic models, such as those we have discussed, will be one of the challenges faced by the systems biology field. It can be done notably using stochastic models taking into account the inherent noise occurring in biological systems. Increasing evidence suggests that transcriptional noise can have a major impact on gene network behavior, in particular at the single-cell level (Raj and van Oudenaarden, 2008; Eldar and Elowitz, 2010). As stochastic models are of a quantitative essence, their development requires advanced knowledge of systems under consideration and their study incurs a significant computational overhead. A notable recent example showed that stochasticity is a plausible explanation for several experimental observations on circadian oscillations at the cell population level (Guerriero et al., 2012). As the understanding of other regulatory systems in plants increases, the constant evolution in computational capacities should allow more in-depth exploration of how much additional knowledge can be gained from stochastic models.

In parallel, a long-term trend to ever larger networks is evident and is raising the question of the number of network components that need to be considered. The answer to this is context dependent, but it is important to recall that simply increasing the number of components in a network does not automatically produce models that yield more information on the system dynamics. As discussed earlier, in some cases, sets of genes and gene families can be subdivided into subsets with similar functionality to derive simplified models that still capture the system dynamics with sufficient accuracy.

Constructing models for larger networks will likely rely on coupling several small gene network models corresponding to specific modules, such as the auxin, cytokinin, and GA signaling pathways. This modularity offers the possibility to parameterize submodels in isolation (which reduces the complexity of parameter estimation), before combining models together. A challenge for the community is to effectively share parameterized models in a way that allows them to be connected together. Considerable progress in this regard is being made for nonspatial models via tools such as SBML (Hucka et al., 2003), CellML (Cuellar et al., 2003), and the BioModels database (Li et al., 2010), but there is an ongoing challenge to do this in a spatial context. Another major challenge for the systems biology community is indeed to develop efficient multiscale modeling approaches that allow integrating these models. This should help us understand the emergent properties of the biological system at the different scales. This requires building models that allow realistic simulations of growth and development. The foundations of such approaches are being established in plants, thanks to recent image analysis techniques that allow building realistic computer representations of three-dimensional plant tissues (Fernandez et al., 2010). For further details, we refer the reader to the review by Band et al. (2012a) in this issue.

However, it is important to stress that at present the extent to which large-scale networks can be studied by dividing them into modules and reassembling them remains to be fully understood, in plants or, in fact, any organism. Even in traditional biology, understanding a system by studying its parts independently is a hypothesis upon which many studies are based. Gene regulatory networks for the processes we have discussed have all been studied in a modular fashion. In reality there will be a degree of crosstalk between them. For example, the circadian clock and auxin signaling are traditionally studied independently, even though there is known to be interplay between the two (Covington and Harmer, 2007). Very few examples of small-scale plant networks have been studied beyond the initial stages of modeling, and subjected to experimental validation, with the most notable exception of the circadian network we have discussed. Despite the obvious success obtained using small-network modeling, a full evaluation of this approach for gene network analysis will not be possible until a number of such small modules have been studied in depth and coupled to test their predictive value.

Testing model prediction requires the continuous production of relevant quantitative biological data. This is a major challenge for biologists, but constant innovations (Ehrhardt and Frommer, 2012) are opening fantastic opportunities for plant scientists. In particular, these will likely make it possible (in the near future) to follow in vivo a variety of variables at different scales, from the subcellular scale to entire plants. For gene regulatory networks, progress in live imaging techniques should make it feasible to follow dynamically a significant number of the variables in small networks. Models will be essential in highlighting which are the most important variables to focus on, at least in the first steps of an analysis.

The spatial organization of plants presents additional challenges in the use of small-scale networks. As we have seen, cells in different locations may have different functional networks (due to expression of different network components). To date, much of the work on model parameterization has relied on data from whole plants, or at least whole tissues, but the anticipated progress in experimental innovations means that in the future we should consider that parameters or the networks themselves differ in different cells.

Even for small-scale networks, it is likely that not all the interactions will be known. In this case, one approach is to generate a selection of mechanisms that account for existing experimental observations. Mathematical models can then be used to generate predictions based on the different mechanisms and therefore suggest further experiments that help to distinguish between them. The simplest case is where an experiment can be designed so that two competing mechanisms generate qualitatively distinct outputs (this being the case in Savage et al. [2008], as discussed above). However, competing mechanisms may only generate quantitatively (but not qualitatively) different outputs. In this case, more sophisticated techniques are required to distinguish between the models based on the data. At present, statistical tools exist or are in development to address this (see Toni and Stumpf, 2010; Toni et al., 2012). In turn, however, these will challenge the experimental community to produce additional data that help justify model extensions on rigorous grounds. Such statistical approaches should also allow prior knowledge (not necessarily quantitative) to be built in.

Finally, we draw attention to what was, and still is, a major challenge for the future of systems biology (that we hope this review helps to address), namely, that of training plant scientists with the skills to engage with mathematical model development and analysis. The scope of small-scale networks is ideal in this context; the models presented here, and others of similar complexity, represent exemplars of modeling and model analysis that are possible to study without the use of heavy mathematics or intensive computation. Furthermore, they illustrate the kinds of phenomena (like steady states, stability, and bifurcations) that should become familiar to the plant science community, so that when, inevitably, larger scale models are used, we do not simply simulate them in a blind fashion. In addition, the plant science community has been particularly active in promoting training in mathematical modeling for life scientists, and funding bodies are increasingly demanding that postgraduate training in life sciences include some element of mathematical modeling and systems approaches. Ultimately, it is hoped that systems approaches become strongly embedded in our fundamental approach to practicing plant science.