Fragment-based quantum mechanical methods for periodic systems with Ewald summation and mean image charge convention for long-range electrostatic interactions

Abstract

We describe an Ewald-summation method to incorporate long-range electrostatic interactions into fragment-based electronic structure methods for periodic systems. The present method is an extension of the particle-mesh Ewald technique for combined quantum mechanical and molecular mechanical (QM/MM) calculations, and it has been implemented into the explicit polarization (X-Pol) potential to illustrate the computational details. As in the QM/MM-Ewald method, the X-Pol-Ewald approach is a linear-scaling electrostatic method, in which the short-range electrostatic interactions are determined explicitly in real space and the long-range Ewald pair potential is incorporated into the Fock matrix as a correction. To avoid the time-consuming Fock matrix update during the self-consistent field procedure, a mean image charge (MIC) approximation is introduced, in which the running average with a user-chosen correlation time is used to represent the long-range electrostatic correction as an average effect. Test simulations on liquid water show that the present X-Pol-Ewald method takes about 25% more CPU time than the usual X-Pol method using spherical cutoff, whereas the use of the MIC approximation reduces the extra costs for long-range electrostatic interactions by 15%. The present X-Pol-Ewald method provides a general procedure for incorporating long-range electrostatic effects into fragment-based electronic structure methods for treating biomolecular and condensed-phase systems under periodic boundary conditions.

1. Introduction

The explicit polarization (X-Pol) theory^1–6 is a fragment-based quantum mechanical method using block localization of molecular orbitals (BLMO) in wave function theory^7–9 or block localization of Kohn–Sham (BLKS) orbitals in density function theory.^10,11 X-Pol can be used as a next-generation force field for statistical mechanical Monte Carlo and molecular dynamics simulations of condensed-phase and biomolecular systems with electronic structure theory as the fundamental framework.^1–6 In X-Pol, a biopolymer is divided into molecular blocks that are also called fragments; each fragment can be a single solvent molecule, an amino acid unit, a nucleotide, or a group of these entities. The electron density or electronic wave function of each molecular fragment is optimized in the presence of the instantaneous electric field of the rest of the system.^1,4 Many-body polarization effects are treated explicitly by electronic structure calculations that couple all the fragments of the system. The feasibility of using such a quantum mechanical force field has been demonstrated for computer simulations of liquids^2,12 and solvated proteins.⁵

A crucial component in dynamics simulation of polar solutions such as biopolymers in aqueous solution is the treatment of long-range electrostatic interactions,^13–16 and this has been facilitated by the development of efficient linear-scaling particle-mesh Ewald (PME) techniques,^17–22 which greatly enhanced the stability of long-time dynamics trajectories and the accuracy of computational results.^23–26 The importance of including long-range electrostatic interactions in dynamics simulations has been demonstrated in numerous applications, and interested readers are directed to some of the original studies.^{18,19,27–32} The original PME method of Darden and coworkers,^17–19 designed for molecular mechanics force fields, has been incorporated into combined quantum mechanical and molecular mechanical (QM/MM) potentials.³³ In this article, we describe a further extension of the QM/MM-PME technique to the fully quantum mechanical X-Pol potential for condensed-phase simulations.

In the past decade, a number of fragment-based methods have been developed,³⁴ and we will comment on only a few of them. Zhang and coworkers developed a molecular fractionation with conjugated caps (MFCC) approach to treat proteins and protein–ligand interactions.^35,36 In this method, the individual fragments are capped with a structure representative of the local functional group of the original system, and the total energy is obtained by subtracting the energies of the common fragments used in the “caps”. The method provides a way to evaluate interfragment interactions and a straightforward procedure to incorporate the local electronic structure into a fragment-based molecular orbital approach.^37,38 Another way of separating the total energy into fragmental contributions is the general interaction energy expansion approach described by Stoll and Preuss.³⁹ The key to achieving fast convergence in this method, in contrast to early schemes,⁴⁰ is to optimize the monomer, dimer, and many-body fragment molecular orbitals in the presence of all other fragments, rather than using gas-phase fragments. There are a number of similar strategies, including the fragment molecular orbital (FMO) method^41,42 and the electrostatically embedded many-body (EE-MB) expansion method.^43–46 The double SCF procedure used in the FMO model^41,42 is identical to that developed in the earlier X-Pol method,^1–3 whereas two-body or three-body exchange and charge transfer corrections are added in the FMO2 or FMO3 implementation.³⁹ Although fragment-based methods have been applied to large systems, it appears that none of the previous biological applications have included long-range electrostatic effects.

The present paper describes an efficient linear-scaling Ewald method for incorporating long-range electrostatic interactions into the X-Pol theory. The present model is an extension of a method developed for combined QM/MM-Ewald simulations,³³ and it can be applied to any fragment-based model to treat long-range electrostatic effects in condensed-phase and biomolecular systems. As the original QM/MM-Ewald method,³³ the present X-Pol-Ewald approach is not restricted to using a specific QM method in the fragment model, and the QM method can be ab initio or semiempirical molecular orbital theory or density functional theory. Electronic structure methods that incorporate the Ewald potential in integral evaluations are available,^47,48 and embedding schemes based on multipole expansions or the use of Madelung constant have been reported.^49–54 The present approach avoids the direct calculation of electronic integrals with the Ewald potential. The aim of this article is to present the theoretical and computational algorithm for including long-range electrostatic forces into fragment-based quantum mechanical methods, and studies of the properties of liquids and biomacromolecular systems will be reported in future publications.

In the following we first introduce the theoretical background for the QM/MM-Ewald method. Then, we present the theory and computational details for the present X-Pol-Ewald approach. Next, we illustrate the performance of the X-Pol-Ewald method and discuss ways of achieving efficiency. Finally, the paper concludes with a summary of the main findings and highlights directions of future research.

2. Method

We first briefly summarize the Ewald summation techniques used with classical force fields. Then, we present the X-Pol Hamiltonian as a general fragment-based quantum mechanical approach for periodic systems including long-range electrostatic interactions. Next, we describe the procedure used in combined QM/MM-Ewald calculations, presented in the context of the X-Pol method. Finally, we highlight the extension of the QM/MM-Ewald method to the X-Pol potential. Throughout this paper, we use the same notations as used ref. 33 for convenience of the reader.

2.1. The Ewald summation method

The electrostatic energy for a periodic system, consisting of N particles with point charges {q_i; i = 1, ⋯, N} at positions {r_i; i = 1, ⋯, N} in a unit cell, can be evaluated using the Ewald lattice sum technique:^13,14,17

$$U_{\text{elec}}=\frac{1}{2}{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}{q}_i{q}_j{\mathrm{\Phi }}_{\mathrm{E}}({\mathbf{r}}_{\mathit{\text{ij}}})$$ (1)

where r_ij = r_i − r_j, and Φ_E(r_ij) is the Ewald pair potential, which is split into short-range and long-range sums, both rapidly converging:

$${\mathrm{\Phi }}_{\mathrm{E}}({\mathbf{r}}_{\mathit{\text{ij}}})={\mathrm{\Phi }}_{\text{SE}}({\mathbf{r}}_{\mathit{\text{ij}}})+{\mathrm{\Phi }}_{\text{LE}}({\mathbf{r}}_{\mathit{\text{ij}}})$$ (2)

The long-range Ewald (LE) pair potential (also called reciprocal or “k-space” pair potential) can be determined using the Fourier series:

$${\mathrm{\Phi }}_{\text{LE}}({\mathbf{r}}_{\mathit{\text{ij}}})=\frac{4\pi }{V}{\displaystyle \sum _{|\mathbf{k}|\ne 0}^{\mathrm{\infty }}}\frac{e^{-k^2/4{\kappa }^2}}{k^2}\text{cos}(\mathbf{k}·{\mathbf{r}}_{\mathit{\text{ij}}})$$ (3)

where k = 2πn with n summing over all integer translations, (n₁, n₂, n₃), of the reciprocal lattice n = n₁b₁ + n₂b₂ + n₃b₃. The reciprocal space vectors are related to the real space vectors {a₁, a₂, a₃} by {b_i·a_j = δ_ij;i,j = 1,2,3}, and V is the volume of the unit cell.

The short-range Ewald (SE) pair potential (or real-space potential) is given by

$${\mathrm{\Phi }}_{\text{SE}}({\mathbf{r}}_{\mathit{\text{ij}}})={\displaystyle \sum _{\mathbf{n}=0}^{\mathrm{\infty }}}\prime \frac{\mathit{\text{erfc}}(\kappa |{\mathbf{r}}_{\mathit{\text{ij}}}+\mathbf{n}|)}{|{\mathbf{r}}_{\mathit{\text{ij}}}+\mathbf{n}|}-\frac{2\kappa }{\sqrt{\pi }}{\delta }_{\mathit{\text{ij}}}\approx \frac{(1-{\delta }_{\mathit{\text{ij}}})\mathit{\text{erfc}}(\kappa |{\mathbf{r}}_{\mathit{\text{ij}}}|)}{|{\mathbf{r}}_{\mathit{\text{ij}}}|}-\frac{2\kappa }{\sqrt{\pi }}{\delta }_{\mathit{\text{ij}}}$$ (4)

where the prime on the summation indicates that self-interaction in the primary unit cell, i.e., the r_ii term with n = 0, is ignored, erfc(r) is the complementary error function defined as erfc(r) = 1 − erf(r),⁵⁵ which rapidly decays to zero as r increases, and the second term $2\kappa /\sqrt{\pi }$ is the self-interaction energy.^13,14 In eqn (3) and (4), the parameter κ is introduced to adjust the relative rates of convergence of the two summations; it is typically chosen in such a way that only the primary unit cell (n = 0 term) is retained in the real-space sum (eqn (4)).¹⁷ The total energy is independent of the choice of κ as long as both summations are converged. Efficient Ewald sum algorithms have been designed such that the Ewald pair potential is pre-computed on a grid,^16,17,19,56 which allows for rapid evaluation through multidimensional interpolation procedures.

A surface energy term, which arises from the |k| = 0 term in the reciprocal sum, should be included if the unit cell has a non-vanishing dipole moment.¹⁴ In practice, the surface energy has little effect on dynamics trajectories⁵⁷ and is neglected in most simulations employing the so-called tin-foil boundary conditions.^13,14,26

2.2. The X-Pol Hamiltonian for periodic systems

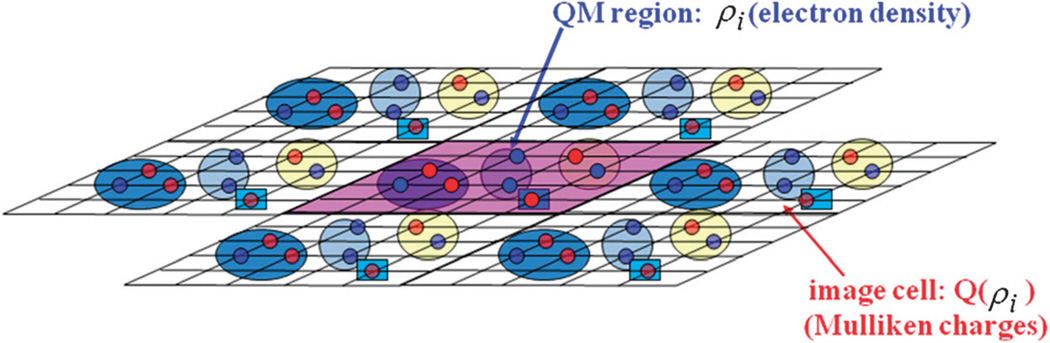
The X-Pol method for systems with the nearest image convention in which the interactions between different fragments are treated using spherical truncation at a cutoff distance has been described previously.^2,5,12 Here, we consider interfragment interactions that extend to the entire periodic system over all lattice vectors. Let M be the number of molecular fragments, and ρ_I(r) be the charge distribution of fragment I, including both the smooth electron density and the core nuclear charges, where I = 1, ⋯, M (Fig. 1). The effective X-Pol Hamiltonian per unit cell for the periodic system is

$$Ĥ={\displaystyle \sum _I^M}{Ĥ}_I+\frac{1}{2}{\displaystyle \sum _I^M}{\displaystyle \sum _{J\ne I}^M}{Ĥ}_{\mathit{\text{IJ}}}^{\text{int}}+E^{\text{XD}}$$ (5)

where Ĥ_I is the electronic Hamiltonian of fragment I which includes the interactions with its own periodic images, Ĥ_IJ represents the interactions between fragments I and J and their images, and E^XD is the sum of the exchange-dispersion (XD) interaction energies of all fragments; E^XD is computed empirically in the present implementation.^1–3,6 (Methods for computing long-range E^XD have been well-established² and will not be further discussed in this paper.) The interaction Hamiltonian between fragment I and the rest of the periodic system depends on both electronic and nuclear degrees of freedom, and it can be expressed as follows:

$${Ĥ}_{\mathit{\text{IJ}}}^{\text{int}}=-{\displaystyle \sum _{i=1}^{N_I}}{\displaystyle \int }d{\mathbf{r}}_J{\mathrm{\Phi }}_{\mathrm{E}}[{\mathbf{r}}_{\mathit{\text{Ji}}}]{\rho }_J({\mathbf{r}}_J)+{\displaystyle \sum _{\alpha =1}^{A_I}}{Z}_{\alpha }^I{\displaystyle \int }d{\mathbf{r}}_J{\mathrm{\Phi }}_{\mathrm{E}}[{\mathbf{R}}_{J\alpha }]{\rho }_J({\mathbf{r}}_J)$$ (6)

where N_I and A_I are, respectively, the number of electrons and nuclei of fragment I, $Z_{\alpha }^I$ is the nuclear charge of atom α at ${\mathbf{R}}_{\alpha }^I$, and Φ_E[r_Jx] is the Ewald pair potential.

Fig. 1.

Schematic depiction of the X-Pol-Ewald method. Fragments in the primary unit cell are explicitly treated by a quantum mechanical model specified with a smooth charge density ρ_i, whereas their periodic images are represented by the partial atomic charges derived from the corresponding charge density. In the present study, Mulliken population charges are used to approximate the image charges. Each fragment is specified by a circle or box and all fragments (molecules) in the system are treated by electronic structure theory.

The total X-Pol energy for the periodic system can be written as follows:

$$E=\langle {\mathrm{\Psi }}_{\text{XPol}}|\mathrm{H̑}|{\mathrm{\Psi }}_{\text{XPol}}\rangle ={\displaystyle \sum _I^M}{E}_I^{\text{Ew}}[{\rho }_I,{\rho }_I]+\frac{1}{2}{\displaystyle \sum _I^M}{\displaystyle \sum _{J\ne I}^M}{E}_{\mathit{\text{IJ}}}^{\mathrm{E}w,\text{int}}[{\rho }_I,{\rho }_J]+E^{\text{XD}}$$ (7)

where Ψ_XPol is the total X-Pol wave function of the periodic system in the unit cell, $E_I^{\mathit{\text{Ew}}}[{\rho }_I,{\rho }_I]$ is the energy of fragment I plus the interactions with its own images (emphasized by the superscript Ew for including the corresponding Ewald potential), and $E_{\mathit{\text{IJ}}}^{\mathit{\text{Ew}},\text{int}}[{\rho }_I,{\rho }_J]$ is the interaction between fragments I and J under periodic boundary conditions. In eqn (7), we have used the notation introduced by Nam et al.,³³ in which E[A,B] denotes the electrostatic interaction energy between two generalized charge distributions evaluated either directly in real space or under periodic boundary conditions with the Ewald sum.

In X-Pol, the Coulomb interactions between two quantum mechanical fragments I and J are not directly computed by evaluating the corresponding two-electron integrals (except when the nearest buffer residues are used in a polypeptide chain),^58,59 but they are determined by one-electron integrals using the electrostatic potential due to atomic partial charges on the second fragment (J).^1,2,4,6 This corresponds to the Level 2 approximation in the X-Pol theory.⁶ The atomic partial charges, Q_J(ρ_J), are obtained to best represent the electrostatic potential of the instantaneous charge density (wave function) of fragment J.^1,2 This approximation greatly reduces the computational costs without sacrificing accuracy. Therefore, the X-Pol energy in eqn (7) is given as follows, replacing the smooth densities by partial atomic charges for interfragment interactions:

$$E={\displaystyle \sum _I^M}{E}_I^{\text{Ew}}[{\rho }_I,{\mathbf{Q}}_I]+\frac{1}{2}{\displaystyle \sum _I^M}{\displaystyle \sum _{J\ne I}^M}{E}_{\mathit{\text{IJ}}}^{\text{Ew},\text{int}}[{\rho }_I,{\mathbf{Q}}_J]+E^{\text{XD}}$$ (8)

where Q_J = Q_J(ρ_J) is a column vector of atomic partial charges on fragment J, derived from the instantaneous electron density ρ_J. In eqn (8), $E_{\mathit{\text{IJ}}}^{\mathit{\text{Ew}},\text{int}}[{\rho }_I,{\mathbf{Q}}_J]$ is defined as follows, which is a one-electron integral in electronic structure theory:

$$E_{\mathit{\text{IJ}}}^{\text{Ew},\text{int}}[{\rho }_I,Q_J]={\displaystyle \int }d{\mathbf{r}}_i{\rho }_I({\mathbf{r}}_i)\{{\displaystyle \sum _{\beta =1}^{A_J}}{\mathrm{\Phi }}_{\mathrm{E}}({\mathbf{r}}_{\beta i})Q_{\beta }^J\}$$ (9)

Notice that the expression in parentheses is the electrostatic potential at r_i due to the rest of the periodic system;² this corresponds to the standard set of QM/MM interactions in that approach.^33,60,61

Although the electronic structure of each fragment can be determined by the double self-consistent field (DSCF) method,^1–5 eqn (8) is not computationally efficient because one has to evaluate the electronic integrals involving the Ewald pair potential in the effective Hamiltonian (eqn (6)). On the other hand, the calculation of the X-Pol energy in “real space” without the image potentials is straightforward and has already been implemented and shown to be computationally efficient.^2,4–6,12 The same observation was also made in the development of the combined QM/MM-Ewald method.³³ Following this strategy,³³ we re-write eqn (8) as

$$E={\displaystyle \sum _I^M}{E}_I^{\text{RS}}[{\rho }_I]+{\displaystyle \sum _I^M}\{E_I^{\text{Ew}}[{\rho }_I,{\mathbf{Q}}_I]-E_I^{\text{RS}}[{\rho }_I]\}++\frac{1}{2}{\displaystyle \sum _I^M}{\displaystyle \sum _{J\ne 1}^M}{E}_{\mathit{\text{IJ}}}^{\text{RS}}[{\rho }_I,{\mathbf{Q}}_J]+\frac{1}{2}{\displaystyle \sum _I^M}{\displaystyle \sum _{J\ne I}^M}\{E_{\mathit{\text{IJ}}}^{\text{Ew},\text{int}}[{\rho }_I,{\mathbf{Q}}_J]-E_{\mathit{\text{IJ}}}^{\text{RS}}[{\rho }_I,{\mathbf{Q}}_J]\}+E^{\text{XD}}$$ (10)

where the superscript RS is used to emphasize that the corresponding energy is computed in “real space” using the Coulomb potential in the primary unit cell, $E_I^{\text{RS}}[{\rho }_I]=\langle {\mathrm{\Psi }}_I|{\mathrm{H̑}}_I^O|{\mathrm{\Psi }}_I\rangle$ is the electronic energy of fragment I as determined by using the fully polarized fragment wave function (Ψ_I), including long-range electrostatic effects, and $E_{\mathit{\text{IJ}}}^{\text{RS}}[{\rho }_I,{\mathbf{Q}}_J]$ is the X-Pol interaction energy between fragments I and J in the primary unit cell. Notice that the quantities $E_I^{\text{RS}}[{\rho }_I]$ and $E_{\mathit{\text{IJ}}}^{\text{RS}}[{\rho }_I,{\mathbf{Q}}_J]$ are different from those computed using the short-range part of the Ewald pair potential Φ_SE(r_ij) in eqn (4) because Coulomb interactions in the RS calculation are not scaled by the complementary error function. We denote the sum of these two energy terms as the real-space X-Pol energy, and it has a formal expression that is identical to that of the X-Pol energy determined with a spherical cutoff^2,5 (but the energies are different here because the wave function used in eqn (11) is polarized with the inclusion of long-range electrostatic contributions):

$$E_{\mathit{\text{XPol}}}^{\text{RS}}={\displaystyle \sum _I^M}{E}_I^{\text{RS}}[{\rho }_I]+\frac{1}{2}{\displaystyle \sum _I^M}{\displaystyle \sum _{J\ne I}^M}{E}_{\mathit{\text{IJ}}}^{\text{RS}}[{\rho }_I,{\mathbf{Q}}_J]+E^{\text{XD}}$$ (11)

The two energy differences in eqn (10) represent the long-range electrostatic energy correction (LEC) to the real-space X-Pol energy (eqn (10)).³³ They include the interactions between the smooth electron distribution of fragment I, (I = 1, ⋯, M), and the partial atomic charges on its own images and on all other fragments; these mimic the electrostatic potentials of the corresponding “QM” charge distributions. For such a long-range type of potential correction, accounting for fragment pairs separated by distances of the order of, or longer than, a full unit cell, a fully classical charge representation of all fragments, rather than the smooth electron densities, would be sufficient (Fig. 1). Consequently, the Ewald-LEC terms can be approximated as follows:

$$\mathrm{\Delta }{E}_I^{\text{LEC},\text{image}}=E_I^{\text{Ew }}[{\rho }_I,{\mathbf{Q}}_I]-E_I^{\text{RS }}[{\rho }_I]\approx E_I^{\text{Ew }}[{\mathbf{Q}}_I,{\mathbf{Q}}_I]-E_I^{\text{RS}}[{\mathbf{Q}}_I]$$ (12)

$$\mathrm{\Delta }{E}_I^{\text{LEC},\text{int}}=\frac{1}{2}{\displaystyle \sum _{J\ne I}^M}\{E_{\mathit{\text{IJ}}}^{\text{Ew},\text{int}}[{\rho }_I,{\mathbf{Q}}_J]-E_{\mathit{\text{IJ}}}^{\text{RS}}[{\rho }_I,{\mathbf{Q}}_J]\}\approx \frac{1}{2}{\displaystyle \sum _{J\ne I}^M}\{E_{\mathit{\text{IJ}}}^{\text{Ew},\text{int}}[{\mathbf{Q}}_I,{\mathbf{Q}}_J]-E_{\mathit{\text{IJ}}}^{\text{RS}}[{\mathbf{Q}}_I,{\mathbf{Q}}_J]\}$$ (13)

With these discussions, we can now write the total X-Pol energy of eqn (10) with the full long-range electrostatic contributions as

$$E[\{\rho \}]=E_{\mathit{\text{XPol}}}^{\text{RS}}+{\displaystyle \sum _I^M}(\mathrm{\Delta }{E}_I^{\text{LEC},\text{image}}+\mathrm{\Delta }{E}_I^{\text{LEC},\text{int}})+E^{\text{XD}}$$ (14)

where we have used E[{ρ}] to emphasize that the X-Pol energy is a functional of the electron densities of all fragments. In eqn (14), we have also decomposed the LEC contributions to each fragment into a term due to its own images and a term originating from interactions with the images of all other fragments. This makes it convenient for comparison with the combined QM/MM-Ewald method.³³

2.3. Long-range electrostatic corrections to the Fock matrix

The elements of the effective Hamiltonian (Fock) matrix of fragment I in the X-Pol method incorporating long-range electrostatic effects are defined by eqn (15)

$$F_{\mu \nu }^I=\frac{\delta E[\{\rho \}]}{\delta P_{\mu \nu }^I}=F_{\mu \nu }^{I,\text{RS}}+\mathrm{\Delta }{F}_{\mu \nu }^{I,\text{LEC}}$$ (15)

where the first term, $F_{\mu \nu }^{I,\text{RS}}$, has an expression identical to that of the Fock matrix of the X-Pol method in the primary unit cell without including long-range electrostatic effects.^4,6

The correction term in eqn (15) consists of two components (from eqn (12) and (13), see also eqn (14)), which can be grouped together (see below), but it is informative to discuss them separately. The first component is the interaction between fragment I and its own periodic images, and it is given by³³

$$\mathrm{\Delta }{E}_I^{\text{LEC},\text{image}}=\frac{1}{2}{\displaystyle \sum _{\alpha =1}^{A_I}}{\displaystyle \sum _{\beta =1}^{A_I}}{Q}_{\alpha }^I\mathrm{\Delta }{\mathrm{\Phi }}_E({\mathbf{R}}_{\alpha \beta }^{I,I})Q_{\beta }^I$$ (16)

The long-range correction of the Ewald pair-potential, ΔΦ_E, has been derived previously in the combined QM/MM-Ewald method,³³ and is

$$\mathrm{\Delta }{\mathrm{\Phi }}_E({\mathbf{R}}_{\alpha \beta }^{I,I})=\frac{4\pi }{V}{\displaystyle \sum _{|\mathbf{k}|\ne 0}}\frac{e^{-k^2/4{\kappa }^2}}{k^2}\text{cos}[\mathbf{k}·{\mathbf{R}}_{\alpha \beta }^{I,I}]-\frac{\mathit{\text{erf}}(|{\mathbf{R}}_{\alpha \beta }^{I,I}|)}{|{\mathbf{R}}_{\alpha \beta }^{I,I}|}$$ (17)

and we have the Fock matrix correction due to self-images:

$$\frac{\delta \mathrm{\Delta }{E}_I^{\text{LEC},\text{image}}}{\delta P_{\mu \nu }^I}={\displaystyle \sum _{\alpha \in \mu ,\nu }}\frac{\delta Q_{\alpha }^I}{\delta P_{\mu \nu }^I}\left({\displaystyle \sum _{\beta =1}^{A_I}}\mathrm{\Delta }{\mathrm{\Phi }}_E({\mathbf{R}}_{\alpha \beta }^{I,I})Q_{\beta }^I\right)$$ (18)

In general, it is convenient to use a charge model that depends linearly on the one-particle density matrix to avoid complications in the charge derivatives and Fock matrix update.

As in the QM/MM-Ewald method,³³ the correction to the Fock matrix must be updated at every SCF iteration as the charge density ρ_I is being optimized. However, the computational cost is rather small since the potential can be precomputed and stored as an A_I × A_I matrix and the Fock matrix update involves simply a multiplication of the correction matrix of the Ewald correction potential with the charge vector Q_I. In the QM/MM method with a single QM fragment, this only needs to be done for the one QM fragment,³³ but in X-Pol, all fragments need to be updated. In practice, this suggests designing a parallel algorithm that distributes the fragments over processors.

The second correction term involves interactions among all “QM” fragments in X-Pol

$${\displaystyle \sum _I^M}\mathrm{\Delta }{E}_I^{\text{LEC},\text{int}}=\frac{1}{2}{\displaystyle \sum _I^M}{\displaystyle \sum _{\alpha =1}^{A_I}}{\displaystyle \sum _{J\ne I}^M}{\displaystyle \sum _{\beta =1}^{A_J}}{Q}_{\alpha }^I\mathrm{\Delta }{\mathrm{\Phi }}_E({\mathbf{R}}_{\alpha \beta }^{I,J})Q_{\beta }^J$$ (19)

and the Fock matrix correction for fragment I is given as

$$\frac{\delta \left({\displaystyle \sum _L^M}\mathrm{\Delta }{E}_L^{\text{LEC},\text{int}}\right)}{\delta P_{\mu \nu }^I}={\displaystyle \sum _{\alpha \in \mu ,\nu }}\frac{\delta Q_{\alpha }^I}{\delta P_{\mu \nu }^I}\left({\displaystyle \sum _{J\ne I}^M}{\displaystyle \sum _{\beta =1}^{A_J}}\mathrm{\Delta }{\mathrm{\Phi }}_E({\mathbf{R}}_{\alpha \beta }^{I,J})Q_{\beta }^J\right)$$ (20)

Note that the main difference between the present X-Pol-Ewald method and the combined QM/MM-Ewald³³ approach is in the variation of all surrounding charges for a given “QM” fragment. In QM/MM, the classical charges are fixed (i.e., $Q_{\beta }^J\equiv q_{\beta }^{\mathit{\text{MM}}}$), thereby the quantity in parentheses in eqn (20) is invariant during the SCF procedure. Since the charge densities, and therefore the partial atomic charges, of all fragments in X-Pol are mutually polarized and change during the SCF procedure, it is necessary to update the LEC term for each fragment based on the changes in all other fragments. As a result, in contrast to the combined QM/MM-Ewald method, there is no distinction between QM-QM (eqn (18)) and QM-MM (eqn (20)) interactions in the X-Pol-Ewald method. Consequently, eqn (18) can be included in eqn (20) with the restriction J ≠ I removed in the second summation:

$$\mathrm{\Delta }{F}_{\mu \nu }^{I,\text{LEC}}={\displaystyle \sum _{\alpha \in \mu ,\nu }}\frac{\delta Q_{\alpha }^I}{\delta P_{\mu \nu }^I}\left({\displaystyle \sum _{J=1}^M}{\displaystyle \sum _{\beta =1}^{A_J}}\mathrm{\Delta }{\mathrm{\Phi }}_E({\mathbf{R}}_{\alpha }^I,{\mathbf{R}}_{\beta }^J)Q_{\beta }^J\right)$$ (21)

Here, the Fock matrix update requires a matrix multiplication of the Ewald correction potential (ΔΦ_E) of dimensions N × N(i.e., all atoms, N = ∑A_I, in the unit cell) by the charge vector (Q). This would be a computational bottleneck for large systems, and in the next section, we discuss approximations to circumvent this high computation cost.

2.4. The mean image charge (MIC) approximation

Although the X-Pol-Ewald method of eqn (15) based on a Fock matrix correction for the long-range electrostatic contributions (LEC), is fast due to employing the PME method, it nevertheless is an order N² algorithm. As noted above, in the combined QM/MM-Ewald method,³³ the update of the LEC correction to the Fock matrix at each SCF iteration is needed for the QM fragment, but this does not pose computational difficulty because the matrix work is small in comparison to that involved in treating the rest of the MM system. The LEC corrections due to all MM charges just needs to be computed once at each dynamics step, and it is not required to update them during the SCF cycle. Consequently, the computational scaling for the QM/MM-Ewald method is essentially the same as the standard PME method for classical force fields. In X-Pol, however, all charges in the system vary during the SCF procedure, and hence an update of eqn (21) is required for all fragments, and this would be limiting for large systems.

Recall that “short-range” interactions within the primary unit cell, which have the dominant effects, are already explicitly and fully accounted for in the RS term, $F_{\mu \nu }^{I,\text{RS}}$, of eqn (15). The correction term, ${\mathrm{\Delta }F}_{\mu \nu }^{I,\text{LEC}}$, although important, represents a secondary effect on the polarization of the Ith fragment. Furthermore, since long-range electrostatic effects are at distances on the order of the length of a unit cell and beyond, the LEC correction on the polarization of the molecular wave function due to fluctuations of the atomic charges between MD steps is expected to be very small. This suggests that it is reasonable to use the fully converged partial atomic charges from the previous MD step to approximate the ${\mathrm{\Delta }F}_{\mu \nu }^{I,\text{LEC}}$ correction without updating during the SCF cycle. A generalization is to employ a running average of the partial atomic charges from the previous T simulation steps for this correction:

$${\mathrm{q̄}}_{\alpha }^I(t;\tau )=\frac{1}{T}{\displaystyle \sum _{s=t-\tau }^t}{Q}_{\alpha }^I(s)$$ (22)

where q̄_α^I(t;τ) is the running average of atomic charge on atom α of fragment I at time t over a period of τ, τ = T × τ₀ with τ₀ being the time step of the MD integration, which is 1 fs in the present study.

If the mean image charges (MIC), q̄(t;τ), are used to replace the instantaneous image charges in eqn (21) for the periodic system, which is equivalent to neglecting the very small variations of the average partial atomic charges from one step to the next during an MD simulation, i.e., $\delta \{{\mathrm{q̄}}_{\alpha }^I(t;\tau )\}/{\delta }_{P\mu \nu }^I\approx 0$, we obtain the following expression for the Ewald-LEC contribution to the Fock matrix at time t:

$$\mathrm{\Delta }{F}_{\mu \nu }^{I,\text{LEC}}(t)={\displaystyle \sum _{\alpha \in \mu ,\nu }}\frac{\delta Q_{\alpha }^I}{\delta P_{\mu \nu }^I}({\displaystyle \sum _{J=1}^M}{\displaystyle \sum _{\beta =1}^{A_J}}\mathrm{\Delta }{\mathrm{\Phi }}_E({\mathbf{R}}_{\alpha \beta }^{I,J}){\mathrm{q̄}}_{\beta }^J(t;\tau ))$$ (23)

Here, the corresponding Ewald correction for long-range electrostatic effects to the Fock matrix does not need to be updated during the SCF procedure, as in the QM/MM-Ewald method.³³ The physical interpretation of eqn (23) is that the long-range electrostatic correction (LEC) acts as a mean field that varies slowly with a correlation time of τ, which affects and polarizes the wave function of each quantum fragment. In this case, eqn (23) needs to be computed only once as an N × 1 vector at the first iteration of the SCF cycle in each MD step, which is part of the standard operation in PME for classical force fields. The memory requirements are storage of T copies of partial atomic charges.

It is interesting to note that most molecular dynamics simulations of biological systems are concerned with non-crystalline environments. Although the Ewald summation provides the electrostatic energy for a perfectly periodic system, in reality, the instantaneous charge variations due to microscopic dynamic fluctuations in a crystal or a solution are not synchronously propagated over to the macroscopic scale. However, the inclusion of the mean field effect of long-range electrostatic interactions is important for the polarization of the molecular wave function for polar liquids and electrolyte solutions.^16,23,25,62 It is important to emphasize again that short-range electrostatic interactions are evaluated explicitly (not scaled by the erfc function as in the Ewald short-range potential) in the primary unit cell in the present X-Pol-Ewald procedure. Consequently, the present X-Pol-Ewald method provides an accurate and efficient linear-scaling electrostatic approach employing the PME algorithm¹⁷ for periodic systems.

3. Computational details

The X-Pol-Ewald method has been incorporated into a developmental version of CHARMM,⁶³ in which the original X-Pol method utilizing semiempirical NDDO Hamiltonians has been implemented.^3,5 To illustrate the procedure, we carried out test simulations of liquid water with and without long-range electrostatic effects using Ewald summation. The main purpose of this test is to show that the X-Pol-Ewald method is an efficient and practical approach for including long-range electrostatic effects into a full quantum mechanical force field in condensed phase simulations. In the present study, a spherical cutoff scheme was used to evaluate the van der Waals potential to account for the exchange-repulsion and dispersion interactions and to determine the real-space X-Pol energy. In all calculations, a group-based cutoff at 9 Å between the oxygen atoms of two water molecules was used; each water is one interaction group. The non-bonded list and crystal images were updated in every 25 steps during the dynamics simulation.

For the Ewald summation, a κ value of 0.340 Å⁻¹ was employed, and the smooth particle mesh Ewald (PME) method of Darden et al.,^17–20 which has been implemented into CHARMM, was used for the long-range (reciprocal) part of the summation. An approximate grid size of 0.945 Å was used on a 20 × 20 × 20 FFT grid in one case, and a grid size of ca. ~0.756 Å was adopted on 50 × 50 × 50 FFT grid in a second case.

All simulations were performed with the leapfrog Verlet integration algorithm and a time step of 1 fs in the constant volume and constant temperature (NVT) ensemble at a temperature of 298 K that is maintained by a Hoover thermostat. The simulations were carried out for two cubic boxes of 18.9 × 18.9 × 18.9 ų and 37.8 × 37.8 × 37.8 ų, consisting of 216 and 1728 water molecules, respectively, modeled by the MODEL² water potential with the semiempirical AM1 Hamiltonian.⁶⁴ The partial atomic charges used to represent the electrostatic interactions of other fragments with the currently considered fragment are obtained by Mulliken population analysis of the NDDO-based AM1 wave function (see the Appendix for details).

4. Results and discussion

The main goal of this study is to present the theory and implementation of long-range electrostatic interactions into the explicit polarization (X-Pol) method, employing the particle-mesh Ewald method. The importance of including long-range electrostatic interactions in biomolecular simulations such as nucleic acids and electrolyte solutions with PME is well known. Here, we illustrate the performance of the present X-Pol-Ewald method on simulations of liquid water. Table 1 shows the computed numerical and analytic forces (negative gradients) on two water molecules (atom numbers 100 through 105) in the simulation with 216 molecules under periodic boundary conditions. The differences are typically below 10⁻⁴ kcal mol⁻¹ Å⁻¹; this is slightly greater than that (10⁻⁵ kcal mol⁻¹ Å⁻¹) using the standard spherical cutoff scheme, but the small error is consistent with the numerical uncertainties in the PME algorithm.¹⁷

Table 1.

Analytic and numerical forces (kcal mol⁻¹ Å⁻¹) calculated by the X-Pol-Ewald method for two water molecules (water number 34 and 35) in a cubic box consisting of 216 water molecules. Numerical forces are determined by finite difference from displacements of atomic positions and differences specify the deviation of analytic forces from the numerical ones

Atom number	dimension	analytic	numerical	difference
100	X (O34)	−0.96117	−0.96109	0.00008
100	Y (O34)	−2.14231	−2.14238	−0.00006
100	Z (O34)	0.40245	0.40233	−0.00012
101	X (H34)	1.41450	1.41454	0.00004
101	Y (H34)	−1.15551	−1.15545	0.00006
101	Z (H34)	−1.24614	−1.24613	0.00001
102	X (H34)	1.07218	1.07211	−0.00008
102	Y (H34)	−1.27491	−1.27476	0.00016
102	Z (H34)	−1.01582	−1.01575	0.00006
103	X (O35)	4.73798	4.73802	0.00004
103	Y (O35)	0.96007	0.96017	0.00010
103	Z (O35)	−3.78347	−3.78341	0.00007
104	X (H35)	0.78805	0.78800	−0.00005
104	Y (H35)	−1.64549	−1.64555	−0.00007
104	Z (H35)	−1.01468	−1.01458	0.00010
105	X (H35)	−0.24715	−0.24712	0.00003
105	Y (H35)	−1.55094	−1.55094	0.00000
105	Z (H35)	−0.17444	−0.17460	−0.00017

Using the analytic forces from the X-Pol-Ewald method, we carried out three separate simulations for each of two liquid water systems; one consists of 216 water molecules, and another 1728 water molecules; the latter was generated by doubling the size of the edges of the cubic box of the first system. The first simulation was performed using the standard spherical cutoff scheme that has been used in the initial implementation of the X-Pol method (we use a group-based cutoff of 9 Å), while the second and third simulations were executed with the use of the Ewald correction for long-range electrostatic effects by using, respectively, a full update of partial atomic charges during each SCF iteration and the mean-image-charge (MIC) approximation with a correlation time of τ = 1 ps. The single core CPU (central processing unit) time is recorded in Table 2 for running 100 ps (100 000 integration steps) in each simulation. The computer consists of a Sun Fire X4600 Linux cluster, which has six nodes and 32 cores per node with 2.3 GH AMD Opteron processors; the total memory of the system is 800 GB. The most significant result of Table 2 is that the incorporation of the PME method into X-Pol only increases the computational costs slightly, in particular by about 25–27% relative to using the spherical cutoff. The increase in CPU time is about 9 times in going from the small system (216 water molecules) to the larger system (1728 water molecules) using the X-Pol-Ewald method, slightly greater than the increase in system size. If one only considers the PME part of the computational costs, the scaling is about 8.7 between the small and large systems, and this is well within the performance of the N·log(N) algorithm of the PME method. In both systems, the MIC approximation saves about 15% of CPU time relative to that employing the full SCF update for the Ewald pair-potentials. Thus, the present X-Pol-Ewald is an efficient approach for incorporating long-range electrostatic effects into an electronic structure-based force field for molecular dynamics simulations.

Table 2.

CPU time (hour) needed to run 100 ps molecular dynamics simulations (1 fs integration time step) for cubic boxes of water, consisting of 216 and 1728 water molecules, using the spherical cutoff scheme for column 2 and the X-Pol-Ewald method for electrostatics beyond the nearest neighbor in columns 2 and 3. A real-space Ewald cutoff distance of 9 angstroms was used in all simulations for comparison. The column under Full lists the time using the full update of Ewald long-range electrostatic correction to the Fock matrix at every SCF iteration (eqn (21)), and MIC denotes calculations using the mean-field image-potential correction approximation (eqn (23)). All calculations were performed using the AM1 method and full computation. All calculations were performed using the AM1 method and full computation details can be found in the text

system	X-Pol cutoff	X-Pol-Ewald
		Full	MIC
216	6.4	8.1	7.0
1728	58.5	73.3	65.0

Table 3 compares the results obtained using spherical cut-off approximation and the X-Pol-Ewald approach averaged over 500 ps molecular dynamics trajectories. In X-Pol-Ewald calculations, the “Full” pair-potential update and the “MIC” approximation were considered. Inclusion of long-range electrostatic interactions using the full SCF update with the X-Pol-Ewald method, the average potential energy is about 1.5% lower than that obtained with the spherical cutoff scheme. When using the mean-image charge (MIC) approximation, the average energy is about 0.3% within that of the full SCF update, but it is 15% more efficient computationally. Consequently, we recommend the use of the MIC approximation in the X-Pol-Ewald method for computations of average quantities. If time-dependent properties are evaluated, it is advised to first test the effect of the correlation time of the running average used in the MIC approximation. Both methods have been implemented and are available in CHARMM.

Table 3.

Average total interaction energy and binding energy (E_i), which is defined as the interaction energy of one monomer with the rest of the system, of water in the liquid consisting of 216 molecules over 500 ps molecular dynamics simulations of liquid water with the conventional spherical cutoff approach for treating intermolecular interactions and the X-Pol-Ewald method for including long-range electrostatic contributions. A real-space cutoff distance of 9 angstroms was used in all simulations for comparison. The column under Full lists the results obtained with full update of Ewald long-range electrostatic correction to the Fock matrix at every SCF iteration (eqn (21)), and MIC denotes calculations using the mean-field image-potential correction approximation (eqn (23)). All energies are given in kcal mol⁻¹. Additional computational details can be found in the text

system	X-Pol cutoff	X-Pol-Ewald
		Full	MIC
average	−2179.4	−2211.8	−2205.4
Ei	−10.07	−10.24	−10.21

5. Summary

We have presented an efficient extension of the Ewald summation method to the explicit polarization (X-Pol) method, which is a quantum mechanical force field based on block localization of molecular orbitals for condensed-phase simulations. The present approach follows the ideas developed for the combined QM/MM-Ewald method,³³ in which the short-range electrostatic interactions are determined in exactly the same way as standard QM/MM calculations in real space, and the long-range Ewald pair potential is incorporated into the Fock matrix as a correction. The separation of electrostatic interactions into an explicit, short-range term and a reciprocal-space, long-range correction makes it possible to conveniently use the existing algorithm and implementation of a combined QM/MM method for the former, and to incorporate the computationally efficient particle-mesh Ewald (PME) technique developed for empirical force fields into the electronic structure calculation. While the long-range electrostatic correction in the QM/MM-Ewald method is extremely efficient since the number of QM atoms is small compared to the remaining static MM charges, the X-Pol-Ewald method is complicated by the instantaneous charge variation of all fragments of the system, and in principle, the Fock matrix must be updated over all atomic charges during the self-consistent field procedure.

A mean image charge (MIC) approximation was proposed, in which the running average with a user-chosen correlation time is used to represent to the long-range electrostatic correction (LEC) as an average effect. Consequently, the time-consuming Fock matrix update during the SCF cycles is no longer needed, which greatly enhances computational efficiency.

Test simulations on liquid water indicate that the present X-Pol-Ewald method takes about 25% more CPU time than that using a spherical cutoff truncation for electrostatic interactions (with a group-based cutoff distance of 9 Å), whereas the use of the MIC approximation reduces the extra costs by 15%. The present X-Pol-Ewald method provides a general procedure for incorporating long-range electrostatic effects into fragment-based electronic structure methods for treating biomolecular and condensed-phase systems under periodic boundary conditions.

Appendix

The partial atomic charges used in eqn (12) and (13) can be obtained with a number of approaches, including population analysis, charge mapping, or charge fitting schemes. Here, we outline the use of three charge models for obtaining the external charges, namely Mulliken population analysis,⁶⁵ Mulliken population analysis with the neglect diatomic differential overlap (NDDO) approximation,⁶⁶ and the recent dipole preserving and polarization consistent (DPPC) charge model.⁶⁷ If Mulliken population is used, the atomic charges are given by

$$Q_{\alpha }=Z_{\alpha }-{\displaystyle \sum _{\mu \in \alpha }}{(\mathbf{\text{PS}})}_{\mu \mu }$$ (24)

where S is the overlap matrix. Then, the charge derivative prefactor in eqn (21) and (23) is

$$\frac{\delta Q_{\alpha }}{\delta P_{\mu \nu }}=-\frac{1}{2}(S_{\mu \nu }{\delta }_{\mu \in \alpha }+S_{\nu \mu }{\delta }_{\nu \in \alpha })$$ (25)

where δ_{μ ∈ α} = 1 if the basis function μ is centered on atom α, and it is zero if the basis function is located on a different atom. If the NDDO approximation is applied in the Mulliken population analysis, then the overlap matrix for a minimum basis set is assumed to be unity, and the charge derivative is simplified to

$$\frac{\delta Q_{\alpha }(\text{NDDO})}{\delta P_{\mu \nu }}=-{\displaystyle \sum _{\alpha \in \mu ,\nu }}{\delta }_{\mu \nu }$$ (24)

The dipole preserving and polarization consistent (DPPC) charges consist of two parts, the Mulliken population charges and the hybridization dipole contributions that preserve the total and local hybridization dipole moments:

$$Q_{\alpha }(\text{DPPC})=Q_{\alpha }^{\text{MP}}+{\displaystyle \sum _{\beta }^A}{\displaystyle \sum _{\chi }}{({\mathbf{G}}_{\beta }^T)}_{\chi }{\sigma }_{{\mathit{\text{sp}}}_{\chi }}^{\beta }$$ (25)

where $Q_{\alpha }^{\text{MP}}$ is the Mulliken population charge on atom α, χ = x,y,z, ${\mathbf{G}}_{\beta }^T$ is a 3×1 vector for atom β,⁶⁷ depending on the geometry of the molecule, and ${\sigma }_{{\mathit{\text{sp}}}_{\chi }}^{\beta }=P_{{\mathit{\text{sp}}}_{\chi }}^{\beta }{R}_{{\mathit{\text{sp}}}_{\chi }}$ with R_spχ = 〈s|χ|p_χ〉, which is an atomic hybridization contribution to the molecular dipole moment,⁶⁸ which depends on the sp density matrix elements on atom β. The charge derivative becomes

$$\frac{\delta Q_{\alpha }(\text{DPPC})}{\delta P_{\mu \nu }}=-{\displaystyle \sum _{\alpha \in \mu ,\nu }}{\delta }_{\mu \nu }+{\displaystyle \sum _{\chi }}{\delta }_{\mu s}{\delta }_{{\nu p}_{\chi }}{({\mathbf{G}}_{\alpha }^T)}_{\chi }{R}_{{\mathit{\text{sp}}}_{\chi }}^{\alpha }$$ (26)