Abstract
When event data are retrospectively reported, more temporally distal events tend to get “heaped” on even multiples of reporting units. Heaping may introduce a type of attenuation bias because it causes researchers to mismatch time-varying right-hand side variables. We develop a model-based approach to estimate the extent of heaping in the data, and how it affects regression parameter estimates. We use smoking cessation data as a motivating example, but our method is general. It facilitates the use of retrospective data from the multitude of cross-sectional and longitudinal studies worldwide that collect and potentially could collect event data.
1 Introduction
In this paper we develop methods to deal with a ubiquitous characteristic of survey data - the tendency of respondents to report in units that are rounded or heaped. Our primary goal is to provide methods to estimate how heaping affects parameter estimates in regression models, to quantify the degree to which heaping affects statistical inference, and to provide a method by which to recover parameter estimates of interest that are less biased.
As a motivating example, we use retrospectively reported data on smoking behavior from the Panel Study of Income Dynamics (PSID - http://psidonline.isr.umich.edu) and the Current Population Survey - Tobacco Use Supplements (CPS-TUS - http://riskfactor.cancer.gov/studies/tus-cps). When surveys ask ex-smokers about when they quit, they commonly phrase the question in one of three ways. The PSID survey asks “How old were you when you quit smoking?” Other surveys (like the CPS) ask “How long ago (in years) did you quit smoking?” Some surveys ask: “In what (calendar) year did you quit smoking?” These prototypical questions often result in “heaped” responses – reported answers that tend to have non-smooth distributions with peaks at multiples of five and ten years. These patterns show up in many types of data and there is evidence that heaping does in fact introduce bias into estimates. For example, Wang and Heitjan [1] analyze cigarette count data to show that heaping can attenuate the treatment effect by as much as 20 per cent. Hu and Tsiatis [2] show that in continuous time framework heaping has substantial effect on the estimated survival curve. In their simulations they find that heaping attenuates the Kaplan-Meier curve by 10 to 60%.
Many analyses rely on linear regression where it is conceivable that heaped responses may result in biased estimates. For instance, suppose we convert the reported ages to calendar years and let pt be the probability that a smoker quit in Year=t. One may be interested in fitting the logistic model log (pt/(1 − pt)) = Xtβ where Xt is a design matrix, containing covariates such as age, health status, and cigarette prices to test the hypothesis that smokers will be more likely to quit when tobacco prices increase. To do so, we need to know whether and how estimates of the coefficient on price and its standard error vary when survey respondents heap their reported quit ages. Here we investigate this issue.
We take a model-based approach and assume that, however it is measured, the distribution of quit-times mixes outcomes generated by two processes. The first is a stochastic process that represents quit decisions that occurred for some stochastic reason. As such, they are randomly distributed along the dimension of age, elapsed time, or calendar year. The second normally-distributed component arises when smokers quit in response to some external conditions, such as serious health issues, changes in family or employment status, or, perhaps, due to changes in cigarette prices. We fit the mixture model using the Expectation Maximization (EM) algorithm [3] or a Monte Carlo Markov Chain (MCMC) simulation, and obtain a smooth, parametric distribution of quit-times. We sample from this mixture distribution and fit the linear model to obtain parameter estimates.
We use Monte Carlo methods to simulate data that represent the quit decisions of subjects who respond in a known way when a single covariate of interest changes. We then use (a set of) rules to replicate the heaping we observe in distributions of quit ages from survey data. With these data we test whether our algorithm recovers the true underlying distribution. To estimate the bias due to heaping, we compare the average estimates with the ones we derive from the observed (heaped) data.
We develop a general method that researchers can use to model and control for bias that heaping might introduce in the study of event data of any type. Such studies abound. For example, a Google Scholar (http://scholar.google.com/) article search yields thousands of hits for “age at marriage,” “time of marriage,” “age at birth of first child,” etc. Because event data are the focus of so much attention, there is great value in developing methods to reduce potential bias that heaping introduces.
The paper is organized as follows. In Section 2 we review the extant literature, including studies that suggest methods to mitigate the bias due to heaping. In Section 3 we motivate the analysis with graphic illustrations and several observations using PSID data. In Section 4 we discuss the possibility that some of the observed heaping reflects true behavior. In Section 5 we develop our methods, fit parameters using both EM and MCMC algorithms, describe three parametric mixture models for three common types of smoking cessation data, and estimate mixture distribution parameters. Section 6 contains a simulation study. In Section 7 we describe how one might use our model-based approach to estimate the bias in regression parameter estimation, the classification error rate in the response, and the probability that a person is ‘at risk’ to quit smoking. We conclude with a discussion in Section 8.
2 Background
Our analysis follows and builds on the work of [4, 5, 6]. These studies recognize the potential problem that heaping might cause. Little [4] succinctly reviews event history analysis and missing-data methods. Torelli and Trivellato [5] deal with heaped data on unemployment spells of Italian youth. They specify a parametric model of the errors in the reformulated likelihood function, add a dummy variable to flag youth who heap or do not heap, and smooth the data as recommended by [6]. Heitjan and Rubin [6] attempt to solve the problem of heaping by coarsening data over broad intervals centered around the heaping unit. They use a simple framework in which survey respondents use a single heaping rule. They assume that, within broad intervals, heaping occurs randomly. Crockett and Crockett [7] deal with the consequences of heaping in the British religious census of 1851. They point out that it is implausible that data are “coarsened” randomly, and hence, it is not ‘ignorable’ in the sense of [6]. Lambert [8] deals with a special case of heaping, where there are an excess of observations of 0 in count data. In her analysis, she shows that one has to account for heaping in Poisson regression, in the presence of ‘zero-inflated’ data. In more recent work, Forster and Jones [9] model smoking initiation and smoking cessation using UK data in discrete-time hazard models with and without controls for heaping. They implement solutions proposed by [5] but find little evidence that heaping biases coefficients on cigarette tax in models of smoking duration. However, a recent working paper [10] shows substantial heaping effects, using Monte Carlo simulations. Pudney [11] focuses on heaping in consumption expenditure data, and changes in heaped responses between consecutive waves. Similar to our findings, he notes that in any group of survey respondents, multiple heaping rules are used. His analysis focuses on patterns of transition between heaping points for the same individual.
Although our model-based approach shares features with several studies, it also improves on the other methods in several ways. Schneeweiss et al. [12] develop an estimate for the rounding error, based on a Taylor series, and apply Sheppard’s correction to account for bias in standard deviations that arises from rounding. Neither they nor we assume that rounding occurs in a symmetric fashion around heaping points. Wang and Heitjan [1] discuss the possibility that smokers use multiple heaping rules when they report how many cigarettes they usually smoke. They develop a likelihood function that allows reported cigarette counts that are a multiple of 5 to either be the correct response or a result of one of several heaping rules (e.g. heap to 5, 10, 20). They use zero-inflated Poisson or Negative Binomial models. Our method is similar to theirs because it also accommodates multiple heaping rules. Our method differs because it accommodates a wider range of distributions (discussed below). Furthermore, in our method, one can incorporate covariates into the heaping probability function. Like Wright and Bray [13], we also use MCMC simulations in a hierarchical model to estimate the effect of heaping. However, our method improves on theirs in three ways. First, it accounts for multiple heaping rules. Second, it allows for a mixture distribution of the response. Finally, we implement an empirical Bayes estimation procedure in two ways: via the EM algorithm and a fully Bayesian (MCMC) estimation procedure.
3 Data Explorations
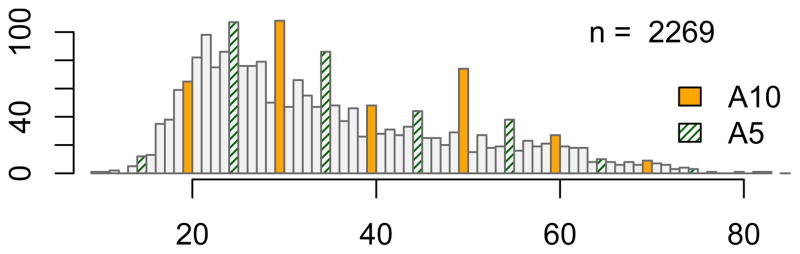
We begin with a number of motivating examples using 1986 PSID data on the age ex-smokers said they quit. In Figure 1 we plot the quit age distribution for 2,269 ex-smokers. The labels ‘A5’ and ‘A10’ correspond to ages that are multiples of five or ten years, respectively. Clearly the data are heaped.
Figure 1.
The distribution of reported quit ages in the 1986 PSID survey.
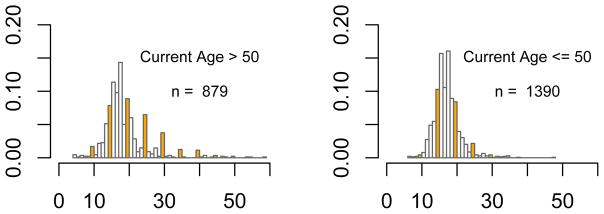
Heaping is also present in Figure 2 where we plot the distribution of start ages, but it is less pronounced and more prevalent among smokers who were older when they responded to the survey (left panel). The right panel shows that, among people interviewed when they were 50 or younger, starting age is distributed approximately normal (mean start age ≊ 17.5 and variance ≊ 11). Such a pattern is consistent with the hypothesis that people are more likely to heap if they remember less well. To formally test this hypothesis, we fit the logistic regression model
Figure 2.
Reported start-smoking ages for two current-age groups.
| (1) |
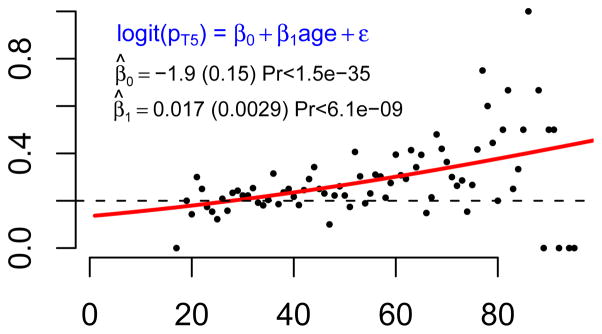
where I [A5] equals 1 if the reported start-age is a multiple of five, and 0 otherwise. We test the null hypothesis that β1 = 0 vs. the alternative, β1 ≠ 0. Figure 3 plots the fitted logit function and the parameter estimates. The horizontal dashed line at .20 represents the proportion of smokers one expects to have started at an age that is a multiple of five. The results confirm the above pattern. The odds a smoker reports he started at an A5 age rise exponentially with age (p < 6.1E − 9). (Note also that people who report a ‘heaped’ starting age are more likely to report a ‘heaped’ quitting age. Both are correlated to a person’s age when surveyed.)
Figure 3.
The probability of a heaped start-smoking age, as a function of current-age.
To motivate the idea of a mixture distribution, we analyze the distribution of a related quantity that combines start and quit ages – the fraction of a person’s lifetime that he has smoked. We define FY S =Fraction of Years Smoking, as
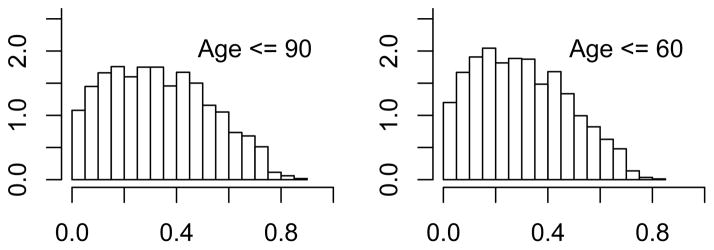
Measured over a person’s whole lifetime, the distribution of this quantity is much less sensitive to the choice of the cohort. Figure 4 demonstrates the distribution of FY S in two age groups – those age 90 or less and those age 60 or less. The distribution for other age groups is practically the same. However, as we show below, if one measures the fraction of life a person has smoked from mid-life forward, one observes a much different distribution.
Figure 4.
The distribution of FY S for different subsets from the sample.
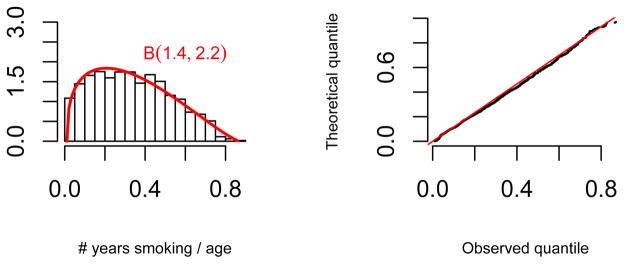
A natural choice for fitting the observed FY S is the generalized beta distribution with support (L, H) where L = min(FY S) > 0 and H = max(FY S) < 1, with the probability distribution function
| (2) |
where B(,) is the Beta function. Figure 5 shows the fitted generalized Beta distribution (left) and a quantile-quantile plot (right).
Figure 5.
Fitting the distribution of FY S.
When we consider the subset of quitters who are at least 49 years old at the time of the survey and plot the fraction of years smoking starting from age 49, i.e.
then the distribution of FY S49 is almost uniform, as can be seen in Figure 6. A possible explanation for the difference between FY S and FY S49 is that the observed distribution of quitting age is actually a mixture of two distributions. This observation motivates our model-based approach.
Figure 6.
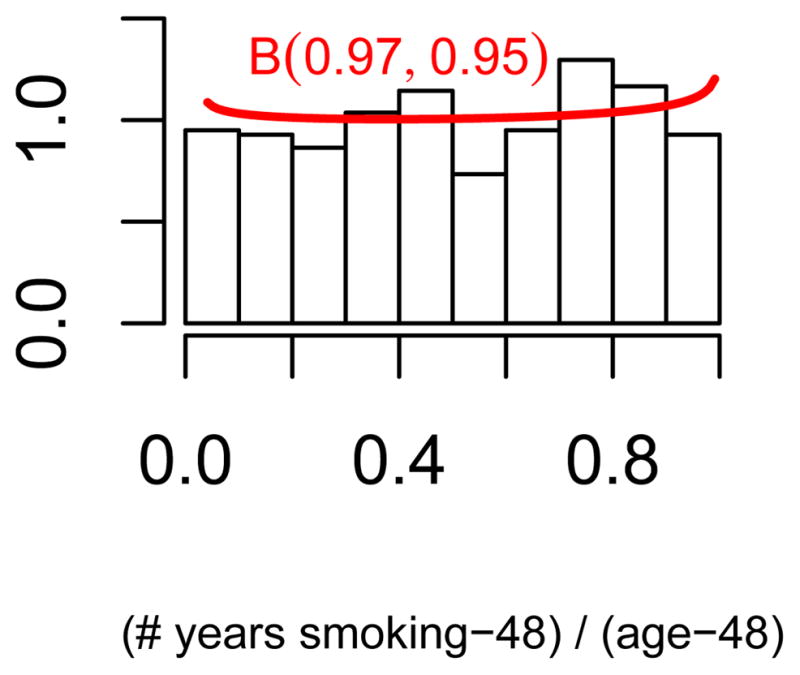
The distribution of FY S49.
Before we develop the model (in Section 5) we summarize the intuition and assumptions that underlie our mixture-distribution approach. We assume that, at any given age, a certain fraction of smokers will randomly quit. They do so according to some stochastic process (or will die without ever quitting). The decision to quit in the first group is related to their start age. We assume that there is a second group for whom the decision to quit is unrelated to their start age. Smokers in this group quit after they experience a significant event (such as heart attack, birth of a child, retirement, a cigarette price increase, etc.). Although we posit the existence of two groups, one can also assume a process where, over the course of an individual’s life, he switches between one of two distributions that govern his decision to quit. In the steady state, each smoker quits according to a random process that is independent of external events. When a shock occurs, some smokers are pushed into the second distribution. Quit decisions for this group are distributed as described above. More generally this structure allows for the presence of a large number of smokers who do not respond to shocks but who still quit according to a random process – a point to which we return later.
4 Heaping and “True Heaping”
While in many cases heaping in observed distributions reflects true behavior, we argue here that most of the heaping shown in Figure 1 probably does not. To differentiate between heaping and actual behavior, analysts must carefully examine both the (assumed) data generating process and the raw data. A failure to do so may cause some analysts to not recognize when observed heaping is more likely the result of misreporting.
When there is ‘true heaping’ the probability of quitting at round ages (e.g. 50) will be higher than expected under a smooth distribution. Sometimes heaping on particular values is expected because of observable characteristics of the data-generating process. For example, the amount of cash that people withdraw from ATM machines is dictated by the menu of options that ATM machines offer [14]. Similarly, there is heaping in the length of unemployment spells that corresponds closely with the maximum time unemployment benefits are paid [15].
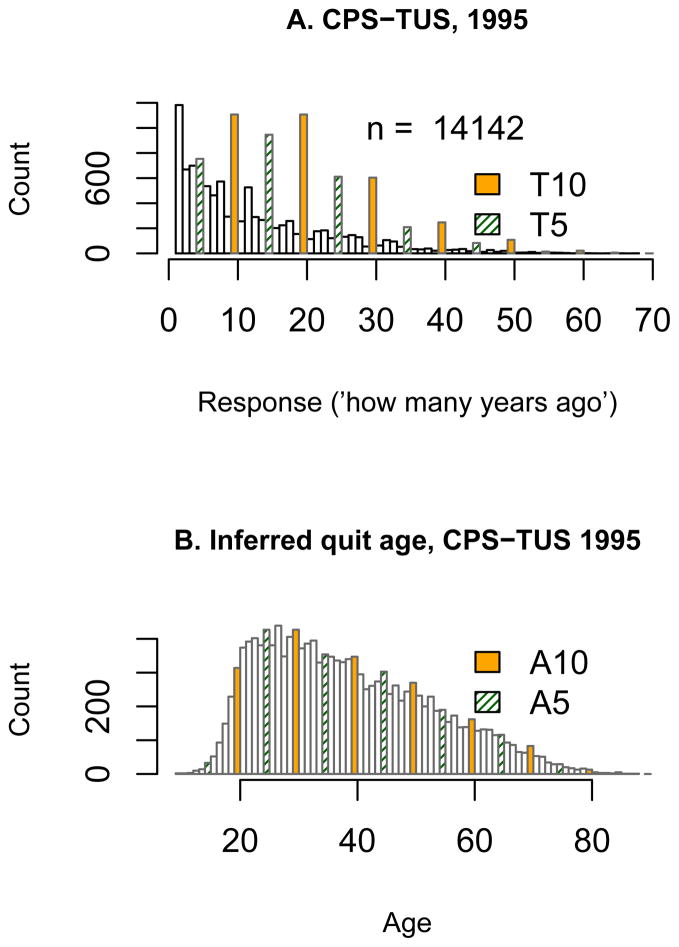
Often heaping is masked by transformations of raw data. The top panel in Figure 7 plots data on time that has elapsed since 14,142 ex-smokers quit. To generate these data the CPS-TUS asked “How long ago did you quit smoking?” One observes significant heaping at T5 and T10 points (corresponding to multiples of 5 and 10, respectively, in terms of number of years since quitting smoking). However, when the response is converted to the age a smoker quit, there appears to be less heaping at A5 and A10 ages than in the PSID data (Figure 1). Because there is no reason to believe that ex-smokers systematically differ in the PSID and CPS samples, it is apparent that, to look for preliminary evidence of heaping, analysts need to examine the distribution of the raw data - on the scale of the responses offered by the survey question.
Figure 7.
The distribution of the response to the question ‘how long ago did you quit smoking’ in the CPS survey (top), and the inferred quitting ages (bottom).
Analysts should also pay attention to how question wording dictates at which points in the distribution one should expect to observe heaping. For example, the 2002 German Socio-Economic Panel survey (SOEP) asks “In which calendar year did you quit smoking?”. One expects (and finds) heaping in calendar years evenly divisible by five.
In any given sample, there may be subsamples that each use a different heaping rule (age, elapsed time, calendar year). For example, in the SOEP, heaping on calendar years divisible by 5 is expected. However, an analyst should also look for evidence of elapsed time heaping in calendar years that end in 2,7,12, etc. Indeed, we observe evidence of heaping from two or more heaping rules in several data sets that we have analyzed.
At least for smoking cessation data there are good reasons to believe that heaping (in the above distributions) did not result from true behavior. The primary reason to suspect heaping rather than true behavior is because of the known process by which smokers quit. On average, smokers attempt to quit three to four times before they succeed and the period between relapses is approximately three to four months [16, 17, 18, 19]. This stylized fact suggests that if smokers did, in fact, have a higher tendency to decide to quit at round ages, we would expect to observe more quits just after A5 ages than just before. Instead, in the distribution of reported quit ages, we find substantially more mass at A5 ages, and no significant differences between the mass at A5−1 and A5+1 ages.
Ultimately analysts need to carefully evaluate what is known about the process that generates their data, the form of survey questions, response categories, and the raw data those questions and categories generate. Heaping is almost always present to some degree. At the same time, there may be reasons to suspect that some heaping results from true behavior. We note again that our proposed model-based approach accommodates “true heaping.”
5 Statistical Models
To develop and test our model, we simulate data that resembles the observed smoking cessation distribution. To assess how heaping affects parameter estimates from models of interest, we propose a parametric model to fit a mixture distribution to the data. The first component represents the population of smokers who quit randomly. The second component represents the population of smokers who quit in response to certain events. The choice of distribution one fits to the first component is dictated by the form of the survey question. The second component allows us to incorporate covariates of interest and assess their effect on people’s decision to quit.
In this section we propose a family of parametric models for fitting distributions to data on the age smokers quit. In Section 7 we describe how we use the models to estimate the attenuation bias due to heaping.
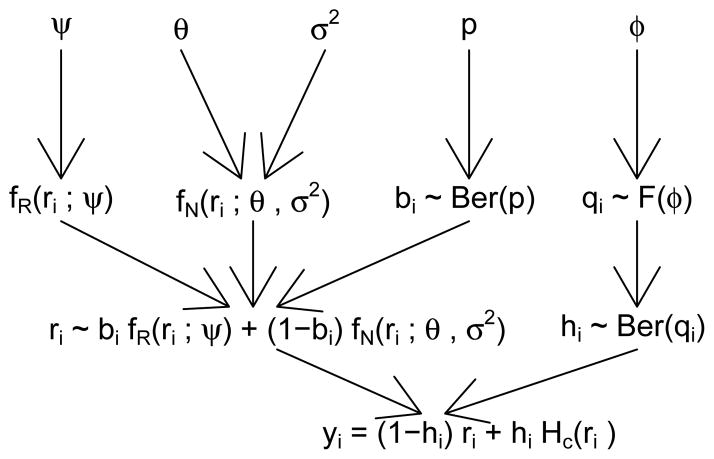
The hierarchical nature of our model-based approach is depicted in Figure 8. Subject i may quit smoking according to either a stochastic process or a process that generates a normal distribution, with probabilities p and 1 − p respectively. We denote the probability distribution function of the stochastic process generically by fR(ri; ψ) where ψ is a set of hyper-parameters. For the normal distribution, we assume mean θ and standard deviation σ. In our model bi is a Bernoulli random variable, so either bi = 1 (the subject belongs to the group of people who quit randomly), or 1 − bi = 1 (the subject belongs to the group of people who quit in response to certain conditions). Hence, ri represents the true quit age (time) of subject i.
Figure 8.
Data generation process for heaped smoking cessation ages
We assume that there is some probability that a subject ‘heaps.’ ‘Heapers’ do not report ri but instead report Hc(ri), where c is a multiple of the time units (e.g., in Model 2 below, we denote the heaped ages by A5 or A10 for multiples of 5 or 10 years, respectively). The probability that a subject heaps is distributed according to a function, F, with a set of hyper-parameters φ. Given the evidence we presented in Section 3 it would be logical to allow F to depend, for instance, on the subject’s age when surveyed. However, it can more generally depend on other factors.
This framework has several attractive features. For example, the normal component of the mixture distribution allows us to incorporate covariates into the model, since it can be written in the usual form in normal linear regression, as Xβ + ε, where β is a vector of effects and ε is the random error. To estimate the coefficients on the covariates while accounting for heaping we take a two-step approach. In the first step we estimate only the overall mean and variance of the normal component in the mixture distribution (using the EM algorithm or MCMC). The parsimony of our model ensures that the complexity of this step does not depend on the number of covariates. In the second step we use a Monte Carlo approach to estimate the regression parameters, as we describe in detail in Section 7.
In addition, as formulated here, our model is quite general. We need not assume particular properties for the function F(φ) (that describes the distribution of the indicator variables hi). For instance, F (φ) does not have to be symmetrical around the heaping points. In the simplest case, we might assume that hi are drawn from a Bernoulli distribution such that person i heaps his response (hi = 1) with probability q (independently of his age or any other covariate). Alternatively, we can assume that qi depends on a person’s age, and use logistic regression as we did in Section 3 (Eq. 1) to estimate a subject-specific heaping probability.
Although we leave the addition of other covariates to future work, there is evidence that a framework that accommodates them will be valuable. Several studies identify factors associated with respondents’ recall accuracy. Recall duration or time since event is a strong predictor of the quality of retrospective reports on marital history in the US Panel Study of Income Dynamics (PSID, [20]), age at first sex in the National Longitudinal Survey of Youth 1979 (NLSY79) in [21], and post-partum amenorrhea (the interval after a pregnancy before menstruation returns) in the Malaysian Family Life Surveys (MFLS) in [22]. Researchers also agree that timing of events are more accurately reported when they are more salient to the respondent. Kenkel et al. [23] find that smokers are more likely to report the same starting age across different waves of the NLSY79 if they are or were heavier smokers. Although marriage and divorce are both salient life events, [20] shows evidence that dates of divorce are reported less consistently than dates of marriage and conjectures that it may be because divorce is less socially acceptable. Researchers have also linked recall accuracy with demographic characteristics such as education and race/ethnicity [23, 20], question wording [20], and even arithmetic facility [21].
In our model we assume that the covariates that affect a person’s decision to quit are independent of the covariates that affect their probability to heap. We recognize that this assumption may not always hold. For example, a person may have quit smoking following a heart attack, the timing of which he recalls perfectly. Such people are more likely to also accurately recall and report the correct quitting age. However, based on the analysis of multiple data sets, we believe our assumption is reasonable for most ex-smokers. In our earlier analysis (available on request) a person’s age when surveyed is the strongest predictor of heaping. In those models, other covariates, like major life events, have significant but much smaller effects on the probability of heaping. Further, in our approach, data on those events can be directly incorporated into the normal component of the mixture as explanatory variables. In ongoing work we relax the independence assumption.
Another advantage of our approach is that one can extend the model to allow for multiple heaping rules and each rule can be modeled with a different probability distribution function, Fc (e.g. A5 and A10 may have different probabilities in Model 2 below.) Although we do not develop the full model with multiple heaping rules here, to do so only requires that we assume that hi follows a multinomial distribution, and yi has the form
where I[No Heap] is the indicator function that takes the value 1 if and only if person i provided the true response, I[Heap Type = u] is the indicator function that takes the value 1 if and only if person i provided a heaped response according to heaping rule u, and H Cu (ri) is the heaped version of the true response, according to rule u.
The mixture-model approach also easily accommodates the existence of two or more groups of people who differ in their response to external events. It is well recognized that, in regression models, the failure to account for such heterogeneity may diminish the power to detect significant effects.
We noted before that our method accommodates “true” heaping - i.e. the case that people may be more likely to quit at certain ages or at certain times. One can incorporate this prior belief into our model-based approach. To do so, one can easily add point-mass mixture components to the model and estimate their probabilities. Alternatively, we could add these ages as fixed effects to the regression model (e.g. I[is 50 ij] = 1 if subject i was 50 years old in time period j, and 0 otherwise).
To summarize, our model-based approach is flexible enough to accommodate a wide range of assumptions about the nature and type of underlying data generating processes.
We use two methods to estimate the mixture-model parameters - the Expectation-Maximization (EM) algorithm and Monte Carlo Markov Chain (MCMC). The EM algorithm is well suited for fitting parametric models to such data because the model explicitly allows for missing data. Specifically, missing data include the mixture component to which each subject belongs and whether an apparently heaped value is in fact heaped. The MCMC approach, while more computationally intensive, allows us to modify the assumed underlying mixture model more easily. One confronts different issues such as computational speed when one implements each method. However, we present both as viable estimation methods, as they share the same underlying (parsimonious) model-based approach. In simulations they both yield excellent results.
5.1 Using the EM Algorithm to Fit Model Parameters
We first use the EM algorithm to obtain the parameter estimates for the generic model in Figure 8. To begin, we write the complete data log likelihood, lC, with two sets of unobserved variables, {bi} (the mixture component indicators), and {hi} (the heaping indicators). To simplify the presentation, we focus here on a single heaping rule (e.g., round to multiples of five years,) but the extension to multiple rules is straightforward. We also simplify the derivations slightly here, by assuming that qi = q (that is, a uniform probability that a person reports a heaped quitting age).
We first set notation. When subject i is in the stochastic component of the mixture distribution the probability of ri (the true response) is given by FR(ri). When he is in the normal component, the probability of ri is FN (ri). Let and respectively be the probabilities that one observes the heaped value yi = HC(ri) rather than the true value ri. Let I5[yi] be the indicator function that takes the value 1 if yi is a multiple of 5, and 0 otherwise.
The complete data likelihood function is:
| (3) |
and the complete-data log-likelihood is
| (4) |
To apply the EM algorithm we construct the Q (ϕ; ϕ (k) function, where ϕ = {ψ, θ, σ, p, φ}, ϕ (k) is the estimate after the k–th iteration of the EM algorithm, and
| (5) |
In every iteration we replace the missing data variables with their expectations, given the current parameter estimates. For the Bernoulli variables, bi, we simply use Bayes rule to find the posterior probability that subject i’s quitting age is distributed through the first component of the mixture distribution. That is, we use the distribution of the stochastic process:
| (6) |
where Prob(CR(i)), Prob(CN (i)) are the posterior probabilities that subject i is in the stochastic or normal component, respectively. Specifically,
| (7) |
| (8) |
For the heaping indicators we set hi = 1 with probability q if a person reported a ‘heaped’ age. As noted before, one can easily specify q=qi so that the heaping probability varies with subject-specific factors such as current age.
To estimate parameters we maximize the Q function with respect to ϕ. Given the parameter estimates in the k-th step of the algorithm, we can express FN and FR in terms of the continuous cumulative distribution functions. We then take the derivatives in order to find the current iteration’s maximum likelihood estimates.
Regardless of the choice of FR, the maximum likelihood estimates for p is
| (9) |
To estimate q we use the current estimates for ϕ to compute Ê5 - the expected number of ages that are multiples of 5. Denote the observed number of multiples of 5 by B5 = ΣI5[yi]. The percentage of heapers is estimated by
| (10) |
We noted above that it is easy to extend the model to allow for multiple heaping rules and estimate the appropriate parameters. For example, suppose that we believe that there are two types of heapers – those who report quit ages (time) on multiples of 10 (A10) and those who report on odd multiples of 5 years. Let q10 be the probability of A10 heapers, and qc be the probability of heaping on odd multiples of 5 years (i.e. Ac where c = 10k + 5 for k = 0, 1, …). We define Êc as the expected number of odd multiples of 5 years (given the current estimates of ϕ), and Ê10 is the expected number of multiples of 10 years, and let Bc = Σ Ic[yi] and B10 = Σ I10[yi] be the observed counts of odd multiples of 5, and multiples of 10, respectively. Then,
| (11) |
| (12) |
To obtain the maximum likelihood estimates of x ∈ {θ, σ2} one maximizes the fourth line in (4) with respect to x. Note that the form of these estimators does not depend on the choice of the stochastic process component. We perform the maximization numerically, expressing FN and in terms of the integral of a normal distribution. In our example, the response is expressed in terms of years (integers) and we are considering only one heaping rule (reporting multiples of five years instead of the true age), so in the our derivation we assume that
for i = 1 … n; and for i ∈ H
If one assumes a different heaping rule, these functions may take other forms. For example, it may be assumed that people only round down (or up), not symmetrically as in this example. The derivation of the maximum likelihood estimates remains (qualitatively) unchanged. However, the limits of the integrals may change according to the assumed heaping scheme.
The estimates one obtains for the remaining parameters varies with the choice of the distribution ofFR and . Generally, the estimation requires that one maximize the fifth line in (4) with respect to the distribution-specific parameters, φ. In practice, we obtain the maximum likelihood estimates numerically using standard maximization methods. We next discuss the application of the model for three distributions that are candidates to fit smoking cessation age data.
5.2 Three Mixture Models
Model 1 – a Beta/Normal Mixture
The first model is motivated by the observations in Section 3 where we saw that the distribution of fraction of years smoking is different for smokers above a certain age. In the stochastic mixture component we use the trivial identity:
| (13) |
As discussed earlier, the distribution of StartAge is approximately normal, and its mean and variance can be estimated using a subset of younger respondents, and Years Smoking/Current Age can be estimated using (2).
For the second mixture component, we assume that quitting ages are distributed normally with mean θ and variance σ2. Hence, given the starting age si and the current age ci, the probability distribution function of the quitting age qi, is
| (14) |
where the unobserved indicator variables bi are distributed Bernoulli (p) and fB() has the form given in (2).
Model 2 – an Inverse-Gaussian/Normal Mixture
Our second model also corresponds to data generated by questions of the form “How old were you when you quit smoking?” We assume that the population of smokers is a mixture of two groups. In this case, we assume that responses in the first group are distributed according to an Inverse Gaussian distribution, with probability distribution function
| (15) |
for x > 0. The Inverse Gaussian distribution (IG) is related to ‘first passage time’ in Brownian motion: given a stochastic process Xt with X0 = 0 and Xt = νt + τWt where Wt is a standard Brownian motion with a positive drift ν, the first passage time is defined as Tα = inf{0 < t|Xt = α}, which is distributed . In the context of smoking cessation, ‘first passage time’ refers to a smoker’s decision to quit. The definition of the IG distribution and its intuitive interpretation make it a natural candidate for modeling event occurrences in general and smoking duration in particular. The IG distribution has been used to model the emptiness of dams [24], purchase incidence [25], and duration of strikes [26]. It is quite popular in the field of finance, where strategies for buying or selling assets are often determined using a ‘first passage time’ rule (buy/sell when the price of a stock reaches a certain threshold). Recently, the IG distribution was also used to model time until the first substitution in soccer games [27]. Folks and Chhikara [28] detail the origin, properties, and applications of the IG distribution. They note that for several data sets which were modeled using the IG distribution, the log normal, the Weibull, and the gamma distributions seemed equally adequate. However, they recommend using the IG distribution to model events that occur over long periods of time because of “its considerable exact sampling distribution theory” and because it is preferable to base the choice on the relation to an underlying physical mechanism. In the case of smoking cessation, the “physical mechanism” may, in fact, be a psychological or social one. In any case, the ‘first passage time’ interpretation makes the IG model a natural choice to model the stochastic process component of our data.
According to our mixture model, given the starting age si, the probability distribution function of the quitting age qi is
| (16) |
As in Model 1, bi are unobserved indicator variables, distributed Bernoulli (p).
Among those in the sample who still smoke at the time of the survey, qi is censored, and we only observe their current age, ci. To estimate the parameters in the model, we consider only the quitters (i = 1, …, m), but in principle, we can include the subset of still-smokers when fitting the model. For the censored qi, i = m + 1, …, n we can find the expected value, given that the subject still smoked at the time of the survey. The expected value is given by
| (17) |
where ci is the person’s age at the time of the survey, and f, F are the probability and cumulative distribution functions, respectively, obtained from (16).
Model 3 – an Exponential/Normal Mixture
The third model corresponds to data generated by questions of the form used in the CPS-TUS. That survey asks ex-smokers, “How long ago did you quit smoking?” In this case we assume that the first group’s stochastic responses (quit time) follow an exponential distribution, with probability distribution function
for x > 0.
5.3 Comparing the EM and MCMC Fitting Procedures
The above model-based approach lends itself quite naturally to a fully-Bayesian framework that uses MCMC simulations algorithms. However, before analysts use MCMC they should consider what they trade when they use MCMC versus the EM algorithm. The EM algorithm is computationally efficient because it provides tractable expressions for parameter estimates. In practice it can be time-consuming to implement because the computer program must maximize the complete data likelihood function with respect to each parameter. This feature means that, when an analyst wants to assume that the data are generated by a different underlying mixture model, he must run a new program. Therefore, when the analyst wishes to use a new specification of the distribution functions in the model in Figure 8 or to implement different heaping rules, MCMC simulations may be preferred.
However, when analysts choose the MCMC approach they trade simplicity for speed. Even though we have described parsimonious models, an MCMC sampling approach tends to be slow since its implementation requires that the algorithm randomly samples from the underlying distributions. By contrast, the EM algorithm analytically derives estimates and therefore converges much faster. Furthermore, MCMC sampling may require multiple runs to assess convergence and to tune up initial values of prior distributions.
Both methods are viable options for the critical step towards bias estimation -recovering the assumed (‘true’) underlying distribution of responses. However, we tend to prefer the EM algorithm implementation for two reasons. First, its speed and scalability is rather important, especially when the sample size is large. Second, the MCMC approach, while easy to set up in principle, can be quite challenging to optimize in terms of the choice of robust priors and achieving convergence.
6 Simulation Study
We stated earlier that two factors can contribute to biased estimates of coefficients on covariates of interest in regression models. First, some of the population may quit smoking according to a stochastic process that does not depend on the covariates in the regression. It is important to separate out the two groups, in order to assess what impact certain policies can have on smoking habits. For example, in the extreme case in which all the subjects quit at random, we cannot expect any policy to affect people’s decision to quit smoking. Second, some respondents heap. Heitjan and Rubin [6] coined the term ‘ignorable coarsening’ to describe a set of conditions under which heaping would introduce no bias. However, as stated here and other places (e.g., [13]), heaping cannot always be ignored. Our goal is to estimate the extent of heaping in data sets and to describe how to use the model to quantify the degree to which regression parameters are biased as a result of heaping.
To assess the performance of our method, we perform simulations in which we vary the distribution of the random process, the mixture proportion, the set of parameters of the two mixture components, and the heaping probabilities. Here, we report two scenarios which demonstrate the power of our method to recover the true parameters.
6.1 Data Generation
Our simulations consist of data generated according to the mixture models described schematically in Figure 8. In each simulated data set, we choose the stochastic mixture component and vary the parameters. Each data set has n = 10000 subjects. To obtain standard errors for the parameters estimates, we ran 30 simulations for each parameter configuration. We run the simulations under two scenarios that use two different distributions for the stochastic process:
To simulate a survey that asks about quitting ages (as in the PSID), we use an Inverse Gaussian distribution with parameters μ = 13 and λ ≈ 61. This scenario represents a situation in which the smokers who draw their quit age from the stochastic distribution, quit, on average, 13 years after they start smoking (with a standard deviation of 6). For the normal component, we vary the mean and variance parameters. Results shown here use values θ = 55 and σ = 5. This represents a group who quit in response to an external event (e.g., disease, birth of a child, etc) on average at age 55 with standard deviation 5.
The second scenario emulates a survey in which people report the time elapsed since quitting (as in CPS-TUS). Here, the stochastic component is assumed to follow an exponential distribution. We use the rate of λ = 1/7 in this scenario. The normal component here represents a ‘one-time shock’, which we think of (simplistically) as the effect of a price increase, θ years ago. We use θ = 14 and σ = 0.2.
To test the accuracy of our estimation procedure under different mixture proportions and different heaping probabilities (denoted by p and q, respectively in our model), we generate data sets according to the above specifications, with p ∈ [0.75, 0.99] and q ∈ [0.15, 0.5].
Note that the purpose of this simulation study is three-fold. First, for any estimation procedure, it is expected that when the correct model is assumed, the estimates will be close to the true values. Hence, the first goal is to verify that, under the right model, our procedure provides accurate results. Second, even under the right model, it is not obvious that the parameter estimates will be accurate in the presence of heaping. Therefore, our second goal is to verify that they are. The third objective is to show that the model-based approach is flexible enough to accommodate different distributional assumptions. This goal is especially important because survey information may often suggest that another distribution better describes the data generating process. The flexibility of our approach in easily accommodating different distributional assumptions is also important because, as is the case with any parametric estimation procedure (for example, least-squares estimation for linear regression), the validity and quality of the estimation depends on the extent to which the distributional assumptions are reasonable approximations of the true underlying distributions.
6.2 Results – IG Distribution
In Table 1 we report how well our algorithm recovers the parameters of the mixture distribution. To evaluate how our algorithm performs, we generate Inverse-Gaussian/Normal mixtures according to the procedure in (6.1), and use the EM algorithm to estimate parameters. Each row reports results for a different combination of p and q (in this simulation the means and variances of both the normal and the IG distributions were fixed, as described above). The first column identifies the true mixture and heaping probability values, respectively. The next four columns report the average bias (and standard error of the bias) of the fitted values of the mean and variance of the Normal and IG components of the mixture distribution. The last two columns report the average bias and standard errors for the estimated mixture and heaping probabilities. The average bias is computed by where ψ stands for any of the estimated parameters, and ψ̂i is the estimate in the i-th simulation. We similarly compute the standard error of the bias.
Table 1.
IG/Normal mixture – average bias of parameter estimates for different heaping and mixture probabilities
| True p, q | Mean(N) | SD(N) | Mean(IG) | SD(IG) | p̂ | q̂ |
|---|---|---|---|---|---|---|
| p=0.7, q=0.15 | 0.05 (0.13) | 0.03 (0.15) | 0.07 (0.16) | 0.18 (0.18) | 0.002 (0.004) | 0.001 (0.005) |
| p=0.7, q=0.48 | 0.06 (0.18) | 0.02 (0.12) | 0.08 (0.14) | 0.03 (0.14) | 0.005 (0.005) | −0.001 (0.006) |
| p=0.85, q=0.16 | 0.05 (0.23) | −0.01 (0.19) | 0.02 (0.14) | 0.13 (0.13) | 0.002 (0.004) | −0.001 (0.005) |
| p=0.85, q=0.49 | 0.08 (0.25) | −0.02 (0.16) | 0.05 (0.11) | 0.29 (0.12) | 0.005 (0.003) | 0.001 (0.007) |
| p=0.95, q=0.16 | 0.23 (0.72) | −0.16 (0.36) | 0.06 (0.10) | 0.17 (0.08) | 0.003 (0.003) | −0.0005 (0.005) |
| p=0.95, q=0.48 | 0.27 (0.65) | −0.31 (0.42) | 0.13 (0.13) | 0.34 (0.14) | 0.005 (0.004) | 0.00006 (0.005) |
| p=0.99, q=0.56 | 0.66 (2.04) | −0.03 (1.46) | 0.02 (0.10) | 0.24 (0.11) | 0.002 (0.002) | 0.0002 (0.007) |
In general, the average bias is very low. For example, in the first row when p = 0.7 and q = 0.15 the average bias of the mean of the normal component (θ) is 0.05 (with standard error of 0.13). The true value of is 55 throughout. Hence, the bias is very small relative to the true value. This pattern holds for all other parameters. Because we get very accurate estimates, we can recover the true mixture distribution. Our estimates are very accurate even in the difficult case in which only 1% of the population quits in response to external shocks and over 56% of respondents report a heaped quitting age. In this case, the estimation procedure is considerably slower.
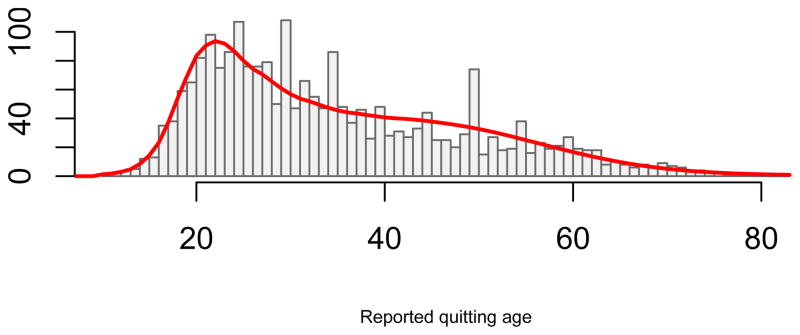
To demonstrate that our algorithm works with survey data we apply the EM algorithm to the PSID data shown in Figure 1. We assume the data are generated by two heaping rules. We assume one group heaps on odd multiples of 5 year ages (with probability q5). The other group heaps on even multiples of 5 year ages (with probability q10). This exercise yields the following estimates:
Normal component: mean 45.9, standard deviation 11.9.
Inverse Gaussian component: mean 11.2, standard deviation 12.16.
The proportion of the stochastic (IG) component is p̂ = 0.65.
Heaping probabilities: q̂5 = 0.038, q̂10 = 0.043.
Hence, 65% of the population quit smoking according to an Inverse-Gaussian random process, approximately 11 years, on average, after they started smoking. The overall proportion of ‘heapers’ is a little over 8%. In the PSID 26.23% of ex-smokers report a heaped quit age, whereas ex ante one expects 20% to report such an age. The excess mass of 6.23% on heaped ages is close to the proportion our model estimates. The fitted distribution is depicted in Figure 9.
Figure 9.
Fitting the PSID 1986 data with an Inverse Gaussian/Normal mixture
6.3 Results – Exponential Distribution
In Table 2 we report how well our algorithm performs with an exponential/normal mixture. We include a simulated ‘one-time shock’ 14 years prior to the survey. Here, we only report results for one combination of p and q (where p = 0.8 and q = 0.2). The average bias and its standard error are computed as above. For all but one parameter our algorithm once again estimates the true parameters accurately. Only the heaping probability, q, is underestimated. On average, it was estimated to be 0.14, when the true probability was 0.2.
Table 2.
Exponential/Normal mixture – average bias of parameter estimates
| True p, q | Mean(N) | SD(N) | Rate (exp) | p̂ | q̂ |
|---|---|---|---|---|---|
| p=0.8, q=0.2 | 0.43 (0.01) | −0.05 (0.02) | 0.0004 (0.0016) | −0.008 (0.002) | −0.067 (0.003) |
Understanding this discrepancy helps to illustrate a very important characteristic of the algorithm and how it interacts with specific features of the data. Two pieces of information are important. First, in this simulation we have a one-time ‘shock’ 14 years prior to the survey. Second, 15 is a heaping point.
When the mean of the normal component is very close to a heaping point, a slight bias (overestimation) of the mean (θ) is translated by the algorithm into a larger proportion of ‘true heapers’. To illustrate this point with a numeric example, consider the following. In one of our simulations the point estimates of the mean and standard deviation of the normal distribution, θ and σ, were 14.43 and 0.15, respectively. The algorithm correctly estimated the proportion of the normal component to be 0.2 (which corresponds to 2,000 subjects). The expected number of subjects in the normal component that are estimated to have quit more than 14.5 year ago is 641. Specifically,
This corresponds to 6.4% of the population, which is very close to the observed average bias in the estimation of q. Because the mean of the normal component is overestimated, the algorithm assigns more of the mass from the normal component to be ‘truly’ at 15, so fewer of the people reporting an A5 age are considered heapers. Generally, our algorithm will estimate the heaping probability more accurately when the normal component is more diffuse or when its mean is not too close to a heaping point.
This observation has important practical implications worth discussing here. First, note that the other estimates are very accurate. The algorithm does a good job recovering the mixture distribution but considers too many people to be ‘true heapers’. Since our main focus is the estimation of the effect of a certain event such as a price increase, the timing of which the analysts will often know, our results show that the algorithm picks up the effect of the event. We can easily correct the estimate of the heaping probability accordingly. Second, this example highlights the importance of allowing the algorithm to specify ‘true heaping.’ For example, if the shock occurred 15 years ago, the estimate for q must reflect the fact that more people truly quit at that time. Lastly, this particular example illustrates the difficulty in unraveling important effects if one does not account for the interaction between the mixture distribution and the heaping behavior.
As a side note, we observe that this situation illustrates a shortfall of one of the main alternative methods for dealing with heaping, namely the “coarsening” of data proposed by [6]. Recall that to apply their method, one averages all data inside the interval over which heaping is assumed to occur. By definition this process throws away information. Under a mixture distribution where behavior occurs both stochastically and in response to events, coarsening not only dilutes the timing of any shock, it also entails an efficiency loss because it combines the random variation from the stochastic component with the systematic variation from the normal component.
We conclude this section by noting that we also fit the data using MCMC simulations and obtained equally good results. In one such simulation we simulated 2000 subjects who reported their quitting time in terms “how long ago.” We set p = 0.9 (1800 subjects quit according to a stochastic process given by an exponential distribution with rate λ = 0.1. 100 subjects quit because of external conditions according to a normal distribution with mean θ = 14 and standard deviation σ = 0.5. We had 34% of people heap their responses (q5 = 0.34). Using the WinBUGS MCMC sampler [29], we set up two chains with 6000 iterations in each, of which the first 3000 were discarded as burn-in iterations. We further thinned the MCMC posterior sample, by keeping one of every three consecutive samples. Thinning MCMC chains is a common practice to reduce the dependence between simulated samples. Hence, each chain provided 1000 samples from the posterior distribution. [29] provides details on the posterior distribution of the parameters and the sampling methods that WinBUGS is using.
A general approach, which we follow, is to use relatively flat priors. However, given the data, one may tweak the prior distributions to gain faster convergence. For instance, we assume that the mean event time has a normal prior distribution. Because in the observed data the mean event time is around 14, we choose to center our prior around that point. We note that in general, if the prior is sufficiently diffuse and the sample size is large enough, the posterior distribution is determined primarily by the data. In this case, the particular form of the prior has a diminishing effect as the sample size gets larger. When the sample size is small, the posterior distribution that results from MCMC depends more critically on the assumed prior distribution. However, the observed distribution always serves as a guide to the choice of the prior.
Here we use a Beta(0.1, 0.9) distribution for elapsed time parameter (λ), a normal distribution with mean 14, and variance 2 for the mean event time (μ), a Beta(0.5, 1.5) distribution for the probability of heaping, and a Beta(0.9, 0.1) for the mixture probability. Since we are simulating a ‘shock event’, we assumed that the prior of the variance of the mean event time is distributed gamma(64, 16). Because our sample size is large, the results are robust to the choice of priors.
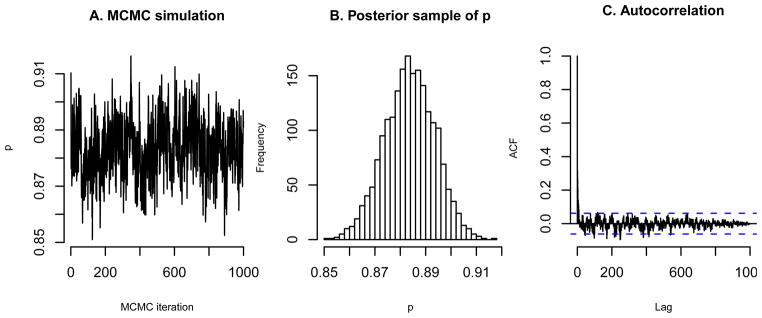
We assessed convergence of the MCMC simulation using autocorrelation and trace plots. Figure 10 shows the trace plot (panel A) and a histogram (panel B) of 1000 samples from one of two chains, and an autocorrelation plot (panel C). The plots for the second chain, as well as for the other parameters, exhibit similar properties. Namely, the plots show good mixing in the simulation, normality of the posterior distribution, and low autocorrelation.
Figure 10.
Sampling from the posterior distribution of p̂ (ptrue = 1).
Furthermore, by using multiple chains we can assess convergence by means of the R̂, which measures the potential scale reduction for each parameter [30, Section 11.6]. The R̂ values for all parameters were 1 (the Bayesian literature recommends using a maximum threshold of 1.1). When the R̂ values are at or below 1.1 taking more samples will not significantly improve inferences based on the posterior distribution of each parameter. Finally, WinBUGS also provides a statistic, n.eff, that is the effective number of independent simulation draws. Ideally n.eff should be as large as the total number of posterior draws (here 2000). We obtained exactly this value for λ, θ, and q. For p n.eff was 880 and for σ−2 (the precision of the normal distribution) it was 220. These values further indicate that convergence has been achieved and that inference based on the posterior distribution is valid.
Table 3 summarizes the results of the MCMC simulation. The posterior means of the five parameters in the model are very close to the true values, even in the presence of significant heaping and with a relatively small proportion of sample in the normal component of the mixture.
Table 3.
Posterior means, standard errors, and 95% Highest Posterior Density (HPD) interval
| Parameter | True Value | Estimate (se) | HPD |
|---|---|---|---|
| p | 0.90 | 0.880 (0.0098) | (0.865, 0.904) |
| q | 0.34 | 0.280 (0.0156) | (0.249, 0.309) |
| θ | 14 | 13.930 (0.0701) | (13.790, 14.060) |
| σ−2 | 4 | 4.790 (0.5583) | (3.581, 5.782) |
| λ | 0.10 | 0.092 (0.0024) | (0.088, 0.097) |
7 Bias Estimation
Our main goal in this paper is to estimate to what extent heaping in surveys can affect parameter estimates in regression models. We begin this section with a brief review of discrete time survival analysis regression. Our notation below follows that in [31], which we summarize here for completeness.
7.1 Discrete-Time Survival Analysis – Brief Review
Let gij = Pr{Ti = j|Ti ≥ j, Z1ij = z1ij, …, ZPij = zPij} be the discrete time hazard function. gij is defined as the conditional probability that person i with covariates Zkij quit smoking in time j, given that he smoked in the previous period. We use the model proposed by Cox [32] and assume that the log-odds of quitting follow a linear model:
| (18) |
where the data are stored in a person-year format. In any given sample, t(1) will be the earliest year a person is at risk to quit (e.g. the year the first person began to smoke) and t(J) is the last year (usually the survey year). The first subscript in Dtij represents the range of time periods in the sample, 1, …, J. Subscript i represents the subject. Subscript j represents the current period. For each subject, the data set contains si rows, where si is the number of years the subject reported to have been smoking. The variable Dtij is set to 1 if subject i has been smoking for j years at time period t, and 0 otherwise. Note that for a fixed t, for each pair ij at most one dummy variable Dtij can be 1. The parameters at represent the baseline hazard in each time period.
The variables Zpij record the values of P covariates for each subject i, in each time period j in which he was ‘at risk’ for quitting. These covariates may be fixed for all time periods (e.g., sex, race, etc.) or time-varying (e.g., cigarette price, or major events such as marriage, heart attack, etc.) The parameters βp describe the effect of the P predictors on the baseline hazard function (on the logit scale).
The observed response, Yij, equals 1 if subject i quit in his j-th year as a smoker and equals 0 if he was still smoking.
The design matrix X for the logistic regression consists of J + P columns where the first J correspond to the smoking duration indicators Dtij. The last P columns correspond to the linear predictors. The number of rows in X equals , the total number of smoker-person-years represented in the sample. To estimate the parameters ϕ = {α1, …, αJ, β1, …, βP }, we maximize the likelihood function
| (19) |
where gij is obtained from (18).
The main goal of most researchers is to estimate the parameters {βp}. The set {αt} can be considered as nuisance parameters. Therefore, to implement our approach we would convert (18) from logit representation to a hazard function in order to use the partial likelihood method, introduced by [32]. This estimation method allows one to consider the nuisance parameters jointly, in the baseline hazard function. It also estimates the regression parameters more efficiently because it uses standard proportional hazard fitting methods, such as coxph in R. Assessing the significance of the predictors is typically done by comparing −2LL of the complete and reduced models, where the latter includes only the intercept parameters, αt, and −2LL is −2 times the log-likelihood. The drop in −2LL is compared with a Chi-square distribution with P degrees of freedom.
7.2 Estimating Heaping-Induced Bias and Misclassification Probabilities
Using the notation in 7.1, it is obvious that heaping (or for that matter, any type of error in reported ages in retrospective surveys) will result in a different design matrix X and response vector Y, and hence may result in biased estimates for {βp}.
To estimate the heaping-induced bias we propose that one use Monte Carlo simulations: recall that in Section 5 we provided a model-based approach to estimate the distribution of quitting ages. One would use these estimates (which we denoted by ϕ̂) to generate random design matrices and response vectors, X(m) and Y (m), respectively. For each such pair, obtain the regression parameter estimates, β̂pm (for m = 1, …, M). Specifically, take the birth years of subjects in the survey, and draw start- and quit-smoking ages according to the fitted distribution for the appropriate model from Section 5 and convert them to calendar years. For each predictor p = 1, …, P then estimate the bias by
| (20) |
where β̂p is the maximum likelihood estimator of βp obtained from the survey data (without accounting for heaping) and β̂pm is the estimator from the m-th random pair (X(m), Y (m)).
Specifically, one could obtain M bootstrap iterations [33] from each column of X to generate the columns X(m). Then, to generate Y (m) proceed as in the data generation process in Figure 8 for each m = 1, …, M: using the estimated regression parameters, β̂, compute the mean of the normal component, θ(m) = X(m)β̂. Draw M random responses from the normal component, ri,N ~ N(θ(m), σ̂2). Also, draw M random samples from the stochastic component, ri,R ~ FR(ψ̂), where ψ̂ is the set of estimated parameters obtained from our fitting procedure. Similarly, generate M mixture component indicators, bi ~ Ber(p̂); and M heaping indicator variables, hi ~ Ber(q̂). For each subject, compute ri = biri,R + (1 − bi)ri,N, and its ‘heaped’ version, H(ri). Finally, obtain .
Using the bootstrap/Monte Carlo simulation approach we could also estimate the response misclassification probabilities, defined for each time period j, as in [34], by γ0,j = Pr(Yij = 1|Ỹij = 0) and γ1,j = Pr(Yij = 0|Ỹij = 1), where Ỹij is the true response (subject i quit in time period j), and Yij is the reported response. Similarly, we could estimate the misclassification probabilities of the ‘at-risk’ set at time t, .
8 Discussion
The above exercise shows that our method recovers the parameters of the underlying distribution in our simulated data. With estimates of the underlying parameters, we can estimate the bias in regression parameters. Our method is similar to the one developed by [13] with two important extensions. Those authors assume there is one underlying distribution and that respondents all use a single heaping rule. Here we assume a mixture of two distributions (that replicate the observed data very well) and we allow for multiple heaping rules. Our approach also relaxes two very strong assumptions of [6] – that respondents only use a single heaping rule and that, within intervals, respondents randomly heap their responses. In most data both assumptions probably do not hold.
We developed a model-based approach that relies on two key assumptions. First, that observed data result from two distinct and separate processes. In one we assume that the behavior of interest occurs stochastically. In the other we assume that observed behavior responds to external shocks. We also assume that survey respondents either report accurately or they fall into (possibly multiple) groups that each use a different heaping rule when responding to survey questions. We fit the model to simulated data to show that we can recover the parameters of the true distribution very accurately, even when the proportion of heaped responses is very high. We also apply the algorithm to retrospectively reported survey data on smoking cessation from the Panel Study of Income Dynamics. We suggest how one can apply our algorithm to estimate the attenuation bias that heaping appears to cause in regression coefficients (shown empirically in [35]).
Our simulation study revealed two important insights that both guide the application of our methods and recommend it over alternative methods. First, we find that when external shocks occur near a heaping point, researchers must take care when applying the algorithm. If researchers fail to incorporate information about the timing of the events when they apply the algorithm, it may underestimate the actual proportion of heaping. Second, our algorithm is preferred over methods such as coarsening because it does not throw away information. Further, our algorithm is flexible. It can accommodate any distributional assumptions researchers believe underlie the data generating process. In addition, the algorithm easily allows one to model heaping probabilities using subject-specific covariates. Finally, the algorithm is not limited to either a single heaping rule or to assumptions about the specific form of the heaping (e.g. symmetry).
Acknowledgments
This research was supported by Awards # R01 HD048828, R01 AG030379, and R03 AG021014 from the National Institutes of Health
We thank Hua Wang for her work on an earlier (empirical) version of this paper, Daniel Heitjan, Donald Kenkel, George Jakubson, Alan Mathios, Martin T. Wells, John Mullahy, and an anonymous referee for comments, Robert Strawderman for his statistical advice, and Eamon Molloy for his programming assistance. We also thank the ASHE 2010 conference discussant, Anna Sommers, for her comments.
References
- 1.Wang H, Heitjan D. Modeling heaping in self-reported cigarette counts. Statictics in Medicine. 2008 Apr;27:3789–3804. doi: 10.1002/sim.3281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hu P, Tsiatis A. Estimating the survival distribution when ascertainment of vital status is subject to delay. Biometrika. 1996;83:371–380. [Google Scholar]
- 3.Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. Journal Of The Royal Statistical Society, Series B. 1977;39 (1):1–38. [Google Scholar]
- 4.Little R. Incomplete data in event history analysis. In: Trussell J, Hankinson R, Tilton J, editors. Demographic applications of event history analysis. Clarendon Press; Oxford, England: 1992. pp. 209–230. [Google Scholar]
- 5.Torelli N, Trivellato U. Modeling inaccuracies in job-search duration data. Journal of Econometrics. 1993;59(1–2):187–211. doi: 10.1016/0304-4076(93)90045-7. [DOI] [Google Scholar]
- 6.Heitjan DF, Rubin DB. Inference from coarse data via multiple imputation with application to age heaping. Journal of the American Statistical Association. 1990;85(410):304–314. doi: 10.2307/2289765. [DOI] [Google Scholar]
- 7.Crockett A, Crockett R. Consequences of data heaping in the british religious census of 1851. Historical Methods. 2006;39(1):24–39. doi: 10.3200/HMTS.39.1.24–46. [DOI] [Google Scholar]
- 8.Lambert D. Zero-inflated poisson regression, with an application to defetcs in manufacturing. Technometrics. 1992;34(1):1–14. doi: 10.2307/1269547. [DOI] [Google Scholar]
- 9.Forster M, Jones AM. The role of tobacco taxes in starting and quitting smoking: duration analysis of british data. Journal of the Royal Statistical Society Series A-Statistics in Society. 2001;164:517–547. doi: 10.1111/1467-985X.00217. [DOI] [Google Scholar]
- 10.Kenkel D, LeCates J, Liu F. Working paper. 2011. Errors in retrospective data on smoking: Comparing maximum likelihood and ad hoc approaches. [Google Scholar]
- 11.Pudney S. Manuscript. Institute for Social and Economic Research, University of Essex; 2007. Heaping and leaping: Survey response behaviour and the dynamics of self-reported consumption expenditure. [Google Scholar]
- 12.Schneeweiss H, Komlos J, Ahmad A. Symmetric and asymmetric rounding: a review and some new results. AStA Advances in Statistical Analysis. Mar; doi: 10.1007/s10182-010-0125-2. [DOI] [Google Scholar]
- 13.Wright D, Bray I. A mixture model for rounded data. The Statistician. 2003;52(1):3–13. doi: 10.1111/1467-9884.00338. [DOI] [Google Scholar]
- 14.Brentall A, Crowder M, Hand D. Predicting the Amount Individuals Withdraw at Cash Macines Using a Random Effects Multinomial Model. Statictical Modelling. 2010;10(2):197–214. doi: 10.1177/1471082X0801000205. [DOI] [Google Scholar]
- 15.Card D, Chetty R, Weber A. The Spike at Benefit Exhaustion: Leaving the Unemployment System or Starting a New Job? The American Economic Review. 2007;97(2):113–118. doi: 10.1257/aer.97.2.113. [DOI] [Google Scholar]
- 16.Center for Disease Control and Prevention [CDC]. . Smoking cessation during previous year among adults – united states, 1990 and 1991. Morbidity and Mortality Weekly Report. 1993;42(26):504–505. [PubMed] [Google Scholar]
- 17.DiClemente C, Prochaska J, Fairhurst S, Velicer W, Valesquez M, Rossi J. The process of smoking cessation: An analysis of precontemplation, contemplation, and preparation stages of change. Journal of Consulting and Clinical Psychology. 1991;59(2):295–304. doi: 10.1037//0022-006x.59.2.295. [DOI] [PubMed] [Google Scholar]
- 18.Hatziandreu E, Pierce J, Lefkopoulou M, Fiore M, Mills S, Novotny T, Giovino G, Davis R. Quitting smoking in the united states in 1986. Journal of the National Cancer Institute. 1990;82(17):1402–1406. doi: 10.1093/jnci/82.17.1402. [DOI] [PubMed] [Google Scholar]
- 19.Prochaska J, DiClemente C. Stages and process of self-change of smoking: Toward an integrative model of change. Journal of Consulting and Clinical Psychology. 1983;51(3):390–395. doi: 10.1037//0022-006X.51.3.390. [DOI] [PubMed] [Google Scholar]
- 20.Peters H. Retrospective versus panel data in analyzing lifecycle events. Journal of Human Resources. 1988;23(4):488–513. doi: 10.2307/145810. [DOI] [Google Scholar]
- 21.Wu LL, Martin SP, Long DA. Comparing data quality of fertility and first sexual intercourse histories. Journal of Human Resources. 2001;36(3):520–555. doi: 10.2307/3069629. [DOI] [Google Scholar]
- 22.Beckett M, DeVanzo J, Sastry N, Panis C, Peterson C. The quality of retrospective data - an examination of long-term recall in a developing country. Journal of Human Resources. 2001;36(3):593–625. doi: 10.2307/3069631. [DOI] [Google Scholar]
- 23.Kenkel D, Lillard DR, Mathios A. Accounting for measurement error in retro-spective smoking data. Health Economics. 2004;13(10):1031–1044. doi: 10.1002/hec.934. [DOI] [PubMed] [Google Scholar]
- 24.Hasofer AM. A dam with inverse gaussian input. Proc Camb Phil Soc. 1964;60:931–933. doi: 10.1017/S0305004100038391. [DOI] [Google Scholar]
- 25.Banerjee AK, Bhattacharyya GK. A purchase incidence model with inverse gaussian interpurchase times. Journal of American Statistical Association. 1976;71:823–829. doi: 10.2307/2286845. [DOI] [Google Scholar]
- 26.Lancaster A. A stochastic model for the duration of a strike. Journal of Royal Statistical Society, A. 1972;135:257–271. doi: 10.2307/2344321. [DOI] [Google Scholar]
- 27.Del Corral J, Barros CP, Prieto-Rodriguez J. The determinants of soccer player substitutions - a survival analysis of the spanish soccer league. Journal of Sports Economics. 2008;9(2):160–172. doi: 10.1177/1527002507308309. [DOI] [Google Scholar]
- 28.Folks JL, Chhikara RS. The inverse gaussian distribution and its statistical application - a review. Journal of Royal Statistical Society, B. 1978;40(3):263–289. [Google Scholar]
- 29.Spiegelhalter D, Thomas A, Best N, Lunn D. WinBUGS User Manual Version 1.4. 2003. [Google Scholar]
- 30.Gelman A, Carlin JB, Stern HS, Rubin DB. Bayesian Data Analysis. 2. Chapman and Hall; 2004. [Google Scholar]
- 31.Singer JD, Willett JB. It’s about time: Using discrete-time survival analysis to study duration and timing of events. Journal of Educational Statistics. 1993;18(2):155–195. doi: 10.3102/10769986018002155. [DOI] [Google Scholar]
- 32.Cox DR. Regression Models and Life-Tables. Journal of the Royal Statistical Society. 1972;34(2):187–220. [Google Scholar]
- 33.Efron B. Nonparametric estimates of standard error: The jackknife, the bootstrap and other methods. Biometrika. 1981;68(3):589599. doi: 10.1093/biomet/68.3.589. [DOI] [Google Scholar]
- 34.Hausman JA, Abrevaya J, Scott-Morton FM. Misclassification of the dependent variable in a discrete-response setting. Journal of Econometrics. 1998;87(2):239–269. doi: 10.1016/S0304-4076(98)00015-3. [DOI] [Google Scholar]
- 35.Lillard DR, Bar H, Wang H. Working paper. A heap of trouble? accounting for mismatch bias in retrospectively collected data 2010. [Google Scholar]