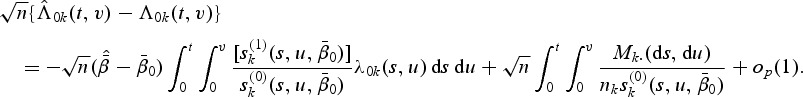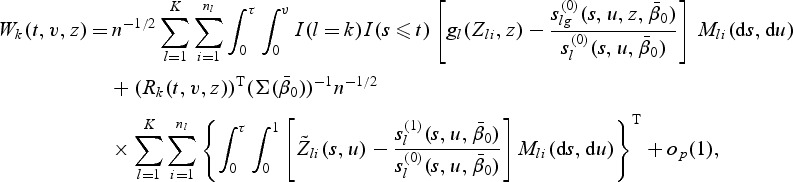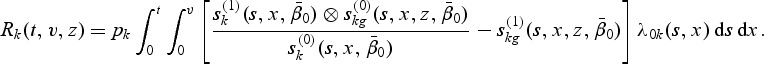Mark-specific proportional hazards model with multivariate continuous marks and its application to HIV vaccine efficacy trials

Abstract

For time-to-event data with finitely many competing risks, the proportional hazards model has been a popular tool for relating the cause-specific outcomes to covariates (Prentice and others, 1978. The analysis of failure time in the presence of competing risks. Biometrics 34, 541–554). Inspired by previous research in HIV vaccine efficacy trials, the cause of failure is replaced by a continuous mark observed only in subjects who fail. This article studies an extension of this approach to allow a multivariate continuum of competing risks, to better account for the fact that the candidate HIV vaccines tested in efficacy trials have contained multiple HIV sequences, with a purpose to elicit multiple types of immune response that recognize and block different types of HIV viruses. We develop inference for the proportional hazards model in which the regression parameters depend parametrically on the marks, to avoid the curse of dimensionality, and the baseline hazard depends nonparametrically on both time and marks. Goodness-of-fit tests are constructed based on generalized weighted martingale residuals. The finite-sample performance of the proposed methods is examined through extensive simulations. The methods are applied to a vaccine efficacy trial to examine whether and how certain antigens represented inside the vaccine are relevant for protection or anti-protection against the exposing HIVs.

1. Introduction

Around 30 years ago, Prentice and others (1978) developed the mark-specific proportional hazard (PH) model for discrete marks, and since then a great deal of work has been done in discrete-mark failure time analysis, cf., Kalbfeisch and Prentice (1980), Sun (2001) and Scheike and others (2008). Alternatively, Huang and Louis (1998) first considered a continuous mark and developed the nonparametric maximum likelihood estimator of the joint distribution of the failure time and the mark. Motivated by applications in preventative HIV vaccine randomized placebo-controlled efficacy trials, Gilbert and others (2004, 2008) developed procedures for testing dependence of mark-specific hazards rates and relative risks (RRs) on the mark variable. Sun and others (2009) developed estimation and hypothesis testing methods for the mark-specific PH model with a univariate continuous mark. The mark variable of interest is a measure of the protein sequence distance between an HIV sequence sampled from a volunteer infected in the trial, to an HIV sequence represented inside the tested vaccine construct. As such, the scientific question is if and how the vaccine's effect to reduce the hazard of HIV acquisition depends on the sequence distance mark; answers to this question may guide vaccine development, as discussed extensively in the above-cited papers and elsewhere.

However, the previous work did not account for multivariate marks. This is a serious limitation given that all of the candidate HIV vaccines tested in HIV vaccine efficacy trials have contained multiple antigens/immunogens, with rational to attempt to elicit multiple types of immune response that recognize and block different types of HIV viruses. The greater the number of virus types that can be recognized and killed by vaccine-induced immune responses, the greater the potential overall vaccine efficacy. In the first two efficacy trials, the HIV vaccine construct contained two Envelope (Env) protein antigens, based on two distinct strains of HIV, such that a two-dimensional mark variable is of interest (Flynn and others, 2005; Pitisuttithum and others, 2006). The vaccine construct evaluated in the third and fourth efficacy trials contained Gag, Pol, and Nef protein antigens, making a three-dimensional mark variable of interest (Buchbinder and others, 2008; Gray and others, 2009). Lastly, the fifth and most recent efficacy trial tested a vaccine that contained Gag, Pol, and Nef protein antigens, as well as three distinct Env protein antigens, making a six-dimensional mark variable of interest (Rerks-Ngarm and others, 2009).

The previous work dealt with the multivariate mark issue by collapsing the multiple distances from an infected subject into a univariate mark—the minimum of the distances to each vaccine antigen. This approach is reasonable under the premise that the only thing that matters for protection is the nearness of the exposing HIV to the closest antigen represented inside of the vaccine (e.g. Gilbert and others, 2008). However, there are many ways in which this assumption may fail. For example, based on host genetics (e.g. HLA type or Fc-γ-receptor type), one subgroup may be protected through immune responses that recognize HIV peptides that are similar to HIV peptides represented in antigen 1, whereas another subgroup may be protected through immune responses that are similar to HIV peptides represented in antigen 2; in this case, the vaccine efficacy depends on both individual distances and less so on the minimum distance. For a second example, there are many ways to define a protein sequence distance to be putatively immunologically relevant [several distances were used in the sequence analysis of the Buchbinder and others (2008) efficacy trial reported in Rolland and others (2011)], and if two distances are used such that the first considers many HIV sites irrelevant for protection whereas the second sagely restricts attention to key HIV sites that are contained in epitopes that cause protection, then the first distance could be shorter even though vaccine efficacy depends only on the second. Therefore, a more general approach to assessing and modeling how vaccine efficacy depends on multiple sequence distances is needed, which does not pre-assume a particular way to collapse the multivariate distances into a univariate distance. Outside of the survival analysis field, Gilbert (2000) studied such a general approach with multivariate marks, based on a semiparametric biased sampling model. However, this method is limited by the fact that the model conditions on infection, so that conditional odds ratios but not prospective RRs of infection can be estimated, and by the fact that the model treats HIV infection as a binary outcome, not accounting for the time to HIV infection.

Let λ(t,v|z) be the conditional mark-specific hazard function, defined as 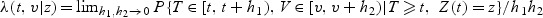, where T is the failure time, V is a continuous mark variable, and Z(t) is a time-dependent p-dimensional covariate. Sun and others (2009) studied the mark-specific PH model

(1.1)

for evaluating the mark-specific vaccine efficacy. Under this model, the ratio of hazard functions for any two individuals is a function of the mark independent of time. This assumption may not always be met in practice, and can be relaxed through stratification (Dabrowska, 1997). Here we propose to study the stratified mark-specific PH model with multivariate marks where the baseline hazard function can vary with stratum. Under the stratified mark-specific PH model, the ratio of hazard functions for any two individuals within same stratum is independent of time. However, it may be time dependent for two individuals from different strata. For simplicity, we consider a two-dimensional mark variable v=(v₁,v₂). The methods for general multivariate mark follow a similar outline. Note that the mark-specific RR function β(v)=β(v₁,v₂) is a p-dimensional function depending on v. Estimation of β(v) without any structural assumptions is possible following the procedure for one-dimensional mark variable by Sun and others (2009). However, this would require a very large sample size due to the curse of dimensionality. In this paper, we consider a parametric model for β(v) as the first-order Taylor approximation of β(v) plus an interaction term that allows investigation of the effects of both marks as well as the interactions. We develop an estimation procedure for the stratified mark-specific PH model under this parametric structure for β(v). We also develop some testing procedures examining how the vaccine efficacy depends on the marks and how relevant the two marks are for protection against HIV infection. The goodness of fit of the proposed model is tested based on the generalized weighted martingale residuals.

The rest of the paper is organized as follows. In Section 2, we develop a partial likelihood procedure for estimating β(v). The asymptotic properties of the proposed estimator are derived. Likelihood-based statistical tests are proposed to examine a variety of null hypotheses to understand whether and how the vaccine efficacy depends on the marks. In Section 3, we propose a procedure for testing goodness of fit of the multivariate mark-specific proportional hazard model based on the generalized weighted martingale residuals. The proposed methods are applied to a vaccine efficacy trial in Section 4. Extensive simulations are conducted to examine the finite sample performance of the proposed methods in Section 5. Proofs of the main results are placed in the supplementary material available at Biostatistics online.

2. Mark-specific PH model with multivariate marks

2.1. Mark-specific PH model

Let λ_k(t,v|z) be the conditional mark-specific hazard function at time t with mark v for a subject in stratum k with covariate z (Sun and others, 2009). We assume that the mark V takes value in the interval [0,1]², rescaled if necessary. The stratified multivariate mark-specific PH model speculates that

(2.1)

for k=1,2,…,K, where K is the number of the strata, λ_0k(t,v) is an unspecified baseline mark-specific hazards function for kth stratum, z is a p-dimensional covariate, and β(v) is a p-dimensional vector of regression functions. Here we assume that β(v) is given by

(2.2)

where each of β₀,β₁,β₂, and β₁₂ is a p-dimensional vector. Thus β(v) is completely specified by the 4×p parameters denoted by 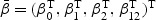. Let z=(z₁,z₂(t))^T, where z₁ is the vaccine group indicator, with z₁=1 for the vaccine group and z₁=0 for the placebo group, while z₂(t) is other possibly time-dependent covariates. Under the mark-specific PH model (2.1), the mark-specific RR is 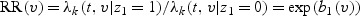, where b₁(v) is the coefficient corresponding z₁. The mark-specific vaccine efficacy VE(v)=1−RR(v) represents the percentage reduction for the vaccine versus placebo in risk of failure at time t with mark v after adjusting for covariates z₂. It does not depend on time t under model (2.1).

Let T_k be the failure time for an individual in the kth stratum, V _k be the mark observed at failure and Z_k be the associated p-dimensional covariate. Assume that (T_k,V _k,Z_k) follows model (2.1). Under right censoring, the observed random variables are (X_k,δ_k,δ_kV _k,Z_k), where 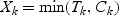, δ_k=I(T_k≤C_k) and C_k is the censoring random variable, which is assumed to be independent of (T_k,V _k) given Z_k. The mark variable V _k is observed if the failure time is uncensored. Let (X_ki,δ_ki,δ_kiV _ki,Z_ki), i=1,…,n_k, be independent identically distributed (iid) replicates of (X_k,δ_k,δ_kV _k,Z_k) from stratum k, for k=1,2,…,K. Let τ be the end of follow-up time, where failure times beyond τ are considered censored. The estimation of model (2.1) for β(v) under parametric structure (2.2) is given next.

2.2. Estimation of the mark-specific PH model

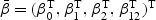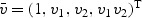Let N_ki(t,v)=I(X_ki≤t,V _ki≤v,δ_ki=1) be the marked counting process for ith individual in stratum k, where the relation V _ki≤v indicates that the inequality holds for each component of the multivariate mark. Let Y _ki(t)=I(X_ki≥t) be the at-risk process. Under (2.2), β(v) is completely specified by . Let and 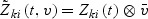with ⊗ being the Kronecker product. Similar to Kalbfleisch and Prentice (1980) for the competing risks model with finite number of causes, the log-partial likelihood function for can be expressed as

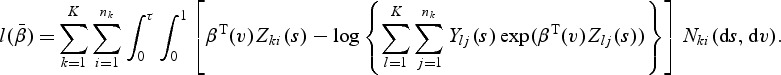(2.3)

Since 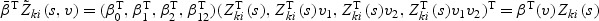, we have

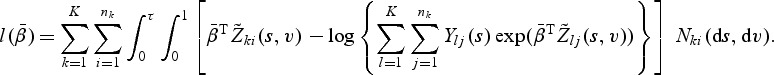(2.4)

The maximum partial likelihood estimator (MPLE) 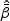for 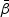is obtained by maximizing 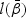given in (2.4). Taking the derivative of 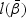with respect to 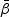, the score function can be written as

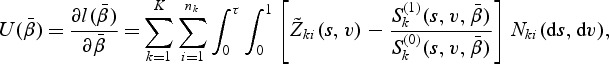(2.5)

where 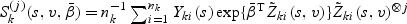 for j=0,1,2. Here for a vector z, z^⊗0=1, z^⊗1=z, and z^⊗2=zz^T. Let 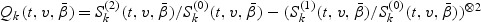. The information matrix is the derivative of 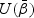with respect to 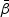given as

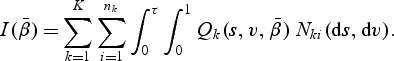(2.6)

The MPLE 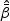for 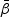is the solution to 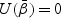. Under condition 1 in Section 2.3, the matrix 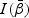is positive definite with probability 1 as 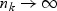for 1≤k≤K. Thus 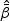exists almost surely and is unique for large sample sizes. The baseline function λ_0k(t,v) can be estimated by smoothing the increments of the following estimator of the doubly cumulative baseline function :

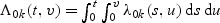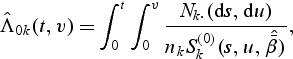(2.7)

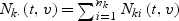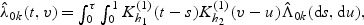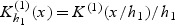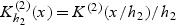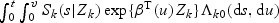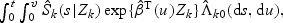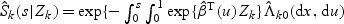where . A kernel estimator of λ_0k(t,v) is given by where and , K⁽¹⁾(⋅) and K⁽²⁾(⋅) are kernel functions, and h₁ and h₂ are the corresponding bandwidths. The cause-related cumulative incidence function P(T_k≤t,V _k≤v|Z_k)= can be estimated by where and .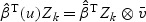

2.3. Asymptotic results

Let 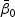be the true value of 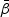under models (2.1) and (2.2). Let 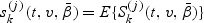, for j=0,1,2, and 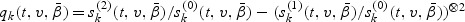. Let 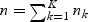. We make use of the following regularity conditions.

Condition 1 —

The covariate process Z_k(t) is left continuous with bounded variation and satisfies the moment condition , where ∥⋅∥ is the Euclidean norm and M is a positive constant such that ( for 1≤k≤K.

Condition 2 —

For 1≤k≤K, λ_0k(t,v) is continuous on [0,τ]×[0,1]², and each component of is continuous on [0,τ]×[0,1]²×ℬ, where ℬ is an neighborhood of .

Condition 3 —

The limit n_k/n→p_k exists as for 0<p_k<1 for 1≤k≤K. The matrix is positive definite for .

The asymptotic results for 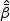and 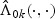, 1≤k≤K, are presented in the following theorems.

Theorem 2.1 —

Under conditions 1–3, converges in probability to as .

Theorem 2.2 —

Under conditions 1–3, as , where can be consistently estimated by .

Theorem 2.3 —

Under conditions 1–3, the following decomposition holds uniformly in (t,v)∈[0,τ]×[0,1] for 1≤k≤K as :

is asymptotically independent of the processes , k=1,…,K, with the latter being asymptotically independent mean-zero Guassian random fields with variances and with independent increments.

2.4. Hypothesis testing

We propose some statistical tests for evaluating whether and how the vaccine efficacy depends on the marks. The following null hypotheses are examined: H₁₀:β₁=β₂=β₁₂=0; H₂₀:β₁₂=0; H₃₀:β₂=β₁₂=0 and H₄₀:β₁=β₁₂=0. The null hypothesis H₁₀ indicates that the RRs do not depend on the marks; H₂₀ implies that the marks v₁ and v₂ do not have interactive effects on RRs; H₃₀ implies that RRs are not affected by v₂; while H₄₀ implies that RRs are not affected by v₁.

Likelihood-based tests such as the likelihood ratio test (LRT), Wald test, and score test are commonly used in the parametric settings. Here we adopt these tests for model (2.1) with β(v) having the parametric structure (2.2). The tests are constructed based on the log-partial likelihood function 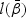given in (2.4). Let 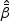be the MPLE maximizing 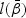. Denote H₀ as one of the null hypotheses H₁₀, H₂₀, or H₃₀. Let 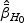be the estimator of 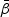under H₀, which is the maximizer of 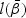under H₀. For example, for H₁₀, 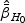is the maximizer of 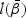under the restriction β₁=β₂=β₁₂=0. The LRT statistic is 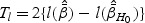. The Wald test statistic is given by 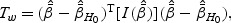where the information matrix 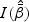is defined in (2.6). The score test statistic is given by 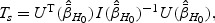where the score function 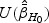and information matrix 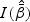are defined in (2.5) and (2.6), respectively.

Routine analysis following Serfling (1980) shows that under H₀, T_l, T_w, and T_s converge in distribution to a chi-square distribution with degrees of freedom equal to the number of parameters specified under H₀. The LRT rejects H₁₀ if 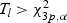, the upper α quantile of the chi-square distribution with 3p degrees of freedom. The corresponding critical values for testing H₂₀, H₃₀, and H₄₀ are 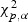, , 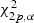and 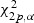, respectively. Similar decision rules hold for the Wald test with test statistic T_w and the score test with test statistic T_s. The parameters β₁,β₂, and β₁₂ specified in the null hypotheses are p-dimensional vectors. The tests can be carried out for the hypotheses that only concern a single component of the coefficients to examine how one particular covariate effect is modified by the marks.

3. Goodness-of-fit tests

The estimation and testing procedures developed in Section 2 are developed under model (2.1) with β(v) having the parametric structure (2.2). The validity of these procedures depends on goodness of fit of the multivariate mark-specific proportional hazard model. This section develops some goodness-of-fit tests of model (2.1) under the parametric structure (2.2) for β(v) following Lin and others (1993). Let 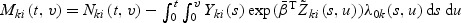. We derive the model checking test statistics based on the cumulative martingale residuals defined as

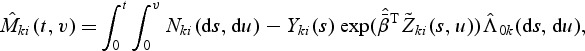(3.1)

where 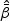is the MPLE given in Section 2, and 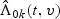is defined in (2.7). 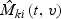may be interpreted as the difference up to time t between the observed and the predicted number of events with marks at failures less than v for the ith subject in kth stratum. Thus the martingale residuals are informative about model misspecifications. It is easy to check that .

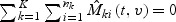For 1≤k≤K, let

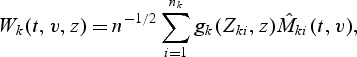(3.2)

where g_k(Z_ki,z) is a 1×r-vector of known bounded functions of Z_ki and z. For example, one may take g_k(Z_ki,z)=f_k(Z_ki)I(Z_ki≤z), where f_k(⋅) is a known function and I(Z_ki≤z)={I(Z_1ki≤z₁),…,I(Z_pki≤z_p)}, in which case r=p. We construct goodness-of-fit test statistics based on the test process W(t,v,z)=(W₁(t,v,z),…,W_K(t,v,z)). If models (2.1) and (2.2) hold, the process W(t,v,z) fluctuates randomly about zero. Various test statistics can be constructed by selecting different weight functions f_k(⋅) and using different functionals of the process W(t,v,z). Here we propose the supremum test statistics to test the overall fit of the model:

(3.3)

The distribution of S under the null hypothesis is complicated and intractable. To calculate the critical value of the proposed test statistic, we consider using the Guassian multiplier method (Lin and others, 1993) that can be applied to approximate the distribution of the process W(t,v,z). The key step toward the application of this method is to approximate W(t,v,z) with the sum of iid processes as shown next.

Let 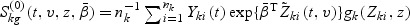and 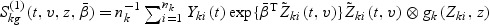, where A⊗B is the Kronecker product of matrices A and B. Let 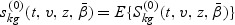and 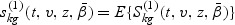. The proof of the following decomposition is given in the supplementary material at Biostatistics online.

Theorem 3.1 —

Assume conditions 1–3. For 1≤k≤K, we have

(3.4)

as where

Expression (3.4) shows that the process W_k(t,v,z) is asymptotically equivalent to the sum of iid terms involving the integrations with respect to M_li(s,u). Donsker's theorem (cf., van der Vaart, 1998) on the weak convergence of empirical processes can be used to show that the process W(t,v,z)=(W₁(t,v,z),…,W_K(t,v,z)) converges weakly to a multi-dimensional Gaussian random field.

Let {ξ_li,i=1,…,n_l,l=1,…,K} be iid standard normal random variables. For 1≤k≤K, let

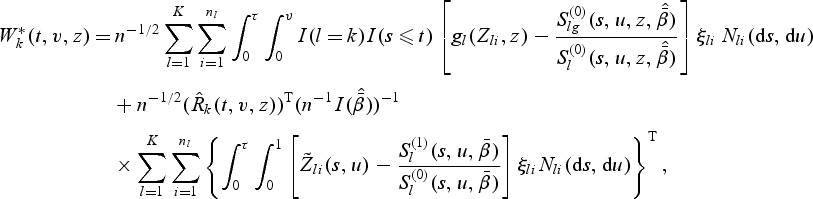(3.5)

where

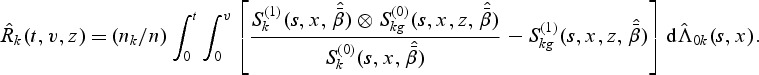Following an application of Sun and Wu (2005, Lemma 1), the distribution of W(t,v,z) can be approximated by the conditional distribution of 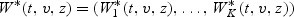given the observed data sequence. The continuous mapping theorem entails that the distribution of S can be approximated by the empirical distribution of 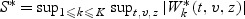obtained through repeatedly generating independent sets of {ξ_li,i=1,…,n_l,l=1,…,K} while holding the observed data fixed. We reject model (2.1) under the parametric structure (2.2) for β(v) at the significance level α if S is greater than the critical value S_α—the upper α quantile of the copies of S* described above.

4. Application to a vaccine efficacy trial

We now illustrate our methods with the analysis of data from a vaccine efficacy trial conducted in North and South America (Buchbinder and others, 2008). The ‘Step’ trial randomized 1836 HIV-negative men to receive either the Merck Adenovirus 5 (Ad5) vaccine (MRKAd5) or placebo. Women were also enrolled, but only one became HIV infected. Of the 1836 men, 87 acquired HIV infection. The sequencing labs attempted to derive single-genome-amplification HIV sequences from all 87 subjects, and were only successful for 65. The 22 men with no sequence data were excluded from the analysis, and therefore for the method to provide consistent estimation the missing completely at random (MCAR) assumption is needed. While MCAR seems reasonable in the application (partial support comes from an analysis of the predictors of missing sequence data, which uncovered no significant predictors), it cannot be assured. Sun and Gilbert (2012) developed an augmented inverse probability-weighted approach to provide consistent estimation and inference in the mark-specific proportional hazards model under a missing at random (MAR) assumption, but this method considered only a univariate mark variable. It would be of interest to extend their method to the multivariate mark setting. Alternatively, it would be of interest to extend the multiple imputation approach of Lu and Tsiatis (2001) from the discrete mark setting to the continuous mark setting. The randomization was stratified by whether a volunteer had pre-existing immunity to the Ad5 vector that was used in the vaccine, defined by an Ad5 neutralization titer greater than 200. The method is implemented accounting for these two strata, where 1058 (778) volunteers had Ad5 below (above) 200. In the data analysis, we focus on men only.

For those with Ad5 ≤200, there were 54 total infections: 29 of 522 in the vaccine group (with 7 missing marks) and 25 of 536 in the placebo group (with 8 missing marks). The annual incidences were 5.6% for the vaccine group and 4.7% for the placebo group. For Ad5>200, there were 33 total infections: 24 of 392 in the vaccine group (with 7 missing marks) and 9 of 386 infections in the placebo group (with 0 missing marks). The annual incidences were 6.1% for the vaccine group and 2.3% for the placebo group.

Two factors motivate the need to consider multiple protein sequence distances for the sieve analysis (Gilbert, 2000). First, the MRKAd5 vaccine contained three HIV-1 proteins: Gag, Pol, and Nef. Each of these proteins stimulates immune responses in vaccine recipients that could plausibly make the vaccine effect on infection vary with genetic distance to the protein. As a control, it is also of interest to evaluate genetic distances to all of the HIV-1 vaccine proteins combined not included in the vaccine, Env-Rev-Tat-Vif-Vpr-Vpu, for which the central HXB2 reference strain was used. Because the vaccine should not be able to stimulate immune responses to these proteins, it is expected that the vaccine effect on infection would not vary with this control genetic distance. Secondly, as described in greater detail in the clinical paper (Rolland and others, 2011), two different bioinformatics methods, NetMHC (Buus and others, 2003) and Epipred (Heckerman and others, 2007), were used to predict, for each infected subject, the set of HIV peptides in the reference sequence that could potentially bind to at least one of his/her HLA alleles. These peptides are the ones that could potentially constitute T-cell epitopes and hence contribute to a vaccine effect on infection.

NetMHC predicts quantitative binding of peptides to four-digit HLA alleles, whereas Epipred identifies known and potential HIV-1 CTL epitope motifs using two-digit HLA information. In addition to the known HLA-restricted epitopes previously reported at the Los Alamos National Laboratory HIV database (HIVDB), we accepted all epitope motifs with a posterior probability of >0.8. HLA-specific epitopes were predicted in the Gag-Pol-Nef protein sequence contained in the tested vaccine (the ‘Step’ reference sequence) and in all proteins from the HXB2 reference sequence (available at the HIVDB, http:www.hiv.lanl.gov). Using Epipred, the first step in computing the distance between a subject's sequences and the reference sequence is to compute the nonparametric maximum likelihood estimate (NPMLE) of the number of peptides shared between the reference sequence and the subject's sequences, defined as the sum of estimated epitope-probabilities across all 8-, 9-, 10-, 11-mers in the reference sequence that are exactly matched in all of the subject's sequences. Then, the distance is the NPMLE of the percent of peptides mismatched in at least one of the subject's sequences, defined as one minus the ratio of the NPMLE of the number of shared peptides (computed in the first step) and the NPMLE of the number of peptides in the reference sequence. Because the NetMHC software categorizes quantitative binding readouts as nonbinder, weak binder, or strong binder, we defined the distance as the estimated percent of epitopes mismatched in at least one of the subject's sequences, the latter defined as the number of weak or strong binding 8-, 9-, 10-, or 11-mers in the reference sequence that mismatch the corresponding peptide in at least one of the subject's sequences.

We consider distances defined using the reference HIV-1 regions Gag, Pol, Nef, Env-Rev-Tat-Vif-Vpr-Vpu, as well as using the two bioinformatics prediction methods. The five selected marks, {v_j,j=1,…,5}, are listed in Table 1. We analyze the data with the mark-specific proportional hazards model (2.1), where the covariate z is the indicator for the treatment, with z=1 for the vaccine group and 0 for placebo group. The K=2 strata are the Ad5≤200 and Ad5>200 groups. We use the standardized marks in the analysis, which are obtained by subtracting the minimum and dividing the range of the measurements for each mark. We perform the backwards model selection procedure by starting the analysis with all five marks in the model (2.1) with 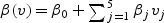. The marks with nonsignificant coefficients are eliminated one at a time, each time the mark with the least significant p-value is eliminated. The backward selection procedure retains the last two marks v₁ and v₂.

Table 1.

The specifications of the five selected marks based on the step data

Mark	Type	Ref†	Protein
v1	Epipred	HXB2	Env-Rev-Tat-Vif-Vpr-Vpu
v2	NetMHC	HXB2	Env-Rev-Tat-Vif-Vpr-Vpu
v3	Epipred	Step	Gag
v4	Epipred	Step	Pol
v5	Epipred	Step	Nef

^†The reference HIV-1 sequence, either a sequence represented in the vaccine tested in the Step trial (Step) or a commonly studiedcentral HIV reference sequence that was not in the vaccine (HXB2).

For the remaining two marks v₁ and v₂, we fit the model (2.1) with β(v)=β₀+β₁v₁+β₂v₂+β₁₂v₁v₂. The goodness of fit of model (2.1) with β(v) given by (2.2) is conducted following the procedure given in Section 3 with the test statistic 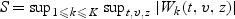. We set f_k(z)=1 and K=2. The p-value is calculated as the percentage of 500 copies of 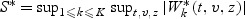greater than S. The p-value for the bivariate mark selection is 0.56. These result supports that the model fit is adequate. The estimates 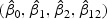are (3.43,−3.40,−10.61,13.90). The standard errors of 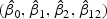are (1.52,2.96,3.63,5.79). Table 2 shows the p-values of the LRT, Wald test (Wald), and score test (Score) for testing H₁₀–H₄₀ described in Section 2.4. All four hypotheses are rejected with borderline significance level near 0.05, with consistent p-values across the three tests.

Table 2.

The p-values of the LRT, Wald test, and score test for testing H₁₀, H₂₀, and H₃₀ for the bivariate marks (v₁,v₂) for the step data

Mark selection	Hypothesis	LRT	Wald	Score
(v1,v2)	H10	0.0357	0.0728	0.0468
	H20	0.0455	0.0779	0.0586
	H30	0.0386	0.0857	0.0483
	H40	0.0152	0.0329	0.0205

Because the overall infection rate was higher in the vaccine than placebo group (Cox model RR = 1.50, 95% CI 0.95–2.41, p=0.06), we estimate the mark-specific RR as RR(v₁,v₂)=exp(β₁(v₁,v₂)) instead of the mark-specific vaccine efficacy; thus for the step trial the analysis focuses on whether and how the vaccine selectively increased the susceptibility to HIV infection. Based on the β point estimates, the estimated RR, 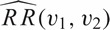(its standard error), equals 3.27 (3.14), 0.91 (1.63), and 3.08 (11.21) for (v₁,v₂) = (0.2,0.2), (0.5, 0.5), and (0.8, 0.8), respectively. Hence the 95% confidence intervals for RR(v₁,v₂) is (−2.88,9.42), (−2.28,4.10), and (−18.89,25.05) at (v₁,v₂) = (0.2,0.2), (0.5, 0.5), and (0.8, 0.8), respectively. The interpretation is that the vaccine had no effect on infection against HIV-1 when both distances are in the range from 0.2 to 0.8.

5. Simulation study

5.1. Numerical performance of estimation and hypothesis testing procedures

In this section, we conduct a simulation study to examine finite sample properties of the proposed estimation and hypothesis testing procedures. The simulations are set up to mimic the step data from the HIV vaccine efficacy trial conducted in North and South America (Buchbinder and others, 2008). We take K=2 strata corresponding to two levels of neutralization titer Ad5. Two sample sizes n_k=250 and 400 are considered for each stratum. The baseline hazard functions λ_0k(t,v) are set as constants λ_0k, with λ₀₁=0.4 and λ₀₂=0.6. The covariate Z_k is a Bernoulli random variable with Z_k=1 corresponding to the vaccine group and Z_k=0 for the placebo group. We take P(Z_k=1)=0.5. The censoring time C_k follows an exponential distribution, independent of (T_k,V _k). We consider the following selections of (β₀,β₁,β₂,β₁₂) under (2.1) and (2.2) to examine the proposed estimation and hypothesis testing procedures:

Here M₁₀ is a model under the null hypothesis H₁₀ which states that β(v) does not depend on either mark v₁ or v₂. Under M₁₁, the mark-specific RR depends on both marks but not the interaction of these marks. Under M₁₂, the mark-specific RR depends on both marks and their interaction. M₂₀ is a model under the null hypothesis H₂₀ where only β₁₂ is zero, and M₃₀ is a model under the null hypothesis H₃₀ where β(v) does not depend on v₂. The overall RRs of the vaccine versus the placebo in most of the settings are around 50%. The percentage of censoring in all settings is about 70% at the end of follow-up τ=2.

Table 3 lists the bias, the sample standard error of the estimates (SSE), the average of the estimated standard errors (ESE), and the coverage probability (CP) for β for sample size n_k=250 and 400. Table 3 shows that the biases of the estimators are small, ESE approximates SSE well, and the coverage probabilities are very close to their nominal level of 0.95. Table 4 summarizes the empirical sizes and powers of the LRT, Wald test, and the score test for testing H₁₀,H₂₀, and H₃₀ at the significance level α=0.05. The average numbers of cases for the vaccine (Vx) and placebo (Plb) groups for are also reported. Each entry of Tables 3 and 4 is calculated based on 1000 simulations. Table 4 shows that the empirical sizes of all these tests are close to 0.05. The LRT has better power than the Wald and score tests. The powers of the tests increase as the simulation model moves from M₁₁ to M₁₂, representing an increased departure from H₁₀. Similarly, the powers of these tests for testing H₂₀ increase in the direction from M₂₁ to M₂₂. The powers for testing H₃₀ also increase in the direction from M₃₁ to M₃₂, and the powers increase as the sample size increases. The coverage probabilities for β₀, β₁, β₂, and β₁₂ are also listed to demonstrate that the proposed maximum partial likelihood methods work very well.

Table 3.

Summary statistics and coverage probabilities of the 95% confidence intervals for (β₀,β₁,β₂,β₁₂) under models M₁₀, M₂₀, and M₃₀

Model	(n1,n2)	Coefficient	Bias	SSE	ESE	CP
M10	(250,250)	β0	-0.0185	0.6904	0.6757	0.960
		β1	0.0125	1.2292	1.1744	0.959
		β2	0.0169	1.2342	1.1817	0.950
		β12	-0.0226	2.1348	2.0509	0.951
	(400,400)	β0	-0.0235	0.5244	0.5275	0.953
		β1	0.0480	0.8983	0.9154	0.958
		β2	0.0283	0.9399	0.9145	0.958
		β12	-0.0619	1.5955	1.5883	0.956
M20	(250,250)	β0	-0.0210	0.7824	0.7884	0.964
		β1	0.0174	1.2611	1.2736	0.968
		β2	0.0100	1.2865	1.2824	0.954
		β12	0.0005	2.0566	2.0802	0.958
	(400,400)	β0	-0.0340	0.6226	0.6171	0.957
		β1	0.0211	0.9909	0.9945	0.962
		β2	0.0308	1.0004	1.0020	0.962
		β12	0.0080	1.6225	1.6216	0.963
M30	(250,250)	β0	-0.0428	0.8601	0.8208	0.957
		β1	0.0686	1.3330	1.2942	0.957
		β2	-0.0021	1.4785	1.4268	0.960
		β12	-0.0177	2.2907	2.4680	0.961
	(400,400)	β0	-0.0179	0.6560	0.6356	0.946
		β1	0.0043	1.0254	1.0026	0.946
		β2	-0.0703	1.1276	1.1045	0.950
		β12	0.0816	1.7516	1.7407	0.954

Table 4.

The empirical sizes and powers of the LRT, Wald test, and score test for testing the null hypotheses H₁₀, H₂₀, and H₃₀ at the significance level 0.05

Model	n1(Vx,Plb)	n2(Vx,Plb)	LRT	Wald	Score
		Testing H10:β1=β2=β12=0
M10	250 (24,46)	250 (34,60)	6.4	4.8	6.2
	400 (39,73)	400 (54,97)	4.7	3.6	4.4
M11	250 (25,46)	250 (35,60)	56.4	53.2	54.9
	400 (41,74)	400 (51,97)	74.1	73.2	73.8
M12	250 (30,46)	250 (42,60)	76.4	72.9	75.9
	400 (49,74)	400 (67,97)	91.7	91.2	91.5
		Testing H20:β12=0
M20	250 (25,46)	250 (36,60)	4.9	4.2	4.6
	400 (41,74)	400 (57,96)	3.9	3.8	3.8
M21	250 (23,46)	250 (32,60)	34.0	39.3	38.2
	400 (37,74)	400 (52,97)	51.0	55.2	54.2
M22	250 (30,46)	250 (41,60)	40.0	43.3	42.0
	400 (48,74)	400 (67,97)	53.7	57.6	56.8
		Testing H30:β2=β12=0
M30	250 (20,46)	250 (29,60)	5.6	4.8	5.5
	400 (33,74)	400 (47.97)	3.9	3.6	3.9
M31	250 (29,46)	250 (41,60)	62.8	60.2	61.8
	400 (48,74)	400 (65,96)	83.0	82.1	82.6
M32	250 (30,46)	250 (41,60)	74.6	73.3	74.2
	400 (48,74)	400 (66,97)	91.3	90.9	91.2

5.2. Numerical performance of goodness-of-fit procedure

In this section, we conduct a simulation study to check the finite sample performance of the proposed goodness-of-fit testing procedure based on the test statistic S=sup_1≤k≤Ksup_t,v,z|W_k(t,v,z)| defined in (3.3). We set f_k(z)=1 and K=2. The size of the test is examined using the following simple stratified mark-specific proportional hazards model:

(5.1)

where λ₀₁=0.4, λ₀₂=0.6 and (β₀,β₁,β₂,β₁₂)=(−1.65,0.4,0.9,1.2). The covariate Z_ki is a Bernoulli random variable with P(Z_ki=1)=0.5. The censoring times are generated from an exponential distribution, independent of (T_ki,V _ki). The first block in Table 5 shows the empirical sizes of the test for sample sizes of n=n₁+n₂=100, 200, and 300. The empirical sizes are calculated based on 1000 simulations and 500 Gaussian multiplier samples, and they are very close to the 0.05 nominal level.

Table 5.

The empirical sizes and powers of goodness-of-fit tests at the significance level 0.05

Model	n1(Vx,Plb)	n2(Vx,Plb)	Size/power
M40	50 (5,9)	50 (8,12)	6.2
	100 (12,18)	100 (16,24)	5.2
	150 (18,27)	150 (25,36)	6.0
M41	50 (4,8)	50 (8,13)	49.8
	100 (9,16)	100 (16,27)	79.0
	150 (14,24)	150 (25,40)	87.4
M42	50 (5,10)	50 (10,15)	61.0
	100 (11,20)	100 (20,31)	87.0
	150 (17,30)	150 (31,47)	92.4
M43	50 (7,12)	50 (11,17)	69.4
	100 (13,24)	100 (23,35)	92.4
	150 (21,36)	150 (36,52)	97.0

To evaluate the power of proposed test, we consider the model

(5.2)

where λ_0k(t,v)=abkt^(b−1)exp{at^b−0.4v₁−0.6v₂}, and a and b are the parameters whose values are to be selected. Again we take Z_ki as a Bernoulli random variable with P(Z_ki=1)=0.5. Model (4.1) is not a mark-specific proportional hazards model since the relative hazard ratio λ_k(t,v|z=1)/λ_k(t,v|z=0)=exp{at^b−0.4v₁−0.6v₂} changes with time. We consider the alternative models specified by the choices of (a,b), defined as M₄₁:(a,b)=(0.20,0.30); M₄₂:(a,b)=(0.25,0.40); and M₄₃:(a,b)=(0.30,0.50). As a and b increase, the rate of change with respect to t of the relative hazard ratio increases, which represents an increased departure from the null hypothesis. For each of the models M₄₁, M₄₂, and M₄₃, random right censoring times are generated from an exponential distribution, independent of (T_ki,V _ki). The empirical powers of the test at the significance level 0.05 under the models M₄₁, M₄₂, and M₄₃ at sample sizes n=n₁+n₂=100, 200, and 300 are given in Table 5. Each entry of the table is based on 1000 simulations and 500 Gaussian multiplier samples. The power of the test increases with increasing (a,b), and also increases with sample size. The limited simulation study demonstrates the validity of the proposed goodness-of-fit testing procedure. The test provides a valuable tool to check the adequacy of the stratified mark-specific proportional hazards model specified in (2.1) and (2.2).

Supplementary material

Supplementary material is available at http://biostatistics.oxfordjournals.org.

Funding

This research was partially supported by the National Institutes of Health (grant number R37 AI054165-09). The research of Y.S. was also partially supported by the National Science Foundation (grant number DMS-0905777).