Unified Resolution Bounds for Conventional and Stochastic Localization Fluorescence Microscopy

Abstract

Superresolution microscopy enables imaging in the optical far field with ~20 nm-scale resolution. However, classical concepts of resolution using point-spread and modulation-transfer functions fail to describe the physical limits of superresolution techniques based on stochastic localization of single emitters. Prior treatments of stochastic localization microscopy have defined how accurately a single emitter’s position can be determined, but these bounds are restricted to sparse emitters, do not describe conventional microscopy, and fail to provide unified concepts of resolution for all optical methods. Here we introduce a measure of resolution, the information transfer function (ITF), that gives physical limits for conventional and stochastic localization techniques. The ITF bounds the accuracy of image determination as a function of spatial frequency and for conventional microscopy is proportional to the square of the modulation-transfer function. We use the ITF to describe how emitter density and photon counts affect imaging performance across the continuum from conventional to superresolution microscopy, without assuming emitters are sparse. This unified physical description of resolution facilitates experimental choices and designs of image reconstruction algorithms.

Exploring the physical bounds on light microscopy has been a mainstay activity in theoretical optics. In classical [1, 2] and in most modern treatments [3] the limits on resolution have been derived using deterministic field theories for optical diffraction. This ignores photon shot noise, the dominant noise source in perhaps most modern microscopy applications. Digital image processing algorithms that take noise into account can achieve subpixel superresolution by combining multiple conventional images of a single sample or scene [4, 5]. However, the poor performance of these techniques in recovering high spatial frequency information led to the recognition that prior information about image structure is generally essential for attaining superresolution [6]. Yet, existing theories do not provide physical limits on image estimation based on the noise and prior information available from specific measurement schemes.

Here we study the physics of superresolution imaging by stochastic localization of single molecules, as in photoactivated localization microscopy (PALM) and stochastic optical reconstruction microscopy (STORM), which achieve superresolution via the spatial localization of single fluorescent molecules [7–10]. We stress that stochastic localization is a distinct measurement and computational analysis procedure that exploits the prior knowledge the active fluorophores are dilute. Previous theories of superresolution from digital image processing do not describe the specific form of prior information that has allowed stochastic localization techniques to successfully achieve tenfold or better superresolution beyond the conventional diffraction limit. Our theory provides unified performance limits for stochastic localization, conventional microscopy, and the entire class of digital image processing algorithms for subpixel superresolution.

Our work builds on earlier applications of estimation theory that amended classical notions of resolution by including fluctuations in the propagating fields [11, 12]. Instead, we consider photon statistics and model the stochastic activation and measurement of individual molecules. Our resolution measure, termed here the information transfer function (ITF), limits how well one can determine a specimen’s features at each spatial frequency. The ITF thus replaces the modulation-transfer function (MTF) but with an expanded range of explanation, covering conventional and stochastic localization microscopy. Importantly, for conventional microscopy the ITF reduces to the square of the MTF, scaled by the number of observed photons, thereby preserving physicists’ basic intuitions about imaging. Overall, our formalism unifies long-standing work on the spatial filtering properties of optical imaging with recent efforts to describe the limits imposed by photon shot noise.

We consider an image taken from a specimen of m fluorophores, all of the same color and located in the sample plane at {x_j}. The experimental data are the counts, {N_l}, of photons detected at pixel l which is located in the image plane at y_l, l = 1…L. The probability, P, of observing the data is

$$\begin{array}{ccc}P(\{N_l\}|\{{\mathbf{x}}_j\})\hfill & =\hfill & {\displaystyle \mathbf{\prod }_{l=1}^L{e}^{-{\lambda }_l}\frac{{\lambda }_l^{N_l}}{N_l!},}\hfill \\ \hfill {\lambda }_l& =\hfill & {\displaystyle \mathbf{\sum }_{j=1}^m{p}_{j}h({\mathbf{y}}_l-{\mathbf{x}}_j)\mathrm{\Delta }{\mathbf{y}}_l}\hfill \end{array}$$ (1)

where p_j is the intensity of the jth emitter, Δy_l is the pixel area, and the point-spread function (PSF), h, is normalized, ${\displaystyle {\mathbf{\sum }}_{l=1}^{L}h({\mathbf{y}}_l)}\mathrm{\Delta }{\mathbf{y}}_l=1$. We idealize the detector by assuming uniformly distributed pixels with infinitesimal area, Δy_l → 0, so thatN_l ∈ {0,1}. This neglects the effect of finite pixel size. In this limit we can rewrite Eq. (1) as a function of the locations in the image plane, {z_k}, of N = ∑_lN_l detected photons: P({N_l}|{x_j}) = P({z_k}|N, {x_j})P(N), where P(N) is the probability that N photons are detected, and

$$P(\{{\mathbf{z}}_k\}|N,\{{\mathbf{x}}_j\})={\displaystyle \mathbf{\prod }_{k=1}^N}{\displaystyle \mathbf{\sum }_{j=1}^m\frac{p_j}{{\displaystyle {\mathbf{\sum }}_{i=1}^m{p}_i}}h({\mathbf{z}}_k-{\mathbf{x}}_j)d{\mathbf{z}}_k.}$$ (2)

This satisfies ∫P({z_k}|N, {x_j})dz₁ … dz_N = 1. Localization microscopy finds estimates, {x̂_j}, of {x_j} based on the observations, {z_k}.

To study the limits of this technique, we use a key tool from estimation theory, the Cramér-Rao lower bound [13] (CRLB), which bounds the accuracy of any estimator, {q̂_i}, of a set of parameters, {q_i}: [E − J⁻¹] ≥ 0. Here E_ij ≡ 〈(q̂_i − q_i)(q̂_j − q_j)*〉 is the estimator covariance matrix, ${\mathbf{J}}_{ij}\equiv {\langle \frac{{\partial }^2}{\partial q_i\partial q_j^{*}}\text{log}P(\{{\mathbf{z}}_k\}|\{q_i\})\rangle }_{\{{\mathbf{z}}_k\}}$ is the Fisher information matrix, and q̂_i is assumed unbiased, i.e., 〈q̂_i〉 = q_i. The angular brackets, 〈···〉, denote averages over the stochastic locations of detected photons, distributed according to Eq. (2). The CRLB states [E − J⁻¹] is positive semidefinite, implying that the diagonal elements (the mean squared errors) obey E_ii = 〈|q̂_i − q_i|²〉 ≥ [J⁻¹]_ii. This inequality bounds estimator accuracy for any set of image parameters, such as the emitters’ locations (q_i ≡ x_i) [14, 15], or, as in our theory, the real-space [q_x ≡ I(x)] or spatial frequency [q_k ≡ I(k)] components.

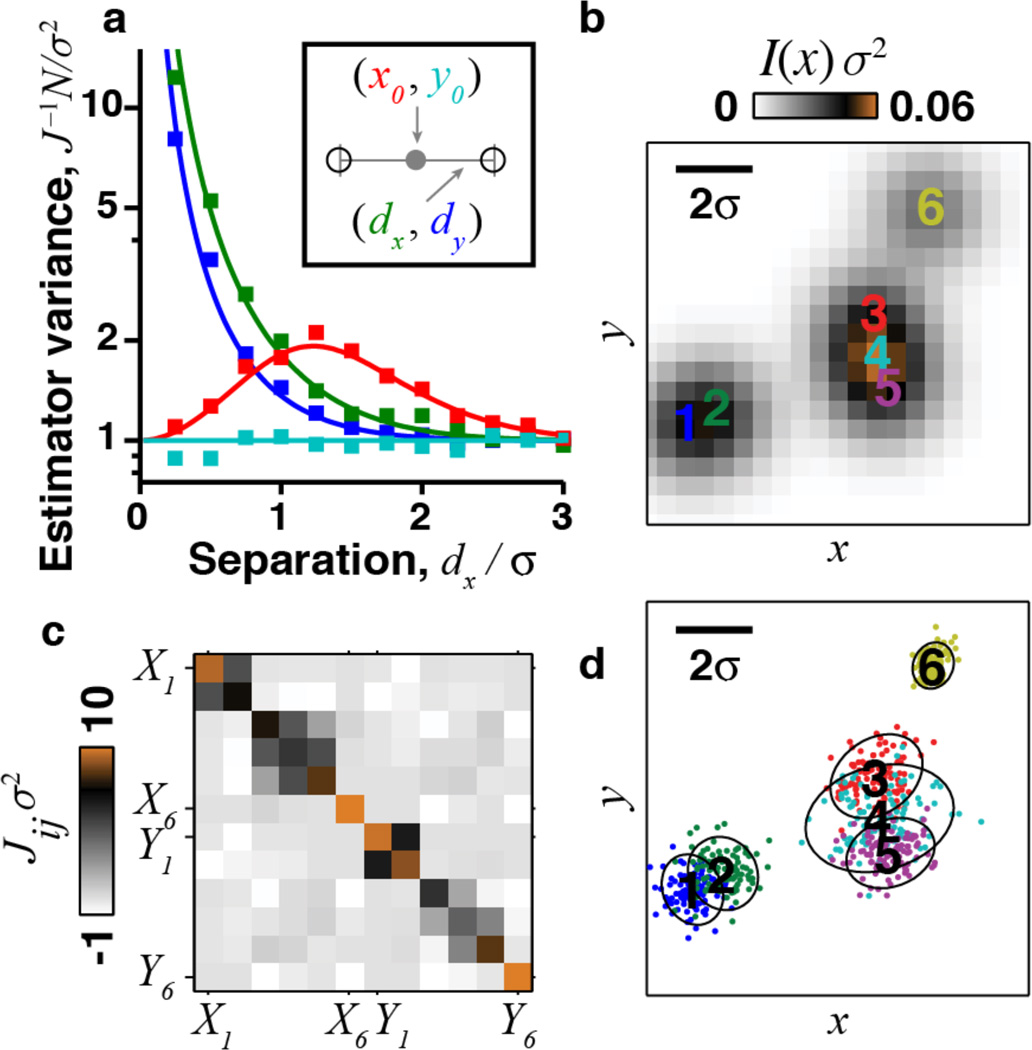
Previous applications of the CRLB to emitter localization did not yield limits on how well entire images can be determined, nor formalism to supersede the PSF and MTF. To illustrate, consider a 2D scene composed of two equally bright emitters [14]. We choose a coordinate system in which the emitters lie on the x axis at (x, y) = (±d_x, 0). J is diagonal in the basis given by the mean position and separation vector [Fig. 1(a), inset]. Figure 1(a) shows the corresponding CRLBs in units of the width of the Gaussian PSF, σ [16]. Similar results hold for an Airy disk PSF, and when the two emitters are not equally bright [16]. If d_x ≫ σ, J ≈ $\frac{N}{{\sigma }^2}$ for each coordinate. When d_x ≪ σ, one cannot unambiguously assign each photon to its correct emitter and J_dy,dy, J_dx,dx both vanish. This is why in stochastic localization microscopy one typically uses a very dilute density of simultaneously active emitters, ρ_a ≪ σ⁻², to prevent emitters’ images overlapping.

FIG. 1.

Real-space analysis of localization accuracy depends on the configuration of emitters. (a) A scene with two emitters has 4 degrees of freedom (inset). The Cramér-Rao lower bound (CRLB) for estimation of each of the 4 coordinates (solid lines; red, x₀; cyan, y₀; green, d_x; blue, d_y) matches the variance of a maximum-likelihood estimator (□). (b)–(d) Real-space analysis for a scene containing 6 emitters. (b) Observed intensity at each pixel. (c) Fisher information matrix for the emitters’ 12 X, Y coordinates. (d) Localization accuracy, determined by simulating 100 independent estimates of the emitters’ locations, with n = 17 photons per emitter, chosen for illustrative purposes. Contours denote 2 s.d. from the true position of each emitter, as determined by [J_ij]⁻¹.

This analysis extends to scenes of more emitters [Figs. 1(b)–1(d)], but in the general case localization accuracy varies with the scene’s details. The Fisher information for m emitters is a 2m × 2m matrix whose entries depend on the emitters’ 2m position coordinates. For m > 2 there is no general coordinate system diagonalizing J. A resolution measure that varies from sample to sample is inconsistent with traditional concepts of resolution and has limited practical utility.

We introduce a measure, the ITF, that gives resolution bounds for all specimens and generalizes the MTF to account for photon statistics. The ITF provides the CRLB for image estimation as a function of spatial frequency; this conception of resolution applies equally well to conventional or stochastic localization microscopy.

Consider an image scene, represented by a positive intensity function, I(x), normalized to have unit integral. In biological microscopy, I may represent the spatial probability density of fluorescently labeled cellular or protein structures. We seek a bound on the squared error of an unbiased estimator, Î(k). The ITF, F(k), bounds the error in estimating the image frequency components: E_I(k) ≡ 〈|Î(k) − I(k)|²〉 ≥ 1/F(k). (In practice it may be impossible to define unbiased estimators for some image components, especially at high spatial frequencies [16]. A generalization of the CRLB relates F(k) to the minimum variance of a biased estimator [13]. Even when no unbiased estimator exists, the ITF provides an objective figure of merit for image resolution that is based on the measurement statistics.)

Physical intuition suggests the ITF should vanish at large k and be proportional to N, since each photon carries equal Fisher information. We first calculate the ITF exactly using three key simplifying assumptions. First, we ignore photons that cannot be assigned to an emitter due to overlap; the case of overlapping emitters will be considered below. This assumption simplifies the probability, Eq. (2). If n_j is the number of detected photons from the jth emitter, and assuming the fluorophores’ locations are randomly sampled from the distribution, I(x), we have [16]:

$$P(\{z_{ij}\}|I)={\displaystyle \mathbf{\prod }_{j=1}^m}{\displaystyle \int d{\mathbf{x}}_j\mathbf{\prod }_{i=1}^{n_j}h({\mathbf{z}}_{ij}-{\mathbf{x}}_j)I({\mathbf{x}}_j).}$$ (3)

Second, assuming the PSF, h, is Gaussian, we can compute the integral:

$${\displaystyle \int d{\mathbf{x}}_j\mathbf{\prod }_{i=1}^{n_j}{e}^{-[{({\mathbf{z}}_{ij}-{\mathbf{x}}_j)}^2/2{\sigma }^2]}I({\mathbf{x}}_j)\propto {\tilde{I}}_{n_j}({\widehat{\mathbf{x}}}_j)\mathbf{\prod }_{i=1}^{n_j}}{e}^{-(1/2{\sigma }^2)({\mathbf{z}}_{ij}^2-{\widehat{\mathbf{x}}}_j^2)}$$ (4)

where ${\widehat{\mathbf{x}}}_j\equiv \frac{1}{n_j}{\displaystyle {\mathbf{\sum }}_{i=1}^{n_j}{\mathbf{z}}_{ij}}$ is the centroid of the observed photons’ locations, and Ĩ_nj (x̂_j) ≡ ∫ dx_jI(x_j)e^{−(n_j/2σ2)(x_j−x̂_j)2} (n_j/2πσ²) is a blurred version of the true image with blurring scale $\sigma /\sqrt{n_j}$ [16]. Third, we assume each emitter emits the same number of photons, n_j = n; numerical results show that a more realistic calculation with Poisson-distributed n_j has a nearly identical result [16]. We find

$${\mathbf{J}}_{I({\mathbf{k}}_1),I*({\mathbf{k}}_2)}=m{e}^{-[{(2\pi \sigma )}^2/2n]({\mathbf{k}}_1^2+{\mathbf{k}}_2^2){\displaystyle \int d\widehat{\mathbf{x}}}\frac{e^{-2\pi i({\mathbf{k}}_1-{\mathbf{k}}_2)\widehat{\mathbf{x}}}}{{\tilde{I}}_n(\widehat{\mathbf{x}})}.}$$ (5)

Using the normalization R of the image and the PSF, ∫dx̂Ĩ_n(x̂) = 1, we invert the Fisher information matrix to compute the ITF:

$$F_0(\mathbf{k})=\frac{1}{{[{\mathbf{J}}^{-1}]}_{I(\mathbf{k}),I*(\mathbf{k})}}=A{\rho }_e{e}^{-{(2\pi \mathbf{k}\sigma )}^2/n}$$ (6)

where A is the field of view area and ρ_e is the total density of emitters; see Fig. 2(a). (Note ρ_e appearing here is the density of all emitters observed in the experiment, whereas ρ_a introduced above is the density of simultaneously activated emitters in a single time frame.)

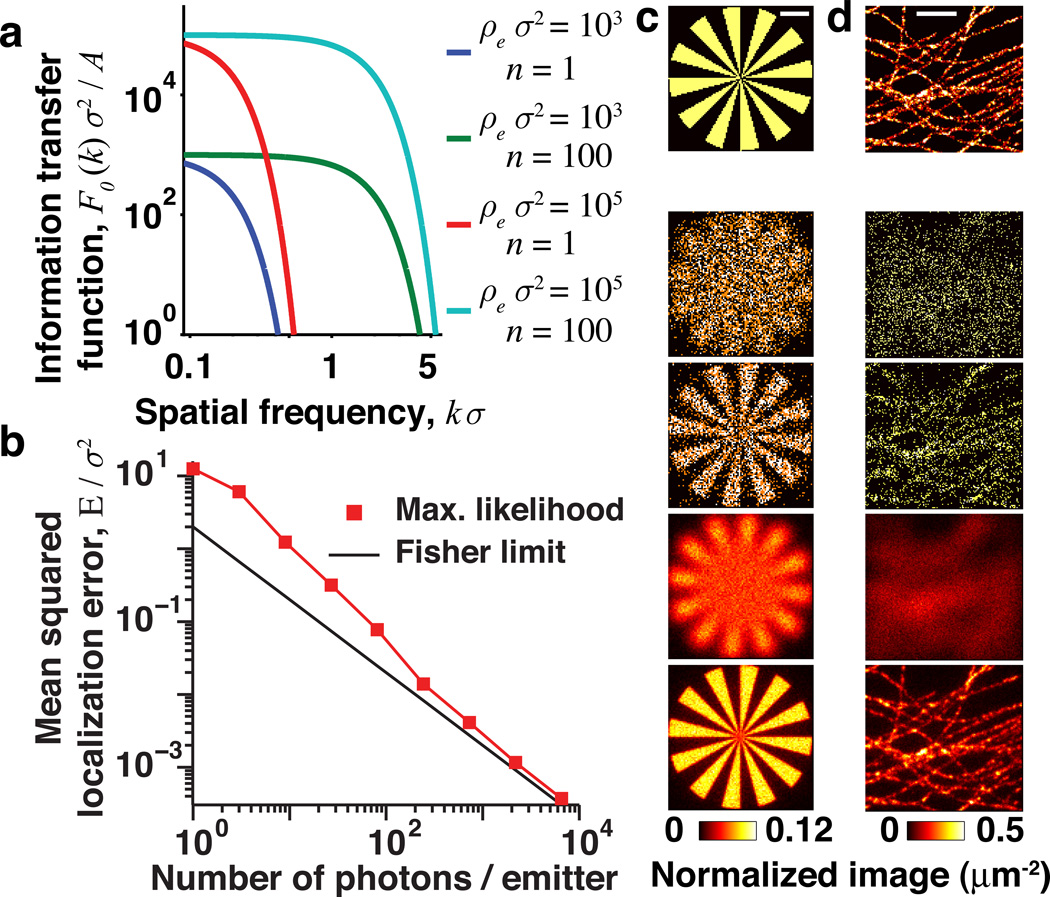
FIG. 2.

The information transfer function, F(k), bounds image estimation accuracy. (a) F₀(k) for conventional imaging (n = 1 photon/emitter; blue and red curves) and superresolution (n = 100, green and cyan). (b) Mean squared localization error for a truncated Airy disk PSF (width parameter σ, defined in [16]) analyzed by maximum-likelihood fitting (red) approaches the Fisher limit for n ≳ 100 photons. The effects of parameters on image quality are shown in simulations of a synthetic image (c), and of microtubules in a mammalian cell (d). The top row shows the true sample, lower rows show estimates using (from the top) ρ_eσ² = {10, 10; 10³, 10³} and n = {1, 100, 1, 100}. Scale bars are 1 µm, ρ_e is the total emitter density and n is the number of photons per emitter. Simulations used an Airy disk PSF (width σ = 200 nm), and the true image in (d) is based on experimental data from [22].

This result is derived more explicitly in [16] and shows that the ITF is an image-independent, universal limit valid for any scene. Equation (6) shows that superresolution hinges on the ability to have n ≫ 1; in practice n ~ 100−10⁴ or more. In conventional microscopy, individual emitters may contribute more than one photon to the image, but since photons cannot be reliably assigned to the correct emitter their statistics are equivalent to the case n = 1. Increasing the emitter labeling density, ρ_e, reduces the error variance at all spatial frequencies but has little effect on the threshold frequency at which the ITF becomes vanishingly small [Fig. 2(a)].

We can also compute the ITF exactly, with no restriction on the PSF, for conventional microscopy (n = 1). In this case Eq. (3) factorizes into a product of independent contributions from each photon, and the ITF is [16]: F(k) = N|h(k)|². This result connects the ITF directly to the conventional MTF.

Both of these exact results are special cases of our main finding, which is a general bound on the ITF for any PSF. If the MTF is bounded by a Gaussian, |h(k)| ≤ e^{−(2πkσ)2/2}, then we find [16]:

$$F(k)\le C{F}_0(k),$$ (7)

where C is a constant that depends on the image but not on k, A or ρ_e.

We now consider how the ITF applies in the case the emitters’ images overlap, which is common when the density of active emitters, ρ_a, approaches σ⁻². Several computational procedures have recently been proposed for analyzing data from such crowded scenes to speed up superresolution image acquisition, but the fundamental limits on resolution and speed remain unknown [17–21]. We show that the spatial frequency-dependent ITF is generally applicable and smoothly depends on ρ_a.

To derive how the ITF depends on ρ_a, we must specialize to images consisting of m emitters. (More generally, the following model applies to images of M emitters obtained in M/m distinct rounds with exactly m active emitters per round. Each round contributes independent information, so the total ITF is the sum of the ITF for each.) The image is $I(\mathbf{x})=\frac{1}{m}{\displaystyle {\mathbf{\sum }}_{j=1}^m\delta (\mathbf{x}-{\mathbf{x}}_j)}$ in real space, or $I(\mathbf{k})=\frac{1}{m}{\displaystyle {\mathbf{\sum }}_{j=1}^m{e}^{-i2\pi \mathbf{k}·{\mathbf{x}}_j}}$ in the frequency domain. We can compute F(k) through its relation to the real-space Fisher information matrix [13, 16]: 1/F(k) ≡ ${\displaystyle {\mathbf{\sum }}_{i,j=1}^m\frac{\partial I(\mathbf{k})}{\partial x_i}{\mathbf{J}}_{ij}^{-1}\frac{\partial I*(\mathbf{k})}{\partial x_j}}.$. Conventional microscopy corresponds to ρ_a ≫ σ⁻². In this limit we may approximate the Poisson statistics of photon shot noise as additive Gaussian fluctuations in intensity, valid when many photons are detected per pixel [16]. The result matches the form derived above for general images when n = 1 photon is observed per emitter [Fig. 3(a), solid black curve].

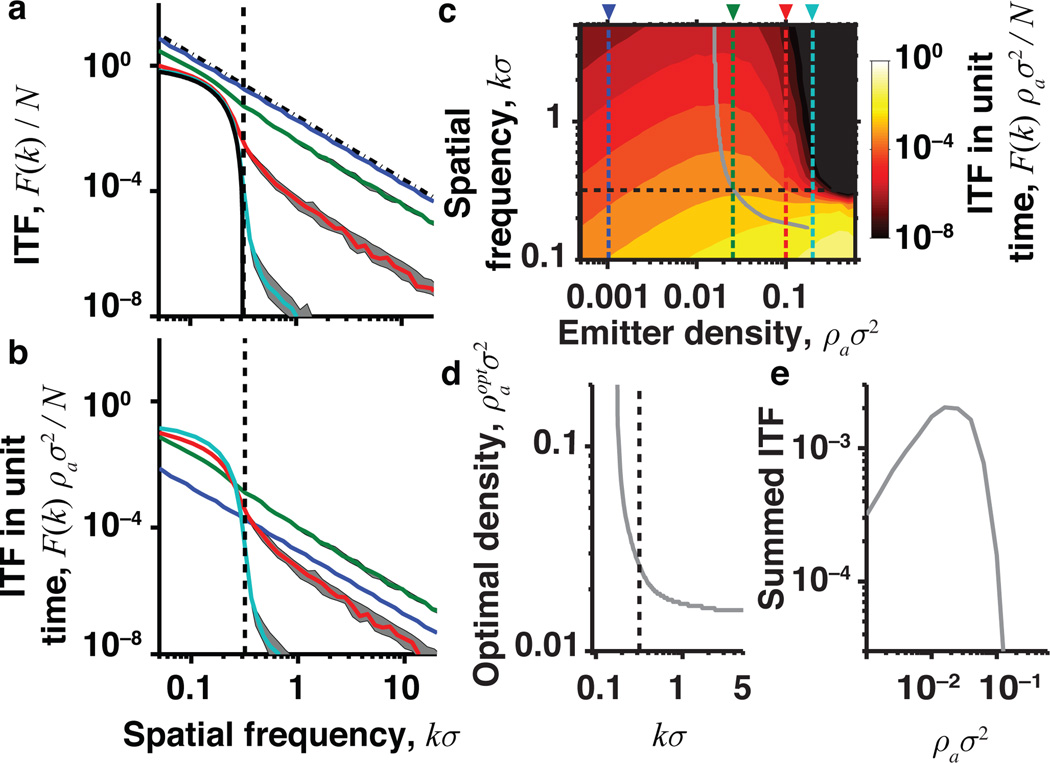
FIG. 3.

ITF for images of discrete emitters reveals the optimal density. (a) ITF for a fixed number of photons, N, with an Airy disk PSF. The Fisher information about emitter location for an isolated emitter is J⁽¹⁾ = σ⁻² per photon, and N = nAρ_e is the total number of observed photons. The ITF declines quadratically for superresolution techniques with sparse labeling (ρ_a ≪ σ⁻², dot-dashed black line). For conventional microscopy with dense labeling (ρ_a ≫ σ⁻²) the ITF declines more sharply (solid black curve) and goes to zero at the diffraction limit (black dashed line). Colored curves show the median ITF taken over an ensemble of random simulated scenes with ρ_aσ² = 0.001 (blue), 0.025 (green), 0.1 (red) and 0.2 (cyan). Error bars are ±1 s:d: (b) ITF for a fixed acquisition time. (c) Contour plot showing the ITF as a function of emitter density and spatial frequency for fixed imaging time. Vertical colored lines correspond to curves in (a) and (b). Black horizontal line denotes the conventional diffraction limit. Gray line indicates the emitter density that maximizes the ITF at each spatial frequency. (d) The optimal emitter density as a function of k. (e) The ITF per unit of image acquisition time, summed over all spatial frequencies greater than the conventional diffraction limit.

We also reconsider superresolution microscopy with sparse emitters, ρ_a ≪ σ⁻². Here the Fisher information matrix is diagonal, J_ij = nJ⁽¹⁾δ_ij, where J⁽¹⁾ is the Fisher information per photon for localizing a single emitter [16]. The ITF, $F(k)=A{\rho }_e\frac{n{J}^{(1)}}{{(2\pi k)}^2},$, declines only quadratically with k [Fig. 3(a), black dot-dashed line]. Prior knowledge that the image structure consists of m discrete emitters improves estimation as compared with a completely general image. Hence, the ITF here is strictly greater than the previous bound, Eq. (7), derived for a general image with n > 1. However, in both cases, the highest resolvable spatial frequency is proportional to $\sqrt{n}$.

Besides providing a unified formalism for these two extremes, the ITF can quantify the trade-off between image resolution and acquisition time as a function of the density of activated emitters. To do this, we computed the ITF for simulated specimens with emitters at a range of densities. The ITF smoothly transitions between the low and high emitter density regimes, Fig. 3(a). In live-cell imaging, the time to acquire an image, T, is a constrained resource. For fixed T, the number of detected photons scales asN ∝ B_ρaT, where B is the average emitter brightness. There is thus a trade-off between achieving superresolution, by working at low ρ_a, and increasing the signal-to-noise ratio by collecting more photons [Figs. 3(b) and 3(c)]. Anextremely low density of emitters is suboptimal, with F(k) falling off as ρ_a (blue curve) for frequencies above the diffraction limit (vertical dashed line). Our simulations reveal the optimal active emitter density, ${\rho }_a^{\text{opt}}$, that maximizes the ITF for each k, Fig. 3(d). The sum of the ITF over all frequencies greater than the conventional diffraction limit, Fig. 3(e), is maximum around ${\rho }_a^{\text{opt}}{\sigma }^2=0.016$, which provides sufficient separability for localizing neighboring emitters without wasting time by overly diluting the emitters.

In summary, we used estimation theory to calculate the ITF, a unified bound on image estimation accuracy, for stochastic localization and conventional fluorescence microscopy. For completely general images, the key parameter is the number of observed photons per emitter, n. In conventional microscopy (n = 1) the ITF reduces to the square of the MTF times the total number of observed photons. This result provides a performance bound for superresolution techniques that combine multiple, shifted images or photographs [4, 5]. Such techniques can overcome undersampling due to finite pixels, but the fundamental resolution limit imposed by optical diffraction is described by the ITF for conventional microscopy [6].

Overall, the ITF formalism reveals fundamental resolution limits on fluorescence microscopy, unifying the conventional concepts of resolution with those developed separately for stochastic localization microscopy. The ITF also fulfills the long-standing goal of characterizing how resolution depends on the unavoidable limitations imposed by photon statistics [3, 11, 12]. Further, the ITF facilitates principled choices of experimental parameters that optimize imaging performance at any chosen length scale. Although improved localization and image estimation algorithms will surely continue to emerge [17–21], our work already provides the fundamental physical limits on the possible improvements. The ITF bounds the performance of any estimation procedure in fluorescence microscopy, regardless of emitter density.