Using the biomass-ratio and idiosyncratic hypotheses to predict mixed-species litter decomposition

Abstract

Background and Aims

A test is made of the acceptability of the biomass-ratio hypothesis (BMRH), operationalized as community-weighted means (CWMs), and of a new hypothesis (idiosyncratic annulment), for predicting the decomposition of multispecies litter mixtures. Specifically, (1) does the BMRH based on monoculture decomposition rates introduce systematic over- or underestimation of rates in mixtures? and (2) does the degree of variability of these rates decrease with increasing species richness (SR) beyond that expected from purely mathematical causes?

Methods

Decomposition rates (mg g⁻¹ d⁻¹) of litter from six tree species in microcosms were measured under controlled conditions during 18 weeks of incubation, alone and in all possible combinations of two, three, five and six species. Observed mixture decomposition rates were compared with those predicted by the BMRH using CWMs calculated from the monoculture rates, and the variability of the differences were compared with the SR of the mixture.

Key Results

Both positive and negative deviations from expectation occurred at all levels of SR. The average differences between observed rates of mixtures and those predicted were approximately zero. Although variability in the prediction errors was independent of the SR, this variability between different mixtures having the same number of species decreased with increasing SR such that mixtures with the most species converged on the predicted values. This decrease in variance was not due to idiosyncratic annulment of higher order interactions between species.

Conclusions

The BMRH described the average response of litter mixtures. The decrease in variance and the convergence to the predicted values based on CWMs was not due to the ‘idiosyncratic annulment’ of species interactions but was a mathematical consequence of CWMs being sums of random variables. Since convergence occurs with increasing SR and since SR increases with increasing spatial scale, the spatial scale will be a determinant in the prediction of ecosystem processes, such as litter decomposition rates.

INTRODUCTION

Understanding and predicting ecosystem processes is a key goal of ecology and has become especially important in the current context of global climate and land-use change. However, the complex dynamics of interacting biological populations that form these ecological systems make predictions difficult and often imprecise. In this context, the recent use of plant functional traits to predict ecosystem processes has generated interest both because of the strength of the correlations that have been found and because the use of plant traits permits generalization beyond taxonomic boundaries (e.g. Keddy, 1990, 1992; Lavorel et al., 1997; Weiher et al., 1999).

The link between a trait, which is defined as any morphological, physiological or phenological feature that is measurable at the individual level (Violle et al., 2007), and a process that occurs at the level of an entire community or ecosystem was provided by the ‘biomass-ratio hypothesis’ of Grime (1998). This hypothesis states that the effect of each species on an ecosystem process is proportional to the relative abundance of the species in the community. Since only physical entities (individuals), rather than conceptual ones (species), can change an ecosystem property, and since individuals affect such changes through their attributes (values of traits), Garnier et al. (2004) reformulated the biomass-ratio hypothesis to state that the effect of each species on an ecosystem process is proportional to the relative abundance of its functional trait values. This leads to the notion of a community-weighted mean (CWM) (or ‘aggregated’) trait as given in eqn (1), in which t_ijc is the average value of trait j for species i in community c, p_ic is the relative abundance of species i and 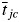is the community-weighted value of trait j over all S species present.

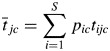1

The goal of this line of research is therefore to compare some ecosystem property across communities differing in community-weighted trait values and to obtain general empirical relationships in the form of a function, usually linear, which links the ecosystem property (E_c) with particular community-weighted trait values:

This possibility of scaling from individual traits to ecosystem properties has already been demonstrated (Vile et al., 2006; Diaz et al., 2007; Garnier et al., 2007; Lavorel et al., 2007; Suding et al., 2008; Hodgson et al., 2011; among others), using various traits and models.

A hypothesis of idiosyncratic annulment

The use of eqn (1) makes an implicit assumption about how the traits of different species interact to produce an ecosystem response. Because a CWM trait is a weighted linear sum of the attributes of each species, this equation assumes that there are no deviations from linearity, i.e. no interactions between species such that the proportional effect of a species changes depending on the other species that are present. Consider the simplest case in which the ecosystem property is a function of a single trait. If the biomass-ratio hypothesis is strictly true, then we have eqn (2), in which ɛ_c is a random sampling error only.

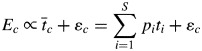2

This equation implicitly means that the proportional effect of each species on the ecosystem property (p_it_i) depends only on its relative abundance and not on the trait values of the other species in the community. The total ecosystem property is a weighted linear sum of the independent effects of the traits of each species measured separately. If this implicit assumption is not true, then the proportional effect of each species will change, depending upon which other species are also in the community and on their relative abundances; this will lead to a deviation (δ_c) between the measured ecosystem property and the effect predicted by the biomass-ratio hypothesis, as specified in eqn (3).

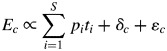3

The total deviation (δ_c) in eqn (3) can be further decomposed. If there are only two species in the community, then the right-hand side of eqn (3) can be written as p₁t₁ + p₂t₂ + δ₁₂ + ɛ_c where δ₁₂ is the two-way interaction between the two species, which describes by how much the ecosystem property changes when the two species are together relative to the proportional effects of each species separately. If there are three species in the community, then the right-hand side of eqn (3) becomes

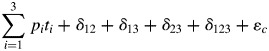Here we have three separate two-way interactions plus a three-way interaction. Using the notation ^xδ_m to mean the deviation from linearity caused by the mth unique group of species taken x species at a time, we can decompose the total deviation (δ_c) from the biomass-ratio hypothesis in a community of S species as given in eqn (4). The total number of such interactions involving S species is 2^S.

δ_c = (Σ²δ_m) + (Σ³δ_m) + …+ (Σ^S−1δ_m) + ^Sδ(4)

Here, in order to evaluate the limits of the biomass-ratio hypothesis, we test a new hypothesis (idiosyncratic annulment) based on the idiosyncratic hypothesis of Lawton (1994), which assumes that while diversity affects ecosystem function, such changes are in an unpredictable direction, due to the complexity and variability of the roles of individual species. More specifically, we hypothesize that the size and direction of each of the possible interactions (^xδ_m) in eqn (4) are uncorrelated and that the distribution of these interactions is symmetrical around zero, i.e. they are equally likely to be positive or negative. When there are only a few species in the mixture, then the total deviation (δ_c) from eqn (2) can be substantial depending on the properties of these few species. However, since increasing the number of species in the community rapidly increases the number of potential interactions, and since each interaction is equally likely to be positive or negative, these interactions will tend to cancel one another more completely. As the total number of species in the community increases, the observed total deviation should therefore tend towards zero and the community-weighted traits should become increasingly accurate predictors of the ecosystem property. If true, then community-weighted traits in multispecies communities would be good predictors of ecosystem properties even when the biomass-ratio hypothesis is not strictly true.

Testing the biomass-ratio and idiosyncratic hypothesis using litter decomposition

The case of mixed-species litter decomposition provides a good system to test the idiosyncratic hypothesis. There is a large literature concerning the determinants of decomposition rates, but these mainly involve experiments containing either single-species litter or only a few species in mixtures (Hättenschwiler et al., 2005). Importantly, species interactions can provide a substantial source of variability in the prediction of the global rate during the decomposition of species litter mixtures (e.g. Hector et al., 2000; Perez-Harguindeguy et al., 2008). Gartner and Cardon (2004) reviewed about 30 studies comparing leaf litter decay rates in mixtures with known decay rates of the component litters decaying alone. Most litter mixtures (108 out of 162) showed non-additive effects, i.e. accelerated (synergistic) or decelerated (antagonistic) responses compared with those estimated from monocultures. Clearly, the assumption of linearity underlying the use of community-weighted trait means, as implied by eqn (2), is wrong because of the ubiquity of such interactions. Despite this apparent ubiquity, the mean bias of the predicted decomposition rate was often weak, as shown by Gartner and Cardon (2004). For example, Perez-Harguindeguy et al. (2008) found a low and non-significant effect of mixing species litters within a functionally homogenous plant composition. More recently, Pakeman et al. (2011) reported a strong correlation (R² = 0·80) between the observed and predicted specific rates of litter mass loss in mixtures using eqn (1). One possible explanation is the hypothesis of idiosyncratic annulment.

This leads to the two working hypotheses that are tested here. (1) The observed specific decomposition rates (k-values) in mixed-species litters are equal to the community-weighted values obtained in monocultures [i.e. the biomass-ratio hypothesis, eqn (2)]. (2) The variation in observed specific decomposition rates between mixtures having the same number of species will decrease as the number of species in the mixture increases due to idiosyncratic annulment. To test these hypotheses, we use a model based on leaf litter mixtures of tree species. The ecosystem property in our study is the actual decomposition constant (k) of a mixed-species litter, obtained from a simple Olson (1963) model of exponential litter decay. Our species-specific trait is the decomposition constant of each species in monoculture (k_i).

MATERIALS AND METHODS

Design of decomposition experiments

The experiment involved a set of six tree species: sugar maple (Acer saccharum), gray birch (Betula populifolia), northern red oak (Quercus rubra), trembling aspen (Populus tremuloides), eastern white pine (Pinus strobus) and jack pine (Pinus banksiana). These species naturally co-occur and were chosen in order to maximize the differences in leaf functional traits known to affect decomposition rate, especially leaf dry matter content (Kazakou et al., 2006; Fortunel et al., 2009; Pakeman et al., 2011), as provided by the TRY database (Kättge et al., 2001).

Leaf litter from approx. 3–6 individuals of each of the six tree species were collected from the local Sherbrooke area (45 °22′N, 71 °55'W, and 45 °20'N, 71 °44'W; Quebec, Canada) every 2–3 d during the peak of litterfall in September 2009 using nets (for leaves) or landscape fabric (for needles), and avoiding direct contact with soil. All leaves were immediately air-dried at 40 °C to stop decay processes before making the litter mixtures and placing them into litterbags. Sugar maple and northern red oak leaves were cut into 2–4 fragments, depending on their original size. A 2 g aliquot of either single or mixed species litter (in equal mass proportions to maximize the magnitude of potential interactions between them) were gently placed in each litterbag. Litterbags were made of fibreglass fabric (approx. 1 mm mesh size, which allowed the greatest litter accessibility to micro- and mesofauna without litter losses) and measured 13 × 15 cm. After being thermo-sealed, each litterbag was weighed and placed upon the surface organic layer in a separate microcosm (described below). We tested all possible combinations of two (15), three (20), five (6) and six (1) mixed species for a total of 42 different litter mixtures. Each combination and harvest time was replicated twice.

The microcosms were based on those described in Taylor and Parkinson (1988) and consisted of a cylindrical drained pot (12 cm height, 15 cm diameter) filled, from bottom to top, with 2–3 cm gravel, 4 cm sand, and 1–2 cm of the organic layer from a forest soil. This soil was collected within a single hectare from a mixed yellow birch–sugar maple forest, typical of southern Quebec. The bulk soil was passed through a 6 mm screen to remove undecomposed leaves, large roots and stones, and then thoroughly mixed before adding it to the microcosms. The microcosms, with one litterbag each, were placed randomly on shelves in a dark room under controlled temperature (18–19 °C) and relative humidity (58 ± 6 %) conditions; the soil was kept moist at all times by regular additions of small amounts of deionized water. At no time did the soil dry out.

Litterbags of each mixture type were destructively harvested after 1, 2, 4, 6, 10 and 18 weeks (i.e. six incubation periods). At each harvest, litterbags were dried for 1 week at 40 °C, then weighed. In total, there were 2 × 6 litterbags per mixture type and 48 different mixture types.

Statistical analysis

We modelled the dynamics of litter decomposition using the simple exponential model (Olson, 1963):

where M_ij(t) is the mass of the litter mixture i in litterbag j at time t, M_ij(0) is the initial mass of litter mixture i (2 ± 0·1 g) in litterbag j, k_i is the estimated average specific decomposition rate (d⁻¹) of litter mixture i, and 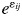is the deviation of litter mixture i in litterbag j from its predicted value. Because there were slight differences in the initial mass of litter between litterbags, we divided the dry mass of the litter in a given litterbag at harvest by its initial dry mass. This ratio was then transformed to logarithms so that Olson's exponential model was linearized:

Obtaining observed monoculture and mixture decomposition rates, and predicted community-weighted mixture decomposition rates

We first fitted a standard linear mixed model regression separately for monocultures and litter mixtures. This was done using the ‘lmer’ function of the lme4 package of R (Pinheiro and Bates, 2000; Bates, 2005; Bates and Sarkar, 2006) in which the grouping factor was ‘species’ (for monocultures) or ‘mixture’ (for litter mixtures). We initially allowed both slopes and intercepts to vary between groups, with no constraints placed on any covariance between slopes and intercepts. However, upon comparing nested models in which the intercepts were free to vary or were fixed to a common value, we found no significant variation of intercepts between groups; this was true for both monocultures and litter mixtures. Therefore, only the slopes were subsequently allowed to vary (model 1). Here, α is the common intercept across groups and k_i is the empirically estimated (i.e. observed) specific decomposition rate of group i. These intergroup decomposition rates are random and follow a normal distribution with mean k and standard deviation σ_δ, while ɛ_ij are normally distributed random within-group deviations with zero mean and standard deviation σ_ɛ.

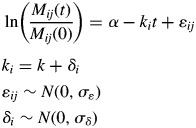For each litter mixture involving at least two species, we calculated the specific decomposition rates 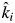that would occur if the mass-ratio hypothesis was strictly true, i.e.

where p_ij = 1/S is the initial mass proportion of species j in the mixture i, and k_j is the empirically estimated (observed) specific decomposition rate of species j when measured in monoculture.

Testing the mass-ratio hypothesis

For each litterbag containing a mixture, we defined a new variable, 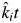as the product of the expected community-weighted decomposition rate 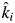of that mixture multiplied by the harvest date t. We then fitted a mixed model regression (model 2) including all of the litter mixtures by regressing the natural logarithm of the mass-ratio on this new variable, so that the empirical estimate of the specific decomposition rate in mixture i became β_i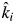. Note that 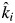is not a fitted parameter in model 2 but is fixed to the predicted value given the biomass-ratio hypothesis and the observed monoculture decomposition rates. Only β_i is empirically estimated from observed values. Thus β_i = 1 means that the empirically estimated decomposition rate in mixture i is the same as that predicted by the biomass-ratio hypothesis (k_i = 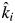); β_i < 1 means that the empirically estimated decomposition rate in the mixture is less than that predicted by the mass-ratio hypothesis (k_i < 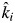); and β_i > 1 means that the empirically estimated decomposition rate is greater than that predicted by the mass-ratio hypothesis (k_i > ).

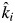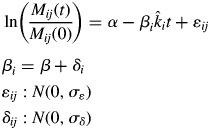If the mass-ratio hypothesis is correct, i.e. the actual decomposition rate equals the community-weighted value 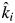that is predicted from the monocultures, then β = 1 and σ_δ = 0; there is no bias on average and no bias in any given litter mixture. Any other result means that the mass-ratio hypothesis is not strictly correct. If β = 1 but σ_δ > 0, then the relationship between observed and predicted (CWM) rates varies across litter mixtures, but the mass-ratio hypothesis is true if averaged across all mixtures. Finally, if β ≠ 1 and σ_δ > 0, then the mass-ratio hypothesis in not true either within particular litter mixtures or as an average claim. The null hypothesis that β = 1 was tested with a t-test using the estimated mean and standard error of β from the fixed term of the mixed-model regression. The null hypothesis that σ_δ > 0 was tested by comparing the change in likelihood between model 2 and the same model in which the between-mixture slope was not random (using maximum likelihood rather than restricted maximum likelihood) and comparing this with a χ² distribution with 2 d.f. using the ‘anova’ function of R.

Testing the hypothesis of idiosyncratic annulment

Idiosyncratic annulment occurs when the biomass-ratio hypothesis is not strictly true, i.e. that the ecosystem response (mixed-species litter decomposition) is not simply the effect contributed by each species weighted by its relative abundance, but when the differences between the two tend to cancel out more completely as the species richness of the community increases. We test this in two ways.

First, we use Monte Carlo simulations to describe the probability distribution of the standard deviation between the community-weighted decomposition rates of different mixtures having the same number of species assuming that this variation is due solely to sampling variation arising from different species compositions in the mixture. Given the same assumptions underlying the mixed-model regressions, the sampling distribution is found to be multivariate normal (Supplementary Data), the dimension of which is equal to the number of unique mixtures having the same number of species. The elements in the covariance matrix are a function of (1) the variance in monoculture decomposition rates (obtained from model 1); (2) the number of species in the mixtures; and (3) the number of species in common between pairs of mixtures. The Monte Carlo simulation generates random draws from this multivariate normal distribution using the ‘mvrnorm’ function of the mass library of R. We then compare the measured standard deviation of mixture decomposition rates with this Monte Carlo distribution.

Secondly, we regress the standard deviation of the observed deviations between observed and predicted (CWM) decomposition rates and the number of species per mixture (two, three or five). We then use a permutation test (Manly, 1997) to compare the slope of this regression assuming that these deviations are independent of the species richness of the mixture; details of this permutation test are given in the Supplementary Data. This simulation was done in R version 2·12·0 (R Development Core Team, 2010).

RESULTS

Testing the biomass-ratio hypothesis

Our first working hypothesis was that the observed specific decomposition rates in mixed-species litters are equal to the community-weighted values obtained in monocultures (the biomass-ratio hypothesis). Table 1 gives the litter decomposition rate k_i of each species in monoculture using model 1. Figure 1A shows the observed decomposition rates of both the monocultures and mixtures and the predicted decomposition rates of mixtures from CWMs. The biomass-ratio hypothesis was tested using model 2, which was applied to the litter mixtures by expressing the empirical estimate of the specific decomposition rate as the product of the value predicted from the mass-ratio hypothesis (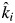) and the bias (β_i). The average bias over all mixtures (the fixed value of β) was not significantly different from the predicted value given the null hypothesis (H₀: β = 1, estimated β = 0·949, s.e. = 0·031, t₅₄₂ = 1·61, P = 0·11; i.e. observed decomposition rate slower than predicted, but not significantly). However, the between-mixture variation in the estimated values of β (i.e. σ_δ = 0·105) was significantly greater than zero (χ² = 6·45, d.f. = 2, P = 0·039), meaning that the bias was not equal to unity in all mixtures. To verify that the average decomposition rate in mixtures did not vary systematically with species richness of the mixture, we added this variable to model 1 for litter mixtures. The slope associated with the number of species in the mixtures was not significantly different from zero (slope = 0·002, s.e. = 0·024, t₅₄₂ = 0·102, P = 0·919; i.e. less slower than predicted with increasing species richness, but not significantly). Therefore, the biomass-ratio hypothesis was consistent with the data on average; this was true irrespective of the species richness of the mixture, but both positive and negative deviations from the biomass-ratio hypothesis occurred in particular litter mixtures.

Table 1.

Decomposition rates (k-values) of single-species litters

Species	ki (mg1 g−1 d−1)
Acer saccharum	3·41
Betula populifolia	1·66
Pinus banksiana	2·08
Pinus strobus	2·26
Populus tremuloides	2·86
Quercus rubra	2·69

Fig. 1.

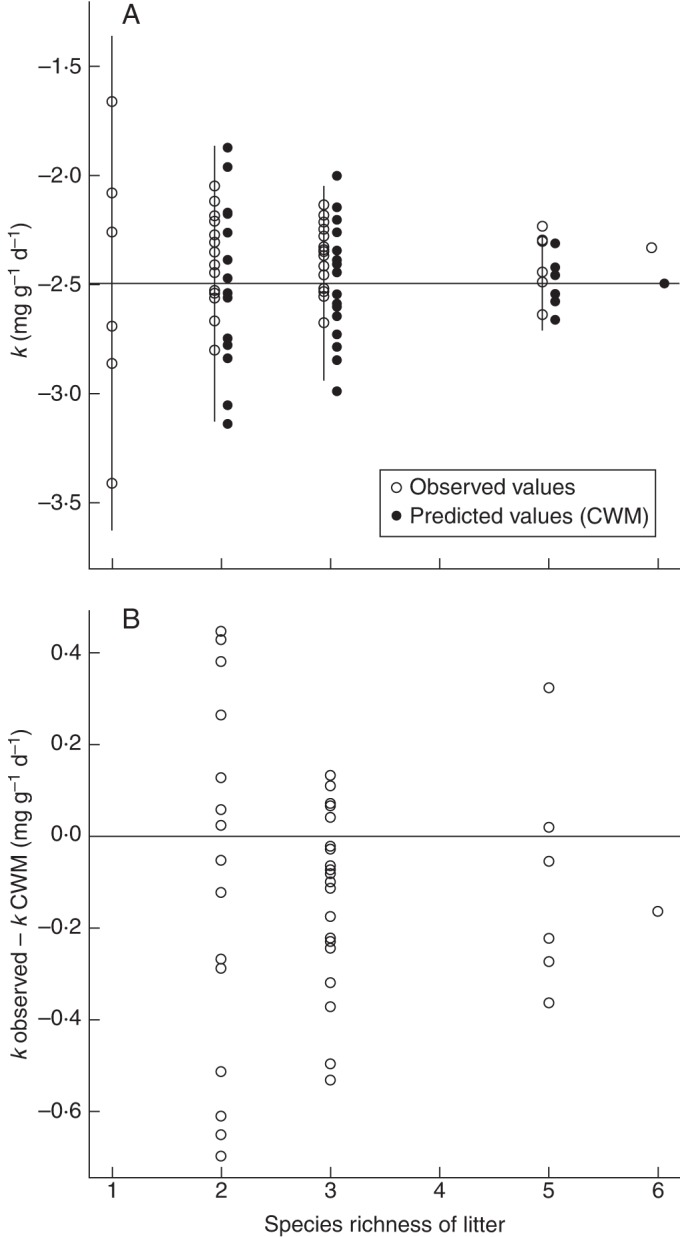
(A) The measured decomposition rates (‘observed’) and the calculated community-weighted mean (CWM) values (‘predicted’) are plotted against the number of species in the litter mixture. The horizontal line is the expected value of the measured rates based on the monoculture values, and the vertical lines show the expected variation (± 2 s.d.), assuming the biomass-ratio hypothesis and normally distributed monoculture rates. (B) Deviations from CWM values due to interactions between species.

Testing the idiosyncratic annulment hypothesis

The second working hypothesis was that variation in the observed decomposition rates would decrease as the number of species in the mixture increases due to idiosyncratic annulment. Figure 1A shows the variation in the observed and community-weighted mixture decomposition rates at each level of species richness. Both the observed and community-weighted values were much less variable in mixtures than were the monoculture values, and this variation decreased with an increasing species richness of the mixture.

The vertical lines in Fig. 1A show the expected range of variation (±2 s.d.), based on 20 000 Monte Carlo simulations. These approx. 95 % confidence intervals assume that the decrease in variation is simply a mathematical consequence of community-weighted values being weighted means with overlapping groups of species (Supplementary Data), rather than being due to any additional decrease caused by idiosyncratic annulment. The levels of variation in both the calculated community-weighted values (P = 0·699, 0·700, 0·701) and the observed values (P = 0·544, 0·110, 0·931) were consistent with Monte Carlo simulations for the two-, three- and five-species mixtures, respectively. Thus, the variability was never significantly lower than that predicted by the Monte Carlo simulations at any level of species richness, contrary to the hypothesis of idiosyncratic annulment.

Figure 1B shows the variation in the deviations between the observed and community-weighted decomposition rates for the two-, three- and five-species mixtures. Both positive (synergistic interactions) and negative (antagonistic interactions) errors were observed at each level of species richness, in about the same proportion. Note that these errors are not residuals from a regression. Rather, the community-weighted decomposition rates were calculated from independently measured monoculture decomposition rates and so there is no logical requirement that such errors be symmetrically distributed around zero. The permutation test, based on 50 000 permutations, showed that there is no significant decrease in the variability of the prediction errors as the species richness increases (P = 0·139).

DISCUSSION

The complexity of ecological systems makes it difficult to predict their processes from a knowledge of the component parts. This is certainly true concerning litter decomposition, where species interactions add an important source of variability (e.g. Hector et al., 2000; Perez-Harguindeguy et al., 2008) and can therefore greatly change predictions of global decomposition rates.

In this study, we were interested in exploring two aspects of the use of the biomass-ratio hypothesis, as operationalized by the notion of community-weighted trait means, in linking traits to ecosystem processes. First, do CWMs, based only on the value of each species in monoculture, introduce a systematic over- or underestimation of the ecosystem process (here, litter decomposition rates in mixtures)? Secondly, do the deviations from the predicted CWMs tend to cancel out more completely as the number of species in the mixture increases (‘idiosyncratic annulment’)?

Before answering these questions, we first measured the decomposition rates of the litter of each species in monoculture. Since the major factors (environmental variables, pool of decomposer species) affecting decomposition were invariant in our experiments, the observed variability in decomposition rates is predominantly due to differences in litter quality between species, i.e. their various physical and chemical properties.

We found that, considering all litter mixtures, the average decomposition rate was equal to the rate predicted by the community-weighted value based on the monoculture values. This agrees with Grime's biomass-ratio hypothesis, in which the contribution of each species to an ecosystem process is equal to its relative abundance in the community (Grime, 1998). However, even though the average response was equal to the community-weighted value, there were substantial deviations between the observed and predicted values between different mixtures having the same total number of species. In other words, the biomass-ratio hypothesis did apply when considering the average response over the entire set of mixtures, but not particularly well to any single mixture. Both synergistic and antagonistic interactions occurred, depending upon the mixture, and resulted in both strong positive and negative deviations from the expected decomposition rates that were predicted by the CWMs. These results showing non-additive effects were consistent with the literature (Gartner and Cardon, 2004; Hättenschwiller et al., 2005).

As expected (Fig. 1; Supplementary Data), the variability in observed and estimated (using monoculture CWMs) mixture decomposition rates decreased with increasing species richness of the mixture. As far as we know, this particular point has been investigated in very few articles within the decomposition literature, but the results were consistent with ours. For example, Keith et al. (2008) (but also Perez-Harguindeguy et al., 2008) found a reduction of variability of observed mass loss with an increasing number of species in the mixtures and a greater effect of species richness on variances than on means.

In part, this result is a necessary consequence of two properties of CWMs. First, the variability of a weighted sum of random variables (i.e. a CWM) is less than the variability of the component variables themselves (the monoculture rates) and is inversely proportional to the number of random variables (i.e. species) in the sum. This is exactly the same reason why the standard error of a sample mean decreases with the square of the sample size. Secondly, when different mixtures contain species in common, this creates a positive covariance that further decreases the variability of the CWMs.

However, we had expected an additional biological effect of mixing litter species (idiosyncratic annulment), which would decrease the variability of the prediction errors below that due to these purely statistical effects. Our Monte Carlo simulations showed that the observed decrease in variability was consistent with those expected purely from these two necessary properties of CWMs. Furthermore, there was no significant trend for the variability in the observed errors (observed – predicted values) to decrease with increasing species richness, based on the permutation test. Thus, we cannot accept the hypothesis of idiosyncratic annulment. If this biological effect does occur, it is too weak to be detected within our experiment.

Even if idiosyncratic annulment does not occur, the mathematically necessary decrease in the variability of CWMs with increasing species richness has important biological consequences that are scale dependent. Consider first a spatial scale in a forest that is small enough so that leaves of only a few different species are found in mixtures (for instance 100 cm², a common size of litterbags). At this scale, we could predict the average decomposition rate using monoculture rates and the biomass-ratio hypothesis, but not the direction or magnitude of actual rates in any particular 100 cm² patch of forest due to the complexity and the variability of the roles of individual component species. Thus, at this scale, our results confirm those of Wardle et al. (1997, p. 254), who found that ‘the effects did not work in easily predictable directions, and both positive and negative effects of litter mixing occurred depending upon the component species.’ This should be true irrespective of the species richness of the entire forest since, at such small scales, one would rarely find the litter of more than only a few species co-occurring. However, at a spatial scale large enough to include many different species, the variance around the average rate predicted by the biomass-ratio hypothesis would be much lower and the accuracy of the prediction, therefore, would be greater (Fig. 1). If one considers a forest with many different mixtures of litter on the forest floor, then this result means that the biomass-ratio hypothesis could be a reasonable approximation at this larger spatial scale, even if it is not very accurate at the very small scales at which individual leaves mix. Furthermore, this increase in accuracy with increasing spatial scale should be more pronounced in species-rich forests.

Certainly, our results must be replicated under variable environmental conditions before we can know if this pattern exists in the more variable environment of a real forest. If so, then we should also be able to use existing databases (e.g. Kattge et al., 2001) to produce aggregated versions of those leaf morphological and chemical traits that cause decomposition rates.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of further details for: the variance of a single community-weighted mean decomposition rate (K_M); covariances; the distribution of K_M in the experiment; and testing the significance of the observed decrease in the prediction errors with increasing species richness of the litter mixture.