Entropy–enthalpy transduction caused by conformational shifts can obscure the forces driving protein–ligand binding

Abstract

Molecular dynamics simulations of unprecedented duration now can provide new insights into biomolecular mechanisms. Analysis of a 1-ms molecular dynamics simulation of the small protein bovine pancreatic trypsin inhibitor reveals that its main conformations have different thermodynamic profiles and that perturbation of a single geometric variable, such as a torsion angle or interresidue distance, can select for occupancy of one or another conformational state. These results establish the basis for a mechanism that we term entropy–enthalpy transduction (EET), in which the thermodynamic character of a local perturbation, such as enthalpic binding of a small molecule, is camouflaged by the thermodynamics of a global conformational change induced by the perturbation, such as a switch into a high-entropy conformational state. It is noted that EET could occur in many systems, making measured entropies and enthalpies of folding and binding unreliable indicators of actual thermodynamic driving forces. The same mechanism might also account for the high experimental variance of measured enthalpies and entropies relative to free energies in some calorimetric studies. Finally, EET may be the physical mechanism underlying many cases of entropy–enthalpy compensation.

The entropic and enthalpic components of free energy can be informative regarding the mechanisms of biophysical processes, like protein folding and protein–ligand binding. Moreover, information on changes in entropy and enthalpy can usefully guide the design of improved drug molecules (1), with advantageous specificity (2) and physical properties (3). However, calorimetric studies of biomolecular binding and folding often reveal unexpected changes in entropy and enthalpy that are difficult to interpret in terms of physical driving forces (4–8). Some of these puzzling results are instances of entropy–enthalpy compensation (9), a common but not universal (10, 11) phenomenon in which perturbations of a system that increase the enthalpy also increase the entropy or vice versa; therefore, the net change in the free energy remains small. Experimental error in measured enthalpies, particularly when obtained by the relatively imprecise van ’t Hoff method, can generate spurious entropy–enthalpy compensation (12); the nonphysical operation of Berkson's paradox (selection bias) (13) can also generate this compensation. However, analysis of collected calorimetric data for protein–ligand binding indicates that entropy–enthalpy compensation is a genuine and common physical phenomenon (13).

Today, novel computational technologies, such as graphical processor units (14–17) and the specialized Anton computer (18), are enabling dramatically longer molecular dynamics (MD) simulations than hitherto feasible. The enormous conformational sampling power of these technologies has the potential to open a new window on the molecular mechanisms underlying the thermodynamics of biomolecular systems. For example, it can provide increasingly accurate estimates of thermodynamic quantities that are notoriously difficult to converge, such as configurational entropy (19–21). Such thermodynamic results, coupled with atomistic structural and dynamical data, hold the potential to address some of the conundrums in calorimetric data outlined above. Recently, a 1-ms MD simulation of a relatively simple protein, bovine pancreatic trypsin inhibitor (BPTI), was released to the scientific community (22). This simulation provides a level of sampling unparalleled by any other biomolecular simulation to date, making it an ideal dataset for gaining a deeper understanding of the thermodynamics of proteins.

Here, we present a statistical thermodynamic analysis of the main conformational clusters observed in the 1-ms BPTI simulation using the maximum information spanning tree (MIST) (23, 24) approach to estimate configurational entropy. A central finding is that even this simple protein is delicately poised between states of similar free energy but very different entropy and enthalpy. We also introduce a method, based on the Jensen–Shannon divergence (25, 26), to show that there exists structural degrees of freedom that can easily be perturbed to drive the system into any of the major conformational states. These observations combine to yield a concept of entropy–enthalpy transduction (EET), in which local thermodynamic driving forces are transduced into different global thermodynamics through conformational selection. Finally, we provide a statistical thermodynamic description of EET that does not rely on the idealization of conformational selection. The methods and results presented here bear on the interpretation of simulation and calorimetry data and the physical basis for entropy–enthalpy compensation.

Results

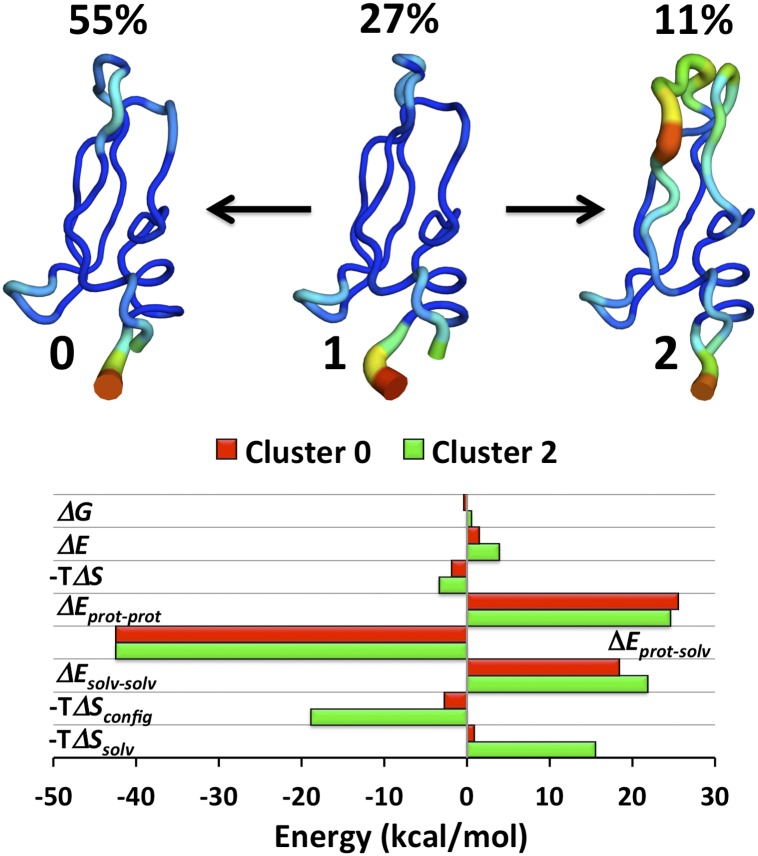
We carried out a thermodynamic analysis of the trajectory of the longest MD simulation of a protein published to date (22), a 1-ms simulation of the small trypsin inhibitor BPTI. The simulation results are available to the scientific community and agree reasonably well with NMR data (27). The previously defined conformational clusters (22) 0, 1, and 2 (C₀, C₁, and C₂) account for 92.3% of the simulation time and include the required number of simulation snapshots for thermodynamic analysis. Cluster C₁ is the most rigid and similar to crystal structures of BPTI bound to trypsin (22), whereas C₂ is the most mobile (Fig. 1, Upper).

Fig. 1.

(Upper) Representative backbone traces of the main conformational clusters C₀, C₁, and C₂ as labeled, and their percent occupancies during the simulation; color and thickness of the traces indicate rms fluctuation of the backbone (narrow blue, 0.4 Å; thick red, 3.7 Å) after structural superposition. (Lower) Bar graph of the computed thermodynamics (kilocalories per mole) of clusters C₀ (red) and C₂ (green) relative to cluster C₁. ΔE, total potential energy; ΔE_prot-prot, potential energy of protein; ΔE_prot-solv, interaction energy of protein and solvent; ΔE_solv-solv, potential energy of solvent; ΔG, free energy; −TΔS, total entropic free energy contribution; −TΔS_config, configurational entropy estimated by MIST at second order and corrected by subtraction of matched results with block-shuffled data; −TΔS_solv, solvent entropy computed as −T(ΔS − ΔS_config).

Although the occupancies (probabilities) of the three conformational clusters vary about fivefold, they are of similar stability, with free energies ranging over only ∼0.95 kcal/mol (1 kcal = 4.18 kJ) because of, essentially, the logarithmic relationship between probability and free energy (Methods). However, considerably larger entropy and enthalpy differences underlie these small free energy differences. For example, although clusters C₁ and C₂ are equistable to within 0.5 kcal/mol, their entropy (−TS) and enthalpy differences are, respectively, −3.2 and 3.7 kcal/mol; their configurational entropy differences are estimated at 19 kcal/mol, and the more mobile C₂ has weaker intraprotein (25 kcal/mol) and intrasolvent (22 kcal/mol) interactions, partly balanced by stronger protein-solvent interactions (−42 kcal/mol). The magnitudes of these thermodynamic components reveal an underlying potential for much larger swings in energy and entropy: even slightly imbalanced perturbation of these terms, such as by mutations or changes in solvent composition, could generate larger net entropy and enthalpy differences between the clusters.

Because the three conformational clusters are so closely balanced in free energy, small perturbations of the system might easily shift their probabilities. Such shifts would then be expected to yield significant changes in the entropy–enthalpy balance at minimal cost in free energy. In particular, we hypothesized the existence of control variables, here defined as geometric variables x_i, whose perturbations could select for one of three main conformational clusters and therefore, influence the global entropy and enthalpy. In searching for such variables, one may use the fact that a canonical MD simulation contains information on how the equilibrium distribution of conformations will respond to local perturbations, because perturbing the marginal probability distribution function (pdf) of a subset of variables x_c from p(x_c) to p′(x_c) will cause the equilibrium joint pdf over all variables x to change from p(x) to p′(x) = p(x|x_c)p′(x_c). The conditional pdf thus represents a response function of the system to shifts in the pdf of the control variables (SI Text shows the derivation). We focus here on perturbations in which the accessible range of a single variable is reduced, because these perturbations are simple to analyze; also, good statistics are available for the associated conditional probabilities. Thus, for each cluster C_a, where a = 0, 1, or 2, we sought a geometric variable x_i, either an interatomic distance or a torsion angle, for which a range R could be identified such that, to good approximation, 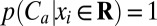and 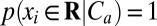. These conditions are best met when there is little overlap of the pdfs of x_i conditioned on the three clusters, p(x_i|C_a). Because the Jensen–Shannon divergence (25, 26) is zero for identical pdfs and reaches its maximum (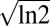) for nonoverlapping pdfs, we used it to define a metric M_ia,

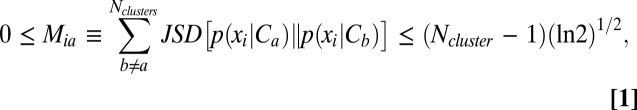which scores the ability of variable x_i to select cluster C_a from all other clusters C_b.

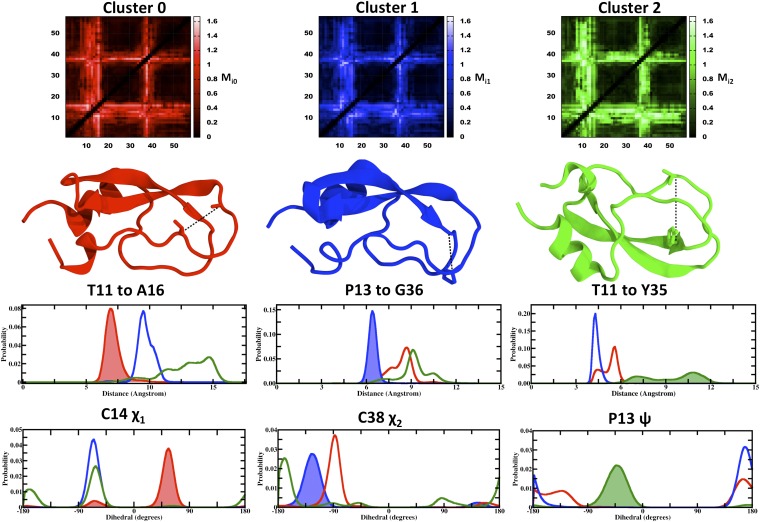
For each cluster, we found multiple carbon α-carbon α distances (x_i) whose M_ia scores are near the theoretical maximum of 1.67 (Fig. 2, row 1) and hence, had low overlap of the pdfs p(x_i|C₀), p(x_i|C₁), and p(x_i|C₂) (Fig. 2, row 3). For example, restricting the Thr11–Tyr35 distance to be greater than 6 Å (Fig. 2, row 2) drives the protein almost entirely into cluster C₂. Interestingly, experiments have shown that the Tyr35Gly mutation makes the loop region of BPTI more flexible (28). Note that the significance of certain carbon α-carbon α distances does not derive from direct energetic interactions between the two corresponding residues, but rather from a complex set of couplings of each distance with the structure as a whole. We also used the same analysis to seek other classes of geometric variable that could yield similarly large values of the M_ia metric and indeed, found a number of torsional pdfs with similarly low overlaps, as shown in Fig. 2, row 4. This result amplifies the observation that many control variables are available to shift the conformational state of this protein.

Fig. 2.

Identification and analysis of control variables. (Row 1) Heat maps of the M_ia values for each cluster a, where the possible control variables x_i are Cα–Cα distances among all 58 residues. The brightest pixels correspond to distances that can best isolate the respective cluster. (Row 2) Representative structure of the respective clusters, with the Cα–Cα distance, x_i, corresponding to the largest M_ia value shown as a dashed line. (Row 3) 1D pdfs of the Cα–Cα distances labeled in the row 2 for all three clusters; the pdf corresponding to the largest M_ia value for a particular cluster is shaded. (Row 4) Analogous pdfs corresponding to the largest M_ia value for each cluster when torsions are used as the x_i instead of Cα–Cα distances.

We validated the ability of the control variables to isolate thermodynamically distinct clusters as follows. For each cluster, we chose the control variable with the greatest value of M_ia (1.55, 1.52, and 1.59 for clusters C₀, C₁, and C₂, respectively). We then reweighted the entire trajectory by imposing on the associated control variable an infinitely high-walled square-well potential positioned to select the bulk of the conformations associated with the desired cluster, while avoiding values of the control variable shared by any other cluster. The thermodynamic quantities of the reweighted trajectory were compared with those quantities associated with the original cluster. The results for the reweighted trajectories agree with the original cluster thermodynamics to within 0.3 kcal/mol for all ΔG_ab, 0.4 kcal/mol for all ΔE_ab, and 0.6 kcal/mol for all −TΔS_ab (Table S1). Thus, the control variables select the intended conformational substates with their respective thermodynamic signatures.

Discussion

Thermodynamic and Structural Analysis of the BPTI Simulation.

The present analysis of a long MD simulation indicates that BPTI can exist in multiple conformational states with distinct thermodynamic signatures, and that a variety of control variables are available to drive it into selected conformational states. Given that BPTI is a small protein rigidified by three disulfide bonds and not normally regarded as allosteric, it seems likely that larger, more flexible proteins have even greater scope to shift among global states of different entropy and enthalpy. If so, then various perturbations of biomolecules, such as ligand binding and mutation, should often be accompanied by changes in entropy and entropy that derive from global population shifts rather than local interactions. Even relatively subtle changes, such as chemical changes across a congeneric series of ligands, could produce large changes in entropy and enthalpy of binding if the global states are of similar free energy. Furthermore, because the local forces driving, for example, ligand binding need not be the same as the global thermodynamic consequences of binding, one may view the biomolecule as transducing the local driving force into a quite different global thermodynamic signature. This phenomenon, essentially a manifestation of thermodynamic linkage (29), may be termed entropy–enthalpy transduction (EET).

Illustration and Implications of EET.

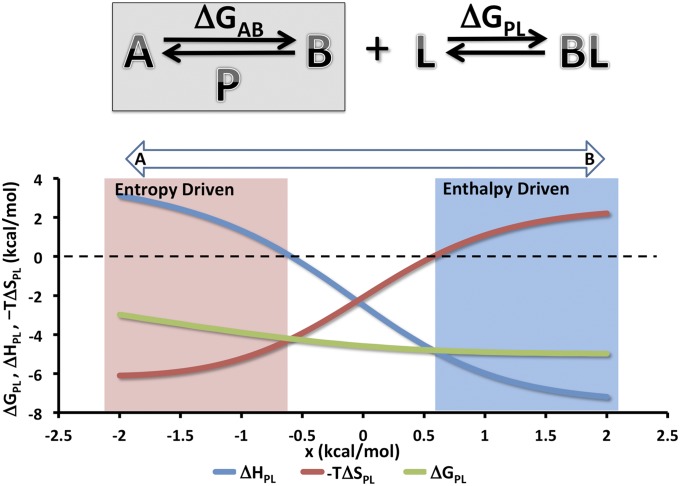
Some of the implications of EET may be illustrated quantitatively by considering a protein P, which can occupy either a low-entropy state, A, or a high-entropy state, B, where the intrinsic free energy difference between the two states is x kcal/mol (Fig. 3, Upper). The ligand L binds exclusively to state B through mainly enthalpic forces. (Note that, as in the BPTI analysis above, the changes in entropy and enthalpy in this model are considered to include contributions from the protein, ligand, and solvent.) When x exceeds thermal energy (RT = 0.6 kcal/mol, and R is the gas constant), the free protein exists primarily in state B, and the overall binding thermodynamics are simply the thermodynamics of the ligand's binding to B and hence are seen to be enthalpy-driven (Fig. 3, Lower). When x < −RT, the free protein exists primarily in state A, but it can switch to the high-entropy state B when L binds; therefore, the binding process now seems entropy-driven. In this way, the protein's ability to switch states on binding enables transduction of the ligand's binding enthalpy into entropy. Conversely, the Tyr35Gly mutant of BPTI, which makes its loops more flexible without visibly perturbing the trypsin-bound conformation (30), causes trypsin binding to become more favorable enthalpically but less favorable entropically (30), which was expected for a mutation that selectively stabilizes a conformational state similar in character to cluster C₂. The EET mechanism can also reinforce or amplify the driving forces of binding and other reactions. In the present example, this would occur if state B, rather than state A, were more stable enthalpically and less stable entropically. The enthalpic driving force for binding would then seem much stronger than the actual enthalpic forces driving ligand binding to the protein. In general, EET can generate shifts in enthalpy and entropy that are opposite to or far larger than expected based on local considerations. This finding implies that calorimetric data alone cannot be relied on to report the actual thermodynamic forces driving binding.

Fig. 3.

Two-state model system illustrating EET. (Upper) The protein P has two states A and B with a free energy difference of ΔG_AB. By construction, state B is higher in entropy and lower in enthalpy than A. Ligand L binds only state B and hence, drives P from a two- to one-state system. The overall binding free energy is ΔG_PL. (Lower) Overall thermodynamics of ligand–protein binding as a function of a small free energy bias, x, added to ΔG_AB to shift the preferred unbound state of P from state A (x < 0) to state B (x > 0). Here, ΔH_BL = −7.5, −TΔS_BL = 2.5, ΔH_AB = 10.0, −TΔS_AB = −10.0, and RT = 0.6, where ΔH_BL and −TΔS_BL correspond to the enthalpy and entropy of the ligand L binding to state B. All quantities are in kilocalories per mole.

Especially when unexpected shifts are observed, a structure-based search for substantial and potentially functionally relevant conformational changes may be fruitful, as illustrated by prior studies of drug binding to various sequences of DNA (31) and the binding of agonists and antagonists to the A_2B adenosine receptor (32). Changes in NMR-order parameters (33) can be informative in this regard. In some cases, they indicate increases in protein flexibility—and hence, presumably in configurational entropy—caused by protein–ligand binding (34–36). However, an increase in configurational entropy identified in this way may be balanced by a decrease in solvent entropy, as in the present calculations and further considered below, leading to either a positive or negative change in the net entropy. It is also worth noting that, although likely cases of EET amounting to 10 kcal/mol or more have been uncovered experimentally (31, 32, 35, 37, 38), identifying them required a combination of calorimetric and noncalorimetric experiments. Thus, there are presumably many systems where EET affects calorimetric results but has not been brought to light. Similarly, although measured changes in heat capacity are often used to elucidate the polar or nonpolar character of a protein–protein binding interface (39), if binding induces a significant conformational change in either protein, then the measured heat capacity may not accurately indicate the nature of the binding interface. The potential significance of this scenario is supported by the present calculations, because the computed heat capacity of conformational cluster C₂ is ∼0.09 and 0.13 kcal/mol per Kelvin greater than the computed heat capacities of clusters C₀ and C₁, respectively (Table S2).

A biomolecular system may access a high-entropy state not only through increased protein motion, but also through a conformational shift that leads to release of water or other solvent molecules far from the site of the inducing perturbation. The potential role of solvent in EET is illustrated by thrombin, whose affinity for dissolved Na⁺ increases when substrate binds (40), leading to possible cobinding of substrate and Na⁺. Because binding of Na⁺ to the enzyme–substrate complex at 300 K is enthalpically favorable (−18 kcal/mol) and entropically unfavorable (15.6 kcal/mol) (40), cobinding of substrate with Na⁺ could cause a substrate with intrinsic binding that is entropy-driven to seem enthalpy-driven. More generally, subtle changes in solvent, or indeed, in other experimental conditions, could lead to marked changes in measured entropy and enthalpy, with minimal change in free energy. Thus, in the scenario of Fig. 3, small changes in experimental conditions may produce small changes in the balance between states A and B (i.e., changes in x) and hence, large variations in the apparent thermodynamics of binding. Such sensitivity to experimental conditions could help explain cases where the variance of calorimetric enthalpies exceeds the variance of free energy (41), although other factors can also contribute (42).

Finally, the EET mechanism could underlie many cases of entropy–enthalpy compensation, a phenomenon in which related processes, such as a drug-like molecule binding various similar biomolecules, are associated with similar free energy changes but seemingly disproportionately large entropy and enthalpy changes that correlate near-linearly with a slope or compensation temperature, 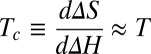. Entropy–enthalpy compensation is often explained on physical grounds by arguing that deeper energy wells are narrower and hence lower in entropy than shallow ones (43, 44). Although this mechanism may indeed play a role, it is not known whether the depths and widths of energy wells in fact anticorrelate or show no correlation at all (45). Moreover, this mechanism would not explain why compensation is usually near-linear with slope 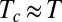. The present analysis of BPTI suggests that a series of related proteins with similar binding sites could readily access different conformations of similar free energy but different enthalpy and entropy. As a consequence, the same ligand could bind the series of proteins with similar free energies but quite different entropies and enthalpies. In this way, the EET mechanism can lead to highly linear entropy–enthalpy compensation. This observation is broadly consistent with prior suggestions, derived from plausible mathematical models rather than detailed simulation, regarding the importance of delicately poised equilibria (46), large fluctuations, and a high density of states (47–51). Although the EET mechanism can, in this manner, generate a highly linear correlation between entropy and enthalpy, it can also generate other thermodynamic patterns. For example, if the various drug-like molecules that bind a protein drive it into global conformational states with free energies that vary substantially, one may still observe a degree of entropy–enthalpy compensation, but it will not be as clear cut as in a system where the protein instead moves among states of very similar free energy.

General Formalism for EET.

To unify and generalize the ideas above, we describe here how the concepts of control variables and response functions allow partitioning of the thermodynamics of protein–ligand binding into an intrinsic part, due to the ligand's direct interactions with the protein, and a transduced part, due to the long-ranged conformational response to the ligand's manipulation of control variables in the binding site: 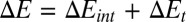, , 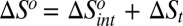and 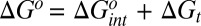. (A detailed derivation is provided in SI Text.) Given the full set of spatial coordinates, x, the coordinates of the atoms local to the binding site are defined as the control variables, x_c, which will be manipulated by the ligand when it binds. The coordinates of the remaining atoms are termed the transducing variables, x_t, which will respond to the manipulation of the control variables. For the free protein, the potential energy function of the whole system 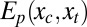is expressed as the sum of a binding site part that depends only on the control variables and a transducing part that depends on the transducing variables as well. For the energy of the ligand–protein complex, 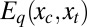, the binding site part also depends on the conformation, position, and orientation of the ligand, 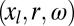, whereas the ligand's long-ranged energetic interactions with atoms beyond the binding site may be approximated as a small constant value, E_lt. Thus, binding of the ligand is approximated as directly affecting only the control variables, while the energy landscape of the transducing variables remains unchanged for any conformation of the control variables. This approximation should be good in a number of cases, such as when a small ligand binds a large protein. Hence,

and

The energetic and entropic contributions of the transducing part of the system may now be expressed as functions of the control variables, 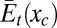and 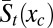, respectively, and these functions can, furthermore, be combined to yield the contribution of the transducing variables to the potential of mean force over the control variable W_t(x_c):

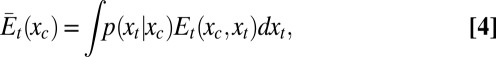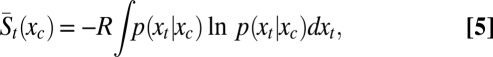where R is the gas constant, and

These thermodynamic response functions, which apply to both the free protein and the complex, are mediated by p(x_t|x_c), the pdf of the transduced variables conditioned on the control variables. The net contribution of the transducing variables to the binding thermodynamics may now be written as

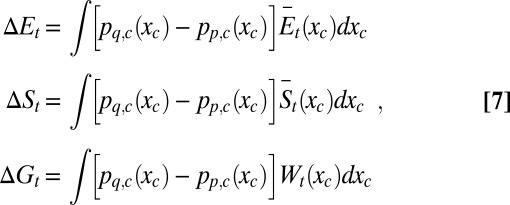where p_q,c(x_c) and p_p,c(x_c) are the marginal pdfs over the control variables for the complex and free protein, respectively, at equilibrium.

The intrinsic binding terms, which make up the remainder of the binding thermodynamics, are as follows:

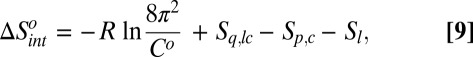and

Here, the angle brackets signify Boltzmann averages for the complex, free protein, and free ligand, respectively; E_l is the potential function of the free ligand, and S_x signifies the Gibbs–Shannon entropies of the subscripted variables for the complex, free protein, and free ligand, respectively. Note that, although the intrinsic and transduced quantities are formally separated, the control and transducing variables are linked in the sense that the potential of mean force of the control variables, which influences both the intrinsic and transduced quantities, is determined jointly by both parts of the system. Thus, the control variables may be viewed as a boundary between two parts of the system, the ligand and transducing part of the protein. The present analysis, thus, is reminiscent of the fluctuating boundary ensemble (48).

The transduction mechanism, then, operates as follows. When a ligand binds, it changes the pdf of the control variables from p_p,c(x_c) to p_q,c(x_c), driving the transducing variables to adopt a new pdf dictated by the response function p(x_t|x_c) and thus, altering the thermodynamic contributions of the transducing part of the protein according to the above expressions. Because there is no requirement that this conformational distribution match any state of the free protein, conformational selection is not an issue. Also note that 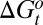can be negative in sign. For example, stabilizing interactions internal to the binding site of the free protein might hold it in a closed conformation that keeps the transducing part in an unstable state; then, binding of the ligand could open up the binding site and allow the transducing part to relax.

Entropy–enthalpy compensation occurs when 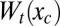, the transducing variables’ contribution to the potential of mean force over the control variables, varies little (e.g., ∼RT or less) over some conformational region R. In this case, the transducing variables permit the conformation of the binding site to rearrange freely within the bounds of R in response to a variety of ligands. However, saying that 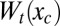varies little with x_c places no constraint on eithe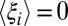r or 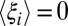individually; therefore, these components can still vary substantially over R. As a consequence, there can be many possible changes in p(x_c) that are associated with small changes in 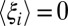but large changes in 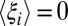and 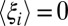. Such changes will lead directly to entropy–enthalpy compensation across the series of ligands, with compensation temperatures, T_c, near unity, as commonly observed experimentally. Deviations from such perfect (or strong) (50) entropy–enthalpy compensation will occur, however, if some ligands drive the binding site conformation (i.e., the control variables) into regions of conformational space associated with large changes in 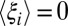and hence, generate different values of 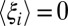or if the intrinsic energy and entropy changes vary substantially across the set of ligands.

Methods

The numerical thermodynamic analysis presented above and detailed in SI Text is based on the recent 1-ms BPTI simulation (22). Because the simulation yields a canonical distribution, the relative free energy ΔG_ab of two clusters a and b can be estimated as −RT ln(n_a/n_b), where n_i is the number of simulation snapshots in cluster i. By the same token, the Boltzmann-averaged potential energy of cluster a, E_a, can be computed as a simple mean over the snapshots in each cluster. The entropy difference between clusters a and b then is given by −TΔS_ab = ΔG_ab − ΔE_ab. Furthermore, we decomposed the total energy into protein–protein, water–water, and protein–water contributions and estimated the protein configurational (19, 20) entropy of each cluster by means of the MIST approach (23, 24). Issues with noise and convergence were minimized by subtracting out the results for block-permuted data (SI Text). Solvation entropy differences were then estimated as differences between total entropy differences and configurational entropy differences (52). Finally, the heat capacity of each conformational cluster was computed by application of existing formulae (53). Fig. 1 and Table S2 summarize the results, and Figs. S1, S2, and S3 provide convergence plots of the various thermodynamic quantities.