Abstract
Prolyl Hydroxylase Domain 2 (PHD2) is deemed a primary oxygen sensor in humans yet many details of its underlying mechanism are still not fully understood. (Fe2++αKG)PHD2 is 6-coordinate, with a 2His/1Asp facial triad occupying 3 coordination sites, a bidentate α-ketoglutarate occupying two sites and an aquo ligand in the final site. Turnover is thought to be initiated upon release of the aquo ligand, creating a site for O2 to bind at the iron. Herein we show that steady-state turnover is faster under acidic conditions, with kcat exhibiting a kinetic pKa = 7.22. A variety of spectroscopic probes were employed to identify the active-site acid, through comparison of (Fe2++αKG)PHD2 at pH 6.50 with pH 8.50. The near-UV circular dichroism spectrum was virtually unchanged at elevated pH, indicating that the secondary structure did not change as a function of pH. UV-visible and Fe X-ray absorption spectroscopy indicated that the primary coordination sphere of Fe2+ changed upon increasing the pH; EXAFS analysis found a short Fe-(O/N) bond length of 1.96 Å at pH 8.50, strongly suggesting that the aquo ligand was deprotonated at this pH. Solvent isotope effects were measured during steady-sate turnover over a wide pH-range, with an inverse SIE of on kcat observed (D2Okcat = 0.91 ± 0.03) for the acid form; a similar SIE was observed for the basic form of enzyme (D2Okcat = 0.9 ± 0.1), with an acid equilibrium offset of ΔpKa = 0.67 ± 0.04. The inverse SIE indicated that aquo release from the active site Fe2+ immediately precedes a rate-limiting step, suggesting that turnover in this enzyme may be partially limited by the rate of O2 binding or activation, and suggesting that aquo release is relatively slow. The unusual kinetic pKa further suggested that PHD2 might function physiologically to sense both intracellular pO2 as well as pH, which could provide for feedback between anaerobic metabolism and hypoxia sensing.
Cellular oxygen-sensing in humans is mediated by enzymes that hydroxylate the α-subunit of the hypoxia inducible factor (HIFα or HIF-1α).(1-3) The human HIF-hydroxylases comprise the factor inhibiting HIF-1 (FIH) and three isozymes of HIF-prolyl hydroxylase (PHD1-3),(4-6) each of which is an Fe(II), α-ketoglutarate (αKG) dependent oxygenase. While all of the PHDs hydroxylate specific Pro residues found within the oxygen-dependent degradation domains of HIF-1α (ODDD), PHD2 is the dominant regulator of HIF-1α.(7) As PHD2 is a key regulator of erythropoeisis and basal metabolism, mechanistic insights into rate-limiting steps during enzyme turnover may point the way to therapeutic control over related biological pathways.
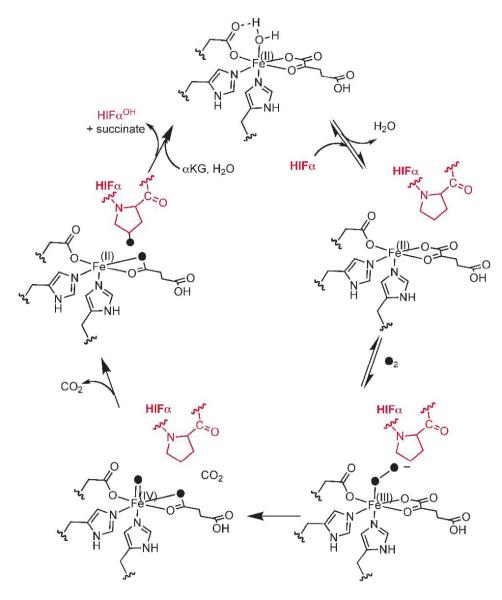
PHD2 is thought to follow the consensus mechanism for αKG-dependent oxygenases, using O2 to decarboxylate αKG, forming succinate, CO2, and a putative high-valent [FeO]2+ oxidant in the decarboxylation half reaction (Scheme 1).(8) PHD2 subsequently hydroxylates Pro402 or Pro564 of HIF-1α, forming a 4-hydoxyprolyl modification that leads to proteasomal degradation of HIF-1α.(9, 10) What makes PHD2 unusual is its regulatory function, in which O2-activation by the enzyme leads to altered gene expression, suggesting that the enzyme may adopt a mechanistic strategy to ensure tight coupling between decarboxylation and hydroxylation. This manuscript describes our efforts to test the rate-limitation of steps early in catalysis, as such a strategy could engender coupled turnover in PHD2.
Scheme 1.
The prevailing model for how αKG-dependent oxygenases achieve coupled turnover relies on an ordered binding of O2 following primary substrate, which is the C-terminal oxygen dependent degradation domain (ODDD) of HIFα in the case of PHD2. The Fe2+ of (Fe+αKG)PHD2 is coordinated by a His2Asp facial triad, a bidentate αKG, and a single aquo ligand;(11) similar structural features are also apparent with PHD2 re-constituted with non-native metal ions or αKG-mimics.(12) In the consensus mechanism, the aquo ligand is released once the primary substrate binds to form a five-coordinate Fe2+ center which is ready to react with O2.(13) Crystal structures of PHD2 (Figure 1) and other αKG-dependent oxygenases support this model,(8, 14-16) as an aquo ligand is frequently modeled into the active site during structural refinement of (M+αKG) forms of enzyme, whereas the aquo ligand is frequently absent from the (M+αKG+Substrate) forms. In addition, spectroscopic studies of related enzymes clearly show that Fe2+ is 6-coordinate in the (Fe+αKG) enzyme form, but 5-coordinate in the (Fe+αKG+Substrate) form of enzyme.(17-19) Poor substrates stimulate uncoupling for PHD2(20) and for related enzymes,(21-24) suggesting that the Fe2+ center becomes reactive toward O2 only after primary substrate, or substrate mimic, binds.
Figure 1.
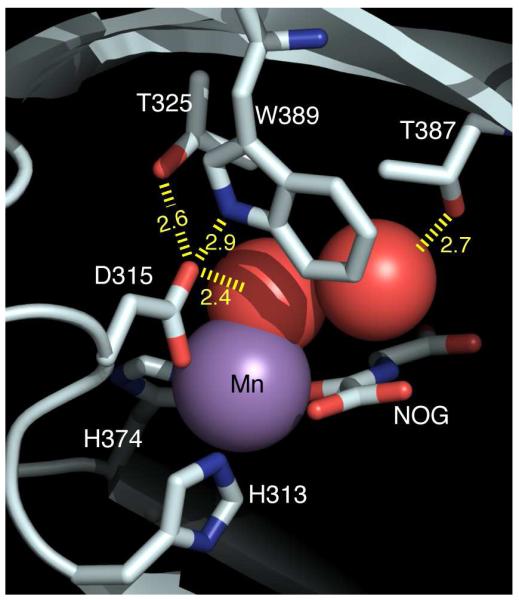
Hydrogen bonding (Å) within the PHD2 active site, for enzyme bound to (Mn+NOG+ODDD). PDBID 3HQR.(12)
Other reports, however, suggest that coordination changes to Fe2+ are not the sole origin of coupled turnover. For example, spectroscopic studies on the (Fe+αKG+Substrate)TauD revealed a mixture of 5-and 6-coordinate Fe2+,(17) indicating that the coordination changes are not absolutely correlated with binding of the primary substrate. Additionally, several enzymes such as TauD and FIH slowly react with O2 in the absence of primary substrate,(25, 26) suggesting that the Fe2+ center equilibrates between a 5- and 6-coordinate center even for the (Fe+αKG) enzyme form. As the rate-limiting step in TauD is thought to be decay of the [FeO]2+ intermediate (27), it appears that coupled turnover in related enzymes may reflect the rates of steps late in the catalytic cycle, Overall, the contrast between turnover that is controlled by an early step such as O2 binding, and turnover that is controlled by a late step such as [FeO]2+ decay, underscore the need to directly test the mechanistic significance of aquo release during turnover in PHD2.
Solvent isotope effects (SIEs) are excellent mechanistic probes for steps associated with aquo release from the Fe2+-OH2 of PHD2, due to the unique fractionation of L2O (L = H or D) within the Mn+-OL2⇌ Mn+ + OL2 equilibrium; aquo release is more favorable in D2O.(28) Consequently, the SIE on steady-state rate constants will be inverse (kH2O/kD2O < 1) when aquo release precedes a rate-limiting step early in turnover. Inverse kinetic SIEs have been used to identify mechanistically significant metal-aquo groups in a point mutant of soybean lipoxygenase(29) and in several metalloproteases(30, 31). Prior studies of the αKG-dependent oxygenases taurine dioxygenase (TauD), xanthine hydroxylase (XanA), and hydroxymandelate synthase (HMS) did not report solvent isotope effects related to fractionation of the metal-aquo group (27, 32, 33), indicating that steps associated with aquo from the Fe2+-OH2 were not rate-limiting for those enzymes.
Recently, Mössbauer spectroscopy and transient kinetics showed that only Fe(II)-containing forms of PHD2 accumulated in the pre-steady state,(34) suggesting that PHD2 turnover was not limited by [FeO]2+ decay. That report suggested that product release was rate-limiting; however, we note that steps early in catalysis, such as O2 binding, could also be rate-limiting. Rate-limiting steps early in catalysis could lead to an inverse SIE, prompting us to measure the SIEs on the steady-state rate constants. Another recent report utilizing a pull down assay suggested that PHD2 required an active site acid to be maximally active,(35) which was puzzling within the context of the consensus mechanism. Along with the SIE experiments, we also measured a kinetic pKa for PHD2 using purified enzyme by a direct kinetic assay. The active site acid was shown to be the Fe2+-OH2 (pKa = 7.22) by X-ray absorption spectroscopy and electronic spectra. Our results showed that the aquo release precedes a rate-limiting step in PHD2, leading to an inverse SIE on the apparent rate constants observed at ambient [O2], kcat and kcat/KM(ODDD). This is the first direct evidence for aquo release during turnover in any αKG-dependent oxygenase, and suggests that PHD2 may exert unusual control over steps early in the catalytic cycle as a strategy for controlling hydroxylation chemistry.
Materials and Methods
Materials and reagents
Buffers and reagents were purchased from commercial sources and used as received. Water was deionized using a Barnstead nanopure system; deuterium oxide (99.9 %) was purchased from Cambridge Isotopes Laboratory.
The peptide substrate for PHD2 was derived from the natural sequence of HIF-1α556-574, which is the C-terminal oxygen dependent degradation domain (ODDD) of HIF-1α. The peptide sequence used in this work (Pro564 of HIF-1α in bold) was DLDLEALAPYIPADDDFQL, in which the termini were not modified, and the natural Met residues were replaced by Ala at the underlined positions. ODDD (99% purity) was purchased from GL Biochem LTD (Shanghai) and was used as received for PHD2 activity assays.
Protein expression and purification
Recombinant human PHD2 was expressed and purified as the catalytic domain (residues 177-426), similar to previous protocols.(36, 37) PHD2 was expressed as an N-terminal GST fusion in E. coli BL21(DE3) cells, using a pGEX-4T-1 vector (Stratagene). The GST-PHD2 was purified using affinity chromatography (GE Bioscience GSTrap), then the GST affinity tag was removed using restriction-grade thrombin. Purified protein was then buffer exchanged into 50 mM HEPES pH 7.00 for storage at -80 °C. Protein purity was assessed by SDS-PAGE gel and mass spectrometry.
Buffer preparation
A three-component buffer solution (MPH buffer) was prepared using 20 mM each of MES, PIPES and HEPES. One portion of MPH buffer was adjusted to pH = 8.88 by the addition of 1 M NaOH, such that the ionic strength was 130 mM. To the acid form of the MPH buffer, solid NaCl was added to match the ionic strength of the base form at 130 mM. These two solutions of buffer of identical ionic strength were then mixed to achieve intermediate pH-values without any variation of the ionic strength.
For assays in D2O, MPH buffer was also prepared as described above except that D2O was substituted for H2O, and NaOH was dissolved in 99.9% D2O. These buffers were used for all solvent isotope experiments, and we estimated that the mole fraction deuterium in each assay as χD = 0.98. For all D2O buffer preparations, the pH electrode was equilibrated in D2O for 30 minutes prior to measuring the actual pD of the full range of prepared buffers, and applying the correction of pD = pH + 0.4.(28)
Reagents for pH-dependence and SIE assays
Working stocks of PHD2 were diluted to a final concentration of 7.5 μM in pL-adjusted MPH buffer containing H2O or D2O as dictated by the assay. The resulting working stocks of PHD2 in D2O-containing buffer contained χD = 0.98. Working stock solutions of ascorbic acid, α-ketoglutarate (αKG), iron and ODDD were prepared in either H2O or D2O as dictated by the experiment. All assays in both H2O and D2O were conducted using 0.3 μM PHD2, and saturating concentrations of ferrous ammonium sulfate (15 μM), ascorbic acid (1 mM) and αKG (200 μM). For all kinetics experiments, ODDD was varied between 1-50 μM. All components of the reaction were mixed at 37.0 °C, and reaction initiated by the addition of ODDD.
Steady-state kinetics assays
Saturating concentrations of Fe(II), αKG, and ascorbate were used throughout. Ambient concentrations of [O2] was used (217 μM at 37 °C), which is sub-saturating for PHD2 (KM(O2) ~ 250 μM) (38), meaning that our reported values are apparent rate constants for kcat and kcat/KM(ODDD). Initial-rates were obtained from quenched reactions in which time points were extracted and quenched in a MALDI matrix consisting of 4-α-cyano hydroxycinnamic acid with a 2:1 ratio of acetonitrile and 0.2% trifluoroacetic acid. Samples were then analyzed on a Bruker Daltonics Omniflex MALDI-TOF. The mole fraction of product (χODDD OH) was obtained from the resulting spectra by comparing the relative intensities of the peak at 2156 m/z, corresponding to (ODDD+Na)1+, to the peak at 2172 m/z, corresponding to (ODDD+O+Na)1+. Product formation was calculated using [ODDDOH] = χ(ODDD OH) × [ODDD]0, and used to determine initial rates.
CD spectroscopy
CD spectra were obtained using 0.1 cm path length quartz cuvettes. PHD2 (2μM) was mixed with (NH4)2Fe(SO4)2 (20 μM) and αKG (100 μM) in 10 mM sodium phosphate buffer (pH 6.50 or pH 8.50) at 20 °C.
UV-Vis absorption
Acid and base forms of PHD2 were prepared anaerobically in a Coy chamber by mixing 50 μM PHD2 with 45 μM ferrous ammonium sulfate and 50 μM αKG in degassed MPH buffer at pH 6.50 or pH 8.50, respectively. The samples were placed in sealed cuvettes, then the optical absorption spectra were measured using an Agilent HP-8453.
Viscosity effect
The initial rate of turnover for PHD2 was assayed in 50 mM HEPES (D2O) at pD = 7.00 by mixing 0.3 μM PHD2, 1 mM ascorbate, 15 μM ferrous ammonium sulfate and 200 μM αKG. All components were prepared in D2O-containing buffer, and reaction was initiated by adding saturating ODDD (15 μM). A matching assay was also performed in 50 mM HEPES at pH = 7.00, containing 10% sucrose as viscosogen. The relative viscosity (η/ηo) of D2O at 37°C is 1.31 mPa•s, which closely matches that of a 10% sucrose solution at 37°C.(39) Assays were conducted as described for other steady-state kinetics assays.
X-ray absorption spectroscopy sample preparation
XAS samples were prepared anaerobically in a Coy chamber by mixing 1 mM PHD2, 0.9 mM ferrous ammonium iron (II) sulphate and 0.9 mM αKG in 50 μL MPH buffer at pH 6.50 for the acid form of the enzyme and pH 8.50 for the basic form. Both samples were diluted with buffer to 500 μL with their respective buffers, then incubated for 15 minutes at room temperature. The samples were treated with chelex (Bio-Rad) for 30 minutes to remove adventitious metal from the samples, then concentrated to a final volume of 50 μL. Each sample was then loaded into a XAS sample holder and immediately submerged in liquid N2 in a Coy chamber and stored at -80 °C until sample analysis could be performed.
X-ray Absorption Spectroscopy
XAS data collection and analysis were performed as reported previously.(40) Data were collected under dedicated conditions on beamline 7-3 at the Stanford Synchrotron Radiation Laboratory (SSRL). X-ray absorption near edge structure (XANES) data was collected from -200 eV to +200 eV with respect to the Fe edge energy (7111.2 eV). Extended X-ray absorption fine structure (EXAFS) data was collected to k = 14 Å−1 above the edge energy. XAS data analysis was performed using EXAFS123(41) for XANES analysis and SixPack(42) for EXAFS analysis. Scattering parameters for SixPack fitting were generated using the FEFF (v. 8.0) software package.(43)
Eight scans were averaged for the (Fe+αKG)PHD2 at pH 6.50 and twelve scans were averaged for (Fe+αKG)PHD2 at pH 8.50. The normalized intensity of the peak associated with a 1s → 3d electronic transition was then used to indicate the coordination number/geometry of Fe(II) sites (2, 3). The energy of Fe K-edge was determined by taking the maximum of the first derivative of the rising edge. For EXAFS analysis of the data collected at the Fe K-edge, a limit of k = 2 – 12 Å−1 was used, with the upper limit determined by the sample with the poorest signal:noise (low pH) and maintained for the purpose of comparison. This data range corresponds to a resolution in the first sphere of ~ 0.16 Å (~ π/(2Δk)). For the high pH data, where a ligand with a short (< 2.0 Å) is found, the data were refit using data over the k = 2 – 14 Å−1 range was used, which improves the resolution to ~ 0.13 Å (see supporting information. Table S3 and Figure S1).
Structural models of the metal sites involving coordination numbers from 2 - 7 were systematically evaluated for all possible combinations of N/O- and S-donors by holding the number of scattering atoms in each shell to integer values. No acceptable fits involving S-donor ligands were obtained. The number of imidazole ligands (Im) in the coordination sphere was estimated by multiple-scattering analysis as previously described (4 - 6). Amplitudes and phase shifts for multiple-scattering paths for the Fe-Im ligands were generated using FEFF (v. 8.0), with the coordinates obtained from the crystal structure of human (Fe+αKG)PHD2 (PDB ID 3OUJ). Scattering paths of similar length were combined in one shell, as described by Tierney et al. (5, 6). During the fitting process, coordination numbers were constrained to integral values and a scale factor of 0.9 was used. Bond lengths, σ2 and a single value of ΔE0 were allowed to vary in each fit. However, acceptable fits with R < 10% could not be obtained without modeling the five-membered O-C-C-O chelate ring that is a feature of αKG (see supporting information). This was previously noted in studies of other non-heme Fe(II) enzymes with αKG bound (35). To model the scattering from the αKG ligand, multiple-scattering analysis derived from a rigid [-O-C-C-O-]Fe five-membered chelate ring was used, with parameters obtained from FEFF (v. 8.0) and the above referenced structure (Table 1), as was previously employed for similar enzyme sites.(35) In this analysis, a single value of σ2 was used for all the atoms in the O-C-C-O chelate ring, and distances in the chelate ring were constrained to vary with a single value of Δr.
Table 1.
XANES and EXAFS analysis of (Fe+αKG)PHD2 at pH 6.50 and pH 8.50.
| (Fe+αKG)PHD | XANES Analysis | EXAFS Analysis | |||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
|||||||||
| Edge (eV) |
1s[barb2right]3d peak area (x10-2 eV) |
Coord. No. |
Shell | r (Å)a | σ2b (x10-3Å2) |
HE0 (eV) |
%Rc | Red. χ2 |
|
| pH 6.5 | 7121.2(2) | 6(1) | 5/6 | 2 N/O | 2.05(6) | 6(1) | 4(3) | 6.4 | 6.7 |
| 2 N/O | 2.21(5) | 6(4) | |||||||
| (2 His) | |||||||||
| 1 O | [2.03(8)]d | 7(1) | |||||||
| 1 O | [2.24(8)] | ||||||||
| 1 C | [2.75(8)] | ||||||||
| 1 C | [2.85(8)] | ||||||||
| pH 8.50 | 7120.9(2) | 7.9(4) | 5/6 | 3 N/O | 2.15(2) | 4(2) | 9(1) | 5.9 | 2.7 |
| (2 His) | |||||||||
| 1 N/O | 1.96(4) | 6(3) | |||||||
|
|
|||||||||
| 1 O | [1.90(6)] | 9(3) | |||||||
| 1 O | [2.11(6)] | ||||||||
| 1 C | [2.62(6)] | ||||||||
| 1 C | [2.72(6)] | ||||||||
r (Å) is the radial distance between metal and ligand.
σ2 is the root mean square disorder in the metal ligand distance.
R is the goodness of fit. Numbers in parentheses represent standard deviation for least square fits.
Distances in [ ] correspond to atoms in a O C C O chelate ring and were constrained to vary with a single value of Δr for the chelate ring.
To compare different models used to fit the data, the R-factor and reduced χ2 parameters were assessed; improved fits minimized both parameters. Although R will always improve with an increasing number of shells (adjustable parameters), the reduced χ2 will increase when a model has too many adjustable parameters. Best fits were judged by using two goodness of fit parameters, reduced χ2 and R, and the deviation of σ2 from typical values.
Results
Activity is pH-dependent
The steady-state rate constants for PHD2 in which ODDD was the varied substrate were measured using saturating concentrations of Fe(II), αKG, and ascorbate at 37 °C in air saturated MPH buffer. As PHD2 was not saturated with respect to O2 (KM(O2) ~ [O2] under our assay conditions (38), our reported rate contants are apparent ones. The initial-rate of turnover was measured as a function of varied [ODDD], and the rate constants kcat and kcat/KM obtained by fitting the data to the Michaelis-Menten equation. The rate at saturating [ODDD], kcat, was pH-dependent over the span of pH 6.5 – 9.0, ranging from a maximum of > 2.5 min−1 at low pH, to a minimum less than 0.5 min−1 at high pH (Figure 2). The fitted values for kcat/K were ~ 1 μM−1 min−1, making the KM less than 2 μM. As it was difficult to obtain high signal/noise in the MALDI spectra at very low [ODDD], the KM values were too uncertain for us to describe the pH-dependence of this kinetic parameter.
Figure 2.
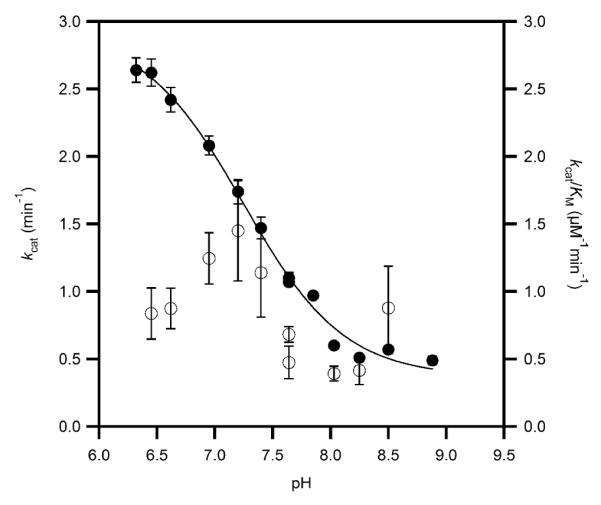
Apparent steady-state rate constants for PHD2 in MPH buffer at 37.0 °C, ambient [O2]; kcat (closed circles) was fitted to pKa = 7.22 ± 0.03, kcat(acid) = 2.99 ± 0.08 min−1; kcat(base) = 0.31 ± 0.02 min−1; kcat/KM (open circles) was not fitted.
The high activity at pH = 6.50 indicated that there was an active site acid in PHD2, which upon deprotonation caused the enzyme to exhibit lower activity. A simplified mechanism that accounts for such behavior is shown in Scheme 2, in which both (Fe+αKG)PHD2 (E) and (Fe+αKG+ODDD)PHD2 (ES) are protonated with the same acid equilibrium constant (Ka) at an acidic position (BH). ODDD binds with equal affinity to either enzyme form, but kcat differs for the acid form (kacid) and base form (kbase).
Scheme 2.
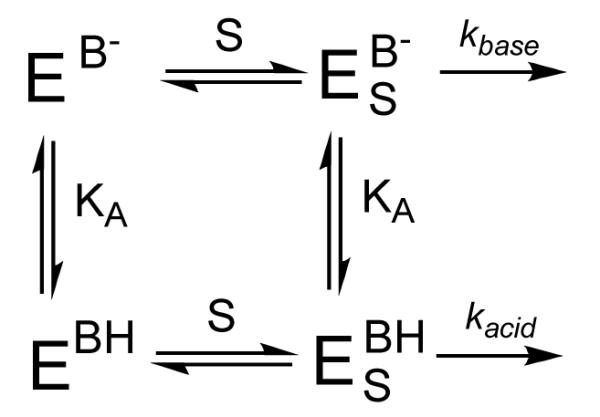
The pH curve of kcat was fitted to an equation which accounted for the pH-independent kcat of the acid form (kacid), and of the base-form (kbase), as well as the protonation equilibrium (Ka) for interconverting these forms.(44) Nonlinear least-squares fitting showed that the acid form of the enzyme exhibited kacid = 2.99 (0.08) min−1, whereas the base form exhibited kbase = 0.31 (0.02) min−1, with pKa = 7.22 (0.03).
| (Eq.1) |
As kcat only reflects steps after substrate binding, this pH-dependent activity must arise from a protonation equilibrium following ODDD binding – a protonation prior to ODDD binding would not affect kcat, but was included in the above scheme for simplicity because it cannot be excluded based upon the kinetics data. As proton transfer is not thought to play a role during the catalytic cycle of αKG dependent dioxygenases, we hypothesized that an acidic group coordinated to the iron center, such as Fe2+-OH2, was the acid involved in turnover. This was tested by spectroscopic measurements at pH 6.50 and pH 8.50.
PHD2 secondary structure is unchanged at pH 8.50
Circular dichroism (CD) experiments were performed to investigate the possible conformational changes of PHD2 upon changing the solution pH. The secondary structures of PHD2 at pH 6.50 and pH 8.50 were monitored in the far-UV spectral region (Figure 3). The CD data were nearly superimposable in both samples, indicating that changing the pH from 6.50 to 8.50 did not cause significant changes in overall secondary structure of PHD2.
Figure 3.
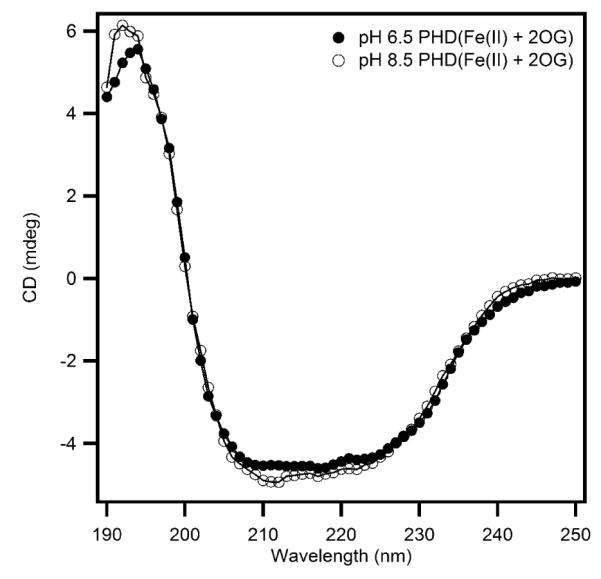
Circular dichroism spectra showing the effect of pH on the secondary structure of (Fe+αKG)PHD2 (2μM) in 10 mM sodium phosphate buffer at pH 6.50 and pH 8.50.
Fe2+ environment changes: UV-Visible absorption spectra
Changes to the Fe2+ coordination environment of many αKG-dependent dioxygenases lead to shifts in the UV-Visible absorption spectra in the 300 - 500 nm range that can be attributed to metal-to-ligand charge transfer (MLCT) transitions. These transitions were observed in (Fe+αKG) enzyme form of FIH at 500 nm, taurine dioxygenase (TauD) at 530 nm and clavaminate synthase 2 (CS2) at 476 nm.(45-47) UV-Visible absorption spectra of anaerobic (Fe+αKG)PHD2 were collected at pH 6.50 and pH 8.50, to test for changes in the electronic environment of Fe(II). Changes in the MLCT region upon increased pH were clearly seen in the difference spectra, ΔAbs = Abs8.50 – Abs6.50 (Figure 4). Absorption peaks shifted at high pH, as shown by the apparent maxima near 342 nm and 485 nm, indicating that the electronic environment of Fe(II) changed due to increased pH. Although we could not assign these shifts to specific MLCT bands, the spectral changes indicated that a ligand to the Fe(II) became deprotonated as pH was increased from 6.50 to 8.50. The most likely candidate is the aquo ligand bound to Fe(II), as the pKa for the facial triad ligands are expected to lie well outside of the 6.50 – 8.50 range, and the calculated pKa for Fe(H2O)62+ only slightly above the physiological range.(48)
Figure 4.
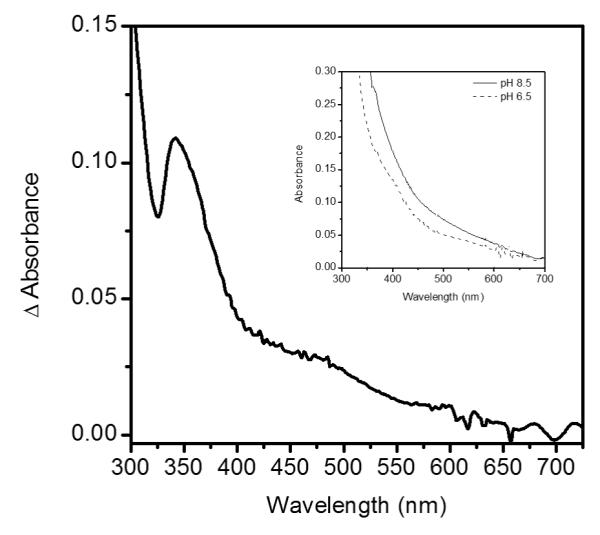
Difference spectra of PHD2 at pH 6.50 and pH 8.50; insert shows raw spectra prior to subtraction. Sample cuvettes contained PHD2 (50 μM), Fe(NH4)2(SO4)2 (45 μM) and αKG (50 μM) prepared anaerobically.
Increased electron density at pH 8.50: XANES Analysis
Fe K-edge XAS experiments were performed to investigate the metal center of (Fe+αKG)PHD2 at pH 6.50 and 8.50. The analysis of XANES data provides information about the coordination number and site symmetry of a metal site (2, 3). Fe(II) has vacancies in the 3d manifold that give rise to peaks associated with 1s → 3d electronic transitions that are observed in the pre-edge XANES region of the K-edge spectra in both the samples (Figure 5). The peak area of the 1s → 3d transition depends on the coordination number and geometry of the metal sites (2, 3). By comparing the 1s → 3d transition peak areas of the PHD2 samples with typical values for known coordination numbers/geometries we were able to determine the coordination numbers of both the PHD2 samples from the XANES data.
Figure 5.
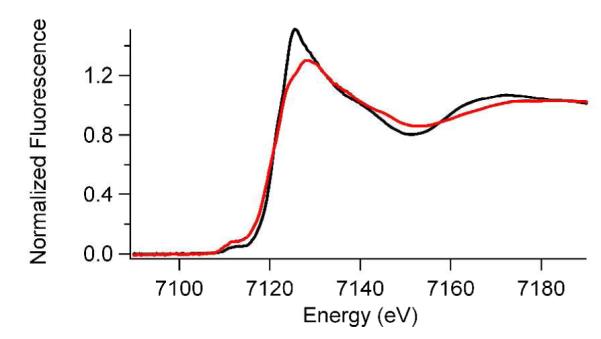
Fe K-Edge XANES spectra of (Fe+αKG)PHD at pH 6.50 (black) and pH 8.50 (red).
The XANES data (Table 1 and Figure 5) showed that the structure of the Fe site became more electron rich upon increased pH. The K-edge energy was lower at pH 8.50 (7120.9 eV) than at pH 6.50 (7121.2 eV), indicating increased electron density at Fe(II) at pH 8.50. This is further supported by the decreased intensity of the white line. This increased electron density did not result from a change in the site symmetry of PHD2, as the 1s → 3d peak areas were similar at pH 6.50 (area = 6 × 10−2 eV) and pH 8.50 (area = 7.9 × 10−2 eV). The higher 1s → 3d peak area at pH 8.5 could be due to higher distortion of the octahedral site as a result of one shorter Fe-N/O bond. Typical 1s → 3d peak areas for octahedral geometries are 3 – 7 × 10−2 eV,(49) whereas lowering symmetry to a five-coordinate geometry is associated with peak areas of 8 – 13 × 10−2 eV (2, 3). The measured peak area for the high pH sample is at the high end of what is typically observed for six-coordinate Fe(II), but could reflect a six-coordinate site with deviations from ideal octahedral symmetry.(50)
Hydroxide ligand at pH 8.50: EXAFS Analysis
The analysis of EXAFS provides information about the number and types of ligands bound to a metal, and metric details of the metal site structure; best fits of the data are summarized in Figure 6 and Table 1. The best fit to the EXAFS data for (Fe+αKG)PHD2 at pH 6.50 consists of six N/O donor ligands, in agreement with the XANES result, of which two are imidazoles from multiple-scattering analysis (Table 1). Using the chelate model for αKG, the two O atoms from αKG were found at 2.03(8) Å and 2.24(8) Å. Two shorter Fe-N/O bonds were found at 2.05(6) Å, and two longer Fe-N/O bonds at 2.21(5) Å. These distances are typical for six-coordinate Fe(II), as seen for the C. elegans dual specificity histone demethylase (CEKDM7A) complexed with αKG(47) and human AlkB human homolog 3 (ABH3) complexed with αKG.(48) For example, the Fe2+-OH2 bond distance in Fe(H2O)62+ is calculated to be 2.16 Å,(48) which in excellent agreement with the bond length found experimentally.(51)
Figure 6.
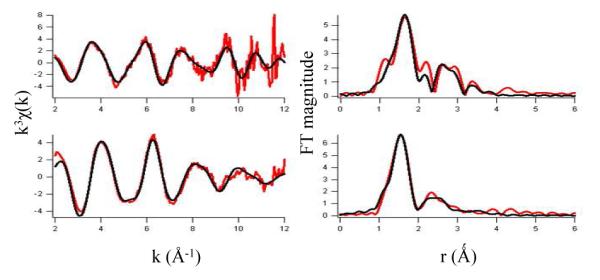
EXAFS analysis. Left: Unfiltered, k3-weighted EXAFS spectra of (Fe+αKG)PHD2 at pH 6.50 (top) and at pH 8.50 (bottom), and fits (black lines, from Table 1). Right: Fourier-transformed EXAFS data and fits.
The best fit to the EXAFS data for (Fe+αKG)PHD2 at pH 8.50 also consisted of six N/O donor ligands of which two were imidazoles from multiple scattering analysis (Table 1). But the average bond lengths at pH 8.50 were shorter than those found at pH 6.50. Using the chelate model for αKG, the two O atoms from αKG were found at 1.90(6) and 2.11(6) Å. In addition, three longer Fe-N/O bonds were found at 2.15(2) Å, and a short Fe-N/O bond was found at 1.96(4) Å. The contraction of the Fe-ligand bond lengths at pH 8.50 nicely agreed with the trends in Fe K-edge energy, as shorter Fe(II)-ligand bond lengths would be expected to increase electron density on Fe(II).
The Fe2+-(OH/OH2) bond length is very sensitive to the aquo/hydroxide protonation status, as shown by calculations for [Fe(OH)n(H2O)6-n](2-n)+ which combined density-functional theory with a continuum dielectric model.(48) This Fe-O bond length was calculated to be 2.16 for the aquo ligand (n = 0), shrinking to 1.80 for the hydroxide ligand (n =1), a reduction which very nicely parallels the trend in bond lengths observed for PHD2. We propose that the unique Fe-O/N bond distance observed at pH 8.50 is an Fe-(OH) bond.
Solvent Isotope Effect
The solvent isotope effects on the apparent rate constants kcat and kcat/KM were measured to test the involvement of solvent-derived protons on turnover. As kcat in H2O was pH-dependent, Michaelis-Menten kinetics were fitted over a full pD range in D2O-containing MPH buffer. The D2O-containing buffers were estimated to contain χD = 0.98, and were treated as being fully deuterated. We observed a kcat ranging from a high value of ~3.1 min−1 at pD = 7.05 to a low value of ~0.5 min−1 at pD = 9.05, with kcat/KM < 2 μM−1 min−1. These trends in D2O were similar to those observed in H2O, but indicated that both kcat and kcat/KM were greater in D2O.
The pD curve of kcat was fitted to Eq. 1, which accounted for the pL-independent kcat of the acid form (kacid) and of the base-form (kbase), as was done for the variable pH data set.(44) The acid form of the enzyme in D2O exhibited kacid = 3.30 (0.06) min−1, whereas the base form exhibited kbase = 0.34 (0.04) min−1, with the protonation equilibrium pKa = 7.89 (0.03).
The solvent isotope effect is the ratio of each rate constant in H2O and D2O, D2Okcat = kcatH2O / kcatD2O. The acid form of the enzyme exhibited an inverse SIE that was observable as the higher plateau for the pD curve (Figure 7), D2Okcat = 0.91 ± 0.03. The SIE for the basic form of the enzyme was indistinguishable from unity, D2Okcat = 0.9 ± 0.1, and the acid equilibrium offset was ΔpKa = 0.67 ± 0.04. The inverse SIE found at acidic pH is unusual, as inverse SIEs have never been observed for any αKG-dependent dioxygenase. Other metalloenzymes with inverse SIEs include stromelysin and a point mutant of soybean lipoxygenase,(29, 30) where metal-aquo centers were invoked during the catalytic cycle.
Figure 7.
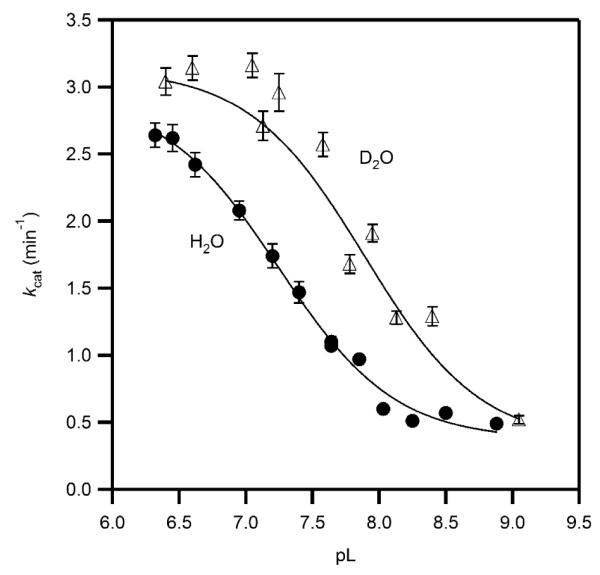
Solvent isotope effect on the apparent kcat for PHD2 in MPH buffer at 37.0 °C, ambient [O2] (D2O, open triangles, H2O, closed circles), fitted to pH-dependent model. The acid form of PHD2 exhibited kcat = 2.99(8) min−1 in H2O, and 3.30(6) min−1 in D2O, for D2Okcat = 0.91(3). The base form of PHD2 exhibited kcat = 0.31(2) min−1 in H2O, and 0.34(4) min−1 in D2O, for D2Okcat = 0.9(1). The pKa = 7.22(3) in H2O; pKa = 7.89(3) in D2O.
The magnitude of the SIE on kcat/KM was subject to large uncertainties due to the very small values for KM. A plot of this data suggested that kcat/KM may have a similar pL-response as seen for kcat, as well as likely exhibiting an inverse SIE (Figure 8); however, we did not attempt to fit this data due to the large uncertainties in many of the data points.
Figure 8.
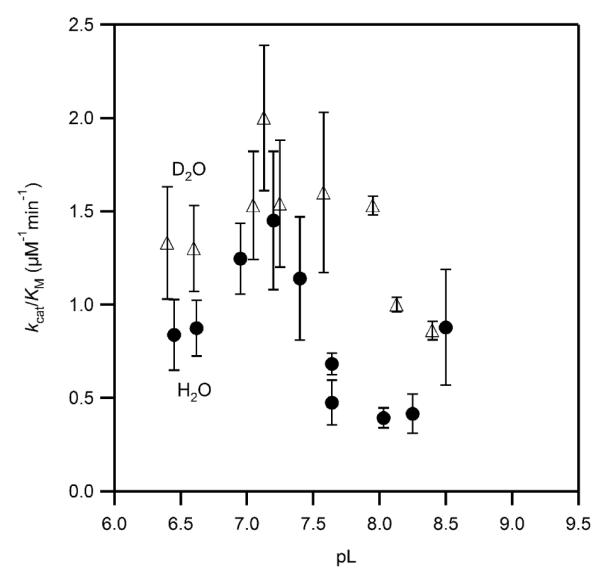
Solvent isotope effect on the apparent kcat/KM for PHD2 in MPH buffer at 37.0 °C, ambient [O2] (D2O, open triangles, H2O, closed circles).
Inverse SIEs are unusual, and can be attributed to one of three chemical origins: fractionation of a solvent derived proton in a CysSH / CysS– + H+ equilibrium, as for a protease; a viscosity-sensitive conformational change; or fractionation of solvent-derived protons in an M-OH2⇌ M + OH2 equilibrium.(28) As there are no Cys residues near the active site, deprotonating CysSH is highly unlikely to lead to the inverse D2Okcat. However, a conformational change does occur when PHD2 binds ODDD, and Fe2+-OH2 dissociation must occur during turnover, making both of these potential origins of the inverse SIE.
In a few notable cases,(52, 53) inverse SIEs were shown to arise from conformational changes linked to solvent viscosity, rather than from a chemical step. Consequently, we performed a control assay comparing the rate of PHD2 turnover in the presence or absence of 10% sucrose in 50 mM HEPES, pH 7.00. The control assays in H2O-containing buffer exhibited v0 = 2.07(5) min−1, and in the same buffer with 10% sucrose v0 = 2.04(2) min−1. The results indicated that the observed SIEs must arise from fractionation of the Fe2+-OH2, rather than from a conformational change.
Discussion
Although aquo release from the Fe2+-OH2 has been proposed as a crucial feature in the consensus mechanism for the αKG-dependent oxygenases to engender coupled turnover, mechanistic data has has either been absent on this point, or else has suggested that steps late in catalysis are rate-limiting (27, 54). Our data establish that aquo release in PHD2 immediately precedes a rate-limiting step, making PHD2 unusual in its control over the Fe2+-OH2 bond. First, the SIE on the apparent kcat is inverse, D2Okcat = 0.91(3), which requires that the Fe2+-OH2⇌ Fe2+ + H2O step equilibrates prior to a rate-limiting step. The simplest explanation is that (Fe+αKG)PHD2 binds the aquo ligand much more tightly than O2, making steps directly involved in O2 binding or activation (partially) rate-limiting. Second, the Fe2+-OH2 can be deprotonated at neutral pH (pKa = 7.22), which we attribute to unique second-sphere hydrogen binding within PHD2. Deprotonation led to decreased rate constants for turnover, which is likely to have physiological significance for hypoxia sensing due to the similarity to the normal physiological pH of 7.4.
The active-site acid is Fe2+-OH2
Electronic transitions in the UV-Visible spectra shifted when the pH increased from 6.50 to 8.50, which we attribute to shifts in charge-transfer transitions. These shifts were due to changes in the energies of metal or ligand-based orbitals at elevated pH, which firmly focused our attention on the ligand environment of Fe(II) as being pH-dependent. The XAS experiments definitively showed decreased bond-lengths to the Fe(II) center at pH 8.50, consistent with altered charge-transfer transitions in the UV-Vis spectrum. Most telling was the unique N/O donor found at 1.96 Å in the pH 8.50 sample, which was consistent with an Fe2+-OH bond.
The pKa of Fe2+-OH2 in PHD2 is unusually low when compared to similar non-heme Fe(II) centers, which likely reflects the second-sphere hydrogen bonds to Fe2+-OH2 in PHD2 (Figure 1). The role of the facial triad in accepting a hydrogen bond from the aquo ligand has been noted in related enzymes, but PHD2 is unusual in the extensive hydrogen bond network observed crystallographically that would be expected to both stabilize the Fe2+-OH2 bond, as well as lower the pKa of the bound aquo ligand. The two hydrogen bonds from Trp389 and Thr325 are oriented such that Asp315 is well-positioned for hydrogen bonding to the aquo ligand, both in structures of (Fe+αKG)PHD2 as well as (Mn+NOG+ODDD)PHD2.(11, 12) Using -5 kcal/mol as a typical hydrogen-bond strength, these three hydrogen bonds may stabilize the Fe2+-OH2 bond by an additional -15 kcal/mol, which would have a significant effect on both the kinetics and thermodynamics of aquo release. An indirect hydrogen bond was also observed between Thr387 and the aquo ligand, via a single localized H2O; while the energetic stabilization of Fe2+-OH2 from this indirect hydrogen bond is harder to estimate due to the entropic cost of the intervening H2O, a reasonable estimate would be -4 kcal/mol. This indirect hydrogen bond is also positioned well to facilitate deprotonation of the aquo ligand, which we propose is the main reason for the low pKa of the aquo ligand.
Examples of the key role of Fe2+-OH2 bond strength and pKa in enzyme function are found in Mn/Fe-SOD, soybean lipoxygenase, and TauD. In each of these enzymes, the Fe(II) is coordinated by an aquo ligand, one or more additional ligands, and a His2(Asp/Glu) facial triad in which the carboxylate ligand is positioned cis to the H2O ligand. Hydrogen bonding within the active site is central to the reactivity of this aquo ligand, which in turn dictates enzyme activity, as maintaining the metal-aquo bond is crucial for Mn/Fe-SOD and lipoxygenase, whereas release of the aquo ligand is thought necessary in TauD. Similarly, the pKa of Fe2+-OH2 moiety has profound effects on the reactivity of Mn/Fe-SOD and lipoxygenase, as these enzymes perform proton coupled redox reactions.
In the case of Mn-SOD and Fe-SOD, the metal center undergoes a reversible M2+-OH2⇌M2+ + OH– 2 + H+ + e– reaction to disproportionate O2•–. The aquo/hydroxo ligand must remain bound during turnover, which is facilitated by a hydrogen bond from the facial triad.(55) Although there is only one anionic ligand in Mn/Fe-SOD, the cationic M2+-OH2 center may be necessary for efficient reaction with the anionic O2•–. Furthermore, an elevated pKa for the aquo ligand is a key factor in determining the redox potential of the metal, and the suitability of either Mn or Fe to be catalytically active in the respective enzyme.(55) Both Mn-SOD and Fe-SOD, when constituted with Fe(II), favor the acid form of the aquo ligand, Fe2+-OH2. However, hydrogen bond donation and steric clashes with a nearby Gln residue shifts the pKa of Fe2+-OH2 from 23.3 for Fe-SOD to 15.6 for Fe-reconstituted Mn-SOD.(56) This decrease in pKa makes the Fe2+-constituted Mn-SOD catalytically inactive, due to an unfavorable redox potential.
Soybean lipoxygenase (SLO) also catalyzes a proton-coupled redox process that is often viewed as an H-atom transfer with 1.4-dienes, but SLO lacks hydrogen bonds to the aquo ligand. There are two anionic ligands, which stabilizes the neutral Fe2+-OH2 center; consequently the pKa is estimated to be higher than the physiological pH range.(57, 58) The aquo ligand remains coordinated throughout turnover, but the high pKa is necessary for an exothermic hydrogen atom abstraction from 1,4-diene containing fatty acids.
The metal center of TauD is the most directly comparable to PHD2, as TauD is an αKG-dependent oxygenase with taurine as primary substrate. The Fe2+ of TauD is bound by the facial triad and αKG, with a sixth coordination site occupied by a weakly bound aquo ligand.(17) In contrast to our observation for PHD2, activity for TauD is pH-independent (pH 6.9 – 8.0) indicating that the pKa of the Fe2+-OH2 moiety is higher than the tested pH range (27). Although aquo release is proposed to be tightly coupled to prime substrate binding in this class of enzyme, TauD undergoes appreciable uncoupled reactions with O2.(59) A rationale for this can be found upon inspection of the X-ray crystal structure,(15) which shows that the facial triad Asp ligand of TauD is oriented such that it cannot hydrogen bond to the aquo ligand, resulting in a high fraction of five-coordinate enzyme even in the absence of taurine,(17) as well as a facile uncoupled O2-activation. It appears that the absence of a hydrogen bonding network to the aquo ligand in TauD shifts the Fe2+-OH2⇌ Fe2+ + H2O equilibrium to favor aquo release.
SIE implicates O2-binding/activation as partially rate-limiting for PHD2
Inverse SIEs are unusual, and therefore our observation of inverse SIEs for PHD2 are diagnostic of aquo release from the Fe2+-OH2 center preceding a mechanistic step that is partially or fully rate-limiting. Reported SIEs for other αKG-dependent oxygenases are either unity, as reported for the pre-steady kinetics of TauD (27), indicating that solvent deuteration has no effect on the measured rate constants; or else are greater than one, as observed for xanthine hydroxylase (XanA) (32) and hydroxymandelate synthase (HMS) (33), indicating that a solvent-exchangeable proton is transferred in a rate-limting step. Proton transfer for product release was shown to be partially rate limiting in HMS, whereas the SIE for XanA remains unexplained. The inverse SIE on kcat for PHD2 indicates that PHD2 exerts unique control over the aquo ligand. We attribute this to the four hydrogen bonds surrounding the aquo ligand (Figure 1), which would stabilize the aquo-bound state by as much as -20 kcal/mol. Inasmuch as PHD2 controls a transcription factor, limiting the rate of overall turnover through a step early in catalysis may constitute a strategy to ensure that O2 is only activated when HIF-ODDD is bound.
As only steps after ODDD binding contribute to the apparent kcat, aquo release cannot be coincident with ODDD binding, as often indicated for the consensus mechanism for αKG-dependent oxygenases. Despite what is thought to be a shared mechanism, inverse SIEs have never been reported by any other αKG-dependent oxygenase, suggesting that the unusual hydrogen-bonding network in PHD2 leads to this unique mechanistic feature.
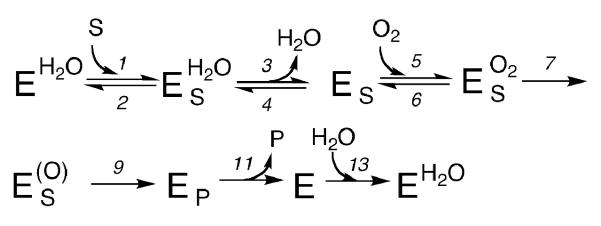
In view of this, a minimal kinetic model for PHD2 turnover at saturating [αKG] contains separate steps for ODDD (S) and O2 binding, water release, and chemical steps to form the active oxidant (O) and ODDDOH (P) (Scheme 3). As our conditions used air-equilibrated buffer, PHD2 was not saturated with O2, and our reported rate constants are apparent ones. Consequently, O2 binding can contribute to the rate at saturating [ODDD], which are the conditions for the apparent kcat.
Scheme 3.
The algebraic expression for the observed SIE takes the form shown in Eq. 2, in which D2Okcat is a function of the kinetic SIE on water release (Dk3), kinetic ratios involving k3 and k4 which are very similar to ‘commitments to catalysis’,(60) the equilibrium SIE on aquo release (DKeq = D2O(k3/k4)), and the kinetic SIE on water re-binding (Dk13). As there are two solvent sensitive steps, the expression for D2Okcat was derived using the net rate method of Tian,(61) which can accommodate such complex mechanisms (Appendix). The kinetic ratios indicate the rate-limiting nature of the solvent-sensitive steps (k3, k4, k13) relative to other steps.
| (2) |
The observed SIE will range between limiting values of ~2 and ~0.5, as Dk3 should be somewhat larger than unity, as seen for aquo release from the Zn2+-OH2 of alcohol dehydrogenase,(62) and we estimate D2OKeq = 0.49 based on fractionation factors (abbreviated as ϕ) for similar metal-aquo complexes.(28, 63) This lower limit depends on the fractionation factor for the Fe2+-OH2 species, which we estimate as ϕFe = 0.7 based on the values experimentally determined for Co2+-OH2 in Co(H2O)62+ and Co2+-reconstituted carbonic anhydrases (ϕ = 0.73 – 0.90).(63)
| (3) |
The observed D2Okcat depends on the relative magnitudes of the commitment-like kinetic ratios. Both kinetic ratios will be relatively large, as the rate constants for ligand exchange on Fe2+ are generally high, making it likely that D2Okcat will be most sensitive to the k3/k4 ratio. When this ratio is small, D2Okcat will be inverse; when large, D2Okcat will approach unity. We conclude that PHD2 exhibited an inverse D2Okcat because the aquo release (k3) was slower than aquo binding (k4), making this equilibrium reactant-favored.
| (4) |
Although current understanding of the rates for individual steps on PHD2 catalysis is poor, we nevertheless can extend what is already known about the overall chemical mechanism of PHD2 through analysis of the SIE. A recent study indicated that only Fe(II) forms of the enzyme accumulated significantly in the pre-steady state.(34) Consequently, steps prior to O2-activation, or product release, are likely rate-limiting steps, as the metal will be in the proper oxidation state preceding these steps. As D2Okcat is slightly inverse, we conclude that a step early in catalysis, such as O2 binding, is at least partially rate-limiting on the apparent kcat for PHD2. This strategy for engendering coupled turnover by making a step early in catalysis (partially) rate-limiting is distinct from that observed for the more thoroughly studied enzyme TauD in which turnover is limited by steps after O2 activation (27, 54).
Potential physiological significance of the Fe2+-OH2pKa
The steady-state rate constants for PHD2 increased at low pH, with a pKa = 7.22 (0.03) that we have assigned to Fe2+-OH2. Consequently, deprotonation of the aquo ligand may constitute a heretoforeunseen strategy to regulate enzyme activity in αKG-dependent oxygenases in response to cellular pH. What might be the physiological consequences for increased PHD2 activity under acidic conditions? The answer may lie in balancing anaerobic metabolism with aerobic metabolism, as PHD2 hydroxylation of the ODDD of HIF-1α destabilizes HIF-1α, thereby decreasing expression of glycolytic genes.
As glycolysis uses no O2, but acidifies the cell, it would seem that feedback between both [O2] and pH-levels would assist in balancing metabolism between aerobic and anaerobic pathways. Our results showed that PHD2 activity is higher at low pH, due to the protonation status of the Fe2+-OH2 center. We propose that this would create a negative feedback in response to the acid produced by glycolysis, making PHD2 more responsive to O2 under acidic conditions. PHD2 may regulate cellular metabolic status through both its sensing of [O2], as well as through a secondary sensing of pH.
Supplementary Material
ACKNOWLEDGMENT
The Stanford Synchrotron Radiation Laboratory (SSRL) is a national user facility operated by Stanford University on behalf of the U.S. Department of Energy, Office of Basic Energy Sciences. The SSRL Structural and Molecular Biology Program is supported by the Department of Energy, Office of Biological and Environmental Research, and by the National Institutes of Health, National Center for Research Resources, Biomedical Technology Program.
Supported by NIH-R01-GM077413
ABBREVIATIONS
- ABH3
AlkB human homolog 3
- CEKDM7A
C. elegans dual specificity histone demethylase
- EXAFS
extended X-ray absorption fine structure
- HEPES
4-(2-Hydroxyethyl)-1-piperazineethanesulfonic acid
- HIF
Hypoxia Inducible Factor
- (HMS)
hydroxymandelate synthase
- MES
2-(N-morpholino)ethanesulfonic acid; non-heme iron
- PHD2
prolyl Hydroxylase domain 2
- PIPES
1,4–piperazinediethane sulfonic acid
- SIE
solvent isotope effect
- XANES
X-ray absorption near-edge structure
- (XanA)
xanthine hydroxylase
- XAS
X-ray absorption spectroscopy
- αKG
alpha-ketoglutarate
Appendix. Derivation of the solvent isotope-effect equation
The solvent-isotope effect equation was derived using the effective rate constant method of G. Tian (Biorganic Chemistry 20, 95-106, 1992) to accommodate multiple isotopically sensitive steps. Assuming that the enzyme is saturated with αKG, the substrates ODDD (S) and O2 bind in separate steps, and the products CO2, succinate (succ) and hydroxylated ODDD (P) are released separately, the overall mechanism for PHD2 is as follows:
The apparent maximal initial rate (V) at saturating [S] but ambient [O2] is related to the effective rate constants for each step of the mechanism as below:
| (A1) |
The steps that may be solvent dependent are aquo release (k3, k4, K3) and water binding (k13) which cause the indicated rate constants and equilibrium constant to be isotopically sensitive. The apparent isotope effect is obtained by taking the ratio of the observed SIE on the apparent maximal rate (DV) to the maximal rate:
| (A2) |
Simplifying the above expression provides the observed SIE on the apparent maximal rate (DV) in a more tractable form:
| (A3) |
The SIE expression found in the main text is obtained by re-labeling K3 as Keq, and by dividing DV by the total enzyme concentration, [E]T (D20kcat = DV/[E]T):
| (A4) |
Although equation A4 has many parameters to explain the SIE, it can be broken down into a few essential components to illustrate the limiting values of DV. DV will take on limiting values of either Dk3 or DKeq, provided that the k3/k13 ratio is small. The limiting values will be governed by the relative magnitudes of the forward commitment-like term (contains k3) and the reverse commitment-like term (contains k4).
When the k3 term and the k4 term are smaller than one, the observed SIE will approach the kinetic isotope effect on k3 (Dk3). This situation is very unlikely to be observed for PHD2, as both k3 and k4 are likely to be large in magnitude.
| (A5) |
When the k3 term is much larger than the k4 term, and much larger than 1, then eq. A4 simplifies to give an observed SIE of unity; remember that Dk3 is on the order of magnitude 1.
| (A6) |
Conversely, should the k4 term be larger than 1 and larger than the k3 term, the observed SIE will equal the intrinsic equilibrium isotope effect (DKeq).
| (A7) |
The only way to explain the inverse SIE on the apparent kcat, as observed for PHD2, is to invoke a large k4 commitment like term. One way to explain this would be for one or both steps immediately following aquo release (k5, O2 binding; or k7, O2 activation) to be very slow. However, these steps contribute to both commitment-like terms. In order for the SIE to approach the limit shown in Eq. A7, aquo release must also be must slower than aquo rebinding (k3/k4 << 1).
Footnotes
Supporting Information: Tables of fitted values for kcat and kcat/KM at varied pH. Tables of EXAFS fits for samples with k = 2 – 12 Å−1; Table of EXAFS fits for sample at pH = 8.5 with k = 2 – 14 Å−1; Figure of EXAFS data and fits with k = 2 - 14 Å−1. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Bruick RK. Oxygen sensing in the hypoxic response pathway: regulation of the hypoxia-inducible transcription factor. Genes Dev. 2003;17:2614–2623. doi: 10.1101/gad.1145503. [DOI] [PubMed] [Google Scholar]
- 2.Ozer A, Bruick RK. Non-heme dioxygenases: cellular sensors and regulators jelly rolled into one? Nat. Chem. Biol. 2007;3:144–153. doi: 10.1038/nchembio863. [DOI] [PubMed] [Google Scholar]
- 3.Semenza GL. Hydroxylation of HIF-1: Oxygen sensing at the molecular level. Physiology. 2004;19:176–182. doi: 10.1152/physiol.00001.2004. [DOI] [PubMed] [Google Scholar]
- 4.Hewitson KS, McNeill LA, Riordan MV, Tian YM, Bullock AN, Welford RW, Elkins JM, Oldham NJ, Bhattacharya S, Gleadle JM, Ratcliffe PJ, Pugh CW, Schofield CJ. Hypoxia-inducible factor (HIF) asparagine hydroxylase is identical to factor inhibiting HIF (FIH) and is related to the cupin structural family. J. Biol. Chem. 2002;277:26351–26355. doi: 10.1074/jbc.C200273200. [DOI] [PubMed] [Google Scholar]
- 5.Bruick RK, McKnight SL. A conserved family of prolyl-4-hydroxylases that modify HIF. Science. 2001;294:1337–1340. doi: 10.1126/science.1066373. [DOI] [PubMed] [Google Scholar]
- 6.Ivan M, Kondo K, Yang H, Kim W, Valiando J, Ohh M, Salic A, Asara JM, Lane WS, Kaelin WG., Jr. HIFalpha targeted for VHL-mediated destruction by proline hydroxylation: implications for O2 sensing. Science. 2001;292:464–468. doi: 10.1126/science.1059817. [DOI] [PubMed] [Google Scholar]
- 7.Appelhoff RJ, Tian YM, Raval RR, Turley H, Harris AL, Pugh CW, Ratcliffe PJ, Gleadle JM. Differential function of the prolyl hydroxylases PHD1, PHD2, and PHD3 in the regulation of hypoxia-inducible factor. J. Biol. Chem. 2004;279:38458–38465. doi: 10.1074/jbc.M406026200. [DOI] [PubMed] [Google Scholar]
- 8.Hausinger RP. FeII/alpha-ketoglutarate-dependent hydroxylases and related enzymes. Crit. Rev. Biochem. Mol. Biol. 2004;39:21–68. doi: 10.1080/10409230490440541. [DOI] [PubMed] [Google Scholar]
- 9.Maxwell PH, Jaakkola P, Mole DR, Tian YM, Wilson MI, Gielbert J, Gaskell SJ, von Kriegsheim A, Hebestreit HF, Mukherji M, Schofield CJ, Pugh CW, Ratcliffe PJ. Targeting of HIF-alpha to the von Hippel-Lindau ubiquitylation complex by O-2-regulated prolyl hydroxylation. Science. 2001;292:468–472. doi: 10.1126/science.1059796. [DOI] [PubMed] [Google Scholar]
- 10.Kaelin WG, Ivan M, Kondo K, Yang HF, Kim W, Valiando J, Ohh M, Salic A, Asara JM, Lane WS. HIF alpha targeted for VHL-mediated destruction by proline hydroxylation: Implications for O-2 sensing. Science. 2001;292:464–468. doi: 10.1126/science.1059817. [DOI] [PubMed] [Google Scholar]
- 11.Rosen MD, Venkatesan H, Peltier HM, Bembenek SD, Kanelakis KC, Zhao LX, Leonard BE, Hocutt FM, Wu XD, Palomino HL, Brondstetter TI, Haugh PV, Cagnon L, Yan W, Liotta LA, Young A, Mirzadegan T, Shankley NP, Barrett TD, Rabinowitz MH. Benzimidazole-2-pyrazole HIF Prolyl 4-Hydroxylase Inhibitors as Oral Erythropoietin Secretagogues. ACS Med. Chem. Lett. 2010;1:526–529. doi: 10.1021/ml100198y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chowdhury R, McDonough MA, Mecinovic J, Loenarz C, Flashman E, Hewitson KS, Domene C, Schofield CJ. Structural Basis for Binding of Hypoxia-Inducible Factor to the Oxygen-Sensing Prolyl Hydroxylases. Structure. 2009;17:981–989. doi: 10.1016/j.str.2009.06.002. [DOI] [PubMed] [Google Scholar]
- 13.Solomon EI, Brunold TC, Davis MI, Kemsley JN, Lee SK, Lehnert N, Neese F, Skulan AJ, Yang YS, Zhou J. Geometric and electronic structure/function correlations in non-heme iron enzymes. Chem. Rev. 2000;100:235–350. doi: 10.1021/cr9900275. [DOI] [PubMed] [Google Scholar]
- 14.Dann CE, Bruick RK, Deisenhofer J. Structure of factor-inhibiting hypoxia-inducible factor 1: An asparaginyl hydroxylase involved in the hypoxic response pathway. Proc. Natl. Acad. Sci. USA. 2002;99:15351–15356. doi: 10.1073/pnas.202614999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Elkins JM, Ryle MJ, Clifton IJ, Dunning Hotopp JC, Lloyd JS, Burzlaff NI, Baldwin JE, Hausinger RP, Roach PL. X-ray crystal structure of Escherichia coli taurine/alpha-ketoglutarate dioxygenase complexed to ferrous iron and substrates. Biochemistry. 2002;41:5185–5192. doi: 10.1021/bi016014e. [DOI] [PubMed] [Google Scholar]
- 16.Muller I, Kahnert A, Pape T, Sheldrick GM, Meyer-Klaucke W, Dierks T, Kertesz M, Uson I. Crystal structure of the alkylsulfatase AtsK: insights into the catalytic mechanism of the Fe(II) alpha-ketoglutarate-dependent dioxygenase superfamily. Biochemistry. 2004;43:3075–3088. doi: 10.1021/bi035752v. [DOI] [PubMed] [Google Scholar]
- 17.Neidig ML, Brown CD, Light KM, Fujimori DG, Nolan EM, Price JC, Barr EW, Bollinger JM, Krebs C, Walsh CT, Solomon EI. CD and MCD of CytC3 and taurine dioxygenase: Role of the facial triad in alpha-KG-dependent oxygenases. J. Am. Chem. Soc. 2007;129:14224–14231. doi: 10.1021/ja074557r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhou J, Kelly WL, Bachmann BO, Gunsior M, Townsend CA, Solomon EI. Spectroscopic studies of substrate interactions with clavaminate synthase 2, a multifunctional alpha-KG-dependent non-heme iron enzyme: Correlation with mechanisms and reactivities. J. Am. Chem. Soc. 2001;123:7388–7398. doi: 10.1021/ja004025+. [DOI] [PubMed] [Google Scholar]
- 19.Pavel EG, Zhou J, Busby RW, Gunsior M, Townsend CA, Solomon EI. Circular dichroism and magnetic circular dichroism spectroscopic studies of the non-heme ferrous active site in clavaminate synthase and its interaction with alpha-ketoglutarate cosubstrate. J. Am. Chem. Soc. 1998;120:743–753. [Google Scholar]
- 20.Myllyharju J, Li DX, Hirsila M, Koivunen P, Brenner MC, Xu L, Yang C, Kivirikko KI. Many amino acid substitutions in a hypoxia-inducible transcription factor (HIF)-1 alpha-like peptide cause only minor changes in its hydroxylation by the HIF prolyl 4-hydroxylases - Substitution of 3,4-dehydroproline or azetidine-2-carboxylic acid for the proline leads to a high rate of uncoupled 2-oxoglutarate decarboxylation. J. Biol. Chem. 2004;279:55051–55059. doi: 10.1074/jbc.M410287200. [DOI] [PubMed] [Google Scholar]
- 21.Counts DF, Cardinale GJ, Udenfriend S. Prolyl hydroxylase half reaction: peptidyl prolyl-independent decarboxylation of alpha-ketoglutarate. Proc. Natl. Acad. Sci. USA. 1978;75:2145–2149. doi: 10.1073/pnas.75.5.2145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Rao NV, Adams E. Partial reaction of prolyl hydroxylase. (Gly-PRO-Ala)n stimulates alpha-ketoglutarate decarboxylation without prolyl hydroxylation. J. Biol. Chem. 1978;253:6327–6330. [PubMed] [Google Scholar]
- 23.Saari RE, Hausinger RP. Ascorbic acid-dependent turnover and reactivation of 2,4-dichlorophenoxyacetic acid/alpha-ketoglutarate dioxygenase using thiophenoxyacetic acid. Biochemistry. 1998;37:3035–3042. doi: 10.1021/bi972388p. [DOI] [PubMed] [Google Scholar]
- 24.Welford RW, Schlemminger I, McNeill LA, Hewitson KS, Schofield CJ. The selectivity and inhibition of AlkB. J. Biol. Chem. 2003;278:10157–10161. doi: 10.1074/jbc.M211058200. [DOI] [PubMed] [Google Scholar]
- 25.Liu A, Ho RY, Que L, Jr., Ryle MJ, Phinney BS, Hausinger RP. Alternative reactivity of an alpha-ketoglutarate dependent iron(II) oxygenase: enzyme self-hydroxylation. J. Am. Chem. Soc. 2001;123:5126–5127. doi: 10.1021/ja005879x. [DOI] [PubMed] [Google Scholar]
- 26.Chen YH, Comeaux LM, Herbst RW, Saban E, Kennedy DC, Maroney MJ, Knapp MJ. Coordination changes and auto-hydroxylation of FIH-1: uncoupled O2-activation in a human hypoxia sensor. J. Inorg. Biochem. 2008;102:2120–2129. doi: 10.1016/j.jinorgbio.2008.07.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Grzyska PK, Ryle MJ, Monterosso GR, Liu J, Ballou DP, Hausinger RP. Steady-state and transient kinetic analyses of taurine/alpha-ketoglutarate dioxygenase: Effects of oxygen concentration, alternative sulfonates, and active-site variants on the fe(IV)-oxo intermediate. Biochemistry. 2005;44:3845–3855. doi: 10.1021/bi048746n. [DOI] [PubMed] [Google Scholar]
- 28.Quinn DM, Sutton LD. Theoretical Basis and Mechanistic Utility of Solvent Isotope Effects. In: Cook PF, editor. Enzyme Mechanism from Isotope Effects. CRC Press; Boca Raton: 1991. pp. 73–126. [Google Scholar]
- 29.Tomchick DR, Phan P, Cymborowski M, Minor W, Holman TR. Structural and functional characterization of second-coordination sphere mutants of soybean lipoxpgenase-1. Biochemistry. 2001;40:7509–7517. doi: 10.1021/bi002893d. [DOI] [PubMed] [Google Scholar]
- 30.Harrison RK, Chang B, Niedzwiecki L, Stein RL. Mechanistic Studies on the Human Matrix Metalloproteinase Stromelysin. Biochemistry. 1992;31:10757–10762. doi: 10.1021/bi00159a016. [DOI] [PubMed] [Google Scholar]
- 31.Born TL, Zheng RJ, Blanchard JS. Hydrolysis of N-succinyl-L,L-diaminopimelic acid by the Haemophilus influenzae dapE-encoded desuccinylase: Metal activation, solvent isotope effects, and kinetic mechanism. Biochemistry. 1998;37:10478–10487. doi: 10.1021/bi9806807. [DOI] [PubMed] [Google Scholar]
- 32.Montero-Moran GM, Li M, Rendon-Huerta E, Jourdan F, Lowe DJ, Stumpff-Kane AW, Feig M, Scazzocchio C, Hausinger RP. Purification and characterization of the Fe-II- and alpha-ketoglutarate-dependent xanthine hydroxylase from Aspergillus nidulans. Biochemistry. 2007;46:5293–5304. doi: 10.1021/bi700065h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.He PQ, Conrad JA, Moran GR. The Rate-Limiting Catalytic Steps of Hydroxymandelate Synthase from Amycolatopsis orientalis. Biochemistry. 2010;49:1998–2007. doi: 10.1021/bi901674q. [DOI] [PubMed] [Google Scholar]
- 34.Flashman E, Hoffart LM, Hamed RB, Bollinger JM, Krebs C, Schofield CJ. Evidence for the slow reaction of hypoxia-inducible factor prolyl hydroxylase 2 with oxygen. FEBS J. 2010;277:4089–4099. doi: 10.1111/j.1742-4658.2010.07804.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Dao JH, Kurzeja RJM, Morachis JM, Veith H, Lewis J, Yu V, Tegley CM, Tagari P. Kinetic characterization and identification of a novel inhibitor of hypoxia-inducible factor prolyl hydroxylase 2 using a time-resolved fluorescence resonance energy transfer-based assay technology. Anal. Biochem. 2009;384:213–223. doi: 10.1016/j.ab.2008.09.052. [DOI] [PubMed] [Google Scholar]
- 36.McDonough MA, Li V, Flashman E, Chowdhury R, Mohr C, Lienard BMR, Zondlo J, Oldham NJ, Clifton IJ, Lewis J, McNeill LA, Kurzeja RJM, Hewitson KS, Yang E, Jordan S, Syed RS, Schofield CJ. Cellular oxygen sensing: Crystal structure of hypoxia-inducible factor prolyl hydroxylase (PHD2) Proc. Natl. Acad. Sci. USA. 2006;103:9814–9819. doi: 10.1073/pnas.0601283103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Flagg SC, Martin CB, Taabazuing CY, Holmes BE, Knapp MJ. Screening chelating inhibitors of HIF-Prolyl Hydroxylase Domain 2 (PHD2) and Factor Inhibiting HIF (FIH) J. Inorg. Biochem. 2012 doi: 10.1016/j.jinorgbio.2012.03.002. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ehrismann D, Flashman E, Genn DN, Mathioudakis N, Hewitson KS, Ratcliffe PJ, Schofield CJ. Studies on the activity of the hypoxia-inducible-factor hydroxylases using an oxygen consumption assay. Biochem. J. 2007;401:227–234. doi: 10.1042/BJ20061151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.CRC Reference Book. 61 ed CRC Press Inc.; Boca Raton: 1980-1981. [Google Scholar]
- 40.Giri NC, Sun H, Chen H, Costa M, Maroney MJ. X-ray Absorption Spectroscopy Structural Investigation of Early Intermediates in the Mechanism of DNA Repair by Human ABH2. Biochemistry. 50:5067–5076. doi: 10.1021/bi101668x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Padden KM, Krebs JF, MacBeth CE, Scarrow RC, Borovik AS. Immobilized metal complexes in porous organic hosts: Development of a material for the selective and reversible binding of nitric oxide. J. Am. Chem. Soc. 2001;123:1072–1079. doi: 10.1021/ja003282b. [DOI] [PubMed] [Google Scholar]
- 42.Webb SM. SIXpack: a graphical user interface for XAS analysis using IFEFFIT. Phys. Scr. 2005;T115:1011–1014. [Google Scholar]
- 43.Ankudinov AL, Ravel B, Rehr JJ, Conradson SD. Real-space multiple-scattering calculation and interpretation of x-ray-absorption near-edge structure. Phys. Rev. B. 1998;58:7565–7576. [Google Scholar]
- 44.Cleland WW. Determining the Chemical Mechanisms of Enzyme-Catalyzed Reactions by Kinetic Studies. Advances in Enzymology. 1977. pp. 273–387. [DOI] [PubMed]
- 45.Saban E, Chen YH, J AH, C YT, Holmes BE, Knapp MJ. The Second Coordination Sphere of FIH Controls Hydroxylation. Biochemistry. 50:4733–4740. doi: 10.1021/bi102042t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Ryle MJ, Padmakumar R, Hausinger RP. Stopped-flow kinetic analysis of Escherichia coli taurine/alpha-ketoglutarate dioxygenase: interactions with alpha-ketoglutarate, taurine, and oxygen. Biochemistry. 1999;38:15278–15286. doi: 10.1021/bi9912746. [DOI] [PubMed] [Google Scholar]
- 47.Zhou J, Gunsior M, Bachmann BO, Townsend CA, Solomon EI. Substrate Binding to the α-Ketoglutarate-Dependent Non-Heme Iron Enzyme Clavaminate Synthase 2: Coupling Mechanism of Oxidative Decarboxylation and Hydroxylation. J. Am. Chem. Soc. 1998;120:13539–13540. [Google Scholar]
- 48.Li J, Fisher CL, Chen JL, Bashford D, Noodleman L. Calculation of redox potentials and pK(a) values of hydrated transition metal cations by a combined density functional and continuum dielectric theory. Inorg. Chem. 1996;35:4694–4702. [Google Scholar]
- 49.Bertini I, Briganti F, Mangani S, Nolting HF, Scozzafava A. X-Ray-Absorption Studies on Catechol 2,3-Dioxygenase from Pseudomonas-Putida Mt2. Biochemistry. 1994;33:10777–10784. [Google Scholar]
- 50.Westre TE, Kennepohl P, DeWitt JG, Hedman B, Hodgson KO, Solomon EI. A multiplet analysis of Fe K-edge 1s->3d pre-edge features of iron complexes. J. Am. Chem. Soc. 1997;119:6297–6314. [Google Scholar]
- 51.Ohtaki H, Radnai T. Structure and Dynamics of Hydrated Ions. Chemical Reviews. 1993;93:1157–1204. [Google Scholar]
- 52.Townsend CA, Raber ML, Freeman MF. Dissection of the Stepwise Mechanism to beta-Lactam Formation and Elucidation of a Rate-determining Conformational Change in beta-Lactam Synthetase. J. Biol. Chem. 2009;284:207–217. doi: 10.1074/jbc.M805390200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Karsten WE, Lai CJ, Cook PF. Inverse Solvent Isotope Effects in the Nad-Malic Enzyme Reaction Are the Result of the Viscosity Difference between D2o and H2o - Implications for Solvent Isotope Effect Studies. J. Am. Chem. Soc. 1995;117:5914–5918. [Google Scholar]
- 54.Price JC, Barr EW, Tirupati B, Bollinger JM, Jr., Krebs C. The first direct characterization of a high-valent iron intermediate in the reaction of an alpha-ketoglutarate-dependent dioxygenase: a high-spin FeIV complex in taurine/alpha-ketoglutarate dioxygenase (TauD) from Escherichia coli. Biochemistry. 2003;42:7497–7508. doi: 10.1021/bi030011f. [DOI] [PubMed] [Google Scholar]
- 55.Miller AF. Redox tuning over almost 1 V in a structurally conserved active site: Lessons from Fe-containing superoxide dismutase. Acc. Chem. Res. 2008;41:501–510. doi: 10.1021/ar700237u. [DOI] [PubMed] [Google Scholar]
- 56.Brunold TC, Grove LE, Xie J, Yikilmaz E, Miller AF. Spectroscopic and computational investigation of second-sphere contributions to redox tuning in Escherichia coli iron superoxide dismutase. Inorg. Chem. 2008;47:3978–3992. doi: 10.1021/ic702412y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Knapp MJ, Klinman JP. Kinetic studies of oxygen reactivity in soybean lipoxygenase-1. Biochemistry. 2003;42:11466–11475. doi: 10.1021/bi0300884. [DOI] [PubMed] [Google Scholar]
- 58.Holman TR, Zhou J, Solomon EI. Spectroscopic and functional characterization of a ligand coordination mutant of soybean lipoxygenase-1: First coordination sphere analogue of human 15-lipoxygenase. J. Am. Chem. Soc. 1998;120:12564–12572. [Google Scholar]
- 59.Ryle MJ, Liu A, Muthukumaran RB, Ho RY, Koehntop KD, McCracken J, Que L, Jr., Hausinger RP. O2- and alpha-ketoglutarate-dependent tyrosyl radical formation in TauD, an alpha-keto acid dependent non-heme iron dioxygenase. Biochemistry. 2003;42:1854–1862. doi: 10.1021/bi026832m. [DOI] [PubMed] [Google Scholar]
- 60.Northrop DB. The Expression of Isotope Effects on Enzyme-Catalyzed Reactions. Ann. Rev. Biochem. 1981;50:103–131. doi: 10.1146/annurev.bi.50.070181.000535. [DOI] [PubMed] [Google Scholar]
- 61.Tian GC. Effective Rate Constants and General Isotope Effect Equations for Steady-State Enzymatic-Reactions with Multiple Isotope-Sensitive Steps. Bioorg. Chem. 1992;20:95–106. [Google Scholar]
- 62.Taylor KB. Solvent Isotope Effects on the Reaction Catalyzed by Alcohol-Dehydrogenase from Equine Liver. Biochemistry. 1983;22:1040–1045. doi: 10.1021/bi00274a007. [DOI] [PubMed] [Google Scholar]
- 63.Kassebaum JW, Silverman DN. Hydrogen-Deuterium Fractionation Factors of the Aqueous Ligand of Cobalt in Co(H2O)62+ and Co(II)-Substituted Carbonic-Anhydrase. J. Am. Chem. Soc. 1989;111:2691–2696. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.