MR Chemical Exchange Imaging with Spin-Lock Technique (CESL): A Theoretical Analysis of Z-spectrum using a Two-Pool R_1ρ Relaxation Model beyond the Fast-Exchange Limit

Abstract

Chemical exchange (CE) process has been exploited as a novel and powerful contrast mechanism for MRI, which is primarily performed in the form of chemical exchange saturation transfer (CEST) imaging. Spin-lock (SL) technique can also be used for CE studies, although traditionally performed and interpreted quite differently from CEST. Chemical exchange imaging with spin-lock technique (CESL), theoretically based on the Bloch-McConnell equations common to CEST, has potentials to be used as an alternative to CEST and to better characterize CE processes from slow and intermediate to fast proton exchange rates through the tuning of spin-lock pulse parameters. In this study, Z-spectrum and asymmetric magnetization transfer ratio (MTR_asym) obtained by CESL are theoretically analyzed and numerically simulated using a general two-pool R_1ρ relaxation model beyond the fast-exchange limit. The influences of spin-lock parameters, static magnetic field strength B₀ and physiological properties on Z-spectrum and MTR_asym are quantitatively revealed. Optimization of spin-lock frequency and spin-lock duration for the maximum CESL contrast enhancement is also investigated. Numerical simulation results in this study are compatible with the findings in the existing literatures of CE imaging studies.

INTRODUCTION

MRI provides a variety of image contrasts to distinguish the diseased tissues from healthy tissues based on different mechanisms like relaxation times of T₁, T₂ and T₂^*, diffusion, and perfusion. Recently, chemical exchange (CE) has been exploited as a novel and powerful contrast enhancement mechanism in addition to normal MRI contrast mechanisms. The principle of CE based MRI relies on the proton exchange process between free water and biological molecules containing exchangeable labile protons resonating at a frequency different from that of water. Proton exchange between them leads to the magnetization attenuation of water that is detectable by the means of normal MR acquisition method. Currently, CE based MRI is mostly performed in the form of chemical exchange saturation transfer (CEST) imaging (Ward et al., 2000; van Zijl and Yadav, 2011). In CEST imaging, different irradiation frequencies of the long and weak saturation radiofrequency (RF) pulse are applied to obtain the signal intensity ratios compared to the unsaturated signal intensity as a function of frequency offset (ΔΩ) with respect to water, often referred as the Z-spectrum. Quantitatively, the magnetization transfer ratio (MTR) is defined as:

$$\mathit{\text{MTR}}(\mathrm{\Delta }\mathrm{\Omega })=1-M(\mathrm{\Delta }\mathrm{\Omega })/M_0,$$ (1)

where M(ΔΩ) and M₀ denote magnetization or image intensity at frequency offset of ΔΩ and without RF irradiation, respectively. To eliminate direct water saturation (DS) effect, asymmetric MTR is proposed as:

$${\text{MTR}}_{\text{asym}}(\mathrm{\Delta }\mathrm{\Omega })=\text{MTR}(\mathrm{\Delta }\mathrm{\Omega })-\text{MTR}(-\mathrm{\Delta }\mathrm{\Omega }).$$ (2)

The voxel-wise map of asymmetric MTR is normally used to visualize the CE-based contrast for lesion detection and tissue characterization.

Spin-lock technique, traditionally applied for the study of relaxation time (T_1ρ) or relaxation rate (R_1ρ) in the rotating frame, could also be used for chemical exchange imaging. In traditional SL imaging, a stronger but much shorter spin-lock pulse than CEST imaging is applied, and the image intensities at different spin-lock pulse times (TSL) are fitted to a mono-exponential decay model to quantify T_1ρ or R_1ρ:

$$M(\mathit{\text{TSL}})=M_0·e^{-\mathit{\text{TSL}}/T_{1\rho }}=M_0·e^{-\mathit{\text{TSL}}·R_{1\rho }},$$ (3)

where M(TSL) and M₀ denote the magnetization or image intensity at spin-lock times of TSL and zero, respectively. T_1ρ-weigthed image or T_1ρ map has been widely used for many clinical applications involving various organs (Li et al., 2008; Johannessen et al., 2006; Borthakur et al., 2008; Wang et al., 2011). Actually, CE information could be reflected by T_1ρ or R_1ρ dispersion, which is the T_1ρ or R_1ρ change as a function of the spin-lock field strength B_1SL or spin-lock frequency FSL, where FSL=γ B_1SL and γ is the gyromagnetic ratio of protons (42.576 MHz/T).

Despite the different acquisition and interpretation form by CEST and SL imaging, both offer chemical exchange information of physiological systems. CEST is normally described sensitive to the processes when the proton exchange rate is much smaller or comparable to the offset frequency of labile protons, often referred to slow or intermediate exchange, while SL imaging is considered to be more sensitive to probe fast proton exchange processes in which case the proton exchange rate is much larger than the offset frequency.

Unlike the SL imaging, CEST typically uses much lower RF pulse field strength and longer duration for the study of slow to intermediate CE processes (Jin et al., 2012). In theory, the Bloch-McConnell equations form the theoretical basis for the quantitative analysis of chemical exchange for both. The underlying equivalence of spin-lock and CEST irradiation schemes has also been revealed (Zaiss and Bachert, 2012). Based on these equations, current CEST models can well describe slow CE processes in a simple form (van Zijl and Yadav, 2011; Zhou et al., 2003b; Zhou et al., 2003a). However, it becomes difficult to quantify intermediate or fast CE processes (Jin et al., 2012) due to the extremely complicated form after extension (Zhou et al., 2004). As comparison, the dynamic magnetization evolution under wide ranges of chemical exchange rates could be more conveniently quantified and interpreted by a general two-pool R_1ρ relaxation model (Trott and Palmer, 2002).

In practice, the full acquisition of T_1ρ dispersion by measuring T_1ρ values at multiple FSLs to quantify proton exchange could be very time consuming even with the limited TSLs at each FSL for acceleration (Yuan et al., 2012b), so usually not practical for routine patient scan. Meanwhile, unlike MTR_asym map for CEST, neither T_1ρ map nor T_1ρ dispersion curves straightforwardly visualize CE-based contrast on image. Therefore, analysis of Z-spectrum and MTR_asym obtained by spin-lock technique provides an efficient and intuitive mean for CE quantification and CE-based image contrast visualization, and has raised more research interests recently (Jin et al., 2012; Jin et al., 2011; Kogan et al., 2012).

The purpose of this study is to theoretically investigate the Z-spectrum and asymmetric MTR of chemical exchange imaging with spin-lock technique (CESL) using the two-pool R_1ρ model beyond fast-exchange limit (Trott and Palmer, 2002). The influences of various parmaeters, including SL parameters of FSL, TSL, static magnetic field strength B₀, offset of labile proton pool, proton exchange rate, population ratio of labile proton pools, as well as intrinsic relaxation time T₂, on Z-spectrum and asymmetric MTR are numerically simulated and quantitatively analyzed. Optimization to maximize the CE-based contrast by adjusting the spin-lock pulse parameters is investigated. The theoretical correlations between CEST models and R_1ρ model are revealed.

METHODS

Theoretical Analysis

We consider a two-pool model that proton exchanges between pool A and Pool B with distinct Larmor frequencies of Ω_a and Ω_b, respectively. The population ratios of A and B are p_a and p_b=1−p_a, respectively. The resonance offsets in the rotating frame for A and B are expressed as:

$${\delta }_a={\mathrm{\Omega }}_a-{\omega }_{\mathit{\text{rf}}}\text{ and }{\delta }_b={\mathrm{\Omega }}_b-{\omega }_{\mathit{\text{rf}}},$$ (4)

where ω_rf is the transmitter frequency of the applied RF pulse. The first-order forward proton exchange rate from A to B and reverse proton exchange rate from B to A are defined as k_a and k_b. The total exchange rate is k=k_a+k_b. To achieve dynamic equilibrium, it is required that:

$$p_a·k_a=p_b·k_b.$$ (5)

By substituting k=k_a+k_b and p_a+p_b=1 into Eq. [5]:

$$p_a=\frac{k_b}{k}\text{ and }{p}_b=\frac{k_a}{k}.$$ (6)

The proton exchange process is referred to slow, intermediate and fast if k<<|Ω_a−Ω_b|, k~|Ω_a−Ω_b|, and k>>|Ω_a−Ω_b|.

The Bloch-McConnell equations quantitatively describe the time evolution of the magnetization of pool A (M_a) and B (M_b) under proton exchange. When the RF pulse is applied in x direction, it is written as:

$$\frac{d}{\mathit{\text{dt}}}\left[\begin{array}{c}\hfill M_{\mathit{\text{ax}}}\hfill \\ \hfill M_{\mathit{\text{bx}}}\hfill \\ \hfill M_{\mathit{\text{ay}}}\hfill \\ \hfill M_{\mathit{\text{by}}}\hfill \\ \hfill M_{\mathit{\text{az}}}\hfill \\ \hfill M_{\mathit{\text{bz}}}\hfill \end{array}\right]=\left[\begin{array}{cccccc}\hfill -k_a-R_2\hfill & \hfill k_b\hfill & \hfill -{\delta }_a\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill k_a\hfill & \hfill -k_b-R_2\hfill & \hfill 0\hfill & \hfill -{\delta }_b\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\delta }_a\hfill & \hfill 0\hfill & \hfill -k_a-R_2\hfill & \hfill k_b\hfill & \hfill -{\omega }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\delta }_b\hfill & \hfill k_a\hfill & \hfill -k_b-R_2\hfill & \hfill 0\hfill & \hfill -{\omega }_1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\omega }_1\hfill & \hfill 0\hfill & \hfill -k_a-R_1\hfill & \hfill k_b\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\omega }_1\hfill & \hfill k_a\hfill & \hfill -k_b-R_1\hfill \end{array}\right]\left[\begin{array}{c}\hfill M_{\mathit{\text{ax}}}\hfill \\ \hfill M_{\mathit{\text{bx}}}\hfill \\ \hfill M_{\mathit{\text{ay}}}\hfill \\ \hfill M_{\mathit{\text{by}}}\hfill \\ \hfill M_{\mathit{\text{az}}}\hfill \\ \hfill M_{\mathit{\text{bz}}}\hfill \end{array}\right]+R_1\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill M_{a0}\hfill \\ \hfill M_{b0}\hfill \end{array}\right]$$ (7)

where M_a0 and M_b0 are the original thermal equilibrium magnetization of A and B along the B₀ direction and t is the time. ω₁ is the Rabi frequency of the SL pulse and ω₁=2πγB_1SL=2πFSL. γ is the gyromagnetic ratio of protons (42.576 MHz/T) and FSL is the spin-lock frequency. R₁ and R₂ are understood as population averaged spin-lattice and spin-spin relaxation rates. For the first-order linear differential equations shown in Eq. [7], R_1ρ is derived as:

$$R_{1\rho }=-\lambda ,$$ (8)

where λ is the largest real eigenvalue of the matrix in Eq. [7]. The detail derivation could be referred to the literature (Trott and Palmer, 2002). Assuming R₂−R₁<<k, the general R_1ρ model is expressed in a linearized from as given by:

$$R_{1\rho }=R_1{\text{cos}}^2\theta +R_2{\text{sin}}^2\theta +\frac{p_a{p}_b{\delta }^{2}k{\text{sin}}^2\theta }{\frac{{\omega }_{\mathit{\text{aeff}}}^2{\omega }_{\mathit{\text{beff}}}^2}{{\omega }_{\mathit{\text{eff}}}^2}+k^2}=R_1{\text{cos}}^2\theta +(R_2+R_{\mathit{\text{ex}}}){\text{sin}}^2\theta .$$ (9)

Eq. [9] is compatible with the result derived in the reference (Zaiss et al., 2012). ω_aeff, ω_beff and ω_eff are the effective spin-lock frequencies in the rotating frame for pool A, B and bulk average, respectively. δ is the Larmor frequency difference between Pool A and B. Exchange relaxation rate R_ex reflects the relaxation variation due to chemical exchange. Relationships between parameters in Eq. [9] are listed as:

$${\omega }_{\mathit{\text{aeff}}}^2={\delta }_a^2+{\omega }_1^2={\delta }_a^2+{(2\pi ·\mathit{\text{FSL}})}^2\text{ and }{\omega }_{\mathit{\text{beff}}}^2={\delta }_b^2+{\omega }_1^2={\delta }_b^2+{(2\pi ·\mathit{\text{FSL}})}^2,$$ (10)

$$\delta ={\delta }_b-{\delta }_a={\mathrm{\Omega }}_b-{\mathrm{\Omega }}_a,$$ (11)

$$\mathrm{\Delta }\mathrm{\Omega }=p_a{\mathrm{\Omega }}_a+p_b{\mathrm{\Omega }}_b-{\omega }_{\mathit{\text{rf}}},$$ (12)

$${\omega }_{\mathit{\text{eff}}}^2=\mathrm{\Delta }{\mathrm{\Omega }}^2+{\omega }_1^2=\mathrm{\Delta }{\mathrm{\Omega }}^2+{(2\pi ·\mathit{\text{FSL}})}^2,$$ (13)

$$\theta =\text{arctan}\left(\frac{{\omega }_1}{\mathrm{\Delta }\mathrm{\Omega }}\right)=\text{arctan}\left(\frac{2\pi ·\mathit{\text{FSL}}}{\mathrm{\Delta }\mathrm{\Omega }}\right),$$ (14)

where ΔΩ is the offset frequency of the spin-lock pulse with respect to the population averaged Larmor frequency. Note that Eq. [9] is generally valid for description of slow, intermediate and fast proton changes and has no assumption on the ratio of pool population. It is only required for the derivation that R₂−R₁<<k. Considering that most biological tissues have T₂ longer than 40ms (Stanisz et al., 2005), quite independent of B₀, and much longer T₁ than T₂, quantification by Eq. [9] is still accurate even for very slow exchange rates.

Under the application of a spin-lock pulse, magnetization along the effective spin-lock field direction would decay at the rate of R_1ρ to a steady state. The magnetization evolution is written as:

$$M=(M_0-M_{\mathit{\text{ss}}})·e^{-R_{1\rho }·\mathit{\text{TSL}}}+M_{\mathit{\text{ss}}},$$ (15)

where M_ss is the steady-state magnetization. By using the normal Bloch equations with dM_ss/dt=0, it can be derived that (Jin et al., 2012; Desvaux and Berthault, 1999):

$$M_{\mathit{\text{ss}}}=M_0·\frac{R_1·\text{cos }\theta }{R_{1\rho }}\text{ if }{\mathrm{R}}_2^2\ll {\omega }_1^2+\mathrm{\Delta }{\mathrm{\Omega }}^2.$$ (16)

Note that relevant parameters like R₁, θ, and M₀ in Eqs. [15–16] are understood as population averaged values.

By substituting Eq. [9] and Eq. [16] into Eq. [15], Z-spectrum obtained by a spin-lock pulse could be analytically expressed as:

$$\frac{M}{M_0}=1-\mathit{\text{MTR}}(\mathit{\text{TSL}},\mathit{\text{FSL}},\mathrm{\Delta }\mathrm{\Omega })=(1-\frac{R_1·\text{cos }\theta }{R_{1\rho }})·e^{-R_{1\rho }·\mathit{\text{TSL}}}+\frac{R_1·\text{cos }\theta }{R_{1\rho }}=(1-\frac{R_1·\text{cos }\theta }{R_1{\text{cos}}^2\theta +(R_2+R_{\mathit{\text{ex}}}){\text{sin}}^2\theta })·e^{-(R_1{\text{cos}}^2\theta +(R_2+R_{\mathit{\text{ex}}}){\text{sin}}^2\theta )·\mathit{\text{TSL}}}+\frac{R_1·\text{cos }\theta }{R_1{\text{cos}}^2\theta +(R_2+R_{\mathit{\text{ex}}}){\text{sin}}^2\theta }.$$ (17)

Note MTR is expressed as a function of adjustable spin-lock parameters of TSL, FSL and ΔΩ, although in fact it is also dependent on many other factors. Accordingly, asymmetric MTR (MTR_asym) is given as:

$${\mathit{\text{MTR}}}_{\mathit{\text{asym}}}(\mathit{\text{TSL}},\mathit{\text{FSL}},\mathrm{\Delta }\mathrm{\Omega })=\mathit{\text{MTR}}(\mathit{\text{TSL}},\mathit{\text{FSL}},\mathrm{\Delta }\mathrm{\Omega })-\mathit{\text{MTR}}(\mathit{\text{TSL}},\mathit{\text{FSL}},-\mathrm{\Delta }\mathrm{\Omega }).$$ (18)

Numerical Simulation

Numerical programs using MATLAB v7.9 (MathWorks, Natick, MA, USA) were developed to simulate the Z-spectrum obtained by the spin-lock technique. Z-spectrum and asymmetric MTR under the influence of B₀, spin-lock parameters including TSL, FSL and ΔΩ, and tissue properties including intrinsic relaxation times, pool population ratio, Larmor frequency difference between two pools and proton exchange rate, were individually investigated and illustrated. To acquire Z-spectrum that could be modeled by Eq. [17], the flip-down and flip-up angle α for spin-lock pulse should be adjusted at each offset frequency ΔΩ of the spin-lock pulse as α=arctan(2πFSL/ΔΩ) to make sure that the magnetization is flipped to the nominal effective spin-lock field direction and experiences pure T_1ρ relaxation along this direction. The deviation between the flipped magnetization and the effective spin-lock field strength induced by B₀ or B₁ inhomogeneities was not taken into account for simulation. In the simulation of Z-spectrum acquisition, a step of 0.01ppm (parts per million) of B₀ Larmor frequency (γB₀) was used to obtain the smooth MTR and MTR_asym curves. In the illustration of Z-spectrum and MTR_asym, 0ppm corresponded to the B₀ Larmor frequency. Without losing generality, pool A could be considered as the pool of free water in biological tissues, on resonance with B₀ Larmor frequency. Pool B is the chemical exchange agent of interest containing labile protons, resonant at an offset frequency (δ_b) of 3ppm relative to pool A, such as Glutamate (Cai et al., 2012). Pool population is assumed to be highly asymmetric with p_a=0.99 and p_b=0.01 for simulation unless particularly specified, similar to the normal tissue microenvironment with a large pool of water and a small pool of labile protons. Theoretical Z-spectra obtained at B₀ of 9.4T (~400MHz) were simulated unless particularly specified. The default proton exchange rate was assumed to be 500/s (or ~3143rad/s) in simulation unless particularly specified. The default spin-lock frequency and spin-lock time were set as 500Hz (corresponded to spin-lock field strength of ~11.74µT and angular frequency of ~3143rad/s) and 50ms, respectively.

Numerical simulation indicated that Z-spectrum and MTR_asym were relatively insensitive to the typical T₁ ranges (from a few hundred milliseconds to three thousand milliseconds) for various tissues at different B₀ for intermediate and fast exchange. Therefore, the effect of T1 on Z-spectrum was not shown in the results. The population averaged T₁ was assumed to be 1500ms for all simulations. However, the effect of population averaged T₂ on Z-spectrum and MTR_asym may not be negligible in the typical ranges for tissues (less than 100ms and relatively independent of B₀). The population averaged T₂ was assumed to be 80ms in simulations unless particularly specified.

RESULTS

Influence of spin-lock parameters on Z-spectrum and MTR_asym

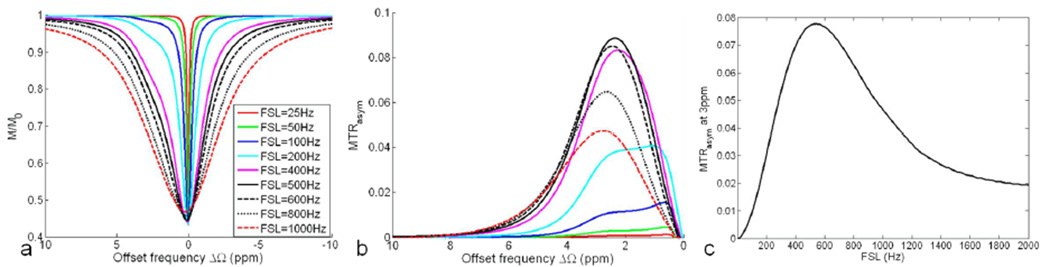
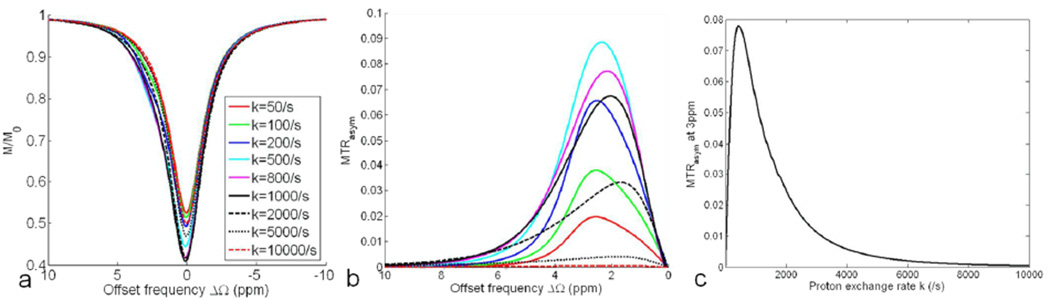
Figure 1 shows the simulated Z-spectrum (a) and MTR_asym (b) under the applications of spin-lock pulses with different FSLs but a fixed TSL of 50ms at 9.4T. As shown in Fig. 1a, the saturation peak width of the Z-spectrum increases with FSL. When FSL is smaller than 100Hz (FSL<<k), MTR_asym is generally smaller than 0.02M₀ that is obtained without spin-lock pulse, or when the spin-lock offset frequency Ω is set sufficiently far from the resonance. When FSL is comparable with k (400<=FSL<=600), MTR_asym is enhanced dramatically and the maximum MTR_asym is larger than 0.08M₀. When FSL is even larger than 600Hz, the maximum MTR_asym begins to reduce with the increasing FSL. The variation of MTR_asym at 3ppm with FSL is illustrated in Fig. 1c. The maximum MTR_asym at 3ppm occurs at the FSL of 527Hz, close to the proton exchange rate k.

Fig. 1.

Simulated Z-spectrum (a) and MTR_asym (b) for a two-pool system (p_a=0.99, p_b=0.01, δ_b=3ppm) under the application of spin-lock pulses with different FSLs but a fixed TSL of 50ms at 9.4T. The variation of MTR_asym at the 3ppm offset of pool B versus FSL is illustrated in (c).

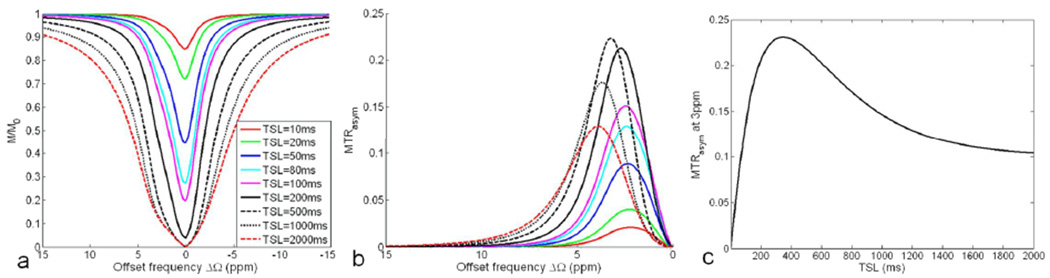
Figure 2 shows the influence of TSL on the Z-spectrum (a) and MTR_asym (b) at a fixed FSL of 500Hz. As seen in Fig. 2a, the longer the TSL, the more completely pool A is suppressed. With the TSL longer than 500ms, pool A is almost completely saturated by the on-resonance spin-lock pulse. However, the maximum MTR_asym does not monotonically increase with TSL (Fig. 2b). In addition, the location of the maximum MTR_asym is shifting to higher off-resonance with the increasing TSL, not always at 3ppm. The maximum MTR_asym could be over 0.2M₀ when the TSL is optimized. Fig. 2c illustrates the variation of MTR_asym at 3ppm with TSL. The MTR_asym at 3ppm is maximized at the TSL around 350ms.

Fig. 2.

Simulated Z-spectrum (a) and MTR_asym (b) for a two-pool system (p_a=0.99, p_b=0.01, δ_b=3ppm) under the application of spin-lock pulses with different TSLs but a fixed FSL of 500Hz at 9.4T. The variation of MTR_asym at the 3ppm offset of pool B versus TSL is illustrated in (c).

Influence of B₀ field strength on Z-spectrum and MTR_asym

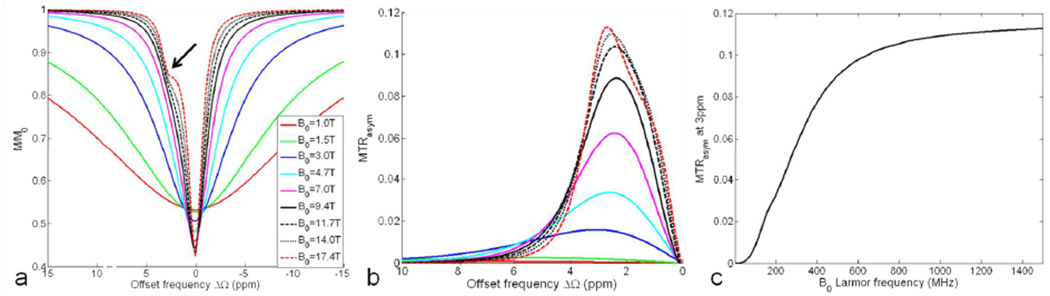
The dependence of Z-spectrum and asymmetric MTR on the main magnetic field strength B₀ under the application of a spin-lock pulse with the FSL of 500Hz and the TSL of 50ms is shown in Fig. 3. The on-resonance saturation rate of pool A increases with B₀. The increase of absolute offset frequency in Hz of pool B with B₀ makes it easier to recognize pool B on the Z-spectrum, as indicated by the arrow. It is expected that a more pronounced saturation of pool B closer to its offset frequency (3ppm) would appear on the overall Z-spectrum at an even stronger B₀, and hence leads to the enhanced MTR_asym and image contrast. As demonstrated in Fig. 3b, the maximum MTR_asym increases with B₀, with its location closer to 3ppm. Meanwhile, the shape width of the MTR_asym curve becomes narrower with B₀, indicating a higher specificity for the detection of pool B. Fig. 3c shows the monotonically increasing MTR_asym at 3ppm is always with the B₀ Larmor frequency, but with a slower increasing rate at higher B₀.

Fig. 3.

Simulated Z-spectrum (a) and MTR_asym (b) for a two-pool system (p_a=0.99, p_b=0.01, δ_b=3ppm) under the application of a spin-lock pulse (FSL=500Hz, TSL=50ms) at different B₀. (c) MTR_asym at the 3ppm offset of pool B versus TSL is always increasing with B₀.

Influence of tissue properties on Z-spectrum and MTR_asym

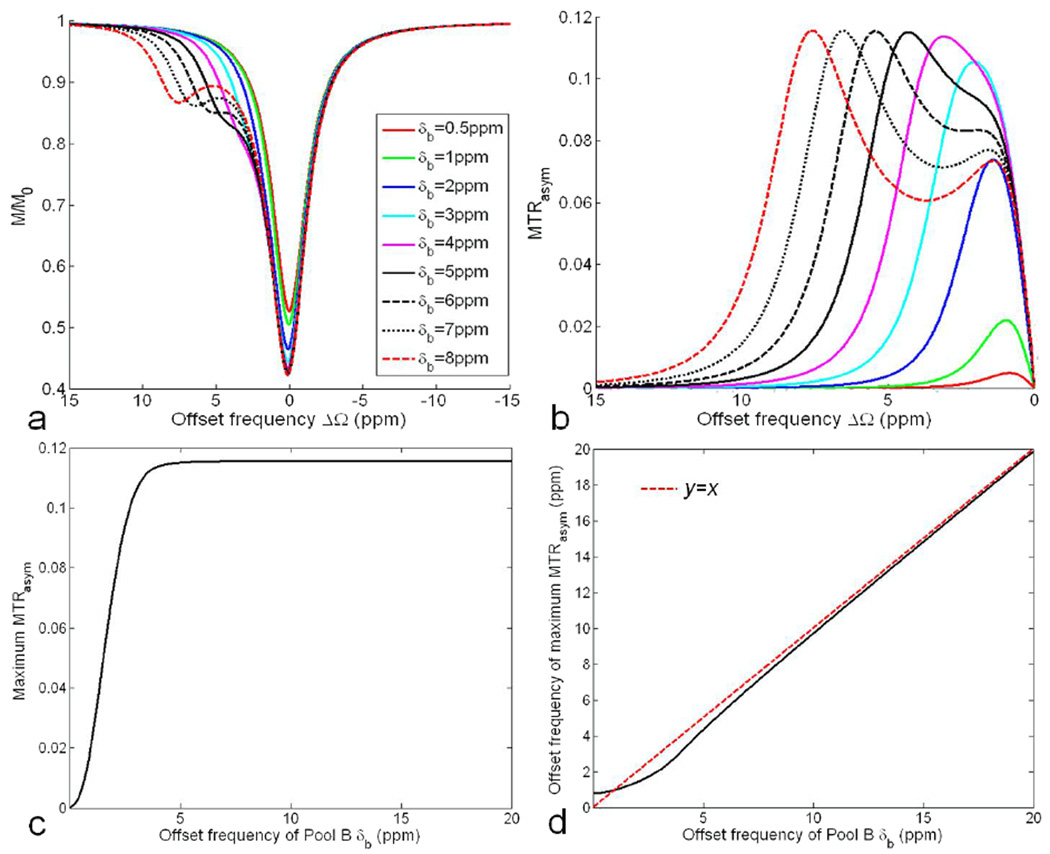
Figure 4a shows the Z-spectra if pool B resonates at different offset frequencies δ_b under the application of a spin-lock pulse with the FSL of 500Hz and the TSL of 50ms. Similar to Fig. 3a, the increase of absolute offset frequency in Hz of pool B, makes it easier to recognize pool B on the Z spectrum. The MTR_asym curves shown in Fig. 4b illustrate that the image contrast is very small if the offset frequency of pool B is too close to the resonant frequency, while with the increasing δ_b, the maximum MTR_asym increases rapidly. However, when δ_b is larger than 5ppm, the maximum MTR_asym becomes stable, no longer increasing with δ_b (Fig. 4c). Fig. 4d shows that the location of the maximum MTR_asym approaches to the exact offset frequency of pool B if δ_b is sufficiently large due to the reduced direct saturation effect, indicating a better specificity.

Fig. 4.

Simulated Z-spectrum (a) and MTR_asym (b) for a two-pool system (p_a=0.99, p_b=0.01) under the application of a spin-lock pulse (FSL=500Hz, TSL=50ms) at 9.4T when pool B resonates at different offset frequencies δ_b. (c) Variation of maximum MTR_asym versus δ_b. (d) The location of maximum MTR_asym approaches the exact offset frequency of pool B with increasing δ_b.

Proton exchange rate k between pool A and B also has the effect on the Z-spectrum appearance, which is denoted in Fig. 5a. Although it may be not easy to visually recognize the apparent differences between Z-spectra at different proton exchange rates, MTR_asym curves for different ks shown in Fig. 5b clearly demonstrate that a more pronounced maximum MTR_asym could be achieved around δ_b when the FSL approximates k, similar to Fig. 1b. Note that the slight shift of the maximum MTR_asym may be primarily caused by the direction saturation effect since the saturation peak for pool B is so small. The MTR_asym at 3ppm is maximized at around 440/s (Fig. 5c), similar to the FSL of 500Hz. Meanwhile, the value of MTR_asym at 3ppm decreases rapidly when k is much smaller or much larger than FSL.

Fig. 5.

Simulated Z-spectrum (a) and MTR_asym (b) for a two-pool system (p_a=0.99, p_b=0.01, δ_b=3ppm) under the application of a spin-lock pulse (FSL=500Hz, TSL=50ms) at 9.4T for different proton exchange rates k. (c) MTR_asym at 3ppm versus k first increases and then decreases with k.

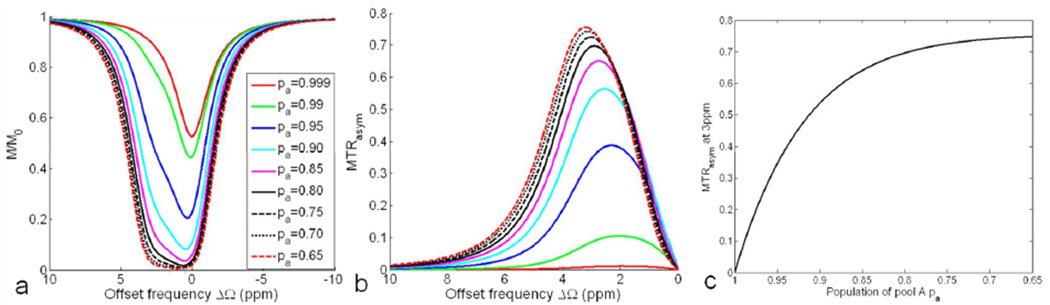
Figure 6 denotes the effect of a decreasing population of pool A p_a (or increasing p_b) on the overall Z-spectrum and MTR_asym. With the decrease of p_a, the saturation on pool B is more prominent (Fig. 6a), which overlaps with the saturation on pool A due to the relatively small δ_b of 3ppm, and broadens the peak of the overall Z-spectrum. Fig. 6b and 6c show that the maximum MTR_asym and the MTR_asym at 3ppm both increase with the larger p_b. As seen in Fig. 7c, MTR_asym at 3ppm is a monotonically decreasing function of p_a (note the reversed x axis).

Fig. 6.

Simulated Z-spectrum (a) and MTR_asym (b) for a two-pool system (δ_b=3ppm) under the applications of a spin-lock pulse (FSL=500Hz, TSL=50ms) at 9.4T. (c) MTR_asym at 3ppm decreases monotonically with p_a (note the reversed x axis).

Fig. 7.

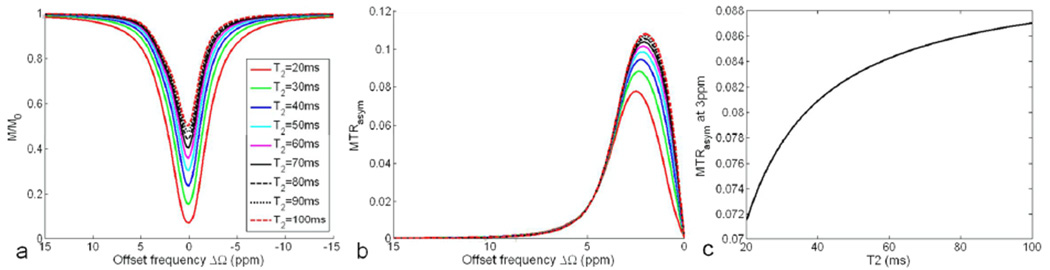
Simulated Z-spectrum (a) and MTR_asym (b) for a two-pool system (p_a=0.99, p_b=0.01, δ_b=3ppm) with different population-averaged T₂ values under the application of a spin-lock pulse (FSL=500Hz, TSL=50ms) at 9.4T. (c) MTR_asym at 3ppm increases monotonically with the population averaged T₂.

Figure 7 denotes the effect of the population averaged T₂ on the overall Z-spectrum and MTR_asym. The increase of T₂ reduces the saturation rate of Z spectra (Fig. 7a), but enhances the maximum MTR_asym (Fig. 7b). However, the location of the maximum MTR_asym shifts to lower offset with the increase of T₂. As a consequence, the MTR_asym at 3ppm although monotonically increases with T₂, the enhancement rate is generally low (Fig. 7c).

Summary of parameter influence on Z-spectrum

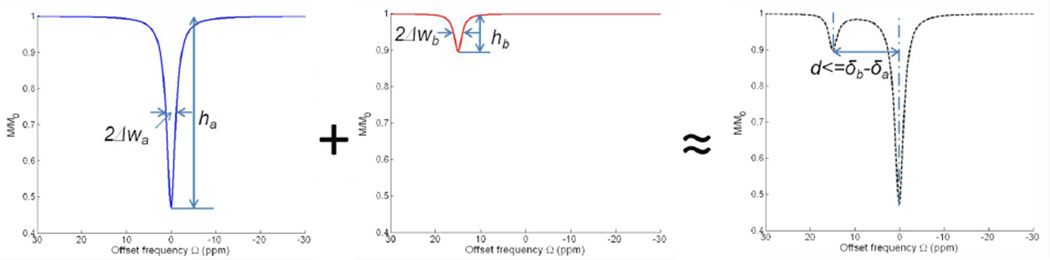
The Z-spectrum of a two-pool model could be imagined as the coupling of the Z-spectra of two individual single pools through chemical exchange and spill-over effect between them (Fig. 8). The Z-spectrum of pool A reflects direct water saturation and the spectrum of the much smaller pool B is more sensitive to the chemical exchange effect. Without chemical exchange and spill-over effect, the composite two-pool Z-spectrum is exactly the sum of Z-spectrum for each single pool. In Fig. 8, Z-spectrum peak height and half width at half maximum for two pools are defined as h_a,b and Δw_a,b respectively. The frequency difference between two peaks is defined as d. Due to chemical exchange as well as spill-over effect, d is usually smaller than δ_b−δ_a. Theoretically, h_b and Δw_b could be used to evaluate the sensitivity and specificity of chemical exchange image contrast if DS is assumed to be symmetric and its effect could be completely compensated through asymmetric analysis. For the better characterization of chemical exchange effect, a Z-spectrum with high values of h_b/h_a, h_a/Δw_a and h_b/Δw_b is preferable. Meanwhile, it is also preferable that Δw_a+Δw_b<<d. The effects of each factor increase on the composite Z-spectrum appearance are summarized in Table 1 as the rule of thumb in the practical experiment settings.

Fig. 8.

The overall Z-spectrum can be considered as the composition and coupling of two individual Z-spectra of pool A and B under the chemical exchange and spill-over effect. An ideal Z-spectrum for better characterization of chemical exchange should have high values of h_b/h_a, h_a/Δw_a and h_b/Δw_b. Δw_a+Δw_b is preferable to be much smaller than the saturation peak difference d as well.

Table. 1.

The summary of the effect of each increasing factor on the composite Z-spectrum.

	ha	Δwa	ha/Δwa	hb	Δwb	hb/Δwb	hb/ha	d(ppm)
FSL	↑→	↑	↓	↑	↑	↑↓	↑	→↓
TSL	↑→	↑	→↓	↑→	↑	→↓	→↑	→
B0	→	↓	↑	→	↓	↑	→	↑→
δb	→	→	→	→	→	→	→	↑
k	↑↓	↑↓	→	↑↓	↑	↑↓	↑↓	→
pb	↑	↑	→	↑	↑	↑→	↑	→
T2	↓	↓	→	→	→	→	↑	→

↑, ↓, and → indicate increase, decrease and no or very small change, respectively. ↑↓ indicate increase first and then decrease, and so on. Note that this table only provides the rough guideline and is applicable for the situations when two pool peaks are recognizable on the composite Z-spectrum.

Optimization of the spin-lock time and frequency for MTR_asym measurements

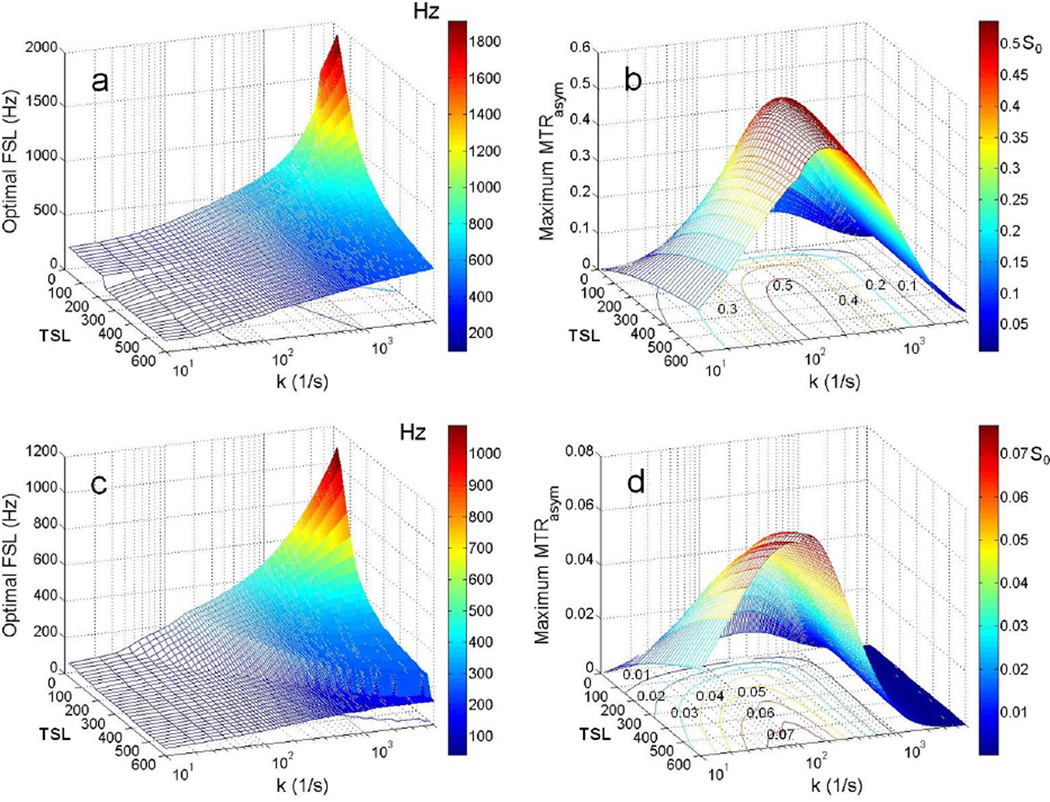
To achieve maximum MTR_asym and hence image contrast for chemical exchange characterization is one of the key aims for chemical exchange imaging. For CESL, adjustments of TSL, FSL and ΔΩ could be employed for this purpose. The offset frequency of pool B usually could be determined from in vitro characterization, so is assumed to be known. For this numerical simulation, an optimal FSL was defined as the FSL that maximizes the MTR_asym at exactly the offset frequency of pool B (3ppm) for a specific proton exchange rate k and a fixed TSL. Optimal FSLs for proton exchange rates from 10/s to 5000/s (at a resolution of 10/s) and TSLs from 20ms to 600ms (at a resolution of 20ms) were numerically searched within the FSL range of 1Hz to 4000Hz at a search step of 1 Hz. The optimal FSLs and the corresponding maximal MTR_asym at 3ppm were depicted in Fig. 9 for 9.4T (a, b) and 3T (c, d), respectively. As seen in Fig. 9a and c, for both 9.4T and 3T, optimal FSL is much dependent on k when TSL is shorter than 100ms. Higher FSL is required to enhance the maximum MTR_asym for high proton exchange rate. In other word, FSL could be tuned to better characterize different proton exchange rates. On the other hand, when a longer TSL is applied, a lower optimal FSL is required to obtain the maximum MTR_asym. Meanwhile, the dependence of optimal FSL on k is also reduced. With a very long TSL like 600ms, a quite universal FSL, in particular at lower B₀ (e.g. ~130Hz at 3T), may be applied to achieve maximum MTR_asym for wide proton exchange rate ranges. For low to intermediate proton exchange rates, e.g. 0–500/s at 3T, the difference of the optimal FSLs is small, while this difference becomes large for high proton exchange rates. As seen in Fig. 9b and d, it is expectable that larger maximum MTR_asym could be achieved at 9.4T than at 3T, which may be attributed to the significantly reduced direct saturation or spill-over effect due to the increase of the absolute offset frequency of labile protons at the higher field. Overall, the greatest maximum MTR_asym is achieved by the optimal FSL with long TSL for low to intermediate proton exchange rates. For fast proton exchange rates, although FSL could be adjusted to enhance MTR_asym, the maximum MTR_asym values are generally quite uniform for different TSLs, and much smaller than the corresponding ones for lower proton exchange rates.

Fig. 9.

The optimal FSL and the corresponding maximal MTR_asym at 3ppm achieved for different proton exchange rates k and different TSLs at 9.4T and 3T. (a) Optimal FSL at 9.4T; (b) maximal MTR_asym achieved by the optimal FSL at 9.4T; (c) optimal FSL at 3T; (b) maximal MTR_asym achieved by the optimal FSL at 3T. The contours plotted in the transverse plane in (b) and (d) are labeled with the level of the maximal MTR_asym. The area inside a contour has the maximal MTR_asym values higher than the corresponding level.

DISCUSSION

Since the Bloch-McConnell equations form the theoretical basis of chemical exchange quantification for both CEST and CESL, the theoretical derivation and simulation results shown in this study are compatible with many findings of CEST imaging in literatures.

As for the theoretical derivation, when the spin-lock pulse is applied at the offset of pool B (ΔΩ=δ_b) for an asymmetric population two-pool system (p_b<<p_a, p_a≈1 and p_ap_b≈p_b/p_a), under the assumption of R₂<<R_ex, it is derived from Eq. [16] that:

$$M_{\mathit{\text{ss}}}=M_0·\frac{R_1·\text{cos }\theta }{R_1{\text{cos}}^2\theta +\frac{p_a{p}_b{{\delta }_b}^{2}k}{{\omega }_1^2+k^2}{\text{sin}}^2\theta }.$$ [19]

With the further assumption of k<<ω₁ and ω₁<<δ_b for slow exchange processes at very high field B₀, cosθ≈1 and sinθ≈tanθ=ω₁²/δ_b², then Eq. [19] is further simplified as:

$$\frac{M_{\mathit{\text{ss}}}}{M_0}\approx \frac{1}{\text{cos }\theta +T_1\frac{p_a{p}_b{{\delta }_b}^{2}k}{{\omega }_1^2}{\text{tan}}^2\theta }\approx \frac{1}{1+T_1{p}_a{p}_{b}k}\approx \frac{1}{1+T_1{k}_a}=\frac{{\tau }_a}{{\tau }_a+T_1}.$$ [20]

Eq. [20] is exactly the Eq. [23] in the literature (Woessner et al., 2005), where τ_a is the lifetime of proton in pool A, except that the average T₁ (very closed to T_1a due to the asymmetric population) is used in Eq. [20]. Similarly, by combining Eq. [15], it is easily derived that:

$$M=(M_0-M_{\mathit{\text{ss}}})·e^{-R_{1\rho }·\mathit{\text{TSL}}}+M_{\mathit{\text{ss}}}=M_0(\frac{{\tau }_a}{T_1+{\tau }_a}+\frac{T_1}{T_1+{\tau }_a}{e}^{-\frac{T_1+{\tau }_a}{T_1·{\tau }_a}·\mathit{\text{TSL}}}),$$ [21]

which is exactly the Eq. [24] for modeling of CEST in the literature (Woessner et al., 2005).

Assuming no spill-over effect and MTR(−ΔΩ)≈1, it is also derived by substituting Eq. [21] into Eq. [18] (τ_a>>T₁):

$${\mathit{\text{MTR}}}_{\mathit{\text{asym}}}(\mathrm{\Delta }\mathrm{\Omega })=1-(\frac{{\tau }_a}{T_1+{\tau }_a}+\frac{T_1}{T_1+{\tau }_a}{e}^{-\frac{T_1+{\tau }_a}{T_1·{\tau }_a}·\mathit{\text{TSL}}})=\frac{T_1}{T_1+{\tau }_a}(1-e^{-\frac{T_1+{\tau }_a}{T_1·{\tau }_a}·\mathit{\text{TSL}}})\approx \frac{1}{1+k_a{T}_1}{k}_a{T}_1(1-e^{-\frac{\mathit{\text{TSL}}}{T_1}})$$ [22]

which is equivalent to the well-known analytical solution for CEST imaging (van Zijl and Yadav, 2011; Zhou et al., 2003b; Zhou et al., 2003a). The derivation of Eqs. [20–22] shows that CEST model is compatible with CESL theory, and could be considered as a simplified case of CESL model for slow exchange rate processes.

It has been also shown (Jin et al., 2011) that the proposed linear plot of M_ss/(M₀−M_ss) versus 1/ω₁² (Dixon et al., 2010), which could be used for concentration independent quantification of proton exchange rates in CEST, could also be derived from the asymmetric two-pool R_1ρ model under the slow exchange assumption.

As for numerical simulation, the MTR_asym dependence on FSL as depicted in Fig. 1c is compatible with the theoretical analysis (Sun et al., 2005) and experiment result (Sun et al., 2007b) in the previous CEST studies. The MTR_asym dependence on TSL as depicted in Fig. 2c is also compatible with the TSL optimization analysis in the literature (Jin et al., 2012). The optimal TSL occurs when ∂MTR_asym/∂TSL=0 by using Eqs. [17–18]. For slow exchange rates and low FSL cases like those in many CEST studies, the MTR_asym usually monotonically increases with TSL and the optimal TSL approaches infinite. For intermediate to fast exchange rates and high FSLs, the optimal TSL becomes complicated, dependent on many factors such as T2, exchange rate and labile pool population p_b. As revealed by the two-pool R_1ρ model, the proton exchange rate k is possible to be quantified by using the CE dependence on either FSL or TSL, consistent with the QUESP and QUEST methods proposed for CEST imaging (McMahon et al., 2006). The influence of p_b on Z-spectrum is compatible with the simulation result in the literature (Zaiss et al., 2012). In addition, the labile proton concentration (proportional to p_b), could also be further independently determined by using the optimal FSL (Sun, 2010).

According to the numerical simulation results in Fig. 1 to Fig. 7, it was found that the maximum MTR_asym does not always appear at the offset of pool B, the value and the location of the maximum MTR_asym could be a complicated function of many factors. MTR_asym at the offset of pool B encounters the similar problem. Therefore, in practice, the sensitivity and specificity of CE based image contrast, no matter by CEST or CESL, are often compromised, although could be improved by the tuning of spin-lock parameters. The interpretation of the CE based image contrast should be also very careful due to the non-monotonic nature of CE-based contrast function and the possible contrast contamination due to the spill-over effect, shifting and broadening of the Z-spectrum and the presence of multiple pools and different proton exchange rates.

B₀ and B₁ inhomogeneities could have pronounced influence on the appearance of Z-spectrum and compromise CE quantification. In particular, B₀ inhomogeneity may simulate the offset frequency of pool B, and B₁ inhomogeneity leads to the deviation of the actual FSL from the nominal FSL. Moreover, θ could be contaminated by both. Some methods have been proposed for this issue in CEST imaging (Scheidegger et al., 2011; Kim et al., 2009; Sun et al., 2007a). For CESL, this issue could also be addressed and alleviated by the improved design of spin-lock pulses and the advanced quantification methods (Chen et al., 2011; Witschey et al., 2007; Charagundla et al., 2003; Yuan et al., 2012a).

There are some practical implications as revealed by the numerical analysis of the spin-lock pulse optimization for CESL (Fig. 9). As indicated by Fig. 9, slow, intermediate, and fast exchange may be imaged optimally with long TSL and low FSL, intermediate TSL and FSL, and short TSL and high FSL in theory, respectively, consistent with the results in a recent CESL study (Jin et al., 2012). Quite similar optimal FSLs could be used to maximize the MTR_asym for slow to intermediate proton exchange rates (Fig. 9a, c). Meanwhile, maximum MTR_asym increases mainly with longer TSL in this case (Fig. 9b, d). These findings are well supported by the existing CEST studies. The strong dependence of optimal FSL on proton exchange rates (Fig. 9a, c) with short TSL is also consistent with the traditional spin-lock T_1ρ imaging (Duvvuri et al., 2001). Generally, CE image contrasts as revealed by MTR_asym, is much smaller for high proton exchange rates than for slow to intermediate proton exchange rates (Fig. 9b, d). Therefore, even with the optimized adjustment of FSL and TSL, it is still technically challenging to visualize the high exchange rate on image contrast by using MTR_asym. This challenge becomes more severe at lower B₀ field strength like 3T (Fig. 9d). By the limitation of hardware capability of a typical clinical 3T MRI scanner, a spin-lock pulse with FSL higher than 500Hz and TSL longer than 200ms may be impractical for excitation by using the body coil. Referring to the MTR_asym contours in Fig. 9d, an image contrast higher than 0.03 could be difficult to achieve even with the spin-lock pulse optimization, particularly for intermediate to fast CE rates (k>500/s in Fig. 9d), making the translation of CESL for clinical studies in this CE range technically challenging. Meanwhile, the strict regulation on specific absorption rate (SAR) of RF pulse has to be satisfied during patient scan for safety reason, which also imposes the difficulty of CESL for clinical studies. Numerical simulation also suggests that a large offset of pool B from water resonance and the increase of pool population ratio of labile protons by using exogenous CE agents (Zhang et al., 2003; Sherry and Woods, 2008) both benefit CE contrast enhancement at clinical field strength.

The major limitation of this theoretical study is the absence of experiment for validation because there is no MRI scanner over 3T and dedicated powerful RF transmitter at our site. Therefore, theoretical derivation and numerical simulation, although compatible with previous CEST studies indirectly, should be further validated by experiments in future studies. Meanwhile, the precision of the simulation result may also be compromised by the limitation of the simplified solution for the Bloch-McCornell equations. For some particular cases, the deviation of the simplified solution from the full Bloch numerical analysis may not be negligible. For instance, the deviation of maximum MTR_asym upon convergence of the two pool frequencies as shown in Fig. 4d may be carefully interpreted when the resonant frequency of pool B approaches pool A (Zaiss et al., 2012). This study only discusses the effect of parameters involved in the two-pool R_1ρ relaxation model on the Z-spectrum and MTR_asym. Actually, concentration of the labile proton pool (only indirectly reflected by p_b) (Zhou et al., 2011), pH value (Ward and Balaban, 2000) and temperature (Zhang et al., 2005) should have remarkable influence on chemical exchange and image contrast, which are not yet discussed in this study. In practice, cross-relaxation (Davis and Bax, 1985), represented by nuclear Overhauser enhancement (NOE) effect (Ling et al., 2008) may also contaminate Z-spectrum and compromise MTR_asym analysis. It is also not involved in the R_1ρ model used in this study and has to be investigated in future experimental studies. The results in this study are only valid for a two-pool model. The extension to multi-pool model should be further developed in the future.

In summary, CESL, an alternative to CEST, should be promising as a powerful chemical exchange imaging tool. In this study, Z-spectrum and asymmetric MTR obtained by CESL are theoretically analyzed and numerically simulated using a general two-pool R_1ρ relaxation model outside of fast-exchange limit. The influence of spin-lock parameters, B₀ field strength and physiological properties on CESL Z-spectrum and MTR_asym are quantitatively revealed. Theoretical analysis shows that the classical analytical CEST model could also be derived from the R_1ρ relaxation model for CESL. Numerical simulation results in this study are compatible with and well supported by the existing chemical exchange imaging studies. Further experimental validations of CESL should be performed in future studies.