Abstract
We have developed a computational approach for predicting protein-protein association rates (Alsallaq and Zhou, Structure 2007, 15, 215). Here we expand the range of applicability of this approach to protein-RNA binding and report the first results for protein-RNA binding rates predicted from atomistic modeling. The system studied is the U1A protein and stem/loop II of the U1 small nuclear RNA. Experimentally it was observed that the binding rate is significantly reduced by increasing salt concentration while the dissociation changes little with salt concentration, and charges distant from the binding site make marginal contribution to the binding rate. These observations are rationalized. Moreover, predicted effects of salt and charge mutations are found to be in quantitative agreement with experimental results.
Introduction
Protein-RNA interactions play central roles in regulation of gene expression and mediation of other essential cellular functions. The complex between the spliceosomal protein U1A and its target on the U1 small nuclear RNA has served as a model system for many studies.1–18 In this complex, the N-terminal RNA recognition motif of U1A interacts in a sequence-specific manner with stem/loop II (U1SLII) of the U1 small nuclear RNA (Figure 1). Both experimental and computational studies have probed determinants of the binding affinity, and a number of experimental studies1,7,9,10,13–15 have been carried out to dissect the binding rate. However, no atomistic modeling of any protein-RNA binding rate has so far been reported. We have developed a computational approach for predicting protein-protein association rates,19–21 which enabled us to elucidate the molecular basis for the association rates of a number of protein-protein complexes.22,23 Here we expand the range of applicability of our computational approach to protein-RNA binding, and report the first realistic modeling of protein-RNA binding rate on the U1A-U1SLII system.
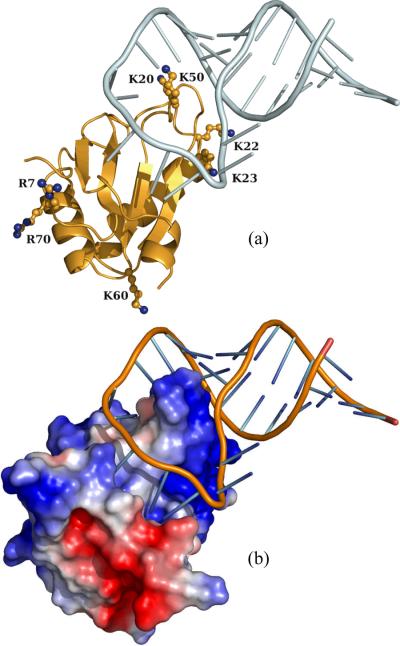
Figure 1.
The native complex of U1A and U1SLII. (a) Locations of mutated residues. (b) Electrostatic surface of U1A.
The stereospecific complex of a protein, A, and a binding partner, B, can be envisioned to occur in two distinct steps.20,23–25 First, the two molecules approach each other via translational and rotational diffusion to reach a region in configurational space where they have near-native separations and orientations. We refer to the ensemble of configurations in this region collectively as the transient complex,22,24 which will be denoted as A*B. (In the past this ensemble was also referred to as the transition state;19–22 the current terminology will avoid unintended connotations of that overused term.26) From the transient-complex ensemble, conformational rearrangement can lead to the stereospecific native complex (C). Accordingly we have the kinetic scheme
| (1) |
where kD is the diffusion-controlled rate constant for reaching the transient complex, and kc is the rate constant for reaching the native complex through conformational rearrangement; the rate constants for the reverse steps are denoted by k−D and k−c, respectively. The overall binding rate constant is given by
| (2) |
and the overall dissociation rate constant is
| (3) |
In the diffusion-controlled limit, kc ⪢ k−D, and we have ka ≈ kD and kd ≈ k−Dk−c/kc.
In our computational approach we obtain kD by modeling overall translational and rotational diffusion and accounting for long-range electrostatic interactions. To use kD as an estimate for ka, the placement of the transient complex in configurational space is as close to the native complex as it is possible to still avoid treating short-range interactions and conformational rearrangement.20,21,23 If the resulting transient complex involves severe translational and rotational constraints between the binding molecules, then the diffusion-controlled rate constant for reaching the transient complex can be calculated as
| (4) |
where kD0 is the diffusion-controlled rate constant in the absence of any biasing force, β = (kBT)−1 is the inverse of the thermal energy, Uel is the electrostatic interaction energy, and <…>* signifies averaging over the transient-complex ensemble. The accuracy of eq (4) has been demonstrated by both analytical results and Brownian dynamics simulations, as long as the transient complex is severely constrained in relative translation and rotation and the interaction force is long-ranged.24,27–31 Note that, since electrostatic interactions contribute a factor exp(−β<Uel>*) to the “equilibrium constant” kD/k−D, when eq (4) is valid, k-D will be independent of long-range electrostatic interactions.
It was noted previously that, when the transient complex is close to the stereospecific native complex and is hence severely constrained in translation and rotation, protein-protein association shows a telltale sign in the effects of salts on the association and dissociation rates.20,32 That is, ka is significantly reduced by increasing salt concentration but kd is only marginally affected by salt concentration. When the transient complex is close to the native complex, salts are not expected to have a significant influence on the transition rate constants kc and k−c. At the same time k−D becomes independent of long-range electrostatic interactions and is thus not affected by salt screening. The only rate constant affected by salts is kD, which is reduced due to weakened electrostatic attraction between the binding molecules. The disparate salt effects on ka and kd are observed on many protein-protein pairs.33–48 The binding of U1A with U1SLII shows exactly this salt behavior7,14 and is thus expected to be modeled by a transient complex close to the native complex.
We have developed a sampling procedure to map the interaction energy landscape and locate the transient-complex ensemble.21–23 The transient-complex ensemble is located at the outer boundary of the native-complex interaction energy well. The average electrostatic interaction energy within the transient complex is then calculated by solving the Poisson-Boltzmann equation and used in eq (4) to predict the diffusion-controlled rate kD, which in turn is taken as an estimate for the overall binding rate constant ka. An alternative approach to predicting kD is through Brownian dynamics simulations, which have been applied to study the association of many protein-protein pairs.27,49–59 Because it is prohibitively expensive to calculate force and torque by solving the Poisson-Boltzmann equation on the fly during a Brownian dynamics simulation, one has to rely on approximations, such as treating one of the proteins as a set of test charges49 (which leads to significant errors from neglecting the low-dielectric region of the protein interior27) or a more elaborate effective-charge model.60 The approximations are worst when the proteins are in close proximity, precisely where electrostatic interactions are expected to have the strongest influence on kD. The problem would be much worse for protein-RNA binding since the large charge density on the RNA demands the use of the nonlinear Poisson-Boltzmann equation, which is much more difficult to approximate than the linearized version typically used for proteins. In our approach the problem is circumvented because the effect of electrostatic interactions is captured by the Boltzmann factor exp(−β<Uel>*). A rigorous treatment of electrostatic interactions is essential for the accuracy of calculated kD. For protein-protein association, the difference in electrostatic interaction energies calculated by the nonlinear Poisson-Boltzmann equation and the linearized version are modest; we found that even the modest difference leads to a clear improvement in agreement between calculated and experimental results for association rates.23
Theory and Implementation
U1A-U1SLII Complex and Mutations
The systems studied here were taken from a previous study of the effects of salts and mutations on the binding affinity.17 Briefly, the U1A-U1SLII native complex was built from the B and Q chains of the X-ray structure of human U1A complexed with RNA step/loop 5'-AAUCCAUUGCACUCCGGAUUU-3' (Protein Data Bank entry 1urn).2 The RNA used in the experimental studies7,14 was 5'-AGCUUAUAUCCAUUGCACUCCGGAUGAGCU-3'. To better match the latter RNA, the 5' adenine and two 3' uracils in 1urn were removed and a 5 basepair duplex RNA (5'-AGCUU paired with AAGCU-3') was added in InsightII (Accelrys Software Inc., San Diego). Two mutations in 1urn, His31 and ARG36, were mutated back to the wild-type residues, Tyr31 and Gln36, respectively. Finally hydrogens were added and the complex was energy minimized with Amber 9.61 For compatibility with the Amber force field, the phosphate at the 5'-end of U1SLII was removed; the net charge on the RNA was −27e. The protein had a net charge of +6e.
Mutations were modeled in InsightII and then energy-minimized within Amber 9.61 Only mutated side chains were allowed to move during minimization; otherwise the energetic contribution of the mutation would be overwhelmed by those from changes in other parts of the molecule. Because of concerns for potential inadequacy in the modeling of mutations, our study was restricted to seven single mutations and just one double mutation (K20A/K22A). The locations of the mutated residues are shown in Figure 1a.
Interaction Energy Landscape
As noted in the Introduction, the transient complex is located at the outer boundary of the native-complex interaction energy well. The identification of the transient-complex ensemble, as described previously for protein-protein association,21–23 is based on mapping the interaction energy landscape over the configurational space of the native complex and the surrounding region. We followed the same procedure here for protein-RNA binding. The protein and RNA subunits were treated as rigid; therefore there were only six relevant degrees of freedom: three for relative translation and three for relative rotation. Each subunit was frozen in its conformation found in the native complex, leading to a smoothed interaction energy landscape.
The six translational and rotational coordinates were defined relative to the native-complex configuration built from the X-ray structure. The translation was represented by the relative displacement vector r; its magnitude r measures the separation between the surfaces of the two subunits. The rotation was represented by three Euler angles (ξ, ζ, χ); χ is the rotation angle around a body-fixed unit vector. The X-ray configuration corresponds to r = 0, ξ = 0, and χ = 0. To sample the configurational space of the native complex and the surrounding region, the six translational and rotational coordinates were randomly generated, with only one restriction: r ≤ r0. Values of r0 in the range of 6 to 11 Å were tested; results obtained with r0 = 8 Å are reported in this paper.
A realistic interaction-energy function would require careful calibration. In our approach we instead use Nc, the number of contacts, as a surrogate, which captures the essence of interactions stabilizing the native complex.21 In Nc both native and nonnative contacts between the two subunits were included. For any configurations in which the two subunits clashed, the interaction energy was set to infinity. Contacts were calculated between 20 representative (known as interaction locus) pairs of interfacial atoms. Each interaction-locus atom was assigned a contact radius, taken to be half of the distance from its native contact partner in the X-ray configuration. In any of the sampled configurations, a native contact was considered formed when the distance between the native partners was less than the sum of their contact radii plus 3.5 Å. A nonnative contact was formed between nonnative pairs of interaction-locus atoms when their distance was less than the sum of their contact radii plus 2.5 Å. In the X-ray configuration, Nc = 41. Nc was recorded for each clash-free configuration.
In the conformational sampling, most of the computational time was spent in detecting clashes and only a tiny fraction of randomly generated configurations passed the clash test. For example, out of 107configurations generated with r0 = 8 Å, only 511 survived the clash test. In the past clash detection has been done through an exhaustive atom by atom detection.21–23 In this work we introduced a procedure to filter out an overwhelming majority of the clashing configurations, which led to a speed up of ~500-fold in mapping the interaction energy landscape. The filtering procedure was based on a grid representation of the binding molecules. One subunit (in our case the protein) was fixed in space, and grid points inside any of its atoms were labeled as interior. For the other subunit (in our case the RNA), grid points representing the molecule's surface were identified in the following way. After labeling all interior points, a sphere with a 1.4 Å was placed in each exterior point. If the sphere did not enclose any interior point, all grid points inside were labeled as solvent. Every interior point with at least one solvent point at one of the six neighboring positions was relabeled as surface. This use of the solvent probe reduced the chance of grid points in small internal crevices being labeled as solvent. The grid representation of this subunit's surface was generated once and stored for later use. Grid representations for both subunits had a spacing of 0.5 Å in each direction.
In mapping the interaction energy landscape, the first subunit was fixed in space while the second subunit was mobile, with configurations generated by randomly sampling the six translational and rotational coordinates. In each configuration, the surface points of the mobile subunit were tested against the interior points of the fixed subunits (note that the surface points of the mobile subunit in general would not fall on grid points of the fixed subunit). Clash was reported if all eight grid points around any surface point of the mobile subunit were interior points of the fixed protein. The surface points were presorted in a specific order to make the clash test as efficient as possible. The structure of the sorted surface points had a hierarchical order. The first batch of points were collected from a 3 × 3× 3 grid representation of the mobile subunit; the second batch of points were collected from a 5 × 5× 5 grid representation, minus those already in the first batch. This sequence continued until all the surface points were collected.
After the filtering procedure, all remaining configurations were further tested for clash by the exhaustive atom by atom detection.
Specification of Transient Complex
The identification of the transient complex was based on the following crucial observation: inside the native-complex interaction energy well, relative translation and rotation are restricted, but once outside the binding molecules gain translational and rotational freedom.21 Thus the outer boundary of the native-complex interaction energy well coincides with the onset of translational and rotational freedom. Translational and rotational freedom was measured by σχ(Nc), the standard deviation of χ among all the sampled configurations at a contact level Nc. A sharp increase in σχ with decreasing Nc marks the onset of translational and rotational freedom. The onset corresponds to the maximum in the difference, Ξ, between σχ and its average at all lower contact levels. The transient-complex contact level, Nc*, was thus identified from the maximum of Ξ as a function of Nc. For r0 = 8 Å, a total of 1,307,285 clash-free configurations were accumulated. From these we found Nc* = 19; 7,830 of the sampled configurations were at this contact level. The value of Nc* was stable when r0 was varied from 6 to 11 Å.
Calculation of Electrostatic Interaction Energy
The transient-complex ensemble was represented by randomly selected 100 configurations at the contact level Nc*. The electrostatic interaction energy in each configuration was calculated as
| (5) |
The three terms on the right-hand side represented the electrostatic energies of the protein-RNA complex and the two subunits each by itself, respectively. The same 100 configurations were also used for all the mutants. This use amounts to assuming that the transient-complex ensemble is not perturbed by the mutations. The average electrostatic interaction energy, <Uel>*, of the transient complex was calculated over the 100 configurations.
Electrostatic energies were calculated by solving the nonlinear Poisson-Boltzmann (PB) equation using the UHBD program.62 The calculation protocol was the same as in an earlier study.17 Each calculation began with a coarse grid with a 1.5-Å spacing, and then a finer grid with 0.5-Å spacing, both centered at the geometric center of the solute molecule. A final grid with a 0.25-Å spacing was centered at the site of mutation. The dimensions of all the three grids were 140 × 140 × 140. The ion exclusion radius in the first calculation was 2 Å. Unless specifically indicated, results were obtained using the van der Waals surface as the boundary between the solute low dielectric and the solvent high dielectric. Some calculations were also done by using the solvent-exclusion surface (also known as the molecular surface) as the dielectric boundary.
In all electrostatic calculations, protein atoms were assigned AMBER charges63 and Bondi radii.64 The temperature was set to 298 K, and the solute and solvent dielectric constants were 4 and 78.5, respectively. The buffer for the experimental studies7,14 on the U1A-U1SLII complex was 10 mM Tris-HCl and 150 mM (or a higher concentration) NaCl. The ionic strength of the buffer with 150 mM NaCl was taken to be 160 mM and increased commensurately at higher NaCl concentrations.
Results and Discussion
Transient Complex of U1A and U1SLII
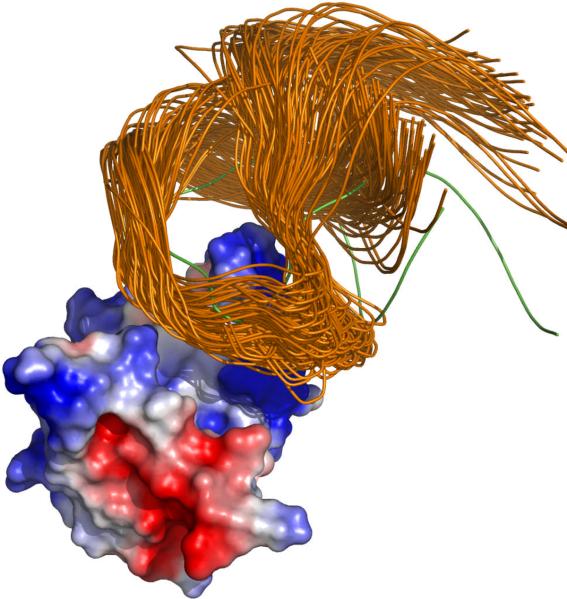
From the structure of the native complex shown in Figure 1a, it can be seen that the loop between β strands 2 and 3 of U1A, crowned by residues L49 and K50, protrudes into the loop of U1SLII. Representative configurations in the transient complex are shown in Figure 2. In the transient complex, the RNA is moved away from the position in the native complex by 5.7 ± 0.9 Å, and the average and standard deviation of the rotation angle χ, around an axis roughly parallel to the U1A protrusion, is 22° and 15°, respectively. These values are mostly in line with corresponding results previously found for protein-protein pairs.23 An exception worth noting is the relatively large value of the average χ found here; in the transient complexes of the protein-protein pairs χ typically averaged around 0°, though in one of them the averaged was −9°. It should be recalled that χ = 0 ° in the native complex.
Figure 2.
Representative configurations in the transient complex of U1A and U1SLII.
Among the transient-complex configurations accumulated, only 5% had negative χ values. The asymmetry between positive and negative χ values, leading to the relatively large positive average χ, can be traced to clashes between the RNA and the U1A protrusion. It is easier to avoid the clash by having positive χ values (i.e., rotating the RNA clockwise). Among the configurations shown in Figure 2, the one with the most negative χ value is singled out by displaying the RNA in green.
Effect of Salt on Binding Rate
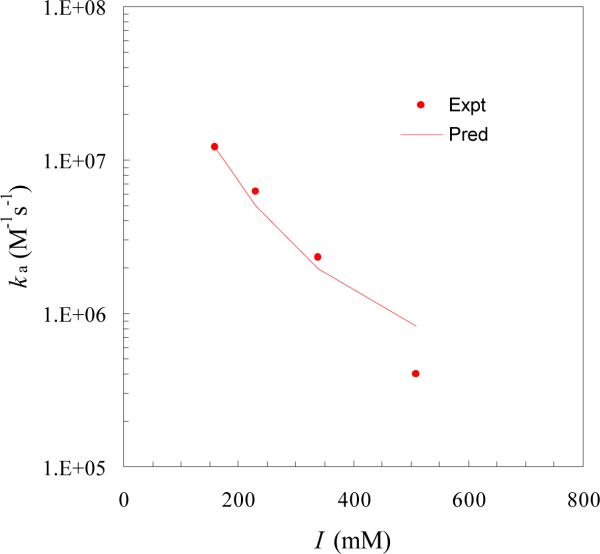
As alluded to in the Introduction, the disparate effects of salt on the binding and dissociation rates of U1A and U1SLII observed experimentally7,14 qualitatively supports our structural model for the transient complex. Upon calculating the average electrostatic interaction energy <Uel>* and using eq (4), we found that the experimental results for the salt dependence of ka can be quantitatively explained (Figure 3). The values of <Uel>* were −3.4, −2.9, −2.3, and −1.8 kcal/mol at ionic strengths of 160, 230, 340, and 510 mM, respectively. The fit to the experimental results led to a basal rate constant of kD0 = 4 × 104 M−1s−1. This value falls on the low end of expected values (105 to 106M−1s−1) of basal rate constants.30,50,65 The low kD0 perhaps is a reflection of the particular tight fit between the subunits studied here, featuring the protrusion of U1A into the U1SLII loop. It may also be an indication that conformational rearrangement, which serves to slow down the binding, perhaps contributes to the measured binding rate.66 There is experimental evidence indicating that parts of U1A, in particular, the protrusion, undergo rearrangement upon RNA binding.2,12,67 It should be noted internal dynamics of the protein or RNA occurring on the sub-nanosecond time scale has little impact on the binding rate.68,69
Figure 3.
Comparison of predicted and experimental ionic-strength dependences of the U1A-U1SLII binding rate.
It is interesting to note that, despite the large magnitude of the net charge on the RNA (−27e; pairing with a partner with a net charge of +6e), the magnitudes of <Uel>* found here for the U1A-U1SLII system are comparable to those found for protein-protein pairs exhibiting charge complementarity.22,23 This points to the dominant roles of specific interactions in electrostatic rate enhancement. Experimentally, Law et al.15 studied the effect of RNA net charge on the binding rate by extending the U1SLII stem, which points away from U1A (Figure 1), and found only a very modest increase in ka.
The results for <Uel>* reported above were calculated from solving the nonlinear Poisson-Boltzmann equation with the dielectric boundary set to the solute van der Waals surface. A widely-used alternative choice for the dielectric boundary is the molecular surface, which treats the many small crevices not accessible to a spherical solvent probe as part of the solute dielectric. In a number of studies on binding affinity and binding rate,17,23,70,71 we have found the van der Waals protocol gives better agreement with experimental results. In particular, we found that, for protein-protein pairs exhibiting charge complementarity, the molecular surface protocol gave positive <Uel>* and thus predicted electrostatic rate retardation instead of enhancement.23 Here we again found for the protein-RNA system that <Uel>* became positive (5.2 kcal/mol at an ionic strength of 160 mM) when the molecular surface protocol was used. Reconciliation of the consequent 6000-fold rate retardation with the experimental result for ka, which is over 107 M−1s−1, would run into considerable difficulty.
Effect of Mutations on Binding Rate
As shown in Figure 1, U1A presents a positive electrostatic surface to complement the negatively charged phosphates of U1SLII. Both the binding site, as represented by K20, K22, K23, and K50, and the backside, as represented by R7, K60, and R70 are coated with basic residues. It was thus of interest to find the relative contributions of the binding site and backside basic residues to electrostatic rate enhancement.
As can be expected from the earlier discussion regarding net charges, the backside acidic residues were found to make marginal contributions to <Uel>*. Neutralizing the basic residues R7, K60, and R70 by glutamine mutations increased <Uel>* by only 0.1 to 0.2 kcal/mol and the binding rate was predicted to barely change. This is in full agreement with the experimental results for these mutants.14
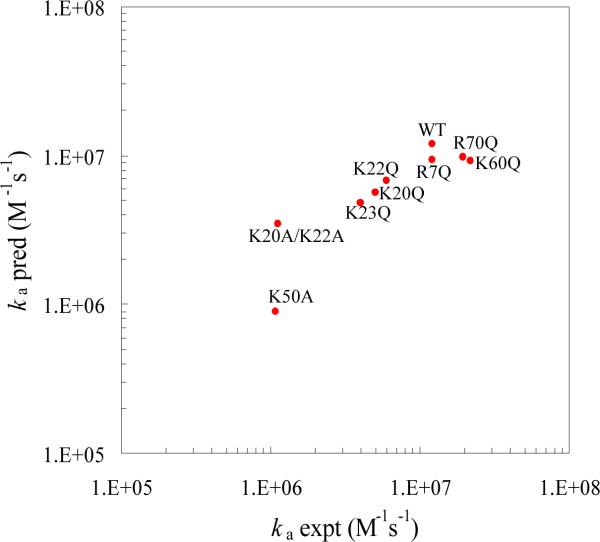
On the other hand, the effect of neutralizing the binding site basic residues is significantly stronger. <Uel>* increased by ~0.5 kcal/mol for the K20Q, K22Q, and K23Q mutations, 0.7 kcal/mol for the K20A/K22A mutation, and 1.5 kcal/mol for the K50A mutation. It is interesting to note that the order of the effects of the K20A/K22A and the K50A mutations in the transient complex is reversed from that in the native complex as found in our previous study.17 The reversal can be attributed to by the location of residue K50 in the protrusion (see Figure 1). In the transient complex, the RNA is moved away from the protein, positioning K50 in close proximity of the RNA (see Figure 2). The predicted effects of the binding site mutations on the binding rate are in good agreement with the experimental results7,14 (Figure 4). The agreement provides important validation of our structural model for the transient complex.
Figure 4.
Comparison of predicted and experimental results for the binding rates of wild-type U1A and seven mutants with U1SLII. The ionic strength was 160 mM.
Compact versus Diffuse Transient-Complex Ensemble
A significant decrease in ka and a marginal change in kd with increasing salt concentration are a telltale sign for a compact transient-complex ensemble, i.e., one involving severe constraints in relative translation and rotation between the binding partners. This salt behavior of the binding and dissociation rates has been observed on many protein-protein pairs and on the protein-RNA pair of U1A and U1SLII. Other protein-nucleic acid pairs have also been found to conform to this salt behavior,72,73 again implicating compact transient-complex ensembles.
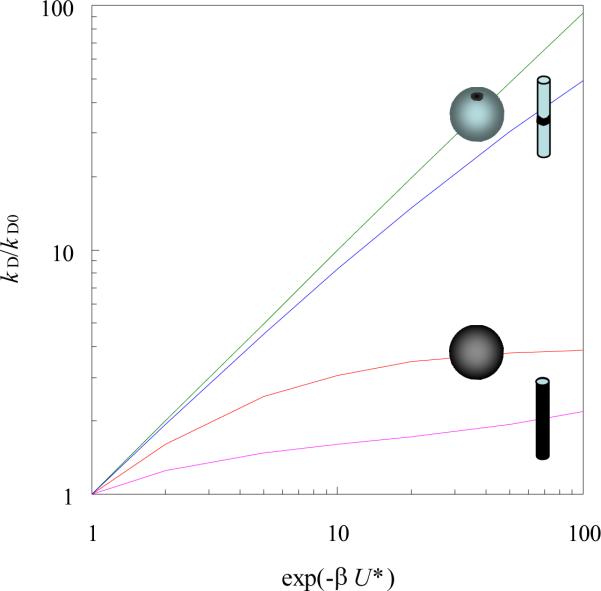
Our rationalization of a significant decrease in ka and a marginal change in kd with increasing salt concentration is based on eq (4), which requires a compact transient-complex ensemble as a precondition (the other prediction is a long-ranged interaction potential).20 When this condition is not met, eq (4) will no longer be valid. For example, the effect of a square-well interaction potential on the diffusion-controlled rate of a pointlike ligand binding to a small binding site on the surface of a spherical target (modeling a protein or RNA) or a cylindrical target (modeling a DNA) is well described by eq (4) (Figure 5). However, when the whole surface of the spherical target or a long length of the cylindrical target becomes the binding site, the rate enhancement is significantly less than what is predicted by eq (4) (Figure 5). In the case of a uniformly binding spherical target, the effect of a centrosymmetric interaction potential U(r) on the diffusion-controlled binding rate is given the well-known Debye result74
| (6) |
where D is the diffusion constant of the ligand and R is the radius of the spherical target. For a Coulomb interaction potential U(r) = −Q/r, eq (6) gives kD/4πDR = β|U*|/[1 − exp(βU*)], with U* = −Q/R, whereas eq (4) predicts kD/4πDR = exp(−βU*). At βU* = −10, the correct result for kD/4πDR is 10, but eq (4) predicts 2 × 104, which is a 2000-fold overestimate.
Figure 5.
Comparison of rate enhancements for compact and diffuse transient-complex ensembles. For the spherical target with radius R, the interaction potential is given by U = U* for R < r < 4R and 0 elsewhere (r: radial distance). The binding site is either a patch with an area fraction of 2.5 × 10−5 or is the whole surface. The cylindrical target features a binding site on an infinite cylinder with radius R. The binding site length is either 0.02R or 200R. The interaction potential is given by U = U* for R < ρ < 7R and 0 elsewhere (ρ: distance to the cylinder axis). The results were obtained from analytical solutions given by Zhou and Szabo.76
The conclusion is then that, when the transient complex is diffuse, electrostatic rate enhancement is expected to be very modest. In this situation we can further deduce that the binding rate will decrease only modestly but the dissociation rate will increase significantly with increasing salt concentration. This type of salt behavior was observed in the binding of the single-stranded binding protein with a single-stranded DNA.75 Since the single-stranded DNA is unstructured in the unbound state and protein binding can be initiated by contacting any point along the length of the DNA, it is quite reasonable to characterize the transient-complex ensemble of this system as diffuse.
In conclusion, we have extended our computational approach for predicting protein-protein association rates to protein-RNA binding and reported the first results on protein-RNA binding rates predicted from atomistic modeling. The study has provided rationalizations for the major experimental findings and the predictions are in quantitative agreement with experiments.
Acknowledgment
It is great pleasure to dedicate this paper to Attila Szabo, mentor and friend, on his 60th birthday. This work was supported in part by grant GM058187 from the National Institutes of Health.
References and Notes
- (1).Hall KB, Stump WT. Nucl. Acids Res. 1992;20:4283. doi: 10.1093/nar/20.16.4283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Oubridge C, Ito N, Evans PR, Teo CH, Nagai K. Nature. 1994;372:432. doi: 10.1038/372432a0. [DOI] [PubMed] [Google Scholar]
- (3).Hermann T, Westhof E. Nat. Struct. Biol. 1999;6:540. doi: 10.1038/9310. [DOI] [PubMed] [Google Scholar]
- (4).Reyes CM, Kollman PA. J. Mol. Biol. 2000;295:1. doi: 10.1006/jmbi.1999.3319. [DOI] [PubMed] [Google Scholar]
- (5).Olson MA. Biophys. J. 2001;81:1841. doi: 10.1016/S0006-3495(01)75836-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Blakaj DM, McConnell KJ, Beveridge DL, Baranger AM. J. Am. Chem. Soc. 2001;123:2548. doi: 10.1021/ja005538j. [DOI] [PubMed] [Google Scholar]
- (7).Katsamba PS, Myszka DG, Laird-Offringa IA. J. Biol. Chem. 2001;276:21476. doi: 10.1074/jbc.M101624200. [DOI] [PubMed] [Google Scholar]
- (8).Showalter SA, Hall KB. J. Mol. Biol. 2002;322:533. doi: 10.1016/s0022-2836(02)00804-5. [DOI] [PubMed] [Google Scholar]
- (9).Katsamba PS, Bayramyan M, Haworth IS, Myszka DG, Laird-Offringa IA. J. Biol. Chem. 2002;277:33267. doi: 10.1074/jbc.M200304200. [DOI] [PubMed] [Google Scholar]
- (10).Shiels JC, Tuite JB, Nolan SJ, Baranger AM. Nucl. Acids Res. 2002;30:550. doi: 10.1093/nar/30.2.550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).McConnell TS, Lokken RP, Steitz JA. RNA. 2003;9:193. doi: 10.1261/rna.2136103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Rupert PB, Xiao H, Ferre-D'Amare AR. Acta Crystallogr. D Biol. Crystallogr. 2003;59:1521. doi: 10.1107/s0907444903011338. [DOI] [PubMed] [Google Scholar]
- (13).Law MJ, Chambers EJ, Katsamba PS, Haworth IS, Laird-Offringa IA. Nucl. Acids Res. 2005;33:2917. doi: 10.1093/nar/gki602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Law MJ, Linde ME, Chambers EJ, Oubridge C, Katsamba PS, Nilsson L, Haworth IS, Laird-Offringa IA. Nucl. Acids Res. 2006;34:275. doi: 10.1093/nar/gkj436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Law MJ, Rice AJ, Lin P, Laird-Offringa IA. RNA. 2006;12:1168. doi: 10.1261/rna.75206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Dobson N, Dantas G, Baker D, Varani G. Structure. 2006;14:847. doi: 10.1016/j.str.2006.02.011. [DOI] [PubMed] [Google Scholar]
- (17).Qin SB, Zhou H-X. Biopolymers. 2007;86:112. doi: 10.1002/bip.20708. [DOI] [PubMed] [Google Scholar]
- (18).Kormos BL, Benitex Y, Baranger AM, Beveridge DL. J. Mol. Biol. 2007 doi: 10.1016/j.jmb.2007.06.003. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Vijayakumar M, Wong KY, Schreiber G, Fersht AR, Szabo A, Zhou H-X. J. Mol. Biol. 1998;278:1015. doi: 10.1006/jmbi.1998.1747. [DOI] [PubMed] [Google Scholar]
- (20).Zhou H-X. Biopolymers. 2001;59:427. doi: 10.1002/1097-0282(200111)59:6<427::AID-BIP1047>3.0.CO;2-7. [DOI] [PubMed] [Google Scholar]
- (21).Alsallaq R, Zhou H-X. Biophys. J. 2007;92:1486. doi: 10.1529/biophysj.106.096024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Alsallaq R, Zhou H-X. Structure. 2007;15:215. doi: 10.1016/j.str.2007.01.005. [DOI] [PubMed] [Google Scholar]
- (23).Alsallaq R, Zhou H-X. Proteins. 2007 in press. [Google Scholar]
- (24).Zhou H-X, Wong KY, Vijayakumar M. Proc. Natl. Acad. Sci. USA. 1997;94:12372. doi: 10.1073/pnas.94.23.12372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Huang X, Dong F, Zhou H-X. J. Am. Chem. Soc. 2005;127:6836. doi: 10.1021/ja042641q. [DOI] [PubMed] [Google Scholar]
- (26).As noted previously,23 what hinder the diffusion-controlled rate constant kD for reaching the transient complex are orientational constraints within the transient complex, not activation to a high-energy barrier. The transient complex can therefore not be identified as a transition state in the sense of Eyring (Eyring, H. J. Chem. Phys. 1932, 3, 1917). Neither is it useful to identify the orientational constraints in the transient complex as constituting an entropy barrier. On the other hand, the conformational rearrangement that brings the binding molecules from the transient complex to the native complex might be an activated process, and a transition state could be considered in the calculation of the rate constant kc.
- (27).Zhou H-X. Biophys. J. 1993;64:1711. doi: 10.1016/S0006-3495(93)81543-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Zhou H-X. J. Chem. Phys. 1996;105:7235. [Google Scholar]
- (29).Zhou H-X, Briggs JM, McCammon JA. J. Am. Chem. Soc. 1996;118:13069. [Google Scholar]
- (30).Zhou H-X. Biophys. J. 1997;73:2441. doi: 10.1016/S0006-3495(97)78272-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Zhou H-X, Briggs JM, Tara S, McCammon JA. Biopolymers. 1998;45:355. doi: 10.1002/(SICI)1097-0282(19980415)45:5<355::AID-BIP4>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- (32).Zhou H-X. Protein Sci. 2003;12:2379. doi: 10.1110/ps.03216203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Miller C. Biochemistry. 1990;29:5320. doi: 10.1021/bi00474a016. [DOI] [PubMed] [Google Scholar]
- (34).Candia S, Garcia ML, Latorre R. Biophys. J. 1992;63:583. doi: 10.1016/S0006-3495(92)81630-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Goldstein SAN, Miller C. Biophys. J. 1993;65:1613. doi: 10.1016/S0006-3495(93)81200-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Schreiber G, Fersht AR. Biochemistry. 1993;32:5145. doi: 10.1021/bi00070a025. [DOI] [PubMed] [Google Scholar]
- (37).Escobar L, Root MJ, MacKinnon R. Biochemistry. 1993;32:6982. doi: 10.1021/bi00078a024. [DOI] [PubMed] [Google Scholar]
- (38).Murrell-Lagnado RD, Aldrich RW. J. Gen. Physiol. 1993;102:977. doi: 10.1085/jgp.102.6.977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Wallis R, Moore GK, James R, Kleanthous C. Biochemistry. 1995;34:13743. doi: 10.1021/bi00042a004. [DOI] [PubMed] [Google Scholar]
- (40).Shen BJ, Hage T, Sebald W. Eur. J. Biochem. 1996;240:252. doi: 10.1111/j.1432-1033.1996.0252h.x. [DOI] [PubMed] [Google Scholar]
- (41).Wendt H, Leder L, Harma H, Jelesarov I, Baici A, Bosshard HR. Biochemistry. 1997;36:204. doi: 10.1021/bi961672y. [DOI] [PubMed] [Google Scholar]
- (42).Radic Z, Kirchhoff PD, Quinn DM, McCammon JA, Taylor P. J. Biol. Chem. 1997;272:23265. doi: 10.1074/jbc.272.37.23265. [DOI] [PubMed] [Google Scholar]
- (43).Baerga-Ortiz A, Rezaie AR, Komives EA. J. Mol. Biol. 2000;296:651. doi: 10.1006/jmbi.1999.3447. [DOI] [PubMed] [Google Scholar]
- (44).Darling RJ, Kuchibhotla U, Glaesner W, Micanovic R, Witcher DR, Beals JM. Biochemistry. 2002;41:14524. doi: 10.1021/bi0265022. [DOI] [PubMed] [Google Scholar]
- (45).Walker D, Moore GR, James R, Kleanthous C. Biochemistry. 2003;42:4161. doi: 10.1021/bi0273720. [DOI] [PubMed] [Google Scholar]
- (46).Stewart RC, Van Bruggen R. J. Mol. Biol. 2004;336:287. doi: 10.1016/j.jmb.2003.11.059. [DOI] [PubMed] [Google Scholar]
- (47).Gianni S, Engstrom A, Larsson M, Calosci N, Malatesta F, Eklund L, Ngang CC, Travaglini-Allocatelli C, Jemth P. J. Biol. Chem. 2005;280:34805. doi: 10.1074/jbc.M506017200. [DOI] [PubMed] [Google Scholar]
- (48).Hemsath L, Dvorsky R, Fiegen D, Carlier MF, Ahmadian MR. Mol. Cell. 2005;20:313. doi: 10.1016/j.molcel.2005.08.036. [DOI] [PubMed] [Google Scholar]
- (49).Northrup SH, Reynolds JCL, Miller CM, Forrest KJ, Boles JO. J. Am. Chem. Soc. 1986;108:8162. [Google Scholar]
- (50).Northrup SH, Erickson HP. Proc. Natl. Acad. Sci. USA. 1992;89:3338. doi: 10.1073/pnas.89.8.3338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Gabdoulline RR, Wade RC. Biophys. J. 1997;72:1917. doi: 10.1016/S0006-3495(97)78838-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (52).Elcock AH, Gabdoulline RR, Wade RC, McCammon JA. J. Mol. Biol. 1999;291:149. doi: 10.1006/jmbi.1999.2919. [DOI] [PubMed] [Google Scholar]
- (53).Altobelli G, Subramaniam S. Biophys. J. 2000;79:2954. doi: 10.1016/S0006-3495(00)76532-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).Fogolari F, Ugolini R, Molinari H, Viglino P, Esposito G. Eur. J. Biochem. 2000;267:4861. doi: 10.1046/j.1432-1327.2000.01542.x. [DOI] [PubMed] [Google Scholar]
- (55).Gabdoulline RR, Wade RC. J. Mol. Biol. 2001;306:1139. doi: 10.1006/jmbi.2000.4404. [DOI] [PubMed] [Google Scholar]
- (56).Zou G, Skeel RD. Biophys. J. 2003;85:2147. doi: 10.1016/s0006-3495(03)74641-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (57).Lin J, Beratan DN. J. Phys. Chem. B. 2005;109:7529. doi: 10.1021/jp045417w. [DOI] [PubMed] [Google Scholar]
- (58).Spaar A, Dammer C, Gabdoulline RR, Wade RC, Helms V. Biophys. J. 2006;90:1913. doi: 10.1529/biophysj.105.075507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (59).Haddadian EJ, Gross EL. Biophys. J. 2006;91:2589. doi: 10.1529/biophysj.106.085936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (60).Gabdoulline RR, Wade RC. J.Phys.Chem. 1996;100:3868. [Google Scholar]
- (61).Case DA, Darden TA, Cheatham TE, III, Simmerling CL, Wang J, Duke RE, Luo R, Merz KM, Pearlman DA, Crowley M, Walker RC, Zhang W, Wang B, Hayik S, Roitberg A, Seabra G, Wong KF, Paesani F, Wu X, Brozell S, Tsui V, Gohlke H, Yang L, Tan C, Mongan J, Hornak V, Cui G, Beroza P, Mathews DH, Schafmeister C, Ross WS, Kollman PA. Amber 9 University of California; San Francisco, CA: 2006. [Google Scholar]
- (62).Madura JD, Briggs JM, Wade RC, Davis ME, Luty BA, Ilin A, Antosiewicz J, Gilson MK, Bagheri B, Scott LR, McCammon JA. Comput. Phys. Comm. 1995;91:57. [Google Scholar]
- (63).Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. J Am Chem Soc. 1995;117:5179. [Google Scholar]
- (64).Bondi A. J Phys Chem. 1964;68:441. [Google Scholar]
- (65).Schlosshauer M, Baker D. Protein Sci. 2004;13:1660. doi: 10.1110/ps.03517304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (66).When conformational rearrangement is accounted for, the basal rate constant is given by ka0 = kD0kc/(k−D + kc) [see eq (2)], which can still be considered “basal” as long as kc and k−c are not significantly affected by salt. That possibility seems justified when the transient complex is close to the native complex.
- (67).Avis JM, Allain FH, Howe PW, Varani G, Nagai K, Neuhaus D. J. Mol. Biol. 1996;257:398. doi: 10.1006/jmbi.1996.0171. [DOI] [PubMed] [Google Scholar]
- (68).Zhou H-X, Wlodek ST, McCammon JA. Proc. Natl. Acad. Sci. USA. 1998;95:9280. doi: 10.1073/pnas.95.16.9280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (69).Zhou H-X. J. Chem. Phys. 2003;118:2010. [Google Scholar]
- (70).Dong F, Vijayakumar M, Zhou H-X. Biophys J. 2003;85:49. doi: 10.1016/S0006-3495(03)74453-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (71).Dong F, Zhou H-X. Proteins. 2006;65:87. doi: 10.1002/prot.21070. [DOI] [PubMed] [Google Scholar]
- (72).Milev S, Bosshard HR, Jelesarov I. Biochemistry. 2005;44:285. doi: 10.1021/bi048907n. [DOI] [PubMed] [Google Scholar]
- (73).Auweter SD, Fasan R, Reymond L, Underwood JG, Black DL, Pitsch S, Allain FH. EMBO. J. 2006;25:163. doi: 10.1038/sj.emboj.7600918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (74).Debye P. Trans. Electrochem. Soc. 1942;82:265. [Google Scholar]
- (75).Kozlov AG, Lohman TM. Biochemistry. 2002;41:6032. doi: 10.1021/bi020122z. [DOI] [PubMed] [Google Scholar]
- (76).Zhou HX, Szabo A. Phys. Rev. Lett. 2004;93:178101. doi: 10.1103/PhysRevLett.93.178101. [DOI] [PubMed] [Google Scholar]