Demographic Inference Reveals African and European Admixture in the North American Drosophila melanogaster Population

Abstract

Drosophila melanogaster spread from sub-Saharan Africa to the rest of the world colonizing new environments. Here, we modeled the joint demography of African (Zimbabwe), European (The Netherlands), and North American (North Carolina) populations using an approximate Bayesian computation (ABC) approach. By testing different models (including scenarios with continuous migration), we found that admixture between Africa and Europe most likely generated the North American population, with an estimated proportion of African ancestry of 15%. We also revisited the demography of the ancestral population (Africa) and found—in contrast to previous work—that a bottleneck fits the history of the population of Zimbabwe better than expansion. Finally, we compared the site-frequency spectrum of the ancestral population to analytical predictions under the estimated bottleneck model.

TO date, several studies have confirmed that Drosophila melanogaster originated in sub-Saharan Africa and spread to the rest of the world (Lachaise et al. 1988; David and Capy 1988; Begun and Aquadro 1993; Andolfatto 2001; Stephan and Li 2007). With its cosmopolitan distribution we expect that different populations have evolved and adapted differently to distinct environments, making D. melanogaster a perfect study system for both adaptation and population history. Extensive research has been performed to detect signatures of adaptation at the genome level (Sabeti et al. 2006; Li and Stephan 2006; Zayed and Whitfield 2008). Such detection usually depends on the underlying demographic scenario, since demographic events can leave similar patterns on the genome as adaptive (selective) events (Kim and Stephan 2002; Glinka et al. 2003; Jensen et al. 2005; Nielsen et al. 2005; Pavlidis et al. 2008, 2010a). Therefore, a better understanding of the demography of a population will not only allow us to estimate past and present population sizes and the times of the population size changes but will also decrease the rate of false positives of signatures of adaptation. Here we study the demography of African, European, and North American populations, with an emphasis on the North American population.

There is evidence that D. melanogaster colonized North America <200 years ago (Johnson 1913; Sturtevant 1920; Keller 2007). D. melanogaster (then known as D. ampelophila) was first reported in New York in 1875 by New York State entomologist Lintner (Lintner 1882; Keller 2007). In the year 1879 several articles were published indicating the appearance of D. melanogaster in several parts of eastern North America, including Connecticut and Massachusetts (Johnson 1913). At that time the dipteran fauna was very well described. It is therefore unlikely that entomologists would have overlooked D. melanogaster for long (Keller 2007). Less than 25 years after its introduction, D. melanogaster became the most common dipteran species in North America (Howard 1900). Johnson (1913) suggested that North America could have been colonized from the tropics, since the first specimen of D. melanogaster in the new world was first described from Cuba (possibly following routes from Central or South America). However, the same author also suggests that the first individuals could have come in vessels from southern Europe during the Spanish regime or from western Africa during the slave trade.

Even if there is agreement regarding the origin of D. melanogaster, the demographic history of North American flies is still poorly understood, and population genetic analyses of both the ancestral and derived populations are required to tackle this problem. Begun and Aquadro (1993) and Andolfatto (2001) showed that variation in non-African populations (including North America) is a subset of that found in African populations. They suggested a simple “out-of-Africa” bottleneck scenario. Later, Kauer et al. (2002) and Caracristi and Schlötterer (2003) used microsatellite data for 40 X-linked loci to study several populations worldwide. Caracristi and Schlötterer (2003) found that some North American populations present only African alleles, whereas other North American populations present only European alleles. Based on the proportion of shared alleles and F_ST values, their study shows that American populations are closer to African populations than to European populations. Baudry et al. (2004) and Haddrill et al. (2005) analyzed 4 and 10 X-linked loci, respectively, but this time using sequence data. Baudry et al. (2004) suggested that rare alleles shared between non-African and African populations might represent immigrants from Africa. This agrees with the hypothesis of admixture between European and African flies suggested by Caracristi and Schlötterer (2003). Furthermore, Haddrill et al. (2005) found in their North American sample higher diversity and larger linkage disequilibrium than in their European sample, which is also compatible with an admixture scenario.

To infer the population history of North America, we also revisit the demography of the likely source populations from Africa and Europe. Concerning the demography of African D. melanogaster Glinka et al. (2003) and Pool and Aquadro (2006) found that African samples have an excess of rare derived mutations when compared to the standard neutral model. This excess can be generated by population expansion or a bottleneck. Li and Stephan (2006) proposed a population expansion model for the African population. However, it is still unclear if Zimbabwe is the center of origin. If Zimbabwe lies outside the center of origin we may expect that a bottleneck model would fit the data of the Zimbabwe population better than expansion, since range expansions are usually associated with bottlenecks and founder effects (Excoffier et al. 2009). Therefore, we decided to revisit the expansion scenario proposed by Li and Stephan (2006).

In this study we focus on modeling and inferring the demography of D. melanogaster using approximate Bayesian computation (ABC) (Tavaré et al. 1997; Pritchard et al. 1999; Beaumont et al. 2002). First, we revisit the demography of the Zimbabwe population and compare a model of instantaneous population expansion with a population bottleneck. Second, having found the best model for our ancestral population we model the joint demography of Africa, Europe, and North America. Finally, we analyze the observed site-frequency spectrum (SFS) of the Zimbabwe population and compare it to analytical predictions.

Materials and Methods

SNP data

Individuals come from three populations: Zimbabwe in Africa (sample size n = 12), The Netherlands in Europe (n = 12), and Raleigh in North America (n = 37). Sequence data consist of 242 intronic and intergenic X-linked loci from each population. African and European loci were originally target sequenced by Glinka et al. (2003), Ometto et al. (2005), and Hutter et al. (2007), while North American loci were extracted from full-genome sequences (publicly available from the Drosophila Population Genomics Project at http://www.dpgp.org) that were created using Illumina next-generation sequencing (NGS) technology. As a first quality control step for the NGS data, all bases with a Phred quality control score <20 were masked. All 242 orthologous loci extracted from the North American data were then aligned to the European and African sequences using MUSCLE (Edgar 2004) to account for insertion/deletion polymorphism. Drosophila simulans has been used as an outgroup sequence. As a second quality control step, the alignments were inspected for singleton polymorphisms private to the North American sample and these positions were removed from further analysis. We believe that a sizable fraction of these singleton polymorphisms are created by sequencing errors. This is reflected by the fact that the average quality score of a base causing a singleton polymorphism is significantly lower than the quality of bases creating variants segregating at higher frequencies (Mann–Whitney U-test: P < 2.2 × 10⁻¹⁶) (Supporting Information, Figure S1). From all these loci we computed the mean and the variance of the following summary statistics: the number of segregating sites S_n, Watterson’s Θ_W (Watterson 1975), the average number of pairwise differences in all pairwise comparisons of n sequences Π_n, Tajima’s D (Tajima 1989), the number of haplotypes K (Depaulis and Veuille 1998), the linkage disequilibrium statistic Z_nS (Kelly 1997), and the distance of Nei as a measure of population differentiation (Nei and Li 1979). Summary statistics of the North American population after exclusion of singletons are also reported. Additionally, we computed the joint site-frequency spectrum (JSFS) of all three pairs of populations, namely: Africa–Europe, Africa–North America, and Europe–North America (Figure S2). Each JSFS was summarized in four classes according to the Wakeley–Hey model (Wakeley and Hey 1997). These summaries are W1 (private polymorphisms in population 1), W2 (private polymorphisms in population 2), W3 (fixed differences between populations), and W4 (shared ancestral polymorphisms). This group of summary statistics, plus the summaries of the JSFS, constitutes our “observed vector” or “observed data” (Tables 1 and 2).

Table 1 . Mean and variance (in parentheses) of observed summary statistics over all 242 fragments.

	Africa (n = 12)	Europe (n = 12)	North America (n = 37)	Africa (no singletons)	Europe (no singletons)	North America (no singletons)
No. of segregating sites Sn	17.55 (81.31)	6.35 (29.31)	13.10 (50.22)	10.70 (42.45)	4.11 (18.30)	7.47 (29.57)
Watterson’s ΘW	5.91 (9.40)	2.11 (3.30)	3.22 (3.12)	3.57 (4.72)	1.36 (2.01)	1.83 (1.79)
Πn	5.13 (9.06)	2.18 (4.81)	2.52 (3.64)	3.92 (6.35)	1.36 (2.56)	2.05 (3.16)
Tajima’s D	−0.67 (0.34)	−0.09 (1.43)	−0.77 (1.05)	0.33 (0.43)	−0.006 (1.56)	0.21 (1.15)
No. of haplotypes K	9.46 (5.26)	3.87 (3.71)	10.31 (23.24)	8.09 (9.47)	2.85 (2.62)	6.98 (19.25)
Kelly’s ZnS	0.15 (0.01)	0.43 (0.075)	0.21 (0.055)	0.23 (0.03)	0.53 (0.08)	0.38 (0.16)

Table 2 . Comparisons between pairs of populations.

	Africa–Europe	Africa–North America	Europe–North America
Distance of Nei (with singletons in North America)	0.78 (0.66)	1.12 (1.38)	0.59 (1.15)
Distance of Nei (without singletons in North America)	0.69 (0.44)	1.01 (0.93)	0.53 (0.72)
W1 (private polymorphisms of population 1)	2278	1961	214
W2 (private polymorphisms of population 2)	363	743	924
W3 (fixed differences between populations)	17	86	89
W4 (shared polymorphisms between poulations)	647	990	809

The first two lines denote mean and variance (in parentheses) of Nei’s distance, and lines 3 to 6 the observed classes of the JSFS.

Demographic models of Africa

We first analyzed the data from the ancestral population in Africa. We tested whether an instantaneous expansion or a bottleneck fits better the observed data. The instantaneous expansion model had three parameters: ancestral population size, current population size, and time of expansion (Figure S3). The bottleneck model includes the severity as an additional parameter, which is defined as the ratio of the bottleneck duration and the population size during the bottleneck (Figure S3). We fixed the duration of the bottleneck to 1000 generations (Laurent et al. 2011).

Demographic models of North America–Europe–Africa

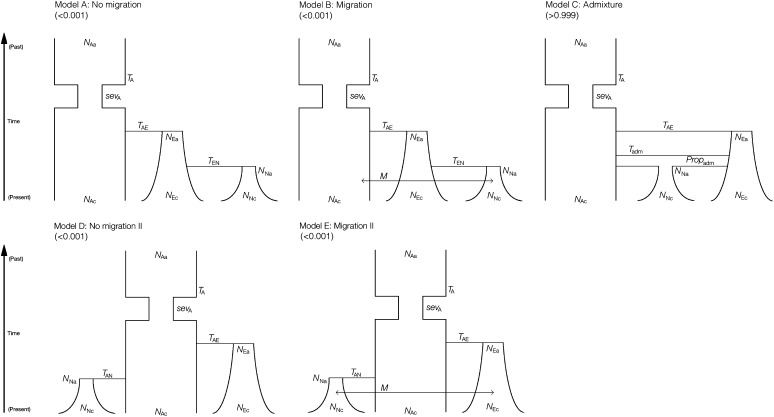
Based on the best model for the ancestral population we tested five different models that included all three populations (Figure 1 and Table S2). These five models are: model A (“no migration”), which comprises Africa as the ancestral population; the colonization of Europe is followed by exponential growth, and the colonization from Europe to North America with subsequent exponential growth. Model B (“migration”) matches model A but adds an equal migration rate between all populations starting at the colonization time of North America (we assumed that migration between continents increased significantly with human dispersal, which started a few centuries ago). Model C (“admixture”) equals the previous models until North America is founded through an admixture between Africa and Europe followed by exponential growth in North America. In model C, we estimated the proportion of European and African ancestry in the founding population of North America. Model D (“no migration II”) has Africa as the ancestral population with North America and Europe splitting independently from Africa. Finally, model E (“migration II”) matches model D but adds an equal migration rate between all populations starting at the colonization time of North America. Models A and D have 10 parameters, and models B, C, and E have 11 parameters each (Figure 1). In all models the time of colonization of North America was given a very small prior around 200 years ago (the time of the reported colonization of North America). We also let migration due to human-associated dispersal start at this same time (for models B and E). Model selection was performed with all models. For further analysis we selected only models A to C because of the biological assumptions that were already presented in the Introduction. A thorough explanation of the reasons why we discarded other models is presented in the Discussion. A more detailed description of all analyzed models can be found in the supporting information (Table S2) and in Figure 1.

Figure 1 .

Three-population models. Numbers in parentheses are the posterior probabilities of each model. The symbols are explained in Table 3.

ABC simulations

We simulated 100,000 data sets for each of the models described above following the protocol of Laurent et al. (2011). Each simulated data set consisted of 242 loci with individual per locus sample sizes, as well as mutation and recombination rates identical to the ones found in the observed data set. Mutation and recombination rates per site per generation for each locus were taken from Laurent et al. (2011). Our primary tool was the coalescent simulator ms by Hudson (2002). Each parameter was chosen from uniform prior distributions (see Table S1). Missing nucleotides (mostly present in the North American population) were also simulated at the same positions as they occur in the observed data. We accomplished this by following two steps: (1) from the observed data set we generated a missing-nucleotide table with the relative positions (beginning and end) of each chunk of missing nucleotides and recorded this information for each line and for each fragment and (2) by a simple manipulation of the ms output we masked all simulated polymorphisms that occurred at the same relative positions that were indicated in the missing-nucleotide table. From the ms output we also excluded all singletons that occurred in the simulated North American population. Following the same procedure as with the observed data set we calculated the summary statistics, the SFS, and the JSFS from the modified ms output, taking into account missing data in all calculations. Handling of priors, simulation of missing data, exclusion of singletons, and calculation of summary statistics was coded by ourselves. The software msABC (Pavlidis et al. 2010b) is able to perform similar simulations but does not calculate the JSFS. However, we still used msABC to validate our prior distributions. We launched simulations on a 64-bit Linux cluster with 510 nodes (at the Leibniz-Rechenzentrum LRZ, Munich).

Model choice

Model selection was also performed within an ABC framework. Posterior probabilities for each model were calculated according to Fagundes et al. (2007). Model selection was done based on the mean and the variance of S_n, mean and variance of Tajima’s D and linkage disequilibrium (Z_nS). In our analysis (see Results) Watterson’s Θ_W, Π_n, and K were correlated with S_n and therefore its inclusion did not change the results of the model choice procedure. Model selection was also performed separately using the summaries of the JSFS of all pairs of populations. The model with the highest posterior probability when comparing bottleneck and expansion for the African population as well as the three-population models was chosen as the best fit to the observed data. A validation for using 100,000 simulations for model choice was also performed: we conducted model choice for bottleneck/expansion and between all three-population models A to E for varying numbers of simulations ranging from 10,000 to 200,000 simulations. For the bottleneck vs. expansion case we show that starting at 50,000 simulations the posterior probability of the best model does not change significantly when the number of simulations is increased (Figure S4). For the three-population model choice the posterior probability of the best model is always >0.999 if the number of simulations is 10,000 or higher. Therefore a choice of 100,000 simulations for model choice is enough. Model choice performance was assessed by simulating 1000 different pseudo-observed data sets under models A, B, and C (samples for each parameter were taken from the prior distributions as well as from the posterior distributions based on the rejection method). Model choice was performed using the same method as above for each simulated vector of summary statistics. We considered one model to be preferred over the other if the Bayes factor of the models under comparison was above 3.

Parameter estimation

We estimated population parameters of the best African model and of the best three-population model. The number of simulations for parameter estimation was increased to 1,000,000. To validate the use of 1,000,000 simulations for parameter estimation we calculated the mean square error (MSE) of model parameters for varying numbers of simulations, ranging from 100,000 to 1,000,000 simulations (Table S3). Additionally, we also plot the mode and the 95% confidence intervals for varying numbers of simulations (Figure S5). We show that the MSE of each estimate and the estimated mode stay both relatively constant (Table S3 and Figure S5). Therefore, 1,000,000 simulations are enough for parameter estimation. Estimation was based on ABC rejection (Tavaré et al. 1997; Pritchard et al. 1999) and regression (Beaumont et al. 2002) methods. Both methods were performed using Wegmann’s ABCtoolbox (Wegmann et al. 2009) and checked with Csilléry’s abcR (Csilléry et al. 2012). First, we pooled all statistics and checked for correlations with the parameters. We did not keep statistics that did not correlate with any parameter, because keeping them does not provide information for the estimation and would only add noise to the final estimates. All these statistics were transformed using partial least squares (p.l.s.) as implemented in Wegmann et al. (2009). This transformation is advantageous because it extracts a small number of orthogonal components from a highly dimensional array of summary statistics. The new set of transformed statistics (with reduced dimensionality) reduces the noise produced by uninformative summary statistics. Moreover, the p.l.s.-transformed statistics are completely uncorrelated with one another ensuring the assumption of singularity, which is required for estimating parameters according to the regression method (Beaumont et al. 2002).

Predictive simulations

To check for the quality of our parameter estimates we took two approaches: (1) we sampled parameter values from the posterior distributions (based on the regression method) of each parameter estimate and resimulated data sets, and (2) we plotted the distributions of summary statistics directly from the set of the 5000 simulations closest to the observed data (which represents a sample of the joint posterior distribution based on the rejection method). The resulting distributions of summary statistics were compared to the observed ones for both approaches and plots were generated (see Results). Both approaches were performed only under the best model, since this is a test to see how well the best model fits the observed data. The same predicitive simulations were also performed for autosomal data (50 intergenic and intronic loci from chromosome 3R) to check how good our best model can predict autosomal summary statistics. For the sake of computational simplicity we assumed a relative effective population size (N_e) ratio of 0.75 for X-linked vs. autosomal loci in our simulations. This assumes a 1:1 male/female ratio in all populations even though we have evidence that actual sex ratios might deviate from these expectations (Hutter et al. 2007). However, we expect that this simplification should have only minor effects on our ability to predict the autosomal data since even in extreme cases of sex bias the X/A ratio of N_e can never drop below 0.5625 or exceed 1.125 (Hedrick 2011, Chap. 4).

Prediction of the site-frequency spectrum of Zimbabwe

Our available sequence data not only allow us to summarize genetic diversity with S_n, Θ_W, or Π_n, but also allow us to compute the observed SFS of the African population (Figure 2) and compare it to predictions under a given demographic model. Analytical methods for predicting the SFS of one population for arbitrary deterministic changes in population size have been successfully developed (Griffiths and Tavaré 1998; Živković and Wiehe 2008; Živković and Stephan 2011) and are briefly revisited as follows. Let T_n, …, T₂ be the time periods during which the genealogy has n, …, 2 lineages, respectively. Furthermore, let λ(t) = N(t)/N denote the ratio of the population sizes at time t in the past and the present. The probability p_n,k(i) that a randomly chosen line of waiting time T_k, k = n, …, 2, has i descendants, i = 1, …, n − 1, during time T_n (Fu 1995; Griffiths and Tavaré 1998) is

$$p_{n,k}\left(i\right)=\left(\begin{array}{c}n-i-1\\ k-2\end{array}\right)/\left(\begin{array}{c}n-1\\ k-1\end{array}\right).$$ (1)

The mean waiting times are given by

$$E\left(T_k\right)={\displaystyle \sum _{j=k}^n{\left(-1\right)}^{j+k}{\alpha }_{n,j,k}{\displaystyle {\int }_0^{\mathrm{\infty }}\exp \left\{-\left(\begin{array}{c}j\\ 2\end{array}\right){\displaystyle {\int }_0^t\frac{1}{\lambda \left(u\right)}du}\right\}dt}},$$ (2)

where

$${\alpha }_{n,j,k}=\frac{\left(2j-1\right)n!\left(n-1\right)!\left(k+j-2\right)!}{\left(j-k\right)!k!\left(k-1\right)!\left(n-j\right)!\left(n+j-1\right)!}.$$

The integral in (2) can be solved explicitly for models that consist of multiple instantaneous changes in population size and be evaluated numerically for models that include phases of exponential growth. Let L_i be the total length of branches leading to i descendants, where i represents singletons, doubletons, etc. Then,

$$E\left(L_i\right)={\displaystyle \sum _{k=2}^{n-i+1}k{p}_{n,k}\left(i\right)E\left(T_k\right)}.$$ (3)

Assuming an infinitely many sites mutation model (Kimura 1969), the expected unfolded site frequency ξ_i for each class i is given by

$$E\left({\xi }_i\right)=\frac{E\left(L_i\right)}{{\displaystyle {\sum }_{k=2}^{n}k\hspace{0.17em}E\left(T_k\right)}}.$$ (4)

We use the ABC parameter estimates obtained for Zimbabwe as an input to the equations shown above, calculate the SFS based on Equation 4, and compare it to the observed SFS.

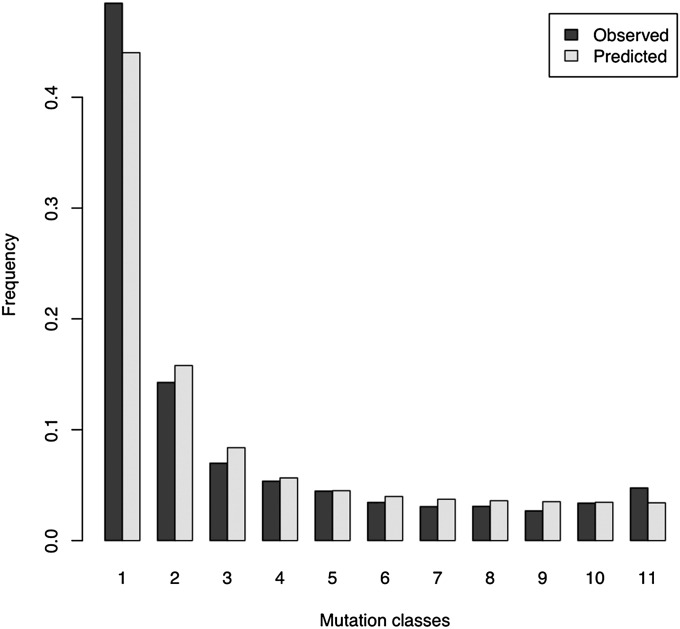
Figure 2 .

Observed (solid) and predicted (shaded) site-frequency spectrum of the African population. To calculate the frequency classes Equation 4 was used.

Results

Observed data

A first examination of the observed summary statistics (Table 1) shows that Africa is the most diverse population (based on the number of segregating sites), followed by North America and Europe. Watterson’s Θ_W and Π_n follow the same pattern. Tajima’s D is most negative in North America (−0.77), followed by Africa (−0.67) and Europe (−0.09). Linkage disequilibrium (Z_nS) is highest in Europe (0.43) compared to North America (0.21) and Africa (0.15). Population differentiation (Table 2) is highest between Africa and North America (distance of Nei = 1.12), followed by Africa–Europe (0.78) and North America–Europe (0.59). All these comparisons are based on the observed data set that included singletons in North America. The resulting statistics of North America after excluding singletons can also be found in Table 1.

The SFS of the African population is shown in Figure 2. Regarding the JSFS (Table 2) we observe an excess of private polymorphisms in Africa when compared to private polymorphisms in Europe (2278 vs. 363) and North America (1961 vs. 743) (W1 vs. W2). We must keep in mind that singletons were excluded from the North American population, and these singletons are mostly private to North America. The opposite pattern is seen when comparing private polymorphisms in Europe to private polymorphisms in North America (214 vs. 924). Shared polymorphism (W4) has its lowest value between Africa and Europe (647) when compared to Africa–North America (990) and Europe–North America (809). The number of fixed differences between populations is small in all pairwise comparisons (W3).

African demography

Model choice results show that a population bottleneck in Africa (P = 0.987) fits the observed data better than an expansion (P = 0.013). We used the following statistics for parameter estimation of the best model: mean and variance of S_n, mean and variance of Tajima’s D, and mean Z_nS. We estimated these parameters (Table 3) using the priors listed in Table 4. After the reduction of dimensionality using partial least squares (see Materials and Methods) we kept three components from the original five statistics used. The estimated ancestral and current N_e are 4.9 million and 5.2 million individuals, respectively. The bottleneck severity (Log₁₀ scale) was estimated as 0.21, which corresponds to ∼620 individuals for a fixed bottleneck duration of 1000 generations. The estimated time of the bottleneck is ∼200,000 years ago, assuming 10 generations per year (Table 4 and Figure S6). Predicted distributions of summary statistics for the bottleneck and the expansion models overlap significantly. However, observed Tajima’s D as well as the mean and the variance of S_n are reproduced more often by the bottleneck model than by the expansion model (Figure S7). Estimations of the African parameters were also performed using the classes of the folded SFS of Zimbabwe but the results do not vary significantly (data not shown).

Table 3 . Parameters used in models A, B, C, D, and E.

Abbreviation of parameter	Explanation
NAa	Ancient population size of Africa
sevA	Severity of the bottleneck in Africa
TA	Time of the bottleneck in Africa
NAc	Current population size of Africa
TAE	Time of split between Africa and Europe
TAN	Time of split between Africa and North America
NEa	Starting population size of Europe
NEc	Current population size of Europe
TEN	Time of split between Europe and North America
NNa	Starting population size of North America
NNc	Current population size of North America
M	Migration rate between all populations
Tadm	Time of admixture between Africa and Europe
Propadm	Proportion of European admixture in North America

Table 4 . Parameter estimates of the African population.

Parameter	Prior	Mode	95% quantiles
NAc	unif(1 × 105, 1 × 107)	4,975,360 individuals	(2.40 × 106, 9.13 × 106)
TA (in years)	unif(1 × 102, 4 × 105)	237,227 years ago	(0.82 × 105, 3.45 × 105)
NAa	unif(1 × 105, 1 × 107)	5,224,100 individuals	(1.98 × 106, 9.55 × 106)
sevA (Log10)	unif(−2,2)	0.21	(−0.15, 0.57)

Site-frequency spectrum

The SFS of the observed African data has an excess of high-frequency-derived variants (Figure 2, solid bars), while the predicted SFS under a bottleneck does not show such a large excess (Figure 2, shaded bars). Predicted values were calculated using the modes of the parameter estimates under the bottleneck scenario (Table 4) and applying Equation 4. Predicted values fit the observed SFS better than the expansion model of Li and Stephan (2006) for the intermediate-frequency classes, but not for the low-frequency variants. The largest relative discrepancies are found for both models for the high-frequency variants that make the SFS slightly U shaped.

North American demography

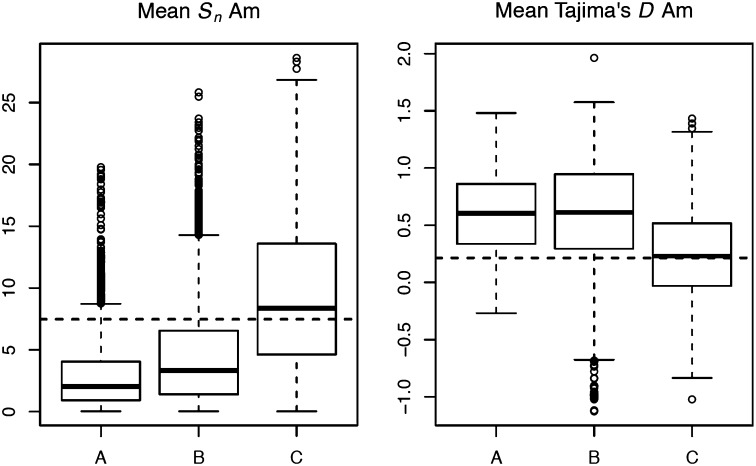
The model with the highest posterior probability is the admixture model C with P > 0.999. Model choice yields the same results when using summary statistics and also when using the JSFS (in both cases the posterior probability of model C is >0.999). Parameters of this model are explained in Table 3. Predictive simulations based on both the regression and rejection methods show that admixture is the only model that can explain the diversity observed in North America (Figure 3 and Figure S8). Admixture can also explain better the observed Tajima’s D in America (Figure 3). It is important to remember at this point that diversity in North America is higher than in Europe, although the colonization of North America has been much more recent than the one inferred for Europe. It is thus reasonable to believe that admixture is playing an important role in this case.

Figure 3 .

Predicted summary statistics under models A, B, and C for the North American population based on the rejection method. The horizontal dashed line represents the observed value.

Other parameters, such as diversity in Africa and Europe can be explained by both admixture and nonadmixture models (Figure S8 and Figure S9). The accuracy of the model choice procedure shows that the simulated model could be correctly identified in 90% of the cases. The cases in which model C is not preferred occur when one or a combination of the following events happen: (a) the time of split between African and European populations is very young (about 1000 to 2000 years ago), (b) the proportion of European ancestry in the North American population is very high (above 90%), and (c) the founding population of Europe is large (in the order of 100,000 individuals). The results of model choice performance when sampling from the posterior distributions of each parameter do not vary significantly with the ones we provide here (see Materials and Methods).

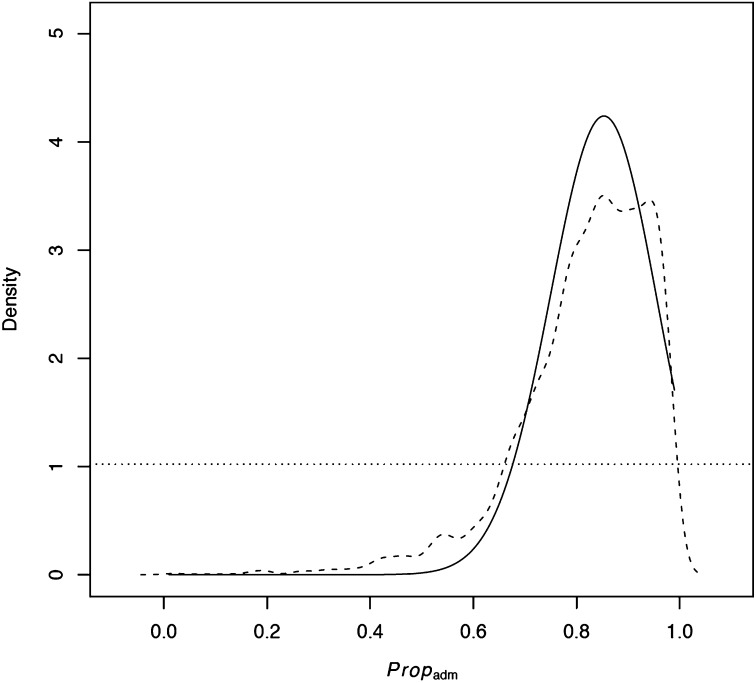
For estimating the parameters of model C, we used the following statistics: mean and variance of S_n in Africa, mean and variance of Tajima’s D in Africa, mean K in Africa, mean and variance of Tajima’s D in Europe, mean and variance of K in Europe, mean Z_nS in Europe, mean S_n in North America, mean and variance Tajima’s D in North America, mean and variance of K in North America, mean Z_nS in North America, mean distance of Nei Africa–Europe, mean distance of Nei Africa–North America, mean distance of Nei Europe–North America, W1 Africa–North America, W2 Africa–North America, W4 Africa–North America, W1 Africa–Europe, W2 Africa-Europe, and W2 Europe–North America. The above-mentioned statistics were chosen after pooling all statistics and checking for correlations between statistics and parameters (see Materials and Methods). After dimensionality reduction using partial least squares we kept six components. Parameter estimates (Table 5 and Figure S10) imply that African and European populations split around 19,000 years ago and Europe was founded with around 17,000 individuals. These estimates are in agreement with previous studies (Li and Stephan 2006; Laurent et al. 2011). The North American population was founded by ∼2500 individuals from which ∼85% are of European ancestry and the remaining of African ancestry (Figure 4). The current population sizes of Europe and North America cannot be estimated accurately.

Table 5 . Joint parameter estimates of the European and North American populations.

Parameter	Prior	Mode	95% quantiles
TAE (decimal log generations)	unif(4,7)	5.29 (∼19,000 years ago)	(4.69, 5.86)
Tadm (decimal log generations)	unif(2,4)	3.16	(2.08, 3.82)
NEc	unif(1x104,1 × 107)	3,122,470 individuals	(0.39 × 106, 9.55 × 106)
NEa (decimal log)	unif(2,5)	4.23 (∼17,000 individuals)	(3.58, 4.83)
NNc	unif(1x104,3 × 107)	15,984,500 individuals	(1.11 × 106, 28.8 × 106)
NNa (decimal log)	unif(2,5)	3.40 (∼2500 individuals)	(2.20, 4.79)
Propadm	unif(0.01,0.99)	0.85	(0.64, 0.97)

Figure 4 .

Probability density of the proportion of European admixture based on the regression method (solid line) and rejection method (dashed line). The horizontal dotted line represents the uniform prior distribution.

Predictive simulations of model C (Figure S11 and Figure S12) were generated by sampling parameters from the posterior distributions (based on the regression method). These parameters were used to simulate data sets and calculate summary statistics and JSFS statistics (see Materials and Methods). The resulting distributions show that all summary statistics can be well predicted by the admixture model (Figure S11 and Figure S12). The only statistics that are overestimated are the number of fixed differences (W3) between Africa and North America or Europe and North America and the distance of Nei between Europe and America. W3 and distance of Nei are related to each other, and an increase in one involves always an increase in the other. An improvement of the model in this aspect is discussed below (see Discussion). Model C was also able to predict autosomal summary statistics quite accurately (Figure S13 and Figure S14) even under the simplified assumption of equal sex ratios in all populations (see Material and Methods).

Discussion

The demography of the Zimbabwe population was modeled in several studies as a simple expansion process (Glinka et al. 2003; Ometto et al. 2005; Laurent et al. 2011). However, it is still unclear if the Zimbabwe population is the source from which all other D. melanogaster populations derive. Based on this scenario we may expect that a bottleneck model would fit the data of the Zimbabwe population better than expansion, since range expansions are usually associated with bottlenecks and founder effects (Excoffier et al. 2009). Indeed, what we find here is exactly that pattern: the bottleneck model is significantly preferred over the expansion model.

The predictive simulations of models A, B, and C show that all models are able to explain the diversity observed in Africa and Europe (Figure S8 and Figure S9). However, only model C (including admixture) is able to fully explain the diversity observed in North America. Model A involves a recent foundation of North America from Europe, but North America shows currently greater diversity. This is hard to explain without considering an input from the ancestral population. Model B provides this input from Africa through migration, but to be able to reach the levels of diversity observed in North America we would need unrealistically high rates of migration. However, this would not be compatible with the observed values of population differentiation. Model C is in accordance with the observed data in this aspect. Another aspect that favors the admixture model over the others is that the values of Tajima’s D in North America and Europe can also be better explained. We do not have an intuitive explanation why a recent admixture event has an influence on Tajima’s D in one of the parental populations (i.e., the European one).

Among all tested models (Table S2), we selected models A, B, and C for two main reasons. First, there is evidence that North American D. melanogaster has been introduced from Europe (see Introduction) and we have strong biological reasons to believe that North American diversity was generated through admixture and/or migration with African populations. Second, we wanted to keep the models as simple as possible. When we examined the data we observed that the North American population shares polymorphisms mostly with the European population and, to a lesser extent, with the African population. This observation fits the hypothesis of a European contribution. A model in which North America is derived from the African population without any European contribution would not be able to explain the shared polymorphism between North America and Europe in the observed data.

In addition to the three main demographic models (i.e., models A, B, and C), we examined two more models in which the North American population derives directly from the African one. This alternative topology of the population’s genealogy was tested without migration (model D, Table S2) and considering a simple migration process, identical to the one used in model B (model E, Table S2). These models represent possible alternative explanations for the high diversity harbored by the North American population. However, when compared to model C, models D and E are less supported by the data set as indicated by their associated posterior probabilities (>0.999, <0.001, and <0.001, respectively).

We note here that our modeling of the dispersal patterns between worldwide populations of D. melanogaster is a crude simplification of the real, but unknown migratory processes characterizing this species. It is well possible that more complex demographic models allowing specific, and potentially asymmetric, migration rates between all pairs of populations might be a more accurate representation of reality. However, in our case, these more sophisticated models have the property of having divergence time and specific migration rates as free parameters for several pairs of populations. A recent simulation study showed that the joint estimation of these two parameters in an ABC framework does not yield satisfying results (Tellier et al. 2011). Indeed, it is not clear at the present time which summarization of the raw data set would allow for an accurate joint estimation of divergence times and migration rates within an ABC framework. Although more work is needed to develop methods that allow for the estimation of more complex models, the analysis presented in this study shows that the history of the North American population is well characterized by an admixture of alleles coming from European and African populations.

The admixture model C can predict most of the observed summary statistics and JSFS equally well or better than the other models, except for the observed population differentiation (distance of Nei) between Africa and North America, which is better explained by model A or B (Figure S8). This higher simulated population differentiation in model A or B is associated with lower values of diversity in North America than the observed one, which is still a drawback for these models. We investigated this fact by adding more parameters to the model. We tested three variations of model C: model C1 has an extra bottleneck during the colonization of North America from Africa, model C2 has an extra bottleneck during the colonization of North America from Europe, and model C3 has both bottlenecks (Figure S15). While including the additional bottlenecks can account for the observed population differentiation they also reduce diversity below the observed values. Therefore, when compared to the original admixture model, models C1, C2, and C3 were not favored.

Another possible model in which higher values of population differentiation could be expected is a scenario in which samples are considered to be taken from demes in a metapopulation. If we have samples from different demes from different populations we may not expect migration or admixture to take place equally between all sampled demes, which may lead to higher values of population differentiation. Even though population differentiation in African populations is minimal (Yukilevich et al. 2010) this hypothesis still needs to be investigated further, with additional analyses of populations from Africa, Europe or North America, which is beyond the scope of this study.

To obtain further insight into the demography of the Zimbabwe population, we compared the SFS of this population with that predicted under a bottleneck. Regarding the input parameters for this prediction we used the modes (as point estimates) of the posterior distributions that were generated by the ABC regression step (see Table 4). Figure 2 shows the observed SFS compared to the predicted SFS under the conditions described above. Li and Stephan (2006) fitted a population expansion model to this same observed SFS (Figure 3 of Li and Stephan 2006). The bottleneck model in our study fits the intermediate-frequency classes better, whereas the population expansion model is more compatible with the classes of the singletons and doubletons. However, for the high-frequency variants both models show relatively large discrepancies. According to Li and Stephan (2006), this may indicate evidence for positive selection, a hypothesis that needs to be further tested. An alternative explanation for the excess of high-frequency variants may be ancestral state misidentification (Hernandez et al. 2007). Note that ancestral misidentification does not change our main ABC results, since the summary statistics used (including the folded SFS) are unaffected by polarization.

Although our modeling approach takes into account the combined effects of mutation, genetic drift, and migration we point out that we did not consider any form of natural selection in this analysis. This omission does not reflect that we believe that the impact of selection is minimal in our data set but rather the lack of available methods to estimate demographic and selective forces simultaneously. We think that such methods would greatly improve the interpretation of data sets like the one we present here, since several studies recently reported evidence that, contrary to previous beliefs, negative and positive selection have a substantial impact on the genetic variation harbored by natural populations of D. melanogaster (Macpherson et al. 2007; Jensen et al. 2008). Until such methods are available it is hard to predict to what extent the results presented in this study are affected by a reduction of the evolutionary history of D. melanogaster to a strictly neutral nonequilibrium model.

Nonetheless, we stress that the main result of this study, which is the identification of a substantial contribution of the African gene pool to the North American population, cannot be invalidated by including selection in our analysis. The reason for this is that the above-mentioned result relies on the observation that the level of genetic diversity found in the North American population is too high compared to expectations under a model in which the North American population would derive exclusively from the European one.

In conclusion, this study generated the first joint demographic analysis of African, European and North American populations of D. melanogaster. We analyzed the African population and found that a bottleneck fits the observed data better than an instantaneous population expansion. Regarding the North American population, we found that an admixture model fits the observed data significantly better than models involving colonization only from Europe or migration. We estimated the population parameters of all populations, from which we highlight the time of split between Africa and Europe (∼19,000 years ago) and the proportion of European and African ancestry in the North American population (85% and 15%, respectively). The time of colonization of North America was given a very small prior because we know it took place ∼200 years ago. In general, having described such a demographic model for North America, Africa, and Europe will be of valuable importance when looking for signatures of adaptation in any of these populations.