Tuning ion correlations at an electrified soft interface

Abstract

Ion distributions play a central role in various settings—from biology, where they mediate the electrostatic interactions between charged biomolecules in solution, to energy storage devices, where they influence the charging properties of supercapacitors. These distributions are determined by interactions dictated by the chemical properties of the ions and their environment as well as the long-range nature of the electrostatic force. Recent theoretical and computational studies have explored the role of correlations between ions, which have been suggested to underlie a number of counterintuitive results, such as like-charge attraction. However, the interdependency between ion correlations and other interactions that ions experience in solution complicates the connection between physical models of ion correlations and the experimental investigation of ion distributions. We exploit the properties of the liquid/liquid interface to vary the coupling strength of ion–ion correlations from weak to strong while monitoring their influence on ion distributions at the nanometer scale with X-ray reflectivity and the macroscopic scale with interfacial tension measurements. These data are in agreement with the predictions of a parameter-free density functional theory that includes ion–ion correlations and ion–solvent interactions over the entire range of experimentally tunable correlation coupling strengths (from 0.8 to 3.7). This study provides evidence for a sharply defined electrical double layer for large coupling strengths in contrast to the diffuse distributions predicted by mean field theory, thereby confirming a common prediction of many ion correlation models. The reported findings represent a significant advance in elucidating the nature and role of ion correlations in charged soft matter.

The works by Gouy (1) and Chapman (2) introduced the Poisson–Boltzmann (PB) equation to describe the distribution of ions and the accompanying variation of electric potential at the interface between a charged planar electrode and an electrolyte solution (1, 2). This seminal theory considered point-like ions interacting through their mean electric field in a continuum solvent but neglected both chemically specific ion–solvent interactions and correlations between ions. Specific ion interactions are exemplified by the well-known Hofmeister series (3). The study of ion correlations has been motivated by observations of the reentrant condensation of DNA (4) and proteins (5) in solution, in which like-charged biomolecules aggregate in the presence of multivalent ions, and reports of charge reversal in colloidal suspensions, in which the sign of the screened charge on a colloid can be changed by varying the surrounding electrolyte solution (6, 7).

Correlations between ions that are caused by their electrostatic interactions are expected to be important when the average electrostatic interaction energy between neighboring ions is larger than the thermal energy 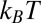. This result is characterized by a coupling strength

where d is the average separation between ions, and 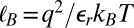is the Bjerrum length at which the electrostatic energy between two ions of charge q in a medium of relative permittivity 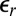is equal to 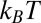(8). Ion–ion correlations are relevant when 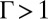, whereas the mean field PB theory should hold in the opposite limit.

Despite the broad interest in this subject, little is known about the role of ion–ion correlations in the structure of the electrical double layer from direct measurements. Here, we report a quantitative experimental test of the effect of ion–ion correlations on the ion density profile 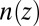at the electrified liquid/liquid interface. Application of an electric potential difference across a liquid/liquid interface is used to vary the interfacial ion density, thereby changing the average ion–ion separation d and tuning the correlation coupling strength 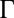at the interface (Eq. 1). The accessible range of 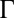, from 0.8 to 3.7, represents ion–ion correlations that vary from weak to strong. The effect of correlations on the ion density profile 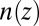is quantified by X-ray reflectivity, which is sensitive to the density distribution on the subnanometer scale, in the direction normal to the interface. In addition, interfacial tension measurements are used to characterize the variation of the total interfacial excess charge density with the electric potential difference. The combination of X-ray and interfacial tension measurements probes the ion density profile on length scales that span the molecular to thermodynamic domains, and therefore, it places stringent constraints on the theoretical model. These measurements are quantitatively consistent with the predictions of a weighted density functional theory that includes ion–ion correlations and specific ion–solvent interactions.

Results

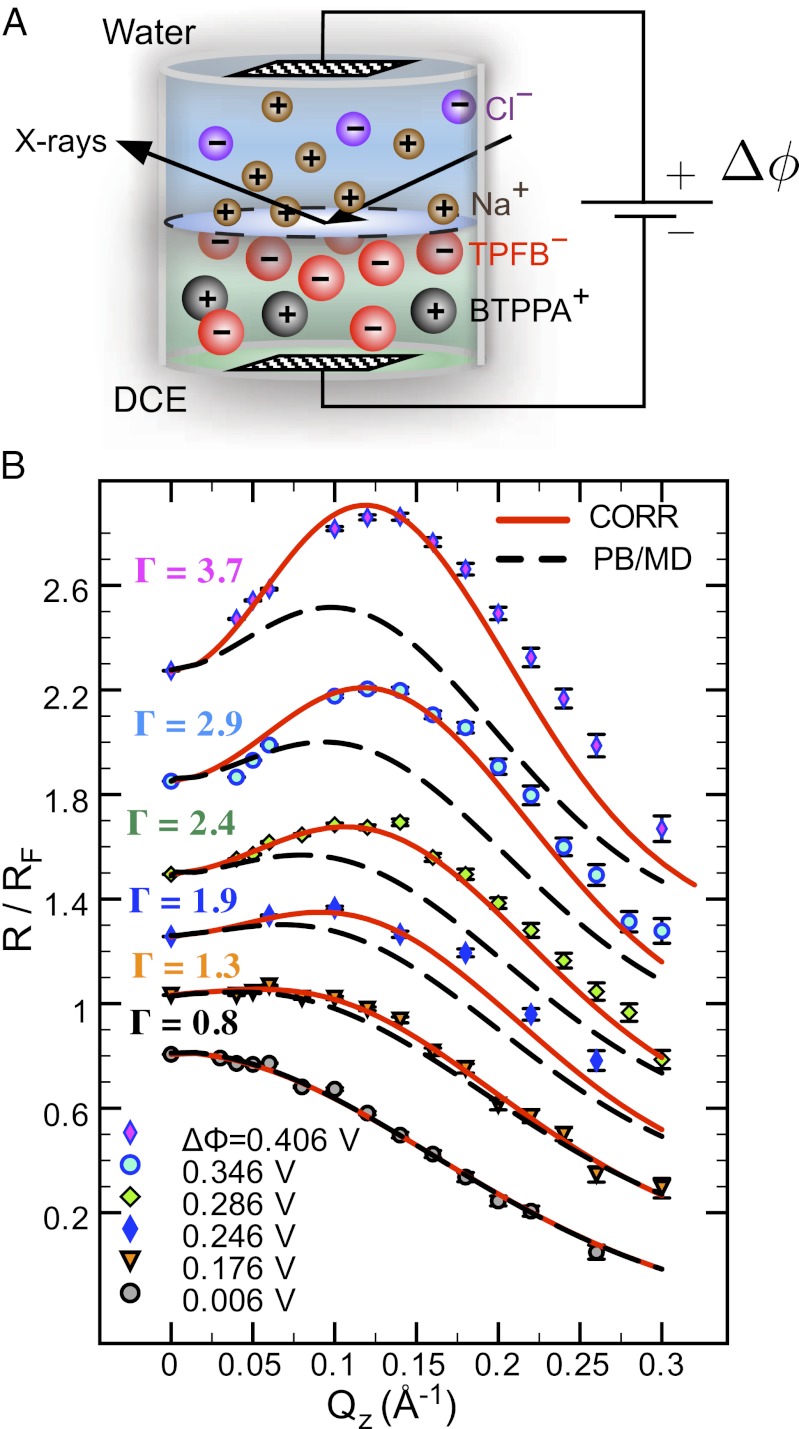
Our experimental system consists of the liquid/liquid interface between two immiscible electrolyte solutions: a 10 mM NaCl aqueous solution and a 5 mM bis(triphenylphosphoranylidene) ammonium tetrakis(pentafluorophenyl)borate (BTPPA-TPFB) solution in 1,2-dichloroethane (DCE). The organic ion of importance in this study, TPFB⁻, is nearly spherical with a van der Waals diameter 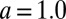nm. An electric potential difference 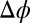is applied between the bulk phases with a four-electrode potentiostat by inserting electrodes into the bulk liquids (Fig. 1A) (9, 10). If 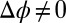, two back-to-back electrical double layers are formed at the liquid/liquid interface. As illustrated in Fig. 1A, when 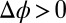, the density of TPFB⁻ is enhanced (and BTPPA⁺ is depleted) near the interface in the DCE, and the density of Na⁺ is enhanced (and Cl⁻ is depleted) near the interface in water.

Fig. 1.

(A) Illustration of the electrified aqueous electrolyte/organic electrolyte interface for 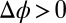, with ions represented by spheres. Arrows represent incident and reflected X-rays. The two grids represent the working electrodes that are ∼1 cm from the liquid/liquid interface; reference electrodes are not shown (10). Electrical double layers (not illustrated) are also formed on the working electrodes. (B) X-ray reflectivity R normalized to the Fresnel reflectivity 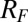from the electrified water (10 mM NaCl)/DCE (5 mM BTPPATPFB) liquid/liquid interface as a function of wave vector transfer 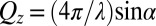(wavelength 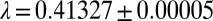Å; angle of incidence α) for different electric potential differences 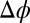(increasing from bottom to top) and TPFB⁻ interfacial ion–ion correlation coupling strengths 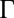. Data are offset for clarity (without the offset, 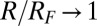as 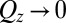). Data at 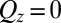are measurements of the beam transmitted, without reflection through the upper phase. Lines illustrate the reflectivity predicted from a model with (solid lines, CORR) and without (dashed lines, PB/MD) ion correlations.

The variation of ion concentration along the interfacial normal z produces a gradient in the electron density profile 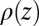(averaged over the 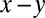plane of the interface) that is probed by synchrotron X-ray reflectivity measurements. Fig. 1B illustrates the reflectivity 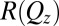normalized to the Fresnel reflectivity, 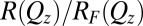, as a function of wave vector transfer 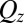normal to the interface. The increase in peak amplitude with 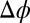corresponds to an increase in density of an interfacial layer of TPFB⁻ ions. These ions provide the largest contribution to the electron density gradient.

The conventional method of fitting X-ray reflectivity data involves postulating a parameterized model for the electron density and then fitting the parameters to the data (11). Instead, we take the approach of comparing the measured reflectivity directly with values calculated from a theory for the ion distribution. This theory predicts the ion number density profiles 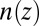, which are then used to calculate electron density profiles 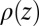(12, 13). X-ray reflectivity is determined from 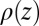by use of the Parratt algorithm (14). The predicted X-ray reflectivity curves are then compared with the data in Fig. 1B.

Ion Distribution Theory.

Earlier X-ray reflectivity studies showed that ion distributions at the liquid/liquid interface can be modeled accurately by a PB equation that has been modified to include ion–solvent interactions when ion–ion correlations are negligible (12, 13). Excellent agreement was obtained between experiment and theory, without adjustable parameters, when ion–solvent interactions near the interface were modeled by a molecular dynamics simulation of the potential of mean force of a single ion in the vicinity of the interface between pure solvents (12, 13). Here, we will show that ion–ion correlations, in addition to ion–solvent interactions, are required to explain the data in Fig. 1B.

Although ion–ion correlations are usually considered to be irrelevant for monovalent ions in aqueous solution, the lower relative permittivity of the organic DCE (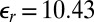) generates a large coupling strength 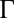. Analysis of the X-ray reflectivity data indicates that the average distance d between neighboring TPFB⁻ ions at the interface is 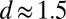nm for the highest 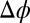( 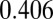V). This value of d and the small 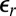of DCE lead to 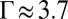for TPFB⁻ ions, which suggests that ion correlations are important. As expected, the much higher relative permittivity of water, 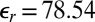, leads to weak correlations (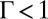) for Na⁺ ions on the aqueous side of the interface, even at the highest 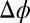. In addition, 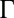is small and correlations are negligible for ions far from the interface, because the bulk concentrations are low.

Ion density profiles are predicted from the free energy functional per unit area

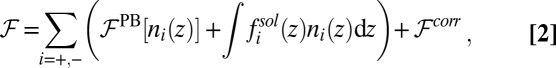where 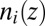is the number density profile of ion i, and the z axis is normal to the interface. The first term, 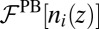, is the standard PB free energy composed of the ideal gas entropy of the ions and the potential energy caused by the electrostatic potential 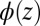that satisfies Poisson’s equation,

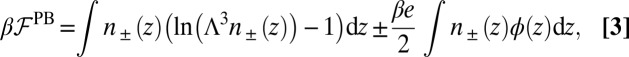where 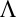is the thermal wavelength, and 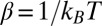. This term by itself leads to the Gouy–Chapman mean field theory that neglects ion and solvent correlations (1, 2), effects that are also ignored in various mean field (PB) approaches developed to describe the spontaneous segregation of ions at liquid/liquid interfaces (15–17). The ion–solvent potentials of mean force 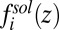in Eq. 2 describe the interactions of each ionic species with the solvent (18), and they are calculated within the atomistic classical molecular dynamics (MD) simulation described below. The last term, 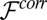, is the free energy contribution from ion–ion correlations that will also be discussed below. The model in Eq. 2 describes a system of interacting ions in an electric field 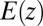that also interacts independently with the solvent.

The number density profile 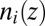is found by minimizing 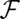, subject to the constraint of charge neutrality within each bulk liquid phase, to yield

where 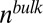is the bulk electrolyte concentration, e is the fundamental charge, and 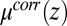is the excess chemical potential caused by ion–ion correlations. The density profiles and the electrostatic potential distribution 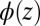are related through Poisson’s equation

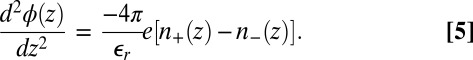If 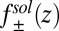and 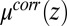are known, the ion density profiles at the liquid/liquid interface are predicted from Eqs. 4 and 5 for both liquid phases, with the interface located at 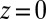. Over the experimental range of 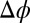, the ions remain in their original phases; therefore, for 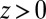, + and − (Eq. 4) refer, respectively, to Na⁺ and Cl⁻ in water, whereas for 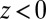, + and − refer to BTPPA⁺ and TPFB⁻ in DCE. A numerical solution of 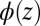across the interface is found subject to the following conditions: (i) the potential difference 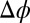(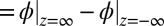) between the bulk liquids on either side of the liquid/liquid interface, which is determined from the applied voltage as described in Materials and Methods; (ii) the constraint of bulk electroneutrality (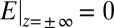); and (iii) electrostatic boundary conditions (10). Note that 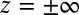refers to the bulk liquids that are far from the liquid/liquid and liquid/electrode interfaces.

Ion–Solvent Interactions.

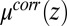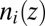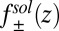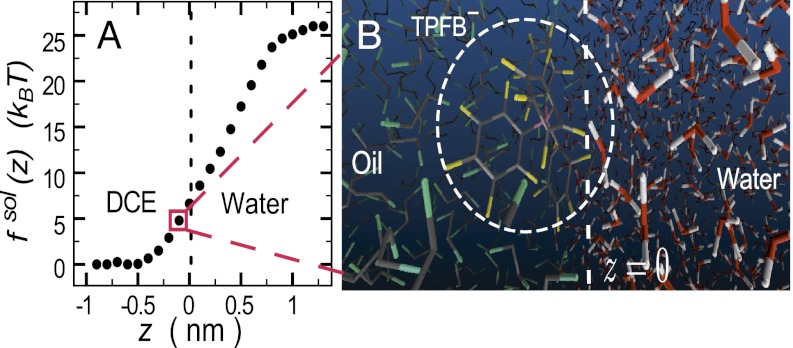
We discuss first the model for which ion correlations are ignored [denoted as the PB/MD model, for which in Eq. 4 is set to zero]. In this case, the ion density profiles can be predicted from the ion–solvent potentials of mean force for each of the four types of ions. The 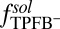shown in Fig. 2A is determined by an MD simulation of the potential of mean force of a single TPFB⁻ ion at the DCE/water interface (Materials and Methods). The rise in 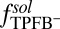near 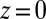indicates unfavorable interactions of TPFB⁻ with water. The difference between the values in the two bulk phases, 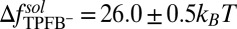, is comparable with the experimental value of the free energy of transferring TPFB⁻ from bulk DCE to bulk water, namely 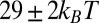(19). Similarly, the 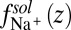for Na⁺ is given by a previously published potential of mean force (19). The very small interfacial densities of the Cl^– and BTPPA+ ions that are depleted from the interface for 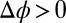justify a mean field (PB) description, for which .

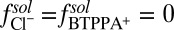Fig. 2.

(A) Ion–solvent potential of mean force 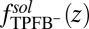of one TPFB⁻ ion at the water/1,2-dichloroethane interface. Each point is calculated by an MD simulation. (B) Snapshot from the MD simulation for the interfacial depth z of the TPFB⁻ ion (circled) shown in A.

As described earlier, the ion density profile 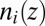(from the PB/MD model) is converted to a prediction for the X-ray reflectivity and compared with the data in Fig. 1B. However, comparison of the X-ray reflectivity data with the prediction from the PB/MD model also requires consideration of the thermal capillary wave roughness of the interface (20). The roughness reduces the measured X-ray reflectivity by scattering X-rays out of the angular range accepted by the X-ray detector (11). Interfacial roughness is included in our model by convoluting the predicted electron density profile with a Gaussian function whose width is the interfacial roughness (11). This roughness is the only fitting parameter used to compare the theoretical density profiles to the reflectivity data in Fig. 1B. The fitted values of roughness (4.2 → 4.9 Å) for all fits of the PB/MD model are within 2 SDs (i.e., within Å) of the values calculated from capillary wave theory using our interfacial tension measurements (10, 21) (Table S1).

The best fits of the PB/MD model shown by the dashed lines in Fig. 1B do not match the data except at the lowest , where 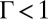and ion–ion correlations are expected to be weak. The amplitudes of the predicted reflectivity peaks are too small, indicating that the predicted interfacial density of ions is too small. Previous theoretical discussions of ion correlation models show that local ion densities can be increased by correlations (8), and we now consider the effect of the correlation free energy 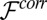in our analysis.

Ion–Ion Correlations.

Different models are available to describe the free energy 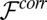that determines correlations in the positions of TPFB⁻ ions (8, 22–30). The particular model that we chose, the Debye–Hückel–Hole (DHH) model of the one-component plasma in a weighted-density approximation, provides an expression for the excess chemical potential caused by ion–ion correlations that can be simply combined (Eq. 4) with an ion–solvent potential to account for both effects. Because our experiments indicate that 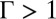for only TPFB⁻ ions, we consider correlations for only this ion. Calculation of the correlations starts with the DHH theory of the homogeneous one-component plasma (31). This model follows from the postulate of a correlation hole around an ion that accounts for mutual electrostatic repulsions with other TPFB⁻ ions. In the limit of weak correlations, 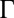<< 1, thermal fluctuations dominate over electrostatic repulsions, and the size of the correlation hole is comparable with the Bjerrum length 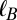. However, in the opposite limit 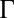>> 1, the correlation hole size is proportional to 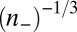, where 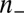is the homogeneous density of the plasma (of TPFB⁻ ions). It has been shown that the homogeneous free energy per ion 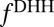in the DHH theory is given by (22),

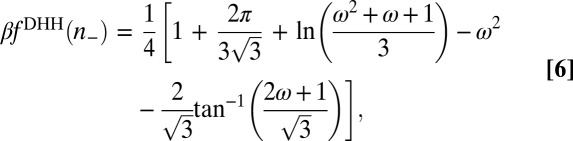where 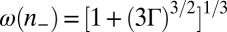. In the limit of strong ion–ion correlations, Eq. 6 converges to the electrostatic energy, 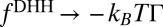, as expected.

The equivalent of Eq. 6 for an inhomogeneous system of ions, such as an interfacial ion distribution with density that varies with depth, is found in the weighted density approximation (23, 32, 33) by the replacement 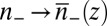in Eq. 6, where 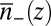is a coarse-grained density. The fact that 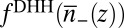is now a function of a nonlocal density can be interpreted as the consequence of introducing a correlation hole, which induces a nonlocal character to the ion correlations. The weighted density is found by averaging over the local density 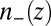in the region of the correlation hole (34),

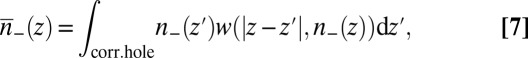where the weight function w (equation 29 in ref. 34) depends on the local density (23, 35). The correlation free energy functional 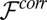in Eq. 2 is then given by

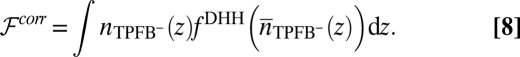The excess chemical potential 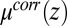caused by TPFB⁻ ion–ion interactions (Eq. 4) is found by taking the functional derivative of the correlation free energy with respect to the local density

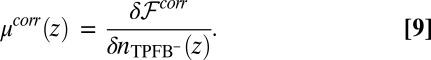The TPFB⁻ density profile is now determined by Eq. 4 with 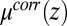given above, whereas the profiles of the other ions are also determined by Eq. 4 but with 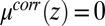. Correlations in the TPFB⁻ ion positions depend on the density 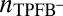, which is expressed by Eq. 9; hence, the equilibrium density profiles and the dependence of 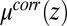on z must be determined from a self-consistent numerical solution of Eqs. 4–9. This procedure defines the Correlation (CORR) model. A standard iteration algorithm used here is included in SI Text.

Analysis of X-ray reflectivity data using the CORR model involves one-parameter fits of the interfacial roughness, which was previously explained for the PB/MD model. Note that there are no other adjustable parameters within the CORR model. These fits show good agreement over the full range of electric potentials (Fig. 1B) that correspond to coupling strengths up to 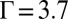. Similar to the PB/MD model, the roughness values are within 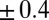Å of the predictions of capillary wave theory (Table S1). The improved fitting of the X-ray reflectivity by the CORR model is entirely caused by introducing electrostatic correlations between TPFB⁻ ions through 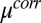, and it represents the only difference between the two models. The reflectivity curves predicted by the CORR model are progressively higher than those curves from the PB/MD model as the coupling strength 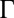increases, indicating that enhanced ion–ion correlations increase the ion density at the interface.

Interfacial Excess Charge.

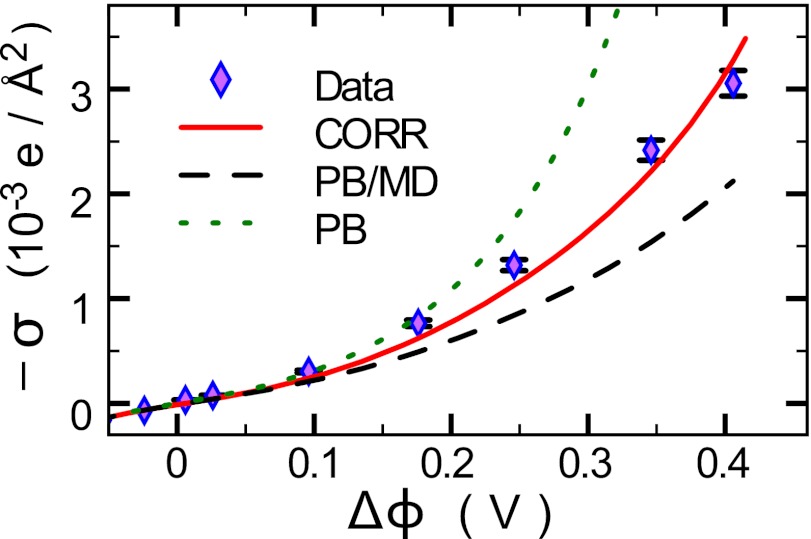
In contrast to X-ray reflectivity data, which probe the nanoscale spatial variation of the density, macroscopic measurements of capacitance or interfacial excess charge σ probe the integral of the ion density profiles, where 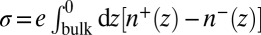. Fig. 3 illustrates 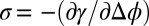, which is a result of measurements of interfacial tension γ over a range of 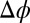(Fig. S1). Excellent agreement between the interfacial excess charge predicted by the CORR model and the data is found without adjustable parameters. Fig. 3 shows that ion–ion correlations as well as ion–solvent interactions are required to explain the variation of the interfacial excess charge with potential.

Fig. 3.

Interfacial excess charge σ of ions accumulating at the interface in response to the electric potential difference 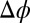. Lines represent predictions of the PB (electrostatics and ion entropy), PB/MD (including ion–solvent interactions), and CORR (adding correlations) models.

Discussion

The predictions of the density functional model in Eq. 2 of the electrical double layer have been shown to be consistent with X-ray reflectivity measurements that probe the interfacial electron density profile and interfacial tension measurements that probe the integrated interfacial excess charge density. The PB (or Gouy–Chapman) model, which consists of only the first term in Eq. 2, overestimates the X-ray reflectivity by a factor of five or more for 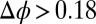V, because it produces unrealistically large ion densities at the interface (Fig. 4D) (19). Adding the second term, which describes ion–solvent interactions, leads to the PB/MD model. Use of all terms in Eq. 2, including the third term, which describes correlations, is referred to as the CORR model. If ion–solvent interactions were ignored and only ion–ion correlations were added to the PB model, the predictions for the reflectivity and excess charge density would deviate from the data by an even greater amount than predicted by the PB model.

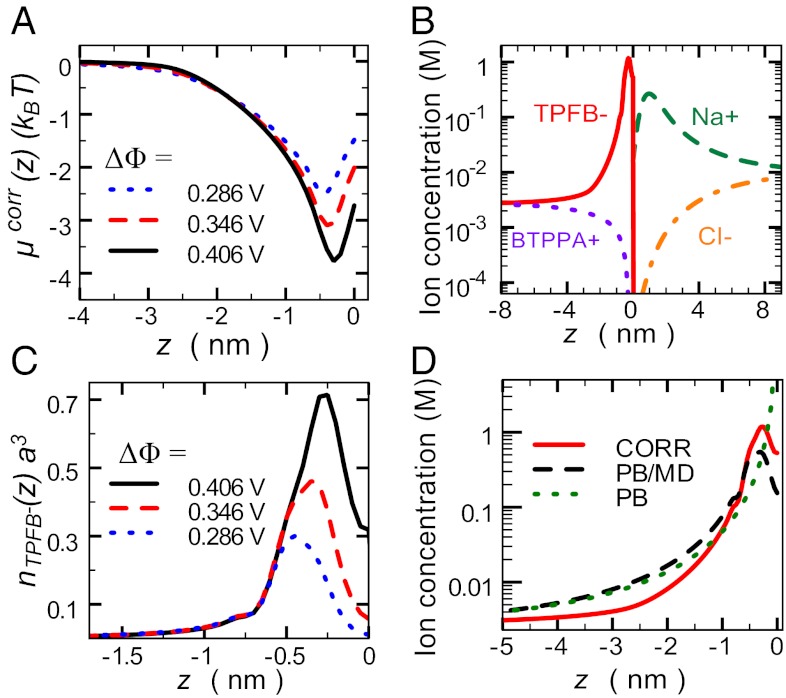
Fig. 4.

CORR model calculations. (A) Excess chemical potential 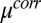for TPFB⁻ for three values of 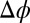. (B) Ion distributions at the water (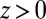)/DCE (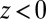) interface illustrate back-to-back electrical double layers at 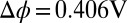in units of molarity. (C) TPFB⁻ number density profile 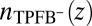times the volume 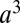, where 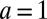nm is the ion diameter, for three values of 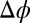. (D) Comparison of the PB (Gouy–Chapman), PB/MD (PB plus ion–solvent interactions), and CORR (PB/MD plus ion–ion correlations) models for the TPFB⁻ ion concentration (in molarity units) near the interface at .

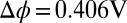Ion–Solvent Interactions.

The PB/MD model predicts that the density profile of Na⁺ and TPFB⁻ ions, which mostly increases on approach to the interface, falls slightly just before reaching the interface at 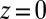(Fig. 4 B and D, where the Na⁺ distribution in Fig. 4B is qualitatively similar to the distribution for the PB/MD model). This effect is the result of ion repulsion from the interface as indicated by the monotonic rise of the potential of mean force (illustrated for 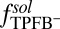in Fig. 2A). In the case of Na⁺, a strongly hydrated ion, this energy barrier can be attributed to its preference for the highly polar aqueous environment. On the organic side of the interface, repulsion of TPFB⁻ by water is likely caused by the disturbance of the water hydrogen bonding network by a large organic ion. These repulsive interactions are strong enough in the PB/MD model to counteract the potential gain in electrostatic energy achieved by a closer approach to the interface at 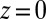. In the absence of ion–solvent interactions, the PB model predicts that the density rises monotonically to 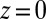(Fig. 4D). Farther from the interface, ion distributions in the PB/MD model decay slowly in a manner similar to PB theory.

Earlier work on ion distributions at the nitrobenzene/water interface had shown agreement of the PB/MD model with X-ray reflectivity data (12). As a result of the higher relative permittivity of nitrobenzene (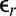 = 34.8) and the lower range of electric potential ( 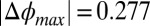V), the correlation coupling strength in those experiments was small ( 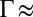0.7), and it was shown that the effect of correlations was negligible (13). However, the reflectivity data in Fig. 1B are taken over a range of 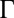up to 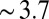, and demonstrate that the PB/MD model is inadequate when 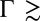2.

Ion–Ion Correlations.

The agreement between the predictions of the CORR model and the data is due to two essential features of the ion density profiles. First, the appearance of a dense layer of TPFB⁻ ions near the interface is a consequence of the minimum in the excess chemical potential 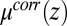(Fig. 4A). Eq. 4 indicates that the progressively deeper minima that appear in 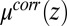with increasing 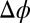lead to an enhanced density of TPFB⁻ ions in this layer. Comparison of Fig. 4A with Fig. 4C reveals that TPFB⁻ density profiles reach their maxima at the same positions as the minima in 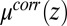. Fig. 4B shows that the enhanced density of TPFB⁻ ions takes the form of a narrow peak that decays rapidly to its bulk value, which is a signature prediction of theories of ion correlations (24); it differs from the broader diffuse electrical double layers of Gouy–Chapman (PB) theory and PB/MD theory (Fig. 4D). The correlation energies (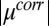) for the three highest applied electric potentials become larger than thermal fluctuations within 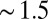nm of the interface, and they approach a maximum value of 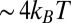when 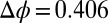V (Fig. 4A).

The second important feature of the TPFB⁻ density profile is the decrease in density illustrated in Fig. 4C for small values of z in the range 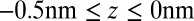. The agreement between the CORR model and the X-ray data suggests that ion–solvent interactions described by 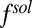play a role in shaping the behavior of correlations near the interface. The z dependence of the excess chemical potential caused by correlations 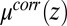, shown in Fig. 4A, is qualitatively a mirror image of the TPFB⁻ density profile: after reaching a minimum at 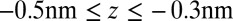, 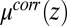increases to a higher value at 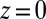. The weakening of the correlations is caused by the repulsive TPFB⁻ interactions with interfacial water molecules as described by 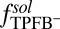(Fig. 2A). This predicted interplay between ion–ion and ion–solvent interactions at a liquid/liquid interface is consistent with the experimental data. We emphasize that, if correlations were considered without ion–solvent interactions, then both the correlation energy and the electric potential would have an extremum at 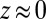, leading to densities that are even higher than predicted by PB theory and a very poor agreement with the data.

The distance of closest approach to the interface is similar to the radius of TPFB⁻ (0.5 nm), even though the radius does not enter explicitly into Eq. 2. Although the correct ionic size that should be used in an electrical double-layer model is a matter of debate (36), an advantage of the current model is that the arbitrariness in defining an ionic diameter is removed. In this approach, the role of the size of ions is determined by the molecular modeling and intermolecular interactions, which are used in the MD simulations of .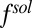

The small deviations at high 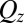between the CORR model and the reflectivity data (Fig. 1B) for the highest potentials most likely indicate that the electrical double layer is slightly thinner (by 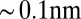) than predicted by the model. Correlations between TPFB⁻ and Na⁺ across the interface could thin the double layer, but they were not included in our analysis. The deviations could also be caused by a breakdown of the approximation used in arriving at the free energy functional in Eq. 2, where we assumed that the ion–solvent interactions are independent of the density and consequently, ion–ion interactions. This dependence on the ionic density should become more prominent as the latter reaches close packing, 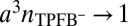. In the cases investigated here, the maximum packing density is 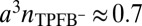(Fig. 4C). Additional theoretical and experimental work is needed to understand these issues.

In summary, we have measured the effect of ion–ion correlations on the microscopic ion distributions and the total interfacial excess charge while varying the coupling strength of ion–ion correlations over a range from weak to strong (i.e., 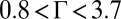). These data cannot be explained by the standard Gouy–Chapman (PB) approach, even when supplemented by ion-specific interactions with the solvent. We have tested only one of many different descriptions of ion–ion correlations in the literature, although it will be interesting to test others against these data (8, 22–30). However, it is important to note that these theories of ion–ion correlations do not include a realistic representation of ion–solvent interactions. This work shows that the interplay between ion–solvent interactions and ion–ion correlations is necessary to quantitatively describe the distribution of ions in this strongly correlated system. We anticipate that these results will also be relevant for understanding correlations of divalent and trivalent ions in aqueous solution, which are of importance for colloid and biomolecular interactions and have coupling strengths that are comparable with those coupling strengths investigated in this work.

Materials and Methods

Materials and Solutions.

Sodium chloride, purchased from Fisher Scientific (certified American Chemical Society, crystal), was dissolved in water from a Nanopure UV Barnstead system to produce a 10 mM solution. The organic solvent 1,2-dichloroethane, purchased from Aldrich (CHROMASOLV, for HPLC, 99.8%), was purified by multiple passes through a column of basic alumina. The organic salt BTPPA-TPFB was synthesized from BTPPACl (Aldrich) and KTPFB (Boulder Scientific Company) (37). A solution of BTPPATPFB in DCE was prepared at a concentration of 5 mM. However, because of the low dielectric constant of DCE, only partial dissociation into BTPPA⁺ and TPFB⁻ occurs. The dissociated fraction was determined to be 54% ± 1% (from solution conductance measurements) (38), which produces an organic solution with a dissociated ionic concentration of 2.7 mM. The aqueous and organic electrolyte solutions were separately placed in contact with pure solvent of the other phase in a beaker and rocked for 10 h to equilibrate.

Electrochemical Cell.

Each phase from the equilibrated solution is extracted separately and placed in contact in a cylindrical glass sample cell of 7-cm diameter for electrochemical and X-ray reflectivity studies (19). The potential difference of the galvanic cell, Ag|AgCl | 10 mM NaCl (water) || 5 mM BTPPATPFB (DCE) | 10 mM LiCl + 1 mM BTPPACl (water) | AgCl | Ag (where || represents the interface under investigation), was controlled by a four-electrode potentiostat using a Solartron 1287. The electric potential difference between the bulk liquid phases 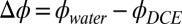is calculated from the measured electrochemical cell potential and potential of zero charge (pzc), 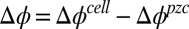, where 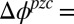0.374 V is determined from the potential-dependent interfacial tension (Fig. S1) (9). The Gibbs free energy of transfer for each of the four ions is at least 23 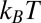; therefore, the ions remain in their original aqueous or organic phase over the experimental range of 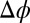(≲ 0.4 V ∼ 16 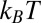per charge), which contrasts with experiments that use ion partitioning between bulk phases to establish the potential difference (12, 13).

X-Ray Measurements.

X-ray reflectivity, 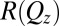, is measured as a function of wave vector transfer normal to the interface, 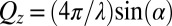, where λ is the X-ray wavelength and α is the angle of incidence. X-ray reflectivity measurements were carried out at the ChemMatCARS Sector 15 of the Advanced Photon Source on a liquid surface reflectometer at an X-ray energy of 30 keV (11, 39). Reflectivity is defined as the reflected intensity normalized to the incident intensity (after subtraction of background scattering) (40). The data are presented in the form of reflectivity normalized to the Fresnel reflectivity, 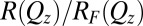, calculated for an ideal structureless interface (11).

MD Simulations.

Ion–solvent interactions are simulated in classical MD by the potential of mean force technique. This potential is sampled by inserting an ion into a simulation box at a specific interfacial height z in the bulk liquids. With the ion position fixed, the overall system is equilibrated for 200–400 ps followed by a simulation run of 2 ns. The force acting on the ion center of mass, from Coulomb and Lennard–Jones interactions with all of the solvent molecules, is ensemble-averaged at the end of the simulation, 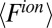(Fig. S2). This procedure is then repeated with the ion placed at a different z position. The heights are chosen to vary from one bulk liquid to the other. The ion–solvent potential of mean force 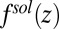is found from the following expression

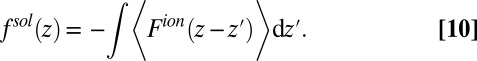MD simulations were performed using the simple point charge force field to model water (41) and a fully flexible 1,2-dichloroethane force field derived in the work by Benjamin (42). A custom computer code was used to simulate a water/DCE box containing a total of 2,424 water molecules and 844 DCE molecules in the (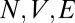) ensemble (Fig. 2B). A fully atomistic and flexible TPFB⁻ ion was added to the system, with Lennard–Jones parameters taken from the Amber force field (43) or the literature (44) (Table S2). The atomic partial charges on the TPFB⁻ atoms (C₂₄F₂₀B⁻) were determined from a computation of the quantum molecular electrostatic potential (Table S2). Intramolecular potentials consist of bond bending, stretching, and torsion, with force constants taken from the Amber force field or derived from vibrational analysis (Table S3).