Measuring forces at the leading edge: a force assay for cell motility

Abstract

Cancer cells become mobile by remodelling their cytoskeleton to form migratory structures. This transformation is dominated by actin assembly and disassembly (polymerisation and depolymerisation) in the cytoplasm. Synthesis of filamentous actin produces a force at the leading edge that pushes the plasma membrane forward. We describe an assay to measure the restoring force of the membrane in response to forces generated within the cytoplasm adjacent to the membrane. A laser trap is used to form a long membrane nanotube from a living cell and to measure the axial membrane force at the end of the tube. When the tube, resembling a filopodium, is formed and in a relaxed state the axial membrane force exhibits a positive stationary value. This value reflects the influence of the cytoskeleton that acts to pull the tube back to the cell. A dynamic sawtooth force that rides upon the stationary value is also obseved. This force is sensitive to a toxin that affects actin assembly and disassembly, but not affected by agents that influence microtubules and myosin light chain kinase. We deduce from the magnitude and characteristics of dynamic force measurements that it originates from depolymerisation and polymerisation of F-actin. The on- and off-rates, the number of working filaments, and the force per filament (2.5 pN) are determined. We suggest the force-dependent transitions are thermodynamically uncoupled as both the on- and off-rates decrease exponentially with a compressive load. We propose kinetic schemes that require attachment of actin filaments to the membrane during depolymerisation. This demonstrates that actin kinetics can be monitored in a living cell by measuring force at the membrane, and used to probe the mobility of cells including cancer cells.

Introduction

Actin remodeling is a characteristic of cell motility¹, and occurs during the invasive stage of carcinoma when transformed epithelial cells produce migratory structures² (e.g. filopodia³). Migration from the primary site of the tumour into the surrounding stroma requires cancer cells to produce conduits either chemically (e.g., enzymatic degradation of the basement membrane) or biophysically through generation of force⁴. The force produced by a cancer cell within its surrounding environment is the resultant of three components: adhesive traction, protrusive and resistive viscous drag⁵. Recent experimental evidence shows the magnitude of the adhesive force integrated over the area of the cell (nN) increases with the metastatic potential of cells within two-dimensional⁶ and 3-dimensional⁷ migration space. The adhesive force was measured with traction force microscopy⁸ which monitors the imprint left on a substrate (or matrix) by contractile stresses of the cell propelling itself within the matrix ⁹. We describe a force assay to measure the magnitude and time course of the second component of the protrusive force (pN) which results from actin polymerisation at a leading edge of a cell. We describe this methodology with results from a hematopoietic cell.

Theory

F-actin is a globular protein that polymerizes into a linear, two-stranded double helix. The length of each monomer is ~ 5.4 nm where the addition of one monomer increases the overall length of the polymer by ~ 2.7 nm¹⁰. Actin is a chemical motor; the free energy available during polymerisation and depolymerisation of actin can be used to do work^{11, 12}. Mechanical work, i.e., force × length, arises because of the difference in the chemical potential of the monomer in the biopolymer (F-actin) versus that in solution¹¹. The direction of the (mechanical) force depends upon the concentration of monomer, c, relative to a critical concentration, c_o (also referred to as the dissociation constant for the polymerisation reaction, c_o = k_off ÷ k_on where k_off and k_on are off and on-rate constants). The expression for the force, f is

$$f=-\frac{k_{B}T}{\lambda }ln\left[\frac{c}{c_o}\right]$$ E.1

where λ: is the length constant; k_B is Boltzmann’s constant; and T is temperature.

In cells, the fast growing barbed end of the filament points towards the plasma membrane. For an F-actin bundle enclosed by a membrane tube as found in filopodium the membrane axial force, F will act to restore the polymerisation force¹³ and the depolymerisation force will act in the same direction as F, then for a change in the membrane axial force, ΔF we write

$$\begin{array}{l}\mathrm{\Delta }\text{F}=-f,\{c>c_o\}\\ \mathrm{\Delta }\text{F}=f,\{c<c_o\}\\ \mathrm{\Delta }\text{F}=0,\{c\equiv c_o\}.\end{array}$$ E.2

Evidence that actin polymerisation produces a protrusive force arose from experiments with model systems, including giant liposomes where actin polymerisation changed the shape of the membrane and the vesicles moved with velocities similar to that observed in cells¹⁴. Other experiments show that bacteria (e.g., Listeria monocytogenes), can propel through their host driven by polymerisation^15–17. Force measurements found that ~1 pN of force stalls isolated growing filaments^{18, 19}. More recent measurements estimate the force per filament at 5–11 pN when actin filaments are allowed to polymerize between two mica surfaces²⁰. One measurement of force produced by actin polymerisation in living cells estimates the force per filopodium at 3 pN²¹. There are no estimates of the pulling force as a result of depolymerisation of actin.

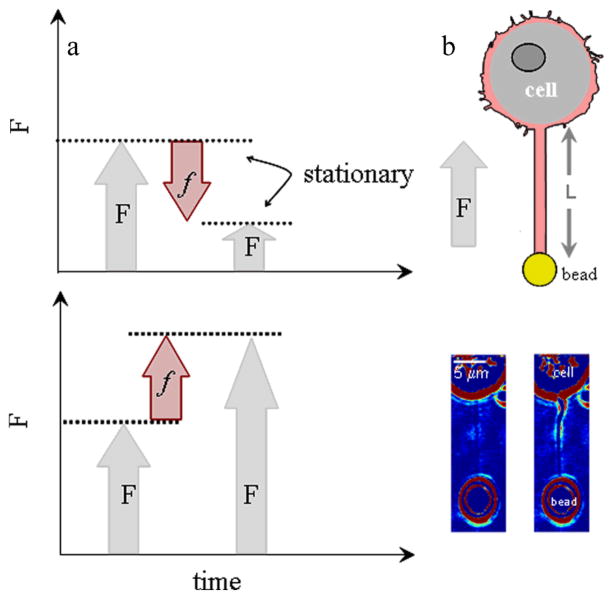
E.1 and E.2 predict that depolymerisation of F-actin if attached to the membrane^{11, 12} could pull the membrane axially whereas polymerisation of monomeric actin would push the membrane (Fig. 1a). The expressions suggest the magnitude of the actin-based force can be obtained upon measuring ΔF. The impediment is to develop an assay to demonstrate that the plasma membrane can monitor actin kinetics within a living cell.

Fig. 1.

a. Pushing force as a result of polymerisation causes a more negative membrane force, F (upper panel), while pulling force as a result of depolymerisation causes a more positive, F (lower panel). b. Optically trapped bead attached to membrane tube of length L and filled with F-actin (noted by magenta). The direction of the axial membrane force, F is positive. Bright-field images of membrane tubes formed from cell. Images were obtained at the end of tube elongation (image on left) and when the stationary force (image on right) was monitored (ESI Movie S.1).

Recently Pontes and colleagues²² show that F-actin filled membrane tubes (~10–15 μm in length) form from cultured fibroblasts by use of laser tweezers, where an optically trapped bead is used as a handle to manipulate the membrane of cells^{23, 24}. They use confocal microscopy to reveal F-actin has grown within the membrane tubes²². This observation is in agreement with earlier studies with neutrophils where it was suggested that F-actin may form in the tube²⁵ and a second study which shows that F-actin can grow to form arrays within the tube²⁶. Specifically, polymerisation of actin was observed within the lumen of tubes formed from neutrophils. This polymerisation occurred up to lengths of 10–20 μm and at a rate of 0.07 μms⁻¹ upon applying a significant local stress (> 600 Pa) to the cell. This force was suggested to originate from cell contraction²⁶.

We form membrane tubes (15–40 μm in length) from a living cell with laser tweezers. We also suggest that F-actin grows within the tubes. This is deduced from the characteristics of the axial membrane force when it relaxes to a stationary value. It is during this phase that we observe a dynamic sawtooth force riding upon the stationary value. This dynamic force has a different magnitude and time course to that observed for cell contraction²⁶ and we reason that it originates from actin polymerisation and depolymerisation (Fig. 1). By monitoring the change in magnitude of the stationary-axial membrane force (ΔF) with laser tweezers and the time course of ΔF we uncover the magnitude of f and characteristics of the rates under a compressive load.

Methods

Solutions

Experiments were conducted in saline containing in mM: 150 NaCl, 2 CaCl₂, 1 MgCl₂, 1.5 NaOH, 2.8 KOH, and 10 HEPES (300 mOsmkg⁻¹, pH 7.2). In some experiments the drugs cytochalasin E, or nocodazole or ML-7 (5-iodonaphthalene-1-sulfonyl homopiperazine, HCl) all purchased from Calbiochem (EMD Chemicals Inc., an Affiliate of Merck KGaA, Darmstadt, Germany) were added to a final concentration of 1–10, 10 and 2–20 μM, respectively. The drugs were dissolved in dimethyl sulfoxide (DMSO). The drugs were added 15 minutes before the onset of the experiment.

Cells

Mast cells were isolated from peritoneum of normal mice (strain C57BL) by peritoneal lavage with CO₂ independent medium with 1% bovine serum albumin (BSA) dissolved (Invitrogen, CA). The suspension was centrifuged at 100 × g for 15 minutes and the pellet dissolved in CO₂ independent medium without BSA. The cell supernatant was plated on Petri-dishes rinsed with saline solution and visualized on an inverted microscope with bright-field optics at 22°C. The data reported were obtained from 32 animals. These included: 23/32 (control), 17/32 (cytochalasin E), 4/32 (nocodazole), 3/32 (ML-7) and 5/32 (DMSO) animals. The sawtooth data presented were obtained from 11 animals (22 cells); specifically from 8/11 (control), 1/11 (nocodazole) 2/11 (ML-7) and 3/11 (DMSO) animals. Baylor College of Medicine Animal Care and Use Committee approved the care and use of the animals. Sawtooths were detected about 1/3 of the time for tubes ≤ 25 μm according to the protocol (see Analysis of the Force).

Beads

Sulphate-coated polystyrene micropsheres (radius: 2 μm Fluospheres sulfate, F8858, Invitrogen, Carlsbad, CA) were used as handles to form the tubes. They were utilized according to the instructions of the manufacture. No additional surface treatments were made.

Laser Tweezers

The trap was formed with a continuous wave titanium-sapphire laser tuned to 830 nm (Newport Corporation, Spectra-Physics, Model 3900S, Irvine, CA) and pumped by a 5 W solid state frequency doubled Nd:YVO₄ laser (Newport Corporation, Spectra-Physics, Model 3900S, Irvine, CA)²⁷. Images of the cells and trapped beads were projected on a monitor and recorded by a S-VHS recorder. Before each experiment, the trap was calibrated perpendicular to the focal direction²⁷. The calibration ranged from 0.6–1.5 pNmV⁻¹. The power at the objective was between 100–200 mW. The trap stiffness was 0.1–0.2 pNnm⁻¹ and was linear for displacements approaching the radius (2 μm) of the polystyrene microspheres. Data from the quadrant photo diode, QPD was amplified by a circuit and digitized with an A/D converter (Iotech, Wavebook512, Cleveland, OH) and collected at a sampling rate of 1 kHz. Calibration of the laser-trap; movement of the piezoelectric stage, PZT (Physik Instrumente, Model P-527.C3L, Waldbronn, Germany) and data collection were controlled by algorithms written in LabView, v7 (National Instruments, Austin TX). Because the image of the bead monitored by the QPD is affected by objects close to the bead (< 10 μm), only measurements made when the cell was > 15 μm from the centre of the bead are reported. Incidental movement of cell debris close to the trapped bead during an experiment was monitored with the SVHS video and when observed these measurements were discarded. Force was calculated from the product of the position data sensed by QPD (mV) and the calibration (pNmV⁻¹) constant.

Formation of Membrane Tubes

Experiments were conducted at room temperature at 22°C. Cells that adhered to glass and exhibited bright luminescent secretory granules were chosen for tube extraction. A bead was trapped, and a cell was brought towards the trapped bead with PZT at a velocity of 1 μms⁻¹. The cell and bead were held in contact for 5 to 15 s to promote adhesion. The cell was then moved away from the bead at a velocity of 1 μms⁻¹ forming a membrane tube of length 15, 25 or 40 μm. The bead was continually monitored for an additional 3–10 minutes to measure the axial membrane force during tube relaxation. We report the force measured at the end of tube elongation and during tube relaxation.

Analysis of the Force

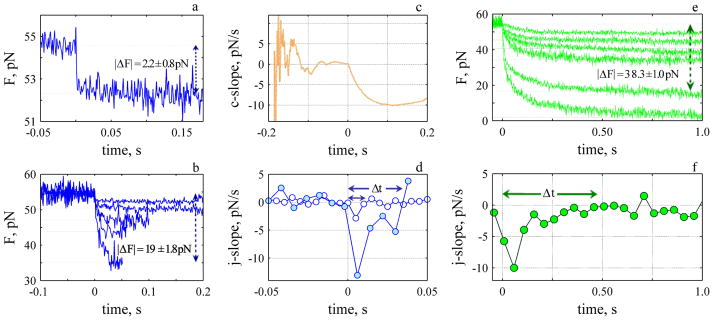
Position data collected from the QPD was processed off-line with MATLAB R2007b (The Mathworks, Natick, MA). To determine the magnitude of the stationary force the position data were digitally filtered at 100 Hz with low-pass Butterworth filter in MATLAB. The magnitude and time course of dynamic events were determined from the raw position data. We developed a list of protocols to discriminate a dynamic event from the inherent noise in the force (see Fig. 3a) and to characterise the event: i) Establish if there is a sawtooth within the time series data. To do this the gradient of the force with respect to time (ΔF/Δt) was calculated. The jump-slope (j-slope) of ΔF was calculated with a constant number of points (1000–1500) for the entire extent of the recording (see Fig 3a), i.e., 1 point every 1 to 1.5 seconds. The gradient was then examined as a function of time. An event was counted if the j-slope (calculated with at most 1000 points, resolution 1 second) was visible above the j-slope noise (Fig 3a); (ii) Determine the onset, t ≡ 0, lifetime, Δt and magnitude, ΔF of the rise of any sawtooths found. To establish t ≡ 0 we calculated the cumulative slope, (c-slope, Fig. 4b) before the rise. The slope (ΔF/Δt) was calculated starting with two points about 2–3 seconds prior to a rise. For this small number of points the c-slope exhibits a mean value close to zero with a large variance. The number of points for each subsequent calculation increased incrementally and the variance on the slope decreased (Fig 4b). The c-slope exhibits a final ascent with a value close to zero at the onset of a rise. This time was considered t ≡ 0. To establish Δt the j-slope was calculated. We considered the lifetime of the rise to occur when the j-slope was greater than zero (calculated with at most 1000 points for the rise). When the j-slope dropped below zero it was considered to be the start of a stall or a stationary state; (iii) Bundle and average all rise events that exhibit similar time course and magnitude, and determine t ≡ 0, Δt and, ΔF of the averaged events as described in (ii). The time resolution of all averaged rise events was 250 to 1000 ms; (iv) Determine the onset, t ≡ 0, lifetime, Δt and, magnitude ΔF of the decay. We used the same procedure as (ii) with some changes. We started the calculation ~ 0.2 seconds prior to the onset of the decay. Five to eight points (5 to 30 ms of data) were used to calculate the j-slope. Linear interpolation was used to determine when the j-slope reached zero because of the faster rate. All similar events were averaged and the process repeated.

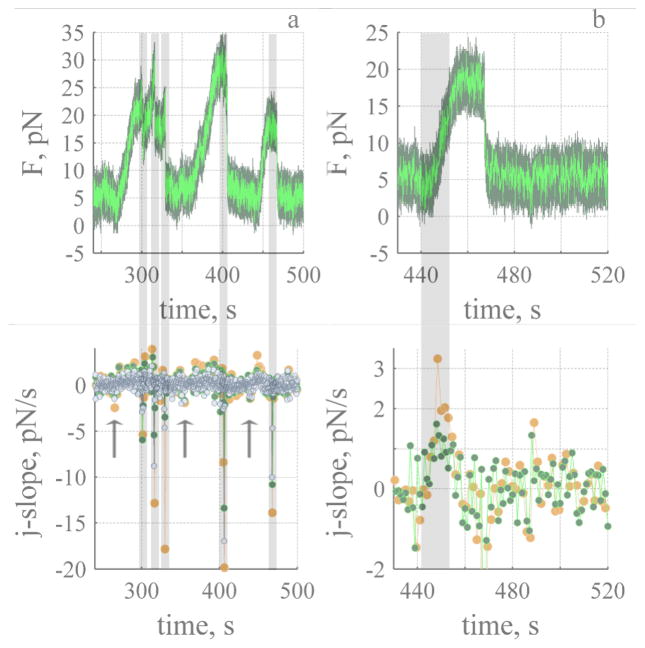
Fig. 3.

Dynamic sawtooth force rides on top of the stationary value. a. Analysis of sawtooths, bottom panel shows the j-slope calculated with 0.5 (500 points, ash), 1.0 (1000 points, green) and 1.5 (1500 points, orange) seconds of data. Five significant decay events (grey) are evident. The arrows indicate a decrease in force before the onset of rise. Dark green lines represent recorded data (1 pt ms⁻¹) and light green lines 1 pt 100 ms⁻¹ of the recorded data. b. Third sawtooth and j-slope determined during the rise. The grey line represents the time course of rise (13 seconds) determined from j-slope (green). Tube was 15 μm in length. Time is measured relative to end of tube elongation.

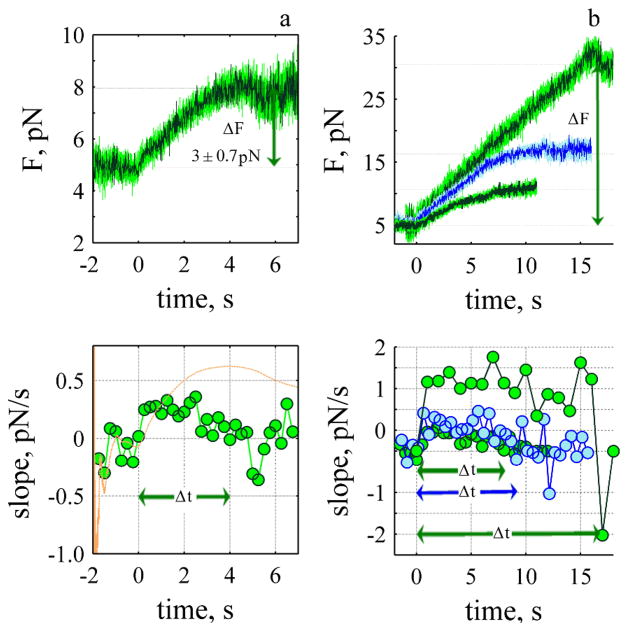
Fig. 4.

Rate of rise depends upon the force. a) Smallest change in force during the rise (N: 41). The onset of the rise was determined from the c-slope (orange line bottom panel) where t=0 is defined as the time when the c-slope begins its final rise. Δt is the time the j-slope (green, bottom panel) remained positive after the onset of rise, each point was calculated with 250 ms of data. b) Three rise-events (upper panel) and their corresponding j-slopes (bottom panel). ΔF 5.7 ± 0.92 pN (N: 27, 500 ms, Δt: 8s), 10.8 ± 1.07 pN (N: 19, 500 ms, Δt: 9.2 s) and 25.4 ± 2.2 pN (n: 4, 1000 ms, Δt: 17 s).

Imaging

Images of the cell-tube-bead assembly were obtained with a CCD camera DAGE-MTI, CCD100, Michigan City, IN) connected to microscope and recorded on SVHS tape recorder. The videos were digitally processed and split by Adobe Premiere Pro (v 2.0, Adobe Systems Inc.). The audio video interleave (avi) files were then processed in MATLAB (v7.0, The Mathworks, Natick, MA) by use of the Image Toolbox. Processing involved digitally averaging 15–30 images (about 0.5 to 1 second of video data) subtracting the digitally averaged images obtained when the bead and tube were not in the field of view from subsequent signals, and reducing the colour map range. To estimate the retraction rate of the tube back to the cell upon removal of the trap, we monitored the position of the bead with the CCD camera. In this case the images were not averaged and the time resolution was 30 frames per second.

Results

Stationary Force

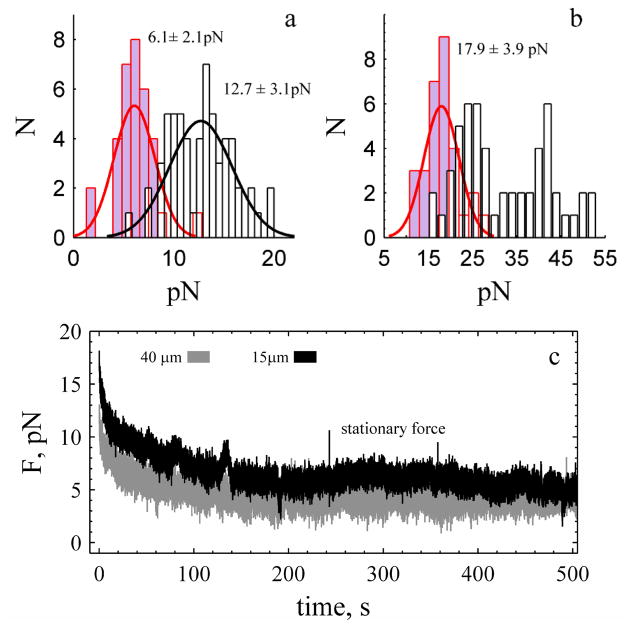
Long membrane tubes were formed with laser tweezers and the force monitored as the tube relaxed at constant length²⁸. Typically, tubes that are not cylindrical exhibit a stationary force centred at 12.7 ± 3.1 pN (Fig. 2a) and are stable for times in excess of 500 s (Fig. 1b, ESI Movie S1), as expected for saline-filled tubes (see ESI Movie S2)²⁹. There is no statistically significant difference (α: 0.05) in the value of the stationary force for tubes of different length, but there is a numerical trend; shorter tubes tended to exhibit a lower force (L: 15 μm 11.6 ± 2.3 pN,) and longer tubes (L: 25 μm 12.6 ± 3.7 pN, L 40 μm 13.8 ± 3.0 pN) tended to exhibit a higher force. The forces measured at the end of tube elongation were dependent upon the length; this force exhibits two normal distributions centred at 25 and 43 pN. The shortest tubes (15 μm) exhibit the lowest value 23.4 ± 3.6 pN (N: 17/18) while the longest tubes (40 μm) exhibit the higher value 45 ± 5.9 pN (N: 14/18). No length-dependent discrepancies were observed when cytochalasin E was added to the bath (Fig. 2c). Cytochalasin E binds to the barbed end of F-actin and disrupts actin bundle formation and forms membrane blebs and invaginations in the plasma membrane (ESI, Fig. S1). The force measured at the end of elongation and the stationary force was 17.9 ± 3.9 pN and 6.1 ± 1.4 pN (Fig. 2). Because the stationary force in the presence of cytochalasin E is independent of length (∂F/∂L=0) we are able to calculate membrane tension, γ with γ=F/(4πR_t) at 4 ± 3 μNm⁻¹ with the experimentally determined diameter, 2R_t at 310 (± 80) nm (ESI, Fig. S2).

Fig. 2.

Stationary force is independent of tether length with and without cytochalasin E in the bath. a. Stationary force for tubes of all lengths under control (white, N: 60) and in presence of cytochalasin E (lavender, N: 33). b. Force measured at end of tube elongation. In presence of cytochalasin E the force exhibits a single distribution (N: 30), white represents the control. Solid black and red lines are normal probability distribution functions. c. Force measured during relaxation in presence of cytochalasin E. The stationary values are 3.7 ± 0.9 pN (grey) and 6.2 ± 1.0 pN (black). The force measured at zero time represents the force at the end of tube elongation.

Under control conditions the classical expressions²⁹ may not be valid because of evidence of F-actin growth within the tube. This was apparent due to tube shape (Fig. 1d, see ESI Movie S1). It was also evident when we removed the trap, and monitored collapse of the tube back to the cell. The rate of tube collapse was faster under control conditions (ESI, Movie S4) compared to the case when the actin cortex of the cell was disrupted (ESI Movie S2 and S3, Fig. S3). We were able to measure the collapse rate for some events and found it to decrease with time. At 1 second it was about 9 and 4 μm/s for control and cytochalasin E treated cells (ESI Fig. S3 long tubes (40 μm). Similar differences were observed for shorter tubes (15 μm) where the rate of retraction was ~2 μm/s for control and 0.6 μm/s in presence of cytochalasin E. Indeed, for shorter tubes and when cortical actin was disrupted the tube-bead assembly appeared to drift back to the cell (lower panel, Movie S2) clearly indicating a diminished cortical-actin effect compared to the control. The third observation that suggests F-actin was forming in the tube was the presence of a dynamic force riding upon the stationary value (Fig. 3a). We describe a sawtooth transient of the dynamic force as this was the most apparent and clearly repeated pattern in the time series data.

Description of the Sawtooth Force

The dynamic force exhibits sawtooth behaviour that increases slowly (tens of seconds) in a step-like fashion, stalls and decays much more rapidly back to a stationary value (ms). Dynamic stalls are also observed (Fig. 3a, sawtooth 1). To detect and determine the onset and lifetime of a dynamic event the gradient of the force with respect to time (ΔF/Δt) was calculated (see Methods). Dynamic events were detected because of a rapid decay rate (ms) compared to a slow rise (see Fig. 3b). The magnitude and sign of the j-slope is used to estimate Δt and determine the change in the force between two stationary states (E.2) and to specifically discriminate between an event that is slowing down and an event that has reached a stationary value. We considered the lifetime of the rise to occur when the j-slope was greater than zero. When the j-slope dropped below zero it was considered to be the start of a stall or a stationary state. We confirmed that a drop was not an isolated anomoly by verifying the j-slope with different numbers of points (e.g., 500–1500). This is shown in Fig. 3b for j-slopes calculated every 1 (green) and 1.5 seconds (orange). In the example shown the j-slope (green) is near zero for 6.5 seconds shows a small rise and decay for 3 seconds and then increases above zero to a maximum of 1.0–1.5 pNs⁻¹, and then returns to zero. Δt for the rise (shown in grey) is 13 seconds.

The smallest change in the force during the rise is shown in Fig. 4a; the mean change in the force is 3 ± 0.7 pN. To determine the time course we calculate the j-slope (Fig. 4, bottom panels). The slope increases reaching a maximum and then decreases to reach a value less than zero, and hovers at a stationary state for 2 seconds. The lifetime of the event, Δt was 4s. Three other mean rise events are shown (Fig. 4b, right panel) with their corresponding j-slopes.

We performed similar analysis when we analyzed the decay of the sawtooth. However, in contrast to the rise we observed two different events during the decay that are discriminated by their rate. There is a step-like decay with ΔF between 2–19 pN and Δt up to 38 ms (Fig. 5a and 5b), and a slower decay which starts like a step but exhibits a slower decay back to the stationary value (Fig. 5e and f). ΔF for this slower phase ranged from 5 to 52 pN with Δt up to 670 ms. Events with a time course between the two extremes were also observed. We calculated the c-slope to determine the onset of the decay (Fig. 5c) and the j-slope to determine Δt (Fig. 5d) and averaged events with similar Δt and ΔF.

Fig. 5.

The rate of decay depends upon the force and exhibits a fast (a–d) and slow (e–f) time course. a. Fastest and smallest decay average of 24 events. b. Five fastest decay events. c. The c-slope for decay shown in a. d. j-slopes for the smallest (open circles) and largest (closed circles) events shown in b. e. Six slowest decay events and (f) corresponding j-slope for one of them, Δt: 489 ms average of 3 events.

Rate of Rise and Decay Depends Upon ΔF

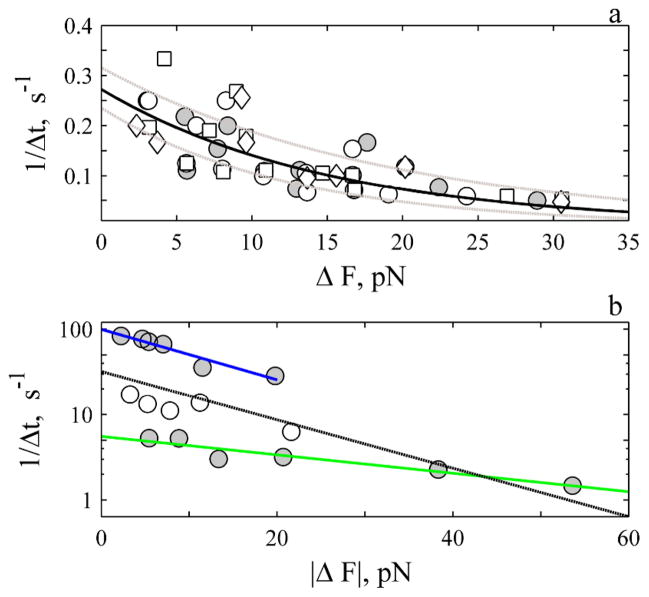
A plot of the rate of rise (1/Δt) versus ΔF is shown in Fig. 6a. The rate decreases exponentially with ΔF to exhibit a constant of ~ −0.066 ± 0.014 pN⁻¹. A rate of 0.27 ± 0.04 s⁻¹ is determined when the exponential relationship is extrapolated to zero change in force. These constants were unaffected by addition of nocodazole, or ML-7 (Fig. 6a) or the solvent DMSO (data not shown). We describe the rate of rise i.e., 1/Δt = k_d in terms of the change in the membrane axial force with ΔF

Fig. 6.

The rate of rise (a) and decay (b) decreases exponentially with magnitude of ΔF. a. Open symbols are events under control conditions (circles, N: 71), in presence of 2–20 μM ML-7 (squares, N: 44) and 10 μM nocodazole (diamonds, N: 18). There is no difference between control and treatments (P-value > 0.8). The solid circles represent average of all events (control and treatments) that exhibit the same force and time course. The solid line is best fit of all events to E.3. The dashed grey lines are the confidence interval of the estimates. The j- slope was determined with up to 500 ms of data for events ΔF < 20 pN and with 1 s of data for events ΔF > 20 pN. b. The solid circles represent the average decay for the fast (upper N: 41) and slower (lower N: 18) events. The open symbols represent events in-between the two extremes (N: 19). The j-slope was calculated with 5 and 8 ms of data for fast events and with 30 ms of data for the slow events. The blue (fast) and green (slow) lines are best-fit of data to E. 4. The black line is average fit, (see ES1, Table S1).

$$\frac{1}{\mathrm{\Delta }t}=k_d=k_{\mathit{off}}exp\left[\frac{-\lambda }{k_{B}T}\frac{1}{N_T}\frac{\mathrm{\Delta }F}{1}\right]$$ E.3

where N_T is the total number of working objects. A length constant of ~0.269 nm per working object is determined upon fitting the slope to E.3 (ESI, Table S1). This expression states that the load affects the off-rate and is dependent upon the magnitude of the exponent. The larger the exponent, (−λ/N_Tk_BT) the slower the off-rate. The results show the rate of rise slows 3-fold under a compressive load (Fig. 6a).

A plot of the rate of decay (1/Δt) versus |ΔF| for the fastest and slowest events is shown in Fig. 6b. The rate decreases exponentially with ΔF to exhibit a constant of −0.066 pN⁻¹ (Fig. 6b, blue) and 0.0254 pN⁻¹ (Fig. 6b, green). We write the decay rate, k_p in terms of the change in the membrane axial force

$$\frac{1}{\mathrm{\Delta }t}=k_p=c{k}_{on}exp\left[\frac{\lambda }{k_{B}T}\frac{1}{N_T}\frac{-\mathrm{\Delta }F}{1}\right]$$ E.4

where c is the concentration of monomer at the tip. Length constants of 0.276 and 0.103 nm per working object are determined for the slow and fast phases. An on-rate in theabsence of compressive load ranges from 5.6 to 99 s⁻¹. This expression also states that the on-rate is slowed by the compressive load. Note the different emphasis of the sign in E.4 compared to E.3. For the decay the length constant is positive and the force is negative. For the rise the length constant is negative and the force is positive (Fig. 1).

Number of Working Objects

Expressions E.3 and E.4 state that the magnitude of N_T will affect the rate of rise and rate of fall provided the length constant is the same. The larger N_T the less the rates are influenced by the load because more working objects cooperate to reduce the decline. To estimate the number of working objects we re-write E.2 in terms of the values of the stationary force between two adjacent stationary states. Namely

$$\begin{array}{l}\mathrm{\Delta }\text{F}={\text{F}}_{\text{fn}}-{\text{F}}_{\text{in}}=-n_{i}f,\{\text{c}>c_0\}\\ \mathrm{\Delta }\text{F}={\text{F}}_{\text{fn}}-{\text{F}}_{\text{in}}=n_{i}f,\{c<c_0\}\end{array}$$ E.5

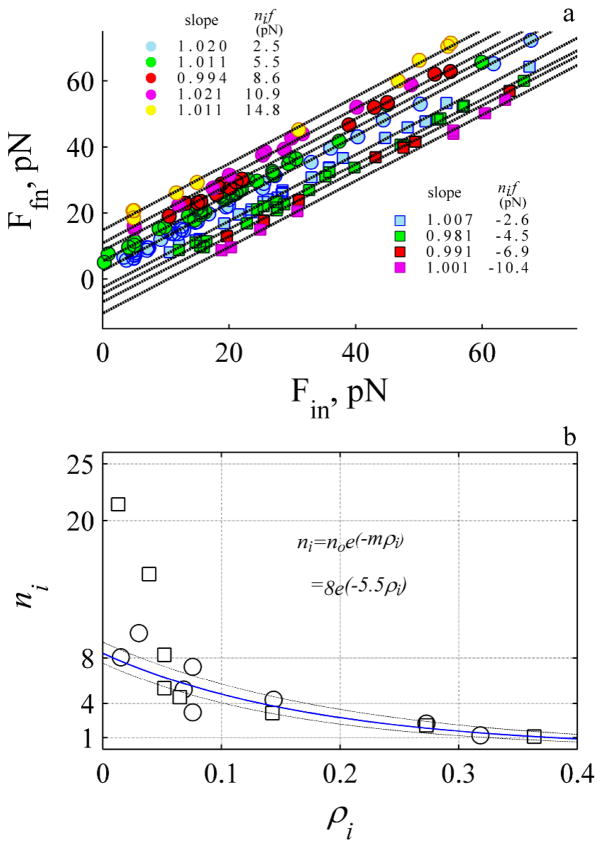
where F_fn and F_in are the magnitude of the final and initial stationary force between two states and n_i is an integer that reflects the number of independent working objects. This expression suggests that F_fn should exhibit a linear relationship with respect to F_in with a slope of ~ 1 and a negative or positive intercept with magnitude n_if. The data was grouped according to the magnitude of ΔF, and the relationships shown in Fig 7a.

Fig. 7.

The force is discrete with a mean value of 2.5 pN where 8 objects work cooperatively. a. The initial and final stationary values for single events (e.g. Fig. 4b) where the circles and squares represent rise and decay. The data was grouped according to the mean ΔF. The solid dashed lines represent the best fit to linear relationship (P- values for slope and intercept always >0.001). b. The number of working objects, n_i decreases exponentially with the probability, ρ_i. The blue line is fit to an exponential function (see inset) (p-values >0.001). The two decay events that exhibit value > 9 were not included in fit. The dashed lines are confidence intervals of the fit. Circles and squares represent rise and decay events.

The data exhibits several straight lines with a slope close to 1 and an intercept that depends upon the magnitude of the step. This suggests F increases by stepping up and decreases by stepping down by a common difference of ~ 2.5 pN like an arithmetical progression. Because the common difference is the same as the initial value, the magnitude of the intercepts at 2.5, 5, 7.5, 10, 12.5, 15 pN reflect a series {a, 2a, 3a, 4a, 5a, 6a..} where the leading integer is a function of the number of force-bearing objects. The maximum leading integer for the events shown in Fig. 7a is six, suggesting the maximum number of working objects is six.

We also estimate the number of working objects by counting the number of events detected within the same force range. The number of working objects is calculated assuming one object is equivalent to 2.5 pN (i.e., n_i ≡ ΔF/2.5). We find the probability of observing an event depends upon the magnitude of ΔF. The greater the magnitude the lower the probability of observing a decay (squares) or rise (circles) event. We find n_i decreases exponentially with probability exhibiting a similar slope for the rise and decay events. Extrapolating to zero probability a maximum of eight working objects is determined, except for the data observed during the slow decay (Fig. 7b) where a much faster decrease (about 5 fold) with a greater number of working objects 36 ±13 is required to explain the data (fit is not shown in Fig. 7b). This analysis suggests there are six to eight working objects. If the objects are working actin protofilaments where N_T ≡ 8 (see E. 3 and E.4) then a length constant of 2.1–2.2 nm (Table S1) is calculated with the experimental derived slopes (Fig. 6). This calculated length scale is 0.7 fold of the expected half length of a single subunit of G-actin at 2.7 nm¹⁰. During the slow on-phase (Fig. 5c and 5f) we calculate a length constant of 1 nm which is much less than single subunit of G-actin.

We investigated whether myosin II via the myosin light chain kinase pathway (MLCK) was responsible for the dynamic force and found the sawtooth transients were also observed in presence of ML-7. In addition, the stationary force and force obtained at end of tube elongation were of similar magnitude to the control at 12 ± 2.6 (n: 5) and 30.1 ± 5.3 (n: 7) (Fig. 2a). Likewise the tube shape and movement were also similar to that observed under control conditions (i.e, Movies S1). We also did not detect a difference in the time course of the sawtooth at least within the noise of our measurements and at the concentrations of ML-7 examined, 2 and 20 μM³⁰ (Fig 6). MLCK is found associated with cortical actin. When mast cells are triggered to undergo exocytosis, calcium and calmodulin bind to MLCK to induce F-actin disassembly³⁰. In the presence of ML-7 this activation of MLCK is inhibited and F-actin concentration increases. When the cells are not activated ML-7 has no effect on F-actin disassembly³⁰. If myosin II via MLCK pathway was directly responsible for the sawtooths we would expect them to diminish and not be observed or observed rarely. Although it is likely that ML-7 had some other subtle effects it did not appear to dimish the dynamic force, especially the sawtooth.

Because the cells were not activated it is also improbable that the discrete force (Fig 3) is due to tension change as a result of exocytosis or endocytosis of secretory vesicles. If exoxytosis occurs it should increase the amount of plasma membrane available (decrease the force) while endocytosis should decrease the amount of plasma membrane available (increase the force). The stationary force is low (12 pN) and independent (statistically) of the length of the tube (Fig. 2a) indicating there is excess membrane to form tubes and buffer³¹ any incidental endocytotic event. In addition cytochalasin E³² does not inhibit exocytosis and the dynamic events should still have been observable in the presence of this drug.

We investigated if nocodazole which inhibits depolymerisation of microtubules³³ was responsible for the dynamic force and found the dynamic force was also observed with this toxin. The stationary force and the force obtained at end of elongation in the presence of 10 μM nocadazol were also similar to the control values at 13.6 ± 2.5 (N: 5) and 32.7 ± 1.09 (N: 4). In mast cells nocodazole disrupts microtubules near the centrosome and within the endoplasmic reticulum to affect calcium release³⁴.

We also considered that unconventional myosins (e.g., myosin 1, myosin V, and myosin X) may be participating as they are present in filopodia³⁵, but suggest they are an unlikely candidate because of the magnitude of the force measured in the experiments. Briefly, about 25% of the events exhibited a ΔF with magnitude greater than 10 pN. This contrasts the maximum force expected for a myosin molecule at 3 pN³⁶. Although unconventional myosins can produce a significant force under isometric conditions, there is a low probability that two or more myosin molecules would simultaneously go through their working-stroke to produce a discrete force step > 10 pN.

Having considered the above possibilities and deemed them not compelling explanations we propose the rising phase of the sawtooth force results from depolymerisation of F-actin where the decay phase originates from polymerisation of F-actin. This suggests that actin is attached to the membrane and the concentration of monomeric actin at the tip of the tube hovers below but near the critical concentration. The measured value of ΔF = f ~ 2.5 pN (E.2, Fig. 7) is comparable to the force per filopodium at 3 pN produced by actin polymerisation by growing dorsal root ganglia²¹. The force is 3-fold more than the value obtained from isolated filaments at ~1.0 pN for both a single filament attached to formin¹⁹ or a growing bundle of filaments polymerizing¹⁸. In the latter report they suggest cooperativity was absent and only one filament was in contact with the barrier. We suggest cooperativity is present (Fig. 6, ESI Table S1) and there is more than 1 filament in contact with the membrane.

Discussion

Filaments are Not Always Treadmilling

We report the measurement of a pulling force which we associate with depolymerisation of actin (Fig. 1, 3–4). This suggests that F-actin is attached to the membrane during depolymerisation and the filaments are not always treadmilling^37,38. This (lack of treadmilling) is an unexpected result as head-to-tail polymerisation of actin is considered to be the dominant mode of actin turnover in cells¹. One reason for this observation may be that the flux of monomeric actin to the tip of the long membrane tube is low, thereby increasing the probability of detecting actin depolymerisation. This reasoning is analogous to the strategy used to measure depolymerisation rates in isolated filaments. The concentration of monomeric actin is lowered to determine off-rates of actin^39–41. Another possibility is that the gradient force due to the light may influence growth especially at the edge of the bead adjacent to the tube. It was shown that actin polymerization-driven lamellipodia growth is stimulated by low power (20–120 mW) light in growth cones⁴². However, recent results in hair cells show that actin turnover in stereocilia does not necessarily occur by treadmilling. They suggest depolymerisation of actin (not just polymerisation) may account for the turnover at the tip of the stereocilia⁴³.

We did not measure sawtooth transients for longer tubes (~40 μm in length) suggesting that a length of ~ 25 μm may represent a limit, which is consistent with other experiments^{22, 44}. The growth rate of F-actin within the tubes (0.15 to 0.25 μm/s⁴⁵) is also similar to reported rates^{22, 26}. An intact cortical actin is required to support the growth of the F-actin bundle within the tube. This was apparent when we removed the trap, and monitored collapse of the tube back to the cell where a faster rate was found under control conditions. Further examination and modelling of the time course of the rate of tube collapse should reveal the viscoelastic properties of the actin cortex and indicate the presence of F-actin growth within the tube.

On and Off Transitions are Thermodynamically Uncoupled

Kinetic arguments predict that an axial membrane compressive load should affect the rate of depolymerisation as well as the rate of polymerisation^{11, 12}. This prediction is in agreement with our observations (Fig. 6). The unexpected result of this work is the evidence that transitions appear to be thermodynamically uncoupled (Fig. 6, Table S1). We suggest this because the exponents of E.3 and E.4 have the same negative sign; the compressive load slows both the on and off-rates (Fig. 6, Table S1). This decrease is 3-fold. Theory shows that kinetics transitions that traverse the same free energy barrier should exhibit an exponent of different sign or be independent of the load. For example, if the on-rate decreased with load then the off-rate should increase with load or not be affected by load¹¹. This result suggests at least for the compressive load on the membrane that the on and off transitions are thermodynamically uncoupled and traverse different free-energy pathways.

The influence of load on the kinetics of microtubule growth shows that a load either slows the on-rate and does not affect the off-rate, or slows the on-rate and quickens the off-rate⁴⁶. In models for actin polymerisation it is usually assumed that a load only slows the on-rate^47–49. In their examples, the on and off processes are coupled and describe forward and backward transitions over the same free-energy barrier. In contrast, our results suggest that the on and off transitions traverse different free-energy pathways. Although more data is required to verify this result, if correct it implies that bundled structures found in cells exhibit elaborate kinetics compared to those of isolated filaments.

Mechanism for Actin Polymerisation and Depolymerisation

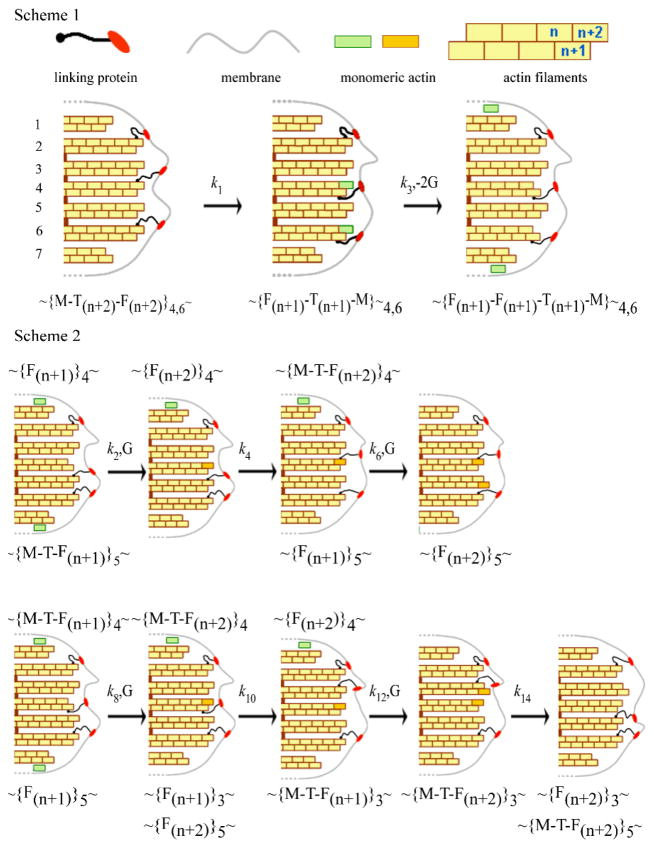
There are several mechanisms to explain how actin filaments push the membrane upon polymerisation^{47, 49}, but none of them consider the opposite possibility of pulling the membrane during depolymerisation. This observation requires that filaments are attached to the membrane during depolymerisation and exhibit a type of stepping-end-tracking mechanism⁴⁷ (Fig. 8, Scheme 1). This scheme requires linker proteins to attach the actin filaments to the membrane. Although several proteins may participate, for simplicity we only include one flexible linker. During depolymerisation we suggest that the linker detaches from the n+2 position of the filament and binds to n+1 position, after which the monomer escapes. We frequently observed a decrease in the force prior to the rise (Fig. 3, black arrows) and speculate that this could represent the linkers re-arranging prior to binding at the n+1 position.

Fig. 8.

Pathway for actin depolymerisation (Scheme 1) and polymerisation (Scheme 2). Scheme 1 Two of the protein linkers, crisscross from the (n+2) to the (n+1) position and pull the membrane towards the cell with rate constant k₁, and the same two monomers at position (n+2) escape to the cytoplasm with rate constant k₃. Scheme 2. Upper: Monomers bind only to filaments without linkers. A monomer binds at the (n+2) position of the 4^th filament after which a protein linker dissociates from the 5^th and binds to the 4^th pushing the membrane forward. A second monomer then binds to the (n+2) position of the 5^th filament. Lower: binding of monomer to filaments with a linker attached. A monomer binds at the (n+1) position (4^th filament) and this linker then moves to the adjacent filament pushing the membrane forward. A second monomer binds to the (n+2) position of the 3^rd filament and the linker on this filament dissociates and rebinds to the (n+2) position of the 5^th filament pushing the membrane forward. The symbols represent G: monomeric actin, M: membrane, F: filament; T: protein linker and the subscript the filament number. The rate constants, k are shown where odd and even subscripts represent depolymerisation and polymerisation.

Because the transitions appear uncoupled we suggest different pathways for polymerisation. We propose linkers first detach from one of the protofilaments and attach to a surrounding filament, and then either polymerize on the filament they just detached from as proposed by the Brownian tethered ratchet mechanism⁴⁹ (Fig. 8., Scheme 2 upper) or polymerise on the newly attached filament⁴⁷ (Fig. 8., Scheme 2 lower). Our data cannot discriminate between the two common mechanisms used to describe actin polymerisation.

Linkers convert chemical energy to kinetic energy that drives the mechanical motion of the membrane. We do not suggest that ATP hydrolysis is required (cf.⁴⁷) rather that monomer addition and removal provides the energy to push and pull the membrane. A likely candidate for one of the transducer molecule(s) are the formin family of proteins especially Diaphanous-related formins (Drf) as they nucleate and track processively at the barbed-end of linear actin arrays^{50, 51} and allow for the assembly of long F-actin arrays in filopodia⁵². Models for processive association suggest the translation of the formin (FH2 dimer) is equivalent to the length of a G-actin molecule^{50, 51}. However, their models do not consider movement of the plasma membrane. In addition, there is paucity of evidence that formins support membrane binding. There is evidence that one of the formins binds to the membrane via a membrane protein⁵³ and that phospholipids may bind to the protein⁵⁴. If formins are indeed the transducers it is more likely that a protein-membrane linker is attached to each protofilament because they exist as dimers⁵⁵. An alternative explanation is that there is a second linker between the membrane and formin, as suggested for N-WASP capture of branched actin filaments⁵⁶.

A first order rate constant for actin polymeristion of 7.4–10 μMs⁻¹ is determined in isolated filaments,^39–41. We did not determine this rate constant only the product of the local concentration and the rate constant (see E.4). Although the fastest on-rate (100 s⁻¹) is comparable to values found in cells⁵⁷, the sampling rate (1 kHz) and noise of our recording (the j-slope was calculated with at least 5 ms of data, Fig 5) limits the robustness of this estimate. Our recent measurements with a similar laser trap indicate the dynamical response of the trap is > 3000 s⁻¹ suggesting the response of the trap was not limiting⁵⁸. We determine an off-rate (0.27 s⁻¹) which is 2–4 fold less than that measured on isolated actin filaments at 0.64–1.4 s⁻¹,^39–41. The off-rate has not been reported in cells. This estimate is not limited by sampling rate.

Several studies suggest that the moving object (e.g. bead or membrane) is tethered to the actin network (Fig 7) for robust actin-based motility^{56, 59, 60}. There is a debate whether the discrete movement of the object should reflect the size of monomeric actin. One experimental report supports the suggestion¹⁶ while other experimental and computational studies disagree^59–61. A length constant between 0.1 to 0.27 nm per working object is calculated from the kinetic data (ESI, Table S.1). This suggests 10–28 protofilaments (N_T ≡ 10–28) would need to be attached to the membrane to achieve a λ equivalent to half a G-actin subunit at 2.7 nm. Although this is a reasonable number for filopodia, the maximum number of protofilaments detected was about eight from which we estimate a λ of ~1–2 nm (Fig. 7). Although we favour the idea that the filaments are cooperating to prevent the rate from decreasing, i.e. exp(−n_iΔFλ/N_Tk_BT), (ΔF = 2.5 pN, n_i working filaments, Fig. 6 and 7). We acknowledge that the experiments cannot discriminate if the slope reflects the cooperative decrease, i.e., exp(−n_iΔFλ/k_BT) in the rate as a result of breakage and formation of many attachments bonds. The latter describes the cooperative thermal breakage model⁶⁰. Further studies are required to determine if the discrete nature of motility is a direct correspondence of the G-actin subunit length and/or reflective of the other participants, (e.g., the putative protein linkages that connect actin to the membrane and determine the transduction efficiency).

Determine Chemical Kinetics of Actin Polymerisation in Cancer Cells

One objective is to develop this methodology to measure the rate constants in cancer cells, and establish if the magnitude and time course of the protrusive force correlates with the mobility of cancer cells^{6, 7}. Additional experimental manipulations are to be conducted. They include: (i) contolled manipulation of biological pathways (e.g., epidermal growth factor pathway) to form the F-actin-filled tubes at physiological temperature of 37°C; (ii) establishing if the chemistry and size of the bead affect the time course, where a large bead improves the dynamic range of the force⁶² while a smaller bead improve the fidelity of the time course⁵⁸; (iii) examine the spectral components of the force to reveal additional states not apparent with time domain analysis; (iv) use of fluorescence microscopy to image F-actin and other key proteins (eg., formins) in the tube, and speckle fluorescence microscopy⁵⁷ to measure rates concurrently with the force.

Conclusions

1. The plasma membrane reflects force production that occurs within the cytoplasm adjacent to the membrane. In this example the force arises from synthesis and break-down of F-actin. This assay could be adapted to measure other cytoskeletal-based forces.

2. The rate of bond formation and breakage is revealed from the time course of the membrane force. Development of methodology to reduce the noise and expand the bandwidth should improve the fidelity of the measured rate and rate constants.

3. We observe separate pathways that we associate with actin polymerisation and depolymerisation. This suggests the kinetics within cells is more complex than that described for isolated filaments and requires theoretical development

4. The observation of the pulling force which we associate with depolymerisation implies the membrane is attached to the bundle and the filaments are not always treadmilling. This could be a function of experimental manipulation. Further studies will establish if this pulling force contributes to cell contraction during cell mobility.