Bacterial Cell Surface Deformation under External Loading

ABSTRACT

Viscoelastic deformation of the contact volume between adhering bacteria and substratum surfaces plays a role in their adhesion and detachment. Currently, there are no deformation models that account for the heterogeneous structure and composition of bacteria, consisting of a relatively soft outer layer and a more rigid, hard core enveloped by a cross-linked peptidoglycan layer. The aim of this paper is to present a new, simple model to derive the reduced Young’s modulus of the contact volume between adhering bacteria and substratum surfaces based on the relationship between deformation and applied external loading force, measured using atomic force microscopy. The model assumes that contact is established through a cylinder with constant volume and does not require assumptions on the properties and dimensions of the contact cylinder. The reduced Young’s moduli obtained (8 to 47 kPa) and dimensions of the contact cylinders could be interpreted on the basis of the cell surface features and cell wall characteristics, i.e., surfaces that are more rigid (because of either less fibrillation, less extracellular polymeric substance production, or a higher degree of cross-linking of the peptidoglycan layer) had shorter contact cylinders and higher reduced Young’s moduli. Application of an existing Hertz model to our experimental data yielded reduced Young’s moduli that were up to 100 times higher for all strains investigated, likely because the Hertz model pertains to a major extent to the more rigid peptidoglycan layer and not only to the soft outer bacterial cell surface, involved in the bond between a bacterium and a substratum surface.

IMPORTANCE

The viscoelastic properties of the bond between an adhering bacterium and a substratum surface play a role in determining bacterial detachment. For instance, removal of an oral biofilm proceeds according to a viscoelastic failure model, and biofilm left behind after toothbrushing has been found to possess expanded bond lengths between adhering bacteria due to viscoelastic deformation. Current elastic deformation models are unable to distinguish between the soft outer bacterial cell surface and the hard core of a bacterium, enveloped by a peptidoglycan layer. Therefore, here we present a simple model to calculate the Young’s modulus and deformation of the contact volume between an adhering bacterium and a substratum surface that accounts for the heterogeneous structure of a bacterium.

Introduction

Microbial adhesion takes place on all natural and man-made surfaces (1) and poses considerable threats in food processing, drinking water systems, and human health to mention a few. These threats are not always associated with adhering organisms, but often with their detachment causing contamination elsewhere. In human health for instance, contact lens-related microbial keratitis is caused by bacterial adhesion to and detachment from the contact lens case to the contact lens onto the cornea (2). In food processing, pasteurized milk can become bacterially recontaminated by detachment of thermoresistant streptococci from heat exchanger plates in the downward, cooling section of pasteurizers (3). Bacterial detachment occurs through a viscoelastic failure model (4), and oral biofilm left behind after toothbrushing has been found to possess expanded bond lengths between adhering bacteria due to viscoelastic deformation (5). Although more prominently demonstrated for bacterial detachment, viscoelastic deformation may also play a role in bacterial adhesion to substratum surfaces, since it increases the contact area between a bacterium and the surface. Recently, it has been suggested (6) that deformation of bacterial cell surfaces during adhesion may result in so-called stress deactivation of the adhering organisms, making them more susceptible to antimicrobial agents which may provide new clues to prevent antibiotic resistance. Deformation of the bacterial cell surface and an associated change in contact area in response to an applied external force are hard to model and require knowledge of the viscoelasticity of the bacterial cell surface.

In colloid science, several deformation models (e.g., the Hertz, Johnson-Kendall-Roberts, and Derjaguin-Muller-Toropov models) have been developed to describe the deformation of an elastic sphere under an applied external loading force (7–10). All models have in common that they require a priori knowledge of the reduced Young’s modulus E* of the particle (i.e., a bacterium), and substratum in order to calculate deformation and possible changes in contact area during loading (11, 12). Note that there is a subtle difference between the reduced Young’s modulus E* and Young’s modulus E, according to the following equation:

$$E*=\frac{E}{1-{\upsilon }^2}$$ (1)

where ν is Poisson’s ratio of the material under consideration (for most materials, ν is between 0 and 0.5). Poisson’s ratio accounts for the fact that a material compressed or stretched in one direction usually tends to expand or become compressed, respectively, in the other two, perpendicular directions. Poisson’s ratio is the ratio of the fractional expansion divided by the fractional compression or vice versa (13).

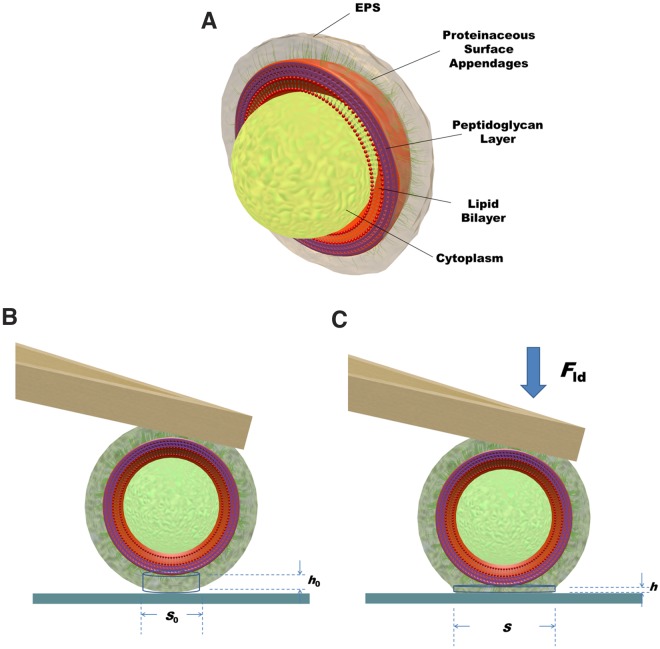
Use of atomic force microscopy (AFM) allows control of the applied external force and measurement of the induced deformation. Such data in combination with any of the deformation models mentioned above can be applied to determine the reduced Young’s modulus of both hard and elastic materials (14–16). Application of these models assumes that the particles examined are homogeneous with respect to their composition and viscoelastic properties, but this is not the case for bacteria. Bacteria can either be rod shaped or spherically shaped and are by no means structurally homogeneous. Gram-positive bacteria consist of a cytoplasmic, intracellular fluid contained within a hard core, enveloped by a lipid bilayer or membrane covered by a thick and relatively rigid, cross-linked peptidoglycan layer (Fig. 1a). Gram-negative strains possess a double membrane with a thin layer of peptidoglycan between the two membranes. The outermost bacterial cell surface may consist of proteinaceous surface appendages of different diameters and lengths of up to hundreds of nanometers or by a layer of extracellular polymeric substances (EPS), produced by the organisms (17). As a consequence of the structural and compositional heterogeneity of bacterial cell surfaces, there is no homogeneous stress distribution upon external loading, and the softer outer layer may deform to concentrate the stress toward the more rigid, hard core. Therefore, the contact volume and its reduced Young’s modulus are beyond experimental reach for bacterial cell surfaces using AFM and existing deformation models.

FIG 1 .

(a) Three-dimensional (3D) schematics of a Gram-positive bacterium, consisting of intracellular cytoplasmic fluid contained within a hard core, composed of a lipid bilayer or membrane covered by a thick and rigid, cross-linked peptidoglycan layer. The softer, outermost cell surface may consist of a combination of proteinaceous surface appendages combined with EPS (extracellular polymeric substances). (b) Bacterium upon initial contact with a substratum surface in the absence of an external deformation force. The contact volume is represented by a cylinder with an initial area S₀ and initial height h₀. (c) Deformation of the bacterial contact cylinder upon application of an external force F_ld to an area S and height h.

In this paper, we present a new, simple model to derive the reduced Young’s modulus of the contact volume between an adhering bacterium and a substratum surface. Our model is based solely on the assumption that contact is established through a cylinder with constant volume during deformation upon application of an external loading force. Importantly, the model does not a priori require any assumptions on the properties and dimensions of the contact cylinder and is applicable to different bacterial strains and species, regardless of whether they are Gram positive or Gram negative, whether they are rod shaped or coccal, and other details of their surface structure and composition. The model requires measurement of force-distance curves using AFM between a bacterial probe and a substratum surface and is applied here on six strains that allow pairwise comparisons to identify the effects of the following: (i) the absence or presence of fibrillar surface appendages (two isogenic Streptococcus salivarius strains) (18, 19), (ii) slime production (two Staphylococcus epidermidis strains) (20), and (iii) the degree of cross-linking in the peptidoglycan envelope (two isogenic Staphylococcus aureus strains) (21).

A summary of the relevant cell surface features of the different strains is given in Table 1. Note that we confined our experiments to this selection of Gram-positive cocci, because they have pairwise unique properties that contribute to the interpretation and validation of the results based on our knowledge of their cell wall properties. Also, reproducible preparation of bacterial probes for rod-shaped organisms is more difficult than for coccal organisms.

TABLE 1.

Structural features of the different pairs of bacterial strains included in this study^a

Bacterial species and strain	Structural feature	Proposed elastic deformation model			E* (kPa)b calculated by the Hertz model
		h0 (nm)b	S0 (104 nm2)	E* (kPa)b
S. epidermidis
ATCC 35983	Poor slime producer	11 ± 2	1.8	22 ± 4	7,190 ± 1,718
ATCC 35984	Strong slime producer	53 ± 7	8.3	8 ± 2	510 ± 160
S. salivarius
HB-C12	Nonfibrillated	28 ± 3	4.4	13 ± 2	1,320 ± 254
HB-7	Fibrillated (91 nm long)	44 ± 1	6.9	7 ± 1	593 ± 151
S. aureus
NCTC 8325-4	Wild-type	12 ± 2	2.0	47 ± 26	5,472 ± 3,020
NCTC 8325-4 Δpbp4	Deficient in peptidoglycan cross-linking	91 ± 2	14.2	10 ± 1	170 ± 62

^aStructural features of the different pairs of bacterial strains included in this study together with dimensions and reduced Young’s moduli of the contact cylinder between adhering bacteria and a glass substratum. The reduced Young’s moduli were obtained from the proposed elastic deformation model of the contact cylinder and from Hertz modeling of the compression data, pertaining to the soft, outermost cell surface and for an unknown part to the bacterial hard core (Fig. 1). 

^bThe values for h₀ and E* are means ± standard deviations for deformation measurements taken over 24 different spots on the glass substratum, comprising eight different bacteria.

RESULTS

Derivation of mechanical properties of the bacterial contact volume mediating adhesion using a new, elastic deformation model.

A bacterial probe attached to a tipless AFM cantilever is compressed against a glass surface under the external loading force of the AFM, yielding deformation of an assumed contact cylinder from an initial area S₀ and height h₀ (Fig. 1b) to their deformed values S and h (Fig. 1c). Assuming that the volume of the contact cylinder remains constant during adhesion and associated deformation, its initial and final dimensions can be related to the deformation equation δ = h₀ − h according to

$$S=\frac{S_0{h}_0}{h_0-\delta }$$ (2)

while by equating the volume of the spherical cap contacting the substratum with the volume of a cylinder of equal height, S₀ can be estimated as

$$S_0=\pi R{h}_0$$ (3)

in which R is the bacterial cell radius, taken as 500 nm for all strains employed in this study (12, 18, 22). As long as the bacterium is in contact with the substratum surface, δ can be calculated from the displacement of the sample stage as measured with the piezo-transducer of the AFM, Δz, and the cantilever deflection d

$$\delta =\Delta z-d$$ (4)

Equating the elastic force F_cant exerted by the cantilever with the force arising due to deformation of the contact volume according to Hooke’s law yields

$$F_{\text{cant}}=kd=E*S\frac{\delta }{h_0}$$ (5)

where k is the spring constant of the cantilever and E* is the reduced Young’s modulus of the contact cylinder. By combining equations 2, 3, and 5, F_cant can be expressed as

$$F_{\text{cant}}=E*\frac{S_0{h}_0}{\mathrm{(}{h}_0-\delta \mathrm{)}}\frac{\delta }{h_0}=\pi RE*\frac{h_0\delta }{h_0-\delta }$$ (6)

Subsequently, fitting of the experimental data for F_cant and the deformation δ yields the reduced modulus E* and the initial dimension h₀.

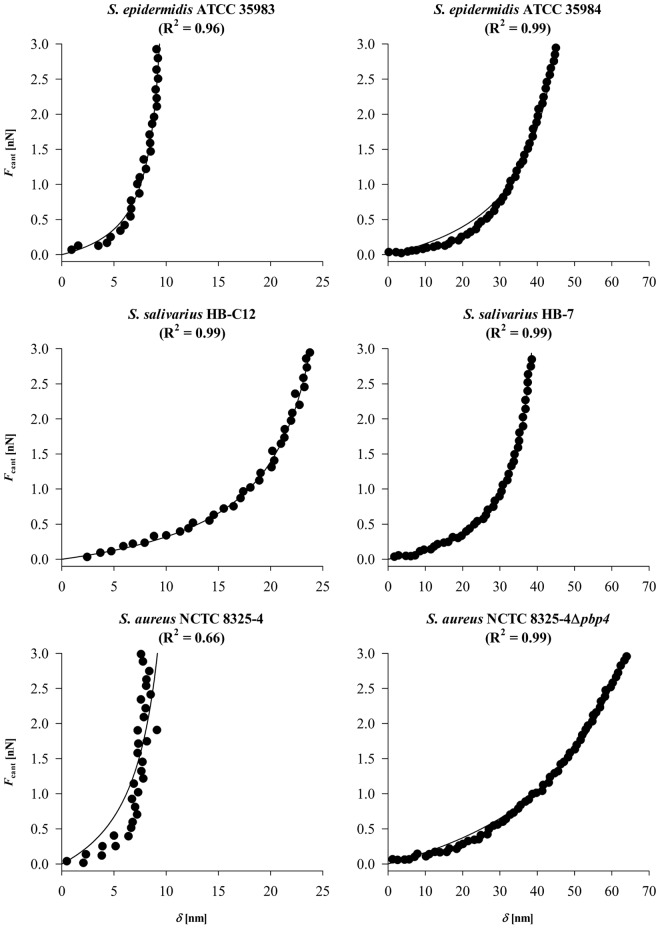
In Fig. 2, the force sensed by the AFM cantilever, F_cant, upon deforming an adhering bacterium is presented as a function of the deformation δ. Since the strains included in this study are pairwise selected with respect to differences in cell surface features (see Table 1), the graphs have been arranged so that strains showing the largest deformation within a pair are presented on the right. Large differences in deformation were observed both within pairs and between pairs.

FIG 2 .

Deformation force exerted by the cantilever F_cant as a function of the bacterial deformation δ applied to two strains of S. epidermidis (ATCC 35983 and ATCC 35984), S. salivarius (HB-7 and HB-C12), and S. aureus (NCTC 8325-4 and its isogenic Δpbp4 strain). Note that the x axes have different scales. The R² values are given in the graphs.

Data could be well fitted to equation 6, yielding values of E* and h₀ for the contact cylinders. The data are summarized in Table 1, together with values for the initial contact areas S₀ calculated from equation 3. Note that the quality of the fit to equation 6 is generally good, except for S. aureus NCTC 8325-4, probably as a result of its relatively small deformation upon external loading. The reduced Young’s moduli calculated by our proposed deformation model vary by a factor of 7 among this collection of strains, and within the pairs of staphylococci and streptococci, it is lower in bacteria that produce EPS, possess fibrils, and lack cross-linking in the peptidoglycan layer. An important feature of the model is that the dimensions of the contact cylinder at zero external loading force are obtained as well. Within each pair, a decrease in reduced Young’s modulus is accompanied by a larger height and contact area of the initial contact cylinder.

Derivation of reduced Young’s moduli using AFM in the Hertz model.

The reduced Young’s moduli of soft materials can also be obtained using the Hertz model (8, 23), assuming the adhesion force arising from the contact can be neglected. When applying the Hertz model to bacteria, a bacterium is simply considered a uniform, elastic sphere and approach force-distance curves are fitted to

$$F_{\text{cant}}=\frac{4}{3}E*R^{1/2}{\delta }^{3/2}$$ (7)

Fitting of the experimental data for F_cant and the deformation δ using the Indentation module of NanoScope Analysis software (Bruker) then directly yields the reduced Young’s modulus E*.

Analysis according to the Hertz mode yields reduced Young’s moduli of the adhering bacteria only as a whole, and accordingly, as shown in Table 1, these values are about 3 orders of magnitude larger than obtained from our proposed deformation model. The measured adhesion forces for the strains involved in this study were generally less than 2 nN (data not shown), which justifies the use of the Hertz model.

DISCUSSION

We propose a simple model to evaluate the elastic deformation of a bacterial cell surface upon external loading using AFM. The model is based on the assumption that the contact between an adhering bacterium and a substratum surface can be represented as a cylinder having a constant volume during deformation, while the rigid, hard core of a bacterium (Fig. 1) does not a priori participate in the deformation unless severely softened, as for instance when cross-linking of the peptidoglycan in the cytoplasmic envelope is absent. The model allows for derivation of the reduced Young’s modulus of the contact volume from the relationship between the external loading force F_cant and the deformation. Like the Hertz model, our model accounts only for elastic deformation, although it has been argued that bacteria should be regarded as being viscoelastic (12). Retardation time constants of bacteria based on standard solid models (24) are reported to be around 1 to 2 s, which is at least 10 times longer than the time scale in which we apply our external loading force. Thus, considering the relatively high frequencies applied, a viscous contribution toward the bacterial cell surface deformation can be neglected using the current protocol. It could be argued (Fig. 1) that during application of an external loading force, not only is the contact volume between the rigid, hard core of a bacterium and the substratum surface deformed, but the volume between the bacterium and the AFM cantilever is also deformed. However, the adhesion force of a negatively charged bacterium to a positively charged cantilever (due to the adsorbed α-poly-l-lysine layer) is much stronger than to a negatively charged glass surface (25–27), while furthermore, the bond between the cantilever and bacterium has had ample time to mature. From this, we conclude that the contact volume between the bacterium and cantilever can be considered undeformable. Nevertheless, the equations presented can be easily adjusted to include deformation of the contact volume between a bacterium and a cantilever. When for instance, both contact volumes would contribute equally to the deformation measured, δ should be replaced by δ/2, which would yield 2-fold-smaller values for h₀ and S₀, while reduced Young’s moduli would double.

In order to judge whether the results obtained using our new model are realistic, we selected pairs of bacterial strains with distinctly different cell surface features and cell wall characteristics within each pair. Within the pair of S. epidermidis strains, S. epidermidis ATCC 35983 produces the least EPS (20), explaining why the height of its contact cylinder is found to be smaller and its reduced Young’s modulus is higher than that for S. epidermidis ATCC 35984. Similarly, the differences in height and elasticity modulus between the isogenic S. salivarius strains can be ascribed to the difference in fibrillation of these strains. S. salivarius HB-7 possesses fibrils with a uniform length of 91 nm (18), and the contact cylinder, with a calculated height of 44 nm, is fully located within the fibrillar layer. However, at the surface of S. salivarius HB-C12, there are no fibrils (19), and the contact cylinder with a height of 28 nm extends well into the peptidoglycan layer of the bacterial cell wall, giving rise to a higher reduced Young’s modulus than for HB-7. The isogenic S. aureus strains differ with respect to the degree of cross-linking of their peptidoglycan layer. The peptidoglycan in the wall of S. aureus NCTC 8325-4 is highly cross-linked, whereas that of the isogenic mutant (Δpbp4 mutant) is deficient in cross-linking (21). Accordingly, the bacterial cell wall of S. aureus NCTC 8325-4 is more rigid than the cell wall of the Δpbp4 mutant, as indicated by the higher reduced Young’s modulus. Furthermore, the different values of the height of the contact cylinder reflect the difference in softness of the bacterial cell walls between the two strains and how far it extends toward the peptidoglycan layer (if not encompassing it). The fact that the method self-defines the dimensions of the contact cylinder is an important feature, as it makes the method applicable to highly complex bacterial cell walls, including those of Gram-negative strains that possess a double lipid membrane.

Application of the established Hertz model to our experimental data also yields pairwise differences in reduced Young’s moduli, demonstrating differences in cell surface features and cell wall characteristics within each pair of strains, similar to our new, elastic deformation model (Table 1). However, the reduced moduli derived from the Hertz model are orders of magnitude larger than those obtained from our proposed elastic deformation model. Thwaites and Mendelson (28) reported 10 MPa for the Young’s modulus of the peptidoglycan thread in Bacillus subtilis cell walls, which is in the same order of magnitude as obtained for the present collection of strains using the Hertz model. The high reduced Young’s moduli arrived in the Hertz model likely pertain mostly to the bacterial hard core. On the other hand, our model self-defines the dimensions of the contact volume. The heights of the contact cylinder derived are limited to several tens of nanometers and therefore clearly refer to the features of the outermost cell surface (with the evident exception of the staphylococcal strain that is deficient in peptidoglycan cross-linking). Accordingly, reduced Young’s moduli of bacterial contact volumes involved in adhesion derived by our model fall within the range of data published for the Young’s moduli of biopolymer gels (29, 30) and polyelectrolyte multilayers (31), generally ranging from 1 to 100 kPa. Thus, we believe that our elastic deformation model yields advantages over the use of other models like the Hertz model, as it accounts for the heterogeneous composition and viscoelastic properties of bacteria, which is especially important to identify the elastic properties of the bond between an adhering bacterium and a substratum surface.

In conclusion, a simple model is proposed to determine reduced Young’s modulus of the bond between adhering bacteria and substratum surfaces. The model is based on the measurement of the elastic deformation of an assumed cylindrical contact of constant volume and defines its own initial cylinder height. The resulting reduced Young’s moduli and the dimensions of the contact cylinders could be interpreted on the basis of the cell surface features and cell wall characteristics, i.e., surfaces that are more rigid (because of either lower fibrillation, lower EPS production, or higher degree of cross-linking of the peptidoglycan layer) have shorter contact cylinders and higher reduced Young’s moduli. Unlike the values found using the Hertz model, Young’s moduli derived for the contact volumes in our elastic deformation model correspond with Young’s moduli from the literature for biopolymer gels and polyelectrolyte multilayers. Application of the established Hertz model to our experimental data yields higher reduced Young’s moduli of all strains investigated, likely because the Hertz model pertains to a major extent to the more rigid peptidoglycan layer surrounding the bacterial cytoplasm and, unlike our elastic deformation model, does not distinguish between the soft outer bacterial cell surface and the hard core of bacterial cells.

Although our model is applicable to different bacterial strains and species, regardless of whether they are Gram positive or Gram negative, rod shaped or coccal, and the details of their surface structure and composition, it is more difficult to apply to rod-shaped organisms, because the orientation of a rod-shaped organism with respect to the AFM cantilever needs to be established and controlled. Moreover, for rod-shaped organisms, other assumptions may have to be made with respect to the geometry of the contact volume, which does not necessarily need to be cylindrical as was assumed for coccal organisms. However, as long as the assumption of constant volume for the contact volume during deformation is made, our proposed method can be applied without further modification or difficulty.

MATERIALS AND METHODS

Bacterial strains and culture conditions.

Three pairs of strains with different surface features were involved in this study. (i) S. epidermidis ATCC 35983 and ATCC 35984 are known as a poor and strong EPS producer, respectively (20). (ii) Isogenic S. salivarius HB-7 and HB-C12 are two related strains that differ in their possession of fibrillar surface appendages (18, 19). (iii) S. aureus NCTC 8325-4 and its isogenic Δpbp4 mutant differ in the degree of cross-linking of their peptidoglycan layer (21). Staphylococci were precultured from blood agar plates in 10 ml tryptone soya broth (Oxoid, Basingstoke, England), while streptococci were precultured from blood agar plates in 10 ml Todd-Hewitt broth (Oxoid). All precultures were grown for 24 h at 37°C. After 24 h, 0.5 ml of a preculture was transferred into 10 ml fresh medium, and the main culture was grown for 16 h at 37°C. Bacteria were harvested by centrifugation at 5,000 × g for 5 min, washed twice with 10 mM potassium phosphate buffer (pH 7.0) and finally suspended in the same buffer. When bacterial aggregates or chains were observed microscopically, the suspension was sonicated for 10 s at 30 W (Vibra Cell model 375; Sonics and Materials Inc., Danbury, CT) intermittently three times while the suspension was cooled in a water/ice bath.

AFM force spectroscopy.

Bacterial probes were prepared by immobilizing a bacterium to an NP-O10 tipless cantilever (Bruker, Camarillo, CA). Cantilevers were first calibrated by the thermal tuning method, and spring constants were always within the range given by the manufacturer (0.03 to 0.12 N/m). Next, a cantilever was mounted to the end of a micromanipulator and using a microscope to observe, the tip of the cantilever was dipped into a droplet of a 0.01% α-poly-l-lysine solution with a molecular weight (MW) ranging from 70,000 to 150,000 (Sigma-Aldrich, St. Louis, MO) for 1 min to create a positively charged layer. After 2 min of air drying, the tip of the cantilever was carefully dipped into a bacterial suspension droplet for 1 min to allow bacterial attachment through electrostatic attraction and dried in air for 2 min. Bacterial probes were always used immediately after preparation.

All force spectroscopy measurements were performed in 10 mM potassium phosphate buffer (pH 7.0) at room temperature on a BioScope Catalyst AFM (Bruker). In the method proposed, the bacterial probe was moved toward a glass microscope slide cleaned to a zero degree water contact angle (Gerhard Menzel GmbH, Braunschweig, Germany) at a constant velocity of 1 µm/s. During deformation, the force F_cant that was exerted by the cantilever was recorded as well as the displacement Δz of the sample stage as measured with the piezo-transducer of the AFM until a maximum loading force of 3 nN.

In order to verify that a bacterial probe enabled a single contact with the surface, a scanned image in AFM contact mode with a loading force of 1 to 2 nN was made at the onset of each experiment and examined for double contour lines. Double contour lines indicate that the AFM image is not prepared from the contact of a single bacterium with the surface but that multiple bacteria on the probe are in simultaneous contact with the substratum. Any probe exhibiting double contour lines were discarded. At this point, however, it must be noted that double contour line images seldom or never occurred, since it represents the unlikely situation that bacteria on the cantilever are equidistant to the substratum surface within the small range of the interaction forces, which is unlikely because the cantilever is contacting the substratum at an angle of less than 15°.

Before the actual deformation measurements were taken, five force-distance curves of a bacterial probe toward a clean glass surface were measured at a loading force of 3 nN, and the maximal adhesion forces upon retraction were recorded. After each deformation measurement on a new spot on the glass slide and after increase of the external loading force on a bacterium up to 3 nN, the bacterial probe was retracted from the glass substratum, and the maximal adhesion force was measured again. Whenever the maximal adhesion force recorded differed more than 1 nN from the initial value, the bacterial probe was regarded as damaged and replaced by a new one.