An efficient sequential design of clinical trials

Abstract

We propose an efficient group sequential monitoring rule for clinical trials. At each interim analysis both efficacy and futility are evaluated through a specified loss structure together with the predicted power. The proposed design is robust to a wide range of priors, and achieves the specified power with a saving of sample size compared to existing adaptive designs. A method is also proposed to obtain a reduced-bias estimator of treatment difference for the proposed design. The new approaches hold great potential for efficiently selecting a more effective treatment in comparative trials. Operating characteristics are evaluated and compared with other group sequential designs in empirical studies. An example is provided to illustrate the application of the method.

1. Introduction

With large numbers of experimental agents in the developing process, there is an increasing need for innovative clinical trial designs that allow effective agents to be identified more efficiently compared with the standard designs. Group sequential designs have the flexibility to use cumulated information to modify the subsequent course of the trial. Monitoring a group sequential clinical trial is a dynamic process. The time of performing an interim analysis in a group sequential trial is a natural time to update and combine the information from prior experience and accumulated data using Bayesian methods. The decision-theoretic approach has the potential ability to concurrently consider efficacy, futility and cost (Berry, 1994). Although there is no explicit specification for the type I and II error rates when determining the maximum sample size, the decisions leading to false-positive and false-negative conclusions may be taken into account through a loss structure to satisfy regulatory settings (Berry and Ho, 1988; and Lewis and Berry, 1994).

In contrast to previous work in the area, Cheng and Shen (2005) proposed an adaptive design using the Bayesian decision-theoretic approach, which allowed the maximum sample size to be random. The design keeps the virtue of the self-designing trial in the frequentist framework (Fisher, 1998; Shen and Fisher, 1999). An algebraic expression that connects the overall type I error rate and the parameters of the loss function was established, so that the desired frequentist properties can be satisfied for regulatory settings. Later, the possibility of inefficient performance by the adaptive designs was raised by Jennison and Turnbull (2006). We recognized the limitations in terms of efficiency in the work of Cheng and Shen (2005), similar to the design of Shen and Fisher (1999). The realized type I error rate is often smaller than the specified significance level. Moreover, the procedures that are based on the non-sufficient statistics may increase the type II error rate with or without the decreased type I error rate. The monitoring procedures for continuing or stopping the trial based on the loss function alone are often not sensitive enough to fully reflect the evidence of operation characteristics at interim analysis. This issue motivated us to search for a more efficient group sequential design within this framework. Our goal of efficient clinical trial design is to minimize the overall sample size while maintaining the specified error rates under regulatory settings (Jennison & Turnbull, 2000, Ch.10). By combining the strengths of the Bayesian approach in establishing a procedure and the frequentist approach in evaluating the procedure, we propose a design that assesses the predicted power and the expected loss at each interim analysis and makes decisions based on these two factors. The maximum sample size is sequentially determined using interim data. The overall type I error rate can be controlled by choosing related designing parameters.

Similar to other sequential clinical trials, the standard estimator of the treatment difference, such as sample mean or posterior mean in this setting, is often biased. Methods in the literature for constructing unbiased or nearly unbiased estimators are not directly applicable to the estimator of parameter following the proposed design because of the random maximum sample size. In this article, we develop a new procedure of estimation aimed at minimizing the bias. The proposed estimation procedure is general and may be applied to other group sequential designs.

The remainder of this article is organized as follows. In Section 2 we present the proposed design, decision rules and the related properties. In Section 3 we derive the critical region and evaluate the frequentist properties with normal responses. We describe a new estimation procedure for the proposed design in Section 4. We conduct a simulation study and compare our inference with the existing adaptive and classical group sequential designs in Section 5. We apply the proposed design to an example in Section 6 and conclude in Section 7.

2. New design and main results

Consider a clinical trial that compares a new treatment T with a control C, where the individual treatment response is X_T and the individual control response is X_C. For notation simplicity, we assume a design with equal randomization, which can be easily extended to more general two-arm trials. The block size at each stage is 2B_i, i = 1, 2, …, where B_i for each treatment arm is fixed before the trial starts, but the maximum number of blocks is not predetermined and is determined using interim data.

Let X̄_Ti and X̄_Cibe the observed mean responses in the ith block. Given the parameter of interest, θ, which is a measure of the treatment difference, let

$$X_i={\overline{X}}_{T_i}-{\overline{X}}_{C_i}~F_i(·\mid \theta ),\text{and}\theta ={\int }_{-\infty }^{\infty }{\mathit{xdF}}_i(x\mid \theta ).$$

The one-sided hypothesis to be tested is

$$H_0:\theta \le 0\text{versus}{H}_1:\theta >0.$$

Within a Bayesian framework, assume that θ has a prior distribution π with E(θ|π) = δ.

2.1. Decision Rule

The loss structures may be devised from the perspective of the investigators, patients, and/or stockholders via the data monitoring committee (Gittins & Pezeshk, 2000). It has become a common practice to include patient advocates on data and safety monitoring committees for the conduct of clinical trials. We define a loss structure consisting of the respective cost of making a false-positive conclusion, a false-negative conclusion, and the cost of the total sample, in which the risk and benefit of the new agent under investigation should be balanced via these cost parameters.

Let D be the decision of either accepting (A) or rejecting (R) null hypothesis. At the jth interim analysis, the loss function is defined by

$$L(\theta ,D,j)=L(\theta ,D)+2K_2\sum _{i=1}^j{B}_i,$$ (2.1)

where

$$L(\theta ,D)=K_0{h}_0(\theta )I\{\theta \le 0,D=R\}+K_1{h}_1(\theta )I\{\theta >0,D=A\},$$

K₀ is a constant and positive penalty for each unit of h₀(θ) when H₀ is incorrectly rejected, and K₁ is a positive penalty for each unit of h₁(θ) when H₀ is incorrectly accepted. Here, h₀(·) and h₁(·) are positive and continuous functions, and the positive loss may change with the actual value of θ. One sensible choice is to allow the loss function to change with the magnitude of θ, such as h₀(θ) = h₁(θ) = |θ|^w + c with c ≥ 0 and w > 0. In this case, the loss to accept the null hypothesis increases as the distance of a positive θ to zero gets larger. Similarly, the loss to reject H₀ increases as a negative θ deviates from zero further. The unit cost of each sample, K₂, is relative to K₀ and K₁, which should be much smaller than K₀ and K₁. Another special case for the type of loss functions is the commonly used 0-K_i loss, with h₀(θ) = h₁(θ) = 1. Following a common convention that making a false-positive conclusion leads to a more severe penalty than making a false-negative conclusion, we let K₀ > K₁.

Let = {X_1, …, X_j} be the accumulated data up to step j, where X_j represents data from the jth block. At each interim analysis the study will be terminated for futility or for efficacy if the evidence is strong enough. Otherwise, the study will continue to (j + 1)th block. The loss function related to the above two decisions at the jth interim analysis is defined as the expected loss of stopping the trial and accepting the null hypothesis, that is,

$$L_A({\mathcal{X}}_j)=E\left\{L(\theta ,A,j)\mid {\mathcal{X}}_j\right\},$$

and the predicted loss of continuing the trial to the (j + 1)th block,

$$L_{\mathit{cont}}({\mathcal{X}}_j)=E\left[\underset{D=AorR}{min}E\{L(\theta ,D,j+1)\mid {\mathcal{X}}_{j+1}\}|{\mathcal{X}}_j\right].$$ (2.2)

To better achieve the targeted power while minimizing the total sample size, we incorporate the predicted power into the monitoring rules. We consider this type of the group sequential designs motivated by internal reasons in view of the interim data on the primary endpoint. As discussed by Jennison & Turnbull (2006), it is proper to increase the remaining sample size if continuing as planned would give low conditional power under θ = δ; an interim estimate of θ̂ still represents a worthwhile clinical improvement. In this case, extending the study could ensure the desired power under the estimated effect size. Our goal is to achieve a desired power at an anticipated effective size with the flexibility that the desired power may be preserved at the true effective size (θ) when the true effective size deviates from the anticipated size within a certain extension. Of course, there is a realistic limitation to such a deviation. In our numerical study (Section 5), the values of θ are mostly limited to the set {θ: |θ − δ| < 0.5δ}. Since the proposed design is intended to achieve the desired power at θ, the true efficacy value in a given range, it is natural to use the current posterior mean as an estimator of θ to evaluate the conditional power.

Given data observed up to the jth block, letting δ_j be the posterior mean of θ given , the predicted power related to the critical region R_j+1, is defined as P(R_j+1|θ = δ_j, ), where

$$R_{j+1}=\left\{{\mathcal{X}}_{j+1}:E\{L(\theta ,A,j+1)\mid {\mathcal{X}}_{j+1}\}>E\{L(\theta ,R,j+1)\mid {\mathcal{X}}_{j+1}\}\right\}.$$ (2.3)

Definition 2.1

The proposed design follows a two-step decision rule described below, where M is the total number of interim analysis and the procedure starts from j = 1.

1. If L_A( ) ≤ L_cont( ), terminate the trial and accept H₀ at the jth step, let M = j.

2. If L_A( ) > L_cont( ), evaluate the predicted power.

   1. If the predicted power P(R_j+1| θ = δ_j; ) ≥ 1 − β, terminate the trial, let M = j. If E{L(θ, A, M)| 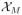} > E{L(θ, R, M)| 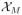}, reject H₀, otherwise accept H₀.

   2. If P(R_j+1|θ = δ_j, ) < 1 − β, continue the trial to the j + 1th analysis and repeat 1 and 2.

Remark 2.1

In our earlier work (Cheng and Shen, 2005), the decision at block j to stop the trial and reject null hypothesis for efficacy is only based on L_R( ) = E{L(θ, R, j)| }, if it is no greater than L_cont( ). The design parameters, such as penalties for making wrong decisions in the typical decision-theoretic approaches are often searched empirically to match with the specified error rates by trial and error. As a result, the design may not be efficient regarding the sample size. One advantage of using the predicted power directly in the course of procedure is the ability to stop the trial whenever evidence favoring the experimental treatment is sufficient. Otherwise, we continue the trial to gain more information about the treatments. Further comparison is presented in the numerical study section of this paper.

2.2. Properties

Some practical concerns need to be addressed, specifically, whether the trial will be terminated with a finite number of interim analysis and whether the decision rules lead to a correct recommendation with the specified probabilities. The following Theorems 2.1 and 2.2 confirm that these desirable properties hold asymptotically with the proposed design. The proofs of the theorems are given in Appendix A.

Theorem 2.1

Let M be the total number of blocks following the proposed decision procedures. Assuming that the prior density of θ, π(θ), satisfies certain regularity conditions, h₀(θ) and h₁(θ) are positive and continuous functions of θ, there exists a positive w such that

$$\underset{0\to -\infty }{lim}{h}_0(\theta )/(1+{\mid \theta \mid }^w)=0,\underset{\theta \to \infty }{lim}{h}_1(\theta )/(1+{\mid \theta \mid }^w)=0$$

almost surely, and that K₀, K₁ and K₂ are positive, then

$$P_{\theta }(M<+\infty )=1$$

if θ ≠ 0; When θ = 0, P₀(M < +∞) = 1 if K₁h₁(0) < 2BK₂, where 2B is the minimum block size.

Theorem 2.1 shows that with probability 1 the trial will be terminated with a finite number of interim analysis. The regularity conditions are specified by Schervish (1995, p. 429).

Theorem 2.2

Under the conditions of Theorem 2.1, let θ* denote the true treatment difference, then

$$\underset{j\to \infty }{lim}\left[E\{L(\theta ,A,j)\mid {\mathcal{X}}_j\}-E\{L(\theta ,R,j)\mid {\mathcal{X}}_j\}\right]=\{\begin{array}{ll}-K_0{h}_0({\theta }^{\ast }),\hfill & \text{if}{\theta }^{\ast }<0;\hfill \\ K_1{h}_1({\theta }^{\ast }),\hfill & \text{if}{\theta }^{\ast }>0\hfill \end{array}$$ (2.4)

almost surely. When θ* > 0, $\underset{j\to \infty }{lim}{P}_{{\theta }^{\ast }}(R_{j+1}\mid \theta ={\delta }_j,{\mathcal{X}}_j)=1$ almost surely. When θ* = 0,

$$\underset{j\to \infty }{lim}{P}_0\left[E\{L(\theta ,A,j)\mid {\mathcal{X}}_j\}-E\{L(\theta ,R,j)\mid {\mathcal{X}}_j\}<0\right]=\frac{K_0{h}_0(0)}{K_1{h}_1(0)+K_0{h}_0(0)}.$$

The condition on K₂ > 0, i.e., a positive cost for enrolling each patient, is critical to avoid unnecessary extension of the trial under H₀. Theorem 2.2 ensures that with the proposed monitoring strategies, it is expected that E{L(θ, A)| } > E{L(θ, R)| } (since K₁h₁(θ*) > 0) and the predicted power P_θ^* (R_j+1| θ = δ_j, ) will be near 1 asymptotically under the alternative hypothesis. When the true treatment difference θ* < 0, we should expect that E{L(θ, A)| }< E{L(θ, R)| }(since −K₀h₀(θ*) < 0) and the predicted power remains small, so that the trial will conclude futility with enough data. When θ* = 0, where zero is the boundary value for the two hypotheses, the probability to conclude futility approximates to K₀h₀(0)=(K₁h₁(0) + K₀h₀(0)), which is connected to the type I error rate. For a special case in which h₀(0) = h₁(0), this limit becomes K₀=(K₀ + K₁). We will give more details of this matter in Section 3.2.

2.3. Computation

There are three key elements in the decision rule, L_A( ), L_cont( ), and the predicted power P(R_j+1|θ = δ_j, ). We derive the computational formulation for each as follows. Given data observed up to the jth block and loss function defined in (2.1), the expected loss of accepting H₀ can be expressed as

$$L_A({\mathcal{X}}_j)=E\left\{L(\theta ,A,j)\mid {\mathcal{X}}_j\right\}=2K_2\sum _{i=1}^j{B}_i+K_1{\int }_0^{\infty }{h}_1(\theta )\pi (\theta \mid {\mathcal{X}}_j)d\theta ,$$ (2.5)

where π (·| ) is the posterior density function of θ given . Similarly,

$$L_R({\mathcal{X}}_j)=E\left\{L(\theta ,R,j)\mid {\mathcal{X}}_j\right\}=2K_2\sum _{i=1}^j{B}_i+K_0{\int }_{-\infty }^0{h}_0(\theta )\pi (\theta \mid {\mathcal{X}}_j)d\theta .$$ (2.6)

Expressions (2.5) and (2.6) provide the computational formulation for the two components, E{L(θ, A, j + 1)| } and E{L(θ, R, j + 1)| 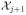}, of L_cont( ) defined in (2.2). The outside expectation on the right-hand side of (2.2) is determined with respect to the conditional distribution of X_j+1 given . When F(·|θ) has a density function f(·|θ), the conditional density of X_j+1 given can be expressed as:

$$g(x\mid {\mathcal{X}}_j)={\int }_{-\infty }^{\infty }\pi (\theta \mid {\mathcal{X}}_j)F(x\mid d\theta )={\int }_{-\infty }^{\infty }f(x\mid \theta )\pi (\theta \mid {\mathcal{X}}_j)d\theta .$$

The last element is the predicted power P(R_j+1|θ = δ_j, ), where R_j+1 is defined in (2.3), and can be expressed as

$$R_{j+1}=\left\{{\mathcal{X}}_{j+1}:{\int }_0^{\infty }{h}_1(\theta )\pi (\theta \mid {\mathcal{X}}_{j+1})d\theta >\frac{K_0}{K_1}{\int }_{-\infty }^0{h}_0(\theta )\pi (\theta \mid {\mathcal{X}}_{j+1})d\theta \right\},$$ (2.7)

for j = 0, 1, …, M − 1.

3. Applications with normal responses

To illustrate the design procedures in application, we assume that the outcomes follow normal distributions. For simplicity of notation, let

$$\begin{array}{l}{\overline{X}}_{T_i}~N({\mu }_{\text{T}},{\sigma }^2/(2B_i)),{\overline{X}}_{C_i}~N({\mu }_{\text{C}},{\sigma }^2/(2B_i)),\\ X_i={\overline{X}}_{T_i}-{\overline{X}}_{C_i}~N(\theta ,{\sigma }^2/B_i),\end{array}$$

where σ² is known. (It is not conceptually different with an unknown variance.) The prior distribution for θ is assumed to be N(δ, σ²/B₀), where B₀ can be interpreted as the equivalent sample size on which the prior information is based (Spiegelhalter et al, 1994). Typically, B₀ is much smaller than B_j so that the prior information plays a minor role in the decision process. We let X₀ = δ to keep the notation for prior information coherent with that from the interim analysis. After data from the first j blocks are observed, letting $n_j={\sum }_{i=0}^j{B}_i$, the posterior distribution of θ is $N({\delta }_j,s_j^2)$, where

$${\delta }_j=\frac{{\sum }_{i=0}^j{B}_i{X}_i}{n_j}\text{and}{s}_j^2=\frac{{\sigma }^2}{n_j}$$

are the posterior mean and variance, respectively.

Consider the following function in the loss structure: h₀(θ) = h₁(θ) = h(θ) = |θ| + c, where c is a nonnegative constant. This function increases linearly with the distance of θ from zero, when an incorrect action is taken. It satisfies the conditions of Theorems 2.1 and 2.2 when cK₁ < 2BK₂.

3.1. Expected losses and predicted power

For h(θ) = |θ| + c and normal responses, we provide explicit expressions for the three key elements, L_A( ), L_cont( ) and the predicted power P(R_j+1|θ = δ_j, ), in the decision rule through the following three propositions, respectively.

Proposition 3.1

Let h₀(θ) = h₁(θ) = |θ| + c. We have

$$L_A({\mathcal{X}}_j)=2K_2\sum _{i=1}^j{B}_i+K_1\left\{{\delta }_j\mathrm{\Phi }({\delta }_j/s_j)+s_j\phi ({\delta }_j/s_j)+c\mathrm{\Phi }({\delta }_j/s_j)\right\},$$ (3.1)

$$L_R({\mathcal{X}}_j)=2K_2\sum _{i=1}^j{B}_i+K_0\left\{-{\delta }_j\mathrm{\Phi }(-{\delta }_j/s_j)+s_j\phi ({\delta }_j/s_j)+c\mathrm{\Phi }(-{\delta }_j/s_j)\right\}.$$ (3.2)

where φ(·) and Φ (·) are the standard normal probability density function and cumulative distribution function, respectively.

Proof

Since the posterior distribution of θ given follows $N({\delta }_j,s_j^2)$, it can be verified that

$$\begin{array}{l}{\int }_0^{\infty }\theta \pi (\theta \mid {\mathcal{X}}_j)d\theta ={\delta }_j\mathrm{\Phi }({\delta }_j/s_j)+s_j\phi ({\delta }_j/s_j),\\ {\int }_0^{\infty }\pi (\theta \mid {\mathcal{X}}_j)d\theta =\mathrm{\Phi }({\delta }_j/s_j).\end{array}$$ (3.3)

Applying the result of (3.3) to the right-hand side of (2.5). The expression of (3.1) is obtained. By a similar argument, noting that 1 − Φ(x) = Φ(−x), expression (3.2) can be obtained as well.

The computational formula for L_cont( ) defined by (2.2) is derive by the following proposition.

Proposition 3.2

Let h₀(θ) = h₁(θ) = |θ| + c. Then

$$L_{\mathit{cont}}({\mathcal{X}}_j)=2K_2\sum _{i=1}^{j+1}{B}_i+{\int }_{-\infty }^{\infty }min\{l_A(x\mid {\delta }_j),l_R(x\mid {\delta }_j)\}\frac{1}{{\sigma }_{j+1}}\phi \left(\frac{x-{\delta }_j}{{\sigma }_{j+1}}\right)dx,$$ (3.4)

where ${\sigma }_{j+1}^2=s_j^2+{\sigma }^2/B_{j+1}$.

Proof

Let l_D(x|δ_j) define the integral term of L_D( 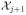) given by the right-hand side of (2.5) and (2.6), where D = A or R. Substituting j by j + 1 in equations (3.1) and (3.2), the second term on the right-hand side of each equation gives, respectively, the expression of l_A(x|δ_j) and l_R(x|δ_j) below:

$$\begin{array}{l}{l}_A(x\mid {\delta }_j)=K_1\left\{({\delta }_{j+1}+c)\mathrm{\Phi }\left(\frac{{\delta }_{j+1}}{s_{j+1}}\right)+s_{j+1}\phi \left(\frac{{\delta }_{j+1}}{s_{j+1}}\right)\right\},\\ l_R(x\mid {\delta }_j)=K_0\left\{(-{\delta }_{j+1}+c)\mathrm{\Phi }\left(-\frac{{\delta }_{j+1}}{s_{j+1}}\right)+s_{j+1}\phi \left(\frac{{\delta }_{j+1}}{s_{j+1}}\right)\right\}.\end{array}$$ (3.5)

Given and X_j+1 = x, the posterior mean δ_j+1 satisfies the following recursive equation in terms of δ_j and x:

$${\delta }_{j+1}=\frac{B_{j+1}{s}_{j+1}^2}{{\sigma }^2}x+\frac{s_{j+1}^2}{s_j^2}{\delta }_j.$$

It is known that the conditional distribution of X_j+1 given is also normal, specifically,

$$X_{j+1}\mid {\mathcal{X}}_j~N({\delta }_j,s_j^2+{\sigma }^2/B_{j+1}).$$

Thus, we have (3.4) since ${\sigma }_{j+1}^2=s_j^2+{\sigma }^2/B_{j+1}$.

The next proposition provides a recursive expression for the estimated probability of the rejection region.

Proposition 3.3

Let h₀(θ) = h₁(θ) = |θ| + c. Then

$$P\left(R_{j+1}\mid \theta ={\delta }_j,{\mathcal{X}}_j\right)=\mathrm{\Phi }\left(\frac{{\delta }_j\sigma -{\xi }_{j+1}\sigma s_{j+1}}{s_{j+1}^2\surd B_{j+1}}\right),$$ (3.6)

where ξ_j is the unique solution of the following equation in variable x:

$$(1-2r)\left\{s_{j}x\mathrm{\Phi }(x)+s_j\phi (x)\right\}+c\mathrm{\Phi }(x)+r{s}_{j}x=cr$$

and r = K₀=(K₀ + K₁).

Proof

In view of (3.3) and that h(θ) = |θ|+c, the critical region R_j defined by (2.7) can be expressed as

$$\begin{array}{l}{R}_j=\left\{{\mathcal{X}}_j:{\int }_0^{\infty }h(\theta )\pi (\theta \mid {\mathcal{X}}_j)d\theta >\frac{K_0}{K_1}\left\{E(h(\theta )\mid {\mathcal{X}}_j)-{\int }_0^{\infty }h(\theta )\pi (\theta \mid {\mathcal{X}}_j)d\theta \right\}\right\}\\ =\left\{{\mathcal{X}}_j:{\int }_0^{\infty }(\theta +c)\pi (\theta \mid {\mathcal{X}}_j)d\theta \ge r\left\{-{\delta }_j+2{\int }_0^{\infty }\theta \pi (\theta \mid {\mathcal{X}}_j)d\theta +c\right\}\right\}\\ =\left\{{\mathcal{X}}_j:(1-2r)\left\{{\delta }_j\mathrm{\Phi }\left(\frac{{\delta }_j}{s_j}\right)+s_j\phi \left(\frac{{\delta }_j}{s_j}\right)\right\}+c\mathrm{\Phi }\left(\frac{{\delta }_j}{s_j}\right)+r{\delta }_j\ge cr\right\},\end{array}$$ (3.7)

where r = K₀=(K₀ + K₁). For given constants c > 0, s > 0, and 0 < r < 1, it can be verified that the continuous function

$$u(x,s,r)=(1-2r)\{sx\mathrm{\Phi }(x)+s\phi (x)\}+c\mathrm{\Phi }(x)+\mathit{rsx}$$ (3.8)

increases in x, lim_x→−∞ u(x, s, r) = −∞, and lim _x→+∞u(x, s, r) = +∞. By the intermediate value theorem, there exists a unique real number ξ_j such that

$$R_j=\{{\mathcal{X}}_j:u({\delta }_j/s_j,s_j,r)>rc\}=\{{\mathcal{X}}_j:{\delta }_j/s_j>{\xi }_j\},$$ (3.9)

where ξ_j is obtained by solving equation u(x, s_j, r) = rc for x. It is easy to see that

$$X_{j+1}|\theta ={\delta }_j,{\mathcal{X}}_j~N\left({\delta }_j,\frac{{\sigma }^2}{B_{j+1}}\right).$$ (3.10)

The posterior mean satisfies the following recursive equation:

$${\delta }_{j+1}=\frac{B_{j+1}{s}_{j+1}^2}{{\sigma }^2}{X}_{j+1}+\frac{s_{j+1}^2}{s_j^2}{\delta }_j.$$

In addition to the fact that ${\sigma }^2/s_j^2+B_{j+1}={\sigma }^2/s_{j+1}^2$, we have

$$\frac{{\delta }_{j+1}}{s_{j+1}}=\frac{s_{j+1}\surd B_{j+1}}{\sigma }\left(\frac{X_{j+1}-{\delta }_j}{\sigma /\surd B_{j+1}}\right)+\frac{{\delta }_j}{s_{j+1}}.$$ (3.11)

Following (3.9) through (3.11), the predicted power, P(R_j+1| θ = δ_j, ), after observing j blocks of data can be expressed as

$$P\left(\frac{{\delta }_{j+1}}{s_{j+1}}>{\xi }_{j+1}|\theta ={\delta }_j,{\mathcal{X}}_j\right)=\mathrm{\Phi }\left(\frac{{\delta }_j\sigma -{\xi }_{j+1}\sigma s_{j+1}}{s_{j+1}^2\surd B_{j+1}}\right).$$

Hence, (3.6), the following expression for the predicted power, is derived.

The expressions (3.1), (3.4), and (3.6) are computationally straightforward and hence the decision procedures are user-friendly to carry out.

3.2. Connection to type I error rate

Our goal in this section is to find a connection between the type I error rate and K₀/K₁ in the loss function, so that the operating characteristic can be directly assessed and ensured.

Recall that K₀/(K₀ + K₁) = r, equivalently,

$$K_0/K_1=r/(1-r).$$ (3.12)

The following two terms are defined for the preparation of Proposition 3.4 and its proof.

Let

$$\xi =\{\begin{array}{ll}\sqrt{Z_{\alpha /2}+n_0{\delta }^2/{\sigma }^2},\hfill & \text{if}{n}_1\le {\sigma }^2{Z}_{\alpha /2}/{\delta }^2+n_0;\hfill \\ Z_{\alpha /2}\sqrt{1-n_0/n_1}+\frac{n_0\delta }{\sigma \surd n_1},\hfill & \text{if}{n}_1>{\sigma }^2{Z}_{\alpha /2}^2/{\delta }^2+n_0\hfill \end{array}$$ (3.13)

and

$$r=\{\begin{array}{ll}\mathrm{\Phi }(\xi ),\hfill & \text{if}\mathrm{\Phi }(\xi )>v(\xi );\hfill \\ \frac{s_1\{\xi \mathrm{\Phi }(\xi )+\phi (\xi )\}+c\mathrm{\Phi }(\xi )}{s_1\{2\xi \mathrm{\Phi }(\xi )+2\phi (\xi )-\xi \}+c},\hfill & \text{if}\mathrm{\Phi }(\xi )\le v(\xi ),\hfill \end{array}$$ (3.14)

where

$$v(\xi )=\frac{\xi \mathrm{\Phi }(\xi )+\phi (\xi )}{2\xi \mathrm{\Phi }(\xi )+2\phi (\xi )-\xi }.$$ (3.15)

Proposition 3.4

Let h₀(θ) = h₁(θ) = |θ| + c. For K₀=K₁ defined by (3.13) through (3.12), the probability of having a false positive conclusion is controlled under the nominal significance level α. Moreover, the probability to conclude futility at θ = 0 in Theorem 2.2 with h₀(0) = h₁(0) is K₀=(K₀+K₁), which is greater than or equal to 1 − α.

Proof

In light of (3.7), the probability to reject the null hypothesis can be expressed as

$$P(R_j\mid \theta =0)=P\left\{u({\delta }_j/s_j,s_j,r)>rc|\theta =0\right\}.$$

Since u(x, s, r) defined by (3.8) is increasing in x and linear in s, noting that 0 < s ≤ s₁, u(δ_j/s_j, s_j, r) > rc leads to

$$max\left\{u({\delta }_j/s_j,s_1,r),u({\delta }_j/s_j,0,r)\right\}>rc,$$ (3.16)

we have

$$P(R_j\mid \theta =0)\le P\left(\frac{{\delta }_j}{s_j}>\xi |\theta =0\right)=\mathrm{\Phi }\left\{\frac{n_0\delta -\xi \sigma \surd n_j}{\sigma \surd (n_j-n_0)}\right\},$$ (3.17)

where ξ = min{u⁻¹(rc, s₁, r), u⁻¹(rc, 0, r)}. The last equation holds due to the fact that

$$\frac{{\delta }_j}{s_j}|\theta =0~N\left(\frac{n_0\delta }{\sigma \surd n_j},\frac{n_j-n_0}{n_j}\right).$$

For a given upper boundary (e.g. α) to the probability in the right-hand side of (3.17), the corresponding quantile ξ can be derived. Once ξ is obtained, we can calculate r and then the ratio of K₀ and K₁ subsequently.

Because efficacy is assessed at each interim analysis, we shall use α (j) at the jth interim in order to control the overall type I error rate at α (Slud and Wei, 1982). Let

$$\alpha (0)=0,\mathrm{\hspace{0.17em} }\alpha (j)=\sum _{i=1}^j\frac{1}{2^i}\alpha ,\text{for}j=1,2,3,\dots ,$$

where α (j) monotonically increases in j and lim_j→∞ α (j) = α (i.e. α (M) ≤ α). Use the conservative upper boundary α (1) for all j ≥ 1 in the above inequality,

$$\underset{n_j:j\ge 1}{sup}\mathrm{\Phi }\left\{\frac{n_0\delta -\xi \sigma \surd n_j}{\sigma \surd (n_j-n_0)}\right\}\le \alpha (1),$$ (3.18)

which leads to P(R_j|θ = 0) ≤ α (1) < α for all j.

We need to solve the inequality (3.18) for ξ. Following the argument of the first derivative, it can be shown that the component inside of Φ, which is (n₀δ − ξσ√n_j)/{σ√ (n_j − n₀)}, as a function of n_j, increases when 0 < n_j < (ξσ/δ)² and decreases when (ξσ/δ)² < n_j < ∞. Therefore,

$$\underset{j\ge 1}{sup}\mathrm{\Phi }\left\{\frac{n_0\delta -\xi \sigma \surd n_j}{\sigma \surd (n_j-n_0)}\right\}\le \{\begin{array}{ll}\mathrm{\Phi }\left\{-\frac{\surd ({\xi }^2{\sigma }^2-n_0{\delta }^2)}{\sigma }\right\},\hfill & \text{if}{n}_1\le {(\xi \sigma /\delta )}^2;\hfill \\ \mathrm{\Phi }\left\{\frac{n_0\delta -\xi \sigma \surd n_1}{\sigma \surd (n_1-n_0)}\right\},\hfill & \text{if}{n}_1>{(\xi \sigma /\delta )}^2.\hfill \end{array}$$

Letting each expression on the right-hand side of the last inequality be less than or equal to α (j), it yields

$$\xi \ge \{\begin{array}{ll}\sqrt{Z_{\alpha (j)}^2+n_0{\delta }^2/{\sigma }^2},\hfill & \text{if}{n}_1\le {\sigma }^2{Z}_{\alpha (j)}^2/{\delta }^2+n_0;\hfill \\ Z_{\alpha (j)}\sqrt{1-n_0/n_1}+\frac{n_0\delta }{\sigma \surd n_1},\hfill & \text{if}{n}_1>{\sigma }^2{Z}_{\alpha (j)}^2/{\delta }^2+n_0.\hfill \end{array}$$

By using the conservative upper boundary α (1) = α/2 instead of α (j) in the above derivation, (3.13) is verified. Next, we find the algebraic expression for r. In light of (3.16) and (3.17), ξ and r satisfy the equation:

$$max\{u(\xi ,s_1,r),u(\xi ,0,r)\}=rc,$$

where u is defined by (3.8). For the scenario of max{u(ξ, s₁, r), u(ξ, 0, r)} = u(ξ, 0, r) = cΦ(ξ), cΦ(ξ) = rc implies r = Φ(ξ). For the complementary scenario of max{u(ξ, s_1, r); u(ξ, 0, r)} = u(ξ, s₁, r), it occurs if and only if r ≤ v(ξ), where v(ξ) is defined by (3.15). Hence (3.14) can be verified after working out the algebra in solving u(ξ, s₁, r) = rc for r.

In general, the choice of constants K_i depends on the objectives of a trial. In a special case: when h_i(θ) = 1 for i =0, 1, K₀ and K₁ are the costs of making type I and type II errors, respectively, relative to the cost of enrolling a patient, K₂.

4. Estimation following the proposed design

After the inference, the estimation of θ is often of interest. It is well known that the naive estimate of θ (sample mean) following a classical group sequential design is biased. This phenomenon also occurs with the posterior mean of θ following the proposed design. Typically, θ is overestimated for trials concluding efficacy and underestimated for trials concluding futility.

We take a different perspective and approach to all existing methods. Since θ is the treatment difference, it is reasonable to assume that the domain of θ, denoted as 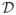, is bounded and can be predetermined. Let δ_M and s_M be the posterior mean and posterior standard deviation of θ from the original data at the end of the trial that follows the proposed design. We perform a grid search to find a near unbiased estimator of θ in 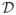based on Monte Carlo simulations.

Because the proposed efficient design (ED) is uniquely determined by a set of design parameters, we denote such a design as ED(δ, K₀, K₁, K₂, B₀, B₁, B, β). Let 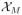be the original data collected under the specified design ED(δ, K₀, K₁, K₂, B₀, B₁, B, β). To perform a grid search, we divide 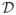into N subintervals with an equal length. The partition is fine enough, so that the midpoint θ_n in the nth subinterval is representative for the nth interval and θ_n, n = 1, · · ·, N, should cover the whole .

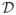Definition 4.1

The simulation based estimation procedure follows:

1. For each θ_n, we simulate one data set from N (θ_n, σ²/B_i) by applying the same monitoring rules of ED(δ, K₀, K₁, K₂, B₀, B₁, B, β) as in the original trial. At the end of the simulated trial, compute the posterior mean of θ_n. To stabilize the estimation, we repeat the procedure for L times and denote the posterior mean from the lth simulation as ${\widehat{\delta }}_{{\theta }_n}^{(l)}$ for each θ_n. We denote the average of the posterior means from the L simulations as

   $${\zeta }_{MC}({\theta }_n\mid L)=\frac{1}{L}\sum _{l=1}^L{\widehat{\delta }}_{{\theta }_n}^{(l)}.$$
2. When ζ_MC(θ_n|L), n = 1,…, N, are computed, the estimator θ̂ will be searched from {θ₁,· · ·, θ_N} with the following criterion: among all candidates in {θ₁, · · ·, θ_N}, ζ_MC(θ̂|L) is the closest to δ_M, where δ_M is the posterior mean obtained from the observed data, i.e.,

   $$\widehat{\theta }=arg\underset{{\theta }_n\in \mathcal{D}}{min}\left|{\zeta }_{MC}({\theta }_n\mid L)-{\delta }_M\right|=arg\underset{{\theta }_n\in \mathcal{D}}{min}{\left\{{\zeta }_{MC}({\theta }_n\mid L)-{\delta }_M\right\}}^2.$$ (4.1)

We reason that the θ̂ proposed in (4.1) is a reduced-bias estimator. Let g(θ) = E_θ (δ_M). For any given θ_n, we have

$$E_{{\theta }_n}\left\{{\zeta }_{MC}({\theta }_n\mid L)\right\}=\frac{1}{L}\sum _{l=1}^L{E}_{{\theta }_n}({\widehat{\delta }}_{{\theta }_n}^{(l)})=g({\theta }_n).$$

It is realistic to assume that the ${\mathit{Var}}_{{\theta }_n}({\widehat{\delta }}_{{\theta }_n}^{(1)})$ is uniformly bounded when θ_n takes a value in a predetermined bounded domain 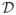. Based on the above estimation procedure (1), we have

$${\mathit{Var}}_{{\theta }_n}\left\{{\zeta }_{MC}({\theta }_n\mid L)\right\}=\frac{1}{L^2}\sum _{l=1}^L{\mathit{Var}}_{{\theta }_n}({\widehat{\delta }}_{{\theta }_n}^{(l)})=O(1/L)$$

uniformly for θ_n in 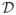. Moreover,

$$\begin{array}{l}{E}_{\theta ,{\theta }_n}{\left\{{\zeta }_{MC}({\theta }_n\mid L)-{\delta }_M\right\}}^2=E_{\theta ,{\theta }_n}{\left\{{\zeta }_{MC}({\theta }_n\mid L)-g({\theta }_n)+g({\theta }_n)-{\delta }_M\right\}}^2\\ ={\mathit{Var}}_{{\theta }_n}\{{\zeta }_{MC}({\theta }_n\mid L)\}+{\mathit{Var}}_{\theta }({\delta }_M)+{\{g(\theta )-g({\theta }_n)\}}^2.\end{array}$$ (4.2)

The last equality follows from the facts that

$$\begin{array}{l}{E}_{\theta ,{\theta }_n}{\{{\delta }_M-g({\theta }_n)\}}^2=\mathit{Var}({\delta }_M)+{\{g(\theta )-g({\theta }_n)\}}^2,\\ E_{\theta }[E_{{\theta }_n}\{{\zeta }_{MC}({\theta }_n\mid L)-g({\theta }_n)\}\{g({\theta }_n)-{\delta }_M\}\mid {\delta }_M]=0.\end{array}$$

Since Var_θ(δ_M) is free of θ_n and Var_θn {ζ_MC (θ_n|L)} = O(1/L), for sufficiently large L, choosing θ_n to minimize E_{θ; θn} {ζ_MC (θ_n|L) − δ_M}², the left-hand side of (4.2), is asymptotically equivalent to choosing θ_n to minimize {g(θ_n)−g(θ)}².

The above proposed estimation procedure has the flavor of a bootstrap procedure in the resampling part (Wang & Leung, 1997). The main difference between our procedure and their procedure is that we use a searching step to locate the estimator of θ that is closest to the posterior estimator; whereas Wang and Leung (1997) used the maximum likelihood estimator.

5. Numerical studies

Using Monte Carlo simulations, we compare the performance of the proposed efficient design (ED) with existing group sequential designs in a similar setting. The OBF design (O’Brien & Fleming, 1979) is a classical group sequential design with a fixed maximum sample size. The self-designing trial of Shen & Fisher (1999) is a frequentist adaptive design, and the Bayesian adaptive design (Cheng & Shen, 2005) is based on the decision-theoretic approach. The ED, Bayes adaptive design and self-designing trials do not enforce a maximum sample size, in contrast to the O’Brien-Fleming (OBF) design, in which the maximum sample size is estimated given the design parameters: δ, α and β.

It is worth noting that the original OBF design is two-sided. DeMets and Ware (1982) extended the results of the OBF design to the one-sided version of the symmetric OBF design. Our numerical study is based on the one-sided boundaries proposed by DeMets and Ware (1982).

For each scenario, the same type I and II error rates, δ, and block sizes are used among the four designs under comparison. The block sizes are prespecified, B₀ = 1, B_i = B = 6, for i ≥ 2. For the OBF design, let B₁ = B for simplicity. For the remaining three designs, B₁ = 15 in order to have a more stable estimator of θ at the first step. The Bayesian adaptive design uses the loss structure with h₁(θ) = h₀(θ) = 1, while K_i is chosen to achieve the corresponding α and β, respectively. The number of interim analysis of the OBF design is backward derived given the block size B and the fixed maximum sample size. The asymptotic boundary for the one-sided OBF test is obtained from DeMets & Ware (1982) and Shen & Fisher (1999) with the given design parameters.

The values of θ are mostly limited to the set {θ: | θ − δ| < 0.5δ}. For a fair comparison among the methods, the true values of θ are given as fixed when the X_i’s are generated from a normal distribution with σ² = 1. We used mean θ = 0 under the null hypothesis, and mean θ = 0.5 under the alternative hypothesis. The design parameters are specified as follows: α = 0.025, β = 0.1, and δ = 0.4 or 0.7. Since the type I error rate in the proposed designs depends on K₀ and K₁ only through the ratio K₀/K₁, we let K₁ = 1 and K₀ = r=(1 − r), where r is computed from (3.14). Let h₀(θ) = h₁(θ) = | θ| + c and c = BK₂, which satisfy the conditions of Theorems 2.1 and 2.2.

The empirical type I error rate, power and average sample number (ASN) of each design are summarized in Table 1 with 10,000 repetitions. The proposed efficient design maintains the nominal level at α = 0.025, and achieves the specified power. Among the designs under comparison, the ED is the most robust one to different values of δ. It can achieve the specified power even if δ is considerably optimistically planned, compared with the true θ. When δ (= 0.7) overestimates θ, the ED and Bayesian designs are the two designs that can still maintain the power at 0.9, but the ASN of ED is 17% lower than the ASN of the Bayesian design. When δ is underestimated relative to the true θ (at δ = 0.4), ASNs for ED are at least 25% lower than those for the other designs under the alternative.

Table 1.

The comparison of power and average sample number (ASN) between the proposed design and other group sequential designs with one-sided α = 0.025, B = 6, and true θ = 0 under null and θ = 0.5 under the alternative.

Design	δ	α̂	ASNα	1−β̂	ASNβ
OBF	0.4	0.023	68.7	0.983	84.2
Self-designing	0.4	0.010	85.4	0.923	87.2
Bayes Adaptive	0.4	0.014	55.3	0.949	75.0
ED	0.4	0.025	42.9	0.908	55.0
OBF	0.7	0.024	26.9	0.644	38.2
Self-designing	0.7	0.017	49.0	0.798	62.6
Bayes Adaptive	0.7	0.014	45.4	0.912	66.4
ED	0.7	0.019	42.7	0.901	54.8

Monte Carlo simulation based on 10,000 repetitions. B₀ = 1, B₁ = 15, σ = 1, K₁ = 1, K₂ = 3 * 10⁵, c = BK₂, and K₀ = r/(1 − r), where r is defined by (3.14). ASN_α and ASN_β are average sample sizes under θ = 0 and θ = 0.5, respectively.

While all sequential methods typically lead to savings in sample size compared with the standard fixed sample design, ED performs the best among the designs we investigated. As noted in Table 1, type I error rates of all designs under comparison are under control. The proposed design with assessment of predicted power at each interim analysis results in some further saving in the ASN while achieving the specified power.

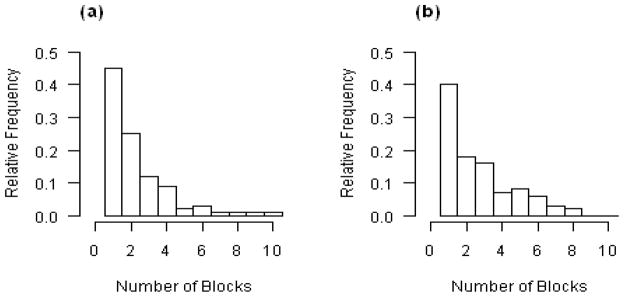
The cost of each patient, K₂, relative to the cost of making a wrong conclusion is chosen to match the specified power. In general, the larger K₂ is, the less power the trial has. We found that K₂ should be in the magnitude of 0.1⁵ of K₁, the cost of mistakenly concluding a negative trial. The results show that the proposed design is quite robust when K₂ varies in the range of 0.1⁵ to 5(0.1)⁵ over different values of θ and δ. We performed following sensitivity analysis based on simulations (not shown in tables due to space limitation). The role of c is relatively minor other than that c should satisfy the inequality 0 ≤ cK₁ < 2K₂ min{B_j, j ≥ 1}, which is one of the conditions for Theorem 2.1. The performance of the proposed design is quite robust when c varies within its domain. When the block size is increased from B = 6 to 16, we found that the performances were also similar for the two settings. The only difference is that average sample size increased by 10 under H₀ and by 6 under H₁ with slightly higher power. Figure 1 shows two histograms of the total number of blocks for the proposed design without a constraint on the maximum number of blocks. Our numerical studies also shows little difference in the error rates or the average sample size if the number of blocks is truncated at 15 for the scenarios shown in the histograms.

Figure 1.

The histogram of the number of blocks as relative frequencies for (a) under H₀, θ = 0 and (b) under H₁, θ = 0.5. For both (a) and (b), α = 0.025, β = 0.1, δ = 0.5, B₁ = 15, B = 8, σ = 1, K₂ = 3 * 10⁵, c = BK₂, K₁ = 1 and K₀ = r/(1 − r), where r is defined by (3.14).

We also assess the bias of the proposed estimator and compare it with the posterior mean. Table 2 presents the proposed estimate and the naive posterior mean estimate for θ, along with their empirical estimates of the standard error with β = 0.1, δ = 0.6, and α =.025 or .05. The true underlying θ varies from 0 to 0.6. The grid search was conducted over the predetermined interval [−0.5, 1] with an equal subinterval length of 0.005. To obtain the the reduced-bias estimator, we used 10,000 repetitions for each grid point. The obtained estimator, θ̂, has a substantially reduced bias compared with that of the posterior mean, denoted by δ_M in Table 2. The standard deviation of the proposed estimators are not significantly different from the standard deviation of the posterior mean.

Table 2.

The comparison of proposed estimate θ̂ and posterior mean δ_M following an ED with β = 0.1, B = 6 and the assumed treatment difference δ = 0.6.

α	θ	θ̂		δM
0.025	0.0	−0.018	0.213	−0.026	0.186
	0.3	0.295	0.235	0.300	0.257
	0.4	0.416	0.230	0.436	0.250
	0.5	0.519	0.224	0.549	0.231
	0.6	0.625	0.214	0.658	0.205
0.05	0.0	−0.015	0.212	−0.025	0.194
	0.3	0.304	0.235	0.320	0.258
	0.4	0.425	0.230	0.455	0.244
	0.5	0.523	0.219	0.558	0.218
	0.6	0.616	0.218	0.645	0.202

Monte Carlo simulation based on 10,000 repetitions. B₀ = 1, B₁ = 15, σ = 1, K₁ = 1, c = BK₂, K₂ = 3 * 10⁵ and K₀ = r/(1 − r), where r is defined by (3.14).

6. Example

We apply the proposed design to a randomized, placebo-controlled, double-blind trial involving patients with acne papulopustulosa of Plewig’s grade 11–111. Investigators examined the effect of treatment under a combination of 1% chloramphenicol and 0.5% pale sulfonated shale oil versus an alcoholic vehicle (placebo) (Lehmacher & Wassmer, 1999; Fluhr et al., 1998). After 6 weeks of treatment, the level of bacteria was compared to the baseline level for patients in the active treatment group versus those in the placebo group. With α= 0.01 and 1− β = 0.95, h₀(θ) = h₁(θ) = | θ|+c, we used K₂ = 3*10⁵, c = BK₂ = 0.00018, K₁ = 1 and K₀ = r/(1 − r) = 1933.9, where r = 0.9995 is calculated from expression (3.14). Assume that δ = 1 and σ̂₀ = 2 based on the prior information. The quantities needed for conducting the proposed design are listed in Table 3, where σ̂_j is the sample standard deviation from the cumulatiive data and Pred. Power is the notation for the predicted power P(R_j+1|θ = δ_j, ). The block means, not cumulative means, are denoted by x_j = x̄_Tj − x̂_Cj.

Table 3.

Illustration of the steps of the ED procedures.

j	Bj	xj	σ̂j	LA	Lcont	Pred. Power	LR	Decision
1	12	1.549	1.861	1.507	0.210	0.946		Continue
2	6	1.580	1.932	1.530	0.051	0.997	0.061	Stop; D=R

In the first interim analysis, L_A( 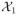) = 1.507 > L_cont( 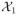) = 0.210, therefore, the next step is to check the predicted power. Since the predicted power, 0.946, is less than 1 − β = 0.95, the trial continues to the next block. At the second interim analysis, L_A( 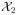) > L_cont( 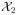), and the predicted power is 0.997, which is great than 0:95. Therefore, we stop the trial. Because L_R( 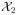) = 0.061 < L_A( 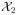) = 1.530, the conclusion is to reject H₀: θ ≤ 0. The procedure is robust in terms of the choices of δ and σ̂₀. When δ varies from 0.5 to 2.5 and σ̂₀ varies from 1 to 2.5, the conclusion remains the same and the trial is always terminated after no more than two interim analyses.

7. Discussion

We have proposed an efficient design with the new aspects of allowing the investigators to evaluate both efficacy and futility at each interim analysis, which leads to a saving in sample size. The one-stage-ahead expected loss and predicted power assessment allow the trial to be terminated once evidence favoring a treatment, or not, is sufficient. The proposed design has the following desirable merits. First, the method can terminate a trial as soon as the evidence is sufficient to show the efficacy of a treatment. Second, the method ensures the control of the type I error rate, which is a practical requirement for trial designs under the regulatory setting, whether Bayesian or frequentist. Third, the proposed method avoids premature decisions with a flexible maximum sample size by relying on the mechanism of assessing the conditional probability. Compared with the other two adaptive designs in simulations, the proposed design is more robust to a range of assumed prior distributions, but more sensitive to the current data.

We have provided a new estimation procedure to obtain a reduced-bias estimator for the parameter of interest. One major advantage of this method is that the estimation procedure takes into account the whole process of the complicated stopping rule through Monte Carlo simulations. The empirical studies have shown that the estimator behaves well under various scenarios. Although this estimation procedure is developed for the proposed design, the methodology of searching for an unbiased parameter estimator may be applied to other Bayesian group sequential designs, as well as classical group sequential designs with the posterior mean replaced by its naive estimate, as in (4.1).

Although we assumed normal observations in illustrating the design, the large sample properties in Section 3 only require independent increments from each block of data to be approximately normally distributed, which will allow extension of the method to outcomes with other distributions and time-to-event outcomes with staggered entry using log-rank type test statistics (Tsiatis et al., 1985 and Shen & Cai, 2003).

The maximum number of blocks is sequentially determined using interim data. When the maximum number of interim analyses is fixed, optimizing the block size B is possible theoretically, but could be difficult computationally. At the first interim analysis, the conditional power can be variable if the size of the first block of data is small. That is why we recommend choosing a relatively larger block size initially, but a constant, smaller block size later. Beyond the initial block, the smaller the block size, the more efficient is the procedure. The most efficient block size would be one, if we do not take the cost of the interim analysis into consideration. But such a fully sequential design after the first block may not be practical in clinical trial conduct. Therefore, we recommend a small block size, such as 5 to 10, after the first block.

We recognize the tradeoff between efficiency and flexibility for clinical trial designs. While being more flexible, the proposed group sequential design may not be the most efficient design as defined in the mathematical sense by Tsiatist and Mehta (2003). As shown in several recent papers (e.g., Bauer, Brannath and Posch, 2001; Brannath, Bauer and Posch, 2006), the most efficient design (in a mathematical sense), however, relies on many underlying assumptions such as the right spending functions and that the sample sizes should be specified a priori. The designs could be poorly underpowered if any of these design parameters were misspecified in the planning phase, which is very likely in practice.

There are different approaches to specifying δ, at which the power is set for group sequential designs, such as using a minimal clinical significant treatment difference (Barber and Jennison, 2002) or an anticipated effective size. Achieving the desired power at the true effective size in a neighborhood of δ has gained more attention for its practicality and flexibility in clinical trial designs in recent years. That is the rationale we use as we set our objectives for the proposed design.

Appendix A. Proofs of Theorems 2.1 and 2.2

For the natural flow of the proofs, we prove Theorem 2.2 first and Theorem 2.1 next.

Proof of Theorem 2.2

We prove (2.4) first. Assume that θ* > 0. For any given positive ε, there exists an N > ε such that h₁(θ)=(1 + |θ|^w) < ε whenever θ > N. Let

$$U_{h_1}(N)=max\{h_1(\theta ):\mid \theta -{\theta }^{\ast }\mid \le N\},U=\underset{j\to \infty }{limsup}\left\{E\left({\mid \theta \mid }^w\mid {\mathcal{X}}_j\right)\right\}.$$

Under the regularity conditions (Schervish, 1995, p. 429, 450),

$$\underset{j\to \infty }{liminf}P(\mid \theta -{\theta }^{\ast }\mid <\epsilon \mid {\mathcal{X}}_j)=1$$

almost surely and E(|θ |^w| ) differs from |θ̂|^w by $O(m_j^{-1})$, where θ̂ is MLE of θ and $m_j={\sum }_{i=1}^j{B}_i$. Hence, U is finite almost surely and we have

$$\begin{array}{l}\underset{j\to \infty }{limsup}{\int }_0^{\infty }{h}_1(\theta )\pi (\theta \mid {\mathcal{X}}_j)d\theta \\ \le \underset{j\to \infty }{limsup}[\{h_1({\theta }^{\ast })+O(\epsilon )\}P(\mid \theta -{\theta }^{\ast }\mid <\epsilon \mid {\mathcal{X}}_j)\\ +U_{h_1}(N)P\left(\mid \theta -{\theta }^{\ast }\mid \ge \epsilon \mid {\mathcal{X}}_j\right)+{\int }_{\mid \theta -{\theta }^{\ast }\mid \ge N}\frac{h_1(\theta )(1+{\mid \theta \mid }^w)}{(1+{\mid \theta \mid }^w)}\pi (\theta \mid {\mathcal{X}}_j)d\theta ]\\ \le \left[\{h_1({\theta }^{\ast })+O(\epsilon )\}+\epsilon (1+U)\right]\end{array}$$ (A.1)

almost surely. A similar argument holds for lim inf. Letting ε approach to zero, we obtain the following inequalities:

$$h_1({\theta }^{\ast })\le \underset{j\to \infty }{liminf}{\int }_0^{\infty }{h}_1(\theta )\pi (\theta \mid {\mathcal{X}}_j)d\theta \le \underset{j\to \infty }{limsup}{\int }_0^{\infty }{h}_1(\theta )\pi (\theta \mid {\mathcal{X}}_j)d\theta \le h_1({\theta }^{\ast }).$$

Hence,

$$\underset{j\to \infty }{lim}{\int }_0^{\infty }{h}_1(\theta )\pi (\theta \mid {\mathcal{X}}_j)d\theta =h_1({\theta }^{\ast })$$ (A.2)

almost surely when θ* > 0. Similarly, we can show the follows:

$$\begin{array}{ll}\underset{j\to \infty }{lim}{\int }_{-\infty }^0{h}_0(\theta )\pi (\theta \mid {\mathcal{X}}_j)d\theta =h_0({\theta }^{\ast })\hfill & \text{a}.\text{s}.,\text{if}{\theta }^{\ast }<0;\hfill \\ \underset{j\to \infty }{lim}{\int }_0^{\infty }{h}_1(\theta )\pi (\theta \mid {\mathcal{X}}_j)d\theta =0\hfill & \text{a}.\text{s}.,\text{if}{\theta }^{\ast }<0;\hfill \\ \underset{j\to \infty }{lim}{\int }_{-\infty }^0{h}_0(\theta )\pi (\theta \mid {\mathcal{X}}_j)d\theta =0\hfill & \text{a}.\text{s}.,\text{if}{\theta }^{\ast }>0.\hfill \end{array}$$ (A.3)

Since

$$\left[E\{L(\theta ,A,j)\mid {\mathcal{X}}_j\}-E\{L(\theta ,R,j)\mid {\mathcal{X}}_j\}\right]=K_1{\int }_0^{\infty }{h}_1(\theta )\pi (\theta \mid {\mathcal{X}}_j)d\theta -K_0{\int }_{-\infty }^0{h}_0(\theta )\pi (\theta \mid {\mathcal{X}}_j)d\theta ,$$

(2.4) is a direct result of (A.2) and (A.3).

For the second part of Theorem 2.2, assuming θ* > 0, since

$$\underset{j\to \infty }{lim}\left[E\left\{L(\theta ,A,j+1)\mid {\mathcal{X}}_{j+1}\right\}-E\left\{L(\theta ,R,j+1)\mid {\mathcal{X}}_{j+1}\right\}\right]=K_1{h}_1({\theta }^{\ast })>0$$

almost surely, we have

$$\underset{j\to \infty }{lim}{I}_{R_{j+1}}({\mathcal{X}}_{j+1})=1\text{a}.\text{s}.,$$

where

$$I_{R_{j+1}}({\mathcal{X}}_{j+1})=\{\begin{array}{ll}1,\hfill & \text{if}E\{L(\theta ,A,j+1)\mid {\mathcal{X}}_{j+1}\}-E\{L(\theta ,R,j+1)\mid {\mathcal{X}}_{j+1}\}>0;\hfill \\ 0,\hfill & \text{elsewhere}.\hfill \end{array}$$

Hence,

$$\underset{j\to \infty }{lim}P(R_{j+1}\mid \theta ={\delta }_j,{\mathcal{X}}_j)=\underset{j\to \infty }{lim}E(I_{R_{j+1}}({\mathcal{X}}_{j+1})\mid \theta ={\delta }_j,{\mathcal{X}}_j)=1$$

almost surely.

For the last part of Theorem 2.2, assuming θ* = 0, by a similar argument of (A.1), we have

$$\begin{array}{l}E\{L(\theta ,A,j)\mid {\mathcal{X}}_j\}-E\{L(\theta ,R,j)\mid {\mathcal{X}}_j\}=K_1{h}_1(0)P(0\le \theta \le \epsilon \mid {\mathcal{X}}_j)-K_0{h}_0(0)P(-\epsilon \le \theta <0\mid {\mathcal{X}}_j)+O(\epsilon )+o_{\epsilon }(1)\\ =\{K_1{h}_1(0)+K_0{h}_0(0)\}P(0\le \theta \le \epsilon \mid {\mathcal{X}}_j)-K_0{h}_0(0)+O(\epsilon )+o_{\epsilon }(1),\end{array}$$ (A.4)

where o_ε(1) converges to 0 almost surely as j approaches to infinity for any given ε > 0. The last equality of (A.4) follows from the facts that

$$P(-\epsilon \le \theta <0\mid {\mathcal{X}}_j)=1-P(0\le \theta \le \epsilon \mid {\mathcal{X}}_j)-P(\mid \theta \mid >\epsilon \mid {\mathcal{X}}_j)$$

and

$$\underset{j\to \infty }{lim}P(\mid \theta \mid >\epsilon \mid {\mathcal{X}}_j)=0\text{a}.\text{s}\mathrm{..}$$

Letting θ̂_mj be the MLE and I(θ) be the Fisher information number, we have

$$\underset{j\to \infty }{lim}\underset{x}{sup}\left|P\left(\frac{\sqrt{m_j}(\theta -{\widehat{\theta }}_{m_j})}{I^{-1/2}(0)}\le x|{\mathcal{X}}_j\right)-\mathrm{\Phi }(x)\right|=0\text{a}.\text{s}.$$ (A.5)

(Bickel, 2001, p. 339). In light of (A.5),

$$P(0\le \theta \le \epsilon \mid {\mathcal{X}}_j)=1-\mathrm{\Phi }\left(-\frac{\sqrt{m_j}{\widehat{\theta }}_{m_j}}{I^{-1/2}(0)}\right)+o_{\epsilon }(1).$$ (A.6)

Moreover, $\mathrm{\Phi }(-\sqrt{m_j}{\widehat{\theta }}_{n_j}/I^{-1/2}(0))$ converges to Φ(Z) in distribution, where Z follows a standard normal distribution. As a result of (A.4) and (A.6),

$$\underset{j\to \infty }{limsup}P\left[E\{L(\theta ,A,j)\mid {\mathcal{X}}_j\}-E\{L(\theta ,R,j)\mid {\mathcal{X}}_j\}<0\right]=\underset{j\to \infty }{limsup}P\left[\{K_1{h}_1(0)+K_0{h}_0(0)\}\{1-\mathrm{\Phi }(Z)\}-K_0{h}_0(0)+O(\epsilon )<0\right].$$

Let ε go to zero. Noting that 1 − Φ(Z) follows a uniform distribution on (0, 1) and that the above argument also holds for lim inf, we have

$$\underset{j\to \infty }{lim}P\left[E\{L(\theta ,A,j)\mid X_j\}-E\{L(\theta ,R,j)\mid X_j\}<0\right]=P\left\{1-\mathrm{\Phi }(Z)<\frac{K_0{h}_0(0)}{K_1{h}_1(0)+K_0{h}_0(0)}\right\}=\frac{K_0{h}_0(0)}{K_1{h}_1(0)+K_0{h}_0(0)}.$$ (A.7)

Hence, the last part of Theorem 2.2 is proved.

Proof of Theorem 2.1

When θ* < 0, in view of the second equation in expression (A.3),

$$\underset{j\to \infty }{lim}\left\{L_A({\mathcal{X}}_j)-L_{\mathit{cont}}({\mathcal{X}}_j)\right\}\le \underset{j\to \infty }{lim}\left[{\int }_0^{\infty }{h}_1(\theta )\pi (\theta \mid {\mathcal{X}}_j)d\theta -2B_{j+1}{K}_2\right]\le 0-2B{K}_2<0$$

almost surely. Consequently, P_θ^*(M < ∞) = 1.

Next, assuming θ* > 0, the trial stops at M = j if

$$P(R_{j+1}\mid \theta ={\delta }_j,{\mathcal{X}}_j)\ge 1-\beta .$$

In the second part of Theorem 2.2, we proved that

$$\underset{j\to \infty }{lim}P(R_{j+1}\mid \theta ={\delta }_{j,}{\mathcal{X}}_j)=1$$

almost surely. Subsequently, P_θ^*(M < ∞) = 1.

Finally, if θ* = 0 and K₁h₁(0) < 2B_j+1K₂ for j ≥ 1,

$$\underset{j\to \infty }{liminf}{P}_0\left\{L_A({\mathcal{X}}_j)-L_{\mathit{cont}}({\mathcal{X}}_j)<0\right\}\ge \underset{j\to \infty }{liminf}{P}_0\left[E\{L(\theta ,A,j)\mid {\mathcal{X}}_j\}<2B_{j+1}{K}_2\right]=\underset{j\to \infty }{liminf}{P}_0\left[{\int }_0^{\infty }{h}_1(\theta )\pi (\theta \mid {\mathcal{X}}_j)d\theta <2B_{j+1}{K}_2\right]$$ (A.8)

By a similar argument that yields (A.4) through (A.7), we have

$$\begin{array}{l}\underset{j\to \infty }{lim}{P}_0\left[{\int }_0^{\infty }{h}_1(\theta )\pi (\theta \mid {\mathcal{X}}_j)d\theta <2B_{j+1}{K}_2\right]=P\left[K_1{h}_1(0)\{1-\mathrm{\Phi }(Z)\}<2B_{j+1}{K}_2\right]\\ =P_0\left[\{1-\mathrm{\Phi }(Z)\}<\frac{2B_{j+1}{K}_2}{K_1{h}_1(0)}\right]=1.\end{array}$$ (A.9)

The last equality follows from the facts that 1 − Φ(Z) follows a uniform distribution on (0, 1) and that 2B_j+1K₂=K₁h₁(0) > 1. Combining (A.8) and (A.9), we have

$$\underset{j\to \infty }{lim}{P}_0\left\{L_A({\mathcal{X}}_j)-L_{\mathit{cont}}({\mathcal{X}}_j)<0\right\}=1,$$

which implies P(M < ∞) = 1.