Detecting and Exploiting Etiologic Heterogeneity in Epidemiologic Studies

Abstract

Contemporary searches for new risk factors frequently involve genome-wide explorations of very large numbers of candidate risk variants. Given that diseases can often be classified into subtypes that possess evidence of etiologic heterogeneity, the question arises as to whether or not a search for new risk factors would be improved by looking separately within subtypes. Etiologic risk heterogeneity inevitably increases the signal in at least one of the subtypes, but this advantage may be offset by smaller sample sizes and the increased chances of false discovery. In this article, the authors show that only a relatively modest degree of etiologic heterogeneity is necessary for the subtyping strategies to have improved statistical power. In practice, effective exploitation of etiologic heterogeneity requires strong evidence that the subtypes selected are likely to exhibit substantial heterogeneity. Further, defining the subtypes that demonstrate the most heterogeneous profiles is important for optimizing the search for new risk factors. The concepts are illustrated by using data from a breast cancer study in which results are available separately for estrogen receptor-positive (ER+) and -negative (ER−) tumors.

Epidemiologic studies of cancer have traditionally focused on the anatomic site of origin of the primary tumor as the criterion for defining the case group. Thus, we have a long history of epidemiologic research on breast cancer, lung cancer, colon cancer, and so forth. Occasionally, investigations have focused on subgroups defined by tumor characteristics, such as tumor histology. As a result, we know, for example, that smoking history has distinctive influences on the risks of adenocarcinomas and squamous cell carcinomas of the lung (1). The impetus to examine tumor subtypes to identify distinct etiologies has increased in recent years as we have learned more about molecular tumor characteristics using genomic techniques. In breast cancer, these techniques have suggested a broad reclassification into 4 subtypes on the basis of the relation of genomic profiles with clinical characteristics (2). These subtypes can be characterized approximately by routinely collected hormone receptor levels into luminal A (estrogen receptor positive (ER+) or progestin receptor positive (PR+) and human epidermal growth factor receptor 2 negative (HER2/neu−)), luminal B (ER+ or PR+ and human epidermal growth factor receptor 2 positive (HER2/neu+)), nonluminal (estrogen receptor negative (ER−), progestin receptor negative (PR−), and HER2/neu+), and triple negative (ER−, PR−, and HER2/neu−), and an increasing focus of breast cancer epidemiologic research involves study of the distinctive influence of known risk factors on these subtypes (3–11).

Given that tumor subtypes may possess some distinctions in etiology on the basis of known risk factors, the question arises as to whether undiscovered risk factors may be more or less likely to have distinct risks for the subtypes. As the credibility of the hypothesis that undiscovered risk factors may influence only one subtype or may have a differential effect on different subtypes becomes more plausible, the strategy of searching for new risk factors separately within subtypes becomes a more attractive one. However, expanding the set of candidate subtypes in this way carries significant potential costs in statistical efficiency. First, the subtypes necessarily have smaller sample sizes than the aggregated case group, reducing the power for detecting specific effect sizes. Second, increasing the number of statistical comparisons increases the chances of false discovery. Indeed, controlling the chances of false discovery is a prominent and challenging feature of current research to identify genetic risk loci via genome-wide association studies. Conversely, the promise of a strategy of testing new risk factors within subtypes separately is that one of the subtypes will have a greatly enhanced risk signal, and that this will more than offset the losses in power due to decreased sample size and chances of false discovery. This strategy can also potentially lead to greater accuracy in risk prediction.

Our goal in this article is to conduct some simple statistical power comparisons in order to shed light on the potential gains and losses of statistical testing strategies that involve the use of tumor subtypes. We explore configurations of risk factor prevalence, overall odds ratio, and risk heterogeneity to determine the circumstances in which a search for etiologic heterogeneity is likely to lead to improved statistical power compared with a traditional strategy in which all cases are aggregated in a unitary case group.

MATERIALS AND METHODS

We investigate 2 different alternatives to a conventional case-control analysis in which all cases are aggregated in a single case group. In the first strategy, each tumor subtype is compared separately with the controls. The risk factor is identified as being significantly associated with disease if any one of the subtype analyses is significant, after adjustment for multiple comparisons. In our calculations below, we identify the smallest range of odds ratios that leads to a significant test of association with equivalent or greater power than the conventional test of the overall (aggregated) odds ratio. For calculating power, we make the assumption that one of the subtypes has an elevated odds ratio compared with all the remaining subtypes (if there are more than 2 subtypes) and contrast high and low odds ratios in the subtypes with the overall odds ratio. In the second strategy, we evaluate the subtypes using a case-only approach in which we test the hypothesis that there is no difference in the risk profiles among the tumor subtypes; that is, we test for the presence of etiologic heterogeneity directly (12). For conceptual clarity and analytical convenience, our calculations are defined initially in terms of tests of a binary risk factor. Later we show briefly that the results are broadly replicated in genetic trend tests of additive allelic effects.

Consider a case-control study with m controls and n cases. We are evaluating a risk factor with population prevalence p and odds ratio φ. The risk factor frequency in cases is therefore given by q, where q = pφ/(1 − p + pφ). The asymptotic power for detecting this association is given by Φ(−z_α/2 + log(φ)/v^1/2), where z_α/2 is the normal deviate for a 2-sided test at the α significance level, v = (nq)⁻¹ + (n(1 − q))⁻¹ + (mp)⁻¹ + (m(1 − p))⁻¹, and where Φ(·) is the normal distribution function. Suppose now that there are 2 tumor subtypes, denoted A and B, and that there are n_A cases of tumor type A and n_B cases of tumor type B. Further, let the relative frequencies of the risk factor in subtypes A and B be q_A and q_B, respectively. The corresponding odds ratios are thus φ_A = q_A(1 − p)/p(1 − q_A) and φ_B = q_B(1 − p)/p(1 − q_B). Note that these terms are constrained by the fact that

(1)

Using the Bonferroni adjustment to account for multiple comparisons, we found that the power to detect an association of the risk factor with either of these subtypes is

where v_i = (n_iq_i)⁻¹ + (n_i(1 − q_i))⁻¹ + (mp)⁻¹ + (m(1 − p))⁻¹, i = A, B. For this strategy to have equivalent or better power than the conventional, aggregated test, we need configurations of relative frequencies and odds ratios within the subtypes to be such that

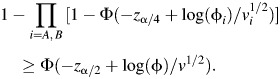Assuming, without loss of generality, that the higher odds ratio occurs in subtype A, we can find the minimum range of odds ratios in the subtypes that delivers equivalent power to the conventional test for a given relative frequency of type A tumors (i.e., n_A/n) and significance level α by solving for φ_A, φ_B the following equation:

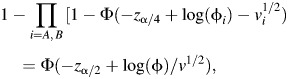(2)

where φ_A, φ_B are constrained by equation 1. We note that the solution to equation 2 depends on the choice of significance level α. However, α has only a modest impact. We present in the Results solutions for α = 0.05.

If there are more than 2 subtypes under consideration, the risks of false discovery will increase. We explore the consequences of this by considering configurations in which the relative frequency of subtype A, the subtype with the elevated odds ratio, remains the same, but the cases in subtype B are further classified into additional subtypes of equal frequencies of occurrence and equal odds ratios. We recognize that these configurations are somewhat artificial, but the setup is constructed merely to obtain an approximate understanding of the impact of the additional multiple testing in this context. In this framework, if there is a total of k subtypes, the minimum range of odds ratios in the subtypes that delivers equivalent power to the conventional test involving all cases, adjusted for multiple comparisons, can be obtained approximately by solving for φ_A, φ_B the equation:

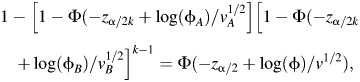(3)

where φ_B is the true odds ratio in the k − 1 subtypes other than subtype A.

A different strategy for utilizing etiologic heterogeneity to detect new risk factors is simply to perform a case-only analysis, comparing the relative frequencies of the risk factor in the different subtypes. The question is, how different must the odds ratios in the subtypes be in order that this test has equivalent power to the conventional approach of testing all cases versus the controls? Given the relative frequencies of the subtypes (i.e., n_A/n and n_B/n), we can find the minimum range of odds ratios by solving for φ_A, φ_B the equation:

(4)

where

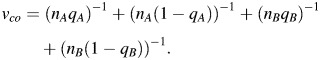Finally, we have adapted the preceding concepts to the setting in which we wish to perform a Cochran-Armitage test of linear genetic effect. That is, we wish to perform linear trend tests to compare cases and controls in a 2 × 3 table with respect to the numbers of variant alleles. In our calculations, the control frequencies are determined by using Hardy-Weinberg equilibrium, based on the underlying population allele frequency of the variant allele (denoted a), and the case frequencies are determined by the “per allele” odds ratio (denoted by φ). We then harmonize the elements in the 2 subtype 2 × 3 tables to make sure they both conform to a linear genetic model (in which each additional allele confers the same per-allele effect). As before, we then find the detectable per allele odds ratio in the subtype analysis that has equivalent power to that of the overall analysis. Further details of these calculations are provided in the Appendix. The power formulas for the Cochran-Armitage test are available in the article by Slager and Schaid (13).

RESULTS

Power comparisons

Results for some plausible configurations are presented in Table 1. As an example, in the first row of the table, we consider a risk factor with population frequency of 10% and an odds ratio of 1.2. The cases belong to 2 subtypes with distinct odds ratios where the subtype with the greater odds ratio (defined as subtype A) occurs in 20% of the cases. In this setting, subtype A must have an odds ratio of at least 1.51 in order for a case-only test for etiologic heterogeneity to have equivalent power to the conventional (case vs. control) test of the overall odds ratio. In these circumstances, the odds ratio of subtype B is 1.13. If, on the other hand, we compare each of the subtypes separately with the controls and adjust for multiple comparisons, the odds ratio for subtype A need only be 1.28 or greater in order for this strategy to have superior power to the conventional approach. In this case, the odds ratio of subtype B is 1.18. If there are 3 or 4 subtypes overall, the minimum odds ratios in subtype A to achieve equivalent power increase to 1.32 and 1.35, respectively, and the corresponding odds ratios of the remaining subtypes decrease to 1.17 and 1.16. For configurations with 2 subtypes and higher baseline odds ratios, the required odds ratio in the high-risk subtype must be at least 1.67 for an aggregate odds ratio of 1.5 and 2.22 for an aggregate odds ratio of 2.0. Examining the rest of the table, we observe that the relation between the required heterogeneity for the subtyping strategy versus the conventional aggregated strategy is nonlinear, but over most of the configurations examined the required heterogeneity to achieve equivalent power is modest, especially when the subtype with the elevated risk (subtype A) is relatively common.

Table 1.

Equivalent Detectable Odds Ratios

Frequencies			Overall Odds Ratio	Equivalent Detectable Odds Ratiosa
pb	Subtype A, %	Subtype B, %		Case Only	2 Subtypes	3 Subtypes	4 Subtypes
0.10	20	80	1.20	1.51 (1.13)	1.28 (1.18)	1.32 (1.17)	1.35 (1.16)
0.10	20	80	1.50	2.37 (1.30)	1.67 (1.46)	1.75 (1.44)	1.85 (1.42)
0.10	20	80	2.00	4.05 (1.58)	2.22 (1.95)	2.31 (1.93)	2.60 (1.87)
0.10	50	50	1.20	1.35 (1.05)	1.23 (1.17)	1.26 (1.14)	1.28 (1.13)
0.10	50	50	1.50	1.91 (1.11)	1.53 (1.46)	1.64 (1.37)	1.69 (1.32)
0.10	50	50	2.00	2.93 (1.19)	2.00 (1.99)	2.24 (1.77)	2.37 (1.66)
0.10	80	20	1.20	1.28 (0.91)	1.23 (1.09)	1.24 (1.04)	1.25 (1.01)
0.10	80	20	1.50	1.71 (0.74)	1.57 (1.22)	1.61 (1.09)	1.63 (1.01)
0.10	80	20	2.00	2.52 (0.31)	2.15 (1.44)	2.24 (1.17)	2.29 (1.00)
0.25	20	80	1.20	1.53 (1.13)	1.29 (1.18)	1.33 (1.17)	1.36 (1.16)
0.25	20	80	1.50	2.52 (1.30)	1.73 (1.45)	1.84 (1.42)	1.95 (1.40)
0.25	20	80	2.00	5.01 (1.57)	2.49 (1.89)	2.72 (1.87)	3.01 (1.84)
0.25	50	50	1.20	1.36 (1.05)	1.24 (1.16)	1.26 (1.14)	1.28 (1.12)
0.25	50	50	1.50	1.95 (1.12)	1.58 (1.41)	1.66 (1.35)	1.72 (1.30)
0.25	50	50	2.00	3.14 (1.22)	2.12 (1.89)	2.37 (1.67)	2.48 (1.65)
0.25	80	20	1.20	1.28 (0.91)	1.23 (1.09)	1.24 (1.04)	1.25 (1.02)
0.25	80	20	1.50	1.72 (0.79)	1.58 (1.21)	1.62 (1.09)	1.64 (1.02)
0.25	80	20	2.00	2.53 (0.59)	2.18 (1.39)	2.27 (1.16)	2.33 (1.03)
0.50	20	80	1.20	1.56 (1.12)	1.31 (1.17)	1.35 (1.17)	1.39 (1.16)
0.50	20	80	1.50	2.86 (1.30)	1.85 (1.43)	2.01 (1.40)	2.13 (1.39)
0.50	20	80	2.00	10.91 (1.52)	3.16 (1.80)	3.76 (1.78)	4.41 (1.77)
0.50	50	50	1.20	1.37 (1.06)	1.24 (1.16)	1.27 (1.13)	1.29 (1.12)
0.50	50	50	1.50	2.03 (1.13)	1.63 (1.39)	1.71 (1.33)	1.76 (1.28)
0.50	50	50	2.00	3.56 (1.24)	2.36 (1.71)	2.57 (1.64)	2.74 (1.50)
0.50	80	20	1.20	1.28 (0.93)	1.23 (1.08)	1.24 (1.04)	1.25 (1.01)
0.50	80	20	1.50	1.74 (0.85)	1.59 (1.20)	1.63 (1.11)	1.66 (1.03)
0.50	80	20	2.00	2.63 (0.77)	2.23 (1.34)	2.33 (1.16)	2.39 (1.20)

^a Minimum heterogeneity of relative risks for the subtypes required for a strategy of comparing the subtypes individually with the controls (or with each other in the case-only design) to achieve equivalent power to a test of the corresponding overall relative risk (i.e., comparing all cases vs. controls) at the 5% level. The numbers in parentheses are the corresponding relative risks for subtype B.

^b Population prevalence of the risk factor.

In Table 2, we show corresponding results for the Cochran-Armitage trend test. The results are broadly similar. The per-allele odds ratio in subtype A only needs to be modestly elevated when this subtype is relatively common (50%), but it needs to be higher as its frequency decreases.

Table 2.

Equivalent Detectable Odds Ratios for Genetic Tests

Allele Frequency	Frequencies		Per-Allele Odds Ratios
	Subtype A, %	Subtype B, %	Overall	Subtypesa
0.10	20	80	1.20	1.29 (1.18)
0.10	20	80	1.50	1.73 (1.45)
0.10	20	80	2.00	2.42 (1.90)
0.10	50	50	1.20	1.24 (1.17)
0.10	50	50	1.50	1.58 (1.42)
0.10	50	50	2.00	2.11 (1.90)
0.30	20	80	1.20	1.31 (1.18)
0.30	20	80	1.50	1.83 (1.43)
0.30	20	80	2.00	2.83 (1.85)
0.30	50	50	1.20	1.24 (1.16)
0.30	50	50	1.50	1.61 (1.40)
0.30	50	50	2.00	2.26 (1.78)
0.50	20	80	1.20	1.32 (1.17)
0.50	20	80	1.50	1.94 (1.42)
0.50	20	80	2.00	3.64 (1.80)
0.50	50	50	1.20	1.25 (1.16)
0.50	50	50	1.50	1.64 (1.38)
0.50	50	50	2.00	2.43 (1.70)

^a The minimum heterogeneity of per-allele odds ratios required (subtype A; subtype B in parentheses) for a strategy of comparing subtypes individually versus controls in order to possess equivalent power to an overall test of association.

Example

As an example to illustrate the relevance of these concepts, we examine some published data from a recent study that explored the odds ratios of breast cancer single nucleotide polymorphisms (SNPs) in tumor subtypes (14). The authors presented per-allele odds ratios of the top 8 SNPs identified from previous genome-wide association studies (GWAS), stratified by various tumor characteristics including estrogen receptor status. In this study, 83% of the cases were ER+. In Table 3, we reproduce the overall per-allele odds ratio estimates for breast cancer and the estimates specific for ER+ and for ER− tumors. The critical data for our purposes are the extent to which the odds ratios for ER+ and ER− subtypes differ with respect to each other and to the overall odds ratio. We also recognize that the estimated subtype odds ratios presented are derived from models that adjust for other risk factors, and so the 3 odds ratios are not perfectly constrained as in the equations in the Appendix. The results are simply intended to show in general terms the design trade-offs in the context of real data. For each of the 8 SNPs, we first calculate the sample size required to identify with 90% power at the 5% significance level the overall odds ratio that was actually observed and, then, based on this sample size, we calculate the corresponding power of the strategy in which each of the subtypes is separately compared with controls and adjusted for the fact that there are 2 comparisons. The results show that the subtyping strategy would have been more powerful for 5 of the 8 SNPs and would have had equivalent power for a sixth.

Table 3.

Power for Testing ER + /ER− Subgroups in Breast Cancer for 8 Known SNPs^a

SNP	Allele Frequencyb	Per-Allele Odds Ratiosc			Subtype Power, %d
		Overall	ER+ (83%)	ER− (17%)
rs2981582	0.38	1.23	1.27	1.01	90
rs3803662	0.26	1.20	1.24	1.07	92
rs13387042	0.50	1.16	1.18	1.17	92
rs889312	0.28	1.13	1.15	1.11	92
rs13281615	0.40	1.09	1.12	1.05	97
rs4666451	0.60	1.08	1.08	1.19	99
rs981782	0.54	1.06	1.05	1.12	87
rs1045485	0.87	1.05	1.04	1.16	58

Abbreviations: ER + , estrogen receptor positive; ER − , estrogen receptor negative; SNP, single nucleotype polymorphism.

^a Data adapted from Reeves et al. (14). For each row, we determine the sample size needed to achieve 90% power for detecting the “overall” relative risk in a conventional comparison of all cases versus controls.

^b Allele frequency in the control group.

^c We used the odds ratios appearing in Figure 1 of the report by Reeves et al. (14), recognizing that these are adjusted odds ratios.

^d We used the allele frequency and overall odds ratio to calculate the sample size required to deliver 90% power to detect the “overall” odds ratio in a conventional analysis of all cases versus controls using Appendix equation A2. We then used this overall sample size and equation A3 in the Appendix to calculate the power of the subtyping strategy, recognizing that “A” in the formula represents the larger of the odds ratios for ER+ and ER− in the table.

DISCUSSION

Although much is known about the factors influencing cancer risk, it is widely believed that there may be many undiscovered risk factors, especially genetic factors with relatively low penetrance. Thus, an important contemporary research agenda involves the search for genetic associations in GWAS of SNPs (15). In the future, this agenda is likely to increasingly involve the search for rare risk variants within genes using new sequencing technologies (16, 17). In parallel with this trend, investigators are increasingly exploring the possibility that subtypes of cancers may exhibit distinct risk profiles. Genome-wide searches present formidable statistical challenges, in that real risk variants of low penetrance are hard to distinguish from the much larger numbers of variants that inevitably provide effect estimates that are significant simply because of chance (false positives). An important strategic question is whether or not it is advantageous to perform genome-wide searches within tumor subtypes where the effect sizes of individual risk variants may be relatively large. The trade-off in this approach is that the subtypes have smaller sample sizes than the aggregate set of cases, and the exploration of subtypes increases the number of comparisons and the chances of false discovery. Our goal in this article has been to shed some light on this issue, by calculating the extent of heterogeneity necessary to offset these disadvantages.

Broadly speaking, the results show that the degree of heterogeneity necessary to provide search strategies that utilize the subtyping with superior power is relatively modest. Larger degrees of heterogeneity are needed if the key subtype with the distinct relative risk is either overwhelmingly common or relatively rare. In general, strategies that test the subtypes separately against a common control group seem to have better power than case-only strategies, at least among the configurations that we explored. In our anecdotal example involving data from studies of 8 breast cancer SNPs, we see that the heterogeneity displayed by most of these leads to power for the subtyping strategy that is somewhat higher than the conventional aggregated test.

We envisage analyses of etiologic heterogeneity that utilize a common control group, since the cases of the distinct tumor subtypes are assumed to arise from the same “at risk” population. This is the reason that the standard epidemiologic approach to evaluating etiologic heterogeneity involves polytomous logistic regression, which utilizes a common control group (18). Many investigators have been concerned that the genetic substructure in this population could invalidate simple statistical tests of individual SNPs, and methods have been developed to use multiple loci to adjust for variance inflation due to such substructure in GWAS investigations (19). The use of genomic control of this nature is equally applicable to studies that make use of etiologically distinct subtypes as it is to conventional GWAS that aggregate the cases in a single case group.

Our studies have been focused on calculations addressing the power trade-offs for detecting a single risk variant. In practice, genome-wide searches seek to identify all variants, and the true risk variants are likely to exhibit broad ranges of risk heterogeneity, with many having no heterogeneity at all. Thus, a search strategy that has superior power for some variants is likely to have inferior power for others. Consequently, in the absence of knowledge of the ranges of risk heterogeneity of the unknown variants that we seek to identify, it is a challenge to formulate a plan for how to optimize the search strategy overall. More importantly, we need to know which subtypes of tumors are good candidates for providing the basis for an analysis. In the breast cancer example in Table 3, we focused on results that distinguish the risks for ER+ versus ER− tumors, when in fact the investigators explored numerous other ways to subtype the cases, including progestin receptor status, histologic classification, grade, invasiveness, status of the v-erb-b2 erythroblastic leukemia viral oncogene homolog 2 gene (ERBB2), and presence of bilaterality (14). In practice, one would want to select a subtyping taxonomy for which strong evidence of etiologic heterogeneity exists. A growing literature in breast cancer is providing evidence that many known risk factors have distinct relative risks for ER+ versus ER− tumors (20–24). This evidence supports search strategies for genetic factors on the basis of estrogen receptor status on the indirect supposition that, if these tumor types differ with respect to known risk profiles, they are more likely also to differ with respect to unknown risk factors. A more direct approach has also been proposed, whereby the fundamental etiologic heterogeneity of different subtyping taxonomies can be ranked on the basis of the extent to which the subtypes are correlated in pairs of double primaries (25). In general, before electing to perform broad searches for risk associations in tumor subtypes, it is advisable to first have strong evidence that the subtypes are etiologically distinct.

APPENDIX

Calculations for the Cochran-Armitage Test

As in the main text, we define m to be the number of controls, n to be the number of cases, and n_A and n_B to be the numbers of cases in subtypes A and B, respectively. Let the population allele frequency be “a” and the per-allele odds ratio be “φ.” The population frequencies of individuals with 0, 1, and 2 alleles, respectively, based on Hardy-Weinberg equilibrium, are as follows: p₀ = (1 − a)², p₁ = 2a(1 − a), and p₂ = a². The corresponding frequencies among incident cases can be calculated by using the following:

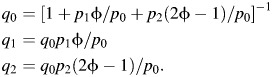Likewise, for subtypes A and B, we have the following:

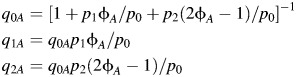and

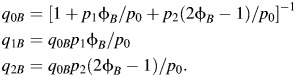These equations ensure that cases in both subtypes A and B and all cases aggregated conform to a linear “per-allele” risk model and that, for each grouping, the probabilities add to 1. However, in order that the estimates of φ_A and φ_B are congruent and simultaneously satisfy the preceding equations, it is necessary that φ_A and φ_B are related through the following equation:

(rmA1)

Power

The power for a 2-sided test at the 5% significance level is as follows (13):

(rmA2)

For our aggregated test, the parameters in the power formula can be expressed in terms of our parameters as follows:

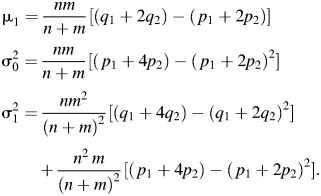For testing subgroup i with correction for the fact that 2 tests rather than 1 will be applied, the power is given by

(rmA3)

where

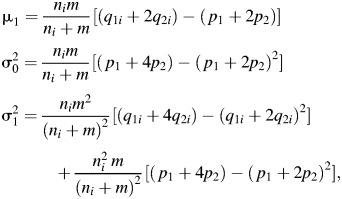where i = A, B. The solutions in Table 2 are obtained by selecting a power of 90%, calculating the required sample size using equation A2, and then using equation A3 iteratively to determine the combination of φ_A, φ_B with minimum value of φ_A > φ that delivers equivalent power where φ_A = q_1A p₀/p₁(1 − q_1A) and the corresponding φ_B is determined by using equation A1.