A simple decision analytic solution to the comparison of two binary diagnostic tests

Abstract

One of the most basic biostatistical problems is the comparison of two binary diagnostic tests. Commonly, one test will have greater sensitivity and the other greater specificity. In this case, the choice of the optimal test generally requires a qualitative judgment as to whether gains in sensitivity are offset by losses in specificity. Here we propose a simple decision-analytic solution in which sensitivity and specificity are weighted by an intuitive parameter, the threshold probability of disease at which a patient will opt for treatment. This gives a net benefit that can be used to determine which of two diagnostic tests will give better clinical results at a given threshold probability, and whether either is superior to the strategy of assuming that all or no patients have disease. We derive a simple formula for the relative diagnostic value, which is the difference in sensitivities of two tests divided by the difference in the specificities. We show that multiplying relative diagnostic value by the odds at the prevalence gives the odds of the threshold probability below which the more sensitive test is preferable, and above which the more specific test should be chosen. The methodology is easily extended to incorporate combination of tests, and the risk or side-effects of a test.

Introduction

One of the most basic biostatistical problems is the comparison of two binary diagnostic tests. Common metrics for the performance of a single test include sensitivity, specificity, positive and negative predictive value and positive and negative likelihood ratio. Application of these metrics to the comparison between two tests is rarely straightforward. Our choice is clear if one of the tests has higher sensitivity and non-inferior specificity, or higher specificity and non-inferior sensitivity. Furthermore, if Youden’s index, that is, sensitivity plus specificity - 1, for the tests was identical, we would choose the more sensitive or specific test depending on whether sensitivity or specificity was more highly valued in the clinical context to which the test would be applied. It has also been argued that both the positive and negative likelihood ratio of one test can be superior to another, even if it has higher sensitivity but lower specificity, or vice versa[1].

Yet such situations are rare. Far more common is where one test is more sensitive, the other more specific, Youden’s index is non-identical and the positive and negative likelihood ratios discordant. As a typical example from the literature[2], the sensitivity and specificity of a repeat Pap smear and a HPV test for high-grade cervical lesions are, respectively, 88% and 57% vs. 75% and 64%, with positive and negative likelihood ratios of 2.04 and 0.22 vs. 2.07 vs. 0.39. To determine whether the repeat Pap smear or HPV test is superior, we need to decide whether a 13% increase in sensitivity is worth a 7% decrease in specificity or, alternatively, how the differences in likelihood ratios trade off.

Previous statistical approaches to the comparison of two binary tests have focused on inference. For example, Bennett[3] gives χ2 statistics for the comparison of sensitivity, specificity, positive or negative predictive value. Nofuentes and de Dios Luna del Castillo[4] propose hypothesis tests for positive and negative likelihood ratios. Other authors[5] have proposed tests that simultaneously compare both sensitivity and specificity.

We believe that an inference based approach is indeed justified in certain specific contexts. For example, if there is an established test that is widely used in practice, it seems reasonable that any new test should be shown to be convincingly superior to the current standard. Alternatively, one test might be more costly, inconvenient or invasive than another and there would clearly be a need to demonstrate benefit. However, there are clearly cases in which there would be no preference between two tests in the absence of data, because neither has become established as a clinical standard or because there is no compelling rationale to choose one or the other in terms of harms or costs. In our view, choosing the preferable test in such cases requires a decision-analytic solution. We define this as an analysis that views the result of a test as informing a decision, such as whether to give a patient a treatment, and which evaluates the consequences of that decision.

In section 2, we give the motivating example. In section 3, we introduce some straightforward notation and describe a decision analytic approach to the comparison of two diagnostic tests. We use this approach in section 4 to derive some simple, intuitive statistics that can used to determine the relative value of two diagnostic tests. In section 5, we incorporate harms and costs of tests. In section 6, we apply our findings to the question of whether tests should be combined.

Motivating example

Blood levels of prostate-specific antigen (PSA) are used to identify men with prostate cancer. However, only a minority of men with elevated PSA, defined as 3 ng/ml or higher, have prostate cancer. This has led to the search for additional markers to determine indication for a prostate cancer biopsy. We analyzed a data set from the Gothenburg arm of the European Randomized Study of Prostate Cancer screening[6]. We explored two markers, free-to-total PSA ratio (FT) and human kallikrein 2 (HK), with a positive test defined as <20% and >0.075ng/mL respectively.

Table 1 gives the crosstable from the study. There were 740 biopsies in total, of which 192 (26%) were positive for cancer. Table 2 gives a variety of statistics typically reported in studies of diagnostic tests. FT is the more sensitive test, and HK has greater specificity; FT has the superior negative predictive value and negative likelihood ratio, HK the superior positive predictive value and positive likelihood ratio. In terms of global statistics, FT has a slightly better Youden index and correlation, but HK a far superior Brier score.

Table 1.

Outcome of 740 biopsies for two binary tests based on free-to-total PSA ratio (FT) and hK2 (HK)

		No cancer			Cancer
		FT			FT
hK2		+	−	Total	+	−	Total
	+	51	67	118	91	6	97
	−	279	151	430	83	12	95
	Total	330	218	548	174	18	192

Table 2.

Test characteristics of binary diagnostic tests based on free-to-total PSA ratio (FT) and hK2 (HK). The BOTH test is positive only if FT and HK are both positive; the EITHER test is positive unless either FT or HK are positive.

	FT	HK	BOTH	EITHER
Sensitivity	91%	51%	47%	94%
Specificity	40%	78%	91%	28%
Positive predictive value	35%	45%	64%	31%
Negative predictive value	92%	82%	83%	93%
Positive likelihood ratio	1.52	2.32	5.22	1.31
Negative likelihood ratio	0.23	0.63	0.58	0.21
AUC (Youden)	0.65	0.64	0.69	0.61
Brier	0.47	0.29	0.21	0.55
Correlation	0.29	0.28	0.42	0.23

We believe that table 2 provides no basis for a choice between the two tests. Indeed, perhaps the only thing we can glean from the table is that FT is more sensitive and HK more specific. This suggests that we should choose based on whether we think that specificity or sensitivity is more important for prostate cancer biopsy. Doing so requires a parameter to quantify the relative importance of finding cancers and avoiding unnecessary biopsy.

Threshold probability

A diagnostic test is given to inform a subsequent course of action, such as surgery, drug therapy or, as is the case in the prostate cancer example, further work-up such as a biopsy. We will use the term “treatment” to describe any action taken on the basis of a positive test.

A simple, intuitive parameter to weight sensitivity and specificity is the threshold probability, which we denote p_t. A patient given a probability of disease $\widehat{p}$ at or above his or her threshold probability will opt for treatment; if $\widehat{p}<p_t$ then the patient will decline further treatment.

The threshold probability p_t can vary from patient to patient and from doctor to doctor depending on personal preferences as to the risks and benefits of treatment. As such, we are defining threshold probability in a decision analytic context, it cannot be derived from the results of a diagnostic study (such as table 1) by maximizing the Youden index or looking for an optimal cut-point on a Receiver Operating Characteristic curve[7]. Threshold probability is entirely dependent on additional information as to the benefits and harms of treatment. To choose a suitable p_t for our prostate cancer biopsy example, we have to take into consideration that biopsy is fairly safe, with <5% incidence of adverse events such as infection[8]. On the other hand, biopsy is an uncomfortable experience, involving a probe being inserted into the rectum, and then needles being fired through the rectum into the prostate. We also have to take into account that prostate cancer is a relatively slow growing disease, such that if we do not biopsy straight away, a future biopsy is still likely to catch disease at a curable stage.

An individual’s own threshold probability can be assessed in several different ways. It can ascertained directly, such as by asking, “What is the lowest risk of cancer at which you would still advise a patient to have a biopsy?”, or by deriving from a question about odds: “What is the maximum number of biopsies you would do in order to find one cancer?”. Where a threshold probability is derived from a patient, it is naturally possible that this might be irrational, or incongruent with the patient’s true preferences. But it is up to the physician, as part of shared decision-making, to help patients become better informed and explore their preferences carefully. Moreover, note that the concept of a threshold probability is fundamental to the use of any form of medical prediction model. Whether the model gives a patient’s risk of a cardiovascular event[9], the likelihood of cancer recurrence after surgery[10] or the probability of prostate cancer[11], decisions about primary prevention, adjuvant chemotherapy or biopsy depend, implicitly or explicitly, on comparing the output of the prediction model with a threshold probability.

After discussions with urologists, we propose that a typical p_t for prostate cancer biopsy is 20%, in other words, a well-informed patient would opt for biopsy if told that his risk of prostate cancer was 20% or more but decline if given a risk of less than 20%. A patient who was averse to medical procedures might require a high p_t such as 30%, before agreeing to put himself through biopsy; a patient who particularly feared cancer might have a lower p_t such as 15%. We note that if prostate cancer was a more aggressive disease, these threshold probabilities would be lower. Indeed, this can be directly observed in the literature. It has been suggested[12] that physicians should be prepared to do up to 10 biopsies to find one ovarian cancer. This is a p_t of 10 %, lower than the 20% p_t for prostate cancer, reflecting that ovarian cancer is a far more aggressive disease.

It is easily shown that the odds at p_t gives the relative harms and benefits of a true and false positive. Denote u_xy as the utility to the patient of the outcome where x is the treatment and y is the true disease state. We assume that treatment is determined by the diagnostic test result, such that x = 0 and x = 1 constitute negative and positive test results respectively. The expected utility of an outcome is simply the probability of the outcome multiplied by its utility. Hence the expected utility of treatment and no treatment are given as:

$$\begin{array}{cc}\hfill \text{Expected utility of treatment}=& u_{11}\widehat{p}+u_{10}(1-\widehat{p})\hfill \\ \hfill \text{Expected utility of no treatment}=& u_{01}\widehat{p}+u_{00}(1-\widehat{p})\hfill \end{array}$$

Take the case where a patient undergoes a diagnostic test and is given a probability of disease identical to their threshold probability, that is, $\widehat{p}=p_t$. We know that if $\widehat{p}>p_t$ a patient will choose treatment and that where $\widehat{p}<p_t$ the patient will decline treatment. So where $\widehat{p}=p_t$, the patient is indifferent. This implies that the expected utility of treatment and the expected utility of no treatment are similar. Hence:

$$u_{11}\widehat{p}+u_{10}(1-\widehat{p})=u_{01}\widehat{p}+u_{00}(1-\widehat{p})$$

As $\widehat{p}=p_t$ this gives:

$$u_{11}{p}_t+u_{10}(1-p_t)=u_{01}{p}_t+u_{00}(1-p_t)$$

This can be rearranged as:

$$\frac{u_{00}-u_{10}}{u_{11}-u_{01}}=\frac{p_t}{1-p_t}$$ (1)

In other words, the odds at the threshold probability p_t gives the benefit of a true positive (compared to a false negative) relative to the benefit of a true negative (compared to a false positive). This relationship has been described previously to determine the most appropriate threshold for a continuous diagnostic test[13].

Here we use (1) to weight the clinical consequences of a binary diagnostic test. There are four possible outcomes of a binary diagnostic test: true positive, false negative, false positive and true negative. Using T for the test result and D for true disease status, this gives:

$$\begin{array}{cc}\hfill \text{True Positive}=& \mathrm{P}(\mathrm{T}=1\mid D=1).P(D=1).u_{11}\hfill \\ \hfill \text{False Negative}=& \mathrm{P}(\mathrm{T}=1\mid D=1).P(D=1).u_{01}\hfill \\ \hfill \text{False Positive}=& \mathrm{P}(\mathrm{T}=1\mid D=0).P(D=0).u_{10}\hfill \\ \hfill \text{True Negative}=& \mathrm{P}(\mathrm{T}=0\mid D=0).P(D=0).u_{00}\hfill \end{array}$$

Assuming the test is itself associated with zero utility, that is, it has trivial costs, harms and inconvenience, the expected utility of the test (u_test) is:

$$\begin{array}{cc}\hfill u_{test}=& \mathrm{P}(\mathrm{T}=1\mid D=1).P(D=1).u_{11}+\mathrm{P}(\mathrm{T}=0\mid D=1).P(D=1).u_{01}+\hfill \\ \hfill & \mathrm{P}(\mathrm{T}=1\mid D=0).P(D=0).u_{10}+\mathrm{P}(\mathrm{T}=0\mid D=0).P(D=0).u_{00}\hfill \end{array}$$

This gives:

$$u_{test}=\mathrm{P}(\mathrm{T}=1\mid D=1).P(D=1)(u_{11}-u_{01})+\mathrm{P}(\mathrm{T}=1\mid D=0).P(D=0).(u_{10}-u_{00})+P(D=1).u_{01}+P(D=0).u_{00}$$

The utility of treating no patient is:

$$u_{none}=P(D=1).u_{01}+P(D=0).u_{00}$$

Hence the utility of the test compared to treating no patient is given by:

$$u_{test}-u_{none}=\mathrm{P}(\mathrm{T}=1\mid D=1).P(D=1)(u_{11}-u_{01})+\mathrm{P}(\mathrm{T}=1\mid D=0).P(D=0).(u_{10}-u_{00})$$

This gives:

$$u_{test}-u_{none}=\mathrm{P}(\mathrm{T}=1\mid D=1).P(D=1)+\mathrm{P}(\mathrm{T}=1\mid D=0).P(D=0).\frac{u_{00}-u_{10}}{u_{11}-u_{01}}$$

From (1):

$$u_{test}-u_{none}=\mathrm{P}(\mathrm{T}=1\mid D=1).P(D=1)+\mathrm{P}(\mathrm{T}=1\mid D=0).P(D=0).\frac{p_t}{1-p_t}$$

Using π for prevalence of disease P(D=1), sensitivity for P(T=1|D=1) and specificity for P(T=0|D=0), we get:

$$u_{test}-u_{none}=\pi .sensitivity-(1-\pi )(1-specificity)\frac{p_t}{1-p_t}$$ (2)

We will denote (2) as “net benefit” to reflect that the quantity reflects a gain minus a loss: true positives minus false positives. By definition, “treat none” is zero and treat all is given by:

$$u_{treatall}-u_{none}=\pi -(1-\pi )\frac{p_t}{1-p_t}$$

We can then plot net benefit of u_test, u_{treat all} and u_none against threshold probability p_t (see figure 1). In the context of evaluating models with a continuous predictor, we have previously described figure 1 as a “decision curve”[14]. Because net benefit combines benefits and harms, decision theory has it that the optimal strategy is that with the greatest net benefit, irrespective of the size of the difference in net benefit.

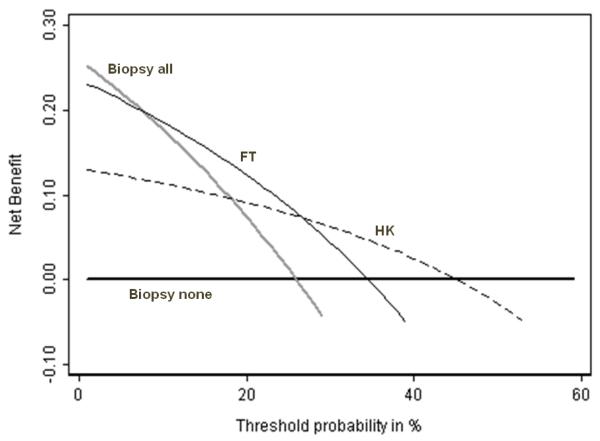
Figure 1. Net benefit against plotted against threshold probabilityfor molecular markers of prostate cancer.

Grey line: biopsy all men. Thick black line: biopsy no men. Thin black line: biopsy if FT test positive. Dashed line: biopsy if HK test positive. The optimal strategy is to biopsy all men if the threshold probability is below 10%; biopsy on the basis of FT is threshold probability is 10 – 25%; biopsy by HK if threshold probability is 25 – 45% and biopsy no man if threshold probability is greater than 45%.

The decision curves in figure 1 show that the optimal strategy changes from the most sensitive (treat all) to the most specific (treat none) as threshold probability increases. This is intuitive: a low threshold probability implies that missing disease is far worse than unnecessary treatment, that it is therefore important to find as many cases of disease as possible and that sensitivity is favored; a high threshold probability implies that treatment is harmful or costly or inconvenient and therefore that specificity is important. The key message of figure 1 is that if p_t is less than about 10%, all patients should be biopsied without testing; if p_t is between approximately 10 – 25% patients positive for FT should be biopsied; if p_t is between 25 – 45%, biopsy should be based on HK; and if p_t is greater than 45%, no patient should be biopsied.

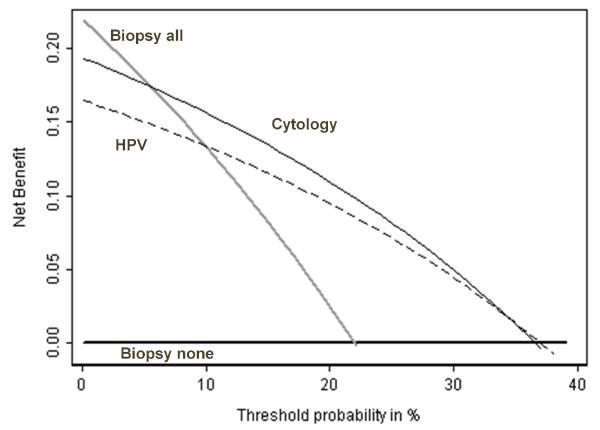
Figure 2 shows net benefit against threshold probability for the example described in the introduction comparing a repeat Pap smear to an HPV test for colposcopy[2]. A repeat PAP smear is of value if the threshold probability for colposcopy is between 10 – 35%; there is essentially no value to an HPV test.

Figure 2. Net benefit against plotted against threshold probability for repeat tests for cervical abnormalities.

Grey line: colposcopy for all women. Thick black line: colposcopy for no women. Thin black line: colposcopy if HPV test positive. Dashed line: colposcopy if repeat cytology positive. A repeat PAP smear is of value if the threshold probability for colposcopy is between 10 – 35%; there is no value to an HPV test.

Using threshold probability as a parameter has allowed us to make a decision as to which of two diagnostic tests we should use under quantitatively defined circumstances. Moreover, our method allows us to specify quantitatively the circumstances under which neither test should be used at all.

Relative diagnostic value

Figure 1 suggests that, in the comparison of two diagnostic tests, there is a cut-point of threshold probability that determines which test should be used. In addition to visual inspection of the decision curve, this cut-point can be determined analytically. Take two tests, test₁ and test₂, where test₁ is more sensitive and test₂ more specific.

The net benefits of the two tests are equal when:

$$\pi .sensitivit{y}_1-(1-\pi )(1-specificit{y}_1)\frac{p_t}{1-p_t}=\pi .sensitivit{y}_2-(1-\pi )(1-specificit{y}_2)\frac{p_t}{1-p_t}$$

This gives:

$$\pi .(sensitivit{y}_1-sensitivit{y}_2)+(1-\pi )(specificit{y}_1-specificit{y}_2)\frac{p_t}{1-p_t}=0$$

Under the assumption that the specificities of the two tests differ, each side can be divided by (1 − π)(specificity₂ − specificity₁) to give

$$\frac{(sensitivit{y}_1-sensitivit{y}_2)}{(specificit{y}_2-specificit{y}_1)}\frac{\pi }{(1-\pi )}-\frac{p_t}{1-p_t}=0$$

We denote:

$$RelativeDiagnosticValue=\frac{(sensitivit{y}_1-sensitivit{y}_2)}{(specificit{y}_2-specificit{y}_1)}$$

Hence

$$RelativeDiagnosticValue\frac{\pi }{(1-\pi )}=\frac{p_t}{1-p_t}$$ (3)

Or alternatively:

$$p_t=\frac{k}{1+k}\text{where}k=RelativeDiagnosticValue\frac{\pi }{(1-\pi )}$$

Equation 3 can be expressed as simple rule of thumb: the relative diagnostic value of two tests is the difference in sensitivity divided by the difference in specificity; the relative diagnostic value multiplied by the odds of the prevalence gives the threshold odds of disease below which the more sensitive test is preferable and above which the more specific test should be used.

An appealing feature of this methodology is that where it would not be rational to calculate relative diagnostic value, doing so involves division by zero, or gives a negative or zero threshold probability. For example, if two tests have the same specificity, the preferable test is the one with the higher sensitivity, independent of threshold probability. In this case, calculation of relative diagnostic value would involve division by zero. If one test has both a superior sensitivity and specificity than another, threshold probability would be negative.

Application of this method leads to several intuitive results. First, consider the cut-point at which treat none is preferable to a diagnostic test. The relative diagnostic value is simply sensitivity divided by 1 - specificity. Using D for disease and T for test result, we get:

$$\frac{p_t}{1-p_t}=\frac{P(T=1\mid D=1)}{P(T=1\mid D=0)}\frac{P(D=1)}{P(D=0)}$$

Using Bayes’ theorem gives:

$$\frac{p_t}{1-p_t}=\frac{P(D=1\mid T=1)P(T=1)÷P(D=1)}{P(D=0\mid T=1)P(T=1)÷P(D=0)}\frac{P(D=1)}{P(D=0)}$$

$$\frac{p_t}{1-p_t}=\frac{P(D=1\mid T=1)}{P(D=0\mid T=1)}$$

$$p_t=P(D=1\mid T=1)$$

That is, the threshold probability above which it is preferable just to treat no-one, rather than to treat according to a diagnostic test, is the positive predictive value of the test. In the case of FT for example, a patient with a positive test is given a probability of cancer at the positive predictive value of 35%. If the patient’s personal threshold probability for biopsy is above 35% he should not undergo testing, because his actions are the same for a positive and negative test.

We can also examine the cut-point below which treat all is preferable to a diagnostic test. The relative diagnostic value is now (1 − sensitivity) divided by specificity. This gives:

$$\frac{p_t}{1-p_t}=\frac{P(T=0\mid D=1)P(D=1)}{P(T=0\mid D=0)P(D=0)}$$

Using Bayes’ theorem again, we get:

$$p_t=P(D=1\mid T=0)=1-P(D=0\mid T=0)$$

Thus, the threshold probability below which it is preferable just to treat all patients, rather than to treat according to a diagnostic test, is 1 minus the negative predictive value of the test. In the case of FT for example, a patient with a negative test is given a probability of not having cancer at the negative predictive value of 92%. The patient’s probability of cancer is thus 8% and if his personal threshold probability for biopsy is below 8%, testing is not of benefit and the patient should be simply be referred to biopsy.

Comparing treat all to treat none, the relative diagnostic value is 1. This gives:

$$\frac{p_t}{1-p_t}=\frac{P(D=1)}{P(D=0)}$$

And thus:

$$p_t=P(D=1)$$

In other words, in the absence of a diagnostic test, the decision to accept treatment depends on whether the threshold probability is above or below the prevalence. Again, this makes clear intuitive sense, because in the absence of a diagnostic test, the patient’s risk is given as the prevalence.

Applying our methodology to figure 1, we order tests from most to least sensitive and calculate relative diagnostic value between adjacent pairs. This gives p_t ’s as follows: treat all vs. FT = 7%; FT vs. HK = 27%; HK vs. treat none = 45%.

Confidence intervals for relative diagnostic value can be calculated as follows. Table 3 is a duplicate of Table 1, except that the entries are denoted by letters to introduce the necessary notation. The specificity of test 1 is (c₀+d₀)/n₀ and the specificity of test 2 is (b₀+d₀)/n₀. The difference between two specificities (denominator of relative diagnostic value) then is (c₀−b₀)/n₀. Similarly, the sensitivity of test 1 is (a₁+c₁)/n₁ and the sensitivity of test 2 is (a₁+b₁)/n₁. The difference between two sensitivities (numerator of relative diagnostic value) then is (b₁−c₁)/n₁.

$$R=\frac{n_0(c_1-b_1)}{n_1(c_0-b_0)}$$

It will be clear later that it is easier to work with R⁻¹ instead of R.

$$R^{-1}=\frac{n_1(c_0-b_0)}{n_0(c_1-b_1)}$$

Table 3.

Notation for derivation of the variance of relative diagnostic value

		No disease			Disease
		FT			FT
hK2		+	-	Total	+	-	Total
	+	a0	b0	a0+b0	a1	b1	a0+b1
	−	c0	d0	a0+b0	c1	d1	a0+b1
	Total	a0+c0	b0+d0	n0	a0+c1	b0+d1	n1

To derive the variance of R⁻¹, first note that the difference between the two specificities is simply the difference between two paired binomial proportions, a quantity extensively studied in various derivations of the asymptotic power function of McNemar’s test and the corresponding confidence interval construction. Fleiss (Statistical Methods for Rates and Proportions, 1981, 2^nd [15], p117) shows that the asymptotic variance of this difference is given by:

$$Var\left(\frac{c_0-b_0}{n_0}\right)=\frac{n_0(b_0+c_0)-{(b_0-c_0)}^2}{n_0^3}$$ (4)

Applying the same principles, the asymptotic variance of the difference in sensitivities can be written similarly as:

$$Var\left(\frac{c_1-b_1}{n_1}\right)=\frac{n_1(b_1+c_1)-{(b_1-c_1)}^2}{n_1^3}$$ (5)

To derive the asymptotic variance of R⁻¹ from (4) and (5) we apply the multivariate delta method (see, for example, Casella and Berger, Section 5.5.4)[16]:

$$Var\left(R^{-1}\right)=Var\left(\frac{[{\mathrm{c}}_0-{\mathrm{b}}_0]{\mathrm{n}}_1}{[{\mathrm{c}}_1-{\mathrm{b}}_1]n_0}\right)={\left(\frac{[{\mathrm{c}}_0-{\mathrm{b}}_0]{\mathrm{n}}_1}{[{\mathrm{c}}_1-{\mathrm{b}}_1]n_0}\right)}^2\left(\frac{Var([{\mathrm{c}}_0-{\mathrm{b}}_0]∕{\mathrm{n}}_0)}{{[{\mathrm{c}}_0-{\mathrm{b}}_0]}^2∕{\mathrm{n}}_0^2}+\frac{Var([{\mathrm{c}}_1-{\mathrm{b}}_1]∕{\mathrm{n}}_1)}{{[{\mathrm{c}}_1-{\mathrm{b}}_1]}^2∕{\mathrm{n}}_1^2}\right)$$

Substituting (4) and (5) we get:

$$\begin{array}{c}\hfill Var\left(R^{-1}\right)=Var\left(\frac{[{\mathrm{c}}_0-b_0{\mathrm{n}}_1]}{[{\mathrm{c}}_1-b_1]{\mathrm{n}}_0}\right)\hfill \\ \hfill ={\left(\frac{[{\mathrm{c}}_0-{\mathrm{b}}_0]{\mathrm{n}}_1}{[{\mathrm{c}}_1-{\mathrm{b}}_1]{\mathrm{n}}_0}\right)}^2\left(\frac{{\mathrm{n}}_0({\mathrm{b}}_0+{\mathrm{c}}_0)-{({\mathrm{b}}_0-{\mathrm{c}}_0)}^2}{{\mathrm{n}}_0{[{\mathrm{c}}_0-b_0]}^2}+\frac{{\mathrm{n}}_1({\mathrm{b}}_1+{\mathrm{c}}_1)-{({\mathrm{b}}_1-{\mathrm{c}}_1)}^2}{{\mathrm{n}}_1{[{\mathrm{c}}_1-{\mathrm{b}}_1]}^2}\right)\hfill \end{array}$$

Recall that p_t = Rπ/(1+ Rπ−R) = [1+R⁻¹(π⁻¹−1)]⁻¹. Another application of the delta method gives:

$$Var\left(p_t\right)={p_t}^{4}Var\left(p_t^{-1}\right)={p_t}^4{({\pi }^{-1}-1)}^{2}Var\left(R^{-1}\right)$$

By virtue of the delta method, the asymptotic distribution of p_t is normal with variance as above. Therefore, an approximate 95% confidence interval for p_t can be formed by:

$$p_t\pm 1.96\times \sqrt{Var\left(p_t\right)}$$

Incorporating test harm

The previous equations assume that the test is associated with trivial cost, harm and inconvenience. To incorporate the disutility of a test, we propose that analysts obtain from physicians a clinical estimate of harms in the units of net benefit, that is, true cases found. A physician can be asked, “If this test was perfect, how many patients would you subject to the test in order to find one case of disease?”. The reciprocal of this number is the test harm and is subtracted from net benefit.

$$u_{test}-u_{none}=\pi .\text{sensitivity}-(1-\pi )(1-\text{specificity})\frac{p_t}{1-p_t}-\text{Test Harm}$$

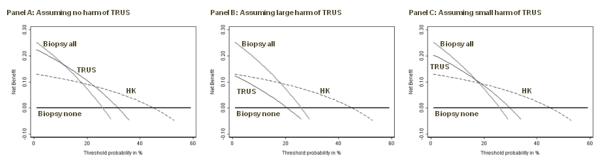
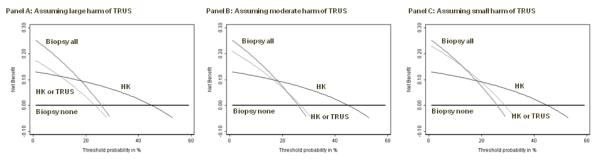
As an example, certain clinicians have advocated the use of transrectal ultrasound (TRUS) to determine whether elevated PSA was due to benign enlargement of the prostate gland, rather than cancer. We defined a positive ultrasound as a TRUS volume less than 50 cc, a cutoff that has similar properties to FT (sensitivity 84%, specificity 34%). The problem with TRUS is that involves placing a probe into the patient’s rectum, which is unpleasant and inconvenient for the patient, and time-consuming for the doctor. We consulted with a urologist, who told us that he would do no more than 10 ultrasounds to detect a prostate cancer if the ultrasound was a perfect test. This gives a test harm of 0.1. We calculated decision curves for TRUS, in comparison to HK, in figure 3, both with and without test harm. There is no level of threshold probability for which TRUS has higher net benefit than any alternative strategy, even under the very liberal assumption that a physician would conduct 50 ultrasounds to find one cancer.

Figure 3. Net benefit against plotted against threshold probabilityfor a molecular marker of prostate cancer compared to an invasive diagnostic test.

Grey line: biopsy all men. Thin black line: biopsy no men. Dashed line: biopsy if HK test positive. Thick black line: biopsy if TRUS test positive, assuming no harm of TRUS (left panel); a physician would do not more than 10 TRUS to find one cancer (center panel); a physician would do no more than 50 TRUS to find one cancer (right panel). TRUS is of some benefit (left panel) unless one takes into account harm: even under the very liberal assumption that a physician would conduct 50 TRUS to find one cancer (right panel), TRUS has highest net benefit for no threshold probability.

Test harm can be incorporated into relative diagnostic value as follows.

$$\frac{\text{sensitivity}1-\text{sensititvity}2-(\text{harm}1-\text{harm}2)∕\pi }{\text{specificity}2-\text{specificty}1}=\frac{1-\pi }{\pi }\frac{p_t}{1-p_t}$$

Combining tests

It is arguable that the comparison between two tests is an arbitrary one, because a physician could always order both. Yet there would still need to be an algorithm to determine treatment on the basis of the test results. Previous literature has compared the EITHER test (e.g. biopsy if either FT or HK are positive) or the BOTH test (e.g. biopsy if both FT and HK are positive). We will further examine conditional testing (e.g. test HK; if positive biopsy, otherwise conduct a TRUS; biopsy if TRUS positive, otherwise no biopsy).

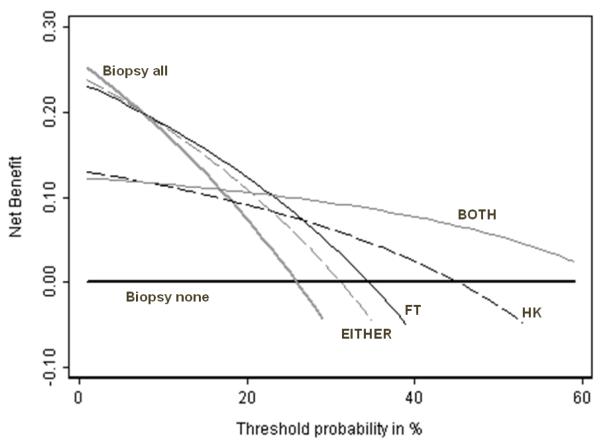
We propose that the EITHER and BOTH tests should be considered as binary tests. The operating characteristics of EITHER and BOTH are shown in table 2. BOTH appears by far the best test, with the highest Youden index and lowest Brier score. But Figure 4 shows the plot of net benefit against threshold probability and BOTH is not universally the optimal strategy. If p_t is less than about 10%, all patients should be biopsied without testing; if p_t is between approximately 10 – 25% patients positive for FT should be biopsied; if p_t is between 25 – 65%, biopsy should be given only to patients who test positive for both FT and HK; and if p_t is greater than 65%, no patient should be biopsied. Note that for no important range of threshold probability do HK or EITHER have the highest net benefit, suggesting that it is never of value to use these tests. The p_t’s below which the more sensitive test should be used and above which the more specific test is optimal, are as follows: treat all vs. EITHER = 7%; EITHER vs. FT = 8%; FT vs. BOTH = 23%; BOTH vs. treat none = 65%.

Figure 4. Net benefit against plotted against threshold probability for molecular markers of prostate cancer.

Thick grey line: biopsy all men. Thick black line: biopsy no men. Thin black line: biopsy if FT test positive. Dashed black line: biopsy if HK test positive. Thin grey line: biopsy if EITHER FT or HK positive. Dashed grey line: biopsy if BOTH HK and FT positive. The highest net benefit is for biopsying all men (threshold probability less than 10%); FT (threshold probability 10 – 25%) and BOTH (threshold probability 25% +). For no threshold probability do HK or EITHER have the highest net benefit, suggesting that neither HK alone nor a test of either HK or FT should be used.

The value of conditional testing would be if one test was harmful or expensive, such as TRUS. The harms of testing in a conditional (“CONDITIONAL”) strategy - such as test HK, test TRUS if HK negative - are reduced because only a subgroup of patients with negative HK receive TRUS. If we set the harm of a TRUS at 0.1, the value of Test Harm for EITHER is also 0.1; Test Harm for CONDITIONAL is 0.1 multiplied by the probability of negative HK, that is, 0.071.

Figure 5 shows net benefit against threshold probability for HK and CONDITIONAL, for Test Harms for TRUS of 0.1, 0.05 and 0.02. Even if TRUS is considered of relatively little disbenefit, its use cannot be justified for what would appear to be the clinically sensible strategy of only applying TRUS where HK is negative.

Figure 5. Net benefit against plotted against threshold probability for a molecular marker of prostate cancer, with an invasive diagnostic test conditional upon the marker findings.

Thick grey line: biopsy all men. Thick black line: biopsy no men. Thin black line: biopsy if HK test positive. Thin grey line: biopsy if HK test positive or TRUS following a negative HK test is positive, assuming a physician would do not more than 10 TRUS to find one cancer (left panel); a physician would do no more than 20 TRUS to find one cancer (center panel); a physician would do no more than 50 TRUS to find one cancer (right panel). Even if TRUS is considered of relatively little disbenefit, its use cannot be justified for what would appear to be the clinically sensible strategy of only applying TRUS where HK is negative.

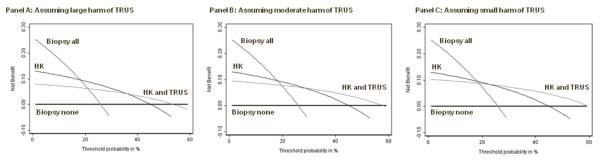
However, we could test an alternative CONDITIONAL strategy: administer HK; if negative, don’t biopsy, if positive give TRUS; biopsy if TRUS also positive. Figure 6 shows the result of this strategy: it is found to be preferable to all alternatives for certain probability thresholds.

Figure 6. Net benefit against plotted against threshold probability for a molecular marker of prostate cancer, with an invasive diagnostic test conditional upon the marker findings.

Thick grey line: biopsy all men. Thick black line: biopsy no men. Thin black line: biopsy if HK test positive. Thin grey line: biopsy if HK test positive and a TRUS given after a positive HK test is also positive, assuming a physician would do not more than 10 TRUS to find one cancer (left panel); a physician would do no more than 20 TRUS to find one cancer (center panel); a physician would do no more than 50 TRUS to find one cancer (right panel).The conditional strategy is now found to be preferable for certain threshold probabilities.

Conclusions

The choice of which of two binary diagnostic tests is preferable, or if the tests should be combined in some way, would appear to be one of the most basic of biostatistical problems. Here we argue that the tools we as biostatisticians have been using to solve this problem – descriptive statistics of test accuracy, and inference thereon – have not been up to the job. We give a specific example using a real data set where statistics such as sensitivity, specificity or Brier score give unclear and even contradictory findings.

It is our view that such statistics have limited ability to guide clinical decisions because they do not incorporate any information on the clinical consequences of diagnostic tests. We introduce a parameter, the threshold probability, which can describe the clinical consequences of using a test in a simple, intuitive manner: a low threshold probability implies that it is very important to find all or nearly all cases of disease; a higher threshold probability implies that treatment or further work-up is associated with significant harms, and that false positives are important to avoid. We go on to show that this parameter can be used to weight true and false positives to provide a single statistic, the net benefit, which may be used to determine which of two diagnostic tests is preferable. Because this statistic has a straightforward interpretation – the number of true positives per patient if the false positive rate was zero – it can easily incorporate simple estimates of the harm of a test. Moreover, the method is naturally extended to combinations of tests, such as where positives on both or either of two tests are required for a clinician to take further action. Net benefit can also be used to derive a simple statistic to compare two tests, relative diagnostic value, which defines when the more sensitive test should be used and where the more specific test would be preferable. We hope our work encourages other biostatisticians to investigate straightforward decision analytic approaches to the comparison of diagnostic tests.