Biomolecular electrostatics and solvation: a computational perspective

Abstract

An understanding of molecular interactions is essential for insight into biological systems at the molecular scale. Among the various components of molecular interactions, electrostatics are of special importance because of their long-range nature and their influence on polar or charged molecules, including water, aqueous ions, proteins, nucleic acids, carbohydrates, and membrane lipids. In particular, robust models of electrostatic interactions are essential for understanding the solvation properties of biomolecules and the effects of solvation upon biomolecular folding, binding, enzyme catalysis, and dynamics. Electrostatics, therefore, are of central importance to understanding biomolecular structure and modeling interactions within and among biological molecules. This review discusses the solvation of biomolecules with a computational biophysics view towards describing the phenomenon. While our main focus lies on the computational aspect of the models, we provide an overview of the basic elements of biomolecular solvation (e.g., solvent structure, polarization, ion binding, and nonpolar behavior) in order to provide a background to understand the different types of solvation models.

Introduction and overview

An understanding of molecular interactions is essential for insight into biological systems at the molecular scale (Baker, 2005a; Baker,2005b; Baker et al., 2006; Baker, 2004; Davis & McCammon, 1990; Dong et al., 2008; Draper et al., 2005; Feig & Brooks, 2004; Feig et al., 2008; Fogolari et al. 2008, 2002; Gilson & Honig, 1987; Honig & Nicholls, 1995; McLaughlin, 1989; Prabhu & Sharp, 2006; Schutz & Warshel, 2001; Sheinerman et al., 2000; Simonson, 2001; Simonson, 2003; Warshel & Papazyan, 1998). Molecular interactions determine the structure, dynamics, and binding of biomolecules, and therefore play a central role in how cells develop, operate, communicate, and control their activities. Such interactions include several components (Leach, 2001; Schlick, 2002): contributions from linear, angular, and torsional forces in covalent bonds; and non-bonded van der Waals and electrostatic forces (Stone, 1996). Among the various components of molecular interactions, electrostatics are of special importance because of their long-range nature and their influence on polar or charged molecules, including water, aqueous ions, proteins, nucleic acids, carbohydrates, and membrane lipids. In particular, robust models of electrostatic interactions are essential to understand the solvation properties of biomolecules and the effects of solvation upon biomolecular folding, binding, enzyme catalysis, and dynamics. Therefore, electrostatics are of central importance to understanding biomolecular structure and modeling interactions within and among biological molecules.

This paper discusses the solvation of biomolecules, and focuses on electrostatics from a computational perspective. We provide a brief overview of various biomolecular solvation models based on their level of detail. Advantages and caveats of different solvation models are discussed. Nonpolar contributions to the solvation are also considered for the models. While our main focus lies on the computational aspect of the models, we summarize the basic elements of biomolecular solvation (e.g., solvent structure, polarization, ion binding, and nonpolar behavior) in order to provide a background to understand the solvation models. Examples such as titration state prediction and biomolecular recognition are provided to exhibit the application of the solvation models. This review concludes with a short summary, and the directions of future research are stated as concluding remarks.

Characteristics of biomolecular solvation by water

Water solvation influences all aspects of biology, ranging from cellular function (Parsegian & Rau, 1984) to biomolecular interactions (Auffinger & Hashem, 2007; Prabhu & Sharp, 2006), to biopolymer stability (Ben-Naim, 1997) and the solvation of simple solutes (Dill et al., 2005). In general, an interaction between solute and solvent is of great importance to understand the solvation. For biomolecular solvation where water is a major solvent, water is not only a passive medium but also actively exhibits unique nature that greatly influences the solvation of biomolecules. To understand this ubiquitous role of water, it is important to appreciate some of its most basic properties.

Solvent and ion interactions influence nearly all aspects of biomolecular structure and function. As a result, it is impossible to provide a comprehensive review of biomolecular solvation. Instead, we focus on those aspects of solvation most amenable to computational treatment. While this discussion includes acid/base chemistry and biomolecular titration state prediction, it exclude several other interesting areas including the role of solvent and ions in catalysis (Bombarda & Ullmann, 2010; Di Cera, 2006; Garcia-Viloca et al., 2004; Martick et al., 2008; Niu et al., 2009; Page et al., 2006; Rhodes et al., 2006; Warshel & Dryga, 2011; Wells & Di Cera, 1992), spectroscopic probes of biomolecular electrostatics (Ensign & Webb, 2011; Hu & Webb, 2000; Stafford et al., 2000; Webb et al., 2011), solvent influences on biomolecular dynamics and flexibility (Bone, 2008; Fenimore et al., 2004; Lubchenko et al., 2005; Lucent et al., 2007), and cosolute influences on biomolecular stability (Drozdov et al., 2004; England et al., 2008; Harries & Rosgen, 2008; Rösgen et al., 2007; Rösgen et al., 2005; Tran et al., 2008).

Water structure

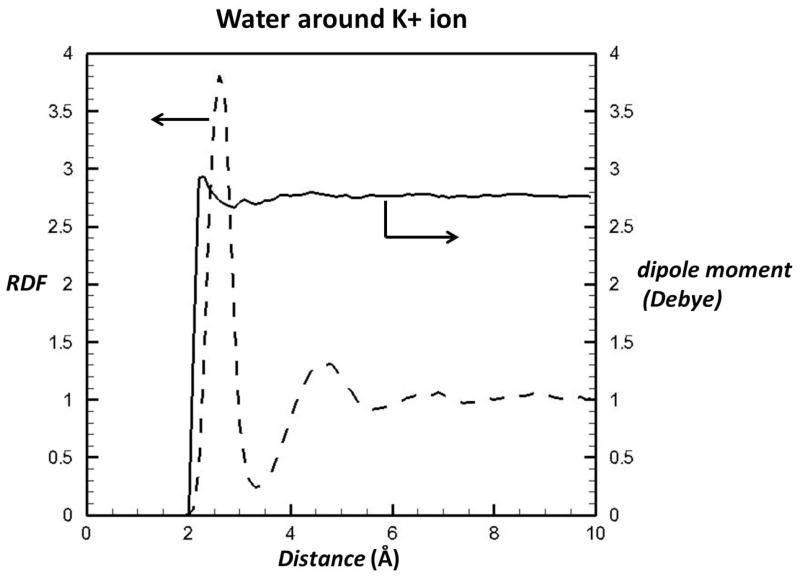
Water is a unique, small molecule with all three constituent atoms capable of forming hydrogen bonds. As a result, water molecules can cluster together in various arrangements, driven by their cooperative tendency to maximize the number of hydrogen bonds formed. Ab initio calculations suggest that a water hexamer (H₂O)₆ has several stable configurations of comparable energies that include cage, cyclic, chair, boat, and prismatic conformations (Moore Plummer & Chen, 1987; Xantheas et al., 2002; Xantheas & Dunning, 1994). Neutron and x-ray scattering have been used to characterize the average structure of bulk water. The radial distribution functions of OO, OH, and HH derived from these measurements provide valuable insight into local water structures (Root et al., 1986; Soper, 2000; Soper & Phillips, 1986; Sorenson et al., 2000). As an illustration, Figure 1 shows the oxygen radial distribution function or RDF around K+, denoting that the first peak of oxygen RDF around K+ is at an average separation of ~2.8 Å between the closest water pair. The first peak extends to a minimum at ~3.3 Å, indicating approximately 4.5 water molecules in the nearest coordination shell. The local structure of water has been rationalized as a “dynamic” mixture of two states: one corresponds to a rigid ice-like structure, Ice I_h, a hexagonal crystal form of ordinary ice (Fletcher, 1970) with four nearest neighbors at 2.8 Å; another corresponds to a denser ice-like structure, Ice II, a rhombohedral crystalline form with four water molecules at 2.8 Å plus another at 3.3 Å. Data from isochoric temperature differential experiments near the maximum-density-temperature peak, where the same densities can be achieved at two nearby temperatures, support the two-state theory (Bosio et al., 1983; Robinson et al., 1999; Sciortino et al., 1990). Within this framework, properties such as the anomalous temperature dependence of the density can be interpreted as the dynamic competition between the two types of hydrogen-bonding networks in response to changes in temperature (Schmid et al., 2001).

Figure 1.

Water structure and average dipole moment around a K+ ion. The radial distribution function (RDF) of O…K+ and water dipole moment were computed from molecular dynamic simulations of K+ in water using a polarizable potential (Grossfield et al., 2003; Ren & Ponder, 2003). Note that the average dipole moment of the water in the first solvation shell is roughly similar to that of bulk water.

Bulk water polarization

One of the fundamental properties of water is its role as an excellent solvent for polar molecules. Some aspects of this favorable polar molecular solvation can be understood from the very macroscopic continuum perspective of water bulk polarization. Water molecules have a dipole moment that varies between 1.8 Debye (D) in vacuum (Clough et al., 1973) to estimates of nearly 3 D in bulk water (Ren & Ponder, 2003; Silvestrelli & Parrinello, 1999). In a liquid environment, the molecular dipole moment of water will reorient in response to the application of an external field or the introduction of a solute charge distribution. The resulting reorientation creates a polarization (or dipole) density or so-called “dielectric response” (Bottcher, 1952; Hansen & McDonald, 2000; Jackson, 1975) (see Figure 1 and Figure 2). From the perspective of continuum electrostatics, this dielectric behavior is modeled as a linear relationship between the local field and electric displacement field because of local polarization—the coefficient of this relationship is the “dielectric coefficient,” or permittivity. Dielectric coefficients of pure solvent depend on a variety of molecular properties of the solvent, including structure, density, permanent charge distribution, and molecular polarizability. Dielectric coefficients range from values as small as 1 for a vacuum, to values of 2–4 for nonpolar solvents (alkanes), 10–20 for weakly polar molecules such as ammonia and ethanol, to approximately 80 for water at room temperature, and even larger values for some polar liquids such as formamide (105).

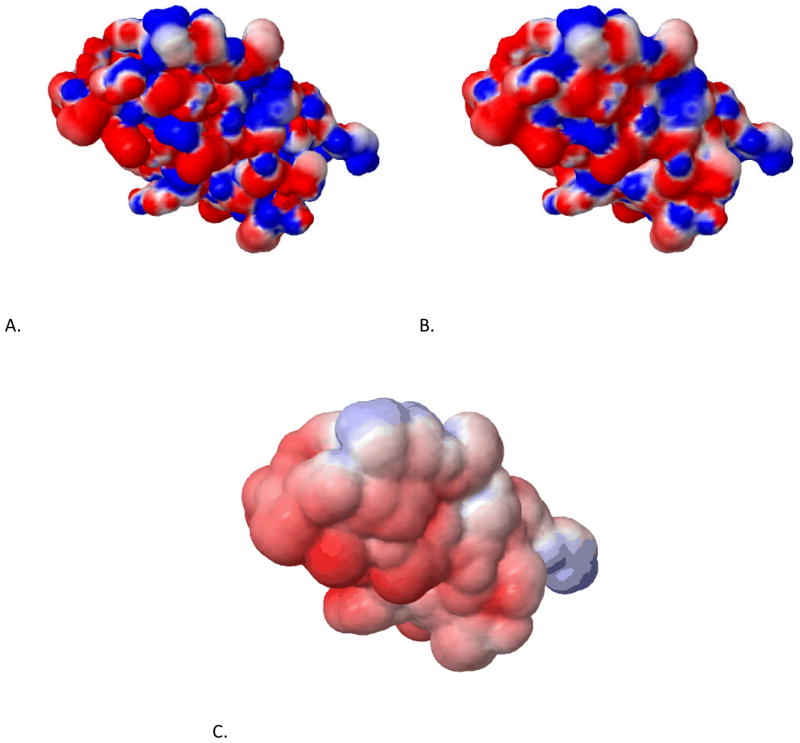
Figure 2.

The reorientation and polarization response of water upon the insertion of a cation (K+) into the bulk water. The yellow vector on each water molecule represents the net induced dipole moment because of the electric field of the ion and other water molecules. The white vector is the permanent (gas-phase) dipole moments (1.8 D) of the water molecule. The average dipole moment of a water molecule in liquid is 2.6–3.0 D according to various theoretical calculations. The snapshot is taken from molecular dynamics simulations of K+ in water using the AMOEBA potential (Ren & Ponder, 2003).

Electronic and nuclear water polarization

In addition to the bulk polarization of solvent, the charge distributions of solvent and solute molecules interact via mutual polarization; i.e., the reorganization of their electronic charge distributions. The reorganization of electrons is much faster than the overall reorientation and redistribution of solvent molecules (Nicol, 1974). It has been estimated that electronic solvation (as opposed to reorganization solvation) could account for as much as half of the overall electrostatic solvation free energy (Cukier & Zhang, 1997). Processes such as photoexcitation and electron and proton transfers occur on timescales between or close to those of electronic and nuclear responses (Cramer & Truhlar, 2001). Theoretical frameworks have been devised to separate the solvent electronic and nuclear response either adiabatically or nonadiabatically (Marcus & Sutin, 1985; Moser et al., 1992). In theoretical studies, continuum or molecular mechanics solvent often supplements quantum mechanical treatment of the solutes (reactants).

Nonpolar solvation by water

Another important aspect of solvation involves the mechanism of solvent interactions with uncharged solutes. This type of solvation phenomenon has many names including hydrophobic, apolar, and nonpolar; we refer to it as nonpolar solvation in this review. Nonpolar solvation has been extensively studied and modeled and there are many good references available for interested readers to explore, the following citations are only a few (Ben-Naim, 2006; Hummer et al.; Pratt, 2002; Pratt & Chandler; Pratt & Pohorille, 2002). This section focuses on the basic properties of nonpolar solvation important for the general aspects of biomolecule-solvent interactions.

Water’s small size and flexibility in forming infinite hydrogen-bonding networks around solutes contribute to the hydrophobic effect that is widely appreciated in biology. Nuclear magnetic resonance (NMR) (Mizuno et al., 1995), liquid chromatography (HPLC) (Silveston & Kronberg, 1989), and neutron scattering (Soper, 2000; Soper & Phillips, 1986) experiments suggested that water structure is different around a hydrophobic solute. Atomic and Monte Carlo simulations also support such structural change in water molecules, depending on surrounding environment (Lynden-Bell & Rasaiah, 1997; Madan & Sharp, 1996). Efforts to understand hydration based on water structure and entropy changes date back several decades (Frank & Evans, 1945). Sophisticated theories have been evolved to delineate the entropy and enthalpy contributions to solvation, the influence of dispersion and electrostatics, the effect of solute-length scale, temperatures and other external factors to understand solvation phenomenon (Chandler, 2005; Garde et al., 1996; Hummer et al., 2000; Schmid et al., 2001). Advancements in molecular simulations have and will continue to help further our understanding of the role of solvation in biomolecular structure and dynamics.

Pioneering work by Pratt and Chandler (Pratt, 2002; Pratt & Chandler, 1977; Pratt & Chandler, 1980; Pratt & Pohorille, 1992; Pratt & Pohorille, 2002) identified some of the fundamental determinants of nonpolar solvation. Not surprisingly, a major contribution to the energetics of solvating an uncharged molecule is the energy required to create a cavity in the solvent. This cavity-creation term describes the work involved with accommodating within the solvent: purely strong solute-solvent repulsive interactions. Later work by Hummer et al. (Hummer et al., 1996) translated this model in an information theory context by noting that the energetics of cavity creation are intrinsically encoded in the density fluctuations of the solvent. The energetics of cavity creation in water is strongly dependent on both the size and the shape of the nonpolar solute with a crossover in energetics and solvent density near the solute interface when the solute size approaches nanometer-length scales (Ashbaugh, 2009; Ashbaugh & Pratt, 2006; Ben-Amotz, 2005; Berne et al.,2009; Choudhury & Pettitt, 2007; Ewell et al., 2008; Hummer & Garde, 1998; Li et al., 2006; Lum et al., 1999; MacCallum et al., 2007; Rajamani et al., 2005). Another important aspect of nonpolar solvation is the attractive nature between the solute and the solvent. For nonpolar solvation, these attractive interactions are (by definition) not because of the electrostatics of static charge distributions on the solute and solvent, but are generally associated with weak dispersion interactions between solvent and solute originated from the fluctuation of induced dipoles within solvent and solute molecules (Boström & Ninham, 2005; Curutchet et al., 2006; Floris & Tomasi, 1989; Floris et al., 1991; Gallicchio et al., 2000; Levy et al., 2003; Pratt & Chandler, 1980). If sufficiently weak, such attractive nonpolar interactions are generally assumed not to affect the density of solvent around the solute but instead simply change the energetics of solvation for a solvent density distribution determined by repulsive solvent-solute interactions. Note that nonpolar solvation cannot be easily decoupled from the polar solvation process: strong attractive solute-solvent interactions can significantly affect local solvent densities and change the nonpolar properties of the solvation process (Dzubiella & Hansen, 2004; Dzubiella et al., 2006a; Dzubiella et al., 2006b). Therefore, while the decomposition of solute-solvent interactions into polar and nonpolar components is a useful conceptual device, the actual solvation process is much more complicated (Cramer & Truhlar, 2008; Cramer & Truhlar, 1999).

Many biological phenomena are associated with nonpolar solvation, ranging from protein folding to protein-protein to the fundamental structure and energetics of lipid bilayers and assemblies (Thirumalai & Hyeon, 2005; Yeagle, 2004; Zhou et al., 2004). A full discussion of the influence of nonpolar solvation on the numerous aspects of biomolecular structure, function, and energetics would fill several reviews. Therefore, interested readers are referred to the excellent discussion of the topic provided by Pratt and Pohorille (Pratt & Pohorille, 2002).

Site-specific binding and recognition

The discussion above has largely focused on the bulk properties of solvent and its non-specific interaction with solutes. However, a solvent such as water can also play a ligand-like role and interact with solutes in a decidedly non-bulk and site-specific manner. Perhaps the most familiar example of such site-bound solvent molecules are the crystallographic waters present at the surface (Kuhn et al., 1992; Merzel & Smith, 2002; Smolin & Winter, 2004) and in cavities (Damjanović et al., 2005; Damjanovic et al., 2005; Damjanović et al., 2007; Imai et al., 2005; Imai et al., 2007a) of many higher-resolution x-ray structures. While the physical and functional properties of such waters can be a subject of debate (Nayal & Di Cera, 1996), they are illustrative of the ways in which water can play structural as well as bulk roles in biomolecules. Nucleic acids provide another good illustration of how water can interact with biomolecular surfaces in a non-bulk-like and often sequence-specific manner (Arai et al., 2005; Auffinger & Hashem, 2007; Auffinger & Westhof, 2000a; Auffinger & Westhof, 2000b; Auffinger & Westhof, 2001; Bastos et al., 2004; Bonvin et al., 1998; Fuxreiter et al., 2005; Mikulecky & Feig, 2006; Rhodes et al., 2006; Yonetani et al., 2008), such as the zig-zag spine of hydration in the minor grove of B-DNA (Drew et al., 1982). Structurally or specifically bound water can also play an important role in protein structure and function, including allosteric regulation (Bone, 2006; Guinto & Di Cera, 1996; Krem & Di Cera, 1998; Royer et al., 1996) and stability/flexibility (Fischer & Verma, 1999). Finally, water can play a very important role in molecular recognition; ranging from the binding of small molecules and peptides (Barillari et al., 2007; Hamelberg & McCammon, 2004; Kuhn et al., 1992; Petrone & Garcia, 2004; Samsonov et al., 2008; Thilagavathi & Mancera, 2010; van Dijk & Bonvin, 2006; Villacanas et al., 2009), to protein-protein complexes (Ikura et al., 2004), to protein-nucleic acid binding (Billeter, 1996; Fried et al., 2002; LiCata & Allewell, 1997), and water itself in the form of ice-binding and anti-freeze proteins (Doxey et al., 2006; Jorov et al., 2004; Liu et al., 2005; Yang & Sharp, 2004). Such specific characteristics of the solvent obviously need detailed molecular descriptions of the solvent, as described later in this review.

Modeling ionic solutions

Ions play an essential role in biomolecular solvation and have a dramatic influence on the stability and function of a wide range of protein (Arakawa & Timasheff, 1984; Baldwin, 1996; Boström et al., 2005b; Boström et al., 2003a; Chen et al., 2007b; Friedman, 2000; Lund et al., 2008a; Ninham & Yaminsky, 1997; Pegram & Record, 2008; Shimizu et al., 2006; Vrbka et al., 2006), membrane (Aroti et al., 2007; Aroti et al., 2004; Berkowitz & Vácha, 2000; Boström et al., 2003b; Chen et al., 2007b; Clarke & Lüpfert, 1999; Gurau et al., 2004; Petrache et al., 2006; Sachs & Woolf, 2003), and nucleic acid structures (Anderson & Record, 1990; Anderson & Record, 1995; Auffinger & Hashem, 2007; Ballin et al., 2004; Chen et al., 2009a; Chen et al., 2009b; Draper, 2008; Draper et al., 2005; García-García & Draper, 2003; Gavryushov, 2009; Grilley et al., 2007; Grilley et al., 2006; Leipply & Draper, 2000; Misra & Draper, 2000; Misra & Draper, 2001; Ni et al., 1999; Olmsted et al., 1991; Record et al., 1978; Record et al., 1995; Tikhomirova & Chalikian, 2004). Several excellent reviews have been written on this subject (Anderson & Record, 1990; Anderson & Record, 1995; Draper, 2008; Draper et al., 2005; Ni et al., 1999; Record et al., 1978); we provide only a broad overview here.

Non-specific screening

One of the simplest aspects of ionic behavior is the non-specific “mean field” screening embodied in Debye-Hückel or Poisson-Boltzmann treatments of ionic solutions (Baker, 2004; Gilson & Honig, 1988; Grochowski & Trylska, 2008; Lamm, 2003; Lamm & Pack, 2010). Such treatments assume ideal ion behavior where each ion experiences the average influence of its surrounding ionic environment. Therefore, this “mean field” assumption implies no ion-ion correlations or fluctuations, effects that have been shown to be important in systems with high ion charge density (Angelini et al., 2006; Angelini et al., 2003; Ben-Yaakov et al., 2009; Ben-Yaakov et al., 2011; Butler et al., 2003; Holm et al., 2001; Jho et al., 2008; Kanduč et al., 2008; Podgornik & Dobnikar, 2001; Todd et al., 2008; Todd & Rau, 2008), as discussed later in this review. Additionally, these models assume no specific ion-ion, ion-solvent or ion-solute interactions; with a few exceptions (Baer & Mundy, 2011; Boström & Ninham, 2004; Boström et al., 2003; Jancovici, 2006; Parsons et al., 2011), ions are typically treated as inert hard spheres with generic solute interactions based only on charge and steric repulsion. While the assumption of ideality makes such theories very convenient to implement and use, such assumptions are rarely valid in actual biomolecular systems (Anderson & Record, 1995; Collins, 1995; Marcus, 2006; Overman & Lohman, 1994; Record et al., 1978). Nevertheless, these models are very popular and have been successfully used to describe some aspects of ionic effects on biomolecular systems—particularly in highly dilute and low-charge density settings.

Site-specific binding

Unlike the non-specific aspects of ionic behavior discussed above, many ions interact with protein and nucleic acids in a site-specific manner. About one third of all proteins contain metal ions as integral components (Chaturvedi & Shrivastava, 2005; Waldron & Robinson, 2009). These metalloproteins—as well as other proteins that transiently bind ions—recognize and associate with only specific types of ions. This specificity allows them to discriminate and bind particular ion species, even in a solution of other ions of similar properties (e.g., charge and size). Specific interactions between ions and biomolecules can be critical for maintaining structure and are often directly involved in function as well. There are several examples where specific ion binding plays a key role in biomolecular structure. These include RNA tertiary structure stability (Adams et al., 2004; Auffinger & Hashem, 2007; Cate et al., 1996; Conn et al., 2002; Draper; Draper et al.; Grilley et al.; Leipply & Draper) as well as several protein assembly and stability examples (Calimet & Simonson, 2006; Ding & Dokholyan, 2008; Li et al., 2008; Wong & Pollack, 2010). Additionally, the functions of many proteins are affected by specific ion binding. For example, thrombin, a key enzyme in blood coagulation, is allosterically activated by Na⁺ (Guinto & Di Cera, 1996; Wells & Di Cera); the NikR DNA binding protein is activated by Ni²⁺ binding (Benanti & Chivers, 2007; Bradley et al., 2008; Carrington et al., 2003; Chivers & Sauer, 2000); and calmodulin undergoes significant conformational transitions in response to calcium binding (Bertini et al., 2004; Evans et al., 2011; Mori et al., 2004). Many other systems are also regulated by ion binding (Benanti & Chivers; Carrington et al.; Chivers & Sauer; Gohara & Di Cera; Hedstrom et al.; Niu et al.; Page et al.; Reyes-Caballero et al.; Shults et al.).

The definition of site-specific binding can be broadened somewhat to also include the specific recognition and binding of particular ions to more generic structural features of nucleic acids and lipid bilayers. For example, different species of ions are known to compete for binding to the DNA minor groove, leading to a preferential accumulation of particular cation species in this region of DNA molecules (Auffinger & Westhof, 2001; Marincola et al., 2004; Savelyev & Papoian, 2006; Tikhomirova & Chalikian, 2004). Such specificity is also observed around other nucleic acid structures, including RNA (Chen et al., 2009a; Chen et al., 2009b; Chen & Honig, 1997; García-García & Draper, 2003; Grilley et al., 2007; Misra & Draper, 1999; Misra & Draper, 2000; Misra & Draper, 2001; Misra & Draper, 2002; Misra et al., 2003; Savelyev & Papoian, 2006; Soto et al., 2007). Ion specificity for particular regions of nucleic acid and protein structure can also manifest itself in effects on protein-DNA recognition (Kozlov & Lohman, 1998; Mauro & Koudelka, 2004; Overman & Lohman, 1994; Record et al., 1978), although such effects can often arise from a wide range of interaction types (Overman & Lohman, 1994; Record et al., 1978; Record et al., 1995; Zhang et al., 1999). In a similar manner, the differential interface-perturbing behavior of monovalent cations on membrane surface properties and membrane curvature is associated with their different hydration tendencies that will modulate the extent and stability of the hydrogen-bond network along the charged membrane surface (Kraayenhof, 1996).

Ion-water interactions

Many species-specific ion effects are governed, in part, by ion-water interactions. Studies of such preferential hydration are far too numerous to include in a single review; indeed, many excellent manuscripts and texts have been written on the basic physical chemistry of these interactions (Kielland, 1937; Nightingale; Robinson & Stokes, 2002) as well as their biophysical implications (Courtenay et al., 2001; Record et al., 1978; Record et al., 1995; Timasheff, 1998; Timasheff, 2002). Ions are known to significantly perturb the structure of water (Ansell et al., 2006; Hribar et al., 2002; Zangi et al., 2007) and the strength of their interaction with water can significantly influence their affinity for interfaces (Collins, 1995; Pegram & Record, 2006; Pegram & Record, 2007). One of the most famous observations of this behavior is the Hofmeister effect (Baldwin, 1996; Hofmeister, 1888), which ranks ions based on their ability to precipitate or destabilize protein structures (Baldwin, 1996; Collins; Timasheff, 1992), or partition to aqueous interfaces (Chen et al., 2007b; Pegram & Record, 2006; Pegram & Record, 2007; Pegram & Record, 2008). Hofmeister-like behavior also correlates with specific tendencies to enter the Stern layer and to bind the surface for charge neutralization. Roughly speaking, the Hofmeister effect can be described as a rank of ions (given valence) to adsorb in directly proportional to their unhydrated size. Hofmeister effects are particularly prevalent when local ion concentrations are high and play a role in a wide range of biological processes, including protein folding (Baldwin, 1996; Timasheff, 1992), protein-DNA interactions (Hong et al., 2004; Kozlov & Lohman, 1998; Shimizu, 2004a; Shimizu, 2004b; Shimizu et al., 2006; Shimizu & Smith, 2004; Timasheff, 2002), nucleic acid stability (Pegram et al., 2010; Pincus et al., 2008), and biomembrane behavior (Aroti et al., 2007; Aroti et al., 2004; Boström & Ninham, 2005; Boström et al., 2003b; Clarke & Lüpfert, 1999; Fukuma et al., 2007; Leontidis et al., 2007; Sachs & Woolf, 2003; Vácha et al., 2009). While there are a number of theories for the detailed physical basis of the Hofmeister effect (Baldwin, 1996; Boström & Ninham, 2004; Boström et al., 2003; Parsegian et al., 2000; Parsons et al., 2011; Parsons et al., 2010; Pegram & Record, 2008; Shimizu et al., 2006; Tang & Bloomfield, 2002; Zhou, 2005), there is not yet broad consensus on the best way to model this phenomenon in computational treatments of biomolecular electrostatics. Perhaps the most straightforward model currently available uses dispersion effects to reproduce Hofmeister trends in continuum models of ion behavior (Boström & Ninham, 2004; Boström et al., 2005; Boström et al., 2003; Parsons et al., 2001; Parsons et al., 2001). While dispersion forces have been implicated in Hofmeister-like behavior (Boström et al., 2005; Boström & Ninham, 2004; Boström & Ninham, 2005; Boström et al., 2005; Boström et al., 2003a; Boström et al., 2003b; Gurau et al., 2004; Ninham & Yaminsky, 1997; Parsons et al., 2011; Parsons et al., 2010), they are unlikely to be the only contributing interaction (Lund et al., 2008a; Lund et al., 2008b; Shimizu et al., 2006; Tobias & Hemminger, 2008). Therefore, it is unlikely that any current continuum solvation model completely describes these types of preferential solvation and Hofmeister effects.

Modeling biomolecular charge distributions

Generally, we are interested in the behavior of the solute molecules even though there is a clear understanding that the role of solvent is indispensable. Here we describe the classical models for solutes that have been the dominant approaches in modeling and simulations of macromolecules.

Electric moments and Coulombic interactions

The importance of Coulombic interactions in molecular energies and forces has been recognized for a long time. Feynman discussed the importance of such interactions in 1939 (Feynman, 1939) while Buckingham (Buckingham, 1967) began his 1967 seminal paper with the statement, “There is now general agreement that the significant forces between atoms and molecules have an electric origin.” Quantum mechanical forces that act among molecules are electrostatic in nature. For example, repulsion results from electron overlap when atoms approach each other without forming chemical bonds; dispersive attraction can arise from interactions from instantaneous fluctuation of charge distribution inside molecules. In classical mechanics, the non-covalent interatomic interactions are partitioned into electrostatics as described by Coulomb’s law, van der Waals exchange-repulsion and dispersion, as well as secondary contributions such as induction and charge transfer (Stone, 1996). Although all major contributions need to be represented effectively in modeling molecular interactions, a consistent and transferable treatment of electrostatic interaction has been particularly challenging. The key issues include representation of charge distribution, efficient and accurate description of long-range interactions, and solvent effects.

The first molecular dynamics simulation of water was reported by Rahman and Stillinger in 1971 (Rahman, 1971). Four artificial point charges (± 0.19 e) were placed 1 Å away from the oxygen atom to model the electrostatic interaction between water molecules. The use of effective point charges to represent the charge distribution of atoms and molecules greatly reduces the computational needs for to study large molecules and condensed matters in comparison to quantum mechanical methods where electrons are considered in detail. The application of quantum-mechanics-derived point charges to investigate molecular systems dates back at least to the mid-1960s (Bradley et al., 1964; Kimel, 1964; Lifson, 1968) with several important later contributions (Allinger, 1976). The electrostatic interaction is commonly modeled via partial charges located at atomic centers; for example, in the following force fields: AMBER (Assisted Model Building with Energy Refinement) (Case et al.; Cornell et al., 1995), MMFF (Merck Molecular Force Field), OPLS (Optimized Potentials for Liquid Simulations) (Kaminski et al., 2001), CHARMM (Chemistry at HARvard Macromolecular Mechanics) (MacKerell et al., 1998).

The electrostatic potential energy U for a system of point charges follows Coulomb’s law:

$$U=\sum _i\sum _{j>i}\frac{q_i{q}_j}{r_{ij}}$$ Equation 1

where q denotes the charge value and r is the distance between charge locations. The electrostatic potential from atomic partial charges can be systematically improved by using a multipole expansion to describe the charge distribution (Buckingham, 1967). For an arbitrary charge distribution (e.g., an atom or a molecule) described by charges q_i (i=1…n), the electrostatic potential at a distance R away from the particle is given by the sum:

$$V(R)=\sum _i\frac{q_i}{\mid \underset{\_}{R}-{\underset{\_}{r}}_i\mid }$$ Equation 2

where the | | notation refers to Euclidean distance. For a distance R> r, a Cartesian Taylor expansion of the above equation leads to

$$V(R)=\left\{\sum _i{q}_i-\underset{\_}{\mu }·\nabla +\frac{1}{2}\underset{\_}{\underset{\_}{\mathrm{\Theta }}}:{\nabla }^2-\dots \right\}\left(\frac{1}{R}\right)$$ Equation 3

a multipole representation where the symbol ∇ denotes the gradient operator. The first term inside the bracket is the sum of charges of the particle or monopole moment. The dipole moment of the charge distribution μ is a vector with three components: ${\mu }_{\alpha }={\displaystyle \sum _i}{q}_i{r}_{i\alpha }$, where α = x, y, z. The quadrupole moment tensor ( $\underset{\_}{\underset{\_}{\mathrm{\Theta }}}$) has nine components given by ${\mathrm{\Theta }}^{\alpha \beta }={\displaystyle \sum _i}{q}_i{r}_{i\alpha }{r}_{i\beta }$. A traceless form of the quadrupole tensor ${\mathrm{\Theta }}^{\alpha \beta }={\displaystyle \sum _i}{q}_i\left(\frac{3}{2}{r}_{i\alpha }{r}_{i\beta }-\frac{1}{2}{r}_i^2{\delta }_{\alpha \beta }\right)$, instead of the traced one, can be used in Equation 3, along with constant ½ in front of $\underset{\_}{\underset{\_}{\mathrm{\Theta }}}:{\nabla }^2$ replaced by 1/3 (Stone, 1996). A spherical form of multipole expansion can also be obtained by a spherical harmonic expansion (Bottcher, 1952; Hirschfelder et al., 1954; Kirkwood, 1934; Stone, 1996).

Molecular multipole moments can be more efficient than point charges for modeling molecular electrostatic interactions, even though the associated energy and derivatives are more complex. In fact, early simulations of liquid and solid benzene adopted potentials that included a point quadrupole at the center of the benzene molecule (Claessens et al., 1983; Jorgensen & Swenson, 1985; Linse, 1984). It was suggested (Claessens et al., 1983) that the potential with a point multipole was superior to the Lennard-Jones-only potential for crystal structure prediction even though a recent study indicated that electrostatic interactions are not critical in predicting crystal packing of nonpolar molecules (Della Valle et al., 2008). Because of the assumption of R>r in the Taylor expansion in Equation 3, however, the molecular multipole expansion is problematic at the short distances that are often relevant in molecular simulation. The multipole expansion may diverge within the sphere R, and lead to an inaccurate electrostatic potential. The solution to overcome this issue is to distribute the multipole expansion to a collection of sites within the molecule, which effectively reduces the radius of the divergence sphere (Fowler & Buckingham, 1983; Fowler & Buckingham, 1991; Price, 1985; Stone, 1981).

Buckingham and Fowler (Fowler & Buckingham, 1983) were the first to apply distributed multipoles to the study of small molecule complexes. Atomic multipoles can be derived in several ways, including the distributed multipole analysis (DMA) of an ab initio wavefunction (Stone, 1981). The combination of a hard sphere potential with atomic multipoles (up to quadrupole) was rather successful in reproducing experimental geometries including hydrogen bonding distance and angle for several molecular complexes. It has been noted that local atomic charge distributions are usually not spherically symmetrical because of chemical bonding and lone pairs, and thus higher-order electrostatic moments are necessary to describe such features. Systematic study of the accuracy of point multipole models also has been described (Williams, 1988). It was shown that the use of higher-order multipole moments significantly improved the representation of molecular electrostatic potential (ESP) in comparison to ab initio reference potential. When only atomic charges were allowed, the relative root-mean-squared error in the ESP around the molecules was on the order of 10%. With the addition of dipole and quadrupole moments, the error was reduced by orders of magnitude to less than 0.1% (Williams, 1988). Considering that higher-order moments decay faster than monopoles, the advantage of a distributed multipole expansion is to improve the short-range description outside the van der Waals surface of a molecule, which is important for interactions such as hydrogen bonding (Dykstra, 1993).

An alternative to multipole expansion is to use a number of charge sites, which should in principle, offer a similar improvement to the accuracy of the molecular electrostatic potential. A great advantage of using point charges is the simplicity of the energy and atomic gradient; in contrast, the gradient and torque on point multipoles require significantly more algebra. There have been arguments that a point charge model is more efficient for a given level of accuracy, at least for diatomic molecules such as HF and HCl (Brobjer & Murrell, 1982). There are also models that replace multipole moments by distributed point charges (Sokalski et al., 1993). The eXtended Electron Distribution (XED) force field adopts an explicit charge distribution around each atom, which seems to give improvements in interaction energy, conformation, and electrostatic field (Chessari et al., 2002; Vinter, 1996). Some versions of the AMBER force field place charges at important lone-pair sites (Dixon & Kollman, 1997). Another recent example is the TIP5P water model, which employs five charge sites. However, it was shown that the determination of the exact locations of the lone pair charges was not trivial, and involved an extensive fitting procedure to reproduce experimental density-temperature profiles (Mahoney & Jorgensen, 2000; Rick, 2001). Another concern is that charges located away from atomic centers may lead to numerical instability in molecular dynamics or Monte Carlo simulations because of the potential fusion of charge sites.

To evaluate the interaction between multipole moments, Applequist introduced a concise polytensor scheme (Applequist, 1983; Applequist, 1984; Applequist, 1985; Applequist, 1989; Dykstra, 1988). The multipole expansion at site k is written as

$$M_i={\left[q_i,{\mu }_{ix},{\mu }_{ix}{\mu }_{ix},{\mathrm{\Theta }}_{\mathit{ixx}},{\mathrm{\Theta }}_{\mathit{ixy}}\dots \right]}^t$$ Equation 4

where the superscript t indicates transpose. The interaction energy between two multipoles at sites i and j is then given by the matrix formula:

$$U_{ij}=M_i^t{T}_{ij}{M}_j$$

where T is the interaction matrix:

$$\left[\begin{array}{ccccc}1& \frac{\partial }{\partial x_j}& \frac{\partial }{\partial y_j}& \frac{\partial }{\partial z_j}& \cdots \\ \frac{\partial }{\partial x_i}& \frac{{\partial }^2}{\partial x_i\partial x_j}& \frac{{\partial }^2}{\partial x_i\partial y_j}& \frac{{\partial }^2}{\partial x_i\partial z_j}& \cdots \\ \frac{\partial }{\partial y_i}& \frac{{\partial }^2}{\partial y_i\partial x_j}& \frac{{\partial }^2}{\partial y_i\partial y_j}& \frac{{\partial }^2}{\partial y_i\partial z_j}& \cdots \\ \frac{\partial }{\partial z_i}& \frac{{\partial }^2}{\partial z_i\partial x_j}& \frac{{\partial }^2}{\partial z_i\partial y_j}& \frac{{\partial }^2}{\partial z_i\partial z_j}& \cdots \\ ⋮& ⋮& ⋮& ⋮& \ddots \end{array}\right]\left(\frac{1}{{\underset{\_}{R}}_{ji}}\right)$$

The multipole moments here are defined in the same global frame. For example, Price reported distributed multipoles for amides and peptides in predefined molecular axes (Faerman & Price, 1990). Alternatively, it is possible to define the multipole moments for each atom type in a local coordinate frame that is constructed with respect to covalently bonded neighboring atoms. Within this scheme, the oxygen atom in the water molecule may use the so-called bisector frame where the z-axis is the bisector of the HOH angle (Kong, 1997; Ren & Ponder, 2003); the x-axis is perpendicular to z and also lies in the HOH plane; and the y-axis is determined via the right-hand rule. For chemical systems without such symmetry, a generic z-then-x local frame can be used, in which one chemical bond to a neighboring atom is selected to define the z-axis.

A rotation matrix converts local multipole moments into the global frame prior to computation of the electrostatic interaction energies. Many algorithms require the evaluation of the analytic electrostatic forces for each molecular configuration. For the atomic charge model, the force is simply the negative derivative of Coulomb energy (1/r) with respect to atomic coordinates. For an atomic multipole expansion, forces are derived in a similar fashion by taking the derivative of the interaction matrix T and, using the relationships T^{(n + 1)} = ∇(Tⁿ), and T⁽ⁿ⁺¹⁾ = ∇(Tⁿ), and T⁰ = 1/R. Expressions for the first few derivatives are available (Kong, 1997). A further complication must be considered for dipole and higher-order moments. From a physics point of view, a dipole moment placed in an external field will experience a torque that favors rotation of the site (and its local frame defining neighbors). It is possible to convert each torque into forces at frame-defining sites to permit standard molecular dynamics integration schemes or optimization algorithms (Ren & Ponder, 2003). There is an alternative approach to understand these extra forces mathematically. If the multipole moments defined within their local frames are explicitly included in the energy expression with their rotation matrix, which is a function of atomic coordinates, the product rule leads to these additional forces (Kong, 1997). Besides the Cartesian poly-tensor approach explained above, the spherical tensor formulations of the multipole interaction energy, force and torque, are available (Price et al., 1984).

Note that even with the better convergence of atomic multipole at short range, there are errors associated with the point approximation of the charge distribution. At a distance where electron density is penetrated, a negative (attractive) penetration effect is missing from the point multipole potential energy (Stone, 1996). It has been suggested that the penetration effect could be absorbed by the repulsive term or possibly by damping the Coulomb energy (Klopper et al., 2000; van Duijnen & Swart, 1998). Wheatley and Mitchell (Wheatley & Mitchell, 1994) proposed replacing the point multipole with Gaussian multipoles to correctly model the penetration effect at short range. Piquemal et al (Piquemal et al., 2003) used s-type Gaussian functions distributed at multi-sites to represent the charge density. In the recent development of QMPFF (Donchev, 2006; Donchev et al., 2005), a model was developed that consists of a nuclear charge and a negative electron cloud of exponential form located off the nuclear center. These more sophisticated treatments are likely to provide greater flexibility and higher accuracy for modeling electrostatics, within the limits of the ab initio data to which they are fit, although at higher computational cost.

When formulating a molecular mechanics potential, conventional wisdom is that intramolecular short-range electrostatic interactions should be masked (scaled), based on the rationale that bond and angle energy terms already include these interactions. However, details of the masking schemes vary among different force fields. For example, charge interactions between the 1–2 (directly bonded) and the 1–3 (separated by two bonds) atoms are almost universally omitted. The 1–4 (atoms separated by three bonds) interaction is scaled down by 5/6 in Amber94, by 1/2 in OPLS-AA, and is not modified in CHARMM. These scaling factors are determined empirically to best reproduce conformational energy profile of flexible molecules.

Parameterization of realistic charge distributions, in the forms of point charges or higher-order moments, is essential to the accuracy of electrostatic energetics. Although atomic charges are not measurable physical quantities (physical observables), it is possible to derive meaningful values from quantum mechanical calculations. A method such as Mulliken population analysis or Bader’s Atoms-in-Molecules (AIM) theory partitions electron density into atomic contributions (Bader, 1990). However, different partitioning schemes lead to substantially different atomic charges. Momany first treated atom charges as adjustable parameters and derived values by fitting to ab initio electrostatic potential (ESP) (Momany, 1978). Unlike atomic charges, ESPs are physical observables and are directly associated with intermolecular interactions. Cox and Williams (Cox & Williams, 1981) pointed out that ESPs from Mulliken charges generally had significant errors. Variants of ESP fitting approaches include CHELP, CHELPG (Breneman & Wiberg, 1990), MK and RESP (Bayly et al., 1993). These methods differ mostly with respect to the choice of grid points to which the ESP is fit, typically residing in a shell immediately outside the van der Waals surface. Note that at very close distances, the ESP is not as relevant to molecular interactions because the actual wave functions of molecules will overlap, leading to penetration and other effects. In RESP, hyperbolic restraints are applied to heavy atoms to avoid artificially large charges obtained for atoms buried inside the molecule during fitting. This type of approach works reasonably well for small molecules, but is inherently limited for larger molecules. In the latter case, such as proteins, model compounds (e.g., dipeptides) are used to derive charges for common molecular fragments.

Various charge parameterization schemes have been compared for their ability to reproduce molecular dipole moments and ESP (Bayly et al., 1993; Martin & Zipse, 2005; Masamura, 2000; Wiberg & Rablen, 1993). Wiberg and Rablen (Wiberg & Rablen, 1993) suggested that atomic charges alone are insufficient to accurately model the anisotropic molecular charge distribution and ESP near the van der Waals surface. They concluded it is necessary to include at least atomic dipoles or even higher-order terms. This is consistent with Williams’ conclusion mentioned above (Williams, 1988). Sun et al. (Sun, 1998) showed that ESP charges were unable to provide quantitatively ion-spherand interaction free energies, unless the region near oxygen was weighted higher than the rest, which is another indication of an over simplification of the spherically symmetric atomic charge approximation. A pitfall of ESP charges is that they may not respond consistently to structural changes such as substituents, which is problematic for developing transferable force field parameters. Even determination of charges from quantum mechanics for water alone can be a difficult task (Martin & Zipse, 2005).

Additional complications arise from the dependency of charge distributions on intramolecular geometry and conformation. This short-range effect is of quantum mechanical origin and is not directly related to through-space induction. Dinur and Hagler reported empirical formulation that couples geometry to charge distribution (Dinur & Hagler, 1995). Palmo et al. showed that such a coupling allows a classical water model to capture the expansion of the H-O-H angle moving from gas phase to liquid (Palmo et al., 2006). In most classical potentials, this conformation dependence is handled by simultaneous fitting to multiple conformations of a flexible molecule (Reynolds et al., 1992a; Reynolds et al., 1992b; Söderhjelm et al., 2007).

Because of their simplicity and efficiency, partial atomic charge models have been adopted by the majority of common biomolecular force fields including AMBER, CHARMM, GROMOS, and OPLS-AA. Since most of the force fields target the condensed-phase, charges derived from gas-phase, quantum mechanics calculations are not suitable and further adjustments must be made to account for solvent and other environmental effects. AMBER force fields have traditionally fit charges to ESPs calculated from the HF/6-31G* basis set. It has been argued that because the HF theory overestimates molecular dipole moments, the amplified charges effectively capture the solute polarization response in condense-phase. CHARMM first optimizes the charges to gas-phase molecular interactions and subsequently scales the charges for the neutral polar molecules by 1.16. The OPLS force field adjusts the charges by fitting to neat liquid properties such as density and heat of vaporizations. This process is tedious but has the advantage of producing reliable condensed-phase properties. We emphasize an important rule, which is not to mix charges from different parameterization strategies (i.e., from different force fields) into a single calculation because each method has its own systematic errors that are more likely to cancel when used consistently. There is also interest in using semi-empirical methods such as AM1 to estimate atomic charges quickly. This can be potentially useful for studying a large number of small molecules. AM1-BCC and CM2 are two examples of such schemes (Jakalian et al., 2000; Jakalian et al., 2002; Li et al., 1998a; Li et al., 1998b).

As discussed previously, electrostatic models beyond fixed atomic charges have also been explored in recent years. In addition to the work that incorporates electronic polarization, distributed atomic multipoles have been applied to represent electrostatic interactions within molecular mechanics force field (Burnham & Xantheas, 2002; Freitag et al., 2000; Grossfield et al., 2003; Holt & Karlström, 2008; Jiao et al., 2008; Jiao et al., 2006; Jiao et al., 2009; Kong, 1997; Ren & Ponder, 2002; Ren & Ponder, 2003; Xantheas et al., 2002). Similar to point charges, distributed multipole moments can be derived via population analysis or an ESP fit. Although it is known that charges from Mulliken population analysis do not produce an accurate ESP because the method is truncated at monopole order, its extension to distributed multipole analysis as proposed by Stone (Stone, 1981) permits systematic convergence of the ESP. Alternatively, atomic multipoles can be obtained from Bader’s AIM theory, which partitions electron density based on zero-flux surfaces (Bader, 1990). Popelier showed that AIM is slow to converge compared to DMA and therefore requires higher-order moments (Popelier et al., 2001). Convergence of AIM multipole expansion can be achieved by adding additional sites at bond midpoints (Joubert & Popelier, 2002). To handle large basis sets in ab initio calculations, a recent modification to DMA, that uses a grid-based quadrature for partitioning the contributions to the charge density from diffuse basis functions, was introduced (Stone, 2005). Other methods to derive atomic multipoles include natural atomic orbitals (NAO) analysis (Reed et al., 1988) and a recently developed method called LoProp (Gagliardi et al., 2004; Söderhjelm et al., 2007).

Polarizability and other many-body effects

The Coulombic energy expression makes use of the assumption that the electrostatic energy is pair-wise additive. In reality, a charge distribution changes under the influence of an electric field produced by the surrounding environment, which can include contributions from solvent, intra-molecular sources or externally applied potential differences. For example, the molecular dipole moment of a water molecule increases from 1.8 D to 3.0 D when immersed in bath of water (Ren & Ponder, 2003).

Different methods exist to incorporate the polarization effect in molecular mechanic framework, by means of induced dipole, fluctuating charge or Drude oscillator. Stone (Stone, 1981; Stone, 2005; Stone & Alderton, 2002) also proposed a more sophisticated treatment. Fluctuating charge and Drude oscillator based methods are easier to implement within the existing fixed-charge force field framework while the induced dipole approach is a natural choice for models based on atomic multipoles. Detailed discussion and comparison of the different treatments of polarization can be found in the recent reviews (Cieplak et al., 2009; Halgren, 1992; Lopes et al., 2009; Ponder & Case, 2003; Rick, 2001). Below we offer a brief account for polarizable force field development and fundamental methodology based on distributed induced dipole model.

In very early studies of enzymatic reactions (Warshel, 1976) and prototype molecular dynamics algorithms (Vesely, 1977), polarization effect was already considered explicitly. In early 1990s, Gresh and colleagues developed THE SIBFA (Sum of Interactions Between Fragments Ab initio computed) potential, which treats the polarization, charge transfer effect, and other second order electrostatic interactions (Gresh, 1997). Karlström and coworkers have been devoting considerable effect to incorporate induced-dipole based polarization models into classical force fields (Åstrand et al., 1995; Brdarski et al., 2000; Holt & Karlström, 2009). Friesner and coworkers also reported models that use both fluctuating charges and atomic induce dipole to account for polarization (Kaminski et al., 2002; Stern et al., 2001). Patel et al. (Bauer et al., 2011; Bauer & Patel, 2009; Patel & Brooks, 2004; Patel et al., 2009; Patel et al., 2004) take a fluctuating charge approach that is based on the charge equilibration scheme (Rappe & Goddard, 1991). MacKerell and Roux base their polarizable potentials on the Drude Oscillator approach (Baker et al., 2010; Harder & Roux, 2008; Jiang et al., 2011; Lamoureux & Roux, 2006; Lopes et al., 2007; Roux et al., 2011; Yu et al., 2010). Ren and Ponder have been developing classical force fields that combine the induced dipole with permanent atomic multipoles to represent the electrostatic interactions (Jiao et al., 2008; Kong, 1997; Ren & Ponder, 2002; Ren & Ponder, 2003; Ren et al., 2011). Duan and AMBER community are also continuing with their effort in polarizable force field development (Wang et al., 2011a; Wang et al., 2011b; Wang et al., 2006). Inclusion of polarization allows more rigorous parameterization and validation of the force field against a wide range of molecular systems in different environment, from small molecules to macromolecules, from gas-phase to condensed-phase properties. The advantages of polarizable force fields have been demonstrated for water (Lamoureux et al., 2003; Ren & Ponder, 2003; Stern et al., 2001), amides and other organic molecules (Brdarski et al., 2000; Hagberg et al., 2005; Harder et al., 2008; Lopes et al., 2007; Ren et al., 2011; Wang et al., 2011a; Wang et al., 2011b), ions (Grossfield et al., 2003; Jiao et al., 2008; Patel et al., 2009; Wu et al., 2010; Yu et al., 2010), membranes (Bauer et al., 2011), and ligand-protein complexes (Jiao et al., 2008; Roux et al., 2011). Of equal importance is the development of efficient particle-mesh. Ewald has enabled accurate treatment of long-range electrostatic interactions of partial charges or point multipoles in the simulations of large biomolecules (Darden et al., 1993; Sagui et al., 2004). However, developing and parameterizing a consistent force field for biomolecular simulations are still daunting tasks because of the extra complication in a more elaborated physical model. There is no consensus on where the polarization effect would be the most important and what is the best way to treat the polarization effect in classical simulations. As we push for more accurate physical potentials, it is also important to keep in mind the limitation of other contributions in the potential energy function such as partial atomic charge representation, van der Waals interactions and empirical valence functions. At the molecular level, an induced dipole moment can be approximated through a linear relation with the total field E:

$${\mu }^{\mathit{ind}}=\alpha E$$

where α is the molecular polarizability of the molecule, which can be measured by experiment or calculated from ab initio theory. Following Buckingham, we define the ground state electron distribution of a molecule as its permanent charge distribution. When several molecules approach each other, each permanent charge distribution will produce an electric field on the others. The induced dipole at each molecule resulting from the total permanent field produces an induced field:

$${\mu }_i={\alpha }_i\left(\sum _{j\ne i}{E}^{\mathit{perm}}+\sum _{k\ne i}{T}_{ik}^{11}{\mu }_k\right)$$

where T¹¹ is the dipole field operator (e.g., Applequist et al., 1972). Since the induced dipole appears on both sides of the equation, it can be solved self-consistently by iteration or by direct matrix inversion. The energy from the mutual induction is

$$U^{\mathit{ind}}=\frac{1}{2}{\mu }^{\mathit{ind}}{E}^{\mathit{perm}}$$

Although induction always lowers the system energy, the factor ½ reflects the positive work required to distort the molecular charge distribution.

While molecular polarization response is a physical observable, measurable from experiment or computed from ab initio quantum mechanics, polarization at the atomic level is modeled empirically by inducing a dipole moment at each atom or charge flow between atoms. To model the molecular dipole polarizability, distributed atomic models – both additive and non-additive (interactive) – have been proposed. In an additive model, the molecular polarizability is the sum of individual bond, atom, or group contributions (Dykstra, 2001). Anisotropic atomic polarizabilities in tensor forms are used to produce anisotropic molecular response (Birge, 1980; Stout & Dykstra, 1995; Stout & Dykstra, 1998). Applequist et al. (Applequist et al., 1972) devised a non-additive model in which atomic response is relayed via neighboring atoms and, as a result, anisotropic molecular response can be captured (Stout & Dykstra, 1995; Stout & Dykstra, 1998). Applequist further incorporated monopole polarizability (atomic charge transfer) into the dipole polarizability model to handle out-of-plane charge flow in the aromatic rings (Applequist, 1993). Thole proposed a damping scheme to handle numerical problems in the interactive model associated with the polarizability catastrophe at the short range (polarization energy approaches negative infinity) (Thole, 1981; van Duijnen & Swart, 1998). Physically, the catastrophe is a consequence of point polarizability approximation and the damping is effectively to replace the point charge with a distribution. Thole’s approach has been adopted by several researchers in empirical force fields for classical simulations or quantum mechanics/molecular mechanics (QM/MM) approaches (Åstrand et al., 1995; Bernardo et al., 1994; Brdarski et al., 2000; Burnham & Xantheas; Engkvist et al., 1996; Grossfield et al., 2003; Holt & Karlström, 2009; Jiao et al., 2008; Jiao et al., 2006; Ren & Ponder, 2002; Ren & Ponder, 2003; Van Duijnen & de Vries, 1996; Xantheas et al., 2002). The advantage of additive models is the computational simplicity, whereas the interactive models require the solution of self-consistent mutual induction equations. However, in the interactive polarizability model, the molecular response has explicit dependence of molecular geometry, which is often lacking in the additive models. In addition to the empirical models mentioned above, Stone proposed a more sophisticated distributed polarizability model based on perturbation theory which systematically treats polarization response in monopole to higher order moments (Stone, 1996).

Different methods exist to incorporate the polarization effect in molecular mechanic framework, by means of induced dipole, fluctuating charge or Drude oscillator. The latter two are easier to implement within the existing fixed-charge force field methodology, while the induced dipole approach makes it a natural choice for models based on atomic multipoles. Detailed discussion and comparison of the different treatments of polarization can be found in the recent reviews (Halgren, 1992; Ponder & Case, 2003; Rick, 2001). Stone (Stone, 1981; Stone, 2005; Stone & Alderton, 2002) proposed a more sophisticated treatment.

Efforts to develop classical force fields that explicitly treat the electronic polarization effect are increasing. Ren and Ponder are developing a classical force field that combines the induced dipole with permanent atomic multipoles to represent the electrostatic interactions (Jiao et al., 2008; Kong, 1997; Ren & Ponder, 2002; Ren & Ponder, 2003). Friesner and coworkers also reported models that merge fluctuating charges and atomic induce dipole models together (Kaminski et al., 2002; Stern et al., 2001). Patel et al. (Patel & Brooks, 2004; Patel et al., 2004) take a fluctuating charge approach that is based on the charge equilibration scheme (Rappe & Goddard, 1991). MacKerell and Roux base their polarizable potential on the Drude Oscillator approach (Lamoureux & Roux, 2006; Lopes et al., 2007). In principle, the inclusion of polarization should provide a more realistic representation of electrostatic interactions and better transferability of force field parameters. Ren and co-workers have shown that electronic polarizability needs to be considered in order to achieve reliable and accurate results in small molecules binding to proteins (Jiao et al., 2008; Jiao et al., 2009). Polarization allows more rigorous parameterization and validation of the force field against a wide range of molecular systems in different environment, from small molecules to macromolecules, from gas-phase to condensed-phase properties. Of equal importance is the development of efficient particle-mesh Ewald has enabled accurate treatment of long-range electrostatic interactions of partial charges or point multipoles in the simulations of large biomolecules (Darden et al., 1993; Sagui et al., 2004). However, developing and parameterizing a consistent force field for biomolecular simulations are still daunting tasks because of the extra complication in a more elaborated physical model. It is also important to keep in mind the limitation of other representations in the potential energy function such as van der Waals interactions and short-range valence term.

Modeling biomolecular titration states

One of the most important aspects of biomolecular charge states is their sensitivity to pH and other environmental influences. The presence of ionizable groups (side chains of acidic and basic amino acids) in a protein affects the protein’s electrostatic properties and its solvation in aqueous media. The two types of ionizable groups in proteins are titratable and redox groups. Titratable groups participate in acid-base (protonation/de-protonation) reactions to exchange (bind or release) a proton. Redox groups participate in redox reactions to exchange (bind or release) an electron. Therefore, these ionizable groups can acquire charge states that determine the stability, solubility, and enzymatic properties of the proteins important in several biological processes (e.g., enzymatic catalysis, respiration, etc.). In fact, several pH-dependent phenomena associated with proteins have been attributed to the presence of titratable groups. To understand the mechanisms of biological phenomena that depend on the ionization states of proteins, it is important to predict accurately these ionization states and understand the factors that affect the ionization behavior of proteins.

The ionization behavior and the corresponding charge state of an ionizable group can be different when it is part of a protein compared to when it exists independently as part of its model compound (side chain in a blocked peptide) in aqueous solutions. Several factors alter the charge state of ionizable groups in a protein: electrostatic interactions between charges of ionizable groups in the same protein, electrostatic interactions between charges on the ionizable group and the partial charges on non-ionizable groups and backbone atoms, location of the group in the protein, changes in the protein’s conformational state, pH of the solution, and polarizability/polarity of the protein’s microenvironment.

The ionization behavior of an ionizable group (titratable or redox) can be characterized by the proton/electron binding affinities of the titratable/redox group. The binding affinity of a group can change depending on whether the group is part of a protein or is left free in solution. These affinities can be quantified using ionization equilibrium constants. For instance, Equation 5 is for an acid-base equilibrium (protonation/de-protonation) reaction, where AH denotes the acid, A− represents the conjugate base, and H+ is the proton:

$$AH\stackrel{K_a}{\leftrightarrow }{A}^{-}+H^{+}$$ Equation 5

K_a is the equilibrium constant, defined as $K_a=\frac{[A^{-}][H^{+}]}{[HA]}$, where the terms in the numerator and denominator are species activities, and K_a determines the strength for the dissociation of the acid into its conjugate base and a proton. Taking negative logarithm on both sides of Equation 5 yields

$$-{\mathit{log}}_{10}{K}_a=-{\mathit{log}}_{10}\left(\frac{[A^{-}]}{[HA]}\right)-{\mathit{log}}_{10}[H^{+}]$$ Equation 6

The free energy (ΔG) required to de-protonate one mole of an acid is given by the relation

$$\mathrm{\Delta }G=-2.303k_{B}T{\mathit{log}}_{10}\left(\frac{[A^{-}]}{[HA]}\right),$$ Equation 7

where k_B is the Boltzmann’s constant, T is the temperature of the solution. Rearranging these equations gives

$$\mathrm{\Delta }G=2.303k_{B}T(-{\mathit{log}}_{10}{K}_a+{\mathit{log}}_{10}[H^{+}])$$ Equation 8

Substituting −log₁₀K_a and −log₁₀[H⁺]with pK_a and pH, respectively, we get the relation between free energy and pK_a

$$\mathrm{\Delta }G=2.303k_{B}T({pK}_a-pH)$$ Equation 9

The ionization state of a protein is characterized by the pK_a values of all the ionizable groups in the protein. We can write the relation between pK_a (pK_a,i) of a titratable group (i) in a protein (p) and the change in free energy ( $\mathrm{\Delta }{G}_i^p$) required to protonate the titratable group, as shown below:

$$\mathrm{\Delta }{G}_i^p=2.303k_{B}T(pH-{pK}_{a,i})$$ Equation 10

Similarly, the pK_a (pK_a,mi) of the same titratable group (i) in a reference or model state (m) is related to the change in free energy ( $\mathrm{\Delta }{G}_i^m$) required to protonate the titratable group, as shown below:

$$\mathrm{\Delta }{G}_i^m=2.303k_{B}T(pH-{pK}_{a,mi})$$ Equation 11

Subtracting these two relationships and rearranging gives

$${pK}_{a,i}={pK}_{a,mi}-\frac{\mathrm{\Delta }{G}_i^p-\mathrm{\Delta }{G}_i^m}{2.303k_{B}T}$$ Equation 12

Equation 12 provides the thermodynamic basis for understanding the differences between the ionization behavior of a titratable group in a protein and that of the same group in its model compound.

A common assumption in pK_a calculations is that the contributions to the free energy of charging a site in the protein or model compound from zero to unit charge (positive or negative) are purely electrostatic in nature (Bashford & Karplus, 1990). These electrostatic contributions include the solvation energy of the charge at the ionizable site (Born), the electrostatic interaction between the charge and the partial charges of backbone atoms and other non-ionizable groups (ic-p interactions), and the electrostatic interaction between the charge and charges on other ionizable groups (ic-jc interactions).

Thus, the pK_a of a titratable state becomes

$${pK}_{a,i}={pK}_{a,mi}-\frac{\mathrm{\Delta }{G}_{i,\mathit{Born}}^p+\mathrm{\Delta }{G}_{i,ic-p}^p+\mathrm{\Delta }{G}_{i,ic-jc}^p-\mathrm{\Delta }{G}_{i,\mathit{Born}}^m-\mathrm{\Delta }{G}_{i,ic-p}^m}{2.303k_{B}T}$$ Equation 13

To calculate the pK_a,i value of the titratable group i, we need to know the values for pK_a,mi and for each free energy term in equation above. The pK_a,mi value can be obtained experimentally; however, the free energy terms have to be computed using a suitable electrostatic solvation model, as discussed in the subsequent sections. Note that the term $\mathrm{\Delta }{G}_{i,ic-jc}^p$ is pH-dependent, which also implies the need to sample against the large space of biomolecular titration states to accurately model the pK_a value (Antosiewicz, 2008).

Significant efforts have been made to accurately measure (Baran et al., 2008; Castañeda et al., 2009; Denisov et al. 2004; Fitzkee & García-Moreno E, 2008; Harms et al., 2009; Harms et al., 2008; Isom et al., 2008; Isom et al., 2011; Isom et al., 2010; Karp et al., 2007; Karp et al., 2010) and predict (Alexov et al., 2011; Antosiewicz, 2008; Antosiewicz et al., 1996a; Antosiewicz et al., 1996b; Bashford & Karplus, 1990; Bryce et al., 1998; Carstensen et al., 2011; Flanagan et al., 1981; Georgescu et al., 2002; Karp et al., 2007; Khandogin & Brooks, 2006; Laurents et al., 2003; Li et al., 2002; Li et al., 2004; Li et al., 2005; Mehler & Guarnieri, 1999; Mitra et al., 2011; Nielsen et al., 2011; Nielsen, 2007; Nielsen, 2009; Nielsen & McCammon, 2003; Nielsen & Vriend, 2001; Shan & Mehler, 2011; Tang et al., 2007; Tynan-Connolly & Nielsen, 2006; Wallace & Shen, 2011; Witham et al., 2011) protein titration states to understand the determinants of pK_a values for the amino acids in the interior and exterior of proteins. A recent special issue of Proteins (Alexov et al., 2011) provides an excellent review of the state of the art in the area of biomolecular titration state modeling.

Modeling solvation with high detail: explicit models

Explicit water models

Water has long been recognized as an important part of biomolecular systems (Kauzmann, 1959). Early theoretical studies of proteins ignored the solvent because of the prohibitive computational cost (McCammon et al., 1977). However, with the advancement of computer technology and quest for realistic simulations, it is now common to represent the solvent explicitly with atomic models.

Numerous water models have been developed over the years beginning with Bernal and Fowler’s attempt in 1933 (Bernal, 1933). A detailed review of nearly 50 water models was given by Guillot in 2002 (Guillot, 2002). It would likely require another full-length review to discuss the new models developed since. The water models introduced to date differ from each other in electrostatic representation (number of charge sites, polarizability), internal geometry (angle and flexibility), and the ways by which the parameters were derived.

TIP3P (Jorgensen et al., 1983) and SPC (Berendsen et al., 1981) are two, three-site, fixed charge models commonly used in biomolecular simulations. The two models have the same equilibrium OH bond lengths and very similar atomic charges but different van der Waals parameters and equilibrium HOH angle values. While the TIP3P adopts a value of 104.52° for the HOH angle, SPC uses 109.47°; the experimentally measured geometry of liquid water at room temperature is 106° (Ichikawa et al., 1991). Both water models were derived originally as rigid water models. A variant of SPC, SPC/E (Berendsen et al., 1987), was developed to take into account the cost of bulk polarization ignored by SPC and other fixed-charge models. Effectively, the correction makes the bulk potential energy of SPC/E model lower than the others. This procedure has not been consistently applied to other liquids or biomolecular systems.

The effort to improve TIP3P has led to four-site (Jorgensen et al., 1983), five-site (Mahoney & Jorgensen, 2000), and even six-site (Nada, 2003) water models, with additional charge sites for better electrostatic descriptions. An extensive reparameterization of TIP4P was made by fitting to properties over a wide range of temperatures and using the Ewald treatment of electrostatics, as opposed to the cutoff scheme used in earlier model development (Horn et al., 2004). TIP5P is one of the best-performing fixed charge water models that reproduces a range of condensed-phase structural, energetic, and dynamic properties including the temperature of maximum density. The use of TIP5P in biomolecular simulations has been limited because of the cost arising from the additional charge sites and concerns about compatible parameterization of amino and nucleic acid residues with this water model.

Recent advancements in water models continue to focus on the electrostatic representation, especially the electronic polarization effect. Water is a high-dielectric solvent and is also very polarizable itself. Examples of water models that explicitly account for polarization include BSV (Jedlovszky, 2001; Jedlovszky & Vallauri, 1999), POL5/TZ(QZ) (Stern et al., 2001), PPC (Svishchev et al., 1996), TIP4P/FQ (Rick, 2001), POL5 (Stern et al., 2001), TTM2 (Burnham & Xantheas, 2002), AMOEBA (Ren & Ponder, 2003), and SWM4-DP (Lamoureux et al., 2003). Parameterization of these models relies on both quantum mechanical ab initio calculations and experimental bulk thermodynamic properties, although to different extents. Overall, these studies have demonstrated that a polarizable water model is able to provide a better representation of electrostatic response, and good transferability among different chemical environments.

Explicit ion models

When explicit water models are used, ions are also typically modeled in atomic detail. Theoretical treatment of specific ion interactions is complicated as the strong electrostatic field around the ions poses challenges to the standard physical water models. Nonetheless, computational studies have offered valuable insights at the atomic details of ion solvation and the interaction of ions with biomolecular solutes.

Specific ion binding to proteins or DNA is a dynamic competition between the biomolecular and aqueous environments. Therefore, it is essential to accurately describe the hydration thermodynamics of single ions. However, this task is not straightforward as only the total solvation free energies of a neutral salt can be measured directly from experiment. As a result, published single ion solvation values differ widely when different parameterizations are employed (Patra & Karttunen, 2004). Furthermore, ion behavior can be very sensitive to the force field, and subtle differences in ion and solvent parameterization may lead to significant ion pairing and clustering problems during simulation (Alejandre & Hansen, 2007; Auffinger et al., 2007; Chen & Pappu, 2007a; Chen & Pappu, 2007b; Joung & Cheatham, 2008).

Recent studies using ab initio QM/MM models, quasi-chemical theory, and polarizable force fields have demonstrated improved accuracy in explicit ion models. The ab initio QM/MM approach has been reviewed extensively (Friesner, 2005; Friesner & Guallar, 2005; Hu & Yang, 2008; Kamerlin et al., 2009; Lin & Truhlar, 2007; Riccardi et al., 2006; Senn & Thiel, 2009). For example, Rode and coworkers have characterized the dynamics and solvation properties of solvated ions by treating the primary region of interest, the first hydration shell of the ions, quantum mechanically and other region using molecular mechanics (Azam et al., 2009; Rode et al., 2006). Unfortunately, most QM/MM calculations are restricted to small systems or short trajectories since quantum mechanical calculations are extremely expensive.

Aqvist has pioneered the work of applying free energy perturbation approaches to derive ion-water potential parameters that can reproduce the experimental solvation free energies of alkali and alkaline earth metal ions in water (Aaqvist, 1990). While there are still efforts to push the limits of the additive nonpolarizable force fields for ionic interactions (Joung & Cheatham, 2008), it is generally accepted that polarizability and perhaps even quantum mechanical treatments are essential for accurate descriptions of ion behavior (Halgren & Damm, 2001) in aqueous solutions (Chang & Dang, 2006; Grossfield et al., 2003; Lamoureux & Roux, 2006; Stuart & Berne, 1996) and for more complex environments such as ion-protein interactions (Li et al., 2008) and ion channels (Allen et al., 2000; Bucher et al., 2006; Illingworth & Domene, 2009; Noskov et al., 2004; Roux et al., 2004; Warshel et al., 2007).

Several groups have performed molecular dynamics simulations using polarizable force fields to study ion behavior or to determine ion solvation energies. For example, Dang and co-workers used many-body polarizable potential models in molecular dynamics simulations to study the solvation behavior of Li⁺, Na⁺, Cl⁻, and F⁻ in water clusters (Dang, 1992; Dang et al., 1991) and the significant role that polarization plays in ion binding to the liquid/vapor interface (Chang & Dang, 2006; Dang & Chang, 2001). A protein Langevin dipole model, developed by Aqvist and Warshel (Aqvist & Warshel, 1989) has been used to calculate the solvation energy of a Na⁺ ion inside the Gramicidin A channel and in water, and similar methods have been applied to model the polarization effect in the KcsA channel (Burykin et al., 2003; Luzhkov & Åqvist, 2000). Additionally, a polarizable molecular mechanic model based on induced dipole approach was successfully applied to study the absolute solvation free energies for K⁺, Na⁺, and Cl⁻ (Grossfield et al., 2003), as well as Mg²⁺ and Ca²⁺ (Jiao et al., 2006). Using a Drude oscillator model for polarizability, Roux and co-workers have developed a polarizable potential function for the hydration of alkali halide salts (Lamoureux & Roux, 2006; Whitfield et al., 2007), which gives results consistent with ab initio calculations. In addition, the fluctuating charge method of polarization has been applied to ionic systems (Bryce et al., 1998; Ribeiro, 1999) and has been used to extend classical force fields to include polarization effects (Patel & Brooks, 2004; Patel et al., 2004; Warren & Patel, 2007). Despite all these efforts, modeling explicit ions remains a considerable challenge, owing to the complex, dynamic, and subtle nature of ions, and it is expected that the future direction will be focused on using ab initio treatment and polarizable force fields.

Modeling solvation with intermediate detail: integral equation and density functional theories

Solvent distributions from integral equations

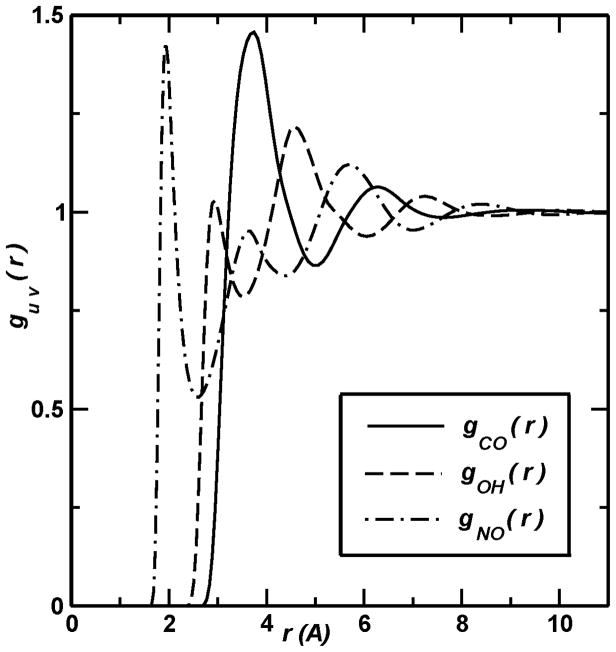
As discussed above, modeling explicit solvent effects via computer simulation techniques can be costly since the resulting systems involve a large number of particles with long-range interactions and demand substantial computational resources. An alternative route to solvation is provided by integral equation theories (IETs), which simplify the all-atom description of explicit solvation into a probabilistic treatment of distributions between solute and solvent. As a result of this simplification, these methods generally require less computational expense than explicit solvent methods but offer more detail than the continuum models discussed below (Attard, 2002; Hansen & McDonald, 2000; Hirata, 2003). Because of this compromise, IETs can be efficient and powerful tools to predict the three-dimensional spatial organization of the solvent density around large molecular solutes of irregular shape as well as related thermodynamic solvation quantities (Beglov & Roux, 1997; Chandler et al., 1986; Du et al., 2000; Harano et al., 2001; Imai et al., 2001; Kovalenko & Hirata, 1998; Kovalenko & Hirata, 1999; Kovalenko & Hirata, 2000a; Kovalenko & Hirata, 2000b; Kovalenko & Hirata, 2000c). A particularly popular set of integral equations are the interaction site models (Chandler, 1978; Hirata, 2003; Rossky et al., 1983) that specifically model the probability distribution of specific atomic sites on the solvent around atomic sites on the solute. The 1D-RISM (Reference Interaction Site Model) theory provides site-site radial distribution functions coming from an angular average over the orientation of both solute and solvent molecules (see Figure 3). This approach has been successfully applied to small molecules in general (Chuev & Fedorov, 2004; Du et al., 2008; Du et al.,2000; Freedman & Truong, 2004; Frolov et al., 2011; Imai et al., 2007; Imai et al., 2000; Kiyota et al., 2009; Kiyota et al., 2011; Kovalenko & Hirata, 1998; Kovalenko & Hirata, 1999; Kovalenko & Hirata 2000a; Kovalenko & Hirata, 2000c; Kovalenko & Hirata, 2000b; Maruyama et al., 2010; Miyata & Hirata, 2008; Nishiyama et al., 2009; Stumpe et al., 2011; Woelki et al., 2008; Yoshida et al., 2006). Unlike the 1D model, 3D-RISM keeps the orientational dependence of solute molecules, which is necessary to properly describe solvation properties of large molecular solutes. This more accurate three-dimensional integral equation demands a higher computational cost when compared with the one-dimensional theories (Perkyns & Pettitt, 1992). It provides not only an accurate site-site radial pair correlation functions but also the correct dielectric properties of polar liquids, which is a key element to properly describe the solvent effects on solutes. Integral equations specify formulae for the total and direct solvent correlation functions. Once solved, these quantities can be used to calculate the solvation chemical potential (Imai et al., 2004; Kovalenko & Hirata, 1999), the potential of mean force for solutes degrees of freedom (Kovalenko & Hirata, 1999; Kovalenko & Hirata, 2000b; Kovalenko & Hirata, 2000c), solvation coordination numbers (Kovalenko & Hirata, 1998) and hydration shells (Imai et al., 2007a), hydrophobic effects (Howard et al., 2008; Kovalenko & Hirata, 2000a) as well as many other quantities.

Figure 3.

This figure represents the solute-solvent site-site pair correlation functions g_uv(r) as a function of the separation distance r predicted by 1DRISM for N-Methyl Acetamide immersed in water at infinite dilution. For instance, g_NO(r) is the pair correlation function for a nitrogen atom in N-Methyl Acetamide molecule and an oxygen atom in water molecule

Despite the successes achieved by IETs in predicting solvation properties, there remain deficiencies that need to be corrected. A serious problem associated with these approaches is that, when they fail to yield physically reasonable predictions, there are no straightforward, systematic methods to improve IET predictive accuracy. A useful avenue to remedy this situation has been to construct thermodynamically consist integral equation theories for interaction site fluids in which the optimal closure approximation is determined by first principles (Marucho et al., 2008; Marucho & Pettitt, 2007). The reanalysis of the interaction-site formalism has also led to the development of more sophisticated (diagrammatically proper) integral equations eliminating diagrams that are not present in the exact theory (Marucho et al., 2008; Marucho & Pettitt, 2007). Another challenge for IETs lies in the inclusion of solute flexibility; however, some progress has been made in this area. IETs can be properly combined with other methodologies such as Monte Carlo simulations which project solvent degrees of freedom onto the solute at the level of site-site pair correlation functions (Freedman & Truong, 2004; Kinoshita et al., 1999; Kovalenko & Hirata, 2000b; Kovalenko & Hirata, 2000c). Alternatively, dynamical solute processes in solution can be treated by incorporating the IETs into a generalized Langevin equation, which describes the time evolution of solvent densities (Chong & Hirata, 1998).

Ion distributions from integral equations and density functional theories

Like solvent, ion distributions can also be modeled by IETs; for example, by the DRISM introduced in section above, which has been shown to account for changes in the water structure caused by the addition of salts near a protein and associated changes in the solvation free energy from the evaluation of site-site total and direct correlation functions (Imai et al., 2000; Perkyns & Montgomery Pettitt, 1994; Perkyns & Pettitt, 1996; Perkyns & Pettitt, 1995). While more computationally efficient, the 1D RISM theory suffers from its inability to model the solvent inaccessibility of buried solute atoms accurately. There have been several efforts to correct this problem (Imai et al., 2000); however, the 3D RISM theory described above is somewhat more computationally expensive but free from this problem and provides more accurate predictions of ionic behavior (Imai et al., 2004; Yonetani et al., 2008).

Classical density functional theory (DFT) (Chandler et al., 1986) provides another powerful tool for describing ionic behaviors through ion distributions. This approach is based on the simple thermodynamic principle that the system reaches the equilibrium as its grand canonical potential reaches minimum. In particular, for a fluid subject to an arbitrary potential V_ext(r, Ω), the grand canonical free energy can be written as a functional of the one-particle density. This free energy functional is minimized at the thermodynamic equilibrium density. Thus, its knowledge of this functional and the equilibrium density characterize the fluid completely. However, this functional is not known for most complex systems and, instead, is approximated in various ways. Different approaches and approximations based on DFT have been proposed to evaluate the excess free-energy and the density profile depending on the complexity and features of the system. For example, Gao and coworkers (Wang et al., 2004) use the weighted-density approximation to describe the structure and thermodynamics properties of small ions around a polyelectrolyte immersed in a continuum media, observing the charge inversion phenomena of DNA at moderate concentrated solution. Ramirez and Borgis (Ramirez & Borgis, 2005) use the homogeneous reference fluid approximation to develop a general approach that includes the microscopic structure of the solvent, the dipolar saturation effects, and the non-local character of the dielectric constant in the calculation of the average solvent structure solvation properties of molecular solutes of irregular shape. Eisenberg and coworkers (Gillespie et al., 2002) combine a one-dimensional drift-diffusion (Poisson–Nernst–Planck or, PNP) transport system and DFT to model ion transport in biological ion channels. These examples show the theoretical versatility of DFT for describing ionic solvation in complex systems. However, the same energy functional may not be accurate for all applications and systematic improvements of the functional are not generally possible, instead requiring ad hoc corrections.

Modeling solvation with low detail: continuum approximations

While models of higher resolution can ideally provide better accuracy and quantitative predictions, their computational cost often precludes use in many biomolecular applications. Instead, it is often essential to reduce computational costs by accounting solvent and ion effects in an implicit or continuum manner (Baker, 2005a; Baker, 2005b; Baker et al., 2006; Baker, 2004; Cramer & Truhlar, 1999; Marenich et al., 2008; Onufriev et al., 2002). Implicit solvent methods have been very successful with a multitude of applications in computational chemistry and biology. However, these models are highly approximate and often empirical; as such, there are several caveats that potential users should keep in mind. First, most implicit solvent models uncouple polar and nonpolar interactions, even though such a separation can be problematic and unphysical (Cerutti et al., 2007; Chen et al., 2011; Chen et al., 2010; Dzubiella & Hansen, 2004; Dzubiella et al., 2006a; Dzubiella et al., 2006b). Additionally, as discussed in more detail below, implicit models for nonpolar and polar solvation are—by their very nature—approximate with several sources of ambiguity in the choice of model parameters and geometries (Swanson et al., 2005; Swanson et al., 2007; Teixeira et al., 2005; Tjong & Zhou, 2008). However, despite these caveats, implicit solvent models are very popular and valuable for a variety of biophysical studies.

While continuum models of solvent polarization have had many successes, they provide an incomplete description of water behavior—particularly at small-length scales and in the presence of strong electrostatic fields. In particular, continuum models are limited by their assumption of linear and local solvent polarization in response to electrostatic perturbations (Beglov & Roux, 1996; Beglov & Roux, 1997; Hansen & McDonald, 2000; Roux, 1999). The continuum dielectric assumption of local response implicitly neglects the role of detailed solvent-solvent interactions (e.g., hydrogen bonds, steric clashes, etc.) and solvent molecular shape (Mobley et al., 2008) in dielectric behavior. The continuum assumption of linear response ignores the finite density, dipole moment, and polarizability of solvent by neglecting the nonlinear phenomena of electrostriction and dielectric saturation. Finally, the polarization of molecular solvents is also closely linked to variations in local density (Ashbaugh & Truskett, 2001; Beglov & Roux, 1996; Beglov & Roux, 1997; Dzubiella & Hansen, 2004; Dzubiella et al., 2006a; Dzubiella et al., 2006b; Paliwal et al., 2006); e.g., the presence of cavities or other solutes. In particular, the introduction of a cavity or uncharged solute into a polar solvent such as water can create significant interfacial polarization, often resulting in a positive potential inside the cavity (Ashbaugh, 2009; Cerutti et al., 2007; Harder & Roux, 2008; Martin et al., 2011).

The Poisson equation for polar solvation

The Poisson equation is a fundamental equation of continuum electrostatics (Bottcher, 1952; Jackson, 1975). It is a linear second-order partial differential equation

$$-\nabla ·(\epsilon (\overrightarrow{r})\nabla \phi (\overrightarrow{r}))=\rho (\overrightarrow{r})\text{for}\overrightarrow{r}\in \mathrm{\Omega }$$

which expresses the electrostatic potential φ terms of a dielectric coefficient ε and a charge distribution ρ for all points r in some domain Ω. This differential equation must be combined with additional constraints on the potential in order to provide well-posed solutions. These constraints usually take the form of boundary conditions specifying the value of the potential or its derivatives on the boundary ∂Ω of the domain. The most common boundary conditions for biomolecular electrostatics problems are the simple Dirichlet condition which constrains the potential to an asymptotic approximation on the boundary of the domain.

The biomolecular structure and chemistry are introduced into the Poisson equation through the dielectric and charge coefficients. The charge distribution is often represented by a sum of atomic monopoles or higher-order multipoles as described in the “Modeling biomolecular charge distributions” section. The dielectric coefficient is generally a sharply varying function that assumes bulk solvent values outside of the biomolecular surface and other values inside the biomolecule. The value of the dielectric coefficient determines the polarization response of the material when subject to an electric field; more easily polarizable materials have higher dielectric values. While the bulk values of the dielectric are straightforward to determine, based on the properties of the homogeneous solvent, the dielectric values inside the biomolecule are much more difficult to interpret and have been subject to much debate and analysis (Roux, 1999; Schutz & Warshel, 2001; Sham et al., 1998; Simonson, 1999; Simonson, 2001; Simonson, 2003; Simonson, 2008; Teixeira et al., 2005; Tjong & Zhou, 2008). In particular, the choice of internal dielectric coefficient values is usually very dependent on the specific application. If the only polarization response of the biomolecular interior results from electronic reorganization, then the most appropriate value of the biomolecular dielectric coefficient should be between 2 and 4 (Landau et al., 1982). Such low dielectric models are appropriate for simulations and calculations such as MM/PBSA (Molecular Mechanics/Poisson-Boltzmann Surface Area) where the molecular flexibility of the molecule is modeled explicitly through conformational sampling. Higher values of the internal biomolecular dielectric are intended to mimic additional relaxation properties, including orientational changes in molecular dipoles, side-chain rearrangement, and even penetration of water into the biomolecular interior. Values from 4 to 20 have been regularly used in a variety of biomolecular applications with lower values generally being successful for protein-ligand interactions (Kollman et al., 2000; Massova & Kollman, 2000), moderate values of 10–12 necessary for protein-protein binding energies (Elcock et al., 2001), and values 20 or higher needed for titration state and pK_a predictions (Chimenti et al., 2011; Schutz & Warshel, 2001).

In addition to the variety of dielectric coefficient values, there are also many choices available for the functional form and shape of the biomolecule-solvent dielectric boundary (see Figure 4) (Chen et al., 2011b; Chen et al., 2010; Grant et al., 2001; Grant & Pickup; Im, 1998; Tjong & Zhou, 2008). The results of most biomolecular solvation and electrostatics calculations are very sensitive to the definition of this boundary, so it is not surprising that the optimal choice of biomolecular parameters and dielectric value are dependent on the particular dielectric boundary of choice (Nina et al., 1999; Swanson et al., 2007). As with the dielectric value, the choice of a particular boundary geometry is dependent on many factors, including the specific problem under consideration, the original geometry definitions used to optimize the parameters desired for the given calculation. The most popular biomolecular dielectric interface definition is the molecular surface (Connolly, 1983; Connolly, 1985) which was used to parameterize the PARSE parameter set for biomolecular solvation calculations (Sitkoff et al., 1994). Zhou and co-workers have suggested the use the van der Waals surface as an alternative to the molecular surface for several different applications (Dong et al., 2003; Tjong & Zhou, 2008). Both the molecular and van der Waals surfaces can introduce significant conformational sensitivity that can be problematic for applications that explicitly sample different conformational states. As a result, a number of smoother surfaces have also been introduced, including Gaussian (Grant et al., 2001; Grant & Pickup, 1995) and spline-based representations (Im, 1998; Schnieders et al.). These surfaces require a distinct set of parameters for accurate calculations, as described in (Grant et al.; Grant & Pickup) for Gaussian interfaces and by others (Nina et al., 1999; Swanson et al., 2007) for spline-based representations. Finally, new generations of molecular surface definitions that are designed to minimize noise from topological artifacts (Bajaj, 2003; Zhang et al., 2006) and to provide a clear physical basis for coupling to nonpolar representations (Chen et al., 2001; Chen et al., 2010; Dzubiella & Hansen, 2004; Dzubiella et al., 2006a; Dzubiella et al., 2006b) are appearing. In particular, new surfaces based on geometric flow (Chen et al., 2001; Chen et al., 2010) provide a self-consistent description of the biomolecular interface that is compatible with the continuum polar and nonpolar energy functions. While these new surfaces appear very promising, they will require parameterization before they can be used optimally in biophysical calculations.

Figure 4.

Images of the varying definitions for the biomolecular surface of fasciculin-2 (PDB ID: 1FAS) with electrostatic potential shown ranging from −5 kT/e (dark red) to +5 kT/e (dark blue). A. van der Waals surface. B. Solvent-excluded, molecular, or Connolly surface. C. Solvent-accessible surface.

The linear and local nature of the dielectric coefficient introduces two major assumptions into the model (Beglov & Roux, 1996; Beglov & Roux, 1997). Linear response implies a proportional increase in system polarization for all strengths of electric field. This approximation clearly breaks down near highly charged interfaces (e.g., nucleic acids or strongly charged proteins) where dielectric saturation and electrostriction processes can become important. Several models have been developed to provide for nonlinear response, generally in the form of a Langevin response function (Azuara et al., 2008; Papazyan & Warshel, 1997; Papazyan & Warshel, 1998). The second major approximation is the local nature of the dielectric constant which implies that local changes in the electric field have only local influences on polarization. However, the molecular nature of water and its associated network of hydrogen bonding and extended structure at interfaces clearly indicate that this approximation is incorrect, particularly at very small (molecular) length scales. Nonlocal features have also been introduced into the Poisson equation but incur increased computational expense (Bardhan, 2011; Basilevsky & Parsons, 1998; Rottler & Krayenhoff, 2009).

The Poisson-Boltzmann equation for polar solvation

The Poisson equation only includes the influence of solvent on the electrostatic properties of a solute. However, as discussed in earlier sections of this review, mobile ions also play a very important role on biomolecular electrostatics and solvation. The Poisson-Boltzmann (PB) model was developed to address the need to include simple effects from low valency ions in dilute solutions (Baker, 2005a; Baker, 2005b; Baker et al., 2006; Baker, 2004; Davis & McCammon, 1990; Dong et al., 2008; Grochowski & Trylska, 2008; Honig & Nicholls, 1995; Honig et al., 1986; Sharp & Honig, 1990). One of the best reviews of the model and its caveats was written by Fixman (Fixman, 1979). The PB model essentially relates the local electrostatic potential to the average mobile charge densities. Several important approximations are associated with the PB model (Baker, 2004; Beglov & Roux, 1996; Beglov & Roux, 1997; Fixman, 1997; Holm et al., 2001).

The first approximation, similar to the Poisson equation, is that system solution can be described a continuum, including the dielectric response described above as well as an average density of point-like ions. This density model precludes the treatment of site-specific ion-solute interactions as well as other phenomena which involve details of ionic shape. The PB model cannot explain differences between ion species in solution and thereby prevents effects analysis of specific ion species and the associated phenomena described earlier in this review.

The second approximation models the distribution of ions in terms of single-species average distribution functions. In other words, ions interact with each other only through their average densities rather than through the steric, Coulombic, and solvent-mediated correlations that occur in real electrolyte systems. As a consequence, the PB model cannot capture a number of phenomena (Chen & Weeks, 2006; Savelyev & Papoian, 2007; Tan & Chen, 2005), including charge inversion (Besteman et al., 2004; Besteman et al., 2005; Goel et al., 2008; Kim & Sung, 2005; Luan & Aksimentiev, 2010; Martin-Molina et al., 2009; Nguyen et al., 2000; Qiao & Aluru, 2004; Taheri-Araghi & Ha, 2005; Wen & Tang, 2004) and like-charge attraction (Angelini et al., 2003; Kim et al., 2008; Mukherjee; Netz & Naji, 2004; Pietronave et al., 2008; Podgornik & Dobnikar, 2001; Qiu et al., 2010; Todd et al., 2008; Zelko et al., 2010), that can be important for highly-charged systems. Such systems include solutes such as DNA, charged biomembrane interfaces, and solutions with even moderate concentrations of di- or multi-valent ions. Ionic correlations and fluctuation corrections have been considered in previous studies. Based on the Kirkwood hierarchy (Kirkwood, 1934), a fluctuation potential and an excluded-volume factor have been added to the potential of mean force to represent the effect of ion correlations (Burley et al., 1974; Carnie & Torrie, 2007; Grochowski & Trylska, 2008). The fluctuation potential is associated with the energy for charging ions and implicitly takes into account the inter-ion Coulomb correlations. This modification provides improved predictions for ion distribution and mean electrostatic potential profile with multivalent ions, as compared to the conventional PB model (Carnie & Torrie, 2007). However, since the fluctuation potential itself is coupled to the electrostatic potential, the three-dimensional numerical solution becomes computationally very expensive and is impractical for applications such as nucleic acid structures (Gavryushov, 2008). Other approaches such as the density functional and integral equation methods were discussed earlier; however, the computational complexity for these approaches is still problematic for many applications.

Another important approximation involves the assumption of infinitesimal ion size which can produce arbitrarily large ion concentrations near highly charged solutes. Borukhov et al (Borukhov et al., 1997) developed a simple analytical approach to include the finite ion size in the original PB model. The modified formula was developed for asymmetric and symmetric electrolytes and matched with the original PB equation when an ionic concentration is low. The size effect was introduced as additional correction terms in the entropic contribution of the total free energy. Such corrections were employed by considering the lattice gas formalism, where each lattice site is occupied at most by one ion; the standard PB model corresponds to one with unlimited number of ions in each lattice site. A similar approach based on the lattice gas formalism was used in other studies (Borukhov et al., 2000; Chaudhry et al., 2011; Coalson et al., 1995; Coalson & Duncan, 1992) to incorporate the finite size effect. This size-modified PB model showed appreciable improvements in predictions for ion-binding properties of monovalent counterions, especially at high-salt concentration, which involves the saturation effect for ion binding. However, the consideration of the finite ion size still cannot capture the binding of the divalent and multivalent ions, which may be because of the absence of ion-ion correlations (Chu et al., 2007).

Despite the caveats and approximations described above, the PB model is simple and captures enough basic solvation behavior to be a popular choice for describing many biomolecular systems. While there are many more interesting ways to drive the PB equation (Holm et al., 2001), the simplest method starts with the Poisson equation, repeated here:

$$-\nabla ·(\epsilon (\overrightarrow{r})\nabla \phi (\overrightarrow{r}))=\rho (\overrightarrow{r}),$$

In the Poisson discussion above, we considered only a single contribution to the charge density ρ(r⃗) due to the solute. For the PB equation, the charge distribution is assumed to consist of two separate contributions: the solute charges ρ_s(r⃗) and the mobile ions in an aqueous medium ρ_m(r⃗). The charge distribution of the solute was discussed previously; for a simple monopole approximation, the charges Q_i located at each solute atom’s position r_i can be modeled via a delta function:

$${\rho }_s(\overrightarrow{r})=\sum _i{Q}_i\delta (\overrightarrow{r}-{\overrightarrow{r}}_i)$$

For a mean-field approximation, the charge distribution associated with the mobile ions can be described by a Boltzmann distribution. For m ion species with charges q_j, bulk concentration $c_j^b$ and steric potential V_j(r⃗) (a potential to describe nonpolar interactions with the solute), the charge for the mobile ions is

$${\rho }_m(\overrightarrow{r})=\sum _j^m{c}_j^b{q}_{j}exp\left[\frac{-q_j\phi (\overrightarrow{r})}{k_{B}T}-\frac{V_j(\overrightarrow{r})}{k_{B}T}\right]$$

where k_B is the Boltzmann’s constant and T is the system temperature. Substituting the two charge distributions into the Poisson equation, one obtains the full PB equation:

$$-\nabla ·(\epsilon (\overrightarrow{r})\nabla \phi (\overrightarrow{r}))=\sum _i^N{Q}_i\delta (\overrightarrow{r}-{\overrightarrow{r}}_i)+\sum _j^m{c}_j^b{q}_{j}exp\left[\frac{-q_j\phi (\overrightarrow{r})}{k_{B}T}-\frac{V_j(\overrightarrow{r})}{k_{B}T}\right]$$

Note that the full PB equation is a nonlinear second-order elliptic differential equation, which cannot be solved analytically for most realistic biomolecular geometries.

A simplification to the full PB equation can be made if the exponential term is approximated by the linear term in its Taylor series expansion. This assumption, which is made in addition to those described above, requires |q_jφ(r⃗)/k_BT| ≪ 1. Also assuming identical steric contributions for all ions, the full PB equation becomes the linearized PB equation:

$$-\nabla ·(\epsilon (\overrightarrow{r})\nabla \phi (\overrightarrow{r}))+\epsilon (\overrightarrow{r}){\kappa }^2(\overrightarrow{r})\phi (\overrightarrow{r})=\sum _i^N{Q}_i\delta (\overrightarrow{r}-{\overrightarrow{r}}_i)$$

where κ(r⃗) is a modified inverse Debye-Hückel length represented by

$$\kappa (\overrightarrow{r})={\left(exp\left[-\frac{V(\overrightarrow{r})}{k_{B}T}\right]\frac{2I^2{e}_c^2}{k_{B}T\epsilon (\overrightarrow{r})}\right)}^{1/2}$$

where $I=\sqrt{{\sum }_i\frac{c_j^b{q}_j^2}{2e_c^2}}$ is the ionic strength and e_c is the electron charge. The Debye-Hückel length is considered as a length scale below which mobile ions experience the electrostatic potential of the solute and interact with it.

Using the potential obtained by solving the PB equation, the electrostatic free energy can be obtained via a variety of integral formulations (Chen et al., 2011b; Chen et al., 2010; Gilson, 1995; Holm et al., 2001; Micu et al., 1997; Sharp & Honig, 1990a). These free energy expressions arise both from physical considerations as well as from a purely mathematical standpoint. Statistical physics can derive the PB equation and its associated free energy from a saddle-point approximation of a more complicated description of the electrolyte system (Holm et al., 2001). Functional minimization of the resulting free energy gives rise directly to the PB equation. It is also possible to differentiate these integral formulations of the electrostatic energy with respect to atomic position in order to obtain the electrostatic (i.e., polar) solvation mean force on each atom (Gilson et al., 1993; Im, 1998; Wagoner & Baker, 2004; Wagoner & Baker, 2006).

While the PB equation may be solved analytically for very simple cases (e.g., flat plate with a single symmetrical electrolytes), analytical solutions of the PB equation are not available for biomolecules with realistic shapes and charge distributions. Therefore, a numerical method is a necessary tool for biomolecular electrostatics. After Warwicker and Watson (Warwicker & Watson, 1982) first introduced numerical methods to solve the PB equation at the active site of an enzyme, many different numerical methods have been developed and are being modified. Most numerical methods for the PB equation depend on the discretization of computational domain/space (i.e., a distribution of points and their connections), which is critical to both accuracy and efficiency. These methods include finite differences (Baker et al., 2001b; Davis & McCammon, 1989; Holst & Saied, 1993; Holst & Saied, 1995; Nicholls & Honig, 1991), finite elements (Baker et al., 2000; Baker et al., 2001a; Cortis & Friesner, 1997a; Cortis & Friesner, 1997b; Dyshlovenko, 2002; Holst et al., 2000), and boundary elements (Bajaj et al., 2011; Bordner & Huber, 2003; Boschitsch & Fenley, 2004; Juffer et al., 1991; Zauhar & Morgan, 1988).

Because of their simpler spatial discretization of the computational domain, finite differences have been the most popular numerical methods for the PB equation in bimolecular electrostatics. Finite difference-based PB solvers include APBS (Baker et al., 2001b), MIB (Chen et al., 2001; Yu et al., 2007a; Yu & Wei, 2007; Yu et al., 2007b; Zhou & Wei, 2006), DelPhi (Klapper et al., 1986; Rocchia et al., 2002), MEAD (Bashford, 1997), UHBD (Madura et al., 1995), ZAP (Grant et al., 2001), the PBEQ (Im, 1998) module in CHARMM (Brooks et al., 2009), and the PB solver in AMBER (Luo et al., 2002). The APBS solver provides scalable electrostatics by uniquely combing standard finite difference focusing techniques (Gilson & Honig, 1987) and the Bank-Holst algorithm (Bank & Holst, 2003) into a parallel focusing method that allows solution of the PB equation for molecules of arbitrary size. A new matched interface and boundary (MIB) method, (Chen et al., 2001; Geng & Wei, 2001; Xia et al., 2011; Yu et al., 2007; Zhou & Wei, 2006) implemented the analytical molecular surface in their interface method for solving the PB equation. This method was the first biomolecular PB solver enforcing the continuity conditions of both the electrostatic potential and its flux at the molecular surface. Wei et al. (Yu et al., 2007a; Yu & Wei, 2007; Yu et al., 2007b) extended their work to further develop MIB-based PB solvers called MIBPB-II and MIBPB-III in order to accommodate geometric and charge singularities respectively.

Finite element methods provide more flexibility than finite differences by permitting adaptive mesh refinement in regions of high error. The local nature of this refinement, together with robust multilevel solvers (Holst, 2001), provides unique multiscale capabilities. Significant finite element work related to the PB equation was performed by Holst and co-workers (Baker et al., 2000; Baker et al., 2001; Holst; Holst et al., 2000; Holst & Saied, 1993; Holst & Saied, 1995). More recently, Chen et al. (Chen et al., 2007a) have provided the first complete convergence result for a numerical discretization technique for the nonlinear PB equation with delta distribution sources and introduced the first convergent adaptive method for the PB equation. Finite element solutions are currently available through the FEtk solver (http://www.fetk.org/) with a biomolecular electrostatics interface provided APBS (http://www.poissonboltzmann.org/).

Boundary element methods (BEM) use Green’s theorem to reformulate the linear PB equation as boundary integral equations (Allison, 2001; Altman et al., 2009; Bajaj et al., 2011; Bharadwaj et al., 1995; Boschitsch & Fenley, 2004; Boschitsch et al., 2002; Juffer et al., 1991; Lu et al., 2010; Yoon & Lenhoff, 1990; Zauhar, 1995; Zauhar & Morgan, 1985; Zauhar & Morgan, 1988; Zhou, 1993). Unlike finite differences and finite elements, the unknowns and domain discretization are only on a two-dimensional surface rather than a three-dimensional volume. For the nonlinear PB equation, three-dimensional volume integrals are involved in the integral equations, which reduce the efficiency of the methods, but still require a smaller number of unknowns than finite difference or finite element methods. BEMs assume a discontinuous dielectric function at the molecular interface with the solvent; as such, they are suitable for a relatively narrow range of dielectric formulations. Advantages of BEM include (i) the reduction of the unknowns, (ii) exact treatment of boundary conditions at infinity, (iii) and explicit treatment of the physical interface conditions (continuity in potential and jump in its normal derivative). However, Green’s functions are not available for the nonlinear PB equation and the BEM may not be efficient because of numerous boundary integral operations and singular boundary integrals that can affect the accuracy and/or stability. Recently, a hybrid finite difference BEM approach was introduced to improve computational efficiency (Boschitsch & Fenley, 2004). This approach is based on the separation of electrostatic potential into a linear component satisfying the linear PB equation and is solved using a fast boundary element method and a correction term accounting for nonlinear effects and optionally, the presence of an ion-exclusion layer.

A completely different approach to solution of the linearized PB equation has been suggested by Mascagni and co-workers (Mascagni & Simonov, 2004; Simonov et al., 2007). Their technique uses Monte Carlo methods that simulate random walks in the problem domain to solve the linear PB equation. This random walk approach is sufficiently flexible to work with complicated biomolecular geometries and can be used to calculate the molecular electrostatic properties for a series of salt concentration values simultaneously.

Simpler models for polar solvation

In addition to the PB model, simpler models have also been developed based on continuum electrostatics principles. These simple models include distance-dependent dielectric functions, analytic continuum methods (Schaefer & Karplus, 1996), the so-called EEF approach (Lazaridis & Karplus, 1999) and the improved ABSINTH model (Vitalis & Pappu. 2009) and generalized Born models. The generalized Born (GB) model is one of the most popular such models and was developed by Still et al. in 1990 (Still et al., 1990) and subsequently revised by several others (Anandakrishnan et al., 2011; Bashford & Case, 2000; Brown & Case, 2006; Chen, 2010; Chen et al., 2006; Clark et al., 2009; Dominy & Brooks, 1999; Feig & Brooks, 2004; Feig et al., 2004; Feig et al., 2008; Gallicchio et al., 2009; Gallicchio et al., 2002; Grant et al., 2007; Grycuk, 2003; Im et al., 2003b; Jorgensen et al., 2004; Labute, 2008; Lee et al., 2002; Onufriev et al., 2000; Onufriev et al., 2002; Osapay et al., 1996; Tjong & Zhou; Tjong & Zhou, 2007b; Tsui & Case, 2000; Xu et al., 2011; Zhu et al., 2005). The GB model describes the solvent as a continuum medium, similar to the PB model, but provides a faster calculation of solvation energies and forces. The model is an approximation to the Poisson equation energy; it models a solute particle as a sphere whose internal dielectric permittivity coefficient is different from that of the external solvent. Specifically, it uses the analytical solvation energy resulting from the solution of the Poisson equation for a simple sphere (Born, 1920).

Analytical solutions to electrostatic problems associated with various simple dielectric boundary conditions are discussed in many textbooks (Bottcher, 1952; Jackson, 1975). A simple electrostatic model of a biomolecule in solution is a cavity with a charge distribution embedded in a high-dielectric continuum medium. The problem can be further simplified by considering a spherical cavity within which electrostatic interactions are calculated explicitly. By Gauss’ Law, the electrostatic potential outside the sphere is given by the usual Coulomb formula. However, since electric charges within the cavity polarize the high-dielectric medium, the total electric potential inside the cavity includes this effect as well as the direct Coulomb interactions between charges within the cavity. The electric potential associated with the polarization is called the “reaction field” potential and can be represented by a summation of Legendre polynomials (Kirkwood, 1934) or by the Coulomb potential associated with image charges outside the cavity.

The image charge approach is usually formulated when the dielectric constant of medium is much larger than that of the cavity, the reaction-field (RF) potential inside the cavity is approximately (Deng & Cai, 2007; Friedman, 1975)

$$\begin{array}{c}{\mathrm{\Phi }}_{RF}(r)=\sum _{i=1}^N\frac{{q_i}^{\prime }}{{\epsilon }_{in}\mid \underset{\_}{r}-{{\underset{\_}{r}}_i}^{\prime }\mid }\\ {\mathrm{\Phi }}_{RF}(r)=\sum _{i=1}^N\frac{{q_i}^{\prime }}{{\epsilon }_{in}\mid \underset{\_}{r}-{{\underset{\_}{r}}_i}^{\prime }\mid }\\ q_i^{\prime }=\frac{{\epsilon }_{in}-{\epsilon }_o}{{\epsilon }_{in}+{\epsilon }_o}\frac{R}{r_i}{q}_i\\ {\underset{\_}{r}}_i^{\prime }={(R/r_i)}^2{\underset{\_}{r}}_i\end{array}$$

where q′ is the image charge that will interact with the solute and r′ is the location of the image charge outside the cavity. The total energy of the system, including both the gas-phase interaction energy of source charges and the reaction-field energy, becomes (Wang & Hermans, 1995):

$$U=\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N\frac{q_i{q}_j}{{\epsilon }_{in}\mid {\underset{\_}{r}}_i-{\underset{\_}{r}}_j\mid }+\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N\frac{q_i{q_j}^{\prime }}{{\epsilon }_{in}\mid {\underset{\_}{r}}_i-{{\underset{\_}{r}}_j}^{\prime }\mid }$$

where the sums implicitly exclude self-interactions for i = j. The first term of this energy expression indicates the direct electrostatic interactions between source charges in the cavity, whereas the second term includes the reaction field effect through the interactions between the source charges and image charges. Note that the second term includes not only the interaction between each source charge with the image charges of other source charges but also that between each source charge with its own image charge. By placing solute molecules in a spherical water droplet, Wang and Hermans adapted the Friedman’s image charge method in molecular dynamic simulations to account for the dielectric effect outside the simulated sphere (Wang & Hermans, 1995). Deng and Cai showed that Friedman’s formula is the zero order term in the Kirkwood series expansion with respect to ε_in/ε₀. (Deng & Cai, 2007). It is also noted that Friedman’s approximation is inconsistent with Born formula when all the charges are located at the center of the spherical cavity. Based on the work by Neumann (Neumann, 1883), a multiple image of charge method was proposed whereby the single image charge is replaced by a charge distribution extending from the image charge position to infinity in the radial direction (Lindell, 1992; Norris, 1995). An efficient fast multipole algorithm was developed to take advantage of the accuracy of the multiple image method while making it computational tractable for simulation purposes (Cai et al., 2007; Deng & Cai, 2007).

The Legendre polynomial solution the spherical system was given by Kirkwood in 1934 (Kirkwood, 1934). For a system with a set of point charges q_k in a spherical cavity of radius a, the reaction-field potential at r inside the sphere is given by

$$V(r)=\frac{1}{{\epsilon }_{in}}\sum _{l=0}^{\infty }\frac{(l+1)({\epsilon }_{in}-{\epsilon }_0)}{(n+1){\epsilon }_o+n{\epsilon }_{in}}\frac{r^l}{a^{2l+1}}\sum _{k=1}^N{q}_k{r}_k^l{P}_l(\mathit{cos}\theta )$$

In the equation above, the dielectric constants inside the spherical cavity is ε_in. The terms $q_k{r}_k^l(l=0,1,2\dots )$ are the multipole moments of the charge distribution inside the sphere. The expansion reduces to the Born (Born, 1920) or Onsager (Onsager, 1936) approximation in the special case of a single ion or dipole buried at the center of the spherical cavity.

With growing interests in sophisticated electrostatic models involving point multipoles and electronic polarization, the Kirkwood’s reaction-field theory has been extended beyond partial charges. Orttung generalized the Kirkwood-Westheimer model (Kirkwood, 1938) for different shapes, charges, and polarizabilities (Orttung, 1978). Warshel developed a multiscale model to describe the interactions among explicit solute (point charge), immediate solvation shell (point dipole) and the surrounding continuum (reaction-field) (Warshel, 1979). Felder and Applequist introduced inducible dipoles to represent the solute electrostatics and derived the corresponding reaction-field expressions for spherical and ellipsoidal cavities (Felder & Applequist, 1981). Kong and Ponder obtained the reaction-field energy and force for arbitrary point multipole distributions located off the center of the spherical cavity (Kong, 1997). Nymand and Linse developed a reaction-field model for solutes of point charges, dipoles and polarizabilities (Nymand & Linse, 2000). Recently, Schnieders and Ponder introduced generalized Kirkwood (GK) model to eliminate the partial charge restriction inherent to generalized Born (GB) analytic continuum electrostatics (Schnieders & Ponder, 2007). GK defines a self-consistent reaction field for solutes modeled by polarizable atomic multipoles, which are more accurate and transferable than partial charges, but also more expensive. Davis developed an inducible multipole solvation model that exhibits an exact series representation of the external electrostatic field for a collection of dielectric cavities with centrosymetric internal charge distributions and arbitrary external charge distributions (Davis, 1994). Fenley et al. (Fenley et al., 2008) derived a closed-form analytical approximation to the Poisson equation for an arbitrary distribution of point charges and a spherical dielectric boundary. Their simple, parameter-free formula was obtained from the Kirkwood solution by an approximate summation method and presents continuous electrostatic potential everywhere in space.

The generalized Born (GB) model can be thought of as a good analytical approximation to the analytical models described above. In particular, it uses the analytical solvation energy resulting from the solution of the Poisson equation for a simple sphere and needs a much lower computational cost, compared to solving the PB equation. Using the GB model, the electrostatic solvation free energy can be approximated by a modified form of the analytical solvation energy for a sphere (Still et al., 1990):

$$G_{el}\cong -\frac{1}{2}\left(1-\frac{1}{{\epsilon }_{\mathit{sol}}}\right)\sum _{i,j}\frac{Q_i{Q}_j}{f_{ij}^{GB}}$$

where $f_{ij}^{GB}$ denotes the effective Born radii (when i = j) and the effective interaction distance (when i ≠ j) respectively. The most common form given by Still et al (1990) is

$$f_{ij}^{GB}={\left[r_{ij}^2+R_i{R}_j\text{exp}\left(-\frac{r_{ij}^2}{4R_i{R}_j}\right)\right]}^{1/2}$$

where R_i are the effective radii of the atoms and r_ij are the distance between atom i and j. It is essential to calculate the effective radii of the atoms efficiently and accurately. A previous study (Onufriev et al., 2002) demonstrated that the GB model can provide comparable results to the Poisson equation when one uses perfect GB radii that reproduce the atoms’ self-energies as obtained from the Poisson equation. This observation implies that an accurate estimation of the radii is critical for reliability of the GB model. Many studies have been performed to improve the GB model with general corrections (Mongan et al., 2007) but also with revised formulations aiming at biomacromolecules such as proteins and nucleic acids (Dominy & Brooks, 1999; Onufriev et al., 2000; Sigalov et al., 2006) and biological membranes (Im et al., 2003; Tanizaki & Feig, 2005). The GB model has also been extended to provide approximations to the full nonlinear PB (NLPB) equation because of its computational benefit (Tjong & Zhou, 2007a; Tjong & Zhou, 2007b)

Continuum models for nonpolar solvation

The low-detail continuum polar solvation models above are generally decoupled from the nonpolar energetics of the system. Therefore, nonpolar contributions must be added into the system to complement the polar energetics. The importance of nonpolar solvation is well-known but has often been treated with a very simple approximation that assumes nonpolar energy is proportional to solvent-accessible area (Chothia, 1974; Massova & Kollman, 2000; Sharp et al., 1991a; Sharp et al., 1991b; Wesson & Eisenberg, 1992)

$$G_{\mathit{nonpolar}}(\overrightarrow{x})\cong \gamma A(\overrightarrow{x})$$

This approximation is motivated by the solvation area of linear alkanes in water. Here γ is a microscopic solvent surface tension parameter (not a macroscopic surface tension of solvent) which can be chosen to reproduce the solvation free energy of nonpolar molecules (Sharp et al., 1991a; Sharp et al., 1991b; Simonson & Brunger, 1994; Sitkoff et al., 1994b), including model side chain analogues (Wesson & Eisenberg, 1992; Wimley et al., 1996). The surface tension parameter can be modeled as a single universal value used for all atoms or different values may be assigned for each atom type. While the simplest description has been successful, it has several caveats, including the difficulty of rationalizing surface tension parameter values (Chothia, 1974; Eisenberg & McLachlan, 1986; Sharp et al., 1991a; Sharp et al., 1991b; Sitkoff et al., 1994b) as well as inaccurate descriptions of detailed aspects of nonpolar solvation energies (Gallicchio & Levy, 2004), peptide conformations (Su & Gallicchio, 2004), and nonpolar solvation forces (Wagoner & Baker, 2006).

Recent work (Gallicchio et al., 2000; Gallicchio & Levy, 2004; Levy et al., 2003; Wagoner & Baker, 2006) has built upon a significant amount of existing research into nonpolar effects (Ashbaugh, 2009; Ashbaugh & Pratt, 2006; Ben-Naim, 2006; Chandler, 2005; Gu et al., 2004; Huang et al., 2001; Huang & Chandler, 2002; Hummer, 1999; Hummer & Garde, 1998; Hummer et al., 1996; Hummer et al., 2000; Pitera & van Gunsteren, 2001; Pratt, 2002; Pratt & Chandler, 1977; Pratt & Pohorille, 1992; Pratt & Pohorille, 2002; Rajamani et al., 2005; Tan et al., 2007) to develop computationally efficient, but more energetically complete, models for nonpolar solvation energy that include important attractive van der Waals interactions between solvent and solute (Gallicchio et al., 2000; Gallicchio & Levy, 2004; Gallicchio et al., 2002; Wagoner & Baker, 2006) and repulsive solvent-accessible volume terms (Wagoner & Baker, 2006). For example, Wagoner and Baker proposed a nonpolar solvation model based on the free energy functional (Wagoner & Baker, 2006):

$$G_{\mathit{nonpolar}}(\overrightarrow{x})\cong \gamma A(\overrightarrow{x})+pV(\overrightarrow{x})+\overline{\rho }\sum _{i=1}^N{\int }_{\mathrm{\Omega }}{u}_i^{\mathit{att}}({\overrightarrow{x}}_i,\overrightarrow{y})\theta (\overrightarrow{x},\overrightarrow{y})d\overrightarrow{y}$$

where p is a solvent hydrodynamic pressure parameter, V is a solvent accessible volume, and ρ̄ is the bulk solvent density. Here Ω denotes the solvent accessible region outside the solute, $u_i^{\mathit{att}}(x_i,\overrightarrow{y})$ is the attractive component of the nonpolar interaction potential (for atom i) between a solute in conformation x⃗ and solvent at position y⃗, and θ(x⃗, y⃗)is a characteristic function defined as a product of per-atom characteristic functions θ_i. This model showed very good agreement with explicit solvent results, which suggests that the addition of appropriate dispersion and volume terms is essential to describe atomic scale nonpolar forces.

Recent studies on the solvation of atomistic and nanoscale solutes reveal that a coupling exists between the hydrophobic, dispersion, and electrostatic contributions to the solvation free energy. The fact that the effective location of the solvent-solute interface can rely on the local electrostatic and dispersive (Huang & Chandler, 2002) potentials suggests that such polar and nonpolar components should be coupled in implicit solvent models. For example, Ashbaugh et al. (Ashbaugh & Paulaitis, 1998) pointed out that a correct balance between nonpolar and polar (or electrostatic) contributions is critical in their study of amphiphiles. To take into account polar-nonpolar coupling, Dzubiella et al (Dzubiella et al., 2006a; Dzubiella et al., 2006b) proposed a theoretical formalism based on the minimization of the Gibbs free energy of the solvent with respect to a solvent volume exclusion function. Unlike existing implicit solvent approaches, the solvent-solute interface is an output of the model. Therefore, the coupling is indeed implemented by the geometrical description of capillary interfaces. The formalism captures the sensitivity of hydration to the particular form of the solute-solvent interactions in agreement with recent computer simulations. More recently, as discussed above, Wei, Baker, and Chen have combined the nonpolar free energy functional introduced above with the PB polar solvation free energy functional for a self-consistent description of solvation and biomolecular surfaces (Chen et al., 2011; Chen et al., 2010).

Hybrid models: the best of both worlds?

In a hybrid approach, physical models of different resolutions are used to treat different regions of the molecular system. The region of interest is often modeled with a high level of detail, using techniques such as quantum mechanics or explicit solvent, while the remainder of the system is treated at lower levels of resolution. Such models are intrinsically multiresolution and therefore include a wide range of multiscale simulation methodologies that have been recently developed. This section will focus on a few key hybrid methodologies that are either commonly used or particularly interesting as a complete review of this broad field of multiscale modeling is infeasible.

Quasi-chemical theory

Many solute-solvent interactions, typically short-ranged and structurally specific, can be characterized as chemical associations. Therefore, it is feasible to identify an inner shell around the solute that will accommodate strongly associating solvent molecules, and an outer shell that corresponds to the rest of the system, so that these regions can be treated with high-detail and low-detail models, respectively (Pratt & Laviolette, 1998; Pratt et al., 2001). Quasi-chemical theory provides a framework for such decomposition. The solvation free energy of Li⁺, Na⁺, K⁺, Zn²⁺ and other alkaline divalent metal cations in water have been successfully predicted on the basis of quasi-chemical theory and ab initio molecular dynamics and provided good agreement with experiment (Asthagiri et al., 2004; Rempe et al., 2004). The quasi-chemical method can provide a level of accuracy comparable to that reported in QM, but it is far less expensive than the standard QM/MM method. However, this method still has several limitations, including difficulty treating strongly disordered solvation shells and heterogeneous environments.

Implicit-explicit solvation models

Over the years, a number of generalized reaction field methods have been implemented in molecular simulations based on the continuum Kirkwood expansion (Tironi et al., 1995) with a variety of applications in explicit solvent molecular simulation methodology (Alper & Levy, 1993; Baker et al., 1999; Beglov & Roux, 1994; Brooks, 1985; Brooks, 1987; Hünenberger & Gunsteren, 1998; Lau et al., 1994; Schreiber & Steinhauser, 1992a; Schreiber & Steinhauser, 1992b; Steinbach & Brooks, 1994; Tironi et al., 1995). However, such reaction field methods also have a natural application to hybrid models. One such example is the general solvent boundary potential (GSBP), where a sphere contains an explicit solvent region while reaction influence of the surrounding environment is represented by a continuum model (Im et al., 2001). The generalized solvent boundary model has been applied to the calculation of protein-ligand binding free energy (Banavali et al., 2002; Deng & Roux) and recently extended to QM/MM settings (Schaefer et al., 2005).

Lee et al. developed a hybrid solvation scheme to incorporate a continuum reaction field via GB theory and use a generalized sum-over-spheres boundary, where water molecules are constrained with respect to their closet solute atom location (Lee et al., 2004). The hybrid method was first tested on single ion and protein L simulations; and the results achieved similar equilibrium and dynamical observables as the conventional explicit solvent simulations except with some deviations near the boundaries. The hybrid solvent model combined with Replica Exchange Molecular Dynamics has been used to study the free energy of formation of ion pairs using model peptides. This work suggested that the structure of salt bridge in explicit solvent can be reproduced by the hybrid solvent approach, but not by GB alone (Okur et al., 2006; Okur et al., 2008).

An important long-standing difficulty of mixed resolution solvent models are structural artifacts near the explicit-implicit solvent boundary. A promising approach to solve this challenging problem is the smoothly decoupled particle interface (SDPI) described recently by Wagoner and Pande (Wagoner & Pande, 2011) that introduces a third, buffering shell between an inner region of explicit solvent and an outer continuum solvent. The function of the buffering shell is to transition smoothly the explicit particle density between that of the innermost region to zero at the interface with the outer continuum.

Particle-based continuum models

An interesting particle-based macroscopic solvent model, which represents electronic and oriental polarization of water molecules by an ensemble of polarizable pseudo-particles (PPP) (Basdevant et al., 2004; Basdevant et al., 2006) in a framework that bears some similarity to the polarizable Langevin dipoles of Warshel (Papazyan & Warshel, 1997; Papazyan & Warshel, 1998) has recently been proposed. In this approach, the solute electric field induces dipoles at the centers of the solvent PPPs which, in turn, interact with the solute charge distribution. However, the solvent PPPs only interact with each other through the van der Waals interactions. The theoretical foundation is built upon on Marcus’ functional for solvation free energy (Marcus, 1956). The functional is minimized to the equilibrium condition following the Coulomb field approximation and a localized, off-lattice Langevin dipole approach (Florián & Warshel, 1997) in which the solvent-solvent polarization is ignored.(HaDuong et al., 2002). This novel approach has the potential to bridge the gap between implicit and explicit solvent-based solvent methods. The PPP is computationally more efficient than explicit solvent methods as it produces the macroscopic dielectric response instantaneously. However, unlike implicit solvent methods, it aims to directly capture nonpolar influences via solvent-solute van der Waals interactions without resorting to additional approximations. While this method shows lower computational cost than explicit models and can be extended to coarse-grained solutes (Basdevant et al., 2007; Ha-Duong et al., 2009), the parameterization of the model is complicated, involving empirically scaling the van der Waals radius based on the Born energy of ions and charges of solute atoms to match Kirkwood solvation energy of a spherical cavity.

Outlook and future directions

Despite the underlying assumptions and inconsistencies, researchers are dedicated to develop and refine implicit models to be more accurate. Therefore, further research efforts based on implicit solvent models should continue to focus on modifications to overcome such limitations without significantly reducing the computational efficiencies of these models.

Additionally, there is increasing effort to incorporate explicit polarization into the general classical mechanics in different forms such as point dipole induction and Drude oscillators to improve the electrostatic representation of biomolecules. Adoption of such polarizable potentials in routine studies remains limited, mostly because of concerns about the computational expense. Advances in computing power and efficient simulation algorithms; however, will continue to reveal shortcomings of oversimplified fixed-charge potentials and remind us of the missing physics. Additionally, development of advanced classical electrostatic model beyond simple polarization is ongoing. In addition to polarization effect, the local charge-transfer (CT) and penetration effects are demonstrated to play important role for short-range molecular interactions in water (Kumar et al., 2010), aromatics (Tafipolsky & Engels, 2011) and high-valence ions (Cisneros et al., 2008; Wu et al., 2010). Incorporation of such effects significantly improves the accuracy in modeling the structural and energetic details of these molecular clusters. Empirical, additive terms for CT (Hagberg et al., 2005; Kumar et al., 2010) and penetration effects (Cisneros et al., 2008; Tafipolsky & Engels, 2011) have been shown to be rather effective. Because of their short-range nature, these interactions can be treated with local cutoffs and incur negligible additional computational cost relative to polarizable electrostatics treated with particle-mesh Ewald summation.

Advancements in the electrostatic representation of biomolecules and their solvent environment have led to successful applications including small molecule solvation, pK_as and protein-ligand binding affinity prediction (Jiao et al., 2008; Jiao et al., 2006; Jiao et al., 2009; Ren et al., 2011; Shi et al., 2011; Yang et al., 2011). Computational sampling can however be the next bottleneck in achieving more accurate thermodynamic quantities in complex molecular systems. Advancements in statistical mechanics theories are as important. Although approaches such as free energy perturbation (FEP) (Grossfield et al., 2003; Jorgensen, 1985; Postma et al., 1982; Torrie & Valleau, 1974) and application of Bennett’s acceptance ratio (BAR) (Charles H, 1976; Jiao et al., 2008) may require little additional work beyond what is required for molecular dynamics, methods such as thermodynamic integration, lambda dynamics(Kong & Brooks Iii, 1996), meta-dynamics(Barducci et al., 2011; Laio & Parrinello, 2002) and the orthogonal space random walk (OSRW) strategy are more time-consuming to implement for polarizable atomic multipole descriptions of electrostatics (Zheng et al., 2008; Zheng et al., 2009). Tenable, but nontrivial, complications arise with the latter methods because of their dependency on the derivative of the potential energy with respect to the state variable λ. For example, to the best of our knowledge, a soft-core method to smoothly decouple atomic multipolar interactions with respect to λ has yet to be described. Given the power of metadynamics-based methods to enhance molecular dynamics sampling and reconstruct the free energy surface along a few collective variables (Barducci et al., 2011), there is great motivation for force field experts to work closely with developers of the leading statistical mechanics algorithms in the future.