Abstract
The work presented herein describes system design and performance evaluation of a miniaturized near-infrared fluorescence (NIRF) frequency-domain photon migration (FDPM) system with non-contact excitation and homodyne detection capability for small animal fluorescence tomography. The FDPM system was developed specifically for incorporation into a Siemens microPET/CT commercial scanner for hybrid small animal imaging, but could be adapted to other systems. Operating at 100 MHz, the system noise was minimized and the associated amplitude and phase errors were characterized to be ±0.7% and ±0.3°, respectively. To demonstrate the tomographic ability, a commercial mouse-shaped phantom with 50 μM IRDye800CW and 68Ga containing inclusion was used to associate PET and NIRF tomography. 3-D mesh generation and anatomical referencing was accomplished through CT. A simplified spherical harmonics approximation (SP3) algorithm, for efficient prediction of light propagation in small animals, was tailored to incorporate FDPM approach. Finally, PET-NIRF target co-localization accuracy was analyzed in vivo with a dual-labeled imaging agent targeting orthotopic growth of human prostate cancer. The results obtained validate the integration of time-dependent fluorescence tomography system within a commercial microPET/CT scanner for multimodality small animal imaging.
1. Introduction
Hybrid tomography systems that provide anatomical information through computed tomography (CT) or magnetic resonance (MR) and molecular biochemical information through positron emission tomography (PET) or single-photon emission computed tomography (SPECT) can accelerate pre-clinical discovery by offering features of quantitative imaging and by enabling direct translation of discoveries via clinical imaging systems. As bioanalytical techniques have migrated from assays using radionuclides to assays employing fluorescence and bioluminescence, small animal imaging systems have likewise begun to transition from planar to tomographic fluorescence (for review see Leblond, et. al, 2010) and bioluminescence techniques (Contag, et. al, 2002, Wang, et. al, 2006). In addition, planar near-infrared fluorescence (NIRF) has been successfully translated into humans using microdoses of contrast agent (Sevick-Muraca, et. al, 2008).
Recent work in pre-clinical imaging increasingly incorporates optical imaging with other complementary techniques including combinations such as bioluminescence-PET imaging (Prout, et. al, 2004), fluorescence-CT (Grimm, et. al, 2005), fluorescence-MRI imaging (Stuker, et. al, 2011), and bioluminescence-diffuse optical tomography (DOT)-CT (Yan et. al, 2012) for acquiring and interpreting meaningful functional images. While fluorescence, bioluminescence, and nuclear imaging techniques provide excellent molecular sensitivity, CT and MRI provide high resolution and accurate anatomical referencing along with surface boundary delineation. However for time-independent fluorescence and bioluminescence techniques, heterogeneous optical properties associated with different tissue structures and organs can attenuate light, confounding image reconstruction. Schulz et. al, in 2010, have shown that in vivo fluorescence reconstruction can be improved upon incorporating segmented CT images as a priori information for use in optical reconstruction algorithms. Barber et. al, in 2010, have taken a step further by utilizing structural a priori information in the form of CT derived anatomical map along with functional a priori information using scattering and absorption coefficients estimated from DOT to further enhance the imaging performance. This work was recently demonstrated in vivo (Lin et. al, 2010); and extended to bioluminescence in phantoms (Yan et. al, 2012). Although CT and MRI may provide complementary anatomical tissue information, neither offers contrast that is dependent directly on tissue optical properties that impacts optical imaging.
Nuclear, bioluminescence, and fluorescence techniques provide functional information arising from probes with different emission energies. Li et. al, 2011, recently demonstrated simultaneous PET-fluorescence imaging using a conical shaped mirror placed within the PET scanner to generate separate 18FDG-PET scans and IRDye800-DG 3D fluorescence tomographs from an animal in a rotation-free gantry implementation. Interferometry provided surface information for fluorescence image reconstruction and although not identical, the two scans employing different modalities and different imaging agents with varied pharmacokinetics showed some similarities. Using phantoms, Cao et. al, 2010, utilized SPECT priors for suppressing reconstruction related artifacts and for achieving quicker solution to the fluorescence inverse imaging problem. It is notable that improvements were made by integrating non-contact fluorescence and gamma collection within the same rotating gantry capable of projections over 360°. Instrumentation for different imaging techniques such as CT, PET, SPECT, and NIRF can be efficiently designed and operated to work as stand-alone modalities. Suitable co-registration approaches, such as use of fiducial markers, must be used to perfectly co-register the data acquired from all modalities. However, combining these distinct modalities into a single gantry-based system offers advantages such as (i) optimizing cost by housing multiple electronics together and reduced instrumentation space, (ii) enabling a one-time calibration to generate transformation matrix that allows precise and repeatable data co-registration between different modalities, and (iii) automating and speeding-up entire imaging session by minimizing the time associated with animal handling. The reduced footprints of optical devices, such as diodes, photomultiplier tubes (PMTs), avalanche photodiodes (APDs), and fiber couplers permit integration of hybrid modalities within the gantries of conventional small animal scanners.
Despite the progress in the area, the validation of quantitative fluorescence tomography results against the conventional PET or SPECT standard uptake value (SUV) units remains to be conducted. Current validation limitations include: (i) the continuing need for dual-labeled agents for direct correlation of quantitative nuclear and fluorescence imaging modalities (for review see Azhdarinia, et. al, 2012), (ii) the confounding effects of heterogeneous tissue optical properties on intensity-based or continuous wave (CW) measurements, and (iii) the space limitations of the bulky components necessary for time-dependent measurement techniques such as time-domain photon migration (TDPM), based on pulsed laser excitation, or frequency-domain photon migration (FDPM) techniques, based on intensity modulated excitation. Although PMTs and APDs can provide a small footprint for fluorescence detection, they lack the integrating capacity of the bulkier intensified charge-coupled devices (ICCD). TDPM and FDPM techniques may be less sensitive to heterogeneous optical properties (Sahu, et. al, 2005) because of the added contrast provided by the fluorescence lifetime of a fluorophore (Sevick-Muraca, et. al, 1997, Li, et. al, 1998). TDPM approaches require time consuming single photon counting, thus FDPM approaches may be best suited for rapid quantitative tomography. Yet the large equipment footprint associated with FDPM methods has been largely prohibitive for direct integration into the gantries of conventional imaging modalities.
Herein, we report the development of a new design and miniaturized FDPM fluorescence tomography system for incorporation into a commercial small animal microPET/CT scanner. The incorporation of the optical system within the scanner enables (i) automated and controlled animal bed movement prompting quicker image acquisitions and data co-registration between the three modalities, (ii) use of CT to define volumetric meshes for fluorescence tomographic image reconstruction, and most importantly, (iii) comparison of the reconstructed values of fluorescent probe absorption with %ID/gm of radio-labeled agents for future validation of quantitative imaging. The FDPM tomography system uses a contact-free excitation source and a gain-modulated, NIR-sensitive ICCD camera for homodyne detection of fluorescent phase and amplitude. Section 2 describes development of FDPM system, data acquisition parameters, integration of the optical instrumentation into the CT gantry, and generation of transformation matrix for repeatable mapping of optical signals onto CT derived volume. Section 3 describes strategy for modifying CW-based reconstruction algorithm for FDPM tomography, and selection of optimal acquisition parameters as they relate to evaluating measurement precision for the system and target reconstruction accuracy. Section 4 compares tomographic reconstructions made from two sets of phantom measurements: (i) within the stationary benchtop configuration, and (ii) within the gantry where FDPM instrumentation was mounted on a rotating microCT gantry. In addition, target co-localization using PET and optical tomographies has also been demonstrated for phantom and preliminary in vivo study. Finally, in Section 5, we discuss and conclude the outcomes from this study.
2. FDPM hardware design and system implementation
2.1. Components of the NIRF planar imaging system
Figure 1 shows the primary components of the NIRF imaging system commonly used for CW planar (within the dashed box) and FDPM measurements (within the solid box). The CW components of the system have been validated and implemented in pre-clinical murine (Kwon, et. al, 2007) imaging as well as clinical studies for planar NIRF imaging of human lymphatics (Rasmussen, et. al, 2009). Excitation light is provided by a 500 mW 785 nm laser diode (1005-9MM-78503, Intense Inc., North Brunswick, NJ), a laser diode mount, diode driver, and temperature controller (TCLDM9, LDC205, and TED200 respectively, Thorlabs, Newton, NJ). An aspheric lens (C240TME-B, Thorlabs, Newton, NJ) is used to collimate the laser beam and a 785±10 nm bandpass filter (LD01-785/10-12.5, Semrock Inc., Rochester, NY) reduces light emanating from the “side-band” wavelengths and thus minimizes the background noise from backscattered light.
Figure 1.
Schematic of experimental setup used for planar NIRF imaging (within the dashed box) and additional circuitry required for FDPM (within the solid box).
The resultant fluorescence signal emanating from the animal is collected by a NIR-sensitive Gen III image intensifier (FS9910C, ITT EXELIS, Roanoke, VA) optically coupled to a customized 16-bit, frame-transfer CCD camera (Princeton Instruments, Trenton, NJ) with a 1024 x 1024 pixel area. The CCD camera was repackaged into a smaller unit for integration into the gantry reducing the original camera size from 12 lbs and ~2040 cm3 to 2 lbs and ~820 cm3. For CW measurements, a high voltage power supply (PS20060500, GBS Micro Power Supply, San Jose, CA) provides the intensifier photocathode with a maximum DC control voltage of −250 V, the multichannel plate (MCP) with a variable gain between 0–1000 V (referred henceforth as the intensifier gain), and the output phosphor screen with 4000 V. A 28 mm wide angle lens (Nikkor f2.8D AF, Nikon) attached to the front-end of the detector assembly allows collection of the focused image. Additionally, suitable 830 nm bandpass filter (10±2 nm bandwidth and optical density (OD) > 5 outside the passing band) combinations were used to efficiently collect the weak emission signals while reducing the excitation light leakage and thus improving the image quality.
2.2. RF components of FDPM system
The components within the solid box shown in Figure 1 represent the radiofrequency (rf) circuitry required for frequency-domain measurements. Unlike the past work which used two phase-locked rf oscillators (Godavarty, et. al, 2003), this FDPM system utilized a single-frequency, 100 MHz rf oscillator (PL0X100-10, Luff Research, Floral Park, NY) and a two-way power splitter (ZX-10-2-12, Mini-Circuits, Brooklyn, NY) for simultaneous modulation of the laser diode and demodulation of the detected signal at the intensifier photocathode. This homodyne configuration produced a steady-state image at the intensifier phosphor screen that was efficiently captured through integration of the CCD array to maximize the signal-to-noise ratio (SNR). Laser modulation was accomplished using a bias tee to superimpose the rf signal from the power-splitter onto the laser diode DC bias. The DC bias and the rf signal strength were chosen so as to maximize the source modulation depth (AC/DC) in order to enhance SNR and hence improve the measurement precision. The desired power level of +22 dBm to the laser diode was achieved by amplifying the rf output from the power-splitter using a 5 W rf amplifier (ZHL-03-5WF, Mini-Circuits, Brooklyn, NY).
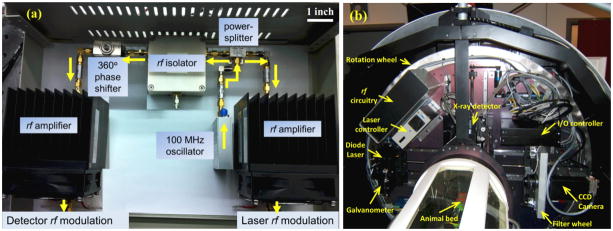
An analog phase-shifter (9520-37, Emhiser Tele-Tech Inc., Belgrade, MT) was used to introduce a series of phase-delays from 0° to 360° to the rf signal modulating the image intensifier with respect to the laser diode signal. The non-linear behavior of the phase-shifter in response to the control voltage was calibrated using a network analyzer and then programmed into LabVIEW (National Instruments, Austin, TX) to control the phase-delay. To prevent temporary noise to laser diode control, a unidirectional rf circulator (RFLC-HXD-7A, RF-Lambda Inc., Plano, TX) was used to isolate any reflected rf signals due to impedance mismatch from feeding back to the laser diode. Coaxial attenuators (VAT-X+, Mini-Circuits, Brooklyn, NY) were placed between different circuit components to dissipate excess rf power and ensure that the required power levels were delivered to the devices. The output from the phase-shifter (+6 dBm) was amplified to +40 dBm using a 20 W rf amplifier (ZHL-20W-13, Mini-Circuits, Brooklyn, NY). This rf signal was superimposed onto −36 V DC bias of intensifier photocathode via custom biasing circuit. Figure 2(a) shows a photograph of the assembled rf components within a 14 inch x 10 inch x 5 inch rectangular box designed for mounting into the CT gantry. Because of the potential for variable rf interference in the rotating CT gantry, the system and resulting imaging performance were tested in a stationary configuration on the benchtop prior to incorporation into the CT scanner.
Figure 2.
(a) A photograph of actual implementation of the rf circuitry components for FDPM as represented in Figure 1. Arrows indicate the flow of the rf signal. (b) Photograph shows the rf circuitry from Figure 2(a) mounted within the Siemens Inveon CT scanner along with the rest of the NIRF imaging instrumentation (dotted box from Figure 1). Additional electronics such as galvanometer (for laser scanning), instrumentation controllers, filter wheel (for switching between white-light and emission wavelength), and CT detector are also seen.
2.3. Integration of NIRF FDPM system within the gantry
Inveon CT scanner (Siemens, Knoxville, TN, USA) is designed to house CT instrumentation and an optional SPECT device on a single rotation wheel which rotates around the horizontally placed animal bed. To integrate FDPM-based NIRF imager with the scanner, the required optical and electronic components illustrated in Figure 1 were mounted in the space originally reserved for the SPECT instrumentation, although additional engineering could conceivably enable SPECT, NIR, and CT components within the same gantry. An automated filter wheel placed before the ICCD detector selects the appropriate filters: 830 nm bandpass filter assembly for fluorescence imaging and a neutral density filter (OD = 7) for white light imaging. The ICCD camera was mounted on a motorized linear stage for translation in the radial direction allowing control over the camera field of view (FOV) without having to exchange the optical components. A compact, combinational controller (ITC133, Thorlabs, Newton, NJ) was used to provide the laser DC bias and to maintain the diode temperature. A dual-axis galvanometer (MicroMax 673 Series, Cambridge Technology, Lexington, MA) mounted near the laser mount scanned the modulated excitation point source across the phantom surface. Multifunction data acquisition interfaces (USB-6009, USB-6216, National Instruments, Austin, TX) provided external control and monitoring of the FDPM instruments via a USB cable mounted in the CT cable carrier. The FDPM control computer was also interfaced to the Inveon system thus allowing an integrated workflow for CT and FDPM modalities. Figure 2(b) shows a photograph of the rotation wheel and the FDPM instrumentation installed inside the CT gantry. When docked to the CT scanner, the dedicated PET scanner (Siemens, Knoxville, TN, USA) enables sequential CT, FDPM, and PET measurements by automated translation of the animal bed between the dedicated CT and PET gantries.
2.4. Mapping of FDPM and CT measurements
To enable image reconstruction, the algorithm utilizes a 3-D CT-defined volumetric mesh as tomographic input in addition to the multiple 2-D projections of the acquired emission signal, and precise mapping of excitation light distribution onto the 3-D tissue surface. For benchtop FDPM measurements, a mouse-shaped phantom (described in section 3.3.1 below) was independently scanned using the microCT to gather volumetric information as well as to precisely determine the location of the fluorescent target within the phantom. A tetrahedron-based volumetric mesh was then generated using the Amira 5.0 software (Mercury Computer Systems Inc., Chelmsford, MA). The mesh comprised of 25,000 discrete points and 116,725 elements. In order to map the 2-D FDPM projection images onto the 3-D CT-derived surface, a white-light image of the phantom using the same FOV as NIRF image was first recorded prior to the fluorescence measurements. The white-light image was then manually co-registered with the generated mesh. In order to determine the surface distribution of the excitation light, a sheet of paper was placed at the same location as the phantom and the incident light image on the paper was used to estimate the excitation location for registration with the 3-D surface.
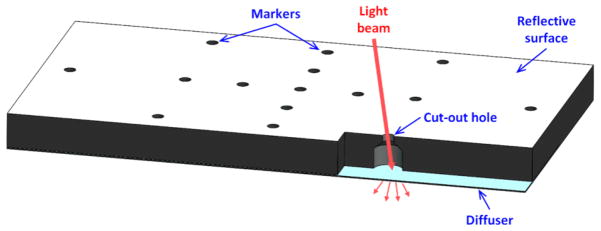
For FDPM measurements conducted within the gantry, a transformation matrix was generated to map the 2-D FDPM measurements onto the 3-D surface. CT scan (voxel size: cube of 0.11 mm) and 2-D optical images (512 x 512 pixels) with different FOVs (pixel sizes: squares of 0.2 – 0.34 mm length) were acquired for a customized phantom made of black plastic (75 x 32 x 5 mm) with a white (highly reflective) top surface, and 25 drilled holes. Figure 3 shows phantom schematic with only a few hole openings illustrated for brevity. The 0.6 mm diameter openings of the holes on the reflective surface act as fiducial markers for both CT and optical. The contrast between air and plastic allowed easy identification of the openings in the 3-D CT image. The reflective surface and the black plastic exposed through the holes created high contrast and allowed easy identification of the openings in 2-D optical images. The coordinate data of the markers on the reflective surface was manually measured from CT and 2-D optical imaging. By tracing the coordinate data of the markers in the 2-D images for different FOVs, the distance in the radial direction between the center of the gantry and the optical camera was estimated (150 – 260 mm) with an accuracy of 1.1 mm standard deviation (STD). This allowed the estimation of the position of the optical camera relative to the CT FOV and the focal length and detector size for the camera. By matching the coordinate data of all the openings in both modalities, the transformation matrix was created by calculating the location and orientation of the camera relative to the CT gantry coordination system with an estimated error of 1 pixel (STD) on CCD. The transformation matrix allows accurate mapping of the 2-D fluorescence intensity distribution from CCD camera onto the 3-D volumetric mesh obtained from the CT scan. In addition, to register placement of incident excitation light on the phantom surface via the scanning galvanometer, optical data was acquired to correlate the galvanometer position with the alignment of the collimated laser beam through the openings. Upon matching the parameters of galvanometer with the 3-D coordinate data of the holes, a formula for tracing the exact ray position for the excitation light distribution on the 3-D surface was obtained.
Figure 3.
Schematic of the customized phantom used for generating transformation matrix between CT and 2-D FDPM images within the gantry.
The protocol associated with PET-CT image co-registration involved sequential CT and PET scanning of a standard cylindrical phantom with four embedded point-sources (Na-22). The offset and orientation for the acquired PET images were then manually adjusted in order to align them with the CT images. ASIPro (CTI Concorde Microsystems) software was used for this purpose and the matching was accomplished with a translation resolution of 0.1 mm and rotational resolution of 0.1°.
2.5. Acquisition of FDPM parameters
In order to record the time-dependency, N phase-delays over a complete cycle of 0° to 360° were imposed on the rf signal driving the intensifier as described previously by Thompson, et. al, 2003. For each phase-delay, a steady-state image at the intensifier phosphor screen was captured by the CCD array. To account for the ambient, readout, and dark current noise, a baseline image was acquired, by turning off the excitation light, and subtracted from all subsequent phase-sensitive images. The modulation amplitude (IAC) and phase (θ) were then calculated by performing fast Fourier transform (FFT) on the FDPM measurements (Thompson et. al, 2003).
3. Experimental Setup
3.1. Theory for tomographic reconstruction
Owing to the imprecision of the diffusion equation to predict light propagation for certain cases (Lu et. al, 2010, Gibson et. al, 2005), we developed a linear tomographic reconstruction algorithm based upon simplified spherical harmonics (SP3) approximation to the radiative transfer equation (RTE) for CW-based fluorescence tomography (Lu, et. al, 2011). In this work, we further extend this reconstruction methodology for application to FDPM measurements. Readers are referred to the supplementary section S1 of this paper for a brief discussion highlighting the changes for adaptation to FDPM tomography. It should be noted that we do not use regularization term for the reconstruction approach. For the animal study, the uniform optical properties of the live mouse were assumed to be 0.057 mm−1 (absorption coefficient, μa) and 8.50 mm−1 (scattering coefficient, μs) at both excitation and emission wavelengths as derived by Vo-Dinh et. al, 2004. As described below, deviations from these values created little or no difference in the reconstructed values.
3.2. Assessing FDPM measurement precision
Since the accuracy of tomographic reconstructions depends critically on quality of the input data it is necessary to benchmark the precision of the FDPM system by evaluating and reducing the errors associated with the measurement of IAC and θ. A procedure similar to that described by Thompson et. al, 2003 was adopted to assess the measurement errors. Readers are referred to the supplementary section S2 for details. Since intensifier gain impacts the measurement noise, IAC and θ precision were first determined over a range of gains by appropriately varying the lens aperture and CCD integration times so as to maintain constant photon counts. The optimal intensifier gain was identified as the highest gain that did not result in significant loss of IAC and θ precision. This gain was then held constant for all the subsequent measurements. The acquisition parameters that provided the least IAC and θ errors with the shortest acquisition times were considered optimal and their impact on accuracy of target reconstruction was then assessed.
3.3. Assessing reconstruction accuracy through phantom measurements
3.3.1 Benchtop setup
The time-dependent setup (as shown in Figure 1) developed for this study makes use of a combination of low and high power rf signals driving the optical instrumentation. The issue of this rf signal interfering with other electronics coupled with the changing environment in the rotating scanner could therefore impact reconstruction accuracy and measurement precision. Thus, we first constructed and assessed the system performance in a stationary benchtop environment. A benchtop replica of the gantry-installed devices was created with the ICCD and laser diode in transillumination geometry and the phantom placed directly in the line between them at a distance of 10 inches from the laser. The laser diode and the ICCD were separated by 17 inches and corresponded to their installed positions within the CT gantry. Instead of rotating the laser and ICCD, as would be the case within the gantry, the phantom was positioned vertically on a rotational stage to obtain image projections while the laser and ICCD remain fixed in space. A mouse-shaped phantom (XFM-2 Fluorescent Phantom, Caliper Life Sciences, Hopkinton, MA) with realistic and relevant complex geometry was selected to mimic emission signals emanating from the non-planar tissue surfaces. As provided by the manufacturer, at excitation (785 nm) and emission wavelengths (830 nm) μa for this homogeneous phantom are 0.0066 mm−1 and 0.0077 mm−1, respectively, while μs are 9.5 mm−1 and 7.4 mm−1, respectively. The excitation beam was collimated to obtain a point source with an approximate diameter of 1 mm using an aspheric lens. A polyethylene tube, 2.5 mm in length and 1 mm diameter, was then filled with 50 μM IRDye800CW (LI-COR Biosciences, Lincoln, NE) and sealed. This fluorescent target was then inserted into a pre-drilled hole inside the phantom. For testing we selected two projections on the ventral side of the phantom with each projection comprising of unique excitation beam position. For each projection, images were acquired by varying the phase on the rf signal to the intensifier over 0–360° in N (N = 16, 32, 64, 128) steps. This procedure was then repeated five times to improve information reliability through data averaging.
3.3.2 Gantry setup
For data acquisition inside the gantry, the phantom/mouse was suspended on a customized bed consisting of thin wires and rods, to evenly support the object being imaged. This setup allowed unimpeded passage of excitation light to the phantom and collection of emission signals from its surface over several projection angles. The modified animal bed was compatible with all the three imaging modalities. The flowchart in Figure 4 gives an overview of the general protocol followed for carrying out FDPM-based measurements within the gantry. To account for the implicit phase-delay associated with the involved instrumentation, homodyne detection was first conducted at the excitation wavelength without the intervening phantom. This baseline phase-delay in each projection was then subtracted from the delay computed from the actual emission signals at the corresponding projections. After baseline phase-delay measurements, the phantom was moved into the CT FOV for imaging. Next, for a stationary bed position, 2-D FDPM projections of the emission photon distribution were collected at different projection angles. The transformation matrix, as described above, was used for mapping the 2-D optical images onto the surface of the phantom. Two projections targeting the ventral side of the phantom, similar to the two projections acquired in the benchtop implementation, were repeated in the gantry setting with each projection comprising of a single point excitation source. This experiment sought to verify whether the optical system was able to replicate the tomographic reconstructions from the benchtop setup to within the gantry. In addition, reconstruction with four projections spaced out over a gantry rotation of 360° (0°, 180°, +45°, and −45°) were also carried out to ascertain the effect of increased projections on tomography.
Figure 4.
Flowchart depicting the overall protocol for hybrid imaging of PET/CT and NIRF tomography using FDPM approach.
Evaluation of target co-localization accuracy between PET and fluorescence tomography was implemented by loading the phantom inclusion with 50 μM IRDye800CW dye and 8 μCi 68Ga. The phantom was then placed on the animal bed and sequentially imaged inside the CT/optical gantry followed by automated translation of the bed to the docked PET system for acquisition of the nuclear signal.
3.4. In vivo imaging
As part of preliminary in vivo animal studies, a primary prostate tumor mouse model injected with dual-labeled targeting agent was imaged. 106 PC3 cells from human prostate cancer cell line were orthotopically implanted into a nu/nu mouse (Charles River, Wilmington, MA). For this study, epithelial cell adhesion molecule (EpCAM) that is often over-expressed in most human cancers was chosen as a molecularly specific target. A dual-labeled PET-NIRF imaging agent was generated by conjugating EpCAM specific antibody (anti-EpCAM) to NODAGA with a chelator ratio of 1.1, and IRDye800 with a ratio of 2.1 per antibody and then later radiolabeled with a nuclear agent 64Cu to obtain (64Cu- NODAGA)1.1 – anti-EpCAM – (IRDye800)2.1. Detailed information regarding synthesis of the imaging agent can be found in Hall et. al, 2012. 173 μCi 64Cu and 40 μg antibody in 170 μL solution was then intravenously injected into the mouse 11 weeks post implantation. CT-NIRF-PET imaging was then sequentially conducted 24 hours post administration. Similar to the phantom measurements explained earlier, we used four projections (0°, 45°, 180°, and −45°) for in vivo NIRF imaging with each projection comprising of a single point excitation source.
4. Results
4.1. FDPM measurement precision
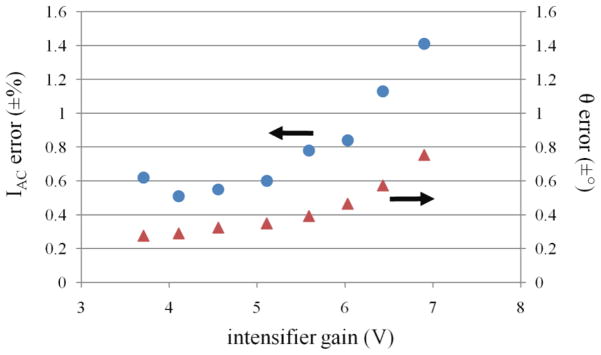
Figure 5 depicts the calculated errors for IAC and θ plotted as a function of the intensifier gain. To minimize the errors, it was imperative to operate the intensifier at the lowest gain settings. However, because lower intensifier gain reduces phosphor intensity and SNR, CCD integration times must be increased to compensate. Increasing CCD integration times however results in increased total data acquisition times. Therefore, we sought a balance between increased CCD integration times and intensifier gain setting. Based on our results in Figure 5, we selected the maximum gain setting of 5.5 V which did not result in significant increase in IAC and θ errors.
Figure 5.
IAC errors represented by ‘●’ markers and θ errors indicated by ‘▲’ markers are plotted as a function of the intensifier gain.
With the intensifier gain held constant the IAC and θ errors were then analyzed using different N and CCD integration times and the results are documented in supplementary section, Table S1. Data shows that upon increasing N, the IAC and θ errors reduce proportionally. In addition, measurements showed that measurement precision was positively affected by capturing more photons (refer supplementary section, Figure S1) implying that a higher SNR considerably reduces the measurement errors. This can be achieved by increasing the CCD integration times at the expense of longer animal imaging times. The result suggests that it may be necessary in the future to implement an algorithm that automatically identifies and discriminates measurements with lower SNR from the input to the tomographic reconstruction so as to obtain a faithful reconstruction with minimal false representation of the fluorescent target (i.e. artifacts). The IAC and θ errors for our system were minimized to ±0.7% and ±0.3°, respectively, for CCD integration time of 800 ms using N = 128. The precision described herein is comparable to the earlier work carried out by Thompson, et. al, 2003, using a previous system prototype. We also found that since we used ICCD-based detection, the system noise will always be limited by the fundamental photon generated noise (refer supplementary section, Figure S2).
4.2. Reconstruction accuracy with phantom measurements
4.2.1 Benchtop results
Based on the measurements of precision, we selected the following conditions for optimal image acquisition: 200 – 1200 ms CCD integration times, bin factor of 4 (256 x 256 pixel area), N = 128, and intensifier gain of 5.5 V. An excitation beam collimated to an approximate diameter of 1 mm was incident on the mouse-shaped phantom at two different locations on its ventral side, as shown in Figures 6(a, b), and emission signal was then collected from the dorsal side of the phantom. In keeping with the view on the importance of phase for reconstructions, experiments were conducted to study the effect of using variable N to extract the target phase information and study its impact on the quality of reconstructions.
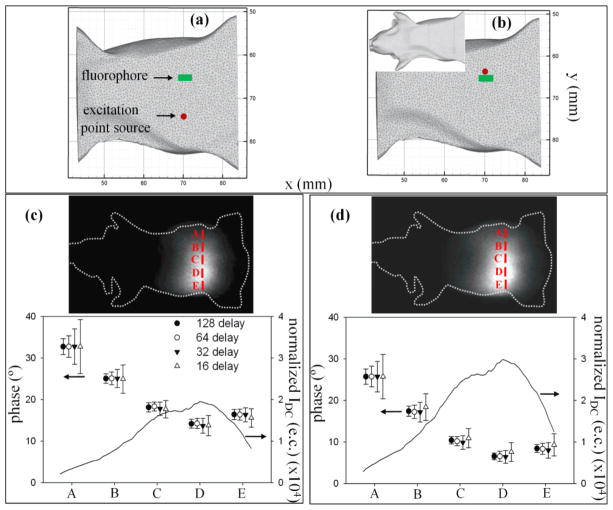
Figure 6.
Phantom measurements with benchtop setting. Figures (a) and (b) indicate the position of the excitation point source (red colored circle) at positions 1 and 2, respectively, on ventral side of the mesh-generated mouse-shaped phantom. The fluorophore location (green colored rectangle) is also shown. Inset to (b) shows the phantom orientation. Images of the emission signal collected from the dorsal side of the phantom can be observed in (c) and (d) along with the plots for normalized IDC, and STD in phase (θ) for different N (16, 32, 64, 128), corresponding to the source locations 1 and 2, respectively. The profiles are plotted along the line A-E that passes through the peak emission photon distribution.
Figures 6(c) and (d) show the 2D images of the emission signal collected from the dorsal surface of the phantom in response to excitation locations (i.e. positions 1 and 2 shown in Figures 6 (a) and (b), respectively) on its ventral side. Furthermore, data subsets with N = 64, 32, and 16 were chosen through down-sampling of the data acquired with N = 128 delays. After computing FFT on the phase-delayed images, the absolute θ and its STD were calculated over five sets for different N. For illustration purposes, the phase was computed at five locations (A-E) along the peak of the emission photon distribution on the mouse surface. The varying phase information measured with FDPM, as shown in Figures 6(c) and (d), over the selected region of interest (ROI) were then used along with IAC to accurately localize the fluorophore position. The IDC (units: excitation counts (e.c.)) profile, normalized with respect to the CCD integration times, is also plotted over the same ROI and shows good correlation between reduced STD in θ and increased IDC, thus suggesting that the higher photon counts aptly reduce the phase noise. Furthermore, one can also observe that N = 128, and 64 exhibit the lowest STD in θ and upon further reducing N to 32 and 16, the phase error deteriorates further. A higher photon count is visible for position 2 (Figure 6(d)) compared to position 1 (Figure 6(c)) because of the proximity of the incident excitation beam to the fluorophore location.
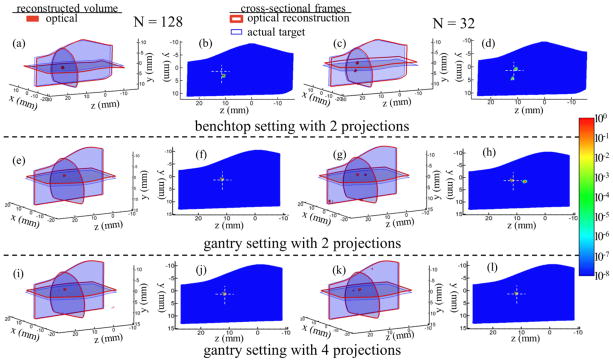
Figure 7 shows reconstructions carried out using SP3-based algorithm for the mouse-shaped phantom after sampling the data with different N and under different settings. For brevity, Figure 7 highlights only two scenarios: N = 128 (left two columns) and N = 32 (right two columns). The 3D views highlight the fluorophore localization within the reconstructed volume while the 2D slices, plotted using logarithmic scale along the phantom sagittal plane, indicate the fluorophore distribution and artifacts generated within the reconstructed volume. Figure 7 (row 1) shows reconstructions with benchtop setting. It can be observed that when compared to N = 32 (Figures (c, d)), reconstructions using data with N = 128 (Figures (a, b)) provide high measurement precision ensuring better localization accuracy along with artifact free reconstruction within the generated volume. All results presented here have a set threshold for neglecting artifacts below 20% of the maximal reconstructed value. Artifacts that occur on the surface of the reconstructed volume are not considered on the basis of their surface location. Table 1 compares the root-mean-square (rms) errors between the actual and reconstructed fluorophore locations for different N. It also lists the peak value for artifacts present within the reconstructed volume as compared to the maximum value on the reconstructed fluorophore. From the results, it is evident that benchtop configuration with N = 64 dataset yields consistent accuracy similar to N = 128, however, with additional reconstruction artifacts. In the case of reconstruction with N = 64, the peak value on the artifact accounts to 37% of the maximum value on the reconstructed target and increases considerably to 64% for N = 32. As seen from Table 1, upon further reducing N, the artifacts increase proportionally in addition to reduced localization accuracy for the reconstructed target. Finally, when the benchtop data with N = 16 subset was used for tomography, the target position could not be ascertained suggesting poor measurement precision (data not included here).
Figure 7.
Tomographic reconstructions using: (1) benchtop system (1st row, Figures a–d), and gantry installed system with (2) 2-projections (2nd row, Figures e–h) and (3) 4-projections (3rd row, Figures i–l). For brevity, reconstructions with only N = 128 and N = 32 are included. The 3D figures highlight the fluorophore localization within the reconstructed volume. Target localization errors are represented by the cross sectional frames with thin (blue color) and thick (red color) boundaries for 3D figures indicating the center position of the actual (CT derived) and optically reconstructed target, respectively. The volumetric mesh denotes the top 80% of the contour levels for the reconstructed fluorophore distribution. 2D slices show logarithmic intensity maps of the fluorophore along with the artifacts generated internal to the reconstructed volume. The cross-hairs on the 2D plots indicate the actual position of the fluorophore.
Table 1.
Target localization accuracy and generated artifacts for FDPM-based system.
| Number of phase-delays N (−) | Benchtop | Gantry-two projections | Gantry-four projections | |
|---|---|---|---|---|
| 128 | 2.38 | 1.41 | 1.41 | rms error (mm) |
|
| ||||
| 0 | 0 | 0 | artifacts (%) | |
| 64 | 2.38 | 1.41 | 1.41 | rms error (mm) |
|
| ||||
| 37 | 28 | 0 | artifacts (%) | |
| 32 | 2.65 | 1.38 | 1.39 | rms error (mm) |
|
| ||||
| 64 | 36 | 0 | artifacts (%) | |
4.2.2 Gantry results
After incorporating the new FDPM system into the rotating gantry it was critical to track its performance by comparing it to the stationary benchtop environment in order to ensure that the instrument performance did not deteriorate with gantry rotation. The phantom experiment previously conducted on the benchtop was hence repeated within the CT gantry (Figure 7, row 2). Translation from benchtop (row 1) to gantry (row 2) showed improved reconstruction accuracy (see also Table 1) since the instrumentation within the gantry was rigidly fixed and the source-detector locations could be precisely determined along with improved surface mapping. Upon implementing better control over the physical setup and improved CT-NIRF co-registration, the quality of reconstruction from the benchtop setup could be improved. To characterize the performance of the new instrument design and to ensure that the rf instrument performance did not deteriorate after integrating it within the gantry, the benchtop assessment was conducted. Tomography performed within the gantry with four angular projections (row 3) show equivalent reconstruction accuracy to the case with two projections in addition to no artifacts within the generated volume even upon using data subset with reduced N.
The results from Figure 7 show that by optimizing the number of projections used for data acquisition and the value of N set for each projection, we can improve the reconstruction quality without significantly compromising on the image acquisition times. The optimal settings need to be further assessed depending on performance criteria, number of targets to be resolved, target to background ratios, etc. Nonetheless, taking parameters such as total data acquisition time, reconstruction accuracy, and artifacts into consideration, N = 32 phase-delays and 4 angular projections seems an adequate choice for in vivo testing of small animals.
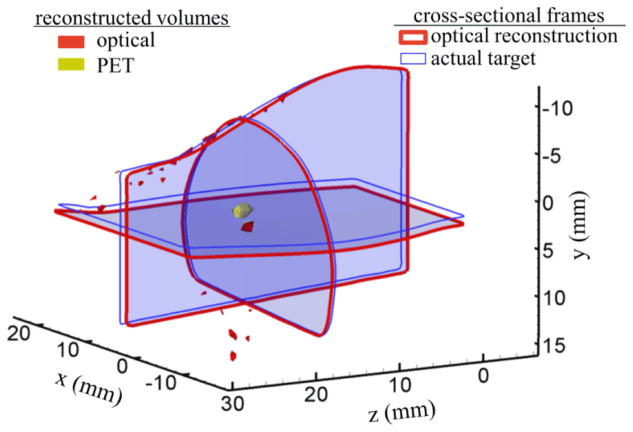
In subsequent studies using the optimal experimental parameters previously selected, we compared PET and NIRF tomography by repeating the PET/NIRF/CT measurements three times to assess reproducibility. The optical signal threshold was set to top 80% of its maximum reconstructed value while the PET was thresholded such that the nuclear signal stays confined to the tube (as determined from CT). Supplemental section S3 presents tomographic images at varying threshold limits. Figure 8 shows the reconstructed volumes from both modalities. For each case the co-localization errors were calculated by determining the rms offset between the reconstructed volumes from each modality. The mean co-localization error between the PET and optical modalities was calculated to be 1.51± 0.13 mm.
Figure 8.
Assessment of tomographic co-localization accuracy using a nuclear (68Ga) and optical (IRDye800CW) agent placed within the homogenous mouse-shaped phantom. Target localization errors are represented by the cross sectional frames with thin (blue color) and thick (red color) boundaries indicating the center positions of the actual (CT derived) and optically reconstructed target, respectively. The reconstructed target volumes from PET (yellow) and optical (red) modalities are also included.
4.3. In vivo imaging
A preliminary study with prostate tumor-bearing mouse model injected with dual-labeled targeting agent was also conducted. Figure 9 shows the optical signal reconstructed near mouse prostate region and its co-localization with PET signal. The co-localization error between PET and NIRF in this case was computed to be 2.15 mm. Because only the pelvic region was imaged in the NIRF scan, Figure 9 shows only those regions with hybrid imaging information. NIRF imaging was unaffected by variation of assigned endogenous properties within the range reported by Vo-Dinh (data not shown for brevity). Although artifacts can be observed on the surface of the mouse, there are no artifacts present within the reconstructed volume. The in vivo co-localization result demonstrates the ability to take into account inherent optical heterogeneity associated with biological models for precise reconstruction of primary tumors located deep within the small animal volume.
Figure 9.
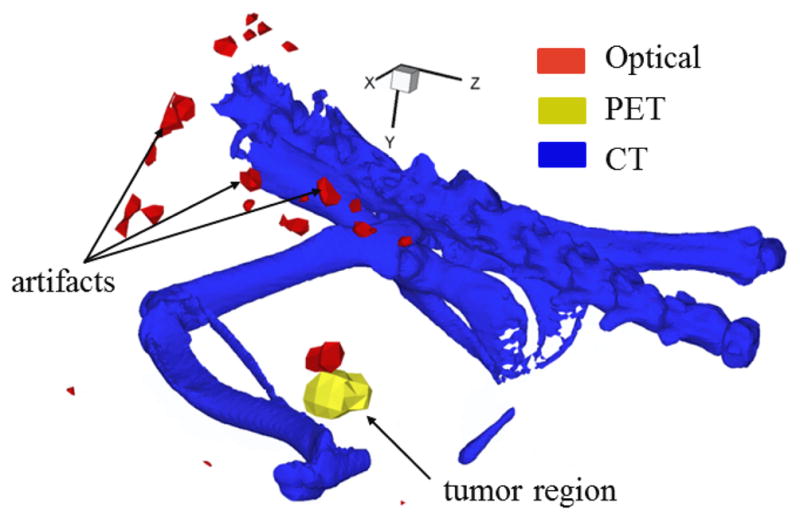
Tomographic PET-optical co-localization accuracy demonstrated in a tumor-bearing mouse model. The figure shows co-localization of primary prostate tumor using a dual-labeled ((64Cu-NODAGA)1.1 – anti-EpCAM – (IRDye800)2.1) agent conjugated to antibody. Artifacts generated from optical tomography can be seen on the animal surface.
5. Discussion
Animal studies for qualitative assessment of nuclear and NIRF imaging with dual-labeled imaging agents have shown that the sensitivity of NIRF may rival that of nuclear imaging technologies in planar imaging systems (Houston, et. al, 2005; Sampath, et. al, 2007). The development and validation of NIRF tomography systems could facilitate pre-clinical discovery research owing to the greater simplicity of handling a non-radioactive contrast agent or even the combination of different targeting agents to provide greater information. However, fluorescence small animal tomography needs to be validated against the known pre-clinical standard of PET or SPECT. In this work, we sought to improve the sensitivity of the imaging system that was developed for investigational NIRF imaging and tomography in humans and re-engineered it for installing into a commercial microPET/CT system for hybrid small animal imaging.
Free-space, non-contact excitation and detection are necessary for systems installed within the gantry. Specifically, the first challenge was to integrate the most sensitive detector which could be used within the gantry. While the photon count rate of fluorescence is high in comparison to that from radioactive decay, the use of an integrating camera such as a CCD provides even better sensitivity than APD or PMT, but offers footprint challenges. Use of fibers for collecting emitted fluorescence from the tissue surface and redirecting it to an externally placed CCD facilitates the use of the camera system and may also reduce excitation light leakage that governs the noise level, however, the fiber placement on animals in the gantry becomes cumbersome and based on a study by Schulz et. al, 2006, provides reduced reconstruction quality compared to non-contact detection. For NIR excitation (>750 nm), confounding tissue autofluorescence is minimal, but the spectral sensitivity of CCDs at NIR wavelengths is not superior. While EMCCD’s have improved spectral characteristics, a recent study by Zhu, et. al, 2012, showed that SNR for NIR ICCDs is superior to EMCCDs owing to the readout noise present in the EMCCD systems. Herein, we have therefore incorporated an NIR-sensitive ICCD system engineered with reduced footprint for enabling its integration into the gantry. In addition, the size on the rest of the optical imaging electronics was also reduced in an effort to fit them into the limited space of a commercially available microCT gantry.
As described earlier, many groups have previously attempted hybrid imaging modalities by adopting CW approach in optical tomography, however, very few groups have worked on adding a time-dependency feature to optical tomography. While CW is generally confounded by tissue optical heterogeneity, the image contrast for time-dependent techniques is primarily influenced by the fluorophore lifetime rather than the tissue optical properties. Thus TDPM or FDPM can be used to tomographically quantify fluorescent targets present deep within the tissue. Recently Nahrendorf, et. al, 2010, have shown that the correlation between concentration of a hybrid nuclear/fluorescence imaging agent probed by PET and CW-fluorescence DOT reduces as the target position changes from subcutaneous to deeper regions within the mouse. Thus, for such scenarios TDPM and FDPM approaches may enable successful target quantification. Use of such time-dependent approaches within the gantry for hybrid tomography can be largely accelerated by active work on instrumentation engineering for accommodating the complicated electronics associated with them. Time-domain approaches typically make use of PMT-based time-correlated single photon counting (Ntziachristos et. al, 1998; Kepshire, et. al, 2009) or ICCD-based, time-gated integration measurements (Kumar et. al, 2008) to collect the emission photons. However, they collect only a fraction of the emission photons, and consequently have reduced photon count compared to CW and FDPM approaches. They are therefore susceptible to low SNR and need to be compensated at the expense of long image acquisition times. In this work, we have hence worked on developing novel rf circuit design to efficiently perform time-dependent fluorescence studies using FDPM approach. Among the other unique features of this system is the use of a single rf frequency oscillator that avoids the need to maintain precise phase synchronization between dual rf sources that were used in previous design. Godavarty, et. al, 2003, used such a FDPM prototype along with approximate extended Kalman filter algorithm to successfully demonstrate target reconstruction in clinically relevant volumes. Our current miniaturized FDPM system exhibits noise characteristics that are comparable to this bulky prototype and can be operated within realistic time frames. As with all ill-posed problems, the correct forward problem in combination with high quality dataset is critical for faithful image reconstruction. We therefore focused on improving IAC and θ precision by minimizing the errors associated with them to ±0.7% and ±0.3°, respectively. In addition, we demonstrated that the imaging quality can be enhanced by (i) judiciously selecting intensifier gain settings, (ii) setting measurements parameters such as number of phase-delays and measurement repetitions, and (iii) choosing pixels that are associated with elevated mean DC pixel intensities as indicated by our SNR studies of the system.
Another unique aspect of this work is the use of higher-order approximation to RTE for a proper forward model for model-based reconstruction. During early stages of development for fluorescence tomography, the diffusion approximation (DA) was popular due to its simplicity and ease of implementation. However, the imprecision associated with DA became more distinct for tomographic reconstructions for small volumes (such as mice) and for organs with wide range of optical properties. For FDPM simulations, our forward solution demonstrated that the simplified spherical harmonics approximation (SPn) can effectively correct for the limitations from DA model especially in highly absorptive domains or at high modulation frequencies (Lu, et. al, 2010). For our current work with SP3 approximation, a linear reconstruction algorithm was developed that significantly improves the reconstruction quality for FDPM-based fluorescence tomography. Successful reconstruction of targets in homogeneous (phantom) and heterogeneous (mouse) conditions without relying on any regularization term demonstrates the utility of our forward light prediction model to FDPM approach for NIRF tomography.
Future work will involve systematically testing resolution limits for different tissue cross-sections, and for multiple targets. While reasonable acquisition times have been recorded for imaging specific tissue volumes, it is necessary to speed up full-body imaging by trying various illumination patterns or through multiple excitation locations. For exhaustive comparison of PET-optical modalities, it is also imperative to quantitatively evaluate acquisition times, sensitivity versus specificity, and resolution through use of multimodal imaging agents.
The contribution of this work to the field of NIRF optical tomography is through: (i.) implementing hardware design with system miniaturization, and noise characterization for a novel design FDPM system for time-dependent tomography, (ii.) development of SP3 based reconstruction algorithm specifically tailored for FDPM approach to effect regularization-free fluorescence tomography in homogeneous and heterogeneous media, and (iii.) incorporating optical instrumentation with a commercially available microPET/CT scanner for future time-dependent quantitative optical-nuclear studies using an integrated workflow approach.
Supplementary Material
Acknowledgments
This work was supported in parts by NIH R01CA135673 (Eva Sevick-Muraca and Anne Smith), the Texas Star Award, and training fellowship from the Keck Center Computational Cancer Biology Training Program of the Gulf Coast Consortia (CPRIT Grant No. RP101489) (Yujie Lu).
References
- Azhdarinia A, Ghosh P, Ghosh S, Wilganowski N, Sevick-Muraca EM. Dual-labeling strategies for nuclear and fluorescence molecular imaging: a review and analysis. Mol Imaging Biol. 2011:1–16. doi: 10.1007/s11307-011-0528-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barber WC, Lin Y, Nalcioglu O, Iwanczyk JS, Hartsough NE, Gulsen G. Combined fluorescence and X-ray tomography for quantitative in vivo detection of fluorophore. Technol Cancer Res Treat. 2010;9:45–52. doi: 10.1177/153303461000900105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson SJ, Moré J. Tech Rep. Mathematics and Computer Science Division, Argonne National Laboratory; 2001. A limited-memory variable-metric algorithm for bound-constrained minimization. ANL/MCS-P909-0901. [Google Scholar]
- Cao L, Peter J. Bayesian reconstruction strategy of fluorescence-mediated tomography using an integrated SPECT-CT-OT system. Phys Med Biol. 2010;55:2693–2708. doi: 10.1088/0031-9155/55/9/018. [DOI] [PubMed] [Google Scholar]
- Chu M, Vishwanath K, Klose AD, Dehghani H. Light transport in biological tissue using three-dimensional frequency-domain simplified spherical harmonics equations. Phys Med Biol. 2009;54:2493–509. doi: 10.1088/0031-9155/54/8/016. [DOI] [PubMed] [Google Scholar]
- Contag CH, Bachmann MH. Advances in in-vivo bioluminescence imaging of gene expression. Annu Rev Biomed Eng. 2002;4:235–60. doi: 10.1146/annurev.bioeng.4.111901.093336. [DOI] [PubMed] [Google Scholar]
- Frenkel A, Sartor MA, Wlodawski MS. Photon-noise-limited operation of intensified CCD cameras. Appl Optics. 1997;36:5288–97. doi: 10.1364/ao.36.005288. [DOI] [PubMed] [Google Scholar]
- Gibson AP, Hebden JC, Arridge SR. Recent advances in diffuse optical imaging. Phys Med Biol. 2005;50:R1–43. doi: 10.1088/0031-9155/50/4/r01. [DOI] [PubMed] [Google Scholar]
- Godavarty A, Eppstein MJ, Zhang C, Theru S, Thompson AB, Gurfinkel M, Sevick-Muraca EM. Fluorescence-enhanced optical imaging in large tissue volumes using a gain-modulated ICCD camera. Phys Med Biol. 2003;48:1701–20. doi: 10.1088/0031-9155/48/12/303. [DOI] [PubMed] [Google Scholar]
- Grimm J, Kirsch DG, Windsor SD, Kim CFB, Santiago PM, Ntziachristos V, Jacks T, Weissleder R. Use of gene expression profiling to direct in vivo molecular imaging of lung cancer. Proc Natl Acad Sci. 2005;102:14404–09. doi: 10.1073/pnas.0503920102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gurfinkel M, Thompson AB, Ralston W, Troy TL, Moore AL, Moore TA, Gust JD, Tatman D, Reynolds JS, Muggenburg B, Nikula K, Pandey R, Mayer RH, Hawrysz DJ, Sevick-Muraca EM. Pharmacokinetics of ICG and HPPH-car for the detection of normal and tumor tissue using fluorescence, near-infrared reflectance imaging: a case study. Photoch Photobio. 2000;72:94–102. doi: 10.1562/0031-8655(2000)072<0094:poiahc>2.0.co;2. [DOI] [PubMed] [Google Scholar]
- Kepshire D, Mincu N, Hutchins M, Gruber J, Dehghani H, Hypnarowski J, Leblond F, Khayat M, Pogue BW. A microcomputed tomography guided fluorescence tomography system for small animal molecular imaging. Rev Sci Instrum. 2009;80:043701–10. doi: 10.1063/1.3109903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klose AD, Larsen EW. Light transport in biological tissue based on the simplified spherical harmonics equations. J Comput Phys. 2006;220:441–70. [Google Scholar]
- Kwon S, Sevick-Muraca EM. Noninvasive quantitative imaging of lymph function in mice. Lymphat Res Biol. 2007;5:219–31. doi: 10.1089/lrb.2007.1013. [DOI] [PubMed] [Google Scholar]
- Kumar ATN, Raymond SB, Dunn AK, Bacskai BJ, Boas DA. A time domain fluorescence tomography system for small animal imaging. IEEE Trans Med Imaging. 2008;27:1152–63. doi: 10.1109/TMI.2008.918341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leblond F, Davis SC, Valdés PA, Pogue BW. Pre-clinical whole-body fluorescence imaging: review of instruments, methods and applications. J Photoch Photobio B. 2010;98:77–94. doi: 10.1016/j.jphotobiol.2009.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li C, Yang Y, Mitchell GS, Cherry SR. Simultaneous PET and multispectral 3-dimensional fluorescence optical tomography imaging system. J Nucl Med. 2011;52:1268–75. doi: 10.2967/jnumed.110.082859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Chance B, Yodh AG. Fluorescent heterogeneities in turbid media: limits for detection, characterization, and comparison with absorption. Appl Optics. 1998;37:6833–44. doi: 10.1364/ao.37.006833. [DOI] [PubMed] [Google Scholar]
- Lin Y, Gao H, Nalcioglu O, Gulsen G. Fluorescence diffuse optical tomography with functional and anatomical a priori information: feasibility study. Phys Med Biol. 2007;52:5569–85. doi: 10.1088/0031-9155/52/18/007. [DOI] [PubMed] [Google Scholar]
- Lin Y, Barber WC, Iwanczyk JS, Roeck WW, Nalcioglu O, Gulsen G. Quantitative fluorescence tomography using a trimodality system: in vivo validation. J Biomed Opt. 2010;15:040503–3. doi: 10.1117/1.3467495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu Y, Zhu B, Shen H, Rasmussen JC, Wang G, Sevick-Muraca EM. A parallel adaptive finite element simplified spherical harmonics approximation solver for frequency domain fluorescence molecular imaging. Phys Med Biol. 2010;55:4625–45. doi: 10.1088/0031-9155/55/16/002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu Y, Zhu B, Darne C, Tan I-Chih, Rasmussen JC, Sevick-Muraca EM. Improvement of fluorescence-enhanced optical tomography with improved optical filtering and accurate model-based reconstruction algorithms. J Biomed Opt. 2011;16:126002, 1–4. doi: 10.1117/1.3659291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall MA, Kwon S, Robinson H, Lachance P-A, Azhdarinia A, Ranganathan R, Price RE, Chan W, Sevick-Muraca EM. Imaging prostate cancer lymph node metastases with a multimodality contrast agent. Prostate. 2012;72:129–46. doi: 10.1002/pros.21413. [DOI] [PubMed] [Google Scholar]
- Houston JP, Ke S, Wang W, Li C, Sevick-Muraca EM. Quality analysis of in vivo near-infrared fluorescence and conventional gamma images acquired using a dual-labeled tumor-targeting probe. J Biomed Opt. 2005;10:054010. doi: 10.1117/1.2114748. [DOI] [PubMed] [Google Scholar]
- Nahrendorf M, Keliher E, Marinelli B, Waterman P, Feruglio PF, Fexon L, Pivovarov M, Swirski FK, Pittet MJ, Vinegoni C, Weissleder R. Hybrid PET-optical imaging using targeted probes. Proc Natl Acad Sci. 2010;107:7910–15. doi: 10.1073/pnas.0915163107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ntziachristos V, Ma X, Chance B. Time-correlated single photon counting imager for simultaneous magnetic resonance and near-infrared mammography. Rev Sci Instrum. 1998;69:4221–33. [Google Scholar]
- Prout DL, Silverman RW, Chatziioannou A. Detector concept for OPET - a combined PET and optical imaging system. IEEE Trans Nucl Sci. 2004;51:752–56. doi: 10.1109/TNS.2004.829736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasmussen JC, Tan I–C, Marshall MV, Fife CE, Sevick-Muraca EM. Lymphatic imaging in humans with near-infrared fluorescence. Curr Opin Biotech. 2009;20:74–82. doi: 10.1016/j.copbio.2009.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sahu AK, Roy R, Joshi A, Sevick-Muraca EM. Evaluation of anatomical structure and nonuniform distribution of imaging agent in near infrared fluorescence-enhanced optical tomography. Opt Express. 2005;13:10182–99. doi: 10.1364/opex.13.010182. [DOI] [PubMed] [Google Scholar]
- Sampath L, Kwon S, Ke S, Wang W, Schiff R, Mawad ME, Sevick-Muraca EM. Dual-labeled trastuzumab-based imaging agent for the detection of human epidermal growth factor receptor 2 overexpression in breast cancer. J Nucl Med. 2007;48:1501–10. doi: 10.2967/jnumed.107.042234. [DOI] [PubMed] [Google Scholar]
- Schulz RB, Peter J, Semmler W, D’Andrea C, Valentini G, Cubeddu R. Comparison of noncontact and fiber-based fluorescence-mediated tomography. Opt Lett. 2006;31:769–71. doi: 10.1364/ol.31.000769. [DOI] [PubMed] [Google Scholar]
- Schulz RB, Ale A, Sarantopoulos A, Freyer M, Soehngen E, Zientkowska M, Ntziachristos V. Hybrid system for simultaneous fluorescence and X-ray computed tomography. IEEE Trans Med Imaging. 2010;29:465–73. doi: 10.1109/TMI.2009.2035310. [DOI] [PubMed] [Google Scholar]
- Sevick-Muraca EM, Lopez G, Reynolds J, Troy T, Hutchinson C. Fluorescence and absorption contrast mechanisms for biomedical optical imaging using frequency-domain techniques. Photochem Photobiol. 1997;66:55–64. doi: 10.1111/j.1751-1097.1997.tb03138.x. [DOI] [PubMed] [Google Scholar]
- Sevick-Muraca EM, Sharma R, Rasmussen JC, Marshall MV, Wendt JA, Pham HQ, Bonefas E, Houston JP, Sampath L, Adams KE, Blanchard DK, Fisher RE, Chiang SB, Elledge R, Mawad ME. Imaging of lymph flow in breast cancer patients after microdose administration of a near-infrared fluorophore: feasibility study. Radiology. 2008;246:734–741. doi: 10.1148/radiol.2463070962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuker F, Baltes C, Dikaiou K, Vats D, Carrara L, Charbon E, Ripoll J, Rudin M. Hybrid small animal imaging system combining magnetic resonance imaging with fluorescence tomography using single photon avalanche diode detectors. IEEE Trans Med Imaging. 2011;30:1265–73. doi: 10.1109/TMI.2011.2112669. [DOI] [PubMed] [Google Scholar]
- Thompson AB, Sevick-Muraca EM. Near-infrared fluorescence contrast-enhanced imaging with intensified charge-coupled device homodyne detection: measurement precision and accuracy. J Biomed Opt. 2003;8:111–20. doi: 10.1117/1.1528205. [DOI] [PubMed] [Google Scholar]
- Vo-Dinh T. Biomedical photonics handbook. J Biomed Opt. 2004;9:1110. [Google Scholar]
- Wang G, Cong W, Durairaj K, Qian X, Shen H, Sinn P, Hoffman E, McLennan G, Henry M. In vivo mouse studies with bioluminescence tomography. Opt Express. 2006;14:7801–09. doi: 10.1364/oe.14.007801. [DOI] [PubMed] [Google Scholar]
- Yan H, Lin Y, Barber WC, Unlu MB, Gulsen G. A gantry-based tri-modality system for bioluminescence tomography. Rev Sci Instrum. 2012;83:043708–8. doi: 10.1063/1.3698295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu B, Tan I–C, Rasmussen JC, Sevick-Muraca EM. Validating the sensitivity and performance of near-infrared fluorescence imaging and tomography devices using a novel solid phantom and measurement approach. Technol Cancer Res Treat. 2012;11:95–104. doi: 10.7785/tcrt.2012.500238. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.