Abstract
The glucocorticoid receptor (GR) is a member of the steroid receptor family of ligand-activated transcription factors. A number of studies have shown that steroid receptors regulate distinct but overlapping sets of genes; however, the molecular basis for such specificity remains unclear. Previous work from our laboratory has demonstrated that under identical solution conditions, three other steroid receptors – the progesterone receptor A-isoform (PR-A), the progesterone receptor B-isoform (PR-B), and estrogen receptor-α (ER-α) – differentially partition their self-association and promoter binding energetics. For example, PR-A and PR-B generate similar dimerization free energies but differ significantly in their extents of inter-site cooperativity. Conversely, ER-α maintains inter-site cooperativity most comparable to PR-A, yet dimerizes with an affinity orders of magnitude greater than either of the PR isoforms. We have speculated that these differences serve to generate receptor-specific promoter occupancies, and thus receptor-specific gene regulation. Noting that GR regulates a unique subset of genes relative to the other receptors, we hypothesized that the receptor should maintain a unique set of interaction energetics. We rigorously determined the self-association and promoter binding energetics of full-length, human GR under conditions identical to those used in our earlier studies. We find that unlike all other receptors, GR shows no evidence of reversible self-association. Moreover, GR assembles with strong inter-site cooperativity comparable to that seen only for PR-B. Finally, simulations show that such partitioning of interaction energetics allows for receptor-specific promoter occupancies, even under conditions where multiple receptors are competing for binding at identical sites.
Keywords: Glucocorticoid receptor, thermodynamics, protein-DNA interactions, quantitative footprinting, analytical ultracentrifugation
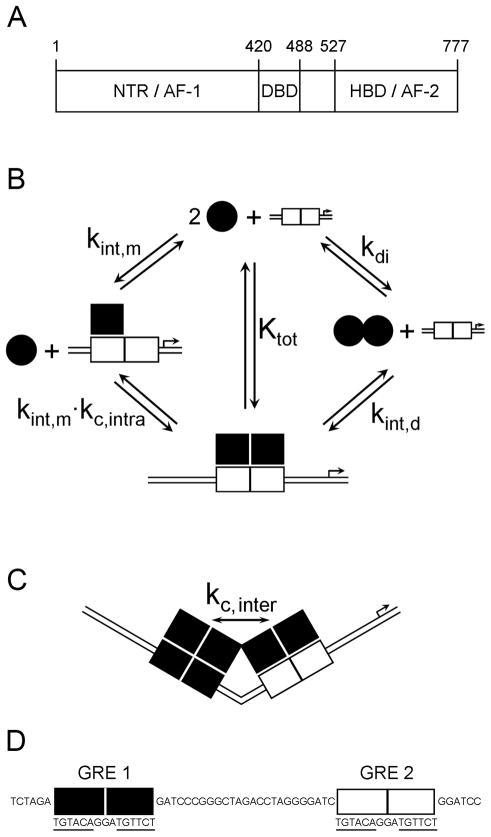
The glucocorticoid receptor (GR) is a member of the steroid receptor family of ligand-activated transcription factors.1 The remaining members include the androgen receptor (AR); the mineralocorticoid receptor (MR); the two isoforms of the progesterone receptor (PR-A and PR-B); and the two isoforms of the estrogen receptor (ER-α and ER-β). The domain structure of GR is shown in Figure 1A. GR has a highly conserved DNA binding domain (DBD), a modestly conserved hormone binding domain (HBD), and a poorly conserved N-terminal region (NTR). Located within the N-terminal region and the HBD are transactivation functions AF-1 and AF-2, respectively.
Figure 1. GR domain structure and promoter assembly states.
(A) Schematic of GR primary sequence with the domains labeled as follows: NTR, N-terminal region; DBD, DNA binding domain; HBD, hormone binding domain. Activation functions (AF-1 and AF-2) are contained within the NTR and HBD, respectively. (B) Schematic describing binding models for assembly onto a palindromic response element. Filled circles represent GR monomers. Filled squares represent GR dimers. The series of reactions to the left describe a monomer-binding pathway, whereby GR monomers assemble sequentially at the response element. The first GR monomer binds with a monomer intrinsic affinity, kint,m, whereas the second monomer binding event is described by kint,m and a cooperative interaction between adjacently bound GR monomers (kc,intra). The center reaction describes the total binding affinity (Ktot) for saturating a single response element with two GR monomers. The series of reactions to the right describe a dimer binding pathway, whereby GR solution dimerization (kdi) precedes dimer binding to a response element (kint,d). (C) Schematic describing the GR binding assembly at a two-site promoter. All binding constants described in panel B apply at each site on the promoter. Additionally, saturation of both promoter sites may be accompanied by an inter-site cooperative interaction (kc,inter), which is depicted by protein-protein contacts between adjacently bound GR proteins and bending of the DNA. (D) Sequence of the GRE2 promoter sequence proximal to the two response element binding sites, with each half-site underlined.
The biochemical understanding for steroid receptor action is as follows: ligand-bound receptors dimerize, assemble at palindromic response elements typically located upstream of a transcriptional start site, and then recruit coactivator proteins to initiate transcription. This model nonetheless remains incomplete. For example, all steroid receptors bind identical or nearly identical DNA response elements in vitro, yet activate distinct but overlapping sets of genes in vivo.2–4 How then does an individual receptor maintain specificity of gene control – the ability to activate only a subset of potential genes? And how does this occur when multiple types of receptors may be present and thus competing for binding at identical response elements? We are focused on determining the quantitative mechanisms responsible for such promoter- and receptor- specific gene regulation.
Shown in Figure 1B are the assembly states and interaction parameters for receptor binding to a single palindromic response element. Receptors may dimerize in the absence of DNA (kdi) and then bind as pre-formed dimers (kint,d), or bind as successive monomers (kint,m) via DNA-induced intra-site cooperativity (kc,intra). These events each constitute a microscopic interaction, whereas the total binding affinity (Ktot) describes the macroscopic reaction for two monomers assembling at a response element regardless of pathway. Finally, shown in Figure 1C is the fully ligated state for a promoter containing two hormone response elements. Complete occupancy of receptor dimers at the promoter may be accompanied by inter-site cooperativity (kc,inter). We note that all of these parameters, including the total binding affinity, have a precise molecular interpretation. By contrast, an apparent binding affinity – the parameter historically measured in nearly all steroid receptor-DNA binding studies – is a composite of some or all of these values and thus offers little molecular insight.
We previously dissected the microscopic energetics of PR-A and PR-B binding to the promoter in Figure 1D consisting of two palindromic response elements.5, 6 Under identical conditions, the two isoforms bind the promoter with similar apparent binding affinities; however, the microstate energetics are dramatically different. In particular, the B-isoform generates significantly increased inter-site cooperativity (kc,inter) relative to PR-A. We subsequently found that differences in microstate energetics applied not just to different isoforms but also to different receptors. Under conditions identical to our work on the PR isoforms, we found that ER-α maintained inter-site cooperative energetics much weaker than either PR-A or PR-B, but dimerization energetics orders of magnitude greater.7
These studies demonstrated that homologous transcription factors were capable of differentially partitioning their microscopic interaction energetics. This led us to speculate that such differences might serve to generate receptor-specific promoter occupancy, and thus receptor-specific gene regulation. For example, if multiple receptors are present at identical total concentrations, stronger dimerization energetics by one (e.g. ER-α), will generate a greater concentration of active dimers. Consequently, promoter layouts containing an abundance of palindromic response elements should allow preferential binding by that receptor over all others. By contrast, promoters containing a higher proportion of half-site response elements should generate preferential monomer binding by that subset of receptors with weak dimerization energetics (e.g. PR-A and PR-B). Receptor-specific differences in inter-site cooperativity should serve as an additional mechanism for controlling receptor-specific promoter occupancy.5
As a step toward determining whether such a framework might be generalized to all members of the steroid receptor family, we dissected the energetics of GR binding to the promoter in Figure 1D (herein defined as GRE2). We hypothesized that GR, which regulates a unique subset of genes relative to the PR isoforms,4 should maintain a unique set of microstate interaction parameters. Consistent with this hypothesis, we found that GR dimerization energetics are considerably weaker than those of any of the other receptors, including PR-A and PR-B. In fact, we were unable to detect reversible GR self-association regardless of protein concentration. Furthermore, although GR inter-site cooperativity is comparable to that of PR-B, it is much greater than that of PR-A and ER-α. Simulations reveal that such unique partitioning of microstate energetics allows for receptor-specific promoter occupancy, even in the presence of competitive binding by another receptor. Our results thus suggest that the ability of homologous receptors to differentially partition their microscopic energetics may serve as the basis for receptor-specific and promoter-specific gene control.
Materials and Methods
Expression & purification of full-length, human GR
A pBAC baculovirus vector (EMD, formerly Novagen) containing human GR (amino acids 1-777) fused to an N-terminal hexa-histadine tag (His-GR) was generated in-house. A vector containing human GR fused to an N-terminal FLAG tag (FLAG-GR) was donated by Dr. Steven Nordeen (University of Colorado Anschutz Medical Campus). Both constructs were expressed in baculovirus-infected Sf9 cells using a multiplicity of infection of 1. Cells were treated with 1 μM triamcinolone acetonide (TA) twenty-four hours post-infection and harvested twenty-four hours later.
All purification steps were carried out at 4°C and in the presence of 10 μM TA. Cells containing His-GR were Dounce homogenized in a buffer containing 20 mM Tris (pH 8.0 at 4°C), 10% glycerol (w/v), 10 mM NaCl, 10 mM β-ME, 10 μM TA and protease inhibitors (Complete, EDTA-free, Roche). The nuclear-localized fraction of His-GR was pelleted, and the receptor was released from the nuclei in an extraction buffer containing 20 mM Tris (pH 8.0 at 4°C), 10% glycerol (w/v), 500 mM NaCl, 10 mM β-ME, 10 μM TA, 25 mM imidazole and protease inhibitors. Following centrifugation, His-GR was purified from the supernatant using Ni–NTA agarose resin (Qiagen). The resin was washed extensively with extraction buffer, and receptor was eluted using the same buffer now containing 250 mM imidazole. His-GR then was chromatographed on a Sephacryl S-300 HR size exclusion column (GE Healthcare) equilibrated in the extraction buffer less imidazole and protease inhibitors. The fractionated protein was dialyzed into 20 mM Tris (pH 8.0 at 4°C), 10% glycerol (w/v), 85 mM NaCl, 10 mM β-ME and 10μM TA, and concentrated using Q-Sepharose (Amersham Biosciences). After elution with a 500 mM NaCl step gradient, His-GR was flash-frozen and stored in liquid nitrogen. The receptor was judged to be approximately 95% pure by quantification of Coomassie Blue stained SDS–PAGE. Concentration was determined using a calculated extinction coefficient of 71,280 M−1 cm−1.8 Final yields were 0.3–0.5 mg of His-GR/liter of cell culture.
FLAG-GR was purified as described for His-GR with the following modifications. After the initial pelleting step, FLAG-GR was extracted from the nuclei using the previously described extraction buffer less imidazole. After centrifugation, the receptor was partially purified from the supernatant using Anti-FLAG M2 Affinity Gel (Sigma). The resin was washed extensively, and the receptor was eluted using 0.25 mg/ml FLAG peptide (Sigma). Eluted receptor was then chromatographed and concentrated as described for His-GR. FLAG-GR was judged to be approximately 95% pure by quantification of Coomassie Blue stained SDS–PAGE. FLAG-GR concentration was determined using a calculated extinction coefficient of 72,270 M−1 cm−1.8 Final yields were comparable to those of His-GR.
Analytical ultracentrifugation
All sedimentation analyses were carried out on a Beckman XL-A analytical ultracentrifuge equipped with absorbance optics and an An-50 Ti rotor. Two- and six-channel Epon centerpiece-containing cells were used for sedimentation velocity and sedimentation equilibrium experiments, respectively. All studies were carried out in a buffer containing 20 mM Tris (pH 8.0 at 4°C), 100 mM NaCl, 1 mM DTT, 1 mM CaCl2, 2.5 mM MgCl2 and 10 μM TA.
For sedimentation velocity, three GR samples at 10.0, 5.0 and 2.0 μM were sedimented at 4°C using a rotor speed of 50,000 rpm. Data was collected at 280 nm, with scans taken as quickly as the instrument would allow (typically every four minutes). Sedimentation coefficient distributions (c(s)) were calculated using the program Sedfit.9 The c(s) distribution was corrected to 20°C and water (s20,w) using standard methods,10 where s20,w is defined as:
| (1) |
and M is the weight-average molecular weight, ν̄ is the partial specific volume of GR, ρ is the solvent density, and N is Avogadro’s number. The density was calculated from the buffer composition and temperature,11 and the partial specific volume was calculated by summing the partial specific volume of each amino acid (0.7223 mL/g at 4°C).12
For sedimentation equilibrium, three GR samples at 9.3, 4.2 and 0.9 μM were equilibrated at 4°C, using rotor speeds of 15,000, 18,000 and 21,000 rpm. Samples were judged to be at equilibrium by successive subtraction of scans. All data were analyzed using nonlinear least-squares (NLLS) parameter estimation as implemented in the program NONLIN.13 NONLIN uses the following equation to resolve the reduced molecular weight (σ):
| (2) |
where Yr is the absorbance at radius r, δ is the baseline offset, and α is the absorbance at the reference radius, r0. The reduced molecular weight, σ, is defined as:
| (3) |
where M is the weight-average molecular weight, ν̄ is the partial specific volume of GR, ρ is the solvent density (calculated from the buffer composition and experimental temperature)11, ω is the angular velocity, R is the gas constant, and T is the absolute temperature in Kelvin.
DNA preparation for DNase I footprinting
A promoter vector containing two tandemly-linked glucocorticoid response elements (GRE2; see Figure 1D) was donated by Dr. Kathryn Horwitz (University of Colorado Anschutz Medical Center). Each GRE corresponds to an imperfect palindrome derived from the tyrosine aminotransferase promoter, TGTACAGGATGTTCT14 spaced 25 base pairs apart. A reduced-valency template (GRE1−) containing a G-to-T point mutation in each half-site of the distal GRE (designated as site 1) was created in-house. Each template was excised from its respective vector using Hind III and Aat II to generate a 1 kb promoter fragment and end-labeled with 32P using a Klenow fill-in reaction. The proximal GRE of each fragment (site 2) was positioned 100 bp from the 3′ end of the labeled strand. The GRE2 promoter sequence is identical to the PRE2 promoter used in our earlier work on the two PR isoforms,5, 6 and differs only in response element sequence when compared to the ERE2 promoter used in our work on ER-α.7
Individual-site binding experiments
Experiments were carried out using quantitative DNase I footprint titrations as originally described by Ackers and co-workers15, 16 with minor modifications.17 All reactions were carried out in an assay buffer containing 20 mM Hepes, pH 8.0, 100 mM NaCl, 1 mM DTT, 1 mM CaCl2, 2.5 mM MgCl2, 10 μM TA, 100 μg/mL BSA, and 2 μg/mL salmon sperm DNA. Each reaction contained 15,000 cpm of freshly labeled DNA. GR was added to each reaction mix, covering a concentration range from sub-nanomolar to low micromolar. Because GR reaches micromolar concentrations in the footprint titration, the concentrated receptor stock was dialyzed into the assay buffer minus BSA and salmon sperm DNA prior to equilibration with promoter DNA. Samples were allowed to equilibrate at 4°C for at least 1 hour. DNase I (Invitrogen) was diluted to a concentration of 0.025 units/μL using the assay buffer less BSA and salmon sperm DNA. 5 μL of the diluted DNase I solution was added to each 100 μL sample, and the reaction was allowed to proceed for exactly 2 min. Digestion products were electophoresed on 6% acrylamide-urea gels and visualized using phosphorimaging. Individual-site binding isotherms were calculated as described by Brenowitz et al.16 using the program ImageQuant (Molecular Dynamics).
The thermodynamic validity of the quantitative DNase footprint titration technique is based upon the testable assumptions that the system of interest is at equilibrium and the DNase exposure does not perturb that equilibrium.16 In the present study, the resolved binding isotherms were independent of equilibration times from 1 to 2 hours. All studies were carried out with DNase concentrations low enough to ensure “single-hit kinetics” and therefore thermodynamically valid binding isotherms.15 Finally, promoter DNA concentrations (maximally 10 pM) were estimated to be well below the estimated GR DNA binding affinity, thus justifying the assumption that GRfree ≈ GRtotal.
Resolution of microscopic interaction free energies
The DNase I footprint titration technique resolves the fractional occupancy of GR binding at each response element site. The statistical thermodynamic expressions that describe the individual-site binding isotherms are constructed by summing the probabilities of each microscopic configuration that contributes to binding at that site. A detailed approach for generating each mathematical formulation has been presented previously.18 Briefly, the probability (fs) of any microscopic configuration is defined as:19
| (4) |
where ΔGs is the free energy of configuration state s relative to the unliganded reference state, x is the free GR monomer concentration, and j is the stoichiometry of GR monomers bound to a response element. R is the gas constant, and T is the temperature in Kelvin. The relationship between each free energy change and its association constant is described by the equation ΔGi = −RT ln ki.
The GRE1− binding isotherms were first analyzed using the model-independent Hill equation:
| (5) |
where Ȳ Hill is the fractional saturation at the response element, x is the free GR monomer concentration, and K is an apparent dissociation constant. This analysis yielded a Hill coefficient (n) statistically indistinguishable from 2, indicative of strong cooperativity between adjacently bound monomers at a palindrome (see Results). Thus, the singly ligated monomer GR-DNA species is not significantly populated, and the affinity for monomer half-site binding is not well constrained. All isotherms were therefore analyzed using a contracted Adair equation to resolve the total binding affinity (Ktot) for assembling two GR monomers at a palindromic response element (Table 1). For the GRE1− data sets, the following equation was used:
| (6) |
where x is the free GR monomer concentration and Ktot is as described in Figure 1B.
Table 1.
Species distributions, binding constants, and free energy changes for GR assembly on the GRE2 promoter
| Species Number | Species Schematic | Macroscopic constant | Free Energy Contribution |
|---|---|---|---|
| 1 |
|
-- | reference state |
| 2 |
|
Ktot | ΔGtot |
| 3 |
|
Ktot | ΔGtot |
| 4 |
|
Ktot2 · kc,inter | 2 · ΔGtot + ΔGc,inter |
The free energy change is related to each macroscopic association constant through the relationship ΔGi = −RT ln ki, where R is the gas constant and T is the temperature in Kelvin.
For the GRE2 data sets, Equation 7 describes binding to both sites 1 and 2 of the GRE2 promoter. Since the two sites are identical (Figure 1D), Ktot is assumed to be the same for each GRE. An additional term, kc,inter, was included to describe potential cooperativity between the palindromes:
| (7) |
The GRE2 and GRE1− datasets were then globally fit to resolve Ktot and kc,inter.
Finally, because protein interactions at DNA binding sites do not afford complete protection from DNase activity, binding data were treated as transition curves fitted to upper (m) and lower (b) end points:
| (8) |
Analyses of binding isotherm data were carried out using the program Scientist (Micromath, Inc.).
Results
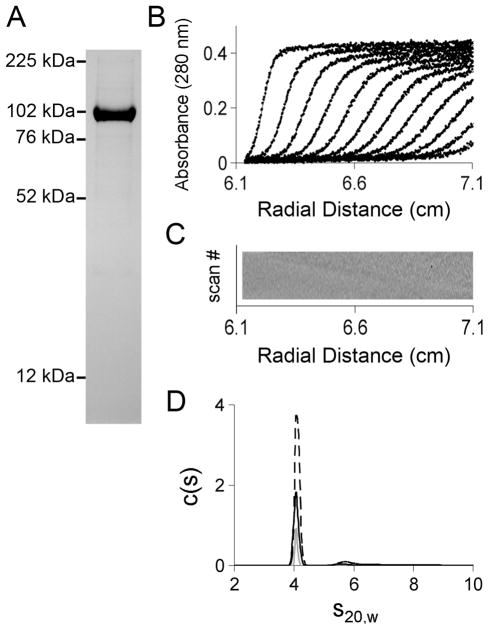
Full-length, human GR (both His- and FLAG-tagged) was purified from baculovirus-infected Sf9 insect cells using three chromatographic steps. For His-GR, densitometric analysis of Coomassie Blue stained SDS-PAGE gels indicated that the receptor was at least 95% pure (Figure 2A). Mass spectrometry analysis of trypsin-digested His-GR resolved masses with the highest probability of corresponding to residues 5-777. The presence of the N-terminal His-tag was confirmed by immunoblotting. FLAG-GR was purified to an identical degree and generated identical ultracentrifugation and DNase footprinting results, suggesting that the tags have little influence on receptor function.
Figure 2. Purification of full-length, human GR and analysis by sedimentation velocity.
(A) Baculovirus-expressed GR was purified as described in Materials and Methods. The purified protein (8 μg) was resolved by 4–12% gradient SDS-PAGE and Coomassie-stained. Molecular mass markers are indicated to the left. (B) Sedimentation velocity data collected using 5 μM GR, at 100 mM NaCl, pH 8.0 and 4°C. Filled circles represent the individual data points from scans taken at 50,000 rpm, plotted as a function of time and radial position. Solid lines represent the best fit from a c(s) analysis as implemented by Sedfit.9 Only every eighth scan is shown for clarity. (C) The residuals of the fits as represented by bitmap. Residuals are shown on a grey-scale as a function of radius (x-axis) and scan number (y-axis). (D) C(s) distributions determined from Sedfit9 for three GR concentrations: 10.0 μM (dashed black line), 5.0 μM (solid black line), and 2.0 μM (solid gray line).
GR is a structurally homogenous monomer
Sedimentation velocity was used to examine the hydrodynamic and self-association properties of His-GR. These studies were carried at concentrations ranging from 2.0 to 10.0 μM. Figure 2B shows representative sedimentation velocity absorbance data, with the solid lines representing the best fit via c(s) analysis as implemented by Sedfit.9 The residuals of the fit, as represented by a bitmap, are shown in Figure 2C. Figure 2D shows the resolved sedimentation coefficient distributions for three GR concentrations. It is evident that regardless of concentration, the vast majority of GR sediments as a single species with a temperature and buffer corrected sedimentation coefficient (s20,w) of 4.1 s. A c(M) analysis of the 4.1 s peak resolved a molecular weight of 80,407 Da, slightly less than the calculated monomer molecular weight of 90,925 Da. We routinely observe a minor peak at 5.7 s, corresponding to a molecular weight of 159,241, and thus consistent with a GR dimer. However, the percentage of the dimer (~7%) is always invariant of receptor concentration, suggesting that it reflects an irreversible, functionally incompetent species. Thus the velocity results indicate that contrary to dogma, ligand-bound GR exists almost exclusively in a monomeric state. An identical result was observed regardless of salt concentration and pH (data not shown).
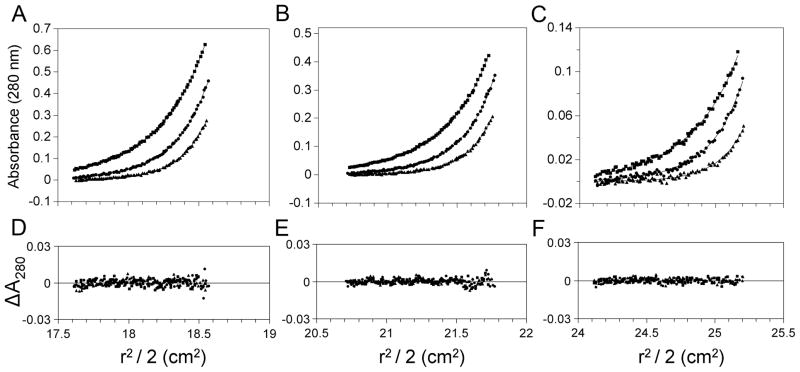
Sedimentation equilibrium was used to directly measure the molecular weight of the putative monomer species observed in the velocity studies. We carried out sedimentation equilibrium at three GR concentrations (9.3, 4.2, and 0.9 μM) and at three rotor speeds (15,000, 18,000 and 21,000 rpm), using buffer conditions identical to those in the velocity studies. Global fitting of the nine data sets to a single-species model resolved an average molecular weight of 96,400 ± 3,400 Da, slightly above that of a GR monomer (SDfit = 0.0033 AU). Analyses using more complex interaction models (e.g. monomer-dimer equilibrium) offered no improvement to the fit. However, since the velocity data detected a larger, non-interacting species consistent with that of a dimer, we also fit the equilibrium data to a model allowing for two non-interacting species. Shown in Figure 3 are the results of that analysis. It is evident that the non-interacting, two species model describes well all the data (SDfit = 0.0024 AU). Moreover, the resolved molecular weight of the monomer species is 87,972 ± 2,900 Da, within 3% of the calculated molecular weight of the monomer. Finally, the resolved stoichiometry from the two species fit was determined to be 2.0 ± 0.4, strongly suggesting that the larger sedimenting species is indeed the GR dimer. Consistent with this, fitting of the individual data sets to a monomer-dimer model resolved binding constants that weakened with increased receptor concentration. Thus the ratio of monomer to dimer was constant as a function of total protein concentration, indicative of an irreversible dimer species. We therefore conclude that GR is overwhelmingly monomeric with only a small population of incompetent, irreversible dimer.
Figure 3. Sedimentation equilibrium analysis of GR, plotted as absorbance versus r2/2.
(A–C) Sedimentation equilibrium data for GR at three different initial loading concentrations: 9.3 μM (A), 4.2 μM (B), and 0.9 μM (C). Symbols represent GR absorbance at 15,000 (squares), 18,000 (circles), and 21,000 rpm (triangles). Solid lines represent simultaneous analysis of all nine data sets to a non-interacting, two species model. The square root of variance was 0.0024 absorbance units. (D–F) Residuals from the single-species model plotted as change in absorbance versus r2/2 for the three initial loading concentrations: 9.3 μM (D), 4.2 μM (E), and 0.9 μM (F).
Finally, the good agreement in molecular weight estimates between the velocity and equilibrium studies suggests that the GR monomer is structurally homogenous, since even small amounts of structural heterogeneity (e.g. incompetent dimer) tend to dramatically underestimate molecular weight estimates when determined by sedimentation velocity.9, 20 If GR is indeed a homogenous monomer, this allows for a number of physically meaningful hydrodynamic calculations. For example, the monomer has a Stokes radius of 54 Å and a frictional ratio of 1.59, indicative of significant asymmetry. Thus if modeled as a prolate ellipsoid, GR has a major:minor axial ratio of 11:1. These results are summarized in Table 2.
Table 2.
Hydrodynamic properties of GR
| s20,w | 4.1 |
| f (g/s) | 1.03 × 10−7 |
| f/f0 | 1.59 |
| Stokes radius (Å) | 54 |
| Axial ratio | 11:1 |
| MW (Da)a | 80,407 |
| MW (Da)b | 87,972 ± 2,900 |
Estimated by a c(M) analysis of the 4.1 s peak as implemented in Sedfit.
Resolved molecular weight from sedimentation equilibrium.
GR assembles at a two-site promoter with substantial cooperativity
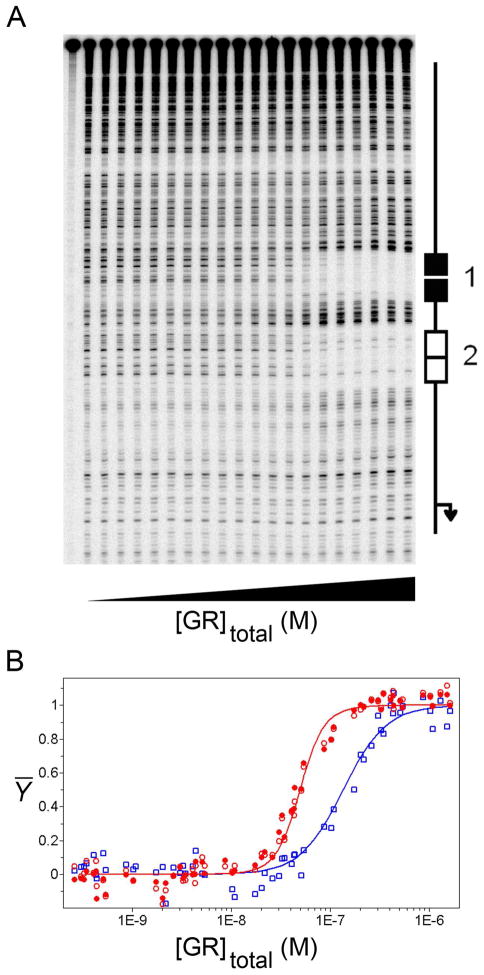
Quantitative DNase footprint titrations were used to resolve the energetics of GR assembly at a promoter containing two palindromic response elements (GRE2). Shown in Figure 4A is a representative titration of the GRE2 promoter in buffer conditions identical to the sedimentation studies. It is evident that GR binding is highly specific, and sequencing studies confirm that the protected regions correspond to the two GREs. Receptor-induced DNase hypersensitivity adjacent to the response elements are also evident. This was seen in our earlier work on ER-α and the two PR isoforms,5–7 and has been previously attributed to receptor-induced DNA bending.21, 22
Figure 4. Quantitative DNase footprint titrations and individual-site binding isotherms determined from global analysis of the GRE1− and GRE2 promoters.
(A) Representative DNase footprint titration image of GR binding to the GRE2 promoter in 100 mM NaCl. GR concentration increases from left to right. Positions of the two GREs (site 1, filled rectangle; site 2, open rectangle) are indicated to the right. (B) Individual-site binding isotherms generated from analysis of the footprint titration images. Solid red circles represent binding to site 1 and open red circles represent binding to site 2 of the GRE2 promoter (three independent footprint titrations); open blue squares represent binding to the GRE1− promoter (three independent footprint titrations). The red and blue lines represent the best global fit to all binding isotherms using the macroscopic binding model described by Equations 6 & 7. The sequences are identical for both sites of the GRE2 promoter, thus the fit lines for site 1 and site 2 overlay.
Our standard approach to quantify steroid receptor-promoter interactions has been to independently determine receptor dimerization affinity (kdi), and then fix this value in a global nonlinear least-squares analysis of the individual-site binding isotherms to resolve the intrinsic (kint,d) and inter-site cooperative (kc, inter) binding constants (Figure 1B).5–7 Such an analysis resolves the microscopic energetics of response element binding using a model that assumes pre-formed dimers bind to the palindromic response elements. However, since we found no evidence for reversible self-association of receptor, this approach was not ideal. Attempts to fit the data using a sequential monomer-binding model were also unsuccessful. This was due to the strong DNA-induced cooperativity known to exist between adjacently bound GR monomers.23 Consistent with this, fitting the single response element GRE1− isotherms to a model-independent Hill equation resolved an n of 2.2 ± 0.2.
We therefore globally fit the individual-site binding isotherms (Figure 4B) to a contracted Adair equation (Equations 6 & 7). This approach allowed us to resolve the total affinity for loading two GR monomers on a single palindromic sequence (Ktot), and the extent of GR cooperativity between adjacent palindromic sites (kc,inter). Using this approach, we find that GR assembles at a palindromic response element with a Ktot of 5.18 × 1013 M−2. This corresponds to a binding free energy of −17.4 kcal/mol, and an apparent dissociation constant of 140 nM or −8.7 kcal/mol.24
The inter-site cooperativity (kc,inter) associated with binding the GRE2 promoter was determined to be 69 ± 20, which corresponds to a free energy of −2.3 kcal/mol. Consistent with this, global fitting of the GRE2 binding isotherms to the Hill equation resolved an n of 2.5 ± 0.1. The increase in n above that reported for the GRE1− template is consistent with the moderate to strong cooperativity associated with fully loading the GRE2 promoter. All binding parameters and their associated errors are summarized in Table 3. Finally, the standard deviation for the global fit was 0.068 fractional saturation units.
Table 3.
Resolved free energy changes (kcal/mol) for GR-GRE2 binding interactionsa
| ΔGdi | ≥ −5.1 |
| ΔGtot | −17.4 ± 0.1 |
| ΔGc,inter | −2.3 ± 0.2 |
Errors correspond to 67% confidence intervals.
Discussion
Cooperative binding energetics of GR
Previous biochemical studies of GR have used either isolated domains or partially purified holo-proteins.14, 23, 25, 26 This study represents the first dissection of GR-promoter energetics using highly purified and rigorously characterized full-length receptor. Using analytical ultracentrifugation to determine GR self-assembly state, we found that GR exists as a structurally homogenous monomer up to protein concentrations of at least 10 μM. Using quantitative footprinting to measure GR-promoter binding energetics, we found that GR assembles at a multi-site promoter with strong binding affinity and with significant inter-site cooperativity.
With regard to GR self-association, since sedimentation analyses are capable of detecting at least 10% dimer, the dimerization constant of GR must be no stronger than 100 μM (if it is even capable of dimerizing). Our results thus contradict earlier semi-quantitative studies indicating that GR dimerizes with nanomolar affinity,25, 26 and raise questions as to the physiological relevance of the dimeric GR hormone-binding domain observed by crystallographic analysis.27 The origins of these differences are unclear; however, we note that biochemical estimates of GR dimerization used either partially purified receptor derived from animal tissue25 or unpurified receptor generated by recombinant expression.26 With regard to the crystallographic results, GR dimerization may have been induced by the high concentration of protein needed for crystallization. Alternatively, the dimeric state may be a consequence of crystal packing or non-physiological buffer conditions. Nonetheless, despite these discrepancies, the hydrodynamic asymmetry seen in our sedimentation velocity studies (thus indicative of a non-globular GR structure) is entirely consistent with the natively unfolded N-terminal regions known to exist for GR and other receptors.28–31
Comparison to homologous receptors
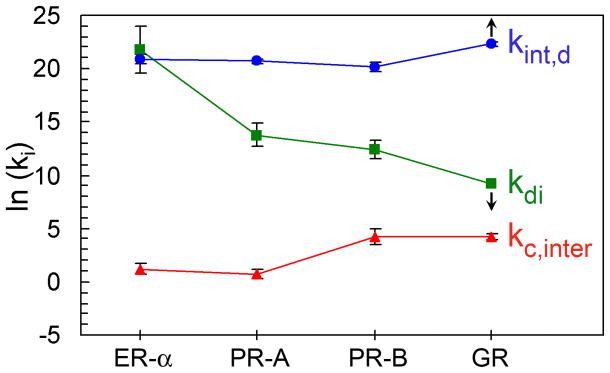
Plotted in Figure 5 are the microstate interaction energetics for PR-A, PR-B and GR binding to the promoter sequence shown in Figure 1D. Also shown are the microstate interaction energetics for ER-α binding to a promoter which differs only in response element sequence.7 All parameters were determined using highly purified receptor preparations analyzed under conditions identical to those used here.5–7 The energetics for ER-α and the two PR isoforms were determined using the well-accepted dimer-binding model: receptors dimerize in the absence of DNA (kdi) and only the pre-formed dimers assemble at DNA binding sites (kint,d). For comparative purposes, we therefore fit the GR footprinting data to the same model assuming the strongest possible dimerization constant consistent with our sedimentation data (100 μM). Interestingly, such a fit reports an intrinsic binding affinity (kint,d) for GR dimer binding of 0.2 nM, comparable to the nanomolar affinities of ER-α, PR-A and PR-B.5–7 This concordance suggests that if GR dimerizes in the absence of DNA, the dimerization affinity is unlikely to be significantly weaker than 100 μM, since that would greatly increase the intrinsic binding affinity. Finally, the dimer-binding model resolved a GR inter-site cooperativity term of −2.3 kcal/mol, unchanged from the Adair fit.
Figure 5. Distribution of microscopic promoter binding affinities for ER-α, PR-A, PR-B, and GR dimer assembly at a two-site promoter.
Individual constants are as follows: Blue circles represent pre-formed dimer binding affinity (kint,d); Green squares represent receptor dimerization affinity (kdi); and red triangles represent inter-site cooperativity (kc,inter). Error bars represent 67% confidence intervals. All parameters were determined under identical solution conditions using either a PRE2 promoter5, 7 or an ERE2 promoter.7 Arrows associated with the GR kdi and kint,d parameters indicate that these values can only decrease or increase, respectively, since the minimum assumed dimerization constant of 100 μM can only become weaker.
Visual inspection makes clear that all the receptors maintain similar intrinsic dimer binding affinities (kint,d). This is not surprising, since the receptor DNA binding domains are highly conserved by sequence, and are structurally similar by crystallographic analysis.32–34 By contrast, the dimerization energetics (kdi) vary dramatically. For example, the nanomolar dimerization affinity seen for ER-α is ~1,000-fold stronger than that of the two PR isoforms, and at least 100,000-fold stronger than that of GR. The inter-site cooperative binding energetics (kc,inter) also vary significantly. For example, ER-α and PR-A show essentially no cooperativity whereas both PR-B and GR exhibit strong cooperative stabilization of ~70-fold. Although cooperativity varies much less than that seen for dimerization, this does not diminish its importance – it is well established that only small changes in cooperative energetics generate dramatic functional consequence for genetic switching mechanisms.18
Functional implications of differential promoter binding energetics
As noted in the Introduction, we are focused on determining the quantitative principles responsible for specificity of steroid receptor-mediated gene regulation. In particular, we are interested in the basis of functional specificity in the face of competitive DNA binding by homologous receptors. Here we attempt to model different competitive binding scenarios that might occur in vivo. We speculate that the large differences in microstate binding energetics seen in Figure 5 serve as the basis for generating receptor-specific and promoter-specific gene regulation. Here we use PR-B and GR as an example – both receptors are strong transcriptional activators, yet are capable of activating overlapping but distinct gene networks.4 The two proteins thus serve as a model system for exploring possible mechanisms of specificity in steroid receptor function.
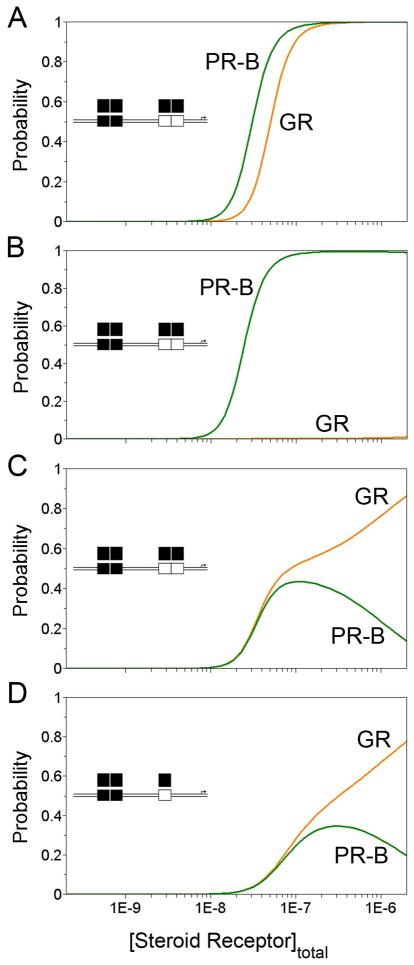
Shown in Figure 6 are the calculated probabilities of the fully-ligated state (e.g. the presumptive transcriptionally active microstate) for GR and PR-B assembly at various promoter layouts, using the experimentally determined binding energetics determined here and in Ref. 7. We simulated both non-competitive and competitive receptor binding to the promoters. In the non-competitive binding scenario (Figure 6A), each receptor is allowed to assemble at the promoter in the absence of the other. In the competitive binding scenarios (Figures 6B–D), the receptors compete for binding sites, assuming that both exist at equimolar concentrations at all points along the simulation. (The equations used for all simulations are presented in Supporting Information.) It is clear that the probability and half-saturation values of the fully-ligated (i.e. transcriptionally active) microstate are similar for both receptors. This is the case regardless of whether one assumes that the receptors bind DNA as pre-formed dimers or by successive monomer binding, thus suggesting that the binding pathway (successive monomer versus pre-formed dimer) is unimportant in receptor function. However, shown in Figure 6B is the same simulation now under competitive binding conditions. To better illustrate how dimerization energetics influence promoter occupancy, we assumed that pre-formed PR-B and GR dimers compete for DNA binding with identical intrinsic binding affinities (0.8 nM) and inter-site cooperative affinities (kc,inter = 70); thus the only difference is in dimerization affinity (4.3 μM for PR-B versus 100 μM for GR). Clearly, PR-B easily outcompetes GR for binding. This is simply because the stronger dimerization energetics of PR-B generate a greater dimer population (i.e. active binding species) relative to GR at identical total protein concentrations. Thus receptor-specific promoter occupancy – and perhaps receptor-specific gene regulation – may be generated even if both receptors exhibit identical intrinsic DNA binding affinities toward the promoter.
Figure 6. Predicted probabilities of the fully-ligated promoter state when bound by either PR-B or GR.
(A) Simulation of non-competitive PR-B (green line) and GR (orange line) binding to the GRE2 promoter using the experimentally determined Ktot values. (B) Simulation of competitive PR-B and GR binding to the GRE2 promoter assuming both receptors bind via a dimer-binding pathway. Simulations were carried out using dimerization constants of 4.3 and 100 μM for PR-B and GR, respectively; intrinsic binding affinities were kept identical. Heterologous promoter occupancy (e.g. PR-B and GR dimers occupying an identical promoter) was not considered since there is no evidence to support this assumption. (C) Simulation of competitive PR-B and GR binding to the GRE2 promoter assuming both receptors bind the promoter via a monomer-binding pathway. Simulations were carried out using dimerization constants of 4.3 μM and 100 μM for PR-B and GR, respectively; identical intra-site cooperativity terms (kc,intra) of 1000; and the assumption that monomer affinity (kint,m) was identical for both half-sites within a palindrome. (D) Simulation of competitive PR-B and GR binding to a promoter containing a single response element and an adjacent half-site, assuming both receptors bind the promoter using a monomer-binding pathway and assumptions described for panel C.
Shown in Figure 6C is the same simulation as in 6B, but now assuming that PR-B and GR bind as successive monomers to the promoter. Monomer binding affinities were determined as follows: 1) PR-B and GR binding isotherms were fit to a monomer-binding model using 4.3 μM and 100 μM dimerization constants, respectively; 2) identical intra-site cooperativity terms (kc,intra) of 1000 were assumed; and 3) monomer binding affinity (kint,m) was assumed to be identical for both half-sites within a single response element. Using these assumptions, similar monomer binding affinities and inter-site cooperativity values were resolved for the two receptors (data not shown). We then carried out the simulations assuming that kint,m, kc,intra and kc,inter were identical, thus the only difference between the receptors was again that of dimerization affinity (kdi). We now see that GR effectively competes for binding at lower protein concentrations and eventually outcompetes PR-B at higher concentrations. In this case, the concentration of assumed DNA binding species (monomer) is decreased for PR-B due to its stronger dimerization energetics. These results point out the importance of determining the rules and states associated with receptor assembly at a promoter – depending upon pathway, a promoter may be preferentially bound by one receptor (Figure 6B) or be competitively bound by both receptors (Figures 6C). Finally, the simulations emphasize the need for kinetic studies to determine the extent to which steroid receptors follow successive monomer versus pre-formed dimer binding pathways.
Finally, shown in Figure 6D is a different promoter layout consisting of a combination of a palindromic and a half-site response element. This type of architecture is seen in natural PR- and GR-regulated promoters such as MMTV35 and in genome-wide computational analyses of receptor binding sites.36 Using a monomer-binding model for both PR-B and GR, we see that the receptors equally compete for binding until receptor concentrations reach supra-physiological. At these concentrations, GR begins to dominate binding due to its weaker dimerization constant and thus larger monomer population. Thus differences in promoter layout, as well as microstate energetics, lead to different outcomes in receptor-specific promoter occupancy.
In summary, combining different microstate energetics with different promoter architectures predicts PR-B-dominated binding in one scenario (Figure 6B) and competitive PR-B and GR binding in a second (Figure 6C and D). Moreover, promoter occupancy is initiated at the tens of nanomolar receptor concentrations thought to exist intracellularly.37 We note that the parameter that differs most between PR-B and GR is dimerization affinity; however, differences in inter-site cooperativity as seen between the PR isoforms and ER-α should allow even greater specificity of promoter occupancy. These results therefore suggest a quantitative framework for considering receptor-specific and promoter-specific gene regulation. It may eventually be possible to predict the receptor-specific transcriptional behavior of natural promoters or design synthetic promoter architectures capable of receptor-specific gene activation – even when multiple receptors are present and active.
Supplementary Material
Acknowledgments
We thank Dr. N. Karl Maluf and Dr. Keith Connaghan for critical discussions. We thank Ms. Fran Crawford and the Kapplar/Marrack Laboratory (National Jewish Medical and Research Center, Denver, CO) for assistance and training in insect cell/baculovirus protein expression systems.
Abbreviations
- AR
androgen receptor
- ER-α
estrogen receptor α-isoform
- ER-β
estrogen receptor β-isoform
- GR
glucocorticoid receptor
- MR
mineralocorticoid receptor
- PR
progesterone receptor
- PR-A
progesterone receptor A-isoform
- PR-B
progesterone receptor B-isoform
- DBD
DNA binding domain
- HBD
hormone binding domain
- AF
activation function
- TA
triamcinolone acetonide
- DTT
dithiothreitol
- β-ME
2-mercaptoethanol
- GRE
glucocorticoid response element
- HRE
hormone response element
- PRE
progesterone response element
- MMTV
mouse mammary tumor virus
Footnotes
This work was supported by NIH grants DK61933 and DK88843 and the Avon Foundation for Women (D.L.B.). J.P.R. was supported by NRSA training fellowship DK897922.
In Figure 6, we simulate the probability of the fully-ligated state for GR and PR-B assembly at various promoter layouts. The equations necessary for modeling the different competitive binding scenarios are shown in Supporting Information. This material is available free of charge via the Internet at http://pubs.acs.org
References
- 1.Tsai MJ, O’Malley BW. Molecular mechanisms of action of steroid/thyroid receptor superfamily members. Annu Rev Biochem. 1994;63:451–486. doi: 10.1146/annurev.bi.63.070194.002315. [DOI] [PubMed] [Google Scholar]
- 2.Monroe DG, Getz BJ, Johnsen SA, Riggs BL, Khosla S, Spelsberg TC. Estrogen receptor isoform-specific regulation of endogenous gene expression in human osteoblastic cell lines expressing either ERalpha or ERbeta. J Cell Biochem. 2003;90:315–326. doi: 10.1002/jcb.10633. [DOI] [PubMed] [Google Scholar]
- 3.Richer JK, Jacobsen BM, Manning NG, Abel MG, Wolf DM, Horwitz KB. Differential gene regulation by the two progesterone receptor isoforms in human breast cancer cells. J Biol Chem. 2002;277:5209–5218. doi: 10.1074/jbc.M110090200. [DOI] [PubMed] [Google Scholar]
- 4.Wan Y, Nordeen SK. Overlapping but distinct gene regulation profiles by glucocorticoids and progestins in human breast cancer cells. Mol Endocrinol. 2002;16:1204–1214. doi: 10.1210/mend.16.6.0848. [DOI] [PubMed] [Google Scholar]
- 5.Connaghan-Jones KD, Heneghan AF, Miura MT, Bain DL. Thermodynamic analysis of progesterone receptor-promoter interactions reveals a molecular model for isoform-specific function. Proc Natl Acad Sci U S A. 2007;104:2187–2192. doi: 10.1073/pnas.0608848104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Heneghan AF, Connaghan-Jones KD, Miura MT, Bain DL. Cooperative DNA binding by the B-isoform of human progesterone receptor: thermodynamic analysis reveals strongly favorable and unfavorable contributions to assembly. Biochemistry. 2006;45:3285–3296. doi: 10.1021/bi052046g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Moody AD, Miura MT, Connaghan KD, Bain DL. Thermodynamic dissection of estrogen receptor-promoter interactions reveals that steroid receptors differentially partition their self-association and promoter binding energetics. Biochemistry. 2012;51:739–749. doi: 10.1021/bi2017156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gill SC, von Hippel PH. Calculation of protein extinction coefficients from amino acid sequence data. Anal Biochem. 1989;182:319–326. doi: 10.1016/0003-2697(89)90602-7. [DOI] [PubMed] [Google Scholar]
- 9.Schuck P. Size-distribution analysis of macromolecules by sedimentation velocity ultracentrifugation and lamm equation modeling. Biophys J. 2000;78:1606–1619. doi: 10.1016/S0006-3495(00)76713-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.van Holde KE. Physical Biochemistry. 2. Prentice-Hall; Englewood Cliffs, CA: 1985. [Google Scholar]
- 11.Laue TM, Shah BD, Ridgeway TM, Pelletier SL. Analytical Ultracentrifugation in Biochemistry and Polymer Science. Royal Society of Chemistry; Cambridge, UK: 1992. [Google Scholar]
- 12.Cohn EJ, Edsall JT. Proteins, Amino Acids, and Peptides. Reinhold; New York, NY: 1943. [Google Scholar]
- 13.Johnson ML, Correia JJ, Yphantis DA, Halvorson HR. Analysis of data from the analytical ultracentrifuge by nonlinear least-squares techniques. Biophys J. 1981;36:575–588. doi: 10.1016/S0006-3495(81)84753-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Jantzen HM, Strahle U, Gloss B, Stewart F, Schmid W, Boshart M, Miksicek R, Schutz G. Cooperativity of glucocorticoid response elements located far upstream of the tyrosine aminotransferase gene. Cell. 1987;49:29–38. doi: 10.1016/0092-8674(87)90752-5. [DOI] [PubMed] [Google Scholar]
- 15.Brenowitz M, Senear DF, Shea MA, Ackers GK. “Footprint” titrations yield valid thermodynamic isotherms. Proc Natl Acad Sci U S A. 1986;83:8462–8466. doi: 10.1073/pnas.83.22.8462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Brenowitz M, Senear DF, Shea MA, Ackers GK. Quantitative DNase footprint titration: a method for studying protein-DNA interactions. Methods Enzymol. 1986;130:132–181. doi: 10.1016/0076-6879(86)30011-9. [DOI] [PubMed] [Google Scholar]
- 17.Connaghan-Jones KD, Moody AD, Bain DL. Quantitative DNase footprint titration: a tool for analyzing the energetics of protein-DNA interactions. Nat Protoc. 2008;3:900–914. doi: 10.1038/nprot.2008.53. [DOI] [PubMed] [Google Scholar]
- 18.Ackers GK, Johnson AD, Shea MA. Quantitative model for gene regulation by lambda phage repressor. Proc Natl Acad Sci U S A. 1982;79:1129–1133. doi: 10.1073/pnas.79.4.1129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hill TL. An Introduction to Statistical Thermodynamics. Dover Publications; New York, NY: 1960. [Google Scholar]
- 20.Philo JS. A method for directly fitting the time derivative of sedimentation velocity data and an alternative algorithm for calculating sedimentation coefficient distribution functions. Anal Biochem. 2000;279:151–163. doi: 10.1006/abio.2000.4480. [DOI] [PubMed] [Google Scholar]
- 21.Nardulli AM, Greene GL, Shapiro DJ. Human estrogen receptor bound to an estrogen response element bends DNA. Mol Endocrinol. 1993;7:331–340. doi: 10.1210/mend.7.3.8483477. [DOI] [PubMed] [Google Scholar]
- 22.Petz LN, Nardulli AM, Kim J, Horwitz KB, Freedman LP, Shapiro DJ. DNA bending is induced by binding of the glucocorticoid receptor DNA binding domain and progesterone receptors to their response element. J Steroid Biochem Mol Biol. 1997;60:31–41. doi: 10.1016/s0960-0760(96)00171-9. [DOI] [PubMed] [Google Scholar]
- 23.Hard T, Dahlman K, Carlstedt-Duke J, Gustafsson JA, Rigler R. Cooperativity and specificity in the interactions between DNA and the glucocorticoid receptor DNA-binding domain. Biochemistry. 1990;29:5358–5364. doi: 10.1021/bi00474a022. [DOI] [PubMed] [Google Scholar]
- 24.Wyman J, Gill SJ. Binding and Linkage: Functional Chemistry of Biological Macromolecules. University Science Books; Mill Valley, CA: 1990. [Google Scholar]
- 25.Perlmann T, Eriksson P, Wrange O. Quantitative analysis of the glucocorticoid receptor-DNA interaction at the mouse mammary tumor virus glucocorticoid response element. J Biol Chem. 1990;265:17222–17229. [PubMed] [Google Scholar]
- 26.Segard-Maurel I, Rajkowski K, Jibard N, Schweizer-Groyer G, Baulieu EE, Cadepond F. Glucocorticosteroid receptor dimerization investigated by analysis of receptor binding to glucocorticosteroid responsive elements using a monomer-dimer equilibrium model. Biochemistry. 1996;35:1634–1642. doi: 10.1021/bi951369h. [DOI] [PubMed] [Google Scholar]
- 27.Bledsoe RK, Montana VG, Stanley TB, Delves CJ, Apolito CJ, McKee DD, Consler TG, Parks DJ, Stewart EL, Willson TM, Lambert MH, Moore JT, Pearce KH, Xu HE. Crystal structure of the glucocorticoid receptor ligand binding domain reveals a novel mode of receptor dimerization and coactivator recognition. Cell. 2002;110:93–105. doi: 10.1016/s0092-8674(02)00817-6. [DOI] [PubMed] [Google Scholar]
- 28.Bain DL, Franden MA, McManaman JL, Takimoto GS, Horwitz KB. The N-terminal region of the human progesterone A-receptor. Structural analysis and the influence of the DNA binding domain. J Biol Chem. 2000;275:7313–7320. doi: 10.1074/jbc.275.10.7313. [DOI] [PubMed] [Google Scholar]
- 29.Bain DL, Franden MA, McManaman JL, Takimoto GS, Horwitz KB. The N-terminal region of human progesterone B-receptors: biophysical and biochemical comparison to A-receptors. J Biol Chem. 2001;276:23825–23831. doi: 10.1074/jbc.M102611200. [DOI] [PubMed] [Google Scholar]
- 30.Baskakov IV, Kumar R, Srinivasan G, Ji YS, Bolen DW, Thompson EB. Trimethylamine N-oxide-induced cooperative folding of an intrinsically unfolded transcription-activating fragment of human glucocorticoid receptor. J Biol Chem. 1999;274:10693–10696. doi: 10.1074/jbc.274.16.10693. [DOI] [PubMed] [Google Scholar]
- 31.Hilser VJ, Thompson EB. Structural dynamics, intrinsic disorder, and allostery in nuclear receptors as transcription factors. J Biol Chem. 2011;286:39675–39682. doi: 10.1074/jbc.R111.278929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Luisi BF, Xu WX, Otwinowski Z, Freedman LP, Yamamoto KR, Sigler PB. Crystallographic analysis of the interaction of the glucocorticoid receptor with DNA. Nature. 1991;352:497–505. doi: 10.1038/352497a0. [DOI] [PubMed] [Google Scholar]
- 33.Roemer SC, Donham DC, Sherman L, Pon VH, Edwards DP, Churchill ME. Structure of the progesterone receptor-deoxyribonucleic acid complex: novel interactions required for binding to half-site response elements. Mol Endocrinol. 2006;20:3042–3052. doi: 10.1210/me.2005-0511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Schwabe JW, Chapman L, Finch JT, Rhodes D. The crystal structure of the estrogen receptor DNA-binding domain bound to DNA: how receptors discriminate between their response elements. Cell. 1993;75:567–578. doi: 10.1016/0092-8674(93)90390-c. [DOI] [PubMed] [Google Scholar]
- 35.Connaghan-Jones KD, Heneghan AF, Miura MT, Bain DL. Thermodynamic dissection of progesterone receptor interactions at the mouse mammary tumor virus promoter: monomer binding and strong cooperativity dominate the assembly reaction. J Mol Biol. 2008;377:1144–1160. doi: 10.1016/j.jmb.2008.01.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Jacobsen BM, Jambal P, Schittone SA, Horwitz KB. ALU repeats in promoters are position-dependent co-response elements (coRE) that enhance or repress transcription by dimeric and monomeric progesterone receptors. Mol Endocrinol. 2009;23:989–1000. doi: 10.1210/me.2009-0048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Theofan G, Notides AC. Characterization of the calf uterine progesterone receptor and its stabilization by nucleic acids. Endocrinology. 1984;114:1173–1179. doi: 10.1210/endo-114-4-1173. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.