Finite Element Estimation of Protein-Ligand Association Rates with Post-Encounter Effects: Applications to Calcium binding in Troponin C and SERCA

Abstract

We introduce a computational pipeline and suite of software tools for the approximation of diffusion-limited binding based on a recently developed theoretical framework. Our approach handles molecular geometries generated from high-resolution structural data and can account for active sites buried within the protein or behind gating mechanisms. Using tools from the FEniCS library and the APBS solver, we implement a numerical code for our method and study two Ca²⁺-binding proteins: Troponin C and the Sarcoplasmic Reticulum Ca²⁺ ATPase (SERCA). We find that a combination of diffusional encounter and internal ‘buried channel’ descriptions provide superior descriptions of association rates, improving estimates by orders of magnitude.

1. Introduction and Motivation

Examples abound of proteins that have evolved to maximize substrate association rates. A common factor in fast association rates is the enhanced diffusion of ligands adjacent to a protein’s active site, through favorable electrostatic interactions [46] that counterbalance diffusional barriers imposed by geometry. Dating back to Smoluchowki [37], descriptions for the diffusional encounter rate, k_D, between enzyme and substrate have been proposed; Bashford provides an excellent review of these in [2]. In essence, the formulations describe the interplay of the diffusion constant of the substrate with the geometry of the reacting species.

A common approach for including the contribution of electrostatics proceeds through the Smoluchowski equation given in equation (1), which relates the time-dependent change in substrate concentration due to fluxes arising from the concentration gradient and an electrostatic potential. Recently, a numerical solution to this equation was implemented, which provides an estimate for k_D, given the solvent-accessible surface of a proteins and the electrostatic potential [11]. While this software represents exciting progress toward modeling substrate association at the molecular level, its focus on globular proteins limits its application to non-trivial geometries such as trans-membrane proteins and macro-structures such as DNA and microtubules.

Further complicating this picture are the roles of conformational changes [51] and binding pathways, such as channels, that present diffusional barriers to the active site [4]. The factors can depress observed association rates relative to the diffusional encounter rate between enzyme and substrate. Recent works [4, 3] proposed analytical solutions to the observed association rate, k_on, which treat the association as an external, diffusion-encounter problem followed by an internal, post-encounter problem. The later stage reflects the effects of stochastic gating and potentials of mean force along a pathway bridging the encounter-surface and the active site; both of which can be estimated from molecular dynamics and Brownian dynamics.

Our computational pipeline is based on this mathematical framework developed for binding in gated channels, i.e. narrow regions of the geometry near the active site [3, 4]. We will treat the notion of ‘channel’ more generically as any binding pathway bridging the outer molecular surface and the active site. The results we present here emphasize the importance of these theoretical developments as well as demonstrate the feasibility of integrating the effects of diffusional and post-encounter effects into a suite of algorithms. We use a finite element method to compute the steady state of ionic diffusion in a spatially-realistic three dimensional region exterior the molecule with an absorbing boundary condition taken at the entrance to the channel. Inside the channel, we use a molecular dynamics simulation to approximate the local potential of mean force V (x) which can then be used to estimate the rate of transport of ions from the channel entrance to the active site. If the access to the channel is blocked stochastically by a gating mechanism, we make use of formulas describing how the approximation of the association rate should be modified according to the comparison of gating speed to the characteristic diffusion time.

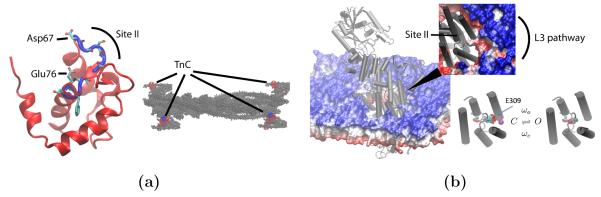
We apply this numerical protocol to two proteins, Troponin C (TnC) and the Sarcoplasmic Reticulum Ca²⁺ ATPase (SERCA), which exemplify the concepts of the electrostatically-driven diffusional encounter and post-encounter effects in binding of Ca²⁺. Troponin C and SERCA serve vital roles in muscle cells by controlling the cell’s contractile function and reabsorbing cytosolic calcium, respectively [7]; molecular-level details of these proteins and Ca²⁺ binding mechanism could improve our understanding of calcium dynamics in contractile cells. We consider TnC both in isolation and bound to a cryo-EM reconstruction of the thin filament (Fig. 1a), as well as SERCA in its native lipid membrane environment (Fig. 1b). To the best of our knowledge, this is the first time substrate association has been modeled using proteins situated in their native environment. In both cases, we consider the contribution of molecular interactions with the proteins, which are captured in a potential of mean force calculations (Fig. 2). For the case of SERCA, we also consider the influence of an apparent gated binding event exemplified in Fig. 1b. We show that accounting for conformational gating and buried binding channels profoundly impacts the association rates.

Figure 1. Troponin C and SERCA molecular structures.

(a) Isolated troponin C molecule structure with Ca²⁺ binding site II (blue).(left) TnC (red, blue) on thin filament (gray) (right) (b) SERCA (gray cartoon) embedded in lipid membrane. Red to blue shading indicates relative height of membrane. Inset magnifies putative L3 pathway leading to Ca²⁺ binding site II; lipid coloring is rescaled to accentuate divot near L3 pathway (left) Putative gating event involving E309 at site II. (right)

Figure 2.

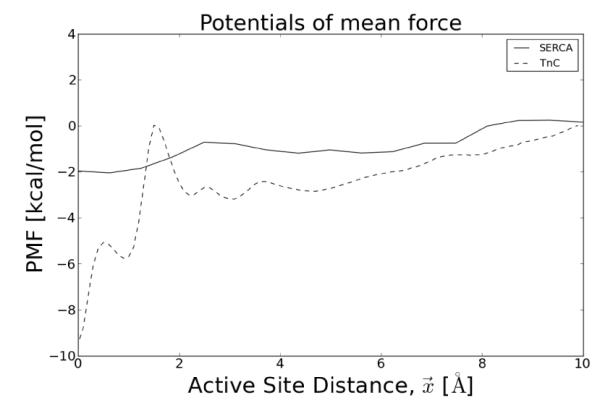
Potentials of mean force. Computed for Ca²⁺ binding to Asp67 in the Troponin C active site (site II) (in preparation) and Asp800 of SERCA site II [25]

The paper is outlined as follows. In Section 2, we explain our algorithms and computational tools. In Section 3, we state and discuss our results. We give concluding remarks and suggest some future research directions in Section 4.

2. Methods and Algorithms

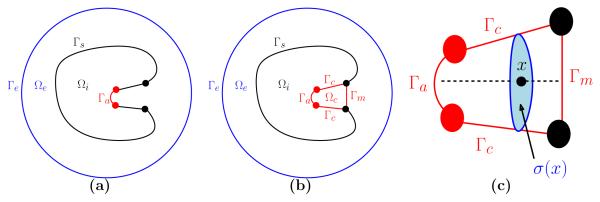
We present a hierarchy of methods for approximating a generic substrate binding rate k_on. The approximation k_D ignores the presence of a buried channel and any effects of a local potential of mean force (PMF). The approximation k_ss accounts for a local PMF in the channel but ignores any gating effects. The approximation k_g includes a local PMF and gating effects. We will describe each algorithm and the supporting mathematical theory at a high level in turn in Sections 2.1-2.3, followed by a more in depth description of the computational tools used to implement each piece. Notation for domains with or without a channel are shown in Fig. 3 and described in the caption. The mathematical framework was introduced by Zhou in [50] and expanded upon recently in [3, 4].

Figure 3.

Notation for our computational domains. (a) First, the domain is treated without a buried channel. The molecular interior Ω_i has an active site Γ_a and a non-reactive boundary Γ_s. (b) When the domain is treated as a buried channel, the molecular interior Ω_i is bounded by Γ_s ⋃ Γ_c ⋃ Γ_a. The active site Γ_a can be accessed from the exterior region Ω_e by passing through the buried channel region Ω_c. Access to Ω_c is through the mouth of the channel Γ_m which may represent a gating mechanism. Both domain types sit inside a large sphere with boundary Γ_e. (c) Inside the channel, the reaction coordinate axis (shown here as a dashed line) is described by the coordinate x ranging from x = 0 (at the active site Γ_a) to the x = L (at the channel entrance Γ_m). The cross-sectional region at a particular x is called σ(x) with area denoted by ∣σ(x)∣.

2.1. Steady state rate constant computation without channels

In the case where no channel is assumed, the time-dependent Smoluchowski problem is formulated as follows: Find an ionic concentration function $\rho :{\overline{\Omega }}_e\times [0,T]\to \mathbb{R}$ such that

$$\frac{\partial \rho }{\partial t}=D(\Delta \rho -\nabla \cdot (\beta \rho \overrightarrow{E}\left)\right)$$ (1)

in Ω_e, where D is the diffusion constant, β := 1/k_BT is the inverse Boltzmann energy with k_B the Boltzmann constant and T the temperature, and ϕ the electrostatic potential, which is related to the electric field, $\overrightarrow{E}$, via the standard equation $\overrightarrow{E}≔-\nabla \varphi$. The boundary conditions are taken to be

$$\overrightarrow{J}\cdot \widehat{n}=0\text{on}{\Gamma }_s,\rho =\alpha \text{on}{\Gamma }_a,\rho =\rho b\text{on}{\Gamma }_e,$$ (2)

where $\overrightarrow{J}≔D({\nabla }_{\rho }-{\beta }_{\rho }\overrightarrow{E})$ is the flux of ρ, α is the relative absorption of substrate at the active site, and ρ_b is the bulk ionic concentration, assumed to be constant outside of Ω_e, and ${\rho }_b$ is the surface normal along Γ. To compute the reaction rate in this context, one solves the steady state problem

$$\frac{\partial \rho }{\partial t}=D(\Delta \rho -\nabla \cdot (\beta \rho \overrightarrow{E}\left)\right)=0,$$ (3)

and computes the accompanying steady state flux ${\overrightarrow{J}}_{\mathit{ss}}$. The reaction rate for the steady state reaction rate with no channel (e.g. the diffusional encounter), k_D is then determined by an area integral of the incident flux [38]

$$k_D=\frac{1}{{\rho }_b}{\int }_{{\Gamma }_a}{\overrightarrow{J}}_{\mathit{ss}}\cdot \widehat{n}\mathit{ds}.$$ (4)

We approximate this by the following algorithm.

Algorithm 1 (Binding site not in a channel)

Input: Hard sphere model of a molecule, with marked boundaries Γ_s and Γ_a

1. Compute the electrostatic potential ϕ on the volumetric mesh using APBS.

2. Compute the steady-state solution ρ from (3) using SMOL.PY.

3. Compute k_D from (4) using SMOL.PY.

Output: Association rate k_D

2.2. Steady state rate constant computation for ungated buried channels

Now we consider the case where the active site lies at the bottom of a buried channel as shown in Fig. 3b, but no gating mechanism is assumed. Suppose that the channel is symmetrical about the x-axis such that the binding site of the molecule is located at the origin and the mouth of the channel, Γ_a, is contained in the plane x = L. Let $\sigma \left(x\right)\subset {\mathbb{R}}^3$ denote the cross-sectional region of the channel for x ∈ [0, L] and ∣σ(x)∣ the corresponding area. Assume that the ligand dynamics are sufficiently fast to ensure local steady state on each cross section σ(x). Let V (x) denote the one-dimensional potential of mean force inside the channel; this can be computed analytically for simple channel geometry (e.g. cylindrical) or approximated using molecular dynamics simulations.

Berezhkovskii et al suggest in [4] that the steady state rate constant for the buried channel domain, k_ss, can be estimating using the formula

$$\frac{1}{k_{\mathit{ss}}}=\frac{1}{k_{\mathit{ext}}}+\frac{1}{k_{\mathit{int}}}+\frac{1}{k_{\mathit{bind}}}\approx \frac{1}{k_{\mathit{ext}}}+\frac{1}{k_{\mathit{int}}}$$ (5)

Here, k_ext denotes the steady state rate constant for ligands outside the channel to be absorbed at the channel entrance Γ_m. This rate can be determined by assigning a fully absorbing boundary condition ρ = 0 on Γ_m and using formula (4) on the modified exterior geometry Ω_e shown in Fig. 3b. The term k_int is the association rate to the active site inside the channel and is estimated by

$$\frac{1}{k_{\mathit{int}}}={\int }_0^L\frac{e^{\beta V\left(x\right)}}{D\mid \sigma \left(x\right)\mid }\mathit{dx}$$ (6)

where integration of the potential of mean force, V (x), is carried out over the length of the channel (from x = 0 to x = L), D is the bulk diffusion constant, and ∣σ(x)∣ signifies the area of the cross-sectional region at x (see Fig. 3c).

The term k_bind is the chemical reaction rate and is given by the formula κ₀σ(0)e^–βV(0) where κ₀ indicates the intrinsic binding rate to the surface of the binding site. We will assume, as is typical in this context [36], that κ₀ is sufficiently large to make the last summand negligible. We thus have the following algorithm.

Algorithm 2 (Binding site in a channel)

Input: Hard sphere model of a molecule, with marked boundaries Γ_s, Γ_a, Γ_c, Γ_m, and value of diffusion constant inside channel Ω_c

1. Compute k_ext using Algorithm 1 with active site replaced by channel entrance.

2. Compute V (x) in Ω_c using an appropriate molecular dynamics simulation.

3. Compute σ(x), i.e. the cross-sectional area as a function of the reaction coordinate.

4. Compute k_int from (6), then k_ss from (5) using CHANNEL SMOL.PY.

Output: Association rate k_ss

2.3. Steady state rate constant computation for gated buried channels

In the event that access to the binding site is intermittently open, we summarize the Smoluchowski equation under gating conditions. To this end we consider open (absorbing) and closed (reflective) states of the active site with a ligand-independent forward rate of ω_a and backward rate of ω_r, as indicated by

$$C\underset{{\omega }_r}{\overset{{\omega }_a}{\leftrightharpoons }}O$$ (7)

The presence of a ligand near a gate can affect the rate at which it opens and closes, hence ω_a and ω_r have a dependence on the spatial variable x. These rates satisfy the detailed balance condition [50, 3, 9]:

$$\frac{{\omega }_a\left(\mathrm{x}\right)}{{\omega }_r\left(\mathrm{x}\right)}=\frac{{\omega }_a}{{\omega }_r}{e}^{-\beta \left[U_a\right(\mathrm{x})-U_r(\mathrm{x}\left)\right]}$$ (8)

where U_a(x) and U_r(x) are the interaction potentials associated with the open (absorbing boundary) and closed (reflective boundary) conformational states, respectively, and are computed using

$${\rho }_a={\omega }_a\left(\mathrm{x}\right)∕\omega \left(\mathrm{x}\right);{\rho }_r={\omega }_r\left(\mathrm{x}\right)∕\omega \left(\mathrm{x}\right)$$ (9)

where ω(x) = ω_a(x) + ω_r(x).

Under this scenario, Barreda et al [3] suggest that the rate constant subject to gating at the active site may be estimated from the coupled PDE system [3]:

$$\frac{\partial {\rho }_a}{\partial t}=D(\Delta \rho -\nabla \cdot (\beta \rho \overrightarrow{E}\left)\right)-{\omega }_r\left(\mathrm{x}\right){\rho }_a+{\omega }_a\left(\mathrm{x}\right){\rho }_r$$ (10)

$$\frac{\partial {\rho }_r}{\partial t}=D(\Delta \rho -\nabla \cdot (\beta \rho \overrightarrow{E}\left)\right)+{\omega }_r\left(\mathrm{x}\right){\rho }_a+{\omega }_a\left(\mathrm{x}\right){\rho }_r$$ (11)

where ρ_a and ρ_r are the pair-wise distributions associated with the absorbing and reflecting boundary conditions at Γ_a, respectively. Note that both ρ_a and ρ_r are distributions for ρ but refer to different boundary conditions on the active site.

The association rate k_g, resulting from the governing equations (10)-(11) can be expressed in a simplified form under two gating limits, which we elaborate upon in Section 6.2. These limits refer to the speed of gating relative to the characteristic diffusion time, τ_d, e.g. the time required for the substrate to diffuse sufficiently far away from the protein. Under a relatively slow gating speed, i.e. when $\omega \gg {\tau }_d^{-1}$, we generalize the result of Barreda et al. [3] equation (3.24a) to yield

$$\frac{1}{k_g^{\text{slow}}}=\frac{1}{p_a}\left(\frac{1}{k_{\mathit{ext}}}+{\int }_0^L\frac{e^{\beta V_a\left(x\right)}}{D\mid \sigma \left(x\right)\mid }\mathit{dx}\right)$$ (12)

where k_ext is as in (5) and V_a(x) represents a 1D potential of mean force that quantifies the attraction of the ligand for the open state of the binding gate. Intuitively, this limit suggests that the probability of reaction is dependent on the whether the slowly gated active site is open for each rapid visit of the substrate to the vicinity of the gate. When $\omega \gg {\tau }_d^{-1}$, the gating speed is fast relative to τ_d, yielding

$$\frac{1}{k_g^{\text{fast}}}=\frac{1}{k_{\mathit{ext}}}+{\int }_0^L\frac{e^{\beta V_{\mathit{eff}}\left(x\right)}}{D\mid \sigma \left(x\right)\mid }\mathit{dx}$$ (13)

where V_eff is determined from

$$e^{-\beta V_{\mathit{eff}}}=p_a{e}^{-\beta V_a}+p_r{e}^{-\beta V_r}.$$ (14)

In this gating extreme, the gate is expected to present an open state before the substrate diffuses away from the reaction vicinity. Thus, from the perspective of the substrate, the gate is always open. While we have considered here only two reacting states, the approach may be extended to an arbitrary number of states as follows from [43, Appendix A].

We summarize this in the following algorithm.

Algorithm 3 (Binding site in a gated channel)

Input: hard sphere model of a molecule, with marked boundaries Γ_s, Γ_a, Γ_c, Γ_m, and gating rates

1. Compute transition rate constants ω_a and ω_r from (7) using molecular dynamics simulations.

2. Compute potentials of mean force V_a and V_r for open and closed states.

3. Compute k_ext using Algorithm 1.

4. Compute V_eff using (14).

5. Compute k_PMF using Algorithm 2, with V_eff in place of V (x).

6. Compute $k_g^{\text{slow}}$ from (12) if ω_a + ω_r >> τ_d or $k_g^{\text{fast}}$ from (13) if ω_a + ω_r << τ_d via GATED.PY.

Output: Association rate k_g

We now explain the details of the methods used in our implementation of Algorithms 1, 2, and 3.

2.4. Molecular mesh

The molecular surface is represented as a mesh approximating the Connolly surface and may be generated by applying the EDTSurf [48] package to Protein Data Bank [5] data of the atomic substructure of the molecule. For this manuscript, we consider three geometry types: globular, linear and planar, which correspond to our isolated TnC (Fig. 5a,b), thin filament (Fig. 5c) and SERCA cases (Fig. 6a), respectively. Using the resulting molecular mesh, we use the BLAMER suite to define an encapsulating region (sphere for a globular protein, cylinder for linear, and rectangular for planar systems). BLAMER is a version of Blender (www.blender.org) which has been bootstrapped with the python implementation of Gamer [49]. While a standalone manuscript is not available, the package has been used in [18]. For globular proteins, the radius of the outer sphere was 10 times the radius of the molecule. For linear proteins, we used a cylinder whose height was equal to the molecule length along the dominant axis, and whose radius was twice the width along the minor axis. For planar geometries, we chose a rectangular box whose x and y dimensions were equal to the dimensions of the modeled lipid bilayer, and whose height was three times the height of the molecule.

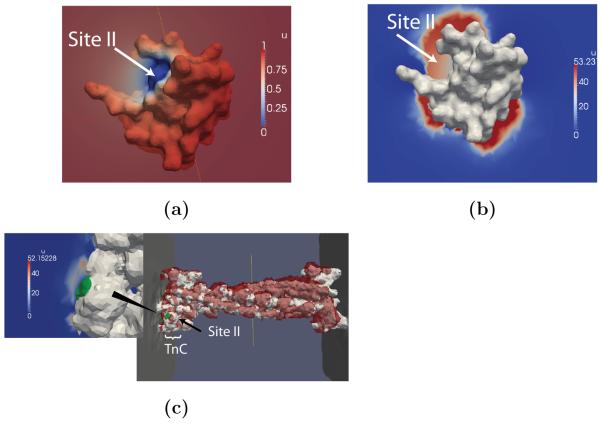
Figure 5.

Steady-state Ca²⁺ distributions about Troponin C. The TnC N-terminal domain in (a) absence and (b) presence of electrostatic potential, as well as (c) TnC on the actin myofilament (left) and with red contours corresponding to 40 M [Ca²⁺] (right)

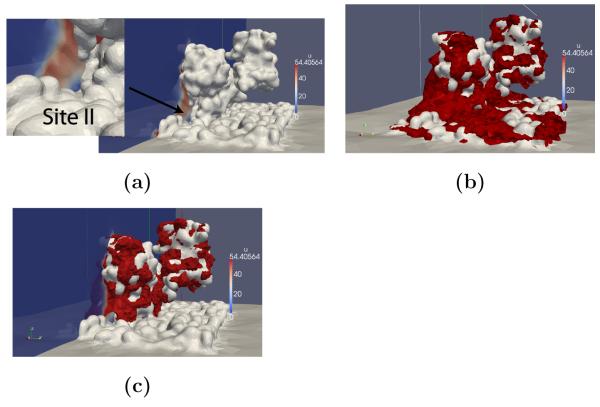
Figure 6.

Steady state Ca²⁺ distributions about SERCA. (a) Ca²⁺ steady-state distribution perpendicular to the SERCA active site (gray). Contours of elevated Ca²⁺ density for the (b) charged and (c) uncharged lipids.

MolecularMesh mesh in the GAMer package [49] (www.fetk.org) can be used to automatically generate finite element-ready meshes for globular proteins. For linear and planar cases, we use the Boolean difference modifier in Blender to create a new mesh based on the encapsulating region and the molecular mesh. The active sites were chosen to coincide with the binding sites of Ca²⁺. For convenience, we labeled the molecular surface comprising the active site with the absorbing condition. Since we are partitioning the diffusion domain into a diffusional encounter region and a post-encounter region, it may be more suitable to position the absorbing boundary for the diffusional encounter at the outer limits of the potential of mean force domain.

Since the diffusional encounter rate scales with the radius of the absorbing center, our approximation likely underestimates the diffusional encounter rate by a factor of (r_m/r_pmf, where r_M and r_pmf reflect the location of the molecular surface and exterior problem interface. All other boundaries, including the molecular surface were assigned reflective boundary conditions. The GAMer package was used within Blender (www.blender.org) to repair and refine the mesh. The refined mesh was tetrahedralized via TETGEN (tetgen.berlios.de).

2.5. Electrostatic potential

APBS provides a standard protocol for computing the electrostatic potential due to a solvated protein via numerical evaluation of the Poisson-Boltzmann equation [1],

$$-\nabla \cdot \left(∊\right(r)\nabla \varphi (r\left)\right)+{\kappa }^2\left(r\right)\sinh \left(\varphi \right(r\left)\right)=\frac{e}{k_{B}T}4\pi \rho \left(r\right)$$ (15)

where ϕ = eΦ/k_BT is the reduced form of the electrostatic potential Φ, ρ is the fixed distribution of charges corresponding to the protein, κ² is the Debye screening parameter due to a monovalent electrolyte solution, and ∊ is the dielectric constant defined over the protein and the solvent domains. For small ψ, the sinh(ψ) contribution from the electrolyte (15) may be linearized to yield the linearized Poisson-Boltzmann equation, which we used for estimating the electrostatic potential for dilute (I = 0 mM) or near physiological (I = 200 mM) ionic strength assuming 2 Å radius monovalent ions.

We computed the electrostatic potential at several grid resolutions ranging from 0.3 Å to 25 Å resolution around the active site, in order to balance higher accuracy required around the active site with a potential defined over the entire simulation domain. This was done by using the MG-AUTO function to first compute the potential on a 1650×1650×1650 Å grid using 65 grid points along each axis, adaptively focus the solution to increasing resolutions until the desired resolution is obtained. The resulting finite-difference APBS grids were interpolated onto the finite element molecule meshes using a tri-linear interpolation algorithm distributed with SMOL [11].

The local concentration of ions, ρ(r), due to a fixed electric potential, ϕ(r), relative to the bulk concentration, ρ_bulk is given by the Boltzmann equation ρ(r) = ρ_bulke^–βqϕ. With this description, the electrostatic potential from APBS predicts unphysically high concentrations of Ca²⁺. In reality, the counter-ion density saturates directly adjacent to the charged molecular surface, giving rise to the Stern layer [24]. Therefore, we assume that the maximum concentration of Ca²⁺ along the molecular surface is 55 M, and truncate the electrostatic potential to limit local [Ca²⁺] to the maximum concentration.

2.6. Potential of mean force

The potential of mean force, V (x), is computed via molecular dynamics simulations along a suitable reaction coordinate, x. Since the purpose of this study is to illustrate the incorporation of estimated PMF data into a numerical model, we are utilizing data from molecular dynamics studies of Troponin C (in preparation) and SERCA [26] for this experiment. In these studies, the PMF along the reaction coordinate was computed using Adaptive Force Biasing [14] and Weighted Histogram Analysis Method [17], respectively, and details of the windows and convergence are described in our manuscripts. In short, for SERCA we performed 6 ns of umbrella sampling at each 0.5 Å interval between the Ca²⁺ site II binding region and the mouth of the binding channel; the potential of mean force was computed with WHAM and confidence intervals were reported based on a bootstrapping procedure included with WHAM. For TnC, we performed ABF calcuations until the potential of mean force changed little between simulations (after roughly 100 ns).

We assume in both cases the the diffusion constant for Ca²⁺ within the binding channel is 60% of its bulk value of 780 μm²/s, findings from [6], where D was explicitly computed within the K+ binding channel. For the computation of k_PMF, we integrate the V (x) and the additional spatially-dependent terms numerically using the numpy trapz trapezoidal integration function. For the case of ligand-induced gating, for simplicity we assume that V_r = 0 and V_a is equal to the potential of mean force at the gate location.

2.7. Gating kinetics

Gating kinetics are determined from molecular dynamics experiments. For our system, we consider two states that are distinguished by a change in side chain position. In practice, more complex gating events could be characterized by partitioning a molecular dynamics trajectory structurally diverse sets based on k-means clustering of the root mean squared deviations. ω_a and ω_r are determined by counting the transitions between the states, yielding a transition probability matrix.

2.8. Numerical solution

We introduce a python-based program dubbed Smolfin, to perform the numerical approximation and computation of the problems described above. The molecular mesh, the electrostatic potential, and, as appropriate, the 1D potential of mean force and gating forward and backward rates, are provided as input. Smolfin has operations for loading the marked finite element mesh corresponding to the simulation domain and defining the Dirichlet boundary conditions at the appropriate boundaries. Smolfin then solves a weak form of the Smoluchowski equation using a piecewise linear Galerkin finite element method with the default direct linear solver. The approach is based on [38], with the exception of using DOLFIN [30], the C++/python interface to the numerical PDE solver FEniCS (http://fenics.project.org), a finite element package. Smolfin obtains k_on by integrating the steady-state flux along Γ_a according to (4). Additional details and references on the Smoluchowski solver are given in the Supplement Section 6.3. Parameters used in this study are summarized in Tbl. 2.

3. Results

3.1. A fully-absorbing, attractively charged sphere

We validate the proposed numerical protocol using a prototypical system for which analytical estimates of the association rate are available. We begin with a neutral and uniformly reacting sphere. We created the mesh for an 12.5 Å radius ion using GAMer. The resulting mesh contained 21,706 vertices and 97,315 simplices. All numerical solutions in this paper were computed in less than 1 min on a single CPU.

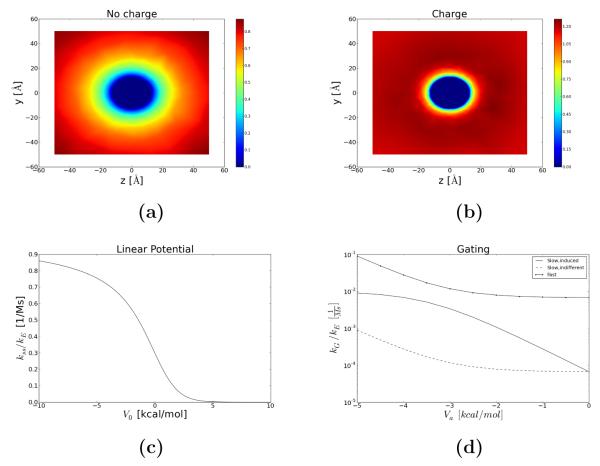
For the spherical case, we chose R=12.25 [Å] for a typical globular protein, D=780 [μm²/s] for Ca²⁺, and an infinitely dilute solution. Using Alg. 1, we predict the steady state distribution, ρ_ss, shown in Fig. 4a. The steady state probability density, ρ_ss approaches the bulk value at the periphery and zero at the active site, as specified by our boundary conditions. Kimball and Collins quantified the association rate for this scenario using

$$k_{\mathit{on}}=4\pi \mathit{DR}$$ (16)

where R is the radius of sphere and D is the diffusion constant for the reacting species [12]. Smolfin predicts k_on = 7.09× 10⁹, which is in almost exact agreement with the analytical estimate of k_on = 7.23× 10⁹ [1/Ms]. We then consider a negatively charged sphere, for which the interaction potential can by described by Coulombic potential of mean force, W(r) = q/r, where q is the effective ligand charge. In Fig. 4b we show that in the presence of an oppositely-charged electrostatic potential, the probability density scarcely deviates from the bulk value except within a few angstroms of the reacting sphere. This leads to a significantly larger concentration gradient adjacent to the active site that contributes to the higher flux at Γ_a and results in an increased value of k_on. Assuming spherical symmetry, Song et al. [38] demonstrate that the analytical solution to the Smoluchowski equation in the presence of a spherically-symmetric electrostatic potential takes the form

$$k=4\pi D{\mathit{qp}}_{\text{bulk}}\left(\frac{e^{q∕r_1}}{e^{q∕r_1}-e^{q∕r_2}}\right)$$ (17)

where r₁ is the radius of the reacting sphere, r₂ is the radius of the outer sphere (we assume r₂ → inf) and q is the effective ligand charge. Our predicted k_on (3.49× 10¹⁰) is slightly larger than the analytical prediction using (17) (9.6× 10⁹) [1/Ms]; the slight error may be due to assuming a linear interpolation scheme for mapping the APBS electrostatic potential onto the finite element mesh, or our truncation of the potential at the molecular boundary to yield a maximum 55M Ca2+ concentration. This case exemplifies the role of favorable electrostatic interactions in driving charged substrates at rates higher than permitted by diffusion alone, as is commonly observed in biological systems.

Figure 4.

Ca²⁺ binding predictions for a uniformly reacting sphere. Steady state ρ distribution around (a) neutral and (b) charged sphere. (c) k_PMF as a function of barrier height, V₀, in a linear potential (d) k_g under ligand-induced slow gating (−), ligand-independent slow gating (−) and fast gating (−.) in a constant binding channel potential with a range of ligand-dependent gating potentials, V_a.

In the following example, we compute the association rate resulting from the diffusional encounter with the molecular surface and subsequent diffusion along a linear potential toward the active site, which is a reasonable approximation to the binding potential of mean force in Fig. 2. We assume energetic barriers ranging from V_a = −10 to V_a = 10 [kcal/mol], which spans the range of PMF barriers encountered in our recent simulation studies (in preparation). We furthermore assume a cylindrical binding channel of length L=10 [Å] and radius R= 5 [Å]. Based on (5), k_on is dominated by the diffusional encounter rate for attractive potentials, while k_pmf dominates when unfavorable barriers are present. Indeed we observe in Fig. 4c that k_ss ≈ k_D for attractive barriers and rapidly decreases as the barrier assumes larger unfavorable values (approximately for V > 2.5 kcal/mol).

Lastly, we consider ligand-independent versus ligand-dependent gating in the fast and slow gating limits. For the slow gating scenario, we choose ω(r) = 0.01 for r far from the protein, while ω(r) at the active site is determined based on the conformation-dependent potentials U_a and U_r in (8). In Fig. 4d, we demonstrate k_on for a range of ligand-dependent potentials, spanning U_a = −5 to U_a = 0 [kcal/mol]. We note that in the fast gating limit, k_on approaches the ungated limit (although still reflecting the time spent diffusing within the channel), whereas the slow gating values report drastically reduce association rates based on the open probability. The ligand-dependent gating rate offers nearly an order of magnitude higher association rate compared to the ligand- independent case for strong potentials. As the attractive U_a diminishes, the ligand-induced gating limit approaches that of the ligand-independent case.

3.2. Troponin C

Myofilaments contract owing to intercalation of the thick filaments, comprised of myosin, and the actin chains forming the thin filament (TF). Contraction is tightly regulated by Troponin proteins tethered to the TF, and in particular, Ca²⁺ binding to TnC sparks the initial stages of the concerted process [15]. Troponin C is a 161 residue protein consisting of two Ca²⁺ binding domains bridged by a linker region [45]. The C-terminal domain is bound to the TF, while the N-terminal domain (Fig. 1a) responds to physiological changes in [Ca²⁺] [45] and induces changes in the Troponin complex. Characterizing the dynamics of Ca²⁺ binding in light of molecular geometry and charge distribution, provides unique insight into muscle cell contraction. To this end, we compute Ca²⁺ association rates to an isolated Troponin C fragment with the active site at the solvent-exposed surface, second to a ’buried’ binding site, and lastly to Troponin C embedded to a complete thin-filament subunit.

We begin with the Ca²⁺-free form of cardiac troponin C (PDB code: 1SPY) determined from NMR [41], This structure consists of the N-terminal domain, which contains the alpha helix-loop EF hand responsible for binding Ca²⁺ at physiological concentrations [35]. We chose Glu76, a residue from site II that directly coordinates Ca²⁺, as the centroid of the active site and labeled the molecular surface within 5 Å of the active site as Γ_a. Using GAMer the resulting mesh had 59,860 vertices and 276,072 simplices.

We apply Alg. 1 to this geometry in absence of the electrostatic potential and obtain the steady-state distribution of ρ shown in Fig. 5a). Here we observe that the [Ca²⁺]≈0 at the active site and is nearly equal to ρ_bulk within 10 Å of the active site; this solution yields a k_D of 4.4× 10⁸ [1/Ms]. The k_D for the uncharged Troponin C is about one order of magnitude smaller than the rate predicted for the uncharged sphere of similar radius and indicates that the non-trivial molecular geometry and smaller active region limit the association rate of Ca²⁺.

Introducing the electrostatic potential into the numerical solution yields the steady state distribution in Fig. 5b. In particular, we observe an accumulation of Ca²⁺ density several-fold higher than the bulk concentration at several regions of the protein, including the active site. Directly adjacent to the active site, we again see large concentration gradients similar to the charged sphere case. Thus the favorable electrostatic potential, which is considerably larger in magnitude than the sphere case, yields a nearly 50-fold increase in the association rate to k_on = 2.14x10¹⁰ [1/Ms]. However, this estimate is nearly 1,000 times faster than experimental estimates (10⁷ to 10⁸ [1/Ms] [35, 19]).

We attribute the disparity between the diffusional encounter rate and experimental estimates to post-encounter interactions that greatly reduce the association rate to the active site. Moreover, prior studies evidence a change in flexibility at site II [40, 28] which we postulate may contribute to an entropic penalty to binding. These effects manifest in a complicated potential of mean force along a reaction coordinate defined as the distance between Ca²⁺ and site II residue D76 in a related study (in preparation).

We note that far from the protein, the potential gradually decreases with smaller values of R, which is indicative of the electrostatic attraction between substrate and TnC. At r ≈ 1.8 [Å] we observe an abrupt barrier of 2.7 [kcal/mol] that that we postulated arises from a competition between the free energy cost upon shifting from coordination state involving water to one involving the binding residues in the active site (Asp65, Asp67, Ser69, Thr71, and Glu76 [45], in preparation) . We include the contribution of this PMF to our estimate of k_on using Alg. 2. For simplicity, we assume a cylindrical reaction path with a radius of 5 Å. We find that the PMF reduces the overall k_on by an order of magnitude and brings our estimates in closer agreement with experiment. Our finding that the observed binding rate is strongly dependent on the potential of mean force barrier associated with dehydration of Ca²⁺ suggests the strong role of water coordination in shaping the kinetics of Ca²⁺ binding.

In an intact myofilament, Troponin C is bound to actin of the thin filament. To determine the extent to which the myofilament geometry impacts the steady state distribution and k_on, we applied our computational protocol to a cryo-EM model of the myofilament from [47] (PDB Code 2W4U). The resulting mesh from Section. 2.4 contained 44,362 vertices and 178940 simplices. We assumed non-periodic boundary conditions, as we expect the contribution of the electrostatic potential from adjacent actin units to be very small, given the Debye length of (λ_d ≈ 6.8 Å) based on physiological ionic strength.

In Fig. 5, we compare ρ in the intact filament versus the N-terminal fragment. We note for the uncharged case that the depletion of ρ extends along the thin filament, suggesting that to some extent its geometry influences local Ca²⁺ dynamics (data not shown). The picture is drastically different when the electrostatic potential is introduced as seen in Fig. 5c. For this case, and in Table 1, we report a k_on value of 1.7× 10⁶ [1/Ms], which is significantly smaller than the k_D value obtained for the charged, isolated Troponin C.The large difference in k_D is surprising, given that we had expected that the electrostatic contribution from the thin filament would be largely shielded by the small Debye length. However, we note in Fig. 5c substantial accumulation of Ca²⁺ (red contours representing 40 M Ca²⁺) that were not observed in the uncharged case. Moreover, the large gradients at the active site observed for the isolated Troponin C case are substantially attenuated in the intact geometry, although the coarser representation of Troponin C on the filament make direct comparisons diffcult. It is possible that the accumulation regions on the thin filament behave as buffers and effectively reduce the available Ca²⁺ for reaction at the active site, as evidenced by the smaller gradients, which thereby reduce the effective association rate. However, it is likely that our simulations over-estimate this bu ering effect, as the counter-ions K⁺ and Mg²⁺ could also compete for these negatively-charged regions.

Table 1.

Predicted kon values for di usional encounter and post-encounter scenarios. Included are applications for TnC (intact geometry) and SERCA (neutral phospholipids).

case	kD, q = 0	kD, q ≠= 0	kss	kg	applications
Sphere(1 x 109)	7.09	3.49
SERCA(1 x 109)	0.10	0.56	0.15	0.03*	2.96
TnC(1 x 109)	0.39	21.5	1.25	NA	0.0015

^*Computed directly from (12).

Our observation that the thin filament geometry impacts Ca²⁺ association rates raises the possibility that changes in the myofilament lattice spacing during rigor [16] could modulate k_on. Decreased lattice spacing, e.g. the distance between adjacent thick and thin filaments, is believed to decrease during contraction and this controversy surrounds whether the decrease is correlated with an increase in Troponin C’s affinity for Ca²⁺[16]. At physiological ionic strengths, we do not expect any significant differences in the electrostatic potential as the thick and thin filaments are still separated by ranges much greater than the Debye length. Alternatively, conformational changes of troponin are known to occur during rigor, including Troponin C (as observed in circular dichroism experiments [31]) and shifting of tropomyosin [8]. Changes to either of these structure’s solvent-exposed surface could alter the electrostatic profile of the system and thereby impact Ca²⁺ association rates. We plan to examine these factors in a follow-up study.

3.3. SERCA

The Sarcoplasmic reticulum Ca²⁺ ATPase (SERCA) is a trans-membrane (TM) Ca²⁺ pump that transports two Ca²⁺ ions into the sarcoplasmic reticulum from the cytosol through ATP-dependent conformational transitions. Previous simulations [32, 21, 13] have explored possible pathways of Ca²⁺ entry. Borrowing the convention proposed in [21] the L3 region (near E309, Fig. 1b) has been suggested as a predominant entryway for Ca²⁺ binding based on molecular dynamics (MD) and solutions of the Poisson Boltzmann equation. For SERCA, we consider association rates to the L3 recognition domain discussed in [26]. This recognition domain is lined with several negatively-charged amino acids, including Glu51, Glu55, Glu58, Asp59 and Asp 109, which contribute to a strongly negative electrostatic potential favoring cation association. Moreover, the prevalence of charged residues along the SERCA transmembrane bundle gives rise to a deformation of the lipid bilayer near the L3 entryway consistent in other studies [39, 27].

We assume here that the effect of the lipid environment is imposed in the ’exterior’ problem (for which the conventional Smoluchowski PDE is used), as the lipids are relatively far from the active site (and outside the L3 binding channel). We created the molecular geometry using a snapshot from our molecular dynamics simulations of the Ca²⁺-bound structure (PDB code: 1SU4) from Obara et al [34] determined at 2.4 Å resolution; details of structure preparation, including embedding in POPC lipid, are available in [26]. For the PDE simulation domain, using Blamer we embedded the lipid head groups and upper transmembrane/cytosolic domains in a rectangular box. The active site was defined on the molecular surface within 5 Å of the mid-point between D55 and D113, which sits in the center of the L3 binding vestibule. The resulting grid contained 88,868 vertices and 360,296 simplices.

Based on this representation, we predict k_on of 5.8× 10⁸ [1/Ms] and the steady state distribution of ρ is shown in Fig. 6a. Particularly interesting is the significant accumulation of Ca²⁺ density along the lipid indentation, which suggests that the deformation may enhance the rate of flux into the active site. Moreover, we note substantial Ca²⁺ density along the lipid bilayer far from the binding site that suggests the negatively charged phosphate heads buffer Ca²⁺. We had anticipated that polar head groups of the lipid bilayer near the L3 site might provide an additional enhancement of the k_on. To probe this, we recomputed the electrostatic potential using uncharged lipids and surprisingly found that k_D improved to 3.0× 10⁹ [1/MS] and accumulation of Ca²⁺ along the lipid was drastically reduced. Thus, it appears that by reducing the buffering capacity of the lipids, more free Ca²⁺ is available to react at the active site, as we had hypothesized for the Troponin C/thin filament system. We note that this phenomenon may serve as physiological purpose, as [7] provides evidence that the sarcolemmal membrane buffers Ca²⁺; while the sarcolemmal lipid composition differs from the POPC assumed in our model, the prevalence of negative charge may help guide cations toward the SERCA binding region.

While it appears that Ca²⁺ can freely diffuse to the binding mouth, the abundance of highly mobile, charged residues in the L3 binding vestibule raises the possibility that they may play a direct role in transferring Ca²⁺ to the active site. To incorporate the influence of these interactions on the association rate, we computed the potential of mean force using molecular dynamics and umbrella sampling in [26]. We found that the potential of mean force did not vary significantly far from the active region where the lipids could be expected to interact with Ca²⁺, which we attribute to the relatively small number of lipids lining the largely solvent-exposed opening of the binding channel. Indeed, we observed a smooth, nearly linear decrease in the potential of mean force at large distances, while a slight barrier was found just outside the Ca²⁺ binding site (≈0.5 [kcal/mol]) at r ≈ 2.5 Å. In [26], we attributed this barrier to a conformational change of E309 that draws Ca²⁺ from the L3 vestibule into the binding site. Based on this PMF, we predict a k_ss of 1.5× 10⁸ [1/Ms] using Alg. 2. Hence, the association rate appears to be only modestly impacted by the molecular interactions within the binding site, which is not unexpected given the vary small barrier height.

Instead, we postulate that gating of Glu309 serves a more prominent role in modulating Ca²⁺ association rates. Prior studies have implicated Glu309 in controlling access to site II , as mutations of the residue to alanine [42] and glutamine [23] resulted in faster Ca²⁺ dissociation rates. We explored this potential gating mechanism in [26] and discovered that the Glu309 side chain oscillates between an open and closed state. In the absence of Ca²⁺, the Glu309 carboxyl terminus tends to favor placement within the L3 vestibule, and as Ca²⁺ approaches the binding site, Glu309 heavily favors the Ca²⁺ binding site, through a conformational change driven by nanosecond-timescale flips in the χ₂ dihedral angle between C_α and C_β. The equilibrium constant for this conformational change was ≈ 20% when Ca²⁺ was far from the active site (R >> 15Å) and approached ≈ 60% (data not shown) just prior to binding at site II. The difference in gating rates implies a gating potential of U(r) ≈ 0.75 [kcal/mol] based on (8). We utilize Alg. 3 to include the effect of this putative gating mechanism. Based on a free Ca²⁺ ion (D=780 μm²), we expect a characteristic diffusion time for Ca²⁺ leaving the active site (r=10Å) of τ_d= 0.2 ns using τ_d = r²/6D, which is within the slow gating regime. In this limit, our analysis would suggest that the binding site is accessible during roughly 20% of the simulation, which would further reduce the observed k_on by nearly an order of magnitude. While we have not estimated gating frequencies for other common ions, such as Mg²⁺ or K⁺, we might expect a less favorable interaction potential between Glu309 and the solvated ion, which in turn would reduce the association rate as we observed in Fig. 4d. If true, this differential in association rates could constitute a mechanism for ion selectivity.

3.4. Limitations

While this numerical approach represents significant progress toward multi-scale modeling of substrate association in realistic molecular scale environments, several limitations should be addressed to improve the approach. For one, we assume in this framework that a 1-D potential of mean force is sufficient to describe diffusion within the binding channel. For SERCA, the binding channel appears to be approximately linear, but for TnC and likely for other systems, the preferred pathway to substrate binding may be very non-linear. Should this be the case, (6) could be modified to include additional degrees of freedom. However, this would likely entail modifying the boundary conditions inherent to the decomposition into interior and exterior problems, which we have not addressed in this study.

An additional complication is that the potential of mean force assumes that fluctuations orthogonal the reaction coordinate are fast relative to the reaction coordinate axis. We have observed in our molecular dynamics simulations of SERCA that gradual changes in the bundle that could invalidate this assumption. However, it may be possible to group these changes into conformational states that inter-convert with some quantifiable equilibrium constant, for which we may estimate k_on in a similar fashion to the gated active site formalism.

We also assume a diffusion constant within the binding channel that is equal to the diffusion in the bulk. Clearly the interactions between Ca²⁺ and the binding site will perturb the diffusion constant in a spatially-dependent fashion. Strategies including estimates based on the mean free passage time [20] or the friction kernel from the velocity autocorrelation function [10] could improve our estimates of D within the binding channel. However, based on a study of the K+ channel in [6], the diffusion constant within the binding channel was at most reduced by 40% relative to the bulk value, hence our estimate of D_channel in this study may be reasonable.

Here in this study we also assumed that the Ca²⁺ probability distribution is determined by its concentration gradient and a simple approximation of the potential based on the linearized Poisson-Boltzmann equation. In reality, additional factors, such as finite-size effects [22], could offer an improved estimate of the probability distribution near the active site. It is likely that including these effect would reduce our estimates of the diffusional encounter and bring our estimates of the overall association rate in line with experiment.

4. Conclusions and Future Work

This paper presents a numerical framework for integrating molecular structural and dynamic data, including binding along gated channels, into continuum models of diffusion. Incorporation of these effects helps bridge the gap between rates predicted by diffusional-encounter models and the actual binding kinetics measured by experiment. We stress that these results are generalizable to variety of ligand-protein biding events are not limited to calcium.

While we have focused here on steady-state solutions to the Smoluchowski equation, we note that the time-dependent case can be addressed by adapting the weak form to include the time-dependent term and using a finite difference time-stepping approach. This modification may offer superior estimates of the association rate when local equilibrium about the receptor is not guaranteed. The advantage of PDE-based estimation of association rates is the flexibility to include more detailed numerical models, such as the Poisson-Nernst-Planck equation to handle ion-ion interactions [33].