On testing an unspecified function through a linear mixed effects model with multiple variance components

Summary

We examine a generalized F-test of a nonparametric function through penalized splines and a linear mixed effects model representation. With a mixed effects model representation of penalized splines, we imbed the test of an unspecified function into a test of some fixed effects and a variance component in a linear mixed effects model with nuisance variance components under the null. The procedure can be used to test a nonparametric function or varying-coefficient with clustered data, compare two spline functions, test the significance of an unspecified function in an additive model with multiple components, and test a row or a column effect in a two-way analysis of variance model. Through a spectral decomposition of the residual sum of squares, we provide a fast algorithm for computing the null distribution of the test, which significantly improves the computational efficiency over bootstrap. The spectral representation reveals a connection between the likelihood ratio test (LRT) in a multiple variance components model and a single component model. We examine our methods through simulations, where we show that the power of the generalized F-test may be higher than the LRT, depending on the hypothesis of interest and the true model under the alternative. We apply these methods to compute the genome-wide critical value and p-value of a genetic association test in a genome-wide association study (GWAS), where the usual bootstrap is computationally intensive (up to 10⁸ simulations) and asymptotic approximation may be unreliable and conservative.

1. Introduction

With a mixed effects model representation of penalized splines (Speed 1991; Ruppert et al. 2003; Wand 2003), we imbed the test of an unspecified function into a test of some fixed effects and a variance component in a linear mixed effects model with multiple variance components. Tests involving variance components have non-standard null distributions because some parameters are on the boundary of the parameter space under the null. When data consists of independent subvectors both under the null and alternative, the asymptotic distribution of a likelihood ratio test (LRT) or a restricted LRT (RLRT) is a 50:50 mixture of chi-square distributions (Self and Liang 1987; Stram and Lee 1994). When the independence assumption is violated, Crainiceanu and Ruppert (2004) and Crainiceanu et al. (2005) discovered that the null distribution of the LRT is different from a 50:50 chi-square mixture in models with a single variance component, and that using a chi-square mixture distribution was conservative. For models with a single variance component, Crainiceanu and Ruppert (2004) took advantage of a spectral decomposition of the likelihood to propose a fast algorithm for computing the exact null distribution of the LRT and RLRT. This non-standard behavior was also observed for the degrees-of-freedom test proposed by Cantoni and Hastie (2002), and the null distribution needed to be computed by bootstrap.

To generalize these results to more complex models with nuisance variance components under the null, Greven et al. (2008) proposed to approximate the null distribution of the RLRT using a pseudo-likelihood ratio test theory (Liang and Self 1996). One constructs pseudo-outcomes by subtracting the best linear unbiased predictors (BLUPs) of nuisance random effects and applying methods developed for models with a single variance component to derive the null distribution of the RLRT. Although the procedure generally works well, in some models with highly correlated covariates and a nuisance variance component that is on the boundary of the parameter space, the regularity conditions of the pseudo-RLRT may not be satisfied and a conservative type I error rate has been observed (Greven et al. 2008; Scheipl et al. 2008). No simple spectral decomposition or exact distribution is available in the literature for testing a variance component in linear mixed models with multiple random effects.

We examine a generalized F-test of a variance component, where there are nuisance random effects under the null. The methods are applicable to testing an unspecified nonparametric function or varying-coefficient through penalized splines with clustered data, comparing two spline functions, testing the significance of an unspecified function in an additive model with multiple components, and testing a row or a column effect in a two-way analysis of variance model. We transform a test of a nonparametric function to a test of some fixed effects and a random effect in a linear mixed effects model with nuisance variance components under the null. We present a spectral decomposition to account for additional variance components in the model and develop a fast algorithm to compute the null distribution of the proposed test. The spectral representation is also used to compare the LRT with the pseudo-LRT, which reveals a connection with methods developed for the single variance component models, and sheds new insights on the geometry of the LRT in multiple variance components models. Compared to the LRT, the generalized F-test has a computational advantage – only a single linear mixed effects model will be fit under the alternative, which is an attractive feature when the test is carried out many times. For example, in a genome-wide association study (GWAS), the procedure is applied to compute the genome-wide critical value of a genetic association test with correlated family data, where the parametric bootstrap is computationally intensive due to the large number of simulations required (up to 10⁸ repetitions) and the asymptotic approximation is unreliable and conservative at the extreme tails.

2. Models and examples

In this section, we first introduce several motivating examples and then describe the general modeling framework.

Example 1: Test an unspecified function in a partially linear mixed effects model

For clustered data, such as samples collected from a family study, let i index families (or clusters) and j index subjects in a family (or a cluster). Consider a partially linear mixed effects model

$$\begin{array}{cc}\hfill & y_{\mathit{ij}}=f\left(s_{\mathit{ij}}\right)+c_{\mathit{ij}}^T\eta +{\alpha }_i+{\epsilon }_{\mathit{ij}},i=1,\cdots ,n,j=1,\cdots ,n_i,\hfill \\ \hfill & {\alpha }_i\sim N(0,{\sigma }_{\alpha }^2),{\epsilon }_{\mathit{ij}}\sim N(0,{\sigma }_{\epsilon }^2),\hfill \end{array}$$ (1)

where α_i’s are independent family-specific random effects, f(s_ij) is an unspecified baseline function relating the outcome to the covariates s_ij, c_ij’s are vectors of fixed effects with coefficients η, and ε_ij’s are independent residual measurement errors. Our goal is to test the significance of the regression function f(s), that is,

$$H_0:f\left(s\right)=0,$$

or the deviation of f(s) from an hth order polynomial function, that is,

$$H_0:f\left(s\right)={\beta }_0+{\beta }_{1}s+\cdots +{\beta }_h{s}^h.$$

Under the alternative, to incorporate a large class of functions, we specify f(s) to be a flexible spline function, such as

$$f\left(s\right)={\beta }_0+{\beta }_{1}s+\cdots +{\beta }_h{s}^h+\sum _{k=1}^K{b}_k{(s-{\tau }_k)}_{+}^h,$$

where τ_k, k = 1, … , K, are a sequence of knots, and ${(s-\tau )}_{+}^h={(s-\tau )}^h$ if s ≥ τ, and 0 otherwise. A sufficient number of knots will be used to guarantee flexibility. Let $x_{\mathit{ij}}={(1,s_{\mathit{ij}},\cdots ,s_{\mathit{ij}}^h)}^T$ and $z_{\mathit{ij}}={\{{(s_{\mathit{ij}}-{\tau }_1)}_{+}^h,\cdots ,{(s_{\mathit{ij}}-{\tau }_K)}_{+}^h\}}^T$. Under the alternative, we have the representation, $f\left(s_{\mathit{ij}}\right)=x_{\mathit{ij}}^T\beta +z_{\mathit{ij}}^{T}b$, where $b={(b_1,\cdots ,b_K)}^T$.

To obtain a smooth fitted curve, one minimizes a penalized weighted least squares (Ruppert et al. 2003),

$$\sum _{i=1}^n{(Y_i-C_i\eta -X_i\beta -Z_i\mathrm{b})}^T{V}_i^{-1}(Y_i-C_i\eta -X_i\beta -Z_{i}b)+\frac{1}{\lambda }{ϴ}^{T}Dϴ,$$

where Y_i = (y_i1, … , y_ini)^T, C_i = (c_i1, … , c_ini)^T, X_i = (x_i1, … , x_ini)^T, Z_i = (z_i1, … , z_ini)^T, Θ = (η^T , β^T , b^T)^T , Vi = cov(Y_i), λ is a smoothing parameter, D = diag(0_m+h+1, ∑⁻¹), m is the dimension of η, and ∑ is a known penalty matrix, depending on the spline basis used. For example, ∑ = I_K with a truncated polynomial basis.

Linear mixed effects model set up for the test

With a mixed effects model representation of splines (Speed 1991; Ruppert et al. 2003; Wand 2003), solutions to the penalized weighted least squares are obtained from a linear mixed effects model, where b_k are treated as random effects and the smoothing parameter is specified as the ratio of two variance components. Specifically, a mixed effects model representation is

$$\begin{array}{cc}\hfill & Y_i=C_i\eta +X_i\beta +Z_{i}b+U_i{\alpha }_i+{\epsilon }_i,i=1,\cdots ,n,\hfill \\ \hfill & b\sim N(0,{\sigma }_b^2\Sigma ),{\alpha }_i\sim N(0,{\sigma }_{\alpha }^2),{\epsilon }_i\sim N(0,{\sigma }_{\epsilon }^2{I}_{n_i}),\hfill \end{array}$$ (2)

where the smoothing parameter $\lambda ={\sigma }_b^2∕{\sigma }_{\epsilon }^2$ and U_i = 1_ni. Through model (2), significance of f(s) can now be tested by

$$H_0:\beta ={({\beta }_0,\cdots ,{\beta }_h)}^T=0,{\sigma }_b^2=0.$$

Testing a nonparametric deviation from a polynomial function is simply through $H_0:{\sigma }_b^2=0$ Note that α_i in model (2) are nuisance random effects under the null hypothesis.

Example 2: Test an unspecified function in a partially linear mixed effects model with multiple variance components

An extension to Example 1 is a partially linear mixed effects model with multiple variance components,

$$\begin{array}{cc}\hfill & y_{\mathit{ij}}=f\left(s_{\mathit{ij}}\right)+c_{\mathit{ij}}^T\eta +{\alpha }_{i0}+{\alpha }_{i1}{u}_{\mathit{ij}}+{\epsilon }_{\mathit{ij}},i=1,\cdots ,n,j=1,\cdots ,n_i,\hfill \\ \hfill & {\alpha }_{i0}\sim N(0,{\sigma }_{\alpha 0}^2),{\alpha }_{i1}\sim N(0,{\sigma }_{\alpha 1}^2),{\epsilon }_{\mathit{ij}}\sim N(0,{\sigma }_{\epsilon }^2),\hfill \end{array}$$ (3)

where α_i0 and α_i1 are independent random effects. It is again of interest to test H₀ : f(s) = 0. Here, there are two nuisance variance components under the null (α_i0 and α_i1). A model similar to (2) can be used to test this hypothesis.

Example 3: Varying coefficient model

In many applications, it is of interest to test an unspecified varying-coefficient or a group difference. Let g_i denote a group indicator. A flexible model with an unspecified baseline function and a varying-coefficient is

$$y_i=c_i^T\eta +f\left(s_i\right)+\beta \left(s_i\right)g_i+{\epsilon }_i,$$

where c_i is a vector of covariates, f(·) is a spline function describing the relationship between the expected outcome and the covariate s_i in the baseline group, and β(·) is the difference between the experiment group and the baseline group. The hypothesis of no group difference is H₀ : β(s) = 0. Using a linear mixed effects model representation of penalized splines on f(·) and β(·), the model under the alternative can be expressed as

$$\begin{array}{cc}\hfill & Y=C\eta +W_1{\beta }_1+W_2{\beta }_2+Z_1{b}_1+Z_2{b}_2+\epsilon ,\hfill \\ \hfill b_1\sim & N(0,{\sigma }_{b1}^2{\Sigma }_1),b_2\sim N(0,{\sigma }_{b2}^2{\Sigma }_2),\epsilon \sim N(0,{\sigma }_{\epsilon }^2{I}_n),\hfill \end{array}$$ (4)

where ∑_j’s are known penalty matrices and W_j and Z_j are related to the basis functions for f(·) and β(·). Testing a group difference is through

$$H_0:{\beta }_2=0,{\sigma }_{b2}^2=0.$$

Here, b₁ are nuisance random effects under the null. In this example, the nuisance variance ratio, $\gamma ={\sigma }_{b_1}^2∕{\sigma }_{\epsilon }^2$, can be regarded as the smoothing parameter for the baseline function.

Example 4: Additive models

Consider an additive model with two covariates,

$$y_i=f_1\left(s_{i1}\right)+f_2\left(s_{i2}\right)+{\epsilon }_i,{\epsilon }_i\sim N(0,{\sigma }_{\epsilon }^2),$$

where f₁(·) and f₂(·) are unspecified spline functions and the covariates s_i1 and s_i2 can be either correlated or independent. When one of the covariates, say s_i2, is of primary interest, one tests H₀ : f₂(s) = 0, which can also be assessed by testing fixed and random effects in a mixed effects model similar to (4).

Another example where this test is useful includes testing a fixed smoothing parameter with longitudinal data, for example, to test λ = λ₀ in model (2). The methods can also be used to test a random slope in the presence of a random intercept, test a row or column effect in a two-way analysis of variance model, or test a random effect in a split-plot design through a two-level random effects model.

2.1 The general problem setting

All the examples above can be summarized as testing a hypothesis in a linear mixed effects model with multiple variance components. To be specific, our goal is to test

$$H_0:{\beta }_2=0,{\sigma }_{b_L}^2=0,\text{or}{H}_0:{\sigma }_{b_L}^2=0$$

in the model

$$\begin{array}{cc}\hfill & Y=X_0{\beta }_1+W{\beta }_2+\sum _{l=1}^L{Z}_l{b}_l+\epsilon ,\hfill \\ \hfill & b_l\sim N(0,{\sigma }_{b_l}^2{\Sigma }_l),\epsilon \sim N(0,{\sigma }_{\epsilon }^{2}I),\hfill \end{array}$$ (5)

where X₀ is the design matrix for the q-dimensional fixed effects under the null, X₁ = (X₀, W) is the design matrix for the p-dimensional fixed effects under the alternative (in some examples p–q = h + 1), b_l, l = 1, … , L, are random effects independent of ε, and ∑_l are known matrices.

3. A generalized F-test

We develop a generalized F-test by comparing the residual sum of squares (RSS) of two models obtained from (5), similar to the classic ANOVA F-tests. Classic F-tests are based on computing RSS under a restricted model and a full model and dividing them by appropriate degrees of freedom. For tests involving variance components, it is unclear what degrees of freedom should be used (Hodge and Sargent 2001; Vaida and Blanchard 2005). Although the test statistic based on comparing RSS under the null and the alternative can still be constructed, its null distribution may be non-standard.

We present the test statistic under the general framework in Section 2.1. For the purpose of illustration, assume L = 2 in model (5). It is easy to generalize to the case where L > 2 (e.g., simulation scenario (c) in Tabel 1). Let γ denote the nuisance variance ratio, ${\sigma }_{b_1}^2∕{\sigma }_{\epsilon }^2$, and let $\gamma ={\sigma }_{b_2}^2∕{\sigma }_{\epsilon }^2$. Under the null hypothesis, the residual sum of squares is

$${\mathit{RSS}}_0\left(\gamma \right)=\frac{1}{{\sigma }_{\epsilon }^2}{\{Y-X_0\widehat{{\beta }_0}(\gamma \left)\right\}}^T{V}_0{\left(\gamma \right)}^{-1}\{Y-X_0\widehat{{\beta }_0}(\gamma \left)\right\},$$

where $\widehat{{\beta }_0}\left(\gamma \right)={\left\{X_0^T{V}_0{\left(\gamma \right)}^{-1}{X}_0\right\}}^{-1}{X}_0^T{V}_0{\left(\gamma \right)}^{-1}Y$ and $V_0\left(\gamma \right)=I_n+\gamma Z_1{\Sigma }_1{Z}_1^T$. Under the alternative, the residual sum of squares is

$${\mathit{RSS}}_1(\gamma ,\lambda )=\frac{1}{{\sigma }_{\epsilon }^2}{\{Y-X_1\widehat{{\beta }_1}(\gamma ,\lambda \left)\right\}}^T{V}_1{(\gamma ,\lambda )}^{-1}\{Y-X_1\widehat{{\beta }_1}(\gamma ,\lambda \left)\right\},$$

where $\widehat{{\beta }_1}(\gamma ,\lambda )={\left\{X_1^T{V}_1{(\gamma ,\lambda )}^{-1}{X}_1\right\}}^{-1}{X}_1^T{V}_1{(\gamma ,\lambda )}^{-1}Y$. When the variance components ratio γ is known to be γ₀, a generalized F-test can be defined as

$$T_1=\frac{{\mathit{RSS}}_0\left({\gamma }_0\right)-{\mathit{RSS}}_1({\gamma }_0,\widehat{\lambda })}{{\mathit{RSS}}_1({\gamma }_0,\widehat{\lambda })∕n},$$

where $\widehat{\lambda }$ is estimated by the restricted maximum likelihood (REML) under the alternative hypothesis. When γ is unknown, the test statistic is

$$T_2=\frac{{\mathit{RSS}}_0\left(\widehat{\gamma }\right)-{\mathit{RSS}}_1(\widehat{\gamma },\widehat{\lambda })}{{\mathit{RSS}}_1(\widehat{\gamma },\widehat{\lambda })∕n},$$

where both $\widehat{\gamma }$ and $\widehat{\lambda }$ are obtained by REML under the alternative. Both test statistics are easy to compute with any standard statistical software. However, deriving their null distributions is not trivial because the null value of ${\sigma }_{b_L}^2$ is on the boundary of the parameter space and the data cannot be partitioned as independent subvectors in certain models, such as (2).

Note that T₁ or T₂ is different from the F or R statistic examined in Cantoni and Hastie (2002). The latter statistics is based on RSS from a conditional model, that is, ${\sum }_{i=1}^n{(Y_i-\widehat{Y_i})}^2$, where ${\widehat{Y}}_i=X_{i1}\widehat{{\beta }_1}+W_i\widehat{{\beta }_2}+{\sum }_{l=1}^L{Z}_{\mathit{il}}{\widehat{b}}_l$ and ${\widehat{b}}_l$ are BLUPs of b_l. The null distributions of these F and R tests are unknown in literature and need to be obtained through bootstrap or permutation to account for uncertainties in estimating smoothing parameters (or variance components). In contrast, the proposed T₁ and T₂ are based on marginal models of Y. Although when there is a non-linear trend, the linear mixed effects model (5) is not the true model under the alternative, it holds exactly under the null. The null distribution of the proposed generalized F-test is computed from a valid model under the null and thereby the test is expected to maintain its size.

3.1 Spectral decomposition of the test statistic

Here we present a spectral decomposition to obtain the null distribution of T₁ and T₂ that accounts for the nuisance variance components still under the general framework (5) with L = 2.

Theorem 1

Let π_s(γ) denote the sth eigenvalue of ${\sum }_2^{-1∕2}{Z}_2^T{P}_{V_0}{Z}_2{\sum }_2^{-1∕2}$, where $P_{V_0}=\{V_0{\left(\gamma \right)}^{-1}-V_0{\left(\gamma \right)}^{-1}{X}_1{\left(X_1^T{V}_0{\left(\gamma \right)}^{-1}{X}_1\right)}^{-1}{X}_1^T{V}_0{\left(\gamma \right)}^{-1}\}$. Let ω_s denote the eigenvalues of ${\Sigma }^{1∕2}{Z}_1^T{P}_1{Z}_1{\Sigma }^{1∕2}$, where $P_1=I-X_1{\left(X_1^T{X}_1\right)}^{-1}{X}_1^T$. Then under the null hypothesis (3), the generalized F-test T₁ has the exact distribution

$$T_1{=}^d\left\{\sum _{s=1}^K\frac{\widehat{\lambda }{\rho }_s\left({\gamma }_0\right)}{1+\widehat{\lambda }{\rho }_s\left({\gamma }_0\right)}{u}_s^2+\sum _{s=1}^{p-q}{\upsilon }_s^2\right\}/\left\{\sum _{s=1}^K\frac{1}{1+\widehat{\lambda }{\rho }_s\left({\gamma }_0\right)}{u}_s^2+\sum _{s=K+1}^{n-p}{u}_s^2\right\},$$ (6)

where =^d denotes equality in distribution, u_s^i.i.d. ~ N(0, 1), s = 1, … , n–p, v_s ~^i.i.d., N(0; 1); s = 1; … ; p – q, $\widehat{\lambda }={\max }_{\lambda }{f}_n({\gamma }_0,\lambda )$, and

$$\begin{array}{cc}\hfill f_n(\gamma ,\lambda )=& -(n-p)\log \left\{\sum _{s=1}^K\frac{u_s^2}{1+\lambda {\rho }_s\left(\gamma \right)}+\sum _{s=K+1}^{n-p}{u}_s^2\right\}\hfill \\ \hfill & -\sum _{s=1}^K\log \{1+\lambda {\rho }_s(\gamma \left)\right\}-\sum _{s=1}^K\log (1+\gamma {\omega }_s)\hfill \end{array}$$ (7)

is the spectral decomposition of the log-profile restricted likelihood under the alternative up to a constant. The null distribution of T₂ is obtained by replacing γ₀ by $\widehat{\gamma }$ in (6) and computing $\widehat{\gamma }$ and $\widehat{\lambda }$ by max_γ,λ f_n(γ,λ). The proof of Theorem 1 is in the Online Appendix A.1. These decompositions allow for fast computation of the null distribution of T by avoiding permutation.

A similar decomposition can be used to obtain the distribution of the test statistics under the alternative, that is,

$$T_1{=}^d\left\{\sum _{s=1}^K\frac{(\widehat{\lambda }-{\lambda }_0){\rho }_s\left({\gamma }_0\right)}{1+\widehat{\lambda }{\rho }_s\left({\gamma }_0\right)}{u}_s^2+\sum _{s=1}^{p-q}{({\theta }_s+{\upsilon }_s)}^2\right\}/\left\{\sum _{s=1}^K\frac{1+{\lambda }_0{\rho }_s\left({\gamma }_0\right)}{1+\widehat{\lambda }{\rho }_s\left({\gamma }_0\right)}{u}_s^2+\sum _{s=K+1}^{n-p}{u}_s^2\right\},$$

where γ₀ and λ₀ are the true values of γ and λ, and θ_s are related to the noncentrality parameter defined in the Online Appendix A1. This expression is useful for the fast computation of power under the alternative hypothesis without bootstrap. The distribution of T₂ under the alternative has a similar representation, with γ₀ replaced by $\widehat{\gamma }$, and $\widehat{\gamma }$ and $\widehat{\lambda }$ computed by max_γ,λ, f_n(γ,λ).

3.2 Fast algorithm to compute the null distribution

Taking advantage of the decompositions (6) and (7), one can obtain the exact null distribution of T₁ rapidly with the following Algorithm A:

A0. Pre-simulation step: Compute eigenvalues ρ_s(γ₀).

A1. Simulate n–p independent standard normal random variables, u_s, and p–q independent standard normal random variables, v_s.

A2. Choose γ by maximizing f_n(γ₀,λ) in (7) over grid points λ₁, … , λ_m.

A3. Compute the test statistic by (6) using the γ selected in step A2.

A4. Repeat the above steps 1-3 for required number of repetitions.

Note that this algorithm is extremely fast, since both (6) and (7) only involve arithmetic operations and their computations are instantaneous. Using R (R Development Core Team, 2012), we were able to obtain about 80,000 simulations per minute on a Dell computer with 2.67GHz CPU and 4Gz memory.

To obtain the null distribution of T₂, the steps A0, A2, and A3 in the Algorithm A are replaced by the following Algorithm B:

B0. Pre-simulation step: Compute eigenvalues π_s(γ_j) at grid points γ₁, … γ_m.

B2. With pre-computed ρ_s(γ_j), choose γ and λ through maximizing f_n(γ,λ) in (7) over grid points γ₁, … , γ_m and γ₁, …, λ_m.

B3. Compute the test statistic by (6) using γ and λ selected in step B2.

There are several desirable features regarding the numerical efficiency of Algorithm B. The eigen-decomposition to compute π_s(γ) in step B0 only needs to be done once before the simulation starts and the simulation replications are only applied to steps B1 through B3. The speed of eigen-decomposition depends on the column dimension of Z₂ (or the number of knots), which does not increase with the sample size or the number of nuisance variance components. The algorithm depends on the sample size through simulating n–p standard normal random variables, thus computation time increases minimally when n increases. In contrast, a permutation or bootstrap based approach for a mixed effects model may be slower when the number of random effects is large.

The major computational step in Algorithm B is to maximize f_n(γ,λ) in (7). After obtaining π_s(γ_j), computing f_n(γ_j, λ_l) only involves arithmetic operations, which can be done extremely rapidly. In addition, we studied a search algorithm with respect to λ at a fixed value of $\widehat{\gamma }$ in step B2 and found satisfactory performance in many simulation settings that offers further improvement on the numerical efficiency. In our data analysis example with a large sample size (n = 6309), reduction in computing time was more than 3000 folds using the proposed algorithm when compared to the bootstrap. We obtained about 60,000 simulations per minute on a Dell computer with 2.67GHz CPU and 4Gz memory using R.

Under a special case, one can further speed up the pre-simulation step of Algorithm B. We show in the Online Appendix A2 that when $Z_1\Sigma Z_1^T$ and $Z_2{\Sigma }_2{Z}_2^T$ can be simultaneously diagonalized, one obtains

$${\rho }_s\left(\gamma \right)=\frac{{\mu }_s}{1+\gamma {\omega }_s},$$ (8)

where μ_s is the sth eigenvalue of ${\Sigma }_2^{1∕2}{Z}_2^T{P}_1{Z}_2{\Sigma }_2^{1∕2}$. Therefore π_s(γ) has an explicit expression as a function of γ in this case. With this explicit formula, the eigen-decomposition to obtain μ_s and ω_s only needs to be done once in step B0 for all grid points of γ. Two matrices can be simultaneously diagonalized if they commute. In example 4 (additive model), for a balanced design where the two covariates are equally spaced and the knots are also equally spaced, the matrices ${\Sigma }_1^{-1∕2}{Z}_1^T{P}_1{Z}_1{\Sigma }_1^{-1∕2}$ and ${\Sigma }_2^{-1∕2}{Z}_2^T{P}_1{Z}_2{\Sigma }_2^{-1∕2}$ commute; therefore, they can be simultaneously diagonalized and the relation (8) holds.

Another speed up of the algorithm is useful when there is more than one nuisance variance component. In this case, step B2 of the algorithm can be replaced by a one-dimensional search where we fix nuisance parameters at values estimated under the alternative hypothesis. We present an example of an additive model with multiple nuisance variance components in Section 4.

3.3 Distribution of the (R)LRT with multiple variance components

The decomposition (6) allows a direct comparison between LRT and pseudo-LRT approximation. Let L(γ,λ) = −nlog{RSS(γ,λ)} −log∣V₁(γ,λ)∣ denote the profile log-likelihood under the model (2) obtained by substituting the weighted least square estimate ${\widehat{\beta }}_1(\gamma ,\lambda )$ into the likelihood. When the variance ratio γ₀ is known, the likelihood ratio test is LRT₁ = sup_λ≥0 L(γ₀, λ) − sup_λ=0 L(γ₀, λ). We show in Online Appendix A4 that under the null hypothesis, LRT₁ has the exact distribution

$$\begin{array}{c}\hfill {\mathit{LRT}}_1{=}^{d}n\log \left(1+\frac{\sum _{s=1}^{p-q}{\upsilon }_s^2}{\sum _{s=1}^{n-p}{u}_s^2}\right)+\underset{\lambda }{\sup }{g}_n({\gamma }_0,\lambda ),\hfill \\ \hfill g_n(\gamma ,\lambda )=n\log \left\{1+\frac{\sum _{s=1}^K\frac{\lambda {\rho }_s\left(\gamma \right)}{1+\lambda {\rho }_s\left(\gamma \right)}{u}_s^2}{\sum _{s=1}^K\frac{u_s^2}{1+\lambda {\rho }_s\left(\gamma \right)}+\sum _{s=K+1}^{n-p}{u}_s^2}\right\}-\sum _{s=1}^K\log \{1+\lambda {\phi }_s(\gamma \left)\right\},\hfill \end{array}$$ (9)

and φ_s(γ) are the eigenvalues of ${\Sigma }_2^{-1∕2}{Z}_2^T{V}_0^{-1}{Z}_2{\Sigma }_2^{-1∕2}$. When γ is unknown, we show in the Online Appendix A3 that the null distribution of LRT₂ can be obtained as

$${\mathit{LRT}}_2{=}^{d}n\log \left(1+\frac{\sum _{s=1}^{p-q}{\upsilon }_s^2}{\sum _{s=1}^{n-p}{u}_s^2}\right)+\underset{\lambda ,\gamma }{\sup }{g}_n(\gamma ,\lambda ).$$

When the hypothesis of interest only involves a variance component without fixed effects, RLRT is used instead of LRT. We cab show that the exact null distribution of RLRT with γ known is

$$\begin{array}{c}\hfill {\mathit{RLRT}}_1{=}^d\underset{\lambda \ge 0}{\sup }{h}_n({\gamma }_0,\lambda ),\hfill \\ \hfill h_n(\gamma ,\lambda )=(n-p)\log \left\{1+\frac{\sum _{s=1}^K\frac{\lambda {\rho }_s\left(\gamma \right)}{1+\lambda {\rho }_s\left(\gamma \right)}{u}_s^2}{\sum _{s=1}^K\frac{u_s^2}{1+\lambda {\rho }_s\left(\gamma \right)}+\sum _{s=K+1}^{n-p}{u}_s^2}\right\}-\sum _{s=1}^K\log \{1+\lambda {\rho }_s(\gamma \left)\right\},\hfill \end{array}$$ (10)

and the null distribution of RLRT with γ unknown is RLRT₂ =^d sup_γ≥0,≥0 h_n(γ,λ).

Greven et al. (2008) computed the null distribution of RLRT by applying methods for the single variance component model (Crainiceanu and Ruppert 2004) through a pseudo-LRT using pseudo-outcomes ${\tilde{Y}}_i=Y_i-{\sum }_{l=1}^{L-1}{Z}_{\mathit{il}}{\widehat{b}}_l$, where ${\widehat{b}}_l$ are BLUPs of b_l. From (9), it is easy to see that by replacing μ_s,n in Crainiceanu and Ruppert (2004) with π_s(γ), we arrive at their equation (9). Note that μ_s,n are eigenvalues of ${\Sigma }_2^{1∕2}{Z}_2^T{P}_1{Z}_2{\Sigma }_2^{1∕2}$ denoted by μ_s in this work. Since π_s(γ) are eigenvalues of ${\Sigma }_2^{1∕2}{Z}_2^T{P}_{V_0}{Z}_2{\Sigma }_2^{1∕2}$, it follows that

$${\rho }_s\left(0\right)={\mu }_{s,n}.$$

Therefore, when γ₀ = 0 or $\widehat{\gamma }=0$, RLRT₁ and RLRT₂ reduce to the equation (9) in Crainiceanu and Ruppert (2004). In general, when γ > 0 there is no explicit expression relating π_s(γ) to μ_s,n. However, when relation (8) in Section 3.2 holds, we substitute (8) into (11) to arrive at the null distribution representation

$${\mathit{RLRT}}_1{=}^d\underset{\lambda \ge 0}{\sup }\left[(n-p)\log \left\{1+\frac{\sum _{s=1}^K\frac{\lambda {\mu }_{s,n}∕c_{0,s}}{1+\lambda {\mu }_{s,n}∕c_{0,s}}{u}_s^2}{\sum _{s=1}^K\frac{u_s^2}{1+\lambda {\mu }_{s,n}∕c_{0,s}}+\sum _{s=K+1}^{n-p}{u}_s^2}\right\}-\sum _{s=1}^K\log \{1+\lambda {\mu }_{s,n}∕c_{0,s}\}\right],$$

where the constants c_0,s = (1 + γ₀ω_s). Therefore, scaling μ_s,n by 1 + γ₀ω_s would equate the exact null distribution of the RLRT₁ and the pseudo-RLRT in this case. The close relationship between (9) and equation (9) in Crainiceanu and Ruppert (2004) sheds lights on the validity of approximating LRT in the multiple variance components model by a single variance component based approach in some cases observed in Greven et al. (2008).

4. Simulations

4.1 Overview of the simulation experiments

We performed simulation studies to examine the type I error rate and power of the generalized F-test and compare them with the 50:50 chi-square approximation and the pseudo-LRT (or pseudo-RLRT when applicable). In all simulations, we assume the nuisance variance ratio γ to be unknown and examine the performance of T₂. Performance of T₁ is similar and results are omitted. In all experiments, we simulated covariates s_i from a uniform distribution with support [0,1]. We used a linear truncated polynomial basis with K = min(n/10, 35) knots, and examined two sample sizes for each scenario. We obtained 5,000 replications to compute the null distribution of T₂, 5000 replications to compute the empirical rejection rate to assess type I error rate, and 1000 replications to assess power.

We considered five simulation scenarios: (a) Testing ${\sigma }_{\alpha }^2=0$ in model (2) of Example 1; (b) Testing f(s) = 0 in model (1) of Example 1; (c) Testing f(s) = 0 in model (3) of Example 2; (d) Testing β(t) = 0 in Example 3; and (e) Testing linearity of f₂(t) in Example 4. The parameters common to the next two subsections are as follows. For case (a) through (d), we let η = 1 and simulated c_ij from a uniform distribution with support [0,1]. We fixed β = (−0.2, 0.2)^T and ${\sigma }_b^2=1$. For case (c), the nuisance random intercepts in model (3) have variance ${\sigma }_{\alpha 0}^2=1$. For case (d), coefficients β₁ = (1, −0.5) in the varying coefficient model (4). We generated the binary group indicator from a Bernoulli distribution with a success probability of 0.5, and used the effect coding (−1/1 coding). For case (e), we generated covariates (s_i1, s_i2) from uniform distributions with a correlation of 0.7. For (d) and (e), we centered the covariates s_i or (s_i1, s_i2) to improve numerical stability. Lastly, we fixed ${\sigma }_{\epsilon }^2=1$ in all experiments.

4.2 Type I error rates

Here we examine the sensitivity of type I error rates of various tests to the presence of the nuisance random effects under the null. The empirical type I error rate was evaluated at a nominal level of 5% and at various values of the variance of the nuisance random effects that ranged from 0 to 100. We show the empirical type I error rates in Table 1 and show the confidence intervals of the error rates computed based on the exact binomial distribution in the Online Supplementary Material (Tables A1 and A2). From these tables, it is seen that the 50:50 chi-square approximation of Stram and Lee (1994) is conservative, regardless of the sample size and the value of the nuisance variance component, except in case (a) with a relatively large sample size. Similar to Greven et al. (2008) and Scheipl et al. (2008), the pseudo-LRT and pseudo-RLRT behave satisfactorily across various settings, except in case (e): a conservative type I error was observed for pseudo-RLRT when the nuisance variance is small and the covariates s_i1 and s_i2 are highly correlated in the additive model. In this case, when the nuisance variance component ${\sigma }_{b1}^2=0,{10}^{-4}$ and 0.01, and n=500, the type I error rate of the pseudo-RLRT is smaller than the nominal level (i.e., the upper bound of the exact 95% confidence interval is smaller than 5%, Table A2 in the Online Supplementary Material). For other values of ${\sigma }_{b1}^2$, the type I error rate of the pseudo-RLRT adheres to the nominal level. In this scenario, the proposed procedure is robust to the presence of nuisance variance component in the sense that it maintains the correct size for all values of ${\sigma }_{b1}^2$.

Table 1.

Type I error of testing linearity (an unspecified function) or a random effect in five examples, based on 5,000 simulations.

(a) Partially linear model			n = 10	ni = 5			n = 100	ni = 5
σ b	0	0.01	0.1	1	10	0	0.01	0.1	1	10
Generalized F	0.052	0.052	0.054	0.053	0.054	0.054	0.052	0.047	0.053	0.049
pseudo-RLRT	0.050	0.049	0.052	0.052	0.054	0.051	0.050	0.048	0.052	0.050
$.5{\chi }_0^2+.5{\chi }_1^2$	0.040	0.043	0.043	0.042	0.046	0.048	0.048	0.045	0.050	0.047
(b) Partially linear model			n = 10	ni = 5			n = 100	ni = 5
σ α	0	0.01	0.1	1	10	0	0.01	0.1	1	10
Generalized F	0.052	0.052	0.048	0.050	0.055	0.046	0.050	0.047	0.054	0.048
pseudo-LRT	0.050	0.046	0.049	0.055	0.054	0.040	0.045	0.041	0.048	0.052
$.5{\chi }_2^2+.5{\chi }_3^2$	0.038	0.035	0.036	0.043	0.040	0.023	0.025	0.023	0.033	0.033
(c)Partially linear model			n = 40	ni = 5			n = 100	ni = 5
σ α 1	0	0.01	0.1	1	10	0	0.01	0.1	1	10
Generalized F	0.050	0.047	0.047	0.052	0.050	0.052	0.056	0.050	0.050	0.056
pseudo-LRT	0.052	0.047	0.054	0.053	0.058	0.050	0.050	0.046	0.048	0.055
$.5{\chi }_2^2+.5{\chi }_3^2$	0.032	0.030	0.031	0.034	0.035	0.030	0.033	0.029	0.031	0.037
(d) Varying coefficient model			n = 50					n = 500
σ b 1	0	0.01	0.1	1	10	0	0.01	0.1	1	10
Generalized F	0.052	0.048	0.055	0.053	0.049	0.052	0.046	0.048	0.048	0.052
pseudo-LRT	0.051	0.050	0.054	0.054	0.053	0.051	0.052	0.051	0.054	0.049
$.5{\chi }_2^2+.5{\chi }_3^2$	0.041	0.040	0.043	0.042	0.041	0.031	0.032	0.031	0.032	0.030
(e) Additive model			n = 50					n = 500
σ b 1	0	0.01	0.1	1	10	0	0.01	0.1	1	10
Generalized F	0.049	0.052	0.047	0.055	0.051	0.046	0.050	0.051	0.052	0.051
pseudo-RLRT	0.046	0.046	0.045	0.050	0.054	0.039	0.040	0.042	0.050	0.051
$.5{\chi }_0^2+.5{\chi }_1^2$	0.023	0.026	0.026	0.029	0.032	0.018	0.019	0.017	0.027	0.027

(a). Testing for the random intercept with a nuisance unspecified function in example 1.

(b). Testing for an unspecified function with a nuisance random intercept in example 1.

(c). Testing for an unspecified function with nuisance random intercept and random slope in example 2.

(d). Testing for a varying coefficient with a nuisance smooth term in example 3.

(e). Testing for linearity of a smooth additive function with a nuisance smooth term in example 4; corr(t_i1; t_i2)=0.7.

In other simulation settings where the covariates have low correlation or the nuisance variance component is not on the boundary of the parameter space, the generalized F-test also has type I error close to the nominal level. For example, with the partially linear model, case (a) and (b) in Table 1 show that both the generalized F-test and the pseudo-RLRT maintain the nominal level of the type I error rate at all the values of nuisance variance. However, the 50:50 chi-square approximation is still conservative. In these settings, we investigated a speed-up of Algorithm B by replacing Step B2 with a one-dimensional search of λ over λ₁, … , λ_m, while fixing $\widehat{\gamma }$ as estimated under the alternative. The procedure is instantaneous and provides satisfactory type I error rates similar to those reported in Table 1. In case (c), we investigate the performance of the proposed procedure when there are multiple nuisance variance components under the null (random intercepts and random slopes), and show that the proposed test maintains the correct type I error rate.

4.3 Power of the tests

The next six sets of simulations compare the power of various tests. The true models under the alternative hypothesis are specified as follows. For case (a), we simulated data from model (2) with ${\sigma }_b^2=1$ and let ${\sigma }_{\alpha }^2$ take different values. For case (b), we fixed ${\sigma }_{\alpha }^2=1$ and let f(t) = d * sin(2πt) in the partially linear mixed effects model (1). The parameter d serves as a measure of the effect size. For case (c), we fixed both variances ${\sigma }_{\alpha 0}^2$ and ${\sigma }_{\alpha 1}^2$ at one in the partially linear model (3). We let β = (0.3, 0.3)^T for the case n = 40, n_i = 5; β = (0.1, 0.1)^T for the case n = 100, n_i = 5; and let the variance ${\sigma }_b^2$ take different values. For the varying coefficient model, we fixed the nuisance variance component at ${\sigma }_{b1}^2=1$ and let β(t) = d * sin(2πt) in scenario (d), let β(t) = d * (t+t²) in scenario (e), and let d range from 0.1 to 1. For case (f), we fixed the nuisance variance component at ${\sigma }_{b1}^2=1$ in the additive model and let the variance component of interest, ${\sigma }_{b2}^2$, take different values.

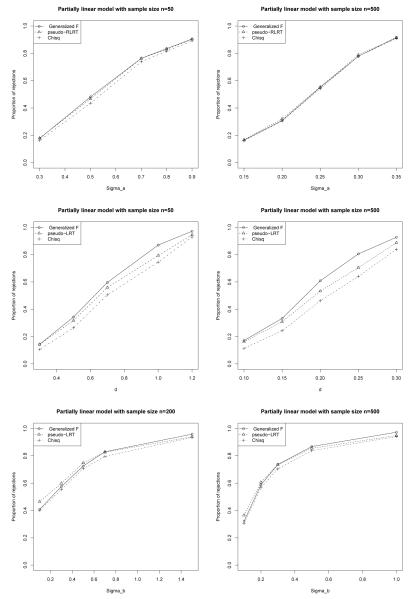
We present the numerical results in Tables A3 and A4 in the Online Appendix A.4 and depict the power comparisons in Figure 1 and Figure 2. We see that in all six scenarios, the 50:50 chi-square approximation is less powerful because it is a conservative procedure. The loss of power can be up to 16% compared to the proposed test. Depending on the hypothesis being tested and the true underlying model, there are some differences in power between the generalized F-test and the pseudo-LRT or RLRT. For example, in scenario (a), when testing for the random intercepts in model (2), there is no difference between the proposed and RLRT. In scenario (b), when testing the presence of a sine function in a partially linear model, the LRT is less powerful than the generalized F-test for several values of d. For scenario (c) and with a sample size of 200, the LRT appears to be slightly more powerful than the generalized-F when ${\sigma }_b^2=0.01$.

Figure 1.

Power of various tests in scenarios (a) (top two panels), (b) (middle two panels), and (c) (bottom two panels) based on 1,000 simulations.

(a): Testing for the random intercept with a nuisance unspecified function in example 1.

(b): Testing for an unspecified function with a nuisance random intercept in example 1.

(c): Testing for an unspecified function with nuisance random intercepts and random slopes in example 2.

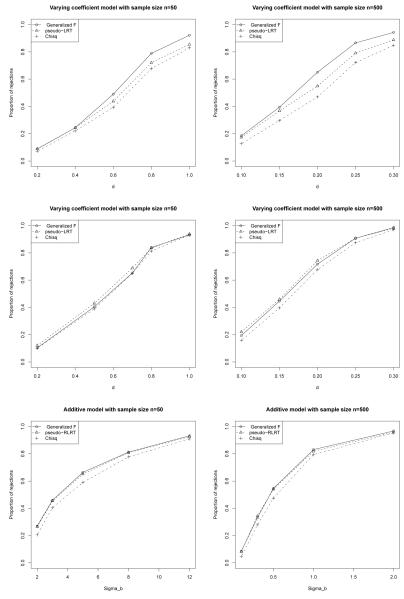
Figure 2.

Power of various tests in scenarios (d) (top two panels), (e) (middle two panels), and (f) (bottom two panels) based on 1,000 simulations.

(d): Testing for a varying coefficient with a nuisance smooth term in example 3, sine function.

(e): Testing for a varying coefficient with a nuisance smooth term in example 3, polynomial function.

(f): Testing for linearity of a smooth additive function with a nuisance smooth term in example 4; corr(t_i1, t_i2)=0.7.

For the varying coefficient model in case (d), when the function being tested is a sine function, the proposed test has a greater power than the pseudo-LRT. The power gain is up to 10%. When the function being tested is simpler (less number of modes), such as a quadratic function in scenario (e), the pseudo-LRT is slightly more powerful than the proposed F-test. For the additive model in case (f), the proposed test behaves similarly to the pseudo-RLRT. A computational advantage of the generalized F-test is that it requires fitting only one linear mixed effects model. The reduction in computational burden is important when the test is applied many times, such as in a GWAS, where T₁ or T₂ is computed for up to a million single nucleotide polymorphisms (SNPs) along the genome.

5. Data analysis

In 2007, dense SNP genotyping (550,000 SNPs) was conducted in the Framingham Heart Study (FHS) to map genes associated with risk factors of cardiovascular disease (CVD). In this genome-wide association study (GWAS), the research goal is to test the association between a SNP and a risk factor for CVD. Here the outcome of interest is the systolic blood pressure (SBP), a complex trait influenced by both environmental and genetic factors. In the literature, the heritability of SBP is estimated to be high (between 30% to 60%, Levy et al. 2000), which suggests a substantial genetic contribution. Several GWAS were conducted to identify SNPs that can explain the high heritability (Levy et al. 2009). However, most work in the current literature do not account for the age-specific genetic effect.

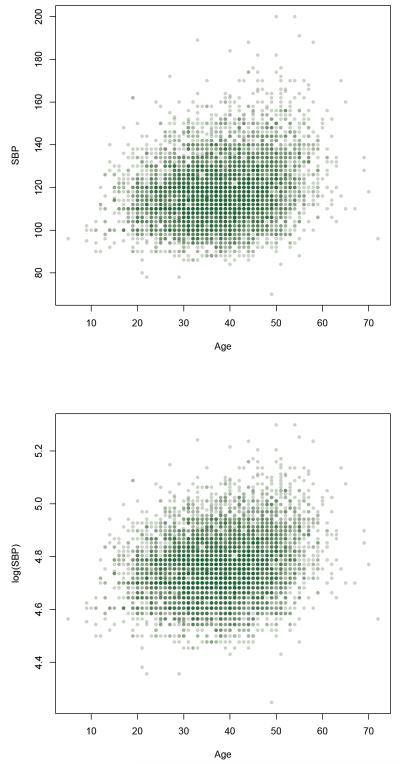
We test for the genetic association by the proposed generalized F-test using the FHS baseline SBP data incorporating the age effect by a varying coefficient mixed effects model. There were 6309 subjects from 951 families with available SBP included in the analysis. In the literature on genetic analysis of SBP, a log-transformation is often applied to better satisfy the model assumptions (Byng et al. 2003; Cui and Sheffield 2003). Therefore, a log-transformation of SBP was also applied in our analysis. We show a scatter plot of SBP and log(SBP) against age in Figure 3.

Figure 3.

Scatterplot of the SBP versus age (top panel) and log(SBP) versus age (bottom panel) in 6309 Framingham samples

Consider the varying-coefficient mixed effects model,

$$y_{\mathit{ij}}=c_{\mathit{ij}}^T\eta +\beta \left(s_{\mathit{ij}}\right)g_{\mathit{ij}}+{\alpha }_i+{\epsilon }_{\mathit{ij}},i=1,\cdots ,n,j=1,\cdots ,n_{\mathit{ij}},$$ (11)

where y_ij is the log-transformed SBP of the jth subject in the ith family, α_i is a family-specific random effect, g_ij is the genotype at a SNP for this subject coded as number of the minor alleles, s_ij is the subject’s age, c_ij are fixed effects (such as gender, age, age-squared, body mass index (BMI) and BMI-squared), and β(s_ij) is an additive genetic effect. It is of interest to test no genetic effect, that is, H₀ : β(s) = 0 in (11). Under the alternative, usual practice specifies β(s) as a linear function. Wang et al. (2012) observed power loss of the linear model analysis when the true genetic effect is nonlinear. Since the true genetic effect is unknown in practice, a flexible model under the alternative is desirable. We specify β(s) using a quadratic truncated polynomial base under the alternative and test the association through penalized spline. With the mixed model representation, the test falls under the general framework in model (5) and we test H₀ : β₂ = 0, ${\sigma }_{b2}^2=0$.

To correct for the large number of tests performed in a GWAS, the genome-wide significance level is usually set as 10⁻⁸ (Levy et al. 2009). We created 10⁸ repetitions to examine the null distribution of the test statistic. The computing time for 10⁸ null distribution simulations was around 28 hours on a Dell computer with 2.67GHz CPU and 4GHz memory, compared to an estimated 10⁵ hours by bootstrap (estimated from performing 100 bootstraps). The long computing time for bootstrap is partially due to a large number of random effects (families). The genome-wide critical value was computed to be 7.84.

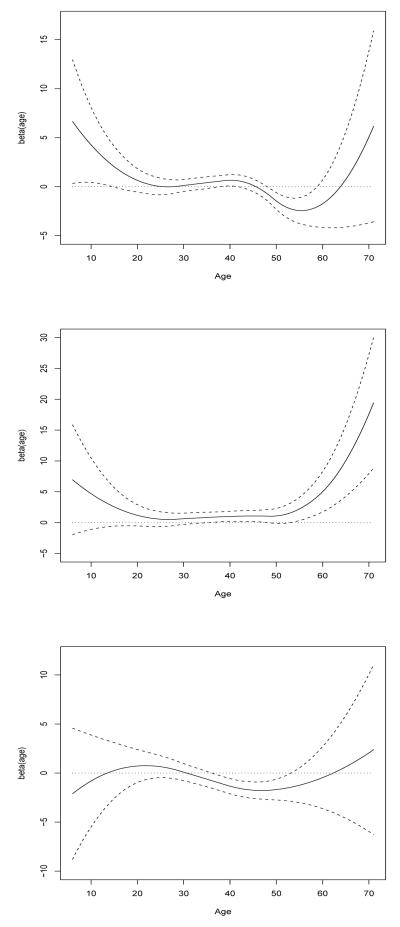
Levy et al. (2009) conducted a meta analysis of six GWAS on blood pressure traits and reported several promising regions that may harbor genes for SBP. We selected two promising candidate regions on chromosome 12 to analyze. There were 42 SNPs available in these regions (19 from region 88485Kb to 88605Kb and 23 from region 110305Kb to 110390Kb). The p-values were computed as the proportions of the simulated null test statistics greater than or equal to the observed. The top ranking SNPs are rs7136259, rs17249754, and rs11065898 with the respective p-values 0.00012, 0.00015, and 0.00068. The minor allele frequencies of these SNPs are 18%, 21%, and 34%, respectively. The first two top-ranking SNPs locate in the gene ATP2B1 (88585Kb and 110347Kb on chromosome 12) and the third one locates in the gene SH2B3 (88605Kb on chromosome 12). Both genes were reported to be associated with hypertension and blood pressure in several studies (Levy et al. 2009; Newton-Cheh et al. 2009). We present the fitted genetic effect $\widehat{\beta }\left(s\right)$ on the original scale for three SNPs in Figure 4, which suggests a nonlinear trend in all three cases. For SNPs rs7136259 and rs17249754, the genetic effect appears to be larger at the early and late ages (before age 20 and after age 50), while for SNP rs11065898, the genetic effect fluctuates across time.

Figure 4.

Fitted age-specific genetic effect $\widehat{\beta }\left(s\right)$ (solid lines) and its pointwise confidence interval (dashed lines) for SNPs rs7136259 (top panel), rs17249754 (middle panel) and rs11065898 (bottom panel)

These analyses provide some evidence of the presence of gene-age interaction, which in some cases may not have been identified if the time-trend had been ignored (Wang et al. 2012). There are reports of empirical evidence and theoretical justification for genetic factors controlling time-varying developmental features of a phenotype in plant, animal, and human genetic literature (Province and Rao 1985, Rice 2002, He et al. 2010). Since aging is a complex biological process during which many physiological changes may take place, age may represent a surrogate of various unmeasured biological factors. Taking into account the gene-age interaction in a genetic association study may help with resolving some of the inconsistencies in replicating a genetic finding, and may increase power of association tests (e.g., Lasky-Su et al. 2008; Wang et al. 2012).

This data analysis example shows that the proposed procedure solves a computational problem encountered in obtaining reliable genome-wide significance level for large-scale studies such as GWAS, where permutation is practically unrealistic and asymptotic approximation may be conservative and unstable.

6. Discussion

In this work, we propose a test of an unspecified function through linear mixed effects models with more than one variance component. We present a spectral decomposition of the test statistic that offers fast computation of the null and alternative distributions and reveals the connection between (R)LRT for single and multiple variance component models. The computational gain over permutation and bootstrap is especially useful for large scale experiments, such as the GWAS or microarray gene expression studies. With a large scale study, improving power is important, therefore an asymptotic chi-square approximation that leads to a conservative decision is highly undesirable. We observe some power differences between the generalized F-test and the (R)LRT depending on the true underlying model. In practice, when the true underlying function is unknown, these tests may supplement each other in terms of power. For the LRT or RLRT, the R package RLRsim (Scheipl et al. 2008) can be used to compute the null distribution efficiently.

Here, we use a reduced-rank penalized spline to represent an unknown function under the alternative. An extension to applying the test and its null distribution computation with smoothing splines or kernel machines is possible through mixed effects model representations. Lastly, the methods can be extended to O’Sullivan penalized splines using the B-splines basis functions through a penalty matrix presented in Wand and Ormerod (2008).