Robust Gaussian Graphical Modeling via l₁ Penalization

Summary

Gaussian graphical models have been widely used as an effective method for studying the conditional independency structure among genes and for constructing genetic networks. However, gene expression data typically have heavier tails or more outlying observations than the standard Gaussian distribution. Such outliers in gene expression data can lead to wrong inference on the dependency structure among the genes. We propose a l₁ penalized estimation procedure for the sparse Gaussian graphical models that is robustified against possible outliers. The likelihood function is weighted according to how the observation is deviated, where the deviation of the observation is measured based on its own likelihood. An efficient computational algorithm based on the coordinate gradient descent method is developed to obtain the minimizer of the negative penalized robustified-likelihood, where nonzero elements of the concentration matrix represents the graphical links among the genes. After the graphical structure is obtained, we re-estimate the positive definite concentration matrix using an iterative proportional fitting algorithm. Through simulations, we demonstrate that the proposed robust method performs much better than the graphical Lasso for the Gaussian graphical models in terms of both graph structure selection and estimation when outliers are present. We apply the robust estimation procedure to an analysis of yeast gene expression data and show that the resulting graph has better biological interpretation than that obtained from the graphical Lasso.

1. Introduction

Gaussian graphical models (GGMs) have been widely used for modeling the dependency structure among a set of variables (Whittaker 1990). Such models use undirected graphs to specify the conditional independence structures among the variables. In genomics, Gaussian graphical models have been applied to analyze the microarray gene expression data in order to understand how genes are related at the transcriptional levels (Segal et al. 2005; Li and Gui 2006; Finegold and Drton 2011). Due to the fact that the number of genes is usually larger than the sample size, regularization methods have been developed in recent years to estimate high dimensional Gaussian graphical models (Yuan and Lin 2007; Meinshausen and Bühlmann 2006; Peng et al. 2009; Friedman et al. 2008). Alternatively, l₁ constrained regularization methods have also be developed for estimating the sparse concentration matrix (Cai et al. 2011). The key of these procedures is to impose a sparse constraint on the concentration matrix of the multivariate variables. Among these, Friedman et al. (2008) developed the graphical Lasso (glasso) procedure that is computationally very efficient through application of the coordinate descent algorithm (Tseng and Yun 2009).

One key assumption of the GGMs and the estimation methods is the multivariate normality of the observations. However, outliers are often observed (Daye et al. 2012) in microarray gene expression data, or the data have longer tail than the normal distribution. Violation of the normality assumption can lead to both false positive or false negative identifications of the edges and biased estimate of the concentration matrix. In particular, contamination of a few variables in a few experiments can lead to drastically wrong inference on graph structures. However, the existing literature on robust inference in graphical models is very limited, especially in high dimensional settings. Finegold and Drton (2011) proposes to use multivariate t-distributions for more robust inference of graphs. However, the zero elements of the inverse of the covariance matrix of a t-distribution do not correspond to conditional independence and the density does not factor according to the graph. Finegold and Drton (2011) show that the zero conditional correlations in the t-distribution entail that the mean-squared error optimal prediction of a given variable can be based on the variables that correspond to its neighbors on the graph.

In this paper, we consider the problem of robust Gaussian graphical modeling and propose a robust estimation of the GGMs through l- penalization of a robustified likelihood function. Different from Finegold and Drton (2011), we still consider the GGMs, however, the estimation procedure is more robust than the standard penalized estimation approaches such as glasso. Our work is partially motivated by the work of Miyamura and Kano (2006), where they improve a Gaussian graphical modeling procedure through a robustified maximum likelihood estimation. In their work the likelihood function is weighted according to how the observation is deviated, and the deviation of the observation is measured based on its own likelihood. However, Miyamura and Kano (2006) did not consider the problem of inferring the graphical structure, especially in high dimensional settings. We propose to develop a l₁ regularization procedure based on the robustified likelihood by a Lasso penalty function on the concentration matrix of the Gaussian graphical model. We develop a coordinate gradient descent algorithm (Tseng and Yun 2009) for efficient computation and optimization. After the graphical structure is obtained, we re-estimate the positive definite concentration matrix using an iterative proportional fitting algorithm that guarantees the positive definiteness of the final estimate of the concentration matrix.

The paper is organized as follows. A brief review the GGMs and key idea of a penalized likelihood approach for robust estimation is first given in Section 2. Some details of coordinate gradient descent algorithm for the robust estimation are presented in Section 3. We evaluate the performance of the methods by simulations and application to a real data set in Sections 4 and 5. Finally, a brief discussion is given in Section 6.

2. Gaussian Graphical Models and Penalized Robust Likelihood Estimation

2.1 Gaussian graphical models

We assume that the gene expression data observed are randomly sampled data from a multi-variate normal probability model. Specifically, let Y be a random p-dimensional normal vector and Y₁, …, Y_p denote the p elements, where p is the number of genes. Let V = {1, …, p} be the set of nodes (genes), and y_k be the vector of gene expression levels for the k-th sample, k = 1, …, n. We assume that

$$Y~N_p(0,{\mathrm{\Omega }}^{-1})$$ (1)

with positive definite concentration matrix Ω = {w_ij}. This model also corresponds to an undirected graph G = (V, E) with vertex set V = {1, …, p} and edge set E = {e_ij}, where e_ij = 1 or 0 according to whether vertices i and j, 1 ≤ i < j ≤ p, are adjacent in G or not. The Gaussian graphical model consists of all p-variate normal distributions N_p(0, Ω^{− 1}), where the concentration matrix Ω satisfies the following linear restrictions:

$$e_{ij}=0\Rightarrow w_{ij}=0.$$

In the Gaussian graphical model, the partial correlation ρ_ij between Y_i on Y_j is defined as Corr(ε_i, ε_j), where ε_i is the prediction errors of the best linear predictors of Y_i based on Y_[−i] = {Y_j: 1 ≤ j ≠ i ≤ p}. It is well known that this partial correlation is also

$${\rho }_{ij}=-\frac{w_j}{\sqrt{w_{ii}{w}_{jj}}},\text{and}\text{Var}({\epsilon }_i)=\frac{1}{w_{ii}}.$$ (2)

2.2 Robustified-likelihood function for robust estimation

Let us consider a parametric statistical model {f_θ(y): θ ∈ Θ } for observations {y_k: k = 1, …, n}, where f_θ(y) is a probability density function and Θ is a parameter space on ℝ^q.

For given data y_k, k = 1, …, n, a modified log-likelihood for robust estimation is defined as

$$l_{\beta }(\theta )=\{\begin{array}{ll}\frac{1}{n\beta }\sum _{k=1}^n{f}_{\theta }{(y_k)}^{\beta }-b_{\beta }(\theta ),\hfill & \text{if}\beta >0\hfill \\ \frac{1}{n}\sum _{k=1}^{n}log{f}_{\theta }(y_k),\hfill & \text{if}\beta =0\hfill \end{array}$$ (3)

where β is a robustness tuning parameter and

$$b_{\beta }(\theta )=\frac{1}{1+\beta }\int f_{\theta }{(y)}^{1+\beta }dy,$$

which was proposed by Basu et al. (1998). Note that β = 0 corresponds to the ordinary log-likelihood. Assuming exchangeability between integration and differentiation, the first differentiation of the likelihood (3) for β > 0 with respective to θ is

$$\frac{1}{n}\sum _{k=1}^n{f}_{\theta }{(y_k)}^{\beta }s(y_k,\theta )-\frac{\partial }{\partial \theta }{b}_{\beta }(\theta )=0,$$ (4)

where

$$\frac{\partial }{\partial \theta }{b}_{\beta }(\theta )=\int f_{\theta }{(y)}^{\beta +1}s(y,\theta )dx=E[f_{\theta }{(y)}^{\beta }s(y,\theta )],$$

and s(y, θ) = ∂ log f_θ(y)/∂θ is the score function. Note that the second component of (4) is the expectation of the first component, and therefore the estimating equation (4) is unbiased and can be viewed as M-estimation (Huber 1981).

The intuition why the modified likelihood function can lead to robust estimation is that the contribution of the outlying observations in the efficient maximum likelihood score equation is down-weighted relatively to the model. Observations that are wildly discrepant with respect to the model get nearly zero weights. In the fully efficient case when β = 0, all observations, including very severe outliers, get weights equal to one. In the GGM, if observations are outliers that deviate greatly from the true model (e.g., observations from another models with different means or concentration matrices), then the density functions evaluated at these outlying observations should be very small and therefore they are downweighted. The idea of downweighting with respect to the model rather than the data is also the motivating principle of Windham (1995). A larger value of β results in more robust estimate of θ. Basu et al. (1998) noted that β > 1 causes a great loss of efficiency for some models.

2.3 Robust Estimation of the GGMs

Using the general robust likelihood formulation (3) of Basu et al. (1998), Miyamura and Kano (2006) proposed a robust estimation method for the concentration matrix of a GGM when the graphical structure is specified. However, estimating the graphical structure of the GGMs is often the goal of many data analysis. Since we expect that the concentration matrix Ω is sparse, we propose a l₁ penalized robust likelihood function to estimate the sparse concentration matrix. Specifically, let σ ≡ {w_ij}_i=j denote the vector of p diagonal elements of the concentration matrix Ω and θ ≡ {w_ij}_i<j denote the vector of q = p(p − 1)/2 off-diagonal elements of the Ω matrix. We estimate θ and σ by minimizing the following l₁ penalized logarithm of the negative robust likelihood function,

$$\begin{array}{l}{Q}_{\lambda ,\beta }(\theta ,\sigma )=-l_{\beta }(\theta ,\sigma )+\lambda {\left|\right|\theta \left|\right|}_1\\ =-c_{\beta }(\theta ,\sigma )\left(\frac{1}{n\beta }\sum _{k=1}^n{e}^{\beta z_k(\theta ,\sigma )}-\frac{1}{{(1+\beta )}^{p/2+1}}\right)+\lambda {\left|\right|\theta \left|\right|}_1,\end{array}$$ (5)

where

$$c_{\beta }(\theta ,\sigma )=\frac{{\mid \mathrm{\Omega }\mid }^{\beta /2}}{{(2\pi )}^{p\beta /2}}\text{and}{z}_k(\theta ,\sigma )=-\frac{1}{2}{y}_k^{\top }\mathrm{\Omega }{y}_k,$$

and λ is the tuning parameter and ||θ||₁= Σ_i≠j |w_ij|. See Web Appendix A for the derivation of the robust likelihood function for the GGMs.

3. A Coordinate Descent Algorithm and Estimation of Ω

3.1 A coordinate descent algorithm

Since the parameter σ is not known, both θ and σ are estimated by a two-step iterative procedure. First, we estimate θ, assuming that σ is fixed, i.e., l_β(θ) = l_β(θ, σ). We employee the (block) coordinate gradient descent method of Tseng and Yun (2009) to obtain the minimizer of the penalized likelihood function (5). The method is designed to solve a non-convex non-smooth optimization problem where the objective function consists of a smooth function and a block separable penalty function like the objective function (5).

The key idea of the method is to replace l_β(θ) by a quadratic approximation to find an improving coordinate direction at θ, and to conduct an inexact line search along a descent direction to ensure sufficient descent. Specifically, using a second-order Taylor expansion l_β(θ) at θ̂, we approximate Q_λ,β(θ) by

$$M_{\lambda ,\beta }(\mathit{d})=-\left\{l_{\beta }(\widehat{\theta })+{\mathit{d}}^{\top }\nabla l_{\beta }(\widehat{\theta })+\frac{1}{2}{\mathit{d}}^{\top }H\mathit{d}\right\}+\lambda {\left|\right|\widehat{\theta }+\mathit{d}\left|\right|}_1,$$

where d ∈ ℝ^q and

$$H=-\text{diag}{\left(max(-{\nabla }^2{l}_{\beta }{(\widehat{\theta })}_{jj},c^{\ast })\right)}_{j\in \{1,\dots ,q\}}.$$ (6)

The derivations of both ∇l_β(θ) and ∇²l_β(θ) are included in Web Appendix A, and c^* > 0 is a lower bound to ensure convergence (See proposition 3.1).

Next, we choose a nonempty index subset $\mathcal{J}\subseteq \mathbb{N}\stackrel{\text{def}}{=}\{1,2,\dots ,q\}$ and denote a minimizer of M_{λ, β} (d) as

$${\mathit{d}}_{\mathcal{J}}(\widehat{\theta })\stackrel{\text{def}}{=}\underset{\mathit{d}}{argmin}\left\{-{\mathit{d}}^{\top }\nabla l_{\beta }(\widehat{\theta })-\frac{1}{2}{\mathit{d}}^{\top }H\mathit{d}+\lambda {\left|\right|\widehat{\theta }+\mathit{d}\left|\right|}_1\right\},{\mathit{d}}_j=0\forall j\notin \mathcal{J}.$$ (7)

This is the estimated descent direction at θ̂, so we should move θ̂ along the direction 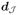(θ̂) to minimize the penalized likelihood. Since H is a diagonal matrix, 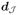(θ̂) has the following closed form

$${\mathit{d}}_j(\widehat{\theta })=-\text{mid}\left[\frac{\nabla l_{\beta }{(\widehat{\theta })}_j-\lambda }{H_{jj}},{\widehat{\theta }}_j,\frac{\nabla l_{\beta }{(\widehat{\theta })}_j+\lambda }{H_{jj}}\right],j\in \mathcal{J},$$ (8)

where mid[a, b, c] denotes the mid-point of (a, b, c).

However, the parameter θ in the Gaussian graphical model is restricted by the partial correlation relation in (2). Suppose that θ_j is the u-th row and v-th column element of Ω. Then, the following inequality must be satisfied;

$$-{\widehat{\theta }}_j-\sqrt{{\sigma }_u{\sigma }_v}\le {\mathit{d}}_j(\widehat{\theta })\le -{\widehat{\theta }}_j+\sqrt{{\sigma }_u{\sigma }_v},$$ (9)

because the partial correlation ρ_uv lies within the interval [−1, 1], and θ̂_j is updated by θ̂_j + d_j(θ̂). Since the minimum of the objective function (7) is one of the three points in (8), attaining the descent direction d_j(θ̂) within the boundaries (9) is still tractable. The condition (9) guarantees that θ̂ gives valid partial correlations in every iteration and the algorithm converges through bounded Ω (See proposition 3.1).

When 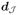(θ̂) ≠ 0, an inexact line search using the Armijo rule is performed to determine an appropriate step-size of the descent direction. Given θ̂ and d = 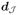(θ̂), let a step-size α be the largest value in {α₀δ^l}_l≥0 satisfying

$$Q_{\lambda ,\beta }(\widehat{\theta }+\alpha \mathit{d})-Q_{\lambda ,\beta }(\widehat{\theta })\le c_0\alpha \mathrm{\Delta },$$ (10)

where 0 < δ < 1, 0 < c₀ < 1, α₀ > 0 and Δ = −d^⊤∇l_β(θ̂) + λ|| θ̂ + d ||₁ − λ||θ̂||₁. The condition (10) requires that the objective improvement obtained by the step αΔ is within a factor c₀ of what is predicted by a linear extrapolation from θ̂. In practice, this step-size α can be computed by a simple backtracking procedure: start with α = α₀; if the condition (10) is not satisfied, set α ← αδ, and repeat until (10) holds. The algorithm is outlined below:

Given θ̂[t], Choose a nonempty index set ⊆ ℕ and H[t] from (6) Solve (7) with θ̂ = θ̂[t], H = H[t], and = to obtain d[t] = (θ̂[t]) Choose a step-size α[t] from (10) with θ̂ = θ̂[t] and d = d[t] Update θ̂[t+1] = θ̂[t] + α[t]d[t] Repeat 1 to 4 until some convergence criterion is met

Tseng and Yun (2009) suggested that a method called the Gauss-Southwell-q rule is the most effective method to select 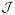on diagonally dominant Hessian from their extensive simulation studies. The Gauss-Southwell-q rule chooses 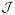to satisfy

$$\left\{j\in \mathcal{J}\mid q_j(\widehat{\theta })\le v\underset{j}{min}{q}_j(\widehat{\theta })\right\},$$ (11)

where 0 < υ ≤ 1, and

$$q_{\mathcal{J}}(\widehat{\theta })\stackrel{\text{def}}{=}{\left\{-{\mathit{d}}^{\top }\nabla l_{\beta }(\widehat{\theta })-\frac{1}{2}{\mathit{d}}^{\top }H\mathit{d}+\lambda {\left|\right|\widehat{\theta }+\mathit{d}\left|\right|}_1\right\}}_{\mathit{d}={\mathit{d}}_{\mathcal{J}}(\widehat{\theta })}-\lambda {\left|\right|\widehat{\theta }\left|\right|}_1.$$

Each iteration 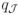(θ̂) measures the magnitude of the descent in Q_λ,β(θ) from θ̂ to θ̂ + 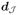(θ̂). So, every θ̂ eventually comes to a stationary point as 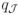(θ̂) goes to 0. We have the following Proposition on the convergence of the algorithm.

Proposition 3.1

If H^[t] and 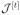are chosen according to (6) and (11), respectively, and ${\mathit{d}}_{\mathcal{J}}^{[t]}$ is bounded by (9) for all t > 0, then every limit point of the sequence {θ̂^[t]}_t>0 is a minimum point of Q_λ,β(θ).

This Proposition directly follows from Theorem 1(d) in Section 4 of Tseng and Yun (2009). In general, because of the non-convexity of the optimization problem, the above algorithm may not achieve the global optimum.

The Armijo rule (10) and the Gauss-Southwell-q rule (11) of the coordinate gradient descent method also requires some tuning values to be fixed. We set them as

$$c_0=0.1,\delta =0.5,{\alpha }_0^{[0]}=1,{\alpha }_0^{[t+1]}=min({\alpha }^{[t]}/0.5,1),$$

and υ^[0] = 0.5,

$$v^{[t+1]}=\{\begin{array}{ll}max({10}^{-4},v^{[t]}/10)\hfill & \text{if}{\alpha }^{[t]}>{10}^{-3}\hfill \\ min(0.5,50v^{[t]})\hfill & \mathit{else}.\hfill \end{array}$$

These settings are suggested by Tseng and Yun (2009) to maintain balance between the number of coordinates updated and step-size based on their experiments. Notice that smaller υ results in more coordinates being updated while a larger value of υ has the opposite effect.

3.2 Estimation of the concentration matrix

Given σ̂^[t] and θ̂^[t], we have estimated θ̂^[t+1] by the coordinate gradient descent method. Given current estimate θ̂^[t+1], we update σ̂^[t] based on (2), where 1/w_ii represents the partial variance of the i-th gene. Based on the nonzero elements of θ̂, we fit the linear regression equation for each gene as response and linked neighboring genes as predictors and obtain the mean squared error which can be used as an estimate of the partial variance. Since we assume that the concentration matrix is sparse, the total number of genes linked to each gene is mostly smaller than the sample size n, so ordinary regression estimation can be made. When a gene has more linked genes than n, then only the n − 2 genes sorted by the largest absolute values of the partial correlations of those linked genes are considered in the regression. The estimate σ̂ quickly stabilizes as nonzero elements and zero elements of θ̂ become fixed regardless of the numerical values of nonzero estimates.

Suppose that the estimates (θ̂_S, σ̂) complete the matrix Ω̂_S, then a graph can be easily constructed based on the nonzero off-diagonal elements of Ω̂_S. However, the resulting estimate Ω̂_S is not guaranteed to be positive definite, while the likelihood based method of glasso (Friedman et al. 2008) assures the positive definiteness. However, we have observed from simulations that Ω̂_S is rarely non-positive-definite under the high dimensional sparse settings that we are interested in. More discussions on this issue can be found in Section 6.

To overcome the potential problem of obtaining a non-positive definite estimate Ω̂_S, we can re-estimate Ω assuming the same zero elements as Ω̂_S using the procedure proposed by Miyamura and Kano (2006). Specifically, given the concentration graph structure estimated based on the algorithm above, the robustified estimating equation (4) of the Gaussian graphical model is

$$\frac{1}{n}\sum _{k=1}^n{e}^{\beta z_k(\theta ,\sigma )}(\mathrm{\sum }-y_k{y}_k^{\top })-\frac{\beta }{{(1+\beta )}^{p/2+1}}\mathrm{\sum }=0,$$ (12)

where Σ = Ω⁻¹ is a covariance matrix. See Web Appendix A for the derivation of the equation above. Given Ω ≡ (θ, σ), suppose that Σ̂ solves the equation (12). Then, the iterative proportional fitting algorithm of Speed and Kiiveri (1986) is applied to update Σ̂ so that Σ̂⁻¹ has the exactly same zero elements as Ω̂_S does. Resetting Ω = Σ̂⁻¹, this step is repeated until Σ̂ converges. Miyamura and Kano (2006) have shown that this procedure always ends up with a positive definite covariance matrix. Let us denote Σ̂_M as the re-estimated robustified covariance matrix, and θ̂ _M and σ̂_M as the off-diagonal and diagonal elements of the inverse of Σ̂_M, respectively.

3.3 Tuning parameter selection

The penalized robust log-likelihood (5) has two tuning parameters β and λ, which controls the robustness and sparsity, respectively. A larger value of β leads to a more robust estimator, but with an inflation of the variance of the resultant estimator. Due to this trade-off of robust and efficiency, Basu et al. (1998) argued that there is no universal way of selecting an appropriate β parameter. We compare the performance of the robust methods with different β values in our simulation study and choose one to apply to the real data analysis.

We use the K-fold cross validation based on the log-robust likelihood criterion with β fixed to choose the sparsity tuning parameter λ. First we divide all the samples in the training dataset into K disjoint subgroups, also known as folds, and denote the index of subjects in the kth fold by T_k for k = 1, 2, ···, K. The K-fold cross-validation score is defined as

$$CV(\lambda )=\sum _{k=1}^K{c}_{\beta }({\widehat{\theta }}_M^{(-k)},{\widehat{\sigma }}_M^{(-k)})\left(\frac{1}{n_k\beta }\sum _{i\in T_k}{e}^{\beta z_i({\widehat{\theta }}_M^{(-k)},{\widehat{\sigma }}_M^{(-k)})}-\frac{1}{{(1+\beta )}^{p/2+1}}\right),$$ (13)

where n_k is the size of the kth fold T_k and ${\widehat{\theta }}_M^{(-k)}$ and ${\widehat{\sigma }}_M^{(-k)}$ are the corresponding estimates of θ and σ based on the sample $({\cup }_{k=1}^K{T}_k)\backslash T_k$ with λ as the tuning parameter. It is well known that cross validation can perform poorly on model selection problems involving l₁ penalties (Meinshausen and Bühlmann 2006) due to shrinkage in the values of the non-zero elements of the concentration matrix. To reduce the shrinkage problem, we replace the non-zero elements of θ̂_S with their non-penalized estimate θ̂_M using the iterative algorithm presented in Section 3.2. We have found that this approach allows us to select sparser network structures than those from using standard cross validation. This two-stage approach was also used for tuning parameter selection in other settings when l₁ penalization is used (James et al. 2010).

4. Simulation Studies

4.1 Simulation setup and results when p < n

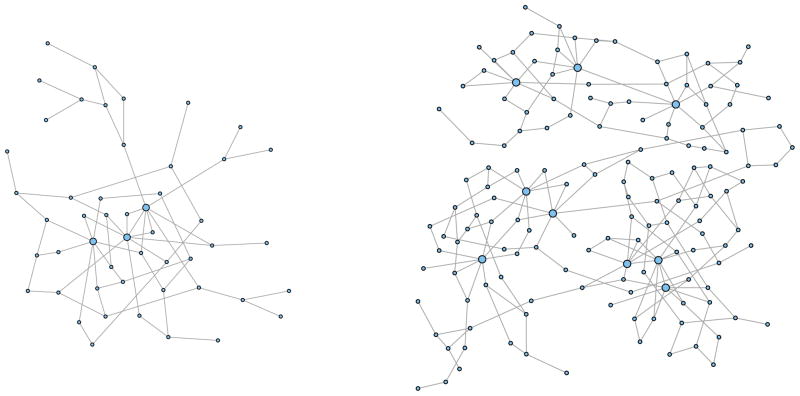
We performed simulation studies to examine the performance of the proposed robust method with some different β values and to compare with the standard penalized likelihood method glasso by Friedman et al. (2008) in terms of both graph structure selection and estimation of the concentration matrix. Our simulation setup is similar to that of Peng et al. (2009). We first randomly generate various network graphs that mimic gene regulatory networks, which typically have a few hub genes with many links and many other genes with only a few edges. For the first set of simulations, each graph consists of p = 50 nodes, and three of them are regarded as hub genes with degrees around 8. The other 47 nodes have 1,2, or 3 degrees so that each graph has about 70 edges (see Figure 1 for an example of such a graph). Based on this network graph we construct a positive definite p×p concentration matrix Ω, where most of elements are zero and the elements corresponding to the edges are nonzero. The simulated nonzero partial correlation ρ_ij of each concentration matrix has ρ_ij ∈ (−0.66, −0.06) for negative correlation and ρ_ij ∈(0.06, 0.66) for positive correlation with mean correlations of about −0.28 and 0.28, respectively.

Figure 1.

Examples of the simulated network graphs: the graph on the left is used in the first set of simulations (single module) and has 50 nodes including 3 hub nodes with around 70 edges; the graph on the right is used in the second set of simulations (triple modules) and has 150 nodes including 9 hub nodes with around 210 edges.

We then simulated i.i.d samples of gene expression data y_k from the multivariate normal distribution, where outliers are added from the same distribution but with different mean vectors. Specifically, each sample was generated from the following mixture distribution,

$$y_k~(1-p_0)N_p(0,{\mathrm{\Omega }}^{-1})+\frac{p_0}{2}{N}_p(-\mu ,{\mathrm{\Omega }}^{-1})+\frac{p_0}{2}{N}_p(\mu ,{\mathrm{\Omega }}^{-1}),k=1,\dots ,n.$$

We fix the mixing proportion p₀ = 0.1, and make four types of outliers: μ^⊤ = (0, …, 0)^⊤, (1, …, 1)^⊤, (1.5, …, 1.5)^⊤, and (2, …, 2)^⊤. They are denoted by model I, II, III, and IV, respectively. This outlying pattern leads to decreasing of the partial correlation coefficients, so the graph structure could be obscured by the outliers. Finally, we re-scaled the data so that each gene has a mean of 0 and standard deviation of 1. The simulated data set consists of a training set for model fit and independent validation set for tuning parameter selection, and both have a sample size of n = 100. For each model, we repeated to generate simulation data 100 times where the network graph was also re-generated each time.

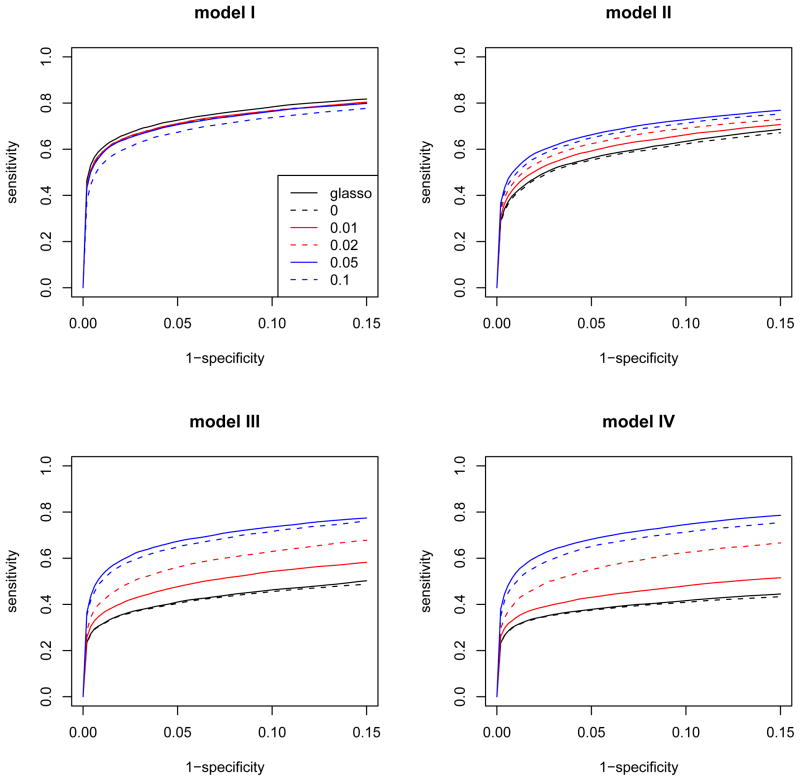
The glasso and robust method with β = 0, 0.01, 0.02, 0.05, 0.07, and 0.1 were fitted for each model. Figure 2 shows the average ROC curves of different methods over 100 simulation data sets for each model as the tuning parameter λ varies. Since no outliers were generated in model I, the standard method glasso performs quite well here, and the other robust methods except β = 0.1 also show similar selection performance as glasso, although they have slightly lower curves. However, in other models II, III, and IV with outliers, we observe that glasso performed very poorly in recovering the true edges. In addition, the robust method with β = 0 results in very similar ROC curves as glasso for all models. This is because the robust penalized estimation with β = 0 simply reduces to ordinary penalized likelihood estimation of glasso. We observe that the robust method with β = 0.05 shows the best performance for gene selection when outliers exist. It is noticeable that the ROC curves from the robust method with β = 0.05 are very comparable for all models, indicating that its selection performances are stable and are not affected by outliers. The ROC curves when β = 0.07 are very similar to those when β = 0.05 and are omitted here. The robust method with β = 0.1 shows the second best performances in models II, III, and IV, but its selection is relatively poor in model I.

Figure 2.

The ROC curves of glasso and the robust method with different robustness tuning parameters, β = 0, 0.01, 0.02, 0.05, and 0.1 for the first set of simulations with p = 50, n = 100. Model I does not have outliers, but Model II, III, and IV has 10% of small, medium and large magnitudes of outliers, respectively. Each curve is an average over 100 simulated data sets.

We then investigate the performance of these methods when the tuning parameter λ is chosen using the cross-validation (13). Table 1 summarizes both selection and estimation performances for four different outlier models. The table includes the average and standard errors of the total number of detected edges, sensitivity, specificity, and the mean squared errors (MSEs) of θ̂_M over 100 simulated data sets. Since θ̂_M is re-estimated for accurate tuning parameter selection, we also re-estimate the matrix Ω of glasso to select the tuning parameter in a similar way, using the iterative proportional fitting algorithm of Speed and Kiiveri (1986). This procedure gives the symmetric positive definite estimate for Ω which is used for the comparison of MSEs among different methods. In each model the results of glasso and the robust methods with β = 0.02, 0.05, and 0.07 are presented in the table. For model I where there are no outliers, all methods perform similarly in terms of both selection and estimation. However, for other three models when the outliers are present, the performances are quite different. The glasso and the robust method with β = 0.02 tend to select many more edges as the magnitudes of outliers increase, which leads to significantly lower specificity and increased MSEs while the sensitivity goes slightly up. In contrast, the robust methods with β = 0.05 and 0.07 show consistent better performances for models II, III, and IV, although both methods still select a few more edges than for model I. The glasso has a little higher sensitivity than the robust methods due to selecting too many edges. In this set of simulations, the best choice of a robustness tuning parameter β appears to be around 0.05 or 0.07.

Table 1.

Simulation results: summary of edge detection under the selected tuning parameter λ by cross-validation for two sets of simulations with p = 50; n = 100 and p = 150; n = 100. The results are the average (standard error) of the number of detected edges, sensitivity, specificity, and mean squared errors(MSE) for θ̂_M over 100 simulation data. Results from glasso and the proposed robust estimation with different specifications of the β value are compared.

Model	Method	# of edges	Sensitivity	Specificity	MSE
p = 50, n = 100
I	glasso	89.22 (1.68)	0.70 (0.0052)	0.97 (0.0012)	0.0032 (0.0000)
	β = 0.02	95.99 (1.83)	0.70 (0.0050)	0.96 (0.0013)	0.0034 (0.0001)
	β = 0.05	94.82 (1.82)	0.69 (0.0053)	0.96 (0.0013)	0.0037 (0.0001)
	β = 0.07	91.10 (1.62)	0.67 (0.0053)	0.96 (0.0011)	0.0039 (0.0001)
II	glasso	306.54 (8.35)	0.76 (0.0065)	0.78 (0.0069)	0.0095 (0.0002)
	β = 0.02	236.82 (11.05)	0.72 (0.0079)	0.84 (0.0092)	0.0083 (0.0002)
	β = 0.05	136.60 (4.67)	0.70 (0.0062)	0.92 (0.0037)	0.0062 (0.0002)
	β = 0.07	110.89 (2.26)	0.68 (0.0058)	0.94 (0.0017)	0.0057 (0.0001)
III	glasso	418.85 (3.22)	0.77 (0.0055)	0.68 (0.0027)	0.014 (0.0003)
	β = 0.02	392.27 (11.99)	0.75 (0.0105)	0.71 (0.0100)	0.014 (0.0003)
	β = 0.05	131.25 (5.35)	0.69 (0.0065)	0.93 (0.0044)	0.0076 (0.0003)
	β = 0.07	105.22 (2.72)	0.67 (0.0057)	0.95 (0.0021)	0.0072 (0.0001)
IV	glasso	441.47 (4.93)	0.77 (0.0079)	0.66 (0.0040)	0.020 (0.0005)
	β = 0.02	430.28 (9.15)	0.75 (0.0107)	0.67 (0.0077)	0.020 (0.0005)
	β = 0.05	133.50 (5.78)	0.70 (0.0071)	0.93 (0.0046)	0.011 (0.0004)
	β = 0.07	109.95 (3.29)	0.68 (0.0069)	0.95 (0.0025)	0.010 (0.0002)
p = 150, n = 100
I	glasso	263.68 (2.38)	0.64 (0.0027)	0.99 (0.0002)	0.0015 (0.0001)
	β = 0.005	281.33 (2.73)	0.64 (0.0027)	0.99 (0.0002)	0.0015 (0.0001)
	β = 0.02	281.94 (2.61)	0.64 (0.0027)	0.99 (0.0002)	0.0016 (0.0001)
	β = 0.03	276.03 (2.82)	0.63 (0.0030)	0.99 (0.0002)	0.0017 (0.0001)
II	glasso	682.78 (1.63)	0.60 (0.0063)	0.95 (0.0002)	0.0030 (0.0001)
	β = 0.005	637.32 (9.14)	0.64 (0.0052)	0.95 (0.0008)	0.0031 (0.0001)
	β = 0.02	427.60 (7.39)	0.65 (0.0034)	0.97 (0.0006)	0.0027 (0.0001)
	β = 0.03	335.24 (4.46)	0.63(0.0033)	0.98 (0.0004)	0.0025 (0.0001)
III	glasso	507.70 (24.71)	0.40 (0.0091)	0.96 (0.0021)	0.0039 (0.0001)
	β = 0.005	672.33 (6.22)	0.54 (0.0087)	0.95 (0.0006)	0.0040 (0.0001)
	β = 0.02	469.63 (10.29)	0.66 (0.0043)	0.97 (0.0009)	0.0037 (0.0001)
	β = 0.03	363.00 (7.63)	0.63 (0.0038)	0.98 (0.0006)	0.0034 (0.0001)
IV	glasso	678.70 (4.00)	0.38 (0.0033)	0.95 (0.0004)	0.0046 (0.0001)
	β = 0.005	673.54 (2.46)	0.52 (0.0081)	0.95 (0.0003)	0.0049 (0.0001)
	β = 0.02	487.78 (12.59)	0.66 (0.0041)	0.97 (0.0011)	0.0038 (0.0001)
	β = 0.03	370.41 (9.31)	0.63 (0.0042)	0.98(0.0008)	0.0033 (0.0001)

4.2 Simulations when p > n

In the next set of simulations, we demonstrate that the proposed robust method performs consistently better than glasso even when p > n. We generate graphs with triple modules in this simulation (See right plot of Figure 2) so that each simulated network graph has p = 150 nodes including 9 hub genes and around 210 edges. The concentration matrix in each model is generated so that the distribution of nonzero partial correlations is same as the previous simulation. The gene expression data y_k with n = 100 are also generated in exactly the same way for each of the four outlier models.

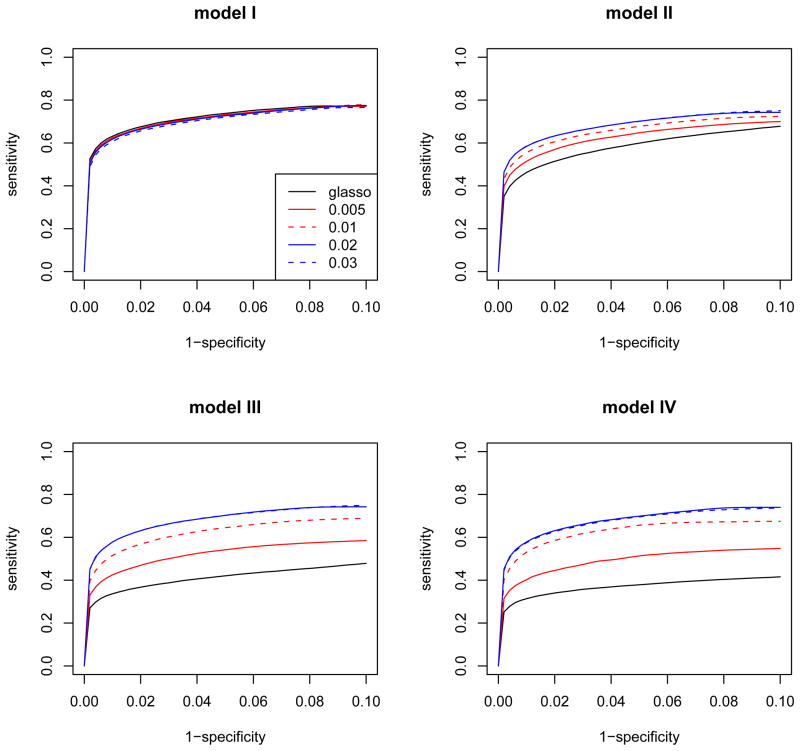
Figure 3 presents the average ROC curves of glasso and the robust methods with β = 0.005, 0.01, 0.02, and 0.03 over 100 simulation data sets for each model as the tuning parameter λ varies. Similar to the first set of simulations, glasso shows the worst selection performance for the models where outliers are present. The robust methods with both β = 0.02 and 0.03 have the best ROC curves, although β = 0.02 is slightly preferred in model I. In this simulation, we observe that the robust methods with β > 0.03 performed worse than method with β = 0.03. Basu et al. (1998) have also discussed that the robust estimation in multivariate normal distribution models loses efficiency for increasing p when β is fixed. Thus, the parameter β should be carefully selected depending on the multivariate dimension p.

Figure 3.

The ROC curves of glasso and the robust method with different robustness tuning parameters, β = 0.005, 0.01, 0.02, and 0.03 for the second set of simulations with p = 150, n = 100. Model I does not have outliers, but Model II, III and IV has 10% of small, medium and large magnitudes of outliers, respectively. Each curve is an average over 100 simulated data sets.

Table 1 summarizes both selection and estimation performance of detecting the edges under the selected λ using cross-validation for four different outlier models. All methods performed similarly for model I. It is clear that the robust methods with both β = 0.02 and 0.03 outperformed glasso on both selection and estimation for all models where outliers were present. Compared to the first set of simulations, glasso recovers relatively few true edges when p > n, but the robust methods consistently have higher level of sensitivity and specificity for all models and for large p.

4.3 Simulations with different concentration matrices for the outliers

In the next set of simulations, we consider four different models where the outliers are generated from models with different concentration matrices while differing the magnitude of μ’s. These models mimic the scenarios where the outliers come from models with different graphical structures. The last model assumes that the outliers are not symmetric about the mean to mimic the scenarios that the outliers can affect both the means and also the concentration matrix. We again observe that our proposed robust method still recovers more true edges than glasso for the same false positive rates even when the Markov structures are blurred by the outliers or when the outliers are not symmetric about the means. Details of the models and simulation results are presented in Web Appendix B.

These simulation studies have clearly demonstrated that the robust method with an appropriate robustness tuning parameter gives much better performance than glasso in terms of both graphical structure selection and estimation of the concentration matrix when the data have some outliers. Since our algorithm only guarantees convergence to a stationary point, we explore different starting values for the concentration matrix, including both the identity matrix and the estimate from the glasso, we did not observe any differences in the final estimates. Choosing the identity matrix as the starting value performs well in all simulation examples. Finally, the algorithm is very fast. For a given tuning parameter λ, it took 1.2–1.7s and 2.2–2.4s for the simulated data sets when p = 50 and p = 150 using the R codes that we implemented.

5. Analysis of Yeast Gene Expression Data Set

To demonstrate the proposed robust estimation method, we present results from an analysis of a data set generated by Brem and Kruglyak (2005). In this experiment, 112 yeast segregants, one from each tetrad, were grown from a cross involving parental strains BY4716 and wild isolate RM11-1a. RNA was isolated and cDNA was hybridized to microarrays in the presence of the same BY reference material. Each array assayed 6,216 yeast genes. Genotyping was performed using GeneChip Yeast Genome S98 microarrays on all 112 F₁ segregants. Due to small sample size and limited perturbation to the biological system, it is not possible to construct a gene network for all 6,216 genes. We instead focus our analysis on a set of 54 genes that belong to the yeast MAPK signaling pathway provided by the KEGG database (Kanehisa et al. 2010). We aim to understand the conditional independence structure of these 54 genes on the MAPK pathway.

The yeast genome encodes multiple MAP kinase orthologs, where Fus3 mediates cellular response to peptide pheromones, Kss1 permits adjustment to nutrient-limiting conditions and Hog1 is necessary for survival under hyperosmotic conditions. Lastly, Slt2/Mpk1 is required for repair of injuries to the cell wall. A schematic plot of this pathway is presented in Figure 2 of the Web Appendix C. Note that this graph only presents our current knowledge about the MAPK signaling pathway. Since several genes such as Ste20, Ste12 and Ste7 appear at multiple nodes, this graph cannot be treated as the “true graph” for evaluating or comparing different methods. In addition, although some of the links are directed, this graph does not meet the statistical definition of either directed or undirected graph. Rather than trying to recover exactly the MAPK pathway structure, we choose this set of 54 genes on the MAPK pathway to make sure that these genes are potentially dependent at the expression level. We evaluate whether the genes on the same signaling path of the MAPK pathway tend to be linked on the graphs estimated from the GGM based on the gene expression data.

We apply both glasso and the robust method to these 54 genes in the MAPK pathway to study their conditional independence structure. For each of the 54 genes, we first re-scale the data so that each gene has a mean of 0 and a standard deviation of 1. Figure 3 of Web Appendix C shows the histogram of re-scaled real gene expression data excluding 5 extreme values and two histograms of data sets simulated from models III and IV presented in previous section. The shapes of histograms are quite similar, and the number of genes (p = 54) and sample size (n = 112) in real data are also comparable to those in the first set of simulations (p = 50, n = 100). The histograms of these genes and their skewness (Web Appendix C) indicate that the expressions of some genes are not symmetric about their means and include outliers. Based on the simulation results, we fix the robustness tuning parameter β = 0.05, which gave the best performance in the simulation studies. We use 5-fold cross validation to choose the optimal tuning parameter for both glasso and robust estimation. After the λ is chosen, we rerun both glasso and robust method using the full samples and obtain the final estimates of the concentration matrix with glasso identifying 163 links and the robust method identifying 100 links.

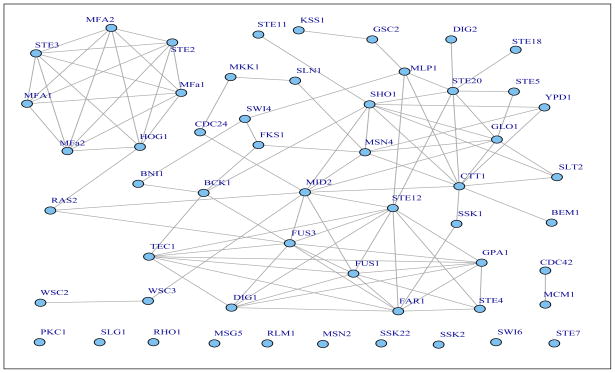
Clearly, glasso results in a much denser graph than the robust estimation, which makes it difficult to interpret biologically. The mean, median and maximum degree the graph is 6, 6.03 and 14 based on glasso, and 3, 3.7 and 10 based on the robust estimation, respectively. We observe that 87 edges are identified by both glasso and the robust method, 76 links are identified only by glasso and 13 links are identified only by the robust method. Figure 4 shows the undirected graph of 54 genes based on the estimated sparse concentration matrix from the robust method, where a total 100 links are observed among 44 genes. This undirected graph can indeed recover lots of links among the 54 genes on the KEGG MAPK pathway. Most of the links in the upper part of the MAPK signaling pathway are recovered by the estimated graph. For example, the kinase Fus3 is linked to its downstream genes Dig1, Ste12, FAR1 and Fus1, and the MFA1 (MATα1)/MFA2 genes and STE2 and STE3 form an interconnected subgraph. This part of the pathway mediates cellular response to peptide pheromones. Similarly, the kinase Slt2/Mpk1 is linked to its downstream genes Swi4 and Rlm1. The Sho1 gene on the second layer of the pathway is linked to many of its downstream genes, including Ste11, Ste20, Cttl, Glo1 and MSN4. These linked genes are related to cell response to high osmolarity.

Figure 4.

The genetic networks identified based on the proposed robust penalized estimation with β = 0.05 for the 54 genes of the KEGG MAPK pathway.

6. Discussion

Gaussian graphical models have been widely used in modeling the conditional independency structures of the data and have been applied to analysis of gene expression data. We have proposed a l₁ penalized robust likelihood estimation procedure for the GGMs in order to achieve the robustness and to maintain the efficiency. Our simulations demonstrated that when there are outliers in the data, the proposed estimation procedure can greatly outperform the graphical Lasso for GGMs. The method also resulted in much fewer number of links for the yeast MAPK gene expression data than glasso, which makes it easier to interpret biologically. Many of the links identified by the robust method agree with the current knowledge of the MAPK pathway and have a clear biological interpretation.

As discussed earlier, one limitation of the penalized robust likelihood estimate of the concentration matrix is its lack of assurance of positive definiteness. This is certainly not unique to our proposed estimator. Except for the glasso estimate, many other estimators of the concentration matrix in the GGM setting (Peng et al. 2009; Cai et al. 2011) are not guaranteed to be positive definite either. However, for simulations reported above, the corresponding estimators we have examined are all positive definite. This suggests that, for the sparse and high dimensional regime that we are interested in, non-positive-definiteness does not seem to be a big issue for the proposed method, as it only occurs when the resulting model is huge and thus very far away from the true model. As long as the estimated models are reasonably sparse, the corresponding estimators by the penalized robust likelihood remain positive definite. After the graph structure is determined, we proposed to obtain the final estimate of the concentration matrix using the procedure of Miyamura and Kano (2006) that is guaranteed to be positive definite.

As with all the robust procedures, there is a trade-off between robustness and efficiency, which is controlled by the parameter β in our proposed penalized robust likelihood estimation. The methodology affords a robust extension of the powerful penalized maximum likelihood estimation of the Gaussian graphical models when β = 0. We notice that when the data are indeed normal, the results from the robust estimation are not effected by the choice of the β value. When there are outliers, the performance of the robust estimation depends on the β value, however, is always better than glasso in recovering the graph structure and in estimation of the concentration matrix as long as the β is not too large. From our simulations, it seems that choosing β between 0.03 and 0.07 affords considerable robustness while retaining efficiency. How to best choose this parameter requires further research.