Mechanism-Based Model of Parasite Growth and Dihydroartemisinin Pharmacodynamics in Murine Malaria

Abstract

Murine models are used to study erythrocytic stages of malaria infection, because parasite morphology and development are comparable to those in human malaria infections. Mechanism-based pharmacokinetic-pharmacodynamic (PK-PD) models for antimalarials are scarce, despite their potential to optimize antimalarial combination therapy. The aim of this study was to develop a mechanism-based growth model (MBGM) for Plasmodium berghei and then characterize the parasiticidal effect of dihydroartemisinin (DHA) in murine malaria (MBGM-PK-PD). Stage-specific (ring, early trophozoite, late trophozoite, and schizont) parasite density data from Swiss mice inoculated with Plasmodium berghei were used for model development in S-ADAPT. A single dose of intraperitoneal DHA (10 to 100 mg/kg) or vehicle was administered 56 h postinoculation. The MBGM explicitly reflected all four erythrocytic stages of the 24-hour P. berghei life cycle. Merozoite invasion of erythrocytes was described by a first-order process that declined with increasing parasitemia. An efflux pathway with subsequent return was additionally required to describe the schizont data, thus representing parasite sequestration or trapping in the microvasculature, with a return to circulation. A 1-compartment model with zero-order absorption described the PK of DHA, with an estimated clearance and distribution volume of 1.95 liters h⁻¹ and 0.851 liter, respectively. Parasite killing was described by a turnover model, with DHA inhibiting the production of physiological intermediates (IC₅₀, 1.46 ng/ml). Overall, the MBGM-PK-PD described the rise in parasitemia, the nadir following DHA dosing, and subsequent parasite resurgence. This novel model is a promising tool for studying malaria infections, identifying the stage specificity of antimalarials, and providing insight into antimalarial treatment strategies.

INTRODUCTION

Malaria remains a major health concern in countries where the disease is endemic, and optimized dosing strategies are therefore required for effective treatment (1, 2). The artemisinins are currently first-line malaria treatment, due to their more rapid killing of parasites than any other available antimalarial drug (3, 4). A further benefit is that the artemisinins are active against parasites resistant to traditional antimalarials, although emerging resistance has been reported recently (5–7). However, their short elimination half-lives in vivo make them inadequate for use as monotherapy, due to recrudescence of infections after a standard 3-day dosing regimen (8). For this reason, artemisinin combination therapy (ACT) with longer-acting partner drugs has been recommended for the treatment of malaria (1). Nevertheless, ACT dosing regimens have been challenging to develop and have at best been empirically derived, primarily due to the lack of pharmacokinetic (PK) and pharmacodynamic (PD) data to guide dose optimization (9).

Murine models are useful tools for investigating malaria infection, because parasite morphology and development in mice are comparable to those in human malaria infections (10). The limitations of murine models are well documented and have repercussions for pathogenesis (including cerebral malaria), immunity, and vaccine testing (11, 12). Nevertheless, murine models have a well-established role in drug discovery and chemotherapy research programs and may support the development of future mathematical models for patients (11, 12). Plasmodium berghei belongs to a group of Plasmodium species that infect rodents and is extensively used in preclinical drug testing (13). For translational PK-PD, the main difference is the time to complete asexual schizogony, which takes 18 to 24 h for P. berghei in rodents and 48 to 72 h for Plasmodium falciparum in humans (13). The key advantage of using P. berghei in murine models is that all erythrocytic stages of the parasite life cycle are observable in thin blood films and are easily differentiated by light microscopy (10). Thus, murine malaria studies can generate robust PK-PD data, as has been reported for dihydroartemisinin (DHA) (14, 15), chloroquine (16), and piperaquine (17), which could be used to optimize dosing. However, traditional animal studies do not allow the evaluation of all doses and are unable to dissect immune elimination of parasite or the contributions of individual antimalarials in combination therapy. Thus, the sole use of animal models to inform ACT dosing has limitations, and mechanism-based mathematical models offer significant advantages in the development of antimalarial dosage regimens.

Mechanism-based models describe the time course of drug effects and disease, thereby maximizing the information gained from experimental data (18–20). However, mechanism-based models that account for multiple stages of the parasite life cycle are lacking (21), despite the potential for optimizing ACT strategies (9, 22–25). Murine models with P. berghei are particularly valuable in this regard, since the effects of antimalarials on specific stages of the parasite life cycle can be well resolved. Mechanism-based models of murine malaria must therefore simultaneously consider the parasite life cycle, the delayed onset of drug effect in relation to its plasma PK, and the stage specificity of antimalarials (26, 27). Once developed, these models can be used to simulate effective dosing strategies to guide the choice of antimalarial monotherapy and combination therapy in patients (9).

The purpose of this study was to develop a mechanism-based growth model (MBGM) for P. berghei in murine malaria and incorporate the parasite-killing effect of DHA (MBGM-PK-PD). We discuss the utility of the model for other antimalarials and the potential for dose optimization of ACT in humans.

MATERIALS AND METHODS

Source of data.

Parasite density data were obtained from a previously reported study that investigated P. berghei growth and the subsequent effect of DHA in malaria-infected mice (15). Briefly, male Swiss mice (6 to 7 weeks old) were infected with an inoculum of 10⁷ P. berghei parasitized erythrocytes by intraperitoneal (i.p.) injection. The mice then received a single i.p. dose of either 0 (control), 10, 30, or 100 mg kg⁻¹ DHA (dissolved in 60:40 DMSO-polysorbate 80) at 56 h following inoculation (parasitemia, 2 to 5%). Peripheral blood smears for the determination of parasitemia were prepared every 12 h prior to DHA dosing, every 4 h for the first 52 h after drug treatment, and then twice daily until euthanasia (15). Parasitemia was determined, and organisms were classified as one of four erythrocytic stages (ring, early trophozoite, late trophozoite, and schizont [13]) by an experienced microscopist. To facilitate the modeling, a linear correlation was used to convert the percentage of infected erythrocytes to parasite density (the number of parasitized erythrocytes per μl of whole blood) (14). The limit of detection was 1,000 parasites/μl.

In an independent study, plasma concentration-time data were obtained following i.p. administration of DHA (100 mg kg⁻¹) to mice (28). Blood was collected by cardiac puncture at 2, 5, 10, 15, 30, 45, 60, 90, and 120 min after DHA dosing, and plasma was analyzed using a validated high-performance liquid chromatography (HPLC) method (29). The limit of quantitation (LOQ) was 90 μg/liter, and assay precision was 9%.

Mathematical modeling.

Initially, a mechanism-based growth model (MBGM) for P. berghei was developed independently of that for DHA PK. Logarithmically transformed parasite density-versus-time data were analyzed by nonlinear mixed-effects modeling in S-ADAPT (version 1.57) (30), using the SADAPT-TRAN facilitator tool (31). Parasite density data from control and treatment mice were then combined and linked to the DHA PK model, to simultaneously describe parasite growth and drug killing (MBGM-PK-PD). Data below the LOQ were handled using an established likelihood-based (M3) method (32).

Model selection was based on visual inspection of diagnostic scatter plots, the objective function value (OBJ; reported as −1 × log likelihood in S-ADAPT), and the biological plausibility of parameter estimates. Statistical comparison of nested models was performed using a χ² test, in which a decrease in the OBJ of 1.92 units (α = 0.05) was considered significant.

The final models were evaluated by performing a visual predictive check (VPC) (33). For this, 1,000 data sets were simulated from the final parameter estimates using the original data. The median and the 25th and 75th percentiles of simulated predictions were then computed and plotted against observed values. For the PK model only, a nonparametric bootstrap method was used to assess the uncertainty of all parameter estimates in the model (34). The 2.5th, 50th, and 97.5th percentiles were calculated from the empirical posterior distribution of 1,000 bootstrap replicates. However, this bootstrapping method was not performed for the MBGM-PK-PD, because of the long estimation time (1 to 2 days) associated with a single run of the full model. All reported parameter estimates and VPCs are from the simultaneous modeling of parasite growth and DHA PK-PD.

Mechanism-based growth model (MBGM).

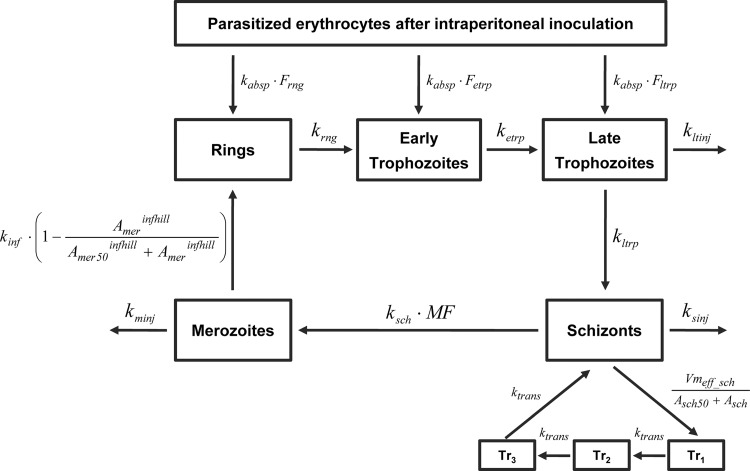
A model reflecting all four erythrocytic stages (ring, early trophozoite, late trophozoite, and schizont) of the parasite life cycle was initially developed to describe P. berghei growth. The structure of the final growth model is illustrated in Fig. 1.

Fig 1.

Structure of the mechanism-based growth model (MBGM) for Plasmodium berghei in murine malaria. The four erythrocytic stages (ring, early trophozoite, late trophozoite, and schizont) were classified according to established guidelines (13, 15). Abbreviations are defined in the text (see the equations), and mean times corresponding to first-order rate constants are provided in Table 2.

Changes in the numbers of parasitized erythrocytes (A_{ip_par}) after i.p. inoculation and the associated initial condition (IC) were calculated as follows:

$$\begin{array}{cc}\frac{d{A}_{\text{ip}\_\text{par}}}{dt}=-k_{\text{absp}}·A_{\text{ip}\_\text{par}}& \text{IC}:A_{\text{ip}\_\text{par}}\left(0\right)={\text{dose}}_{\text{par}}·F_{\text{total}}\end{array}$$

where k_absp is the first-order rate constant for absorption of parasitized erythrocytes and F_total is the sum of bioavailability for rings (F_rng), early trophozoites (F_etrp), and late trophozoites (F_ltrp). The number of schizonts in the initial inoculum (dose_par = 10⁷ parasites) was assumed to be negligible, since this parasite stage is a small component of the inoculum (<5%) and is less likely to survive the centrifugation and passaging process due to erythrocyte fragility (35, 36).

The rates of merozoite (A_mer) formation from schizonts (A_sch), their subsequent infection of erythrocytes to form rings, and loss of noninfecting merozoites are calculated as follows:

$$\frac{d{A}_{\text{mer}}}{dt}=\text{MF}·{\text{k}}_{\text{sch}}·{\text{A}}_{\text{sch}}-\left[k_{\inf }·\left(1-\frac{A_{mer}{{\displaystyle }}^{\text{infhill}}}{A_{\text{mer50}}{{\displaystyle }}^{\text{infhill}l}+A_{mer}{{\displaystyle }}^{\text{infhill}}}\right)·A_{\text{mer}}\right]-k_{\text{minj}}·A_{\text{mer}}$$

where MF is the multiplication factor for the number of merozoites formed per schizont and k_sch is the first-order rate constant for schizont transfer. Infection of erythrocytes (quantified as observed rings) was described by a first-order rate constant (k_inf), which declined with increasing parasite density (merozoites in the model). In this term, A_mer50 is the amount of merozoite at half-maximal infection rate and infhill is the Hill coefficient. The elimination of noninfecting merozoites is represented by the first-order rate constant k_minj.

Changes in the numbers of rings (A_rng), early trophozoites (A_etrp), late trophozoites (A_ltrp), and schizonts (A_sch) through one life cycle is described by equations 3 to 6:

$$\begin{array}{c}\frac{d{A}_{\text{rng}}}{dt}=A_{\text{ip}\_\text{par}}·k_{\text{absp}}·F_{\text{rng}}+\left[k_{\inf }·\left(1-\frac{A_{mer}{{\displaystyle }}^{\text{infhill}}}{A_{\text{mer50}}{{\displaystyle }}^{\text{infhill}l}+A_{mer}{{\displaystyle }}^{\text{infhill}}}\right)·A_{\text{mer}}\right]-k_{\text{rng}}·A_{\text{rng}}\\ \frac{d{A}_{\text{etrp}}}{dt}=A_{\text{ip}\_\text{par}}·k_{\text{absp}}·F_{\text{etrp}}+k_{\text{rng}}·A_{\text{rng}}-k_{\text{etrp}}·A_{\text{etrp}}\\ \frac{d{A}_{\text{ltrp}}}{dt}=A_{\text{ip}\_\text{par}}·k_{\text{absp}}·F_{\text{ltrp}}+k_{\text{etrp}}·A_{\text{etrp}}-k_{\text{ltrp}}·A_{\text{ltrp}}-k_{\text{ltinj}}·A_{\text{ltrp}}\\ \frac{d{A}_{\text{sch}}}{dt}=k_{\text{ltrp}}·A_{\text{ltrp}}-k_{\text{sch}}-k_{\text{sinj}}·A_{\text{sch}}-\frac{V_{\max \_\text{eff}\_\text{sch}}}{A_{\text{sch}50}+A_{\text{sch}}}·A_{\text{sch}}+k_{\text{trans}}·A_{\text{tr}3}\end{array}$$

where k_rng, k_etrp, k_ltrp, and k_sch are the first-order rate constants for parasite maturation through the ring, early trophozoite, late trophozoite, and schizont stages, respectively. First-order rate constants for elimination by the host immune system of injured late trophozoites (k_ltinj) and schizonts (k_sinj) were also included. The last two terms in equation 6 describe saturable efflux of schizonts with first-order return to the central circulation. In the absence of this pathway, schizont amounts were drastically underpredicted at late times (>100 h) after parasite inoculation. The inclusion of these two terms resolved this underprediction, where V_{max_eff_sch} is the maximal rate of schizont efflux, A_sch50 is the schizont amount at half-maximal efflux, and k_trans is the first-order rate constant for return from 3 transit compartments. Schizont transfer through the 3 transit compartments (tr1 to tr3) is calculated as follows:

$$\begin{array}{c}\frac{d{A}_{\text{tr}1}}{dt}=\frac{V_{\max \_\text{eff}\_\text{sch}}}{A_{\text{sch}50}+A_{\text{sch}}}·A_{\text{sch}}+k_{\text{trans}}·{\text{A}}_{\text{tr}1}\\ \frac{d{A}_{\text{tr}2}}{dt}=k_{\text{trans}}·{\text{A}}_{\text{tr}1}-k_{\text{trans}}·{\text{A}}_{\text{tr}2}\\ \frac{d{A}_{\text{tr}3}}{dt}=k_{\text{trans}}·{\text{A}}_{\text{tr}2}-k_{\text{trans}}·{\text{A}}_{\text{tr}3}\end{array}$$

All first-order rate constants (k) were parameterized and estimated as mean times (1/k), to facilitate the interpretation of parameter estimates. The parasite amount at each time was scaled to the apparent volume into which it distributes (V_rbc), to obtain a prediction in parasite density units (parasites/μl) (for example, the predicted concentration of rings equals A_rng/V_rbc).

DHA PK and PD model.

One- and two-compartment models were tested to describe the disposition of DHA in mouse plasma. Drug input from the i.p. dosing compartment was modeled as zero- or first-order absorption. The final PK model was then linked to the above structural growth model (MBGM) to simultaneously model parasite growth and DHA killing (MBGM-PK-PD).

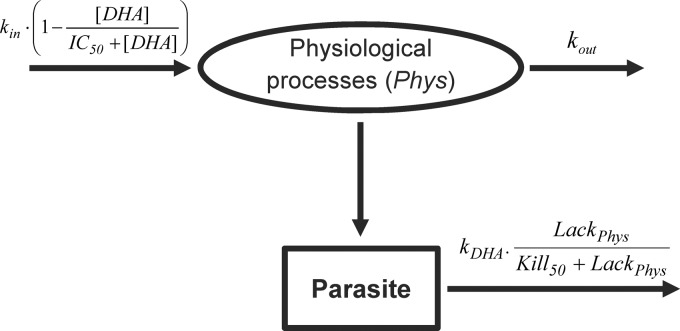
Drug killing of parasites was described by a turnover model, to account for the delay between the DHA dose and parasite death. In this model, DHA inhibited the production of a hypothetical physiological intermediate. Changes in the amount of the physiological intermediate (A_phys) were modeled using a turnover compartment, arbitrarily initialized at a steady-state value of 1. In this system, the effect of DHA is:

$$\begin{array}{cc}\frac{d{A}_{\text{phys}}}{dt}=k_{\text{in}}·\left(1-\frac{\left[\text{DHA}\right]}{{\text{IC}}_{50}+\left[\text{DHA}\right]}\right)-k_{\text{out}}·A_{\text{phys}}& \text{IC}:A_{\text{phys}}\left(0\right)=1\end{array}$$

where k_in is the zero-order rate constant for A_phys production, IC₅₀ is the DHA concentration at half-maximal A_phys inhibition, and k_out is the first-order rate constant for A_phys loss. At steady state, the rate of production of the physiological intermediate equals that of its loss, resulting in a unity ratio of rate constants (k_in/k_out = 1). Thus, the apparent lack in A_phys is

$${\text{lack}}_{\text{phys}}=1-A_{\text{phys}}$$

Equation 11 was then incorporated into a “kill” function that stimulated the DHA elimination of parasite (A_par) as follows:

$$\frac{d{A}_{\text{par}\_\text{DHA}}}{dt}=-k_{\text{DHA}}·\left[\frac{{\text{lack}}_{\text{phys}}}{{\text{kill}}_{50}+{\text{lack}}_{\text{phys}}}\right]·A_{\text{par}}$$

where k_DHA is the first-order rate constant for parasite elimination by DHA and kill₅₀ is the amount of physiological intermediates at half-maximal killing. For each of the four erythrocytic stages, A_par corresponded to the respective amount of parasite in that compartment. The kill function is incorporated in large parentheses and ensures zero killing of parasite in the absence of DHA, where A_phys is arbitrarily defined at a steady state of 1 (lack_phys = 0). A schematic representation of the DHA PK-PD model is provided in Fig. 2.

Fig 2.

Schematic representation of the turnover model describing parasite elimination after dihydroartemisinin dosing of malaria-infected mice. Abbreviations are defined in the text, and mean times corresponding to first-order rate constants are provided in Table 2.

Between-subject variability and residual error models.

The between-subject variability (BSV) was assumed to follow a lognormal distribution and was estimated for all parameters. For convenient interpretation, BSV is reported as the square root of the estimated variance, as this approximates the apparent coefficient of variation (CV) of a normal distribution on log scale.

Residual unexplained variability (RUV) for logarithmically transformed parasite density data was estimated using exponential random error. For the DHA PK model, exponential and additive components were fixed to assay precision (9%) and LOQ (90 μg/liter), respectively. This allowed calculation of BSV, as only a single observation was obtained from each mouse due to sampling by terminal bleeds (28).

RESULTS

P. berghei growth model (MBGM).

Parasite density-time data from seven untreated malaria-infected mice were used to develop the growth model for P. berghei. The final model explicitly incorporated all four maturation stages of the parasite life cycle, as well as release of merozoites and their subsequent infection of erythrocytes. Absorption of parasitized erythrocytes was rapid and first order (T_absp = 0.0522 h; BSV, 22%), with the bioavailability of rings (F_rng = 0.568) far exceeding that for early (F_etrp = 0.101) and late (F_ltrp = 0.0289) trophozoites. The apparent volume into which the parasite distributes (V_rbc) was estimated at 1180 μl (BSV, 18%), which approximates the red blood cell volume in mice.

The estimated mean time to complete one life cycle of asexual schizogony for P. berghei was 24.6 h. Merozoite infection of erythrocytes to rings was described by a first-order process (T_inf = 0.0446 h; BSV 12%) that declined with increasing parasitemia. This decline function significantly improved the model (ΔOBJ, −31.8) for merozoite invasion of erythrocytes and the corresponding formation of rings. Immune elimination of merozoites (T_minj = 5.99 h) was faster than that for schizonts (T_sinj = 115 h), which in turn was more rapid than the estimate for late trophozoite loss (T_ltinj = 2,390 h). The inclusion of similar first-order elimination pathways for rings and early trophozoites did not significantly improve the structural growth model (ΔOBJ, −0.725), and these pathways were therefore not included in the final model. Saturable schizont efflux with first-order return through 3 transit compartments was included to resolve the drastic underprediction of schizont amounts at late times (>100 h) after inoculation. Statistical inferiority was obtained when this route was excluded (ΔOBJ, −108) from the MBGM, or when schizont efflux was first-order (ΔOBJ, −65.4), suggesting that inclusion of these processes significantly improved the final model (Fig. 1). This pathway represents parasite sequestration or trapping in the microvasculature, with subsequent return to the circulation. The incorporation of this efflux return pathway to other stages of the P. berghei life cycle did not improve the model, and it was therefore not included.

DHA PK model.

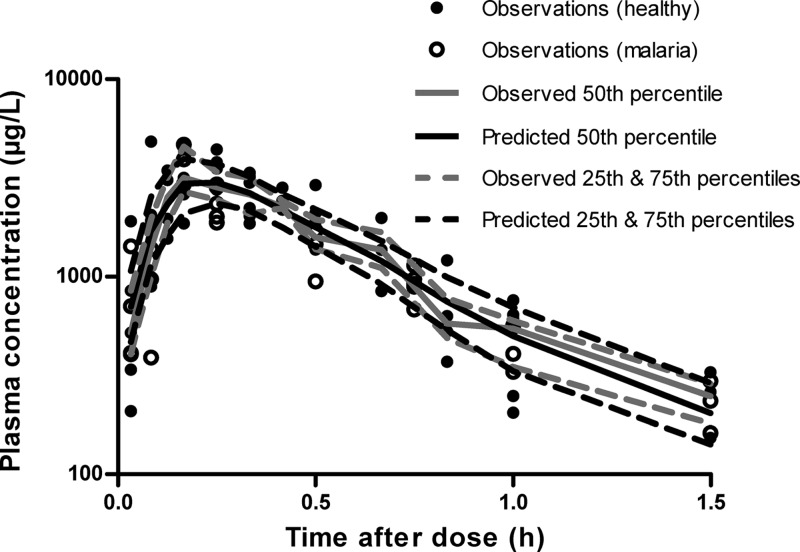
Plasma concentration-time data from 65 healthy and 33 malaria-infected mice were used to independently develop the PK model for DHA. Drug absorption was fitted by a zero-order process, with an estimated duration of 0.224 h (BSV 48%). The disposition of DHA in plasma was best described by a one-compartment model, which included estimation of BSV on all parameters. Addition of a second compartment did not significantly improve the disposition model (ΔOBJ, −0.128), and other structural models were therefore not tested. In malaria-infected mice, the estimated clearance of DHA was 1.95 liters h⁻¹, which was approximately 1.3 times faster than that in healthy mice (CL_healthy = 1.48 liters h⁻¹). Similarly, the estimated volume of distribution (V_malaria = 0.851 liter) was 1.6 times larger in malaria-infected mice than in healthy controls (V_healthy = 0.535 liter). Table 1 provides a summary of parameter estimates from the final PK model.

Table 1.

Population parameter estimates for the dihydroartemisinin (DHA) pharmacokinetic model and the 1,000 bootstrap runs

Parameter	Description	Unit	Estimate (% RSE)a	Value for 1,000 bootstrap replicates
				Median	95th percentilec
CLhealthy	Clearance of DHA in healthy mice	Liters/h	1.48 (6.37)	1.41	1.32–1.54
CLmalaria	Clearance of DHA in malaria mice	Liters/h	1.95 (12.0)	1.98	1.67–2.52
Vhealthy	DHA distribution vol in healthy mice	Liters	0.535 (9.28)	0.550	0.487–0.608
Vmalaria	DHA distribution vol in malaria mice	Liters	0.851 (17.9)	0.861	0.631–1.19
Durabs	Duration of zero-order DHA absorption	h	0.224 (16.0)	0.209	0.185–0.253
BSV CL	Between-subject variability in clearance	CV%b	8.20	10.6	1.05–11.6
BSV V	Between-subject variability in distribution vol	CV%	26.6	31.9	22.7–32.3
BSV Durabs	Between-subject variability in zero-order absorption	CV%	47.8	48.9	40.4–62.7

^aRSE, % relative standard error.

^bCV, % coefficient of variation.

^c2.5th and 97.5th percentile range.

DHA PK-PD model (MBGM-PK-PD).

Parasite density data from 7 untreated and 20 treated mice were combined to simultaneously model P. berghei growth and DHA killing. The concentration-effect relationship used for driving DHA elimination of parasite was defined by linking the developed structural growth model (MBGM) to that for drug PK in malaria-infected mice. A delayed effects model described DHA PK-PD and was statistically superior (ΔOBJ, −148) to a corresponding model in which drug killing was immediate. The delay in onset of parasite killing in relation to maximal drug concentration was best described using a turnover model, with DHA inhibiting the production of hypothetical physiological intermediates (IC₅₀, 1.46 ng/ml; BSV, 37%). This turnover was incorporated into a kill function that stimulated parasite elimination (equation 12 and Fig. 2), and was necessary for all stages of the P. berghei erythrocytic cycle. While stage-specific differences in the rates of parasite killing were evaluated, a single first-order rate constant (mean time for parasite elimination by DHA [T_DHA] = 5.66 h; BSV, 17%) adequately described the elimination of all erythrocytic maturation stages. Goodness-of-fit plots from the simultaneous modeling of P. berghei growth and DHA killing (MBGM-PK-PD) suggested an acceptable performance of the final model (see Fig. S1 to S4 in the supplemental material), which simultaneously fitted four dependent variables. The parameter estimates for the final model are provided in Table 2.

Table 2.

Population parameter estimates for the final mechanism-based model describing the growth cycle of P. berghei and the parasite-killing effect of dihydroartemisinin (DHA)

Kinetic process	Parameter	Description	Unit	Estimate (% RSE)a	BSV (CV%)b
Parasite absorption	Tabsp	Mean time for parasite absorption	h	0.0522 (35.7)	22.4
	Frng	Bioavailability of rings		0.568 (64.6)	18.8
	Fetrp	Bioavailability of early trophozoites		0.101 (28.4)	27.4
	Fltrp	Bioavailability of late trophozoites		0.0289 (7.12)	20.8
	Vrbc	Volume of parasite distribution	μl	1180 (4.54)	18.1
P. berghei life cycle	Trng c	Mean time for rings transfer	h	1.10 (5.49)	15.3
	Tetrp	Mean time for early trophozoite transfer	h	3.31 (4.41)	16.3
	Tltrp	Mean time for late trophozoite transfer	h	16.6 (2.86)	5.54
	Tsch	Mean time for schizont transfer	h	3.60 (2.88)	9.18
	MF	Number of merozoites per schizont		22.0 (1.46)
Merozoite infection	Tinf	Mean time for infection of erythrocytes	h	0.0446 (17.2)	11.5
	Amer50	Log10 of merozoites at half-maximal infection decline		5.86 (1.46)	10.3
	infhill	Hill coefficient for decline in infection		0.766 (1.92)
Parasite elimination	Tltinj	Mean time for late trophozoite elimination	h	2390 (31.9)	43.6
	Tsinj	Mean time for elimination of schizonts	h	115 (37.2)	25.2
	Tminj	Mean time for elimination of merozoites	h	5.99 (12.0)	15.1
Schizont efflux	Vmax_eff_sch	Log10 of maximal schizont efflux per hour		7.31 (0.132)
	Asch50	Log10 of schizonts at half-maximal efflux		6.95 (0.321)
	MTTtrans	Mean transit time of schizonts	h	7.49 (11.3)	39.8
Pharmacodynamics	IC50	DHA concn at 50% killing	ng/ml	1.46 (45.8)	36.5
	Kill50	Lack of physiological intermediate at 50% kill		0.00872 (29.4)	15.8
	TDHA	Mean time for parasite elimination by DHA	h	5.66 (5.45)	16.9
	Tout	Half-time for elimination of turnover model	h	3.20 (15.2)	59.2
Residual error	SDinrng	Exponential error for rings	CV%		25.8
	SDinetrp	Exponential error for early trophozoites	CV%		19.9
	SDinltrp	Exponential error for late trophozoites	CV%		19.4
	SDinsch	Exponential error for schizonts	CV%		32.5

^aRSE, relative standard error.

^bCV, coefficient of variation for between animal variability.

^cAll first-order rate constants (k) were parameterized and estimated as mean times (1/k), to facilitate the interpretation of parameter estimates.

Model evaluation.

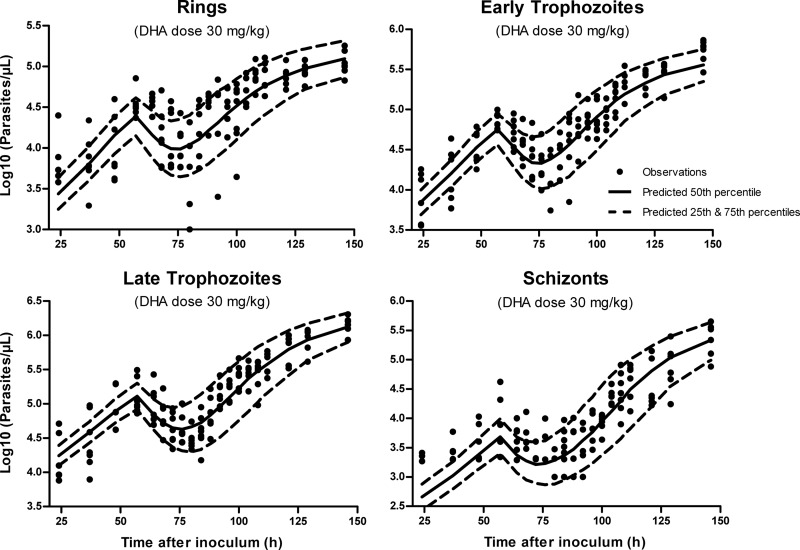
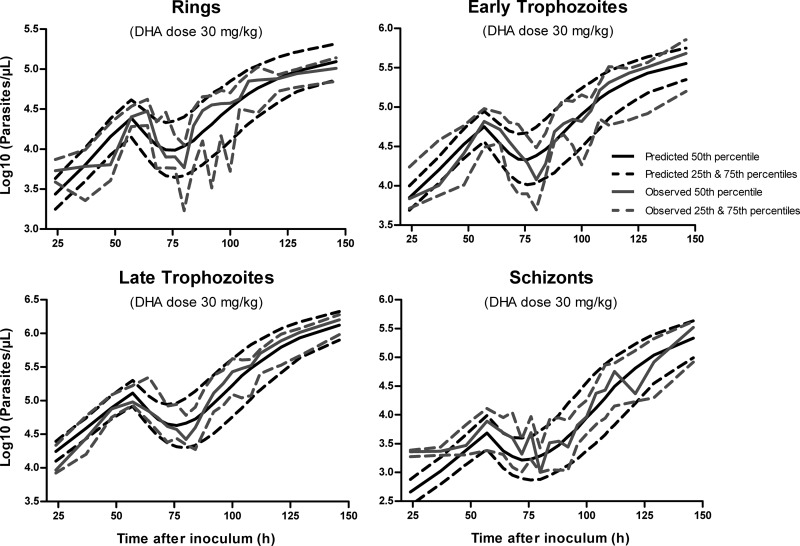
The VPCs for DHA in plasma for healthy and malaria-infected mice are presented in Fig. 3. Representative VPCs at the intermediate dose of 30 mg kg⁻¹ DHA are also provided for the P. berghei growth and parasite killing model (Fig. 4 and 5). These plots illustrate that 20 to 25% of the data lie outside the predicted 25th and 75th percentiles, with the majority of observations being evenly distributed around the median. In addition, all of the prediction percentiles broadly match their corresponding observed percentiles. These VPCs therefore demonstrated a reasonable predictive performance of the models, with prediction percentiles describing the central tendency and variability in the data. For all PK parameters from the bootstrap analysis, the median values were similar to that in the final model (Table 1).

Fig 3.

Visual predictive check for dihydroartemisinin plasma concentration in mice. The model-predicted median and 25th and 75th percentiles closely match corresponding observed percentiles, indicating the suitability of the PK model. Closed circles represent actual observed data in healthy and malaria-infected mice.

Fig 4.

Visual predictive check (scatterplot) for the mechanism-based model (MBGM-PK-PD) at the representative dose of 30 mg/kg dihydroartemisinin. Predicted medians and 25th and 75th percentiles demonstrate that the model reasonably describes both the central tendency and variability in the observed data.

Fig 5.

Visual predictive check (percentile plot) for the mechanism-based model (MBGM-PK-PD) at the representative dose of 30 mg/kg dihydroartemisinin. Predicted percentiles broadly match corresponding observed percentiles, illustrating reasonable predictive performance of the final model.

DISCUSSION

In the present study, we developed a novel, mechanism-based population model that describes the rise in parasitemia following murine inoculation with P. berghei, the nadir after DHA dosing, and subsequent parasite resurgence. This model explicitly incorporated four distinct erythrocytic stages of P. berghei, merozoite release from schizonts and subsequent erythrocyte invasion, as well as the PD effect of parasite killing by DHA. While the parasiticidal effect of DHA was demonstrated for all four erythrocytic stages, our model offers the advantage of testing antimalarial stage specificity on the parasite life cycle.

The structural growth model for P. berghei (MBGM) in murine malaria demonstrated biological and physiological plausibility for a number of reasons. First, parasites and/or parasitized erythrocytes are rapidly absorbed after i.p. inoculation (T_absp = 0.0522 h), possibly via the lymphatic system (37–39). Furthermore, the dominance in bioavailability of rings (F_rng = 0.568) is expected, since these are most likely to survive the inoculation process relative to early or late trophozoites (F < 0.11). The latter are more susceptible to physical and chemical breakage, due to their larger size and maturation in the parasite life cycle (14). In addition, the apparent red blood cell volume into which the parasite distributes (V_rbc = 1180 μl) is consistent with the theoretical erythrocyte volume in mice (40). However, a possible limitation is that this V_rbc estimate does not include changes in red blood cell homeostasis, which may occur with malaria pathophysiology. Second, the high rate of merozoite infection (T_inf = 0.0446 h) and elimination of noninfecting merozoites is likely, given the known mechanism of invasion of erythrocytes (41). A decline in the rate of infection with increasing merozoite is also appropriate, since the pool of uninfected erythrocytes will be depleted with increasing parasite density (14, 26). Third, a faster elimination of schizonts (T_sinj = 115 h) is expected relative to late trophozoites (T_ltinj = 2,390 h), as schizonts are more readily detected by the host reticuloendothelial system (13, 26). In contrast, immune elimination of rings and early trophozoites was not supported by the model for the present data set in mice, since these are considered pliable when passing through the spleen (15, 42). Finally, the sequestration or trapping of parasites in the microvasculature is a known phenomenon and is a potential mechanism by which the parasite avoids immune detection (43, 44).

Inclusion of schizont efflux into the model was a relatively minor quantitative component, because schizonts comprised an average of 5 to 7% of the total parasite density. Moreover, while sequestration of P. berghei is considered negligible in Swiss mice, parasite trapping could explain our finding that schizont transfer through transit compartments improved the growth model (15, 43, 45). However, in studies where sequestration is a more significant factor, schizont efflux or a similar strategy may be an essential component of the model. Furthermore, in the DHA PD model, this schizont efflux pathway could potentially include parasite dormancy, which is induced by the artemisinin drugs (46–48).

Population PK analysis demonstrated that a 1-compartment model adequately described the disposition of DHA in mice. The estimated clearance (1.95 liters h⁻¹) and volume of distribution (V = 0.851 liter) in malaria-infected mice were consistent with the original study (28), hence the use of population PK parameters to develop the MBGM-PK-PD model. The time course of DHA killing of parasite was described by a turnover model, with DHA inhibiting the production of hypothetical physiological intermediates. This concentration-effect relationship is indirect and is a well-established tool for describing the delay between drug PK and PD (18). Although there are several proposed mechanisms of action for artemisinin drugs, the DHA turnover model utilized in this model encompasses all probable theories associated with its antimalarial activity (49–51). However, the IC₅₀ (1.46 ng/ml) was difficult to estimate in this study, because the concentrations of DHA achieved after dosing greatly exceeded its independently determined IC₅₀ (1 to 4 nM) in vitro (52, 53). Given its low in vitro IC₅₀ estimate and the high plasma protein binding (90% [54]), further experimentation at lower doses is required to elucidate the IC₅₀ of DHA in vivo. Nonetheless, the kill function for DHA was required for all stages of parasite elimination, consistent with its broad stage specificity (52).

Evaluation of the final mechanism-based model by VPC (Fig. 4 and 5), as well as the goodness-of-fit plots (see Fig. S1 to S4 in the supplemental material), demonstrated a reasonable predictive performance of the model. However, some model misspecification is apparent at early times (24 h postinoculation), with an underprediction of measured parasite density data. This limitation is likely related to the lack of data to accurately identify the kinetics of parasite absorption after inoculation, which, combined with the asynchronicity of infection, may explain the higher estimated multiplication factor (MF = 22), compared to reports of 6 to 20 (55) and 12 to 18 merozoites per schizont (13) for P. berghei. Nonetheless, while low parasite counts are difficult to obtain because they are close to the limit of detection, the estimated bioavailability and first-order absorption of parasite appear to be plausible. Further model misspecification is apparent at 60 to 65 h and 80 h (nadir) for rings and early trophozoites (Fig. 5; also, see Fig. S1 and S2 in the supplemental material). A probable explanation is that at all administered doses (10 to 30 mg/kg), the concentrations of DHA achieved exceeded the concentration required for near-maximal parasite killing. As a consequence, the estimation of IC₅₀ and k_DHA was challenging in this study and could be better carried out with the administration of DHA at lower (and potentially more clinically relevant) doses. These experiments would also assist with specifying the schizont PD model, which appears to overpredict parasite killing where the data are at the limit of parasite density detection (log₁₀ of 3.0).

Our mechanism-based model for P. berghei growth and DHA PD is potentially applicable to the development of ACT dosing guidelines in malaria chemotherapy. Its structure is adaptable to the quantitative evaluation of other parasite strains and antimalarials for both preclinical and human studies. However, for clinical studies, the counts of circulating parasites must be considered because, unlike P. berghei, not all of the erythrocytic stages of P. falciparum can be measured. Other differences in malaria infections between mice and humans also may need to be considered for translation of the present model to humans. Nevertheless, the proposed model could be a valuable tool in the development of antimalarial treatment strategies, because there is scope to simulate and design effective single-agent, multiple-dose or combination therapy studies. A further benefit is the capacity of the model to dissect the contributions of individual antimalarials in combination therapy, as well as parasite elimination by the host immune system. Without a modeling approach, it is essentially impossible to obtain this information from traditional preclinical studies or from human clinical trials. Therefore, this model can be a cost-effective tool to expedite the translation of antimalarial drug development and to rationally design effective ACT regimens.