Resonance-induced multimodal body-size distributions in ecosystems

Abstract

The size of an organism reflects its metabolic rate, growth rate, mortality, and other important characteristics; therefore, the distribution of body size is a major determinant of ecosystem structure and function. Body-size distributions often are multimodal, with several peaks of abundant sizes, and previous studies suggest that this is the outcome of niche separation: species from distinct peaks avoid competition by consuming different resources, which results in selection of different sizes in each niche. However, this cannot explain many ecosystems with several peaks competing over the same niche. Here, we suggest an alternative, generic mechanism underlying multimodal size distributions, by showing that the size-dependent tradeoff between reproduction and resource utilization entails an inherent resonance that may induce multiple peaks, all competing over the same niche. Our theory is well fitted to empirical data in various ecosystems, in which both model and measurements show a multimodal, periodically peaked distribution at larger sizes, followed by a smooth tail at smaller sizes. Moreover, we show a universal pattern of size distributions, manifested in the collapse of data from ecosystems of different scales: phytoplankton in a lake, metazoans in a stream, and arthropods in forests. The demonstrated resonance mechanism is generic, suggesting that multimodal distributions of numerous ecological characters emerge from the interplay between local competition and global migration.

Multimodal body-size distributions, in which a population exhibits several peaks of abundant sizes, characterize local ecosystems and have puzzled ecologists for many years (1–4). To resolve this puzzle, most previous studies concentrated on one important aspect of body size, namely resource partitioning or niche separation: larger individuals consume certain resources more efficiently than smaller ones, whereas smaller individuals have access to some resources that are unavailable to larger individuals. As a result, multimodal size distributions may originate from community-wide character displacement, in which natural selection pushes species to assort into packs, each of which fits to a particular niche (1, 4, 5).

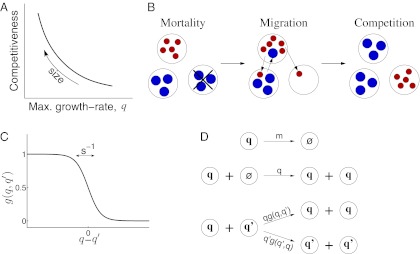
Another aspect of size, however, relates to a growth-vs.-efficiency tradeoff (6, 7). Smaller individuals generally invest less effort in their development and have a higher maximal growth rate when the resource is abundant (8–12), whereas larger individuals have more efficient metabolism and are more successful in direct competitive interferences (Fig. 1A) (6, 13, 14). As a result, smaller individuals are more likely to be the first to populate newly formed patches, and the larger individuals follow only later. In this study, we show how this tradeoff may promote multimodal body-size distributions, and we identify several characteristics of the underlying dynamics.

Fig. 1.

Stochastic colonization-competition model. (A) Body size is associated with a tradeoff between maximal growth rate, q, and competitiveness abilities such as direct interference. (B) Schematic illustration of the dynamic processes. Mortality (or path destruction and creation): occupied patches are emptied at a rate m. Migration: each species spreads migrants from its home patch to random patches at a rate proportional to its maximal growth rate q. Competition: if the destination patch is empty, the migrant invades; if the patch is already occupied by a 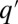-species, the q-migrant takes over with a probability 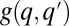and is being eliminated otherwise. (C) The invasion probability 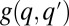has a sigmoidal shape with a width ∼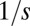, which corresponds to stochasticity. Species with higher q have a smaller chance of taking over occupied patches. (D) Competition is much faster than migration, which implies that each patch is either empty () or occupied by a single species, entitled by its maximal growth rate (q). The resulting dynamics are that of a well-mixed population of patches subject to the illustrated rate equations for all q and 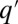: exchange (up), colonization of empty patches (middle), and invasion into occupied patches (down). The corresponding mean-field equation is Eq. 2.

Stochastic Subdivided Population Model

To examine how the growth–efficiency tradeoff leads to multimodal body-size distributions, we considered a population that is subdivided into several habitable resource patches. As in Levins’s classic metapopulation framework, we assume each patch is either empty or occupied by a single species (15–17). In our model, each species is specified by its maximal growth rate q, which is negatively correlated with its body size. The higher growth rate of smaller individuals results in more migrants sent to other patches. Larger individuals, on the other hand, are advantageous in interference and exclude the smaller individuals during within-patch competitions.

Specifically, we considered the following processes (Fig. 1): First, occupied patches are emptied at a rate m. This may occur because of mortality or because of path destruction and creation in which occupied patches vanish and new patches enter the system. Second, a patch occupied by a q-species spreads its offspring as migrants at a rate q. Each migrant arrives at a randomly picked patch. If the destination patch is empty, the migrant takes over. If it is occupied by a 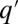-species, the invasion probability is given by the sigmoidal function (Fig. 1C)

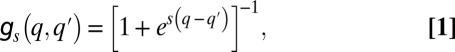where 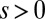measures the selection strength. This function may be seen as a phenomenological rule reflecting stochastic competition in which a species with an inferior fitness (higher q) still may take over, but also may be derived from microscopic dynamics of competition between the resident and migrant subpopulations. In the deterministic limit, 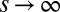, the dynamics are reduced to the “colonization-competition” model of Hastings (16) and Tilman (17): the sigmoid (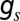) becomes a step-function and the larger species (lower q) always takes over.

To examine the possibility of multimodal distributions, we solve the long-term evolution of the entire size spectra. The hallmark of multimodal distributions is the emergence of discrete peaks within the continuous spectrum of possible q-values, 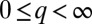. When the number of patches is large, the normalized distribution of patch occupancy (relative abundance), 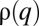, evolves according to the dynamics:

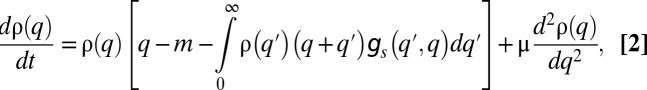where the term q corresponds to colonization without competition, the term m to mortality, the negative integral term to inhibition of colonization by competition, both due to the invasion of competing migrants and due to the inability to invade into already occupied patches, and the last term corresponds to mutations that slightly tune q at a rate μ (SI Methods).

Emergence of Multimodal Size Distributions

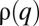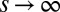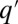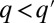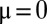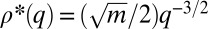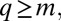In the long term, the distribution approaches a unique steady state that we examine for multimodality. The case in which competition over patches is deterministic (), i.e., a q-migrant invades a populated patch if and only if (16, 17), exhibits a monotonous steady-state solution (Fig. 2A). For , this solution is if and 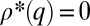otherwise (18): species with 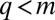vanish whereas species with 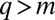distribute smoothly. (Evolution pushes species to differ, i.e., to become further away from their neighboring species along the q-axis.)

Fig. 2.

Emergence of multimodal body-size distributions. Steady-state distributions of the model (Eqs. 1 and 2) are demonstrated when the selection strength (s) is varied. When competition is deterministic, the distribution is smooth (A). However, when competition is sufficiently stochastic, multimodal patterns emerge (B–D): peaks appear near the singularity at 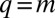, followed by smooth tails on the right. The distance between consecutive peaks is of the order of 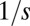, and the width of the peaks is affected by the mutation rate (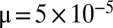) (see also Fig. S1).

In contrast, when the competition becomes stochastic, as the selection strength s decreases below a certain threshold, peaks emerge and the steady-state distribution becomes multimodal (Fig. 2 B–D). For s just below the transition, peaks are most prominent near the singularity at 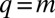. As s decreases further, the peaks become significant even further away from the singularity. This implies species packing: evolution pushes species toward the peaks even when they already are populated by other species. Peaks are located at approximately equal distances that are of the order of the q range over which competition is stochastic, .

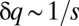The width of the peaks and their abundance are affected by the mutation rate μ (Fig. S1): without mutations (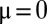), the distribution is discretized with many sharp zero-width peaks; whereas as μ increases, peaks are smeared and apparent only near the singularity. This can be understood by dimensional analysis, which shows that the width of the first peak scales approximately are like 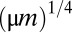(see Supporting Information). This width becomes comparable to the interpeak distance 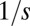at , which is the critical mutation rate for the appearance of lumpiness. Equivalently, this determines the scaling of the critical selection strength 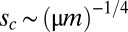. To show generality, we also examined other sigmoidal invasion probabilities g, and very similar patterns emerged (Fig. S1).

Comparison with Measurements

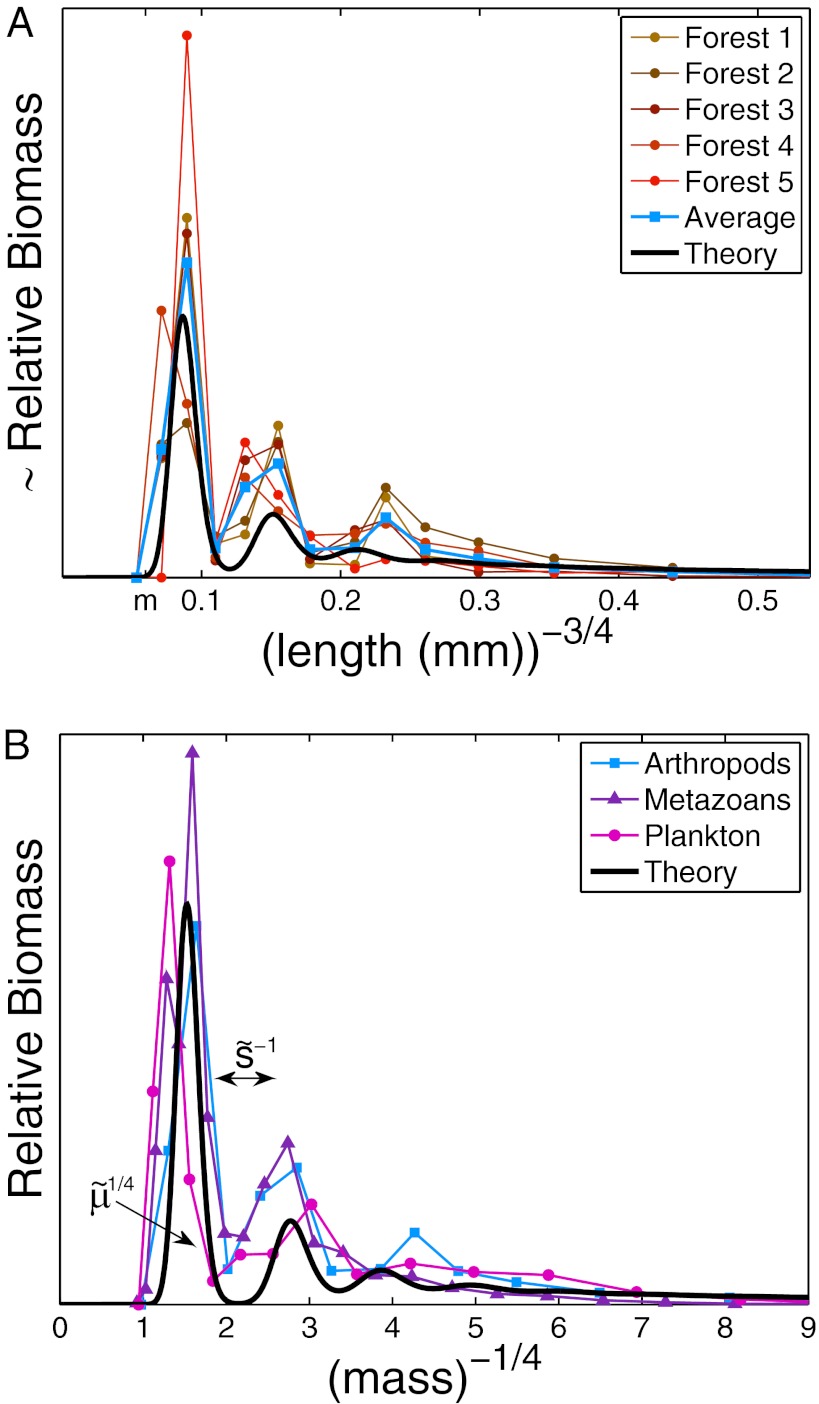
To test the validity of our model, we first examined the empirical data by Janzen, who measured body lengths of thousands of randomly sampled arthropods from several forests (19). To estimate the maximal growth rate q, we used the well-established empirical relation 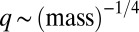(8–12) and estimated 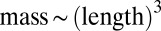(20, 21). The resulting distribution of biomass vs. maximal growth rate is multimodal, periodically peaked at larger sizes, and followed by a smooth tail at smaller sizes, just like the steady-state distributions exhibited by our model (Fig. 3A). Qualitative agreement was achieved by fitting the three model parameters, m, s, and μ.

Fig. 3.

Universal body-size distribution. Demonstrated are histograms of biomass as a function of maximal growth rate q, estimated by the well-established empirical relation 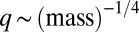(8–12). (A) Arthropods from five different regions [data from Janzen (19), biomass estimated as 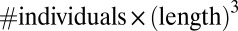: forest 1-TPR; 2-OS; 3-TPH; 4-SVP; 5-TAP]. To fit the data, we used exchange rate m corresponding to 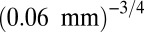, which is about 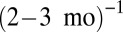(see Methods). (B) Biomass distributions of arthropods (average), phytoplankton [wet weight, 4-y average from Lake Kinneret (22)], and metazoans [dry weight, 1-y average from the Lone Oak stream (23)] are plotted on the same graph. All distributions are lumpy and nearly periodic on the left, followed by a smooth curve on the right, which agrees with our theory (black solid line). To fit all datasets simultaneously, we use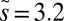d and 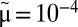, and rescaled the q-axis by the exchange rates m of approximately 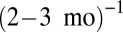(arthropods), 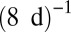(metazoans), and 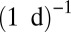(phytoplankton) (see Methods).

Our model also fits well to two other datasets: the time-averaged weight distributions of phytoplankton in Lake Kinneret and of metazoans in the Lone Oak stream (Fig. 3B) (22, 23). Moreover, we were able to universally fit all three distributions simultaneously by a single graph (Fig. 3B) via scaling all rates by the mortality m, as 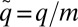, , 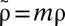, 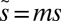and (SI Methods). The shape of this distribution is independent of m, which merely scales the q-axis by a value specific to each ecosystem. The scaled parameter 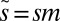corresponds to the number of offspring an organism must renounce within a time window to guarantee taking over a patch within that time.

In addition to 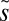and 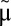, which seem to be nearly the same for all three ecosystems, our model may predict via scaling the resource exchange rate m of each ecosystem (see Methods): ∼ 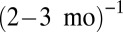for arthropods, ∼ 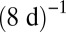for metazoans, and ∼ 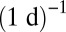for phytoplankton. A careful empirical examination still is needed to verify these predictions, but the predicted exchange rates appear to be plausible. First, arthropods usually have an annual or seasonal life cycle, after which they lay eggs and sometimes migrate; moreover, their resources are plant products that often are also annual or seasonal (24). Second, the phytoplankton turnover rate is about 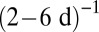(25). The lower bound of this rate, which corresponds to small phytoplankton, may fairly estimate the resource exchange rate because of the relatively poor ability of small phytoplankton to persist without resources. This turnover rate also may approximate the resource exchange rate in the metazoans’ ecosystem, in which phytoplankton is a primary resource. More generally, our results are supported by the observation that turnover rates in plants also scale approximately like 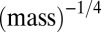(12).

Resonance Mechanism for Multimodal Distributions

The underlying “microscopic” dynamics of species competition has a natural effective frequency, which is exhibited at the “macroscopic” scale as the width over which the invasion probability g varies (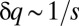, Fig. 1C). This frequency is inherent in the competition, and its resonance with colonization rates leads to a nearly periodic discrete pattern with a corresponding period 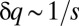(see Supporting Information). Although competition in our model is fast, its characteristic frequency persists at the macroscopic scale because of its stochastic nature. Indeed, similar periodic patterns appear if we modify the model and assume that selection is deterministic but occurs over a nonnegligible period s, during which both competing species spread migrants from the same patch.

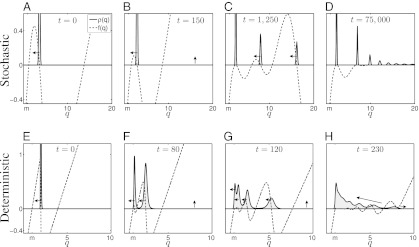
This resonance is evident in the dynamics (Fig. 4 and Movies S1 and S2). Assume that initially all individuals are “packed” and have the same maximal growth rate 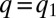(Fig. 4A). As long as is sufficiently large, mutants with 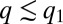have a considerable competitive advantage and they invade the population, thereby pushing 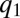to lower values (Fig. 4 A and B). As 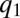decreases, the fraction of occupied patches decreases (Fig. S2) and the competition with the 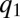-pack becomes less important. Consequently, the pack stops moving as 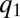approaches 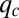, where the competitive advantage of lower q-individuals is sufficiently low and is balanced by their reduced colonization rate. Meanwhile, species with sufficiently large q can proliferate by occupying the patches left unoccupied by the 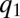population (17), thereby creating new packs, which in turn also propagate to lower q (Fig. 4 B and C). Eventually, each pack stops at a q-value at which the benefit from the reduced inhibition of the pack itself is compensated by the cost of slower colonization (Fig. 4 C and D). Nevertheless, if competition is deterministic (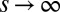), then every mutant with invades 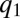-patches in every competition; hence, the population becomes more competitive and less fertile until it vanishes as 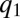approaches m [Fig. 4 E–G; “evolutionary suicide” (26)]. The succeeding packs undergo similar dynamics, which result in a series of evolutionary suicides, and no single pack is sustained. Eventually, newer packs catch the preceding ones, and a smooth distribution is obtained (Fig. 4H). Note that for stochastic competition, the transition from an initially smooth distribution into a lumpy one also is through a cascade of moving packs (Movie S3).

Fig. 4.

Species packing vs. evolutionary suicide. Graphed are time evolutions of the distribution (solid line) and of the corresponding per capita growth rate, 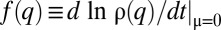(dashed line). (A–D) Stochastic competition (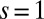, 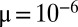). At 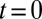, the entire population is packed around 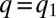. Mutants with 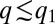have a substantial competitive advantage (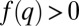), and they push the pack leftward to lower q (A and B). As the pack moves leftward, the proportion of patches occupied by the 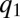-pack decreases until their advantage from better competitiveness is sufficiently small and is compensated by the cost of slower colonization ( has a local maximum at 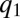) and the pack stops (C). Meanwhile, new packs with much larger q emerge, and, in turn, also propagate leftward (C). This process ensues until a stationary, multimodal pattern is obtained, in which each pack is located at a local maximum of 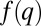(D). (E–H) Deterministic competition (, 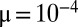). Evolution pushes the initial packs leftward until they vanish as their q-values approach m (evolutionary suicide). Eventually, newly emerged packs reach the preceding ones, which results in a smooth distribution. See also Movies S1, S2, and S3.

We derived an analytic steady-state solution of Eq. 2 for the multimodal distribution (see Supporting Information) assuming and the mutation rate is small enough to allow adiabatic adjustment of population abundance [adaptive dynamics (27)]. In this limit, the fraction of patches occupied by species from the first pack at 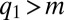(the area of the peak) is 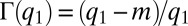(Fig. S2). At steady state, this pack is located at 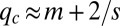, and consequentially, 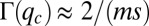. The following few peaks are periodically located at distances of approximately 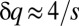from one another, which supports the numerical solution (Fig. 2 and Fig. S1).

Discussion

Our examination of body-size distributions of species competing over the same resources in a local environment, such as a forest or a lake, revealed a universal body-size distribution that holds for various taxa. We suggest that this is a natural consequence of the tradeoff between growth rate and competitiveness. We also found some characteristics of size distributions mediated by that tradeoff. First, multimodality appears at larger body sizes, whereas the distribution of smaller sizes is smooth. Second, evolution entails directional dynamics toward larger sizes, which is consistent with fossil records showing that species tend to increase in size during evolution (Cope’s rule) (14, 28). Our study suggests that examining biomass distributions plotted vs. 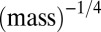may reveal features that are less apparent in the traditional 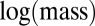plot. On a 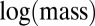plot, peaks are still evident, but their periodicity may be masked and some extra peaks may appear at larger masses because of stochasticity. Hence, the 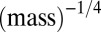transformation may enable meaningful comparison among several distributions.

Our model cannot fit all body-size distributions, particularly certain seemingly unimodal body-size distributions with a long tail at large sizes, which were found by several studies (29, 30). This may result from three possible effects. First, some of the analyzed ecosystems are much larger than a typical dispersal length, so large that the environmental conditions vary throughout the ecosystem. In contrast, our model assumes global connectivity and identical patches; therefore, it should be examined in relatively small, homogeneous regions. Indeed, Brown and Nicoletto (31) found that peaks become evident when the system size decreases. Second, our model disregards the possibility of resource partitioning within a niche or a patch, which is relevant in many ecosystems. Third, several studies examine the number of species (instead of the biomass) as a function of the mass (32, 33). Fitting to such available data of species size distributions requires further formulation of the speciation processes. Nevertheless, note that species spectra are known to exhibit multimodality in local ecosystems (1–4).

In a broader context, our study suggests an alternative, generic mechanism for emergence of species assembly (multimodality) in trait space. Mechanisms that induce discreteness in trait space are of central importance in ecology and evolution, and were examined in previous studies. In particular, it is known that resource partitioning may result in community-wide character displacement, even along a homogeneous resource axis (4). To model this effect, several studies considered dynamics somewhat formally similar to Eq. 2, but with a symmetric kernel (usually Gaussian) (4, 34). This equation also may represent a single-species population competing over a one-dimensional, homogeneously distributed resource, in which the initially homogeneous population may undergo Turing instability and become patchy (35–37). In contrast, in our model the competition is asymmetric and entails essentially different dynamics—specifically, no smooth solution exists near the singularity at 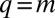and peak dynamics are directional.

Our study suggests that species assembly is naturally mediated by the interplay between local competition and global migration. The possibility that asymmetric competition may induce a discrete community pattern, such as the one exhibited in the present work, was shown by Geritz et al. (38), and general criteria for such discretization were derived by Gyllenberg and Meszéna (34). We focused on a prototypic model in which local competition takes place rapidly, but multimodality also appears if we relax this assumption and allow several species to compete within the same patch. The combination of local competition and global migration is central in many ecological processes; therefore, the mechanism we suggest may promote multimodality in a large variety of traits other than body size, including dispersal rates, seed sizes, and more.

Methods

The theoretical results are numerical solutions of Eq. 2 with invasion probability (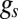) given by Eq. 1. These equations incorporate the tradeoff between having a larger maximal growth rate q (smaller individuals) and having better local competitive interference abilities (larger individuals; Fig. 1). To compare our theory with empirical data (Fig. 3), we used the well-established empirical relation 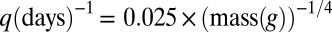(8–12), and used the rescaled equation Eq. S1 to simultaneously fit distributions from various scales (Fig. 3B).