High-resolution single-molecule characterization of the enzymatic states in Escherichia coli F₁-ATPase

Abstract

The rotary motor F₁-ATPase from the thermophilic Bacillus PS3 (TF₁) is one of the best-studied of all molecular machines. F₁-ATPase is the part of the enzyme F₁F_O-ATP synthase that is responsible for generating most of the ATP in living cells. Single-molecule experiments have provided a detailed understanding of how ATP hydrolysis and synthesis are coupled to internal rotation within the motor. In this work, we present evidence that mesophilic F₁-ATPase from Escherichia coli (EF₁) is governed by the same mechanism as TF₁ under laboratory conditions. Using optical microscopy to measure rotation of a variety of marker particles attached to the γ-subunit of single surface-bound EF₁ molecules, we characterized the ATP-binding, catalytic and inhibited states of EF₁. We also show that the ATP-binding and catalytic states are separated by 35±3°. At room temperature, chemical processes occur faster in EF₁ than in TF₁, and we present a methodology to compensate for artefacts that occur when the enzymatic rates are comparable to the experimental temporal resolution. Furthermore, we show that the molecule-to-molecule variation observed at high ATP concentration in our single-molecule assays can be accounted for by variation in the orientation of the rotating markers.

1. Introduction

The rotary molecular motor F₁F_O-ATP synthase is a nanoscale machine responsible for ATP production in bacteria and eukaryotes. Driven by the electrochemical gradient across cytoplasmic, mitochondrial or chloroplast membranes, ATP synthase generates ATP from ADP and inorganic phosphate. It is composed of two co-axial rotary motors, the catalytic F₁ and membrane-embedded F_O sectors. The flux of ions down an electrochemical gradient through F_O provides the energy to synthesize ATP within F₁. When isolated from F_O, F₁ behaves as an ATP-hydrolysing enzyme.

The cyclical conformational changes proposed by Boyer in the ‘binding change mechanism’ [1–3] and the crystal structure of bovine mitochondrial F₁ determined at high resolution [4] predicted that internal rotation within the F₁ enzyme would be required for catalytic function. The first direct visualization of this rotation was achieved for F₁ derived from the thermophilic Bacillus PS3 (‘TF₁’) [5]. Following this landmark single-molecule work, various similar biophysical studies have led to a detailed understanding of the mechanism governing the TF₁ motor (for reviews see [6–8]). Briefly, the three β-subunits act cooperatively to coordinate the binding of ATP from the medium (in β-subunit 1), ATP hydrolysis (in β3) and product release (in β2, and possibly β3) with the relative rotation of the  γ-subunit [9,10]. In this numbering scheme the γ-subunit rotates in the direction β1 → β2 → β3 → β1. Rotation rates of single surface-immobilized TF₁ molecules follow Michaelis–Menten kinetics over a range of substrate (ATP) concentrations [11–13], with discrete 120° steps observed at low ATP concentrations owing to rate-limiting ATP binding. The 120° steps have been further resolved into approximately 80°/40° substeps [12], with the intermediate dwell (the ‘catalytic dwell’) assigned to ATP hydrolysis and phosphate release [10,14,15]. ADP release is thought to occur at the 0° ATP-waiting angle [16]. Extensive work has also been presented detailing the rates of substrate binding and product release [10]. The rotation of TF₁ has been shown to be unidirectional but not continuous, with stochastic transitions into a non-rotating state owing to Mg²⁺ADP inhibition [17]. The reversibility of F₁ has been demonstrated by isolating TF₁ within femtolitre chambers [18] and externally rotating the γ-subunit in the opposing direction using magnetic tweezers to synthesize ATP [19,20].

TF₁ is obtained from a bacterium that lives at up to 75°C [21], which offers several advantages for single-molecule studies. The enzyme's high stability helps to retain its function during purification, reconstitution, preparation of surface-immobilized single-molecule assays and extended single-molecule observation and manipulation. At room temperature, relatively slow enzyme kinetics and high-mechanical stiffness both make it easier to resolve transitions in the mechano-chemical cycle of TF₁ that lead to rotation of the γ-subunit. These factors have contributed to TF₁ becoming the archetype for detailed biophysical characterization of the mechanism of F₁. Single-molecule studies of mesophilic F₁ are less complete. Rotation of large actin markers (typically 1–3 μm) attached to F₁ isolated from Escherichia coli (‘EF₁’) [22–25] and from spinach chloroplasts [26] has been demonstrated, in addition to the rotation of EF₁ with the actin filament replaced by small gold beads [27–29]. This has shown that EF₁ generates a similar torque to TF₁ when rotating a large viscous load, and rotates approximately four times faster in the limit of low load at room temperature. Rotation of high-load actin markers attached to F₁F_O from E. coli (‘EF₁F_O’) [30,31] has shown that EF₁F_O generates similar torque to F₁ under conditions of ATP hydrolysis, in the absence of a membrane potential to energize F_O. The torsional stiffness of various mechanical parts of EF₁F_O has been measured by analysis of Brownian motion of similar markers [32]. The equivalent experiment with TF₁ [33,34] confirms that the internal torsional stiffness of TF₁ is 3–4 times greater than that of EF₁, as expected for a thermophilic enzyme at room temperature.

The experiments above track F₁ rotation by measuring the position of a relatively large marker attached to one extreme of F₁ (e.g. the F_O-binding part of the γ-subunit) relative to the opposite extreme of F₁ (e.g. the N-terminus of the α- or β-subunits) immobilized on a surface. An alternative method uses single-pair Forster resonant energy transfer (sp-FRET) to measure distances between two fluorescent markers attached to different parts of EF₁F_O reconstituted in phospholipid vesicles. The γ [35,36] and ε [37] subunits of EF₁F_O rotate relative to the β-subunit through three states per revolution, in both the hydrolysis and synthesis directions. By contrast, the C-terminus of the α-subunit rotates relative to one of the 10 subunits in the membrane-embedded c-ring through 10 states per revolution during ATP synthesis [38]. sp-FRET allows single-molecule observation of F₁F_O in energized bilayers, which has so far not been possible using larger markers. It also allows a wider range of marker locations and the advantage of observing rotation without external load. However, the low brightness and relatively fast photobleaching of fluorescent marker molecules severely limit the spatio-temporal resolution and quantity of data respectively; larger markers are still required to measure in detail the kinetics of single F₁ molecules operating over a full range of loads and speeds. A related method measures F₁ rotation via the polarization of light scattered by gold nanorods, with dimensions of tens of nanometres, attached to F₁ in the same way as other large markers [39–41]. This offers the advantage of measuring rotation angle directly, rather than inferring it from the position of the marker, and promises extremely high temporal resolution. However, technical difficulties in unambiguous determination of the rotation angle have to date limited the usefulness of this method.

In this study, we present conclusive evidence that EF₁ rotation is governed by the same mechanism that controls the well-studied TF₁. In particular, we quantify the lifetimes of the ATP-binding, catalytic and inhibited states of EF₁. We use computer simulations to quantify and compensate for the effects of experimental sample rates that are similar to the kinetic transition rates of the enzyme. We also demonstrate that the typical molecule-to-molecule speed variations observed in surface-bound F₁ assays at high [ATP] and/or high load, where viscous drag of the marker determines speed, can be assigned primarily to different attachment geometries of the observation marker.

2. Material and methods

Experimental methods and data acquisition are included in the electronic supplementary material.

(a). Estimating the drag coefficient of the attached markers

The rotational viscous drag coefficient of a rotation marker ξ is defined by T = ξω, where T is the torque exerted by F₁ and ω is the angular velocity of rotation. For a single sphere of radius r rotating far from any surface, with eccentricity R (defined as the shortest distance between the rotation axis and the centre of the sphere), an exact solution can be obtained; 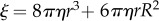[42], where η is the viscosity of the medium.

(i). Single beads

The eccentricity of a single bead (figure 1a) is given by R(ϕ) = r cos(ϕ). If we assume that the surface is flat, ϕ will range from ϕ_min up to π/2, where 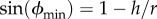and h is the height of the streptavidin–EF₁ complex. In our calculations, we take h = 15 nm. Assuming no preferred attachment orientations, the vector connecting the point of attachment to a marker with the marker centre will be distributed isotropically about a shell of solid angle and the density of states 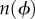will be proportional to 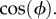Therefore, the mean eccentricity is

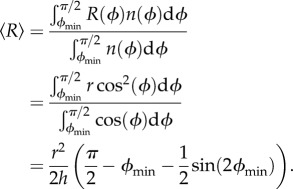2.1

If we ignore any interactions with the surface, the mean drag coefficient is

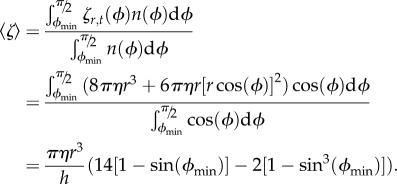2.2

Figure 1.

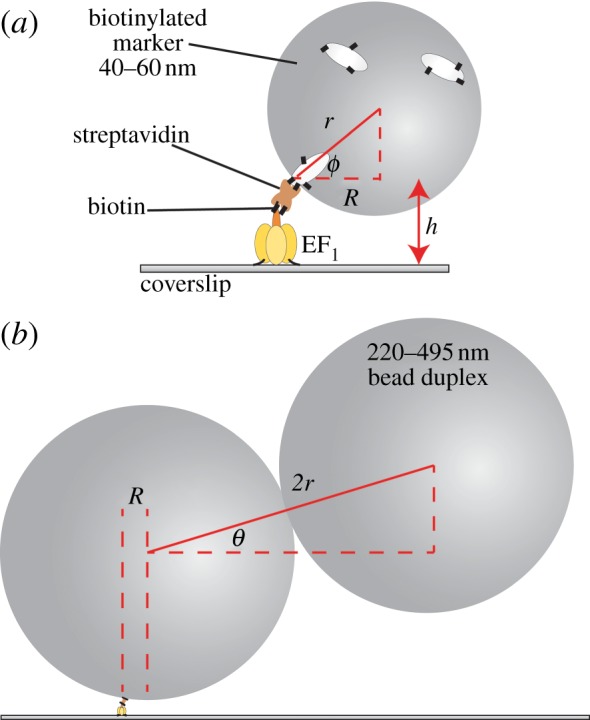
The experimental set-up for observing the rotation of markers attached to surface-immobilized EF₁ molecules. (a) A single bead (d = 2r = 40 nm shown) can only reach a minimum gyration angle ϕ_min of sin(ϕ_min) = 1 − h/r, where h is the height of the F₁–streptavidin attachment point. (b) A bead duplex formed from two biotinylated polystyrene beads (d = 220 nm shown) will, in general, form a rise-angle of θ with the surface plane. The beads are attached via streptavidin (brown) and biotin (black lines). Cream spheroids represent biotinylated bovine serum albumin.

(ii). Bead duplexes

Still neglecting surface interactions, we estimate ξ for a bead duplex (figure 1b) as the sum of the individual drag coefficients of the two beads in the duplex (ξ_inner+ξ_outer), each rotating with the eccentricity that it has in the duplex, as

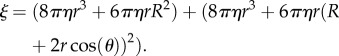2.3

We have ignored the hydrodynamic interactions between the two beads that can lead to underestimation (θ = 0) or over-estimation (θ = π/2) of the drag by upto 10 per cent [43]. Again assuming no preferred attachment orientations, the vector connecting the two bead centres will be distributed isotropically about a hemisphere of solid angle 2π and the density of states n(θ) will be proportional to cos(θ), with θ defined in figure 1b. Setting R = 〈R〉, a calculation similar to that leading to equation (2.2) (refer to full integrals in SI) gives

2.4

for the average drag coefficient of a duplex of beads of radius r, with 〈R〉 given by equation (2.1). We also estimated the distribution of rotation speeds 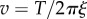predicted for a particular duplex size, assuming constant torque T and no surface interaction. The dominant source of variation in ξ  for a duplex is variation in θ, and typically the terms containing R in equation (2.3) are small compared to the other terms. Setting in equation (2.3) gives

2.5

Given that the total number of molecules is 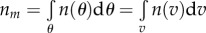and remembering 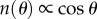, the fraction of molecules rotating with speeds in the range 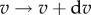is expected to be

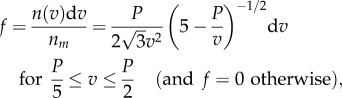2.6

where 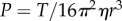is the expected rotation speed of a single bead with R = 0 (see electronic supplementary material).

The above expressions ignore any effects of interactions between markers and the surface. We estimate that hydrodynamic surface effects should be small (less than 20%) for single beads and ‘tall’ duplexes , but would increase the drag coefficient of ‘flat’ duplexes 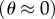by over twofold (see electronic supplementary material), as demonstrated recently [44]. By consideration of the density of states, the hydrodynamic surface effect will increase the average drag coefficient by approximately 40 per cent. Unless otherwise stated, we have used the drag coefficients calculated in the absence of a surface (see electronic supplementary material, tables S1 and S2) but then taken care to note the requirement for the surface correction factor.

3. Results

Single (40–200 nm) or duplex (220–495 nm) beads attached to the γ-subunit of surface-immobilized EF₁ molecules (figure 1) rotated counter-clockwise (viewed from the γ-subunit side) in the presence of ATP. We measured the dependence of rotation speed on ATP concentration ([ATP]) over an approximately 10⁶-fold range, and upon the beads' viscous drag coefficient over an approximately 10⁴-fold range.

(a). [ATP] dependence

Figure 2 shows the Michaelis–Menten dependence of EF₁ rotation speed upon [ATP] over six orders of magnitude for four different marker sizes. Similar single-molecule experiments on TF₁ also showed Michaelis–Menten kinetics [11,12]. This is consistent with a simple phenomenological model of rotation where the time taken for each revolution is equal to

3.1

Figure 2.

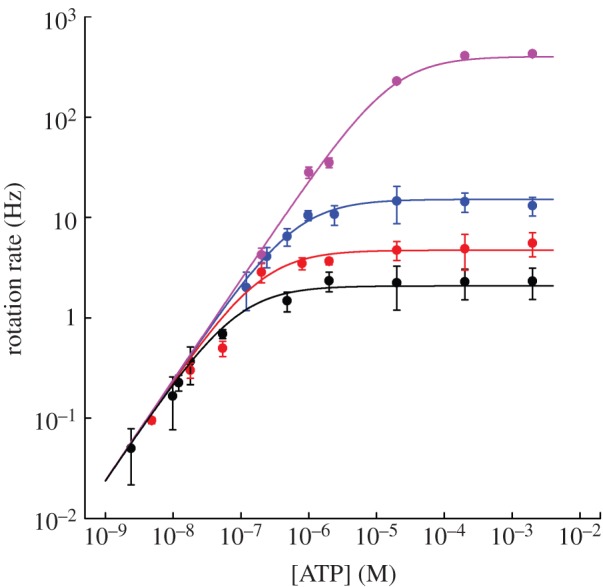
The average rotation rate versus [ATP] for 60 nm (pink) and 220 nm (blue) single beads, and 340 nm (red) and 495 nm (black) duplexes (mean±s.e. for n = 8–15 molecules, except at low [ATP] where n = 3–10). Lines are weighted global fits to equation (3.2) using the full dataset (see text for details). Fitted parameters: v_max = 449±15, 16.0±0.8, 4.98±0.25 and 2.22±0.07 Hz; K_M = 21.1±0.5 μM and 752±11, 234±11 and 104±3 nM for 60 nm single beads and 220, 340 and 495 nm duplexes, respectively. Some data for 40 and 60 nm beads were reproduced from Nakanishi-Matsui et al. [27].

where t_ATP is the time for ATP binding, t_i is the time for internal catalytic processes and product release, and t_r is the time required for the rotation of the marker through the viscous medium. Assuming that ATP binding is first-order with respect to [ATP] gives 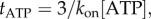and equation (3.1) can be rearranged to give

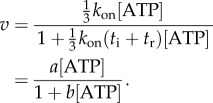3.2

Equation (3.2) is the Michaelis–Menten equation with 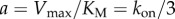and .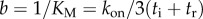

We assumed that k_on, and, therefore, parameter a, in equation (3.2) is independent of marker size, while parameter b depends on marker size via t_r. A global nonlinear fit to the data with a single a parameter and separate b parameters for each marker dataset is shown in figure 2. Estimates of the corresponding fitted kinetic parameters V_max and K_M for each marker size are listed in figure 2 legend.

(b). Load dependence

Figure 3a shows the relationship between speed and the average viscous drag coefficient 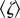of each type of marker, estimated as described in §2, at saturating ATP (2 mM). In these conditions 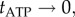and the rotation rate is given by

3.3

Figure 3.

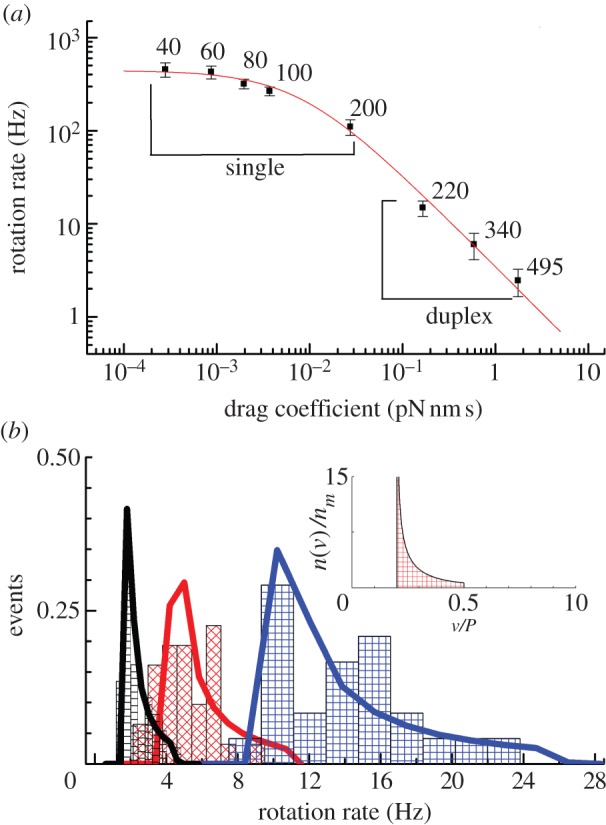
The effect of viscous drag on the rotation rate of EF₁. (a) The rotation rate versus average viscous drag coefficient (no surface correction) at 2 mM ATP (mean±s.e.). The numbers next to each data point specify the diameter in nm of the beads used to observe rotation. A nonlinear best-fit of equation (3.3) (red line) implies a maximum average rotation speed of 442±15 Hz, corresponding to an ATPase rate of approximately 1350 s⁻¹ for active EF₁ molecules, and a torque of 21.9±1.8 pN nm. (b) The distribution of rotation rates observed with different size duplexes attached (blue, 220 nm; red, 340 nm; black, 495 nm). The normalized density of states, n(v)/n_m (equation (2.6)), is shown in the inset as a function of the ratio of the duplex speed to the maximum single bead speed (v/P). For each marker size, the histogram is fitted with a discrete version of equation (2.6) (see electronic supplementary material). EF₁ torque estimates are 21.5±2.3 pN nm (495 nm, n_m = 37), 17.2±2.0 pN nm (340 nm, n_m = 31) and 10.8±0.7 pN nm (220 nm, n_m = 24). Errors estimates were obtained from 1000 bootstrapped resamples.

For large markers (220–495 nm bead duplexes), speed is inversely proportional to drag coefficient; for small markers (60 nm gold beads or smaller), speed is approximately 450 Hz, independent of drag coefficient, consistent with the simple model of equations (3.1) and (3.3). At high load, the marker rotation time becomes the dominant factor determining the rotation speed, i.e. 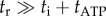and thus 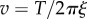. At low load, 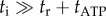, the internal catalytic processes are rate-limiting, and thus 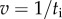is independent of ξ. A nonlinear least-squares fit to equation (3.3) describes the data well (figure 3, red line). Together with the fit in figure 2, this indicates that the simple model is a good description of the [ATP] and load dependence of EF₁ rotation: as for TF₁, the enzyme binds [ATP] with first-order kinetics and generates approximately constant torque while moving the marker against viscous drag, and the time required for further rate-limiting internal catalytic steps is independent of load and [ATP].

The fit to the data of figure 3a gives t_i = 0.75±0.03 ms and T = 21.9±1.8 pN nm. t_i corresponds to rotation at 442±15 Hz in the absence of external load, in agreement with the previously published figure of approximately 450 Hz [27]. This is 3–4 times faster than the equivalent speed for TF₁ at room temperature [12], as expected given that TF₁ normally works at much higher temperatures than EF₁. Considering the hydrodynamic surface effect on the rotational drag coefficient increases our torque estimate to approximately 30 pN nm. This is at the lower end of the range previously reported for F₁ from various organisms (see §4). Surface interactions could also possibly explain the slight deviations from the fit in figure 3a—for example, the low average speed of 220 nm duplexes compared with the fit might indicate that the drag coefficient is underestimated by a larger factor for these markers than for the larger duplexes. To investigate this possibility, we obtained estimates of T separately for each type of duplex. Figure 3b shows histograms of the fraction of duplexes of a particular size that rotated in various speed ranges (black = 495 nm, red = 340 nm, blue = 220 nm). The inset shows the normalized density of speed states (n(v)/n_m) expected for a particular duplex size under the assumption that all duplex orientations are equally probable (§2, equation (2.6)), and the solid lines show fits of this distribution to the histograms (see electronic supplementary material for fitting procedure), each with torque T as the single adjustable parameter. The fits are reasonable, indicating that our model is adequate to explain most of the variability in speed for a particular duplex size. The values of T obtained from the fits in figure 3b decrease with bead size (21.5±2.3, 17.2±2.0 and 10.8±0.7 pN nm for the 495, 340 and 220 nm duplexes, respectively). The simplest explanation for this trend is a selection bias for ‘flat’ duplexes 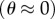of smaller beads, which are easier to identify by eye and which have larger hydrodynamic drag coefficients.

(c). 120° steps at low [ATP]

At 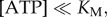ATP binding is rate-limiting 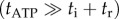and the rotation rates for all marker sizes converge, as can be seen in the bottom-left corner of figure 2, Figure 4a,b show examples of step-wise rotation of EF₁ molecules under these conditions (18 nM ATP, 495 nm duplexes in a, 1 μM ATP, 60 nm single beads in b). Dwell times at discrete 120° steps are exponentially distributed (figure 4c,d), consistent with first-order ATP binding. We confirmed this by analysis of 20 EF₁ molecules that showed clear stepping behaviour at various 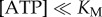. Figure 4e shows the apparent unimolecular rate constant of ATP binding (k_ATP) for each molecule versus [ATP], derived from the set of dwell times using maximum-likelihood estimation (see the electronic supplementary material). Data points corresponding to the two traces illustrated in figure 4a,b are indicated by arrows in figure 4e. The line in figure 4e is a fit to 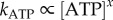, with x = 1.03±0.03, confirming that ATP binding is first-order with respect to [ATP]. Assigning 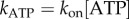gives k_on = (4.3±0.2) × 10⁷ M⁻¹ s⁻¹, in excellent agreement with the rate obtained in previous bulk studies [45]. Note that we could also estimate k_on from the slope of the curve in figure 2 as [ATP]→0 (following equation (3.2), k_on = 3a). However, this estimate is sensitive to large uncertainties in average speed measurements, particularly at low [ATP] (figure 2). By contrast, single-molecule events are very well defined temporally, and thus we have high confidence in the accuracy of our estimate of k_on above.

Figure 4.

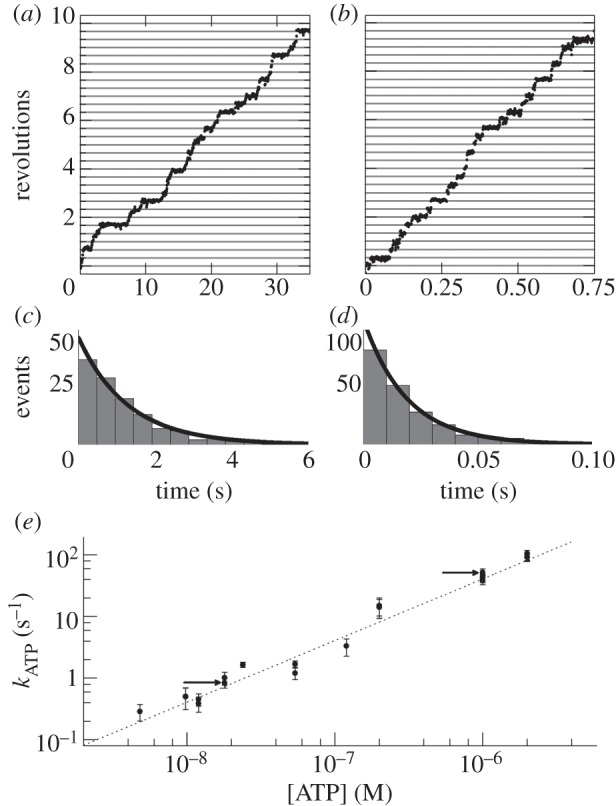
Step-wise rotation of two typical EF₁ molecules at low [ATP]: (a) 18 nM ATP, 495 nm bead duplex, (b) 1 μM ATP, single 60 nm bead. (c,d) Distributions of dwell times for the molecules of (a,b), respectively. Lines in (c) and (d) are exponential functions 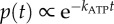obtained by maximum-likelihood estimation, with (c) k_ATP = 0.84±0.16 s⁻¹ and (d) k_ATP=52.1±7.4 s⁻¹. (e) k_ATPversus [ATP] for 20 molecules across a range of beads sizes, obtained as in (c,d). (error estimates in panels c–e are 95% confidence levels). First-order kinetics were confirmed by a fit to k_ATP = k_on[ATP]^x (grey dashed line), with x = 1.03±0.03 and k_on = 4.3±0.2 × 10⁷ M⁻¹ s⁻¹. The two example molecules from (a) and (b) are indicated by the black arrows in (e).

We estimated the angular stiffness of EF₁ in the ATP-binding state, using the principle of equipartition of energy and angular Brownian motion of the probe during dwells [32], taking care to ensure that our sampling rate was adequate to sample fully the Brownian motion [33] (see electronic supplementary material). Our estimated stiffness of 26.5±1.8 pN nm rad⁻² combines the compliance of linkers between the surface or marker and EF₁, with compliances within EF₁, and is consistent with previous stiffness estimates in EF₁F_O.

(d). 120° steps at high [ATP]

Single 40–60 nm beads do not slow the rate of rotation of EF₁ significantly (see the plateau in figure 3a). At saturating [ATP], we observed step-wise rotation of single 60 nm beads attached to EF₁ (figure 5a). With k_on = 4.3±0.2 × 10⁷ M⁻¹ s⁻¹, ATP binding occurs within approximately 10 μs at 2 mM ATP and is not resolved at the sampling rates used in this study (up to 4 kHz). Because the viscous load is also negligible, the rate of rotation is dominated by the internal chemical processes of the enzyme. Equation (3.1) becomes 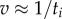. The dwells observed under these conditions are the EF₁ equivalent to the catalytic events observed in TF₁ [12].

Figure 5.

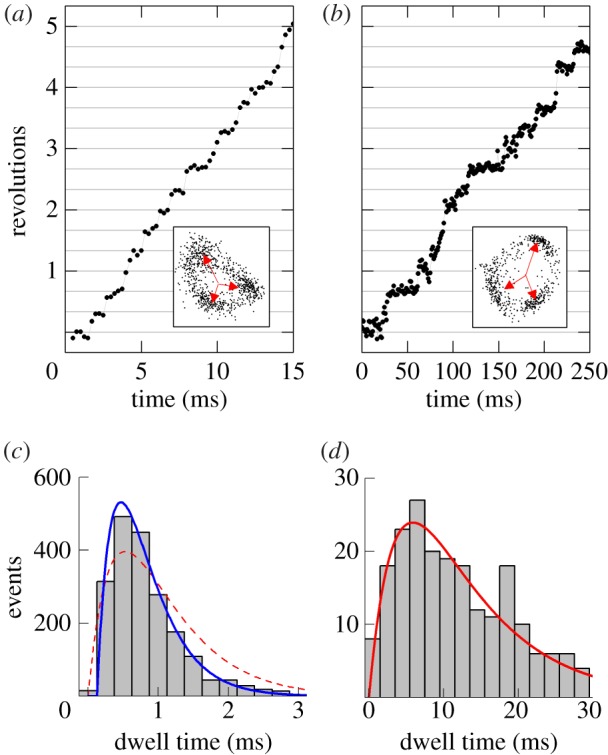
(a,b) Examples of 120° steps observed at (a) high [ATP] (2 mM) and (b) high [ATPγS] (1 mM) with a single 60 nm bead attached. The insets show the xy orbits of the probe centroid and the three dwell positions (red arrows). Note the different timescales in (a) and (b). (c,d) The distribution of dwell times observed (c) at 2 mM ATP for 2003 steps in 3 molecules and (d) at 1 mM ATPγS for 206 steps in 3 molecules. In (c), the catalytic dwells do not follow a ‘double exponential’ (red dotted line) owing to a lack of short dwells but are well described by the inclusion of a fixed transit time for the probe movement throughout the 120° step, τ_m. For t > τ_m, p(t)∝ 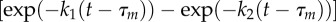and is shown by the blue line. Obtained parameters are 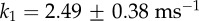, 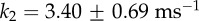and 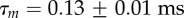. The ratio of the sum-of-squared-errors of the two parameter fit to the three parameter fit is 12.0, indicating a much better fit when the extra time constant is included. In (d), substitution of ATP with ATPγS lengthens the catalytic dwell. Owing to the longer catalytic dwells, the transit time τ_m cannot be resolved. A fit with 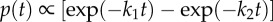(red line) gives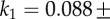 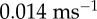and .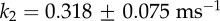

On average, the dwells at each 120° position lasted approximately 0.8 ms, only slightly longer than three frames of our video recordings (one frame = 0.25 ms). This is consistent with the full speed rotation of 450 Hz observed in figure 3a (t_i = 3 × 0.8 ms = 2.4 ms = 1/(417 Hz)). With events lasting on the order of the experimental sample time (in this case a single video frame), observed dwell times are, in general, a complicated function of the true dwells and the effect of discrete sampling. We used a kernel density technique to map the observed dwells back to the true underlying dwells and verified the accuracy of this method using Monte Carlo simulations of stepping data (see electronic supplementary material for a full discussion).

Two unresolved sequential Poisson processes, each of length approxiamtely 1 ms, were postulated to account for the catalytic dwells in TF₁ [12], giving a ‘double-exponential’ dwell time distribution

3.4

The EF₁ distribution that we observe is not well described by this function owing to a lack of very short dwells, even after accounting for sampling effects (figure 5c, red dotted line; see electronic supplementary material). Adding a constant time τ_m for the transit of the marker through 120° [34] gives

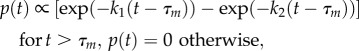3.5

which fits the observed distribution well with 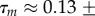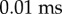, 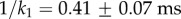and 1/k₂= (figure 5c, blue line). The use of simulated data suggests that τ_m obtained from the fitting process is always approximately 50 per cent longer than expected from the model parameters (see electronic supplementary material for full discussion). Accounting for this, our estimated 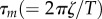is approximately as expected for a constant torque of 20 pN nm and no surface drag, consistent with our estimates from figure 3. A third rate constant (analogous to our τ_m) has been required in previous bulk [45] and single-molecule [29] EF₁ assays to account for a partial rotation of the γ-subunit. By contrast, our results are consistent with assignment of this third process to viscous drag without the requirement for an additional enzymatic step.

In TF₁, the two Poisson processes have been ascribed to ATP hydrolysis [14] followed by phosphate release [10]. ATPγS, a slowly hydrolysing analogue of ATP, slows the rotation of TF₁ by approximately 30-fold [14]. Under conditions of saturating ATPγS (1 mM) and in the low load regime, the rotation rate of EF₁ was 16.8±1.7 Hz (a reduction of approximately 30-fold when compared with the rate when powered by ATP hydrolysis), and dwells were approximately 30 times longer, as evidenced in figure 5b. ATPγS dwells were long (typically greater than 10 ms) compared to τ_m, and we fit them using equation (3.4) with time constants of 3.1±0.7 and 11.3±1.7 ms (figure 5d, red line).

(e). 35° steps at intermediate [ATP]

For 60 nm beads at intermediate [ATP], the catalytic and ATP-binding dwells take similar times, and both states may be resolved in a single trace. For ATP concentrations between 20 and 50 µM, we collected seven traces clearly showing both the ATP-binding state and the catalytic dwell (figure 6). After filtering the angle–time data, we fit six Gaussian peaks to the angle distribution to estimate the position of both states. The mean angular difference between adjacent states was 35.3°, with a standard deviation of 12° and standard error of the mean of 2.7° (n = 21).

Figure 6.

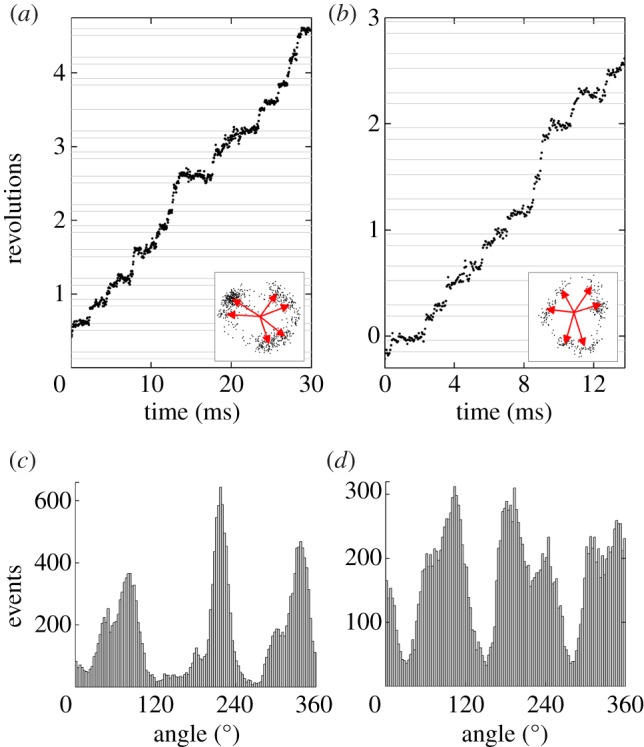
(a,b) Examples of substeps observed at intermediate [ATP] (a; 20 µM and b; 50 µM) with a single 60 nm bead attached. The insets (a; 60 nm and b; 40 nm wide) show the xy orbits of the probe over the time shown and the six dwell positions as assessed from the full recording (0.93 s). (c,d) The histogram of angles at which the probe was observed (3° bins, 0.93 s with pauses excluded) clearly shows evidence of six peaks with overlapping distributions. The average angular separation between the catalytic and ATP-binding state was (a) 33° and (b) 42°, compared with the average measured over seven traces of 35°.

We constructed dwell histograms for the catalytic and ATP-binding dwells for each observed bead, and tested fits of single and double exponential states to both dwells, using the Bayesian Information Criterion to judge whether the addition of extra fitting parameters was justified. There was no single model that fits all seven beads well, which we attribute to difficulty in precisely resolving the transition between two closely separated and overlapping states; however, the fits are compatible with the one and two state models presented earlier. We therefore consider the analysis of 120° steps at high and low ATP concentrations, above, to be the best estimate of the kinetics of these states (see electronic supplementary material for a full discussion).

(f). The inhibited state of EF₁

Individual EF₁ molecules exhibit a dynamic equilibrium between a non-rotating, paused or inhibited state and the active rotating state, in both bulk [46] and single-molecule [22,23] EF₁ assays. Recently it has been shown that on short timescales (1–10 s), EF₁ under low load converts between the active and paused states approximately once per second and that this pause state is coincident with the angular position of the catalytic dwells [47]. TF₁ has been reported to have a similarly short-lived pause state but also to have an unrelated longer-lived paused state of length 32 s on an alternative inhibition pathway [17].

We studied the pausing behaviour of EF₁ in 72 molecules at 2 mM ATP using 220–495 nm bead duplexes over long timescales. Because the mechanical relaxation time of these large markers made accurate determination of pauses shorter than 1 s difficult, pauses shorter than 1 s were ignored and intervals between pauses were not analysed owing to the likely concatenation of adjacent intervals. Missed pauses were, however, accounted for in the analysis of the lifetimes and relative populations of the active and inactive states (see the electronic supplementary material). Because pauses can last for tens of seconds, all molecules were recorded for at least five minutes, unless they detached from the surface during this period.

In total, EF₁ spent 49.8 per cent of the observation time paused at 2 mM ATP. The distribution of pause durations is shown in figure 7. We found no dependence of the pause durations upon the viscous load over the range of marker sizes used (see the electronic supplementary material, figure S4). Similar to [17], we observed too many long pauses (greater than 15 s) to be explained by a single Poisson process. Instead, the distribution of pause lengths was well fit (figure 6a, red lines) by

3.6

Figure 7.

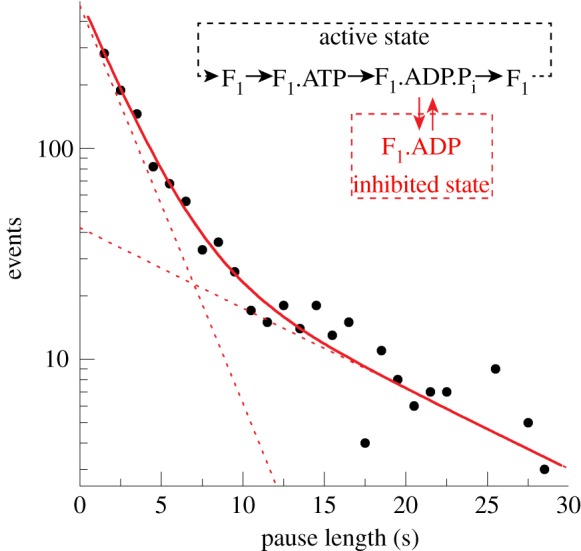
The pause length distribution of the inhibited state at 2 mM ATP. Black dots represent histogram values with bin width 1 s. The distribution is consistent with an inhibited state that is composed of two unresolved states (inset). A possible reaction scheme is shown where EF₁ spontaneously fails to release Mg²⁺ADP post-hydrolysis at +80°.

consistent with two unresolved paused states of lifetimes τ₁ = 2.3±0.2 s and τ₂ = 11.4±3.7 s. Under these conditions, each EF₁ molecule spent twice as long in the short state as in the long state (given by 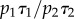). The lifetime of the active state can be found by considering the rate of decay of the inhibited states and their relative populations (see the electronic supplementary material). We have calculated that active EF₁ enzymes become inhibited with a rate of approximately 0.3 s⁻¹ at 2 mM ATP.

We observed similar pausing behaviour at 20 μM ATP, close to the transition between double and triple nucleotide occupancy for F₁ with no load [48]. The paused state again appeared to be composed of a short and a long state (τ₁ = 1.0±0.1 s, τ₂ = 15.0±2.5 s). In total, EF₁ was paused 56 per cent of the time at 20 μM ATP, of which approximately two-thirds of the paused time was spent in the short state, and active EF₁ became inhibited with a rate of approximately 0.9 s⁻¹.

A large majority of the molecules (55 out of 72) we studied showed preferential angles for pausing, with over half of all molecules displaying clear pauses at angles separated by approximately 120°. See the electronic supplementary material for example pauses. To investigate the angle of the pauses relative to known states within the EF₁ catalytic cycle, records exhibiting 120° step-wise rotation (either owing to ATP binding at low [ATP] or catalytic dwells observed with 60 nm markers) were analysed for pauses that were too long to belong to the underlying stepping distribution (see the electronic supplementary material). The average pause angle was 82±3° forwards of the ATP-binding state, and 2±4° forwards of the catalytic state. Because we analysed only pauses that were statistically determined to be long, there remains a possibility that only the longer pause state has been analysed. Thus this state at least can be attributed to failure of product release at the catalytic dwell angle.

4. Discussion

Single-molecule experiments on TF₁ in the past 10 years have given a comprehensive picture of the mechanism of F₁. The mesophilic EF₁ shares considerable homology with TF₁ (53% α-subunit, 67% β-subunit, 37% γ-subunit) but the two enzymes function at very different natural temperatures, and consequently have significantly different activities at room temperature. In this study, we demonstrate that despite their different native conditions, EF₁ and TF₁ essentially share a common mechanism.

It appears likely that, at the limit of high load, F₁ from all species produce approximately equal torque, and that the torque is set by the requirement that the Stokes efficiency is less than or equal to 1, so that the work done in one revolution is less than or equal to the free energy released by the hydrolysis of three ATP molecules. However, the determination of torque from a single-molecule rotation assay is limited by considerable uncertainty in the estimation of the drag coefficient close to the coverslip surface, mainly owing to unknown marker geometry and possible interactions with the surface. These uncertainties are evident in the previously published estimates: EF₁ using actin filaments, 33–50 pN nm [13,22,23]; TF₁ using actin filaments, 40 pN nm [7,11]; TF₁ using nano-engineered gold rods [49], 20 pN nm; F₁ from spinach chloroplasts using actin filaments, 10–40 pN nm [26]; and our estimates for EF₁ using beads (approximately 30 pN nm). We have demonstrated that natural random variation in marker orientation is sufficient to explain the molecule-to-molecule speed variation observed in our single-molecule assays under conditions where viscous drag is rate-limiting. Panke et al. [31] bypassed the problem of unknown surface drag by using the curvature of long actin filaments to estimate torque without needing to know the drag coefficient of the marker. Their estimate of 50 pN nm for the torque generated by EF₁F_O during ATP hydrolysis corresponds to a Stokes efficiency close to 1, and is probably the most accurate estimate to date. If we accept this value, our results indicate that our estimated drag coefficients are approximately 60 per cent of the true value. There are two possible explanations of how this could arise. Selection bias for flat duplexes would increase the true average drag coefficient compared with our estimate, which assumes isotropic distribution of duplex orientations. Also, direct interactions with the surface could increase the drag coefficient beyond the value estimated by considering hydrodynamic interactions.

At room temperature, the main differences between the mesophilic EF₁ and the thermophilic TF₁ are the rates at which the mechanical steps occur. Binding of ATP molecules occurs twice as fast in EF₁ compared with TF₁ (EF₁: (4.3±0.2) × 10⁷ M⁻¹ s⁻¹; TF₁: (2.2–2.7) × 10⁷ M⁻¹ s⁻¹) [11–13]. If ATP binding was solely limited by diffusive processes, an approximate calculation suggests that the rate of binding would be approximately 10⁹ M⁻¹ s⁻¹, almost two orders of magnitude faster. All residues found within the binding pocket of the bovine mitochondrial structure [4] are conserved in TF₁ and EF₁ as determined by sequence alignment. It would therefore appear likely that the free energy of ATP binding would essentially be the same between TF₁ and EF₁. The difference in the rates of binding of ATP could be due to a higher energy barrier that the ATP molecule must overcome before it reaches the binding pocket or slower protein dynamics within the TF₁-binding site. Both are consistent with the three- to fourfold greater stiffness measured for TF₁ compared with EF₁. Our estimate of the angular stiffness in the ATP-binding state based on Brownian motion and equipartition of energy is 26.5±1.8 pN nm rad⁻². Sielaff et al. [32] used a similar method to estimate a stiffness of approximately 30 pN nm rad⁻² in the ATP-binding state of rotating F₁F_O molecules. Using disulphide crosslinking, they attributed this to two compliances in series, corresponding to the rotor–stator interaction in F₁ and the link between F₁ and F_O, each with a stiffness of approximately 60 pN nm rad⁻². Given the estimate of approximately 60 pN nm rad⁻² for the internal stiffness of F₁, our result implies that the linking stiffness is also approximately 60 pN nm rad⁻². A recent crosslinking study of TF₁ at high sampling rates showed a stiffness in the ATP-binding state of approximately 55 pN nm rad⁻², attributed to internal and linking stiffnesses of 223 and 73 pN nm rad⁻², respectively [33]. The linking stiffnesses are similar in EF₁ and TF₁ experiments, while the internal stiffness is 3–4 times greater in the thermophilic enzyme, at room temperature. This is consistent with the high temperature stability of TF₁, and the possibility remains that the internal stiffnesses of TF₁ and EF₁ are similar at their natural operating temperatures.

In the limit of small attached viscous loads and saturating [ATP], EF₁ rotates at approximately 450 Hz at room temperature, almost four times as fast as TF₁ under the same conditions. The rate-limiting step is the approximately 0.7 ms catalytic dwell, which consists of at least two processes each lasting approximately 0.35 ms. In TF₁, the two processes have been assigned to ATP hydrolysis and phosphate release, each lasting approximately 1 ms [12]. We also observed a third rate-limiting process, mechanical relaxation lasting approximately 0.1 ms, similar to recent direct observations in TF₁ [34]. At 50°C, TF₁ has been reported to rotate at over 700 Hz [50]. An Arrhenius extrapolation to physiological temperatures (75°C) predicts that TF₁ could rotate at over 1000 Hz. Rotation rates of EF₁ show approximate Arrhenius dependence between 10°C and 31°C [29], suggesting a rotation speed of approximately 650 Hz at 37°C. The substitution of ATP with its slow hydrolysing analogue ATPγS resulted in an approximately 30-fold decrease in EF₁ rotation rate, in agreement with published results with TF₁ [14]. The two EF₁ catalytic processes were lengthened from approximately 0.35 ms to 4–9 ms suggesting that both the hydrolysis and (thio)phosphate release are slowed in this instance. Determination of which time constant corresponds to ATP hydrolysis and which to (thio)phosphate release is not possible with our current data.

Dynamic equilibrium between the rotating and paused states has been reported in both bulk [46] and single-molecule [22,23] EF₁ assays. We have shown that the paused state is composed of two unresolved states with lifetimes 2.3±0.2 s and 11.4±3.7 s at 2 mM ATP, with the short-lived state being twice as populous. It should be noted that load-dependent short pauses have been reported for TF₁ [13], implying that one of the reactions at +80° is sensitive to mechanical hindrance; however, we have not observed a similar pause in EF₁. In conjunction with the recently published study on the short paused state [47], we can conclude that both the long and short pauses occur at the catalytic dwell angle. This conclusion is in agreement with the angular location of the paused state found in TF₁ [17,51] and within EF₁F_O [32].

Pauses are thought to be due to inhibitory Mg²⁺ADP in the active binding site. EF₁ shows [Mg²⁺ADP]-dependent inhibition of catalytic turnover in bulk assays [52], and [Mg²⁺]-dependent activity [53] and inhibition [54,55] are thought to be due to stabilization of the inhibitory ADP molecule by Mg²⁺ [56]. The propensity of TF₁ to lapse into the long pause was greatly increased by the presence of Mg²⁺ADP [17]. Re-activation from the inhibited state has been previously reported by applying external torque to TF₁ with magnetic tweezers [57]. We have observed a similar re-activation in EF₁, by forced forwards rotation by optical tweezers (see electronic supplementary material), demonstrating that the angular dependence of the binding pocket for Mg²⁺ADP is common to both enzymes.

In summary, using high-temporal resolution and modelling, we have presented conclusive evidence that the mesophilic EF₁ shares the same mechanism as the thermophilic TF₁ when assayed under the same conditions. Our data are consistent with the following mechanism of EF₁. ATP binding at the 0° position initiates rotation to the catalytic dwell angle at +80°. During this rotation, EF₁ produces essentially constant torque of magnitude 50 pN nm [31]. At the catalytic dwell angle, at least two sub-millisecond (0.2–0.4 ms) processes occur before the enzyme is reset by rotation to the rotationally symmetric +120° position. During this final rotation, a third process may also occur as reported previously [29,45], but our data do not provide strong evidence for the existence of any such extra processes. An alternative, off-pathway, route from the catalytic dwell state is for EF₁ to enter into the ADP-inhibited state before spontaneous re-activation. This mechanism is summarized by the reaction scheme in figure 7 (inset). The results for EF₁ are quantitatively different from the thermophilic TF₁ at room temperature, however, including faster rotation rates, faster ATP hydrolysis and faster ATP-binding. This study provides a quantitative wild-type reference for future single-molecule studies of EF₁ mutants and for F₁ from other species that live at mesophilic temperatures.