Eco-evolutionary feedbacks, adaptive dynamics and evolutionary rescue theory

Abstract

Adaptive dynamics theory has been devised to account for feedbacks between ecological and evolutionary processes. Doing so opens new dimensions to and raises new challenges about evolutionary rescue. Adaptive dynamics theory predicts that successive trait substitutions driven by eco-evolutionary feedbacks can gradually erode population size or growth rate, thus potentially raising the extinction risk. Even a single trait substitution can suffice to degrade population viability drastically at once and cause ‘evolutionary suicide’. In a changing environment, a population may track a viable evolutionary attractor that leads to evolutionary suicide, a phenomenon called ‘evolutionary trapping’. Evolutionary trapping and suicide are commonly observed in adaptive dynamics models in which the smooth variation of traits causes catastrophic changes in ecological state. In the face of trapping and suicide, evolutionary rescue requires that the population overcome evolutionary threats generated by the adaptive process itself. Evolutionary repellors play an important role in determining how variation in environmental conditions correlates with the occurrence of evolutionary trapping and suicide, and what evolutionary pathways rescue may follow. In contrast with standard predictions of evolutionary rescue theory, low genetic variation may attenuate the threat of evolutionary suicide and small population sizes may facilitate escape from evolutionary traps.

1. Introduction

Population viability is determined by the interplay of environmental influences and individual phenotypic traits shaping life histories and behaviour. A long-standing view in evolutionary ecology has been that adaptive evolution would optimize a population's phenotypic state in the sense of maximizing some suitably chosen measure of fitness (such as its intrinsic growth rate, r, or its basic reproduction ratio R₀ [1–3]). On this basis, it was largely expected that adaptive evolution would always improve the demographic balance of a population, resulting in, e.g. higher population size, lower extinction risk or larger geographical spread.

This picture is reflected in our current theory of evolutionary rescue. In the most general terms, evolutionary rescue occurs when a population subject to environmental change ‘performs better’ under the operation of evolutionary processes than without these processes; typically, the currency of ‘population performance’ is the population size or persistence time [1] (see also [4]). Historically, there have been two main theoretical approaches to evolutionary rescue. One approach capitalizes on a well-established modelling tradition in population genetics to investigate how mutations may reduce the extinction risk of a population reaching low size or negative growth upon some abrupt change in the environment [5–9]. The other approach uses quantitative genetics to study the conditions under which selection enables a population to track a moving evolutionary optimum as the environment changes gradually [10–13]. These two theoretical views of evolutionary rescue show interesting conceptual differences in (i) the type of environmental change (abrupt versus gradual), (ii) threat (an actual demographic deficit versus a risk of demographic deficit), and (iii) rescue pathway (returning to demographic balance versus avoiding demographic imbalance). But they both are grounded in the notion that adaptive evolution inherently tends to enhance population viability.

Despite the long tradition of describing evolutionary processes through concepts of progress and optimization, as early as in 1932 J. B. S. Haldane pointed out that there was no general principle preventing adaptive evolution from harming population performance [14]. A verbal example comes from considering overtopping growth in plants. Taller trees get more sunlight while casting shade onto their neighbours. As selection causes the average tree height to increase, fecundity declines because more of the tree's energy budget is diverted from seed production to wood production. Under these circumstances, it may also take longer for the trees to reach maturity. Thus, arborescent growth as an evolutionary response to selection for competitive ability can cause population abundance and/or the intrinsic rate of population growth to decline. The logical conclusion of this process may even be population extinction, as was first explained by Haldane [14].

The past two decades of research in theoretical evolutionary ecology have done much to flesh out this picture. The concept of the ‘eco-evolutionary feedback loop’ has been introduced to link the joint operation of ecological and evolutionary processes to the dynamics of populations (figure 1). The selection pressures driving phenotypic evolution should be derived from models that describe the whole eco-evolutionary feedback loop [15–20]. The structure of the loop determines whether an optimization principle can be found in the first place, and, if so, what specific fitness measure it ought to be based on [21–25]. Departure from optimization occurs when selection is frequency-dependent [1,23,26–28].

Figure 1.

Eco-evolutionary feedback loop. Complex selective pressures on individuals' phenotypic traits emanate from the interaction of individuals (I) with their local environment (E)—consisting of conspecifics, prey and predators, mutualists and parasites, in their ecosystem context. Heritable variation in adaptive traits responds to these pressures, and in turn affects how these individuals impact their environment. This feedback loop—from the environment to the individuals, and back—intimately links ecological and evolutionary processes.

Frequency dependence is responsible for remarkable eco-evolutionary dynamics such as rock–paper–scissor cycles in allele frequencies (with well-studied examples in real life [29,30]). But frequency dependence, broadly defined, pervades eco-evolutionary feedback loops way beyond those causing non-equilibrium dynamics, such as cycles in allele frequencies [23]. A necessary and sufficient condition for selection not to be frequency-dependent is that the adaptive traits affect fitness effectively in a one-dimensional monotone manner; that is, fitness must be an increasing or decreasing function of a single variable that compounds the effect of all adaptive traits under consideration [26]. From a modelling point of view, this combination of one-dimensionality and monotony is quite special. Yet optimization arguments have widely been used in evolutionary ecology. ‘It may well be that our limited perception of the range of feedback scenarios actually existing in nature biases our models toward the simplest subset that conveniently obeys optimization principles’ (J. A. J. Metz 1996, personal communication).

Thus, realistic eco-evolutionary feedbacks are expected to generate frequency dependence, and under frequency dependence there is no optimization principle to predict the outcome of adaptive evolution. Even when the adaptive process does optimize, phenotypic evolution maximizes the population's intrinsic growth rate (r or R₀) or size (equilibrium or average) only if the eco-evolutionary feedback loop possesses special features regarding how density dependence affects transitions in the life cycle, and how traits influence invasion fitness [21,23]. And in the rare cases where adaptive evolution gradually tends to improve population viability, one cannot exclude that the process ends with the population's sudden demise [1,31]. It has thus become clear that the relationship between adaptive evolution and population persistence is complex. How then can we define and study evolutionary rescue? Adaptive dynamics theory provides a mathematical framework to design and analyse models of phenotypic evolution in which all components of the eco-evolutionary feedback loop are integrated. This article is a conceptual synthesis intended to provide a brief introduction to the framework and to show how the current theoretical approaches to evolutionary rescue can be recast in that framework, and then extended as part of a broader investigation of the influence of adaptive evolution on ecological dynamics.

2. The adaptive dynamics framework

Adaptive dynamics is an extension of evolutionary game theory to general models of ecological interactions between individual organisms and their environment [32,33]. Adaptive dynamics modelling typically starts with an abstract description of the eco-evolutionary feedback loop (figure 1), involving three ingredients [16,34,35]: (i) a description of the individual phenotype by adaptive, quantitative traits of interest; (ii) an ecological dynamic model that relates the individual traits to population, community and/or ecosystem properties (depending on the question of interest and available empirical knowledge); and (iii) a model of trait inheritance. Parameters are used to describe features of the ‘external’ environment that may influence the eco-evolutionary feedback loop but are not influenced by the loop itself. For the given environmental conditions (i.e. fixed parameters for the external environment), the eco-evolutionary feedback loop drives the dynamics of the distribution of trait values in the phenotype space. These so-called ‘adaptive dynamics’ unfold within the set of feasible phenotypes—the boundary of which is shaped by physiological and genetic constraints and ecological viability.

Adaptive dynamics are driven by the local selection gradient, which depends on (and hence varies with) the phenotypic and ecological state of the current population (the ‘resident’ population). Phenotypes where the local fitness gradient vanishes are called ‘evolutionary singularities’. The central goal of adaptive dynamics theory is to identify and classify the stability properties of evolutionary singularities [16,32,36]. The classification is complete for one-dimensional traits [16,37,38]; the multi-dimensional case is found in the studies of  Leimar [39,40]. In general, multiple evolutionary singularities may occur, some attractive, some repelling. Here, ‘attractive’ means that the singular phenotype can be reached from nearby phenotypes by a sequence of small mutation–selection steps; ‘repelling’ means that any sequence of small mutation–selection steps initiated near the singularity will move the population away from the singularity. Alternatively, there may be no singularity at all, in which case long-term evolution is predicted to drive the population to the boundary of the set of feasible phenotypes.

An important application of adaptive dynamics theory is to provide joint predictions for the evolutionary response of a population to new environments and how this evolutionary response influences the ecological state of the population. The ecological state is described by the population, community and ecosystem properties that are involved in the eco-evolutionary feedback loop. This may include population size and structure, diversity and abundance of interacting species and ecosystem functions such as inorganic nutrient flow or primary productivity; in the context of evolutionary rescue studies, this may just be the demographic viability (or lack thereof) of the evolving population.

3. Recasting current evolutionary rescue theory in the adaptive dynamics framework

Dieckmann & Ferriere [1] introduced ecology–evolution–environment diagrams, or E³-diagrams for short, as a graphical way of presenting the eco-evolutionary predictions made by adaptive dynamics models. Current theoretical approaches to evolutionary rescue can be interpreted using this graphical tool (figure 2). Environmental change is assumed to degrade the species' demographic viability, causing the expansion of the non-viable region. Initially, the population experiences environmental conditions e₁ and sits at an evolutionary attractor residing at a safe phenotypic distance from the non-viable region. Environmental conditions are assumed to change from e₁ to e₂, either abruptly or gradually. If environmental conditions change abruptly, the initial trait value in the new environment e₂ is assumed to be demographically non-viable, i.e. the corresponding point in the E³-diagram lies in the non-viable region; while it is also assumed (explicitly or implicitly) that there exists a safe evolutionary attractor under the new environmental conditions e₂, corresponding to a point located outside the non-viable region. Then the question that existing theory has tackled is, what is the probability that the population evolves between these two points and exits the non-viable region before extinction actually occurs? This problem requires a population (or quantitative) genetics approach, which has been developed, in the wake of Gomulkiewicz & Holt [5], by e.g. Boulding & Hay [6], Orr & Unckless [9] and Gomulkiewicz et al. [41]. A population-genetics approach to rescue is the focus of several articles in this special issue [42,43].

Figure 2.

E³-diagram for current evolutionary rescue theory. E³-diagrams (short for ecology-evolution-environment diagrams) describe the adaptive dynamics of a population for viable combinations of phenotypes and environmental conditions. The environmental and evolutionary components of change are represented by the horizontal and vertical axes, plain thin arrows show the direction of selection, line styles indicate the type of evolutionary singularity (solid thick lines for attractors, dashed thick lines for repellors), and shading shows the demographically non-viable region. Abrupt environmental change (horizontal dotted arrow) from environmental condition e₁ to e₂ (marked with vertical dotted lines) exposes the population to the demographic threat of extinction (light grey star). Evolutionary rescue may occur (light grey arrow), that would take the population out of the non-viable region, from where it could converge to a safe evolutionary attractor. With gradual environmental change, evolutionary rescue may occur (dark grey arrow) or not (dark grey star) depending on whether the population can track its safe evolutionary attractor fast enough.

If environmental conditions change smoothly, it is assumed that the safe evolutionary attractor also changes smoothly while remaining at a safe distance from the (expanding) non-viable region. Thus, it is assumed that the eco-evolutionary feedback loop is somehow shielding the population from extinction. Then the question that existing theory has addressed is, given the rate of environmental change from e₁ to e₂, can evolution be fast enough to track the safe evolutionary attractor closely enough and thus avoid colliding with the non-viable region? Questions of this kind are best analysed using techniques of quantitative genetics [11,12].

This theory thus adheres to the conventional view that adaptive evolution tends, by itself, to favour population viability; and that the question of evolutionary rescue boils down to deciding the outcome of a temporal race between the ‘bad’ pull of demographically lethal environmental change and the ‘good’ pull of evolutionary change. Taking the eco-evolutionary loop into account and using the adaptive dynamics toolbox, however, alters the terms of the problem. Population genetics and quantitative genetics do not close the loop: they both ignore how evolution-driven population changes that affect viability may feed back on the very selection pressures that act on heritable variation and drive these changes. Closing the loop has the important consequence, adaptive dynamics theory tells us, that only under exceptional circumstances is population size or viability maximized at an evolutionary attractor (see §1 and references therein).

4. Extending evolutionary rescue theory in the adaptive dynamics framework

By accounting for the eco-evolutionary feedback loop, adaptive dynamics theory predicts that, as the environment changes, the evolutionary attractor may approach the non-viable region and eventually collides with it, a phenomenon called ‘evolutionary trapping’ [1,44]. Even under fixed environmental conditions, successive trait substitutions driven by the eco-evolutionary feedback loop can gradually erode population size, thus potentially raising the population's extinction risk (this is ‘evolution to self-extinction’ in terms of  Matsuda & Abrams' [45]). An adaptive dynamics model of such gradual effects of adaptation on population size is studied in [46]. Furthermore, a single trait substitution event can suffice to degrade population viability drastically at once, by causing a crash in population size [47] or by putting the population in a demographically non-viable state [48,49], a phenomenon dubbed ‘evolutionary suicide’ [1,31,44,50] (for the related notion of ‘Darwinian extinction’ see [51]).

Evolutionary suicide thus occurs when a trait substitution sequence driven by mutation and selection in a constant (external) environment takes a population towards and across a boundary in the population's trait space beyond which the population cannot persist. Once the population's phenotypic traits have evolved close enough to this boundary, ‘kamikaze’ mutants can invade that are viable as long as the current resident trait value abounds, but that are not viable on their own [48,49]. This means that crossing the boundary causes a catastrophic shift of the population from a stable positive equilibrium density to extinction, and requires that the ecological system demonstrates positive density dependence at low density, i.e. an Allee effect [52,53]. More generally, for ecological systems with multiple stable equilibria, an invading mutant may shift the population catastrophically to a low-density population equilibrium (rather than outright extinction), rendering the population highly susceptible to extinction by stochastic causes [47]. Thus, evolutionary suicide extends into the notion of ‘evolutionary collapse’ [1] which concerns an even wider class of multistable ecological systems.

By confining adaptive evolution to the role of the Good and environmental change to the Bad, current evolutionary rescue theory is at risk of missing the Ugly: challenges to population viability raised by the evolutionary process itself. Even in the absence of negative effects of environmental change on the species' demography, evolutionary trapping and suicide can, by themselves, be the driving forces towards extinction. When environmental change does degrade population demography (the usual assumption in current models of evolutionary rescue), evolutionary trapping and evolutionary suicide can suppress the potential for evolutionary rescue altogether. The occurrence of evolutionary repellors determines whether evolutionary rescue remains possible, and how evolutionary trapping and suicide influence the chance of rescue in response to, respectively, gradual and abrupt demographic degradation.

(a). Evolutionary trapping and suicide as driving forces to extinction

Evolutionary trapping occurs when an evolutionary attractor collides with a non-viable region as environmental conditions are changed. This may happen even if the non-viable region does not expand in response to environmental change (figure 3a). It is evolutionary suicide that ‘terminates’ the population when its evolutionary attractor hits the non-viability region. Hence, evolutionary trapping generally implies evolutionary suicide, in the sense that evolutionary trapping requires the existence of a region in the environment-trait (e, x) space where evolutionary suicide occurs. Yet in contrast with evolutionary trapping, evolutionary suicide per se can occur in the absence of any extrinsic environmental change, as it is intrinsically driven by the feedback between an evolving populations and its environment (figure 3a). The fingerprint of evolutionary suicide in E³-diagrams is directional selection pointing towards a non-viable region. Evolutionary suicide can be induced by environmental change when an evolutionary attractor collides with an evolutionary repellor, such that a population that is tracking the attractor as environmental conditions change suddenly becomes exposed to directional selection towards the non-viable region. As in the case of evolutionary trapping, this may occur while the non-viable region remains unaffected by environmental change (figure 3b).

Figure 3.

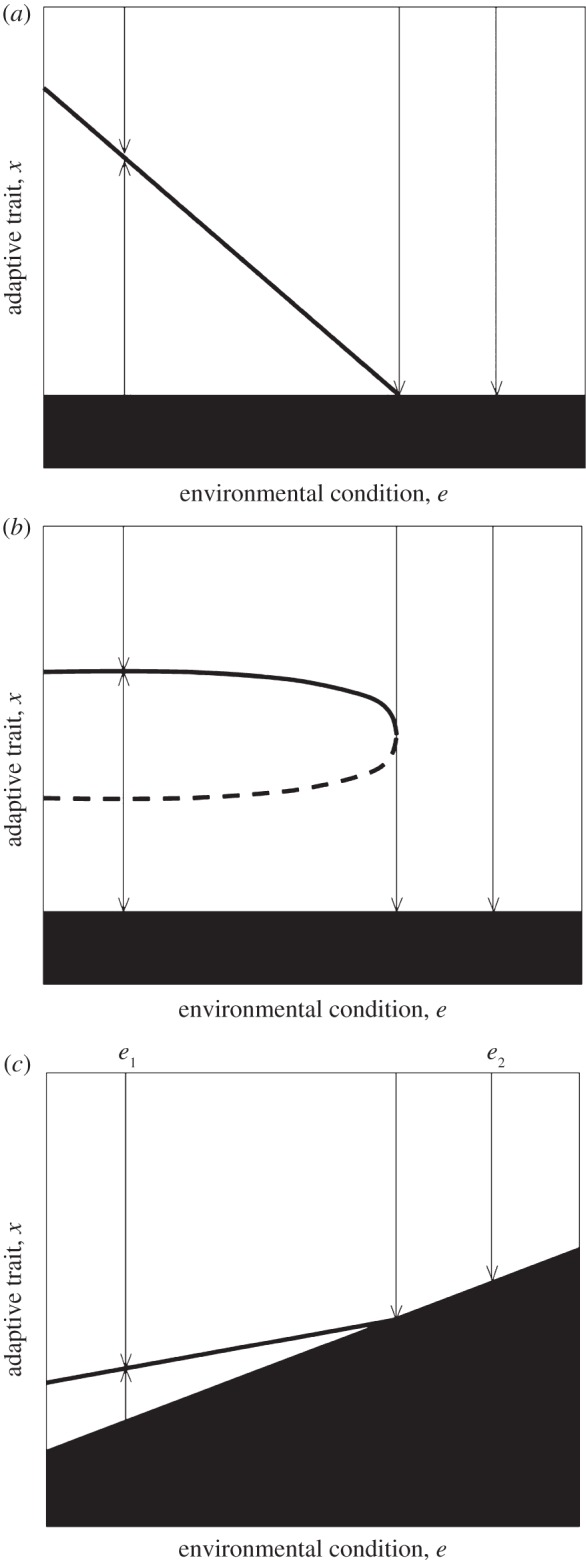
Evolutionary threats: trapping and suicide. Evolutionary trapping and evolutionary suicide are generated by eco-evolutionary feedbacks and predicted by adaptive dynamics theory. (a) Evolutionary trapping and suicide. As the environment changes, the evolutionary attractor collides with the non-viable region. The plot shows a case where beyond the environmental condition for which the collision happens, selection uniformly presses towards the non-viable region, causing inevitable evolutionary suicide. (b) Evolutionary suicide induced by environmental change without evolutionary trapping. As the environment changes, the safe evolutionary attractor collides with an evolutionary repellor, subjecting the population to selection towards extinction, hence evolutionary suicide. (c) Potential for evolutionary rescue suppressed by evolutionary trapping and suicide. The plot depicts a simple and general scenario whereby, as the environment changes from e₁ to e₂, evolutionary rescue could not occur, neither by tracking the attractor (owing to evolutionary trapping) nor by escaping the non-viability region (owing to evolutionary suicide).

In the context of current evolutionary rescue theory, where the changing environment does beget the non-viable region to expand, evolutionary trapping and suicide can suppress the potential for rescue. This is illustrated in figure 3c. In the case of gradual environmental change, owing to evolutionary trapping there is no viable evolutionary attractor that the population could track from environmental condition e₁ all the way to e₂. In the case of abrupt environmental change from e₁ to e₂, the positive density dependence (Allee effect) responsible for evolutionary suicide opposes rescue: owing to positive density dependence, mutants' invasion and fixation is very unlikely given their initial low density, unless the mutation process, by its rate or its phenotypic magnitude, could generate mutants that are phenotypically distant enough from the non-viable region to escape the Allee effect. Even if the population were to escape from the non-viable region thanks to rapid arising and fixation of ‘rescue mutants’, the selection gradient associated with evolutionary suicide would pull it back to extinction.

(b). The key role of evolutionary repellors

Evolutionary trapping and suicide can compromise the potential for evolutionary rescue, but the occurrence of evolutionary repellors may restore it. Evolutionary repellors typically separate regions in trait space with different long-term evolutionary outcomes, such as convergence to alternative evolutionary attractors, or convergence to an evolutionary attractor in one region versus evolutionary suicide in another. Thus, the occurrence of evolutionary repellors opens the possibility that an evolutionary trap coexists with a persistently viable evolutionary attractor (figure 4a).

Figure 4.

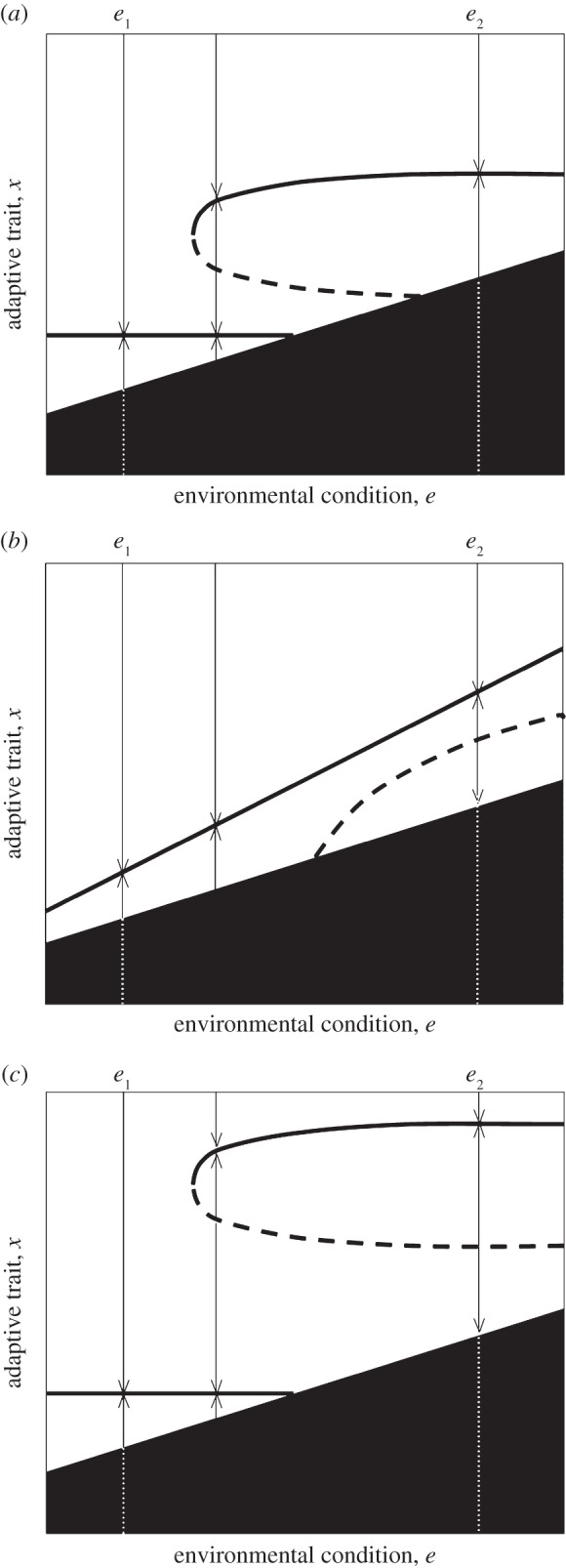
Evolutionary threats and evolutionary rescue: The key role of evolutionary repellors. The geometry of repellor lines determines whether evolutionary rescue is possible. (a) Here the problem of rescue after abrupt environmental change from e₁ to e₂ conforms to current evolutionary rescue theory. In contrast, rescue from gradual environmental change requires that the population switches to a different evolutionary attractor by evolving across the evolutionary repellor. (b) Here the problem of rescue under gradual environmental change from e₁ to e₂ conforms to current evolutionary rescue theory. In contrast, rescue from abrupt environmental change requires that the population escapes from the non-viable region and overcomes the pull of evolutionary suicide by evolving across a repellor. (c) Combining geometric features of (a) and (b): the problem of rescue departs from current theory in both cases of abrupt and gradual environmental change. See figure 2 for graphical details.

In this case, the question of evolutionary rescue in response to abrupt environmental change may be the same as in current rescue theory (i.e. whether the population under environmental condition e₂ can escape the non-viable region while selection acts directionally towards a safe evolutionary attractor), but the problem of rescue is fundamentally different in the case of gradual environmental change. It becomes whether or not the population may drift away from the evolutionary trap and across the evolutionary repellor fast enough, so that from there selection could drive it to the safe evolutionary attractor. Evaluating the likelihood of rescue and its determinants then relates to an exercise in population genetics, on the effect of mutation, selection and drift on the genotypic distribution of a population across a fitness valley (the evolutionary repellor) under directional environmental change [54]. Population genetics then tell us that population size, rate and fitness effects of mutations and the pace and fitness effects of environmental change will be critical factors (see [42,43,55] in this special issue). In particular, lower population size, by making genetic drift more effective, might facilitate this route to rescue.

Alternatively, an evolutionary repellor can arise without altering the problem of evolutionary rescue in gradually changing environments (i.e. whether the population can evolve fast enough so as to track a safe but changing evolutionary attractor) while introducing a new evolutionary hurdle to populations subject to abruptly changing environments. This is the case when evolutionary rescue is so perilous as to require that the population both escapes extinction while in the non-viable region and then drifts against the opposing selective force of evolutionary suicide so as to cross the repellor (figure 4b). Figure 4c depicts the combined case where both gradual and abrupt environmental change exact those new requirements for evolutionary rescue to take place. This happens when the range of environmental condition e over which the evolutionary repellor exists is broad enough.

5. Examples: theoretical and empirical

Evolutionary suicide occurs for a rich variety of ecological systems which set the stage for some form of a ‘tragedy of the commons’ [56] whereby new phenotypes that are demographically advantageous against the rest of the population turn out to be demographically lethal when dominating the population. This accounts for the fact that models of evolutionary suicide often involve traits related to cooperation that begets Allee effects, such as positively density-dependent dispersal [49,57], group effects against enemies such as predators [47], altruism [58,59], mutualism [50,60,61] and facilitation [62]. These traits shape ecological interactions and generate Allee effects. For example, a population of altruists may only be viable if the population density is above some threshold, such that on average an individual receives enough altruistic benefits from others to compensate for its own cost of altruism. In all these models, evolutionary trapping and induced evolutionary suicide are generic outcomes. In the rest of this section, we elaborate on two theoretical examples and end with an empirical prospectus.

(a). Adaptive dynamics of altruism in social networks

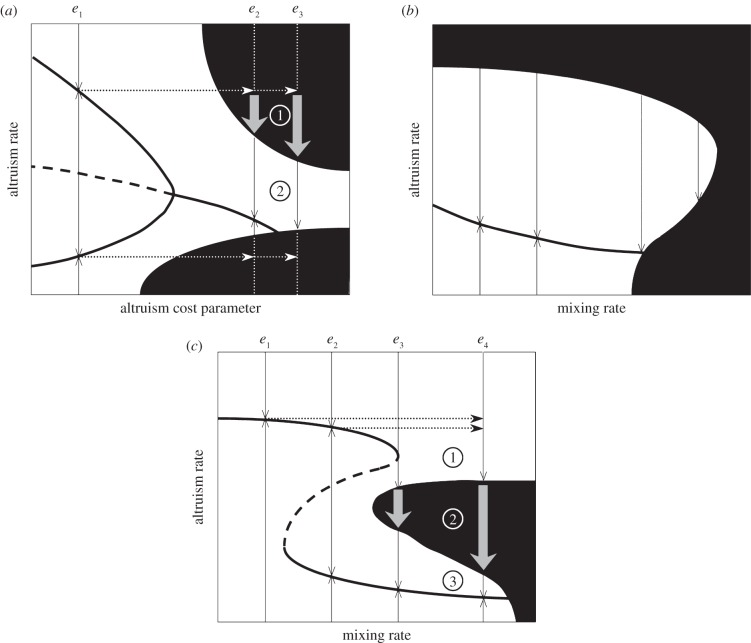
The role of evolutionary repellors in shaping patterns of evolutionary trapping and suicide and determining the requirements for evolutionary rescue is well exemplified by Le Galliard et al.'s model of altruism adaptive dynamics in heterogeneous populations [58,59] (see also [25]). Figure 5 displays E³-diagrams for this model. Here, heterogeneity means that each individual interacts with others within its ‘social network’. Altruism, by definition, contributes to the demographic success of connected individuals at a demographic cost for the altruist. Individuals quit their current social network and join new ones at a given rate that quantifies the degree of social mixing in the population. The cost function of altruism and degree of mixing are strong influences of both the population's demographic viability and the adaptive dynamics of altruism (figure 5), and can be impacted by environmental change via physiological factors and physical or cultural factors, respectively. Because mixing has a cost (due, e.g. to delays in re-establishing one's social network), the population is not demographically sustainable at high mixing rates without a substantial degree of altruism between individuals (figure 5b,c). When the cost of strong altruism is very large, high levels of altruism may also preclude demographic viability irrespective of mixing rates (figure 5b). For slowly accelerating cost of altruism, an evolutionary repellor appears over a range of intermediate mixing rates, and comes to separate a high-altruism evolutionary attractor from a ‘quasi-selfish’ evolutionary attractor at very low altruism (figure 5a,c).

Figure 5.

E³-diagrams for the adaptive dynamics of altruism in social networks. (a) Environmental change makes the cost of altruism steeper (model from [58] with mixing rate m = 10 and altruism cost parameter 1 < γ < 5). A population adapted to environmental condition e₁ may sit on a high- or low-altruism attractor. Starting in e₁ at either attractor and undergoing an environmental change to e₂ (gradual or abrupt) sets up the classical scenarios for evolutionary rescue. In contrast, the change from e₁ to e₃, either gradual or abrupt, leaves no chance for rescue. With abrupt environmental change, a population initially at high-altruism may still experience ‘transient rescue’ if it survives its passage though the upper non-viable region (phase (1)); but this would only be next to experiencing evolutionary suicide (phase (2)). (b,c) Environmental change makes the mixing rate larger (model from Le Galliard et al. [58] with mixing rate 1 < m < 5 and altruism cost parameter γ = 3 in (b) and γ = 1.2 in (c)). In (b) the cost of altruism is rapidly accelerating. This leaves no chance for rescue. In (c) the cost of altruism is slowly accelerating. The e₁ mixing condition selects for a high-altruism attractor, whereas a population adapted to e₂ could sit on a high- or low-altruism attractor. Starting in e₂ at low-altruism and undergoing an environmental change to e₃ (gradual or abrupt) is a classical case of evolutionary rescue. In contrast, starting in e₂ at high-altruism or in e₁ (hence necessarily at high-altruism) and undergoing the change to e₄ now exposes the population to the evolutionary threat of suicide (phase (1)). Rescue remains possible though, since the evolutionary attractor at e₄ is viable (phase (3)); but the rescue likelihood will depend on whether the environmental change is gradual or abrupt, which determines the range of non-viable phenotypes that the population would have to move across—possibly narrow if environmental change is gradual, but maximally large if the change is abrupt (phase (2)). See [57] for detail about the model, and fig. 5 therein for parameter values corresponding to this figure.

The model exemplifies the evolutionary threats of suicide and trapping, features the classical routes to rescue in abruptly or gradually changing environments and also reveals more complex pathways evolution may have to take in to rescue the population. As predicted by general theory, the risk of evolutionary suicide may be averted by rescue that takes the population through a non-viable region and eventually exposes it to selection towards a viable attractor. In an abruptly changing environment, a population driven out of a non-viable region (see figure 5a, phase (1)) by rescue may only find itself exposed to selection towards another non-viable region (figure 5a, phase (2)). Moreover, evolutionary rescue in a gradually changing environment may be seriously impeded when it involves switching to a new attractor (figure 5c, phases (1) and (3)), for a non-viability zone may lie in between (figure 5c, phase (2)).

(b). Adaptive dynamics of the maturation reaction norm in fisheries

In the study of Bürger [54] and other previously cited adaptive dynamics models, the evolving trait is defined as unconditional. The (common) assumption is thus made that there is initially no plasticity in the trait, and no plasticity can evolve. How plasticity and genetic adaptation interact and jointly shape a population's evolutionary trajectory is a fundamental issue in evolutionary biology [63–65], yet one for which our theoretical understanding is still limited [66]. Perhaps even more so is our appreciation of how plasticity and genetic adaptation together influence the ecological properties of a population. Using the quantitative genetics approach, the question was tackled by Chevin & Lande [67] and is addressed in this special issue by Chevin et al. [68] and Kovach-Orr & Fussmann [69].

In the adaptive dynamics framework, the mathematical toolbox to deal with plastic traits, and plasticity as a trait, has been assembled [70–72]. A remarkable application has been developed to understand the eco-evolutionary consequence of overharvesting fisheries [73–75]. Here, the maturation reaction norm (the function describing maturation size in dependence of maturation age) is the (plastic) trait around which the eco-evolutionary feedback loop revolves. Ernande et al. [73,74] show that when the evolving population is exposed to harvesting, the maturation reaction norm evolves such as to allow individuals to mature at younger ages and smaller sizes. At a certain point, this adaptation may cause the entire population to go extinct, thus showing that plasticity and its evolution do not make the population proof against evolution-driven extinction.

(c). Empirical prospectus

On the empirical side, case studies of evolutionary suicide and evolutionary trapping remain more suggestive than demonstrative. Early examples were discussed in Ferriere et al. [76] and Dieckmann & Ferriere [1]. Delgado et al. [77] discussed evolutionary suicide and rescue when individual dispersal is the target of the adaptive process. They used predictions from general theory [48,49,78] and from more organism-specific models [79] to show (theoretically) that evolution tends to favour dispersal rates that are considerably lower than the rates that would maximize ‘population performance’ (e.g. patch occupancy, metapopulation persistence). Then they examined empirical evidence for such discrepancy: vertebrates and insects form well-studied taxa for dispersal in relation to habitat fragmentation and local population size. In these data, Delgado et al. [77] found tangential support for the predictions, but no direct evidence.

Specifically, experimental evidence that individual fitness would not increase if dispersal rates were higher, whereas population performance would, is lacking [77]. We suggest that the common lizard (Lacerta vivipara) offers a promising model, for which long-term observations on individual traits and environmental conditions are available, alongside experimental data and population mathematical models. Using such a combination of observation, experiment and modelling, Massot et al. [80] concluded that dispersal has been decreasing across years in response to climate warming, that such decrease could cause extinction through an Allee effect, and that higher values of dispersal would ensure longer population persistence under continued climate change. Although this could be an example of evolutionary suicide or trapping in action, the data at hand could not reveal whether the lizards' dispersal response was genetic or plastic.

The same system (common lizard) seems also prone to evolutionary suicide and trapping through sexual selection [81]. Le Galliard et al. [82] showed that male–male competition can reduce the availability of females, owing to harassment that elevates female mortality, and hence turn sexual conflict over mating into a tragedy of the commons [83,84]. Combining data with population models, Le Galliard et al. [82] concluded that exacerbating the conflict can lead to extinction via an Allee effect. Rankin et al. [81] took the modelling work one step further to show that evolutionary suicide could ensue, driven by selection acting on male harassment behaviour. Interestingly, they also showed that the coevolution of female resistance could avert the risk of evolutionary suicide.

Micro-organisms may offer the best bet for direct experimental evidence. Using experimental populations of a bacterium (Pseudomonas fluorescens) and a bacteriophage, Zhang & Buckling [85] studied how bacterium–virus coevolution impacts viral population persistence in the face of gradually increasing temperature. They garnered evidence that the virus persisted much longer when its infectivity evolved in the presence of an evolutionarily constant host genotype. This suggests a case of ‘coevolutionary trapping’: in response to increasing temperature, a consumer (phage) tracks an evolutionary attractor that reaches extinction as the resource (bacterium) coevolves, but over the same temperature range the consumer's evolutionary attractor remains viable if coevolution is blocked in the resource (see the electronic supplementary material, figure S1). Further progress in understanding the underlying ecological and evolutionary mechanisms involved in this and the previous examples is likely to benefit from a stronger integration of experimental data and mathematical models.

6. Further perspectives on adaptive dynamics and evolutionary rescue theory

(a). New questions for population and quantitative genetics

The theoretical example presented in §5a shows how adaptive dynamics further broaden the problem of evolutionary rescue as currently addressed by quantitative genetics and population genetics. When evolutionary rescue requires that a population tracking a due-to-disappear evolutionary attractor switches to another, safe evolutionary attractor, gradual evolutionary change towards the safe attractor may, by itself, take the population into the non-viable region (see figure 5c, phase (1)–(2) under environment e₃). Furthermore, rescue out of the non-viable region may take the population to an evolutionary trap (see figure 5c, phase (3) under environment e₃), or expose the population to selection towards another non-viable region (figure 5a, phase (2) after the environment has changed from e₁ to e₃).

In §4a, we pointed out that when the population is pulled into a non-viable region around which selection drives evolutionary suicide, the probability of exit from that region is seriously compromised. What about the extinction risk of an ecologically viable population undergoing evolutionary suicide—for example, taking the case depicted in figure 5c, when abrupt environmental change occurs between e₁ or e₂ and e₄? As shown in [1], this is an open problem for sexually reproducing organisms. In populations characterized by small genetic variation, evolution towards the boundary of the viability region may further reduce genetic variation, thus slowing down the evolutionary trajectory and perhaps bringing it to a halt before hitting the viability boundary [45,86]. Another mechanism whereby evolutionary suicide might be delayed was described in [1] for populations that have large genetic variation (figure 6). When a broad phenotypic distribution approaches the non-viable region, it extends its head tail beyond the viability boundary. The loss of individuals in this tail will then affect the selective pressures acting on the rest of the population. In particular, the release of density dependence through very low reproductive success in the head tail may boost the reproductive success of individuals in the rear tail. This source–sink dynamics across the viability boundary may lead to a stable phenotypic distribution hovering at the brink of extinction. The smaller the population's phenotypic variance, the closer it gets to extinction. Achieving a general, quantitative description of this phenomenon is a problem for population and quantitative genetics, but one in which eco-evolutionary feedbacks lay at the core and must be fully accounted for.

Figure 6.

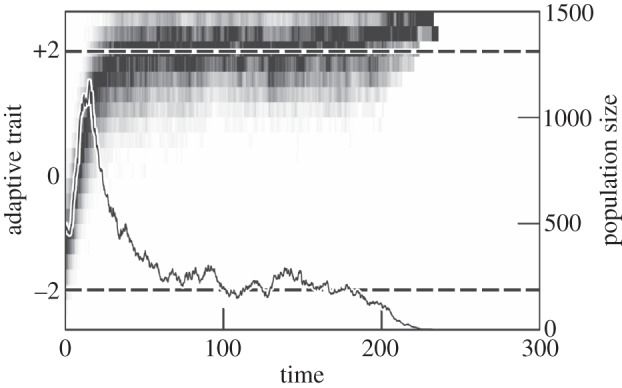
Example of evolutionary suicide in sexual populations (from [1]). The ecology of the system involves asymmetrical competition and an Allee effect. The adaptive trait x is a measure of competitive ability, e.g. body size. There is an optimal value of the trait but the greater the difference in trait values between any two individuals, the lesser competition they experience. The death rate captures the direct fitness effect of the trait and the ecological effect of asymmetrical competition, as in [87]; the birth rate bears the Allee effect and is trait-independent. See box 11.6 in [1] for detail. In their simulations, the adaptive trait x is polygenic, determined by 10 diploid loci with free recombination and additive effects. Loci are diallelic, with allelic values +1 and −1 and the set of trait values is scaled to −2 < x < +2. Mutations occur with probability 10⁻³ per locus. The polymorphic distribution of adaptive trait values, depicted by grey scales, starts out on one side of the optimum at x = 0. Owing to asymmetric competition, the evolutionary process drives the distribution towards and then beyond the optimum, until it reaches the non-viable boundary (near x = 1.5). The model has two viability boundaries, depicted by dashed lines. The black solid curve shows the changes in actual population size resulting from the trait's evolution. The genetic architecture of trait x results in large phenotypic variance that maintains through time. The loss of individuals in the tail of the phenotypic distribution that extends beyond the viability boundary enhances reproductive success in the remainder of the poupulation. As a result, the population lingers at the brink of extinction, before perishing eventually. Adapted from [1] (Cambridge University Press).

(b). Evolutionary trapping, suicide and rescue in polymorphic populations

The case of sexually reproducing organisms that we just broached addresses the phenomenon of evolutionary suicide in populations that are polymorphic yet phenotypically unimodal. Does the threat of evolutionary suicide extend to polymorphic populations distributed around multiple phenotypic modes? Such multimodal polymorphism may provide a form of ‘evolutionary insurance’ [44] since evolutionary suicide would require the rather unlikely event that all phenotypic modes hit the viability boundary of their (now multi-dimensional) phenotype space at once. The phenomenon of evolutionary branching, as predicted by adaptive dynamics theory, can turn a monomorphic population into a multi-morphic one. The simplest case is that of a one-dimensional trait driven to an evolutionary singularity where selection turns from directional to disruptive; two phenotypic branches result and diverge as evolution proceeds. The population now evolves in a two-dimensional phenotype space, which possesses its own non-viable region. Evolutionary suicide in this case would require that the (dimorphic) population hitting the boundary of this (new) non-viable region would go extinct. But non-viability of a dimorphic population does not necessarily mean extinction of the whole population; it may simply entail that the population collapses back to a viable but monomorphic state [36,88]. Evolutionary cycles of branching–extinction may result [89,90].

To our knowledge, all adaptive dynamics models in which branching was followed by collision with the non-viable boundary have been of that kind: loss of one type and return to a monomorphic population (or in the case of larger degrees of polymorphism, loss of p types among p + q, p ≥ 1, hence return to a viable, q-morphic population). However, recent models of mutualism evolution hint at evolutionary suicide (and trapping) in polymorphic multimodal populations. For example, Jones et al. [61] focused on mutualism in plant–insect interactions. In their model, two seed–parasite insects can coevolve; one is a pure parasite of the plant and the other is mutualistic. Evolutionary suicide of the two-type community is a generic outcome, and environmental change that affects the competitive asymmetry between insect types can cause evolutionary trapping and induce evolutionary suicide of both types.

In figure 7, we report what may be the first example of induced evolutionary suicide in a population shaped originally by evolutionary branching. The model (derived from [50]) describes the adaptive dynamics and diversification of a cooperation trait. Starting with a monomorphic ancestral population, seven phenotypic branches evolve in a constant environment. An episode of gradual environmental change is then imposed. The effect of environmental change on two different parameters was considered. The first led to evolutionary suicide (figure 7a,b). Without evolution (figure 7a), five out of seven phenotypic branches survived the environmental change and the remaining five-branch community persisted in the long run. With adaptive evolution (figure 7b), the community responded to the period of environmental change with the loss of one branch. Interrupting the environmental change exposed the remaining six-branch polymorphism to a strong regime of directional selection, which led to the loss of one more branch and the eventual collapse of the entire population. With the second kind of environmental change, a form of evolutionary rescue was discovered (figure 7c,d). Without evolution (figure 7c), all seven branches went successively extinct and the whole population was lost. With evolution (figure 7d), the six upper branches were lost as the environment changes but the lowest branch could survive and spring a new episode of diversification, leading to a new polymorphism complement, in a (within-species) process akin to (between-species) classical ‘incumbent replacement’ [91]. This evolutionary rescue happens with a certain probability which can be estimated by Monte-Carlo simulations.

Figure 7.

Evolutionary trapping, suicide and rescue in polymorphic populations. Distribution of phenotypes (vertical axis) across time (horizontal axis) generated by a model of cooperation evolution (see appendix A). The system is seeded with a monomorphic ancestral population. The environment is constant over the first 21 000 generations and changes gradually between time 21 000 and 22 000. (a,b) Evolutionary suicide. Environmental change is mimicked by increasing parameter a geometrically (from −9.16 to −0.454). (a) Evolution stops at time 21 000 (mutation rate set to zero). A five-branch population persists in the long run. (b) With continued adaptive evolution, the entire population collapses around time 46 000. (c,d) Evolutionary rescue. Environmental change is mimicked by increasing parameter θ geometrically (from 0.01 to 0.11). (c) Evolution stops at time 21 000 (mutation rate set to 0). The whole population is lost. (d) With continued adaptive evolution, one branch survives to environmental change and springs a new episode of diversification. The probability of evolutionary rescue (estimated by Monte-Carlo simulations) is 0.83.

It is interesting to look at the pattern exemplified in figure 7c,d in the light of the results of Geritz et al. [36] and Kisdi [88] (see fig. 6 therein) on the extinction of evolutionary branches. In these studies, a population first evolves into a dimorphic state by evolutionary branching; one of its branches then evolves to extinction; this is followed by the remaining branch converging towards the population's final (monomorphic) evolutionary state. Thus, for some ancestral phenotypes far from the evolutionary attractor, branching and dimorphism can be a necessary but transient phase on the way to the monomorphic attractor. Given such findings, simulations as in figure 7 make us wonder whether in polymorphic multimodal populations, the loss of branches during gradual environmental change might facilitate switching to and tracking an alternative, safe evolutionary attractor (which may or may not be polymorphic too).

(c). Evolutionary rescue theory at the community level

The question of evolutionary rescue, as posed by current theory, can be carried over to the community level (see also [69]): the threat may be direct demographic imperilment of individual species, and rescue may be the persistence of all species initially present. But the threat may also act indirectly, by altering interactions between species, or even more indirectly by impacting basic ecosystem functions and flows of matter and energy between guilds. Rescue may be defined in new ways, e.g. by the persistence of a fraction of the species originally present simply greater that the proportion that would remain in the absence of evolution; or by no diversity loss, but accepting that the species composition of the community could be different [92,93].

A remarkable example has been provided along these lines by Tilman & Lehman [94] who modelled the exposure of a formerly nitrogen-poor community of terrestrial plants to a large increase in the rate of nitrogen deposition, and examined the community's response both at the ecological and the evolutionary time-scale. Unsurprisingly, the model predicts that the short-term effect of the environmental change is the take-over of a few formerly rare, but now fast-growing and rapidly dispersing species. The differential success of these plants is enhanced by asymmetric competition for light. After the initial ecological response, evolutionary processes come into play and reshape the entire community. On the basis of a trade-off between competitive ability and dispersal, the model predicts that the winners of the short-term round gradually reduce their capacity for dispersing and evolve into better local competitors.

Under such conditions, evolution first establishes two distinct morphs: a good disperser that is a poor competitor and a good competitor that is a poor disperser. Afterwards, the former morph again evolves towards better competitive ability and thus allows a well dispersing third morph to invade with traits similar to those the first and second morph had both expressed initially. Thus, the range between the two extreme strategies successively fills up with a collection of intermediate species. Tilman & Lehman describe this pattern as the result of a speciation process that eventually yields a local flora that is as species-rich as the one present before the environmental change. The far-reaching conclusion from this theoretical study is that rapid speciation processes can drive evolutionary rescue of community diversity by conferring high long-term resilience to the diversity of natural communities against the immediate negative impacts of ecosystem degradation.

Stegen et al. [95–97] have combined such eco-evolutionary models with eco-physiology theory to predict the evolution of species richness in trophic networks as environmental temperature increases globally. As this happens, evolution changes the network's species complement but yields a net gain in species richness, up to a threshold beyond which the balance between the (temperature-increasing) speciation rate and extinction rate tilts in favour of the latter. Such developments will contribute to a theoretical underpinning for the empirical investigation, as undertaken by Lavergne et al. [98], of how species' eco-evolutionary history shapes the impact of current environmental change on contemporary communities.

7. Implications for conservation and management

Such an adaptive dynamics approach to evolutionary threats and rescue raises important challenges for conservation and ecosystem management. First, what systems are more at risk? The key ecological mechanism underlying evolutionary suicide and, more generally, evolutionary collapse, is the existence of alternative stable states. Positive ecological feedbacks (e.g. positive density dependence) are often necessary for alternative stable states [99,100], and play key roles in the organization and function of various important ecosystems [101]. When shifts between alternative stable states can be triggered by adaptive traits or by some ecological parameters which they influence, then the stage is set for evolutionary suicide or collapse [62]. Can we then diagnose the evolutionary threats? This may not be easy when the environment changes gradually. Monitoring the direct effect of environmental change on population demography will be of little value. Indeed, environmental change can drive a population to extinction through evolutionary trapping while shrinking, rather than expanding, the hazardous region of demographic non-viability [61]. And as evolutionary trapping occurs, there may be very little change in the phenotypic or ecological state of the population, rendering the diagnosis difficult. Close to evolutionary suicide, however, the population is expected to show the early warning signals of systems approaching a ‘tipping point’ in ecological state [100,102]. There is increasing evidence [103,104] that generic statistical indicators, based on ‘critical slowing down’ [105–107], can provide advance warning of catastrophic collapse. These tests could be adapted to detect the risk of evolutionary suicide as well.

What factors may attenuate (or worsen) evolutionary threats, and can we predict important influences of the likelihood of rescue? According to current evolutionary rescue theory for gradually changing environments, rescue should be more likely under slower environmental change. In contrast, evolutionary rescue from the threat of trapping may be more likely under faster environmental change. Rapid environmental change may leave the population lagging so much behind its dangerous evolutionary attractor that the population may end up under selection towards an alternative, safe evolutionary attractor. Reduced genetic variation, which would impede rescue under current theory, may similarly be advantageous. As discussed in §6a, very small genetic variation can delay the extinction outcome of evolutionary suicide; in sexual organisms, large genetic variance will have the same effect (figure 6). The findings of Rankin et al. [81] also suggest that the structure of genetic covariance between adaptive traits could radically alter the likelihood of evolutionary suicide. Evolutionary rescue essentially amounts to crossing a fitness valley (evolutionary repellor) to escape an evolutionary trap or an immediate suicide. Somewhat paradoxically, small population size, by amplifying genetic drift, may facilitate evolution to an alternative evolutionary attractor and thus foster evolutionary rescue. Realizing that genetic variance, population size and the direction of selection are variables and outputs of eco-evolutionary feedbacks, rather than parameters or external inputs, should encourage future research to use insights into the eco-evolutionary feedback loop to design unconventional conservation or restoration methods.

8. Concluding remarks

The question of the potential for evolutionary adaptation to rescue populations from deleterious effects of environmental change is usually asked under the (oft-implicit) assumption that adaptive evolution is, if anything, bound to improve the demographic fate of the population. But this conventional view ignores eco-evolutionary feedbacks. The eco-evolutionary feedback loop is responsible for frequency-dependent selection, broadly defined [23], and this has important consequences for our understanding of the interaction between evolutionary adaptation and population persistence.

Adaptive dynamics theory provides a framework to model phenotypic evolution driven by eco-evolutionary feedbacks and investigate the resulting ecological changes in population dynamics. This framework shows that the question of evolutionary rescue does not reduce to whether or not a population can track a moving evolutionary attractor fast and closely enough, or whether or not demographically viable mutants can arise and invade soon enough to prevent extinction of an otherwise non-viable population. The operation of eco-evolutionary feedbacks readily generates evolutionary repellors that can delineate conditions on the environment and the population's phenotypic composition under which the population is either safe or at risk of evolutionary trapping and suicide. In the face of trapping and suicide, evolutionary rescue is not only a matter of a population taking advantage of the evolutionary process to survive or avoid demographic threats; it requires that the population overcomes evolutionary threats generated by the process of adaptive evolution itself.

By being explicit about ecological processes, adaptive dynamics theory makes it possible to investigate the effect of different types of environmental change (differing in how they impact the various ecological processes that drive population dynamics and generate selective pressures; whether they affect one and not the other, directly or indirectly) and discover and address evolutionary rescue phenomena that may differ in the mechanisms of threats (e.g. demographic versus evolutionary), the manifestation of these threats at different levels of ecological organization (e.g. population demography, community structure, ecosystem function), and the evolutionary path away from those threats. The emerging picture of evolutionary rescue is one of a complex, multi-faceted process, the study of which raises the challenging but exciting task of bridging and unifying important areas of ecological and evolutionary theory.

Appendix A. A model of suicide and rescue in populations undergoing evolutionary branching

Ferriere et al. [50] studied evolutionary branching in a model of two-species mutualism adaptive dynamics. We simplified their system into a one-species model of cooperation. The adaptive trait now measures the individual investment in some public goods that benefit the entire population. Dependence on the public goods causes an Allee effect and raises asymmetrical competition. For a resident population with trait x and density n, the ecological model is given by

A1

and for a rare mutant with trait x‘ and density n‘, per capita population growth is

A2

Here, c and θ are positive constants, r is the constant function of the trait. Function α has a sigmoid shape accounting for the assumption that investing more in public goods gives a competitive advantage; 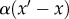is the intensity of asymmetrical competition experienced by an individual with trait x‘ interacting with a population of individuals with trait x, and 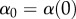. Functions α and r and their parameters are chosen as in [50]: 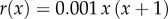, 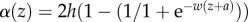. Parameter values used in figure 7 are: c = 2, h = 2.05, w = 0.4, a = −9.16 and θ = 0.01. Simulations were performed using ZEN software (http://www.biologie.ens.fr/~legendre/zen/zen.html) with initial trait value = 100, initial population size = 3000, mutation rate = 0.001, mutation standard deviation = 1, carrying capacity = 1000 and integration step = 0.01.