A test of the influence of continental axes of orientation on patterns of human gene flow

Abstract

The geographic distribution of genetic variation reflects trends in past population migrations, and can be used to make inferences about these migrations. It has been proposed that the east-west orientation of the Eurasian landmass facilitated the rapid spread of ancient technological innovations across Eurasia, while the north-south orientation of the Americas led to a slower diffusion of technology there. If the diffusion of technology was accompanied by gene flow, then this hypothesis predicts that genetic differentiation in the Americas along lines of longitude will be greater than that in Eurasia along lines of latitude. We use 678 microsatellite loci from 68 indigenous populations in Eurasia and the Americas to investigate the spatial axes that underlie population-genetic variation. We find that genetic differentiation increases more rapidly along lines of longitude in the Americas than along lines of latitude in Eurasia. Distance along lines of latitude explains a sizeable portion of genetic distance in Eurasia, whereas distance along lines of longitude does not explain a large proportion of Eurasian genetic variation. Genetic differentiation in the Americas occurs along both latitudinal and longitudinal axes and has a greater magnitude than corresponding differentiation in Eurasia, even when adjusting for the lower level of genetic variation in the American populations. These results support the view that continental orientation has influenced migration patterns and has played an important role in determining both the structure of human genetic variation and the distribution and spread of cultural traits. (240 words)

Interest in the relationship between genetic differentiation and geography has been longstanding in human population genetics (Lawson Handley et al., 2007; Novembre and Di Rienzo, 2009). Empirical studies have shown that genetic differentiation between human populations increases with geographic distance (Cavalli-Sforza et al., 1994; Cavalli-Sforza and Feldman, 2003) and that within-population genetic diversity decreases with increasing distance from Africa (Prugnolle et al., 2005; Ramachandran et al., 2005).

Menozzi et al. (1978) introduced the idea of inferring geographic “axes” underlying human genetic variation by using principal components analysis (PCA) to study allele frequency patterns in various geographic regions. In models in which migration among populations occurs isotropically on a lattice, recent theoretical analysis predicts that the first two principal components will correspond to perpendicular geographic axes (Novembre and Stephens, 2008). The resurgence of PCA with genetic data in this and other work (e.g., Price et al., 2006; Patterson et al., 2006; Paschou et al., 2007; McVean, 2009), together with advances in high-throughput genotyping technology that permit fine-scale inferences about genetic similarities and differences among sampled individuals, has led to increased interest in the investigation of spatial axes of variation in genomic data.

Studies performed globally (Zhivotovsky et al., 2003; Ramachandran et al., 2005; Jakobsson et al., 2008; Li et al., 2008; Xing et al., 2009; Auton et al., 2009; Biswas et al., 2009; Xing et al., 2010) and, more recently, within Africa (Tishkoff et al., 2009; Bryc et al., 2010), East Asia (Yamaguchi-Kabata et al., 2008; Tian et al., 2008a; Xu et al., 2009; Chen et al., 2009), Europe (Lao et al., 2008; Novembre et al., 2008; Heath et al., 2008; Gayán et al., 2010; Tian et al., 2008b), Finland (Jakkula et al., 2008), Iceland (Price et al., 2009), and India (Reich et al., 2009), all observe that, to varying degrees, two-dimensional summaries of population-genetic differentiation largely recapitulate relative geographic locations. Further, the studies in Europe find that the first two principal components largely reflect latitudinal and longitudinal gradients in genetic differentiation (Lao et al., 2008; Novembre et al., 2008; Heath et al., 2008), which may imply a singular role for these axes in the demographic history of Europeans (Menozzi et al., 1978; Novembre et al., 2008).

Here we perform a comparative analysis of the spatial distribution of genetic variation in Eurasia and the Americas. These continental regions differ in geographic orientation: the major axis of orientation lies east-west in Eurasia, and north-south in the Americas. This difference is significant, as it has been hypothesized that the east-west orientation of the Eurasian landmass facilitated a rapid spread of agriculture and other technological innovations, while the north-south orientation of the Americas led to a slower diffusion of technology (Crosby, 1986; Diamond, 1997). We are interested in the effect of continental axis of orientation on the spatial distribution of human genetic variation in these regions, and in whether continental axes of orientation have influenced the spread of human populations and, consequently, their cultural traits.

Diamond (1997) suggested that continental axes of orientation expedited technological diffusion in Eurasia and delayed it in the Americas because populations with the same latitude experience similar photoperiods and climates; this similarity could have made adaptation to new locations comparatively easier for domesticated animals and plants — and consequently for humans — when migrating along lines of latitude rather than along lines of longitude (Crosby, 1986; Diamond, 1997). If Diamond’s hypothesis that the ease of technological diffusion was greater along latitudinal lines than along longitudinal lines is correct, and if the diffusion of technology was accompanied by human migrations, then ancient human migration along longitudinal lines in the Americas would have occurred at a slower rate than migration along latitudinal lines in Eurasia. It would then follow that a comparative study of genetic variation will reveal a signature of greater genetic differentiation between populations along lines of longitude in the Americas than that in Eurasia along lines of latitude.

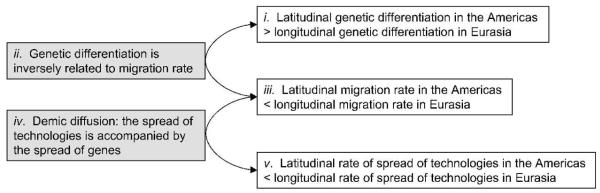
Figure 1 illustrates how spatial patterns of human genetic variation can be connected to the diffusion of technologies. If extant indigenous human populations are descended largely from ancestral populations in their same locations, and if the ancient movement of technologies and crops occurred via the movement of human individuals and their genes, then we can use genetic data to test whether continental axes of orientation have influenced technological diffusion.

Fig. 1.

The connection between spatial patterns of genetic variation and the spread of technologies. The figure illustrates that conditional on (ii) and (iv), a test of (i) provides a test of (v). This line of reasoning suggests a genetic approach to testing the argument that continental axes of orientation explain relative differences in the spread of technologies in Eurasia and the Americas.

The utility of genetic data for this test relies on an assumption that technologies traveled largely by demic diffusion (Fig. 1), in which technologies are spread by migration of peoples and their genes, rather than by cultural diffusion, in which technologies are adopted by imitation of neighboring cultures in the absence of genetic exchange. For the most extensively studied case, the Neolithic transition in Europe, it has been argued that observed archaeological and genetic data are compatible with a pattern of demic diffusion (Childe, 1925; Clark, 1965; Ammerman and Cavalli-Sforza, 1971; Renfrew, 1973; Ammerman and Cavalli-Sforza, 1984; Dupanloup et al., 2004; Pinhasi et al., 2005). Even for this well-studied example, however, the debate about the relative importance of demic diffusion and cultural diffusion remains unresolved (Fix, 1996; Richards et al., 2000; Barbujani and Bertorelle, 2001; Haak et al., 2005; Barbujani and Chikhi, 2006). Rather than evaluating the evidence for demic diffusion as a general phenomenon, our interest is in testing whether continental axes of orientation affected the rates of gene flow among human populations — and by extension, the spread of technologies — conditional on the assumption that ancient technology spread largely by demic diffusion (Fig. 1). We use a genetic variation dataset from the Americas and Eurasia consisting of 678 autosomal microsatellites in 68 populations (Ramachandran et al. 2005; Rosenberg et al. 2005; Wang et al. 2007), and we consider a variety of analyses of the relationship between genetic variation and geography.

MATERIALS AND METHODS

Data

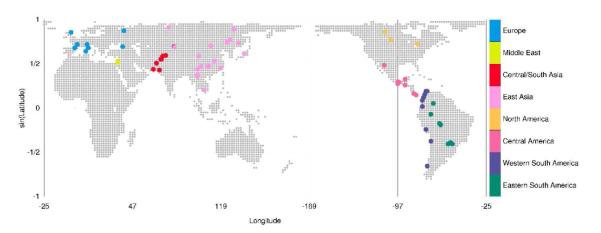
The 39 populations described here as “Eurasian” are those in the Human Genome Diversity Panel (HGDP) (Cann et al., 2002) from Europe, Central/South Asia, the Middle East (excluding the Mozabites in North Africa), and East Asia, as well as the Tundra Nentsi (Wang et al., 2007). Combining these populations with 29 Native American populations (Wang et al., 2007), our analysis examined genotype data from 404 Native American individuals and 740 Eurasian individuals, a subset that excluded first- and second-degree relationships (Rosenberg, 2006) from the combined Native American and HGDP data studied by Wang et al. (2007) (Fig. 2).

Fig. 2.

Populations included in this analysis. The world map shows locations of the 39 Eurasian and 29 American populations used in this study, color-coded by geographic region (these colors are used in subsequent figures). Population coordinates were the same as those used by Rosenberg et al. (2005) and Wang et al. (2007).

Geographic distance calculations

Let population 1 have latitude θ₁ and longitude ϕ₁, measured in degrees. We write the coordinates of population 1 as (θ₁, ϕ₁). Let population 2 have coordinates (θ₂, ϕ₂). We calculated three types of geographic distance between each pair of populations (measured in kilometers). First, pairwise great circle distances were calculated as in equation (2) of Rosenberg et al. (2005). Second, latitudinal distance was calculated as the great circle distance between (θ₁, ϕ₁) and (θ₂, ϕ₁) (see the red dashed line in Fig. S1). This distance reduces to ∣θ₁ – θ₂∣Rπ/180, where R is the radius of the earth measured in kilometers (R = 6371 km). Latitudinal distance does not depend on the longitudinal coordinate used in the calculation. Third, longitudinal distance (which varies with latitude) was calculated as the geographic distance between([θ₁+θ₂]/2,ϕ₁) and ([θ₁+θ₂]/2,ϕ₂) along a line of latitude, as shown by the green dashed line in Figure S1. This distance equals

$$\mid {\varphi }_1-{\varphi }_2\mid (R\pi ∕180)\cos \left(\right[{\theta }_1+{\theta }_2]∕2\times \pi ∕180).$$ (1)

We denote latitudes in the southern hemisphere and longitudes in the western hemisphere by negative values. For each population pair, we computed (i) longitudinal distance between coordinates as described in equation 1 and (ii) longitudinal distance between (θ₁, ϕ₁ mod 360) and (θ₂, ϕ₂ mod 360). The smaller of these two distances was taken as the longitudinal distance between the pair.

Population coordinates were the same as those used by Rosenberg et al. (2005) and Wang et al. (2007). We also considered waypoints used in past analyses (Ramachandran et al., 2005; Rosenberg et al., 2005; Wang et al., 2007), performing separate analyses including and excluding the waypoints. When using a waypoint, latitudinal distance, for example, was computed as the sum of the latitudinal distances to the waypoint of the two populations under comparison. In the Americas, a waypoint at Panama City (8.9678° N; 79.5338° W) was used between North and South American populations as in Wang et al. (2007). In Eurasia, a waypoint near Istanbul (41° N; 28° E) was used between European populations (except the Adygei) and populations in the Middle East. Use of the waypoints alters most pairwise geographic distances only slightly; separately in Eurasia and in the Americas the correlation coefficient between any of the three geographic distances without waypoints and its counterpart with waypoints exceeds 0.999. Among all geographic distances, American latitudinal distances and great circle distances were the most strongly affected by the inclusion of waypoints.

Genetic distance calculations

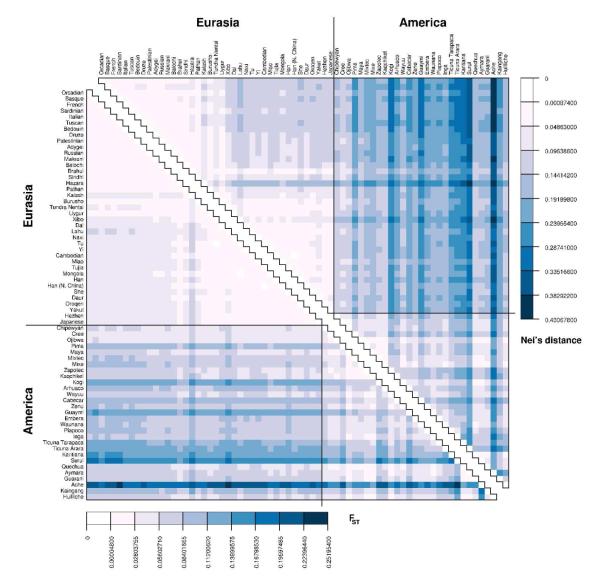
The computer program Genetic Data Analysis (GDA) (Lewis and Zaykin 2001) was used to compute pairwise genetic distances, as measured by F_ST (using equation 5.12 from Weir (1996) for coancestry distance) and Nei’s standard genetic distance (given on page 345 by Nei (1978)), for all pairs of populations in our dataset (Fig. 3).

Fig. 3.

Heat map of pairwise genetic distances between all 68 populations based on 678 microsatellite loci. The lower triangle depicts F_ST (Reynolds et al., 1983); the upper triangle represents Nei’s standard genetic distance (Nei, 1978). Populations are ordered according to longitude in Eurasia (from west to east) and according to latitude in America (from north to south). Colors were chosen to represent equal-sized intervals of genetic distance, based on the range of non-negative genetic distances observed using each estimator; numerical scales for the colors in each triangular matrix are given below the F_ST matrix, and to the right of the Nei’s distance matrix. Diagonal elements in each matrix are zero and are indicated by white squares. The two triangles can be fit together by superposing their diagonals. Genetic distances estimated to be negative are set to zero, and they are also depicted as white squares.

Regression analysis

Choice of regression model

Considering all pairs of populations within a continent, we separately regressed F_ST and Nei’s standard genetic distance on geographic distance. Each genetic distance was regressed onto the sum of: (i) geographic distance (great circle, latitudinal, or longitudinal; each with or without waypoints) and (ii) a term related to heterozygosities for a pair of populations. Term (ii) in our regression analysis had four possible values. It could be nonexistent, resulting in a univariate linear regression of genetic distance on geographic distance. The other possible values were max(het₁; het₂) (which we term “maximum heterozygosity”), min(het₁; het₂) (“minimum heterozygosity”), and (het₁+ het₂)/2 (“mean heterozygosity”); here, “het_i” denotes the unbiased estimator of expected heterozygosity under Hardy-Weinberg equilibrium based on microsatellite allele frequencies for population i, where i is 1 or 2, averaged across loci.

Therefore, for each continent, each of two genetic distances was regressed onto a sum of (i) one of six possible geographic distances and (ii) one of four terms related to heterozygosity. This resulted in 48 different models to explain patterns of genetic distance within Eurasia and within the Americas (Tables S1-S4). When a heterozygosity term was included in the model, we examined the partial Mantel correlation (Mantel, 1967; Smouse et al., 1986) between genetic and geographic distance, controlling for heterozygosity (as represented by term (ii) above). We also obtained the regression coefficient of geographic distance in the multiple regression. We included the heterozygosity term to control for the portion of genetic distance influenced by genetic diversity. This computation was especially relevant here because genetic diversity in Native American populations is reduced, and has greater variance across populations, in comparison with genetic diversity in Eurasian populations (Wang et al., 2007).

Let Y be a vector of observed pairwise genetic distances. We describe Y as a function of geographic distances and heterozygosities by estimating model parameters $\widehat{\theta }$ (regression coefficients, regression constant, and residuals) using linear regression. Akaike’s Information Criterion (AIC) of a regression model is $-2\log \left(L\right(\widehat{\theta }\mid Y\left)\right)+2K$, where $L(\widehat{\theta }\mid Y)$ is the likelihood of the estimated parameters given the data Y and K is the number of estimable parameters in the model (Burnham and Anderson, 1998). Here, K is the number of regression coefficients plus two, to account for the constant and the residual sum of squares. In our models, where n pairs of observed genetic distances in vector Y were regressed onto geographic distance and a heterozygosity term to produce fitted values $\widehat{Y}$, the likelihood function is the product over i of the densities of the observed data points Y_i, which are normally distributed with mean ${\widehat{Y}}_i$ and variance ${\widehat{\sigma }}^2$ (Neter et al., 1996). Therefore, the logarithm of the likelihood function is $\log \left(L\right(\widehat{\theta }\mid Y\left)\right)={\Sigma }_{i=1}^n\left[-{(Y_i-{\widehat{Y}}_i)}^2∕\left(2{\widehat{\sigma }}^2\right)+\log \left(1∕\sqrt[]{2\pi {\widehat{\sigma }}^2}\right)\right]$.

This log-likelihood reduces to

$$\log \left(L\right(\widehat{\theta }\mid Y\left)\right)=n\left[-\frac{1}{2}+\log \left(\frac{1}{\sqrt[]{2\pi {\widehat{\sigma }}^2}}\right)\right],$$

where ${\widehat{\sigma }}^2$ is the maximum-likelihood estimator of the error term in the regression model, equaling the mean of the residual sum of squares, or ${\widehat{\sigma }}^2={\Sigma }_{i=1}^n{(Y_i-{\widehat{Y}}_i)}^2∕n=\mathit{RSS}∕n$

Because values of Akaike’s Information Criterion (AIC) all lie on a relative scale, values were rescaled by subtracting the minimum AIC observed across all 48 models examined for a geographic region (Tables 1, S1-S4). Models with a rescaled AIC ≤ 2 are considered to have equivalent support (Burnham and Anderson, 1998).

Table 1. Regression of genetic distance on geographic distance in Eurasia and the Americas.

The partial Mantel correlation coefficient (Smouse et al., 1986) is given for genetic and geographic distance, controlling for the heterozygosity term. The null hypothesis tested is whether the partial correlation is equal to zero; the test is two-tailed and based on 10⁴ permutations. The regression coefficient is the coefficient of geographic distance in the multiple regression of genetic distance on the sum of geographic distance and the heterozygosity term. 95% confidence intervals are given for regression coefficients. Here we display the models with lowest-rescaled AIC for both latitudinal and longitudinal distance in each continent; the best model overall within each continent has a rescaled AIC of 0. Results from all 48 models considered appear in Tables S1-S4.

Continent	Genetic distance	Geographic distance	Heterozygosity term	Partial Mantel r(p-value)	Regression coefficient x 10−6 (p-value)	95% C.I., regression coeff. x 10−6	R2	rescaled AIC
Eurasia	FST	Latitude, waypoints	Minimum	0.0599 (0.3268)	0.7431 (0.1033)	[−0.1514, 1.6376]	0.2286	609.97
Eurasia	FST	Longitude, waypoints	Minimum	0.7500 (0.0001)	3.7569 (<10−133)	[3.5175, 3.9963]	0.6613	0
America	FST	Latitude, waypoints	Mean	0.6337 (0.0001)	4.8605 (<10−46)	[4.2795, 5.4416]	0.9128	0
America	FST	Longitude, waypoints	Mean	0.3128 (0.0081)	3.8571 (<10−9)	[2.7102, 5.0041]	0.8686	166.67

Robustness of model selection to the exclusion of populations

Due to the relative dearth in our dataset of samples drawn from North America, to assess whether regression model selection was robust to the distribution of populations or altered by excluding populations from analysis, we jackknifed over populations (and sets of two and three populations) in each continent to produce a series of sensitivity analyses (Tables 2, S5, and S6). After each population or set of populations was excluded from the sample, we refit all 48 possible models (6 geographic distances × 4 ways of controlling for heterozygosity × 2 genetic distances). We then compiled the partial Mantel correlations and regression coefficients and 95% confidence intervals from those models with the lowest AIC for each excluded population or set of populations. To generate Table 2, when excluding i populations from the Native American sample and j populations from the Eurasian sample, we examined $\left(\underset{i}{\overset{29}{}}\right)$ models with the lowest AIC in America and $\left(\underset{i}{\overset{39}{}}\right)$ models with lowest AIC in Eurasia. We compared the 95% confidence intervals for the slope of the geographic distance term in the $\left(\underset{i}{\overset{29}{}}\right)$ models for America with the $\left(\underset{i}{\overset{39}{}}\right)$ 95% confidence intervals for the slope of the geographic distance term in the models with the lowest AIC for Eurasia. For each i and j considered, the possible number of comparisons was therefore $\left(\underset{i}{\overset{29}{}}\right)\mathrm{x}\left(\underset{j}{\overset{39}{}}\right)$; the number and proportion among the comparisons for which the 95% confidence interval was greater in the Americas than in Eurasia are given in Table 2, columns 6-8.

Table 2.

Robustness of the observation that 95% confidence intervals for the slope of the latitudinal distance regression term in the Americas are strictly greater than 95% confidence intervals for the slope of the longitudinal distance regression term in Eurasia.

Number of populations excluded		Lowest-AIC model same as in Table 1:			Using whichever models had lowest AIC in each continent
America	Eurasia	Number greater American intervals	Number of comparisons	Proportion of greater American intervals	Number of greater American intervals	Number of comparisons	Proportion of greater American intervals
0	0	1	1	1	1	1	1
0	1	37	37	1	37	39	0.9487
1	0	27	29	0.9310	27	29	0.9310
0	2	671	673	0.9970	671	741	0.9055
1	1	992	1073	0.9245	993	1131	0.8780
2	0	339	406	0.8350	339	406	0.8350
0	3	7759	7881	0.9845	7759	9139	0.8490
1	2	17700	19517	0.9069	17744	21489	0.8257
2	1	12264	15022	0.8164	12295	15834	0.7765
3	0	2656	3653	0.7271	2656	3654	0.7269
1	3	202289	228549	0.8851	203064	265031	0.7662
2	2	218407	273238	0.7993	219366	300846	0.7292
3	1	97123	135161	0.7186	97489	142506	0.6841
2	3	2508097	3199686	0.7836	2527039	3710434	0.6811
3	2	1742920	2458469	0.7089	1754938	2707614	0.6481
3	3	20123630	28789293	0.6990	20355336	33393906	0.6096

Exclusions of zero, one, two, or three populations from one or both continental samples are considered. There are 29 Native American populations and 39 Eurasian populations in the sample. Rows are grouped by the sum across both continents of the number of populations excluded. When excluding populations, the model with the lowest AIC for a continent was sometimes different from the best model overall in the continent, as reported in Table 1. Columns 3-5 reflect comparisons between intervals when the lowest-AIC model in the Americas regressed genetic distance on latitudinal distance (with or without the incorporation of waypoints) and the lowest-AIC model in Eurasia regressed genetic distance on longitudinal distance (with or without the incorporation of waypoints); note that these models were the lowest-AIC models in each continent using the full dataset (see Table 1). Columns 6-8 reflect comparisons between confidence intervals for the coefficient of the geographic distance term in lowest-AIC models — regardless of which models these were — after the exclusion of populations. Entries in column 5 are the ratios of entries in column 3 to entries in column 4; entries in column 8 are the ratios of entries in column 6 to entries in column 7.

When using all Eurasian populations in the regression analysis, genetic distance was best explained by longitudinal distance incorporating waypoints, controlling for minimum heterozygosity (Table 1). Based on rescaled AIC, the same model without waypoints was equivalent to this best model (Table S1). To compare slope intervals between models comparable to the best model for each continent in Table 1, we repeated the $\left(\underset{i}{\overset{29}{}}\right)\mathrm{x}\left(\underset{j}{\overset{39}{}}\right)$ comparisons described in the paragraph above, only considering pairs of reduced data sets for which (i) exclusion of populations in the Americas produced the strongest support for models of genetic distance regressed onto latitudinal distance — with or without incorporating waypoints — controlling for mean heterozygosity, and (ii) exclusion of populations in Eurasia produced the strongest support for models of genetic distance regressed onto longitudinal distance — with or without incorporating waypoints — controlling for minimum heterozygosity. The number of these comparisons and the number and proportion of 95% confidence intervals that were greater in the Americas than those in Eurasia are given in Table 2, columns 3-5.

The inclusion of admixture as a covariate

Because admixture between Europeans and Native Americans occurred during European colonization, we conducted pairwise likelihood-ratio model comparisons (Agresti, 2002) between (i) each of the 48 models discussed above and (ii) four corresponding models that included a term related European admixture estimates (calculated by Wang et al. (2007)). The four models of type (ii) were: the absolute difference in admixture estimates, the minimum of the admixture estimates for each pair of populations in the Americas, the maximum of the admixture estimates for each pair of populations in the Americas, or the average between the two European admixture estimates for each pair of populations in the Americas. Each model of type (i) is nested in the corresponding models of type (ii).

Under the null hypothesis that the model with more parameters holds, the difference in the deviance (Agresti, 2002) of the nested model and the deviance of the models with the admixture term is approximately chi-square distributed, with degrees of freedom equal to the difference between the numbers of parameters in the two models (in our case, df=1). For each of the twelve models (among 48) with lowest rescaled AIC for latitudinal and longitudinal distances in the Americas, we did not find evidence (at the 5% significance level) that the inclusion of any term representing European admixture improves the regression model compared to the model with fewer parameters.

Genetic variation as a function of latitude and longitude using alternative poles

Consider a pole at (latitude, longitude) coordinates (θ₀,ϕ₀), and let ψ₀ be an arbitrary angle (all coordinates here are in degrees). Consider a point (θ,ϕ) whose coordinates are given relative to the north pole (90°, 0°). We are interested in (θ’,ϕ’), the coordinates of (θ,ϕ) relative to the pole (θ₀,ϕ₀). The rotation matrix that rotates rectangular coordinates (x, y, z) about (θ₀,ϕ₀,ψ₀) is (see page 37 of Fisher, Lewis, and Embleton (1987)): A(θ₀,ϕ₀,ψ₀)=

$$\left[\begin{array}{ccc}\hfill \sin {\theta }_0\cos {\varphi }_0\cos {\psi }_0-\sin {\varphi }_0\sin {\psi }_0\hfill & \hfill \sin {\theta }_0\sin {\varphi }_0\cos {\psi }_0+\cos {\varphi }_0\sin {\psi }_0\hfill & \hfill -\cos {\theta }_0\cos {\psi }_0\hfill \\ \hfill -\sin {\varphi }_0\cos {\psi }_0-\sin {\theta }_0\cos {\varphi }_0\sin {\psi }_0\hfill & \hfill \cos {\varphi }_0\cos {\psi }_0-\sin {\theta }_0\sin {\varphi }_0\sin {\psi }_0\hfill & \hfill \cos {\theta }_0\sin {\psi }_0\hfill \\ \hfill \cos {\theta }_0\cos {\varphi }_0\hfill & \hfill \cos {\theta }_0\sin {\varphi }_0\hfill & \hfill \sin {\theta }_0\hfill \end{array}\right].$$ (2)

Therefore, given (θ,ϕ), coordinates (θ’,ϕ’)are found using

$$\left(\begin{array}{c}\hfill \cos {\theta }^{\prime }\cos {\varphi }^{\prime }\hfill \\ \hfill \cos {\theta }^{\prime }\sin {\varphi }^{\prime }\hfill \\ \hfill \sin {\theta }^{\prime }\hfill \end{array}\right)=\mathrm{A}({\theta }_0,{\varphi }_0,{\psi }_0)\left(\begin{array}{c}\hfill \cos \theta \cos \varphi \hfill \\ \hfill \cos \theta \sin \varphi \hfill \\ \hfill \sin \theta \hfill \end{array}\right)$$

Matrix 2 differs slightly from that given by Fisher, Lewis, and Embleton (1987), because here θ denotes latitude, which represents degrees from the equator in geographical coordinates, as opposed to colatitude, the polar angle from the north pole. When latitude equals θ, colatitude is 90° – θ.

We rotated continental population locations about each of 1246 possible poles in the Americas and about 1641 possible poles in Eurasia. These poles were drawn from a grid on the surface of the earth in an equal-area projection as in Ramachandran et al. (2005), ignoring Southeast Asian points on or south of the equator. After rotation, we calculated latitudinal and longitudinal distance between all population pairs using the rotated coordinates, separately with and without waypoints. Waypoints at Panama City (8.9678° N; 79.5338° W) and Istanbul (41° N; 28° E) were also rotated about the pole when included in path calculations.

As before, we performed 48 regressions within each region at each pole (1246 poles in the Americas, and 1641 poles in Eurasia). We determined which models resulted in the highest proportion of partial Mantel correlations significant at the 5% level between genetic distance and rotated latitudinal or longitudinal distance across poles in a continent, and which pole within each continent produced the highest partial Mantel correlation for a particular model (Figs. 4 and 5). Some regression models resulted in few poles within a continent with partial Mantel correlations between genetic and rotated latitudinal or longitudinal distances significant at the 5% level. These corresponded to the models that were found to be poor fits in the earlier regressions done in this study (i.e., regression models with non-significant two-tailed Mantel tests between genetic and unrotated geographic distance in Tables S1-S4). For example, when heterozygosity was not controlled in the Americas, no pole produced a significant Mantel correlation between genetic distance and either rotated latitudinal or rotated longitudinal distance. Many of the models that resulted in very few poles with significant partial Mantel tests within a continent also failed to produced a Mantel correlation significant at the 5% level between genetic distance and unrotated geographic distance terms (Tables S3 and S4).

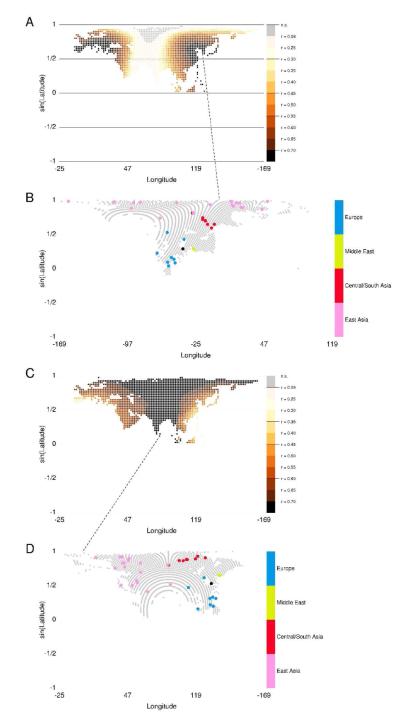
Fig. 4.

Relationship of genetic distance and latitudinal and longitudinal distances based on rotated coordinates in Eurasia. A: Partial Mantel correlations between F_ST and rotated latitudinal distance computed with waypoints, controlling for minimum heterozygosity, at 1641 poles in Eurasia. The color of a point corresponds to the partial Mantel correlation r when population locations in Eurasia are rotated about that point. The range of r values significantly different from zero at the 5% level is [0.0974, 0.7655]; 93.7% of poles produced partial Mantel test results that were significant at the 5% level (among 104 permutations). The model shown had the highest proportion of significant partial Mantel tests of the regressions on latitudinal distance after rotating about poles in Eurasia. B: Rotation of Eurasian population locations about the pole (35.0996° N; 126.2° E), plotted here with ψ₀ = −90°. The pole is indicated by an open circle in A from which a dashed line is drawn to B at (90° N; 0° E). The partial correlation between F_ST and latitudinal distance (controlling for minimum heterozygosity) was calculated using latitudinal distance between population locations after applying the rotation. C: Partial Mantel correlations between F_ST and rotated longitudinal distance with waypoints, controlling for mean heterozygosity, across poles in Eurasia. The range of r values significantly different from zero at the 5% level is [0.2695, 0.8072], and all poles produced significant partial Mantel tests (among 104 permutations). Note that this means no points are colored grey, nor do any points have the lightest pink color, which indicates 0.09 ≤ r < 0.25. D: Rotation of Eurasian population locations about the pole (7.18076° N; 81.2° E), plotted here with ψ₀ = 90°. The pole is indicated by an open circle in C, from which a dashed line is drawn to D at (90° N; 0° E). The waypoint at Istanbul is shown in black in both B and D.

Fig. 5.

Relationship of genetic distance and latitudinal and longitudinal distance based on rotated coordinates in the Americas. A: Partial Mantel correlations between F_ST and rotated latitudinal distance with waypoints, controlling for mean heterozygosity, at 1246 poles in the Americas. The color of a point corresponds to the partial Mantel correlation r when population locations in Eurasia are rotated about that point. The range of r values significantly different from zero at the 5% level is [0.2191, 0.7094]; 91.7% of poles produced significant partial Mantel test results (among 104 permutations). The model shown had the highest proportion of significant partial Mantel tests of the regressions on latitudinal distance after rotating about poles in the Americas. B: Rotation of American population locations about the pole (5.73917° S; 80.8° W), plotted here with ψ₀ = 90°. The pole is indicated by an open circle in A from which a dashed line is drawn to B at (90° N; 0° E). The partial correlation between F_ST and latitudinal distance (controlling for mean heterozygosity) was calculated using latitudinal distance between population locations after applying the rotation. C: Partial Mantel correlations between F_ST and rotated longitudinal distance with waypoints, controlling for mean heterozygosity, across poles in the Americas. The range of r values significantly different from zero at the 5% level is [0.2243, 0.7468], and 79.7% of poles produced significant partial Mantel test results (among 104 permutations). D: Rotation of American population locations about the pole (30° N; 107.8° W), plotted here with ψ₀ = −90°. The pole is indicated by an open circle in C from which a dashed line is drawn to D at (90° N; 0° E). Due to this pole’s location near the Pima population, an angle ψ₀ that placed all populations in the same hemisphere (i.e., with maximal rotated longitudinal distance between a population pair less than 180°) could not be found.

The angle ψ₀ is a rotation about the pole (θ₀,ϕ₀). For plotting rotations in Figures 4B, 4D, 5B, and 5D, we set ψ₀ to values that made the display of the rotated population locations sensible; the value of ψ₀ does not affect geographic distance calculations.

GESTE analysis

We applied a hierarchical Bayesian method that presents an alternative to Mantel tests by estimating separate F_ST values for each local population and relating these estimates to external factors — in this case, latitudes and longitudes — using a generalized linear model. This method is implemented in geste (Foll and Gaggiotti, 2006). The calculation of population-specific F_ST values (Balding and Nichols, 1995; Foll and Gaggiotti, 2006) is intended to account for variability across populations in effective size and geographic isolation that leads to variability in genetic drift processes. geste reports frequencies with which different linear models of the relationship between population-specific F_ST values and external factors were visited by the method over the course of many steps of an iterative estimation procedure. With two external factors, latitude and longitude, five models are possible: (i) constant, (ii) constant plus latitude, (iii) constant plus longitude, (iv) constant plus latitude plus longitude, or (v) constant plus latitude plus longitude plus an interaction term between latitude and longitude. geste also estimates the residual sum of squares (denoted by σ²) and the coefficients of each term in the model when the estimated population-specific F_ST values are regressed onto them. The iterations involving the model most-often visited by the method are used to estimate values and credibility intervals for the regression coefficients, as in Table S7.

Using latitude and longitude measured in degrees for population coordinates, we ran geste for a burn-in of 10,000 iterations followed by 10 pilot runs (each pilot run consisted of 1000 iterations, and served to tune the proposal distributions used in the method, as described in Appendix A of Foll and Gaggiotti (2006)). Pilot runs were followed by 10,000 iterations, with a thinning interval of 10 between iterations. We specified two external factors (population latitudes and longitudes) and that a model with an interaction term between these factors be an option. We also excluded populations from the analysis individually and re-ran geste with these same parameters; results for the 68 leave-one-out analyses appear in Tables S8 and S9.

The deviation from the regression (σ² in Table S7) is higher than that reported by Foll and Gaggiotti (2006) for 377 microsatellite loci in the HGDP populations; one difference between their application of geste and ours is that we left missing data out of the input files, while they coded missing data as another allele in their input. Our exclusion of missing data makes estimates of σ² and credibility intervals for parameters increase.

RESULTS

Genetic distance between pairs of populations

We first examined levels of genetic distance for all pairs of populations. Figure 3 is a visualization of F_ST and Nei’s standard genetic distance (Nei, 1978; Reynolds et al., 1983) matrices between Eurasian and American populations, arranging populations from west to east in Eurasia and from north to south in the Americas. That genetic differentiation is generally greater in the Americas than in Eurasia is visible in Figure 3 from the mostly darker shades for population comparisons within the Americas than for those within Eurasia. In Eurasia, the highest observed genetic distances are between populations in East Asia and populations elsewhere in the landmass; genetic distances between populations on the same side of the Himalayas are quite low, and genetic distances within East Asia and within the rest of the landmass are generally comparable to each other (Fig. 3). In America, the largest genetic distances are comparisons involving the Ache or Surui populations. The 25th percentile of F_ST values between populations in the Americas is 0.0404, exceeding the 75th percentile of F_ST values in Eurasia (0.0385). Similarly, the median of the distribution of Nei’s distance in America (0.1217) is greater than the 75th percentile among Nei’s distances between pairs of Eurasian populations (0.1080) (see Fig. S2).

Based on two-sided Wilcoxon tests, we reject the hypotheses for both F_ST and Nei’s distance that (i) Native American population pairs have the same distribution of genetic distances as Eurasian population pairs, that (ii) the distribution of genetic distances between population pairs within Eurasia is the same as the distribution of genetic distances between population pairs from different continents, and that (iii) the distribution of genetic distances between population pairs within the Americas is the same as the distribution of genetic distances between population pairs from different continents (p < 10⁻¹⁵ for each of these tests).

Regressing genetic distance on latitudinal and longitudinal distance

As the populations in Figure 3 are arranged geographically, the figure suggests that the increase in genetic distances along lines of longitude in the Americas occurs over shorter geographic distances compared to the increase in genetic distances in Eurasia along lines of latitude. To formally test the effects of latitude and longitude suggested by Figure 3, we performed regressions of genetic distance on latitudinal and longitudinal geographic distance.

Variation across comparisons in pairwise genetic distance measures such as F_ST can be affected by differences in the level of genetic variability across populations (Wright, 1978; Balding and Nichols, 1995; Long and Kittles, 2003; Hedrick, 2005; Foll and Gaggiotti, 2006). Among the populations in our analysis, the Ache and Surui have the lowest heterozygosity; this low level of diversity might explain the high genetic distances between these populations and all others.

To access the component of genetic distance not influenced by the level of genetic variation in the populations being compared, we performed multiple regressions and multivariate Mantel tests to choose models for which geographic distance best predicted genetic distances, when controlling for heterozygosity (see Materials and Methods). Separately for Eurasia and for the Americas, 48 models were fitted to explain the geographic distribution of genetic distance (see Materials and Methods and Tables S1-S4). These models consider two different genetic distances, six measures of geographic distance, and four ways of controlling for heterozygosity. The models with the lowest rescaled Akaike Information Criterion (AIC) for each continent are shown in Table 1.

In Eurasia, genetic distance is best explained by longitudinal distance (by which we mean east-west distance between longitudes; see Materials and Methods) incorporating a waypoint in Istanbul, controlling for heterozygosity by using the smaller of the heterozygosities for the two populations being compared. In the Americas, genetic distance is best explained by latitudinal distance including a waypoint in Panama City, controlling for heterozygosity with the mean of the heterozygosities of the two populations under consideration. When using F_ST as the genetic distance in either continent, these models were preferred to models involving great circle geographic distance, which incorporates both latitude and longitude. In both regions, models using Nei’s distance had higher rescaled AIC values, reflecting a poorer fit than models with F_ST (see Tables S1-S4). In each region, however, the rankings by AIC values of models that used Nei’s distance were quite similar to the rankings for corresponding models using F_ST. Kendall’s coefficient of rank correlation for AIC values of models using F_ST and corresponding models using Nei’s distance was 0.8824 in Eurasia and 0.9710 in the Americas.

If, as hypothesized in Figure 1, genetic differentiation is greater along longitudinal lines in the Americas than along latitudinal lines in Eurasia, then we expect such a pattern to be reflected in comparisons of the slopes of the geographic distance terms in the linear regressions of genetic distance on geographic distance. We find that the slope of the latitudinal distance term in the best model for the Americas is greater than the slope of the longitudinal distance term in the best model for Eurasia (Table 1); further, the 95% confidence intervals (in units of contribution to F_ST per kilometer of geographic distance) do not overlap. We interpret this result as meaning that a greater contribution is made to genetic differentiation by additional latitudinal distance between American populations than by additional longitudinal distance between Eurasian populations.

Latitudinal distance in Eurasia does not account for a statistically-significant amount of variation in genetic distance (Table 1). In contrast, longitudinal distance in the Americas still explains a large proportion of variation in genetic distance, although the partial Mantel correlation between genetic distance and longitudinal distance in the Americas, controlling for heterozygosity, is lower than the corresponding correlation involving latitudinal distance.

To assess the robustness of the outcomes of the regression analysis, separately for both continents, we excluded populations from the analysis individually and refit the 48 regression models relating genetic distance to geographic distance and heterozygosity. For each possible exclusion, the model with lowest AIC is reported in Tables S5 and S6. In the Americas, none of the 29 exclusions affected the choice of which among the 48 models had the strongest support according to AIC. For Eurasia, two of 39 exclusions (Cambodian and Kalash) led to the selection of pairwise great circle distance in place of longitudinal distance as the best predictor of genetic distance, and two other exclusions (Palestinian and Tundra Nentsi) led to a minor difference in that longitudinal distance not incorporating waypoints had the strongest support. Among the 37 exclusions that continued to support a choice of longitudinal distance in Eurasia, none resulted in overlapping 95% confidence intervals for the regression coefficient of the geographic distance term and the corresponding coefficient of latitudinal distance for the Americas in Table 1. When excluding Native American populations from the analysis, two of 29 exclusions (Ache and Chipewyan) produced 95% confidence intervals for the regression coefficient of latitudinal distance that overlapped with the corresponding interval for the longitudinal distance slope in Eurasia in Table 1. All other confidence intervals for the regression coefficient of latitudinal distance in the Americas when excluding one population exceeded the 95% confidence interval observed for the longitudinal distance slope in Eurasia in Table 1.

We repeated this analysis to calculate how often the 95% confidence interval for the slope of the geographic distance term in the Americas was strictly greater than the 95% confidence interval for the slope of the geographic distance term in Eurasia in the lowest-AIC models, when excluding sets of two and three populations within each continent (Table 2). After excluding populations from a continent and fitting the 48 regressions, if the model with strongest support when populations were excluded corresponded to the best model for the full data from that continent in Table 1 (see Materials and Methods), we were interested in whether the 95% confidence interval of the latitudinal regression slope for a model fitted after populations were excluded in the Americas was strictly greater than the 95% confidence interval of the longitudinal regression slope for a model fitted after populations were excluded in Eurasia (Table 2). For each configuration of exclusions, excluding 0 to 3 populations in Eurasia and 0 to 3 populations in the Americas, we determined whether the 95% confidence interval of the geographic distance term for the lowest-AIC model in the Americas exceeded the corresponding 95% confidence interval of the geographic distance term for the lowest-AIC model in Eurasia.

Table 2 shows that our observation of a 95% confidence interval for the latitudinal distance term in the best model in America greater than that for the longitudinal distance term in the best model in Eurasia in Table 1 is detected in 92.5% of cases when excluding one population from each continent, 79.9% of cases when excluding two populations from each continent, and 69.9% of cases when excluding three populations from each continent — if the exclusions supported the same models chosen for the full data in Table 1. These results suggest that the observation that latitudinal distance has an effect on Native American genetic distances strictly greater than the effect of longitudinal distance on Eurasian genetic distances is reasonably robust, though partly dependent on the sampling scheme.

Rotating the map to find clines in genetic differentiation

The analyses above have all used the standard map with the north pole at (90° N; 0° E) when computing geographic distances. We applied a new method, an alternative to an analysis proposed by Falsetti and Sokal (1993), the rotation of population locations about alternative poles, to determine whether an axis of orientation might exist that produces a stronger genetic cline with respect to latitude or longitude in Eurasia or the Americas than does the standard north-south or east-west axis (see Materials and Methods). Suppose a “north pole” is found about which latitudinal distances between rotated population coordinate pairs are more closely correlated with genetic distance than when using the standard map; the relative positioning of populations in that rotation suggests the primary axis along which genetic variation is oriented.

After rotating Native American sample locations about each of 1246 possible poles in the Americas and rotating Eurasian sample locations about each of 1641 possible poles in Eurasia (see Materials and Methods), we fit 32 models that regressed genetic distance onto geographic distance between rotated sample locations, controlling for heterozygosity. We considered two different genetic distances, four types of geographic distance, and four ways of controlling for heterozygosity; we did not use great circle distance (with or without waypoints) in this analysis, because rotation of sample locations does not alter that distance measure (assuming a spherical earth), and because our intent was to find “latitudinal” and “longitudinal” axes for which genetic differentiation is clinal.

Among 16 possible models regressing two genetic distances onto two measures of latitudinal distance (i.e., with and without waypoints) with four ways of controlling for heterozygosity, the model with the highest proportion of poles with significant partial Mantel correlations at the 5% level between genetic distance and latitudinal distance in Eurasia is plotted in Figure 4A. This model regresses F_ST onto latitudinal distance incorporating waypoints, controlling for minimum heterozygosity; this is the same model that has the lowest AIC among models involving unrotated latitudinal distance in Eurasia (see Table 1). For each of the 16 models regressing genetic distance onto longitudinal distance in Eurasia, partial Mantel correlations between genetic distance and longitudinal distance at each pole were significant at the 5% level. The highest correlation between genetic and geographic distance, among all models fitted to the data among all poles in Eurasia, occurred when regressing F_ST onto longitudinal distance incorporating waypoints, controlling for mean heterozygosity (Fig. 4C). Figures 4A and 4C each allow us to compare correlations at neighboring poles with the same model, and the rotations of population locations about the poles that produce the highest partial correlations for these models are shown in Figures 4B and 4D.

Recall that regressing genetic distance in Eurasia on unrotated latitudinal distance results in a non-significant Mantel correlation coefficient for the lowest-AIC latitudinal models (Tables S1 and S2). Figure 4A shows that rotated latitudinal distance becomes highly correlated with Eurasian genetic distances (r ≥ 0.7, Mantel p = 10⁻⁴) when populations are rotated about poles in eastern Asia or southwestern Europe (black points in Fig. 4A). The pole about which rotation is performed in Figure 4B, on the Korean peninsula, produces the highest partial correlation between F_ST and rotated latitudinal distance, controlling for minimum heterozygosity (r = 0.7655); the value of this partial correlation coefficient is similar to that of the partial correlation produced for the best longitudinal model in Eurasia with unrotated coordinates (Table 1). The interpretation is that the only way to achieve latitudinal predictors for Eurasian genetic distance is by turning the standard map on its side, effectively changing longitude to latitude.

Using the standard map of Eurasia, the partial Mantel correlation between genetic distance and longitudinal distance is r=0.7500 (Table 1); 17.12% of the poles in Figure 4C produce higher correlations between genetic distance and rotated longitudinal distance than when using unrotated coordinates. The pole that produces the highest partial correlation between genetic distance and rotated longitudinal distance (r=0.8072), controlling for mean heterozygosity, is located in Sri Lanka, and it essentially turns the Eurasian map upside down, preserving the east-west orientation of the continent (Fig. 4D).

In the Americas, the model with the highest proportion of poles with significant partial Mantel correlations between genetic distance and latitudinal distance is plotted in Figure 5A. This model regresses F_ST onto latitudinal distance incorporating waypoints, controlling for mean heterozygosity; this is the model with the lowest AIC among all 48 models in the Americas using the standard map (Table 1). The model resulting in the highest proportion of poles in the Americas with significant partial Mantel correlations between genetic distance and longitudinal distance regresses F_ST onto longitudinal distance with waypoints, controlling for mean heterozygosity (Fig. 5C). The rotations about the poles that produce the highest partial correlations between genetic distance and rotated latitudinal distance and between genetic distance and rotated longitudinal distance are shown in Figures 5B and 5D, respectively.

Using the standard map of the Americas, the correlation between genetic distance and unrotated latitudinal distance, controlling for mean heterozygosity, is r = 0.6337. In Figure 5A, 38 poles produce higher correlations between genetic distance and rotated latitudinal distance. These poles are all located in western South America and, as shown in Figure 5B, rotations about these poles place most South American populations onto a small range of latitudes. The rotation in Figure 5B reflects that population differentiation north-south in South America accounts for relatively little of the observed genetic distances; rather, east-west differentiation, especially between Andean populations such as the Huilliche and South American populations farther to the east (e.g., Karitiana, Surui, and Ache), is more marked.

The partial Mantel correlation between genetic distance and unrotated longitudinal distance in the Americas is r = 0.3128 (Table 1); 75.36% of poles in Figure 5C produce higher correlations between F_ST and rotated longitudinal distance, controlling for mean heterozygosity. The pole that produces the highest partial correlation between genetic distance and rotated longitudinal distance (r = 0.7468), controlling for heterozygosity, places eastern South American populations at a similar longitude, and Andean populations on longitudes further from all other South American populations (Fig. 5D).

In summary, our method of rotating the geographic map about alternative poles allows us to identify “latitudinal” or “longitudinal” axes that predict genetic differentiation between populations. In Eurasia, genetic differentiation is best predicted by “latitude” or “longitude” after rotation about poles that lie at edges of the region, and the analysis of polar rotations generally supports the view that genetic differentiation is predicted by longitudinal distance along the standard east-west axis. In contrast, in the Americas, genetic differentiation is best predicted by “latitude” and “longitude” after rotation about poles lying along an axis running from the northwest to the southeast. These polar locations support the view that genetic differentiation is predicted by distance along a northwest-southeast axis; the locations of these poles partly reflect the differentiation observed between the northernmost populations and populations farther south in the Americas, and the differentiation observed between Andean populations and populations of eastern South America — a pattern seen in other studies of South American variation (Tarazona-Santos et al., 2001; Lewis Jr. et al., 2007; Wang et al., 2007). Thus, as the primary geographic axis in the Americas is perhaps more accurately described as northwest-southeast rather than north-south, in both continents, the analysis of alternative poles finds that continental axis of orientation provides an explanation for patterns of genetic differentiation.

Evaluating the roles of latitude and longitude with an iterative model-based method

An additional method, geste (version 2.0) (Foll and Gaggiotti, 2006), provides an alternative to the multivariate Mantel test for assessing the relative importance of external factors (for example, geographical variables such as latitude and longitude) on the genetic structure of populations. When applied to these data, geste finds longitude to be important in explaining genetic variation between Eurasian populations, matching the result of our Mantel test (Table 1). However this analysis also finds genetic variation in the American sample difficult to relate to latitudinal and longitudinal distances. geste does not recover the strong signature of American latitudinal genetic variation seen with Mantel tests, instead finding that in both continents, genetic variation is best explained by longitude only (Table S7). The differences in results in comparison with the Mantel test could arise from complexities in the pattern of spatial variation in the Americas, or from differences in the way genetic variability is controlled in a regression that treats heterozygosity directly and in a model that incorporates levels of genetic variation when obtaining population-specific values of F_ST.

We jackknifed over populations separately in both regions and re-ran geste, finding that the importance of longitude in explaining Eurasian genetic variation was robust to the exclusion of particular populations, while in America the preferred model sometimes contained no effect for either latitude or longitude (Tables S8 and S9). We note, however, that although the best choice of model often disagreed between the linear regression and geste analyses, the geste results do not contradict the result based on regression analyses that the level of genetic differentiation per kilometer latitudinally in the Americas is greater than the level of genetic differentiation per kilometer longitudinally in Eurasia.

DISCUSSION

Recent advances in genotyping technology and statistical approaches for spatial analysis have led to increased interest in the geographic distribution of human genetic variation. Here we have conducted comparative analyses of geographic and genetic distance in Eurasia and the Americas, and we have developed new approaches for studying the spatial axes that underlie human population genetic variation. This work augments recent investigations of human spatial genetic variation on the basis of such techniques as bearing analysis, principal components analysis and other multivariate analysis techniques (Falsetti and Sokal, 1993; Barbujani and Belle, 2006; Novembre and Stephens, 2008; Lao et al., 2008; Price et al., 2009; Wang et al., 2010; François et al., 2010), spatial simulations (Barbujani, 1987; Edmonds et al., 2004; Liu et al., 2006; Ray and Excoffier, 2009), wave-of-advance differential equations (Novembre et al., 2005; Hallatschek and Nelson, 2008, 2010), and Bayesian model-based strategies (Foll and Gaggiotti, 2006; François et al., 2006; François and Durand, 2010).

We applied our spatial analysis to find a genetic approach for indirectly testing the argument that the east-west orientation of the Eurasian landmass facilitated a rapid spread of agriculture and other technological innovations, while the north-south orientation of the Americas led to a slower diffusion of technology (Crosby, 1986; Diamond, 1997). Diamond suggested that because of the horizontal orientation of the Eurasian continent, the spread of crops in Eurasia was rapid enough to preempt the need for multiple domestications (Diamond, 1997), while claiming that in the Americas, multiple domestications of some plants (e.g., chili peppers, lima beans) resulted from a slower spread of domesticated crops due to the vertical orientation of the landmass.

If an east-west continental orientation in Eurasia made migration easier for humans and their domesticated flora and fauna than did a north-south continental orientation in the Americas, then we expected genetic distances north-south along lines of longitude between Native American population pairs to be greater than genetic distances east-west along lines of latitude between Eurasian population pairs. We found that in general, genetic distances were greater between Native American populations than between Eurasian populations (Figs. 3 and S2). When controlling for the level of genetic variation across populations, genetic differentiation, as measured by F_ST, increased more rapidly with latitudinal distance in the Americas than with longitudinal distance in Eurasia (Tables 1 and 2).

A search for the axes along which genetic variation is oriented revealed that a north-south axis contributes relatively little to the spatial distribution of Eurasian genetic differentiation (Fig. 4). Note that a claim related to Diamond’s hypothesis is that technology will spread more easily east-west in a continent than north-south within the same continent. Under our assumptions (ii and iv in Fig. 1), separately in Eurasia and in the Americas, this claim predicts a genetic signature in which differentiation increases more rapidly along lines of longitude than along lines of latitude. We find support for this prediction in the Americas (Table 1), but we do not find that distance north-south is predictive of genetic differentiation in our Eurasian samples. Previous studies in Europe and East Asia have identified both latitudinal and longitudinal clines in genetic variation (Lao et al., 2008; Novembre et al., 2008; Heath et al., 2008; Tian et al., 2008), and it is possible that with a denser Eurasian sample, we would have detected a more important role for distance along lines of longitude in explaining Eurasian genetic distances.

In contrast, American genetic distances were explained both by latitudinal and longitudinal distances, with genetic differentiation being distributed along a northwest-southeast axis (Fig. 5). The primary axis of genetic differentiation we observed in the Americas is not simply north-south, however. Figures 5B and 5D also reflect genetic differentiation between eastern and western South American populations in the sample (Lewis Jr. et al., 2007; Wang et al., 2007). Although the major axis of the Americas is north-south, in South America the east-west axis may provide a better proxy for change in climatic regime — or geographic barriers that may restrict migration and cultural interaction — than the north-south axis. The geospatial pattern of genetic variation is more complex than envisioned under a simple model with linear effects for latitude and longitude, and testing mechanistic or more complex migration processes could potentially improve our ability to explain the observed pattern.

Genetic variation in the Americas was changed by European colonization, which may have interfered with the ancient population relationships that are of interest here. Previous analysis suggested that for the particular samples we are studying, a systematic relationship of European admixture with geography is not likely to be a serious concern (Wang et al., 2007). Even so, we additionally performed regression analyses of genetic distance on geographic distance in the Americas, accounting for European admixture; model selection did not support the inclusion of the European admixture term to explain Native American genetic distances (see Materials and Methods).

Another potential concern is that we implicitly assume that samples drawn from modern indigenous populations reflect genetic variation from ancestral populations in those same locations. While the validity of this assumption likely varies by population, it is unlikely that recent migrations in the Americas and Eurasia would have occurred systematically with respect to latitude or longitude in a way that could confound our interpretation.

Our approach implicitly assumes that populations have been separated for long enough that genetic distance between a pair of populations primarily reflects the level of gene flow between them, as opposed to the time of their initial divergence. It is possible, however, that our genetic distance data hold relatively little information about post-divergence gene flow between indigenous populations, and instead largely reflect the initial peopling of both continents and the subsequent divergence of the founding populations. Suppose that the typical pattern of range expansion for ancient populations involved considerable isolation of small groups during initial occupation of a habitat, followed by a steady increase in interconnectedness between such groups over time. In this view, because human habitation began much later in the Americas than in Eurasia, the observed patterns of Native American genetic differentiation could largely be remnants of an initial period of isolation of small groups throughout the Americas, rather than reflections of the factors — possibly including continental axis of orientation — that would have influenced migration once the region was fully inhabited. The genetic distances we observed, especially in the Americas, would result primarily from serial bottlenecks or other events early in the initial peopling process, and they would not reflect general influences of migration along continental axes. We would then be unable to evaluate whether migration levels after the initial peopling support or refute Diamond’s hypothesis, under an assumption of demic diffusion. However, some studies suggest based on archaeological sites that the Americas were occupied quickly (Fix, 2002; Miotti and Salemme, 2003), so that the initial phase of isolation may have been short compared to the subsequent phase in which regular influences on migration, such as those due to continental orientation, could have developed. In addition, controlling for heterozygosity, as we have done in our regressions, partly controls for the effects of serial bottlenecks, as a key signal of a serial bottleneck process is a decline in heterozygosity with increasing distance from the source of the expansion (Ramachandran et al. 2005).

We note that in contrast to our other methods, geste did not identify latitudinal distance as the main axis of orientation for genetic variation in the Americas. In Eurasia, our analysis found that the choice of a longitudinal model typically had strong support, whereas the geste analysis was less decisive in the Americas. However, the results from geste do not contradict our claim of greater genetic differentiation along longitudinal lines in the Americas than along latitudinal lines in Eurasia. It is possible that relatively sparse sampling in North America affected the relative signal of latitude and longitude detected by GESTE in the Americas, and that inclusion of additional samples from North America would enable a more complete version of the analysis.

Finally, perhaps the most important caveat in interpreting our results is our interpretation of patterns of genetic variation as supporting the claim that continental axes of orientation led to expedited technological diffusion in Eurasia and delayed technological diffusion in the Americas rests very directly on the assumption that technological diffusion was accompanied by genetic diffusion (Fig. 1). While this assumption may be sensible in various specific cases, its general validity over the large span of time and space required for forming a basis of our test is unknown — see, for example, differing viewpoints on the spread of Clovis technology (Waters and Stafford Jr., 2007; Hamilton and Buchanan, 2007). Its further investigation will be important for reconciling patterns of technological variation, spatial genetic variation, and archaeological data, and for understanding the processes that generated currently-observed patterns of human population-genetic structure.

CONCLUSIONS

Our results suggest a reduced speed for gene flow in the Americas since its initial peopling that, even after accounting for lower levels of genetic diversity in Native American populations, has led to more genetic differentiation in the Americas than that observed between Eurasian populations. Not only is the level of genetic differentiation greater between Native American populations, but it is greater per kilometer of latitudinal distance than genetic differentiation between Eurasian populations per kilometer of longitudinal distance. If a lack of gene flow between populations is an indication of little cultural interaction (i.e., assuming that technologies travel by demic diffusion), then a lower latitudinal rate of gene flow suggested for Native American populations may partly explain the relatively slower diffusion of crops and technologies through the Americas, when compared to the corresponding diffusion in Eurasia. Thus, our result that genetic differentiation increases more with latitudinal distance between Native American populations than with longitudinal distance between Eurasian populations supports the hypothesis of a primary influence for continental axes of orientation on the diffusion of technology in Eurasia and the Americas (Fig. 1).

Supplementary Material

supp. figs+tables+supp. tables

Fig. S1 Example of latitudinal and longitudinal coordinates used for geographic distance calculations. For two populations with coordinates (θ₁, ϕ₁) and (θ₂, ϕ₂) (shown by blue dots), the red dashed line indicates latitudinal distance between the populations. The green dashed line is the longitudinal distance, taken between the two populations’ respective longitudes along the mean of their latitudes.

Fig. S2 Boxplots of genetic distances within and between American and Eurasian populations. “Between” denotes genetic distances between a pair of populations in which one is located in the Americas and the other is located in Eurasia.