Abstract
The spatial organization of stem cells into a niche is a key factor for growth and continual tissue renewal during development, sustenance, and regeneration. Stratified epithelia serve as a great context to study the spatial aspects of the stem cell niche and cell lineages by organizing into layers of different cell types. Several types of stratified epithelia develop morphologies with advantageous, protruding structures where stem cells reside, such as rete pegs and palisades of Vogt. Here, multistage, spatial cell lineage models for epithelial stratification are used to study how the stem cell niche influences epithelial morphologies. When the stem cell niche forms along a rigid basal lamina, relatively regular morphologies are maintained. In contrast, stem cell niche formation along a free-moving basal lamina may prompt distorted epithelial morphologies with stem cells accumulating at the tips of fingerlike structures that form. The correspondence between our simulated morphologies and developmental stages of the human epidermis is also explored. Overall, our work provides an understanding of how stratified epithelia may attain distorted morphologies and sheds light on the importance of the spatial aspects of the stem cell niche.
Introduction
Organic tissues are inherently complex systems as critical processes occur at the biochemical, cellular, and tissue levels. Achieving and maintaining proper homeostatic conditions while carrying out necessary functions, then, follow as important tasks that must be finely tuned and regulated at each of these levels. Several tissues develop or maintain a regenerative capacity through a multistage cell lineage generally consisting of stem cells, transit amplifying (TA) cells, and terminally differentiated (TD) cells. For a multistage cell lineage to regulate the quantities of each cell type throughout the tissue in a precise fashion, morphogens, diffusive molecules secreted by cells, provide feedback upon cellular processes and, as a result, affect the tissue as a whole.
It is widely believed that a key mechanism for proper maintenance of a cell lineage to occur is the formation and sustenance of a stem cell niche (1,2), a microenvironment where stem cells reside in a tissue. Specifically, a combination of extracellular cues from the niche and underlying genetic systems has been identified to be crucial for normal stem cell proliferation and differentiation (3). Outside of the niche, such as in an in vitro setting, stem cells may have a multipotency to behave in a variety of ways and can assume one of many possible fates depending on their external environment (4,5). As a result, a great importance lies in understanding niche behavior in order to harness the potential for the use of stem cells in a nonnative environment in regenerative medical applications (1). Even so, a clear understanding of the niche’s importance has yet to be achieved (6), and only recently has stem cell niche formation been observed in vitro (7).
Stratified epithelia serve as a great model system to study the formation and sustenance of the stem cell niche. Often, epithelia stratify into cell layers with stem cells residing along the adjacent basal lamina, as seen by the epidermis (8), olfactory epithelium (OE) (9), and cerebral cortex (10). The stem cell niche allows the tissue to maintain a regenerative capacity and continually renew other cell layers (11). Beyond this apical-basal stratified organization, epithelia may also exhibit patterns in high spatial dimensions. The tissue may achieve fingerlike structures that protrude into the basal lamina, such as rete ridges (or rete pegs) found in the epidermis (12,13), hard palate (14), cervix (15), and gingiva (16) or palisades of Vogt found in the limbal corneal epithelium (17,18). Generally, stem cells accumulate in a niche along the bottom of these structures near the basal lamina to provide better protection of the basal layer, a greater surface area for stem cells to reside, and a more efficient wound response (18,19). Modeling also suggests that a smaller surface/volume ratio of the niche may correspond to a higher susceptibility to cancer (20).
How these undulating morphologies might develop then arises as an immediate question. Buckling instability has been speculated as a possible mechanism for crypt formation from the single-layered epithelia in the colon (21,22), while mechanical feedback might provide another (23). If proliferative stem cells constitute a single cell layer along the basal lamina of a stratified epithelium and the apical surface of the tissue is fixed, then buckling instability may also prompt undulations in several-layered stratified epithelium. Another possible explanation for these morphologies is derived from hydrodynamic instability that arises from assuming that the epithelia serves as an incompressible fluid that neighbors a viscoelastic stroma (24), though it does not consider the stem cell niche as the source of tissue renewal. Other studies use models to examine how the size of rete pegs are regulated by nitric oxide (25) or may be controlled during psoriasis through radiative treatment (26), but neither explores the mechanisms that drive rete peg formation.
Mathematical modeling and computational studies have begun to examine the role and necessity of feedback upon stem cells in cell lineages (27–29). However, due to their challenging nature, very little of this work accounts for the spatial aspects of the lineage and the role of the stem cell niche. Recent mathematical modeling uses the olfactory epithelium as a vehicle to investigate the spatial aspects of multistage cell lineages and the stem cell niche (30). Using a one-dimensional continuum model, the niche formation, tissue stratification, and homeostasis are achieved within the tissue by two mechanisms that incorporate morphogen gradients formed by assuming a permeable basal lamina.
In this paper, we explore the spatial effects of multistage cell lineages and the stem cell niche in stratified epithelium in two dimensions. We develop mathematical models that explicitly take into consideration the following:
-
1.
A cell lineage comprised of stem, TA, and TD cells;
-
2.
Diffusive signaling molecules produced by cells in the tissue;
-
3.
Regulation of cell proliferation and differentiation rates by these secreted molecules;
-
4.
Two-dimensional growth accounting for the interface between neighboring tissues; and
-
5.
Mechanical forces resulting from cell-to-cell adhesion and internal tissue pressure.
In particular, we study two different types of stem cell niches: one in which the stem cell niche forms at a fixed boundary, and one in which it forms at a free boundary. Our simulations show that when a stem cell niche forms along a fixed basal lamina, the epithelium maintains a regular morphology. On the other hand, when a stem cell niche forms along a free-moving basal lamina, surface tension forces induced by cell-to-cell adhesion may be overcome and fingering may occur in the tissue, giving rise to structures resembling rete pegs and palisades of Vogt. We contextualize each of the two types of niches in distinct stages during human epidermal development and explore relevance of impeding fingering to epithelial diseases. Finally, we provide possible explanations for the morphologies arising from our models to yield a novel, to our knowledge, way of understanding how intertissue signaling at the molecular level may affect the manner in which the stem cell niche organizes a tissue and its resulting morphology.
Material and Methods
The numerical methods used to compute the mathematical models presented here are described elsewhere (J. Ovadia and Q. Nie, unpublished). Computational details are provided in Section SII in the Supporting Material.
Results
A two-dimensional spatial model of a multistage cell lineage
Consider the two-dimensional domain (0,1) × (0,h) as a spatial representation of a multilayered epithelial tissue. Here, the dynamic boundary h = h(x,t) and the boundary y = 0 are interfaces between neighboring tissues or an open external environment while periodicity is assumed along the boundaries in the x direction. Let describe the tissue growth velocity.
Following the literature (27,28,30), the epithelial cell lineage will be comprised of three different cell types: stem, TA, and TD cells with respective densities expressed as C0, C1, and C2. The governing equations for the lineage accounting for growth of the tissue are given by
| (1) |
| (2) |
| (3) |
Here, stem and TA cells proliferate at rates ν0 and ν1 and may either self-replicate upon division with probabilities p0 and p1 or differentiate with probabilities 1 − p0 and 1 − p1, respectively, while TD cells undergo natural cell death at a rate d2 (Fig. 1). No-flux boundary conditions for the cell densities along both y = h and y = 0 are applied when necessary.
Figure 1.
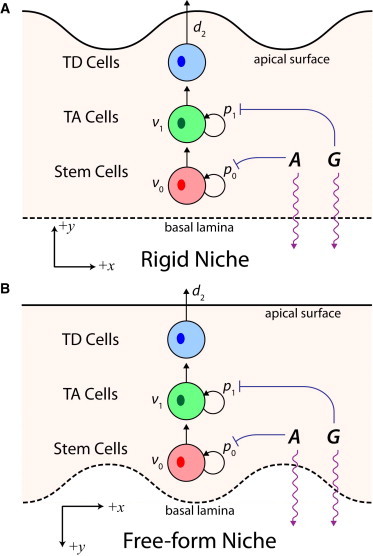
Schematic portraits of a multistage cell lineage in stratified epithelium. Stem and TA cells proliferate with rates ν0 and ν1 and either self-replicate or differentiate upon division while TD cells undergo natural cell death at a rate d2. The regulatory molecules A and G are produced in the epithelium, diffuse throughout the tissue and through a permeable basal lamina (purple arrows), and inhibit the self-replication probabilities of stem and TA cells, p0 and p1 (blue barred arrows). The apical surface serves as a closed tissue surface with tight junctions. (A) The basal lamina is fixed in space while the apical surface is free-moving in the rigid niche structure. (B) The apical surface is fixed in space while the basal lamina is free-moving in the free-form niche structure.
Imposing a uniform density of cells, or incompressibility, in our tissue, which can be interpreted as C0 + C1 + C2 = 1 at each spatial location after normalization of the densities, then Eqs. 1–3 can be summed to obtain
| (4) |
To further describe movement in the tissue, we, also, assume that the flow of cells occurs down pressure gradients as described by Darcy’s law, (32). Taking the vertical tissue velocity to be zero along the bottom of the tissue, w(x, y = 0, t) = 0, fixes this boundary so that no upwards motion occurs. Along the top of the tissue, we include surface tension that may be caused by intercellular forces and cell-surface mechanics (33,34). Thus, we take the pressure along the variable boundary y = h to be directly proportional to the curvature of the boundary, κ, P(x, y = h, t) = ξκ (35). The kinematic condition governing the movement of the dynamic boundary is given by
| (5) |
To describe the tissue morphology at a given time, the variation in tissue size, Th, is defined by a scaled maximum difference in tissue size,
| (6) |
as a measure of the morphology’s distortion or regularity. When Th is zero, the tissue morphology is uniform in the x direction, and h is constant. When Th increases toward a maximum value of 1, the morphology is less regular and a greater spatial variation in tissue size is present.
Stem cell niches are sustained in our models by intercellular signaling of morphogens. We allow the molecules A and G to be produced by the cell type Ci at rates μi and ηi in the epithelium, respectively, and then diffuse throughout the tissue while being degraded with corresponding diffusion coefficients DA and DG and degradation rates adeg and gdeg,
| (7) |
| (8) |
By incorporating A’s inhibition of the self-renewal of stem cells and G’s inhibition of the self-renewal of TA cells,
| (9) |
| (10) |
where A and G regulate the epithelial lineage in our model similarly to the behavior of the morphogens ActivinβB and GDF11 in the olfactory epithelium (36); the coefficients and are the maximal threshold values that p0 and p1 can achieve while 1/γA and 1/γG are the half-maximal effective concentrations (or EC50 values) for the response curves for p0 and p1, respectively; and the parameters m and n are Hill exponents that describe the sharpness of the response curves for p0 and p1.
Adopting a permeable basal lamina across which molecules freely diffuse to and from neighboring tissues, and a closed boundary at the apical surface where tight junctions are present (37,38), may prompt the formation of spatial gradients of A and G that are low along the basal lamina and high along the apical surface of the tissue and, ultimately, the aggregation of stem cells into a niche along the basal lamina. We say that the tissue maintains a rigid niche when stem cells accumulate along the fixed boundary y = 0, indicating that y = 0 is taken to be the basal lamina while y = h serves as the apical surface of the tissue. In contrast, stem cells accumulate along the free boundary y = h in a free-form niche, meaning y = h is taken as the basal lamina and y = 0 as the apical surface. In a rigid niche, stem cell movement is relatively restricted by the rigid boundary and by the zero velocity in the basal-apical direction along y = 0 while stem cells in a free-form niche are more free to move throughout as the tissue and the free boundary h moves. The permeability and closedness of the boundaries can be imposed correspondingly as leaky and no-flux boundary conditions for the rigid niche,
| (11) |
| (12) |
and for the free-form niche,
| (13) |
| (14) |
Here, αA and αG are the coefficients of permeability for the morphogens and denotes the unit outward normal vector to h. The parameters αA and αG represent ratios of the decay lengths of morphogens across the basal lamina and do not approximate the physical permeability (30).
Often, the many processes that occur on the molecular and tissue levels are on distinct timescales, with the former being on the order of hours and the latter in days (39). Also, the ratios of convection timescales to diffusion timescales in epithelia are often quite large (30). For these reasons, Eqs. 7–14, governing the distribution of morphogens in the tissue, are considered at a quasi-steady state by equating the left-hand sides equal to zero.
The rigid niche maintains a regular tissue morphology
Spatial uniformity in the x direction reduces the two-dimensional epithelial model with a rigid niche to a previously studied one-dimensional model (30). Simulations of the two-dimensional rigid niche model with homogeneity in the x direction reveal the same qualitative behavior exhibited by the one-dimensional model, as expected (see Fig. S1 A in the Supporting Material). Just as seen in one dimension, the morphogens A and G form spatial gradients that induce a stratification of cell layers in the tissue, and the system may reach a homeostatic steady state. Stem and TA cells reside along the bottom of the tissue with TD cells occupying the upper regions of the tissue. The rapid uptake of A and G along the fixed basal lamina induces a lower relative concentration of each morphogen in this region. Higher self-replication probabilities, p0 and p1, result along the basal lamina, ultimately prompting the formation of a stem cell niche. Behavior also seen in the one-dimensional case and in a homogeneous two-dimensional case is overgrowth during development (i.e., the ability of the tissue to overshoot its steady-state size while stratification occurs). Simulations beginning with either morphological distortions (Th = 0.4 at ) or a nonuniform distribution of cells in the tissue arrive to the same uniform steady state (Fig. S1, B–D). From here, we then speculate that this stable steady state may be the unique nontrivial one in which homeostasis and tissue stratification are achieved.
When the spatial cues that induce stem cell niche formation are nonuniform in space, a spatially nonuniform tissue morphology results, though morphological distortions are slight. Perturbing αA and αG by a sinusoid in the x direction prompts A and G to leak from the epithelium through basal lamina at faster rates where α-values are higher (Fig. 2 A). As a result, the regulatory molecules A and G attain lower distributions in spatial regions along the basal lamina where the basal lamina is more permeable, prompting the accumulation of more stem and TA cells there due to higher self-replication probabilities p0 and p1. This nonuniformity in the stem cell niche size then associates with a slightly distorted tissue morphology, evident in an increase in the variation in tissue size, Th, from zero to approach an approximate value of 0.07 (Fig. 2 C). The dynamics of the mean tissue size in this case and the case when the permeability of the basal lamina is uniform in space exhibit the same general temporal dynamics with overgrowth during stratification but with different mean steady-state sizes (Fig. 2 D). When other components of the lineage, such as p0, ν0, p1, ν1, or d2, are perturbed in the x direction so that they are spatially varying in the direction parallel to the basal lamina, other nonuniform steady states may also be achieved, though the variance in tissue size and niche size may be observed to different degrees.
Figure 2.
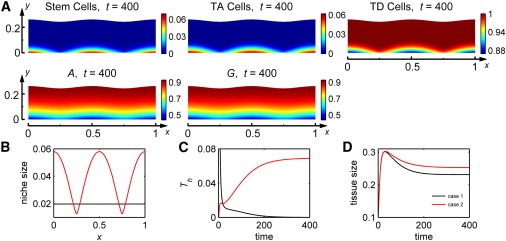
Tissue dynamics and steady-state behavior of the rigid stem cell niche. Two cases are plotted: for Case 1, an initial perturbation to tissue morphology, and for Case 2, a spatial perturbation to the permeability of the basal lamina. Simulation details are listed in Section SIV in the Supporting Material. (A) Approximate steady-state cell and regulatory molecule distributions for case 2. (B) Stem cell niche size at an approximate steady state. (C) Variation in tissue size, Th, over time. (D) Mean tissue size over time.
Overall, at most, minor distortions of the tissue morphology at a steady state result from a rigid stem cell niche. Whether the tissue reaches a uniform or nonuniform steady state, the tissue is able to maintain a relatively regular morphology.
The free-form niche can induce vastly undulating morphologies
Comparing the free-form niche and the rigid niche with spatial homogeneity in the x direction, the free-form niche in two dimensions does not reduce to the one-dimensional model previously studied (30) as the rigid niche does because the basal lamina is free to move in the free-form case. Even so, both cases appear to reach a stratified homeostatic steady state with the same approximate tissue size but through different temporal dynamics (Fig. S2 A). The free-form niche tissue reaches its approximate steady-state size ∼10 times faster, and very little overgrowth occurs in comparison to the rigid niche. This indicates that directional growth of the niche may impact stratification dynamics but not necessarily have a drastic influence on homeostasis.
When the initial morphology of the tissue is slightly distorted by a sinusoid (Th ≈ 0.0488 at t = 0), free-form niche simulations demonstrate a further distortion of the morphology and fingering of the tissue occurs. By time t = 250, structures similar to rete ridges or palisades of Vogt develop (Fig. 3, A and B); the fingers attain a shape with deep wells and steep walls that protrude into the basal lamina in a columnar fashion. However, the tissue does not appear to reach a stable steady state during this process, but instead the morphology of the tissue continually deforms. Initially, Th decreases as growth and stratification occur and then begins to increase rapidly toward 1 after primary growth stages (Fig. 3 D). Stem cells accumulate at the bottom of the fingers just as observed experimentally, and appear to be the driving force behind fingering of the tissue. More specifically, the free-form niche size (defined in Section SII C in the Supporting Material) begins relatively uniform and then attains sharp peaks where fingers form over time, indicating a significantly higher concentration of stem cells in these regions (Fig. 3 E). It is important to note that as the tissue morphology deforms, lower concentrations of A are present within the fingers (Fig. 3 C), which appears to be due to a higher basal lamina/volume in these spatial regions (see an analytical study in Section SIII in the Supporting Material). As a result of stem cells accumulating in the fingers, thinner regions of the epithelia are almost entirely comprised of TD cells where a low basal lamina/volume ratio exists (Fig. S2 B).
Figure 3.
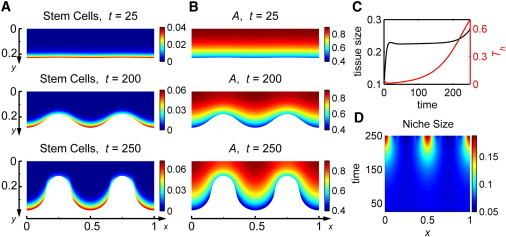
Tissue dynamics and morphological distortions after an initial perturbation to tissue morphology for the free-form stem cell niche. Simulation details are listed in Section SIV in the Supporting Material. (A) Dynamics of the distribution of stem cells. (B) Dynamics of the distribution of panel A. (C) Mean tissue size (black) and variation in tissue size, Th, (red) over time. (D) Heat map for the stem-cell niche size as a function of both x and time.
In a thin epithelium consisting of a large stem cell population, initial low frequency perturbations to tissue morphology may give rise to morphological distortions at higher frequencies. The early dynamics of the morphology of the basal lamina for simulations of this case that begin with morphological distortions at k = 1 and k = 2 wave modes demonstrate a gradual transition to fingering at a k = 4 wave mode (Fig. 4 A). Distributions of cell populations for this particular case demonstrate expanded stem and TA layers with a thinner TD cell layer caused by a higher cell death rate, d2 (Fig. 4 B). This phenomenon of high frequency fingering from an initial low frequency morphological perturbation suggests that an inherent minimal frequency for tissue fingering may be ingrained in the cell lineage and its regulations. As a result, stratified epithelial tissues may have the capacity to regulate the width of their structures that protrude into the basal lamina.
Figure 4.
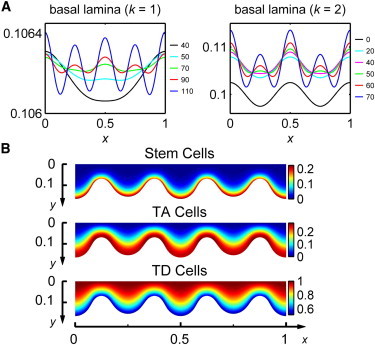
High frequency morphological distortions result from low frequency initial perturbations to tissue morphology when a large stem cell population resides in a free-form niche. Simulation details are listed in SIV. (A) Basal lamina morphologies at different times, t, with a high removal rate of TD cells after an initial tissue morphology perturbation at wave modes k = 1, 2. (B) Distributions of Stem, TA, and TD cell volume fractions at time t = 100 for the k = 2 case.
When components of the system such as proliferation rates and replication probabilities are spatially perturbed in the x direction, morphological distortions of the tissue are induced, similar to the observed effects of varying the permeability of the basal lamina with a rigid niche. Because we have already observed that an initial morphological distortion in a free-form niche may prompt fingering of the tissue, simulations in which the permeability of the basal lamina, p values, ν-values, or d2 values are inhomogeneous in space can lead to the formation of fingers within the tissue as expected, though at distinct rates (Fig. 5 A). In particular, varying p0 and the permeability of the basal lamina prompts fingering to occur the quickest while it takes a long time for fingering to begin when p1 and ν1 are perturbed. We speculate that this difference occurs because stratification and tissue size are most sensitive to p0 and the permeability of the basal lamina, while not necessarily sensitive to p1 and ν1 for the chosen parameters.
Figure 5.
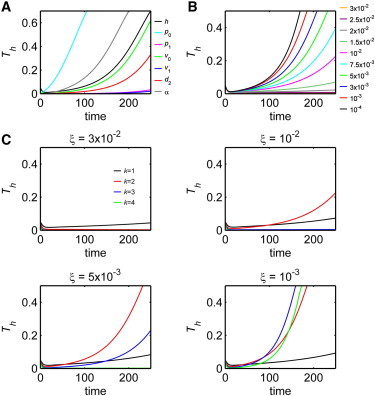
Dynamics of variation in tissue size, Th, for the free-form stem cell niche. Simulation details are listed in Section SIV in the Supporting Material. (A) Components of the system are perturbed in the x direction: h denotes an initial perturbation to tissue morphology; pi, νi, and d2 denote perturbations to respective parameters in the cell lineage; and α denotes a perturbation to the permeability of the basal lamina. (B) Different levels of surface tension chosen by varying the value of ξ. (C) Wave modes k = 1 (black), 2 (red), 3 (blue), and 4 (green) for an initial perturbation to tissue morphology for different surface tension strengths.
With the free-form niche, the imposed surface tension from cell-to-cell adhesion along the basal lamina is a force that maintains the regularity of tissue morphology. For fingering to occur along the basal lamina, surface tension must then be overcome by internal forces from cell proliferation within the tissue. When surface tension is increased, fingering takes longer to occur and can be prevented entirely (Fig. 5 B). More specifically, an approximate eightfold increase in surface tension (from ξ = 4 × 10−3 to ξ = 3 × 10−2) prevents the occurrence of fingering while a uniform morphology is attained at a stable steady state, which is evidenced by Th approaching zero over time. As expected, simulations also show that when surface tension is relaxed by decreasing ξ along the basal lamina, fingering occurs at a faster rate and Th curves increase. So, when surface tension becomes large, there is a similarity between the free-form niche and rigid niche in the notion that flat, regular tissue morphologies can be maintained.
Next, we explore how different spatial frequencies of initial morphological distortions may affect the rate of tissue fingering. For initial morphological distortions of equal magnitude (meaning Th is equal at t = 0), we find that the higher the frequency of the distortion, the higher the curvature of the basal lamina and surface tension forces will be. Simulations for different frequencies with different surface tension forces ranging over a factor of 30 show that low frequency fingering occurs more frequently than high frequency fingering (Fig. 5 C). However, it is important to note that when it does occur, high frequency fingering often occurs at a faster rate, which is shown by comparing the plots that increase sharply for higher wave modes. When the initial morphology is distorted by a sinusoid with an initial wave mode k = 1, Th at t = 250 only increases twofold from a low value when the surface tension forces decrease 30-fold, indicating a relatively low sensitivity of the rate of low frequency fingering to surface tension strength. On the other hand, simulations for both the k = 2 and k = 3 wave modes may finger rapidly, slowly, or not at all depending on the surface tension values in this range. Further examining Th for different wave modes also reveals that the high frequency fingering does not begin as early as low frequency fingering. For example, the value of Th for the k = 4 wave mode with ξ = 10−3 exceeds that of the k = 1 wave mode after ∼t = 80, and then larger fingers form.
Contextualization in the developing human epidermis and relevance to epithelial diseases
Though the behavior of each is quite different, our models for both the rigid and free-form stem cell niches are applicable to the human epidermis during different stages of development. The stratum corneum, or cornified layer, is the outermost layer of the skin consisting of rigid, dead cells that are high in keratin to provide the skin with its barrier function (40,41). This layer begins to form during the second embryonic trimester (40,42). At birth, the epidermis as a whole has almost fully matured, and the stratum corneum has developed to nearly equivalent that of an adult. At this time, the interfollicular epidermis lacks rete ridges, which only develop postnatally (40). From here, we can identify the presence of the stratum corneum in correspondence with the immobile boundary along the apical surface of our model with a free-form niche and the lack thereof in correspondence with the free apical surface in the rigid niche model. Then, we are provided with a possible explanation for why the rete ridges form postnatally; only when growth is restricted to occur inwardly would rete ridges form, as in our free-form niche simulations, and not when outward growth is unimpeded, similar to the rigid niche. Furthermore, it has been demonstrated that the level of integrin expression in the basal layer of the human epidermis varies spatially; integrin expression is relatively higher in cells along rete ridges in the palm and relatively lower in rete ridges in the foreskin and interfollicular scalp relative to cells lining the dermal papillae (13). This evidence of a molecular difference in basal cells based on spatial location may indicate that stem cells along the rete ridges may be subject to different strengths of regulation from signaling molecules, such as feedback from morphogens like A and G from our models that may be more present in one of these regions than the other.
Epithelial dysplasia is often characterized by the presence of larger, drop-shaped rete pegs along with irregular epithelial stratification and differentiation (43,44), often prompting tumor formation (45). Psoriatic epidermis, in which the growth cycle of skin cells is accelerated, exhibits elongated rete ridges along with an absent granular layer (25,46,47). In these cases, tissues may not be able to reap full benefits from a spatially varying architecture that provides better protection and surface area for stem cells and a more efficient wound response (18,19). As a result, the ability for stratified epithelia to control its variance in morphology becomes an important performance objective for the tissue. The free-form niche stratification models presented here provide a framework to understand what mechanisms might control the size of the protrusions into the basal lamina and serve to impede fingering of the tissue. Morphological distortions in our free-form niche models can be slowed significantly or entirely through the stem cell niche’s observed regulation of its own cell cycle length to maintain niche cells in a quiescent, slow cycling state (48,49) by intercellular signaling mediated by morphogens, such as members of the Hedgehog signaling family, which have been identified experimentally to assume such a role in the hematopoietic system (50) (see Section SI A and Fig. S3, A and B, in the Supporting Material). Mechanotransduction may also serve to impede tissue fingering because the inclusion of pressure-induced differentiation (51,52) into our models delayed or prevented fingering (see Section SI B and Fig. S3 C in the Supporting Material). Both the niche’s regulation of its own proliferation and pressure-induced differentiation failed to prompt stable fingering; however, simulations with a mechanism in which the permeability of the basal lamina is proportional to its own curvature was able to approach a stable steady state with a distorted free-form niche morphology (see Section SI C and Fig. S4 in the Supporting Material).
Discussion and Conclusions
In this paper, we explore the two-dimensional spatial effects of the stem cell niche and multistage cell lineages in developing stratified epithelia through modeling. We demonstrate that the morphologies of stratified epithelia depend on the spatial structure of the stem cell niche. In particular, undulating epithelial morphologies may develop when the niche forms along a dynamic, variable basal lamina as opposed to when its movement and formation are restricted by a rigid, fixed basal lamina. These undulating morphologies are in close resemblance with stratified epithelia that maintain rete pegs or palisades of Vogt; stem cells accumulate along the basal lamina in the tips of the fingerlike structures that develop.
We speculate that the regular morphologies maintained with a rigid stem cell niche are primarily due to the lack of proliferating cells near the variable boundary. When a rigid niche is assumed, TD cells accumulate in the outermost layer of the stratified tissue along the free boundary, and do not divide but only die naturally through apoptosis or are sloughed off of the tissue, prompting a low influx of new cells along the top stratified layer. This result allows the surface tension forces and pressure gradients to flatten the apical surface of the tissue, giving rise to a relatively regular tissue morphology.
When stem cells accumulate at the free boundary in the free-form niche, we speculate that the relationship between the convexity of the basal lamina and morphogen distributions gives rise to undulating tissue morphologies. An initial perturbation to tissue morphology in our free-form niche model prompts an initial convexity of the basal lamina and a higher surface area/volume ratio of the basal lamina to the size of the epithelium. Our simulations (Fig. 3 C) and analytical work (see Section SIII in the Supporting Material) hint that a larger tissue interface along the basal lamina allows for a higher leakage of A from the epithelium, and, as a result, a lower distribution of A is present along regions of the basal lamina where its convexity is high. From here, a lower distribution of A prompts stem cells to self-renew more often as opposed to differentiating in these regions, which results in a higher local in-flux of cells and higher local internal tissue pressure along where the basal lamina is convex. This high local pressure, then, may cause an increase in the convexity of the basal lamina if the forces are large enough to overcome surface tension. Overall, this process then may drive fingering of the tissue and the tissue morphology may become further distorted over time (Fig. 6).
Figure 6.
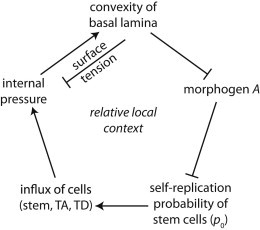
Schematic portrait outlining an explanation for tissue fingering with the free-form stem cell niche.
To experimentally test this hypothesis for the occurrence of undulating epithelial morphologies based on the regulation of stem cell fates by diffusible molecules, one could compare the behavior of stem cells at the tips of developing fingers of the tissue with the behavior of stem cells found in thinner regions of the tissue. If a noticeable difference is found, such as distinct proliferation or stem cell fates, then some indication is provided that stem cells in each of these regions may be subject to different strengths of regulation from signaling molecules. The difference in basal layer integrin expression in cells along the tips of rete ridges of the human epidermis, in comparison to cells along the dermal papillae (13), may be a starting point for experimental work to explore this concept.
Communication between cells through cell-to-cell contact, such as Notch signaling (53) and cellular adhesion (33,34), affects the stratification of epithelia. These local spatial effects, along with the individuality of stem cells, are difficult to incorporate into a continuum approach, such as the one our model assumes here. However, they can be treated much more easily with a discrete model, such as an agent-based model (54,55) or a cellular automata model (56,57). While continuum models can account for the distribution of morphogens throughout the tissue in a simpler fashion (especially when several layers of cells are present), a hybrid approach, accounting for the basal stem cells in a discrete fashion, and the upper tissue layers and morphogen distributions as a continuum, may enable the models to include more detailed mechanistic and stochastic effects. We may further observe new and interesting simulations, such as a natural stabilization of tissue fingers for a free-form niche.
If a cause of undulating epithelial morphologies is inherent within the spatial structure of the stem cell niche, then the question remains as to how such a tissue may simultaneously achieve homeostasis with a spatially varying tissue architecture. Neither mechanistic nor molecular mechanisms from experimental observations that impede tissue distortion with a free-form niche ultimately yield an undulating morphology at a steady state but, instead, continue to distort over time; only a model in which permeability of the basal lamina is proportional to its own curvature provides such a result. Extensions of the current free-form niche model that include two dynamic free boundaries without a rigid apical surface along with adding a third spatial dimension may enable more stable fingering. Incorporating more detailed tissue mechanics and elaborate signaling networks into a continuum model may also help capture simultaneous homeostasis and fingering as well as other intricate three-dimensional epithelial morphologies (22). The overall modeling framework presented here provides an in silico tool for studying healthy and abnormal epithelial tissues, with potential to identify novel, to our knowledge, components that may aid in treatment of epithelial diseases, such as dysplasia and psoriasis.
Acknowledgments
We thank Arthur Lander, Xing Dai, and Anne Calof for helpful discussions.
This work was partially supported by National Institutes of Health grants No. R01GM67247 and No. P50GM76516 and National Science Foundation grant No. DMS-1161621. J.O. has been supported by National Institutes of Health training grants No. T32EB009418 and No. T32HD060555.
Footnotes
This is an Open Access article distributed under the terms of the Creative Commons-Attribution Noncommercial License (http://creativecommons.org/licenses/by-nc/2.0/), which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Supporting Material
References
- 1.Fuchs E., Tumbar T., Guasch G. Socializing with the neighbors: stem cells and their niche. Cell. 2004;116:769–778. doi: 10.1016/s0092-8674(04)00255-7. [DOI] [PubMed] [Google Scholar]
- 2.Moore K.A., Lemischka I.R. Stem cells and their niches. Science. 2006;311:1880–1885. doi: 10.1126/science.1110542. [DOI] [PubMed] [Google Scholar]
- 3.Li L., Xie T. Stem cell niche: structure and function. Annu. Rev. Cell Dev. Biol. 2005;21:605–631. doi: 10.1146/annurev.cellbio.21.012704.131525. [DOI] [PubMed] [Google Scholar]
- 4.Phinney D.G., Prockop D.J. Concise review: mesenchymal stem/multipotent stromal cells: the state of transdifferentiation and modes of tissue repair—current views. Stem Cells. 2007;25:2896–2902. doi: 10.1634/stemcells.2007-0637. [DOI] [PubMed] [Google Scholar]
- 5.Cohen, D. M., and C. S. Chen. 2008. Mechanical control of stem cell differentiation. StemBook. http://www.stembook.org/. 1–16. [PubMed]
- 6.Jones D.L., Wagers A.J. No place like home: anatomy and function of the stem cell niche. Nat. Rev. Mol. Cell Biol. 2008;9:11–21. doi: 10.1038/nrm2319. [DOI] [PubMed] [Google Scholar]
- 7.Chan C.K.F., Chen C.-C., Weissman I.L. Endochondral ossification is required for hematopoietic stem-cell niche formation. Nature. 2009;457:490–494. doi: 10.1038/nature07547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Koster M.I., Roop D.R. Mechanisms regulating epithelial stratification. Annu. Rev. Cell Dev. Biol. 2007;23:93–113. doi: 10.1146/annurev.cellbio.23.090506.123357. [DOI] [PubMed] [Google Scholar]
- 9.Smart I.H. Location and orientation of mitotic figures in the developing mouse olfactory epithelium. J. Anat. 1971;109:243–251. [PMC free article] [PubMed] [Google Scholar]
- 10.Frantz G.D., McConnell S.K. Restriction of late cerebral cortical progenitors to an upper-layer fate. Neuron. 1996;17:55–61. doi: 10.1016/s0896-6273(00)80280-9. [DOI] [PubMed] [Google Scholar]
- 11.Rizvi A.Z., Wong M.H. Epithelial stem cells and their niche: there’s no place like home. Stem Cells. 2005;23:150–165. doi: 10.1634/stemcells.2004-0096. [DOI] [PubMed] [Google Scholar]
- 12.Lavker R.M., Sun T.-T. Epidermal stem cells. Adv. Dermatol. 1983;21(S1):121–127. doi: 10.1111/1523-1747.ep12540880. [DOI] [PubMed] [Google Scholar]
- 13.Jones P.H., Harper S., Watt F.M. Stem cell patterning and fate in human epidermis. Cell. 1995;80:83–93. doi: 10.1016/0092-8674(95)90453-0. [DOI] [PubMed] [Google Scholar]
- 14.Garant P.R., Feldman J., Cullen M.R. Ultrastructure of Merkel cells in the hard palate of the squirrel monkey (Saimiri sciureus) Am. J. Anat. 1980;157:155–167. doi: 10.1002/aja.1001570204. [DOI] [PubMed] [Google Scholar]
- 15.Jordan J.A., Singer A., Shafi M.I. Blackwell/Wiley; New York: 2006. The Cervix. [Google Scholar]
- 16.Karring T., Lang N.P., Löe H. The role of gingival connective tissue in determining epithelial differentiation. J. Periodontal Res. 1975;10:1–11. doi: 10.1111/j.1600-0765.1975.tb00001.x. [DOI] [PubMed] [Google Scholar]
- 17.Goldberg M.F., Bron A.J. Limbal palisades of Vogt. Trans. Am. Ophthalmol. Soc. 1982;80:155–171. [PMC free article] [PubMed] [Google Scholar]
- 18.Dua H.S., Shanmuganathan V.A., Joseph A. Limbal epithelial crypts: a novel anatomical structure and a putative limbal stem cell niche. Br. J. Ophthalmol. 2005;89:529–532. doi: 10.1136/bjo.2004.049742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Low W.C., Verfaillie C.M. World Scientific; Singapore: 2008. Stem Cells and Regenerative Medicine. [Google Scholar]
- 20.Blagoev K.B. Organ aging and susceptibility to cancer may be related to the geometry of the stem cell niche. Proc. Natl. Acad. Sci. USA. 2011;108:19216–19221. doi: 10.1073/pnas.1106105108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Drasdo D. Buckling instabilities of one-layered growing tissues. Phys. Rev. Lett. 2000;84:4244–4247. doi: 10.1103/PhysRevLett.84.4244. [DOI] [PubMed] [Google Scholar]
- 22.Hannezo E., Prost J., Joanny J.-F. Instabilities of monolayered epithelia: shape and structure of villi and crypts. Phys. Rev. Lett. 2011;107:078104. doi: 10.1103/PhysRevLett.107.078104. [DOI] [PubMed] [Google Scholar]
- 23.Shraiman B.I. Mechanical feedback as a possible regulator of tissue growth. Proc. Natl. Acad. Sci. USA. 2005;102:3318–3323. doi: 10.1073/pnas.0404782102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Basan M., Joanny J.-F., Risler T. Undulation instability of epithelial tissues. Phys. Rev. Lett. 2011;106:158101. doi: 10.1103/PhysRevLett.106.158101. [DOI] [PubMed] [Google Scholar]
- 25.Savill N.J., Weller R., Sherratt J.A. Mathematical modeling of nitric oxide regulation of rete peg formation in psoriasis. J. Theor. Biol. 2002;214:1–16. doi: 10.1006/jtbi.2001.2400. [DOI] [PubMed] [Google Scholar]
- 26.Weatherhead S.C., Farr P.M., Reynolds N.J. Keratinocyte apoptosis in epidermal remodeling and clearance of psoriasis induced by UV radiation. J. Invest. Dermatol. 2011;131:1916–1926. doi: 10.1038/jid.2011.134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lo W.-C., Chou C.-S., Nie Q. Feedback regulation in multistage cell lineages. Math. Biosci. Eng. 2009;6:59–82. doi: 10.3934/mbe.2009.6.59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lander A.D., Gokoffski K.K., Calof A.L. Cell lineages and the logic of proliferative control. PLoS Biol. 2009;7:e15. doi: 10.1371/journal.pbio.1000015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Marciniak-Czochra A., Stiehl T., Wagner W. Modeling of asymmetric cell division in hematopoietic stem cells—regulation of self-renewal is essential for efficient repopulation. Stem Cells Dev. 2009;18:377–385. doi: 10.1089/scd.2008.0143. [DOI] [PubMed] [Google Scholar]
- 30.Chou C.-S., Lo W.-C., Nie Q. Spatial dynamics of multistage cell lineages in tissue stratification. Biophys. J. 2010;99:3145–3154. doi: 10.1016/j.bpj.2010.09.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Reference deleted in proof.
- 32.Basser P.J. Interstitial pressure, volume, and flow during infusion into brain tissue. Microvasc. Res. 1992;44:143–165. doi: 10.1016/0026-2862(92)90077-3. [DOI] [PubMed] [Google Scholar]
- 33.Foty R.A., Pfleger C.M., Steinberg M.S. Surface tensions of embryonic tissues predict their mutual envelopment behavior. Development. 1996;122:1611–1620. doi: 10.1242/dev.122.5.1611. [DOI] [PubMed] [Google Scholar]
- 34.Lecuit T., Lenne P.-F. Cell surface mechanics and the control of cell shape, tissue patterns and morphogenesis. Nat. Rev. Mol. Cell Biol. 2007;8:633–644. doi: 10.1038/nrm2222. [DOI] [PubMed] [Google Scholar]
- 35.Greenspan H.P. On the growth and stability of cell cultures and solid tumors. J. Theor. Biol. 1976;56:229–242. doi: 10.1016/s0022-5193(76)80054-9. [DOI] [PubMed] [Google Scholar]
- 36.Gokoffski K.K., Wu H.-H., Calof A.L. Activin and GDF11 collaborate in feedback control of neuroepithelial stem cell proliferation and fate. Development. 2011;138:4131–4142. doi: 10.1242/dev.065870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Dowd C.J., Cooney C.L., Nugent M.A. Heparan sulfate mediates bFGF transport through basement membrane by diffusion with rapid reversible binding. J. Biol. Chem. 1999;274:5236–5244. doi: 10.1074/jbc.274.8.5236. [DOI] [PubMed] [Google Scholar]
- 38.Tang J., Tang J., Liang F. Juxtanodin in the rat olfactory epithelium: specific expression in sustentacular cells and preferential subcellular positioning at the apical junctional belt. Neuroscience. 2009;161:249–258. doi: 10.1016/j.neuroscience.2009.03.051. [DOI] [PubMed] [Google Scholar]
- 39.DeHamer M.K., Guevara J.L., Calof A.L. Genesis of olfactory receptor neurons in vitro: regulation of progenitor cell divisions by fibroblast growth factors. Neuron. 1994;13:1083–1097. doi: 10.1016/0896-6273(94)90047-7. [DOI] [PubMed] [Google Scholar]
- 40.Holbrook K.A. Structure and function of the developing human skin. In: Goldsmith L.A., editor. Vol. 1. Oxford University Press; Cambridge, UK: 1983. (Biochemistry and Physiology of the Skin). [Google Scholar]
- 41.MacKenzie J.C. Ordered structure of the stratum corneum of mammalian skin. Nature. 1969;222:881–882. doi: 10.1038/222881a0. [DOI] [PubMed] [Google Scholar]
- 42.Hardman M.J., Byrne C. Skin structural development. In: Hoath S.B., Maibach H.I., editors. Neonatal Skin: Structure and Function. Marcel Dekker; New York: 2003. [Google Scholar]
- 43.Bánóczy J., Csiba A. Occurrence of epithelial dysplasia in oral leukoplakia. Analysis and follow-up study of 12 cases. Oral Surg. Oral Med. Oral Pathol. 1976;42:766–774. doi: 10.1016/0030-4220(76)90099-2. [DOI] [PubMed] [Google Scholar]
- 44.Nauta J.M., Roodenburg J.L., Vermey A. Comparison of epithelial dysplasia—the 4NQO rat palate model and human oral mucosa. Int. J. Oral Maxillofac. Surg. 1995;24:53–58. doi: 10.1016/s0901-5027(05)80857-4. [DOI] [PubMed] [Google Scholar]
- 45.Tavassoli F.A., Devilee P. World Health Organization Classification of Tumors. IARC Press; Lyon, France: 2003. Pathology and genetics of tumors of the breast and female genital organs. [Google Scholar]
- 46.Helwig E.B. Pathology of psoriasis. Ann. N. Y. Acad. Sci. 1958;73:924–935. doi: 10.1111/j.1749-6632.1959.tb40869.x. [DOI] [PubMed] [Google Scholar]
- 47.Iizuka H., Ishida-Yamamoto A., Honda H. Epidermal remodeling in psoriasis. Br. J. Dermatol. 1996;135:433–438. [PubMed] [Google Scholar]
- 48.Orford K.W., Scadden D.T. Deconstructing stem cell self-renewal: genetic insights into cell-cycle regulation. Nat. Rev. Genet. 2008;9:115–128. doi: 10.1038/nrg2269. [DOI] [PubMed] [Google Scholar]
- 49.Wagner W., Horn P., Ho A.D. Aging of hematopoietic stem cells is regulated by the stem cell niche. Exp. Gerontol. 2008;43:974–980. doi: 10.1016/j.exger.2008.04.007. [DOI] [PubMed] [Google Scholar]
- 50.Trowbridge J.J., Scott M.P., Bhatia M. Hedgehog modulates cell cycle regulators in stem cells to control hematopoietic regeneration. Proc. Natl. Acad. Sci. USA. 2006;103:14134–14139. doi: 10.1073/pnas.0604568103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Altman G.H., Horan R.L., Kaplan D.L. Cell differentiation by mechanical stress. FASEB J. 2002;16:270–272. doi: 10.1096/fj.01-0656fje. [DOI] [PubMed] [Google Scholar]
- 52.Lee I.C., Wang J.H., Young T.H. The differentiation of mesenchymal stem cells by mechanical stress or/and co-culture system. Biochem. Biophys. Res. Commun. 2007;352:147–152. doi: 10.1016/j.bbrc.2006.10.170. [DOI] [PubMed] [Google Scholar]
- 53.Lowell S., Jones P., Watt F.M. Stimulation of human epidermal differentiation by delta-notch signaling at the boundaries of stem-cell clusters. Curr. Biol. 2000;10:491–500. doi: 10.1016/s0960-9822(00)00451-6. [DOI] [PubMed] [Google Scholar]
- 54.Graner F., Glazier J.A. Simulation of biological cell sorting using a two-dimensional extended Potts model. Phys. Rev. Lett. 1992;69:2013–2016. doi: 10.1103/PhysRevLett.69.2013. [DOI] [PubMed] [Google Scholar]
- 55.Christley S., Lee B., Nie Q. Integrative multicellular biological modeling: a case study of 3D epidermal development using GPU algorithms. BMC Syst. Biol. 2010;4:107. doi: 10.1186/1752-0509-4-107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.von Neumann J. University of Illinois Press; Champaign, IL: 1966. Theory of Self-Reproducing Automata. [Google Scholar]
- 57.Alarcón T., Byrne H.M., Maini P.K. A cellular automaton model for tumor growth in inhomogeneous environment. J. Theor. Biol. 2003;225:257–274. doi: 10.1016/s0022-5193(03)00244-3. [DOI] [PubMed] [Google Scholar]
- 58.Silva, H., and I. M. Conboy. 2008. Aging and stem cell renewal. StemBook. http://www.stembook.org/. 1–14. [PubMed]
- 59.Gopinath S.D., Rando T.A. Stem cell review series: aging of the skeletal muscle stem cell niche. Aging Cell. 2008;7:590–598. doi: 10.1111/j.1474-9726.2008.00399.x. [DOI] [PubMed] [Google Scholar]
- 60.Daya-Grosjean L., Couvé-Privat S. Sonic Hedgehog signaling in basal cell carcinomas. Cancer Lett. 2005;225:181–192. doi: 10.1016/j.canlet.2004.10.003. [DOI] [PubMed] [Google Scholar]
- 61.Dupont S., Morsut L., Piccolo S. Role of YAP/TAZ in mechanotransduction. Nature. 2011;474:179–183. doi: 10.1038/nature10137. [DOI] [PubMed] [Google Scholar]
- 62.Wang J., Baker G. A numerical algorithm for viscous incompressible interfacial flows. J. Comput. Phys. 2009;228:5470–5489. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


