Abstract
Cholera reappeared in Haiti in October, 2010 after decades of absence. Cases were first detected in Artibonite region and in the ensuing months the disease spread to every department in the country. The rate of increase in the number of cases at the start of epidemics provides valuable information about the basic reproductive number (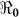 ). Quantitative analysis of such data gives useful information for planning and evaluating disease control interventions, including vaccination. Using a mathematical model, we fitted data on the cumulative number of reported hospitalized cholera cases in Haiti.
). Quantitative analysis of such data gives useful information for planning and evaluating disease control interventions, including vaccination. Using a mathematical model, we fitted data on the cumulative number of reported hospitalized cholera cases in Haiti. 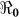 varied by department, ranging from 1.06 to 2.63. At a national level, 46% vaccination coverage would result in an (
varied by department, ranging from 1.06 to 2.63. At a national level, 46% vaccination coverage would result in an (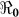 ) <1, which would suppress transmission. In the current debate on the use of cholera vaccines in endemic and non-endemic regions, our results suggest that moderate cholera vaccine coverage would be an important element of disease control in Haiti.
) <1, which would suppress transmission. In the current debate on the use of cholera vaccines in endemic and non-endemic regions, our results suggest that moderate cholera vaccine coverage would be an important element of disease control in Haiti.
A cholera outbreak was confirmed in Haiti on October 21, 2010 by the National Laboratory of Public Health of the Ministry of Public Health and Population (MSPP). Cholera had not been documented in Haiti for decades, and outbreaks had been thought unlikely after the earthquake on 12 January 20101. Cholera was heralded in the Artibonite region, a rural area north of Port-au-Prince, followed in the ensuing months by spread of the disease throughout the country. Spread was facilitated by the earthquake-related disruptions to water and sewage facilities and damage to a local public health infrastructure that was already weak1. Haiti's populations were immunologically naïve to cholera after its long absence, so the potential for a severe cholera epidemic was high, much like recent cholera epidemics in Zimbabwe and other emerging epidemic-prone regions. Following the initial epidemic wave, there were also concerns about the possibility of cholera establishing long-term endemicity in Haiti, marked by the traditional recurrent seasonal epidemics that are characteristic of the disease.
There is an increasing appreciation of the utility of mathematical models in informing public health policy, both in the emergency situation of an initial cholera epidemic2,3,4,5,6 (Table 1), and in long-term public health management of seasonal epidemics. Here, we consider a model that we developed in association with the 2008–2009 Zimbabwe epidemic to explicitly estimate the basic reproductive numbers (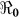 ) for the disease, and make public health recommendations on the usefulness of cholera vaccines on a finer scale. In contrast to earlier models applied to the Haitian epidemic, this model permits incorporation of recently recognized differences in transmission pathways for cholera: a “fast,” or “human-to-human” transmission pathway that takes advantage of the lower infectious dose of hyperinfectious V. cholerae in freshly passed stool, vs. a “slow” transmission pathway that involves movement between environmental reservoirs and human populations. We also explore the impact of variation in parameter estimates, including estimates for rates of asymptomatic carriage, environmental contamination, and infectious dose from environmental exposure. The Haitian Ministry of Health is currently considering implementation of a national vaccination campaign for cholera. Our results underscore the geographic variability in
) for the disease, and make public health recommendations on the usefulness of cholera vaccines on a finer scale. In contrast to earlier models applied to the Haitian epidemic, this model permits incorporation of recently recognized differences in transmission pathways for cholera: a “fast,” or “human-to-human” transmission pathway that takes advantage of the lower infectious dose of hyperinfectious V. cholerae in freshly passed stool, vs. a “slow” transmission pathway that involves movement between environmental reservoirs and human populations. We also explore the impact of variation in parameter estimates, including estimates for rates of asymptomatic carriage, environmental contamination, and infectious dose from environmental exposure. The Haitian Ministry of Health is currently considering implementation of a national vaccination campaign for cholera. Our results underscore the geographic variability in 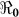 in the initial Haitian epidemic, and the corresponding variability in the needed vaccination coverage for effective disease control.
in the initial Haitian epidemic, and the corresponding variability in the needed vaccination coverage for effective disease control.
Table 1. Haiti 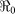 estimates.
estimates.
| Data source | Estimate | |
|---|---|---|
| Bertuzzo et al4 | MSPP | 1.98 |
| Chao et al.5 | MSPP | 2.60 |
| Chunara et al.28 | MSPP | 1.27–3.72 (Before Hurricane Tomas) 1.06–1.73 (After Hurricane Tomas) |
| Chunara et al.28 | Informal sources (HealthMapp & Twitter) | 1.54–6.89 ( Before Hurricane Tomas) 1.04–1.51(After Hurricane Tomas) |
| Tuite et al.3 | MSPP | 2.06–2.78 |
Results
Table 2 provides estimates of the basic reproductive number (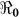 ), and partial reproductive numbers due to “fast” human-to-human transmission (
), and partial reproductive numbers due to “fast” human-to-human transmission (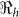 ) and “slow” transmission through the environment (
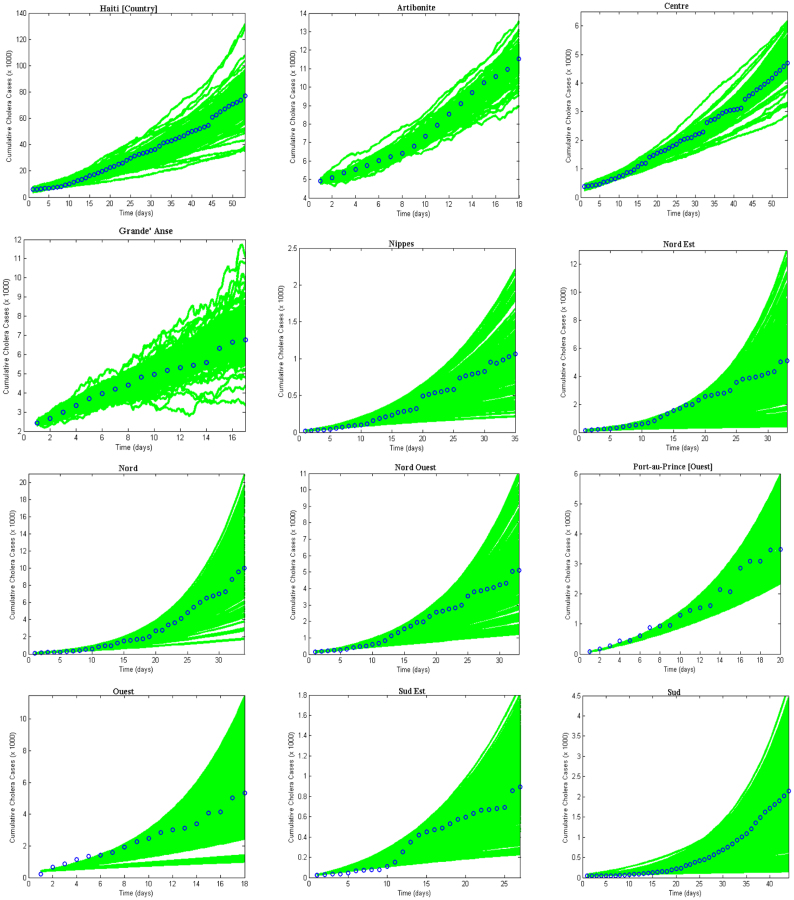
) and “slow” transmission through the environment (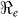 ); it also provides data on the corresponding minimum vaccination coverage needed for a cholera vaccine with an estimated 78% efficacy7 for the 10 departments and the country as a whole. The cumulative cholera cases were fit with mathematical models for each department and for the whole country (Figure 1). The results in Table 2 show that Artibonite department had the highest
); it also provides data on the corresponding minimum vaccination coverage needed for a cholera vaccine with an estimated 78% efficacy7 for the 10 departments and the country as a whole. The cumulative cholera cases were fit with mathematical models for each department and for the whole country (Figure 1). The results in Table 2 show that Artibonite department had the highest 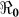 (2.63) and environmental transmission accounted for most of the transmission (≈ 97%) compared to lower values (≈ 9–55%) in other departments. Artibonite department was the first to report cholera cases1 and epidemiological studies have revealed that, the contamination of the Artibonite River and its tributaries (i.e. sources of drinking and cooking water for villagers) triggered the epidemic8. Thus our estimates support the notation that contamination of drinking water sources sparked the outbreak in Artibonite. These results also show that departments neighboring Artibonite had slightly higher
(2.63) and environmental transmission accounted for most of the transmission (≈ 97%) compared to lower values (≈ 9–55%) in other departments. Artibonite department was the first to report cholera cases1 and epidemiological studies have revealed that, the contamination of the Artibonite River and its tributaries (i.e. sources of drinking and cooking water for villagers) triggered the epidemic8. Thus our estimates support the notation that contamination of drinking water sources sparked the outbreak in Artibonite. These results also show that departments neighboring Artibonite had slightly higher 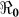 values (1.37–1.73) compared to other departments (1.06–1.44), suggesting that it was the epidemic focal point. Our analysis showed that
values (1.37–1.73) compared to other departments (1.06–1.44), suggesting that it was the epidemic focal point. Our analysis showed that 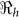 and
and 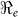 estimates are determined by the time scales of the unfolding epidemic i.e. with fast growing epidemic curves giving a higher percentage of
estimates are determined by the time scales of the unfolding epidemic i.e. with fast growing epidemic curves giving a higher percentage of 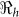 than
than 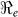 and vice-versa. However the inference about the estimates of
and vice-versa. However the inference about the estimates of 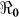 is likely more robust than the estimates of the individual transmission components (i.e.
is likely more robust than the estimates of the individual transmission components (i.e. 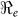 vs.
vs. 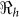 ). Aggregated cholera data for Haiti compared with the department estimates will, on average, overestimate the required country-wide vaccination coverage by about 20% (Table 2). Thus for effective disease control, surveillance and resource allocation there is a need to quantify the magnitude of cholera outbreaks using data on a finer resolution. Analysis of data on a finer grain would likely reveal additional heterogeneities in transmission, but the spatial scales at which it is appropriate to aggregate data for the purposes of planning control interventions remain poorly understood. Since cholera vaccines have different efficacies9,10,11,12, we also carried out sensitivity analysis to show possible scenarios that may arise from using different types of vaccines by considering an efficacy range of 50–100%.
). Aggregated cholera data for Haiti compared with the department estimates will, on average, overestimate the required country-wide vaccination coverage by about 20% (Table 2). Thus for effective disease control, surveillance and resource allocation there is a need to quantify the magnitude of cholera outbreaks using data on a finer resolution. Analysis of data on a finer grain would likely reveal additional heterogeneities in transmission, but the spatial scales at which it is appropriate to aggregate data for the purposes of planning control interventions remain poorly understood. Since cholera vaccines have different efficacies9,10,11,12, we also carried out sensitivity analysis to show possible scenarios that may arise from using different types of vaccines by considering an efficacy range of 50–100%.
Table 2. Estimates of 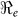 ,
, 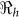 ,
, 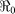 and minimum vaccination coverages. Ouest department includes Port-au-Prince and Ouest** hospitalized cases. The population estimates were extracted from http://www.citypopulation.de/Haiti.html.
and minimum vaccination coverages. Ouest department includes Port-au-Prince and Ouest** hospitalized cases. The population estimates were extracted from http://www.citypopulation.de/Haiti.html.
| Department | Population Size/1000 | 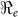 |
SE | % 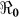
|
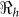 |
SE | % 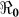
|
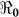 |
SE | Vaccination Coverage Resulting in 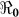 <1 <1 |
|---|---|---|---|---|---|---|---|---|---|---|
| Haiti[Country] | 9923.24 | 0.84 | 7.00 × 10−1 | 54.01 | 0.71 | 0.29 | 45.35 | 1.55 | 0.41 | 45.4 |
| Artibonite | 1571.02 | 2.54 | 2.32 × 10−1 | 96.70 | 0.09 | 0.06 | 3.30 | 2.63 | 0.18 | 79.5 |
| Centre | 678.63 | 0.58 | 4.82 × 10−1 | 42.12 | 0.79 | 0.24 | 57.88 | 1.37 | 0.24 | 34.3 |
| Grande Anse | 425.88 | 0.59 | 4.31 × 10−1 | 46.31 | 0.68 | 0.09 | 53.70 | 1.27 | 0.35 | 27.2 |
| Nippes | 311.50 | 0.09 | 2.84 × 10−4 | 8.86 | 0.96 | 0.21 | 91.15 | 1.06 | 0.21 | 6.9 |
| Nord | 970.50 | 0.16 | 7.79 × 10−2 | 10.24 | 1.37 | 0.24 | 89.76 | 1.53 | 0.23 | 44.4 |
| Nord Ouest | 662.78 | 0.20 | 2.56 × 10−4 | 14.26 | 1.20 | 0.11 | 85.74 | 1.40 | 0.11 | 36.4 |
| Nord Est | 358.28 | 0.22 | 1.43 × 10−3 | 14.99 | 1.22 | 0.21 | 85.01 | 1.44 | 0.21 | 38.9 |
| Ouest**[Ouest] | 1187.83 | 0.45 | 2.04 × 10−4 | 37.67 | 0.74 | 0.16 | 62.33 | 1.18 | 0.16 | 19.9 |
| Port-au-Prince[Ouest] | 2476.79 | 0.74 | 3.68 × 10−4 | 39.27 | 1.15 | 0.13 | 60.73 | 1.89 | 0.13 | 60.5 |
| Sud | 704.76 | 0.21 | 1.32 × 10−3 | 14.65 | 1.23 | 0.19 | 85.36 | 1.44 | 0.19 | 39.5 |
| Sud Est | 575.29 | 0.13 | 2.31 × 10−4 | 11.11 | 1.04 | 0.14 | 88.89 | 1.17 | 0.14 | 18.3 |
| Ouest | 3664.62 | 0.43 | 1.78 × 10−3 | 25.41 | 1.30 | 0.30 | 74.75 | 1.73 | 0.30 | 54.2 |
Figure 1. Cholera model fitting for the cumulative cholera cases where the bold green lines represent the model fit and the blue circles mark the reported data for the cumulative number of cholera cases in the departments for 1000 runs.
The results suggest that a vaccine with 50% efficacy may result in cholera control in most of the departments except for Artibonite, which would require a vaccine with at least 65% efficacy (Table 3). However most of the new-generation cholera vaccines have shown an efficacy more than 65%7,9,10,11,12 for periods sufficient to contain epidemic cholera (i.e. depending on vaccination coverage). But, there are still concerns that most of the studies on vaccine effectiveness were conducted in cholera endemic areas with some degree of immunity within the population, thus these study results may not hold for Haiti where the population was initially immunologically naïve to the disease13,14.
Table 3. Sensitivity analysis of vaccination efficacies from 50%–100% and the corresponding percentage coverage's in the departments and the whole country. Ouest department includes Port-au-Prince and Ouest** hospitalized cases.
Vaccination Coverage (%) Resulting in 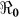 <1 <1 |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Department | 50% | 55% | 60% | 65% | 70% | 75% | 80% | 85% | 90% | 95% | 100% |
| Haiti [Country] | 70.8 | 64.4 | 59.0 | 54.5 | 50.6 | 47.2 | 44.2 | 41.6 | 39.3 | 37.3 | 35.4 |
| Artibonite | >100 | >100 | >100 | 95.4 | 88.6 | 82.7 | 77.5 | 72.9 | 68.9 | 65.3 | 62.0 |
| Centre | 53.6 | 48.7 | 44.6 | 41.2 | 38.3 | 35.7 | 33.5 | 31.5 | 29.8 | 28.2 | 26.8 |
| Grande Anse | 42.4 | 38.6 | 35.4 | 32.6 | 30.3 | 28.3 | 26.5 | 25.0 | 23.6 | 22.3 | 21.2 |
| Nippes | 10.7 | 9.8 | 8.9 | 8.3 | 7.7 | 7.2 | 6.7 | 6.3 | 6.0 | 5.6 | 5.4 |
| Nord | 69.2 | 62.9 | 57.7 | 53.2 | 49.4 | 46.1 | 43.3 | 40.7 | 38.5 | 36.4 | 34.6 |
| Nord Ouest | 56.8 | 51.6 | 47.3 | 43.7 | 40.5 | 37.8 | 35.5 | 33.4 | 31.5 | 29.9 | 28.4 |
| Nord Est | 60.6 | 55.1 | 50.5 | 46.7 | 43.3 | 40.4 | 37.9 | 35.7 | 33.7 | 31.9 | 30.3 |
| Ouest**[Ouest] | 31.1 | 28.2 | 25.9 | 23.9 | 22.2 | 20.7 | 19.4 | 18.3 | 17.3 | 16.3 | 15.5 |
| Port-au-Prince [Ouest] | 94.4 | 85.8 | 78.7 | 72.6 | 67.4 | 62.9 | 59.0 | 55.5 | 52.5 | 49.7 | 47.2 |
| Sud | 61.6 | 56.0 | 51.3 | 47.4 | 44.0 | 41.1 | 38.5 | 36.2 | 34.2 | 32.4 | 30.8 |
| Sud Est | 28.6 | 26.0 | 23.9 | 22.0 | 20.4 | 19.1 | 17.9 | 16.8 | 15.9 | 15.1 | 14.3 |
| Ouest | 84.6 | 76.9 | 70.5 | 65.1 | 60.4 | 56.4 | 52.9 | 49.7 | 47.0 | 44.5 | 42.3 |
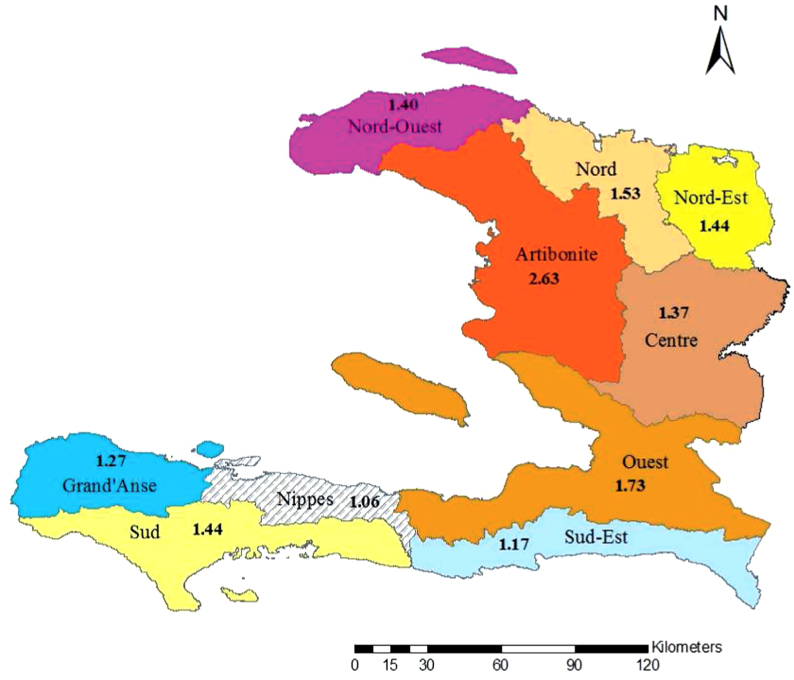
Mapped 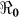 values illustrate the differences in transmission across Haiti (Figure 2). Reproductive numbers were estimated separately for Port-au-Prince (Table 2), and the part of Ouest that does not include Port-au-Prince, as in the data sets on the MSPP website15. We also estimated the reproductive number for the whole Ouest department, combining hospitalized cases from both Port-au-Prince and Ouest**, which was used for mapping (Figure 2).
values illustrate the differences in transmission across Haiti (Figure 2). Reproductive numbers were estimated separately for Port-au-Prince (Table 2), and the part of Ouest that does not include Port-au-Prince, as in the data sets on the MSPP website15. We also estimated the reproductive number for the whole Ouest department, combining hospitalized cases from both Port-au-Prince and Ouest**, which was used for mapping (Figure 2).
Figure 2. Map of Haiti showing corresponding 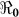 values in the departments.
values in the departments.
We performed sensitivity analysis using a deterministic version of our model to ascertain the robustness of our 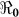 estimates. We carried out sensitivity analysis of κ (the 50% infectious dose for environmental exposure) and χ (the rate of environmental contamination by cholera infected individuals). On the basis of studies conducted by our group in Lima and Bangladesh, peak environmental counts of ctx-positive V. cholerae from pristine areas have been found to range from 101 to 102 cfu/mL16,17; even in areas with heavy sewage contamination, peak environmental counts of ctx-positive V. cholerae were not observed to exceed 106 cfu/ml16. The infectious dose for media-grown V. cholerae ingested by healthy North American volunteers ranges from 108 to 1011 cfu/mL; this drops to 104–108 when the inoculum is given with bicarbonate or food18,19,20. In a series of studies conducted at the Center for Vaccine Development, University of Maryland, the “standard” V. cholerae inoculum in challenges employing health North American volunteers was 106, administered with bicarbonate20.
estimates. We carried out sensitivity analysis of κ (the 50% infectious dose for environmental exposure) and χ (the rate of environmental contamination by cholera infected individuals). On the basis of studies conducted by our group in Lima and Bangladesh, peak environmental counts of ctx-positive V. cholerae from pristine areas have been found to range from 101 to 102 cfu/mL16,17; even in areas with heavy sewage contamination, peak environmental counts of ctx-positive V. cholerae were not observed to exceed 106 cfu/ml16. The infectious dose for media-grown V. cholerae ingested by healthy North American volunteers ranges from 108 to 1011 cfu/mL; this drops to 104–108 when the inoculum is given with bicarbonate or food18,19,20. In a series of studies conducted at the Center for Vaccine Development, University of Maryland, the “standard” V. cholerae inoculum in challenges employing health North American volunteers was 106, administered with bicarbonate20.
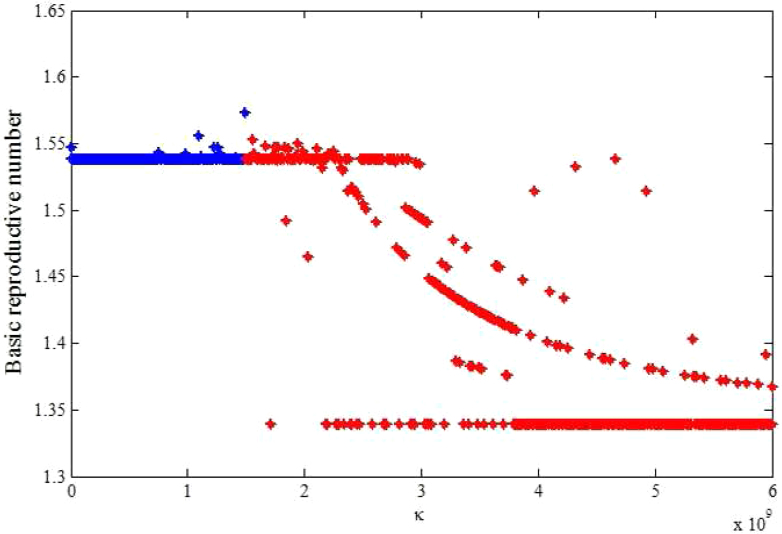
In the context of these data, we carried out sensitivity analysis to explore the effects of κ on 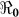 estimates. Results using aggregated data for Haiti are shown in Figure 3, which is a plot of estimated
estimates. Results using aggregated data for Haiti are shown in Figure 3, which is a plot of estimated 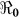 and corresponding values of κ. Varying κ in a plausible range of 105 to 1.5 × 109 cells/ml, which covers the concentration range of vibrios in sewage-contaminated water and also falls within the range of the infectious dose (with bicarbonate, or food) demonstrated among North American volunteers19,20, we note that
and corresponding values of κ. Varying κ in a plausible range of 105 to 1.5 × 109 cells/ml, which covers the concentration range of vibrios in sewage-contaminated water and also falls within the range of the infectious dose (with bicarbonate, or food) demonstrated among North American volunteers19,20, we note that 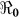 estimates will change by less than 1%. However, these estimates will change by about 13% in vibrio concentration ranging from 1.5 × 109 to 1011 cells/ml. In Figure 4 we present sensitivity analysis results on the effects of χ on
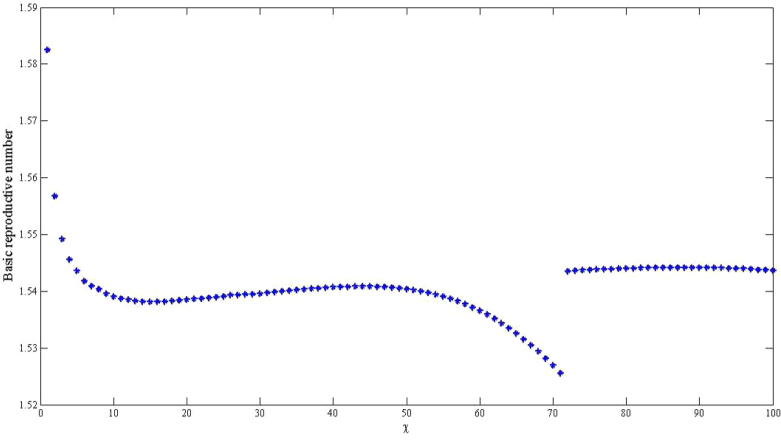
estimates will change by less than 1%. However, these estimates will change by about 13% in vibrio concentration ranging from 1.5 × 109 to 1011 cells/ml. In Figure 4 we present sensitivity analysis results on the effects of χ on 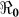 estimates by plotting estimated
estimates by plotting estimated 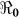 and corresponding values of χ. This parameter may be influenced by a number of socio-economic factors, including adequacy of sewage disposal, and consequently may vary within communities. The distribution of exposure doses would be, in all likelihood, highly skewed. In Figure 4, we note that a change in χ from 1 to 100 only affects our estimates by approximately 3%. Thus, while there may be uncertainty around estimates for κ and χ, changes in these parameters do not substantially affect our results. The discontinuities in Figures 3 and 4 explain points where the curves stops being sensitive to changes in the parameters and the fitting procedure abruptly switches to favor the
and corresponding values of χ. This parameter may be influenced by a number of socio-economic factors, including adequacy of sewage disposal, and consequently may vary within communities. The distribution of exposure doses would be, in all likelihood, highly skewed. In Figure 4, we note that a change in χ from 1 to 100 only affects our estimates by approximately 3%. Thus, while there may be uncertainty around estimates for κ and χ, changes in these parameters do not substantially affect our results. The discontinuities in Figures 3 and 4 explain points where the curves stops being sensitive to changes in the parameters and the fitting procedure abruptly switches to favor the 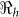 component.
component.
Figure 3. The relationship between the basic reproductive number estimate (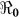 ) and κ using aggregated data for Haiti using population sizes in Table 2 and parameter values in Table 4.
) and κ using aggregated data for Haiti using population sizes in Table 2 and parameter values in Table 4.
The blue line denotes range of κ from 105 to1.5 × 109 cells/ml and the red line denotes range range of κ from 1.5 × 109 to 1011 cells/ml (here our scale only shows 1.5 × 109 to 1010).
Figure 4. The relationship between the basic reproductive number estimate (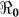 ) and χ using aggregated data for Haiti using population sizes in Table 2 and parameter values in Table 4 and varying χ from 1 to 100.
) and χ using aggregated data for Haiti using population sizes in Table 2 and parameter values in Table 4 and varying χ from 1 to 100.
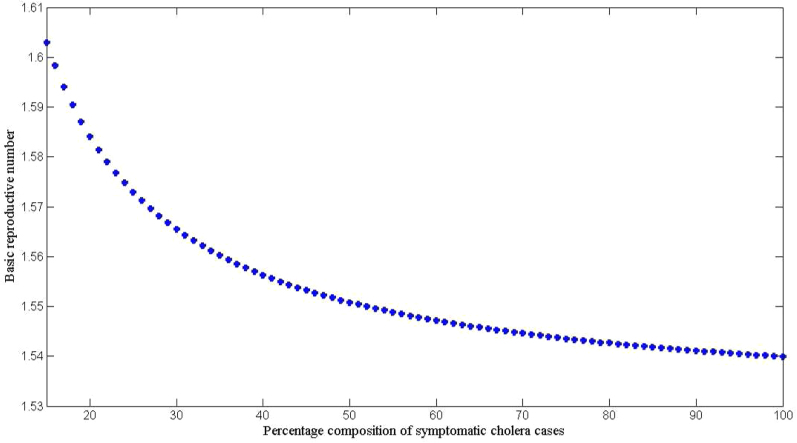
In addition, we also explored the effects of other forms of unreported cholera infection such as asymptomatic colonization on 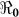 by assuming that the current data represent a certain percentage of reported cases in the clinical spectrum of cholera infection, and then fitting the model to Haitian data. Here, we extend our basic cholera model to incorporate a class of cholera asymptomatic cases as a proportion of total infections. We fit cholera reported data to the class of symptomatic cases in the model based on the assumption that the available reported data only represent a percentage of the total cholera cases. This model also assumes that asymptomatic patients, who shed approximately 103 vibrios per gram of stool for only one day, do not significantly contribute to cholera infection21. Studies in the early 1970s suggested infection with cholera strains of classical biotype (responsible for the sixth cholera pandemic) resulted in severe cholera cases in only 11% of total infections; 59% of infections were asymptomatic and the remainder represented illness of mild to moderate severity. Other studies during the same period showed that only 2% infected with seventh pandemic biotype El Tor strains had severe disease, and 75% of infected persons were asymptomatic22,23. However; recent studies have noted substantial increases in the percentage of patients with severe dehydration24, and the percentage of asymptomatic infected patients appears to be much smaller (<50%, in a recent study by Harris et al. in Bangladesh25), attributed to genetic changes in the organism26,27. Based on these studies we carried out sensitivity analysis to assess the effects of varying the percentage composition of reported symptomatic cases in the range 15–100% on the basic reproductive number. The range of the percentage composition of reported symptomatic cases (15–100%) considered here is consistent with recent findings which suggest an increase in the percentage of severe cases24 and a smaller percentage of asymptomatic carriage (<50%)25. The results in Figure 5 show that incorporating other forms of unreported cholera infection into the model changed
by assuming that the current data represent a certain percentage of reported cases in the clinical spectrum of cholera infection, and then fitting the model to Haitian data. Here, we extend our basic cholera model to incorporate a class of cholera asymptomatic cases as a proportion of total infections. We fit cholera reported data to the class of symptomatic cases in the model based on the assumption that the available reported data only represent a percentage of the total cholera cases. This model also assumes that asymptomatic patients, who shed approximately 103 vibrios per gram of stool for only one day, do not significantly contribute to cholera infection21. Studies in the early 1970s suggested infection with cholera strains of classical biotype (responsible for the sixth cholera pandemic) resulted in severe cholera cases in only 11% of total infections; 59% of infections were asymptomatic and the remainder represented illness of mild to moderate severity. Other studies during the same period showed that only 2% infected with seventh pandemic biotype El Tor strains had severe disease, and 75% of infected persons were asymptomatic22,23. However; recent studies have noted substantial increases in the percentage of patients with severe dehydration24, and the percentage of asymptomatic infected patients appears to be much smaller (<50%, in a recent study by Harris et al. in Bangladesh25), attributed to genetic changes in the organism26,27. Based on these studies we carried out sensitivity analysis to assess the effects of varying the percentage composition of reported symptomatic cases in the range 15–100% on the basic reproductive number. The range of the percentage composition of reported symptomatic cases (15–100%) considered here is consistent with recent findings which suggest an increase in the percentage of severe cases24 and a smaller percentage of asymptomatic carriage (<50%)25. The results in Figure 5 show that incorporating other forms of unreported cholera infection into the model changed 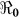 estimate by less than 5%.
estimate by less than 5%.
Figure 5. The relationship between 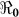 and the percentage composition of reported symptomatic cholera cases reported using aggregated data for Haiti, parameter values from Table 4, and population size from Table 2.
and the percentage composition of reported symptomatic cholera cases reported using aggregated data for Haiti, parameter values from Table 4, and population size from Table 2.
Discussion
Estimated basic reproductive numbers varied across the departments ranging from 1.06 to 2.63. With the exception of the work by Chunara et al.28, these results are in the same general range as the estimates from other mathematical models of the initial Haitian epidemic (Table 1), and are similar to those obtained for the 2008–2009 Zimbabwe outbreak6. However, in our model partial reproductive numbers were also highly heterogeneous suggesting that the patterns of transmission and transmission routes varied by department, and that some departments would be more amenable to vaccination compared with other kinds of interventions. The results in Table 2 suggest that on average, human-to-human transmission accounted for 68% of all the transmission, but both transmission pathways contributed to initiating and sustaining cholera outbreaks across the departments. These quantities of 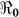 >1 obtained for the departments and the whole country (see Table 2) suggest that future epidemics are highly likely, after population immunity has waned, unless effective control measures are put in place. These patterns address the concern that cholera may become endemic in Haiti because of a combination of a large estuarine system which may act as possible long-term ecological reservoirs for cholera, combined with continued transmission within human populations. In this setting, there would appear to be clear utility in mass vaccination with cholera vaccine with even moderate uptake, particularly in light of the significant herd protection afforded neighboring non-vaccinated individuals noted in prior studies29. However, to achieve optimal protection of the population, vaccination would need to be combined with other measures that permanently improve water systems and/or otherwise decrease the risk of transmission from environmental sources.
>1 obtained for the departments and the whole country (see Table 2) suggest that future epidemics are highly likely, after population immunity has waned, unless effective control measures are put in place. These patterns address the concern that cholera may become endemic in Haiti because of a combination of a large estuarine system which may act as possible long-term ecological reservoirs for cholera, combined with continued transmission within human populations. In this setting, there would appear to be clear utility in mass vaccination with cholera vaccine with even moderate uptake, particularly in light of the significant herd protection afforded neighboring non-vaccinated individuals noted in prior studies29. However, to achieve optimal protection of the population, vaccination would need to be combined with other measures that permanently improve water systems and/or otherwise decrease the risk of transmission from environmental sources.
As alluded to above, the Haitian cholera epidemic has resulted in the development of several mathematical models (Table 1), driven, in part, by the close proximity of Haiti to the United States (with resultant interest in the outbreak), as well as recent developments in modeling techniques. The prediction of the sequence and timing of regional cholera epidemics in Haiti using a spatial approach was reported by Tuite et al.3. A similar spatial transmission model considering hydrologic and human mobility drivers of pathogen dispersal was proposed by Bertuzzo et al.4. Chao et al.5 used an individual, agent-based, dynamic transmission model to understand the dynamics of the of the cholera epidemic in Haiti. Not unexpectedly, these and other models have given somewhat different results (Table 1). Nonetheless, the range of values for 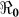 has been fairly consistent; there is also clear convergence in the models related to the importance of vaccination, combined, potentially, with efforts to minimize transmission from environmental sources. The Haiti situation provides a unique opportunity to apply modeling results in development and implementation of practical public health interventions. As the history of cholera plays out in Haiti, it will be important to use the actual outcomes of these interventions to appropriately parameterize and assess the value of this and other models and modeling approaches.
has been fairly consistent; there is also clear convergence in the models related to the importance of vaccination, combined, potentially, with efforts to minimize transmission from environmental sources. The Haiti situation provides a unique opportunity to apply modeling results in development and implementation of practical public health interventions. As the history of cholera plays out in Haiti, it will be important to use the actual outcomes of these interventions to appropriately parameterize and assess the value of this and other models and modeling approaches.
Methods
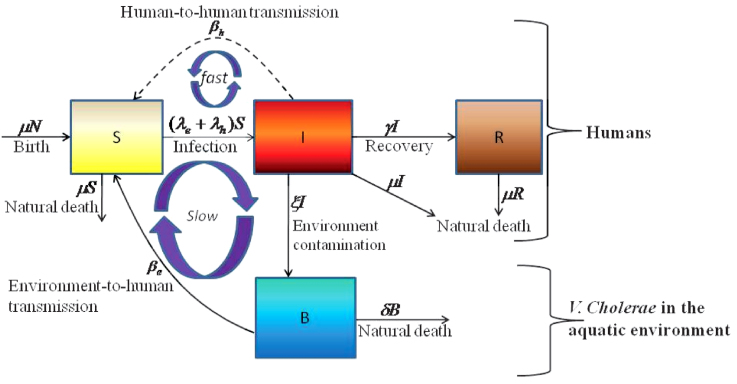
The cholera model compartmentalizes the human population (Figure 6), of density N, into susceptibles S, infected I and recovered R (see on-line supplemental material included with reference6 for a complete mathematical description of the model). The concentration of vibrios in contaminated water is denoted by B. As previously described in application of the model to the Zimbabwe cholera epidemic of 2008-09, susceptible individuals acquire cholera infection either by ingesting environmental vibrios from contaminated aquatic reservoirs (a “slow” transmission route requiring a higher infectious dose) or through close contact with infected humans associated with ingestion of “hyperinfectious” vibrios30,31 (a “fast” transmission route related to the observed decrease in infectious dose seen among V. cholerae within a matter of hours of passage in diarrheal stool) at daily per-capita rates 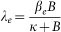 and
and 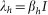 respectively, with the subscripts e and h denoting environment-to-human and human-to-human transmission routes. The constant κ is a shape parameter that determines the human infectious dose: when B equals κ the probability of ingestion resulting in human disease is 0.5. βe and βh are rates of exposure to vibrios from the contaminated environment and through human-to-human interaction respectively. Infected individuals recover from infection at a rate γ. Cholera infected individuals contribute to V. cholerae in the aquatic environment at a daily rate χ and vibrios have a net death rate δ in the environment. Readers interested in the model formulation, parameters and other properties should refer to6,23. The resulting model as a system of coupled stochastic differential equations is as follows.
respectively, with the subscripts e and h denoting environment-to-human and human-to-human transmission routes. The constant κ is a shape parameter that determines the human infectious dose: when B equals κ the probability of ingestion resulting in human disease is 0.5. βe and βh are rates of exposure to vibrios from the contaminated environment and through human-to-human interaction respectively. Infected individuals recover from infection at a rate γ. Cholera infected individuals contribute to V. cholerae in the aquatic environment at a daily rate χ and vibrios have a net death rate δ in the environment. Readers interested in the model formulation, parameters and other properties should refer to6,23. The resulting model as a system of coupled stochastic differential equations is as follows. 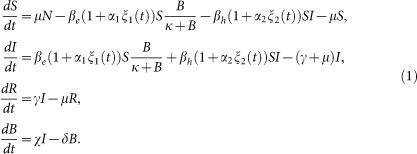 Here, αi for i = 1, 2 are real constants and ξ(t) = (ξ1(t), ξ 2(t)) is the Gaussian white noise process to model environmental stochasticity satisfying < ξ i(t)> = 0 where <> denotes ensemble average. It can also be shown that a solution of model system (Eqs. 1) is Markovian if and only if the external noises are white. We have assumed the Stratonovich interpretation of stochastic differential equations (Eqs. 1), which conserves the ordinary rule of calculus and in this case the stochastic differential equations can be considered as an ensemble of ordinary differential equations32,33. A code in MATLAB (The Mathworks, Inc., Version 7.10.0.499, R2010a) was used to fit the stochastic model system (Eqs. 1) to data and estimate the basic reproductive number and standard error for a given number of iterations. The code uses a fourth order Runge–Kutta numerical scheme for numerical integration and the built-in MATLAB least-squares fitting routine lsqcurvefit. In each iteration:
Here, αi for i = 1, 2 are real constants and ξ(t) = (ξ1(t), ξ 2(t)) is the Gaussian white noise process to model environmental stochasticity satisfying < ξ i(t)> = 0 where <> denotes ensemble average. It can also be shown that a solution of model system (Eqs. 1) is Markovian if and only if the external noises are white. We have assumed the Stratonovich interpretation of stochastic differential equations (Eqs. 1), which conserves the ordinary rule of calculus and in this case the stochastic differential equations can be considered as an ensemble of ordinary differential equations32,33. A code in MATLAB (The Mathworks, Inc., Version 7.10.0.499, R2010a) was used to fit the stochastic model system (Eqs. 1) to data and estimate the basic reproductive number and standard error for a given number of iterations. The code uses a fourth order Runge–Kutta numerical scheme for numerical integration and the built-in MATLAB least-squares fitting routine lsqcurvefit. In each iteration:
Two white noise time series, ξ1(t) and ξ2(t) were generated;
The fitting routine lsqcurvefit found the parameters that minimized the sum of squared errors, including initial conditions (S0,I0,R0,B0) and parameters α1and α2 that scale the variance of ξ1 and ξ2;
The estimates were stored in a table.
Figure 6. Model flow diagram.
This was repeated 1000 times. The means and standard errors of these parameter estimates are reported in Table 2.
We fit the cholera model system (Eqs.1) to cumulative hospitalized cholera cases to estimate the basic reproductive numbers and critical vaccination coverage levels for the geospatially localized cholera outbreaks in Haiti by using daily data on numbers of hospitalized cases published on the MSPP website15. These data may well be underestimates due to the weak health system in Haiti. However, despite quality issues surrounding the data set, it presents the best currently available platform for quantifying the magnitude of the cholera outbreak in Haiti.
The basic reproductive number (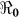 ), is defined as a measure of the average number of secondary cases generated by a primary case. Understanding its magnitude and variation can help to identify cholera “hot spots” and in designing targeted surveillance programs. The two transmission routes of cholera are quantitatively described by partial reproductive numbers,
), is defined as a measure of the average number of secondary cases generated by a primary case. Understanding its magnitude and variation can help to identify cholera “hot spots” and in designing targeted surveillance programs. The two transmission routes of cholera are quantitatively described by partial reproductive numbers, 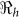 and
and 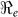 that describe new cases that arise from either the fast human-to-human or the slower environment-to-human transmission routes, respectively. In the fitting, we estimate βe and βh to match the reported hospitalized cases in each department and for the whole country with other parameter values fixed as given in Table 4 and calculate the corresponding values of
that describe new cases that arise from either the fast human-to-human or the slower environment-to-human transmission routes, respectively. In the fitting, we estimate βe and βh to match the reported hospitalized cases in each department and for the whole country with other parameter values fixed as given in Table 4 and calculate the corresponding values of 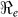 ,
, 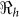 and
and 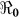 . For each department, we use the data points for the number of days that maximize the basic reproductive number estimate at the onset of an outbreak (i.e. maximizing βe and βh), using data for the period from 30 0ctober 2010 to 25 December 2010. The data sets used for the estimation of
. For each department, we use the data points for the number of days that maximize the basic reproductive number estimate at the onset of an outbreak (i.e. maximizing βe and βh), using data for the period from 30 0ctober 2010 to 25 December 2010. The data sets used for the estimation of 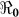 were obtained by systematically testing different subsets of data from the start of an outbreak. We also normalize our population data by 1000 thus computed estimates of βe and βh are per capita.
were obtained by systematically testing different subsets of data from the start of an outbreak. We also normalize our population data by 1000 thus computed estimates of βe and βh are per capita.
Table 4. Cholera model parameters and values.
| Parameter | Symbol | Value | Source |
|---|---|---|---|
| Natural human birth and death rate | μ | 61.2 years | 35 |
| Concentration of V. cholerae in the environment | κ | 106 cells/ml | 36 |
| Rate of contribution to V. cholerae in the aquatic environment | χ | 10 cells/ml-day/person | 36 |
| Rate of recovery from cholera | γ | (5 day) −1 | 37 |
| Death rate of vibrios in the environment | δ | (30 day) −1 | 37 |
The corresponding minimum vaccination coverage's (c) for a cholera vaccine with 78% efficacy7 for the 10 departments and the whole country given are based on the formula in34,
where r is the fraction of the vaccinated population who are completely immunized and s is the proportional reduction of the susceptibility for those partially immunized.
Author Contributions
Dr. Mukandavire was responsible for construction of the model and initial manuscript preparation. Drs. Smith and Morris assisted with conceptualization of the project and preparation of the manuscript.
Acknowledgments
Z.M. and J.G.M. are supported in part by a grant from the National Institute of Allergy and Infectious Diseases (RO1AI097405, awarded to J.G.M.). Z.M. is also supported by the UF Science for Life Program, an interdisciplinary program with support from the Howard Hughes Medical Institute. D.L.S. is funded by the RAPIDD program of the Science and Technology Directorate, Department of Homeland Security, and the Fogarty International Center, National Institutes of Health. The authors acknowledge Nathaniel Hupert, Michael L. Washington and their colleagues at the U.S. Centers for Disease Control and Prevention's Preparedness Modeling Unit and the group of modelers involved in the useful discussions on the cholera outbreak in Haiti.
References
- CDC, Haiti cholera outbreak, http://www.cdc.gov/haiticholera/situation/, Accessed February 10 (2011).
- Andrews J. R. & Basu S. Transmission dynamics and control of cholera in Haiti: an epidemic model. Lancet 377, 1248–1255 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuite A. L. et al. Cholera epidemic in Haiti, 2010: Using a transmission model to explain spatial spread of disease and identify optimal control interventions. Ann. Intern. Med. 154, 293–302 (2011). [DOI] [PubMed] [Google Scholar]
- Bertuzzo E. et al. Prediction of the spatial evolution and effects of control measures for the unfolding Haiti cholera outbreak. Geophysical Research Letters 38, L06403 (2011). [Google Scholar]
- Chao D. L., Halloran M. E. & Longini I. M. Vaccination strategies for epidemic cholera in Haiti with implications for the developing world. Proc. Natl. Acad. Sci. USA 108, 7081–7085 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukandavire Z. et al. Estimating the reproductive numbers for the 2008–2009 cholera outbreaks in Zimbabwe. Proc. Natl. Acad. Sci. USA 108, 8767–8772 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lucas M. E. et al. Effectiveness of mass oral cholera vaccination in Beira, Mozambique. N. Engl. J. Med. 352, 757–767 (2005). [DOI] [PubMed] [Google Scholar]
- Piarroux R. et al. Understanding the cholera epidemic, Haiti. Emerg. Infect. Dis. 17 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sur D. et al. Efficacy and safety of a modified killed-whole-cell oral cholera vaccine in India: an interim analysis of a cluster-randomised, double-blind, pacebo-controlled trial. Lancet 374, 1694–1702 (2009). [DOI] [PubMed] [Google Scholar]
- Thiem V. D. et al. Long-term effectiveness against cholera of oral killed whole-cell vaccine produced in Vietnam. Vaccine 24, 4297–4303 (2006). [DOI] [PubMed] [Google Scholar]
- Clemens J. D. et al. Field trial of oral cholera vaccines in Bangladesh: results from three-year follow-up. Lancet 335, 270–273 (1990). [DOI] [PubMed] [Google Scholar]
- Clemens J. D. et al. Cross-protection by B subunit whole cell cholera vaccine against diarrhea associated with heat-labile toxin-producing enterotoxigenic Escherichia coli: results of a large-scale field trial. J. Infect. Dis. 158, 372–377 (1988). [DOI] [PubMed] [Google Scholar]
- Date K. A. et al. Consideration for oral cholera vaccine use during outbreak after earthquake in Haiti, 2010–2011. Emerg. Infect. Dis. 17 (2011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez J. L. et al. Protective efficacy of oral whole-cell/recombinant-B-subunit cholera vaccine in Peruvian military recruits. Lancet 344, 1273–1276 (1994). [DOI] [PubMed] [Google Scholar]
- MSPP website at: http://mspp.gouv.ht/site/index.php?option=com_content&view=article&id=57&Itemid=1, Accessed February 2 (2011).
- Franco A. A. et al. Cholera in Lima, Peru, correlates with prior isolation of Vibrio cholerae from the environment. Am. J. Epidemiol. 146, 1067–1075 (1997). [DOI] [PubMed] [Google Scholar]
- Huq A. et al. Critical factors influencing the occurrence of Vibrio cholerae in the environment in Bangladesh. Appl. Environ. Microbiol. 71, 4645–4654 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaper J. B., Morris J. G. Jr. & Levine M. M. Cholera. Microbiol. Rev 8, 48–86 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cash R. A. et al. Response of man to infection with Vibrio cholerae. I. Clinical, serologic, and bacteriologic responses to a known inoculums. J. Infect. Dis. 129, 45–52 (1974). [DOI] [PubMed] [Google Scholar]
- Levine M. M. et al. Volunteer studies in development of vaccines against cholera and enterotoxigenic Escherichia coli: A review. In: Holme T, Holmgren J, Merson MH, Mollby R. Acute Enteric Infections in Children. New Prospects for Treatment and Prevention. Elsevier/NorthHolland Biomedical Press, pp 443–459 (1981). [Google Scholar]
- Mosley W. H., Ahmad S., Benenson A. S. & Ahmed A. The relationship of vibriocidal antibody titre to susceptibility to cholera in family contacts of cholera patients. Bull. World Health Organ. 38, 777–785 (1968). [PMC free article] [PubMed] [Google Scholar]
- Gangarosa E. J. & Mosley W. H. Epidemiology and surveillance of cholera. In: Barua D., , Burrows W., editors. Cholera. Philadelphia: W. B. Saunders, pp 381–403 (1974). [Google Scholar]
- Morris J. G. Jr. Cholera: Modern pandemic disease of ancient lineage. Emerg. Infect. Dis. 17, (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siddique A. K. et al. El Tor cholera with severe disease: a new threat to Asia and beyond. Epidemiol. Infect. 138, 347–352 (2010). [DOI] [PubMed] [Google Scholar]
- Harris J. B. et al. Susceptibility to Vibrio cholerae infection in a cohort of household contacts of patients with cholera in Bangladesh. PLoS Negl. Trop. Dis. 2, e221 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nair G. B. et al. New variants of Vibrio cholerae O1 biotype El Tor with attributes of the classical biotype from hospitalized patients with acute diarrhea in Bangladesh. J Clin Microbiol. 40, 3296–3299 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Safa A., Nair G. B. & Kong R. Y. C. Evolution of new variants of Vibrio cholerae O1. Trends Microbiol. 18, 46–54 (2010). [DOI] [PubMed] [Google Scholar]
- Chunara R., Andrews J. R. & Brownstein J. S. Social and news media enable estimation of epidemiological patterns early in the 2010 Haitian cholera outbreak. Am. J. Trop. Med. Hyg. 86, 39–45 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ali M. et al. Herd immunity conferred by killed oral cholera vaccines in Bangladesh: a reanalysis. Lancet 366, 44–49 (2005). [DOI] [PubMed] [Google Scholar]
- Merrell D. S. et al. Host-induced epidemic spread of the cholera bacterium. Nature 417, 642–645 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson E. J., Harris J. B., Morris Jr. J. G., Calderwood S. B. & Camilli A. Cholera transmission: the host, pathogen and bacteriophage dynamic. Nat. Rev. Microbiol. 7, 693–702 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Øksendal B. Stochastic Differential Equations: An Introduction with Applications., (Springer, New York, 1998), 5th edn.
- Samanta G. P. The effect of random fluctuating environment on interacting species with time delay. Int. J. Math. Educ. Sci. Technol. 27, 13–21 (1996). [Google Scholar]
- Dietz K. The estimation of the basic reproduction number for infectious diseases. Statistical Methods in Medical Research 2, 23–41 (1993). [DOI] [PubMed] [Google Scholar]
- UN data, A world of information, http://data.un.org/Data.aspx?q=haiti&d=PopDiv&f=variableID%3A68%3BcrID%3A332. Accessed March 1 (2011).
- Codeço C. T. Endemic and epidemic dynamics of cholera: The role of the aquatic reservoir. BMJ Infect. Dis. 1 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartley D. M., Morris Jr. J. G. & Smith D. L. Hyperinfectivity: A Critical Element in the Ability of V. cholerae to Cause Epidemics? PLoS Med. 3, e7 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]