Slowing and controlling the translocation of DNA in a solid-state nanopore

Abstract

DNA sequencing methods based on nanopores could potentially represent a low-cost and high-throughput pathway to practical genomics, by replacing current sequencing methods based on synthesis that are limited in speed and cost. The success of nanopore sequencing techniques requires the solution to two fundamental problems: (1) sensing each nucleotide of a DNA strand, in sequence, as it passes through a nanopore; (2) delivering each nucleotide in a DNA strand, in turn, to a sensing site within the nanopore in a controlled manner. It has been demonstrated that a DNA nucleotide can be sensed using electric signals, such as ionic current changes caused by nucleotide blockage at a constriction region in a protein pore or a tunneling current through the nucleotide-bridged gap of two nanoelectrodes built near a solid-state nanopore. However, it is not yet clear how each nucleotide in a DNA strand can be delivered in turn to a sensing site and held there for a sufficient time to ensure high fidelity sensing. This latter problem has been addressed by modifying macroscopic properties, such as a solvent viscosity, ion concentration or temperature. Also, the DNA transistor, a solid state nanopore dressed with a series of metal-dielectric layers has been proposed as a solution. Molecular dynamics simulations provide the means to study and to understand DNA transport in nanopores microscopically. In this article, we review computational studies on how to slow down and control the DNA translocation through a solid-state nanopore

1 Introduction

Sequencing DNA with affordable cost is essential to bring routine applications of genomic data to improve human health. Success in this endeavor would allow revolutionary changes in bio-medicine. At present, commercial sequencing techniques are based on Sanger’s method ¹, sequencing DNA by synthesis. All sequencing technology based on this method require extensive sample preparations including amplification, labeling, and ligation of many DNA strands cut from long chromosomes. Over the past two decades, methods of sequencing-by-synthesis have been highly optimized and the cost of sequencing a human genome has dropped dramatically from tens of millions to tens of thousands of dollars. Further reducing the cost is very challenging with classical Sanger type methods.

To achieve low-cost sequencing (such as the 1000$-human-genome), nanopore based DNA sequencing methods have been proposed ^2–5 that can bypass many of the intensive sample preparation steps. A nanopore provides a confined geometry to guide a single-stranded DNA (ssDNA) towards a sensing site in such a way that each DNA base can be identified by an electric sensor in the nanopore. This sequencing process, if practically achieved, could be parallelized and automated, greatly reducing the labor cost and increasing the speed of DNA sequencing.

Nanopore-based DNA sequencing originated in ground breaking proof-of-concept experiments ⁶, showing that a ss-DNA molecule can be driven electrically through an α-hemolysin nanopore. Ideally, nucleotides in a ssDNA molecule pass the constriction site in a protein pore one-by-one and each nucleotide can be detected by variations in ionic current through the pore. The latter has been demonstrated in experiment in both engineered α-hemolysin ^7,8 and MspA ⁹ nanopores. However, it remains a grand challenge to pause each nucleotide at the pore constriction site for sufficiently long times to permit high fidelity sensing.

Inspired by protein nanopores, researchers have deployed advanced nanofabrication techniques to build various electronic devices containing solid-state nanopores for DNA sequencing ^2,10,11. It was suggested theoretically ¹² and has been recently demonstrated experimentally ^13,14 that the type of a DNA nucleotide in the gap of two nano-electrodes can be determined by the tunneling current through the electrodes. As above, the outstanding challenge for methods based on solid-state nanopores is again, how to pause each nucleotide, in turn, in front of a sensor for sufficient time to allow accurate sensing. Therefore, it is critical to control the translocation of DNA strands through a solid-state nanopore.

Experimentally, a DNA molecule can be driven through a solid-state nanopore either mechanically or electrically. The former can be achieved using a magnetic tweezer ¹⁵ or an optical tweezer ^16,17 to pull DNA through the pore. Although the pulling velocity in these single molecule experiments can be very slow, it is difficult to scale up these methods to sequence DNA in parallel, that is simultaneously utilizing thousands of nanopores on a chip ¹⁸. Alternatively, DNA can be driven through a solid-state nanopore by a biasing electric field. For a double stranded DNA (dsDNA) molecule, the typical translocation velocity through a solid-state nanopore is about 30 base-pairs per micro-second if the biasing voltage is a few hundred millivolts. This translocation speed would make nucleotide identification be beyond the capability of current sensors ^13,14. It has been shown experimentally that a viscous solvent (such as an aqueous glycerol solvent) can reduce the translocation velocity of DNA by a factor of 5.5. Additionally, experiments showed that DNA can be trapped in a small nanopore (whose diameter is smaller than that of a DNA duplex), if the biasing electric voltage is below a threshold value ¹⁹.

From a practical point of view, even though different nanopores might have nearly the same diameter, the dynamics of DNA translocation through these pores could be quite different. This is mainly due to different surface properties of nanopores. For example, the translocation velocity can be affected by the surface roughness of a nanopore ²⁰. Charges on a pore surface could be nonuniformly distributed and the charge density may vary among different pores, which affect DNA motion not only electrically but also hydrodynamically through the electro-osmotic flow on a charged pore surface. It is therefore difficult to describe these effects using continuum theory alone. Atomistic molecular dynamics (MD) simulations are a useful tool to study the effects on DNA motion produced by subtle changes of the pore surface, and have provided valuable insights on DNA translocation through solid-state nanopores ^19–25. In this article, we review MD simulation studies of the translocation of DNA through solid-state nanopores and discuss how the motion of DNA can be slowed and controlled to make possible the vision of nanopore-based DNA sequencing. Note that coarsed-grained simualtions based on Langevin dynamics have also provided valuable insights on DNA translocation through a nanopore ^26–28. A review article can be found in ²⁹.

2 Roadmap

In order to best explain the factors affecting DNA translocation through a solid state nanopore, we divide our discussion into three portions. First, the effect of friction, both contact and viscoelastic, are described through the lens of simulation studies. Next, the role of the zeta potential is discussed, followed by a description of recent work using electric trapping fields in a nanopore to control DNA motion. An outlook and discussion is given last which places the work discussed in context and points to possible fruitful future directions. A good description of simulation methods employed in the simulations described herein can be found in Refs. ^21,25.

3 Simulations to gain insight into the control of DNA strand transport through nanopores

DNA translocation through a nanopore can be affected by many factors, such as the temperature, electrolyte viscosity, ion concentration, pore surface charge density and other factors. Additionally, the direct interaction between DNA and a pore surface yields a frictional force. Assuming that a ds-DNA molecule can only move along the symmetry axis of a nanopore and that end effects of the pore are negligible, the translocation velocity of dsDNA driven through the pore by an applied electric field can be determined by solving coupled differential equations ^30,31: (1) Stokes equation for the flow between the DNA and pore surfaces; (2) Poisson equation for the distribution of electric potentials in the pore. With non-slip boundary conditions for flow and with known ζ-potentials on DNA and pore surfaces, the translocation velocity of the ds-DNA molecule is

$$v=\epsilon \frac{{\zeta }_d-{\zeta }_w}{\eta }E,$$ (1)

where ε is the dielectric constant of the electrolyte, η the viscosity of the electrolyte, ζ_d and ζ_w the zeta potentials on DNA and pore surfaces respectively, and E the biasing electric field.

According to Eq. 1, the translocation velocity of a dsDNA or ssDNA molecule (strand) can be reduced by employing the following methods: (1) increasing friction on DNA (such as increasing the viscosity of the electrolyte); (2) adjusting ζ potentials on DNA and pore surfaces; (3) reducing biasing electric field or superimposing electric trapping fields.

3.1 Increasing frictional force

3.1.1 Solvent viscosity

It is reasonable to assume that a DNA strand’s translocation velocity through a nanopore will decrease with increasing solvent viscosity and this was indeed demonstrated experimentally ³²; the translocation velocity of dsDNA in a 1:1 glycerol-water mixture was reduced 5 to 6 times. Using MD simulations, we studied the diffusion coefficient of ssDNA through a 4-nm-diameter SiO₂ nanopore in a 1:2 glycerol-water solution. As shown in Fig. 1a, the ssDNA molecule was confined to the symmetry axis of the nanopore. The thickness of the nanopore is 14.8 nm. Because of the periodic boundary imposed to simulations, the nanopore (without an entrance and an exit) is effectively an infinite nanochannel.

Fig. 1.

MD simulation of ssDNA in the nanopore solvated with glycerol. a) Simulation system. The ssDNA molecule moves along the symmetry axis of a solid-state nanopore (tan). Glycerol molecules are shown as balls-and-sticks. Water and ions are not shown. b) Diffusive motion of ssDNA along the symmetry axis of the nanopore. c) Mean square displacement vs. time interval. The slope of the linear fit (solid line) is twice the diffusion coefficient D~ 1 Ų/ns, or 1×10⁻⁷ cm²/s.

Figure 1b shows the diffusive motion of the ssDNA molecule in the pore. From the simulation trajectory, the distance L moved along the symmetry axis of the nanopore was computed as a function of time, i.e. L=z(t)-z(0). Using this relation, one can calculate the mean square displacement of the ssDNA molecule as a function of a time interval Δt, as shown in Fig. 1c. As < L² > = 2DΔt (where D is the diffusion coefficient), the computed diffusion coefficient is about 1×10⁻⁷ cm²/s, about an order of magnitude larger than that of ssDNA in water ²⁵. Using the fact that D ∝ kT/ξ, we can surmise that the friction coefficient ξ of ssDNA in the glycerol solvent can be 10 times larger and the translocation velocity of ssDNA could be reduced by 10 times.

In this simulation, ssDNA was confined on the central symmetry axis of the nanopore, preventing ssDNA from being stuck on the pore surface. Besides the hydrodynamic friction, the direct interaction between a DNA molecule and the pore surface provides additional contact friction as discussed below.

3.1.2 Contact friction

3.1.2.1 Solid surface of a nanopore

The diameter of a solvated dsDNA helix is about 2.4 nm. When the dsDNA is electrically driven into a 2-nm-diameter nanopore, the dsDNA molecule is locally stretched near the constriction of a double-cone-shaped nanopore (see Fig. 2) to allow dsDNA to squeeze through the constriction area ¹⁹. Thus, the dsDNA molecule is in direct contact with the pore surface as shown in Fig. 2, yielding a contact frictional force on the molecule.

Fig. 2.

MD simulation of the nanopore trap. Left: Snapshots of the simulated systems that include dsDNA and water and ions (not shown) as well as a 2.0 nm diameter pore. Right: The number of base-pairs permeating through the pore in four MD simulations carried out at different biases. The simulations predict a voltage threshold between 500 mV and 1.0 V. Inset: Normalized histogram of the DNA displacement in the pore constriction at a 0 V bias. The solid line shows the distribution expected for a particle restrained by a harmonic spring with a 7.2 nN nm⁻¹ spring constant. Adapted from ref. ¹⁹.

Due to contact friction, the translocation velocity of the ds-DNA molecules is greatly reduced. Fig. 2 shows that when the biasing voltage across the solid membrane is less than 1 V, the dsDNA molecule may remain stuck at the constriction region of the pore. At a higher biasing voltage (2 V), the dsDNA molecule can be driven through the constriction region. By reducing the biasing voltage to 1 V (larger than the threshold voltage), the translocation velocity is approximately 1 base-pair per 30 ns. Experimental studies ¹⁹ of the same system demonstrated that the velocity of dsDNA in the extreme case can be as low as 1 base-pair per 2 ms.

3.1.2.2 Chemically modified surface of a nanopore

The direct interaction between DNA and a pore surface could also occur when DNA moves radially towards the surface. Depending on the adhesion between DNA and the surface, DNA could move away from or be stuck on the pore surface. To slow the translocation velocity of DNA, it is possible to coat the pore surface with polymers containing different functional groups ^24,33, i.e. chemically modifying the pore surface. Thus, the surface properties such as the charge density and hydrophobicity can be properly controlled. Additionally, the self-assembled monolayer (SAM) coating can provide a more benign environment than a solid surface.

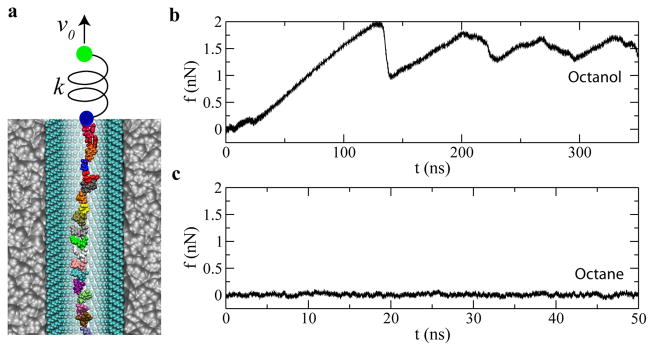
Figure 3 shows the steered MD (SMD) ³⁴ simulations performed to mechanically drive ssDNA through a SAM coated nanochannel mimicking the action of an optical tweezer ¹⁶. Both the hydrophilic octanol-SAM and the hydrophobic octane-SAM coated pores were used in simulations. Figure 3 illustrates the simulation setup. A spring (10 pN/Å) was used to drive ssDNA forward. One end of the spring was attached to a pulling stage that moved at a constant velocity (2 Å/ns), while the other end was attached to the center of mass of all phosphorus atoms.

Fig. 3.

Mechanically driving ssDNA through a SAM-coated nanochannel. (a) simulation setup. v₀ is the pulling velocity of the stage (green dot); k is the spring constant; the blue dot represents the ssDNA position. Water and ions are not shown. (b) Force-time dependence when ssDNA is mechanically driven by the harmonic spring in the octanol-SAM-coated nanochannel. (c) Force-time dependence when ssDNA is mechanically driven by the harmonic spring in the octane-SAM-coated nanochannel. Adapted from ref. ²⁴.

Figure 3b and 3c show time-dependent forces in the spring during pulling processes. Clearly, frictional forces in the two cases considered, hydrophobic and hydrophilic coatings, are quite different and result in different ssDNA translocation dynamics. As shown in Fig. 3b (the hydrophilic case), after ss-DNA diffused away from the symmetry axis and bound to the octanol-SAM, the force in the spring increased linearly with time. When the force in spring was comparable to the friction force, ssDNA quickly caught up with the pulling stage (a slip event) and the force in spring dropped (Fig. 3b). Since the pulling force was smaller than the friction force, ssDNA was stuck again. As the pulling stage kept moving forward, force in the spring built up again and triggered another slip event. Thus, forces in the spring periodically increased and decreased as shown in Fig. 3b, corresponding to the stick-slip motion of ssDNA.

In contrast to about 1.5 nN friction force for ssDNA in octanol-SAM-coated nanochannel, the friction force for ss-DNA in the octane-SAM-coated nanochannel is much smaller (Fig. 3c). Because ssDNA is always near the symmetry axis of the octane-SAM-coated channel, during a pulling process, there is no direct interaction between ssDNA and the SAM. The pulling force in the spring is balanced by the hydrodynamic friction force, ~ 8 pN, about 200 times less in friction.

These simulations indicate that the translocation velocity of ssDNA is much faster in the octane-SAM-coated nanochannel than in the octanol-SAM-coated one. As it is possible to design and synthesize vast varieties of SAMs, the interaction between ssDNA and a SAM can be modified and the translocation speed of ssDNA could be adjusted by the selection of a proper SAM. It is important to note that uncontrolled stick-slip motion would not be a favorable mode of operation in a sequencing technology.

3.2 Modifying surface ζ potentials of dsDNA and a nanopore

3.2.1 Ion concentration

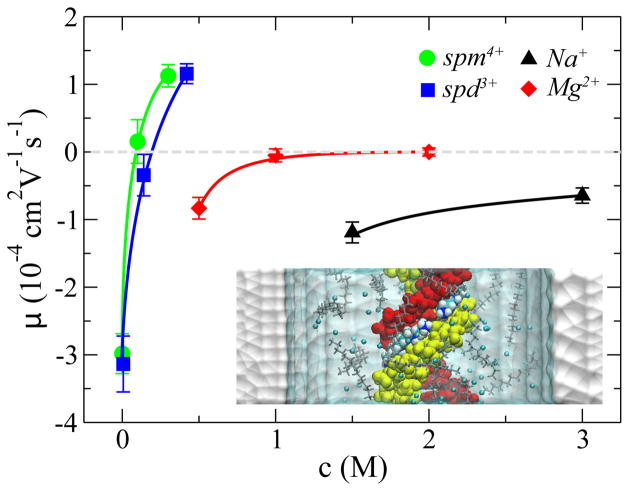
Near a charged surface, such as the DNA surface, counterions form an electric screening “cloud”. The thickness of this “cloud” is characterized by the Debye length that depends on the ion concentration c. This picture is valid for mono- or di-valent counterions near the dsDNA surface, as suggested by the small-angle x-ray scattering experiment ³⁵. The empirical formula ³⁶ to compute a surface ζ potential is that ζ =a–bln(c), where a and b are surface-related coefficients. For multivalent counterions, the ions may even form a condensed layer that tightly binds the dsDNA molecule ³⁷. Thus, the ζ potential on the dsDNA surface depends on both the valence and the concentration of counterions, which was confirmed by MD simulations ²³, as shown in Fig. 4.

Fig. 4.

Electrophoretic mobility μ of DNA versus concentration of counterions: Na⁺ (triangle), Mg²⁺, spd³⁺ and spm⁴⁺. Lines are guides to the eye. inset: A snap shot of the simulation system containing dsDNA (red and yellow), water (cyan and transparent), nanopore (white) Cl⁻¹ and spm⁴⁺ ions. The spm⁴⁺ ions in the minor groove of dsDNA are highlighted and are shown as van der Waals spheres. The rest spm⁴⁺ ions are in the “stick” presentation. Adapted from ref. ²³.

The inset in Fig. 4 illustrates the simulation system, a ds-DNA molecule in the electrolyte confined in a 6-nm-diameter solid-state nanopore. The pore surface is neutral. In simulations, the same electric field (E=78 mV/nm) was applied vertically across the nanopore. The mean velocity < v > of dsDNA translocation was computed from each simulation trajectory and the electrophoretic mobility was obtained using μ =< v > /E. Results for dsDNA in different electrolytes are summarized in Fig. 4.

In a mono- or di-valent electrolyte, the electrophoretic mobilities (in absolute value) of dsDNA decrease with increasing ion concentrations (Fig. 4). For dsDNA in NaCl electrolyte, the negatively charged dsDNA molecule always move opposite the field direction. For dsDNA in MgCl₂ electrolyte, the effect of dsDNA charge screening is more significant. The ds-DNA molecule barely moved in the electric field because of the high ionic strength. Interestingly, in the spermine (spm⁴⁺) or spermidine (spd³⁺) electrolyte, dsDNA could even move in the field direction at the high ion concentration. Thus, the electrophoretic mobility of dsDNA changed its sign (Fig. 4). This indicates that the total charge of the complex of dsDNA and nearby counterions is positive, i.e. charge inversion of ds-DNA. From simulation trajectories, it was found that spd³⁺ or spm⁴⁺ ions could localize in the minor groove of the ds-DNA molecule (see the inset in Fig. 4). These simulations also demonstrate that the counterion condensation on the ds-DNA surface may only occur readily in a multivalent electrolyte. Nonetheless, it is clear that modifying the ζ potential of dsDNA via the ionic screening effect, can slow translocation or even reverse translocation direction of dsDNA through a nanopore.

3.2.2 Charge density of a pore surface

The ζ potential of a nanopore surface depends on the surface charge density σ ³⁸. Normally, the surface of a solid-state pore after TEM (transmission electron microscopy) drilling is negatively charged. However, the surface charge of a pore can be changed by controlling the gate voltage of a buried electrode near the pore ³⁹ or via chemical modification of the pore surface by polymer coating ^25,33. To investigate how the translocation of dsDNA can be affected by the surface charge density of a pore, MD simulations ⁴⁰ were carried out.

The simulation system is shown in the inset of Fig. 5. Five nanopores were constructed “in silico” to have the uniform surface charge density between −0.34 and 0.34 e/nm², where e is the charge of an electron. Similar to simulations illustrated in Fig. 3, a harmonic spring was used to apply a mechanical force on the dsDNA molecule in a biasing electric field. As the spring stretched, the spring force increased and eventually balanced the effective electric driving force on dsDNA. The radius of each nanopore was 3 nm. In 0.1 M and 1 M KCl electrolytes, the Debye lengths are 1 nm and 0.3 nm, respectively. For the dsDNA molecule confined on the symmetry axis of a nanopore, the direct electric interaction between dsDNA and the pore is less important than the electroosmotic effect on a charged surface. When the pore surface is charged, counterions near the surface can be driven by the biasing electric field, yielding an electroosmotic flow in the nanopore. Note that the direction of the electroosmotic flow on the pore surface reverses when the sign of the surface charge changes. Therefore, the hydrodynamic coupling of the electroosmotic flow and the dsDNA motion results in a frictional force on dsDNA. Theoretically, the second term −εζ_wE/η in Eq. 1 is the velocity of an electroosmotic flow on a charged pore surface in the electric field E and the first term εζ_d E/η in Eq. 1 is the electrophoretic velocity of dsDNA in the reference frame fixed to the electroosmotic flow in the nanopore ³⁰.

Fig. 5.

The stall force F on DNA in a nanopore versus the pore surface charge density σ. The direction of the stall force depends on the surface charge density σ. inset: A snapshot of the simulation system showing simultaneous actions of electric and mechanical forces on dsDNA in a nanopore. Adapted from ref. ⁴⁰.

Fig. 5 shows that, when the pore surface charge density changes from the neutral to a positive value, the effective driving force on dsDNA increases. This is due to the fact that the electroosmotic flow (on the positively charged pore surface) moves in the same direction as the dsDNA molecule does in the electric field. Thus, the dsDNA molecule was pushed by such flow and the spring stretched further. The spring force increased until dsDNA stalled again. When the surface charge density is negative, the electroosmotic flow on the pore surface moves opposite the direction of dsDNA motion. Thus, the ds-DNA molecule was pushed back by that flow and the spring was less stretched. Therefore, the stall force in the spring was less for a more negatively charged pore surface (Fig. 5). The stall force in the spring can even change its sign when the surface charge density is negative enough, indicating that the dsDNA molecule reverses its motion and moves in the field direction.

Since the surface charge density of a nanopore can be set through appropriate selection of a SAM coated on the pore surface or can be dynamically adjusted by modifying the gate voltage on the electrode near the pore surface, it is possible to slow or even reverse the motion of dsDNA in a solid-state nanopore. In these simulations, the direct interaction between dsDNA and a charged surface was not considered, which can impose an additional contact friction as discussed above.

3.3 Applying electric fields in a nanopore

3.3.1 Feedback control of the biasing electric field

The entrance of DNA into a solid-state nanopore can be detected by the ionic current through the pore. The open-pore current is reduced once DNA enters the pore because DNA physically and partially blocks the ion pathway through the pore. However, DNA also brings extra counterions into the pore that contribute to the total ionic current. Thus, in a low ionic concentration, a current enhancement may be observed as DNA transits the pore ⁴¹. Nonetheless, once such signal is detected, one can reduce or even reverse the biasing electric field to slow the translocation of DNA in a nanopore, as demonstrated by recent experiments ¹⁹.

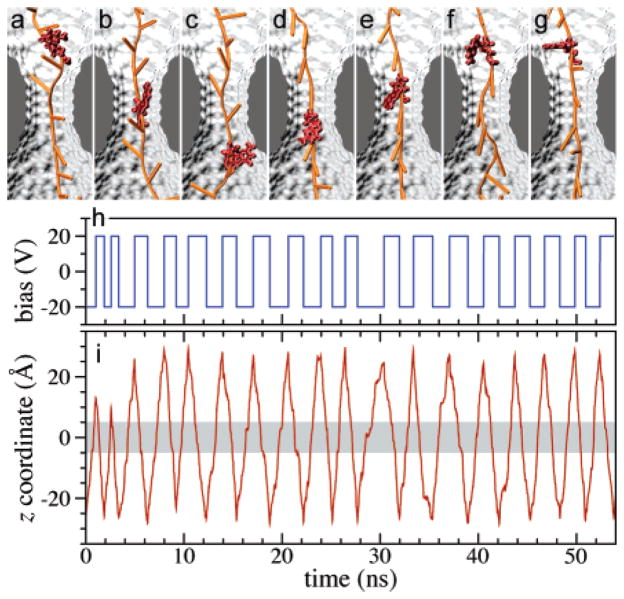
Simulation studies ²², shown in Fig. 6, illustrate that, after ssDNA enters a nanopore, the change from a constant biasing voltage to an alternating voltage across the pore can provide an electric trap for the ssDNA molecule. Figures. 6a–g show the motion of ssDNA during one cycle of voltage oscillation. The same nucleotide can move back and forth through the pore’s constriction region. During many aperiodic cycles of voltage alternating, the ssDNA molecule was able to quickly respond the voltage change, i.e., ssDNA reversed the direction of motion when the voltage changed its sign. Over about 18 cycles, the whole ssDNA molecule oscillated about the pore’s constriction without moving backward or forward. Thus, the ssDNA is effectively trapped by the alternating electric field. However, to trap ssDNA at a single base resolution, it is important to know when to switch the voltage, which might be feasible by detecting electric potential signals generated by different conformations of the same nucleotide ²² while it moves back and forth through the constriction (see Fig. 6).

Fig. 6.

DNA motion under alternating external electric field. (a–g) Typical conformations of a DNA strand during one translocation cycle. The conformations of one nucleotide are highlighted for clarity. (a,b) DNA moves down (toward its 5′ end) with its bases tilted up; (c) the base of the highlighted nucleotide reorients after the voltage polarity has been reversed; (d–f) DNA moves up with its bases tilted down; (g) the base of the selected nucleotide changes its orientation again. (h) The profile of the driving potential. Note that the alternating potential is in this simulation aperiodic. (i) The position of the center-of-mass of a DNA nucleotide from the middle of the DNA strand. The shaded area indicates the location of the pore’s constriction region. Adapted from ref. ²².

Besides the trapping of ssDNA in the alternating electric field, these simulations also demonstrated a possible sequencing method by measuring electric signal generated by the dipole moment of each nucleotide. To sense the electric potential signal, electrodes made of doped semiconductors can be built near a solid-state nanopore, yielding a capacitive device named “nanopore capacitor” ⁴².

3.3.2 Translocation through nanopores dressed with trapping electric fields

3.3.2.1 Trapping ssDNA in the DNA transistor

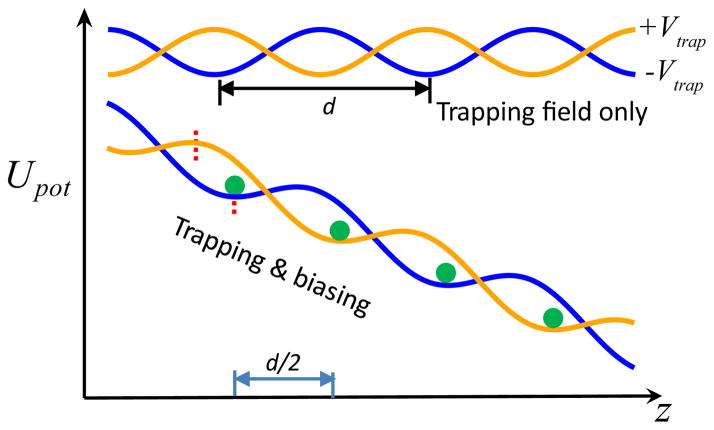
In order to sequence DNA, each nucleotide in a ssDNA molecule should be placed near a sensing site for a sufficiently long time that allows for accurate measurements, and then move the ssDNA by one nucleotide to identify the next nucleotide (adjacent to the previously measured one). Repeating this process would in principle allow for the sequencing of long DNA fragments. However, it is extremely difficult to exert a force on a single nucleotide, limited by spatial fluctuations created in a thermal environment. The DNA transistor ^25,43 was designed to ratchet a ssDNA molecule through a nanopore one nucleotide at a time. Instead of applying a force to one nucleotide, the core idea of the DNA transistor is to apply electric forces in opposite directions to two different segments of ssDNA, containing n and (n+1) nucleotides respectively (where n is an integer). Fig. 7 shows the principle of an electric trap provided by the DNA transistor.

Fig. 7.

Trapping potential of ssDNA in the DNA transistor: when the sidewall length is a half integer (in unit of the distance d between neighboring phosphate groups in ssDNA), and the potential well thickness W is slightly larger than integer length, there are displacements for which the force of the charges (gray arrows) produces a net force on the polymer. Adapted from ref. ⁴³.

The DNA transistor contains metal and dielectric layers, alternatively stacked on top of each other, and a nanopore that is drilled through the multi-layer “sandwich”-like membrane. In the solid membrane, totally, there are three metal layers (or electrodes) that are separated or covered by dielectric layers. Two outer electrodes (not shown in Fig. 7, see Fig. 8 instead) are grounded and the voltage on the middle electrode is set to be positive (Fig. 7). Thus, forces on negatively charged nucleotides in these electric fields point towards the middle electrode. Assuming that ssDNA is in a stretched and linear conformation and the distance between neighboring phosphate groups is d. Fig. 7 shows the basic idea underlying the DNA transistor. If the thickness of each dielectric layer (insulator) is 1.5d and the thickness of the metal layer is 2d, the ssDNA molecule can be trapped in the DNA transistor as follows. In the top panel of Fig. 7, there are two nucleotides in each dielectric region and the total force on ssDNA is zero. After slightly shifting ssDNA to the right, the second panel shows that there are still two nucleotides in the left dielectric region but there is only one nucleotide in the right dielectric region. Therefore the net force can push ssDNA further to the right. This indicates that ssDNA shown in the top panel is at a potential maximum. Further moving ssDNA to the right, the third panel shows that there is one nucleotide in each dielectric region, the net force on ssDNA is zero again. Displacing ss-DNA further to the right (the fourth panel) results in a net force that pushes ssDNA back to the left. This indicates that ssDNA shown in the third panel is at a potential minimum. Therefore, when a ssDNA molecule moves through the DNA transistor, a trapping potential with period d is applied on the ssDNA. Note that the electric trapping force on the ssDNA molecule in the DNA transistor is due to the broken translational symmetry at nanoscale, as shown in Fig. 7.

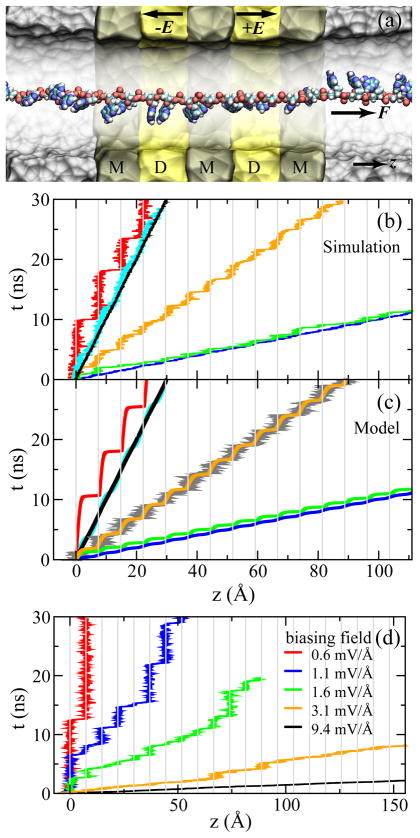
Fig. 8.

Simulations of ssDNA ratcheted through an electrostatic trap in the DNA transistor. (a) A cross-section view of the setup of MD simulations. The metal and dielectric regions are labeled with “M” and “D”, respectively. (b) Simulated time-position dependence of the ssDNA molecule pulled by a harmonic spring. (c) Time-position dependence of the ssDNA molecule that is pulled under the same conditions as in (b), resulting from the model of Eq. 2. According to the pulling velocity, data in each panel are grouped into three sets: (i) v = 1 A/ns and k = 10 (red), 100 (cyan), 1000 (black) pN/Å; (ii) v = 3 Å/ns and k = 33.3 (orange) pN/Å; (iii) v = 10 Å/ns and k = 10 (green), 100 (blue) pN/Å. (d) Thermally activated ratchet-like motion of ssDNA driven by a biasing electric field, changing from a ratcheting to a steady-sliding motion of ssDNA when increasing the biasing electric field from 0.6 mV/Å to 9.4 mV/Å, or the electric driving force on bare ssDNA from 20 to 300 pN. The interval of mesh lines in (b–d) is the interphosphate distance d. Adapted from ref. ²⁵.

The thickness difference between a metal and a dielectric layer should be (m+0.5)d, where m is an arbitrary integer number. Since 0.5d is only about 3.5 Å, to accurately control the thickness of a layer, cutting-edge fabrication techniques such as the “atomic layer deposition” are required.

3.3.2.2 Ratcheting ssDNA in the DNA transistor by thermal activation

When driven by an external force, a ssDNA molecule, that is trapped in the potential provided by the DNA transistor, will experience a tilted periodic potential, with a smaller energy barrier for the forward motion than for the backward motion. When the barrier for the forward motion is low enough to allow ssDNA to be activated thermally, the ssDNA molecule will move forward by one-nucleotide spacing d to be trapped again in a new potential well. Therefore, ssDNA can be base-by-base ratcheted through the DNA transistor.

Fig. 8 shows the simulation studies of the ratcheting motion of ssDNA by the DNA transistor. Fig. 8a illustrates the simulation set-up. the ssDNA molecule is on the central symmetry axis of a 4-nm-diameter nanopore. The thickness of each dielectric layer (labeled with “D” in Fig. 8) is 2d and the thickness of each metal layer (labeled with “M” in Fig. 8) is 2.5d. Two outer metal electrodes are grounded and the voltage on the middle electrode is 2 V. In simulations, uniform trapping electric fields are applied between neighboring electrodes ⁴⁴. These fields have the same strength but are in opposite directions. To demonstrate the ratcheting of ssDNA, ssDNA was driven through the DNA transistor by a mechanical or an electric force F.

Similar to the pulling method shown in Fig. 3a, a harmonic spring was used to pull ssDNA through the electric trap mimicking the action of an optical tweezer. Fig. 8b shows the time-dependent ssDNA position under various pulling conditions. At the same pulling velocity (v=1 Å/ns), Fig. 8b shows that the motion of ssDNA changes from a steady sliding to a ratcheting motion when the spring constant decreases. When the pulling velocity is high (v=10 Å/ns), the ratcheting motion is less obvious even when the spring is weak (k=10 pN/Å).

The ssDNA motion described above can be treated as the motion of ssDNA in a thermal bath and on a periodic potential of mean force modeled by −V_b cos(2πz/d)/2, using

$$m\ddot{z}=-\gamma \stackrel{.}{z}-f^{max}sin(2\pi z/d)-k(z-z_0)+\sqrt{2\gamma k_{\text{B}}T}\xi$$ (2)

where z is the ssDNA position, m the mass of ssDNA, z₀ (= vt) the position of the pulling stage, k_B the Boltzmann constant, T the temperature, and ξ the δ-correlated white noise. The external forces applied on ssDNA are the hydrodynamic friction force, the electric trapping force (f ^max = V_b π /d) and the pulling force from a harmonic spring.

Figure 8c shows the solution of the above model with boundary conditions: z(0) = 0 and ż(0) = 0. No fitting parameter was used and pulling conditions are the same as used in the MD simulations. Predictions of the model at T = 0 (smooth lines) and T = 300 K (grey line) agree well with the simulation results shown in Fig. 8b. Therefore this model accurately captures the dynamics of observed ssDNA motion, the slower motion of ssDNA on the experimental time scale can be investigated simply by integrating the model to a long time scale without performing complicated MD simulations.

Using the same atomistic MD simulation setup as above, a constant biasing electric field E′ across the nanopore can be used to drive ssDNA translocation through the pore. In Fig. 8d, MD trajectories of ssDNA subject to different strengths of the biasing electric field are shown. When ssDNA is driven in a weak biasing electric field [0.6 mV/Å, red line], a ratcheting motion of ssDNA is present. When the biasing electric field increases, these simulations also demonstrate a continuous transition from a ratcheting motion to a steady sliding motion of ssDNA. At intermediate biasing electric fields, a mixing of both types of motion is observed.

It is notable that the trapping time is about tens of nanoseconds. The estimated trapping energy for the ssDNA molecule is about 5 k_BT. Using simulation-determined parameters (such as friction coefficient and electrophoretic mobility) for the ssDNA molecule, the trapping time derived from Kramer’s theory is about 10 ns, consistent with the simulation results. It is therefore possible to find approaches to increase the trapping time, according to predictions of the Kramer’s theory. For example, the trapping energy can be increased by increasing the trapping voltage on the middle electrode in the DNA transistor, or increasing the friction on ssDNA by using an aqueous viscous solvent–glycerol.

3.3.2.3 Actively Ratcheting ssDNA in the DNA transistor

The ratcheting motion of ssDNA discussed above is activated thermally, thus trapping times for the ssDNA molecule in different potential wells (but with the same barrier height) vary statistically (Fig. 8d). To actively control the ratcheting motion of ssDNA, the DNA transistor can be operated in a different mode to enhance the position control of ssDNA. As shown in Fig. 9, the orange and blue curves represent potentials for ssDNA when voltages on the middle electrode are positive and negative, respectively. Note that potential maxima and minima are switched between these two curves. Therefore, the ssDNA molecule diffuses away from a potential well after switching the voltage on the middle electrode. The ssDNA molecule can move either backward or forward by d/2 and is trapped in the new established electric potential. The switching times are ideally much shorter than the barrier crossing time due to thermal activation in order to control the racheting motion.

Fig. 9.

Electric potential energies for ssDNA in the DNA transistor with (lower two lines) and without (upper two lines) a biasing electric field. The voltage on the middle electrode (Fig. 7a) alternates between positive (orange) and negative (blue) values. The position of the ssDNA molecule is represented by the green dot. Each red dashed line shows the position of an extreme value of each potential.

When applying a biasing electric field, trapping potentials are tilted, with the result that the forward barrier is smaller than the backward one. Additionally, positions of the maximum in one potential (orange curve in Fig. 9) and positions of the minimum in the other potential (blue curve in Fig. 9) shift away from each other. Thus, the position of a minimum in one potential (blue curve) corresponds to the position on the downhill edge of another potential (orange curve). As shown in Fig. 9, after a voltage switching, the ssDNA molecule moves forward by d/2 and is trapped again. Then, after switching the voltage on the middle electrode back to the previous value, ss-DNA move forward again by d/2. Therefore, by alternating the voltage on the middle electrode, ssDNA can be actively ratcheted forward, supposing that the thermally activated process is negligible.

During the ratcheting process, the biasing voltage can be temporally turned off to enhance the trapping, which was demonstrated in simulation (Fig. 10). In Fig. 10a and 10b, V_bias is the biasing voltage across a nanopore and V_trap is the voltage on the middle electrode. Time-dependent voltage signals in Fig. 10a and 10b were applied to electrodes to allow the ratcheting motion of ssDNA in the DNA transistor. In the beginning, the ssDNA molecule was trapped since the biasing and trapping voltages were 0 and −4 V, respectively. As shown in the first 6 ns of simulation (Fig. 10c), the position of the ssDNA molecule barely changed. After 6 ns, V_bias was increased to 0.4 V. Although the trapping potential was tilted, the ssDNA molecule was still trapped as shown in Fig. 10c. When the simulation time reached 9 ns, the voltage on the middle electrode was switched to 4 V. Correspondingly, the ssDNA molecule moved forward by d/2 (Fig. 10c) and was trapped again. At 12 ns, the voltage on the middle electrode was switched back to −4 V, the ssDNA molecule moved forward by another d/2 (Fig. 10c) and was trapped again. After that, V_bias was turned off and the ssDNA molecule was trapped for another 6 ns. In this whole process, the ssDNA molecule advanced a distance d, or moved forward by one nucleotide spacing. This controlled process was repeated in simulation three times as shown in Fig. 10c.

Fig. 10.

Actively Ratcheting ssDNA in the DNA transistor. upper panel: Time-dependent set-ups for biasing and trapping voltages. lower panel: Time-dependent ssDNA position from the trajectory of a MD simulation. The interval of mesh lines is d/2.

Note that the voltage signals shown in Fig. 10a and 10b can be modified (such as using a longer time interval) to assist the sensing of a nucleotide adjacent to a sensor. When the ssDNA molecule is trapped (gray stripes in Fig. 10c), the nucleotide in front of a sensor can be measured. After a required time for sensing a DNA base, the ssDNA molecule can be ratcheted forward by one nucleotide and the next DNA base can be measured. Note that by changing the polarity of V_bias, the ssDNA molecule could be ratcheted in the opposite direction, allowing for correction of reading errors. To achieve ssDNA ratcheting in experiments, it is critical to reduce the response time of the DNA transistor ⁴⁵ and protect metal electrodes from electrochemical corrosion ^46,47.

4 Discussion and outlook

In order to sequence DNA using a solid-state nanopore-based device, it is important to ensure both that each DNA strand to be measured has high persistence length so as to cleanly expose each base to a sensor and that the strand’s motion through the pore is controlled to allow high fidelity sensing of each base in turn. The persistence length of ssDNA is about 2 nm in a bulk electrolyte. Therefore, ssDNA is in a coiled conformation. In the confined geometry of the solid-state nanopore, the ssDNA is uncoiled but the persistent length is still on the order of the pore diameter. Therefore, ssDNA could be bent and neighboring ssDNA bases could stack on top of each other ⁴⁸, as in dsDNA. Such conformations are more difficult to sense with high fidelity. Ideally, a ssDNA molecule should be stretched so that neighboring nucleotides are well separated as shown in Fig. 8a, allowing an accurate measurement of, for example, tunneling current^13,14 through each DNA base in turn. Inside a solid-state nanopore, ssDNA could be stretched by a non-uniform biasing electric field in a nanopore ⁴⁹, by electroosmotic flow on ssDNA surface ²⁰, or by two large electrodes embedded in the pore acting to pull DNA.

Adhesion and friction between DNA and a solid pore surface pose difficulties for nanopore-based sequencing technologies. In order to control DNA translocation in a nanopore, it is beneficial to use a weak biasing electric field. However, when the field is weak, DNA could stick to the surface of a nanopore for long times before thermal activation detaches it. Therefore, although the friction between DNA and a pore surface does slow the motion of DNA, the result is non-uniform and uncontrolled transit. Note that a recent experiment ⁵⁰ shows different scaling laws for dsDNA and ssDNA molecules transiting a solid-state nanopore, likely due to the different DNA-pore interactions. An untreated solid-state nanopore might have a hydrophobic surface that can only contact the hydrophilic backbone of a dsDNA molecule. However, for a ssDNA molecule, both the hydrophilic backbone and hydrophobic bases can interact with the hydrophobic solid surface. Therefore, in order to allow for better control of DNA motion through nanopores, the pore surface could be chemically modified (such as the coating of a SAM ^24,33) to make the interaction between DNA and pore surface effectively “repulsive”. In addition, the interaction between the electrolyte and the pore surface should ideally be adhesive such that the pore surface provides a non-slip boundary for the electrolyte, slowing the driven motion of an electrolyte and consequently the motion of DNA.

In order to achieve high fidelity sensing, it is necessary for ssDNA molecules either to move steadily past a continuous-read sensor or move in a ratchet-like way so as to pause each base before a slow-read sensor. While continuuous-read sensors may become possible in the future, current proposed sensors based on tunneling current ^13,14, for example, require a significant averaging time even assuming a fair control of base configuration before the sensor. Thus, it is desirable to develop methods to achieve a ratcheting motion of ssDNA, allowing switching alternatively between a long-time trapped state in front of the sensor and a fast moving state of ssDNA (when ssDNA advances forward by one-nucleotide spacing). The ratcheting motion of a linear, stretched ssDNA molecule can be realized, provided a periodic (trapping) potential for ss-DNA, such as the electric trapping potential in the DNA transistor ⁴³. With advanced fabrication methods, electrodes can be built around a nanopore to control the motion of DNA (as in the DNA transistor) and to sense a DNA base. Finally, the integration of the DNA transistor and a DNA sensor is challenging, but is possible to achieve using currently available fabrication techniques.

A solid-state nanopore is normally made on a Si₃N₄ or a SiO₂ membrane. Recently, a graphene nanopore 51–53 (a single atom thick nanopore), has been suggested for sequencing DNA. Due to the unusual electronic structure of graphene, the electronic conductance of a graphene sheet might be very sensitive to the type of a nucleotide in the graphene pore ⁵⁴. A recently proposed method to circumvent uncontrolled surface properties of nanopores, is to embed a carbon-nanotube in the pore ⁵; transport of a ssDNA molecule through a carbon nanotube has been demonstrated ⁵⁵ experimentally. These new solid-state nanopores are very promising but the factors governing the DNA translocation through these pore are not yet well understood and will require extensive experimental, theoretical and computational studies to understand and control.