Erasing the Engram: The Unlearning of Procedural Skills

Abstract

Huge amounts of money are spent every year on unlearning programs – in drug-treatment facilities, prisons, psychotherapy clinics, and schools. Yet almost all of these programs fail, since recidivism rates are high in each of these fields. Progress on this problem requires a better understanding of the mechanisms that make unlearning so difficult. Much cognitive neuroscience evidence suggests that an important component of these mechanisms also dictates success on categorization tasks that recruit procedural learning and depend on synaptic plasticity within the striatum. A biologically detailed computational model of this striatal-dependent learning is described (based on Ashby & Crossley, 2011, J. of Cognitive Neuroscience). The model assumes that a key component of striatal-dependent learning is provided by interneurons in the striatum called the Tonically Active Neurons (TANs), which act as a gate for the learning and expression of striatal-dependent behaviors. In their tonically active state, the TANs prevent the expression of any striatal-dependent behavior. However, they learn to pause in rewarding environments and thereby permit the learning and expression of striatal-dependent behaviors. The model predicts that when rewards are no longer contingent on behavior, the TANs cease to pause, which protects striatal learning from decay and prevents unlearning. In addition, the model predicts that when rewards are partially contingent on behavior, the TANs remain partially paused leaving the striatum available for unlearning. The results from three human behavioral studies support the model predictions and suggest a novel unlearning protocol that shows promising initial signs of success.

Introduction

Every year society spends huge amounts of money on programs designed to facilitate the unlearning of maladaptive behaviors – in prisons, psychotherapy clinics, drug treatment facilities, and schools. As a more personal example, many golfers spend years and thousands of dollars trying to unlearn a poor golf swing (e.g., a slice). Yet virtually all of these programs must be classified as failures because recidivism rates are high in each of these domains. Why are behaviors so difficult to unlearn? This article proposes a neurobiological theory of why one important class of behaviors – namely, those acquired via procedural learning – may be so resistant to unlearning training. In addition, we use this theory to design a novel training protocol that shows promising initial success at inducing true unlearning of a procedural skill.

To begin, it is important to distinguish between learning and performance. Researchers have long recognized that although the expression of a skilled behavior generally indicates that the behavior has been learned, the absence or failure to produce the behavior after initial learning does not necessarily indicate that the behavior was unlearned. By “unlearning” we mean the erasing or obliterating of the memory traces that encode the behavior. An animal might fail to produce a behavior for many reasons, only one of which is unlearning.

This distinction between learning and performance is well known in the conditioning literature. The best-known example occurs during extinction, in which the removal of reward causes a previously rewarded behavior to disappear. In particular, there is overwhelming evidence that extinction does not cause unlearning (e.g., Bouton, 2002; Konorski, 1948; Pearce & Hall, 1980; Pavlov, 1927; Rescorla, 2001) because a variety of experimental manipulations can cause the behavior to quickly reappear. For example, if the rewards are reintroduced after extinction the behavior is reacquired much faster than during original acquisition (Woods & Bouton, 2007; Bullock & Smith, 1953). Faster reacquisition suggests that the original learning was preserved during the extinction period, even though the behavior disappeared. Other conditioning phenomena widely attributed to a failure of unlearning include spontaneous recovery (Brooks & Bouton, 1993; Estes, 1955; Pavlov, 1927) and renewal (Bouton & Bolles, 1979; Bouton & King, 1983; Nakajima, Tanaka, Urshihara, & Imada, 2000).

One influential account of extinction is that removing rewards causes new learning rather than unlearning (e.g., Bouton, 2002, 2004). The idea is that during original acquisition the animal learns the behavior, and also the context under which the behavior is appropriate (i.e., rewarded). During extinction the animal then learns about a context in which the behavior is inappropriate (i.e., not rewarded). So according to this account, extinction is not primarily an unlearning phenomenon, but rather an example of context learning. The theory proposed in this article is conceptually similar to this context-learning account of extinction. In fact, our theory might be interpreted as a formal neurobiological instantiation of this context-learning account.

The goal of this article is to develop and test a neurobiologically detailed computational model that formally specifies the mechanisms mediating the learning and unlearning of procedural skills, and to use this model to design an effective unlearning protocol. Our empirical domain will be perceptual category learning, and more specifically information-integration (II) category learning, which is known to recruit procedural learning (Ashby, Ell, & Waldron, 2003; Maddox, Bohil, & Ing, 2004).

Operationally, we will follow the instrumental conditioning literature and require two conditions before we conclude that a behavior has been unlearned. First, the behavior must disappear during the unlearning training, and second, if the original training conditions (i.e., reward) are reintroduced then the relearning or reacquisition must occur at the same rate as the original learning. As a further test, some participants in the experiments that we describe will be asked to learn novel categories during the reacquisition phase. If the unlearning training was effective then the performance of participants relearning the original categories should be the same as the performance of participants learning novel categories. Thus, all three experiments described in this article include three phases – an acquisition phase in which the II categories are first learned, an intervention phase in which some feedback change is introduced that causes categorization accuracy to drop, and a reacquisition phase where participants either relearn the original categories or learn a set of novel categories.

The article has a somewhat unusual organization. Following a brief review of procedural learning and II categorization, the third section describes the results of an experiment (Experiment 1) that sets the stage for the formal theoretical development of the model. The fourth section describes the model, which suggests clear behavioral and pharmacological methods to induce unlearning. Sections five and six report the results of two experiments that represent the first demonstration of unlearning in human II categorization. Finally we close with a general discussion and some conclusions.

Procedural Learning and Information-Integration Category Learning

The theory that we propose is restricted exclusively to behaviors acquired via procedural learning that depend on the striatum (a major input structure within the basal ganglia). Procedural learning is often referred to as skill or habit learning. A convenient operational definition is that behaviors acquired via procedural learning improve incrementally and require extensive practice with feedback. Procedural skills cannot be mastered via observation or by listening to a lecture. Prototypical examples include athletic skills (e.g., golf) and playing a musical instrument, but many cognitive skills such as looking for tumors in an x-ray or identifying the variety of grape used to make a wine also meet these criteria. An effective unlearning program is called for anytime such a skill is learned incorrectly (e.g., when a bad habit arises).

The procedural-learning task that we focus on in this article is II category learning. In an II categorization task, stimuli are assigned to categories in such a way that accuracy is maximized only if information from two or more non-commensurable stimulus dimensions is integrated at some pre-decisional stage (Ashby & Gott, 1988). Perceptual integration could take many forms – from computing a weighted linear combination of the dimensional values to treating the stimulus as a Gestalt. Typically, the optimal strategy in II tasks is difficult or impossible to describe verbally (which makes it difficult to discover via logical reasoning).

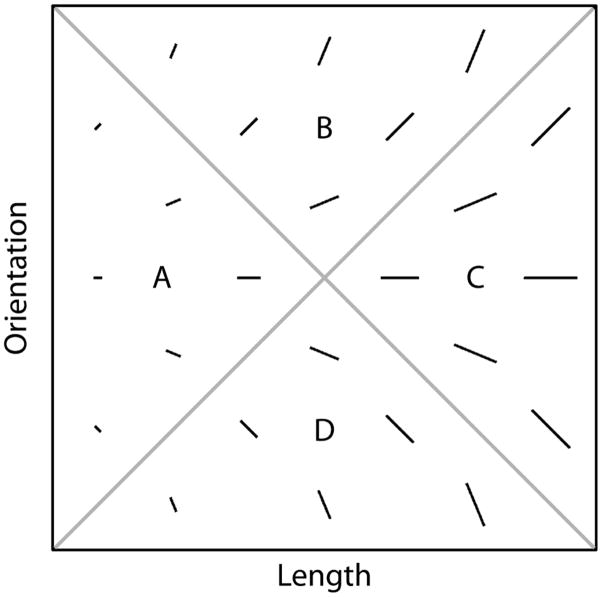
An example of an II task is shown in Figure 1. In this case the four categories are each composed of single black lines that vary in length and orientation. The diagonal lines denote the category boundaries. Note that no simple verbal rule correctly separates the lines into the four categories. Nevertheless, many studies have shown that with enough practice, people reliably learn such categories (e.g., Ashby & Maddox, 2005).

Figure 1.

A few examples of stimuli that might be used in an information-integration (II) category-learning experiment.

II categorization tasks are often contrasted with rule-based tasks, in which the categories can be learned via some explicit reasoning process. Frequently, the rule that maximizes accuracy (i.e., the optimal strategy) in rule-based tasks is easy to describe verbally. In the most common applications, there are two contrasting categories, only one stimulus dimension is relevant, and the participant’s task is to discover this relevant dimension and then to map the different dimensional values to the relevant categories. However, there is no requirement that rule-based tasks be one-dimensional. For example, a conjunction rule (e.g., respond A if the line is short and its orientation is shallow) is a rule-based task because a conjunction can be discovered through logical reasoning (e.g., a conjunction is easy to describe verbally). Many real-world skills seem to include components of both tasks. For example, radiologists can make initial progress in detecting tumors in x-rays by receiving explicit instruction (e.g., via book or lecture), but expertise in this skill requires years of hands-on training (e.g., during a residency).

Many studies have documented a wide variety of qualitative differences in how rule-based and II tasks are initially learned. For example, delaying feedback by a few seconds (Maddox, Ashby, & Bohil, 2003; Maddox & Ing, 2005), switching the location of the response keys (Ashby, Ell, & Waldron, 2003; Maddox, Bohil, & Ing, 2004), or informing participants of the category label before the stimulus rather than after the response (Ashby, Maddox, & Bohil, 2002) all interfere with performance in II tasks much more than in rule-based tasks. In contrast, adding a secondary (dual) task (Waldron & Ashby, 2001; Zeithamova & Maddox, 2006) or reducing the time available to process the feedback (Maddox, Ashby, Ing, & Pickering, 2004) interferes with performance in rule-based tasks much more than in II tasks. These differences are all consistent with the hypothesis that learning in rule-based tasks is mediated by declarative memory systems, whereas learning in II tasks is mediated by procedural memory (Ashby & O’Brien, 2005).

The evidence is also good that the learning of procedural skills depends critically on the basal ganglia, and in particular on the striatum. This is true for instrumental conditioning tasks (Barnes, Kubota, Hu, Jin, & Graybiel, 2005; Divac, Rosvold, & Szwarcbart, 1967; Konorski, 1967; O’Doherty et al., 2004; Yin, Ostlund, Knowlton & Balleine, 2005) and for II category learning (Ashby & Ennis, 2006; Filoteo, Maddox, Salmon, & Song, 2005; Knowlton, Mangels, & Squire, 1996; Nomura et al., 2007; Waldschmidt & Ashby, 2011; Seger & Cincotta, 2005).

Experiment 1

Experiment 1 is a control that will establish a baseline measure of how difficult unlearning is in II categorization. As mentioned above, the experiment includes three phases –acquisition, intervention, and reacquisition – each of which includes 300 trials. During the intervention, the stimuli and category structures are the same as during acquisition. The critical manipulation will be to change the feedback in some way that causes categorization accuracy to drop – ideally to chance levels. Pilot data suggested that simply removing the feedback, as is done for example during extinction training in instrumental conditioning studies, does not cause categorization accuracy to drop significantly, at least not over the course of 300 trials. Therefore, in Experiment 1 we opted for a more active intervention. Specifically, during the intervention phase, without any warning to the participant, the feedback suddenly became random.

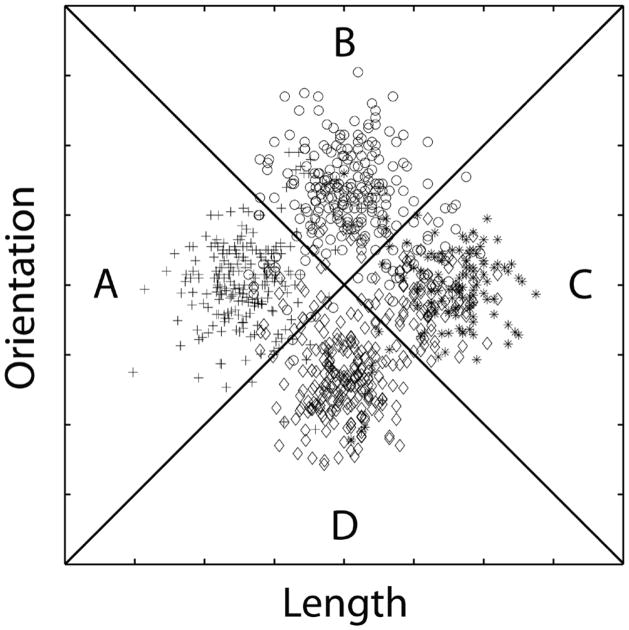
Every stimulus in all three phases of Experiment 1 was a line (as in Figure 1) that varied across trials in length and orientation. Identical II category structures were used in all three phases. These are represented abstractly in Figure 2. Note that these categories are similar to the categories shown in Figure 1, except with more exemplars in each category. Also note that the categories overlap, so perfect accuracy is impossible. In fact, the best possible accuracy with these categories is 95%.

Figure 2.

An abstract representation of the stimuli used in Experiments 1, 2, and 3. All stimuli were single lines that varied across trials in length and orientation. Plus signs denote the length and orientation of exemplars in category A, circles denote exemplars in category B, stars denote exemplars in category C, and diamonds denote exemplars in category D. The diagonal lines denote the optimal decision bounds.

The acquisition, intervention, and reacquisition phases were identical except in the nature of the feedback provided after each response. During acquisition, feedback indicated whether each response was correct or incorrect. As mentioned previously, during the intervention phase, the feedback was random. On each trial, participants were informed that their response was correct with probability ¼ and incorrect with probability ¾, regardless of what response they actually made (i.e., because there were four categories). The transition from the acquisition to the intervention phase occurred without the participant’s knowledge. On trial 301 the feedback rule simply changed without warning. Reacquisition began after the intervention phase was complete, again without warning. During the reacquisition phase, feedback was again veridical. There were two conditions. In the Relearning condition, the category structures remained the same as during acquisition and intervention. Thus, the participants’ task during reacquisition was to relearn the same categories they learned during acquisition. In the Meta-Learning condition, the stimuli were the same during reacquisition but the category labels were switched so that stimuli originally assigned to categories A, B, C, and D were now assigned to categories B, A, D, and C, respectively. Previous research shows that a label switch of this type (i.e., without an intervening intervention phase) causes performance to drop almost to the same level as the first block of acquisition and that learning then proceeds at about the same rate as original acquisition (Maddox, Glass, O’Brien, Filoteo, & Ashby, 2010a). This control condition was included to ensure that fast reacquisition, if it occurs, is not due to some sort of meta-learning. For example, because participants will have had 600 prior trials to familiarize themselves with the stimuli and task instructions, it is feasible that this experience would facilitate the learning even of novel categories. Thus, one critical test of fast reacquisition will be to compare the reacquisition performance of participants in the Relearning condition to the reacquisition performance of participants in the Meta-Learning condition.

Method

Participants

There were 33 participants in the Relearning condition and 20 participants in the Meta-Learning condition. All participants completed the study and received course credit for their participation. All participants had normal or corrected to normal vision. To ensure that only participants who performed well above chance were included in the post-acquisition phase, a learning criterion of 40% correct (25% is chance) during the final acquisition block of 100 trials was applied. Using this criterion, we excluded 3 participants in the Relearning condition and 2 participants in the Meta-Learning condition from further analyses.

Stimuli

Stimuli were black lines that varied across trials only in length (pixels) and orientation (degrees counterclockwise rotation from horizontal). The stimuli are illustrated graphically in Figure 2, and were generated by drawing 225 random samples from each of four bivariate normal distributions along the two stimulus dimensions with means along the x dimension of 72, 100, 100, and 128 and along the y dimension of 100, 128, 72, and 100 for categories A – D, respectively. The variance along the x and y dimensions was 100 and the covariance was 0 for all categories. The random samples were linearly transformed so that the sample means and variances equaled the population means and variances. Each random sample (x, y) was converted to a stimulus by deriving the length (in pixels displayed at 1280 × 1024 resolution on 17″ screens) as l = x, and orientation (in degrees counterclockwise from horizontal) as o = y − 30. These scaling factors were chosen to roughly equate the salience of each dimension. Optimal accuracy was 95%. In each 100 trial block, 25 stimuli per category were randomly sampled without replacement from the original random sample of 225 stimuli. This was done independently for each participant in each block.

Procedure

Participants in both conditions were told that they were to categorize lines on the basis of their length and orientation, that there were four equally-likely categories, and that high levels of accuracy could be achieved. At the start of each trial, a fixation point was displayed for 1 second and then the stimulus appeared. The stimulus remained on the screen until the participant generated a response by pressing the “Z” key for category A, the “W” key for category B, the “/” key for category C, or the “P” key for category D. Following the response, the stimulus was replaced with a 1000 ms feedback display and a 1000 ms blank screen inter-trial-interval. None of these four keys were given special labels. Rather, the written instructions informed participants of the category label to button mappings, and if any button other than one of these four was pressed, an “invalid key” message was displayed.

During the three 100-trial acquisition blocks, the word “correct” was presented if the response was correct or the word “incorrect” was presented if the response was incorrect. Once feedback was given, the next trial was initiated. During the three 100-trial intervention blocks, the feedback was random (i.e., during each 100-trial intervention block, participants were told that they were correct on 25 randomly selected trials and were told that they were incorrect on the remaining 75 trials, regardless of their responses). During the three 100-trial reacquisition blocks, feedback was again veridical.

In the Meta-Learning condition, the acquisition and intervention procedures were identical to those from the Relearning condition, and the reacquisition phase was replaced with three 100-trial blocks of a category-label switch (Maddox et al., 2010). During the category-label switch, the association between stimulus clusters and category labels was changed so that stimuli originally assigned to categories A, B, C, and D were now assigned to categories B, A, D, and C, respectively.

Results

Accuracy-based results

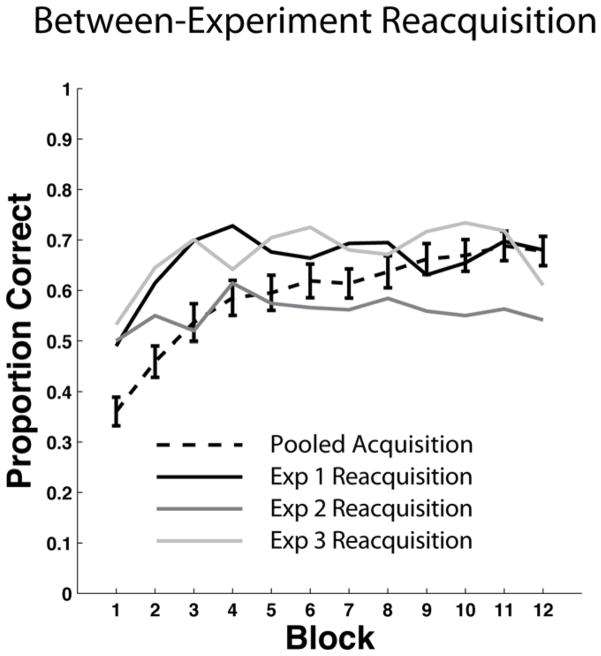
The top panel of Figure 3 shows the mean accuracy for every 25-trial block of each condition. During intervention, a response was coded as correct if it agreed with the category membership shown in Figure 2. Recall that the categories and feedback were identical in the two conditions until the beginning of the reacquisition phase. Note that participants from both conditions were able to learn the categories, reaching their peak accuracy near the end of acquisition, before falling to near chance during intervention. As expected, there are only minor differences between participants in the Relearning and Meta-Learning conditions during the acquisition and intervention phases of the experiment. During reacquisition however, the two learning curves diverge. Participants in the Relearning condition show fast reacquisition while participants in the Meta-Learning condition show slow reacquisition or interference (i.e., both the rate of reacquisition and the asymptote of accuracy are less than their counterparts in the Relearning condition).

Figure 3.

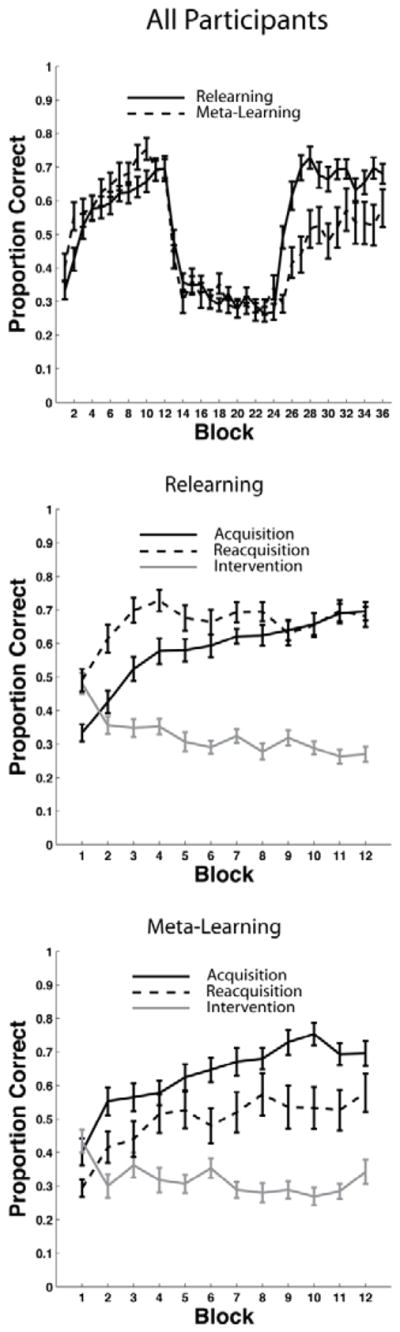
Experiment 1 accuracy. Each block includes 25 trials. Top Panel: Accuracy in both the Relearning and the Meta-Learning conditions throughout the entire experiment. Blocks 1–12 were in the acquisition phase, blocks 13–24 were in the intervention phase, and blocks 25–36 were in the reacquisition phase. Middle Panel: Overlaid accuracy data in the Relearning condition from the acquisition phase, intervention phase, and reacquisition phase. Bottom Panel: Overlaid accuracy data in the Meta-Learning condition from the acquisition phase, intervention phase, and reacquisition phase.

To test these conclusions formally we conducted several statistical tests, including several repeated measures ANOVAs. Note that all ANOVAs reported in this article use the Greenhouse-Geisser correction for violations of sphericity. We first performed a 2 conditions (Relearning versus Meta-Learning) × 36 blocks repeated measures ANOVA. We found no significant effect of condition [F(1,46) = 2.30, p = 0.136, η_p² = 0.05], but the interaction [F(8,407) = 5.24, p < 0.001, η_p² = 0.10] and the effect of block [F(8,407) = 44.20, p < 0.001, η_p² = 0.49] were both significant. We then conducted several 2 conditions (Relearning versus Meta-Learning) × 12 blocks repeated measures ANOVAs, where the 12 blocks corresponded to the acquisition, intervention, or reacquisition phase. In the ANOVA corresponding to the acquisition phase, we found no effect of condition [F(1,46) = 2.38, p = 0.13, η_p² = 0.049], or interaction [F(7,323) = 1.07, p = 0.38, η_p² = 0.02], but the effect of block was significant [F(7, 323) = 27.34, p < 0.001, η_p² = 0.37]. In the ANOVA corresponding to the intervention phase we found no effect of condition [F(1,46) = 0.05, p = 0.83, η_p² = 0.001], or interaction [F(7,361) = 1.32, p = 0.23, η_p² = 0.03], but the effect of block was significant [F(7, 361) = 7.52, p < 0.001, η_p² = 0.14]. In the ANOVA corresponding to the reacquisition phase, we found a significant effect of condition [F(1,46) = 11.14, p < 0.005, η_p² = 0.19], and block [F(6, 312) = 12.01 , p < 0.001, η_p² = 0.21], but the interaction was not significant [F(6,312) = 1.62, p = 0.13, η_p² = 0.03]. The key result from these analyses is that there was only a significant difference between conditions during the reacquisition phase.

Next, we computed several repeated measures t-tests to compare performance between phases (i.e., acquisition, intervention, and reacquisition) within each condition. Note that we report effect size for all repeated measures t-tests as described by Gibbons et al. (1993). For the Relearning condition, mean acquisition performance (across blocks) and mean reacquisition performance were both significantly better than mean performance during intervention [acquisition: t(359) = 17.82, p < 0.001, d = 0.94; reacquisition: t(359) = 25.64, p < 0.001, d = 1.35]. A more important result was that reacquisition was significantly better than acquisition [t(359) = 7.17, p < 0.001, d = 0.38]¹. This difference is clearly seen in middle panel of Figure 3, which superimposes the acquisition, intervention, and reacquisition curves from the Relearning condition. For the Meta-Learning condition, mean acquisition performance (across blocks) and mean reacquisition performance were both significantly better than mean performance during intervention [acquisition: t(215) = 19.22, p < 0.001, d = 1.31; reacquisition: t(215) = 9.15, p < 0.001, d = 0.62]. A more important result was that reacquisition was significantly worse than acquisition [t(215) = 8.95, p < 0.001, d = 0.61]. This difference is clearly seen in the bottom panel of Figure 3. In summary, for both conditions, performance during intervention was significantly worse than performance during acquisition and reacquisition. For the Relearning condition, performance during reacquisition was significantly better than performance during acquisition. For the Meta-Learning condition, performance during reacquisition was significantly worse than performance during acquisition.

Next, we performed two separate tests that more closely examined the effects of the intervention. First, we compared the first block of acquisition to the last block of intervention (i.e., acquisition - intervention). These tests revealed that these two blocks were not significantly different from each other in either the Relearning condition [t(29) = 1.59, p = 0.12, d = 0.29], or the Meta-Learning condition [t(17) = 1.16, p = 0.26, d = 0.27]. Second, we computed t-tests on the null hypothesis that the last two intervention blocks from each condition were generated from a distribution with mean 0.25 (i.e., the accuracy we would expect if performance was truly at chance). These tests revealed that that the last two blocks of intervention were significantly different from chance for the Meta-Learning condition [t(35) = 2.97, p < 0.01, d = 0.49], but not for the Relearning condition [t(59) = 1.02, p = 0.30, d = 0.13]. We also computed this t-test on the pooled the data from the last two intervention blocks from both conditions and found that that the last two blocks of intervention were significantly different from chance [t(71) = 4.24, p < 0.001, d = 0.27]. In summary, random feedback eventually reduced accuracy to the level present in the first 25 trials of acquisition (i.e., before much learning could have occurred), but did not reduce performance to chance levels.

Model-based results

The accuracy-based results show fast reacquisition in the Relearning condition. However, we must be cautious when interpreting this result because of the possibility that at least some participants may have used an II strategy during the acquisition phase and then switched to a rule-based strategy during the reacquisition phase. In Experiment 1, rule-based strategies are suboptimal, but several will yield higher-than-chance accuracy and might be learned quickly. Thus, a participant who unlearned the original categories during the intervention and then switched to an easy-to-learn rule-based strategy during reacquisition would show evidence of fast reacquisition, even though unlearning was successful. To examine this possibility, we partitioned the data from each participant into blocks of 100 trials and fit different types of decision bound models (e.g., Ashby, Waldron, Lee, & Berkman, 2001; Maddox & Ashby, 1993) to each block of data from every participant.² One type assumed a rule-based decision strategy, one type assumed an II strategy, and one type assumed random guessing. See Appendix 1 for details.

Table 1 shows the number of participants in the two conditions best fit by a model of these three types. In the final block of acquisition, about 63% of all participants from the Relearning condition and 61% of all participants from the Meta-Learning condition were best fit by models that assumed information integration³. The remaining participants were best fit by a model that assumed a rule-based strategy. In the first block of reacquisition, about 77% of all participants in the Relearning condition but only 50% of participants in the Meta-Learning condition were best fit by a model that assumed an II strategy. The majority of the remaining participants from the Relearning condition were best fit by a model that assumed a rule-based strategy, whereas most of the remaining participants from the Meta-Learning condition were best fit by a model that assumed a guessing strategy. Thus, the proportion of participants fit best by a model that assumed information integration slightly increased from the last block of acquisition to the first block of reacquisition in the Relearning condition, and slightly decreased in the Meta-Learning condition. Even so, neither the slight increase in the Relearning condition or the slight decrease in the Meta-Learning condition was significant [Relearning condition: t(58) = −1.12, p = 0.13, d = 0.20; Meta-Learning condition: t(34) = 0.67, p = 0.16, d = 0.16].

Table 1.

Proportion of participants in the two conditions of Experiment 1 whose responses were best accounted for by a model that assumed an information-integration (II) decision strategy, a rule-based strategy, or random guessing, and the proportion of responses accounted for by those models.

	Relearning				Meta-Learning
	A3		R1		A3		R1
	%N	%RA	%N	%RA	%N	%RA	%N	%RA
II	.63	.71	.77	.70	.61	.75	.50	.66
RB	.37	.61	.17	.49	.39	.68	.11	.47
Guessing	0	-	.07	-	0	-	.39	-

Note. A3 = the last 100 trials of acquisition, R1 = the first 100 trials of reacquisition, %N = the proportion of participants contained in a given cell, and %RA = the proportion of responses accounted for by a particular model.

The reacquisition responses of more participants in the Relearning condition were best fit by a model that assumed an II strategy than in the Meta-Learning condition. If the intervention had caused complete unlearning then the reacquisition modeling results should have been the same for the two conditions. Also note that the number of participants in the Relearning condition whose responses were best fit by a model that assumed an II strategy remained roughly constant from acquisition to reacquisition. These results suggest that strategy switches from II to rule-based strategies were not driving fast reacquisition.

Since the model developed in the next section is exclusively designed to account for II category learning, it is important to determine if the pattern of results obtained from the accuracy-based analyses from all participants is also observed in the subset of participants that were most likely using an II strategy to learn the categories. To answer this question, we repeated all the accuracy-based analyses reported in the previous section using only the data from the participants from each condition that were best fit by an II strategy during the last block of acquisition. The results of all these statistical tests were qualitatively identical to results obtained by including all participants in the analysis. Specifically, the accuracy of II users in the Relearning condition was not different from the accuracy of II users in the Meta-Learning condition until the reacquisition phase, and neither condition reached chance levels of performance during intervention, although the last block of intervention pooled from each condition was indistinguishable from the first block of acquisition. Importantly, reacquisition performance was better than acquisition performance in the Relearning condition and worse than acquisition performance in the Meta-Learning condition.

Discussion

The results from Experiment 1 indicate fast reacquisition in the Relearning condition and interference in the Meta-Learning condition. It is critical to note that both of these results suggest a lack of complete unlearning during the intervention phase, despite the fact that accuracy fell nearly to chance in both conditions⁴. If the random feedback delivered during the intervention caused complete unlearning of the category structures that were learned during acquisition, then reacquisition should proceed at the same pace as original acquisition and changing the category structures as in the Meta-Learning condition should not produce interference. By definition, interference means that there must be some prior learning that is interfering with new learning.

At first glance, our results echo a classic result within the instrumental conditioning literature. Insofar as II category learning and instrumental conditioning are mediated by similar reinforcement-learning mechanisms, our finding that learning is mostly preserved during unlearning with random feedback may not be that surprising. However, in addition to theoretical difficulties with this view that will be discussed shortly, there are a number of important differences between category learning and instrumental conditioning that need to be appreciated before settling on this conclusion. Aside from being a more cognitively complex task, category learning differs fundamentally from instrumental conditioning in its response characteristics. Instrumental conditioning is free response. Typically the choice is between emitting one response or not responding at all, and learning is characterized by an increase in response rate. During extinction, removing reward is sufficient to make the behavior disappear. Category learning, on the other hand, is forced choice – that is, participants are forced to choose among two or more responses on every trial. Learning is characterized by an increase in correct responding. However, since category learning is forced choice, extinction (or intervention by our terminology) cannot be characterized by the simple absence of responding. Furthermore, as mentioned earlier, unpublished data from our lab indicates that simply removing feedback during the intervention phase in category learning is not sufficient to make accurate II responding disappear. In light of these fundamental differences, the finding of fast reacquisition after intervention with random feedback during category learning is quite unexpected. For example, as we will now show, this result is incompatible with all existing theoretical accounts of category learning. The remainder of this section briefly considers a number of possible accounts of the Experiment 1 results. Readers primarily interested in our theoretical account of Experiment 1 may skip to the section “A Neurobiological Theory of Why Unlearning is so Difficult.”

Strategy Recall

An obvious possibility is that during reacquisition the participants in Experiment 1 simply recalled the categorization rule that they were using at the end of the acquisition period. Thus, no new learning was required, only memory retrieval. This would be a viable hypothesis if the categorization task was rule based, but for several reasons it cannot account for the results of Experiment 1. First, in II categorization tasks, participants do not have conscious awareness of their categorization strategy (e.g., Ashby & Maddox, 2005). In particular, participants cannot recall the strategy that they used immediately after II categorization training, so there is no reason to expect them to be able to do this during the reacquisition phase. Second, participants do not learn rules during II categorization, even if “rule” is interpreted in the most abstract, mathematical sense. Several studies have presented strong evidence that participants do not learn decision bounds in II categorization tasks or any other decision rule that can be specified by a specific mathematical function (Ashby & Waldron, 1999; Casale, Roeder, & Ashby, 2012). Thus, there is no “rule” to recall in II categorization. Furthermore, as we will see, Experiment 2 uses the theory developed in the next section to design conditions that cause fast reacquisition to disappear. Thus, a strategy recall hypothesis would have to explain why recall succeeds in Experiment 1 but not in Experiment 2.

Single Category-Learning Systems Accounts

We know of no existing single-system theories of category learning that can account for fast reacquisition. For example, consider exemplar theory (Brooks, 1978; Estes, 1986, 1994; Hintzman, 1986; Lamberts, 2000; Medin & Schaffer, 1978; Nosofsky, 1986). Exemplar theory assumes that feedback is used to associate a category label with every exemplar encountered. When a new stimulus is seen, its similarity is computed to the memory representation of every previously seen exemplar from each potentially relevant category. The stimulus is then assigned to the category for which the sum of these similarities is greatest. The intervention phase in Experiment 1 randomly reassigns stimuli to each of the four contrasting categories. Exemplar theory predicts that performance will drop to chance during this intervention when every stimulus is equally similar to the stored exemplars that have been associated with each of the four categories. During reacquisition the random category assignments that were learned during the intervention will impair re-learning. In fact, exemplar theory naturally predicts that reacquisition will be slower than original acquisition (i.e., in Experiment 1) because during initial acquisition there are no random category assignments that must be overcome.

Other single-system models of category learning have an equally difficult time accounting for our results (e.g., the striatal pattern classifier of Ashby & Waldron, 1999). This is because in each of these, the intervention period would either cause unlearning or random learning. Reacquisition then becomes either a process of starting over from scratch (in the case of unlearning) or overcoming all the new random associations. In the former case reacquisition should occur at the same pace as original acquisition and in the later case reacquisition should be slower than acquisition.

Multiple Category-Learning Systems Accounts

Existing multiple-systems models of category learning are equally challenged by fast reacquisition. Included in this list are ATRIUM (Erickson & Kruschke, 1998) and COVIS (Ashby et al., 1998). Both models assume two systems – one that is rule based and one that is similarity based. ATRIUM assumes that the similarity-based system is a standard exemplar model, whereas COVIS assumes that it is the striatal pattern classifier.

During acquisition and reacquisition, ATRIUM and COVIS both predict that the similarity-based system will dominate performance (because the categories cannot be learned with a simple rule). For both models there are two possibilities for the intervention phase. One is that the similarity-based system will continue to dominate. In this case the models essentially reduce to single-system accounts because they would predict that the similarity-based system would dominate all phases of the experiment. As single-system models, they both fail to predict fast reacquisition for the reasons described in the preceding section.

A second possibility is that ATRIUM and COVIS might be able predict that participants switch to rule-based strategies during the intervention phase. The problem here is that both models predict independent learning in the two systems. Thus, even if participants switch to rule-based strategies during the intervention phase the models predict that the random feedback will cause unlearning in the similarity-based system. Thus, during reacquisition the similarity-based system will have to overcome this unlearning, which will prevent fast reacquisition.

Other Cognitive Accounts

A variety of mechanisms have been proposed in the cognitive literature that could theoretically account for fast reacquisition by postulating that different cognitive processes are in operation during the intervention phase as compared to the acquisition and reacquisition phases. For example, several categorization models postulate highly flexible attention mechanisms that can be modulated up and down depending on feedback (for a review, see Kruschke, 2011). If the gain on attention was low during the intervention, then the stimuli presented during intervention would have little impact on the category representation and if the gain was turned back up during reacquisition, then fast reacquisition would result.

A similar account is provided by knowledge partitioning, which is the phenomenon in which people break down a task into subtasks, and apply a unique strategy in each subtask that is not influenced by the strategies used in the other subtasks (Lewandowsky & Kirsner, 2000; Yang & Lewandowsky, 2004). If participants are able to create a partition that includes acquisition and reacquisition on one side and intervention on the other, then fast reacquisition should occur in the Relearning condition of Experiment 1. The slow reacquisition results we will present in Experiment 2 could potentially be accounted for by assuming that the conditions present in that experiment somehow impaired the formation of partitions.

Finally, Sanborn, Griffiths, and Navarro’s (2010) version of the rational model may be able to account for fast reacquisition but only if additional post hoc assumptions are included. Sanborn et al.’s model allows multiple candidate categorization strategies to be held in memory and thus it is possible that the model could learn one strategy during initial acquisition, a second strategy during intervention, and then could re-institute the original strategy during relearning.

The attention-learning, knowledge-partitioning, and rational-model accounts are similar in that all three require a cognitive switch to be flipped at the appropriate times during training. In the attention-learning account, flipping the switch at the beginning of the intervention phase would reduce attentional gain, in the knowledge-partitioning account it would create a new knowledge structure, and in the rational model it would trigger the learning of a new strategy. Flipping it again at the beginning of reacquisition would then turn the attentional gain back up, cause a switch back to the original knowledge structure, or to the original strategy. The challenge for all switch-based accounts is to specify a mechanism that would allow the cognitive switch to be flipped on or off at the appropriate times (e.g., at the onset of the intervention and reacquisition phases). To our knowledge, none of the attention-learning, knowledge-partitioning, or rational models predict that simply making the feedback suddenly random will cause such a switch to be flipped. For example, each of the attention learning models assumes that changes in the allocation of attention are mediated by attempts to reduce error (e.g., as in back-propagation). Since the feedback given during the intervention phase in Experiment 1 was random, there is no reallocation of attention that will reduce error and therefore, presumably there would be no attentional relearning (since the gradient is flat). Similarly, most experiments that study knowledge partitioning include one or more cues that signal the participant where to make the partition. In the present studies, the only such cue was a change in the validity of the feedback. Ashby and Crossley (2010) reported the results of several categorization experiments in which knowledge partitioning would have allowed perfect accuracy. Participants in these studies could have used the validity of feedback to construct the partition, or the value of one of the two stimulus features (i.e., large versus small). Despite a variety of attempts to induce knowledge partitioning, only 2 of 53 participants in the Ashby and Crossley (2010) experiments showed any evidence that knowledge partitioning was successful. Thus, the available evidence suggests that the validity of feedback alone is not enough to induce knowledge partitioning.

General Learning Theories

Given the preceding discussion, it is not surprising that fast reacquisition has also posed a difficult challenge for learning theories in general. For example, fast reacquisition disconfirms any theory that assumes learning is purely a process of strengthening associations between stimuli and responses (e.g., Redish, Jensen, Johnson, & Kurth-Nelson, 2007). Partly for this reason, some conditioning researchers have proposed that extinction is not a process of unlearning, but rather a process of new learning (Bouton, 2004; Rescorla, 2001). In particular, Bouton (2004) suggested that conditioned responding is highly context-specific. According to this view, a new context is learned during extinction⁵. This leaves the original learning in the acquisition context intact. This explanation accounts for fast reacquisition as well as a number of other important conditioning phenomena. One shortcoming of this account is that it lacks a formal specification. For example, it is unclear how it might be generalized from simple conditioning to II category learning, and it is unclear how it might be applied to the complex feedback conditions in our experiments. Another shortcoming of this account is that it does not offer much insight into the mechanism of where or how such context learning is mediated (although see Bouton et al., 2006).

Computational and Neurobiological Accounts

There are several computational and neurobiological accounts of fast reacquisition. O’Reilly and Munakata (2000) proposed a computational model in which learning strengthens a connection (i.e., weight) between critical units in a neural network model and extinction weakens this weight. Once the strength falls low enough for the behavior to disappear, however, this weight is no longer weakened by further extinction trials. This allows the model to predict fast reacquisition, because the first rewarded trial following extinction brings the connection strength above threshold, and therefore reinstates the behavior. However, it seems that this model should predict that random feedback would cause the learning of random associations (since rewards are still present), and therefore predict that reacquisition should be slow in Experiment 1. We show in the next section that this is a property of all standard reward-prediction-error models.

Several neural network models have been proposed that can account for fast reacquisition by assuming that extinction is a process of learning that the environmental context has changed (Gershman, Niv, & Blei, 2010; Redish et al., 2007). These models assume two separate processes – a situation recognition process that learns to recognize the current environmental context, and a standard temporal difference reinforcement-learning component. To our knowledge these models have only been applied to standard extinction paradigms, and thus, it is not clear how or whether they could be generalized to account for the results of Experiment 1. Also, the models are not neurobiologically detailed, although Redish et al. (2007) and Gershman et al. (2010) both speculate that the locus of their context-learning module is within prefrontal cortex and/or the hippocampus.

A Neurobiological Theory of Why Unlearning is so Difficult

This section proposes a neurobiologically detailed computational model that describes a mechanism in the striatum that protects procedural learning when rewards are no longer available or when rewards are no longer contingent on behavior. The model therefore explains why the unlearning of procedural skills is so difficult. It also successfully accounts for the Experiment 1 results, and it predicts how the random feedback intervention might be modified to improve unlearning.

The Ashby and Crossley (2011) Model

The only biologically detailed model of II category learning is COVIS (Ashby et al., 1998; Ashby & Waldron, 1999), which assumes that in II tasks a procedural-learning system gradually associates categorization responses with regions of perceptual space via reinforcement learning. The key structures in the COVIS procedural-learning system are the putamen and the premotor cortex (i.e., supplementary motor area and/or dorsal premotor cortex). Early versions of COVIS assumed that the striatal regions most critical to the procedural system were the body and tail of the caudate nucleus (Ashby et al., 1998). More recent evidence however, suggests that the procedural system has a strong motor association (Ashby et al., 2003; Maddox et al., 2004), which caused the focus to switch to the putamen. Recent neuroimaging data support this hypothesis (Waldschmidt & Ashby, 2011). The key site of learning in this model is at cortical-striatal synapses, and this synaptic plasticity is presumed to be facilitated by a DA-mediated reinforcement training signal from the substantia nigra pars compacta. However, COVIS does not account for the fast reacquisition seen in Experiment 1. Instead, like every other existing model of category learning, COVIS predicts that random feedback will cause learning of random stimulus-response associations, and therefore that the correct associations will have to be relearned during the reacquisition phase.

Fast reacquisition is notoriously difficult to model, even when it follows extinction in instrumental conditioning. One of the few models that can account for this phenomenon was proposed by Ashby and Crossley (2011; see also O’Reilly & Munakata, 2000). This model is similar to the procedural learning system of COVIS except it adds cholinergic interneurons (known as TANs, for tonically active neurons) to the striatum. When applied to category learning, the Ashby and Crossley (2011) model is characterized by a number of key features. First, as in COVIS, category/response associations in II tasks are learned at cortical-striatal synapses. Second, the theory assumes that the TANs tonically inhibit cortical input to striatal output neurons. The TANs are driven by neurons in the centremedian and parafascicular (CM-Pf) nuclei of the thalamus, which in turn are broadly tuned to features of the environment. In rewarding environments the TANs learn to pause to stimuli that predict reward, which releases the cortical input to the striatum from inhibition. This allows striatal output neurons to respond to excitatory cortical input, thereby facilitating cortical-striatal plasticity. In this way, TAN pauses facilitate the learning and expression of striatal-dependent behaviors. When rewards are no longer available, the TANs cease to pause, which prevents striatal-dependent responding and protects striatal learning from decay. Third, DA-dependent reinforcement learning occurs at cortical-striatal and CM-Pf –TAN synapses. Fourth, DA release is modeled discretely on a trial-by-trial basis and is proportional to the reward prediction error (RPE; i.e., obtained reward minus predicted reward). Ashby and Crossley (2011) showed that a computational version of this theory predicts fast reacquisition following extinction in instrumental conditioning paradigms at the same time that it correctly accounts for a wide variety of single-unit recording data. Included in this list are single-unit recordings from striatal medium spiny neurons (MSNs) during acquisition, extinction, and reacquisition phases of instrumental conditioning and during category learning.

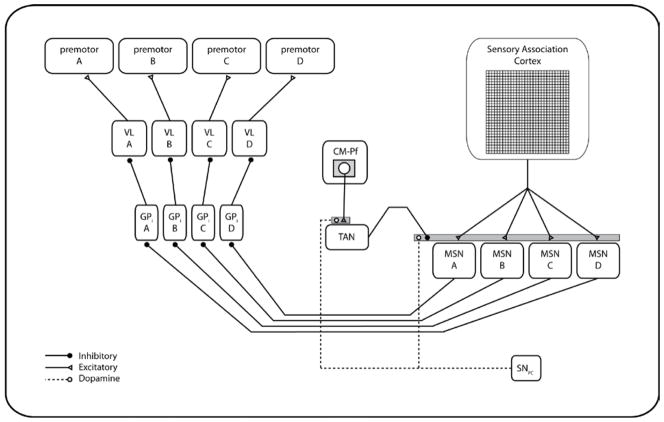
The overall architecture of the model proposed by Ashby and Crossley (2011) when applied to the 4-category task used in Experiment 1 is shown in Figure 4. The idea is that, in the absence of CM-Pf input, the TAN’s high spontaneous firing tonically inhibits the cortical input to the striatal MSNs. When cells in the CM-Pf complex fire, reinforcement learning at the CM-Pf –TAN synapse quickly causes the TAN to pause when in a rewarding environment. This releases the cortical input to the MSNs from tonic inhibition, thereby allowing cortical access to the striatum. Thus, in effect, the TANs serve as a gate between cortex and the striatum. The default state of the gate is closed, but it opens when cues in the environment predict rewards.

Figure 4.

The model architecture of the Ashby and Crossley (2011) model modified for a task with four response options. MSN – medium spiny neuron of the striatum. CM-Pf – centremedian and parafascicular nuclei of the thalamus. TAN – tonically active neuron of the striatum. SN_PC –DA neurons from the substantia nigra pars compacta. GP_i – internal segment of the globus pallidus. VL – ventral lateral nucleus of the thalamus.

The model is described in detail in Ashby and Crossley (2011). Briefly, activation in all sensory and CM-Pf units was modeled with a simple square wave (i.e., on or off). In all other units, spiking neuron models were used. Firing in MSNs and TANs was modeled with a modification of the Izhikevich (2007) spiking model, and firing in all other units was modeled with the quadratic integrate-and-fire model (Ermentrout, 1996).

Learning at the CM-Pf – TAN synapse, and at all cortical-striatal synapses is a function of presynaptic activity, postsynaptic activity, and the DA released on each trial. Specifically, let w_K,J(n) denote the strength of the synapse on trial n between pre-synaptic unit K and post-synaptic unit J. Then we model reinforcement learning as follows:

$$\begin{array}{l}{w}_{K,J}(n+1)=w_{K,J}(n)+{\alpha }_w{I}_K(n){[S_J(n)-{\theta }_{\mathit{NMDA}}]}^{+}{[D(n)-0.2]}^{+}[1-w_{K,J}(n)]\\ -{\beta }_w{I}_K(n){[S_J(n)-{\theta }_{\mathit{NMDA}}]}^{+}{[0.2-D(n)]}^{+}{w}_{K,J}(n)\\ -{\gamma }_w{I}_K(n){[{\theta }_{\mathit{NMDA}}-S_J(n)]}^{+}{[S_J(n)-{\theta }_{\mathit{AMPA}}]}^{+}{w}_{K,J}(n),\end{array}$$ (1)

where I_K (n) and S_J (n) are the total positive activations on trial n in pre-synaptic unit K and post-synaptic unit J, respectively. The function [g(n)]⁺ = g(n) if g(n) > 0, and otherwise g(n) = 0. The constant 0.2 is the baseline DA level, D(n) is the amount of DA released following feedback on trial n, and α_w, β_w, γ_w, θ_NMDA, and θ_AMPA are all constants. The first three of these (i.e., α_w, β_w, and γ_w) operate like standard learning rates because they determine the magnitudes of increases and decreases in synaptic strength. The constants θ_NMDA and θ_AMPA represent the activation thresholds for post-synaptic NMDA and AMPA (more precisely, non-NMDA) glutamate receptors, respectively. The numerical value of θ_NMDA > θ_AMPA because NMDA receptors have a higher threshold for activation than AMPA receptors. This is critical because NMDA receptor activation is required to strengthen cortical-striatal synapses (Calabresi, Pisani, Mercuri, & Bernardi, 1996).

The first line in Equation 1 describes the conditions under which synapses are strengthened (i.e., striatal activation above the threshold for NMDA receptor activation and DA above baseline) and lines two and three describe conditions that cause the synapse to be weakened. The first possibility (line 2) is that post-synaptic activation is above the NMDA threshold but DA is below baseline (as on an error trial), and the second possibility is that striatal activation is between the AMPA and NMDA thresholds.

Note that synaptic strength does not change if post-synaptic activation is below the AMPA threshold. Note that Equation 1 requires that we specify exactly how much DA is released on each trial [i.e., D(n)]. Dopamine neurons are driven by an extensive neural network that is thought to include the prefrontal cortex, hypothalamus, amygdala, and pedunculopontine tegmental nucleus (among other structures). Modeling this network is beyond the scope of this article (for one model, see Brown, Bullock, & Grossberg, 1999). Instead, our focus is on II category (i.e., procedural) learning. Specifically, we propose that the TANs act as a gate that protects striatal-mediated procedural learning when changes in behavior cannot increase the rate of reward. A biologically detailed computational model of II learning is required to verify that the abstract concept of a gate is physically realizable and consistent with known neuroscience. Thus, we will build a biologically detailed model of the gate and of its effects on striatal-mediated learning, but not of the network that drives dopamine neuron firing. Instead we will model the dopamine system using a more abstract, descriptive model (i.e., in the language of Marr, 1982, a computational, rather than an implementational level model).

Ashby and Crossley (2011) also modeled the dopamine system in this descriptive way. Their model was developed to be consistent with a broad array of DA cell firing data. In particular, the model was developed to account for three well replicated results (e.g., Schultz, Dayan, & Montague, 1997; Tobler, Dickinson, & Schultz, 2003): 1) midbrain DA neurons fire tonically, 2) DA release increases above baseline following unexpected reward, and the more unexpected the reward the greater the release, and 3) DA release decreases below baseline following unexpected absence of reward, and the more unexpected the absence, the greater the decrease. One common interpretation of these latter two results is that over a wide range, DA firing is proportional to the reward prediction error (RPE):

$$\text{RPE}=\text{Obtained}\text{Reward}-\text{Predicted}\text{Reward}.$$ (2)

Ashby and Crossley (2011) built a simple model of DA release by specifying how to compute Obtained Reward, Predicted Reward, and exactly how the amount of DA release is related to the RPE. Although the Ashby and Crossley (2011) model easily accounts for fast reacquisition following a traditional no-feedback extinction period, it fails to account for fast reacquisition after a period of random feedback in category learning. This is because random feedback provides sufficient unexpected reward (on average, once every four trials) to keep the DA system fluctuating significantly above baseline. This causes the TANs to maintain their pause. When the TANs are paused, the model unlearns the category structures, and as a result reacquisition is slow.

Extending the Ashby and Crossley (2011) Model

The problem is that the Ashby and Crossley (2011) model was developed exclusively from data collected in traditional instrumental conditioning paradigms in which no feedback of any kind is given during extinction. The model predicts that fast reacquisition will occur in any paradigm where the intervention drives DA cell firing to baseline (assuming the attenuation in DA cell firing proceeds faster than unlearning at cortical-MSN synapses). Thus, one way to modify the Ashby and Crossley (2011) model to account for fast reacquisition in Experiment 1 is to assume that the magnitude of trial-by-trial DA fluctuations decreases when feedback becomes random. We know of no current models of DA release capable of this subtlety.⁶

In Experiment 1, two cues signal participants that the feedback has become random. One is that the probability of receiving positive feedback is at chance. A second is that reward valence is no longer contingent on behavior. For several reasons, we believe the latter of these two cues is more important than the former. First, the probability of receiving positive feedback is also at chance when the experiment begins and at the beginning of reacquisition. Yet in both of these cases, accuracy steadily increases, which by all current DA-mediated reinforcement-learning models can only occur if DA fluctuations are significant. Second, any inference that performance is at chance requires a mental model of the testing conditions. For example, a positive feedback rate of 25% signals chance performance only under the realization that there are four equally likely response alternatives. In contrast, even in the absence of any such model, determining that the feedback is non-contingent on behavior is always a matter of determining whether feedback valence is correlated with expectation. Furthermore, there is evidence that animals are highly sensitive to feedback contingency. In fact, in instrumental conditioning tasks, extinction can be induced simply by suddenly making the rewards non-contingent on behavior (Balleine & Dickinson, 1998; Boakes, 1973; Nakajima, Urushihara, & Masaki, 2002; Rescorla & Skucy, 1969; Woods & Bouton, 2007). Additionally, fMRI studies in humans have shown that activity in the dorsal striatum is correlated with RPE when feedback is contingent on behavior but not when feedback is independent of behavior (O’Doherty et al., 2004; Harunu & Kawato, 2006).

Based on this reasoning, we propose to modify the Ashby and Crossley (2011) model of DA release in the following way. First, Ashby and Crossley used the single-operator learning model (Bush & Mosteller, 1951) to compute predicted reward. The predictions of this model depend only on past reinforcement history. This is sufficient for instrumental conditioning tasks with a single cue and a single response, but not for categorization tasks. One of the most ubiquitous results in the categorization literature is that accuracy, response confidence, and response time are all strongly correlated with the distance from the stimulus to the category decision bound (e.g., Ashby, Boynton, & Lee, 1994). Stimuli far from the bound are easier to categorize and response confidence is higher than for stimuli near the bound. Thus, even if past reinforcement history is identical, reward expectation will be higher for stimuli far from the bound than for stimuli near the bound. In the Figure 4 model, response confidence is determined by the difference between the output magnitudes of the competing motor units. When one unit is much more active than the others, then the model is signaling that the evidence favoring one response is much greater than the evidence favoring the alternative, which is consistent with a state of high confidence. In this case, the expectation of reward should be high. If two units are almost equally active however, then the model is signaling that the available evidence is equivocal. In other words, confidence and reward expectation are both low. Thus, we propose to define predicted reward on trial n in Equation 1, which we denote by P_n, as the normalized difference between the maximum outputs of the two most active motor units. Specifically,

$$P_n=(M_{1,n}-M_{2,n})/M_{1,n},$$ (3)

where M_1,n is the maximum output from the most active motor unit on trial n and M_2,n is the maximum output from the second most active motor unit on that trial. Note that Equation 3 is sensitive both to past reinforcement history and to the identity of the stimulus. We define obtained reward simply as +1 if positive feedback is received and −1 if the feedback is negative (and 0 if no feedback is given).

Second, we assume that the amount of DA release is modulated by reward contingency. When rewards are contingent on behavior, we assume DA fluctuations with RPE are large, whereas if rewards are non-contingent on behavior then we assume that DA fluctuations will be low (regardless of the RPE). An adaptive justification for this assumption is that when rewards are not contingent on behavior then changing behavior cannot increase the amount or probability of reward. As a result, there is nothing of benefit to learn. If DA fluctuates under such conditions then reinforcement-learning models predict that learning will occur, but it will be of behaviors that have no adaptive value.

Computationally, we propose to measure reward contingency by computing the correlation between reward expectation (i.e., P_n) and the valence of obtained feedback. If these are uncorrelated then for example, the probability of receiving positive feedback does not depend on the response of the model because positive feedback is equally likely on trials when model uncertainty is high as when it is low. This is exactly what should happen when rewards are non-contingent on behavior. In contrast, when rewards are contingent on behavior, then positive feedback should be more likely on trials when confidence is high than when confidence is low, and as a result, reward expectation and feedback valence should be positively correlated.

Note that expected reward on trial i, P_i, is a continuous variable and obtained reward (i.e., reward valence) is binary (−1 or 1). Thus, to compute the correlation we used a variation of the point-biserial correlation coefficient. Specifically, we defined r(n) as

$$r(n)=\left|{\overline{P}}^{+}-{\overline{P}}^{-}\right|$$ (4)

where P̄⁺ is the mean response confidence on trials that received positive feedback, and P̄⁻ is the mean response confidence on trials that received negative feedback. Note that if feedback is non-contingent on behavior then P̄⁺ = P̄⁻ and consequently, r(n) = 0. On the other hand, if confident responses are always rewarded with positive feedback then P̄⁺ ≫ P̄⁻ and the correlation will be large. To implement this model we assumed a small value of r(n) = 0.1 during the first 25 trials and thereafter computed r(n) using iterative estimates of P̄⁺ and P̄⁻ that are fully described in Appendix 3.

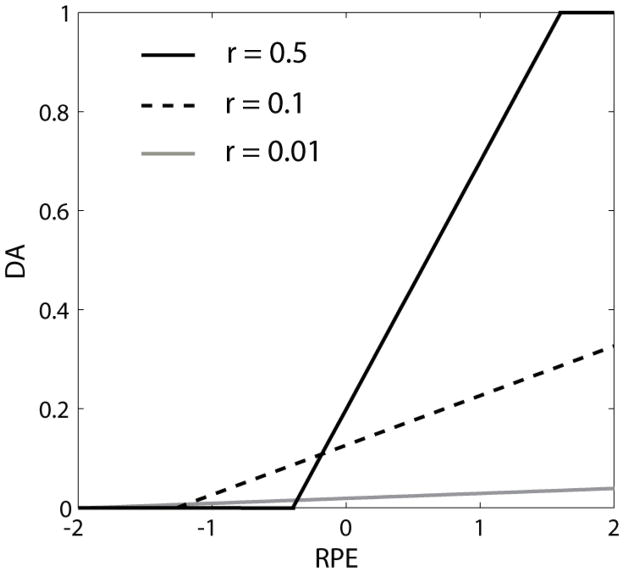
The final step is to determine how these factors affect DA release. Ashby and Crossley (2011) assumed that the amount of DA released on trial n, D(n), was a linear function of RPE between minimum and maximum values of 0 and 1, respectively, with a baseline level of 0.2. This model was chosen to closely match DA single-unit firing data reported by Bayer and Glimcher (2005). We propose that the reward contingency factor r(n) acts as a gain on this linear function – the larger the correlation the greater the fluctuations in DA for the same RPE. More specifically, we propose that:

$$DA(n)=f\left[r(n)\mathit{RPE}+0.2(1-e^{-10r(n)})\right]$$ (5)

where r(n) is a measure of the correlation between the predicted (i.e., P_i) and obtained rewards as of trial n. The function f(x) is equal to 0 if x is less than zero and is equal to 1 if x is greater than 1. Figure 5 shows examples of Equation 5 for a few different values of r(n). Note that as reward contingency increases, the slope of the function relating DA release to RPE increases, as does the amount of DA released on trials when RPE = 0. This latter feature means that as reward contingency decreases, DA release falls below baseline (i.e., 0.2) when RPE = 0. Equation 1 indicates that this condition biases the learning model towards synaptic weakening at low RPE and r(n) values. This assumption is essential to ensure that the TANs can learn to stop pausing during random feedback and thereby protect cortical-MSN synapses from random learning. On the other hand, it should also be noted that the assumption only affects a few trials – that is, when RPE and r(n) are both low. With random feedback, RPE will rarely equal 0. An RPE of 0 means that the reward is perfectly predictable, which is highly unlikely when rewards are non-contingent on behavior. Similarly, since r(n) is an estimate of the true correlation, its value will fluctuate around 0 when the feedback is random, but it will rarely exactly equal zero. Thus, the assumption that r(n) affects the gain (i.e., the slope) of DA fluctuations has much greater effects on the behavior of the model than the assumption that r(n) affects the intercept.

Figure 5.

The amount of DA released at the end of a trial in the model as a function of reward prediction error (RPE) for three different values of the correlation between response confidence and obtained reward (r). In our simulations, the mean value of r during the acquisition and relearning phases did not exceed 0.5 and was about 0.01 during the intervention phase.

An obvious and important question is: how does the brain compute the Equation 4 correlation? The model of Brown et al. (1999) would probably ascribe this function to the prefrontal cortex. But, as mentioned above, answering this question is beyond the scope of this article. Instead our goal is to determine whether the TANs could serve as a gate to the striatum if the dopamine system is described by Equation 5.

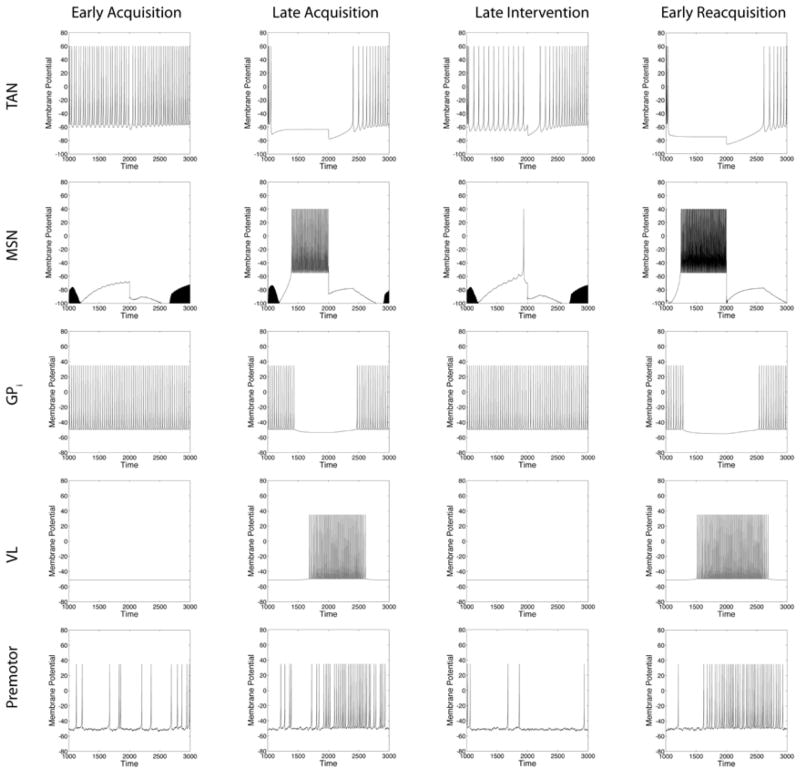
Figure 6 shows an application of the model to Experiment 1. Spiking is shown in each unit type in the model on four separate trials distributed at different points during the experiment. All four trials resulted in an A response, so only the A pathway through the system is shown. The four trials occurred early in acquisition (trial 1), near the end of acquisition (trial 300), near the end of intervention (trial 600), and early in reacquisition (trial 650). Note that the CM-Pf and the sensory cortex activations are both modeled as simple square waves that are assumed to coincide with the stimulus presentation. Early in acquisition, the TAN has not yet learned that the cue is associated with reward, so it fails to pause when the stimulus is presented. As a result of the tonic inhibition from the TAN, the MSN does not fire to the stimulus, and in the absence of any inhibitory input from the striatum, the globus pallidus does not slow its high spontaneous firing rate, and therefore the thalamus is prevented from firing to other excitatory inputs. The premotor unit fires at a slow and noisy tonic rate, but note that this rate does not increase during stimulus presentation. As a result, the model responds A by chance (i.e., the spontaneous firing rate in premotor unit A happens to be higher on this trial than in other premotor units). At the end of acquisition, the TAN pauses when the stimulus is presented, which allows the MSN to fire a vigorous burst, thereby inhibiting the globus pallidus. The pause in pallidal firing allows the thalamus to respond to its other excitatory inputs, and the resulting burst from the thalamus drives the firing rate in premotor unit A above the response threshold. Note that the responses at the end of the random feedback intervention look much the same as at the beginning of acquisition. This is because the TAN fails to pause to the cue. In the absence of a TAN pause the premotor unit is never excited by thalamus, so responding is driven by chance (i.e., by noise in the premotor firing rates). Despite the similarity in firing rates however, the cortical-striatal synaptic strengths are significantly stronger at the end of the intervention than at the beginning of acquisition. The absence of a TAN pause during much of the intervention prevented these synapses from weakening. Thus, just a few trials later when the TAN is pausing again (i.e., early in reacquisition), note that the stimulus again elicits a vigorous burst from the MSN, which results in a strong response from premotor unit A.

Figure 6.

Model dynamics shown at four distinct points in the Experiment 1 simulation. The horizontal axis begins at stimulus onset (i.e., time step 1000), and stimulus offset is at time step 2000. See text for a complete description. MSN – medium spiny neuron of the striatum. TAN –tonically active neuron of the striatum. SN_PC – DA neurons from the substantia nigra pars compacta. GP_i – internal segment of the globus pallidus. VL – ventral lateral nucleus of the thalamus.

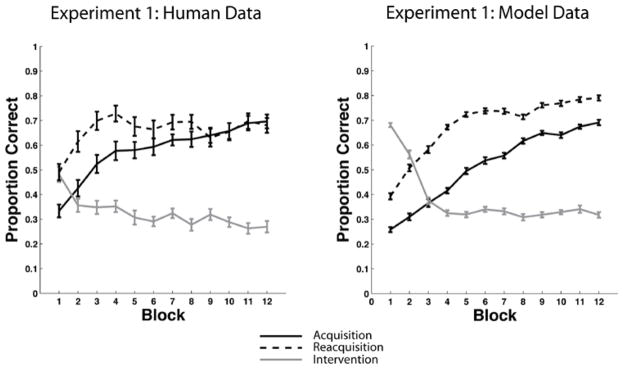
We tested this model against the Relearning data⁷ of Experiment 1. The right panel of Figure 7 shows the predictions of the model and for comparison the left panel shows the human data. The model’s predictions are the means of 50 separate simulations of the experiment (see Appendix 2 for complete simulation details). Note that the model effectively captures the major qualitative properties of the human data – that is, the model learns the categories, performance drops nearly to chance during the intervention phase, and reacquisition is considerably faster than acquisition.

Figure 7.

Behavioral data versus model results in the Experiment 1 Relearning condition. Left Panel: Overlaid accuracy data in the Relearning condition from the acquisition phase, intervention phase, and reacquisition phase in Experiment 1. Right Panel: Overlaid accuracy data in the Relearning condition from the acquisition phase, intervention phase, and reacquisition phase in the model simulation of Experiment 1.

The only major qualitative difference between the model and the human data is that the model’s reacquisition accuracy continuously increases, whereas human reacquisition accuracy asymptotes after about the fourth block. One possible explanation for the human asymptote is fatigue. Of course, the model never gets tired, but by this point in the experiment, the humans have completed 700–800 of their eventual 900 trials. It seems plausible that after so many trials, attention and motivation might wane in some participants. Another possibility is synaptic fatigue. For example, the evidence is good that the threshold on post-synaptic activation that separates LTD from LTP increases after periods of high activity (Kirkwood, Rioult, & Bear, 1996; Bienenstock, Cooper, & Munro 1982). In our model, this threshold is determined by the θ_NMDA. Increasing this parameter decreases learning. It seems likely that allowing θ_NMDA to increase during the experimental session (e.g., as in the BCM model of Bienenstock et al., 1982) would therefore improve the quality of the fits. We chose not to add this feature to the model however, because our major focus is on the rate of acquisition and reacquisition, rather than on the absolute accuracy level at the end of 900 experimental trials. Thus, the most important feature of Figure 7 is that for both the model and the data, reacquisition is considerably faster than acquisition.

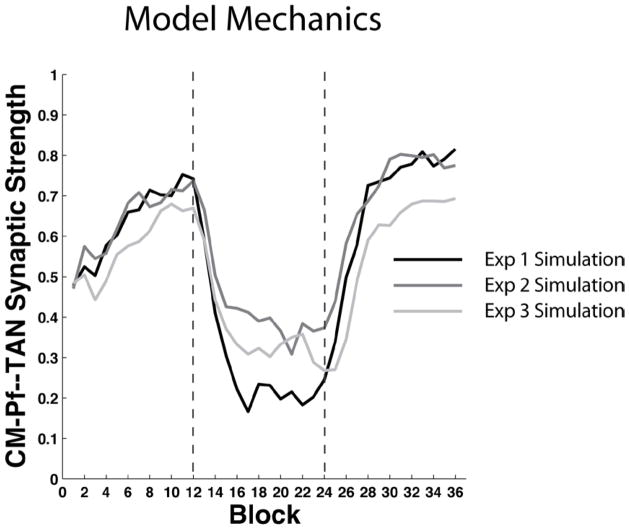
The solid black curve in Figure 8 shows the mean strength of the synapse between the CM-Pf and the TAN across all 36 blocks of the Experiment 1 simulation. Note that the strength of the CM-Pf – TAN synapse quickly falls during the random feedback intervention period. Early during this period, before the model recognizes that the feedback is no longer contingent on behavior, the large increase in the frequency of negative feedback weakens the CM-Pf – TAN synapse because on negative feedback trials DA falls below baseline levels. The same thing happens to cortical-MSN synapses (not shown) but because the sensory cortical neurons are so narrowly tuned only a few of the thousands of cortical-striatal synapses are affected on any one trial. As a result, the overall decay of cortical-MSN synapses is much slower than the decay of the CM-Pf – TAN synapse (which is active on every trial). When the CM-Pf – TAN synapse becomes weak enough, the visual stimulus is no longer able to induce a pause in the TAN firing. In the absence of a pause, the stimulus is effectively invisible to the MSNs, and no further decay occurs in the cortical-striatal synaptic strengths. Note that this is also why the model responds at near chance levels during the intervention phase (i.e., since the cortical input to the striatum is heavily attenuated, the only activity in the premotor unit is due to noise).

Figure 8.

Mean cortical-MSN and CM-Pf—TAN synaptic strengths in the model simulation of Experiments 1 – 3. Top Panel: Simulation of Experiment 1. Middle Panel: Simulation of Experiment 2. Bottom Panel: Simulation of Experiment 3. The vertical lines denote transitions between phases (i.e., acquisition, intervention, reacquisition).

After some number of random feedback trials (e.g., 20–40) the non-contingent nature of the feedback causes the DA system to change its behavior in two critical ways. First, the overall magnitude of the trial-by-trial fluctuations is reduced. This has the effect of reducing the magnitude of changes at all plastic synapses in the model. Second, the average DA release across many trials is suppressed such that the DA release during the intervention phase is usually below baseline DA levels. This has the effect of ensuring that the most frequent synaptic change at vulnerable synapses (i.e., the CM-Pf—TAN synapse) is synaptic weakening. This ensures that the TANs unlearn their pause response and protect cortical-MSN synapses from modification. During reacquisition, the feedback again becomes contingent on behavior, DA fluctuations increase, and the CM-Pf—TAN synapse quickly grows strong enough to induce a TAN pause. At this point the behavior reappears because of the minimal synaptic modification of cortical-MSN synapses during the intervention phase.

Using the Model to Develop an Effective Unlearning Protocol

The model developed in the last section has a number of attractive features. First, it correctly accounts for the behavioral results from II category-learning experiments. The great majority of these experiments include only an acquisition phase where veridical feedback is given after every response. In such experiments, the addition of the TANs do not change the predictions of the model in any significant way, since the model predicts that the TANs would quickly learn to pause and that they would remain paused throughout the course of the experiment. Without the TANs, the model reduces to a biologically detailed version of the striatal pattern classifier (Ashby & Waldron, 1999), which has successfully accounted for II category-learning data for many years (Maddox & Filoteo, 2011; Maddox et al., 2010a; Maddox et al., 2010b; Schnyer et al., 2009; Maddox et al., 2008).

Second, the model is consistent with a wide variety of neuroscience data. For example, 1) it is based on known neuroanatomy, 2) it accounts for single-unit recording data from striatal MSNs and from TANs (in both cases, the model accounts for results from both patch-clamp and learning experiments; see Ashby & Crossley, 2011), 3) the model correctly predicts fast reacquisition following extinction in traditional instrumental conditioning paradigms (Ashby & Crossley, 2011), and 4) the model is roughly consistent with the available neuroimaging data from II tasks – for example, by postulating a key role for the putamen and the premotor cortex (Waldschmidt & Ashby, 2011).

Third, of course, the model successfully accounts for the fast reacquisition observed in Experiment 1. As we have seen, this is a significant accomplishment that makes the model unique among all other category-learning models. As an added benefit, the model specifies a biological mechanism that protects learning during periods when rewards are no longer available or are no longer contingent on behavior (i.e., the TANs).

Given that we have a biologically detailed model of II category learning that specifies a mechanism that protects learning, an obvious question that has both theoretical and practical significance is: how can we use this model to design an effective unlearning protocol? The model hypothesizes that the key to unlearning in procedural skill tasks is the TANs. Specifically, the model predicts that unlearning can be effective only if the TANs pause during the unlearning training. If the TANs do not pause, then the MSNs in the striatum will never “see” the stimuli (because the cortical input will be presynaptically inhibited), and the unlearning training will have no effect.

The model suggests two qualitatively distinct approaches for maintaining a TAN pause during unlearning training – pharmacological and behavioral. We discuss the pharmacological methods in the general discussion. The idea behind the behavioral approach is to arrange conditions so that the TANs pause but unlearning still occurs. The TANs are highly sensitive to cues associated with reward, so to keep the TANs paused it seems vital to deliver some rewards during the unlearning training (i.e., the intervention phase). Experiment 2 explores this possibility.

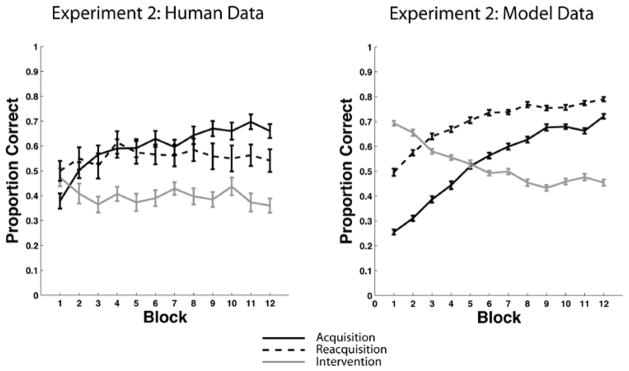
Experiment 2

The results of Experiment 1 suggest that random feedback does not induce true unlearning. Our model accounts for this failure by assuming that the TANs unlearn their pause response during the intervention phase (i.e., they quit pausing). We hypothesize that this occurs because the DA system is highly sensitive to the correlation between the obtained and expected feedback. Thus, since random feedback is not contingent on the subject’s behavior, DA fluctuations decrease, which weakens the CM-Pf—TAN synapse and abolishes the TAN’s pause response. With the TANs tonically active, learning at cortical-MSN synapses is protected. This suggests that one possible method to induce true unlearning might be to make the feedback partially contingent on the behavior of the participant. One way to do this is to include some accurate feedback trials among the random feedback trials that define the intervention period. The idea is to make the contingency between feedback and behavior high enough to keep the TANs paused but low enough to induce some true unlearning. Experiment 2 tests this prediction. The acquisition and reacquisition phases are the same as in Experiment 1, but during the intervention phase, random feedback will be given on 75% of the trials and valid (accurate) feedback will be given on 25% of the trials. The hope is that the true feedback trials will be frequent enough to keep the TANs paused throughout the intervention phase and the random feedback will then overwrite the relevant memory traces with random associations. Experiment 2 also includes a Meta-Learning condition that is similar to the Meta-Learning Control condition of Experiment 1.

Method

Participants

There were 32 participants in the Relearning condition, 27 participants in the Meta-Learning condition. All participants completed the study and received course credit for their participation. All participants had normal or corrected to normal vision. To ensure that only participants who performed well above chance were included in the post-acquisition phase, a learning criterion of 40% correct (25% is chance) during the final acquisition block of 100 trials was applied. Using this criterion, we excluded 4 participants in the Relearning condition, and 3 participants in the Meta-Learning condition.

Stimuli

The stimuli were identical to those from Experiment 1.

Procedure

The procedures were identical to Experiment 1 except for the nature of the feedback during the intervention phase. Specifically, during each of the three 100-trial intervention blocks, valid feedback was provided on 25 trials and random feedback was given on the remaining 75 trials. These 25 trials were randomly distributed within each block⁸.

Results

Accuracy-based results

The top panel of Figure 9 shows the mean accuracy for every 25-trial block of each condition. During intervention, a response was coded as correct if it agreed with the category membership shown in Figure 2. Recall that the categories and feedback were identical in the two conditions until the beginning of the reacquisition phase. Note that participants from both conditions were able to learn the categories, reaching their peak accuracy near the end of acquisition, before falling to about 40% correct by the end of the intervention period. As expected, there are only minor differences between participants in the Relearning and Meta-Learning conditions during the acquisition and intervention phases of the experiment. Interestingly, the two learning curves do not diverge during reacquisition. Participants in both conditions show no evidence of fast reacquisition.

Figure 9.

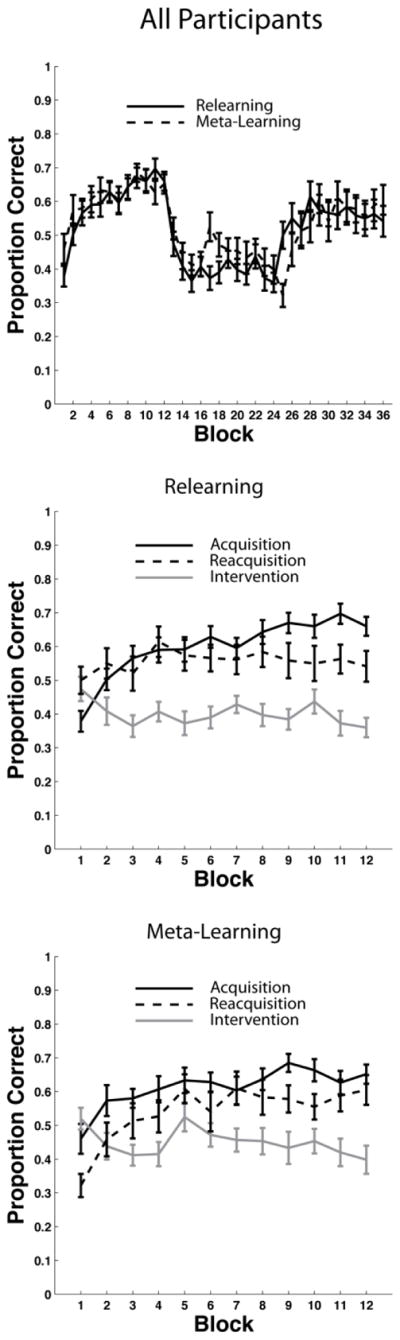
Experiment 2 accuracy. Each block includes 25 trials. Top Panel: Accuracy in the Relearning and Meta-Learning conditions throughout the entire experiment. Blocks 1–12 were in the acquisition phase, blocks 13–24 were in the intervention phase, and blocks 25–36 were in the reacquisition phase. Middle Panel: Overlaid accuracy data in the Relearning condition from the acquisition phase, intervention phase, and reacquisition phase. Bottom Panel: Overlaid accuracy data in the Meta-Learning condition from the acquisition phase, intervention phase, and reacquisition phase.

To test these conclusions formally we conducted a 2 conditions (Relearning versus Meta-Learning) × 36 blocks repeated measures ANOVA. We found no significant effect of condition [F(1,50) = .26, p = .61, η_p² = 0.005], and no interaction [F(7,382) = 1.49, p = .162, η_p² = 0.03], but the effect of block was significant [F(7,382) = 15.94, p < .001, η_p² = 0.24]. We then conducted several 2 conditions (Relearning versus Meta-Learning) × 12 blocks repeated measures ANOVAs, where the 12 blocks corresponded to the acquisition, intervention, or reacquisition phase. In the ANOVA corresponding to the acquisition phase, we found no effect of condition [F(1,50) = .15, p = .70, η_p² = 0.003], or interaction [F(6,302) = 1.34, p = .24, η_p² = 0.03], but the effect of block was significant [F(6,302) = 17.75, p < .001, η_p² = 0.26]. In the ANOVA corresponding to the intervention phase we found no effect of condition [F(1,50) = 2.74, p = .10, η_p² = 0.05], and no interaction [F(5,251) = .79 , p = .56, η_p² = 0.02], but the effect of block was significant [F(5,251) = 2.30, p < 0.05, η_p² = 0.04]. In the ANOVA corresponding to the reacquisition phase, we found no significant effect of condition [F(1,50) = .09, p = .77, η_p² = 0.02], but the interaction and block effects were both significant [Interaction: F(5,297) = 3.40, p < .005, η_p² = 0.06, Block: F(5,297) = 7.21, p < .001, η_p² = 0.13].

Next, we computed several repeated measures t-tests to compare performance between phases (i.e., acquisition, intervention, and reacquisition). For the Relearning condition, mean acquisition performance (across blocks) and mean reacquisition performance were both significantly better than mean performance during intervention [acquisition: t(335) = 13.96, p < 0.001, d = 0.76; reacquisition: t(335) = 10.05, p < 0.001, d = 0.55]. Interestingly, reacquisition was significantly worse than acquisition [t(335) = 3.04, p < 0.005, d = 0.17]⁹. This difference is clearly seen in the middle panel of Figure 9, which superimposes the acquisition, intervention, and reacquisition curves from the Relearning condition. The qualitative pattern of results for the Meta-Learning condition was the same (see the bottom panel of Figure 9). Specifically, acquisition and reacquisition were better than intervention [acquisition: t(287) = 11.68, p < 0.001, d = 0.69; reacquisition: t(287) = 5.24, p < 0.001, d = 0.31], and reacquisition was worse than acquisition [t(287) = 5.01, p < 0.001, d = 0.29]. In summary, for both the Relearning and Meta-Learning conditions, performance during the intervention phase was significantly worse than performance during acquisition and reacquisition, and performance during reacquisition was significantly worse than performance during acquisition.

Next, we performed two separate tests to examine intervention performance. First, we compared the first block of acquisition to the last block of intervention (i.e., acquisition -intervention). These tests revealed that these two blocks were not significantly different from each other in either the Relearning condition [t(27) = 0.46, p = 0.64, d = 0.09], or the Meta-Learning condition [t(23) = 1.25, p = 0.22, d = 0.25]. Second, we computed t-tests on the null hypothesis that the last two intervention blocks from each condition were generated from a distribution with mean 0.25 (i.e., the accuracy we would expect if performance was truly at chance). These tests revealed that that the last two blocks of intervention were significantly different from chance for the both the Relearning condition [t(55) = 5.03, p < 0.001, d = 0.67] and the Meta-Learning condition [t(47) = 5.50, p < 0.001, d = 0.79]. In summary, the intervention eventually reduced accuracy to the level present in the first 25 trials of acquisition training (i.e., before much learning could have occurred), but did not reduce performance to chance levels.

Model-based results

The accuracy-based results show slow reacquisition in both conditions. To determine whether this was due to participants never reacquiring the strategy they learned during acquisition, or because they applied the II strategy they learned during acquisition less successfully, we conducted the same model analyses outlined in Experiment 1.

Table 2 shows the number of participants in the two conditions whose responses were best fit by each of the three model types. In the final block of acquisition, about 64% of all participants from the Relearning condition and about 62% from the Meta-Learning condition were best fit by models that assumed information integration. The remaining participants were best fit by a model that assumed a rule-based strategy, with one participant best fit by a model that assumed a guessing strategy. In the first block of reacquisition, about 43% of all participants in the Relearning condition and about 54% of all participants in the Meta-Learning condition were best fit by a model that assumed an II strategy. About 36% of the remaining participants from the Relearning condition were best fit by a model that assumed a rule-based strategy and about 21% were best fit by a model that assumed a guessing strategy. A similar pattern held true for the Meta-Learning condition. Specifically, about 54% of participants were best fit by a model that assumed an II strategy, 29% by a model that assumed a rule-based strategy, and the remaining 17% were best fit by a guessing strategy during the first block of reacquisition. Thus, the proportion of participants fit best by a model that assumed an information-integration strategy was decreased from the last block of acquisition to the first block of reacquisition in both conditions, although this decrease was only significant for the Relearning condition [Relearning condition: t(54) = 1.88, p < 0.05, d = 0.35; Meta-Learning condition: t(46) = 0.58, p = 0.28, d = 0.12].

Table 2.

Proportion of participants in the two conditions of Experiment 2 whose responses were best accounted for by a model that assumed an information-integration (II) decision strategy, a rule-based strategy, or random guessing, and the proportion of responses accounted for by those models.

	Relearning				Meta-Learning
	A3		R1		A3		R1
	%N	%RA	%N	%RA	%N	%RA	%N	%RA
II	.64	.74	.43	.68	.63	.70	.54	.55
RB	.36	.65	.36	.67	.33	.65	.29	.55
Guessing	0	-	.21	-	.04	-	.17	-

Note. A3 = the last 100 trials of acquisition, R1 = the first 100 trials of reacquisition, %N = the proportion of participants contained in a given cell, and %RA = the proportion of responses accounted for by a particular model.

Since the model developed here deals exclusively with procedural memory, we repeated all the accuracy-based analyses reported in the previous section using only the data from the participants in each condition whose responses were best fit by an II strategy during the last block of acquisition. The results of these statistical tests were qualitatively identical to those reported earlier for all participants. Specifically, the accuracy of II users in the Relearning condition was not different from the accuracy of II users in the Meta-Learning condition during any phase of the experiment, and II users did not reach chance levels of performance during intervention in either condition, although the last block of intervention pooled from each condition was indistinguishable from the first block of acquisition. Importantly, reacquisition performance was worse than acquisition performance in the Relearning condition (not, however, in the Meta-learning condition).

Discussion

A comparison of Figures 3 and 9 shows that relearning was dramatically slower in Experiment 2 than in Experiment 1, and that there was less interference in Experiment 2 when participants were required to learn new categories. Thus, the use of partially contingent feedback during the intervention phase appears to hold promise as a method to induce unlearning. On the other hand, it is also important to acknowledge that unlearning was not complete in Experiment 2. Statistically, reacquisition was less effective than original acquisition and changing the category structures in the Meta-Learning condition produced an interference. In addition, performance did not drop to chance during the intervention. All three of these results suggest a failure of complete unlearning. Even so, it is critical to note that our results do suggest that partially contingent feedback was successful at inducing some degree of either unlearning or new learning capable of interfering with the learning acquired during acquisition.

A Theoretical Account of Experiment 2

The right panel of Figure 10 shows predictions of the model in the Relearning condition of Experiment 2 compared to the human data (left panel). The values shown in the right panel of Figure 10 are the means of 50 separate simulations of the experiment (see Appendix 2 for complete simulation details). Note that the model effectively captures the major qualitative properties of the human data – that is, the model learns the categories, performance drops nearly to chance during the intervention, and reacquisition is not faster than acquisition.

Figure 10.

Behavioral data versus model results in Experiment 2. Left Panel: Overlaid accuracy data in the Relearning condition from the acquisition phase, intervention phase, and reacquisition phase in Experiment 2. Right Panel: Overlaid accuracy data in the Relearning condition from the acquisition phase, intervention phase, and reacquisition phase in the model simulation of Experiment 2.

As in Experiment 1, the only major qualitative difference between the model and the human data is that the model continuously improves its accuracy, whereas human accuracy asymptotes, especially during the reacquisition phase. Note that the higher terminal acquisition accuracy of the model causes accuracy to be higher in the first intervention block than in the human data. But perhaps most striking is the model’s higher reacquisition accuracy. During reacquisition, the model continuously improves, whereas human reacquisition accuracy asymptotes after block 4. Note that the human asymptote is even lower here than in Experiment 1, which favors the synaptic fatigue hypothesis over more general cognitive factors (e.g., reduced attention, motivation). The number of trials is the same in Experiments 1 and 2, so it is not clear why motivation would be lower at the end of Experiment 2 than Experiment 1. But note that our model predicts that the TANs pause more during the intervention phase in Experiment 2 than in Experiment 1, which exposes the cortical-striatal synapses driving the categorization behavior to more activity and therefore more fatigue. Again however, the most important point is that the model nicely accounts for the rates of acquisition and reacquisition. For example, note that the humans increase in accuracy by 0.34 in the first five blocks of acquisition (assuming chance performance on trial 1), and increase by 0.25 during the first five blocks of reacquisition. The model displays a similar pattern, with an increase in accuracy of 0.27 in the first five blocks of acquisition, and an increase of 0.25 during the first five blocks of reacquisition.

The dark grey curve in Figure 8 shows the mean strength of the CM-Pf—TAN synapse across all 36 blocks of the Experiment 2 simulation. Note that the dynamics of the CM-Pf – TAN synapse throughout the intervention phase are highly similar to their behavior under the fully random feedback of Experiment 1 (solid black curve). The main difference is that the strength of the CM-Pf – TAN synapse does not decrease as much under the partially contingent feedback of Experiment 2 as it did during the fully random feedback of Experiment 1. The net result is that the pause response of the TANs is not abolished as completely under partially contingent feedback as it is during fully random feedback, and this leaves the cortical-MSN synapses vulnerable to more unlearning and random learning. Note that the difference in CM-Pf – TAN synaptic strengths in the simulation of Experiment 1 and Experiment 2 (i.e., the solid black and dark grey curves) is why the model generates higher intervention phase accuracy under partially contingent feedback than under fully random feedback. During reacquisition, the feedback again becomes contingent on behavior, DA fluctuations increase, and the CM-Pf – TAN synaptic strength quickly grows strong enough to induce a TAN pause. At this point the behavior reappears, but more slowly than in Experiment 1 because the cortical-MSN synapses have experienced slightly more unlearning.

Experiment 3

The results of Experiment 2 suggest that the use of partially contingent feedback may induce some true unlearning by keeping the TANs paused. However, it is important to note that participants maintained a higher level of accuracy during the Experiment 2 intervention (about 40% correct), than they did in Experiment 1 (about 30% correct). In addition, note that the average positive feedback rate during random feedback is 25%, whereas the average positive feedback rate during the semi-random feedback of Experiment 2 is 28.75%¹⁰. Thus, the results of Experiment 2 do not allow us to determine whether the unlearning that occurred was due to the use of partially contingent feedback or to either the higher accuracy or the higher positive feedback rate during the intervention phase of Experiment 2. Experiment 3 tests between these hypotheses by examining performance in a condition where intervention feedback was completely random, but weighted such that positive feedback was given on 40% of the intervention trials¹¹. If the higher accuracy rate or the higher rate of positive feedback during the Experiment 2 intervention caused the slow reacquisition in that experiment, then we should also see slow reacquisition in Experiment 3. On the other hand, if the slow reacquisition in Experiment 2 was due to the use of partially contingent feedback, then we should see fast reacquisition in Experiment 3.

Method

Participants

There were 24 participants in the Relearning condition and 28 participants in the Meta-Learning condition. All participants completed the study and received course credit for their participation. All participants had normal or corrected to normal vision. To ensure that only participants who performed well above chance were included in the post-acquisition phase, a learning criterion of 40% correct (25% is chance) during the final acquisition block of 100 trials was applied. Using this criterion, we excluded 1 participant in the Relearning condition and 3 participants in the Meta-Learning condition from further analyses.

Stimuli

The stimuli were identical to those from Experiment 1.

Procedure

The procedure was the same as in Experiment 1 except for the nature of the feedback during the intervention phase. In Experiment 3, during each of the three 100-trial intervention blocks, participants were told that they were correct on 40 randomly selected trials and were told that they were incorrect on the remaining 60 trials, regardless of their response.

Results

Accuracy based results

The top panel of Figure 11 shows the mean accuracy for every 25-trial block of each condition. During intervention, a response was coded as correct if it agreed with the category membership shown in Figure 2. Recall that the categories and feedback were identical in the two conditions until the beginning of the reacquisition phase. Note that participants from both conditions were able to learn the categories, reaching their peak accuracy near the end of acquisition. Also note that participants take nearly the entire intervention phase to fall to near-chance accuracy levels, spending the majority of the time well above chance. As expected, there are only minor differences between participants in the Relearning and Meta-Learning conditions during the acquisition and intervention phases of the experiment. During reacquisition however, the two learning curves diverge. Participants in the Relearning condition show fast reacquisition whereas participants in the Meta-Learning condition show interference (i.e., slow reacquisition).

Figure 11.

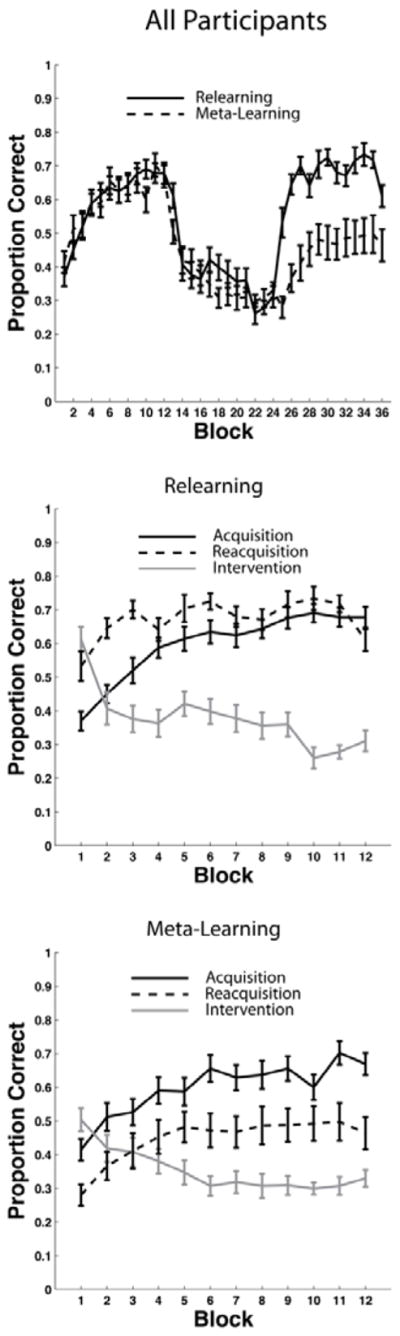
Experiment 3 accuracy. Each block includes 25 trials. Top Panel: Accuracy in both the Relearning and the Meta-Learning conditions throughout the entire experiment. Blocks 1–12 were in the acquisition phase, blocks 13–24 were in the intervention phase, and blocks 25–36 were in the reacquisition phase. Middle Panel: Overlaid accuracy data in the Relearning condition from the acquisition phase, intervention phase, and reacquisition phase. Bottom Panel: Overlaid accuracy data in the Meta-Learning condition from the acquisition phase, intervention phase, and reacquisition phase.

To test these conclusions formally, we conducted a 2 conditions (Relearning versus Meta-Learning) × 36 blocks repeated measures ANOVA. We found a significant effect of condition [F(1,46) = 8.82, p < 0.01, η_p² = 0.16], interaction [F(7,348) = 5.94, p < 0.001, η_p² = 0.11] and block [F(7,348) = 30.12, p < 0.001, η_p² = 0.40]. We then conducted several 2 conditions (Relearning versus Meta-Learning) × 12 blocks repeated measures ANOVAs, where the 12 blocks corresponded to the acquisition, intervention, or reacquisition phase. In the ANOVA corresponding to the acquisition phase, we found no significant effect of condition [F(1,46) = 0.001, p = 0.98, η_p² = 0.0], and no significant interaction [F(7,325) = 1.26, p = 0.27, η_p² = 0.03], but the effect of block was significant [F(7, 325) = 27.15, p < 0.001, η_p² = 0.37]. In the ANOVA corresponding to the intervention phase we found no significant effect of condition [F(1,46) = 0.48, p = 0.76, η_p² = 0.01], but the interaction and block effects were significant [Interaction: F(8,380) = 2.08, p < 0.05, η_p² = 0.04; block: F(8, 380) = 15.35, p < 0.001, η_p² = 0.25]. In the ANOVA corresponding to the reacquisition phase, we found a significant effect of condition [F(1,46) = 22.30, p < 0.001, η_p² = 0.33], and block [F(6, 283) = 9.57 , p < 0.001, η_p² = 0.17], but the interaction was not significant [F(6,283) = 1.16, p = 0.33, η_p² = 0.02]. The key result from these analyses is that there was a significant difference between conditions during the reacquisition phase.

Next, we computed several repeated measures t-tests to compare performance between phases (i.e., acquisition, intervention, and reacquisition) within each condition. For the Relearning condition, mean acquisition performance (across blocks) and mean reacquisition performance were both significantly better than mean performance during intervention [acquisition: t(275) = 12.45, p < 0.001, d = 0.75; reacquisition: t(275) = 17.85, p < 0.001, d = 1.07]. A more important result was that reacquisition was significantly better than acquisition [t(275) = 6.59, p < 0.001, d = 0.40]¹². This difference is clearly seen in middle panel of Figure 11, which superimposes the acquisition and reacquisition curves from the Relearning condition. For the Meta-Learning condition, mean acquisition performance (across blocks) and mean reacquisition performance were both significantly better than mean performance during intervention [acquisition: t(299) = 16.15, p < 0.001, d = 0.93; reacquisition: t(299) = 5.16, p < 0.001, d = 0.30]. A more important result was that reacquisition was significantly worse than acquisition [t(299) = 11.21, p < 0.001, d = 0.65]. This difference is clearly seen in the bottom panel of Figure 11. In summary, for both the Relearning and Meta-Learning conditions, performance during intervention was significantly worse than performance during acquisition and reacquisition. For the Relearning condition, performance during reacquisition was significantly better than performance during acquisition. For the Meta-Learning condition, performance during reacquisition was significantly worse than performance during acquisition.

Next, we performed two separate tests to examine performance during the intervention phase. First, we compared the first block of acquisition to the last block of intervention (i.e., acquisition - intervention). These tests revealed that these two blocks were not significantly different from each other in the Relearning condition [t(22) = 1.80, p = 0.08, d = 0.38], but they were marginally significantly different in the Meta-Learning condition [t(24) = 2.19, p < 0.05, d = 0.44]. However, when the data from the first acquisition block and the last intervention block are pooled across both conditions, the difference between these two blocks is significant [t(47) = 2.86, p < 0.01, d = 0.41]. Second, we computed t-tests on the null hypothesis that the last two intervention blocks from each condition were generated from a distribution with mean 0.25 (i.e., the accuracy we would expect if performance was truly at chance). These tests revealed that that the last two blocks of intervention were significantly different from chance for the both the Relearning condition [t(55) = 5.03, p < 0.001, d = 0.35] and the Meta-Learning condition [t(49) = 3.80, p < 0.001, d = 0.54]. In summary, the intervention eventually reduced accuracy to the level present in the first 25 trials of acquisition training (i.e., before much learning could have occurred), but did not reduce performance to chance levels.

Model-based results

The accuracy-based results show fast reacquisition in the Relearning condition. To test whether this was because participants truly acquired and reacquired an II strategy, or because they switched to a simpler rule-based strategy, we conducted the same model analyses as in Experiment 1.

Table 3 shows the number of participants in the two conditions whose responses were best fit by a model that assumed an II, rule-based, or guessing strategy. In the final block of acquisition, the responses of 78% of the Relearning participants and 64% of the Meta-Learning participants were best fit by an II model. The responses of all but one of the remaining participants were best fit by a model that assumed a rule-based strategy. In the first block of reacquisition, the responses of 74% of the Relearning participants but only 36% of the Meta-Learning participants were best fit by an II model. The responses of the remaining participants from the Relearning condition were all best fit by a model that assumed a rule-based strategy, whereas the responses of most of the remaining participants from the Meta-Learning condition were best fit by a model that assumed a guessing strategy (52% of all participants in this condition). Thus, the proportion of participants whose responses were fit best by an II model remained essentially constant from the last block of acquisition to the first block of reacquisition in the Relearning condition, but decreased in the Meta-Learning condition. There was no difference in the number of participants whose responses were best fit by a model that assumed an II strategy in the Relearning condition [t(44) = 0.35, p = 0.73, d = 0.07], but there was a significant decrease in the Meta-Learning condition [t(48) = 1.98, p < 0.05, d = 0.40]. Since there was no significant change in the number of participants whose responses were best fit by a model that assumed an II strategy from the last block of acquisition to the first block of reacquisition in the Relearning condition, strategy switches from II to rule-based strategies were not driving fast reacquisition.

Table 3.

Proportion of participants in the two conditions of Experiment 3 whose responses were best accounted for by a model that assumed an information-integration (II) decision strategy, a rule-based strategy, or random guessing, and the proportion of responses accounted for by those models.

	Relearning				Meta-Learning
	A3		R1		A3		R1
	%N	%RA	%N	%RA	%N	%RA	%N	%RA
II	.78	.74	.74	.67	.64	.70	.36	.59
RB	.22	.65	.26	.58	.32	.71	.12	.43
Guessing	0	-	0	-	.04	-	.52	-

Note. A3 = the last 100 trials of acquisition, R1 = the first 100 trials of reacquisition, %N = the proportion of participants contained in a given cell, and %RA = the proportion of responses accounted for by a particular model.

As in Experiments 1 and 2, we repeated all accuracy-based analyses using only the data from participants whose responses were best fit by an II model during the last block of acquisition. The results of these statistical tests were nearly identical to those reported earlier for all participants. Specifically, the accuracy of II users in the Relearning condition was not different from the accuracy of II users in the Meta-Learning condition until the reacquisition phase, and neither condition reached chance levels of performance during intervention, although the last block of intervention pooled from each condition was marginally distinguishable from the first block of acquisition. Importantly, reacquisition performance was better than acquisition performance in the Relearning condition and worse than acquisition performance in the Meta-Learning condition.

Discussion

The results from Experiment 3 indicate fast reacquisition in the Relearning condition and interference in the Meta-Learning condition. As in Experiment 1 (i.e., random feedback during intervention), these results imply that the learning that occurred during the acquisition phase was preserved during the intervention. Importantly, these results suggest that the unlearning observed in Experiment 2 was not due to the higher intervention accuracy or to the higher intervention positive feedback rate, but instead support the hypothesis that the unlearning we observed was due to the use of partially contingent feedback. Another hypothesis to consider however, is that the unlearning may have been due to the fact that the use of partially contingent feedback in Experiment 2 increased the number of correct responses that received correct feedback during intervention. This increase could make it more difficult to detect the change in reward contingencies during the Experiment 2 intervention than in Experiment 1 and therefore could be the factor that maintains the TAN pause that is needed for unlearning to occur. In fact, in Experiment 1, 25% of all correct responses received positive feedback during intervention, whereas this percentage increased to 43.75% in Experiment 2. So there were many more correct intervention responses that received positive feedback in Experiment 2 than in Experiment 1. However, in the Experiment 3 intervention there were nearly as many rewarded correct responses as in Experiment 2 (i.e., 40% versus 43.75%). Although we cannot rule out the possibility that this small difference was enough to cause unlearning in Experiment 2 but not 3, we believe this to be unlikely. The main reason is that the Experiment 3 results were virtually indistinguishable to the results of Experiment 1, and qualitatively different from the results of Experiment 2. The correlation between feedback valence and response confidence followed this same pattern – that is, the correlation was 0 in Experiments 1 and 3 (i.e., during intervention) and positive in Experiment 2. In contrast, the percentage of correct intervention responses receiving positive feedback was more similar for Experiments 2 and 3 (43.75% versus 40%) than for Experiments 1 and 3 (25% versus 40%).

A Theoretical Account of Experiment 3

The right panel of Figure 12 shows the predictions of the model proposed above in the Relearning condition of Experiment 3. The human data are shown for comparison (left panel). The values shown in the right panel of Figure 12 are the means of 50 separate simulations of the experiment (see Appendix 2 for complete simulation details). Note that the model effectively captures the major qualitative properties of the human data – that is, the model learns the categories, performance drops nearly to chance during the intervention phase, and reacquisition is faster than acquisition.

Figure 12.

Behavioral data versus model results in Experiment 3. Left Panel: Overlaid accuracy data in the Relearning condition from the acquisition phase, intervention phase, and reacquisition phase in Experiment 3. Right Panel: Overlaid accuracy data in the Relearning condition from the acquisition phase, intervention phase, and reacquisition phase in the model simulation of Experiment 3.

As in Experiments 1 and 2, note that human reacquisition performance asymptotes fairly quickly, whereas the model continues to learn throughout the reacquisition phase. The asymptote is higher here (and in Experiment 1) than in Experiment 2, which is also consistent with the synaptic fatigue hypothesis. The fast reacquisition seen in Experiments 1 and 3 suggest that the cortical-striatal synapses were protected more during the intervention phase of these experiments than in Experiment 2. Thus, synaptic fatigue should be worse in Experiment 2 than in Experiments 1 and 3. The difference in the asymptotes across experiments supports this prediction.

The light grey curve in Figure 8 shows the mean strength of the synapse between CM-Pf and the TAN across all 36 blocks of the Experiment 3 simulation. Note that the dynamics of the CM-Pf – TAN synapse are very similar to the simulation of Experiment 1 and 2 (i.e., the solid black and dark grey curves). The key difference to observe in Figure 8 is that the mean strength of the CM-Pf—TAN synapse during the Intervention phase is lower in the Experiment 1 and Experiment 3 simulations than it was in the Experiment 2 simulation. This means that the TANs did not protect cortico-striatal learning as much in Experiment 2 as they did in Experiments 1 and 3.

Comparing Results Across Experiments

The results presented so far suggest that fast reacquisition occurs anytime the intervention phase consists of non-contingent (i.e., random) feedback, regardless of the positive feedback rate (as in Experiments 1 and 3), and that slow reacquisition occurs if partially contingent feedback is given during the intervention (as in Experiment 2). These results therefore suggest that one key to successful unlearning lies in the contingency parameters of the feedback. However, since this conclusion relies heavily on between-experiment comparisons, this section reports the results of several key statistical comparisons between experiments.

Figure 13 shows the reacquisition curves from all three experiments overlaid on the mean acquisition curve pooled across experiments (since the acquisition phase was identical in all experiments). The main qualitative features of this figure are: 1) reacquisition in Experiments 1 and 3 is better than acquisition; 2) reacquisition in Experiment 2 is worse than acquisition; 3) there is no real reacquisition difference between Experiments 1 and 3, but reacquisition in both of these experiments is better than in Experiment 2. To test these observations formally, we collapsed the data from each curve across blocks and computed several independent sample t-tests between experiments¹³. The mean reacquisition performance in Experiment 1 and in Experiment 3 was significantly greater than the pooled acquisition performance [Experiment 1: t(970) = 4.97, p < 0.001, d = 0.33; Experiment 3: t(970) = 6.34, p < 0.001, d = 0.44], but the mean reacquisition performance in Experiment 2 was significantly worse than acquisition [t(970) = 2.18, p < 0.05, d = 0.15]. Mean reacquisition performance did not differ significantly between Experiments 1 and 3 [t(634) = 0.90, p = 0.37, d = 0.07], but each was significantly higher than reacquisition performance in Experiment 2 [Experiment 1: t(694) = 6.25, p < 0.001, d = 0.46; Experiment 3: t(610) = 6.83, p < 0.001, d = 0.53]. Thus, all of the key qualitative features we wished to test were verified by these statistical tests.

Figure 13.

Between-experiment accuracy. Each block includes 25 trials. The mean acquisition curve was obtained by pooling the acquisition data from all experiments. The reacquisition curves were taken directly from the corresponding experiments. To simplify the appearance of the figure, error bars are only shown for pooled acquisition. Error bars on the other curves are of similar magnitude (but slightly larger).

Comparing Results Across Simulations

The human data from these experiments show large and obvious qualitative differences in support of our theory that feedback contingency determines successful unlearning more than positive feedback rate. The model appeared to display most of the same qualitative differences. As discussed above, its major shortcoming seemed to be that unlike the human participants, the model shows no evidence of synaptic fatigue during reacquisition. But to examine the predictions of the model more carefully, Figure 14 shows the superimposed Acquisition (top panel), Intervention (middle panel), and Reacquisition (bottom panel) curves from all three experiments.

Figure 14.

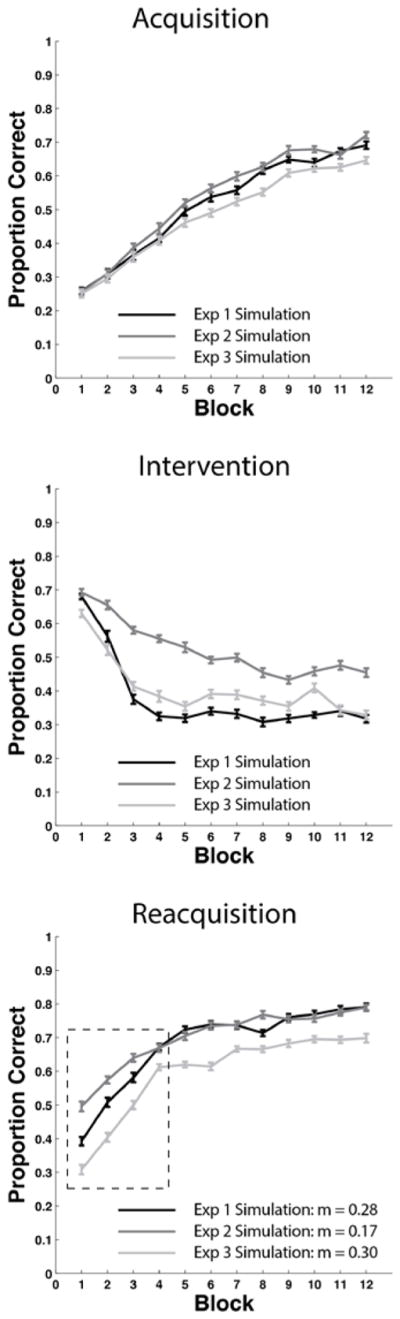
Between-experiment simulations. Curves were taken directly from the simulation results presented in Figures 7, 10, and 12, and sorted to compare phases across experiments. Top Panel: Acquisition phase. Middle Panel: Intervention Phase. Bottom Panel: Reacquisition phase. The dashed box highlights slope differences the first 4 blocks of reacquisition (indicated in the legend by the letter “m”).

Several key results are apparent in Figure 14. First, note that the model shows no real acquisition differences in any of the experiments. Second, performance during the intervention phase is similar in Experiments 1 and 3, but like the human participants, the model’s accuracy in Experiment 2 remains well above chance. Third, and most important, the Experiment 1 and 3 reacquisition curves are parallel to each other, suggesting equal reacquisition rates, whereas the Experiment 2 reacquisition curve is shallower, suggesting slower reacquisition. For example, the slope of these reacquisition curves during the first four blocks is .28 and .30 for Experiments 1 and 3 respectively, but .17 for Experiment 2. This difference shows that the model predicts at least partial unlearning in Experiment 2.

General Discussion

This article proposed a new neurobiologically detailed computational model that describes a mechanism in the striatum that protects procedural learning when rewards are no longer available or when rewards are no longer contingent on behavior. Since traditional unlearning protocols typically attempt to remove reward, the model therefore provides an account of why the unlearning of procedural skills is so difficult. It also successfully accounts for the results of Experiments 1 – 3, and it makes predictions about how to design more effective unlearning protocols.

The three experiments described in this article explored the efficacy of three different possible methods for inducing unlearning of II category structures. Experiment 1 showed that II categorization ability is preserved through a period of random feedback, even though the random feedback makes that ability temporarily disappear. Experiment 3 showed that the key to unlearning is not the positive feedback rate during the intervention. Categorization ability is preserved when the intervention feedback is random, even when positive feedback is frequently delivered. Experiment 2 showed that a key to unlearning is instead to provide a mixture of random and true feedback, thereby guaranteeing that the feedback valence is partially contingent on behavior. Thus, collectively these results show that response-outcome contingency is a critical factor for the induction of unlearning.

The theory that motivated these experiments assumed that II category learning critically depends on synaptic plasticity at cortical-MSN and CM-Pf—TAN synapses. Plasticity at cortical-MSN synapses mediates the learning of procedural skills, whereas plasticity at CM-Pf—TAN synapses mediates the learning of environmental contexts associated with reward. The TANs in the model learn to pause in rewarding contexts, and since they pre-synaptically inhibit cortical input to the striatum, they essentially serve as a gate to the striatum. Under tonic conditions (i.e., when the TANs are active) the gate is closed, which protects cortical-striatal learning from decay. When the environment changes in a way that makes rewards available and this availability is contingent on behavior, then the gate opens (i.e., the TANs pause) and new learning (or unlearning) is possible at cortical-MSN synapses.

The model predicts that unlearning occurs in Experiment 2 because the use of partially contingent feedback keeps the TANs paused during the intervention period. With the gate open, the noncontingent feedback trials will cause the learning that occurred during acquisition to be overwritten by random associations. Thus, the model does not predict that the synaptic changes that occurred during learning are erased, but rather that new, random learning will make it impossible to retrieve the original memory traces.

The rules that guide synaptic plasticity at cortical-MSN and CM-Pf—TAN synapses are identical (i.e., described by Equation 1). A natural question to ask then is why is learning at these two types of synapses qualitatively different? Why do CM-Pf—TAN synapses learn about environmental contexts whereas cortical-MSN synapses learn specific stimulus-response associations? The key is to note that whereas most MSNs fire to a restricted set of stimuli from a single sensory modality (e.g., Caan, Perrett, & Rolls, 1984), many TANs respond to stimuli from a number of different modalities (Matsumoto, Minamimoto, Graybiel, & Kimura, 2001). Thus, a TAN might respond to the discriminative cue associated with reward, but it is also likely to respond to other visual, auditory, and olfactory cues (for example) that occur incidentally at the time of reward delivery. This extremely broad tuning means that the TANs are not learning about specific stimuli, but rather about environmental contexts.

Although the neurobiological model proposed here is novel, at the conceptual level the theory described in this article bears similarity to a number of previous proposals. Perhaps the closest conceptual match is to proposals that during skill acquisition animals not only learn the skilled behavior, but also the context under which the behavior is appropriate (i.e., rewarded). During extinction the animal then learns about a context in which the behavior is inappropriate (i.e., not rewarded). So according to this account, extinction is not primarily an unlearning phenomenon, but rather an example of context learning (e.g., Bouton, 2002, 2004). The theory proposed in this article could be interpreted as a formal neurobiological instantiation of this context-learning account of extinction.

The theory proposed here also bears some similarity to cognitive theories that might assume some sort of switch is flipped at the appropriate times during intervention and reacquisition. For example, this would include theories that assume rapid attentional changes at the beginning of intervention and reacquisition (Kruschke, 2011) and knowledge-partitioning models that assume the knowledge gained during intervention is partitioned off from the knowledge gained during acquisition and reacquisition (Lewandowsky & Kirsner, 2000; Yang & Lewandowsky, 2004). Currently, the primary shortcoming of such models, at least when applied to the results of Experiments 1 – 3, is that they lack a mechanism that would flip the switch at the appropriate times. One interpretation of the model proposed here is that it describes exactly such a switching mechanism.

The model suggests two qualitatively distinct methods to induce the unlearning of striatal-mediated behaviors. One method is to use a behavioral paradigm that somehow keeps the TANs paused (or partially paused) during unlearning training. Experiment 2 showed promising initial results that partially contingent feedback might be such a behavioral manipulation. The significance of this result should not be taken lightly. This is the first and only demonstration of category unlearning to date. Additionally, there have only been a few other hints at successful unlearning protocols in certain areas of the animal conditioning literature (Woods & Bouton, 2007; Brooks & Bouton, 1993, 1994; Gunther et al. 1998). Interestingly, all of the methods used in these simple conditioning experiments to induce some degree of unlearning manipulated the extinction context so that it was more similar to the acquisition context. In a sense, this is similar to our method of including some true feedback trials during the intervention phase in Experiment 2.

A number of unlearning protocols also have been investigated within clinical settings, and some have shown signs of moderate success. Many of these rely on will power (a form of executive control) that is fragile and fails under stress or distraction (Wood & Neal, 2007). Others (e.g., contingency management), which deliver positive reinforcements (e.g., money) for abstaining from bad behaviors, have shown some success in treating alcohol (Petry, 2000), marijuana (Budney, Higgins, Delaney, Kent, & Bickel, 1991) and nicotine (Shoptaw, Jarvik, Ling, & Rawson, 1996) dependence, but the effectiveness of these treatments is suspect as well (Higgins, Budney, & Bickel, 1995).

The model suggests that a second method to induce unlearning is pharmacological, where the idea is to target the neurobiology of the model directly. One possibility would be to direct a selective muscarinic M2 receptor drug at the relevant striatal territory (an agonist or antagonist). The idea is that the drug would bind to the relevant M2 receptors in such a way as to mimic a TAN pause. The model predicts that the drug should be administered at the beginning of an extinction (in the case of instrumental conditioning) or unlearning intervention (e.g., random feedback). The drug would mimic a TAN pause, which according to the model should allow the intervention to succeed (e.g., extinction would weaken synapses, random feedback would overwrite relevant synapses with random associations). Thus, a behavioral consequence of such a treatment should be to abolish fast reacquisition. To our knowledge this prediction has not been tested. At least one study has looked at the effect of M2 antagonists on various aspects of learning and memory (e.g., Buresova, Bures, Bohdanecky & Weiss, 1964), but we know of no studies that have asked whether M2-selective drugs directed at the striatum prevent fast reacquisition of a previously extinguished instrumental behavior.

In conclusion, this article proposed a new neurobiologically detailed computational model that describes a mechanism in the striatum that protects procedural learning when rewards are no longer available or when rewards are no longer contingent on behavior. The model suggests a novel unlearning protocol – namely, that unlearning can be induced by delivering feedback that is partially contingent on the participant’s response. The results from three studies support the model and provide the first demonstration of category unlearning to date.

Appendix 1: Decision Bound Models Used in Experiments 1 and 2

Rule-Based Models

The General Conjunctive Classifier (GCC)

Three versions of the GCC (Ashby, 1992) were fit to the data. One version assumed that the rule used by participants is a conjunction of the type: “Respond A if the length is short and the orientation is shallow (e.g., less than 45 degrees), respond B if the length is short and the orientation is steep (e.g., greater than 45 degrees), respond C if the length is long and the orientation is shallow, or respond D if the length is long and the orientation is steep.” This version has 3 parameters: one for the single decision criterion placed along each stimulus dimension (one for orientation and one for bar width), and a perceptual noise variance. A second version assumed that the participant sets two criteria along the length dimension partitioning the lengths into short, medium, and long, and one criterion along the orientation dimension partitioning the orientations into shallow and steep. The following rule is then applied: “Respond A if the length is short, respond B if the length is short and the orientation is steep, respond C if the length is short and the orientation is shallow, or respond D if the length is long.” A third version assumed that the participant sets two criteria along the orientation dimension partitioning the orientations into shallow (e.g., less than 30 degrees), intermediate (e.g., between 30 and 60 degrees), and steep (e.g., greater than 60 degrees), and one criterion along the length dimension partitioning the lengths into long and short. The latter two models each have four parameters: three decision criteria, and a perceptual noise variance. The assignments of category labels to response regions were modified in the appropriate manner when being applied to the label switch condition.

Information-Integration Models

Striatal Pattern Classifier (SPC)

The SPC (Ashby & Waldron, 1999) has provided good fits to II categorization data in a variety of previous studies (e.g., Ashby et al., 2001; Maddox, Molis, & Diehl, 2002). The model assumes there are decision points that cover the perceptual space, each of which is associated with a response. In the present applications we assumed 4 decision points, one for each category. The SPC assumes that on each trial the participant gives the response associated with the decision point that is nearest to the percept. Because the location of one unit can be set arbitrarily, the model has 6 free response-unit parameters. One additional noise variance parameter is also included for a total of 7 parameters. The optimal model is a special case of the SPC in which the striatal units are placed in such a way that the optimal decision bounds are used. The optimal model contains only one parameter (i.e., noise variance).

Random Guessing Models

Fixed Random Responder Model

This model assumes that the participant guesses randomly and that all responses were equally likely. Thus, the predicted probability of responding “A”, “B”, “C”, or “D” is .25. This model has no free parameters.

General Random Responder Model

This model assumes random guessing, but that some responses are more likely than others. Thus, the predicted probabilities of responding “A”, “B”, “C”, and “D” are parameters that are constrained to sum to 1 (i.e., so this model has three free parameters).

Appendix 2: Simulation Methods

All model simulations were based on the network structure shown in Figure 4. Figures 7, 10, and 12 were generated by simulating the experimental design exactly. Specifically, we simulated 300 acquisition trials, 300 intervention trials, and 300 reacquisition trials. The model was given valid feedback at the end of every acquisition and reacquisition phase trial. The model also received feedback at the end of every intervention phase trial according to the rules from the corresponding experiment. Each simulation was replicated 50 times, the results were averaged, and the average results were then further split into blocks of 25 trials each. The dynamics of the model within a single trial are described by the differential equations described below. The parameter values used for all applications are listed in Table A.1.

Table A.1.

Parameter values used to obtain the fits to Experiments 1 through 3.

Eq. 1 – MSN		Eq. A.7
αw	50.0 × 10−9	αG	0.4175
βw	25.0 × 10−9	Eq. A.8
γw	10.0 × 10−9	βV	0.275
Eq. 2 – TANs		Eq. A.9
αw	1.5 × 10−7	βC	0.35
βw	0.3 × 10−7	γC	0.0
γw	0.125 × 10−7	σS	15.0
Eq. 2 – General		φ	25.0
θNMDA	100.0	CM-Pf Amplitude	55
θAMPA	10.0	Eq. B5
Eq. A.1		θ	0.9
α	160
β	2.5
Eq. A.2
wk,j(0)	0.5
βS	400
γS	1.5
σS	5.0
Eq. A.4
λ	100
Eq. A.5
v(0)	0.2

The activation of all CM-Pf units was either off (with activation 0) or on (see table A.1 for amplitude values) during the duration of stimulus presentation. We model sensory cortex in the same way as in Ashby et al. (2007). Briefly, this means we assumed an ordered array of 40,000 units in sensory cortex, each tuned to a different stimulus. We assumed that each unit responds maximally when its preferred stimulus is presented, and that its response decreases as a Gaussian function of the distance in stimulus space between the stimulus preferred by that unit and the presented stimulus. For the present applications, it sufficed to assume that activation in each unit was either 0 or equal to some positive constant value during the duration of stimulus presentation. Specifically, we assumed that when a stimulus is presented, the activation in sensory cortical unit K at time t is given by

$$I_k(t)=\alpha e^{\frac{d{(K,\mathit{stimulus})}^2}{2{\beta }^2}}$$ (A.1)

where α and β are constants and d(K, stimulus) is the (Euclidean) distance (in stimulus space) between the stimulus preferred by unit K and the presented stimulus. Equation A.1 is a popular method for modeling the receptive fields of sensory units, both in models of categorization (e.g., Kruschke, 1992) as well as other tasks (e.g., Er, Wu, Lu, & Toh, 2002; Oglesby & Mason, 1991; Riesenhuber & Poggio, 1999; Rosenblum, Yacoob, & Davis, 1996).

The activation in striatal unit j at time t, denoted S_j(t), was determined by the following coupled differential equations:

$$50\frac{{dS}_j(t)}{dt}=\sum _k{w}_{k,j}(n)\left[I_k(t)-{\beta }_{S}f[T(t)]\right]-{\gamma }_S\sum _{m\ne j}f[S_m(t)]+[S_j(t)+80][S_j(t)+25]+E-u_S(t)+{\sigma }_S\epsilon (t)$$ (A.2)

$$100\frac{{du}_S(t)}{dt}=-20[S_j(t)+80]-u_s(t)$$ (A.3)

where w_k,j(n) is the strength of the synapse between cortical unit k and striatal unit j on trial n. β_S, ϒ_S, and σ_S are constants, and ε(t) is white noise. T(t) is the membrane potenital from the TAN unit (descitbed below). The third term on the right is the quadratic integrate-and-fire model (Ermentrout, 1996). The function f [x] is called the alpha function and is a standard method for modeling the temporal smearing that occurs postsynaptically when a presynaptic neuron fires a spike (e.g., Rall, 1967). The idea is that every time the presynaptic cell spikes, the following input is delivered to the postsynaptic cell:

$$\alpha (t)=\frac{t}{\lambda }{e}^{\frac{\lambda -t}{\lambda }}$$ (A.4)

Ashby and Crossley (2011) proposed that changes in the TAN membrane potential at time t, denoted T(t), could be modeled via the following two coupled equations:

$$100\frac{dT(t)}{dt}=v(n)Pf(t)+1.2[T(t)+75][T(t)+45]+950-u_T(t)$$ (A.5)

$$100\frac{d{u}_T(t)}{dt}=5[T(t)+75]-u_T(t)+2.7v(n)R(t)$$ (A.6)

where v(n) is the strength of the synapse between the CM-Pf and the TAN on trial n, and Pf(t) is the input from the CM-Pf at time t. The constant 950 models spontaneous firing, and the function R(t) = Pf(t) up to the time when CM-Pf activation turns off, then R(t) decays exponentially back to zero (with rate .0018). To produce spikes, when T(t) = 40 mV then T(t) is reset to T(t) = −55 mV and u_T(t) is reset to u_T(t) + 150. The dynamical behavior of this model that allows it to mimic the unusual firing properties of TANs is described in Ashby and Crossley (2011).

Activation in globus pallidus unit j at time t, denoted by G_j(t), is described by:

$$15\frac{{dG}_j(t)}{dt}=-{\alpha }_{G}f[S_j(t)]+71+0.7[G_j(t)+60][G_j(t)+40]$$ (A.7)

where α_G is a constant. The first term models the inhibitory input from the striatum, the second term ensures a high tonic firing rate. Spikes are produced after G_j(t) = 35 by resetting to G_j(t) = −50. Similarly, activation in thalamus unit j at time t, denoted by V_j(t), is given by

$$\frac{{dV}_j(t)}{dt}=-{\beta }_{V}f[G_j(t)]+71+0.7[V_j(t)+60][V_j(t)+40]$$ (A.8)

where β_V is a constant. The first term models the inhibitory input from the globus pallidus. The constant 71 models excitatory input not explicitly included in the model. Spikes are produced after V_j(t) = 35 by resetting to V_j(t) = −50.

Activation in the jth unit in premotor cortex at time t, denoted by C_j(t), is given by

$$\frac{{dC}_j(t)}{dt}={\beta }_{C}f[V_j(t)]-{\gamma }_C\sum _{k\ne j}f[C_k(t)]+69+0.7[C_j(t)+60][C_j(t)+40]+{\sigma }_C\epsilon (t)$$ (A.9)

where β_C, γ_C, and σ_C are constants, and ε(t) is white noise. As in other units, spikes are produced after C_j(t) = 35 by resetting to C_j(t) = −50. The second term on the right models lateral inhibition in the same way as in Equation A.2. In tasks with two possible responses, evidence suggests that cortical units in premotor areas are sensitive to the cumulated difference in evidence favoring the two alternatives (e.g., Shadlen & Newsome, 2001). We used a more biologically plausible method that is known to simulate this difference process – that is, we placed a separate response threshold (φ) on the activation of each unit, but included lateral inhibition between the units (Usher & McClelland, 2001).

The model was forced to choose one of the four possible response options on every trial. In general, the emitted response corresponded to the first premotor unit (i.e., f[C_j(t)]) to cross the response threshold (φ). If no premotor unit crossed the threshold before the end of the trial, then the model responded according to which unit had the greatest output during the course of the trial.