Evaluating the Effect of Early Versus Late ARV Regimen Change if Failure on an Initial Regimen: Results From the AIDS Clinical Trials Group Study A5095

Abstract

The current goal of initial antiretroviral (ARV) therapy is suppression of plasma human immunodeficiency virus (HIV)-1 RNA levels to below 200 copies per milliliter. A proportion of HIV-infected patients who initiate antiretroviral therapy in clinical practice or antiretroviral clinical trials either fail to suppress HIV-1 RNA or have HIV-1 RNA levels rebound on therapy. Frequently, these patients have sustained CD4 cell counts responses and limited or no clinical symptoms and, therefore, have potentially limited indications for altering therapy which they may be tolerating well despite increased viral replication. On the other hand, increased viral replication on therapy leads to selection of resistance mutations to the antiretroviral agents comprising their therapy and potentially cross-resistance to other agents in the same class decreasing the likelihood of response to subsequent antiretroviral therapy. The optimal time to switch antiretroviral therapy to ensure sustained virologic suppression and prevent clinical events in patients who have rebound in their HIV-1 RNA, yet are stable, is not known. Randomized clinical trials to compare early versus delayed switching have been difficult to design and more difficult to enroll. In some clinical trials, such as the AIDS Clinical Trials Group (ACTG) Study A5095, patients randomized to initial antiretroviral treatment combinations, who fail to suppress HIV-1 RNA or have a rebound of HIV-1 RNA on therapy are allowed to switch from the initial ARV regimen to a new regimen, based on clinician and patient decisions. We delineate a statistical framework to estimate the effect of early versus late regimen change using data from ACTG A5095 in the context of two-stage designs.

In causal inference, a large class of doubly robust estimators are derived through semiparametric theory with applications to missing data problems. This class of estimators is motivated through geometric arguments and relies on large samples for good performance. By now, several authors have noted that a doubly robust estimator may be suboptimal when the outcome model is misspecified even if it is semiparametric efficient when the outcome regression model is correctly specified. Through auxiliary variables, two-stage designs, and within the contextual backdrop of our scientific problem and clinical study, we propose improved doubly robust, locally efficient estimators of a population mean and average causal effect for early versus delayed switching to second-line ARV treatment regimens. Our analysis of the ACTG A5095 data further demonstrates how methods that use auxiliary variables can improve over methods that ignore them. Using the methods developed here, we conclude that patients who switch within 8 weeks of virologic failure have better clinical outcomes, on average, than patients who delay switching to a new second-line ARV regimen after failing on the initial regimen. Ordinary statistical methods fail to find such differences. This article has online supplementary material.

1. INTRODUCTION

The most current method for treating human immunodeficiency virus (HIV)-1 infected patients in clinical practice is through a sequence of antiretroviral (ARV) regimens. After the initial treatment assignment, the sequential treatment strategy is both adaptive and reactive as subsequent regimen change always depends on response to current regimen, medical history, as well as tolerability and toxicity of treatment. In antiretroviral studies and in clinical practice, patients have historically been given treatment choices to sustain virus suppression, maximize adherence, and minimize toxicity which will, it is hoped, result in improved clinical health and long-term survival. In general, patients are encouraged to switch regimens after (confirmed) virologic failure since increased viral replication on the same regimen may compromise therapy, promote drug resistance, increase the possibility of cross-resistance to other agents in the same class, and decrease the likelihood that the patient responds to subsequent antiretroviral therapy (for current treatment guidelines, see AIDSinfo, www.aidsinfo.nih.gov/Guidelines). The negative aspects of staying on a failing regimen are counterbalanced by a patient who may be clinically stable for a prolonged period of time and tolerating their initial regimen despite low levels of viral replication. A final layer of complexity follows from the fact that switching therapy is no panacea to improved intermediate or long-term clinical endpoints. Patient-specific genetic and environmental factors preclude the existence of a single resolution to a complex disease and, hence, switching ARV therapies may not reduce toxicity nor improve tolerability and may, in fact, lead to problems with adherence. Here, our aim is to estimate the expected response for particular ARV treatment sequences and to compare these sequences using the observed clinical data.

In the clinic, it is observed that some patients successfully suppress viral load on their initial ARV regimens while others may fail and switch regimens repeatedly. For those patients who fail virologically and a regimen switch is recommended, the optimal timing of antiretroviral therapy switch is not known, especially in the setting of relatively low-level viremia. Although these sequential treatment strategies have been successfully incorporated in many clinical studies, direct comparisons between different regimens is challenging due to patient- and provider-initiated treatment decisions after the initial treatment assignment. For example, ACTG A5095 was a placebo-controlled randomized clinical trial of three ARV treatment regimens (See Section 2), but the decision of when to switch off a failing first-line ARV regimen was left to the patient and his or her primary-care provider as long as plasma HIV-1 RNA did not exceed 10,000 copies/mL when more decisive action was required. Decisions to stop, continue, or switch treatments, even in the face of incomplete suppression of HIV-1RNA replication, often depend on multiple other factors including a patient’s medical history of ARVs, immunologic and clinical response to those ARVs, or alternatively the desire to limit resistance emergence. Because the same factors that affect a patient’s treatment decision and assignment may subsequently affect patient response, we have a classic case of confounding. By now, statistical techniques to address confounding are well known (e.g., Horvitz and Thompson 1952; Cassel, Särndal, and Wretman 1976; Rosenbaum and Rubin 1983a, 1983b; Rosenbaum and Rubin 1984) and lead naturally to methods of causal inference (Rubin 1974; Holland 1986; Robins 1986).

The premise of our statistical approach is to view regimen change within the context of an intended ARV treatment strategy or treatment policy; that is, a sequence of treatment decisions at fixed or random intervals (e.g., routine clinic visits, benchmarks in disease progression, or some combination thereof) through the follow-up period. We may conceptualize the observed A5095 data through two treatment decisions and define the following ARV regimen strategy accordingly:

Definition 1. (ARV Regimen Change Strategy). An initial ARV regimen “a” followed by a switch to any second-line ARV regimen at time “s,” if virologic failure on the initial regimen.

It is important to note Definition 1 does not require that patients fail on initial regimen but does require that patients switch to second-line regimen if they fail on initial regimen. After the regimen strategy is defined, the goal is to estimate mean outcome for each (a, s)-treatment strategy combination and perform treatment comparisons. Our principal argument is that we can estimate the same intent-to-treat (ITT) population parameters in each of three study designs of increasing complexity—two simplified hypothetical designs and finally the observed data—under statistical assumptions of increasing strength. We outline the three proposed study designs below.

In the ACTG A5095 data, we consider two initial ARV regimens, combined efavirenz-containing regimens (a₁) and the triple nucleoside regimen (a₂), and switching from a failing regimen “early” (s₁, within 8 weeks of confirmed virologic failure) and “late” (s₂).Without loss of generality, define the population means as {μ_jk} ≡ {μ_jk, j, k = 1, 2} for four possible strategies with initial ARV regimen a_j, j = 1, 2, at time s_k, k = 1, 2. Our three study designs are as follows:

• D1A2 × 2 factorial experiment where patients are assigned to one of four treatment groups at baseline. Policy assignment is completely independent of patient and provider input. Parameter estimation and inference is performed under an intent-to-treat (ITT) principle.
• D2A two-stage randomization trial (Stone et al. 1995; Lunceford, Davidian, and Tsitatis 2002), whereby patients are randomly assigned to initial ARV regimen and randomized a second time, to switch ARV regimens earlier or later only after having already failed on their initial ARV regimen. Each randomization is made independent of patient characteristics.
• D3The observed ACTG A5095 data where patients are randomly assigned to initial ARV regimen at baseline and then, if virologic failure, switch to second-line ARV regimen depending on personal decisions and provider input.

In an ITT paradigm, treatment comparisons are made without regard for the success or failure of the initial ARV regimen and, therefore, the estimands {M_ij} reflect the combined influences and ARVs and viral load levels. In Design D1, ordinary sample averages are consistent estimators of the ITT estimands of interest. The second study (D2) is the two-stage randomized design, whereby patients are only randomized to switch early or late if they failed on the first regimen. In order to estimate {μ_jk} in this design, we impose identifiability conditions on potential outcomes (Lunceford, Davidian, and Tsitatis 2002) as described in Section 3.1.2. As in Design D1, patients are not forced to fail on the initial regimen, but it is assumed that patients who do fail will switch regimens.

The existing literature provides methods for regimen strategy comparisons in Designs D1 and D2, but these studies are difficult to implement in therapeutic HIV studies. This is because many ARV regimen transitions require direct patient or provider intervention, there exists no a priori set of treatment rules governing regimen change, and many viremic patients and their providers are unwilling to leave treatment assignment entirely to chance. Recently, the ACTG initiated a clinical trial (protocol A5115) where patients were randomly assigned to new ARV regimen after two confirmed HIV-1 RNA levels > 200 copies/mL (virologic failure) on the current regimen. Unfortunately, patients did not enroll and the study failed to reach target enrollment and subsequently closed with insufficient power to detect significant differences between the two groups (Riddler et al. 2007). The statistical methods proposed here estimate the ITT estimands {μ_jk} while adjusting for the selection bias in how patients were assigned to switch early versus late, if they failed on the initial ARV regimen. A formal connection from the observed data to the second study requires additional technical conditions and is outlined in Section 3.3.

Assessing the benefit of delayed or immediate switching from a failing ARV regimen is an important practical problem in HIV research and has been discussed in the scientific literature previously. The United Kingdom Collaborative HIV Cohort (2008) estimated factors associated with cause-specific, hazard rates for time-to-switch. Petersen et al. (2008) used marginal structural models (cf. Murphy, van der Laan, and Robins 2001, and references therein) to examine the effect on mortality of delayed switch from a failing highly active antiretroviral treatment (HAART) regimen. Our analysis is more similar to one considered by Peterson et al. but differs in a couple of important aspects. Because treatment decisions proceed over two stages in our setting, the additional notation and bookkeeping associated with marginal structural models is superfluous in the current article. Moreover, our estimator is minimum variance in a class of doubly robust estimators while Peterson et al. do not concern themselves with optimal estimation at this level. Furthermore, although mortality is an important endpoint, it tends to play a small role in current HIV studies because mortality rates are so low. For example, in ACTG A5095, only 24 out of 1147 patients (2%) died during a 5-year follow-up.

Our contribution to the literature is threefold. First, we present a systematic framework for switching from a failing ARV regimen using two-stage designs. The framework is based on intent-to-treat population parameters and accommodates the fact that not all patients fail on the current regimen during the study period; however, we do assume that all patients who fail virologically on current regimen switch to a new regimen. As noted by earlier authors (see Murphy, van der Laan, and Robins 2001; Lunceford, Davidian, and Tsitatis 2002), estimating mean potential outcome on treatment strategies differs from conventional analyses—for example, comparing switch-early versus switch-late conditioning on those patients who failed on initial regimen—that do not directly address the scientific question of interest. Second, we propose a one-step regression approximation to the constrained maximum likelihood estimator (Tan 2006) to estimate mean outcome on treatment strategies defined in Definition 1. Our proposal extends Tan’s technique to two-stage designs with selection bias in the second-stage treatment assignment mechanism and continues a recent trend to develop new and improved doubly robust estimators (Robins et al. 2007; Tan 2006, 2007; Tsiatis and Davidian 2007) beyond the ordinary doubly-robust class (Robins, Rotnizky, and Zhao 1994). Third, this is a new and particularly intriguing case study of the ACTG A5095 data. We show that a conventional analysis (one conditioning on only those patients with confirmed virologic failure) fails to find any statistically significant differences between early and late switching. However, using the methodology outlined here, we show that for patients on efavirenz-based ARV regimens, regimen changes made within 8 weeks of confirmed virologic failure on initial ARV regimen are associated with lower HIV-1 RNA levels, higher CD4 cell counts, and spend a larger proportion of the follow-up period with suppressed viral load levels, on average. Finally, our statistical analysis further exemplifies the benefit of using auxiliary covariates in practice and doubly robust estimators, in general. The remainder of the article is organized as follows. We describe the ACTG A5095 data in Section 2 and our methodological approach in Section 3. A summary of our analysis is described in Section 4 and discussion follows in Section 5.

2. THE ACTG A5095 DATA

ACTG A5095 was a randomized, multicenter clinical trial designed to compare three antiretroviral regimens in antiretroviral therapy-naive patients with HIV-1RNAlevels ≥ 400 copies/mL. The three initial regimens were: abacavir (ABC)/ lamivudine (3TC)/ zidovudine (ZDV), 3TC/ZDV+efavirenz (EFV), and ABC/3TC/ZDV+EFV. The goal of the study was to suppress and maintain HIV-1 RNA levels < 200 copies/mL. The primary efficacy endpoint was time to first virologic failure, defined as two subsequent assays with HIV-1 RNA levels ≥ 200 copies/mL at or after study week 16. The study enrolled in 18 months and followed patients for 120 weeks after the enrollment of the last subjects for a median follow-up of approximately three years. At an interim review after a median of 32-week follow-up, 82 of 382 patients (21%) in the triple nucleoside reverse-transciptase inhibitor (NRTI) group versus 85 of 765 patients (11%) in the combined efavirenz-containing groups had experienced virologic failure; hence, the triple NRTI regimen (ABC/3TC/ZDV) appeared inferior when compared to the combined efavirenz-containing regimens. Moreover, the time-to-virologic failure was significantly longer in the combined efavirenz-containing groups. The Data and Safety Monitoring Board recommended that the triple NRTI group be discontinued but that follow-up in the remaining two groups continue for the remaining planned duration of the study. Details of the study results, including the early differences between the triple NRTI and combined efavirenz-containing groups as well as the full comparative follow-up of the efavirenz-containing groups, have been reported elsewhere (Gulick et al. 2004, 2006; Ribaudo et al. 2008).

3. METHODS

In this section, we describe concepts that form the basis of the estimation framework. Due to space limitations, we state and review the basic building blocks for causal inference but do not elaborate; appropriate references are provided for relevant topics. Although our concept builds on a two-stage framework, we are primarily interested in treatment comparisons at the second stage for a particular efavirenz-containing regimen at the first stage. Nevertheless, we conceptualize our framework through two-stage randomized designs and adopt notation similar to that in Lunceford, Davidian, and Tsitatis (2002).

3.1 Causal Model: Notation and Assumptions

3.1.1 Potential Outcome Framework

Throughout this article, we adopt Rubin’s causal model (1974) and the ideas of potential random variables (Neyman 1923; Rubin 1974).We define the potential outcome, Y (a_j, s_k), j, k = 1, 2, as the outcome one would observe if a patient were assigned to an ARV regimen strategy in Definition 1, with initial ARV regimen a_j and regimen switch at time s_k, if virologic failure on a_j. Our notational convention will be to let a₁ denote the two combined efavirenz-containing groups and a₂ denote the triple-nucleoside group, with s₁ and s₂ denoting early and late switch, respectively, after virologic failure. We also define the potential random variable R(a_j) as the failure status indicator on the initial ARV regimen a_j, j = 1, 2; that is, R(a_j) = 1 if a randomly selected patient from the population fails virologically on initial regimen a_j and R(a_j) = 0 otherwise. Hence, the full set of potential random variables for a randomly selected patient from the population is

$$\{R(a_1),R(a_2),Y(a_1,s_1),Y(a_2,s_1),Y(a_1,s_2),Y(a_2,s_2)\}.$$ (1)

3.1.2 Identifiability and Consistency

A noteworthy step in the development below is an identifiability constraint on the potential outcomes Y (a_j, s₁) and Y (a_j, s₂) when virologic failure is unobserved. In particular, we assume that potential outcomes for patients who do not fail on initial ARV treatment would be the same whether they were assigned to a treatment strategy s₁ or s₂ for early or late switch, respectively, and that potential virologic failure R(a_j) is a function of the initial ARV regimen only and not on a patient’s assigned switching time (Lunceford, Davidian, and Tsitatis 2002). Hence, we assume that the distribution of {R(a_j), Y(a_j, s₁), Y(a_j, s₂)} obeys the constraint

$$Y(a_j,s_1)=Y(a_j,s_2)\text{ if }R(a_j)=0,j=1,2.$$ (2)

In ACTG A5095, one does not observe the full set of potential random variables in (1), rather one only observes the initial ARV regimen, switching time if virologic failure, and the clinical endpoint. First, we let A denote the initial ARV regimen which realizes two values, a₁ and a₂.Next, we define the observed indicator of virologic failure, R, which realizes the value 1 if a patient failed virologically on initial ARV regimen and 0 otherwise. As in Lunceford, Davidian, and Tsitatis (2002), we assume that the potential random variables, R(a₁) and R(a₂), satisfy the relation R = 1(A = a₁)R(a₁) + 1(A = a₂)R(a₂). We let S denote a dichotomous random variable for switching early (s₁) versus late (s₂) and is only observed for those patients who failed on the initial ARV regimen. The observed outcome is Y and the random vector X denotes patient characteristics. Furthermore, we assume that potential outcomes Y (a_j, s_k) and observed outcome Y are related through

$$Y=(1-R)Y(a_j,s_1)+R\mathbf{1}(S=s_1)Y(a_j,s_1)+R\mathbf{1}(S=s_2)Y(a_j,s_2),\text{on the event }\{A=a_j\}.$$ (3)

Incidentally, because we assume Equation (2), then we also have that conditional on the event {A = a_j}, Y = (1 − R)Y (a_j, s₂) + R1(S = s₁)Y (a_j, s₁) + R1(S = s₂)Y (a_j, s₂). In contrast to the potential random variables given in (1), the observed random variables are {A, R, RS, Y, X}.

3.1.3 Treatment Assignment

In ACTG A5095, eligible patients were randomly assigned to initial ARV treatment stratified according to their viral load level at screening. Hence, because of randomization, treatment assignment is independent of specific patient characteristics within each stratum, that is, P(A = a_j | Y (a_j, s₁), Y(a_j, s₂), X) = P(A = a_j). Similarly, it is necessary to consider how patients are assigned to switch ARVs early versus late postvirologic failure. Here, patients were not assigned to treatment independent of individual characteristics; rather patients and their attending physicians intentionally chose to switch early or late on a case-by-case basis. Hence, we have P(S = s_k | R = 1, Y(a_j, s₁), Y(a_j, s₂), X) ≠ P(S = s_k | R = 1). However, we do assume that

$$P(S=s_k|R=1,Y(a_j,s_1),Y(a_j,s_k),\mathbf{X})=P(S=s_k|R=1,\mathbf{X})\text{ on the event }\{A=a_j\}.$$ (4)

Expression (4) is often referred to as the no unmeasured confounders assumption or sequential randomization. We interpret Equation (4) as the assumption that a decision to switch early versus late depends on auxiliary variables X up to that point at which a switch is made but unrelated to future events Y (a_j, s₁) and Y (a_j, s₂).

3.2 Estimation in a Hypothetical, Randomized Two-Stage Trial (D2)

To motivate our estimator in Section 3.3 using data from the observational study, we first consider estimation in a hypothetical two-stage randomization trial where treatment assignment to switch early or late is independent of patient characteristics. For clarity, we let E_d̄2 and P_d̄2 denote expectation and probability in the hypothetical two-stage trial, respectively. In the hypothetical randomized study, there are no confounding variables X and the observed data are simply {A, R, RS, Y}. This hypothetical trial is exactly the scenario considered by Lunceford, Davidian, and Tsitatis (2002) where expression (4), with no X, holds easily as a consequence of randomization. Using conditioning arguments via Equations (2) and (3), Lunceford, Davidian, and Tsitatis (2002) show that for each (a_j, s_k) combination, the causal estimand μ_jk is related to the observed data in a two-stage randomized design through

$${\mu }_{\mathit{\text{jk}}}=E_{{\mathrm{d̄}}_2}[Y\mathbf{1}(A=a_j)\times \{(1-R)+\frac{R\mathbf{1}(S=s_k)}{P_{{\mathrm{d̄}}_2}(S=s_k|A=a_j,R=1)}\left\}\right].$$ (5)

Replacing E_d̄2 with the sample average of the random variables on the right-hand side of Equation (5) leads to a consistent and asymptotically normal estimator for the estimand μ_jk under an ITT principle, Equations (2) and (3), and known propensitites. The interpretation of the weighting scheme in Equation (5) is as follows: if a patient does not fail on the initial ARV regimen a_j, then that patient represents him/herself and hence receives a weight of 1; if a patient fails on initial ARV regimen, however, then that patient represents {P_d̄2 (S = s_k | A = a_j, R = 1)}⁻¹ similar patients who could have potentially been assigned to combined sequential first- and second-line ARV regimens (a_j, s_k). In the following section, we show how to extend the expression (5) for the analysis of the ACTG A5095 data.

3.3 Estimation in the Observational Study (D3)

We use results provided by Murphy, van der Laan, and Robins (2001) to derive a consistent estimator of μ_jk using the observed data from the ACTG A5095 study. Under regularity conditions, including P(S = s_k | A = a_j, R = 1, X) > 0, Lemma 4.1 of Murphy, van der Laan, and Robins (2001) asserts that the distribution of (Y, A, R, S) under P_d̄2 is absolutely continuous with respect to the distribution of (Y, A, R, S) under P, and a version of the Radon–Nikodym derivative is E{W_d̄2 (A, R, S, X) | Y = y, A = a, R = r, S = s}, where

$$W_{{\mathrm{d̄}}_2}(a,r,s,\mathbf{x})=\mathbf{1}(A=a)\times \{\mathbf{1}(R=0)+\mathbf{1}(R=1,S=s)\times \frac{P_{{\mathrm{d̄}}_2}(S=s|A=a,R=1)}{P(S=s|A=a,R=1,\mathbf{X}=\mathbf{x})}\}.$$

The Radon–Nikodym derivative can be applied directly to the expression in Equation (5) to show that

$$E_{{\mathrm{d̄}}_2}[Y\mathbf{1}(A=a_j)\times \{(1-R)+\frac{R\mathbf{1}(S=s_k)}{P_{{\mathrm{d̄}}_2}(S=s_k|A=a_j,R=1)}\left\}\right]=E[W_{{\mathrm{d̄}}_2}(A,R,S,\mathbf{X})\times Y\mathbf{1}(A=a_j)\times \{(1-R)+\frac{R\mathbf{1}(S=s_k)}{P_{{\mathrm{d̄}}_2}(S=s_k|A=a_j,R=1)}\left\}\right]=E[Y\mathbf{1}(A=a_j)\times \{(1-R)+\frac{R\mathbf{1}(S=s_k)}{P(S=s_k|A=a_j,R=1,\mathbf{X})}\left\}\right].$$ (6)

The last expression in Equation (6) is a function of the observed data {Y, A, R, RS, X} and a sample average yields a consistent estimator for μ_jk if the propensity score P(S = s_k | A = a_j, R = 1, X) were known.

By definition, the propensity score P(S = s_k | A = a_j, R = 1, X) is estimable only by those patients who failed on their initial ARV regimen and not by the entire sample. Hence, in small samples, estimation and inference for the causal estimand μ_jk may be sensitive to the overall marginal probability of failing on initial ARV regimen. Nevertheless, the propensity score may be modeled parametrically, semiparametrically, or nonparametrically as a function of (A, X). The most common approach is to model P(S = s_k | A = a_j, R = 1, X) using maximum likelihood via generalized linear models (e.g., probit or logistic regression) and separately for each initial ARV regimen a_j. Substituting the fitted propensity score P̂(S = s_k | A = a_j, R = 1, X) in expression (6) and taking a sample average leads to a standard inverse-probability weighted (IPW) estimator

$${\mathrm{\mu ̂}}_{\mathit{\text{jk}}}={ℰ}_n[Y\mathbf{1}(A=a_j)\times \{(1-R)+\frac{R\mathbf{1}(S=s_k)}{\mathrm{P̂}(S=s_k|A=a_j,R=1,\mathbf{X})}\left\}\right],$$

where ℰ_n denotes sample average (i.e., ${ℰ}_{n}f(Z)={\displaystyle {\sum }_{i=1}^n}f(Z_i)/n)$. Assuming that the propensity model is correctly specified and under standard regularity conditions, $\sqrt{n}({\mathrm{\mu ̂}}_{\mathit{\text{jk}}}-{\mu }_{\mathit{\text{jk}}})$ converges in distribution to a mean-zero normal random variable with asymptotic variance that can be derived using standard arguments (e.g., Tsiatis 2006) and consistently estimated from the data (e.g., Lunceford, Davidian, and Tsitatis 2002; Tsiatis 2006).

3.4 Doubly Robust, Locally Efficient, and Optimal Estimation

Semiparametric efficient estimation and double robustness in missing data problems has been an active research area for two decades now following the work of Robins, Rotnizky, and Zhao (1994). The doubly robust estimators of Robins, Rotnizky, and Zhao (1994) are attractive because they provide some robustness to model misspecification and can achieve the semiparametric efficiency bounds when all modeling assumptions are correct. At the same time, several authors have noted that the same estimator can behave poorly in finite samples when one or both modeling assumptions are incorrect. We review and extend these estimators to our analysis of the ACTG A5095 data.

For the purposes of robust and efficient estimation, we drop the indicator 1(A = a_j) from our description with the understanding that estimators are computed separately for each initial ARV regimen; here, we focus on the efavirenz-containing regimens. We define the switch indicator

$$Z=\{\begin{array}{cc}1,\hfill & \text{if }S=s_1(\text{switch early}),\hfill \\ 0,\hfill & \text{if }S=s_2(\text{switch late}),\hfill \end{array}$$

the propensity score P(Z = 1 | R = 1, X) = P(S = s₁ | R = 1, X) = π(X), which is modeled via logistic regression,

$$\text{logit }\pi (\mathbf{X},\mathit{\psi })={\psi }_0+{\psi }_1{X}_1+\cdots +{\psi }_{q-1}{X}_{q-1},$$ (7)

where ψ = (ψ₀, …, ψ_q−1)^T is a q-vector of regression coefficients for 11 potential confounders (see Section 4). Then the inverse-probability weighted (IPW) estimator for an ARV regimen strategy (that switches early) is simply

$${\mathrm{\mu ̂}}_{\text{IPW}}={ℰ}_n\left[Y\right\{(1-R)+\frac{\mathit{\text{RZ}}}{\pi (\mathbf{X},\mathit{\psi ̂})}\left\}\right],\text{ or},$$ (8)

$${ℰ}_n{\left[\right\{(1-R)+\frac{\mathit{\text{RZ}}}{\pi (\mathbf{X},\mathit{\psi ̂})}\left\}\right]}^{-1}\times {ℰ}_n\left[Y\right\{(1-R)+\frac{\mathit{\text{RZ}}}{\pi (\mathbf{X},\mathit{\psi ̂})}\left\}\right].$$ (9)

The analogous IPW estimator for “switch late” to second-line ARV regimen is given by replacing Z/π̂(X) in Equation (8) with (1 − Z)/{1 − π̂(X)}. Next, we show how to construct improved semiparametric estimators by minimizing asymptotic variance.

By applying the theory of Robins, Rotnizky, and Zhao (1994), we know that all regular and asymptotically linear (RAL) estimators μ̂ of μ take the form

$$\{(1-R)+\frac{\mathit{\text{RZ}}}{\pi (\mathbf{X})}\}Y+R(\frac{Z}{\pi (\mathbf{X})}-1)h(\mathbf{X}),$$ (10)

where h(·) is an arbitrary function of X. In the missing data literature, the last expression R{Z/π(X, ψ) − 1}h(X) in Equation (10) is called the augmentation term (Tsiatis 2006).We note that the class of influence functions for μ̂ is {(10) − μ} and the IPW influence function is one that simply has h ≡ 0. The semiparametric efficient estimator is found when h(X) = −m(X), with m(X) = E(Y | R = 1, X). Because the true conditional mean model E(Y | R = 1, X) is unknown, we posit a statistical model for it, say E(Y | R = 1, X; ξ) = m(X, ξ). Here, we model the conditional mean of Y given X for patients who failed on initial ARV regimen linearly as

$$m(\mathbf{X},\mathit{\xi })={\xi }_0+{\xi }_1{X}_1+\cdots +{\xi }_{r-1}{X}_{r-1},$$ (11)

where ξ = (ξ₀, ξ₁, …, ξ_r−1)^T is an r-vector of unknown parameters for covariables including baseline CD4 cell counts and HIV-1 RNA level at virologic failure. Then, replacing h(X) with the posited model m(X, ξ) leads to an augmented inverse-probability weighted (AIPW) class of estimators:

$${\mathrm{\mu ̂}}_{\text{AIPW}}={\mathrm{\mu ̂}}_{\text{IPW}}-{ℰ}_n\left[R\right\{\frac{Z}{\mathrm{\pi ̂}(\mathbf{X})}-1\}m(\mathbf{X},\mathit{\xi ̂})].$$

We know that the AIPW estimator is consistent if either π(X) or m(X) is correctly specified (i.e., double robustness; Robins, Rotnizky, and Zhao 1994; Tsiatis 2006), and the AIPW estimator is semiparametric efficient if π(X) and m(X) are both correctly specified (i.e., local efficiency). Unfortunately, if the conditional mean model m(X) is incorrectly specified, there is no promise that the AIPW estimator is optimal in any sense. Hence, the AIPW estimator class will not include the efficient estimator if m(X) is misspecified even though it does include the efficient estimator when m(X) is correctly specified. These considerations lead to other families of estimators which may be motivated through different considerations.

Noting that the AIPW estimator could be less efficient than the IPW estimator if the conditional mean model m(X) is misspecified, the authors (Robins et al. 1995) considered an adaptive estimator which is guaranteed to be more efficient than the IPW estimator. Here, Robins et al. restricts to the class of estimators whose influence functions are of the form

$$\{(1-R)+\frac{\mathit{\text{RZ}}}{\pi (\mathbf{X})}\}(Y-\mu )+R(\frac{Z}{\pi (\mathbf{X})}-1){\mathit{\xi }}^{\mathrm{T}}\mathbf{X},$$ (12)

which leads to the class of estimators in Equation (10) when h(X) = ξ^TX. Then, the goal is to find the estimator in the restricted class given in Equation (12) whose variance is minimum. One can show that the estimator with minimum variance in the class defined by Equation (12) is

$${\mathrm{\mu ̂}}_{\text{RRZ}}={\mathrm{\mu ̂}}_{\text{IPW}}-\mathrm{\kappa ̂}\times {ℰ}_n\left[R\right\{\frac{Z}{\pi (\mathbf{X},\mathit{\psi ̂})}-1\}m(\mathbf{X},\mathit{\xi ̂})],$$

where κ̂ serves as the first element to the classic multiple linear regression {ℰ_n(VV^T)}⁻¹ℰ_n(V U), U = RZY/π(X, ψ̂), V = R(Z/π(X, ψ̂) − 1) × G, and

$$\mathbf{G}=\left(\begin{array}{c}\hfill m(\mathbf{X},\mathit{\xi ̂})\hfill \\ \hfill \{(\partial /\partial \mathit{\psi })\pi (\mathbf{X},\mathit{\psi ̂})\}/\{1-\pi (\mathbf{X},\mathit{\psi ̂})\}\hfill \end{array}\right).$$

In the two-stage design framework, we note that μ̂_RRZ is similar to the Wahed and Tsiatis (2004) estimator if κ̂ in G is replaced by G^∗ = (1, m(X, ξ̂))^T. The estimator μ̂_RRZ or that proposed by Wahed and Tsiatis (2004) in two-stage designs is no longer consistent if π(X) is incorrectly modeled in Equation (7).

Recently, Tan (2006) proposed estimators that are motivated from a theory of control variates and constrained maximum likelihood. Tan’s preferred estimator (the so-called “tilde” or “regression” estimator) has the same minimum variance property as the estimator proposed by Robins et al. (1995). However, Tan’s estimator is doubly-robust while the estimator by Robins et al. (1995) is not (Tan 2007, Proposition 4). Specifically, the appropriate extension of Tan’s estimator to our particular application is

$${\mathrm{\mu ̂}}_{\text{REG}}={\mathrm{\mu ̂}}_{\text{IPW}}-\mathrm{\kappa ̃}\times {ℰ}_n\left[R\right\{\frac{Z}{\pi (\mathbf{X},\mathit{\psi ̂})}-1\}m(\mathbf{X},\mathit{\xi ̂})],$$

where κ̂ is a scalar defined as the first element of {ℰ_n(VW^T)}⁻¹ℰ_n(V U), W = R(Z/π(X, ψ̂)) × G, and V, U, and G were defined earlier. The form of Tan’s regression estimator is analogous to that proposed by Robins et al. (1995) although it is motivated as a first-order approximation to a restricted maximum likelihood estimator. Both μ̂_REG and μ̂_RRZ are consistent if π(X) is correctly modeled but μ̂_REG has minimum variance. If both π(X) and m(X) are correctly modeled, the differences between the two estimators are asymptotically negligible. Details for estimating the asymptotic variance of μ̂_REG and μ̂_RRZ are provided in the Appendix.

4. ANALYSIS OF THE ACTG A5095 DATA

4.1 The Study Sample

A total of 1147 subjects enrolled in the ACTG A5095 between March 2001 and November 2002. Of the original 1147 patients, 12 patients never started their initial treatments. These 12 patients were removed from our analysis as indicated later.

As mentioned briefly in Section 2, the Data Safety and Monitoring Board recommended that the triple-nucleoside group be discontinued at the second annual review in February 2003 and study investigators followed this recommendation. For ease of exposition, our analysis is therefore restricted to the two combined efavirenz-containing groups (Gulick et al. 2004, 2006). In addition, we excluded 14 patients who did experience virologic failure, are not observed to switch therapy, and are not followed for at least 8 weeks since virologic failure. Thus, our effective sample size is 744 patients on the two combined efavirenz-containing groups, where 137 (18.4% of 744) patients experienced virologic failure on their initial ARV treatment regimens. An additional 45 (6.0% of 744) patients experienced virologic failure but only after a protocol-approved drug substitution in the same drug class for treatment-limiting drug-related toxicity (e.g., stavudine for zidovudine, nevirapine for efavirenz). Hence, they were not following their initial randomized ARV at the time of failure but they were following our working definition of “initial ARV regimen” (see also, Section 4.4).

We quantitatively describe our study sample in Table 1 through a summary of baseline characteristics. Patient age ranges from 18 to 77 years old; weight has a mean of 76 kg with standard deviation of 16 kg. Sex is an indicator variable (1 if male); race is a three-level variable (0 if white, 1 if black, and 2 for any other race); drug history indicates whether a patient ever previously used intravenous (IV) drugs, (1 if ever an IV drug user and 0 otherwise). Baseline HIV-1 RNA and HIV-1 RNA level at virologic failure are presented on the logarithmic scale; baseline CD4 cell counts, baseline CD8 cell counts, and time (in weeks) from baseline to first virologic failure remain their original scales.

Table 1.

Descriptive statistics of auxiliary covariates

		Virologic failure (182)
Covariates	Overall (744) Mean (SD)	Switch early (31) Mean (SD)	Switch late (151) Mean (SD)
Baseline HIV-1 RNA	4.86 (0.73)	5.29 (0.70)	4.81 (0.69)
HIV-1 RNA at virologic failure	3.74†(0.94)	4.17 (0.90)	3.65 (0.92)
Time to virologic failure	55.46†(37.45)	57.08 (39.49)	55.12 (37.15)
Baseline CD4 cell count	241.39 (192.54)	183.05 (165.21)	260.06 (211.52)
Baseline CD8 cell count	846.65 (509.31)	882.61 (598.55)	850.68 (603.72)
Body weight	76.22 (16.21)	70.97 (14.15)	75.25 (14.59)
Age	37.46 (9.26)	38.16 (8.88)	37.33 (9.35)
Sex	80.78	80.65	82.12
Drug history	10.62	19.35	13.91
Race
White	41.27	29.03	37.09
Black	35.08	41.94	43.04
Hispanic or others	23.65	29.03	19.87

^†Descriptive statistics for HIV-1 RNA at virologic failure and time to virologic failure pertain only to 182 patients who experienced virologic failure.

NOTE: Baseline HIV-1 RNA (copies/mL) and HIV-1 RNA (copies/mL) are transformed on a base-10 logarithmic scale, time to first failure is measured in days, body weight in kilograms, age at baseline (age) in years, gender (sex) is reported as proportion male, and drug history is proportion who have ever used intravenous drugs.

4.2 Treatment and Endpoint Definitions

The results of our analyses depend critically on the definitions of virologic failure (R), switching off a failing regimen early versus late (S), and the endpoint (Y). Our definition of confirmed virologic failure follows one defined in theACTGA5095 protocol: lab readings from two consecutive visits where HIV-1 RNA ≥ 200 copies/mL after at least 16 weeks of study treatment. We define “failure” as “confirmed virologic failure on the first-line treatment regimen” and first-line regimen to include initial ARV regimen plus any protocol-approved drug substitutions. Our definitions for “early” versus “late” ARV regimen switch and three different outcomes are described in the paragraphs that follow.

Our preferred definition for switching ARV regimens “early” was switching regimens less than 8 weeks after confirmed virologic failure. In Figure 1, we see that the proportion of patients switching ARV regimen less than 8 weeks was 17.0% (31 of 182) patients in the combined efavirenz-containing group. We considered other cutoffs to define early switch, including 12, 16, and 20 weeks. We chose 8 weeks to define early switch because it agrees with provider’s experience in the clinic and, per the A5095 study design, was equivalent to the clinic visit following the visit at which a confirmatory HIV-1 RNA level above 200 copies/mL was measured (i.e., two clinic visits after the date of virologic failure). We also considered a four-week cutoff but so few patients met the criteria that we did not pursue it further.

Figure 1.

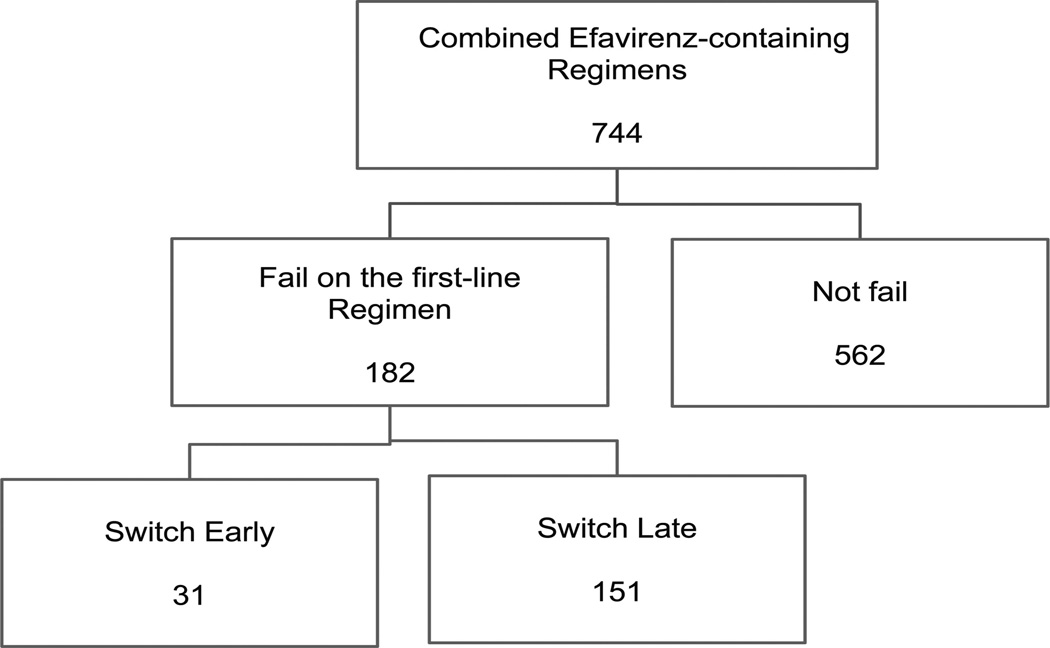
Number of patients at each stage. “Switch early” is defined as switching to second-line regimen less than 8 weeks after confirmed virologic failure.

In two-stage analyses, the endpoint Y must be well-defined for all treatment combinations. Perhaps the most natural endpoint is death or time-to-death (cf. Petersen et al. 2008) but mortality is seldom considered a primary endpoint in most HIV studies due to the successes of ARV regimens. Also, because some HIV studies do not extend beyond two to three years of follow-up, few HIV-related deaths are actually observed. In A5095, for example, only 24 patients died during five years of follow-up. In the sequel, we use length-adjusted area-under-the-curve (AUC) endpoints. Cumulative viral load, cumulative CD4 cell count, or equivalently their AUC counterparts, are sensitive to ARV regimens and valuable scientifically (Fleming 1994; Journot et al. 2001; Fletcher et al. 2008; Marconi et al. 2011; Torti et al. 2011). Cumulative viral load is associated with and often used as an early indicator of virologic failure (cf. Fleming 1994; Journot et al. 2001; Marconi et al. 2011).We used AUC endpoints in our statistical analysis because they are relevant clinically and well-defined for all patients on a particular ARV regimen strategy, including those patients that did not fail their initial regimen.

Let H(t) be the viral load or CD4 cell count at time t and α(t) a nonnegative weight function. A patient’s AUC is defined by the Riemann–Stieltjes integral

$$\text{AUC}={\displaystyle {\int }_0^L}H(t)\alpha (t)\mathit{\text{dt}},$$

where L is the patient’s length of follow-up and follow-up is defined as length from the first viral load drawing date to the off-study date. Our endpoints are defined Y = AUC/L and interpreted as the length-adjusted AUC (cf. Spritzler, DeGruttola, and Pei 2008), where the length-adjustment accounts for differences in follow-up time. In practice, the AUC is approximated through the Riemann sum ${\displaystyle {\sum }_{j=1}^J}{H}_j\mathrm{\Delta }{\alpha }_j$, where H_j = H(t_j) for j = 1, …, J and Δα_j = α(t_j) − α(t_j−1). One conventional definition uses a constant weight α(t) = 1 which implies Δα_j = (t_j − t_j−1) while the modified definition Δα_j = [(t_j+1 − t_j) + (t_j − t_j−1)]/2 leads to the linear trapezoidal rule (Yeh and Kwan 1978); we report results using the latter definition.

We consider three specific endpoints: (i) H(t) is viral load (HIV-1 RNA in copies/mL) at time t and α(t) = 1 for all t; (ii) H(t) = 1 and α(t) = 1{HIV-1 RNA (copies/mL) at time t ≤ 200}; (iii) H(t) is CD4 cell count at time t with α(t) = 1. The first endpoint is interpreted as cumulative viral load with large values suggesting higher viral load levels per unit of time, on average. We interpret the second endpoint “Days below the limit of detection (LOD)” as the proportion of time with suppressed viral load and the third endpoint is the same as the first but with CD4 cell count replacing HIV-1 RNA. Length-adjusted AUC of viral load and CD4 are transformed on a natural logarithmic scale (see also, Section 4.4). The mean and standard deviation of our endpoints are included as part of our analytic results in Table 4. We provide additional comments on our endpoints in the online supplementary material.

Table 4.

Results for combined efavirenz-containing arms using auxiliary variables in Table 1

		HIV-1 RNA		Days below LOD		CD4
Method	Switch	Est. (SE)	T	Est. (SE)	T	Est. (SE)	T
COND	Early	259.56 (18.09)	0.360	55.32 (5.19)	0.937	243.68 (5.52)	0.311
	Late	270.16 (7.11)		49.89 (2.33)		247.29 (2.40)
IPW	Early	181.88 (3.79)	6.576	81.67 (2.26)	3.560	258.53 (6.77)	0.538
	Late	190.14 (3.25)		77.48 (1.10)		253.45 (1.14)
IPW (no Aux)	Early	187.52 (5.12)	0.305	78.89 (1.53)	0.932	253.14 (1.60)	0.355
	Late	190.11 (3.29)		77.56 (1.09)		254.02 (1.11)
AIPW	Early	183.71 (4.29)	3.098	80.82 (1.38)	7.288	255.53 (1.30)	4.274
	Late	190.20 (3.29)		77.50 (1.07)		253.46 (1.11)
RRZ	Early	181.93 (3.78)	6.387	80.90 (1.35)	7.919	255.14 (1.73)	1.332
	Late	190.11 (3.26)		77.48 (1.07)		253.46 (1.12)
REG	Early	182.02 (3.68)	6.998	80.82 (1.07)	13.945	255.59 (1.12)	6.985
	Late	190.18 (3.26)		77.51 (1.08)		253.45 (1.12)

NOTE: The table shows estimates of the mean potential outcome (standard errors) for six estimators and each of three endpoints. Each outcome (HIV-1 RNA, Days below LOD, CD4) is computed as the length-adjusted area under the curve (AUC), i.e., AUC divided by length of follow-up. For HIV-1 RNA (copies/mL), the AUC is computed after transforming HIV-1 RNA on the base-10 logarithmic scale; LOD is limit of detection; length-adjusted AUC for CD4 cell count is computed on the base-10 logarithmic scale. The estimators are conditional mean endpoints (COND) considering only those patients that failed on initial ARV, inverse probability-weighted (IPW) estimator, IPW estimator using no auxiliary variables (IPW no Aux), augmented IPW (AIPW), and the proposed regression (REG) estimator. The Wald-type test statistic (T) tests the null hypothesis that the average causal effect between treatment strategies is zero. Mean and standard error estimates are multiplied by 100.

4.3 Main Analysis

The first step in our statistical analysis is to fit the propensity score (PS) model (7) and the outcome regression (OR) model (11) for 182 patients with virologic failure. Here, we fit the PS model using multiple logistic regression with a binary outcome for the time of ARV regimen change (1 if switched early within 8 weeks after failure and 0 otherwise) and covariables including age, weight, race, sex, time from baseline to the first virologic failure, baseline CD4 cell counts, baseline CD8 cell counts, baseline viral load, and HIV-1 RNA level at virologic failure, drug history. HIV-1RNAlevel at virologic failure is not included when the endpoint is adjusted cumulative viral load. Each of the variables (age, weight, baseline CD4 cell count, baseline CD8 cell count, and time to first failure) are normalized before entering the models. For the OR models, we fit multiple linear regression models for each of our three AUC endpoints using the same covariables as in the PS model. The estimated regression coefficients in the PS and OR models are described in Tables 2 and 3, respectively.

Table 2.

Coefficient estimates from propensity score model P(Z = 1|R = 1,X) for switching within 8 weeks of confirmed virologic failure on the combined efavirenz-containing arm to any second-line ARV regimen

Covariate	Model 1 Est. (SE)	Model 2 Est. (SE)
Intercept	−8.20 (2.21)	−6.64 (2.01)
Baseline HIV-1 RNA	0.80 (0.38)	0.89 (0.37)
HIV-1 RNA at virologic failure	0.54 (0.23)	—
Time to virologic failure	0.15 (0.22)	0.09 (0.22)
Baseline CD4 cell count	−0.18 (0.32)	−0.12 (0.30)
Baseline CD8 cell count	0.02 (0.18)	0.09 (0.18)
Body weight	−0.18 (0.28)	−0.23 (0.28)
Age	0.02 (0.22)	0.05 (0.21)
Sex	0.15 (0.62)	0.18 (0.60)
Drug history	0.50 (0.58)	0.39 (0.56)
Race
White	—	—
Black	0.29 (0.54)	0.37 (0.52)
Hispanic or other	0.50 (0.62)	0.67 (0.59)

NOTE: Propensity model 2 is used when the endpoint is HIV-1 RNA and model 1 is used otherwise.

Table 3.

Coefficient estimates in the conditional mean model E(Y|R = 1, X) for the combined efavirenz-containing arm

	HIV-1 RNA		Days below LOD		CD4
Covariate	Early	Late	Early	Late	Early	Late
Intercept	0.33 (1.87)	1.75 (0.52)	1.58 (0.53)	0.68 (0.18)	3.06 (0.46)	2.71 (0.17)
Baseline HIV-1 RNA	0.26 (0.32)	0.15 (0.10)	0.01 (0.09)	0.01 (0.03)	0.06 (0.08)	−0.01 (0.03)
HIV-1 RNA at virologic failure	—	—	−0.15 (0.07)	−0.05 (0.02)	−0.13 (0.06)	−0.05 (0.02)
Time to virologic failure	−0.16 (0.27)	−0.42 (0.07)	−0.07 (0.08)	0.14 (0.02)	−0.01 (0.07)	0.10 (0.02)
Baseline CD4 cell count	0.08 (0.32)	0.20 (0.07)	0.01 (0.08)	−0.06 (0.02)	0.16 (0.08)	0.21 (0.02)
Baseline CD8 cell count	0.08 (0.19)	0.07 (0.06)	0.03 (0.06)	−0.01 (0.02)	0.01 (0.05)	0.01 (0.02)
Body weight	−0.09 (0.24)	−0.12 (0.08)	−0.04 (0.07)	0.04 (0.02)	−0.01 (0.06)	−0.01 (0.02)
Age	−0.24 (0.21)	−0.09 (0.06)	0.08 (0.06)	0.04 (0.02)	0.04 (0.05)	−0.01 (0.02)
Sex	0.51 (0.67)	−0.02 (0.18)	−0.33 (0.19)	0.05 (0.06)	−0.23 (0.17)	−0.01 (0.05)
Drug use	0.19 (0.53)	0.24 (0.18)	−0.13 (0.14)	−0.08 (0.06)	−0.17 (0.13)	−0.05 (0.06)
Race
White	—	—	—	—	—	—
Black	0.94 (0.59)	0.35 (0.14)	−0.34 (0.16)	−0.10 (0.05)	−0.25 (0.14)	−0.08 (0.04)
Hispanic and others	0.24 (0.65)	0.10 (0.17)	−0.10 (0.17)	0.01 (0.06)	−0.10 (0.15)	−0.03 (0.05)

NOTE: Each outcome (HIV-1 RNA, Days below LOD, CD4) is computed as the length-adjusted area under the curve (AUC), i.e., AUC divided by length of follow-up. For HIV-1 RNA (copies/mL), the AUC is computed after transforming HIV-1 RNA on the base-10 logarithmic scale; LOD is limit of detection; length-adjusted CD4 cell count is reported on the base-10 logarithmic scale.

In Table 2, we found that patients with higher baseline viral load levels are more likely to switch earlier rather than later. Also, HIV-1 RNA level at virologic failure was strongly associated with switching early, with higher levels more likely to switch early. The remaining covariates are not significantly associated with the timing of ARV regimen change among those who failed on first-line regimen. The outcome regression model results are presented in Table 3. First, controlled for other covariates, cumulative viral load is positively associated with baseline viral load level and baseline CD4 cell count; it is negatively associated with the time to virologic failure among patients that changed regimens after 8 weeks. Second, HIV-1 RNA level at virologic failure is negatively associated with the days below the limit of detection. Third, among patients who change regimens after 8 weeks of confirmed virologic failure, patients with longer time to virologic failure and lower baseline CD4 cell counts have a higher proportion of days below the limit of detection during the total follow-up period. Fourth, HIV-1 RNA level at virologic failure is negatively associated with cumulative CD4 cell counts. Finally, time to virologic failure and baseline CD4 cell counts are positively associated with cumulative CD4 cell counts among patients who switch to second-line ARV regimen after 8 weeks.

Table 4 presents the analytic results for three primary endpoints using auxiliary covariates in Table 1. We include parameter estimates from the following six estimators: the sample average conditioning on those patients that failed their initial ARV regimen (COND), inverse-probability weighted (IPW) estimator, the IPW estimator with no auxiliary variables (IPW no Aux) in the propensity score model, the augmented IPW (AIPW) estimator, the minimum variance estimator of Robins et al. (1995, RRZ), and the proposed regression estimator (REG). Note, that an AIPW estimator with no auxiliary covariates in the PS or OR model is numerically equivalent to the “IPW no Aux” estimator. We conduct formal hypothesis tests that the average causal effect equals zero, that is, no difference between regimen strategies that switch early (s = 1) versus late (s = 0). In the case of naive (COND) estimates, we report the squared two-sample t-test statistic so that it is asymptotically distributed ${\chi }_1^2$ under the null hypothesis. Additional details for test statistics reported in Table 4 are provided in the Appendix.

In Table 4, we first note that the conditional (COND) estimates are quite different than all other estimates—HIV-1 RNA estimates are substantially larger, days below LOD estimates shorter, and CD4 estimates are smaller. This observation is because COND is not estimating the same quantity as the other five estimators. The IPW, IPW no Aux, AIPW, RRZ, and REG estimators are estimating the mean outcome for a particular ARV regimen strategy while COND is not. The COND estimator excludes information from all patients who do not experience virologic failure and so the effective sample size is smaller. The COND estimator would only be consistent for ARV regimen strategy in Definition 1 if all patients failed on initial ARV regimen and, additionally in the observed data, the timing of regimen change did not depend on potential confounders.

The next comparison is between two IPW estimators, one that models the propensity score via Table 2 and another (IPW no Aux) that ignores auxiliary covariates altogether. Here, it is clear that at least one of the auxiliary variables is having an impact on the HIV-1 RNA endpoint. Upon closer inspection of Tables 2 and 3, we find that baseline HIV-1 RNA, HIV-1 RNA at virologic failure, and time to virologic failure all appear to play an important role. At the same time, it appears that adjusting for auxiliary variables in the PS model for the IPW estimator has minimal impact on the conclusions for the LOD and CD4 endpoints.

The doubly robust estimators (AIPW, RRZ, and REG) take advantage of the auxiliary variables through the PS and OR model and generally have smaller standard errors than the corresponding IPW estimators. The AIPW estimate for the HIV-1 RNA endpoint within 8 weeks is almost two units larger than the IPW estimate (183.71 versus 181.88) and the AIPW standard error estimate is also larger. This leads to a null finding for the HIV-1 RNA endpoint using AIPW estimates whereas the conclusion using IPW estimates was significantly different. This is due to fact that the AIPW estimate can be adversely affected by small samples in the augmentation; this is also reflected by a larger standard error estimate. However, both the RRZ and REG estimates are similar to the IPW estimates and all three lead to the same conclusion. For days below LOD and the CD4 endpoints, the AIPW, RRZ, and REG estimates are all very similar. The RRZ standard error estimate for early switch in the CD4 endpoint was much larger than AIPW and REG and, therefore, led to a null finding putting it in disagreement with AIPW and REG.

In general, our results suggest there are significant differences in HIV-1 RNA, days below the LOD and CD4 cell counts between patients switching early versus late to second-line ARV regimens in the combined efavirenz-containing groups. In particular, viral load is generally lower while CD4 cell counts are greater for those patients switching earlier rather than later. Our findings also suggest that patients who switch within 8 weeks after confirmed virologic failure spend more days below 200 copies/mL, on average. For example, after one year of follow-up, patients following a treatment strategy which switched to second-line regimen within 8 weeks after virologic failure suppressed viral load levels to below 200 copies/mL for an average 296 days (365 × 0.81, 95% CI: 292–300 days), compared to 285 days (365 × 0.78, 95% CI: 281–289 days) for switching to second-line regimen beyond 8weeks after virologic failure. Hence, on average, patients spend about 11 days more with viral load levels below 200 copies/mL if they switch from a failing ARV regimen within 8 weeks. In conclusion, using our current definitions, we find evidence to suggest switching to second-line ARV regimen within 8 weeks of confirmed virologic failure from an efavirenz-containing regimen is associated with modest improvements in virologic and immunologic endpoints.

4.4 Sensitivity and Secondary Analyses

The sensitivity of our analytic results depend on identifiability assumptions, modeling assumptions, and may further depend on user-specified definitions and variable transformations included at any stage of the statistical analysis. Throughout this article, we work within the ubiquitous causal inference assumptions (3) and (4) and do not dwell on their veracity. All doubly robust estimators are consistent if either the propensity score model (7) or the outcome model (11) are correctly specified. If both Equations (7) and (11) are misspecified, none of the estimators discussed in this article are guaranteed to be consistent. Nonparametric models could be used instead, for example, but the resulting estimator would no longer be regular and asymptotically linear. The foci of our additional analyses are to assess the sensitivity and robustness of our conclusions to alternative treatment definitions, endpoint definitions, and variable transformations. Our findings are tersely summarized below but detailed in the online supplementary material.

The following sensitivity analyses were performed:

• (Subset auxiliary variables) Our main analysis used the same set of baseline covariables (with the exception of HIV-1 RNA level at virologic failure) throughout all propensity and outcome models, and for all three endpoints. Alternatively, we can perform subset selection and retain only significant confounders. We found that point estimates, standard error estimates, and tests of signficance changed only modestly.

• (Alternate definition of treatment policy) Our working definition of treatment strategy allowed all protocol-approved drug substitutions and implied that 45 patients were not actually following their initial randomized treatment at the time of virologic failure. Alternatively, we could have simply removed these patients from the analysis or treated them as a separate subgroup. Using the same auxiliary variables in Tables 2 and 3, we found that most conclusions did not change from the main analysis in Table 4 for cumulative CD4 cell counts and proportion of time with suppressed HIV-1 RNA. However, there is no significant difference for cumulativeHIV-1 RNA between two groups.

• (Alternate definition of endpoint) In Section 4, we computed endpoints calculating length-adjusted AUC of viral load and CD4 cell counts on their logarithmic scale (base 10). Alternatively, we could have first computed length-adjusted AUC on the original scale and then taken up logarithmic transformation. We mainly considered two different methods for computing the outcome not only because of the observed long right tail in the AUC empirical distribution but also because our Wald tests are not invariant to transformation. Nevertheless, all results remained similar except for one. We saw mild deviation in the magnitude of the difference in point estimates for the cumulative viral load endpoint compared to those presented in Table 4 but our tests of significance still rejected the null hypothesis at the nominal level.

Hence, we found that the results reported in Table 4 were generally repeated across the scenarios considered above. This is not proof that the results are correct but it does suggest that conclusions are not easily shaken by modest changes in our variable definitions.

5. DISCUSSION

The primary goal of this article was to address a scientific question in therapeutic HIV research where there is an abundance of conjecture and speculation but limited evidence: is it better to switch early or late from a failing ARV regimen? The ACTG attempted to answer this question through a randomized controlled clinical trial but found the trial difficult to enroll (Riddler et al. 2007). Alternatively, one may perform a secondary analysis on existing data from another study where assignment to change ARV regimen early or late depends on patient-specific characteristics. Although standard sample averages and two-sample tests cannot be used to analyze such data, methods of causal inference may be used and have become a staple of modern statistical inference. To answer the aforementioned scientific question using data from ACTG A5095, we built a statistical framework through potential outcomes (Rubin 1974) and two-stage designs (Lunceford, Davidian, and Tsitatis 2002) and a consistent IPW estimator for an intent-to-treat estimand using theory from Murphy, van der Laan, and Robins (2001). Note, that our intent-to-treat estimand is motivated by and analogous to one that would be estimated if ACTG A5115 (Riddler et al. 2007) had enrolled. Next, we derived a one-step regression approximation to a constrained maximum likelihood estimator (Tan 2006) for this problem and applied it to the A5095 data. Using this combination of techniques, we found that patients who started a standard combination antiretroviral regimen of nucleoside analogs and efavirenz and then employed the strategy to make regimen changes within 8 weeks of confirmed virologic failure on initial ARV regimen had lower cumulative viral load levels, higher cumulative CD4 cell counts, and spent a larger proportion of the follow-up period with suppressed viral load levels, on average. Although no definitive conclusions can be drawn from this secondary analysis, our results do suggest that switching earlier rather than later from a failing ARV regimen was associated with virologic and immunologic benefits.

It is difficult to say for certain whether the average differences in HIV-1 RNA, days below a limit of detection, or CD4 cell count reported in Table 4 are clinically relevant or not. In general, clinically significant differences in HIV-1 RNA and CD4 are discussed as patient-specific changes: < 0.5 log₁₀ change in HIV-1 RNA (copies/mL) are not considered clinically significant and, for CD4 cell count, a 30% change in absolute count or 3% change is deemed clinically significant (AETC National Resource Center, www.aids-ed.org). We concede that average differences in absolute HIV-1 RNA or CD4 may be difficult to translate to the clinical experience and a patient-specific relative measure would have been preferable. However, endpoints defined as functions of a limit of detection are reputable and, historically, have been used in defining primary endpoints for numerous clinical studies including ACTG A5095 (Gulick et al. 2004, 2006). When we began this project several years ago, our scientific objective was to identify treatment strategies that lead to sustained, low levels of HIV-1 RNA below the limit of detection. While this endpoint could not be defined through the available data, we did conceive of another endpoint, “time below the limit of detection,” that could be defined through the observations. In our analysis, we found that patients who switched to second-line ARV regimen within 8 weeks of confirmed virologic failure had viral load levels suppressed below the limit of detection for 11 days more, on average, than patients who delayed switching. In general, lower levels of viremia are indicative of less development of drug resistance, slowed disease progression, and positive response to therapy. Hence, while it is difficult to say whether 11 days of reduced viremia leads to definitive improved clinical benefits, it is reported that viral load reductions of less than 0.5 log copies or less are associated with clinical benefits (Murray et al. 1999).

TheACTGA5095 study is an example of a clinical trial whose primary objective was to test the efficacy of initial regimens but we used it in a secondary analysis of regimen change. If ACTG A5115 is any indication of the future, it will be difficult to design and enroll a completely randomized study of regimen change. In this case, data like that from ACTG A5095 and the framework employed here will be germane for evaluating the effect of early regimen change. As with many clinical studies, however, there are often caveats that make secondary analyses tricky. A limitation of our analysis is that patients who switched to second-line regimen within 8 weeks of initial virologic failure may have more follow-up data post-second-line treatment than do patients who delay switching. We attempted to adjust for the discrepancy by adjusting for length of follow-up but it would have been preferable to measure and analyze an endpoint that was exogenous to the timing of the second-line ARV treatment decision. One response to this potential criticism is that it is not evident, based on the literature or the clinical experience of the coauthors, whether more follow-up necessarily leads to better or worse outcomes and such assumption was one of our working hypotheses when we started this project. A second response to this potential criticism is to increase the sample size from a larger clinical study at the outset or to combine several smaller studies.

In addition to additional analyses listed in Section 4.4, we also considered different thresholds for an early versus delayed regimen change. The decision to define switching early as switching within 8 weeks after failing on the first-line regimen was made by investigators in the ACTG A5095 team and physicians who actually participated in the study. Nevertheless, we tried different thresholds including 90, 120, and 150 days. In general, we found that significance differences between early and late regimen change disappeared as timing of the threshold increases. Other methods that do not require dichotomizing the time of regimen change are desirable but we conjecture would not make a significant impact in the current analysis due to limited numbers of patients who actually changed regimens within several months of confirmed virologic failure.

For some statistical hypotheses within the combined efavirenz-containing group, it may be necessary to account for early stoppage of the triple-nucleoside group. To further elucidate this point, suppose that one had designed a study (analogous to D1 in Section 1) to test early-versus-late regimen change for two treatment groups, perhaps with the null hypothesis of no early-versus-late difference in either treatment group. If one treatment a₂ was stopped early and we proceeded to perform early-versus-late comparisons on treatment a₁ that continued, then these treatment comparisons might be biased and the tests of significance may have the incorrect size. In this case, it would be prudent to consider group sequential methods (cf. Pocock 1977; Tsiatis, Rosner, and Mehta 1984; Emerson 2006) to account for the sequential monitoring that led to the premature discontinuation treatment a₂. In the analysis of the ACTG A5095 data in Section 4, we were primarily concerned with correcting bias due to confounding and robust estimation of mean outcome for a particular treatment strategy defined through Definition 1. Additional statistical issues introduced by sequential monitoring could be an extension of our methods in Section 3 and may be an interesting avenue for future research, but it was beyond the scope of the current article.

APPENDIX

STANDARD ERROR ESTIMATION AND HYPOTHESIS TESTING

Under standard regularity conditions, our estimator behaves asymptotically as if the parameter κ _j, j = 0, 1 were known a priori and defined in Section 3.3.3. For completeness, we define the whole system of estimating equations, 0 = ℰ_nϕ_θ (Z, θ), where ${\mathit{\varphi }}_{\mathit{\theta }}={({\varphi }_{{\mu }_1},{\varphi }_{{\mu }_0},{\mathit{\varphi }}_{\mathit{\psi }}^{\mathrm{T}},{\mathit{\varphi }}_{{\mathit{\xi }}_1}^{\mathrm{T}},{\mathit{\varphi }}_{{\mathit{\xi }}_0}^{\mathrm{T}})}^{\mathrm{T}}$, and,

$${\varphi }_{{\mu }_1}=Y\{(1-R)+\frac{\mathit{\text{RS}}}{\pi (\mathbf{X},\mathit{\psi })}\}-{\mathrm{\kappa ̃}}_1\times R\{\frac{S}{\pi (\mathbf{X},\mathit{\psi })}-1\}{(1,m(\mathbf{X},{\mathit{\xi }}_1))}^{\mathrm{T}}-{\mu }_1,$$

$${\varphi }_{{\mu }_0}=Y\{(1-R)+\frac{R(1-S)}{1-\pi (\mathbf{X},\mathit{\psi })}\}-{\mathrm{\kappa ̃}}_0\times R\{\frac{1-S}{1-\pi (\mathbf{X},\mathit{\psi })}-1\}{(1,m(\mathbf{X},{\mathit{\xi }}_0))}^{\mathrm{T}}-{\mu }_0,$$

$${\mathit{\varphi }}_{\mathit{\psi }}=R\{S-\pi (\mathbf{X},\mathit{\psi })\}\mathbf{X},$$

$${\mathit{\varphi }}_{{\mathit{\xi }}_1}=\mathit{\text{RS}}\{Y-m(\mathbf{X},{\mathit{\xi }}_1)\}\mathbf{X},$$

$${\mathit{\varphi }}_{{\mathit{\xi }}_0}=R(1-S)\{Y-m(\mathbf{X},{\mathit{\xi }}_0)\}\mathbf{X}.$$

Standard arguments lead to the usual sandwich formula for the asymptotic covariance of θ̂ and a consistent estimator given by Σ̂_θ = Â⁻¹B̂(Â⁻¹)T. The asymptotic covariance estimator for μ = (μ₁,μ₀)^T, i.e., ${\mathbf{\Sigma ̂}}_{\mathit{\mu }}=\widehat{\text{cov}}(\mathit{\mu ̂})$, is the upper right 2 × 2 matrix of Σ̂_θ.

A consistent estimator for the average causal effect (ACE) for switching ARV regimens early versus late is given by δ̂ = μ̂₁ − μ̂₀. Our Wald test statistic for the difference between early vs. late switch shows T = (Cμ)^T(CΣ_μC^T)⁻¹(Cμ), where C = (1, −1), is asymptotically distributed as ${\chi }_1^2$ under the null hypothesis of no difference.