Reverse-engineering the genetic circuitry of a cancer cell with predicted intervention in chronic lymphocytic leukemia

Abstract

Cellular behavior is sustained by genetic programs that are progressively disrupted in pathological conditions—notably, cancer. High-throughput gene expression profiling has been used to infer statistical models describing these cellular programs, and development is now needed to guide orientated modulation of these systems. Here we develop a regression-based model to reverse-engineer a temporal genetic program, based on relevant patterns of gene expression after cell stimulation. This method integrates the temporal dimension of biological rewiring of genetic programs and enables the prediction of the effect of targeted gene disruption at the system level. We tested the performance accuracy of this model on synthetic data before reverse-engineering the response of primary cancer cells to a proliferative (protumorigenic) stimulation in a multistate leukemia biological model (i.e., chronic lymphocytic leukemia). To validate the ability of our method to predict the effects of gene modulation on the global program, we performed an intervention experiment on a targeted gene. Comparison of the predicted and observed gene expression changes demonstrates the possibility of predicting the effects of a perturbation in a gene regulatory network, a first step toward an orientated intervention in a cancer cell genetic program.

Cellular behavior is conditioned mostly by functional genetic programs in response to various environmental signals, as initially shown in simple organisms (1, 2). External stimuli activate cellular surface receptors that trigger multiple signaling cascades in cells. The ultimate targets of these cascades are transcription factors that initiate sequential transcriptional activations with high temporal coordination. The first activated genes, at early time-points, after cell stimulation, essentially have a fast and transient expression; their gene products activate expression of various target genes downstream of transcriptional regulation cascades. These latter genes have longer-lasting expression, and their products sustain the adapted cellular response to initial environmental stimulation (3). These functional molecular networks are disrupted in various pathologies (e.g., cancer) where genetic aberrations lead to tumoral cellular programs. Since the first application of high-throughput technologies for measuring gene expression, a number of methods have been proposed to reverse-engineer gene regulatory networks; considered to be the underlying structure of these genetic programs (4). These different methods were developed to infer gene potential interactions and to describe these networks at the system level (5). The next important goal was to develop statistical tools to control these systems (6). One of the key challenges is to determine which critical genes whose perturbed expression drive these pathological genetic programs toward targeted states. We propose here a predictive method that is able to predict changes in gene expression upon intervention in the network. Predicting the resulting dynamic gene expression after specific targeted gene disruption is a first step toward controllability.

Among statistical approaches developed to reverse-engineer statistical links between genes and to infer underlying gene regulatory programs (7) there is as yet no standard method, because each one is based on strong and specific modeling assumptions, indispensable to make the model identifiable (8). As we aimed to understand the temporal dynamic of the network, we focused on methods suited for time-series gene expression data. These methods can be grouped into three categories: (i) information theoretic models, which define a proximity measure between genes, (ii) optimization methods, which use a scoring function to choose the best suited network, and (iii) regression and other systems of equation methods with a prior network structure. Information theoretic models can only be used for descriptive purposes (i.e., no prediction is possible) but are computationally efficient, making them appealing for large data sets. Several proximity criteria may be used, e.g., the partial Pearson correlation coefficient in graphical Gaussian models (9) or entropy in the time-delay ARACNE (TD-ARACNE) method (10). Optimization methods comprise mostly algorithms using discretized gene expression data and are not computationally efficient for large data sets. Equations-based models impose an underlying structure on the gene network (11). These last methods were retained in this study because they have led to promising results due to their flexibility (allowing structural prior information to be incorporated in the model), their ability to infer large-scale networks, and their suitability for prediction purposes (7).

To develop and test such statistical models, we previously developed a pertinent biological model using human blood cancer cells (12). This biological model allowed us to focus on a genetic program that sustains the leukemic process after a cellular stimulation in primary malignant lymphocytes (13, 14). Furthermore, this model includes various cell states, from healthy (normal) lymphocytes to those implicated in indolent and aggressive chronic lymphocytic leukemia (CLL), allowing us to compare the genetic program of these different cell states, which leads in turn to specific proteomic phenotypes (15). CLL is defined by a clonal proliferation of B-lymphocytes, which accumulate in the blood to form a leukemia that progressively evolves and is currently incurable (16). The mechanism of this proliferation is not well understood, but current hypotheses are in favor of a chronic antigenic stimulation of certain lymphocytes as the primary event in tumorigenesis. Indeed, stimulation through the B-cell antigen receptor (BCR) is crucial for physiological development and is the basis of immunological response of these cells. However, in CLL (as in other leukemias and lymphomas) a sustained and chronic stimulation of unknown origin is thought to chronically stimulate some lymphocytes, progressively leading to a cell transformation and finally—with accumulation of genetic abnormalities—to an autonomous leukemic cell expansion program (13, 16). Several prognostic subgroups of CLL have been described, encompassing patients with different survival times (17). Gene expression profiles have been assessed in these different leukemic states (12, 18, 19), but no comprehensive lymphocyte BCR genetic program has been proposed to date. Inferring a statistical model of the BCR gene program to predict the key genes that need to be ultimately silenced to modulate the leukemic genetic program in an oriented way would enable better drug development in this presently incurable disease. Furthermore, such an approach would be transferable to other cancers and nonmalignant complex diseases.

In this study we selected genes using a two-step algorithm, which retains genes with high differential expression and genes with specific temporal patterns. We then reverse-engineered the gene regulatory network with a penalized regression-based method. To assess the possibility of controlling such a genetic program, we performed an RNAi knockdown experiment on a targeted gene, predicting the changes in gene expression from wild-type to the knockdown cells.

Results

Gene Selection and Network Reverse-Engineering.

After cell stimulation, a specific genetic program is initiated by the concerted expression of a limited number of genes. When captured through temporal genome-wide transcriptional data, the expression of these genes of interest needs to be separated from the residual cellular transcription. So, at each time point after stimulation, we studied gene expression both in stimulated cells and in control (unstimulated) cells. Given that several temporal gene expression profiles have revealed complex gene expression after cellular stimulation (3, 20), we considered that genes with both high expression level and those with a specific expression pattern (regardless of their expression level) are relevant in the program (21). Gene selection methods based upon selection of highly differentially expressed genes are widely used. In this study, highly expressed genes are selected using common statistical methods (22), and genes with specific temporal expression patterns are selected with a specific mixture model, which is also used to group genes into time clusters.

After selecting genes that are likely to participate in the genetic program, we specified a regression-based model to reverse-engineer the gene network. To make the model identifiable and interpretable, some biological constraints were assumed. First, we use the time clusters induced by the mixture model to ensure the temporal causality (i.e., if gene n1 is in the time cluster c1 and gene n2 is in the time cluster c2, gene n1 may interact with gene n2 if and only if c2 > c1). More importantly, topological changes have been observed in gene regulatory networks across time (2, 23). This property implies a variance in the links between genes through time, allowing specific links activation at specific periods of time after cell stimulation. There are only a few methods allowing such a temporal rewiring. Assuming the widespread hypothesis of sparsity of large networks (4), we put a Lasso penalty on the model (24). As a result, we propose a scalable time rewiring reverse-engineering method, well-suited for large data sets (Materials and Methods).

Application to Synthetic Data.

To test our model for inference purposes and determine how accurate the inferred network is, compared with the real network, we used synthetic simulated data where the true network is perfectly known. We compared two network topologies for our simulations: W1, which has a scale-free topology, generated with the RANGE algorithm (25); and W2, which has a temporal cascade topology closer to a biological model of transcriptional activation after transient cell stimulation (3, 26). These networks are composed of 500 and 300 genes, respectively, both with four time-points (the number of genes and time points was chosen with the perspective of studying our biological data set). The gene expression was simulated using a nonlinear logistic function (27). We then calculated three usual indicators (10, 28): sensitivity, which describes the proportion of detected links among those that are in the real network; predicted positive value (PPV), which describes the proportion of inferred links that are in the real network; and the F-score (29), which combines both and therefore is a convenient way to assess the global performance of an inference method. With the stable state synthetic network generated with RANGE algorithm, our method achieves an F-score = 0.011 (P = 0.001), which considerably increases with a temporal cascade network reaching an F-score = 0.159 (P < 0.001). To go further in this evaluation with synthetic data, we sought to compare these performances with those of actual benchmarked algorithms encompassing several mathematical approaches: TD-ARACNE, an information theoretic method (10); GeneNet, a graphical Gaussian method (9); GeneReg, a regression-based method (30); and a dynamic Bayesian network method (DBN) by Morrissey et al. (31) (settings and short descriptions of these methods are presented in Tables S1 and S2). Despite the performances of the DBN method (31), its low computational efficiency did not allow us to reach any results with such synthetic data size. GeneReg (30) did not give any significant result for either of the performance indicators. All three remaining methods (TD-ARACNE, GenNet, and our method) performed equally on the RANGE network, with an F-score of 0.01 ± 0.001. One notes that a slight change in F-score (e.g., from 0.011 for our method network to 0.009 for GeneNet) induces an important change in terms of P value (0.001–0.032, respectively), which seems to reveal how difficult it is to reverse-engineer a 500-nodes network. When using a cascade topology network, performances of all methods (TD-ARACNE, GenNet, and our method) increased. Nevertheless, in this case, our method has much better results with an F-score = 0.16, whereas other methods have an F-score less than 0.044. The two proposed network topologies are reliable, and the true targeted network may be halfway between the two. Because our method outperforms the others in both networks, our proposed algorithm appears to be effective in all cases. Detailed results of algorithms comparisons are presented in Table 1.

Table 1.

Modeling performances comparisons on synthetic data with other benchmarked methods

	Sensitivity	PPV	F-score	P value
Our method
Range network topology	0.021*	0.007*	0.011*	0.001
Temporal cascade topology	0.276*	0.111*	0.159*	<0.001
TD-ARACNE (33)
Range network topology	0.062*	0.005*	0.010*	0.006
Temporal cascade topology	0.023*	0.040*	0.029*	<0.001
GeneNet (9)
Range network topology	0.031*	0.005*	0.009*	0.032
Temporal cascade topology	0.071*	0.038*	0.044*	<0.001
GeneReg (33)
Range network topology	0.252	0.003	0.007	0.476
Temporal cascade topology	0.655	0.010	0.019	0.895

*Significant at 0.05; explicit P values are for the F-score.

Application to the CLL Data Set.

We used gene expression data generated and previously reported (12). Briefly, three different cell populations (six healthy B-lymphocytes, six leukemic CLL B-lymphocyte of indolent form, and five leukemic CLL B-lymphocyte of aggressive form) were stimulated in vitro with an anti-IgM antibody, activating the BCR. We analyzed the gene expression at four time-points (two early time-points at 60 and 90 min, one intermediary time-point at 210 min, and one late time-point at 390 min). For each time point, gene expression measurement was performed both in stimulated cells and in control unstimulated cells, and data were then preprocessed using dChip software (32). The gene selection process retained genes that were highly differentially expressed (∼40%) and genes with specific temporal patterns (∼60%). Among the 54,675 probe sets, 960 were retained for further analysis. Approximately 500 genes are retained by cell category; the distribution of these genes within the three cell groups is shown in a Venn diagram in Fig. S1. A core of 183 genes is used by all cell groups. Among these, 118 correspond to unique genes. The exploration of their biological function through the National Institutes of Health’s DAVID database (33) allows evaluation of the significance of biological function enrichment of this list of genes. The majority of these genes are indeed known to be expressed in response to cellular stimulation (51 of 118 genes, P value with false discovery rate correction = 0.0001) and specifically in the gene expression regulation after cell stimulation (44/118, P = 0.0006). Furthermore, the genes shared by the three cell categories are enriched with genes having a transcriptional activity (22/118, P = 0.0003) or a transcriptional regulation activity (26/118, P = 0.0017). As expected, some of these genes are also involved in the BCR signaling regulation through MAP kinase phosphatases (3/118, P = 0.05). Some genes are known to be involved in the biological process of immune regulation (20/118, P = 0.0045), and more specifically in lymphocyte activation (8/118, P = 0.0016). These genes, which are the basis of the response to BCR stimulation within the three cell groups, have labels that are distributed across the four temporal cluster types. Other genes are either shared by two cell groups or are specific to a cell population. More genes (183 + 86) are shared by the aggressive or indolent leukemic cells than by the healthy cells and the leukemic cells. The differential expression levels of the retained genes as a function of time is shown for a representative patient in Fig. 1.

Fig. 1.

Results of gene selection. Representation of selected genes for a representative patient. Graphs A–D successively represent genes that have consistent up-regulation at a given time, noted in bold (t₁–t₄, respectively). Graph E shows genes that are highly expressed through all four time-points. Graph F shows all of the retained genes.

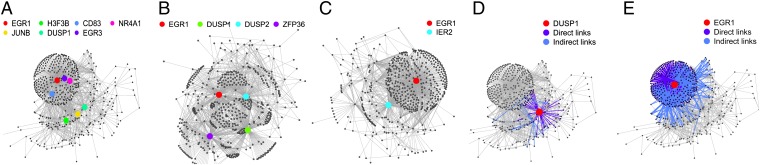
The genetic program induced within each cell group is then inferred with a Lasso regression-based method and is represented by a predictive linear model, adjusted independently on each of the three cell groups (Materials and Methods). Within the model, the expression of one particular gene at a given time-point influences the expression of other genes at subsequent time-points, satisfying the temporal constraint of the gene program. This model defined a network of the probable genetic interactions involved in cell response to antigen stimulation. The inferred network in the three cell categories is shown in Fig. 2. These models show a scale-free–like structure, where a large fraction (93% in the most aggressive leukemic B cells) of genes have a small number of outgoing edges (less than 10) and a small fraction of genes, the so-called hub genes (1%: seven genes), have a large number of outgoing edges (more than 40). There are two hubs in healthy cells, four in indolent leukemic cells, and seven in aggressive leukemic cells. Among these 10 hub genes, four are known genes with transcription factor activity (EGR1, EGR3, JUNB, and NR4A1), involved in transcriptional activation of the JNK MAP kinase signaling and ERK signaling pathways, downstream of the BCR. Some of these genes are also directly involved in MAP kinase signaling (DUSP1 and DUSP2) and in lymphocyte function regulation (CD83). Interestingly, EGR1, which is common to all three cell groups (i.e., it is one of the 183 common genes) appears as a major hub in all three networks. Additionally, the leukemic cells share an important hub gene, DUSP1, as shown in Fig. 2 A and B. The temporal evolution of the signal is shown in Fig. S2. Genes that are active in the two earlier time-points are massively linked, whereas genes that are active in the latest time-points have far fewer connections.

Fig. 2.

Visualization of inferred networks. The gene regulatory network of the most-aggressive leukemic B cells (A), the indolent leukemic B cells (B), and healthy B cells (C) are represented. Nodes represent genes, and edges statistical relationships between genes. For each network, hubs are highlighted in color. As the number of hubs decreases between aggressive, indolent, and healthy networks, the structure of the network is changed. Subnetworks for DUSP1 (D) and EGR1 (E) in the most-aggressive leukemic B-cell networks. The concerned gene is highlighted in red. Direct links are shown in navy blue, and indirect links are shown in pale blue. EGR1 is a gene whose influence is very large, because its subnetwork takes a large part of the complete network. In contrast, DUSP1 has a limited subnetwork. Visualization generated using R and R package igraph.

Though the structure and parameters of such models provide insight into the nature of a cell gene regulatory network under a given stimulation, the predictive aspect is its main interest. However, the nature of the inferred network is essentially statistical, and further experimentation is necessary to distinguish causal from correlated behavior. Perturbation experiments are the usual mechanisms for assessing causal behavior. Consequently, as a feasibility experiment, we examined the structure of the inferred network and identified DUSP1 as a candidate gene. DUSP1 is a hub gene in both aggressive and indolent networks (Fig. 2); it shows up-regulation at the first time-point, which provides opportunities to measure the effect of perturbing it at later time-points on the genes to which it is connected. Furthermore, it has a localized subnetwork (Fig. 2D) so that effects due to perturbation of DUSP1 can be distinguished from effects following general cell perturbation concomitant to cell transfection. We performed a biological intervention experiment using fresh primary negatively selected B cells from one aggressive CLL case (Materials and Methods). We silenced expression of DUSP1 by transfecting DUSP1-specific RNAi and, as a control, transfected cells with a nontargeting RNAi (Fig. S3). We then stimulated the BCR of these cells as previously described (12). Whole-genome expression profiling was performed at four time-points after BCR stimulation, using the same Human Genome U133 Plus 2.0 microarray, and preprocessed using dChip [data accessible in the Gene Expression Omnibus (GEO) database]. Gene expression profiles under DUSP1 silencing were then compared with model predictions in which the expression of DUSP1 is set to zero. In this model, the predicted expression is up-regulated, down-regulated, or constant (Fig. S4). For each probe set, prediction is done for the last three time-point measurements. Consequently, for each probe set, we can have 0–3 correct predictions. Considering our data, where the proportion in the three categories are not equivalent (the number of up-regulated, down-regulated, and constant gene expressions are different), the random prediction of one of these three categories is correct with a probability of 45%. However, the observed modulation of expression in this experiment shows 62% correct predictions for genes with a direct link to DUSP1 at t₂ (P value 0.0041) (Table 2). At later time-points, the predictive accuracy decreases (t₃: 54%, P value = 0.08, and t₄: 43%, P value = 0.7). At t₄, our predictions are not significantly better than noise; this can be explained by a slow accumulation of the errors, because predictions for time t₄ take into account predictions made at time t₂ and t₃. Although the predictive power of our model decreases in the later time-points, results are promising and demonstrate the possibility of an oriented modulation of the gene regulatory network in future work.

Table 2.

Percentage of correct predictions between observed and inferred network after the silencing of DUSP1

	t2, %	P value	t3, %	P value	t4, %	P value
Linked	62	0.004	54	0.08	43%	0.70
Not linked	56	<0.001	59	<0.001	40%	0.97

Discussion

We developed a general statistical method for analyzing gene expression as a means to infer a temporal regulatory network. We first ascertained the performance of this method on synthetic data before analyzing biological data sets. We applied this method to model the response of three different cell groups—healthy B cells, indolent CLL cells, and the most aggressive CLL B cells—in response to an in vitro stimulation. The results demonstrate different patterns of the genetic program used by each cell group after antigenic stimulation, as shown in the graphical representation of the inferred networks (Fig. 2). When focusing on the genetic program of the more aggressive leukemic cells, several points of convergence (overlap) are found in the networks inferred by our method and by other benchmark methods (Table S3). Considering specific topologies of these networks, EGR1 appears as a hub (regulating here more than 10 others genes) for all of the methods, whereas DUSP1 only appears as a hub for our method and GeneNet. Still focusing on the more-aggressive leukemic cells, we used our in silico model to predict the effects of perturbing the genetic program of these cells. This prediction ability imposes specific constraints on model inference (Fig. S5). Obtaining multiple points of measurements via microarray experiments also poses a great challenge when analyzing human cells. Thus, the study deals with a relatively small number of subjects, time points, and points of measurement, including a total of 152 microarrays. The inference method, as a result, explicitly imposes sparseness in the inferred network. The preliminary results suggest the feasibility of such an approach for oriented genetic program modulation. Furthermore, 20% (183 of 960) of the probe sets are shared by the three networks within separate analyses, which suggests the need for further study toward an understanding of how such networks are related and how such networks evolve from a healthy state to the more aggressive state and why, as a consequence, genes are specific to one state (healthy, indolent, or aggressive). To solve this issue we may create a network inferred with all of the patients irrespective of their category. However, in such a model, an interaction between two genes might depend on both the incoming stimulation and the state of the considered cell. Furthermore, as shown in the perturbation experiments, analysis of the network structure of such statistical models identifies target genes, typically hubs, for modulation. Ultimately, we should target those genes whose expression can be perturbed under the model in a way leading to an oriented modulation of the cancer cell phenotype. For the particular genetic background and cancer stage of each patient, the method could be used to generate personalized models enabling patient-specified modulations of these cancer-disrupted cellular programs.

Materials and Methods

Genes are initially under two states: stimulated and unstimulated (control situation). Their differential expression profiles were computed by subtracting unstimulated from stimulated expression levels at each of the measured time-points. Furthermore, a data set X containing N genes, P patients within a subpopulation, and four time points (t₁,…,t₄) was considered. In this study, each subpopulation (healthy, indolent, and aggressive) is modeled separately.

Gene Selection.

Gene selection was done in two steps. First we selected a large number of highly expressed genes based on a Laplace mixture model (step 1) (22). We then used a mixture model, estimated by an expectation-maximization (EM) algorithm, to select, among the remaining genes, those with a specific pattern of expression (step 2). In the mixture model, gene expressions were assumed to come from a finite mixture of probability distributions, with each mixture component m = 1,…,5 corresponding to a different cluster. In our case, clusters m = 1,…,4 indicate localized up-regulation of a gene at time t_m and cluster m = 5 indicates a gene that is not strongly affected by BCR stimulation and is hence excluded from further analysis. Though the parametrization across subpopulations is the same, the actual parameters differ. Formally, we assume that we want to maximize the following likelihood function: 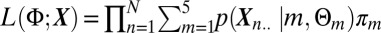, where , , 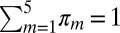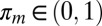for all m, Θ contains all of the parameters Θ₁,…,Θ₅ assumed to be distinct, and X_n.. is the vector expression for gene n across all patients and time points. The mixture proportions for each cluster are π_m. Conditional probability for a given gene X_n.. in a given cluster is defined as . The subscripts on X specify gene n, patient p, and time point t_i. For purposes of categorization only, time points are modeled as independent. Additionally, the model enforces a common labeling of a given gene across all subjects within a subpopulation. Consequently, disease-related genes exhibiting consistent temporal structure across subjects within a given subpopulation will have a sharp posterior probability under the model, whereas those that respond to BCR stimulation but vary in their response within a subpopulation will not. Following convergence of EM-fitting, each gene for all P patients within a subpopulation is assigned to the cluster with maximum a posteriori probability. We developed a simple parameterization of 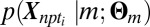to account for the observed predominance of up-regulation at the specified time-points in differential expression. Specifically, genes responding to BCR stimulation are fit to the following model for :

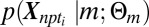where b_m, 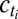, , 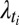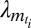are positive real numbers and θ_m are real numbers. These parameters are estimated by the EM algorithm. The use of exponential and Laplacian distributions better captures the heavy-tailed behavior observed in responding genes. The statistical significance of the resulting model was computed using a permutation approach (34, 35), and significance was computed by comparing the log-likelihood score from EM-fitting of the original unpermuted data to the distribution of scores obtained using different permutations for each gene within a trial. Moreover, our clusters are validated by an unsupervised clustering method (Fig. S6). The list of selected genes consists of both the highly differentially expressed genes (step 1) and genes with a specific expression pattern (step 2). Let N_sel be the length of this list. We eventually attribute a categorical label to each selected gene describing at which time-point its expression is the highest. In the following, let m(i) be the categorical label of gene i.

Model Inference.

After selecting the genes as described above, we define a linear predictive model:

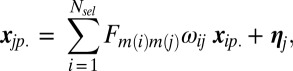where 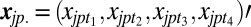and 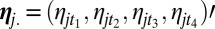is the noise. Two sets of parameters are used with a specific role. The first term, ω_ij, captures the relative influence of one gene on another compared with other genes in the putative network. The second term is the 4 × 4 matrix F_m(i)m(j), which quantifies the mode of interaction and is indexed by the categorical label (1,…,4) m(i), m(j) of genes i and j, inferred during the previous step. Notice that matrix F_m(i)m(j) permits the link between genes i and j to evolve across time; this results in a global optimization criterion over the sets ω_ij and F_m(i)m(j), minimizing the L₂ norm of the residuals. We then set two constraints: (i) 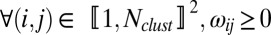and (ii) 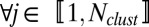, , where d is a nonnegative parameter estimated by cross-validation. The constraints on ω_ij ensure that only a small number of genes will have a significant influence on any one gene, leading to sparse interaction models. The second constraint is a Lasso penalty. However, no constraint is placed on the number of genes that any single gene may influence. Though the full optimization is nonconvex, given the set ω_ij, there is an analytic solution for the set F_m(i)m(j). Similarly, given the set F_m(i)m(j), one can solve for the set ω_ij via a quadratic program, which leads naturally to a coordinate ascent approach. The result of the optimization is a connectivity network described by the nonzero elements of ω_ij combined with a set of cluster-dependent interaction models described by the set F_m(i)m(j). Each matrix F_m(i)m(j) is further constrained to have the following form:

where a_m(i)m(j), b_m(i)m(j), c_m(i)m(j) are reals. This structure has two consequences. From a practical standpoint it reduces the complexity of the optimization from a search over 16 parameters for each F_m(i)m(j) to one over three parameters. Consequently, interactions depend only on time-index differences rather than absolute time index. Matrices are lower triangular with a null diagonal; these conditions ban the possibility of feedback loop. Furthermore, because the categorical label indexes the peak in differential expression within the temporal profile we only consider causal predictor models, which is why we impose 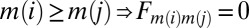. To summarize, results of the clustering are used both to select genes that are the most affected by the stimulation and to impose some constraints on the linear model. The resulting gene regulatory network is then represented by link strength ω_ij.

Simulations.

To evaluate our inference methodology, a simulation step in which the initial gene regulatory network is perfectly known is essential for comparison purposes. To simulate in silico data, we need to choose both a network topology and a dynamic model that spreads the signal from genes to genes. We choose two reliable network topologies: a scale-free topology generated with RANGE (25) and a temporal cascade topology that represents the topology of the network when the cell is stimulated by an environmental stimulus (3, 26). To simulate gene expression, we assume that expression of gene A at time t depends on expression of its regulators at time (t − 1). To make the simulations more realistic, we used a nonlinear function to modelize interactions, , where a has been set to 1/3.5, b has been set to 30, and C has been set 40; this is a logistic function with a sigmoid form, classically used in modeling gene network dynamic (27). Furthermore, we compared our reverse-engineering method with four other algorithms: GeneNet (9), based on graphical Gaussian models; GeneReg (30), a regression-based method that extrapolates the number of time points by B-spline regression; TD-ARACNE (10), the time-course data equivalent of the information theory method ARACNE (36); and a DBN method (31). We then compare the inferred matrix with the real matrix. We calculate the predictive positive value (PPV), defined as TP/(TP + FP), the sensibility, defined as TP/(TP + FN), and the F-score, defined as 2 × sensitivity × PPV/(sensitivity + PPV), where TP represents the true positives, FP the false positives, and FN the false negatives. The F-score combines both sensitivity and PPV and is known to decrease when the number of genes included in the model increases (10). We finally compute a conditional permutation test for all of these indicators of performance.

Microarrays, RNA Interference, and Validation Experiments.

Primary microarray data were extracted from Vallat et al. (12) and consisted of 136 samples [four time-points for both unstimulated (US) and stimulated (S) cells from six healthy donors, six patients with indolent CLL, and five patients with aggressive CLL)]. Patients with indolent CLL (with IGVH gene mutated and ZAP70-negative expression) had stable disease over time, whereas patients with aggressive CLL (4/5 with IGVH gene unmutated and 6/6 with ZAP70-positive expression) had a rapid clinical course (12). For the intervention experiment performed here, peripheral blood was obtained from one patient with aggressive CLL included in our previous study (12). B cells were negatively selected (RosetteSep B-cell enrichment mixture; Stemcell Biotechnologies) and isolated by density gradient centrifugation over Ficoll-Paque PLUS (Pharmacia). Quality of the selection was assessed by flow cytometry on a Cytomics FC500 system (Beckman-Coulter) after CD5-PE/CD19-FITC staining (BD Biosciences) and was >98% of total cells. Cells were cultured at 37 °C in 5% CO₂ for 6 h in RPMI-1640 medium supplemented with 10% heat-inactivated FCS, 2 mM L-glutamine, and 24 μg/mL gentamicin. Cells were transfected with a pool of four designed DUSP1 siRNA (siGenome SMARTpool reagent; Dharmacon Inc.) or with a non–sequence-specific siRNA (siCONTROL nontargeting siRNA no. 1; Dharmacon Inc.) at a final siRNA concentration of 100 nM using the Nucleofector apparatus and cell line Nucleofector kit according to the manufacturer’s instructions (Amaxa Biosystem). Cells were then cultured at 37 °C in 5% CO₂ in supplemented RPMI-1640 culture medium. After 12 h, the cells were recovered by density gradient centrifugation over Ficoll-Paque PLUS (Pharmacia), washed, and starved for 4 h at 37 °C/5% CO₂ in supplemented RPMI-1640. Starved-transfected and mock-transfected B cells at a density of 10⁷cells/mL were divided in two. Half of the cells were BCR-stimulated by goat F(ab′)2 anti-human IgM-BIOT (Southern Biotechnology) at 20 μg/mL and cross-linked by 20 μg/mL avidin (Sigma-Aldrich), washed, and resuspended in supplemented RPMI-1640 (12). At four time-points (60, 90, 210, and 390 min) after BCR stimulation, total mRNA was collected over four experimental conditions [DUSP1 silenced (US/S) and mock-transfected (US/S)]. cRNA was prepared in accordance with the Affymetrix protocol and hybridized to the Human Genome HU133 Plus 2.0 microarray, which contains 54,675 probe sets. We further normalized these 16 microarrays with the previous 136 samples with the invariant set method and the model-based expression index obtained by the perfect-match-mismatch (pm-mm) model using dChip software (32) (all data are accessible in the GEO database under accession no. GSE39411).