Fatigue-Related Gene Networks Identified in CD14⁺ Cells Isolated From HIV-Infected Patients—Part II: Statistical Analysis

Abstract

Purpose

In limited samples of valuable biological tissues, univariate ranking methods of microarray analyses often fail to show significant differences among expression profiles. In order to allow for hypothesis generation, novel statistical modeling systems can be greatly beneficial. The authors applied new statistical approaches to solve the issue of limited experimental data to generate new hypotheses in CD14⁺ cells of patients with HIV-related fatigue (HRF) and healthy controls.

Methodology

We compared gene expression profiles of CD14⁺ cells of nucleoside reverse transcriptase inhibitor (NRTI)-treated HIV patients with low versus high fatigue to healthy controls (n = 5 each). With novel Bayesian modeling procedures, the authors identified 32 genes predictive of low versus high fatigue and 33 genes predictive of healthy versus HIV infection. Sparse association and liquid association networks further elucidated the possible biological pathways in which these genes are involved.

Relevance for nursing practice

Genetic networks developed in a comprehensive Bayesian framework from small sample sizes allow nursing researchers to design future research approaches to address such issues as HRF.

Implication for practice

The findings from this pilot study may take us one step closer to the development of useful biomarker targets for fatigue status. Specific and reliable tests are needed to diagnosis, monitor and treat fatigue and mitochondrial dysfunction.

Genome-wide studies, coupled with clinical and physiological data, provide key information for the determination of biological pathways involved in many critical diseases. Without exception, the data resulting from high-throughput sequencing techniques are characterized by an extremely small number of available samples with respect to the number of candidate factors of interest. This situation leads to substantial difficulties in the subsequent statistical analyses. The overarching goal of such analyses is to select a reduced pool of genes and traits that might play a role in the relevant disease-inducing mechanisms. Based on this initial selection, researchers identify a network of interactions with the goal of generating pertinent conjectures about the underlying biological processes. They further refine these conjectures based on current knowledge and then validate them through additional studies and laboratory experiments.

In the statistical literature, the selection of genes and traits is referred to as a variable selection problem. Univariate rankings of the strength of association between each candidate factor and disease status represent the most straightforward and widespread method for performing variable selection (Dudoit, Fridlyand, & Speed, 2002; Golub et al., 1999; Nguyen & Rocke, 2002; Tusher, Tibshirani, & Chu, 2001). The assessment of the statistical significance of the huge number of null hypothesis tests associated with each individual factor is a complex problem that still lacks a definite solution (Benjamini & Hochberg, 1995; Efron & Tibshirani, 2002; Storey & Tibshirani, 2003). For this reason, univariate rankings often lead to the puzzling conclusion that no factors seem to be significant for the response of interest. Such a claim is not justified for two reasons: (a) the available data might be insufficient to prove the involvement of any single factor in the disease-generating mechanisms, but they could still show what factors are most likely to be involved and (b) combinations of two, three, or more predictors also need to be considered. Complex hypotheses in which several factors contribute together in the progression of a disease compound the variable selection problem because it is no longer computationally feasible to exhaustively explore all the possible candidate models. In the context of linear regression, stepwise methods (Furnival & Wilson, 1974) represent a first solution that allows the identification of the most relevant regressions without listing all candidate regressions. Unfortunately, these methods can handle only small data sets due to their inability to escape local modes created by patterns of collinear factors; hence, they are unlikely to perform well in the context of genome-wide studies.

Markov chain Monte Carlo (MCMC) algorithms were a major step forward. These algorithms explore the model space in a Bayesian framework by sampling from the joint posterior distribution of the regression parameters and the candidate regressions (Chipman, George, & McCulloch, 2001; Clyde & George, 2004; George & McCulloch, 1993). The performance of MCMC methods can be enhanced by integrating out the regression parameters, thereby creating chains that move only in the space of regressions. In this case, sampling from a posterior distribution is no longer required and other stochastic search methods that aggressively move toward regions of high posterior probability in the regressions space are more desirable. Two such algorithms stand out for their performance: the shotgun stochastic search (SSS) of Hans, Dobra, and West (2007) and the bounded mode stochastic search (BMSS) of Dobra (2009). Both algorithms give excellent results when selecting the most promising factors from large data sets involving gene expression, genotype, and clinical and physiological information.

Exploring patterns of covariation in the observed data using genetic networks can further unravel complex biological processes. A network is represented as a graph whose vertices are associated with entities of interest (e.g., disease status, genes, single nucleotide polymorphisms, and body measurements) and whose edges link two vertices if they are considered associated in a certain way. Since the number of available samples is small, the networks must be sparse; most pairs of entities should be considered unrelated and the corresponding edges removed. Sparse networks arise quite often in biology. For example, only a small number of regulatory factors are expected to influence the evolution of any given process. There are numerous ways to build genetic networks from data. Each network should be interpreted based on the procedure employed to construct it. Networks are built from the same data using several statistical approaches that complement each other as they reveal various aspects of the available data. Association networks have edges given by genes whose expression levels exhibit high absolute associations as quantified by Kendall’s τ, Spearman’s ρ, or Pearson’s correlation coefficient. Genes that are linked directly in association networks are likely to share the same biological functions (Butte, Tamayo, Slonim, Golub, & Kohane, 2000; Steuer, Kurths, Fiehn, & Weckwerth, 2003). Genes involved in the same biological pathways can be identified by shortest path analysis (Zhou, Kao, & Wong, 2002).

Another type of genetic network is determined from Gaussian graphical models (Dobra et al., 2004; Schafer & Strimmer, 2005). In this case, the edges in the network correspond with the nonzero elements of the precision matrix associated with a multivariate Gaussian distribution. Liquid association networks (Li, 2002) are constructed with respect to a phenotype of interest. Entities (e.g., genes and phenotypes) are connected if their relationship changes as a function of this phenotype. For example, two genes might exhibit strong co-expression in diseased samples, while in healthy samples their expression levels might be unrelated. As opposed to association networks, liquid association networks capture such a dynamic relationship.

In this article, we focus on the determination of genetic networks associated with fatigue and HIV status. We select the genes to include in the networks through the BMSS algorithm for logistic regressions (Dobra, 2009). Furthermore, we explore whether the edges we uncover from the data actually correspond to true biological processes.

Material and Method

Patient Groups and Blood Draws

As part of a larger National Institutes of Health (NIH) intramural natural history study, “Assessing the Relationship Between Fatigue and Mitochondrial Toxicity in Patients with HIV/AIDS” (05-CC-0127), with a focus on HIV-related fatigue (HRF) and mitochondrial toxicity, we enrolled 46 HIV-positive patients on nucleoside reverse transcriptase inhibitor (NRTI)-containing and protease-inhibitor sparing antiretroviral (ART) regimens and 15 healthy controls. We described the methodologies that we utilized in this study more completely in Part I of this article, “Research Findings.” The results of the complete study were just recently published (Morse et al., in press).

Patients completed self-report evaluations for fatigue, quality of life, and depression. We took muscle and fat biopsies and collected peripheral blood mononuclear cells (PBMCs) via aphaeresis. We evaluated HRF using the revised 26-item Piper Fatigue Scale, which has a range of scores of 0–10, with 0–3 considered no fatigue, 4–7 moderate fatigue, and 8–10 severe fatigue (Piper et al., 1998). For the purposes of this study, we combined patients whose scores indicated moderate or severe fatigue together into the high-fatigue group. In this substudy, we compared three categories of CD14⁺ cell samples: cells from HIV patients with high fatigue (n = 5), from HIV patients with low fatigue (n = 5) and from healthy controls (n = 5). For details on gender, age, CD4 count, viral load, medication regimen, drug use, and hepatitis coinfection status, please see Table 1 in Part I. There were no significant differences among the groups in these characteristics.

CD14⁺ Cell Isolation and RNA Extraction

CD14⁺ cells were isolated from total PBMCs after aphaeresis with a negative CD14⁺ isolation procedure to prevent activation using the Invitrogen Dynabead Monocyte Negative Isolation kit (Invitrogen, Carlsbad, CA) followed by CD14⁺ positive cell sorting, according to the manufacturer’s instructions. In addition, the CD16 monocyte subfraction, an activated subset of monocytes (Alexaki, Liu, & Wigdahl, 2008; Altenburg, Jin, Alkhatib, & Alkhatib, 2010; Crowe, Zhu, & Muller, 2003; Ziegler-Heitbrock, 2007), were selected against using anti-CD16 capture beads. Samples were sorted for CD3⁺/CD14⁺ monocytes using a B-D FACSAria system (Becton-Dickinson, Franklin Lakes, NJ) according to the manufacturer’s protocols. Cells were transferred to a QIASh-redder MiniSpin Column (Qiagen, Valencia, CA) to sheer DNA, then spun, and cell extracts were frozen and stored at −70 °C until RNA extraction. RNA was extracted as previously described (Voss et al., 2008).

Microarray Protocol, Data Processing, and Gene Association Network Determinations

We employed a custom Affymetrix (Santa Clara, CA) microarray design, FATMITO1a520158F, containing 4,712 unique probes for mitochondria-related genes in these experiments (Voss et al., 2008). We described the target synthesis protocol, hybridization, and data extraction previously (Voss et al., 2008). We submitted microarray data to the Gene Expression Omnibus (GEO; http://www.ncbi.nlm.nih.gov/geo/), where they can be found under the accession number GSE18468. We followed a microarray data analysis approach, as previously described (Dobra, 2009).

Bayesian Framework for Genetic Networks

We identified candidate genes related to a binary response variable Y (e.g., HIV status or fatigue status) by following the Bayesian inference methods described in Dobra (2009). Briefly, we assumed that there were p candidate genes X₁, … X_p. We let D be the n × (p + 1) data matrix, where the rows corresponded with samples, the ith column corresponded with variable X_i, and the last column corresponded with variable Y. We denote with [Y|X_A] the logistic regression model

$$\text{log}\mathit{\text{it}}(P(Y=1|X_{\mathrm{A}}=x_{\mathrm{A}}))={\mathrm{\beta }}_0+{\displaystyle \sum _{i\in \mathrm{A}}}{\mathrm{\beta }}_i{x}_i,$$

where A is a subset of {1,2, …, p}. A full Bayesian specification of the logistic regression model [Y|X_A] was obtained by assuming that the regression coefficients follow independent N(0,1) priors, which lead to the marginal likelihood p(D|[Y|X_A]) that is numerically computed through a Laplace approximation (see appendix A in Dobra, 2009). We assumed that all the possible logistic regression models were a priori equally likely; hence the posterior probability of [Y|X_A] was proportional with its marginal likelihood, that is, P([Y|X_A]|D) ∝ P(D|[Y|X_A]).

We made use of the BMSS algorithm to identify high posterior probability logistic regressions. Our candidate genes were those genes that were involved in the top 1,000 logistic regressions identified by BMSS. These regressions could be further combined in a classifier for Y. Each regression [Y|X_A] received a weight proportional with its posterior probability p([Y|X_A]|D). The classifier was obtained by taking the weighted average of the top 1,000 logistic regressions. This technique is called Bayesian model averaging (BMA) and is often used in the literature to build high performance predictive systems (including, for example, weather forecasting tools—see http://probcast.washington.edu/). BMA (Kass & Raftery, 1995) works especially well in the context of genome-wide studies because it avoids picking a single model from the huge pool of candidate regressions. Due to the small sample size, there is not enough information to favor any one given model with respect to the other. Instead, model uncertainty is taken into account by considering a large number of top models. Any subsequent statistical inference (e.g., variable selection or prediction) is performed based on these top models.

BMSS can be further employed to build Bayesian dependency networks (Heckerman, Chickering, Meek, Rounthwaite, & Kadie, 2000). These are joint distributions specified by a collection of regressions of each random variable given the rest. The set of regressions associated with each variable is determined independently of the other collections by an application of BMSS. Once a dependency network has been identified, one can draw random samples from it using an ordered Gibbs sampling algorithm (Dobra, 2009) that sequentially samples from each conditional distribution as follows: (i) sample a regression for the corresponding collection of regressions, (ii) sample from the posterior distribution of parameters of this regression, and (iii) sample a data point from the fully identified regression equation.

Genetic networks can be efficiently estimated based on a large number of samples (>10,000) from a dependency network. Because the conditional distribution of each variable given the rest is identified by a weighted average of the top regressions, the resulting genetic networks are much sparser than the networks that would be constructed by estimating associations directly from the observed data. Most pairwise dependencies are reduced to 0 when the top regressions are determined by BMSS; hence, only the strongest associations are represented through edges. Furthermore, the estimation of associations from data sampled from dependency networks significantly decreases the inherent correlations between the corresponding test statistics; hence, multiple comparison issues (Efron, 2007) are a lot less serious and the use of false discovery rate techniques are no longer required.

Results

HIV Dependent Genes

We first analyzed the microarray data to identify mitochondrial dysfunction genes associated with HIV. In this analysis there were 10 HIV patient samples and 5 HIV-negative controls. We preprocessed the 15 microarray hybridization CEL files (i.e., background corrected and normalized) using GC Robust Multi-array Average. After the removal of 112 control probes included on the Affymetrix custom chip, the resulting data set comprised 4712 probes with 10 HIV cases and 5 controls.

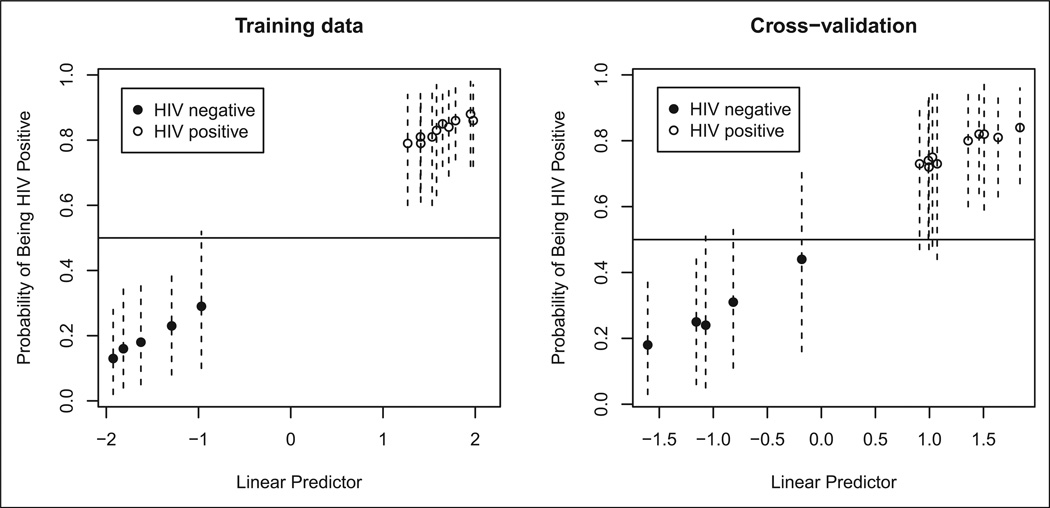
A total of 33 genes were present in the top 1000 highest posterior logistic regressions corresponding with the binary outcome HIV status (see Part I of this article, Table 2). BMA involving these 1,000 logistic regressions led to a classifier that correctly predicted HIV status for all 15 samples. These excellent prediction results held when we performed leave-one-out cross-validation. We show the prediction results in Figure 1, where we coded HIV positive with open circles and HIV negative with solid circles.

Figure 1.

Prediction results for HIV status. The vertical lines are 95% confidence intervals.

We constructed genetic networks that involve the 33 candidate genes and HIV status. The association network involved 286 edges associated with variables whose pairwise Kendall’s τ values were different from 0 at a false discovery rate of 1%. Since highly connected genes (hubs) were more likely to play key roles in the underlying biological processes, we expressed the topology of the resulting association network by the degree of each vertex (i.e., the number of direct neighbors). We sorted the genes in decreasing order with respect to their degrees and to their posterior inclusion probabilities regarding HIV status.

The most relevant genes had larger ranks on both scales: ADCY2, CASC4, YAF2, GOT1, and HDAC6. The 22 genes that were direct neighbors of HIV status in this association network together with those having strong adjacent network association between their expression levels and HIV status (having false discovery rate of 1%) and their Kendall’s τ coefficients are shown in Table 2 (Part I). Positive Kendall’s τ values indicate a positive association, while negative values indicate a negative association. Positive association increases as we go from non-HIV- to HIV-infected expression levels. Negative associations indicate the opposite. Two of these 33 HIV associative gene probes were subsequently identified in the most recent Unigene sequence database (http://www.ncbi.nlm.nih.gov/sites/entrez?db=unigene) to represent the same gene, cofilin 2; 224352_s_at and 224663_s_at. Therefore, we identified 32 unique genes in this analysis of HIV association.

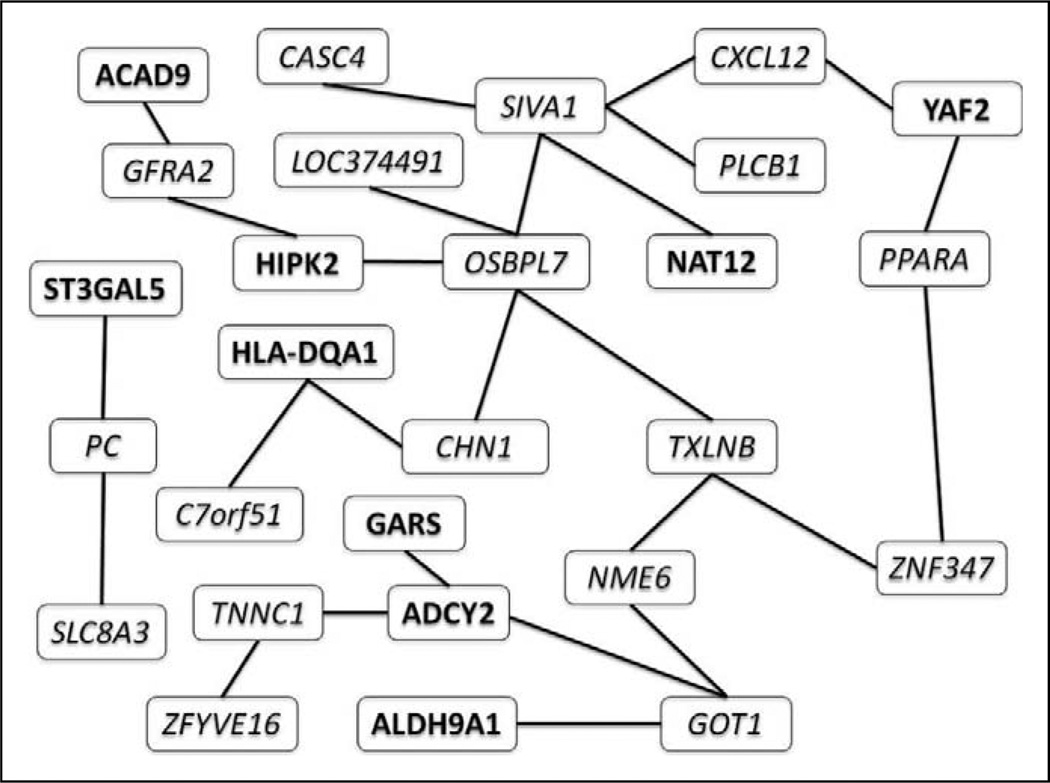
Figure 2 shows the liquid association network corresponding with HIV status. This graph links pairs of genes whose association, as measured by Kendall’s τ, changes with respect to HIV status. The significance level for the corresponding permutation tests was .05. The genes making up the liquid association set for HIV are listed in Table 3 (Part I). The genes that did not have any direct neighbors in this network (i.e., the singletons) are not shown. The direct neighbors of ADCY2 are GARS, TNNC1, and GOT. The hub of this network is OSBPL7, with five direct neighbors. OSBPL7 was ranked high with respect to its degree in the association network.

Figure 2.

Liquid association network for HIV status. Each edge corresponds with a pair of genes whose association differs in HIV-negative and HIV-positive samples. We used italics for upregulated genes and bold for downregulated genes.

Fatigue Dependent Genes

We preprocessed the 10 fatigue CEL files as for HIV analysis (i.e., background corrected and normalized) using GC Robust Multi-array Average (Z. Wu, Irizarry, Gentleman, Murillo, & Spencer, 2004; Z. Wu & Irizarry, 2005). After the removal of 112 control probes included on the Affymetrix custom chip, the resulting data set comprised 4,712 probes with 5 low-fatigue (0–3 fatigue score) samples and 5 high-fatigue (4–10 fatigue score) samples.

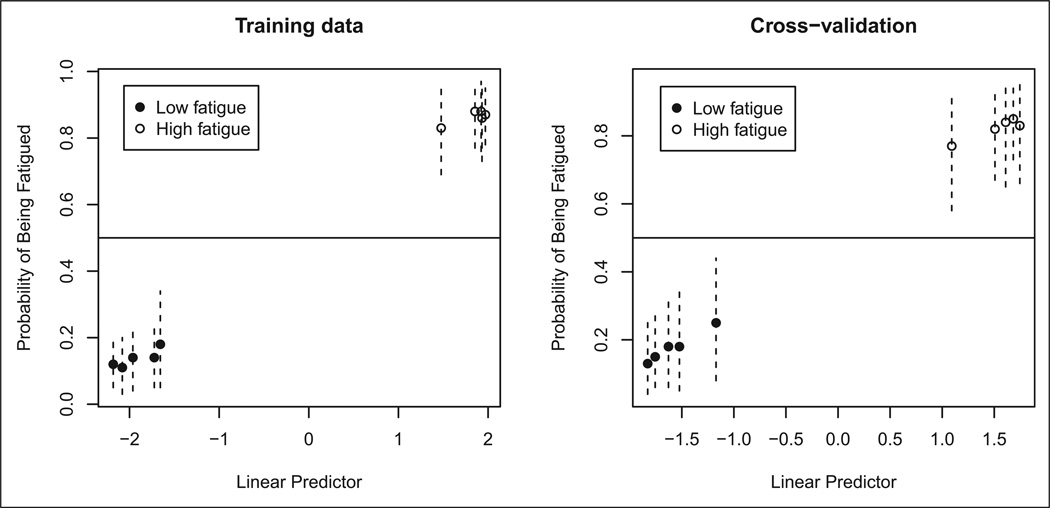
A total of 33 genes were present in the top 1,000 highest posterior logistic regressions corresponding with the binary outcome fatigue status (see Table 3 in Part I of this article). We note that the same number of genes was present in the top logistic regressions corresponding with HIV status. This coincidence might be a consequence of the small number of samples available in our study. BMA involving these 1,000 logistic regressions led to a classifier that correctly predicted fatigue status for all 10 samples. These excellent prediction results held when we performed leave-one-out cross-validation, as shown in Figure 3.

Figure 3.

Prediction results for fatigue status. The vertical lines are 95% confidence intervals for prediction probabilities.

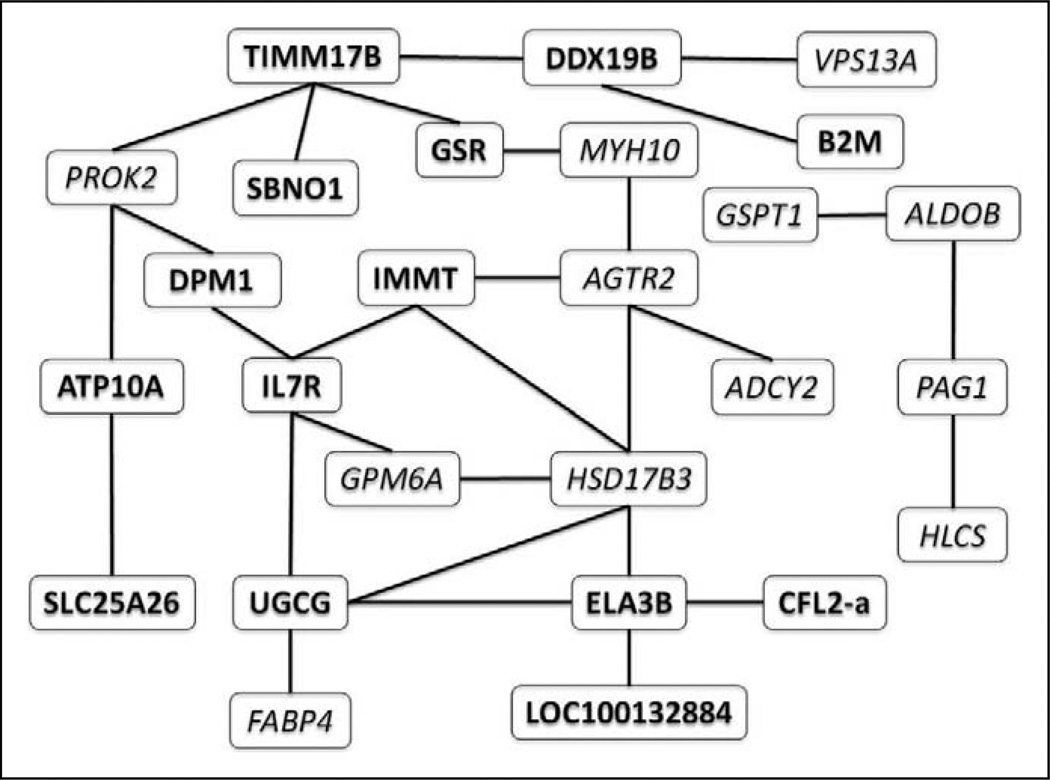
The association network involving the 33 candidate genes and fatigue status had 505 edges that corresponded with pairwise Kendall’s τ values that differed from 0 at a false discovery rate of 1%. We ranked the 33 candidate genes in decreasing order with respect to their degrees in the resulting association network. We also ranked the genes in decreasing order with respect to the posterior inclusion probabilities. The most relevant genes ranked high in both orderings and comprised of two probe sets for CFL2, SULT2B1, and PAG1. Unigene had originally categorized one of the two probe sets for CFL2 as a separate gene and thus we had unintentionally placed CFL2 twice on the array. Both probe sets are located on the long untranslated 3’ terminal exon of CFL2, with the higher Kendall’s τ probe set being close to the poly A tail and thus having a higher rate of reverse transcription into target cDNA. Both targets were associated with HIV status in this analysis. Therefore, we identified 32 unique genes in the fatigue association set. Figure 4 shows the liquid association network corresponding with fatigue status. This graph links pairs of genes whose association as measured by Kendall’s τ changes as fatigue status changes. The significance level for the corresponding permutation tests was .05. ADCY2 has only one neighbor in the liquid association network, namely, AGTR2. However, AGTR2 is a neighbor of HSD17B3, the hub of this network.

Figure 4.

Liquid association network for fatigue status. Each edge corresponds with a pair of genes whose association differs in low fatigued vs. high fatigued patient samples. Italic type indicates upregulated genes; bold type indicates downregulated genes.

Discussion

We showed that Bayesian techniques for variable selection and network determination are a powerful tool for uncovering relevant biological pathways of interest. The edges in our genetic networks no longer represent linear associations; hence, the underlying nature of gene expression data is captured in a more efficient manner in the joint distributions specified by dependency networks. The framework from Dobra (2009) efficiently handles genome-wide studies involving any combination of continuous or discrete factors. The networks are sparse due to the regression selection process behind the BMSS algorithm. BMA properly accounts for the small number of samples.

The methodology described in Dobra (2009) expresses the conditional distribution of each variable, given the rest as a finite mixture of linear regressions. Although extremely flexible, this framework does not reflect the intensity-dependent and nonlinear nature of gene expression data. Furthermore, direct interactions between factors are not allowed under the current model specification. More suitable formulations should allow the inclusion of nonlinear components as well as of interaction terms. Another problem relates to the existence of a joint distribution associated with a dependency network identified by BMSS. Under a general positivity condition, a dependency network uniquely determines a joint distribution up to a normalizing constant (Besag, 1974). This condition is at least loosely satisfied in our approach, although it cannot be guaranteed to always hold. An excellent starting point is the work of Hobert and Casella (1998), in which they study the case when a dependency network determines an improper joint distribution.

Until now there have been few tools to quantify fatigue and no molecular biomarkers of HRF. Our analysis of gene expression in this study allowed us to generate multiple hypotheses for future studies of HIV fatigue etiology. First, SULT2B1, a key enzyme in androgen biosynthesis, is the gene most associated with fatigue status (Croxson et al., 1989; Honour, Schneider, & Miller, 1995). HIV disease is associated with gonadal and adrenal androgen deficiencies, and fatigue in men with HRF is improved with testosterone therapy (Rabkin, Wagner, McElhiney, Rabkin, & Lin, 2004). Our data are consistent with the literature linking androgen levels to HRF and newly implicate SULT2B1 and its role in androgen generation as a factor in hormonal dysregulation in HRF disease. Second, the fatigue association of the actin cytoskeleton polymerization regulators CFL2 and the f-actin binding scaffolding protein PAG1 indicates that cell motility and cytoskeletal structural rigidity, factors controlled by f-actin stability, are involved in the fatigue response in CD14⁺ cells (Itoh et al., 2002; Svec, 2008; Van Troys et al., 2008; Y. Wu et al., 2008). Since f-actin also stabilizes signaling complexes contained in anchored lipid rafts, these complexes can also have effects on the regulation of cell responses to agonist stimulation. Our data suggest that changes in cellular behavior controlled by the state of the actin cytoskeletal network may play a role in HRF, possibly through unknown mechanisms in CD14⁺ cell activity. Finally, PROK2 is a GPCR agonist that controls torpor (state of mental or physical inactivity or insensibility), attenuates circadian rhythms and regulates normal sleep patterns, and potently promotes neutrophil chemotaxis (Gottlieb, O’Connor, & Wilk, 2007; Jethwa et al., 2008; Li et al., 2006; Monnier & Samson, 2008; Zhong, Qu, Tan, Meng, & Ferrara, 2009). This protein was negatively associated with fatigue, indicating that sleep regulation is disturbed in HRF patients and consistent with the literature that sleep patterns are disturbed in HIV disease and HRF. This association also indicates a hormonal defect in HRF. A general hypothesis drawn from our identification of fatigue biomarkers could be that a subset of the genes identified in this study could also be biomarkers of fatigue across many diseases with a chronic fatigue component. Future studies comparing other diseases with associated fatigue will allow us to test this hypothesis.

Conclusion

For this pilot study, we took advantage of rare CD14⁺ cell samples collected by aphaeresis in a natural history study of mitochondrial dysfunction and HRF with the resources of the NIH intramural program and the most meticulous cell sorting techniques of the National Cancer Institute (NCI). The availability of a newly developed mitochondrial gene expression chip (huMITOchip) allowed us to investigate the gene expression patterns of CD14⁺ cells of fatigued and non-fatigued HIV patients compared to healthy controls. Newly developed statistical methods enabled us to analyze these results in a way that regular microarray analyses (false discovery rate and t statistic–based methods) would have not allowed. These new tools and methods are innovations that generated three major new hypotheses to further study HRF in much greater detail and could be of great value for other studies in the future.