Abstract
With increasing urbanization vector-borne diseases are quickly developing in cities, and urban control strategies are needed. If streets are shown to be barriers to disease vectors, city blocks could be used as a convenient and relevant spatial unit of study and control. Unfortunately, existing spatial analysis tools do not allow for assessment of the impact of an urban grid on the presence of disease agents. Here, we first propose a method to test for the significance of the impact of streets on vector infestation based on a decomposition of Moran's spatial autocorrelation index; and second, develop a Gaussian Field Latent Class model to finely describe the effect of streets while controlling for cofactors and imperfect detection of vectors. We apply these methods to cross-sectional data of infestation by the Chagas disease vector Triatoma infestans in the city of Arequipa, Peru. Our Moran's decomposition test reveals that the distribution of T. infestans in this urban environment is significantly constrained by streets (p<0.05). With the Gaussian Field Latent Class model we confirm that streets provide a barrier against infestation and further show that greater than 90% of the spatial component of the probability of vector presence is explained by the correlation among houses within city blocks. The city block is thus likely to be an appropriate spatial unit to describe and control T. infestans in an urban context. Characteristics of the urban grid can influence the spatial dynamics of vector borne disease and should be considered when designing public health policies.
Author Summary
Chagas disease is a major parasitic disease in Latin America. It is transmitted by Triatoma infestans an insect common in Arequipa, the second largest city in Peru. We propose a method to demonstrate that streets strongly affect the spatial distribution of infestation by this insect in Arequipa. The effect of streets may be due to several external factors: 1) houses on different sides of a street may not be equally welcoming to the insects due to the presence of certain materials or animals, 2) people inspecting houses on the two sides of a street may not be equally efficient, and, 3) insects may disperse to neighboring houses but rarely reach houses across a street. We take these aspects into account in a second analysis and confirm that streets are important barriers to these insects. Our finding should allow for improvements in the control of insects that transmit Chagas disease in cities. More generally, our methods can be applied to other pests and disease vectors to better understand and control epidemics in cities.
Introduction
In the context of increasing urbanization worldwide [1]–[4], vector-borne diseases, a significant burden to human and animal populations [5], are quickly emerging in cities [6] and require the adaptation of control strategies to densely populated and highly interconnected environments. Notable examples include Dengue [7]–[9], Malaria [10]–[12] and Chagas disease [13]–[15].
Prevention of vector-borne diseases relies heavily on vector control [8], [16], [17]. Given the substantial resources needed to control vector populations on the city scale, well-managed control strategies based on understanding of vector spatial dynamics can potentially increase cost efficiency [18]–[20]. A central feature of cities is the grid of streets which fractures the environment. Such disjoint landscapes can affect patterns of occurrence and transmission of diseases, both communicable and non-communicable. Assessing the impact of the urban grid on the spatial distribution of diseases could lead to more effective design of surveillance and control programs in cities.
Arequipa, Peru, a city of nearly 1 million inhabitants, is currently experiencing an epidemic of infestation by Triatoma infestans [21], [22], the principal vector of Trypanosoma cruzi [23], the etiological agent of Chagas disease [24]. The spread of T. infestans in Arequipa is accompanied by micro-epidemics of T. cruzi transmission to humans [25], [26]. Control of the vector in the city through insecticide application in households is challenging [20], [27]. Previous work on T. infestans and other Chagas disease vectors have used non-spatial [28], [29] and spatial modeling techniques [19], [30]–[33] to characterize vector population dynamics and propose improvements in control strategies. However, these studies have not considered the impact of an urban grid on vector populations.
The impact of known boundaries such as roads or rivers on epidemics or population dynamics has occasionally been assessed using spatio-temporal modeling to describe spatio-temporal presence-absence data [34]. Using only spatial data, kriging approaches integrated in well known GIS softwares may take into account the presence of known landscape features as impenetrable barriers [35] but do not assess the resistance of these barriers. In landscape genetics, the quantification of the effect of barriers is a central aim of a large and growing field [36]–[38]. These approaches benefit from the complex information present in DNA to infer the impact of barriers. Some of their results, however, depend on the assumption of migration-drift equilibrium which is typically violated in epidemics and highly dynamic human influenced landscapes [39]. In social sciences, disparities among spatially well circumscribed census tracts are commonly quantified using indices of segregation [40], but the borders between such tracts are not usually considered as barriers themselves [41].
Here we propose to quantify the impact of known boundaries by measuring their effect on spatial autocorrelation in presence-absence data. Variations of the autocorrelation over distance have been measured and presented in autocorrelograms [42], [43]. Another approach has been to parameterize kernels describing these variations, notably to produce Bayesian disease risk maps [44]–[46]. We extend both of these approaches to assess the impact of known barriers such as streets on the spatial distribution of binary data, in our case the presence of T. infestans in households of the city of Arequipa. First, we provide a global assessment of the effect of streets on vector infestation using a decomposition of the commonly used Moran's I statistic and corresponding autocorrelograms [47], [48]. Second, we capture the effect of streets on a finer scale and control for cofactors and imperfect detection of vectors by designing a Gaussian Field Latent Class model. Taking into account streets, the kernel of this model describes the spatial correlation through precision matrices [49], [50] in the framework of a spatial Bayesian Generalized Linear Model [51]. Finally, we discuss how surveillance and control of Chagas disease in cities can be better informed by taking into account the impact of streets on infestation.
Materials and Methods
Entomological Data Collection and Mapping
We conducted our study in Paucarpata, the largest district in the city of Arequipa, Peru. The Ministry of Health of Arequipa applied insecticide to 13,917 households in Paucarpata between November 2006 and April 2009. During the insecticide application campaign, household-level data on the presence or absence of T. infestans and relevant risk factors for vector infestation were collected. Risk factors included a description of construction materials in each house and the presence of guinea pigs, dogs, and other domestic animals.
We mapped the position of all households and the delimitation of city blocks in the district comparing satellite imagery in Google Earth™ [52] to field maps drawn by the personnel of the Ministry of Health. Households were then snapped to their city block according to their respective coordinates.
Statistical Analysis
Application of Moran's I to an urban grid
We first assessed the impact of streets on the global spatial autocorrelation of vector infestation as measured by the Moran index (I) [47]. This index reads:
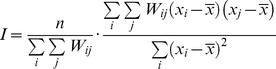 |
where  corresponds to the number of households,
corresponds to the number of households, 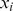 indicates the presence (1) or absence (0) of insects in household
indicates the presence (1) or absence (0) of insects in household  ;
; 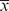 is the mean of the observations over all households, and
is the mean of the observations over all households, and 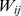 represents the weights describing the spatial relationship between households
represents the weights describing the spatial relationship between households  and
and 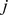 .
. 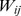 is set to 1 if the distance between point
is set to 1 if the distance between point  and point
and point 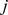 falls within a given range; otherwise, it is set to 0. We calculated autocorrelograms [43], [53] for the occurrence of T. infestans in Paucarpata for successive 15m-wide distance ranges.
falls within a given range; otherwise, it is set to 0. We calculated autocorrelograms [43], [53] for the occurrence of T. infestans in Paucarpata for successive 15m-wide distance ranges.
To determine if streets affect the spatial autocorrelation of infestation, we decomposed the autocorrelation into a within city-block component and an across city-blocks component. We then calculated separate autocorrelograms for pairs of households on the same city block (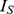 ) and for pairs of households on different city blocks (
) and for pairs of households on different city blocks (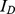 ).
).
We then assessed the significance of the difference  using the following random labeling permutation test [54]. For a given distance range, each household has
using the following random labeling permutation test [54]. For a given distance range, each household has 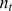 total neighbors, among which
total neighbors, among which 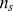 are on the same city block. For each permutation we randomly assigned
are on the same city block. For each permutation we randomly assigned 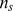 of the
of the 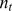 neighbors as occupying the same city block as the index house, and the remainder of neighbors as occupying a different city block. We then calculated the corresponding
neighbors as occupying the same city block as the index house, and the remainder of neighbors as occupying a different city block. We then calculated the corresponding 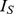 and
and 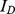 . We repeated this process for 1000 permutations, creating a histogram of the values of
. We repeated this process for 1000 permutations, creating a histogram of the values of  . We determined the p-value of our observed value of
. We determined the p-value of our observed value of  by referencing this histogram. We applied this decomposition of Moran's I to all the households participating in the vector control campaign.
by referencing this histogram. We applied this decomposition of Moran's I to all the households participating in the vector control campaign.
The decomposition of Moran's Index offers a fast, simple way to obtain an estimate of how streets impact the autocorrelation of observations. However, several factors could confound or obscure this estimate. First, well-known risk factors for T. infestans presence, such as construction materials or presence of domestic animals [27], may be more common on some city blocks than others. Such an aggregation of cofactors could contribute to the structure of vector populations. Multivariate methods are needed to tease apart the effect of such cofactors from that of city streets. Second, due to the vast areas surveyed, multiple inspectors are employed to search houses for vectors. These inspectors may vary in their ability to detect insects. If some city blocks are examined by more sensitive inspectors and others by less sensitive ones, the observed spatial distribution of infestation may be structured, even if the full, unobserved distribution of infestation is not.
Beyond these two considerations, there is a third, less obvious limitation to the Moran's I. As a pair-wise statistic, Moran's I, as well as its derivatives described here, measures indirect and direct correlation together: measured correlation could result either from a direct correlation between households or an indirect correlation mediated by the in-between households that are strongly correlated on a small distance scale. The effect of streets can be important simply because streets create a gap in a chain of small distance scale autocorrelations between households (hereafter the “gap effect”). In contrast, streets may, above and beyond the gap effect, serve as a barrier to vector migration (hereafter the “barrier effect”). A spatial field-based measure of autocorrelation accounts for the autocorrelation of neighbors at all distances simultaneously. Such an approach can then detect a barrier effect linked to the presence of streets and not only to the uneven distribution of households induced by streets.
Application of a Gaussian field model to an urban grid
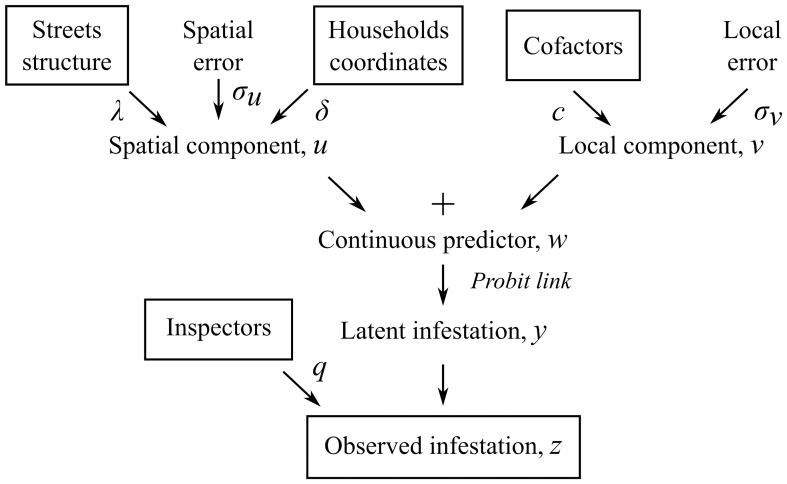
We built a Bayesian generalized linear model describing household infestation status as a discrete manifestation of a continuous predictor of infestation. The predictor of infestation includes a spatial field component [51], accounting for the street network, and a non-spatial component, integrating local cofactors. Additionally, household infestation status is considered as a latent class [55], [56] to account for the imperfect sensitivity of the inspectors surveying the households. We refer to our model, shown in Fig. 1, as a Gaussian Field Latent Class model. Hereafter upper case characters indicate matrices, lower case characters vectors, and Greek letters scalars.
Figure 1. General structure of the Gaussian Field Latent Class model.
Working backward, we consider the infestation data  to be the result of a latent infestation status
to be the result of a latent infestation status 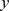 , observed by imperfect inspectors of sensitivity
, observed by imperfect inspectors of sensitivity 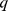 . The true infestation
. The true infestation 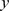 is a binary manifestation of an underlying continuous infestation predictor
is a binary manifestation of an underlying continuous infestation predictor 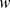 . Cofactors and a local error term,
. Cofactors and a local error term,  , form the local component. The spatial component
, form the local component. The spatial component  is modeled as a Gaussian field. The fit parameters,
is modeled as a Gaussian field. The fit parameters,  and
and 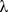 , respectively tune how distances between neighbors and the streets define the spatial dependency between households in the spatial component.
, respectively tune how distances between neighbors and the streets define the spatial dependency between households in the spatial component.
Spatial component. The spatial component u of the infestation predictor 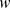 is an auto-regressive Gaussian Markov random field described through its precision matrix [49], [50]: for any household i, the mean of the spatial component,
is an auto-regressive Gaussian Markov random field described through its precision matrix [49], [50]: for any household i, the mean of the spatial component, 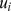 , is a weighted mean of the spatial components of its neighbors, weighted by the distance to them. Normal variations around the spatial mean are allowed, their variance increasing with the isolation of the household (mathematical details on the Gaussian Markov random field are provided in Section 1 in Text S1).
, is a weighted mean of the spatial components of its neighbors, weighted by the distance to them. Normal variations around the spatial mean are allowed, their variance increasing with the isolation of the household (mathematical details on the Gaussian Markov random field are provided in Section 1 in Text S1).
We introduce the effect of streets in a similar way as in the decomposition of the Moran's I – by distinguishing between neighbors within a city block and proximate households separated by streets. The spatial weight 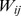 between the households
between the households  and
and 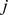 is:
is:
where 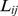 takes the value
takes the value 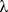 if
if  and
and 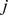 are on different city blocks and the value 1 if they are on the same block;
are on different city blocks and the value 1 if they are on the same block; 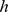 is a spatial kernel of shape factor
is a spatial kernel of shape factor  applied to the distance
applied to the distance 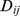 between the households and
between the households and 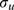 is a scale parameter for the spatial error.
is a scale parameter for the spatial error.
We consider four one-parameter kernels describing a wide range of shapes (Table 1). For computational reasons, when the distance 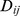 is above a distance threshold
is above a distance threshold 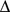 (set at 100 m) the households are considered to have no direct influence on each other and thus their weights are set to 0. A sensitivity analysis (Section 2 in Text S2) shows that the choice of 100 m as a threshold provides in our case a robust estimate of the parameters of interest.
(set at 100 m) the households are considered to have no direct influence on each other and thus their weights are set to 0. A sensitivity analysis (Section 2 in Text S2) shows that the choice of 100 m as a threshold provides in our case a robust estimate of the parameters of interest.
Table 1. Spatial kernels and corresponding fitted parameters.
| Name | Equation, 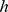
|
Shape | DIC | Shape factora, 
|
Streets factor, 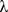
|
Same Block Indexb |
| Exponential |
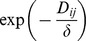
|
Sharp top, thin tail | 2526 | 9.00 (7.04–11.8) | 0.30*** (0.12–0.61) | 94.0% (89.8–96.9) |
| Gaussian |
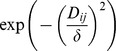
|
Flat top, thin tail | 2553 | 17.3 (14.4–21.2) | 0.52  (0.16–1.24) (0.16–1.24) |
93.7% (88.1–97.3) |
| Cauchy |
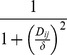
|
Flat top, fat tail | 2553 | 8.25 (5.30–13.0) | 0.08*** (0.04–0.14) | 94.7% (91.4–97.3) |
| Geometric |
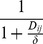
|
Sharp top, fat tail | 2609 | 7.64 (2.08–26.3) | 0.03*** (0.01–0.05) | 95.1% (91.6–98.2) |
The shape factor  is indicated in meters.
is indicated in meters.
Same Block Index: Percent of the spatial component of infestation explained by same city block neighbors (see Section 2 in Text S1). In parentheses are the 95% Credible Intervals (CrI) according to the MCMC sampling. The probability of having no barrier effect of streets is indicated with the values of 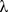 :
: 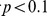 ;
;
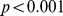 .
.
To assess the relevance of the city-block as a spatial unit of infestation we calculate the “Same Block Index” which we define as the mean percentage of the spatial component of infestation explained by neighbors on the same city block (Section 2 in Text S1).
Local component. We include in a local component  the effects of known cofactors and a local error term
the effects of known cofactors and a local error term  :
:
with 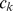 the risk coefficient for the presence of the cofactor
the risk coefficient for the presence of the cofactor 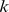 ,
, 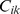 the indicator of presence of the cofactor and
the indicator of presence of the cofactor and  with
with 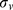 the scaling parameter of the local error (see Section 3 in Text S1).
the scaling parameter of the local error (see Section 3 in Text S1).
Link function. We relate our outcome data, the observed infestation,  , to the continuous infestation predictor
, to the continuous infestation predictor 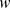 , in two steps. A probit function links the infestation predictor
, in two steps. A probit function links the infestation predictor 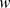 to the latent infestation status
to the latent infestation status 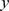 :
: 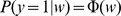 where
where 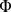 is the Cumulative Distribution Function of the standard normal distribution. The latent infestation is then imperfectly revealed by the inspection: an infested household is observed as infested by an inspector
is the Cumulative Distribution Function of the standard normal distribution. The latent infestation is then imperfectly revealed by the inspection: an infested household is observed as infested by an inspector 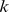 with a probability
with a probability 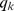 : the sensitivity of the inspector.
: the sensitivity of the inspector.
When infestation data are not available (non-inspected houses), the sensitivity is set to 0 (see Section 4 in Text S1 for more details on the implementation and Section 2 in Text S2 for an analysis of the sensitivity of the results to this modeling choice).
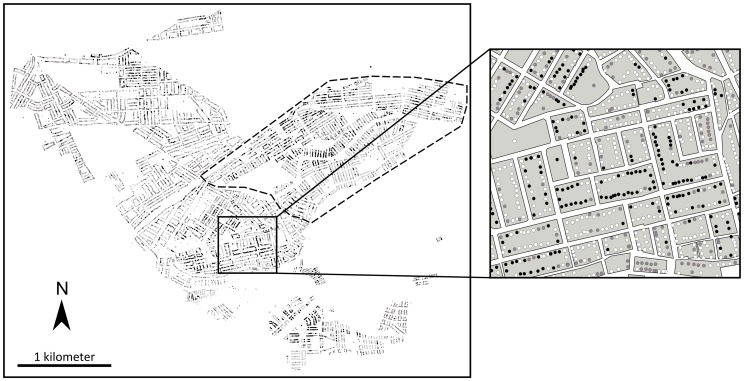
Fitting and validation. We fit the Gaussian Field Latent Class model on a fraction of the map consisting of all of the households inspected between September and December 2007 (Fig. 2). We used the remaining households as a validation dataset. For all priors, we use flat or weakly informative priors [57]. Further mathematical details on the implementation of the sampling are given in Section 5 in Text S1.
Figure 2. Spatial distribution of Triatoma infestans presence in households of Paucarpata, Arequipa, Peru.
Map of the study area. Black indicates infested households, white non-infested households, and grey non-inspected households. The area encircled by dashes was used to fit the Gaussian Field Latent Class model; the remaining area was used as a validation dataset. The close-up shows the urban grid underneath and the aggregation of vectors within city blocks.
We used the validation dataset to determine how well our parameterized model predicted the presence of vectors in unobserved households. To do so, we randomly selected 5% of the houses in the validation set and removed them. We set the sensitivity of inspectors and the spatial parameters to their estimated means, remove the cofactors from the model and refit the spatial component, predicting the observation of infestation in the withheld households. We repeated the process 20 times, without replacement, so that all houses had been selected for prediction exactly once. We then evaluated the predictions using the McFadden index [58].
As a second check, we verified that the Gaussian Field Latent Class model properly reproduced the global autocorrelation of the observed infestation by generating 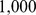 vector infestation maps across the validation dataset and repeating the Moran's I analysis on each.
vector infestation maps across the validation dataset and repeating the Moran's I analysis on each.
All analyses were performed in R [59]; the code is available in Data S1 and updated versions are available at https://github.com/cbarbu/spatcontrol.
Results
During the vector control campaign in Paucarpata, the Ministry of Health sprayed 9,654 houses, among which 1,791 (18.5%) were infested with T. infestans (Fig. 2). Data was unavailable from an additional 4,263 (30%) households, most of which chose not to participate in the spray campaign.
Importance of streets as assessed by the decomposition of Moran's index
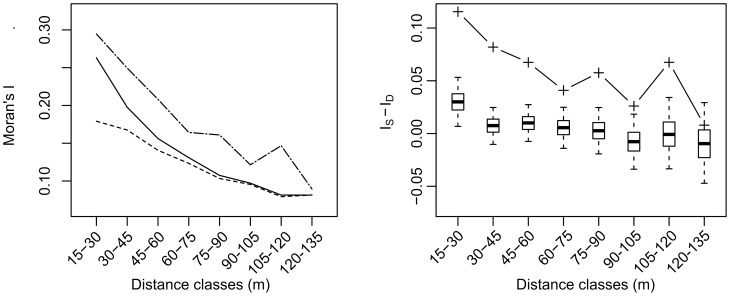
For all distance classes up to 120 m, the autocorrelation among houses within the same city block was significantly greater than that among houses separated by streets (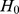 : spatial autocorrelation independent of streets,
: spatial autocorrelation independent of streets, 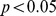 ) (Fig. 3). For the distance class above 120 m, the difference was not significant, probably due to decreased sample size of same city block neighbors. Interestingly, the autocorrelation across a street is consistently similar to the autocorrelation within a same block 30–45 m further.
) (Fig. 3). For the distance class above 120 m, the difference was not significant, probably due to decreased sample size of same city block neighbors. Interestingly, the autocorrelation across a street is consistently similar to the autocorrelation within a same block 30–45 m further.
Figure 3. Spatial autocorrelation of Triatoma infestans presence in Paucarpata, Arequipa, Peru and the effects of streets.
Left: autocorrelation of the infestation status as a function of the distance. Solid line: Global Moran's index. Dot-Dashed line: Moran's Index for within blocks household pairs. Dashed line: Moran's Index for household pairs across streets. All Moran's I values are significantly different from the expected value under hypothesis of no spatial autocorrelation (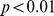 ). Right: significance of the difference between the correlation within city blocks and the correlation across streets. Box plots indicate the expected values under the null hypothesis using a permutation test. The boxes indicate the
). Right: significance of the difference between the correlation within city blocks and the correlation across streets. Box plots indicate the expected values under the null hypothesis using a permutation test. The boxes indicate the 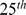 ,
, 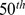 and
and 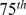 quantiles, and the whiskers depict the 95% CrI.
quantiles, and the whiskers depict the 95% CrI.
Notably the expected difference  under the null hypothesis is positive at short distances. This unintuitive result is due to the non-negligible width of the rings we used to bin our data: at short distances, houses across streets are further from each other than those on the same block, hence there is a slightly positive expectation for the difference in Moran's I. Our permutation test reproduces this effect and thereby controls for it in determining the significance of the impact of streets.
under the null hypothesis is positive at short distances. This unintuitive result is due to the non-negligible width of the rings we used to bin our data: at short distances, houses across streets are further from each other than those on the same block, hence there is a slightly positive expectation for the difference in Moran's I. Our permutation test reproduces this effect and thereby controls for it in determining the significance of the impact of streets.
Importance of the barrier effect of streets as assessed by the Gaussian field model
Controlling for the spatial distribution of cofactors and inspectors, we estimated the barrier effect of streets on infestation to induce a two to thirty fold decrease (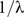 ) in the spatial weight between households for a given distance, depending on the chosen kernel (Table 1). The “Same Block Index”, quantifying the relevance of the city-block as a spatial unit of infestation, exceeded 90% and our estimate was extremely robust across all four kernels considered (Table 1).
) in the spatial weight between households for a given distance, depending on the chosen kernel (Table 1). The “Same Block Index”, quantifying the relevance of the city-block as a spatial unit of infestation, exceeded 90% and our estimate was extremely robust across all four kernels considered (Table 1).
Cofactors
As a part of the fitting process of the Gaussian Field Latent Class model, we assessed the effect of cofactors on the presence of vector infestation. We found that the presence of guinea pigs and the presence of dogs were significant risk factors for vector infestation. Conversely, we found that the presence of plastered walls inside of the house was strongly and significantly protective against infestation. The degree of the effect of these cofactors varied across the four kernels considered (detailed results in Table S1).
Interestingly, for all four kernels, the standard deviation of the continuous infestation predictor induced by the joint effect of all the cofactors and the random effect (0.44–0.54) was threefold less than the standard deviation of the estimated spatial component across households (1.64–1.93).
Inspector sensitivity
We also assessed the quality of inspectors in terms of their sensitivity—the probability that an inspector detects vectors in households that are indeed infested. The mean inspector sensitivity was 70%, with extremes at 41 and 90% (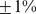 depending on the kernel). The relative ranking of inspectors by their sensitivity was largely preserved across kernels, and the estimates of inspector sensitivities did not vary greatly (
depending on the kernel). The relative ranking of inspectors by their sensitivity was largely preserved across kernels, and the estimates of inspector sensitivities did not vary greatly (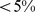 ) between models with alternative kernels.
) between models with alternative kernels.
Model validation
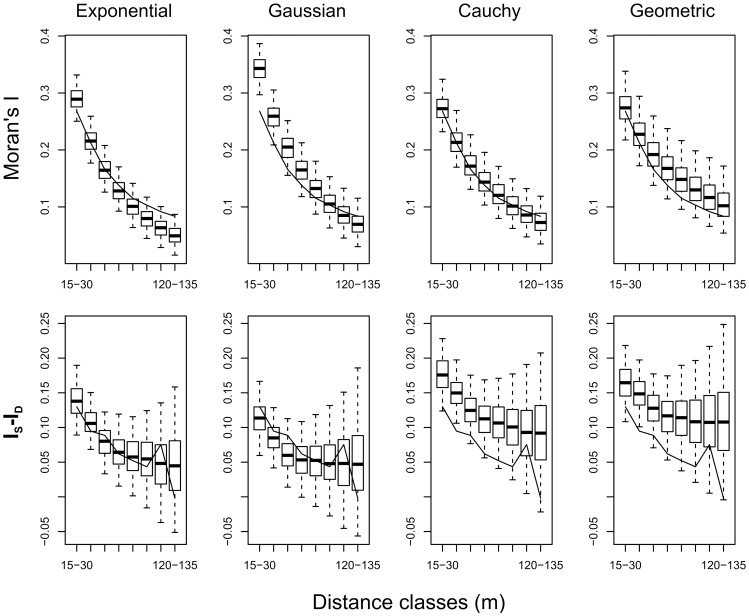
The Gaussian Field Latent Class model allowed us to make generally accurate predictions in hold-out households across the four kernels (McFadden index [58] of 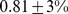 depending on the kernel). The model also reproduced the patterns observed with the Moran's I analysis across all four kernels, both in terms of classical Moran's I and of decomposed Moran's I (Fig. 4). Differences can nevertheless be observed between the kernels. In particular, the exponential kernel closely reproduced the global autocorrelation up to 75 m and the impact of streets on the spatial autocorrelation (
depending on the kernel). The model also reproduced the patterns observed with the Moran's I analysis across all four kernels, both in terms of classical Moran's I and of decomposed Moran's I (Fig. 4). Differences can nevertheless be observed between the kernels. In particular, the exponential kernel closely reproduced the global autocorrelation up to 75 m and the impact of streets on the spatial autocorrelation ( ) at all distances. The DIC values [60] obtained with the respective kernels (Table 1) also indicate particularly good performance of the exponential kernel.
) at all distances. The DIC values [60] obtained with the respective kernels (Table 1) also indicate particularly good performance of the exponential kernel.
Figure 4. Spatial autocorrelation of data simulated with the Gaussian Field Latent Class model of Triatoma infestans distribution.
The autocorrelation of infestation in the generated data is compared to the autocorrelation in observed data. Infestation data were generated on the validation map using the estimated parameters for each of the kernels: exponential (first column), Cauchy (second column), Gaussian (third column), and geometric (fourth column). We calculated the standard Moran's I (first row) and the difference  between within block and across street autocorrelation (second row) as a function of distance. The solid line indicates the values for the observed data. Box plots indicate the values obtained from generated data. The boxes indicate the
between within block and across street autocorrelation (second row) as a function of distance. The solid line indicates the values for the observed data. Box plots indicate the values obtained from generated data. The boxes indicate the 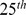 ,
, 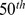 and
and 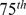 quantiles, and the whiskers depict the 95% CrI.
quantiles, and the whiskers depict the 95% CrI.
Discussion
We observed a significant effect of streets on the spatial pattern of Chagas disease vectors in Arequipa, Peru, and show that greater than 90% of the spatial component of infestation is determined by neighbors on the same city block. In addition, the difference of autocorrelation in the same block and between blocks indicate that the crossing of streets is grossly equivalent to an added distance of 30–45 m in terms of spatial autocorrelation. The limiting effect of streets was consistent across two methodological approaches: a pair-wise analysis (decomposed Moran's I) and a field based model (Gaussian Field Latent Class). The latter approach accounted for known cofactors and imperfect detection, further confirming that streets constitute an important barrier to aggregation of triatomine infestation above and beyond the uneven spatial distribution of urban households.
The underlying cause of the barrier effect of streets on T. infestans remains unclear. As we control for the spatial distribution of known cofactors, and the varying sensitivity of different inspectors surveying houses, the observed autocorrelation and its perturbation by streets are likely to be related to the movements of the insects [34], [61]. We have previously shown that the majority of T. infestans dispersal is due to early-stage nymphs [22]. These insects, the size of a small ant, may simply be unable to cross streets. In addition, it should be noted that the façades of houses are usually plastered, representing a barrier to dispersion of T. infestans, as for other insect species [62]. In contrast, the walls in the back of houses are typically not plastered, loosely stacked stones or bricks that provide hospitable habitats for vectors, and may facilitate insect movement within the block.
Several authors have commented on the need to assess the role of landscape heterogeneity in the context of epidemiological [34], [63] and ecological studies [38]. Previous work evaluating barriers to animal dispersion or disease propagation has focused on a small number of potential barriers using spatio-temporal data [64]–[66], observational and mark/recapture methods [67]–[69], or population genetics [38]. These approaches have been used to characterize the impact of roads on insect populations in rural settings and the connectivity of vertebrate populations in urban environments. Specifically, roads in open fields have been implicated as barriers for a handful of insects, including ground beetles [70]–[72], carabid beetles [67], [73], bumble bees [74], and dragonflies [75]. In urban settings, it has been shown that streets act as a barrier to hedgehog movement [68] and structure rat populations by city block [76]. Our study both extends existing approaches to these questions by providing a methodology to assess the importance of streets in the context of multi-variate models and offers evidence of the strong effect of streets on T. infestans populations.
We have shown previously that the presence of guinea pigs, the presence of dogs and the presence of other animals are risk factors for triatomine infestation and that fully cemented plaster walls are protective [27]. These findings held true in our current analysis, but the influence of cofactors was small compared to the spatial component of our model. Our previous studies were conducted in a peri-urban area where T. infestans populations were established, and exhibited no spatial clustering [27]. In the current study site, which is more urban, vector populations exhibit strong spatial clustering, suggesting that they may be expanding [61]. When populations are in a continuous dynamic of dispersal or redispersal, the effect of heterogeneous habitats is often weak compared with that of the spatial dynamics of colonization [77]. In Paucarpata, we believe vector dynamics trumped the effects of traditional cofactors, which would be more predictive of infestation in a stable system.
There are several limitations to our study. The effect of streets detected in our approach could be confounded by unmeasured cofactors strongly clustered within blocks. Two reasons nevertheless limit the probability of such a scenario. First our Gaussian Field Latent Class model explicitly accounts for the main known cofactors of infestation by Chagas vectors as identified previously [27], [52], [78], [79]. Second, taking into account these known cofactors has a limited influence on the estimated influence of streets (Section 3 in Text S2).
We were only able to obtain binary data on the presence or absence of vectors; data on vector densities could provide more information with which to assess the effect of streets. While our analysis is tailored to binary observations, it could be extended to consider discrete measurements. Our Gaussian Field Latent Class model can be applied to a wide variety of datasets without adaptation of the priors; however, care should be taken to correctly choose the order of magnitude when assigning a prior on the shape factor of the spatial autocorrelation kernel. The use of 100m as a threshold distance beyond which correlation is assumed to be null is a simplification needed to lessen computation time; we assessed the effect of this simplification and determined that our findings were not affected by it.
The flat prior used here for inspector sensitivity may shrink the posterior towards the mean of the prior, 50%. The true sensitivity is then likely greater than the estimate provided here, 70%. However, the strong estimated effect of streets is robust to variations of the prior (Section 4 in Text S2).
Further extension of the model would be necessary to determine whether wider streets pose a greater barrier to insects than narrower ones. Interestingly, if, as we hypothesize, the barrier effect is mainly due to the asymmetry in housing materials in the front and back of houses, broader streets may not pose a greater barrier to insects. Finally, further work is needed to assess if the impact of streets is affected by the seasonality of T. infestans dispersion. This would provide much needed biological insight given the importance of seasonality in triatomine dispersion [29], [33].
Our findings have implications for adapting control strategies to disease transmission dynamics. First, city blocks have been used as a practical unit of study previously [80]–[82], and here we show that they are a relevant spatial unit for the study of urban Chagas disease. Given the high cost of insecticide application, it may be much more efficient to develop targeted control strategies that are appropriate for the urban geography – taking greatest advantage of the barrier effect of streets. More specifically, current practices in such localized interventions are based on ring treatment that ignores the impact of streets. Our results suggest that control efforts may be more effective if they are expanded further within the same city-block (30–45m), before crossing a street: more of an “oval” treatment strategy, giving preference to houses on the same block when resources are limited. Second, as city blocks seem adequate for describing infestation and thus exposure of inhabitants to disease agents, they may also be valuable in modeling parasite transmission [83] and targeting screening for infection [21], [84]. Third, over the long term, it is expected that resistance to pyrethroid insecticides will be observed in urban settings as it has already been in rural areas [85]–[88]. The fragmentation of the vector population by streets may then affect the propagation of resistance alleles [89]. Finally, we expect the distribution of streets to affect the dynamics of the vector spread both in terms of speed, as different localities have different densities of streets, and direction, as city-blocks are usually twice as long as they are wide across a neighborhood.
The difficulties presented in controlling Chagas vectors in cities are similar to those of other urban disease vectors and pests such as the mosquito vectors of Dengue (Aedes aegypti) and bed bugs (Cimex lectularius). The effect of streets and other aspects of the urban environment should be considered when designing control or elimination campaigns against these organisms.
Supporting Information
Annotated code in R with data. Two datasets are given. One corresponds to the original, de-identified data (realData.R) where spatial relationships are given through the distance matrix between points. The second dataset (JitteredDataPaucarpata.csv) corresponds to a generated dataset having the same spatial characteristics as the original dataset. The given examples with this second dataset (example_structuredMI.R and example_fit_GMRF.R) provide a model for application of these methods to new datasets. Please see the README file for details. Updated code can be accessed through github: https://github.com/cbarbu/spatcontrol.
(ZIP)
Detailed parameters estimates. Estimates for each spatial kernel of all fitted parameters with their 95% credible intervals.
(PNG)
Details about the mathematical model. Detailed description of the Latent Class Gaussian Field implementation (model and sampling).
(PDF)
Sensitivity analyses. We further investigate the sensitivity of the Latent Class Gaussian Field model to the distance threshold 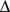 , the handling of missing data, the included cofactors, and the inspector sensitivity prior.
, the handling of missing data, the included cofactors, and the inspector sensitivity prior.
(PDF)
Acknowledgments
We thank Dr. Tony Smith, Dr. Sébastien Goubière, Dr. Vitaliano A. Cama, Ian Spalding, Dr. Chris Paciorek and Katelyn Levy for insightful comments; Katty Borrini-Mayori, Danitza Pamo, Giovanna Moscoso, Lina Mollesaca, Maria Luz Hancco, Manuel Burgos, Renzo Salazar, and the laboratory staff at UPCH-LID. We gratefully acknowledge the work of the following organizations that have organized and conducted the Chagas disease control program in Arequipa: Ministerio de Salud del Perú (MINSA), the Dirección General de Salud de las Personas (DGSP), the Estrategia Sanitaria Nacional de Prevención y Control de Enfermedades Metaxénicas y Otras Transmitidas por Vectores (ESNPCEMOTVS), the Dirección General de Salud Ambiental (DIGESA), the Gobierno Regional de Arequipa, the Gerencia Regional de Salud de Arequipa (GRSA), the Pan American Health Organization (PAHO/OPS) and the Canadian International Development Agency (CIDA). We thank the district of Paucarpata for its participation in this study.
Funding Statement
Funding for this study came from National Institutes of Health (NIH, http://www.nih.gov/) 5K01 AI079162-04 and 05, NIH 3K01AI079162-02S1 and 03S1, NIH P50 AI074285-03, and 04. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Dye C (2008) Health and urban living. Science 319: 766–769. [DOI] [PubMed] [Google Scholar]
- 2.Department of Economic and Social Affairs of the United Nations World urbanization prospects, the 2009 revision. URL http://esa.un.org/unpd/wup/index.htm.
- 3. Kennedy DP, Adolphs R (2011) Social neuroscience: Stress and the city. Nature 474: 452–453. [DOI] [PubMed] [Google Scholar]
- 4. Gong P, Liang S, Carlton E, Jiang Q, Wu J, et al. (2012) Urbanisation and health in china. The Lancet 379: 843–852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Randolph SE, Rogers DJ (2010) The arrival, establishment and spread of exotic diseases: patterns and predictions. Nature Reviews Microbiology 8: 361–371. [DOI] [PubMed] [Google Scholar]
- 6. Enserink M (2008) A mosquito goes global. Science 320: 864–866. [DOI] [PubMed] [Google Scholar]
- 7. Teixeira MG, Barreto ML, Costa MC, Ferreira LD, Vasconcelos PF, et al. (2002) Dynamics of dengue virus circulation: a silent epidemic in a complex urban area. Tropical Medicine & International Health 7: 757–762. [DOI] [PubMed] [Google Scholar]
- 8. Eisen L, Beaty BJ, Morrison AC, Scott TW (2009) Proactive vector control strategies and improved monitoring and evaluation practices for dengue prevention. Journal of medical entomology 46: 1245–1255. [DOI] [PubMed] [Google Scholar]
- 9. Sanchez L, Cortinas J, Pelaez O, Gutierrez H, Concepcion D, et al. (2010) Breteau index threshold levels indicating risk for dengue transmission in areas with low aedes infestation. Tropical Medicine & International Health 15: 173–175. [DOI] [PubMed] [Google Scholar]
- 10. Trape JF, Lefebvre-Zante E, Legros F, Ndiaye G, Bouganali H, et al. (1992) Vector density gradients and the epidemiology of urban malaria in Dakar, Senegal. The American journal of tropical medicine and hygiene 47: 181. [DOI] [PubMed] [Google Scholar]
- 11. Wang SJ, Lengeler C, Smith T, Vounatsou P, Diadie D, et al. (2005) Rapid urban malaria appraisal (ruma) I: epidemiology of urban malaria in Ouagadougou. Malaria Journal 4: 43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Matthys B, Vounatsou P, Raso G, Tschannen AB, Becket EG, et al. (2006) Urban farming and malaria risk factors in a medium-sized town in cote divoire. The American journal of tropical medicine and hygiene 75: 1223. [PubMed] [Google Scholar]
- 13. Carrasco HJ, Torrellas A, García C, Segovia M, Feliciangeli M (2005) Risk of Trypanosoma cruzi I (kinetoplastida: Trypanosomatidae) transmission by Panstrongylus geniculatus (hemiptera: Reduviidae) in Caracas (metropolitan district) and neighboring states, Venezuela. International Journal for Parasitology 35: 1379–1384. [DOI] [PubMed] [Google Scholar]
- 14. Medrano-Mercado N, Ugarte-Fernandez R, Butrón V, Uber-Busek S, Guerra H, et al. (2008) Urban transmission of chagas disease in Cochabamba, Bolivia. Memórias do Instituto Oswaldo Cruz 103: 423–430. [DOI] [PubMed] [Google Scholar]
- 15. Bayer AM, Hunter GC, Gilman RH, Cornejo del Carpio JG, Naquira C, et al. (2009) Chagas disease, migration and community settlement patterns in Arequipa, Peru. PLoS Negl Trop Dis 3: e567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Ranson H, NGuessan R, Lines J, Moiroux N, Nkuni Z, et al. (2011) Pyrethroid resistance in African anopheline mosquitoes: what are the implications for malaria control? Trends in Parasitology 27: 91–98. [DOI] [PubMed] [Google Scholar]
- 17. Dias J, Silveira A, Schofield C (2002) The impact of Chagas disease control in Latin America: a review. Mem Inst Oswaldo Cruz 97: 603–612. [DOI] [PubMed] [Google Scholar]
- 18. Ferguson N, Cummings D, Fraser C, Cajka J, Cooley P, et al. (2006) Strategies for mitigating an inuenza pandemic. Nature 442: 448–452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Barbu CM, Dumonteil E, Gourbière S (2011) Evaluation of spatially targeted strategies to control non-domiciliated Triatoma dimidiata vector of Chagas disease. PLoS neglected tropical diseases 5: e1045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Levy M, Malaga Chavez F, Cornejo del Carpio J, Vilhena D, McKenzie F, et al. (2010) Rational spatio-temporal strategies for controlling a Chagas disease vector in urban environments. Journal of The Royal Society Interface 7: 1061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Levy MZ, Kawai V, Bowman NM, Waller LA, Cabrera L, et al. (2007) Targeted screening strategies to detect Trypanosoma cruzi infection in children. PLoS Negl Trop Dis 1: e103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Levy MZ, Quíspe-Machaca VR, Ylla-Velasquez JL, Waller LA, Richards JM, et al. (2008) Impregnated netting slows infestation by Triatoma infestans. Am J Trop Med Hyg 79: 528–534. [PMC free article] [PubMed] [Google Scholar]
- 23. Schofield CJ, Dujardin JP (1997) Chagas disease vector control in central america. Parasitology Today 13: 141. [DOI] [PubMed] [Google Scholar]
- 24. Chagas C (1909) Nova tripanozomiaze humana. Mem Inst Oswaldo Cruz 1: 159–218. [Google Scholar]
- 25. Bowman NM, Kawai V, Levy MZ, del Carpio JGC, Cabrera L, et al. (2008) Chagas disease transmission in periurban communities of Arequipa, Peru. Clin Infect Dis 46: 1822–1828. [DOI] [PubMed] [Google Scholar]
- 26. Levy MZ, Small DS, Vilhena DA, Bowman NM, Kawai V, et al. (2011) Retracing micro-epidemics of Chagas disease using epicenter regression. PLoS computational biology 7: e1002146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Levy MZ, Bowman NM, Kawai V, Waller LA, Cornejo del Carpio JG, et al. (2006) Periurban Trypanosoma cruzi-infected triatoma infestans, Arequipa, Peru. Emerg Infect Dis 12: 1345–1352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Cohen JE, Gürtler RE (2001) Modeling household transmission of american trypanosomiasis. Science 293: 694–698. [DOI] [PubMed] [Google Scholar]
- 29. Barbu CM, Dumonteil E, Gourbière S (2009) Optimization of control strategies for non-domiciliated Triatoma dimidiata, Chagas visease vector in the Yucatán Peninsula, Mexico. PLoS Negl Trop Dis 3: e416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Vazquez-Prokopec GM, Ceballos LA, Kitron U, Gürtler RE (2004) Active dispersal of natural populations of triatoma infestans (hemiptera: Reduviidae) in rural northwestern argentina. Journal of Medical Entomology 41: 614–621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Cecere MC, Vasquez-Prokopec GM, Gürtler RE, Kitron U (2006) Reinfestation sources for chagas disease vector, triatoma infestans, argentina. Emerg Infect Dis 12: 1096–1102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Zu Dohna H, Cecere M, Grtler R, Kitron U, Cohen J (2009) Spatial re-establishment dynamics of local populations of vectors of chagas disease. PLoS neglected tropical diseases 3: e490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Barbu CM, Dumonteil E, Gourbière S (2010) Characterization of the dispersal of non-domiciliated triatoma dimidiata through the selection of spatially explicit models. PLoS Negl Trop Dis 4: e777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Real LA, Biek R (2007) Spatial dynamics and genetics of infectious diseases on heterogeneous landscapes. Journal of The Royal Society Interface 4: 935–948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Darsow A, Schafmeister M, Hofmann T (2009) An arcgis approach to include tectonic structures in point data regionalization. Ground Water 47: 591–597. [DOI] [PubMed] [Google Scholar]
- 36. Epps C, Palsbll P, Wehausen J, Roderick G, Ramey R II, et al. (2005) Highways block gene ow and cause a rapid decline in genetic diversity of desert bighorn sheep. Ecology Letters 8: 1029–1038. [Google Scholar]
- 37. Storfer A, Murphy M, Evans J, Goldberg C, Robinson S, et al. (2006) Putting the landscapein landscape genetics. Heredity 98: 128–142. [DOI] [PubMed] [Google Scholar]
- 38. Storfer A, Murphy MA, Spear SF, Holderegger R, Waits LP (2010) Landscape genetics: where are we now? Molecular Ecology 19: 3496–3514. [DOI] [PubMed] [Google Scholar]
- 39. Segelbacher G, Cushman S, Epperson B, Fortin M, Francois O, et al. (2010) Applications of landscape genetics in conservation biology: concepts and challenges. Conservation Genetics 11: 375–385. [Google Scholar]
- 40. Massey D, Denton N (1988) The dimensions of residential segregation. Social forces 67: 281–315. [Google Scholar]
- 41. Lee B, Reardon S, Firebaugh G, Farrell C, Matthews S, et al. (2008) Beyond the census tract: Patterns and determinants of racial segregation at multiple geographic scales. American Sociological Review 73: 766–791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Sokal RR, Oden NL (1978) Spatial autocorrelation in biology 1. methodology. Biological Journal of the Linnean Society 10: 199–228. [Google Scholar]
- 43. Oden NL (1984) Assessing the significance of a spatial correlogram. Geographical Analysis 16: 1–16. [Google Scholar]
- 44. Gosoniu L, Vounatsou P, Sogoba N, Maire N, Smith T (2009) Mapping malaria risk in West Africa using a Bayesian nonparametric non-stationary model. Computational Statistics & Data Analysis 53: 3358–3371. [Google Scholar]
- 45. Hay SI, Guerra CA, Gething PW, Patil AP, Tatem AJ, et al. (2009) A world malaria map: Plasmodium falciparum endemicity in 2007. PLoS Medicine 6: e1000048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Vounatsou P, Raso G, Tanner M, N'goran E, Utzinger J (2009) Bayesian geostatistical modelling for mapping schistosomiasis transmission. Parasitology 136: 1695–1705. [DOI] [PubMed] [Google Scholar]
- 47. Moran PAP (1950) Notes on continuous stochastic phenomena. Biometrika 37: 17–23. [PubMed] [Google Scholar]
- 48. Getis A (2008) A history of the concept of spatial autocorrelation: a geographer's perspective. Geographical Analysis 40: 297–309. [Google Scholar]
- 49. Rue H, Tjelmeland H (2002) Fitting gaussian markov random fields to gaussian fields. Scandinavian Journal of Statistics 29: 31–49. [Google Scholar]
- 50. Furrer R, Sain SR (2010) spam: A sparse matrix r package with emphasis on mcmc methods for gaussian markov random fields. Journal of Statistical Software 36: 1–25. [Google Scholar]
- 51. Guisan A, Edwards TC, Hastie T (2002) Generalized linear and generalized additive models in studies of species distributions: setting the scene. Ecological modelling 157: 89–100. [Google Scholar]
- 52.Google Earth (2009) Imagery date Aug. 17 2009.
- 53. Legendre P, Fortin MJ (1989) Spatial pattern and ecological analysis. Plant Ecology 80: 107–138. [Google Scholar]
- 54.Good PI (2005) Permutation, parametric and bootstrap tests of hypotheses. Springer Verlag.
- 55. Goodman LA (1974) Exploratory latent structure analysis using both identifiable and unidentifiable models. Biometrika 61: 215–231. [Google Scholar]
- 56.Kaplan D (2004) The Sage handbook of quantitative methodology for the social sciences. Sage Publications, Inc.
- 57. Gelman A, Jakulin A, Pittau MG, Su YS (2008) A weakly informative default prior distribution for logistic and other regression models. The Annals of Applied Statistics 2: 1360–1383. [Google Scholar]
- 58.McFadden D (1974) Conditional logit analysis of qualitative choice behaviour. In: Frontiers of Econometrics. New York, NY: Academic Press. pp. 105–142.
- 59.R Core Team (2012). R: A language and environment for statistical computing. URL http://www.R-project.org. ISBN 3-900051-07-0.
- 60. Spiegelhalter DJ, Best NG, Carlin BP, Van Der Linde A (2002) Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society Series B, Statistical Methodology 583–639. [Google Scholar]
- 61. Legendre P, Dale MR, Fortin MJ, Gurevitch J, Hohn M, et al. (2002) The consequences of spatial structure for the design and analysis of ecological field surveys. Ecography 25: 601–615. [Google Scholar]
- 62. Peralta G, Fenoglio MS, Salvo A (2011) Physical barriers and corridors in urban habitats affect colonisation and parasitism rates of a specialist leaf miner. Ecological Entomology 36: 673–679. [Google Scholar]
- 63. Ostfeld RS, Glass GE, Keesing F (2005) Spatial epidemiology: an emerging (or re-emerging) discipline. Trends in Ecology and Evolution 20: 328–336. [DOI] [PubMed] [Google Scholar]
- 64. Smith DL, Lucey B, Waller LA, Childs JE, Real LA (2002) Predicting the spatial dynamics of rabies epidemics on heterogeneous landscapes. Proceedings of the National Academy of Sciences 99: 3668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Russell CA, Smith DL, Childs JE, Real LA (2005) Predictive spatial dynamics and strategic planning for raccoon rabies emergence in Ohio. PLoS Biology 3: e88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Vora A, Burke D, Cummings D (2008) The impact of a physical geographic barrier on the dynamics of measles. Epidemiology and infection 136: 713–720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Joyce KA, Holland JM, Doncaster CP (1999) Inuences of hedgerow intersections and gaps on the movement of carabid beetles. Bulletin of Entomological Research 89: 523–531. [Google Scholar]
- 68. Rondinini C, Doncaster CP (2002) Roads as barriers to movement for hedgehogs. Functional Ecology 16: 504–509. [Google Scholar]
- 69. Shepard D, Kuhns A, Dreslik M, Phillips C (2008) Roads as barriers to animal movement in fragmented landscapes. Animal Conservation 11: 288–296. [Google Scholar]
- 70. Keller I, Largiadèr CR (2003) Recent habitat fragmentation caused by major roads leads to reduction of gene ow and loss of genetic variability in ground beetles. Proceedings of the Royal Society of London Series B: Biological Sciences 270: 417–423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71. Melis C, Olsen CB, Hyllvang M, Gobbi M, Stokke BG, et al. (2010) The effect of traffic intensity on ground beetle (coleoptera: Carabidae) assemblages in central Sweden. Journal of Insect Conservation 14: 159–168. [Google Scholar]
- 72. Yamada Y, Sasaki H, Harauchi Y (2010) Effects of narrow roads on the movement of carabid beetles (coleoptera, carabidae) in Nopporo Forest Park, Hokkaido. Journal of Insect Conservation 14: 151–157. [Google Scholar]
- 73. Koivula M, Vermeulen H (2005) Highways and forest fragmentation effects on carabid beetles (Coleoptera, carabidae). Landscape Ecology 20: 911–926. [Google Scholar]
- 74. Bhattacharya M, Primack RB, Gerwein J (2003) Are roads and railroads barriers to bumblebee movement in a temperate suburban conservation area? Biological Conservation 109: 37–45. [Google Scholar]
- 75. Soluk DA, Zercher DS, Worthington AM (2011) Inuence of roadways on patterns of mortality and ight behavior of adult dragonies near wetland areas. Biological Conservation 144: 1638–1643. [Google Scholar]
- 76. Gardner-Santana LC, Norris DE, Fornadel CM, Hinson ER, Klein SL, et al. (2009) Commensal ecology, urban landscapes, and their inuence on the genetic characteristics of city-dwelling Norway rats (Rattus norvegicus). Molecular Ecology 18: 2766–2778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Kareiva P, Mullen A, Southwood R (1990) Population dynamics in spatially complex environments: theory and data [and discussion]. Philosophical Transactions of the Royal Society of London Series B: Biological Sciences 330: 175. [Google Scholar]
- 78. Albarracin-Veizaga H, de Carvalho ME, do Nascimento EMM, Rodrigues VLCC, Casanova C, et al. (1999) Chagas disease in an area of recent occupation in cochabamba, bolivia. Rev Saúde Públ 33: 230–236. [DOI] [PubMed] [Google Scholar]
- 79. Ramsey JM, Alvear AL, Ordoñez R, Muñoz G, Garcia A, et al. (2005) Risk factors associated with house infestation by the chagas disease vector triatoma pallidipennis in cuernavaca metropolitan area, mexico. Medical and Veterinary Entomology 19: 219–228. [DOI] [PubMed] [Google Scholar]
- 80. Childs JE, McLafferty SL, Sadek R, Miller GL, Khan AS, et al. (1998) Epidemiology of rodent bites and prediction of rat infestation in New York City. American Journal of Epidemiology 148: 78–87. [DOI] [PubMed] [Google Scholar]
- 81. Schneider JR, Morrison AC, Astete H, Scott TW, Wilson ML (2004) Adult size and distribution of Aedes aegypti (Diptera: Culicidae) associated with larval habitats in Iquitos, Peru. Journal of medical entomology 41: 634–642. [DOI] [PubMed] [Google Scholar]
- 82. Dibo MR, Chierotti AP, Ferrari MS, Mendonça AL, Chiaravalloti Neto F (2008) Study of the relationship between Aedes (Stegomyia) aegypti egg and adult densities, dengue fever and climate in Mirassol, state of São paulo, Brazil. Memórias do Instituto Oswaldo Cruz 103: 554–560. [DOI] [PubMed] [Google Scholar]
- 83. Dodd P, Ferguson N (2007) Approximate disease dynamics in household-structured populations. Journal of The Royal Society Interface 4: 1103–1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84. Hunter GC, Borrini-Mayorí K, Juárez JA, Neyra RC, Verastegui MR, et al. (2012) A field trial of alternative targeted screening strategies for Chagas disease in Arequipa, Peru. PLoS Neglected Tropical Diseases 6: e1468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85. Vassena CV, Picollo MI, Zerba EN (2000) Insecticide resistance in Brazilian Triatoma infestans and Venezuelan Rhodnius prolixus. Medical and Veterinary Entomology 14: 51–55. [DOI] [PubMed] [Google Scholar]
- 86. Picollo MI, Vassena C, Orihuela PS, Barrios S, Zaidemberg M, et al. (2005) High resistance to pyrethroid insecticides associated with ineffective field treatments in Triatoma infestans (Hemiptera: Reduviidae) from Northern Argentina. J Med Entomol 42: 637–642. [DOI] [PubMed] [Google Scholar]
- 87. Toloza AC, Germano M, Cueto GM, Vassena C, Zerba E, et al. (2008) Differential patterns of insecticide resistance in eggs and first instars of Triatoma infestans (hemiptera: Reduviidae) from Argentina and Bolivia. J Med Entomol 45: 421–426. [DOI] [PubMed] [Google Scholar]
- 88. Germano M, Acevedo GR, Cueto GA, Toloza A, Vassena C, et al. (2010) New findings of insecticide resistance in Triatoma infestans (Heteroptera: Reduviidae) from the Gran Chaco. Journal of medical entomology 47: 1077–1081. [DOI] [PubMed] [Google Scholar]
- 89. Hoy MA (1998) Myths, models and mitigation of resistance to pesticides. Philosophical Transactions of the Royal Society of London Series B, Biological Sciences 353: 1787–1795. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Annotated code in R with data. Two datasets are given. One corresponds to the original, de-identified data (realData.R) where spatial relationships are given through the distance matrix between points. The second dataset (JitteredDataPaucarpata.csv) corresponds to a generated dataset having the same spatial characteristics as the original dataset. The given examples with this second dataset (example_structuredMI.R and example_fit_GMRF.R) provide a model for application of these methods to new datasets. Please see the README file for details. Updated code can be accessed through github: https://github.com/cbarbu/spatcontrol.
(ZIP)
Detailed parameters estimates. Estimates for each spatial kernel of all fitted parameters with their 95% credible intervals.
(PNG)
Details about the mathematical model. Detailed description of the Latent Class Gaussian Field implementation (model and sampling).
(PDF)
Sensitivity analyses. We further investigate the sensitivity of the Latent Class Gaussian Field model to the distance threshold 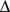 , the handling of missing data, the included cofactors, and the inspector sensitivity prior.
, the handling of missing data, the included cofactors, and the inspector sensitivity prior.
(PDF)