Abstract
The perceived colors of reflecting surfaces generally remain stable despite changes in the spectrum of the illuminating light. This color constancy can be measured operationally by asking observers to distinguish illuminant changes on a scene from changes in the reflecting properties of the surfaces comprising it. It is shown here that during fast illuminant changes, simultaneous changes in spectral reflectance of one or more surfaces in an array of other surfaces can be readily detected almost independent of the numbers of surfaces, suggesting a preattentive, spatially parallel process. This process, which is perfect over a spatial window delimited by the anatomical fovea, may form an early input to a multistage analysis of surface color, providing the visual system with information about a rapidly changing world in advance of the generation of a more elaborate and stable perceptual representation.
Keywords: parallel processing, cone-excitation ratios, surface color, transient chromatic signals
Changes of illumination on a scene occur naturally, as when a cloud passes over the sun, or when a nearer object moves in front of the light and casts a shadow. Given this variation, it might be expected that the visual system would have evolved mechanisms for extracting properties of surfaces that are invariant under these changes. Color constancy is the effect whereby the color of a surface is perceived as invariant despite differences in the color of the illumination (1, 2). The effect is strongest when the illumination remains steady and spatially uniform (3), but it also holds across differently illuminated areas (4–8) and under illumination that changes over time (9). Operationally, color constancy can be measured by asking observers to distinguish between changes in the spectral properties of the illumination on a scene from changes in the spectral properties of the surfaces comprising it (10). Such a task can be performed rapidly and effortlessly (10) and is best with fast reflectance changes (11), which probably generate a transient signal that is exploited by the visual system (12). This ready capacity to detect violations of color constancy during illuminant changes has some of the properties of preattentive vision (13, 14) or vision with distributed attention (15), involving primarily the early stages of visual processing (16–18). The stimulus element with the critical feature or attribute exhibits “pop out” (14, 19–21). A characteristic property of preattentive vision is that search or detection performance is independent of the number of elements in the scene; that is, the visual mechanisms concerned act spatially in parallel over the visual field (21–26).
Are, then, violations of color constancy detected in parallel? The question is important both for identifying those stimulus properties that receive priority in the earliest stages of visual processing and for elucidating how human surface-color perception might proceed as a multistage process (8, 27). The traditional way of addressing this question for stimulus attributes such as shape or orientation has been to measure the time taken to detect a “target” element in an array of “distractor” elements as the number of distractor elements increases (22, 24), although accuracy of detection has also sometimes been used as the dependent measure (23). With a transient event such as an illuminant or spectral-reflectance change, the accuracy of detection rather than time taken to achieve it provides a more natural measure of competence, emphasizing encoding-level processes rather than decision-level processes (28).
In the work reported here, the stimuli were made up of images of differently colored paper patches undergoing an abrupt illuminant change. In the first experiment, the target patch, which appeared in 50% of trials, was defined by a single spectral-reflectance change that took place at the same time as the overall illuminant change; the distractors were the remaining patches, variable in number, undergoing just the illuminant change. The probability of detecting the target was measured as the number of distractors increased. This task is different from detecting a colored target in an array of differently colored distractors, for which detection is already known to be generally parallel (14, 20, 29). In the present task, the target would have been undetectable in the images preceding and following the illuminant change: the target was defined only at the moment of change. Target detectability decreased gradually as the number of distractors increased from 1 to 24, and in a way predictable by a simple probabilistic model of processing that was perfectly parallel over a bell-shaped spatial window of width about 4° visual angle.
Because this window may have covaried with the number of distractors, a second experiment was performed in which target detectability was measured as the number of targets increased and number of distractors decreased so that their total number was conserved. Two sizes of stimulus field were used. Target detectability increased gradually as the number of targets increased, but less rapidly with the smaller field than with the larger field, both increases consistent with perfectly parallel processing over a spatial window of about 4°. To test whether the underlying signals might be restricted to a pure luminance channel, performance was also measured with image changes that were isoluminant. Window width was unaltered.
General Methods
Observers were presented with computer simulations of square patches of illuminated colored papers, each of side 1.2° visual angle, drawn randomly from 1,149 displayable samples of the 1,269 papers in the Munsell Book of Color (30), the spectral reflectances of which were constructed from combinations of eight spectral basis functions (31). (Subsequent references to surfaces and illuminants apply to these computer simulations; little difference has been reported between levels of constancy found with reflected and emitted light, e.g., ref. 7.) The patches were positioned on the vertices of an imaginary 5 × 5 grid. The resulting array appeared on a dark background and was limited to either 6° × 6° or 4.5° × 4.5° visual angle at a viewing distance of 150 cm. The array was uniformly illuminated by randomly selected daylights, the spectra of which were constructed from combinations of three spectral basis functions (32). (Basis functions were used here for computational speed and have no theoretical implications.) Daylights fall about a line on the CIE 1931 (x, y) chromaticity diagram slightly to the green side of the Planckian locus and can therefore be labeled (but not specified) by their x coordinates, which ranged from 0.25 to 0.37, corresponding to correlated color temperatures of 25,000 K to 4,300 K.
The stimuli were generated on the screen of a 19-inch, 1024 × 768 pixels, RGB color display monitor (Trinitron, model GDM-2036S; Sony, Tokyo), controlled by a computer (type 3/160; Sun Microsystems, Mountain View, CA) driving a special-purpose RGB color-graphics system (4660 series; Ramtek, Hampshire, U.K.) providing 10-bit intensity resolution per gun. The screen refresh rate was about 60 Hz, and phosphor decay times were each <1 ms. A telespectroradiometer (SpectraColorimeter, PR-650; Photo Research, Chatsworth, CA), previously calibrated by the National Physical Laboratory, was used to regularly calibrate the display system. Errors in the displayed CIE (x, y, Y) coordinates of a white test patch were ≤0.005 in (x, y) and <2% in Y. The mean luminance of the patches was 16 cd⋅m−2, but individual luminances varied widely (SD 10 cd⋅m−2).
In each trial, the array of papers was displayed for 1 s under one randomly selected, spatially uniform daylight, and then for 1 s under a second randomly selected, spatially uniform daylight; the change in illuminant was abrupt, and total display duration was therefore 2 s. At the same time as this illuminant change, one or more randomly selected papers underwent a spectral-reflectance change, with probability 0.5. The size of the reflectance change was conveniently quantified in CIE (x, y) coordinates by an equivalent localized illuminant change that differed from the spatially uniform illuminant change by an increment Δx in x along the daylight locus (10, 33). The change is not necessarily equivalent to shifting the CIE (x, y) coordinates of the surface color by Δx but depends on the product of the illuminant and surface-reflectance spectra. This shorthand method of quantifying changes in spectral reflectance was used so that they could be related directly to the changes in the x values of the illuminants. It does not affect the data analysis or conclusions. The x values of the uniform illuminant changes were drawn randomly from the values ±0.04 and ±0.10; on the basis of pilot estimates of detection thresholds, the increments Δx were drawn randomly from the values ±0.04 and ±0.08 (or ±0.06), subject to the constraint that the total illuminant x value did not fall below 0.25 or above 0.37.
The task in each trial was to determine whether a reflectance change occurred. Viewing the screen binocularly, the observer fixated a central fixation mark on the screen and, when ready, initiated a trial by pressing a switch on a box connected to the computer. The fixation mark disappeared, and then the array of papers appeared under the two successive illuminants. The observer responded by using the switch box, and, after a few seconds, the fixation mark reappeared indicating that the next trial could be initiated. Observers were encouraged to maintain central fixation, although this proved difficult when there were no patches at the center of the screen.
Different randomly selected surfaces and illuminants were used in each trial. Depending on the experiment, each observer performed, on average, 830–1,760 trials. There were five observers, three female and two male, aged 19–30 yr. Each had normal color vision, verified by Rayleigh and Moreland anomaloscopy. All except observer K.A. (coauthor) were unaware of the purpose of the experiment and unpracticed in making color matches.
Target-detection performance was quantified by the discrimination index d′ from signal-detection theory (34). In brief, let pH be the hit rate, that is, the probability of a “reflectance” response when a reflectance change occurred; let pF be the false-alarm rate, that is, the probability of a “reflectance” response when a reflectance change did not occur; and let z be the inverse of the cumulative unit normal distribution. Then d′ = z(pH) − z(pF). In this way, d′ linearizes and combines responses to target and nontarget arrays and eliminates observer bias (34). A zero value of d′ corresponds to chance performance, and d′ increases monotonically with the detectability of the target (in a two-alternative forced-choice task, a value of d′ of 1.0 corresponds to 76% correct). Observers' levels of performance were found to be similar, and data were pooled. For the purposes of analysis, a psychometric function was fitted to the graphs of d′ against increment Δx and selected values read off. Standard errors were estimated by resampling over observers (35).
One Target, Variable Geometry
In the first experiment, observers were presented with a variable array of square patches of paper undergoing an abrupt illuminant change, as illustrated in Fig. 1. Except for the largest array, patches were grouped into pairs distributed randomly over the field (a pair being the smallest stimulus unit providing the required cue). If a spectral-reflectance change also occurred, it affected only one randomly selected patch [in Fig. 1, it is the patch with grid coordinates (2, 2) counting from bottom left]. The total number of patches present in any trial was 2, 4, 8, 16, or 25. In the last, patches were unpaired and arranged in a 5 × 5 array to provide continuity with the second experiment (for which an array with an odd number of patches was required). The size of the field was 6° × 6°, over which cone-photoreceptor thresholds do not vary too rapidly with eccentricity (see ref. 36 and Discussion). Visual search for targets defined by color is similar when targets and fields are both smaller and both larger than the ones used here (29).
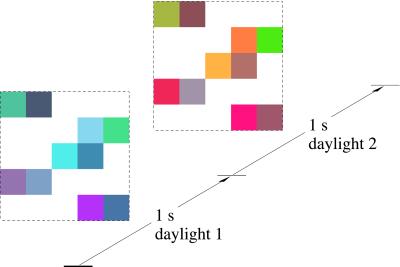
Figure 1.
Example stimulus with variable geometry. The image consisted of an array of randomly positioned square patches of randomly selected colored papers (grouped into pairs) displayed for 1 s under one randomly selected daylight and then for 1 s under another randomly selected daylight. The illuminant change was abrupt. In a target trial, a simultaneous spectral-reflectance change also occurred affecting only one randomly selected patch [here, the patch with coordinates (2, 2), counting from bottom left]. The total number of patches present in any trial varied from 2 to 25, and they were constrained to fall within a field of 6° × 6° visual angle (shown by the broken lines).
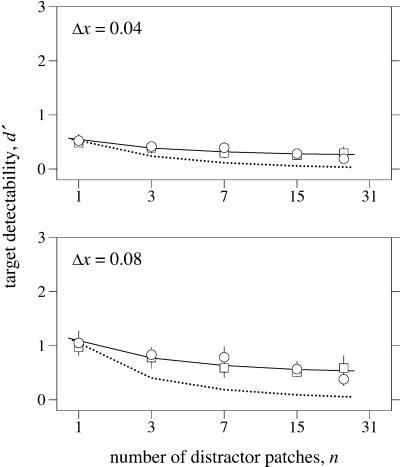
Fig. 2 shows target detectability (circles) plotted against the number n of distractors in the array (squares refer to a control condition and curves to model predictions, both described later; ordinate ranges were chosen to aid comparison with subsequent plots). The upper and lower panels are for data obtained with the different sizes of increments Δx of 0.04 and 0.08 quantifying the target spectral-reflectance changes. With just two patches in the array (n = 1), the detectability of a single reflectance change was well above chance (d′ = 0), but, as n increased, detectability gradually decreased (the gradients in the upper and lower panels were −0.028 and −0.055 per patch). It is not immediately clear, however, if this decrease is as much as would be expected if processing were serial. To resolve this question, one needs a quantitative model of how the probability of detecting the target varies with the number of patches.
Figure 2.
Detectability of a single target (spectral-reflectance change) patch in a variable number of distractor (illuminant change) patches, as in Fig. 1. Discrimination index d′ (○) calculated over five observers is plotted as a function of the number n of distractors. Vertical bars show ±1 SE where sufficiently large. The upper and lower panels are for data derived with different sizes of increments Δx of 0.04 and 0.08 in CIE x-coordinate quantifying the spectral-reflectance change. □, a control condition in which the changes in the images were isoluminant. The continuous curves represent predicted detection performance for perfectly parallel processing over a Gaussian spatial window of width 4.0° visual angle. The dotted curves represent predicted detection performance for serial processing.
A Probabilistic Model of Target Detection
Suppose, first, that processing were indeed serial. As each trial provided a single transient cue, serial processing would amount to processing just one of the pairs of patches present in the image. As argued later, serial processing of other pairs of patches by observers shifting fixation or focal attention seems unlikely, owing to limitations on visual working memory. In a trial with no more than one pair of patches, there would be no uncertainty about which pair to fixate and process (given that observers did not maintain central fixation). For such a trial, let pH(1) be the probability of a hit (the “1” designating a single distractor), and let pF(1) be the corresponding probability of a false alarm. These two probabilities may be estimated by the observed hit and false-alarm rates with a single distractor (together giving the value of d′ at n = 1, plotted in Fig. 2). Now consider a trial with n distractors (n > 1). Let pH(n) be the corresponding probability of a hit and pF(n) be the corresponding probability of a false alarm. The probability pH(n) may be predicted from pH(1) and pF(1) in the following way. By supposition, only one pair of patches can be processed at a time. The total number of patches in the array is n + 1, and therefore the probability of fixating the pair containing the target, if present, is 2/(n + 1) and of not fixating it is 1 – 2/(n + 1). Hence, pH(n) = [2/(n + 1)] pH(1) + [1 – 2/(n + 1)] pF(1) (cf. ref. 23). Assume for the moment that the observer's false-alarm rate is constant with n; that is, pF(n) = pF(1). Predicted detection performance d′ as a function of n is, by definition, then given by z[pH(n)] − z[pF(n)]. This function, shown by the dotted curves in Fig. 2, fell significantly below observed performance [χ2(4) = 39; P < 0.0001]. Processing was clearly not serial. Assume now that the false-alarm rate pF(n) varies with n, which is possible as observers could have shifted their criterion while inspecting the array before and after the illuminant change (in fact, the observed rate increased only slightly with n). Because this criterion shift would have been identical for target and nontarget arrays with the same n, the value of d′ remains the same.
Suppose, next, that processing were parallel, but only within a spatial window of width w, say, centered on the point of gaze. Assume for simplicity that the window has a hard edge; that is, patches within w/2 of the center are processed perfectly in parallel, and beyond that, not at all. Let the maximum width of the stimulus array be W. Consider a target trial with n distractors (n > 1). The probability pH(n) of a hit is given by an expression similar to that for serial processing, but containing terms weighted by the probability (w/W)2 of the pair falling within the window and 1 − (w/W)2 of it not. As before, predicted detection performance d′ as a function of n is given by z[pH(n)] − z[pF(n)]. This function was evaluated numerically with the window width w ranging from 0 to W. The best-fitting function for this hypothetical hard-edged window was obtained with w = 4.3°.
More realistically, assume now that the window is spatially graded, so that the degree of parallel processing declines smoothly with distance, say r, of the patch from the center of the window according to a Gaussian function exp[−r2/(2s2)] with SD s. The full width at half-maximum, say w1/2, of this function is 2.35 s. A Monte-Carlo simulation of the selection procedure was performed, with w1/2 ranging from 0 to more than W, the full width of the array. The best-fitting function for this graded window was obtained with w1/2 = 4.0° and is shown by the continuous curves in Fig. 2. In generating this best fit (and that with the hard-edged window), the probabilities pH(1) and pF(1), estimated by the observed hit and false-alarm rates for a single pair of patches, were allowed to vary by no more than 1 SE, about 4%.
Although the model curves accounted well for the variance in the data [χ2(4) = 2.1, P > 0.5], it is possible that the calculated window merely represented an average of many different windows whose size and shape fluctuated from trial to trial, depending on the number and disposition of the patches in the field. It is also possible that the small decline in detection performance with increasing number of distractors may have had less to do with a spatial limit on perfect parallel processing and more with the perceived “objectness” of the image, that is, the degree to which patches were seen as physical surfaces. This perceptual effect, which could have increased with the total number of patches in the image, might have offset a much stronger underlying decline in detection performance with increasing distractor number. These uncertainties could only be satisfactorily resolved by fixing the geometry of the array. This was done in the next experiment.
Multiple Targets, Fixed Geometry
In this second experiment, observers were presented with a fixed 6° × 6° array of 25 abutting square patches of paper undergoing an abrupt illuminant change, as illustrated in Fig. 3. If a simultaneous spectral-reflectance change also occurred, it affected 1, 2, 4, 8, or 12 randomly selected patches [in Fig. 3, it is the 4 patches with coordinates (1, 2), (1, 4), (1, 5), and (2, 3), counting from bottom left]. Although the size and direction of the spectral-reflectance change varied from trial to trial, within a trial it affected all targets equally; that is, the equivalent localized illuminant change with increment Δx in x along the daylight locus was the same for each. The other conditions of the experiment were unchanged. If, in a target trial with n patches undergoing a spectral-reflectance change, visual processing were parallel over the whole field, then, providing that the cues from the targets were perfectly correlated, the probability of detection with one target should be the same as with 12 targets (the information available being the same).
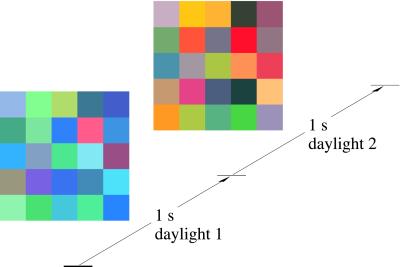
Figure 3.
Example stimulus with fixed geometry. The image consisted of a fixed 6° × 6° array of 25 abutting square patches of randomly selected colored papers displayed for 1 s under one randomly selected daylight and then for 1 s under another randomly selected daylight. The illuminant change was abrupt. In a target trial, a simultaneous spectral-reflectance change also occurred affecting 1, 2, 4, 8, or 12 randomly selected patches [here, the four patches with coordinates (1, 2), (1, 4), (1, 5), and (2, 3), counting from bottom left].
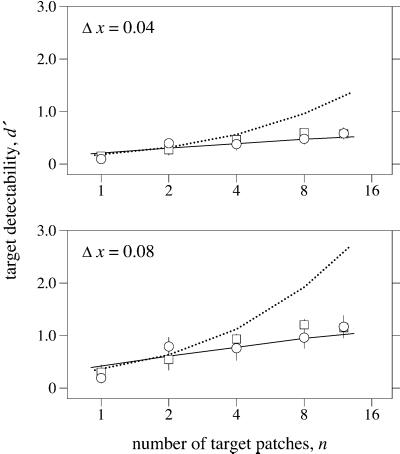
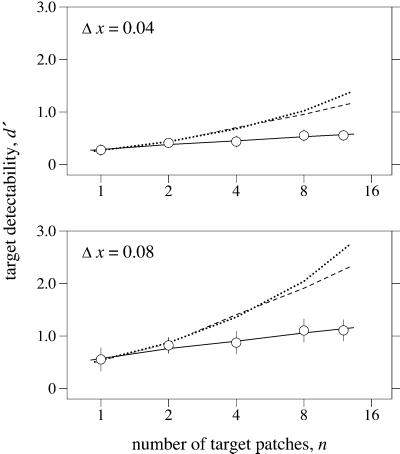
Fig. 4 shows target detectability (circles) plotted against the number n of targets in the array (squares refer to a control condition and curves to model predictions, both described later).
Figure 4.
Detectability of one or more target (spectral-reflectance change) patches within a fixed 6° × 6° array of distractor (illuminant change) patches, as in Fig. 3. Discrimination index d′ (○) calculated over five observers is plotted as a function of the number n of targets. The continuous curves represent predicted detection performance for perfectly parallel processing over a Gaussian spatial window of width 4.3° visual angle. The dotted curves represent predicted performance for serial processing optimized for best fit at low n. Other details as for Fig. 2.
With one target, the detectability of a reflectance change was above chance and increased gradually as n increased (the gradients in the upper and lower panels were 0.034 and 0.067 per patch, respectively). These increases were statistically significant and imply that processing was not perfectly parallel over the whole field, or multiple targets were not perfectly correlated, or both. A small departure from perfect correlation is to be expected as the cue that each target provided depends on the product of the illuminant and surface-reflectance spectra. In terms of cone-photoreceptor activity, this product varied between pairs of patches with SD about 3.7% of the mean. Although these fluctuations are very small (and typical, see ref. 37), they may have an effect when many targets are present (38). For example, with n = 2, the probability of one patch giving a cue 10% larger than the mean for a single patch is about 0.007; with n = 12, this probability rises to 0.04. (For a single target, as in the first experiment, the effect is immaterial. For distractors, the effect in target arrays is negligible in comparison with the target cue, and in nontarget arrays it is constant and may be subsumed in the false-alarm rate.)
A Monte-Carlo simulation of the selection procedure that incorporated these fluctuations was used to predict the probability pH(n) of a hit with n targets based on the probabilities pH(1) and pF(1) of a hit and a false alarm for a single target, as the width w1/2 of the Gaussian window ranged from 0 to more than W, the full width of the array. As observers could maintain central fixation with the 5 × 5 array, it was possible to estimate the probability pH(1) by the observed hit rate for those trials in which a single target fell centrally, where it would have coincided with the center of the Gaussian window (possible with an odd-numbered array). As nontarget arrays were of the same kind for all n, the predicted probability pF(n) of a false alarm was independent of n, so that pF(n) = pF(1), estimated by the observed false-alarm rate over all nontarget trials.
As before, the predicted detection performance d′ as a function of n is given by z[pH(n)] − z[pF(n)]. The best-fitting function was obtained with a window width w1/2 = 4.3° and is shown by the continuous curves in Fig. 4, which accounted well for the variance in the data [χ2(4) = 3.3, P = 0.5]. The width of 4.3° is close to that obtained in the first experiment with a single target and variable number of distractors. Predicted detection performance was also estimated for serial processing, again based on the probabilities pH(1) and pF(1). It fell well below observed performance [χ2(4) = 27; P < 0.0001]. Only if pH(1) and pF(1) were allowed to take extreme values, close to unity and zero, was it possible to fit performance at low n, but the fit then failed at large n, as shown by the dotted curves in Fig. 4. As in the first experiment with a single target and variable-geometry field, processing was clearly not serial.
Given that parallel processing does take place, is the width w1/2 = 4.3° estimated for the Gaussian window an absolute spatial limit? In other words, if the array were scaled down from 6° × 6° to say 4.5° × 4.5°, would the new window for parallel processing remain the same or also scale down? It might be argued that if the window were determined by physical factors, for example, foveal anatomy, then w1/2 should remain the same; alternatively, if it were determined by attentional factors, then, in view of previous results (23, 29), it might scale with the array, from 4.3° to 3.2° [= 4.3° × (4.5°/6°)]. (This inference does not depend on the size of the cue, for the estimated window width was the same with small and large increments Δx quantifying the target spectral-reflectance changes.) To address this question, the experiment was repeated with the array of 25 abutting square patches of paper scaled down to 4.5° × 4.5°.
Fig. 5 shows target detectability (circles) plotted against the number n of targets in the 4.5° × 4.5° array. Predicted detection performance d′ as a function of n was calculated exactly as for the previous experiment. The best-fitting function was obtained with a Gaussian window of width w1/2 = 4.3°, shown by the continuous curves [χ2(4) = 0.2, P > 0.5]. This window width is the same as that with the 6° × 6° array. For comparison, predicted detection performance is shown for the smaller window width w1/2 = 3.2° derived from the scaling assumption (dashed curves) and for serial processing (dotted curves), with pH(1) or pF(1) taking extreme values to fit performance at low n. Both fits were poor.
Figure 5.
Detectability of one or more target (spectral-reflectance change) patches within a fixed 4.5° × 4.5° array of distractor (illuminant change) patches. The continuous curves represent predicted detection performance for perfectly parallel processing within a Gaussian spatial window of width 4.3° visual angle. The dashed curves represent the corresponding performance for a 3.2° window, based on scaling performance with the 6° × 6° array (Fig. 4), and the dotted curves represent the performance for serial processing; both curves are optimized for best fit at low n. Other details as for Fig. 2.
Isoluminant Changes
Previous tests of the detectability of relatively slow “contrary” chromatic changes in Mondrian-like stimuli (33) have suggested that processing is parallel only as a consequence of luminance cues. But, as has been shown elsewhere (39), fast illuminant and spectral-reflectance changes can be discriminated in isoluminant images, which offer no luminance cues, as well as in achromatic images, which offer no chromatic cues. Thus, the detection of violations of color constancy in isoluminant images might still be parallel if image changes were fast. The first and second experiments were accordingly repeated with the images modified so that the luminance of each patch remained constant during illuminant and spectral-reflectance changes. In this way, although the images were not isoluminant, the changes in them were.
Target detectability with these modified images is shown by the squares in Figs. 2 and 4. Performance was almost the same as with the original, chromatically unconstrained images (mean difference in d′ < 0.1). Violations of color constancy seem to be detected in parallel in the absence of luminance cues.
Discussion
Color constancy represents a natural accommodation by the visual system to the invariance of surface spectral reflectance in the environment. When violations of this constancy occur, they appear to be detected by visual mechanisms acting in parallel over the central visual field. Such processing may be thought of as a second-order form (e.g., ref. 40) of the parallel processing involved in simple color discriminations, in which, for example, a green patch can be rapidly and effortlessly detected within an array of red and black patches (14, 20, 29). In first-order processing, what pops out is a difference in color; in second-order processing, a difference in color change, the one sometimes preempting the other (41).
The spatial window for parallel processing of color-constancy violations appears to be limited to about 4° visual angle. The coincidence of this window with the anatomical fovea is consistent with physical factors constraining performance. Beyond the fovea, cone-photoreceptor sensitivity declines rapidly (36), but within the fovea, sensitivity varies rather less, except when determined by short-wavelength-sensitive cones, which contribute little to the present task (38). Except for small fluctuations, the signals from distractors were spatially correlated, as were signals from multiple targets. Therefore, as long as patches fell within the fovea and their sizes exceeded the summation area for detection, signal-to-noise ratios should have been fairly constant, which may account for the invariance of the window with the scale of the array (23, 29). Whether performance can also be constrained by attentional factors in extrafoveal arrays with various geometries remains to be determined.
As already noted, parallel processing of constancy violations is best when changes in surface spectral reflectance are fast, within about 200 ms (11, 12). If spectral-reflectance changes are made gradually, over intervals much greater than 200 ms, performance becomes markedly worse, even though there is no temporal gap between the images or other interruption, as in change-blindness measurements (42–44). Performance is also worse if refixations are made a natural part of the task, as when the two images are presented continuously side-by-side, requiring the observer to look from one to the other (45). The transient nature of the cue and its failure to persist over refixations suggest that visual working memory contributes little, if at all, to performance (46, 47).
What is the origin of the cue? One possibility is that it is a low-level signal based on the computation of spatial ratios of cone excitations or of combinations of cone excitations arising from light reflected from pairs of surfaces in the image (cf. ref. 2). Under illuminant changes, these ratios are preserved almost exactly for pigmented surfaces and for surfaces with random spectral reflectances (37). They provide compelling evidence to observers: deviations in ratios are interpreted as being due to changes in surface reflectance even when they are actually due to changes in illuminant (38). Ratios also predict the variation in discrimination performance with the size of spectral-reflectance change over a wide range of conditions, for example, in isoluminant, achromatic, and colorimetrically unconstrained images of surfaces undergoing illuminant changes (39), for which performance levels may be closely similar, as was observed here with isoluminant and colorimetrically unconstrained image changes. Ratios may also predict the perceived transparency of colored filters placed over illuminated scenes (48).
Such signals, which do not require adaptation to the illuminated scene or knowledge of the illuminant, could be generated early in the visual pathway, perhaps within the eye itself (49, 50), but as illuminant changes can be discriminated moderately well from spectral-reflectance changes with dichoptically viewed images, cone-excitation ratios might also be computed more centrally, as part of a multistage analysis of surface color (27, 51, 52). They cannot, of course, account completely for color constancy, which requires a spectral reference to anchor cone-ratio information (53, 54). Color appearance also depends on the prevailing levels of light (3) and contrast adaptation (55, 56) and on the geometry of the scene (57, 58). The task of the parallel process described here may therefore be to provide the visual system with information about a rapidly changing world as a prerequisite to establishing a more elaborate and stable perceptual representation.
Acknowledgments
We thank A. C. Hurlbert, A. Reeves, S. Westland, and J. M. Wolfe for helpful discussion and J. P. S. Parkkinen, J. Hallikainen, and T. Jaaskelainen for providing data for the spectral reflectances of the Munsell papers. This work was supported by the Biotechnology and Biological Sciences Research Council, the Wellcome Trust, the Centro de Física da Universidade do Minho, Braga, Portugal, and the British Council.
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Young T. A Course of Lectures on Natural Philosophy and the Mechanical Arts. I. London: Joseph Johnson; 1807. , Lecture XXXVIII. [Google Scholar]
- 2.Land E H. Proc Natl Acad Sci USA. 1959;45:636–644. doi: 10.1073/pnas.45.4.636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bramwell D I, Hurlbert A C. Perception. 1996;25:229–241. doi: 10.1068/p250229. [DOI] [PubMed] [Google Scholar]
- 4.Arend L, Reeves A. J Opt Soc Am A. 1986;3:1743–1751. doi: 10.1364/josaa.3.001743. [DOI] [PubMed] [Google Scholar]
- 5.Arend L E, Jr, Reeves A, Schirillo J, Goldstein R. J Opt Soc Am A. 1991;8:661–672. doi: 10.1364/josaa.8.000661. [DOI] [PubMed] [Google Scholar]
- 6.Zaidi Q, Spehar B, DeBonet J. J Opt Soc Am A. 1997;14:2608–2621. doi: 10.1364/josaa.14.002608. [DOI] [PubMed] [Google Scholar]
- 7.Brainard D H, Brunt W A, Speigle J M. J Opt Soc Am A. 1997;14:2091–2110. doi: 10.1364/josaa.14.002091. [DOI] [PubMed] [Google Scholar]
- 8.Kraft J M, Brainard D H. Proc Natl Acad Sci USA. 1999;96:307–312. doi: 10.1073/pnas.96.1.307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Brainard D H, Wandell B A. J Opt Soc Am A. 1992;9:1433–1448. doi: 10.1364/josaa.9.001433. [DOI] [PubMed] [Google Scholar]
- 10.Craven B J, Foster D H. Vision Res. 1992;32:1359–1366. doi: 10.1016/0042-6989(92)90228-b. [DOI] [PubMed] [Google Scholar]
- 11.Linnell K J, Foster D H. Perception. 1996;25:221–228. doi: 10.1068/p250221. [DOI] [PubMed] [Google Scholar]
- 12.Foster D H, Amano K, Nascimento S M C. Color Res Appl. 2001;26,Suppl.:S180–S185. doi: 10.1002/1520-6378(2001)26:1+<::AID-COL39>3.0.CO;2-#. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Julesz B. Biol Cybern. 1981;41:131–138. doi: 10.1007/BF00335367. [DOI] [PubMed] [Google Scholar]
- 14.Treisman A. Comput Vis Graph Image Proc. 1985;31:156–177. [Google Scholar]
- 15.Beck J, Ambler B. Percept Psychophys. 1973;14:225–230. [Google Scholar]
- 16.Julesz B, Schumer R A. Annu Rev Psychol. 1981;32:575–627. doi: 10.1146/annurev.ps.32.020181.003043. [DOI] [PubMed] [Google Scholar]
- 17.Bergen J R, Adelson E H. Nature (London) 1988;333:363–364. doi: 10.1038/333363a0. [DOI] [PubMed] [Google Scholar]
- 18.Treisman A, Gormican S. Psychol Rev. 1988;95:15–48. doi: 10.1037/0033-295x.95.1.15. [DOI] [PubMed] [Google Scholar]
- 19.Nothdurft H-C. Vision Res. 1993;33:1937–1958. doi: 10.1016/0042-6989(93)90020-w. [DOI] [PubMed] [Google Scholar]
- 20.D'Zmura M. Vision Res. 1991;31:951–966. doi: 10.1016/0042-6989(91)90203-h. [DOI] [PubMed] [Google Scholar]
- 21.Li Z P. Proc Natl Acad Sci USA. 1999;96:10530–10535. doi: 10.1073/pnas.96.18.10530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Treisman A M, Gelade G. Cognit Psychol. 1980;12:97–136. doi: 10.1016/0010-0285(80)90005-5. [DOI] [PubMed] [Google Scholar]
- 23.Bergen J R, Julesz B. Nature (London) 1983;303:696–698. doi: 10.1038/303696a0. [DOI] [PubMed] [Google Scholar]
- 24.Sagi D, Julesz B. J Opt Soc Am. 1985;228:1217–1219. doi: 10.1126/science.4001937. [DOI] [PubMed] [Google Scholar]
- 25.Nakayama K, Silverman G H. Nature (London) 1986;320:264–265. doi: 10.1038/320264a0. [DOI] [PubMed] [Google Scholar]
- 26.Wolfe J M, Cave K R, Franzel S L. J Exp Psychol-Hum Percept Perform. 1989;15:419–433. doi: 10.1037//0096-1523.15.3.419. [DOI] [PubMed] [Google Scholar]
- 27.Walsh V. Proc Natl Acad Sci USA. 1999;96:13594–13596. doi: 10.1073/pnas.96.24.13594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rouder J N. J Exp Psychol Hum Percept Perform. 2000;26:359–378. [PubMed] [Google Scholar]
- 29.Nagy A L, Sanchez R R, Hughes T C. J Opt Soc Am A. 1990;7:1995–2001. doi: 10.1364/josaa.7.001995. [DOI] [PubMed] [Google Scholar]
- 30.Munsell Color Corporation. Munsell Book of Color-Matte Finish Collection. Baltimore, MD: Munsell Color Corp.; 1976. [Google Scholar]
- 31.Parkkinen J P S, Hallikainen J, Jaaskelainen T. J Opt Soc Am A. 1989;6:318–322. [Google Scholar]
- 32.Judd D B, MacAdam D L, Wyszecki G. J Opt Soc Am. 1964;54:1031–1040. [Google Scholar]
- 33.D'Zmura M, Mangalick A. J Opt Soc Am A. 1994;11:543–546. doi: 10.1364/josaa.11.000543. [DOI] [PubMed] [Google Scholar]
- 34.Green D M, Swets J A. Signal Detection Theory and Psychophysics. New York: Wiley; 1966. [Google Scholar]
- 35.Efron B, Tibshirani R J. An Introduction to the Bootstrap. New York: Chapman & Hall; 1993. [Google Scholar]
- 36.Stiles W S. Doc Ophthalmol. 1949;3:138–163. doi: 10.1007/BF00162601. [DOI] [PubMed] [Google Scholar]
- 37.Foster D H, Nascimento S M C. Proc R Soc London Ser B. 1994;257:115–121. doi: 10.1098/rspb.1994.0103. [DOI] [PubMed] [Google Scholar]
- 38.Nascimento S M C, Foster D H. Proc R Soc London Ser B. 1997;264:1395–1402. doi: 10.1098/rspb.1997.0194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Nascimento S M C, Foster D H. J Opt Soc Am A. 2000;17:225–231. doi: 10.1364/josaa.17.000225. [DOI] [PubMed] [Google Scholar]
- 40.Lu Z-L, Sperling G. J Opt Soc Am A. 1996;13:2305–2318. doi: 10.1364/josaa.13.002305. [DOI] [PubMed] [Google Scholar]
- 41.Moore C M, Brown L E. J Exp Psychol Hum Percept Perform. 2001;27:178–194. doi: 10.1037//0096-1523.27.1.178. [DOI] [PubMed] [Google Scholar]
- 42.Simons D J, Levin D T. Trends Cognit Sci. 1997;1:261–267. doi: 10.1016/S1364-6613(97)01080-2. [DOI] [PubMed] [Google Scholar]
- 43.Scott-Brown K C, Orbach H S. Proc R Soc Lond Ser B. 1998;265:2159–2166. doi: 10.1098/rspb.1998.0553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Rensink R A. Visual Cognit. 2000;7:345–376. [Google Scholar]
- 45.Foster D H, Amano K, Nascimento S M C. Vision Res. 2001;41:285–293. doi: 10.1016/s0042-6989(00)00239-x. [DOI] [PubMed] [Google Scholar]
- 46.Phillips W A. Percept Psychophys. 1974;16:283–290. [Google Scholar]
- 47.Luck S J, Vogel E K. Nature (London) 1997;390:279–281. doi: 10.1038/36846. [DOI] [PubMed] [Google Scholar]
- 48.Westland S, Ripamonti C. J Opt Soc Am A. 2000;17:255–264. doi: 10.1364/josaa.17.000255. [DOI] [PubMed] [Google Scholar]
- 49.Hurlbert A C, Bramwell D I, Heywood C, Cowey A. Exp Brain Res. 1998;123:136–144. doi: 10.1007/s002210050554. [DOI] [PubMed] [Google Scholar]
- 50.Rüttiger L, Braun D I, Gegenfurtner K R, Petersen D, Schönle P, Sharpe L T. J Neurosci. 1999;19:3094–3106. doi: 10.1523/JNEUROSCI.19-08-03094.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.De Valois R L, De Valois K K. Vision Res. 1993;33:1053–1065. doi: 10.1016/0042-6989(93)90240-w. [DOI] [PubMed] [Google Scholar]
- 52.Moutoussis K, Zeki S. Proc Natl Acad Sci USA. 2000;97:8069–8074. doi: 10.1073/pnas.110570897. . (First Published June 20, 2000; 10.1073/pnas.110570897) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Land E H. Proc Natl Acad Sci USA. 1959;45:115–129. doi: 10.1073/pnas.45.4.636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Gilchrist A, Kossyfidis C, Bonato F, Agostini T, Cataliotti J, Li X J, Spehar B, Annan V, Economou E. Psychol Rev. 1999;106:795–834. doi: 10.1037/0033-295x.106.4.795. [DOI] [PubMed] [Google Scholar]
- 55.Webster M A, Mollon J D. Nature (London) 1995;373:694–698. doi: 10.1038/373694a0. [DOI] [PubMed] [Google Scholar]
- 56.Brown R O, MacLeod D I A. Curr Biol. 1997;7:844–849. doi: 10.1016/s0960-9822(06)00372-1. [DOI] [PubMed] [Google Scholar]
- 57.Williams S M, McCoy A N, Purves D. Proc Natl Acad Sci USA. 1998;95:13301–13306. doi: 10.1073/pnas.95.22.13301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Bloj M G, Kersten D, Hurlbert A C. Nature (London) 1999;402:877–879. doi: 10.1038/47245. [DOI] [PubMed] [Google Scholar]