Acoustic structure of the five perceptual dimensions of timbre in orchestral instrument tones

Abstract

Attempts to relate the perceptual dimensions of timbre to quantitative acoustical dimensions have been tenuous, leading to claims that timbre is an emergent property, if measurable at all. Here, a three-pronged analysis shows that the timbre space of sustained instrument tones occupies 5 dimensions and that a specific combination of acoustic properties uniquely determines gestalt perception of timbre. Firstly, multidimensional scaling (MDS) of dissimilarity judgments generated a perceptual timbre space in which 5 dimensions were cross-validated and selected by traditional model comparisons. Secondly, subjects rated tones on semantic scales. A discriminant function analysis (DFA) accounting for variance of these semantic ratings across instruments and between subjects also yielded 5 significant dimensions with similar stimulus ordination. The dimensions of timbre space were then interpreted semantically by rotational and reflectional projection of the MDS solution into two DFA dimensions. Thirdly, to relate this final space to acoustical structure, the perceptual MDS coordinates of each sound were regressed with its joint spectrotemporal modulation power spectrum. Sound structures correlated significantly with distances in perceptual timbre space. Contrary to previous studies, most perceptual timbre dimensions are not the result of purely temporal or spectral features but instead depend on signature spectrotemporal patterns.

INTRODUCTION

Timbre is foundational to the ability to identify sound sources but may be one of the most intractable auditory perceptions to investigate, due to dynamic contextual factors that interact with the stable source modes in sound production (Handel, 1995). Its definition is negatively posed as all qualities of sound other than pitch, level, duration, and location. Previous researchers making determinations of perceptual timbre space have relied on unlabeled judgments of dissimilarity between tones produced by different musical instruments, so as to avoid adjectives prejudicing listeners toward arbitrary musical concepts as criteria for timbral judgments (Grey, 1977). Researchers then used multidimensional scaling (MDS) of the dissimilarity judgments to describe perceptual timbre space.

The present work makes three major advances in the characterization of perceptual timbre spaces. First, we combine the MDS analysis with a discriminant function analysis (DFA) of subsequent semantic ratings of the same sounds. This allows us to validate the subjective experience described by the MDS and also to obtain a semantic labeling of the axes of the perceptual space. Furthermore, the use of a more complete set of isolated sustained orchestral instrument stimuli (42 tones) makes it possible to treat a wider and more continuous scope of timbral differences (von Bismarck, 1974; Gordon and Grey, 1978), many of which have broader behavioral relevance as structural attributes of resonant sounds in general.

Secondly, we perform a regularized regression analysis to relate the perceptual MDS dimensions to the acoustic properties of the sounds. Current literature describes timbre as a combination of both spectral and temporal features of sound (Sethares, 2005, pp. 27–32) but treats spectral properties separately from temporal properties (Peeters and Deruty, 2010). By applying the spectrotemporal modulation power spectrum (MPS) to the physical characterization of instrumental sounds, our acoustical analysis advances the first comprehensive and unified description of physical sound structure causing listeners' gestalt percept of orchestral timbre.

Thirdly, debate has been unable to resolve the dimensionality of this perceptual space. Researchers have suggested dimensionalities from 2 to 4 [2 dimensions: Rasch and Plomp (1999) and Wessel (1979); 3 dimensions: Gordon and Grey (1978), Grey (1977), Marozeau et al. (2003), McAdams et al. (1995), and Plomp (1970); 4 dimensions: von Bismarck (1974) and Stepanek (2006)] but have never advanced a rigorous analytical argument for the claim. We solve this thorny issue by developing a novel cross-validation methodology for a recently developed nonclassical MDS procedure. The cross-validation results are confirmed by agreement with three further statistical procedures: (1) a more classical MDS model selection, (2) a significance test of the DFA of semantic ratings, and (3) the regression analysis between MDS coordinates and acoustical features. The consistency among these four statistical procedures confirms that 5 dimensions are necessary and sufficient to describe the perceptual timbre space of sustained orchestral tones, a complex yet salient percept underpinning the cognition of music.

METHODS

Subjects

Subjects had at least 3 years of musical or acoustical training (mean ± s.d. 9 ± 5.5 years) and were asked to exclude themselves if they thought they might have any hearing problems. The 33 subjects averaged 24 years in age; 14 were male and 19 female. Subjects gave written consent as approved by the Committee for the Protection of Human Subjects at the University of California, Berkeley.

Stimuli and presentation

We limited our study to the timbre of instruments found in the Western orchestra and used professional recordings of real instruments rather than synthetic sounds, to achieve focused ecological validity. Our sample strove to encompass the range of timbral perceptions at one pitch experienced by typical listeners of orchestral music (Plomp and Steeneken, 1969). The drawback of using stimuli not easily synthesized is the need for fine adjustments to normalize loudness, duration, and pitch.

Recordings that included sustained tones at E-flat in octave 4 (above middle C) were selected from the McGill University Master Samples collection (Opolko and Wapnick, 2006). The total of 66 recordings was reduced to a sample of 42 that would represent the variety of instruments and include muted and vibrato versions where possible (noted parenthetically as m and v, respectively): alto saxophone, alto flute, alto shawm, bass flute (v), Bach trumpet, baritone saxophone, Baroque alto recorder, Baroque tenor recorder, bass viol, B-flat trumpet (m), bass clarinet, bassoon, C trumpet, C trumpet (m), cello, cello (v), cello (mv), Classical oboe, cornet, double bass (m), double bass (v), E-flat clarinet, English horn, French horn, French horn (m), flute, flute (v), oboe, oboe d'amore, pan flute, soprano saxophone, soprano crumhorn, tenor saxophone, tenor trombone, tenor trombone (m), tuba, viola, viola (m), viola (v), violin, violin (m), violin (v). Each tone was re-sampled such that the fundamental peak in the spectral profile was shifted (≤ a whole tone) to 311 Hz.

Tone duration was subjectively shortened to 1 s in the following way. Attack and decay beginning and end points were noted subjectively by a third party. The Hilbert transform of the tones yielded an envelope, and the decay portion was extracted between the demarcated timepoints. The decay envelope was re-scaled in level such that its initial amplitude maximum was 1. The original envelope was then multiplied by the scaled decay envelope starting at a timepoint such that the total envelope length from beginning of attack to end-point of the decay envelope multiplier would equal 1 s, and the sound file was truncated at that point. An undesirable consequence was that this operation failed to preserve the potentially perceptible timbral phenomenon of individual harmonics dropping out at different relative times. However, this concern was surpassed by the concern that differences in duration might dwarf less salient differences in decay; attack properties are thought to more strongly influence perceptions of instrument identity (Saldanha and Corso, 1964).

Tones were then normalized for A-weighted rms sound level. Sounds were presented in a sound-attenuated booth, over Sennheiser HD580 precision (16 subjects) or Sennheiser HD250 linear II (17 subjects) headphones at a level set according to listener comfort by initial subjects and calibrated afterward to ∼65 dB SPL (B&K Level Meter, A-weighting, measured with headphone coupler from B&K, peak level with fast integration). Stimuli were controlled, and keyboard responses recorded, using the Psychophysics Toolbox version 3 (Brainard, 1997) in MATLAB 7.6.0 (R2008a) on a personal computer running Windows XP.

Experimental procedure

Dissimilarity judgments

Subjects first judged the dissimilarity of pairs of the normalized orchestral instrument tones on a differential scale of timbre.

The 42 tone stimuli were divided into three groups of 14 tones, and each subject made every possible unidirectional nonidentical pair-wise comparison (378) within a 28-tone subset comprising two of these groups. Groups were counterbalanced among the 33 subjects, so that the 861 comparisons possible among all 42 stimuli were represented >14 times in the entire data set. The sequence of pairs was pseudorandom and the first pair of stimuli reappeared at the end of the task, so that the difference with the first presentation could be used as a gauge of reliability (the mean difference on z-scored ratings was 0.713, less than 1 s.d.). Only the final response was taken for further analysis.

Instructions to subjects were, “Your task is to click menu buttons to play two tones as many times as you would like in order to judge how different they are in timbre. You will rate the similarity of the pair of tones relative to that of all other pairs of tones you've heard.” As training, subjects heard all of the stimuli in a random order so that they could calibrate their judgment of the average dissimilarity between tones. Subjects were encouraged to take breaks (total sessions were ∼1.8 h). For ease of comparison with previous studies (Wessel, 1979), subjects made the similarity ratings on a scale of 0 to 9 by typing a single digit at the keyboard or number pad: 0 = the same instrument played in the same manner; 1 to 3 = very similar instruments, or one instrument played in slightly different ways; 4 to 6 = an average level of similarity; 7 to 9 = very dissimilar tones. The dissimilarity judgments were transformed into z-scores for each individual.

Semantic judgments

Instructions on the qualitative task, performed after the dissimilarity task on the same 28 tones, were to assign a value to each tone on 16 semantic differential scales between pairs of opposites (e.g., calm vs explosive). Pairs included adjectives and parameters related to the tone color of the sound, spectral and temporal fluctuation, and envelope shape (see Fig. 1 for entire list). Subjects replayed each tone ad libitum and placed it on the semantic scales by typing a digit from 0 to 9 appearing between the pair of polar opposite attributes: for example, “Pleasant 0 1 2 3 4 5 6 7 8 9 Unpleasant.” Tones were presented in random order.

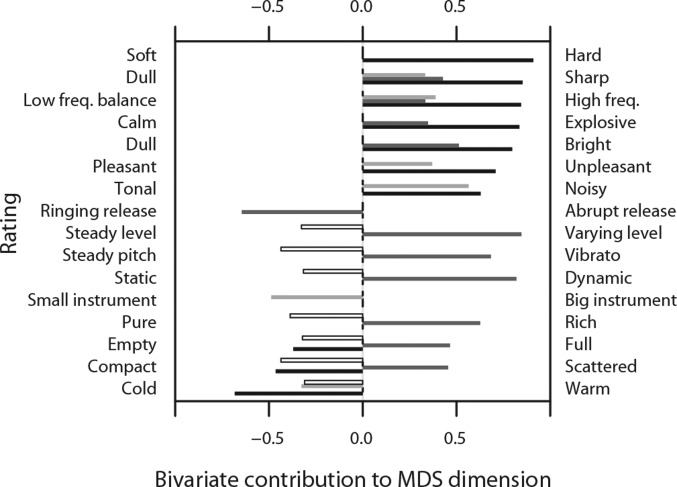
Figure 1.

Bivariate linear regression of semantic ratings on the 5 dimensions of the perceptual timbre space in Fig. 9a shows distinct semantic contributions to the primary 4 dimensions perceived. Black bars = rotated 5D MDS solution D1; dark gray = MDS D2; light gray = MDS D3; and white = MDS D4.

Perceptual analysis

Overview

Taking the two psychophysical tasks separately, first we related tones in a gestalt perceptual space based on an MDS of overall similarity, and second, we found verbally expressed dimensions by plotting tones on discriminant functions of the 16 semantic scales. Finally, we transformed the perceptual space so that instrument distances best matched their relations within the semantic DFA.

MDS algorithm

We used an MDS algorithm developed and implemented by de Leeuw and Mair (2009), called SMACOF, because in contrast to the classical scaling method, this iterative algorithm can perform a multi-way constrained MDS, in which multiple dissimilarity ratings (i.e., from different subjects) are used for each pair of stimuli. The constraint on the individual solutions guarantees that they are simple linear transformations (e.g., scaling and rotation) of a group solution (interpretable as a weighted and scaled average). The original SMACOF algorithm can already incorporate missing ratings, but we modified it to implement transformations for “left-out” subjects as a cross-validation, to obtain measures of predictive power. The algorithm is briefly described here (de Leeuw and Mair, 2009), and our changes in the following section.

In metric MDS, the configuration space X is defined as the position of n objects (here n instruments) in a Euclidean space of p dimensions. The optimal configuration is the one that minimizes the weighted (w_ij) sum of square errors between the empirical dissimilarities, δ_ij, and the distances, d_ij, in the metric space. This error is called the stress and is a function of X:

$$\sigma (X)={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{w}_{\mathit{i}\mathit{j}}{\left[{\delta }_{\mathit{i}\mathit{j}}-d_{\mathit{i}\mathit{j}}(X)\right]}^2}}.$$

The distances d_ij are the Euclidean distances:

$$d_{\mathit{i}\mathit{j}}=\sqrt{{\displaystyle \sum _{s=1}^p{\left(x_{\mathit{i}\mathit{s}}-x_{\mathit{j}\mathit{s}}\right)}^2}}.$$

When multiple subjects, K, are taken into consideration, the stress becomes:

$$\sigma (X)={\displaystyle \sum _{k=1}^K{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{w}_{\mathit{i}\mathit{j}\mathit{k}}{\left[{\delta }_{\mathit{i}\mathit{j}\mathit{k}}-d_{\mathit{i}\mathit{j}}(X_k)\right]}^2}}}.$$

Although each subject is allowed its own configuration, X_k, it is constrained to be a linear transformation of a group configuration, Z:

$$X_k=C_{k}Z.$$

This multi-subject algorithm takes three forms depending on whether the linear transformation C_k is unrestricted [IDIOSCAL (Individual Differences in Orientation Scaling)], diagonal [INDSCAL (Individual Differences in Scaling)], or set to the identity (Carroll and Chang, 1970). Both the group configuration, Z, and the transformation C_k are found by minimizing the stress function using optimization by majorization. In majorization, a two-argument function, τ(X,Y), is designed to be always greater than the function that is being minimized, σ(X), and equal when the two arguments are identical σ(X) = τ(X,X). The advantage of majorization is that although the minimum of σ(X) cannot be found analytically, one could find the minimum of τ(X,Y) with respect to its first argument X. One can then minimize σ(X) by an iterative procedure: (1) Initialize X and Y to X⁰; (2) Minimize τ(X,Y) with respect to X to find X^min; (3) Set X¹ = X^min; (4) Repeat step 2 with τ(X¹,X¹); (5) Iterate until σ(X) stops decreasing by a significant amount.

In the SMACOF algorithm, the (single-subject) stress is rewritten in matrix notation and after normalization (i.e., ${\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{\mathit{i}\mathit{j}}{\delta }_{\mathit{i}\mathit{j}}^2=1$ as $\sigma \hspace{0.17em}(X)=1+tr{X}^{\prime }VX-2tr{X}^{\prime }B(X)X.$

Here tr denotes the trace of a matrix, prime denotes its transpose, and V is the “weight” matrix $V={\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{\mathit{i}\mathit{j}}{A}_{\mathit{i}\mathit{j}}$ with $A_{\mathit{i}\mathit{j}}=(e_i-e_j)(e_i-e_j)\prime$ where e_i means a unit vector along the dimension i. Similarly for the cross-product term, B(X) must be defined as: $B(X)={\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{\mathit{i}\mathit{j}}{s}_{\mathit{i}\mathit{j}}(X)A_{\mathit{i}\mathit{j}}$ where $s_{\mathit{i}\mathit{j}}(X)={\delta }_{\mathit{i}\mathit{j}}/d_{\mathit{i}\mathit{j}}(X)$ if d_ij(X) > 0 and 0 otherwise. The majorization function is then given by:

$$\tau (X,Y)=1+tr{X}^{\prime }VX-2tr{X}^{\prime }B(Y)Y.$$

Minimizing τ with respect to X gives the simple update rule:

$$X^{\text{min}}=V^{-1}B(Y)Y.$$

When multiple subjects are taken into account the same equations are used but with a configuration supermatrix X′ = [X₁X₂… X_K]. Similarly V and B become block diagonal supermatrices.

The iterative process of majorization involves first obtaining an initial classical MDS estimate (Torgerson, 1958, pp. 1–460) for the group space based on the mean dissimilarities and setting all subject configurations to this group space. The majorization step is then used to get better configurations for each subject. The transformation C_k is derived (and updated in later iterations) and a new group configuration and individual configurations are obtained. Optimal C_k are obtained for each subject by finding the best projection onto scaled-and-rotated transformations of the previous group space. The updated group space (Z) is then obtained by inverting this transformation and applying to each subject's configuration and averaging. Each individual configuration is then set again to be equal to X_k = C_kZ. The iteration is then repeated until the stress fails to decrease. In our study, we use an R² measure to quantify the goodness of fit. The R² was defined as the proportional reduction in stress from a null configuration where all instruments are at the same location:

$$R^2=\frac{{\sigma }_T-\sigma (X)}{{\sigma }_T}\hspace{1em}\text{where}\hspace{1em}{\sigma }_T={\displaystyle \sum _{k=1}^K{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{w}_{\mathit{i}\mathit{j}\mathit{k}}{\left({\delta }_{\mathit{i}\mathit{j}\mathit{k}}\right)}^2}}}.$$

Cross-validation

Adding dimensions to the MDS will always reduce stress or equivalently increase R² between observed dissimilarities and the estimated distances. To judge the predictive power of each additional dimension, we used two methods: (a) we modified the SMACOF routine provided by de Leeuw and Mair (2009) to allow for cross-validation across subjects, and (b) we evaluated the goodness of fit as gauged by the Aikake Information Criterion (AIC) at different dimensions. The added complexity of the SMACOF MDS model, inherent to its efficient representation of each subject's individual difference as a rotation and scaling from the group (or average) MDS space, undermines the use of traditional model selection methods like AIC on the MDS solution dimensionality.

SMACOF across-subjects cross-validation.

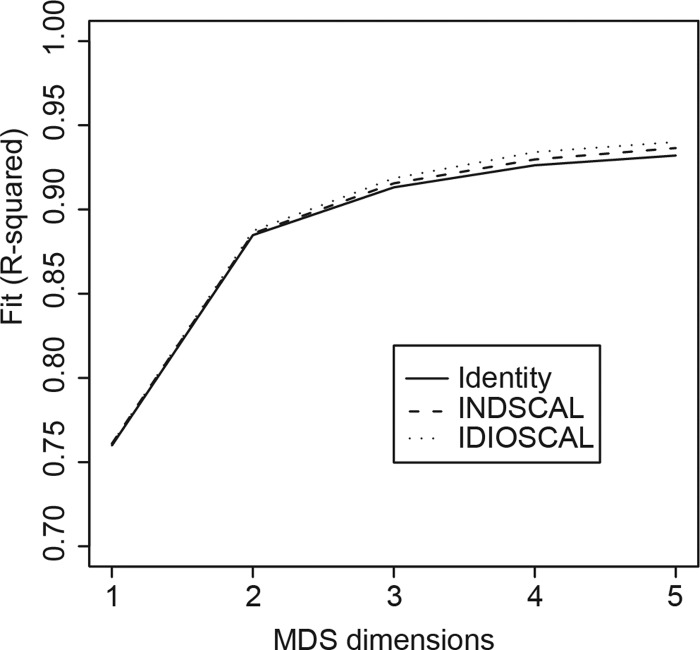
During cross-validation, we left out subjects singly from the optimization while still obtaining a configuration space for each left-out subject as a basis for calculation of R². In the multi-subject algorithm INDSCAL (Fig. 2), we calculated a transformation C_k for the left-out subject that distinguished the group configuration of the others from the SMACOF solution obtained at that particular step for the left-out subject. That solution was itself derived from the group average obtained at the previous iteration from the other subjects. The jackknifing procedure leaves each subject out in turn to determine an average and standard error for the R² of all left-out subjects. The initial starting point for the left-out subjects was also the classical MDS solution obtained from the average distances of the other subjects. In this manner we could apply the scaling and rotation for the left-out subject and obtain values of stress comparable to those obtained from the other subjects, but the data from the left-out subject could be excluded from the estimation of group means and the minimization of stress. This procedure allowed us to estimate the predictive power of the improvement in stress made by each additional MDS dimension. The results obtained with IDIOSCAL, INDSCAL, and the identity matrix were very similar, with the former two introducing small improvements (Fig. 2). In the cross-validation analysis, we chose INDSCAL as a good compromise between goodness of fit and the number of model parameters in the MDS. The cross-validated R² did not increase monotonically with the number of dimensions but plateaued around n = 5 dimensions [Fig. 3a]. This extension of the SMACOF routine is available as an R script upon demand.

Figure 2.

Comparison of IDIOSCAL, INDSCAL, and IDENTITY. The multi-subject algorithms in the SMACOF model, IDIOSCAL and INDSCAL, allow subjects to have different configurations than the “Identity” diagonal matrix alternative. Each algorithm produces a different version of the MDS. But all MDS versions showed similar coefficients of determination R². Fits from all three models plateaued with increasing dimensionality of the solution, corroborating the 5-dimension limit of descriptive power across subjects.

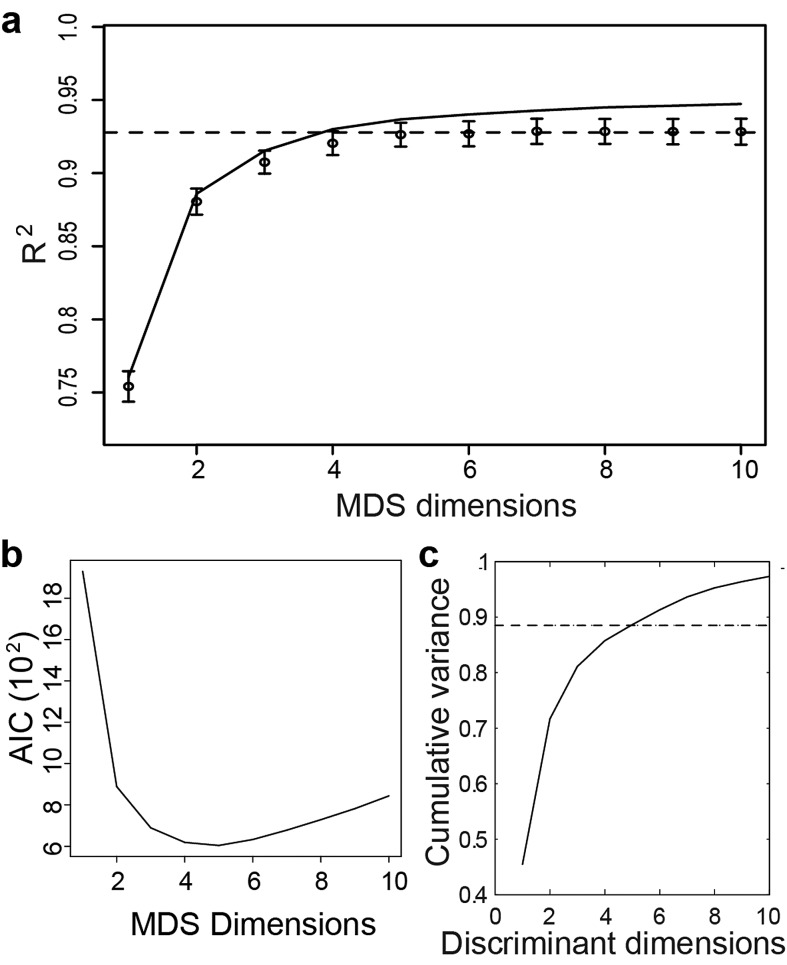
Figure 3.

Predictive power and significance of the number of dimensions in the MDS analysis of dissimilarity judgments (a and b) and in the DFA of semantic ratings (c). Cross-validation, model selection, and MANOVA analyses indicate that a 3D space suffices to describe much of perceptual timbre space as assessed by either dissimilarity judgments or semantic qualifications, but that 5 dimensions in total are merited. (a) The solid line shows the R² obtained for fitted subjects in the MDS analysis of dissimilarities. Circles show the average R² value obtained for the left-out subjects. Error bars represent one SEM. Dotted line represents the average R² value for the 5D through 10D solutions. The cross-validated R² plateaus beyond this point. (b) Aikake information criterion is minimal for 5 MDS dimensions, indicating this model is preferred for its simplicity balanced with goodness of fit. (c) The solid line shows the cumulative variance captured by successive discriminant functions for the normalized ratings in the semantic task. The MANOVA analysis shows that 5 dimensions provide statistically significant discriminations (see Sec. 3). The dotted line is provided for reference in judging that 5 dimensions suffice to describe the variation in qualitative ratings.

Model selection by AIC.

Because the treatment of individual differences played a negligible role (Fig. 2) in the MDS on our data, we also evaluated the goodness of fit of additional dimensions in a more classical MDS analysis (where the same solution is used for each subject) by calculating the AIC of each solution. Among competing models, the best one for the data at hand will produce the minimum AIC value. AIC depends on the log likelihood of the observed data given the model, penalized by the number of parameters in the model:

$$\text{AIC}=2k(p)-2\text{ln}\hspace{0.17em}L.$$

Here p is the dimensionality of the MDS solution, k(p) is the number of free parameters in the MDS model, and L is the likelihood. We calculated the AIC for the simplest MDS method in which the same group configuration is used for all subjects (i.e., C_k is the identity matrix). The use of this simple method allows us to apply AIC because the number of free model parameters becomes easy to estimate and does not increase with the number of observations (which would violate the asymptotic theory for maximum likelihood estimates). Although this is a more restricted case of MDS (and has fewer model parameters), the INDSCAL and the Identity methods generated very similar solutions and R² values from our data (Fig. 2). The number of parameters in the MDS model of dimensionality p is:

$$k(p)=n·p-p(p+1)/2,$$

where n is the number of objects in the space (here sound stimuli). To calculate the likelihood of the observed data given the model, one needs to assume an error model. A commonly used noise model in MDS is the log-normal model (Takane, 1994, p. 385):

$$\text{ln}\hspace{0.17em}{\delta }_{\mathit{i}\mathit{j}}=\hspace{0.17em}\text{ln}\hspace{0.17em}{d}_{\mathit{i}\mathit{j}}+\epsilon \hspace{0.17em}\text{and}\hspace{0.17em}\epsilon \hspace{0.17em}\sim N(0,\sigma ),$$

where δ is the observed responses collected for the perceived distance d_ij between stimuli i and j. The log likelihood is then:

$$\text{ln}\hspace{0.17em}L=-\frac{1}{2}\frac{S}{{\sigma }^2}+M\hspace{0.17em}\text{ln}\hspace{0.17em}{\sigma }^2,\hspace{0.17em}$$

where

$$S={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j>1}^n{\left[\text{ln}\hspace{0.17em}\left({\delta }_{\mathit{i}\mathit{j}}\right)-\text{ln}\hspace{0.17em}\left(d_{\mathit{i}\mathit{j}}\right)\right]}^2}}$$

and M is the number of distance measurements, M = n(n - 1)/2. The AIC calculated from our data was minimal for p = 5 [Fig. 3b], providing an alternative rationale for selecting the 5D MDS model as best for this data set.

Discriminant function analysis of semantic judgments

We also performed a classical DFA to find the smallest number of dimensions that describe the semantic timbre space based on the 16 qualitative descriptor ratings of each tone. The DFA finds the linear combinations of the original ratings that successively maximize the distance between the 42 tones while taking into account subject variability. These linear combinations are called discriminant functions (DF) and the significant DFs define a Euclidean space that captures the signal in the data. Mathematically, classical DFA is obtained by performing a principal component analysis (PCA) on the ratio of the between-variance matrix, obtained from the mean ratings for each instrument, and the within-variance matrix, obtained by averaging the variance across subjects for each instrument. The statistical significance of each dimension is obtained by multivariate analysis of variance (MANOVA): the p-value is obtained after calculating Wilks' Lambda statistic and comparing the results to expected distributions given the null hypothesis. The first several discriminant functions are analyzed because they represent a majority of variation. DFA was performed using the MANOVA function of MATLAB, and the PCA preceding it used raw ratings (without z-scoring) from subjects who completed all ratings.

Synthesis of dissimilarity MDS and semantic DFA via rotation

Isomorphic Procrustes rotation and reflection (performed in MATLAB; Schönemann, 1966) allowed us to cast the first two dimensions of the 5D dissimilarity MDS solution space into a space described by DF1 and DF2 of the semantic ratings. This recasting allowed us to compare the gestalt “timbral” space defined by dissimilarity judgments (MDS space) to the semantic “timbral” space defined by the descriptor ratings (DFA space). Positive results from the comparison permitted application of the semantic labels to the MDS dimensions.

Acoustical analysis

Spectrotemporal MPS

The MPS of a sound is the amplitude spectrum of the two-dimensional Fourier Transform of a time-frequency representation of the sound pressure waveform. The MPS can be taken for a single tone (Fig. 4), or the MPSs of all 42 tones can be averaged. First a spectrogram is calculated using Gaussian windows, which are symmetric in time and frequency domains, resulting in more conveniently invertible representations (Cohen, 1995, p. 108). As in the cepstrum, the logarithm of the amplitude of the spectrogram yields separate additive spectral and temporal modulation terms that would otherwise be multiplicative. For example, the spectral modulations composing the distribution of spectral power related to the percept of spectral balance separate from those composing the fundamental (Fig. 4, right column).

Figure 4.

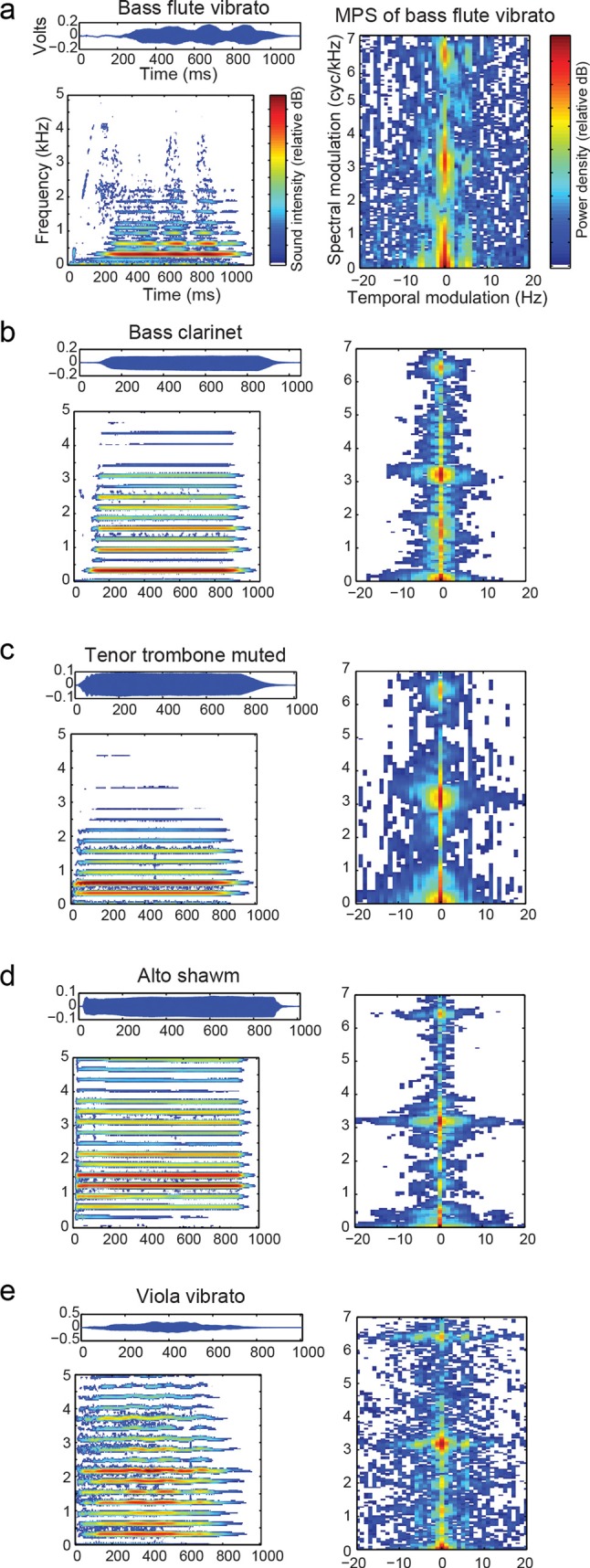
(Color online) Waveforms, frequencies, and spectrotemporal modulations differ between instrument tones normalized for fundamental frequency (311 Hz), sound level and duration. Oscillogram (top left panel), spectrogram (bottom left panel), and spectrotemporal MPS (right panel) of perceptually dissimilar example stimuli representing different instrumental families. (a) bass flute with vibrato; (b) bass clarinet; (c) tenor trombone with mute; (d) alto shawm; and (e) viola with vibrato. White areas represent modulation power below 78 relative dB.

The resulting MPS is the square amplitude as a function of the Fourier pairs of the time and frequency coordinates of a spectrogram of the original log-amplitude spectrogram. The MPS has axes referred to as temporal modulations (in Hz) and spectral modulations (in cycles/kHz). Positive and negative temporal modulations ω_t, by convention, distinguish upward frequency modulations [e.g., cos(ω_sf-ω_tt) for positive ω_t and ω_s] from downward modulations [e.g. cos(ω_sf + ω_tt)] of spectral modulation ω_s. The resolution of the spectrogram in time and frequency, set by the width of the Gaussian window, determines the upper bounds of the temporal and spectral modulation in an inverse relationship known as the time-frequency (TF) tradeoff. The TF scale is necessarily chosen with the modulation frequencies of interest held in mind, so that most of the energy in the MPS is far from these boundaries (Singh and Theunissen, 2003). The TF scale used was given by a Gaussian window of 5 ms in the time domain, or 32 Hz in the frequency domain $\left({\sigma }_t=1/2\pi {\sigma }_f\right)$, with upper bounds of 100 Hz and 64 cycles/kHz, respectively. Modulation patterns important for timbre are better resolved when a spectrogram rather than a cochleogram is taken as the initial time-frequency representation (Fig. 5), because the MPS in cycles/octave units does not reveal harmonic regularities. Cycles/kHz units reveal a separation between formants and power at alternating harmonics, for example.

Figure 5.

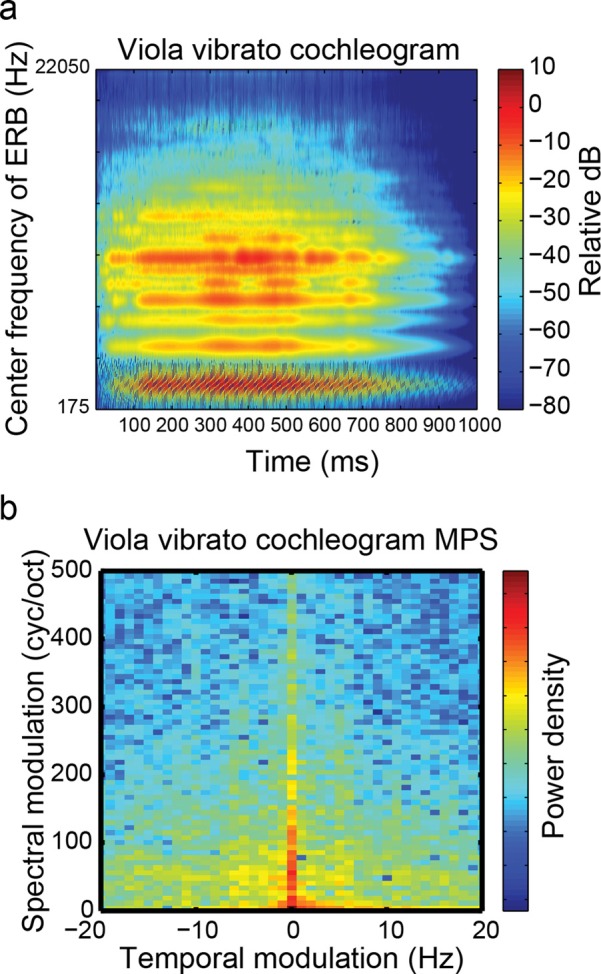
(Color online) Modulation power spectra from cochleograms. Cochleograms (a cochlear filter bank with logarithmically spaced center frequencies) are often used as the initial time-frequency representation of sounds since they better model the peripheral neural representation (Schreiner et al., 2011). In this case the spectral dimension of the MPS yields cycles/octave instead of cycles/kHz. This figure illustrates that the spectral modulation patterns important for timbre are not well resolved using cochleograms. (a) As an example, a cochleogram representing spectral features of the viola vibrato tone across time. Independent filters model the aural output available to the auditory system, based on Patterson's gammatone filterbank (Clark, 2007). (b) MPS of the cochleogram in (a) shows a monotonic decrease in power away from the origin, without distinction between spectral modulations higher or lower than those of the fundamental that we would find in the linear MPS. Thus, although this representation might be more relevant for modeling peripheral neural representation, we find it harder to interpret for acoustic analysis and psychophysical studies such as this one.

PCA of MPS

Before performing the regression between perceptual distances and sound features described by the MPS, we analyzed the principal components of the MPS across the 42 stimuli in order to reduce the dimensionality of that representation.

Of 41 possible principal components (PCs), only the first 20 principal components (PCs) were included for the regression analysis because they represent a reasonable amount of the variance and because they yielded the best cross-validated predictions (adjusted R²) of perceived timbre, as compared with other multiples of 5 PCs up to 40 PCs.

The MPS representation is not, however, a complete description of the physical sound features and in particular the modulation phase could also play an important role. The role of phase may be better captured by other measures such as the spectral mean below.

Alternative spectral and temporal feature calculation

More traditional acoustic features that separately describe the spectral and temporal envelope were calculated for comparison with the MPS analysis.

The shape of these envelopes was quantified by the equivalent of the statistical moments. To describe spectral shape, we first normalized the frequency power spectrum to obtain: p(f_i) where f_i = frequencies and ${\sum }_{i=1}^{N}p(f_i)=1$. One can then define and calculate the mean spectral frequency $\overline{f}={\sum }_{i=1}^N{f}_{i}p(f_i)$ and the standard deviation of the spectrum ${\sigma }_f^2={\sum }_{i=1}^{N}p(f_i){(f_i-\overline{f})}^2$. Using these values, we obtained normalized measures of spectral skew and kurtosis given by:

$$\begin{array}{c}\text{Skew}=\sum _{i=1}^{N}p(f_i){(f_i-\overline{f})}^3\times \frac{1}{{\sigma }^3}\hspace{0.17em}\text{and}\\ \text{Kurt}={\displaystyle \sum _{i=1}^{N}p(f_i){(f_i-\overline{f})}^4\times \frac{1}{{\sigma }^4}}.\end{array}$$

We also used an entropy measure to further characterize finer details in the shape. The spectral entropy was calculated as $-\left\{{\sum }_{i=1}^{N}p(f_i)\hspace{0.17em}{\text{log}}_2\hspace{0.17em}\left[p(f_i)\right]\right\}/{\text{log}}_2\hspace{0.17em}(N)$. Complementary measures were also obtained from a normalized temporal envelope. The entropy measures embody the higher moments and allow one to distinguish envelope profiles with many ripples (e.g., harmonic stacks or tremolo) from more static shapes (e.g., noisy spectral sounds or steady amplitude). The temporal envelope was obtained by rectification of the sound pressure waveform and low-pass filtering below 20 Hz. The spectral envelope was obtained by the Welch's modified periodogram estimation of the power spectral density using a Hamming window of 23 ms. Similar metrics for describing spectral and temporal shape have also been proposed by others (Sueur et al., 2008).

Psychophysical analysis

Ridge regression of perceptual space with either the MPS or a traditional acoustic description

Because multiple linear regression is generally prone to overfitting noise, regularization is used to constrain the complexity of the model while optimizing its fit to the data. The regularization we used combined principal component regression and ridge regression (Hoerl and Kennard, 1970). In ridge regression, also called L2-regularization, the prior probability distribution of predictor weighting (of the 20 PCs representing the MPS, or of the traditional acoustical features) is Gaussian and centered at zero, and a “ridge parameter” (inversely related to the width of the Gaussian) is used to effectively restrict the effect of predictors with low predictive power. We evaluated ridge parameters from 0.1 to 1000. To cross-validate the predictive power of the resulting models in a bias-free manner and to determine model significance, we used a jackknife resampling procedure. In this procedure, one instrument at a time is removed from the regression analysis. The error in those predictions yields an adjusted R² value and is used for evaluating model significance. The best cross-validated predictions from MPS regressors were obtained by using only the first 20 PCs of the MPS (see Sec. 2E) and ridge parameter values of 5 (MDS D1 and D4), 10 (D2) or 50 (D5). D3 did not correlate significantly with the PCs of the MPS, regardless of ridge parameter. For the regression analysis using the more traditional sound features defined in subsection F.3 above, we found that ridge parameter values of 0.1 (D1), 5 (D3), and 10 (D2 and D4) gave maximum R² values in the cross-validation data set. D5 did not correlate significantly with any traditional parameter.

This multivariate linear regression analysis also confirms that the ordering generated in the 5 MDS dimensions is not random, since a significant correlation was found between the coordinates of stimuli in the 5 perceptual MDS dimensions and the physical descriptions of the acoustical features of stimuli obtained either by the MPS (Fig. 6) or by more classical sound features.

Figure 6.

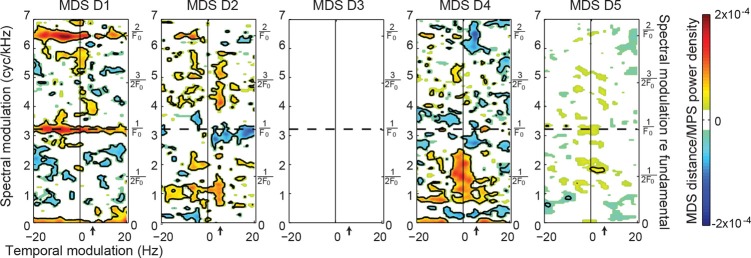
(Color online) Distinct spectrotemporal modulations correlate with relative locations in perceptual timbre space. The first 20 PCs of the MPS of the instrumental tones were regressed with the MDS coordinates for each instrument after rotational scaling. Colors toward red indicate that a power increase in that region of the MPS correlates with positive distance values along that dimension of the 5D MDS solution (plot title); blue indicates that a power increase correlates with negative distances. White indicates areas of low predictive power (<2 s.e.m.); contours enclose smoothed areas above or below 20% of overall maximum. X-axis arrows at 6 Hz are characteristic of vibrato. The right side y-axis labels give spectral modulations in units of the period of the fundamental (1/311 s).

To compare the predictive power of the traditional sound features with the MPS features, we used the same ridge regression algorithm and cross-validation approach. All 11 traditional features were used as regressors, and we compared adjusted R² values between the regressions.

Bivariate regression of perceptual space on traditional acoustic features alone

Bivariate correlation coefficients were calculated to evaluate the potential contribution of each traditional acoustic feature individually to the variation along the 5 dimensions of perceptual timbre space (Fig. 7).

Figure 7.

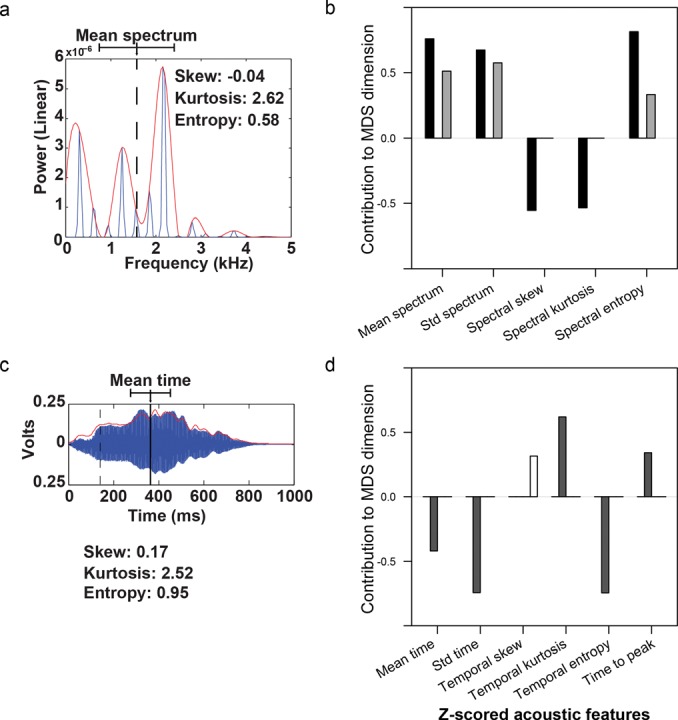
(Color online) Spectral and temporal envelope sound features and timbre. Diagrams of traditional (a) spectral and (c) temporal acoustic features extracted from the stimuli. (a) Spectral acoustic features of the example viola vibrato tone include mean (dashed line) of the power spectral density (blue line; red line its envelope); standard deviation of power spectrum (whiskers around dashed line); and skew, kurtosis, and entropy (inset). (b) Bivariate correlation coefficients between the spectral envelope features and the first 4 dimensions of the rotated MDS solution representing perceptual timbre. Black = D1; dark gray = D2; light gray = D3; and white = D4. Only significant correlation coefficients (p < 0.05) are shown. (c) Temporal features symmetric to those of the same example tone as in a, with mean temporal envelope represented as a solid vertical line. Dashed line shows the end of the attack. (d) Bivariate correlation coefficients of perceptual timbre space on temporal acoustic features as in Fig. 7b.

RESULTS

This study evaluated the dimensionality of perceived orchestral timbre, correlated timbre with differences in comprehensively expressed acoustic properties, and confirmed the ecological validity of the perceptual timbre space using semantics.

Acoustic structure of instrument stimuli

We examined the perceptual and acoustical nature of 42 tones produced by Western orchestral instruments, at the same note (E-flat) with the same intensity and length. Exemplars of the instrument families represented in the tones have distinct spectrograms (Fig. 4, left plots) with unique amplitude envelopes, spectral balance and dynamics. Another exceptionally powerful representation for acoustic analysis of perceptible features, which are often jointly spectrotemopral, is the MPS, because it unifies spectral and temporal domains. The MPS is insensitive to the phase of features, and quantifies power in particular spectrotemporal structures that would often be superimposed in a spectrogram (Elliott and Theunissen, 2009; Singh and Theunissen, 2003). A PCA of the MPS across instruments was performed both to examine the combination of acoustical features that varied the most across instruments and to reduce the dimensionality of this representation for analyzing the relation of the physical structure of the sounds to their perceived timbre. The first 20 PCs were retained for this purpose (see Sec. 2).

The distinctive properties of modulation power, as they appear in the example plots (Fig. 4, right) and the average MPS [Fig. 8a], are as follows. The MPS of each instrument shows a peak spectral modulation power at 3.22 cycles/kHz corresponding to the natural spacing of harmonics of the E-flat fundamental (F₀ = 1000/3.22 = 311 Hz). Spectral modulations at multiples of this 3.22 cycles/kHz peak indicate the spectral shape of harmonic bands whereas power at fractions of 1/F₀ reflect spectral energy balance across harmonics. For example, the suppression of power in even harmonics of the bass clarinet results in a secondary peak at 1/2F₀ [Fig. 4b]. Spectral formants are defined as prominent power in local frequency regions and result from linear filtering properties of the instruments independent of the fundamental (Handel, 1995). Formants appear in the MPS as low spectral modulations (well below 1/2F₀ and with temporal modulation close to 0 Hz). The single formant caused by low spectral balance in flute and trombone [Figs. 4a, 4c], manifests as a wide spread of spectral modulation power from 0 to ∼1 cycles/kHz, whereas the multiple formants present in viola and alto shawm [Figs. 4d, 4e] result in more peaked energy including below 1 cycles/kHz. Spectral distributions change with a temporal dynamic evident in their distance from the y-axis: a relatively delayed onset of higher harmonics with respect to that of the fundamental, representative of the brass family, appears as an upsweep bias of spectral modulations toward the left quadrant at 3.2 cycles/kHz in trombone [Fig. 4c] and other instruments predicted by weighting of PC3. The temporal modulations of tremolo and vibrato characteristic of woodwinds and strings appear laterally at ∼6 Hz (Brown and Vaughn, 1996; Fletcher and Sanders, 1967; Strong and Clark, 1967). Tremolo is a fluctuating change in overall amplitude that can be seen as a peak of energy on the x-axis (0 spectral modulation) ∼6 Hz [bass flute vibrato, Fig. 4a] while a pure vibrato fluctuating in pitch without change in amplitude would appear as a peak also at ∼6 Hz but with spectral modulations corresponding to the fundamental, 1/F₀ and its multiples [viola vibrato, Fig. 4e, see also synthesized sounds in Figs. 8b, 8c]. The fast attack and decay of the alto shawm [Fig. 4d] increases pure temporal modulations from 0 to 20 Hz because of the sudden changes. The slower attack and decay of the viola [Fig. 4e] has more peaked overall amplitude modulations, which resembles intermediate (∼3 Hz) ongoing temporal dynamics as in, e.g., a crescendo.

Figure 8.

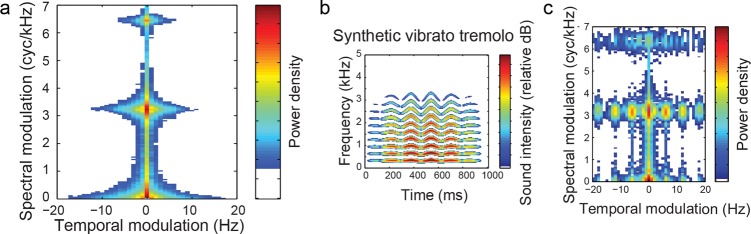
(Color online) MPS of illustrative sounds. General properties of the MPS of the 42 tones reflect their pitch (normalized at E-flat) and their overall envelope shape. (a)The average MPS of all 42 stimuli shows peaks at multiples of spectral modulations associated with the fundamental. (b) For illustration purposes, the spectrogram of a tone synthesized to have cosine ramped amplitude, with overtones' power dropping off as cos², a 0-to 100 cents vibrato, and 0-to-6 Hz tremolo. (c) The MPS of the synthetic tone in Fig. 8b.

Ordination of perceived timbre dissimilarity

We represented the perceived dissimilarities in timbre as distances between tones by fitting the ratings to a model space using MDS. The MDS solutions improve in fit with increasing dimensionality of the space, but solutions with relatively few dimensions represent a substantial portion of the timbral differences judged by listeners [Fig. 3a]. The solution in 3 dimensions explains 91.5% of the squared distance between instruments.

Dimensionality of perceived timbre dissimilarity

Because increasing the dimensions in the MDS analysis always results in improvements in fitting a given set of pair-wise dissimilarities, MDS is prone to overfitting. The benefit from using additional dimensions does not necessarily generalize to another data sample. To study the significance of the various possible dimensionalities of the perceptual timbre space, we examined the predictive power gained by successive dimensions, by (1) developing and implementing a novel cross-validation procedure and (2) evaluating the AIC. In the cross-validation procedure, the dissimilarity ratings by a left-out subject are transformed into coordinates along with other data but are excluded when minimizing the MDS stress function to find the optimal dimensions (see Sec. 2). The cross-validation procedure allows us to estimate the standard error of the goodness of fit and also to determine the upper dimension above which improvement in fit stops increasing. The adjusted R² first decreased at 9 dimensions, so we evaluated the dimensionalities within 1 s.e.m. of this R², namely, 5 to 10 dimensions, whose averaged R² is shown as the dotted line in Fig. 3a. Because the error bars (2 standard errors) of dimensionality 4 just crossed this line, we judged the minimum number of significant dimensions to be five. Together with the fact that the fifth dimension is correlated with acoustical features (below), the evaluation shows that there is no substantial improvement in fit beyond 5 dimensions [Fig. 3a], and 5 dimensions did not overfit the data. Standard errors overlap between adjacent dimensionalities around 5, but not between, e.g., 3 and 5 dimensions. This relative plateau in stress with increasing dimensionality was essentially unchanged even when we removed individual instruments in turn from the MDS analysis (not shown), supporting the notion that our stimulus set was sufficiently large to encompass the perceptual timbre range of the Western orchestra. Evaluation of the AIC led to the same conclusion. The AIC reached its minimum at 5 dimensions, supporting the claim that a 5D timbre space provides the best fit to the data without overfitting.

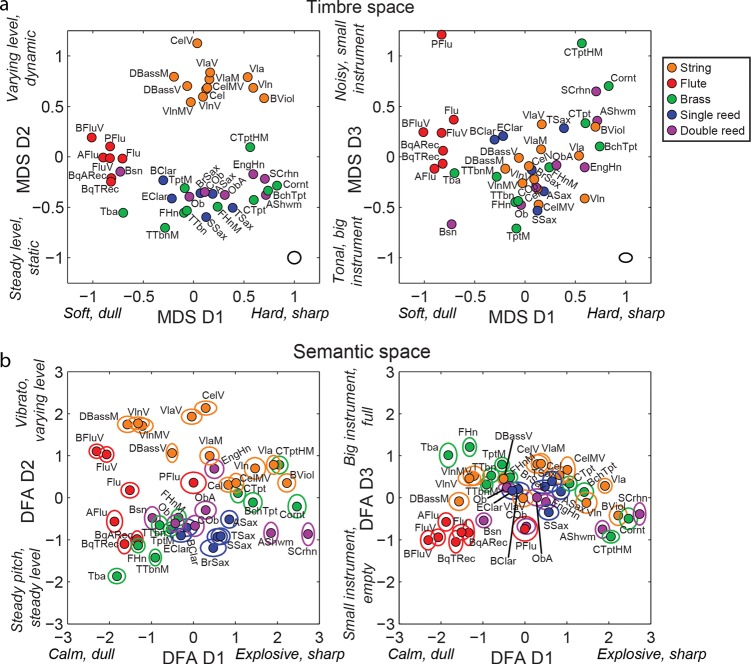
The 5D solution of the MDS converged after 100 iterations and was well correlated with observed dissimilarities (R² = 0.93). Tones ordered by the first 2 dimensions of the 5D MDS solution [Fig. 9a, left] clustered roughly into instrument families, with flutes low on the primary dimension (D1), brass and reeds on a continuum across D1, and strings well separated high on D2. Families overlapped on D3 and D4, but D5 separated the brass (all positive) from the reeds (all negative).

Figure 9.

(Color online) Instrument locations in perceptual timbre space. (a) The first vs second dimensions (left plot), and first vs third dimensions (right), of the five-dimensional MDS solution of the dissimilarity judgments, projected after rotational scaling onto the primary two DFs of the semantic ratings. Tones from different families (“flutes” includes end-blown flutes) are distributed unevenly among the quadrants. Instrument abbreviations (M = muted, V = vibrato): ASax alto saxophone; AFlu alto flute; AShwm alto shawm; BFluV bass flute; BchTpt Bach trumpet; BrSax baritone saxophone; BqARec Baroque alto recorder; BqTRec Baroque tenor recorder; BViol bass viol; TptM B-flat trumpet; BClar bass clarinet; Bsn bassoon; CTpt C trumpet; CTptHM C trumpet with Harmon mute; Cel, CelV and CelMV cello; COb Classical oboe; Cornt cornet; DBassM double bass; DBassV double bass; EClar E-flat clarinet; EngHn English horn; FHn and FHnM French horn; Flu and FluV flute; Ob oboe; ObA oboe d'amore; PFlu pan flute; SSax soprano sax; SCrhn soprano crumhorn; TSax tenor saxophone; TTbn and TTbnM tenor trombone; Tba tuba; V1a, V1aM and V1aV viola; V1n, V1nM and V1nV violin. Black ovals (lower right inset) represent SEM. (b) Semantic ratings for each instrument projected onto the first 3 discriminant functions (DF1, DF2, and DF3). The discriminant functions are the linear combinations of ratings that maximize the normalized distance between instruments. Ovals represent SEM of the average projected ratings. Symbol color shows instrument family as in Fig. 9a.

Discriminant function analysis of semantic timbre characterization

To obtain a qualitative interpretation of timbre space, we performed a DFA on the ratings from the semantic judgment task. The first 5 discriminant functions (DFs) explained 88.6% of the variance. Instruments in the same families grouped together with some proximity [Fig. 9b], but less so than in the MDS solution [Fig. 9a]. Instruments with large DF1 values rated most strongly explosive, sharp and steady pitch. DF2 loaded most heavily ratings of vibrato, varying level, and sharp. DF3 weighted most the descriptors big instrument, full, and tonal.

The DFA can also be used to reduce dimensionality since it ranks dimensions. Here, the significance of the discriminant dimensions was assessed by classical MANOVA: the p-values for 5th and 6th dimension respectively were 0.002 and 0.0938. Thus, as did the dissimilarity MDS, the semantic DFA suggested that a 5-dimensional space suffices to describe much of timbre [Fig. 3c].

Interpreting perceptual timbre space in semantic terms

To compare the ordinations of instruments that resulted from the dissimilarity-based MDS and the semantic DFA, and to assign qualitative labels to the dimensions obtained in the MDS, we reoriented the first two dimensions of the 5D MDS solution by a Procrustes transformation without scaling (reflection and rotation) onto the first two dimensions of the DFA solution. This oriented and labeled version of the MDS solution is what we henceforth call “the perceptual timbre space” and use in all subsequent analyses [Fig. 9a]. In this perceptual timbre space, distances represent quantitative differences in gestalt timbre, and each axis direction best explains the major qualitative differences, or semantic variance, between tones as assessed by the DFA.

The overall arrangement of instruments in the two solution spaces, compared by visual inspection of the rotated MDS solution and the DFA solution, are preserved [Figs. 9a, 9b], although exact distances differed somewhat.

By rotating the MDS solution to the DFA we could assign semantic ratings to it. However, since the similarity between the two resulting solutions is imperfect and since the discriminant functions are composed of potentially redundant rating scales, we also used bivariate linear regression to show contributions of the individual semantic differential scales to the five dimensions of the rotated MDS solution (Fig. 1). This complementary analysis provides a quantitative assessment of the importance of each label to the MDS dimension. In good agreement with the Procrustes rotation of the MDS to the semantic DFA, the bivariate contributions show ratings of hard, sharp, high-frequency energy balance, and explosive contributed the most to D1 of the MDS (Fig. 1, black bars), while ratings of varying level, dynamic, vibrato, and ringing release best accounted for positive values in D2 (dark gray bars). D3 (light gray bars) was explained best by ratings of noisy, small instrument, unpleasant. D4 (white bars) correlates best with ratings of compact, steady pitch, and pure. MDS D5 had no significant correlates among our semantic descriptor pairs.

Subjects segregated their applications of descriptors, according to the bivariate analysis, in correspondence with the mathematical orthogonality of the first two rotated MDS dimensions. With the exception of steady-pitch/vibrato, descriptor pairs with high coefficients for MDS D1 have low coefficients for MDS D2 and vice versa.

Acoustic basis of perceived timbre

The spectral and temporal acoustic information present in the stimuli is most effectively represented by the joint spectrotemporal MPS, so we examined which of these modulations contribute to the orthogonal percepts.

In a ridge regression analysis, the coefficients of the first 20 PCs of the MPS of each tone were used to predict its position in the perceptual timbre dimensions [Fig. 9a]. The 20 regression weights can then be multiplied by the principal component vector to obtain the regression weights in the MPS space (Fig. 6) for each perceptual dimension. Acoustic features of the MPS correlate significantly with four perceptual dimensions after jackknife cross-validation: the maximum adjusted R² was 0.73 for D1; 0.59 D2; 0.6 D4; and 0.1 D5. D3 did not correlate significantly with the PCs of the MPS, regardless of ridge parameter, suggesting either that perceptual ordering of this “noisy, small instrument, unpleasant” dimension does not depend on spectrotemporal modulations, or that it does so in a nonlinear way. Notably, the spectral mean considered among the traditional acoustic features below has no representation in the MPS (except as the phase of the amplitude spectrum, not included in the MPS analysis).

The modulation contributions display distinct patterns (Fig. 6). Percepts high on D1 of the perceptual timbre space (associated with hard) were explained by an increase in broad temporal modulation power from 0 to >20 Hz, corresponding to fast transients both in the overall envelope and individual harmonics. The asymmetric power peaking in the left quadrant (corresponding to up-sweeps) is caused by delays in these transients such as in the arrival of higher harmonics. In an orthogonal pattern to that of D1, contributions to percepts high on D2 included increases in ±2 and ±6 Hz temporal modulations of broad spectral patterns (vertical yellow bands), together with small decreases in fluctuations of individual harmonics (blue areas at dotted reference line). Thus sounds high on D2 have slower than average modulations of partials. D4 entails a distribution of spectral power between alternating (either all odd or even) harmonics (red area at 1/2F₀ cycles/kHz spectral modulation) along with a small decrease in power at slower spectral modulations in the region of formants (lowest blue areas). High-D4 instruments also included amplitude modulations >6 Hz (yellow to the right of arrow on x-axis) corresponding to faster dynamics. Instruments high on D5 have more power in select areas <6 Hz (yellow near the y-axis). The restricted nature of the modulation features appearing in D5 reflect the subtlety of this dimension as compared with acoustical variation along the other dimensions of perceptual timbre space.

Despite the orthogonality between D1 and D2, all 4 correlated dimensions are predicted by complex joint spectrotemporal power related to tonal resonance. On the other hand, there is a segmentation of temporal features below, at, and above ∼6 Hz (arrows) that correlate severally with perceptual dimensions. Similarly, we find a segmentation of spectral structure related to tonal resonance (at ratios and multiples of 1/F_o) and more invariant “fixed” spectral formants (D2 and D4).

Traditional spectral and temporal acoustic features associated with perceptual timbre space

Since previous researchers used purely spectral or temporal terms to describe perceptual qualities of timbre, we extracted 11 such traditional acoustic parameters (Fig. 7) and compared their PCs with distances in perceptual timbre space. The traditional features systematically described the temporal and spectral envelope of each sound, characterized by the moments of their power density distributions (mean, spread, skew, and kurtosis) and an equivalent of the distributions' entropy. We performed two regression analyses with these traditional features on the perceptual MDS dimensions. First, a regularized multivariate regression analysis showed that the combination of these acoustical descriptors can be used to predict the perceptual score of instruments in the MDS space for dimensions 1 to 4 with estimated adjusted R² values of 0.7 for D1, 0.57 for D2, 0.40 for D3, and 0.22 for D4.

Second, to identify contributions of particular features, we then performed bivariate linear regression of the traditional acoustic features on the perceptual timbre space. All 5 spectral features contributed to rotated MDS D1, and D3 was similarly correlated with exclusively spectral features [Fig. 7b], whereas features correlated with D2 and D4 were exclusively temporal [Fig. 7d]. The spectral contrast between MDS D1 and MDS D3 is that only D1 is correlated (inversely) with the spectral measures of skew and kurtosis; sounds high in D1 have relatively more power in higher harmonics than lower harmonics, and greater peakedness in spectrum [Fig. 7b]. However, as discussed below, these spectral features may be only secondary determinants of MDS D1, because in combination with the MPS acoustic analysis it appears that D1 is principally determined by fast spectrotemporal differences including the attack. D3 is more straightforwardly interpretable as purely spectral: instruments that score high in D3 (noisy, small instrument, unpleasant) have a power spectrum where the energy is shifted toward the higher frequencies, resulting in higher mean and greater bandwidth (spectral s.d.).

The regression results for D2 (varying level, dynamic) would initially suggest a perceptual role for the shape of the attack, since both mean time and time-to-peak are significant regressors, except that the time-to-peak coefficient indicates that slower attacks are found for instruments high in D2, whereas the negative mean time contribution indicates the opposite [Fig. 7d]. In fact, as described above and further discussed below, D2 is principally determined by ongoing fluctuations in the temporal envelope, corroborated by the observed temporal envelope entropy. Stimuli that have such dynamic temporal envelopes also tend to have longer times-to-peak, and mean times lying in the first half of the tone.

MDS D4 (steady pitch, compact, pure) shows only weak correlation with the temporal skew, with instruments high on D4 having more positive skew, meaning a slightly longer decay relative to the attack [Fig. 7d].

Contrast of acoustic analyses

The comparison of the two acoustical analyses showed striking contrasts underscoring (1) the power of the MPS to describe perceptually relevant acoustic structure, (2) the utility of complementary measures, and (3) the difficulty in interpreting regression results based on correlated descriptors.

We note that both acoustical analyses resulted in high predictive values in multiple linear regression. However, these predictions can be either similar in quality, as they were for D1, or drastically opposed, as they were for D3 and D4. Whereas MDS D3 was not significantly correlated with the MPS, it correlated highly with spectral envelope attributes (adjusted R² values of 0 vs 0.4, respectively) such as the spectral mean, which is not represented in the MPS. On the other hand, MDS D4 has strong correlations with the MPS, but weak correlations with temporal envelope features (adjusted R² of 0.6 vs 0.2) and none with spectral ones. The MPS analysis shows D4 is strongly affected by the spectral structure corresponding to differential power in odd and even harmonics and this quality is poorly captured by traditional spectral measures.

Thus, comparison revealed that interpretation of either analysis could be misleading on its own, without an account of the other. Combining analyses brought forward that the traditional spectral features contributing to percepts high on MDS D1 are characterized by fast transients (modulations at high temporal frequencies) in both the overall envelope and in the natural harmonic components that were not captured by traditional temporal measures averaging across the entire tone duration. Similarly, combined analyses show that the traditional temporal features uniquely indicated for MDS D2, such as kurtosis and time-to-peak, involve principally low frequency modulations in the amplitude envelope (blue and yellow areas at x-axis, Fig. 6), and particular intermediate (6 Hz) modulations in distribution of power across harmonic partials (yellow indicated by arrow, Fig. 6), rather than traditionally measured envelope changes associated with tremolo, or the duration of attack per se.

In summary, the two acoustic analyses are strongly complementary. When both give positive correlation results, the MPS analysis has the advantage of being more quantitative and detailed. For example, the MPS specifies 4 Hz temporal modulation frequencies at the boundary between perceptual dimensions D2 and D4 (vertical contours, Fig. 6). Furthermore, the combination of analyses shows that diverse acoustical parameters can be correlated and yet some may disappear in the averaging along either the spectral or temporal dimension alone.

DISCUSSION

Our key findings first robustly assess the dimensionality of timbre perceived in instrumental tones, and second, relate the five perceptual timbre dimensions to an unprecedentedly complete physical acoustic structure, quantified by both the MPS and more traditional acoustical measures.

The first limitation of earlier studies that arrived at a timbre map by geometrical scaling analysis (i.e., MDS) of dissimilarities between paired instruments (von Bismarck, 1974; Grey, 1977) has been an inability to demonstrate perceptual sufficiency. Albert Bregman drew attention to the difficulty of making a complete description of timbral dimensions based on such perceptual maps (Bregman, 1990, p. 125), “None of these [MDS] attempts to find a reduced number of dimensions to account for differences in perceived timbre has been able to show that the dimensions identified as the important ones are completely adequate, even within the restricted range of stimuli used, to account for differences in the qualities of the sounds.” In this study, we have addressed this shortcoming for one class of instruments. The sufficiency of 5 dimensions in representing perceptual timbre space is justified by evaluating the changes in predictive power of additional dimensions in the MDS solution. Predictive power is demonstrated both by a well-established model selection statistic, the AIC, and by cross-validation of a nonlinear MDS algorithm incorporating individual differences. As additional evidence that we are not overestimating the number of dimensions, we show that these 5 perceptual dimensions each have correlates with particular physical attributes of the sound.

At the same time, we extend the range of stimuli to a broad set of Western orchestral instruments. Finally, we make a qualitative interpretation by relating the perceptual space to semantic qualifications made by musicians. The DFA of these semantic measures independently supports the sufficiency of 5 perceptual dimensions.

Dimensionality of perceived instrumental timbre

To evaluate the dimensionality of the MDS solution space while addressing the problem of overfitting, we adapted a cross-validation technique to the particular case of subject-weighted MDS. Specifically, the jackknifing cross-validation determines the number of dimensions that can be confidently used to fit SMACOF MDS solutions in which individuals' distance judgments weight dimensions differently. The point at which increased dimensionality makes no improvement in predictions on alternately left-out subjects indicates the upper limit of perceptual dimensionality that can be supported with confidence by judgments across subjects. We further validated this statistical analysis by estimating the AIC for MDS solutions from 1 to 10 dimensions. Here again, in the case of the AIC model selection, the MDS model that best supports the data is five dimensional.

The result that there was no increase in goodness of fit beyond 5 dimensions means that the perception of sustained orchestral instrument timbre that is held in common between our subjects has no more than 5 dimensions [Fig. 3a]. To our knowledge we have made the first cross-validation of an MDS using individual differences, and this method should be widely applicable as an alternative to other model validation methods for classical MDS such as the AIC used here or the Bayesian Information Criterion used in previous research (Winsberg and De Soete, 1993).

The numerosity of the 5 dimensions in the perceptual timbral space is also supported by the DFA of semantic ratings in a subsequent task. The fact that similar arrangements of tones are obtained between the two tasks (Fig. 9) and are justified by the predictive power and significance of the MDS and DFA dimensionality (Fig. 3) further validates our conclusions about the nature of timbre space. It is remarkable that these approaches yield the same result because they differ in: (1) what is measured (gestalt dissimilarities vs semantic ratings), (2) the method for dimensionality reductions (MDS vs DFA), and (3) the statistical analysis (a novel cross-validation or AIC vs classical MANOVA). The methodological approach could suitably be applied to many other complex multidimensional perceptions and actions treated by psychology, such as olfaction (Dravnieks, 1982).

Of the 5 dimensions, the first 3 capture most of the variance and corroborate the 2 to 4 principal dimensions of timbre assessed by previous researchers (von Bismarck, 1974; Caclin et al., 2005; Gordon and Grey, 1978; Grey, 1977; Marozeau et al., 2003; McAdams et al., 1995; Plomp, 1970; Stepanek 2006; Wessel, 1979). Whether or not they treat impulse notes along with the sustained, all such findings have been limited to the timbre of Western music. An all-inclusive timbre space would represent sounds from other musical traditions, vocalizations (Ekholm et al., 1998) and other environmental sounds. The timbre of simultaneously blended sound sources (Kendall and Carterette, 1991) may emerge as a nonlinear combination of the percepts of the components themselves. Finally, timbre perception depends on the pitch context (Marozeau et al., 2003) and is affected by learning and experience (Chartrand and Belin, 2006). Thus, the complete timbre space of potential sounds should have higher dimensionality than the space reported here, and may vary across subjects. Investigating this whole space using naturally produced sounds is challenging because of the difficulty in holding the pitch, duration and loudness constant across diverse kinds of sound production. As an alternative, one can assess synthetic sounds designed to systematically sample specific regions of timbral space. Such approaches may confirm findings from natural sounds (Caclin et al., 2005) or investigate potential extensions of spaces found in other studies (Terasawa et al., 2005).

Perceptual timbre dimensions and their interpretation

Relational tasks (similarity judgments) order stimuli without the classification bias of musical terminology. But the resulting constellation lies within a space detached from the perceptual meaning that we sought to relate to physical sound properties. To express the MDS solution in perceptual terms requires interpretation of the dimensions upon which the stimuli are ordered. To this end, subjects' classification using categorical rating scales results in conceptual distinctions that semantically express the nature of perceived dimensions of timbre. DFA of these semantic results precludes a priori suppositions about which rating scales are perceptually salient or mutually redundant. The DFA weights variables so that those upon which subjects disagree cannot unduly influence the resulting dimensions, which are meant to separate percepts.

By rotating and scaling the semantic space obtained from the DFA into the Euclidean distance model obtained from the MDS, we find that hard/soft, sharp/dull, high-/low-frequency energy balance, and explosive/calm qualities combine to organize instrumental tones along the primary perceptual dimension. Varying/steady level, dynamic/static, vibrato/steady pitch, and ringing/abrupt release commingle in the secondary distinctions we perceive. Add to these the perceptually complementary qualities of noisy/tonal, small/big instrument and unpleasant/pleasant in the third dimension, and compact/scattered and pure/rich in the fourth dimension, and all four dimensions taken together manifest the essential orchestral landscape for us. Only one more dimension held in common by listeners, the fifth, which had no significant correlates among our semantic descriptor pairs, remains for a final, less conspicuous qualification that completes the diversity of our actively constructed experience of timbre in sustained instruments.

We found that the bivariate correlation coefficients of the semantic descriptors with the first two dimensions of the rotated MDS space showed a high degree of orthogonality. This result validates that the MDS approach has extracted perceptual dimensions that we perceive as distinct and are able to describe as such, an idea previously proposed (Stepanek, 2006). The particular verbal expressions of timbral properties that correlated with our first two perceptual dimensions are also in reasonable agreement with previous assessments. Our D1, which is principally influenced by the shape of the overall amplitude envelope, can be related to Wessel's “attack” dimension in (Wessel, 1979) or Kendall et al.'s (1999) “nasal”. Our D2 could be related to the dimension that correlated with spectral variability in time, labeled as “spectral fluctuation” (Grey and Gordon, 1978) or “tremulous,” “brilliant,” and “rich” by (Kendall et al., 1999).

Acoustic structure correlated with timbre percepts

Understanding the relation between acoustical structure and the distinct timbre percepts is an essential part of this psychophysical effort. One difficulty is that acoustic features that affect timbre perception are relatively “high-order” in the sense that most cannot be obtained from the sound pressure waveform or simple linear (and invertible) transformations of the waveform. Previous researchers have therefore relied on operational definitions of particular acoustic qualities of the temporal envelope (e.g., the attack rise-time) or the spectral envelope (e.g., the spectral centroid), or the dynamics of spectral shape (e.g., spectral flux). Although relatively successful, this approach can lead to conflicts between results using different durations or stimulus sets (Hajda et al., 2007) and correlated spectral and temporal features can lead to false conclusions (Fig. 7). Most ad hoc acoustical descriptors are not fully invertible and therefore fall short of examining all the sound parameters that could be of significance.

The MPS overcomes some of these shortcomings because of its completeness and unification of spectral and temporal domains. First, the MPS is an invertible characterization. As long as both the phase and the amplitude are preserved, inversion of the MPS can obtain the original spectrographic representation of the sound. This spectrogram can itself be inverted under certain conditions to recover the original sound. Second, the MPS is a nonlinear transformation of the sound pressure waveform that extracts features that have been shown to be perceptually salient (Chi et al., 1999; Elliott and Theunissen, 2009). Third, high-level auditory neurons are well characterized by their modulation tuning (Elhilali et al., 2006; Escabi et al., 2003) and this characterization has helped link neural representation to perception (Chi et al., 2005; Shamma, 2001; Woolley et al., 2009). However, we find ultimately that because the MPS phase is difficult to interpret, combining MPS analysis with more traditional measures constitutes the best approach to study the acoustical structure correlated with timbre perception.

Our results recapitulate some prior linkages found between acoustics and timbre, but with fundamentally new conceptualization. It is an established finding that both temporal and spectral properties affect timbre (Sethares, 2005, pp. 27–32). For example, the rise-time of the attack amplitude envelope (e.g., log attack time) and balance of power across harmonic components in the spectral envelope (e.g., spectral centroid) have been shown to correlate with the timbre of musical instruments (Grey, 1977; Hajda et al., 1997, 2007; Handel, 1995; Krimphoff et al., 1994; Marozeau et al., 2003; McAdams et al., 1995, 1999; Samson et al., 1997). It has been implied that these temporal and spectral features correspond to separate perceptual dimensions (Caclin et al., 2005; McAdams et al., 1995; Wessel, 1979). Similarly, our analysis brought out a purely spectral dimension (D3) for which the spectral centroid is relevant. The three other main dimensions in our analysis are spectrotemporal rather than isolated to the spectral or temporal domain, a circumstance that could have led to erroneous classification of them in the past. Yet they retain the orthogonality in acoustics that was claimed by previous researchers (i.e., D1, D2, and D4 show little overlap in the MPS analysis). One last dimension distinguishing brass and reeds plays a more minor role and is harder to describe perceptually.

Indeed, although our primary two timbre dimensions show many features of orthogonality, both in the regression with the MPS and semantically, their semantic classifications are both mainly temporal. D1 (hard, sharp) is affected by the shape of the overall envelope (including attacks), but also by differential timing in the envelope of the harmonics. Traditional acoustic feature analysis (Fig. 7) could mistakenly label these features as primarily spectral because delayed onsets of some harmonics change the spectral balance (as in brass “brightness” caused by a relative delay in high partial onsets). The upper extent of temporal modulations in D1 surpasses 20 Hz, encompassing fast transient amplitude changes necessary for a sharp attack. D2 (varying level, dynamic) is associated with dynamic spectral changes on a slow scale that must include the sustain. But these temporal changes affect spectral harmonics differentially (as shown in the broad spectral modulation range) and occur mainly at intermediate temporal modulations (between 2 and 6 Hz). The particular modulation rate of 6 Hz is characteristic of vibrato in woodwinds and strings (Brown and Vaughn, 1996; Fletcher and Sanders, 1967; Strong and Clark, 1967). In summary, classical acoustic analysis may have mislabeled the D1 vs D2 distinction (orthogonal in percept, semantics, and acoustics) as a spectral vs temporal contrast, whereas we distinguish them by the different spectral application of broad vs intermediate temporal ranges: either, in D1, overall amplitude modulations including fast transients applied to the whole tonal resonance structure, or, in D2, 2-to-6 Hz ongoing modulations in the temporal envelope applied to the spectral distribution across broad frequency ranges encompassing multiple harmonics.

The semantic labels of D3, noisy and small instrument, go along with its solely spectral acoustic nature (namely, spectral shifts to more energy at higher frequencies, and greater bandwidth). D4 could similarly be considered mainly “spectral” both in its semantic description, steady pitch, compact, and pure, and in its acoustic correlation with slower spectral modulations (below ∼6 Hz). These spectral modulations are principally centered ∼1/2F₀ corresponding to a prominence of alternating harmonics. The odd harmonics of the clarinet (Fletcher and Rossing, 1998, p. 463) exemplify this as a peak at 1.6 cycles/kHz, or half the spectral modulation corresponding to the resonance at this pitch [Fig. 4b]. Yet MDS D4 is also correlated with temporal amplitude modulations >6 Hz at very low spectral modulations of the overall amplitude envelope. As for MDS D1, these fast modulations distinguish transients in the attack, but in D4 they are further characterized by a positive correlation with temporal skew (although skew plays a small overall role judged by adjusted R²). The last significant dimension (D5) from tuba to oboe d'amore has mostly spectral coefficients concentrated ∼1/2F₀ with slow (<6 Hz) development.

It is worth noting the relatively small effect of pitch invariant spectral modulations at <1/8F₀ of very low temporal modulation (<2 Hz). We ascribe these to linear resonances of the instruments at fixed formants, in contrast with larger nonlinear effects dependent on pitch that cause, e.g., a prominence of alternating harmonics, or nonlinear distortions in brass (Beauchamp, 1979).

Our MPS analysis would need to account for phase in order to detect shifts along the frequency spectrum. Such properties are critical for describing D3, and only the traditional features of the spectral mean and standard deviation captured it. Phase would also be required, e.g., to distinguish temporal modulations due to the attack vs the decay. However, the conclusions from regression did not change significantly when we calculated MPSs for the beginning and end segments of each sound and performed the analysis using both as regressors. Most of the effect is thus caused by differences in ongoing amplitude dynamics but is also influenced by the attack segment of the envelope. This result is not surprising since it has been shown that including attacks improves listener categorization of instrument tones, whereas removal of decay segments does not impair instrument identification (Saldanha and Corso, 1964; Wedin and Goude, 1972).

In summary, through our new methodology for multidimensional psychophysical analysis and our combination of complementary acoustic descriptions of the sounds, we have made an unprecedentedly full account of orchestral timbre perception. We found a five dimensional space with four spectrotemporal dimensions and one mostly spectral. The primary two dimensions are orthogonal in both semantic labeling and sound structure, with one dimension sensitive to faster temporal modulations (>6 Hz) and the other sensitive to slower temporal modulations (≤6 Hz). These signature features correspond to dynamics in the transient and steady-state parts of the sound, respectively. Both dimensions also depend on spectral features: for the first dimension these are related to the harmonic structure of the sound, whereas for the second dimension both harmonic and nonharmonic features are modulated at intermediate rates. The third dimension is mostly “spectral,” driven by energy in higher harmonics. The fourth accompanies energy in alternating harmonics and includes spectral structure related to nonlinear filtering as well as linear formants. Although these dimensions are ordered by fraction of the variance explained, this ordering should differ for other types of sound groups, such as vocalizations in which formants play an important role.

Our results make two predictions for the purpose in auditory neuroscience of uncovering the neural basis of timbre perception. First, we expect there to be two distinct neural populations tuned to temporal dynamics above or below ∼6 Hz. Second, we predict that neural computations relevant to more spectral percepts of timbre will be tightly coupled to pitch computations, whereas those with other relevance will not. For example, representations of both the fast changes in the whole resonance observed in D1, and of the slower spectral changes in D4 ascribed to nonlinear filtering properties, will be tightly coupled to neural representations of the natural harmonic complex at particular pitches. In contrast, low spectral modulations in D1, D2, and D4 ascribed to fixed formants could be uncoupled from pitch computations. An analysis of neural tuning for spectrotemporal modulations could be useful in discovering neural populations that are tuned for timbral features but pitch independent (Woolley et al., 2009). In future investigations of the neural basis of timbre perception, the relationship between timbre and pitch computations should be examined closely.

The traditional and spectrotemporal MPS representations of acoustic features correlating with perceptual dimensions of timbre hold promise for making the first constitutive definition of timbre (Handel, 1995). Psychophysical tests of the perceptual relevance of correlated features could inform synthesis of sounds with extreme timbres. Sustained orchestral timbre could then be defined as some combination of the five essential acoustic patterns associated with each of the five perceptual dimensions (Fig. 10).

Figure 10.

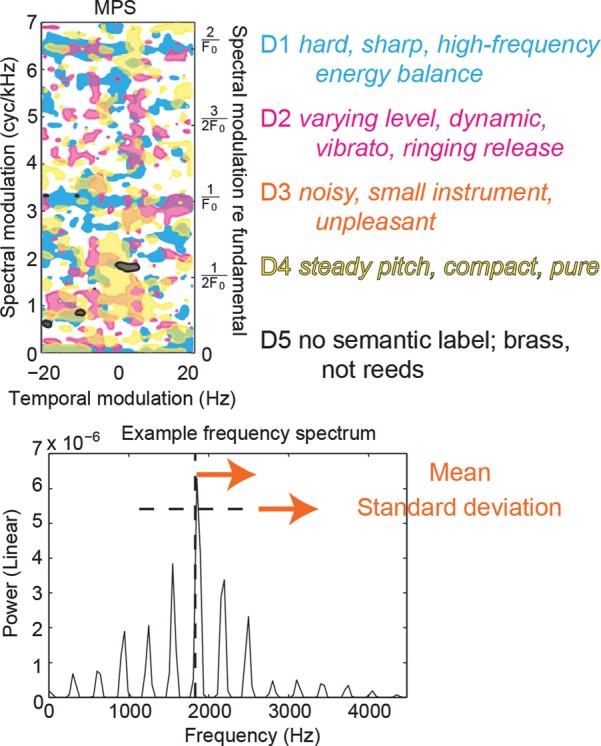
(Color online) The five kinds of timbre percepts in orchestral instrument tones are associated with distinct acoustic features, as depicted in the MPS, and as interpreted semantically (legend color labels). The first perceptual dimension (MDS D1) involves power fluctuations in frequency (“spectral modulations”) associated with amplitude changes in the natural harmonic structure (horizontal purple bands). D2 (overlaid in green) involves 6 Hz amplitude changes (“temporal modulations”) in spectral balance characteristic of vibrato (vertical bands). D3 (orange) overlaid on D4 (red) centers similarly on spectral prominence of alternating harmonics (half the spectral modulation in D1). D5 (blue, the top layer) involves particularly 2 Hz changes (vertical bands). The right side y-axis labels give spectral modulations in units of the period of the pitch fundamental (1/311 s).