Evolving the [Myoglobin, Cytochrome b₅] Complex from Dynamic Toward Simple Docking: Charging the Electron-Transfer Reactive Patch

Abstract

We describe photo-initiated electron transfer (ET) from a suite of Zn-substituted myoglobin (1Mb) variants to cytochrome b₅ (b₅). An electrostatic interface redesign strategy has led to the introduction of positive charges in the vicinity of the heme edge through D/E → K charge-reversal mutation combinations at `hotspot' residues (D44, D60, E85), augmented by the elimination of negative charges from Mb or b<sub>5</sub> by neutralization of heme propionates. These variations create an unprecedentedly large range in the product of the ET partners' total charges: −5 < −q<sub>Mb</sub>q<sub>b5</sub> < 40. The binding affinity (K<sub>a</sub>) increases a thousand-fold as −q<sub>Mb</sub>q<sub>b5</sub> increases through this range, and exhibits a surprisingly simple, exponential dependence on −q<sub>Mb</sub>q<sub>b5</sub>. This is explained in terms of electrostatic interactions between a `charged reactive patch' (crp) on each partner's surface, defined as a compact region around the heme edge that (i) contains the total protein charge of each variant, and (ii) encompasses a major fraction of the `reactive region' (Rr) comprising surface atoms with large matrix elements for electron tunneling to the heme. As −q_Mbq_b5 increases, the complex undergoes a transition from fast to slow exchange dynamics on the triplet ET timescale, with a correlated progression in the rate constants for intracomplex (k_et) and bimolecular (k₂) ET. This progression is analyzed by integrating the crp and Rr descriptions of ET into the textbook steady-state treatment of reversible binding between partners that undergo intracomplex ET, and found to encompass the full range of behaviors predicted by the model. The generality of this approach is demonstrated by applying it to the extensive body of data for the ET complex between the photosynthetic reaction center and cytochrome c₂. Deviations from this model also are discussed.

Introduction

Protein-protein binding is at the heart of much of biology, with affinity constants ranging over many orders of magnitude,^{(1, 2)} and many diseases involving the disruption and/or elimination of vital interactions.^{(3) (4–6)} Two limiting energy landscapes (Fig 1) have been used to describe the correlation between protein-protein binding and inter-protein reactivity): i) weakly-bound complexes can exhibit `dynamic docking' (DD), where reactive configurations are rare and geometrically distinct from more-abundant, thermodynamically favored unreactive configurations, and thus binding and reactivity are decoupled;<sup>(7–10)</sup> ii) tightly-bound complexes can exhibit `simple docking' (SD) where a dominant, strongly-binding configuration is also the most reactive.⁽⁷⁾ We are exploring the principles governing reactive protein-protein binding by undertaking a systematic re-design of the interface of the [myoglobin (Mb), cytochrome b₅ (b₅)] electron transfer (ET) complex, with the aim of taking this weakly-bound complex and strengthening the binding of reactive configurations, so as to evolve the DD landscape on which it functions into an SD landscape and thereby enhance ET.^(11–13)

Figure 1.

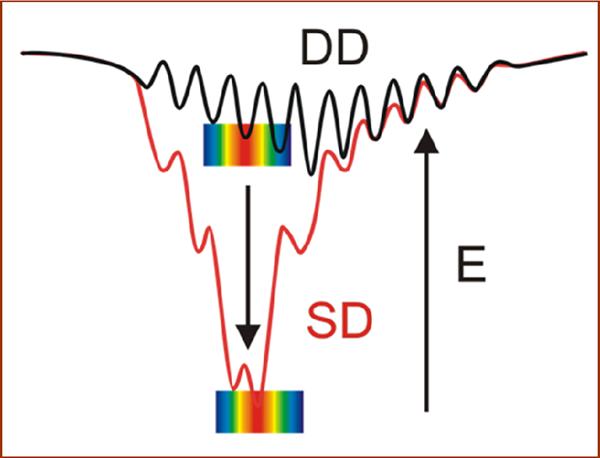
Energy landscapes for DD-type and SD-type reactions. Rainbow indicates ET reactive configurations where red indicates the most ET-active geometries and wells represent stable ones.

A reverse process, the identification of `hotspot' residues that provide the most favorable interactions in the protein-protein interface of a tightly-bound, SD complex, is typically carried out through inspection of an x-ray structure, coupled with a traditional alanine replacement strategy.^{(14, 15) (16, 17)} The studies of Okamura and coworkers with the [photosynthetic reaction center (RC), cytochrome c₂ (c₂)] ET complex provide a compelling example of the use of this crystallographic/mutational strategy to study the coupling between binding affinity and ET. By employing both charged^{(18, 19)} and hydrophobic ⁽²⁰⁾ interface mutants, these workers were able to identify residues essential to tight binding by monitoring mutationally-induced changes in ET, with the elimination of hotspot interactions lowering the binding constant by over three orders of magnitude relative to the wild-type complex. They further developed an empirical function to correlate the corresponding changes in binding affinity and ET reactivity generated by these interface mutations. ⁽²⁰⁾

To take a weakly-bound complex that reacts on a DD landscape, and identify potential `hotspot' surface residues where interactions can be most successfully introduced so as to evolve the complex towards a tight-binding complex with SD behavior, presents a challenge of a different order. Weakly-bound protein pairs such as the [Mb, b<sub>5</sub>] ET complex (K ~10<sup>3</sup> M<sup>−1</sup>)<sup>(21, 22)</sup> do not in general form crystals, precluding the use of X-ray structures to identify sites where modification would stabilize the protein-protein interface and enhance reactivity. Indeed, such complexes do not even have a well-defined `structure'.^{(23, 24)} This has led us to develop an interface redesign strategy that employs Brownian Dynamics (BD) docking simulations to identify residues where charge reversal mutations will strengthen electrostatic interactions^(25–27) in the protein-protein interface of ET-active conformations of such transiently-formed, DD-type complexes.⁽¹³⁾ Application of this strategy to the [Mb, b₅] partners identified residues D44, D60, and E85 of Mb as surface residue `hotspots' where the progressive introduction of D/E → K mutations in the vicinity of the Mb heme edge should create a positively charged `patch'⁽²⁸⁾ on the Mb surface with enhanced Coulombic attraction to the complementary pattern of negative surface charges on the b₅ template, progressively stabilizing reactive configurations of the complex and `evolving' it towards a reactive SD behavior (Fig 1).

Guided by these predictions, we have now prepared all seven mutants in which positive charges have been added to the Mb surface by D/E → K charge-reversal mutations at one, two or all three of the hotspot positions on Mb, augmented with variants in which negative charge is eliminated from the Mb surface by neutralization of the Mb heme propionates. The binding affinity and ET reactivity for each member of this suite have been measured at two different pH values by examination of ET quenching of the Zn-deuteroporphyrin IX (ZnD) or ZnD-(dimethylester)-reconstituted Mb photo-donors by either the ferri-b₅ electron acceptor or its diester heme reconstituted analog.

Whereas b₅(wt) has a large negative total charge, q_b5 e = −5.7 e, Mb(wt) is nearly charge-neutral, q_Mb e = −0.3 e (pH 7; Table SI_1). The charge variation through mutation and/or heme-neutralization yields a set of [Mb, b₅] complexes that spans an unprecedentedly large range in the product of the total charges on the partners: −5 < −q_Mbq_b5 < 40 (Table SI_1). As −q_Mbq_b5 increases within the set, the binding constant (K_a) increases by over three orders of magnitude and the complexes shift from the fast-exchange (FE) dynamics regime to the slow-exchange (SE) regime on the triplet-state ET timescale. The second-order ET rate constant (k₂) concomitantly increases by ~10³; intra-complex protein-protein ET is observed in the SE regime and it too increases with −q_Mbq_b5. The correlated increases in binding and reactivity are found to have remarkably simple dependences on the charge product, −q_Mbq_b5. To describe these consequences of charge buildup, we have been led to extend the idea of a charged patch^(28–31) by defining a charged reactive patch (crp) on each protein that satisfies two criteria. (i) It is the most compact area that surrounds a selected surface point/region and in which the surface charge of the protein equals its total charge. (ii) The selected region, here taken to be the heme edge, is chosen so that the crp encompasses a major fraction of the ET-active surface, the `reactive region (Rr)' comprising the surface atoms with large matrix elements for electron tunneling to the heme (Fig 2). Because the hot-spot mutation sites of Mb and the heme propionates of both partners fall within their WT crp, the crp for each of the ET partners remains compact and essentially invariant as its surface charge is changed. With the crp of each partner of every complex containing its total protein charge, while the remaining surface has no net charge, complex formation can be treated in terms of the interaction between the total charges, localized within the complementary, reactive regions on the protein surface — the crp. The correlated progression of k₂ and K_a with increasing - q_Mbq_b5, and the transition from fast to slow exchange dynamics, then arise naturally when the crp description of protein-protein binding is integrated into the textbook steady-state treatment of reversible pre-equilibrium binding between partners that exhibit intracomplex ET.^(32–34)

Figure 2.

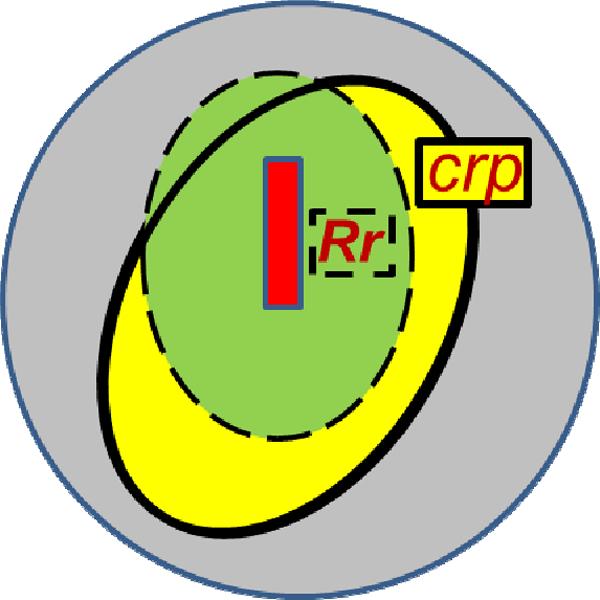
Cartoon of the overlapping charge reactive patch (crp) and reactive regions (Rr).

This simple approach completely captures the global aspects of the correlated electrostatic control of binding and reactivity, while at the same time illuminating the `granularity' that results from alternative arrangements of charges on the Mb surface. The generality of this approach is evidenced by its ability to treat the correlated decreases in binding and ET rate constants between the reaction center (RC) and cytochrome c₂ (c₂), as produced by separate suites of hydrophobic and electrostatic mutations within the interface.

Materials and Methods

Bacterial Strains and Plasmids

Escherichia coli strains used for plasmid propagation and protein expression were DH5a and BL21(DE3) respectively. Coding sequences for target proteins were cloned under control of the T7lac promoter by placing the initiation codon at the NcoI site of pET28a⁽⁺⁾ (Novagen), which confers resistance to kanamycin. The plasmid for expressing horse heart myoglobin (Mb) was obtained from Professor A. Grant Mauk (University of British Columbia, Vancouver). The wild-type gene was then amplified via PCR from the constitutive expression vector pEMBL18 containing the template⁽³⁵⁾ with the forward (ACTAGCCATGGGTCTGTCTGATGGTGA) and reverse (ACTAGGGATCCTTAACCCTGGAAACCCAGTTC) primers. The PCR product was digested with NcoI and BamHI enzymes, and cloned into the pET28a⁽⁺⁾ vector, similarly digested with the same enzymes. Protein mutants were created via site-directed mutagenesis using a Stratagene QuikChange II XL Site-Directed Mutagenesis Kit. The constructs for Mb wild-type and all mutants were verified by DNA sequencing (SeqWright).

Expression and Purification

Terrific broth medium (0.17mM KH₂PO₄, 0.72mM K₂HPO₄, 12g tryptone, 24g yeast extract/L) containing kanamycin (100ug/mL) was inoculated with an overnight culture of BL21(DE3) E. coli transformed with the desired Mb construct. The culture was grown at 37°C, 350rpm until it reached an OD₆₀₀ ~ 2.4–2.7. Protein expression was induced with IPTG (final concentration of 1mM) and an increase in temperature to 42°C. The resulting protein formed inclusion bodies as described by Ribeiro, et al.⁽³⁶⁾ High cell densities (OD₆₀₀ > 6) are desired, so to provide sufficient aeration of the expression culture the volume of culture was limited to < 25% of the flask volume and a high shaking speed (>350rpm) was maintained.

After 3h, the culture was pelleted by centrifugation at 20,000g for 15 minutes, re-suspended in 20ml/L 100mM Tris-HCl, 5mM EDTA, 1% Triton X-100 (pH 8.0) and lysed by sonication. This process was repeated 3 times with the same buffer, taking care to completely re-suspend the pellet after each centrifugation step. The pellet was then re-suspended in water and sonicated twice, as before, to remove excess Triton X-100. Finally, the pellet was re-suspended in 100mM Tris-HCl, 8M guanidine-Cl (pH 8.0) and sonicated to homogeneity.

An excess of the desired metalloporphyrin (Frontier Scientific) was added along with 5mM sodium dithionite, and then very slowly with stirring, the volume was doubled with 100mM Tris-HCl, pH 8.0. This solution was then dialyzed overnight in 14L of 10mM Tris-HCl (pH 7.2) with stirring. The next day, precipitated protein was removed by centrifugation, and the reconstituted Mb was further purified by ion-exchange chromatography, using a CM-52 column equilibrated with 10mM Tris-HCl (pH 7.2). Purity was assayed by measuring the A_414,408/A₂₈₀ ratio and verified by SDS-PAGE. The protein was then exchanged into 10mM KPi, pH 7.0, concentrated, pelleted in liquid nitrogen, and stored at −80°C. The protein yield was found to be mutation-dependent, and decreased with added mutations; wild-type was obtained at about 100mg/L, D44K/D60K/E85K at about 50mg/L. Concentrations were calculated using the Soret absorbance (Zn²⁺-DPIX, Zn²⁺-DPIX dme: ε_{414 nm} = 361 M⁻¹cm⁻¹;⁽⁷⁾ Fe³⁺-PPIX: ε_{408 nm} = 188 M⁻¹cm⁻¹)⁽³⁷⁾.

Bovine Fe³⁺b₅ was expressed in E.coli, isolated and purified according to previously described methods.^{(38, 39)}

Brownian Dynamics Simulations

Mutants were designed as described previously using a Brownian dynamics docking protocol implemented in the Linux version of MacroDox.⁽¹³⁾ Total charges were calculated for each of the Mb and b₅ variants using the Tanford-Kirkwood method(⁴⁰) with the default intrinsic pK_a values, adjusted as implemented in MacroDox,⁽⁴¹⁾ using the experimental parameters: i) pH7, μ = 18 mM, 293K; ii) pH6, μ = 5 mM, 293K. All Arg, Tyr, and Lys residues (including the mutation sites) were fully charged; all Asp and Glu residues were essentially deprotonated with the charge distributed between their carboxylate oxygen atoms. Consistent with the His pKa values measured by NMR for met-Mb(horse),^{(42, 43)} the computed pK_a for His 36 is larger than the default intrinsic pK_a = 6.3, while those for His 48 are less than the intrinsic pK_a. The computed pK_a and corresponding charges on the N_ε and N_δ atoms of the His residues are slightly smaller for the more highly charged mutants in comparison to their values in Mb(wt). The formal charges on the metal atoms in Mb and b₅ were assigned as +2 and +3, respectively. We have suggested previously that the pK_a of charged residues within the protein-protein interface may change upon binding,⁽⁷⁾ but given the diversity of the geometries resulting from the BD simulations, this complication has not been addressed in the current work.

Flash Photolysis Experiments

Cuvettes filled with 2 mL of buffer were stored open to the atmosphere overnight in a N₂-filled glove box. Stock solutions of protein were thawed on a cold block in the glove box for several hours prior to the experiment. The final concentration of Mb in the sample was 5 μM. Protein stock concentrations were determined using a Hewlett-Packard UV-vis spectrophotometer: ε₄₁₄ (ZnDMb) = 361 mM⁻¹cm⁻¹; ⁽⁷⁾ ε₄₁₄ (Fe³⁺b₅) = 117 mM⁻¹cm⁻¹.⁽⁴⁴⁾

Samples were excited with a Nd:YAG Quanta-Ray INDI laser (Spectra-Physics) tuned to 532 nm. The output power was set so that it was approximately 100 mJ at the sample holder. Triplet quenching measurements were performed with an LKS.60 laser flash photolysis spectrometer (Applied Photophysics) fitted with a xenon lamp with pulsing capabilities. For slow triplet decays (<1000 s⁻¹), a setup modified from Applied Photophysic's stopped-flow instrument was employed with a 9-stage photomultiplier tube for detection. Data for shorter timescales was taken with an Agilent Infiniium 600 MHz digitizer and 5-stage photomultiplier tube detector. The xenon lamp was pulsed to achieve the shortest timescales. The triplet decay timecourses were monitored at 475 nm. Typically, 10 shots were averaged on the slow timescale setup and at least 20 shots were averaged for the fast setup data collection. All kinetic experiments were performed at 20°C.

Results and Discussion

Electron Transfer Measurements

In the absence of b₅, the photo-excited triplet states of all the ZnMbs decay exponentially, with a rate constant (k_d) that ranges from 50 to 500 s⁻¹. Upon addition of b₅, photo-initiated ET quenches the triplet excited state, with the form of the resulting triplet decay trace being dependent on the strength of the binding interaction. The traces are exponential throughout a quenching titration when binding is weak and the complex is in fast exchange (FE) with its components; they are bi-exponential when the binding has been strengthened to the point that the complex is in slow exchange (SE) with unbound partners. The upper panel of Fig 3 shows triplet decay traces for a set of Mb surface charge mutants in solutions with excess b₅ ([b₅]/[Mb] = 2). The [Mb, b₅] pairs with low values of the protein-protein charge product (−q_Mbq_b5 ≤ 16.5), e.g., [ZnMb(wt), b₅] and [ZnMb(D44K), b₅] (Table S1), are all in the FE limit, and their triplet decay traces are well described with an exponential function. For these [Mb, b₅] pairs, the quenching rate constant (k_q) obtained by subtracting k_d from the observed rate constant (k_obs) increases linearly (Fig 3, lower) as a function of [Fe³⁺b₅]. The slope of the resultant line gives the bimolecular quenching rate constant, k₂. Complexes with high values of the charge product (−q_Mbq_b > 16.5), e.g., [ZnMb(44/60), b₅] and [ZnMb(44/60/85), b₅], fall in the SE regime, with biphasic triplet decay traces. For these complexes, the rate constant for the faster decay phase (k_f) is invariant with b₅ concentration (Fig 3, lower) and is attributed to protein-protein ET within the pre-formed complex; the rate constant for the slower component (k_s) varies linearly with [Fe³⁺b₅] and like the single kinetic phase exhibited by the FE (DD)-type pairs, its slope (k₂) is associated with second-order ET-quenching of the free ZnMb by Fe³⁺b₅.

Figure 3.

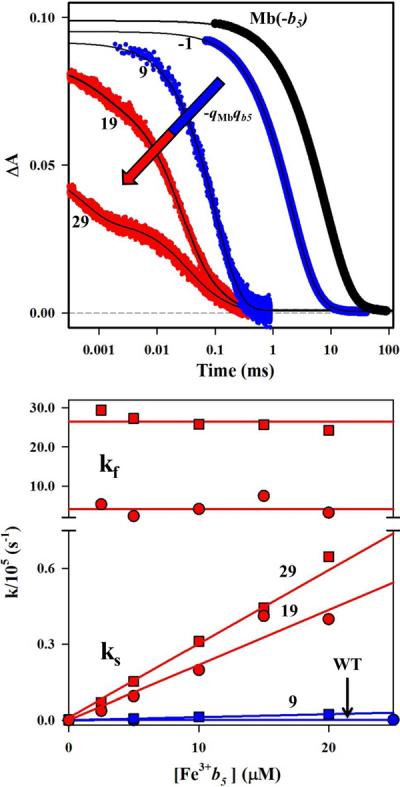
Triplet decay traces at [b₅]/[Mb] = 2 (upper) and fit parameters during titrations of Mb with b₅ (lower). Data for the Mb(wt) (circles) and Mb(+2) (squares) complexes, classified as FE (blue), were analyzed with a single exponential decay function; the Mb(+4) (circles) and Mb(+6) (squares) complexes, classified as SE (red), were analyzed with a bi-exponential decay function. Conditions: 5 μM Mb; 5 mM KPi, pH 6, 20°C, 475 nm.

For the SE complexes, the fraction of the faster phase in the triplet decay typically is taken to correspond to the fraction of bound complex, and the measured variation in this fraction during a titration with an ET quencher is fit to a binding isotherm to determine the protein-protein binding constant, K_a. In contrast, K_a generally cannot be measured from a triplet quenching titration for complexes in the FE regime. However, we have shown that the progressive decrease in the early-time absorbance (A₀) during a triplet-quenching titration results from quenching of the singlet state by b₅.⁽¹³⁾ On the singlet timescale, all the [Mb, b₅] complexes are in SE and as a result, the variation in the absorbance decrease can be fit to a binding isotherm to calculate K_a, regardless of whether the complex is in FE or SE on the triplet timescale. This procedure has been applied to each of the complexes studied here.

The upper panel of Fig 4 is a semi-logarithmic plot of K_a for all the [Mb, b₅] complexes, measured at both pH 6 and 7, as a function of the product of the total protein charges determined from Poisson-Boltzmann electrostatic computations, −q_Mbq_b5. As −q_Mbq_b5 increases from −5 to 40, the [Mb, b₅] binding affinity increases by nearly three orders of magnitude. The exponential increase in K_a revealed in this plot shows that the driving force for complex formation, −ΔG⁰_a = RTlnK_a, increases linearly with the total-charge product for the [Mb, b₅] ET pairs, −q_Mbq_b5. This surprisingly simple dependence on total protein charges confirms that the progressive increase in K_a is electrostatically driven and that the mutations change only the electrostatic interactions between the partners.

Figure 4.

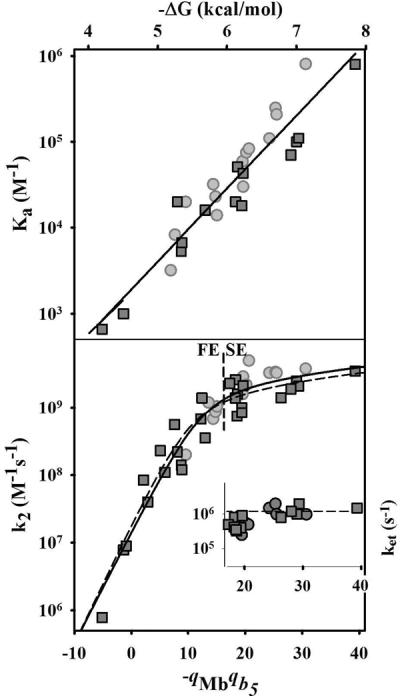
Dependence of K_a (upper), k₂ (lower) and k_et (inset in lower panel) on the negative charge product (−q_Mbq_b5). Dashed line (lower panel) indicates the experimentally observed division between the FE and SE regimes. Conditions: 5 mM KPi, at pH 6 (light-gray circles); 10 mM KPi at pH 7 (dark-gray squares). Solid line running through points of lower panel is a fit of the entire k₂ dataset to eq 7; dashed line, a fit to pH = 7 data. The bimolecular quenching rate constants, ET rate constants, binding affinities and charge products for all the [Mb, b₅] pairs included in this figure are tabulated in Table SI_1. The fit parameters for the entire k₂ dataset are discussed in the text.

The lower panel of Fig 4 is a semi-logarithmic plot of k₂ versus −q_Mbq_b5 for all complexes at both pH 6 and 7. At low values of −q_Mbq_b5, where FE dynamics are obtained, k₂ varies exponentially with −q_Mbq_b5, increasing by over three orders of magnitude, from 8.0×10⁵ M⁻¹s⁻¹ at −q_Mbq_b5 = −5 to 1.2 × 109 M⁻¹s⁻¹ at −q_Mbq_b5 ~ 16. This behavior was observed previously for Mb mutants with −q_Mbq_b5 ≤ 12.^{(7) (45)} As the charge product is increased beyond this value, the [Mb, b₅] pairs show SE-type dynamic behavior (Fig 3) and the increase in k₂ with −q_Mbq_b5 slows markedly, resembling the weak charge dependence expected for the diffusion rate describing the association of charged partners.^{(32, 46, 47)}. The inset to the lower panel of Fig 4 displays the intracomplex ET rate constant, k_et, measured for the complexes in the SE regime as a function of the charge product. Although k_et ~ 10⁶ over the accessible range of −q_Mbq_b5, closer examination reveals that k_et increases nearly an order of magnitude in this range, from k_et ~ 2×10⁵ s⁻¹, toward a limiting rate constant in excess of 10⁶ s⁻¹.

Although k₂ increases smoothly with increasing −q_Mbq_b5, the dynamics of complex formation changes from FE to SE; complexes with −q_Mbq_b5 ≤ 16.5 show FE dynamics; complexes with a larger value show SE dynamics. An interesting aspect of the presentation in Fig 4 is that an apparent pH dependence of k₂ for the [Mb, b₅] pairs (Table S1) is shown to be merely a consequence of the differing pH dependences of −q_Mbq_b5 for each pair: the points for both pH values can be plotted together. Likewise, no special influences of heme neutralizations are seen beyond the resulting changes in −q_Mbq_b5.

Analysis

The interface redesign strategy employed here leads to the progressive generation of a patch in the vicinity of the ET-active Mb heme edge with a high local density of positive charge, complementary to the high negative charge of the b₅ surface. Figure 4 shows that the consequence of this charge buildup is that K_a and k₂ for the suite of [Mb, b₅] complexes can be treated as functions of a single variable, the product of the total charges on the two partners, −q_Mbq_b5. Although this confirms that binding and reactivity are both under electrostatic control, at first glance the simple logarithmic dependence of K_a on −q_Mbq_b5, corresponding to a simple coulombic interaction between total protein charges, is a surprise. One might expect that at relatively low values of −q_Mbq_b5, where there has been little localized charge buildup, the electrostatic interactions would involve charges over a wide area, and not be so simply parametrizable.^{(48)(49, 50)}

The development of a model for the observed behavior begins with the recognition that for all complexes studied, the measurements of both binding affinity and ET probe only configurations of the complex in which b₅ is bound at a site on the Mb surface that has a good ET pathway to the heme⁽⁵¹⁾; such sites comprise a `reactive region (Rr)' on the Mb surface surrounding its exposed heme edge. Considering first the binding constant, K<sub>a</sub>, this restriction arises because binding is assayed by measuring singlet ET quenching. As this quenching process must compete with the intersystem crossing rate (k<sub>isc</sub> ~ 2×10<sup>8</sup> s<sup>−1</sup>), it can only report on complexes with reactive configurations whose pathways for intracomplex ET can compete effectively, namely configurations in which b<sub>5</sub> is bound at the Rr. Fig 5A shows a Pathways coupling map for the Mb surface,<sup>(52)</sup> color-coded according to the magnitude of the matrix element for electron tunneling from that site to the heme-iron. The heme edge, of course has the largest tunneling matrix element, with concentric `rings' of decreasing coupling as the distance from the heme increases. A more precise definition of the Rr could be developed, but for the present purposes, one may loosely imagine that the Rr for Mb comprises the surface atoms colored red and yellow (or yellowish-green) in Fig 5A.

Figure 5.

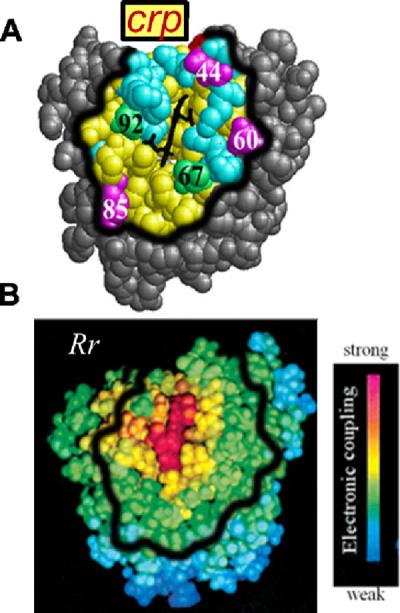
Mb charged reactive patch (crp) and Pathways coupling map. A. The Mb crp defined to include resides such that q_patch ~ q_Mb; this are includes all the surface residues within 10Å of the heme. Color scheme: patch residues (yellow); acidic (red) and basic (blue) residues within the patch; residues outside of the patch (gray); charged hotspot mutation sites (magenta); uncharged mutation sites (green). B. Pathways coupling map and color scheme from Liang, et al.⁽⁷⁾ The thick black line shows the rough outline of the crp in panel A.

A quantitative description of binding in terms of total protein charges is obtained by linking the idea of a Rr around the heme edge to total protein charge, through the definition of a `charged reactive patch (crp)'. Although one might have expected that a wide area of the Mb surface contributes to the energetics of binding at low to moderate values of −q_Mbq_b5, we have examined the surface of Mb and found that a compact surface region that surrounds its heme edge contains a net surface charge equal to the total charge of the wild-type protein, leaving the rest of the protein as charge-neutral. The well-defined surface region identified in this way, shown in both panels of Fig 5, includes the Mb surface atoms that lie within ~10Å of any heme atom. It encompasses: (i) much of the Rr (Fig 5A), and thus an area whose effective ET pathways from the Mb surface support rapid electron tunneling between the heme of a bound b₅ and the Mb heme; and (ii) all of the Mb mutation sites employed in this study (Fig 5B). Thus, the total charge on every Mb charge variant can be treated as being concentrated within the crp. The corresponding crp for b₅ and its heme-neutralized charge variant, likewise defined to contain the total protein charge, is displayed in Fig SI_1. The definition of a crp naturally leads to a picture in which the ET partners react only when the Rr within their complementary crp are electrostatically drawn together.

This picture is supported by the finding that the crp of the two partners are relatively small and have effectively the same solvent-accessible surface area: 1410Ų (Mb) and 1560Ų (b₅) at pH7. The crp on Mb includes only ~22% of the solvent-accessible Mb surface, which supports the physical reality behind the concept of a well-defined patch at which both binding and reactivity occur. Furthermore, BD simulations show that as the charge product is increased, there is a corresponding large increase in the likelihood that a reactive configuration (BD `hit') involves binding through a protein-protein interface that includes the complementary crp of Mb and b₅ (Fig SI_2). We of course recognize that one could use any surface location to define a charged patch that encompasses the total protein charge. What makes the crp construct useful is that reactivity is associated only with the Rr, which mostly is contained within the crp (Fig 2,5).

A simple formulation of the reactive, electrostatic binding between the crp of the partner proteins follows naturally. As ET quenching arises from binding of b₅ at surface sites of the Mb Rr that lie within its crp, and as the total charges for the Mb and b₅ partners are defined to be localized within the relatively small surface areas of their crp, the electrostatic driving force for reactive complex formation must be dominated by the Coulombic interaction between the charges within the complementary crp of the partner proteins. The further simplification of expressing this driving force as the electrostatic interaction of the total protein charges leads to a form for the driving force that corresponds to the experimental findings:

$$\begin{array}{cc}\hfill -\Delta {\mathrm{G}}_{\mathrm{a}}^0& =\mathrm{RT}\ln \left[K_a\right]\hfill \\ \hfill & =-[\Delta {\mathrm{G}}_{\mathrm{hyd}}^0+V\left(q_{\mathrm{Mb}}{q}_{\mathrm{b}5}\right)]\hfill \\ \hfill & =-[\Delta {\mathrm{G}}_{\mathrm{hyd}}^0+q_{\mathrm{Mb}}{q}_{\mathrm{b}5}f({∊}_{\mathrm{o}},{∊}_{\mathrm{i}},{\mathrm{r}}_{i,j})]\hfill \\ \hfill & =\mathrm{RT}\ln {\mathrm{K}}_0-q_{\mathrm{Mb}}{q}_{\mathrm{b}5}f({∊}_{\mathrm{o}},{∊}_{\mathrm{i}},{\mathrm{r}}_{i,j}).\hfill \end{array}$$ (1)

Here we have taken the electrostatic interaction energy, V(q_Mbq_b5), to be proportional to the product of the complementary patch charges (q_Mbq_b5), and a function f that could be formulated at differing levels of sophistication in terms of the distances between charged Mb and b₅ patch residues (r_i,j) and the protein and solvent dielectrics (ε_o, ε_i), but whose modeling is far beyond the scope of this report.⁽⁵³⁾ The additional contribution, ΔG⁰_hyd, takes into account non-electrostatic interactions, as well as an entropy term that reflects the low fractional surface area at which reaction can occur. Definition of such a term represents an extension of the partitioning of the binding free energy, discussed earlier.⁽⁹⁾ With this definition, the last line of Eq 1, rewrites −ΔG⁰_a in terms of K₀, the binding constant that would apply when Mb is completely uncharged (q_Mb = 0).

Eq 1 has been used to fit the dependence of K_a on −q_Mbq_b5 for experiments at both pH 6 and 7. This fit yields K₀ = 2 × 10³ (−ΔG⁰_a = 4.6 kcal/mol), f = 0.093 kcal/mol; as shown in Fig 4, upper panel, it gives an excellent description of the roughly thousand-fold increase in K_a with increasing −q_Mbq_b5 over the entire range explored. Conversely, the experimentally observed linear dependence of −ΔG⁰_a on −q_Mbq_b5 supports the simplified description of electrostatic binding as governed by the total protein charge concentrated within the protein-protein interface formed by the complementary crp. We note, however, that because the actual magnitude of the parameter f is dependent on the spread in −q_Mbq_b5, it might vary somewhat with the method for computing protein charges.⁽⁵⁴⁾ The success of this description (Eq 1) further supports the implicit assumption that hydrophobic interactions between the partners remain largely invariant as the charge in the Mb crp is increased.

We next consider k₂, the bimolecular rate constant for ET. In the FE/DD regime, as we previously discussed,⁽⁷⁾ k₂ can be written as the sum of rate constants for all individual configurations weighted by their individual binding constants (Eq 2). Here, the non-reactive (NR) configurations are in the majority (N_NR in number), but they do not contribute to reactivity as k_NR ~ 0. Instead, the minority of reactive (R) conformations (n_R in number; large intracomplex ET rate constant, k_R) dominate the reactivity, leading to Eq 3,

$${\mathrm{k}}_2=\Sigma K_i{k}_i~n_R{k}_R{K}_R+N_{NR}{k}_{NR}{K}_{NR}$$ (2)

$$~n_R{k}_R{K}_R$$ (3)

As the binding constant measured by ET quenching, K_a, monitors only reactive sites, one may equate, K_a = K_R. Taken together, Eqs 1, 3 then predict the exponential dependence of k₂ on −q_Mbq_b5 in the DD/FE regime that is observed (Fig 4). For the more tightly bound complexes that populate the SE regime, the interface redesign has enhanced binding to the ET-active R-configurations sufficiently so that one directly observes the first-order, intracomplex ET rate constant (Fig 4, inset). As this monitors only configurations in which b₅ is bound to reactive sites within the crp, one can assign k_et = k_R = k_f, which is taken to be invariant with −q_Mbq_b5.

The second-order rate constant (Fig 4, lower) however continues to increase with increasing −q_Mbq_b5 through the FE/SE transition and into the SE regime, but the rate of increase slows markedly. To understand the full −q_Mbq_b5 dependence of k₂, and in particular the transition from FE to SE, requires that the description of the dependence of the electrostatic binding energetics on −q_Mbq_b5 be incorporated into a kinetic scheme. We find that this can be successfully carried out through use of the textbook steady-state treatment of intracomplex ET between partners involved in a binding pre-equilibrium.

$$D+A\underset{k_{off}}{\overset{k_{on}}{\rightleftarrows }}DA\stackrel{k_{et}}{\to }{D}^{+}{A}^{-}$$ (4)

This scheme predicts that in the limit of tight binding, intracomplex, photo-initiated ET will be first order and its rate constant will be k_et = k_R. Most importantly, we find that it provides an excellent description of the variation of k₂ with −q_Mbq_b5 over the full range of behaviors from FE and weak binding through the transition to SE and tight binding, (Fig 4, upper). The scheme of Eq 4 leads to the classical steady-state expression for k₂ as a function of the intracomplex ET rate constant (k_et), the diffusion-limited association rate constant (k_on), and the affinity constant (K_a = k_on/k_off).

$$\begin{array}{cc}\hfill {\mathrm{K}}_2& =k_{et}{k}_{on}∕(k_{et}+k_{off})\hfill \\ \hfill & =k_{et}{k}_{on}{K}_a∕(k_{on}+k_{et}{k}_a)\hfill \end{array}$$ (5)

In the FE limit, defined by the rate ratio, k_et/k_off ⪡ 1, the scheme reduces to k₂ = k_etK_a, as discussed above. In the slow-exchange limit, defined by k_et/k_off ⪢ 1, the rate constant for the second-order ET quenching of unbound, photo-excited ZnMb reduces to the diffusion rate constant, k₂ → k_on.

To apply this model to the experimental results, K_a = K₀ exp(− q_Mbq_b5f/RT), as described in Eq 1, and k_on is given the charge dependence for diffusion of charged species.⁽³²⁾

$$k_{on}-{\mathrm{k}}_{\mathrm{D}}^0\{-a{q}_{\mathrm{Mb}}{q}_{\mathrm{b}5}∕[1-\exp \left(a{q}_{\mathrm{Mb}}{q}_{\mathrm{b}5}\right)]\}\equiv {\mathrm{k}}_{\mathrm{D}}^{0}p\left(q_{\mathrm{Mb}}{q}_{\mathrm{b}5}\right)$$ (6)

Here k_D⁰ is the diffusion-limited rate constant for the proteins that do not interact electrostatically (−q_Mbq_b5 = 0), and p represents the contribution to diffusion from the electrostatic interactions between the partners, with a = f/RT.⁽³²⁾ As a simplifying first approximation, we further take k_et to be identical for all [Mb, b₅] protein pairs, ignoring the small fractional change observed experimentally (Fig 4, inset). Substitution of Eqs 1,6 into Eq 5 leads to the following form for the dependence of k₂ on the product of the charges, q_Mbq_b5, where c = k_D⁰/k_et,

$${\mathrm{k}}_2={\mathrm{k}}_{\mathrm{D}}^{0}p\left(q_{\mathrm{Mb}}{q}_{\mathrm{b}5}\right)K_a∕[cp+K_a]$$ (7)

The fit of Eq 7 to the full dataset composed of k₂ measured for the suite of complexes at both pH = 7 and 6 (Fig 4, solid line) gives a remarkably good description of its overall dependence on −q_Mbq_b5, with equivalent scatter in the data at both pH values (Fig4, Fig SI_4). This fit is essentially identical that obtained with the pH 7 data alone (Fig 4, dashed line); the more limited range in −q_Mbq_b5 available at pH = 6 (noted above) makes an independent fit of this data infeasible.

The parameters that result from the fit of the entire dataset to eq 7 are f = RTa = 0.22 kcal/mol, c = k_d⁰/k_et = 17.3, and k_D⁰ = 2.6×10⁸ M⁻¹s⁻¹. The nominal limiting intracomplex ET rate constant, k_et = k_D⁰/c = 1.5×10⁷ s⁻¹, is ~ 10-fold larger than the intracomplex ET rate constant determined for the SD-type complexes: k_et ~ 10⁶ s⁻¹ (Fig 4, Table SI_1), suggesting that the rapid intracomplex ET reaction obtained in the quenching measurements (Fig 3) may be dynamically controlled, and may actually correspond to a rate constant for conformational interconversion. Motion(s) that might be involved include `diffusion' of b<sub>5</sub> among the ensemble of forms bound to the crp, or the conversion between a weakly-bound `encounter complex' and the ensemble of bound forms (see next subsection). The parameter f ~ 0.2 kcal/mol obtained from the fit of k₂ to Eq 7 is larger than the parameter f ~ 0.1 kcal/mol determined above from the dependence of K_a on −q_Mbq_b5. Further work will be required to determine whether this difference merely reflects experimental limitations, or whether it reflects the fact that K_a is determined from singlet-quenching, while k₂ is determined from triplet-quenching, and the two measurements sample different conformational ensembles.

According to Eq 5, the SE-regime comprises complexes with k_et/k_off ⪢ 1, the FE-regime, complexes with the reverse of this inequality. Surprisingly, the change between regimes occurs without any apparent transitional behavior at −q_Mbq_b5 ~ 16.5, which corresponds to k_et/k_off ~ 250, based on the parameters a, k_D⁰ and k_et determined by the fit to Eq 7. To compare this finding with expectations based on the simple model of Eq 4, the parameters from the fit in Fig 4 were used to calculate values for k_on and k_off as a function of −q_Mbq_b5 and these in turn were used as input parameters for computing kinetic decay traces through numerical solutions of the differential equations for the kinetic scheme of Eq 4. The calculated decay traces were then fit to exponential and bi-exponential decay functions. These fits show that for low values of −q_Mbq_b5 the simulated traces are monophasic throughout a b₅ titration, whereas for high values of −q_Mbq_b5 they are biphasic. Of particular note, they further show that the transition from FE to SE kinetic behavior is sharp, and occurs at a ratio, k_et/k_off ~225, very similar to that found experimentally, but at a slightly lower value of −q_Mbq_b5 ~10.5. This correspondence in the observed and calculated transitions supports the analysis based on the model of Eq 4, with the small differences likely attributable to experimental limitations on the ability to detect a second component in the experimental decay traces because of noise on those traces.

BD Simulations

Fig 4 shows that the complex formation and ET reactivity between Mb and b₅ are governed by electrostatic interactions between the total protein charges, viewed as localized in the crp, and that Eq 4 provides an excellent global characterization of the response of the kinetic behavior of this system to changes in the protein-protein charge product. To explore the structural basis for this relationship between k₂ and −q_Mbq_b5 we have performed paired Brownian Dynamics (BD) simulations of b₅ docking to the series of Mb mutants created using the three hotspot charge residues. Here, as in previous studies,^{(12, 13)} we employ the center-of-mass distance `hit' criterion (d_COM) as a measure of overall binding and a heme propionate – heme propionate distance criterion (d_OO) as a measure of reactive binding. The variation of k₂ with −q_Mbq_b5 can be visualized by comparing the number of reactive OO hits to the number of COM hits (R), with an expectation that the two numbers approach unity as the energy landscape approaches the SD limit in which all hits are reactive.

Fig SI_2 shows the numbers of hits from the two types of simulations as a function of −q_Mbq_b5. With the COM criterion, nearly half of the 10⁴ trajectories result in hits, even for the [Mb(wt), b₅] complex where −q_Mbq_b5 ~ 0, and this number increases only modestly as a function of increasing −q_Mbq_b5. However, the number of hits with the OO criterion is quite low when −q_Mbq_b5 is small, increases rapidly as −q_Mbq_b5 increases, and approaches the COM value as a limiting value at high −q_Mbq_b5.

The global response of k₂ to changes in −q_Mbq_b5 is accompanied by noticeable variations (`granularity') at fixed values of −q_Mbq_b5, which offers additional insights into the overall progression. For example, Fig 4 contains 12 reaction pairs with −q_Mbq_b5 = 19.5 ± 2, among which k₂ varies by roughly an order of magnitude, and similar behavior is observed for the five pairs with −q_Mbq_b5 = 7.5± 2. BD simulations indicate that the variation in k₂ at a given value of −q_Mbq_b5 is not reflective of experimental uncertainties, but arises because the interactions within each pair involves an ensemble of conformations with b₅ bound within the crp, and the nature of the ensemble depends on the number and placement of the surface charges.

The variations in the nature of these ensembles can be understood by comparing `hit profiles' from Brownian Dynamics simulations for protein pairs with similar values of −q<sub>Mb</sub>q<sub>b5</sub>. The insets in Fig 6 show profiles of the reactive hits for the FE/DD-type [Mb(wt), b<sub>5</sub>] complex and three SE/SD-type [Mb(+4), b<sub>5</sub>] complexes with −q<sub>Mb</sub>q<sub>b5</sub> ~19.5 that involve different pairs of altered hotspot residues. For each of these [Mb(+4), b<sub>5</sub>] complexes, the reactive hits have coalesced from the dispersed array seen for the complex with Mb(wt)<sup>(13)</sup> into a `reactive' ensemble (`cluster') of hits in the crp, with the majority of the hits having the requisite short metal-metal distance needed for rapid ET. However, the histograms of the metal-metal distances for the hit ensembles of these three complexes are significantly different.

Figure 6.

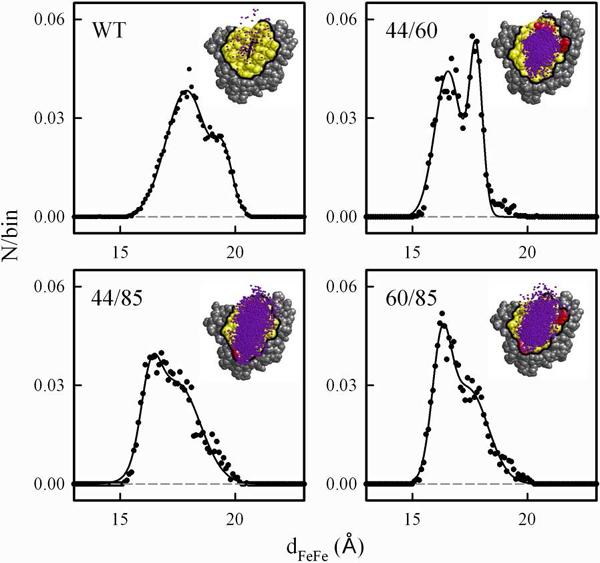
BD hit profiles (insets) and corresponding d_FeFe histograms for Mb(wt) and Mb(+4) mutants with −q_Mbq_b5 = 19.5. The counts/bin was normalized to the total number of hits and the resulting histograms were fit to a sum of two Gaussians (Table 1). Conditions: OO reaction criterion with a 4.0 Å distance cutoff; pH7; μ = 18 mM; 20°C; 10⁴ trajectories; 0.1 Å distance binning. To improve the signal/noise on the histogram for the Mb(wt) complex, a simulation with 10⁶ trajectories was used.

Viewed qualitatively, the distributions for the complexes with Mb(44/85) and Mb(60/85) are expanded in comparison to the distribution for the complex with Mb(44/60), extending towards the E85 hotspot mutation site. Looked at more quantitatively, the histograms for each of the three Mb(+4) mutants are well-described by a sum of two Gaussian functions with peak maxima near 16.5Å and 17.5Å (Table 1). While the breadths of the distributions for the shorter distance component (peak 1) are quite similar among the three pairs, the width at half-maximum (Δw_1/2) for the longer-range component (peak 2) is much smaller for the [Mb(44/60), b₅] pair than it is for the other two pairs. Thus, the differences in the hit profiles largely arise from differences in the less-reactive, longer-range component and in the relative populations of the short and long-range components. Overall, these computations confirm that increasing the charge of the crp serves to increase the attraction of the b₅ partner to this Mb surface region, but variation in the location of the charges within the crp introduces `granularity' into the details of the ensemble of contributing conformations.

Table 1.

Parameters from Double Gaussian fits to d_FeFe Histograms from BD Simulations^a

Protein	Peak 1			Peak 2
	dmax (Å)	Δw1/2 (Å)	hb	dmax (Å)	Δw1/2 (Å)	hb
Mb(wt)	17.9	0.88	0.038	19.5	0.40	0.015
Mb(44/60)	16.5	0.57	0.044	17.8	0.28	0.049
Mb(44/85)	16.3	0.43	0.023	17.5	1.0	0.030
Mb(60/85)	16.3	0.41	0.036	17.4	0.86	0.029

^aOO reaction criterion, d_oo = 4.0; 0.1 Å bins.

^bAmplitudes based on 10⁶ trajectories (wt) or 10⁴ trajectories (mutants).

It is useful to note that this granularity exists within the context of a design strategy that successfully enhances binding/reactivity by making variants with increased total charge. By localizing all mutation sites within the crp, this design strategy generates a progression in charge product while minimizing granularity. With alternative design strategies, it is conceivable that the granularity in k₂ at fixed −q_Mbq_b5 could be made to encompass the full range of behaviors seen in the progression, thus illuminating the importance of the overall pattern of charged residues. Indeed, such an alternative strategy was elegantly implemented by Margoliash and coworkers,^{(55–57) (58)} who mapped the binding interface of Cc with several of its redox partners through kinetic measurements of ET that employed a suite of site-selective, chemically-modified Cc proteins in which the dipole moment of Cc was varied while the charge was fixed.

Generality of the Pre-equilibrium model of Eq 4

It is widely thought that the association and docking of protein partners is a complicated process, with the partners first forming an `encounter complex' before proceeding to the most stable bound state.^{(23, 47, 59–62)} Nonetheless, application of the analysis based on the pre-equilibrium binding/ET scheme of Eq 4 to the [RC, c₂] complex suggests that this simple approach offers a general basis for discussions of protein-protein ET within suites of mutants formed by varying the properties of one or both of the partners. For the [Mb, b₅] system, the linear relationship between the charge product −q_Mbq_b5, and the driving force for binding (−ΔG_a = RT log K_a, Eq 1), allows the abscissa of the semi-logarithmic plot of k₂ to be assigned to either −ΔG_a or −q_Mbq_b5 (Fig 4, top and bottom axes). The use of a free energy axis then permits a comparison of the behavior of the [Mb, b₅] system with ET between other suites of partners where the driving force for binding is varied without such a simple correlation with total-charge product.

The pre-eminent example of such a study involved measurements by Okamura and coworkers of ET between c₂ and a suite of variants of the RC. Guided by the crystallographic structure of the [RC, c₂] complex,⁽⁶³⁾ they initially prepared charged RC interface mutants (Δq = −1,1,2,4), to study long-range electrostatic effects on the formation, stabilization and reactivity of the [RC, c₂] complex.^{(18, 19)} As the crystal structure of the [RC, c₂] complex suggested the presence of hydrophobic residues in the core of the binding interface, they subsequently prepared RC single-site variants at three hydrophobic hotspot positions.⁽²⁰⁾

The inset to Fig 7 presents values of k₂ for ET between c₂ and the suite of RC variants prepared by mutating hydrophobic residues without changing the charge. The parent [RC, c₂] complex is so tightly bound that despite the large decreases in binding affinity that were achieved, all the complexes from this suite remain in the SE regime. For this regime the pre-equilibrium model predicts that k₂ = k_on ~ k_D. As k_D should be independent of the binding free energy for complexes in which the RC differs only through hydrophobic mutations, k₂ should be invariant in this regime, exactly as observed. In short, within this suite, the reactivity is kinetically decoupled from the large changes in binding.

Figure 7.

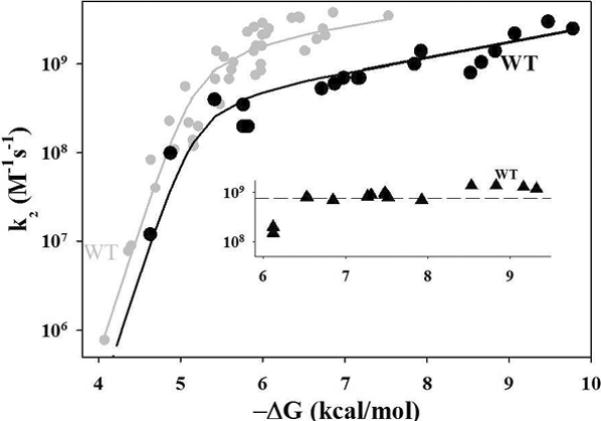
Progression in k₂ as a function of K_a for [Mb, b₅] and [RC, c₂]. Data for charged RC mutants are from ⁽¹⁹⁾; data for hydrophobic mutants (inset) are from ⁽²⁰⁾. The datapoint for the LK(M191) mutant is included with the charged mutants rather than the hydrophobics. The curve through the data for the [RC, c₂] complex is drawn to guide the eye.

The study with the charge-altering RC variation corresponds more closely to the present work with the [Mb, b₅] complex. Fig 7 shows the variation of k₂ as a function of RTlnK_a = −ΔG_a for the suite of RC with charge-altering mutations. As the binding is weakened by mutation, the tightly-bound complex shifts from the SE regime into the FE regime in a progression that reverses the progression from FE to SE generated by the charge reversal mutations in the weakly-bound [Mb, b₅] complex. An independent fit of k₂ vs −ΔG_a for the [RC, c₂] complex to Eq 7 is not feasible, as there are too few points in the FE regime, but the variation of k₂ for the [RC, c₂] complexes with –ΔG_a, nonetheless, is well-described by offsetting the fitting curve for the [Mb, b₅] pair. The offset to lower k₂ reflects, in part, a smaller value of k_et, as might be expected because the bacteriochlorophyll special pair of the RC is buried whereas the Mb heme edge is exposed.

Unlike the driving force for the [Mb, b₅] system, –ΔG_a for the [RC, c₂] complexes does not monotonically follow the nominal mutation-induced changes in RC charge. This difference likely occurs because the `binding patch' of the RC (Fig SI_3) is quite large in comparison with the crp of Mb, and the charged residues on the RC reactive surface are dispersed within this much larger area. In addition, the crp of c<sub>2</sub> is small compared to the RC binding surface, in contrast to the excellent match between the crp of Mb and b<sub>5</sub>. As a result, the binding interfaces between c<sub>2</sub> and different modified RCs will involve residues in different electrostatic microenvironments, with different solvent exposure and different degrees of screening. As a consequence, charge-changing mutations at different sites will have different influences on the binding, preventing any simple correlation between the binding driving force and the product of total charges. Furthermore, the binding affinities for the RC hydrophobic variants span an equally large range in –ΔG<sub>a</sub> as do the complexes with the RC charge variants, yet the hydrophobic variations do not `push' the complex appreciably into the FE regime, whereas the charge variations do.

The large variability in the influence of individual contacts within the [RC, c₂] interface contrasts with the considerably smaller variability/granularity for [Mb, b₅] complexes, discussed above. This difference reflects the fact that the BD,designed Mb mutation sites are not dispersed over a large binding surface, as with the RC, but by design are closely clustered within the small Mb crp.

Summary and Conclusions

We have examined photo-initiated ET quenching within a set of [ZnMb, b₅] complexes prepared from Mb variants identified by our interface electrostatic redesign strategy. The addition of positive charges to the reactive region of the Mb surface through D/E → K charge-reversal mutations at one, two or all three of the hotspot positions (D44, D60, E85), augmented with variants in which negative charge is eliminated from the Mb or b₅ surface by neutralization of their heme propionates, has produced a remarkably large range in the product of the total charges of the two partners, −5 < −q_Mbq_b5 < 40. As −q_Mbq_b5 is increased within this range, the affinity constant for binding of b₅ to Mb increases by 10³ and the complex undergoes a transition from FE to SE kinetic behavior on the triplet ET timescale. The second-order triplet ET quenching rate constant (k₂) is measurable throughout the entire range in −q_Mbq_b5, increasing progressively as −q_Mbq_b5 increases. The rate constant for intracomplex protein-protein ET from the ³ZnP excited state of the ZnMb (k_et) can be directly measured only for complexes in the SE regime where it increases by roughly an order of magnitude (Fig 4, inset). Furthermore, intracomplex ET from the singlet excited state used here to measure the binding constants for the complex (K_a) becomes progressively more effective with increasing total-charge product. Indeed, the singlet ET process has been directly monitored on the ns/ps timescale for the [Mb, b₅] complex with the highest −q_Mbq_b5 value.

The binding affinity (K_a), which probes the population of ET-active configurations of the [Mb, b₅] complex, shows a simple, exponential dependence on −q_Mbq_b5 (Fig 4, Eq 1). To understand this behavior we introduced the idea of a charged reactive patch (crp) on the surface of each partner: the compact surface area around the heme edge that contains a charge equal to the total charge of the wild-type protein and encompassing much of the reactive surface region (Rr). All of the Mb mutation sites employed in this study fall within the crp (Fig 5B), so the total charge on every Mb charge variant can be treated as being concentrated within this surface region. A corresponding crp for b₅ and its heme-neutralized charge variant likewise contains the total b₅ charge and its good ET pathways (Fig SI_1). The crp definition naturally leads to a picture in which the ET partners react only when the Rr within the two complementary crp are electrostatically drawn together.

The progression in k₂ with increasing −q_Mbq_b5 and the transition from FE to SE kinetic behavior (Fig 4) can be understood by integrating the crp description of a protein-protein interface and the corresponding charge-product dependences of the binding free energy (Eq 1) and association rate (Eq 6) into the simplest steady-state, pre-equilibrium treatment of reversible binding between the ET partners (Eq 4). The suite of complexes studied here is found to encompass the full range of behaviors predicted by the model, and as shown in Fig 4, its simple approach captures the global aspects of the correlated electrostatic control of binding and reactivity extremely well. At the same time it reveals a `granularity' in the dependence of k₂ on total charge product - the variations in k₂ at fixed value of −q_Mbq_b5. As illustrated in Fig 6, this variation results from a response of the populations of different bound configurations to variations in the electrostatic surface potentials resulting from the alternative arrangements of charges within the Mb crp.

The general applicability of this simple, textbook, pre-equilibrium model to suites of ET complexes prepared with surface mutants is supported by its ability to fully describe the behavior of ET for suites of [RC, c₂] complexes. The analysis reveals a strong difference between the behavior of the hydrophobic RC mutants and the electrostatic RC mutants, yet the behavior of both subsets can be explained with the pre-equilibrium model. The model further illuminates the basis of the strong variation in the response of the binding affinity to mutations at different sites on the RC surface.

In summary, guided by the BD/mutation surface redesign strategy, we have made considerable progress in electrostatically strengthening the binding of the intrinsically, weakly-bound [Mb, b₅] complex, thereby coupling reactivity to binding at the crp as the total-charge product, −q_Mbq_b5, is increased. The example set by the tightly-bound [RC, c₂] complex shows how much more remains to be achieved in strengthening the binding of the [Mb, b₅] complex, further pushing it toward the SD limit where NMR structure determination or even crystallization of a tightly bound complex will offer a welcome comparison to the ensemble of structures predicted by the BD simulations. It is further anticipated that the strengthened binding will be accompanied by the direct observation of enhanced ultrafast ET on the singlet timescale. As a complement to these efforts, we are employing computational approaches to understand the dynamic and structural factors that govern protein-protein recognition and ET. In particular, the integration of inter-protein pathways and molecular dynamics with Brownian dynamics ensemble-generation provides a promising approach for further exploring the heterogeneity in the electrostatic interactions within the protein-protein interface that govern the progression in behaviors of the [Mb, b₅] complex, and others, and the additional granularity that is not incorporated in the model presented here.

Abbreviations

Mb

Myoglobin

b₅

Cytochrome b₅

RC

Photosynthetic Reaction Center

c₂

Cytochrome c₂

DD

Dynamic Docking

SD

Simple Docking

FE

Fast Exchange

SE

Slow Exchange

ET

Electron Transfer

Crp

Charged Reactive Patch

Rr

Reactive Region

BD

BrownianDynamics