Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ₁ and χ₂ dihedral angles

Abstract

While the quality of the current CHARMM22/CMAP additive force field for proteins has been demonstrated in a large number of applications, limitations in the model with respect to the equilibrium between the sampling of helical and extended conformations in folding simulations have been noted. To overcome this, as well as make other improvements in the model, we present a combination of refinements that should result in enhanced accuracy in simulations of proteins. The common (non Gly, Pro) backbone CMAP potential has been refined against experimental solution NMR data for weakly structured peptides, resulting in a rebalancing of the energies of the α-helix and extended regions of the Ramachandran map, correcting the α-helical bias of CHARMM22/CMAP. The Gly and Pro CMAPs have been refitted to more accurate quantum-mechanical energy surfaces. Side-chain torsion parameters have been optimized by fitting to backbone-dependent quantum-mechanical energy surfaces, followed by additional empirical optimization targeting NMR scalar couplings for unfolded proteins. A comprehensive validation of the revised force field was then performed against data not used to guide parametrization: (i) comparison of simulations of eight proteins in their crystal environments with crystal structures; (ii) comparison with backbone scalar couplings for weakly structured peptides; (iii) comparison with NMR residual dipolar couplings and scalar couplings for both backbone and side-chains in folded proteins; (iv) equilibrium folding of mini-proteins. The results indicate that the revised CHARMM 36 parameters represent an improved model for the modeling and simulation studies of proteins, including studies of protein folding, assembly and functionally relevant conformational changes.

Introduction

Accurate force field parameters are essential for the application of empirical potential energy functions to study protein structure, stability, folding and function. As a result of many years of careful refinement, current additive protein energy functions are of sufficient quality that they may be used predictively for studying protein dynamics, protein-protein interactions and in pharmacological applications.¹ It is clear that the next major step in advancing protein force field accuracy requires a different representation of the molecular energy surface: in particular, the effects of charge polarization must be included, as fields induced by ions, solvent, other macromolecules and the protein itself will affect the charge distribution^2–5. However, since it may be some time before such energy functions are widely available, and computationally accessible for mainstream use, it is important to ensure the highest possible accuracy of current “additive” force fields. Indeed, over the last few years more rigorous evaluation of force fields in the context of conformational sampling of polypeptides and protein folding have lead to new variants of the AMBER and CHARMM22 force fields, including AMBER ff03⁶, ff03*⁷ and ff03w⁸, AMBER ff99SB⁹, ff99SBnmr1¹⁰, ff99SB*⁷, ff99SB*-ILDN¹¹, ff99SB*-ILDN-Q¹² and CHARMM C22*¹³.

From the perspective of protein folding, it has been shown that in long simulations with the additive CHARMM22/CMAP^14–16 force field, certain fast-folding proteins will reach the native state, starting from a completely unfolded configuration (e.g. Villin headpiece subdomain)¹⁷. However, there are some indications of significant deficiencies: examples include misfolding encountered in long simulations of the pin WW domain starting from an unfolded configuration, and differences of the Villin folding mechanism from that inferred experimentally^17,18. In the case of the WW domain, free energy calculations subsequently showed that the misfolded states were in fact lower in free energy than the folded state, confirming that the energy function was at fault¹⁹. A number of studies have suggested that such discrepancies may be largely due to relatively small inaccuracies in the potential for the backbone, resulting in a net “bias” toward either structure, which may be corrected by means of a minor adjustment to the backbone potential^7,20–22.

Here we report a revised set of CHARMM²³ all-atom protein force field parameters (C36) that represents a significant improvement in representing the potential energy surface of proteins, within the context of the current functional form. The changes described in the present work are (i) a new backbone CMAP potential, refined against a range of data for dipeptides as well as experimental data on small peptides such as hairpins and helices and (ii) new side-chain dihedral potentials optimized against quantum mechanical energies from dipeptides and NMR data from unfolded proteins. Other differences from the previous C22/CMAP protein force field include previously published revised Lennard-Jones (LJ) parameters for aliphatic hydrogens²⁴, improved treatment of the internal parameters for the guanidinium ion²⁵ and new parameters for tryptophan²⁶. The backbone and side-chain improvements have been undertaken in parallel such that the new force field is balanced with respect to the contribution of these moieties to protein structure and dynamics. Validation of the C36 force field against a wide range of test systems, including comparison with other state-of-the-art protein force fields, indicates improvements in the quality of the force field in reproducing a number of experimental observables.

Methods

1. Simulation Methods

Several simulation codes were used to perform the calculations in this work, reflecting the packages in which the CHARMM force field is currently implemented: CHARMM²³ itself, NAMD2²⁷, and GROMACS 4.5.3²⁸. All molecular dynamics (MD) simulations were performed in explicit water with periodic boundary conditions, and with long range electrostatics treated using Particle-Mesh Ewald (PME). Non-bonded pair interactions were treated similarly in all packages, as described below. The water model used was TIP3P²⁹: for simulations with CHARMM and NAMD2, a modified TIP3P including Lennard-Jones parameters for hydrogen³⁰ was used, whilst for GROMACS, the standard TIP3P²⁹ was used. Comparison of results with the two TIP3P variants for the Ala₅ and Ac-(AAQAA)₃-NH₂ test cases discussed below showed negligible differences.

(i) Simulations of Ala₅ and other short peptides

Ala₃, Ala₅, Ala₇, Val₃, and Gly₃ were simulated in the NPT ensemble at 298K and 1 atm pressure under periodic boundary conditions. All peptides were unblocked and had protonated C-termini (experimental pH is ~2)³¹. Initial box sizes were 32.13 ų, 34.56 ų, and 38.34 ų for tri-, penta-, and heptapeptides, respectively. PME summation³² was used to calculate the electrostatic interactions with a real-space cutoff set to 12 Å and a 1 Å grid spacing while the LJ interactions were treated with a switching function from 10 to 12 Å. The equations of motion were integrated with a 2 fs time step while SHAKE was used to constrain covalent bonds involving non-water hydrogen bonds and SETTLE³³ was used to maintain rigid water geometries. All of the peptides were simulated for 400 ns each with the new force field. In addition, Ala₅ was also simulated for 200 ns with the previous C22/CMAP force field¹⁶, Amber ff99SB⁹, Amber ff99SB*⁷, OPLS-AA³⁴, and Gromos 53a6³⁵. All of the simulations were carried out with NAMD version 2.7b2. The equilibration protocol for all of the simulations consisted of initial minimization followed by step-wise heating to 298K. Simulations of zwitterionic GPGG were run using GROMACS with a 30 Å cubic box for 100 ns at 300 K, using the same non-bonded treatment, thermostat and barostat as those for Ac-(AAQAA)₃-NH₂ below.

(ii) Replica exchange simulations of Ac-(AAQAA)₃-NH₂

The N-terminally acetylated and C-terminally amidated peptide, initially in a helical conformation, was solvated in a truncated octahedron simulation cell with a distance between nearest faces of 42 Å using GROMACS 4.5.3. The resulting system contained 1833 water molecules. It was found that a larger box size was necessary than was used in earlier work with Amber force fields⁷, as the coil state was more expanded. A 200 ps simulation was run at a constant pressure of 1 bar to obtain equilibrium box dimensions at 300 K. The peptide was then unfolded using a 5 ns constant volume simulation at 800 K. Starting from the final configuration from this simulation (in which all peptide bonds were trans), constant volume replica exchange MD was run using GROMACS 4.5.3, with 32 replicas spanning a temperature range from 278 to 416 K and exchange attempts every 10 ps, for a total of 150 ns per replica. Electrostatic interactions were computed with PME using a real-space cut-off of 12 Å and a 1 Å grid spacing and Lennard-Jones interactions were switched off smoothly between 10 and 12 Å. A Langevin thermostat with a friction coefficient of 1 ps⁻¹ was used, with a time step of 2 fs to integrate the equations of motion. A residue was defined as being helical if it lay within a stretch of at least three residues in the α-helical region of the Ramachandran map, defined as |−65°−φ|< 35° and |−37° −ψ|< 30°. To define residues which lay within the wider α minimum (but not necessarily part of a helix), a larger range of angles, denoted α₊, was used, i.e. −160° < φ < −120° and −120° <ψ < 50°.

(iii) Solute tempering simulation of unfolded proteins in urea

Simulations of unfolded proteins (GB1 and ubiquitin) in urea were performed at a constant pressure of 1 bar using a truncated octahedron cell with a distance between nearest faces of 70 Å using GROMACS 4.5.3. The protein was solvated in an 8 M solution of urea in TIP3P water, with the KBFF³⁶ model being used for urea, based on the favorable results obtained in peptide simulations using this model³⁷. Four potassium ions were added to the GB1 simulation to neutralize the overall charge. Simulations of ~100 ns duration of the unfolded proteins were found to be insufficient to get a representative sampling of side-chain rotamer distributions, particularly for the bulky aromatic side chains. Since for systems of this size (~ 24000 atoms), standard replica exchange would require a very large number of replicas, we instead used the solute tempering replica exchange proposed by Liu et al³⁸. In this scheme, the pairwise forces are split into protein-protein, protein-water and water-water interactions, and the energy of the water-water interactions is scaled in such a way that the water-water energy vanishes from the replica exchange acceptance criterion. Specifically, the potential energy of replica m is given by ³⁹:

$$E_m=E_{pp}+\frac{{\beta }_0}{{\beta }_m}{E}_{ww}+{\left(\frac{{\beta }_0}{{\beta }_m}\right)}^{1/2}{E}_{pw}$$ [1]

In equation 1, E_pp is the sum over all pair interactions between two atoms that are both in the protein, and, similarly, E_ww and E_pw are the sums over water-water and protein-water pair interactions. The particular scaling³⁹ given in the above equation can be implemented by scaling all “solvent” (urea, water and ions) charges by (β₀/β_m)^1/2 and angle terms (urea only) and LJ ε (urea, water and ions) by β₀/β_m, for replica m, where β_m=1/k_BT_m with k_B being Boltzmann’s constant and T_m the temperature of replica m. Replica 0 is the replica for which the correct equilibrium distribution is desired. Sampling was done via a general Hamiltonian replica exchange utility implemented in a modified version of GROMACS 4.5.3. Simulation parameters were the same as for Ac-(AAQAA)₃-NH₂, with a 1 ps interval between replica exchange attempts.

(iv) Replica exchange simulations of HEWL19

REMD simulations were also performed for the unblocked peptide HEWL19, derived from hen egg-white lysozyme with sequence KVFGRC(SMe)ELAAAMKRHGLDN. The structure and parameters for the S-methylated Cys 6 were adapted from those for methionine and are given in the Supporting Information (SI), Figure S1 and Table S1 respectively. Both termini as well as all acidic side chains were protonated, corresponding to the experimental conditions of pH 2³¹. The peptide was solvated in a truncated octahedron simulation cell with a 42 Å distance between nearest faces, and equilibrated at a constant pressure of 1 bar for 200 ps at 300 K. Constant volume REMD was run with 32 replicas spanning the temperature range 278–472 K, for 50 ns, of which the first 10 ns were discarded in the analysis. All other simulation parameters were the same as for Ac-(AAQAA)₃-NH₂.

(v) Crystal Structure Simulations

Simulations of the proteins in their crystal environments (Table 1), which were used previously during optimization of the C22/CMAP force field ⁴⁰, were performed using CHARMM on full unit cells with added waters and counterions to fill the vacuum space. Once the full unit cell was constructed based on the coordinates in the protein databank, a box of water with dimensions that encompassed the full unit cell was overlaid onto the crystal coordinates while preserving crystal waters, ions, and ligands. Water molecules with oxygen within 2.8 – 4.0 Å of any of the crystallographic non-hydrogen atoms were removed, as described below, as well as those occupying space beyond the full unit cell. To neutralize the total charge of each system, sodium or chloride ions were added to the system at random locations at least 3.0 Å from any crystallographic non-hydrogen atom or previously added ions and 0.5 Å from any water oxygen. Final selection of the water molecule deletion distance was performed by initially applying a 2.8 Å criteria to all systems followed by system equilibration and an NPT production run of 5 ns following which the lattice parameters were analyzed. The deletion distances were then increased and the equilibration and 5 ns production NPT simulation were repeated until the final lattice parameters were in satisfactory agreement with experimental data. The final water deletion distances and unit cell parameters from the full 40 ns production simulations are presented in Table S2 of the SI. For the minimization and MD simulations, electrostatic interactions were treated with PME using a real space cutoff of 10 Å. The LJ interactions were included with force switching from 8 Å to 10 Å, while the list of nonbonded atoms was kept for interatomic distances of up to 14 Å and updated heuristically. Each crystal system was first minimized with 100 steps of steepest-decent (SD) with non-water, non-ion crystallographic atoms held fixed followed by 200 steps of SD with harmonic positional restraints of 5 kcal/mol/Ų on solute non-hydrogen atoms. The minimized system was then subject to an equilibration phase consisting of 100 ps of NVT simulation⁴¹ in the presence of harmonic positional restraints followed by 5 ns (100 ps for 135L and 3ICB) of fully relaxed NVT simulation with a time step of 2 fs. During the simulations all covalent bonds involving hydrogens were constrained using SHAKE⁴². Production phase simulations were conducted for 40 ns in the isothermal and isobaric NPT ensemble⁴³. The only symmetry enforced was translational (i.e. periodic boundaries). Reference temperatures were set to match the crystallographic conditions (Table S2) and maintained by the Nosé-Hoover thermostat with a thermal piston mass of 1,000 kcal ps²/mol while a pressure mass of 600 amu was used with the Langevin piston. The first 5 ns of the production simulations were considered as equilibration and therefore discarded from analysis, which was performed on coordinate sets saved every 5 ps. The boundaries for α helices and β strands were obtained from a consensus of author annotations and structural assignments calculated by DSSP⁴⁴ and STRIDE⁴⁵ from the crystal structures.

Table 1.

Protein crystal test systems

PDB ID	Protein	Resolution Å	Unit Cell	Comments	Reference
135L	Lysozyme	1.3	Monoclinic (110.06°)	α-helix, β-sheet, αL, 298K	86
3EBX	Erabutoxin b	1.4	Orthorhombic	antiparallel β-sheet, 298K	81
1EJG	Crambin	0.54	Monoclinic (90.47)	α-helix, β-sheet, 100K	82
1I27	RAP74 Subunit	1.02	Orthorhombic	α-helix, β-sheet, 282K	87
5PTI	Trypsin inhibitor	1.00	Orthorhombic	α-helix, β-sheet, 298K	88
3ICB	Calcium-binding protein	2.30	Orthorhombic	2 EF-hands, α-helix, 298K	89
1BYI	Dethiobiotin Synthase	0.97	Monoclinic (107.24)	α-helix, parallel β-sheet, 100K	90
1BZP	Deoxy and CO myoglobin	1.15	Monoclinic (105.58)	α-helix, 298K	91

(vi) Simulation of a dimeric coiled-coil in solution

Simulation of a dimeric coiled-coil in solution was initiated from model 1 of the NMR structures in 1UOI.⁴⁶ System preparation using CHARMM, with inputs initially generated using the CHARMM-GUI,⁴⁷ involved solvating the dimer with an aqueous solution of approximately 150 mM KCl. All non-hydrogen atoms in the peptides were then harmonically restrained (5 kcal/mol/Ų) and the system subjected to a 500 step SD minimization followed by a 50 ps NPT simulation at 298 K in the presence of the restraints. The final coordinate set was used to initiate the production simulation using NAMD with the coordinates saved every 10 ps for analysis. Simulations involved a 2 fs time step, treatment of electrostatics via PME with a real space cutoff of 12 Å with smoothing of the LJ interactions via a switching function over 10 to 12 Å.

(vii) Simulations of folded proteins in solution

Simulations using Gromacs 4.5.3 were carried out for the following four folded globular proteins: bovine pancreatic trypsin inhibitor (BPTI), ubiquitin, GB3 and hen Lysozyme, starting from the published experimental structures (PDB entries 5PTI⁴⁸, 1UBQ⁴⁹, 1P7E⁵⁰, 6LYT⁵¹ respectively). Each protein was solvated in a truncated octahedron simulation cell filled with TIP3P water, with nearest distance between images of 45 Å for all proteins except for lysozyme, for which the distance was 60 Å. Sodium and chloride ions were added as needed to yield a final salt concentrations of ~100 mM, with adjustments to ensure charge neutrality. For each protein, a 100-step SD energy minimization of the whole system was performed, followed by 200 ps of MD at a constant pressure of 1 bar and temperature of 300 K, in which harmonic positional restraints of 2.39 kcal/mol/Ų were applied to each Cartesian component of each protein non-hydrogen atom using the minimized structure as a reference. Each protein was then simulated at a constant pressure of 1 bar and a temperature of 300 K for 200 ns. Pressure was regulated by a Parinello-Rahman barostat⁵² with a coupling time of 2.5 ps; otherwise all details were as described for Ac-(AAQAA)₃-NH₂ above.

(viii) Replica exchange folding simulation of β-hairpins

REMD simulations were performed on two well-studied β hairpins, the GB1 hairpin (residues 41–56 of protein G)^53,54 and GB1m3^55,56 using Gromacs 4.5.3. Completely unfolded structures obtained from high temperature vacuum simulations were solvated in a 49 Å truncated octahedron box with 2225 water molecules. The REMD simulations spanned a temperature range 278 to 595 K utilizing 40 replicas, sufficient to achieve exchange probability around 0.2, with a frequency of attempted exchanges of 1 ps. An initial sampling of 500 ns per replica was obtained with a preliminary version of the force field, with a further 111 ns per replica obtained with the final parameter set, of which the first 11 ns was discarded as initial equilibration^22,57; all other details were as described for Ac-(AAQAA)₃-NH₂ above.

(ix) Quantum mechanical calculations

Quantum mechanical calculations of the Gly and Pro dipeptides were performed to obtain 2-dimensional (2D) Ramachandran φ,ψ potential energy surfaces. With φ and ψ constrained in 15° increments the dipeptides were optimized at the MP2/aug-cc-pVDZ level of theory using Gaussian 03^58,59. The optimized structures were then subjected to single point energy determinations at the RIMP2/cc-pVTZ and RIMP2/cc-pVQZ levels of theory using QCHEM.⁵⁸ These energies were then used to extrapolate to the complete basis set (CBS) limit using the method of Halkier et al. ⁶⁰ For the Pro dipeptide the surface was limited to φ = −180 to 30° as the remainder of the surface is energetically highly unfavorable. The resulting Gly and Pro RIMP2/CBS//MP2/aug-cc-pVDZ CMAPs were then calculated from the QM surfaces as previously described.^15,16

2. Optimization methods

Backbone Optimization

Optimization of backbone parameters was done via the 2D CMAP potential V_CMAP(ϕ,ψ) ^15,16, for which separate parameters are used for each of (i) non-Gly, Pro residues, (ii) Gly and (iii) Pro. For non-Gly, Pro residues the starting point was the C22/CMAP potential. This CMAP was further optimized, as described further below, to obtain an acceptable match to NMR data for both a short peptide (Ala₅) and a longer helix-forming peptide Ac-(AAQAA)₃-NH₂. The target functions for optimization were the deviations from the experimental observables, i.e. ³J scalar couplings for Ala₅, and carbonyl chemical shifts for Ac-(AAQAA)₃-NH₂. The target function optimized was defined as:

$${\chi }^2=N^{-1}\sum _i\frac{{(F_{\text{obs},i}-F_{\text{calc},i})}^2}{{\sigma }_i^2}$$ [2]

In equation 2, F_obs,i is the experimental data, F_calc,i the data calculated from the simulation, σ_i the error on the ith data point and N the total number of data. The error estimate was based on the uncertainty in the prediction of the experimental observables from the simulation, i.e. the estimated error in the predictions from the Karplus equation and the SPARTA+ algorithm⁶¹. The motivation for this choice is that χ² should be ~1 when the average deviation from experiment is comparable to the error in the prediction, although it differs from the standard definition of the χ² statistic. In most cases, the error of the experimental measurement and the statistical error from the simulation are small, relative to this prediction error. Typical values for the statistical uncertainty of backbone J-couplings from simulations are ~0.05 Hz (e.g. see Table 6) compared with 0.2–0.9 Hz for the error in the Karplus equation prediction, and for chemical shifts ~0.03 p.p.m statistical error compared with ~1 p.p.m prediction error. Values of σ used for each type of scalar coupling and chemical shift are given in Table S3 of the SI. For side-chain J-couplings, the sampling errors can be more significant, due to the slow transitions about χ torsion angles. For these, we have propagated the statistical error in the J-couplings to report an error on the estimate of χ². For Gly and Pro, CMAPs based on the respective RIMP2/CBS//MP2/aug-cc-pVDZ energy surfaces were used without additional modification.

Table 6.

Scalar couplings of the central residue (Ala 10) of HEWL19 in different force fields. All J-coupling values in Hz.

	a expt	σ	b ff99SB	b ff99SB*	c C22/CMAP	c C36
A10 1JNCα (ψ10)	10.58	0.59	10.84 (0.07)	10.27 (0.03)	9.78 (0.02)	10.35 (0.05)
A10 2JNCα (ψ10)	7.24	0.50	7.50 (0.06)	7.06 (0.11)	6.49 (0.06)	7.03 (0.05)
A10 3JHαC (ψ10)	1.72	0.38	2.55 (0.13)	1.82 (0.08)	1.18 (0.04)	2.10 (0.10)
A10 3JHNC (ψ10)	1.33	0.59	1.10 (0.06)	0.65 (0.03)	0.77 (0.02)	0.88 (0.04)
A10 3JHNCβ (ψ10)	2.19	0.39	2.23 (0.12)	3.01 (0.06)	3.73 (0.02)	2.86 (0.06)
A10 3JHNHα (ψ10)	5.10	0.91	5.72 (0.16)	6.46 (0.12)	4.83 (0.04)	6.19 (0.14)
A10 3JHNCα (ψ10,ψ9)	0.46	0.10	0.52 (0.01)	0.39 (0.02)	0.19 (0.01)	0.37 (0.01)
χ2(J) [Hz2]			1.3	1.0	4.7	0.6
% α+	-	-	34.9	69.4	90.3	57.3
% β	-	-	23.5	12.9	2.66	14.6
% ppII	-	-	27.9	15.2	6.67	18.2
% helix	-	-	4.5	30.9	87.0	39.4

^aExperimental data from Graf et al.³¹;

^bData from Ref⁷;

^cData from present work. The set of Karplus parameters denoted “DFT2” in Ref²⁰ was used. χ ² values calculated using equation 2. Statistical errors on individual J-couplings are given in brackets next to the values, based on block error analysis⁹².

Sidechain χ₁ and χ₂ dihedral parameter optimization

Dipeptides corresponding to each residue, excluding Gly, Pro and Ala, were generated with the program CHARMM. The dipeptides contain N-acetylated and N′-methylamidated termini and are representative of the amino acid sidechains in the local environment of peptide backbone. For the initial fitting of χ parameters we used a published set of energy surfaces derived from QM calculations⁶² as target data. The selected QM level, RIMP2/cc-pVTZ//MP2/6-31G* (6-31+G* for the Asp and Glu dipeptides) represents a compromise between accuracy and computational accessability that has been shown to yield conformational energies comparable to CCSD(T)/complete basis sets calculations on complex molecules including those containing anomeric oxygens⁶³. CHARMM potential energy surfaces were generated in a manner consistent with the QM target data which consisted of full 2D scans of the χ₁ and χ₂ dihedral angles in 15° increments for each dipeptide constrained at each of the following backbone conformations: α (−60.0°/−45.0°), β (−120.0°/120.0°), or α_L (63.5°/34.8°). Initial coordinates were obtained from the QM-optimized geometries. Structures were minimized for 500 steps of conjugate-gradient (CONJ) and 500 steps of adopted basis Newton-Raphson (ABNR) with a convergence criteria of the root-mean-square (RMS) gradient < 10⁻⁵ kcal/mol/Å with harmonic dihedral restraints of 10⁴ kcal/mol/rad on the respective dihedrals. The resulting χ₁/χ₂ energy surfaces were offset relative to the respective global minimum for each residue type.

A Monte Carlo simulated annealing (MCSA) automated fitting program⁶⁴ was used for the optimization of sidechain dihedral parameters. This program allows simultaneous fitting of multiple dihedrals for an arbitrary number of dipeptides as required for fitting parameters for dihedrals common to more than one sidechain. During optimization of the dihedral parameters the multiplicities, n, were restricted to 1, 2 and 3, the force constant, K, was limited to K ≤ 3.0 and the phase δ limited to either 0° or 180°. Energy surfaces from all three backbone conformations were considered together as target data. The objective function of the fitting program, shown in equation 3,

$$\mathit{RMSD}=\sqrt{\frac{{\displaystyle \sum _i^N}{w}_i{\left(E_i^{QM}-E_i^{MM}+c\right)}^2}{{\displaystyle \sum _i^N}{w}_i}}$$ [3]

is the RMS energy difference, RMSD, where E^QM and E^MM are the relative QM and MM energies, respectively, for conformation i, c is an offset to minimize the RMSD and w is a weighting factor for conformation i. In practice, the RMSD is calculated with the force constants on the dihedral parameters to be optimized set to zero such that during each iteration of the MCSA only the dihedral energies need to be evaluated and the change in the RMSD calculated in a computationally expedient fashion. During fitting we applied weighting factors of w = 5 on energy surfaces from α and β backbone conformations and w = 1 for data from α_L. Each set of side-chain parameters was fitted with a minimum of 100,000 MCSA steps and an initial temperature of 1,000 K. The initial parameters for condensed phase simulation testing were obtained as the arithmetic mean of five individual MCSA runs that differed by the initial random number seed. Convergence of each run was verified by monitoring the RMSD throughout the optimization. Optimized parameters from the automated fitting program were subsequently subjected to manual adjustments focused on the relative energy of the local minima in the QM surfaces to improve the reproduction of experimental relative rotamer populations in MD simulations as described below.

For comparison of χ₁ and χ₂ from the crystal simulations with experimental data, crystal distributions for χ₁ and χ₂ were obtained from a survey of the protein data bank⁶⁵ with the data converted to probability distributions using a bin size of 15°.⁶² The analogous probability distributions were calculated from the protein crystal simulations. To measure the agreement between the crystallographic and simulated χ distributions, the 1D overlap coefficients (OC) for the two probability distributions were calculated over the sampled grid points as previously described using equation 4.^66,67

$$OC=\frac{\sum p_m·p_n}{\sqrt{\sum {(p_m)}^2·\sum {(p_n)}^2}}$$ [4]

3. Calculation of experimental observables

Residual Dipolar Couplings

Residual dipolar couplings for the folded proteins were calculated as described previously,⁷ by fitting the global alignment tensor that results in the smallest RMS difference between experimental and calculated couplings.

Three-bond Scalar Couplings

Scalar couplings for backbone and sidechains were determined from the torsion angles using Karplus relationships. Ala_n, Gly_n, Val_n: both flavodoxin-based Karplus parameters⁶⁸ and DFT-based Karplus parameters (DFT2) described in Ref⁶⁹ were used as previously described²⁰. Unfolded proteins in urea: the amino acid-dependent Karplus parameters of Perez et al. for sidechain dihedral χ₁ were used.⁷⁰ Folded proteins: the Perez parameters⁷⁰ were used for all J-couplings, with the exception of ³J_NCG and ³J_C′CG couplings, for which the parameters of Chou and Bax were used. ⁷¹

Chemical Shifts

Chemical shifts were calculated with the SPARTA+ empirical shift prediction package⁶¹ for individual structures and ensemble-averaged over the simulation.

Results: Parameter Optimization

The main aim of the optimization was to improve the parameter set for torsion angles in the force field. This was motivated, in the case of the backbone, by the results of folding simulations that showed the backbone parameters for C22/CMAP to have an excessive helical bias^18,19. In addition, since the torsion parameters had never been explicitly optimized in a side-chain specific fashion, it was felt this was an area in which improvements could be made. The backbone and side-chain optimization were initially undertaken independently, and the results then combined – it was found that there was some coupling between the backbone and side-chain parameters as described below. The final optimized C36 parameters may be obtained from the MacKerell Laboratory web page at http://mackerell.umaryland.edu/CHARMM_ff_params.html

Backbone Optimization

The CHARMM additive protein force field contains, in addition to the usual Fourier terms for the backbone torsion angles ϕ and ψ, a two dimensional cubic spline potential or CMAP, V_CMAP(ϕ,ψ) ^15,16. The spline is specified by energies determined on a 2D lattice with a 15° grid spacing. For internal residues, we only modify the CMAP terms for the backbone, since these effectively include any features of the energy surface that could be captured by the backbone torsion terms (some independent optimization of the backbone torsion angles for terminal Gly residues was carried out as discussed below). The previous CMAP, optimized for use with the C22¹⁴ all-atom protein force field, was based on the adiabatic QM vacuum energy surface of alanine dipeptide, with empirical modifications to correct for systematic deviations of protein crystal structure simulations from the X-ray diffraction structure. We had initially aimed to base the new CMAP on the QM dipeptide energy surface once more; however, it was found that the previous empirical corrections captured additional cooperativity that was lacking in the dipeptide-based maps (to be described in a separate publication). We therefore retained the original CMAP as a starting point for further optimization. For completeness, we summarize here the strategy used to derive the C22 CMAP¹⁶. The CMAP was initially fitted to minimize the difference between the MM energy and that obtained from the QM surface (calculated with LMP2/cc-pVQZ(-g)//MP2/6-31G*). Although this brought about some improvements, it was found that simulations of proteins in their crystal environment exhibited systematic deviations from the backbone (ϕ,ψ) angles in the experimental structures. A probable cause of this deviation is that the additive energy function cannot capture many-body effects important in folded proteins⁷². As a compromise, small manual adjustments of the CMAP were made in order to match the minima for regions of canonical secondary structure more closely to those in the PDB. With these changes, the average backbone torsion angles from simulations of folded proteins in their crystal environment now matched those in the experimental structures.

In the present work, the grid energies were initially optimized using an automated Monte Carlo-based protocol to improve agreement with Ala₅-based NMR scalar coupling data. Iterative manual adjustments were then made in order to further improve the match with the experimental NMR data for peptides in solution, specifically the following data sets: (i) an extensive set of 3-bond scalar coupling data for Ala₅ published by the group of Schwalbe³¹ and (ii) a set of chemical shift data reflecting helix formation in the 15-residue peptide Ac-(AAQAA)₃-NH₂⁷³. The purpose of the first data set is to capture “intrinsic” propensity for populating the different minima in the Ramachandran map (in the absence of any significant secondary structure), while the second data set is for a peptide with a significant helical population. In each round of optimization, a perturbation approach⁷⁴ was used to estimate the correction needed to better match experimental data, following which further sampling was performed to test the new parameter set. An important principle that emerged was that one should not apply more than the minimal changes needed to match the experimental data to within the estimated error (in calculating the experimental observables from simulation), since overfitting to one data set may result in deleterious effects. For example, it is possible to match the data for Ala₅ more closely by making the polyproline II region of the map even lower in energy, but we found that this has a very destabilizing effect on β-hairpins: even after formation of interstrand hydrogen bonds, the backbone remains in the polyproline II region of the Ramachandran map.

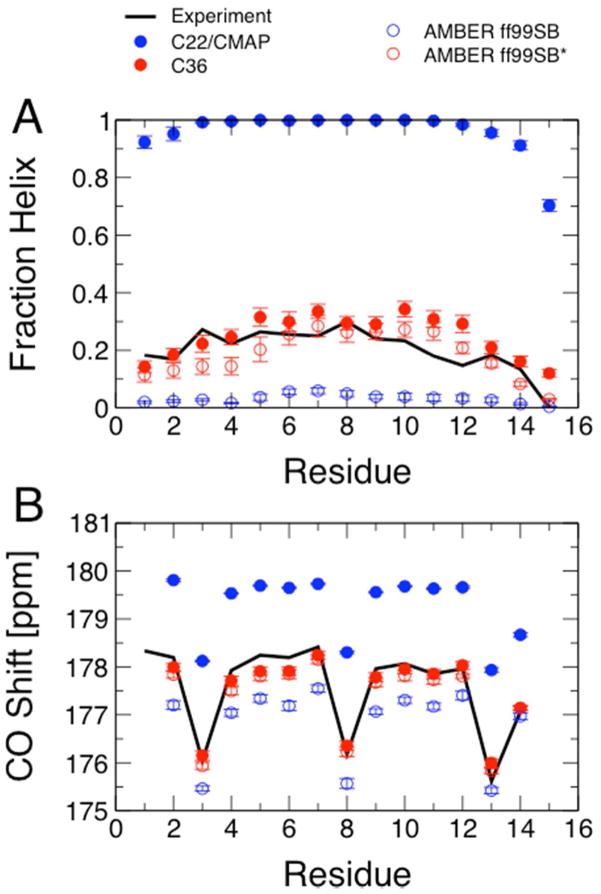
We summarize the final results of the optimization for the two peptides Ala₅ and Ac-(AAQAA)₃-NH₂ in Table 2, together with the analogous statistics for the C22/CMAP^15,16, the Amber ff99SB⁹ and the modified Amber ff99SB* force fields¹¹. We see that the overall agreement with scalar couplings for Ala₅ is much improved relative to C22/CMAP, and also relative to ff99SB and ff99SB*. The individual residues sample more of the “polyproline II” helix region of the Ramachandran map (52%) than any of the other force fields, and less of the enlarged α₊ alpha-helical region (defined as −160° ≤ ψ ≤ −20° and −120° ≤ ψ ≤ 50°). For the longer, helix-forming peptide, Ac-(AAQAA)₃-NH₂ we find that the overall fraction helix at 300 K (21%) is much more reasonable than that (95%) obtained with the previous C22/CMAP, and more in line with the experimental estimate of ~19% obtained by Shalongo and Stellwagen from NMR chemical shifts in D₂O⁷³ and the similar estimate of ~22% which can be interpolated from the circular dichroism data of Scholtz et al. on the related peptide Ac-(AAQAA)₃-Y-NH₂ in water^75,76. This agreement can also be seen at the level of individual residues, as we show in Figure 1A. Since the fraction helix from experiment is only inferred by fitting a thermodynamic model, we have also calculated carbonyl chemical shifts using the SPARTA+ chemical shift prediction program⁶¹. SPARTA+ uses a neural network trained on sets of known folded protein structures and corresponding chemical shifts in order to predict shifts from structure. The estimated error in carbonyl shift prediction is approximately 1 p.p.m. Although the training set does not include weakly structured peptides such as we consider, it does include loops in folded proteins, which are also not in canonical secondary structures. In Figure 1B we compare the predicted shifts with the carbonyl chemical shifts measured in the original experiments⁷³, confirming the improvement afforded by the backbone optimization. A final noteworthy feature of the data for the helix-forming peptide is that the overall fraction helix is slightly higher than that in ff99SB* (21 % vs 14 %), yet the overall population of the α₊ region of the Ramachandran map is lower (44 % vs 48 %). This suggests additional cooperativity as mentioned above, which will be explored further in a future publication.

Table 2.

Properties of peptides used in parameter optimization: Ala₅ and Ac-(AAQAA)₃-NH₂. J-couplings calculated with “DFT2” set of Karplus parameters²⁰ and chemical shifts with SPARTA+⁶¹ at 300 K. Statistical errors from a block error analysis⁹² are given in brackets.

Peptide	Property	ff99SB	ff99SB*	C22/CMAP	C36
Ala5
	% α+	15.7 (1.2)	22.5 (2.2)	41.5 (3.2)	13.1 (1.3)
	% β	37.8 (1.4)	34.5 (1.3)	25.3 (2.2)	30.8 (1.3)
	% ppII	42.3 (1.9)	39.8 (1.6)	26.2 (1.8)	51.9 (1.1)
	% α-helix	0.0 (0.2)	0.6 (0.3)	3.7 (2.1)	0.1 (0.1)
	χ2(J)	1.7	1.7	2.0	1.2
Ac-(AAQAA)3-NH2
	% α+	26.9 (1.2)	48.5 (1.3)	98.7 (0.4)	44.0 (1.8)
	% β	32.4 (0.8)	22.7 (0.7)	0.46 (0.2)	19.1 (0.6)
	% ppII	31.8 (0.9)	21.8 (0.6)	0.41 (0.2)	29.5 (1.2)
	% α-helix	1.8 (0.3)	14.2 (2.1)	95.3 (0.1)	21.0 (1.7)
	χ2(δC′)	0.5	0.06	2.6	0.04

Figure 1.

Helix formation in Ac-(AAQAA)₃-NH₂. (A) Fraction helix per residue estimated from experiment⁷³ at 300 K (black lines) compared with average fraction helix calculated from REMD simulations with C22/CMAP^15,16 (solid blue symbols), C36 (solid red symbols), Amber ff99SB (open blue symbols) and Amber ff99SB* (open red symbols) using the replica closest in temperature to 300 K. (B) Average carbonyl carbon chemical shifts calculated with SPARTA+⁶¹ from the simulations in (A) compared with experimental shifts.⁷³ Color scheme as in (A).

Gly and Pro CMAPs were determined by taking the difference between the target QM and force field energies for Gly and Pro dipeptides, respectively. The new CMAPs were already found to result in good agreement with NMR data for Gly₃ and GPGG, with a significant improvement for Gly, and were therefore not further adjusted. Since the Gly termini are not affected by the CMAP, we have performed a simple optimization on the N-terminal ψ and C-terminal ϕ torsion parameters. In each case, only a single parameter was optimized, namely a dihedral force constant, in such a way as to minimize the χ² between simulated and experimental J-couplings for Gly₃ (each terminus was independently optimized). The old and new parameters are listed in Table S11 in the SI.

Side-chain optimization

Dihedral parameters that modulate sidechain χ₁ and χ₂ conformational energies were initially optimized using QM energy surfaces as target data using a MCSA-based fitting protocol⁶⁴ followed by subsequent empirical optimization targeting the rotamer populations obtained from both solution and crystal simulations, as described below. We note that an alternative method to MCSA for optimizing torsion angle coefficients is linear least squares fitting⁷⁷. We have opted for MCSA as it is more generally applicable and due to the greater flexibility afforded, such as the inclusion of constraints on parameters as was used in the present study. Dihedral parameter multiplicities of up to the third term are used in conjunction with an upper boundary of 3.0 kcal/mol/deg for the force constant (K). The latter constraint reduces the likelihood of overfitting where individual parameters with large K values cancel each other, thereby maintaining parameter transferability. We also limited the phase (δ) to 0 or 180° such that the resulting parameters are not specific to chirality. In addition, during fitting only those χ₁, χ₂ conformations with relative energies less than 12.0 kcal/mol were included in the calculation of the RMSD (eq. 3) to avoid fitting the high-energy regions at the expense of the low energy regions that are accessible during MD simulations. Higher-energy cutoffs (20.0 kcal/mol for Arg and Lys or 25.0 kcal/mol for Asp, Glu and Hsp) were used for the charged sidechains as favorable electrostatic interactions with the backbone in selected conformations led to deep minima in the energy surface such that other local minima are 12.0 kcal/mol above the global minima. In addition to the criteria in the preceding paragraph, χ₁ and χ₂ parameters were grouped based on sidechain type. The groupings are shown in Table S4 of the SI. For example, initially Lys, Arg, Gln, Glu and Met have the same χ₁ parameters. Fitting tests were undertaken in which selected atom types were changed to make the parameters for one or more of the sidechains unique (not shown). Based on this analysis, unique atom types were introduced at the C^β atom of Glu, Asp, and protonated His (Hsp) thereby allowing for improvements in the quality of the fits of those sidechains as well as of the remaining sidechains in the respective groups.

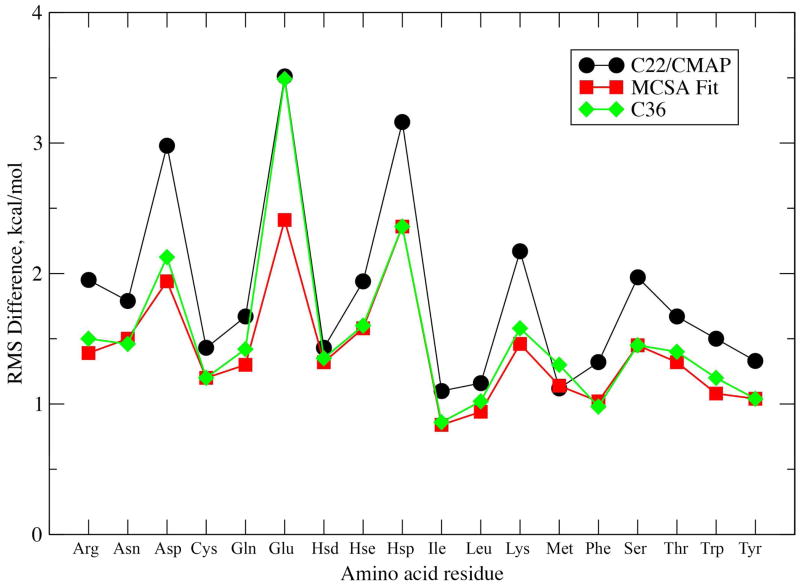
RMS differences between MM and QM energy profiles for those conformations below the relative cutoff energies are shown in Figure 2. As is evident, significant improvement was made in the overall agreement following the initial MCSA fit with respect to C22/CMAP. This is expected as the C22/CMAP χ₁/χ₂ parameters were typically assigned values associated with alkanes and not explicitly optimized targeting QM or other data. In Table 3 the average and RMS differences in relative energies of the expected χ₁/χ₂ minima, or rotamers, between MM and QM levels of theory are presented. The individual relative energies and definitions of the minima for the studied amino acids are shown in Tables S5, S6 and S7 of the SI. The results indicate that although the MCSA-fit brought the energies closer to QM as compared to C22, empirical fitting based on reproduction of the χ₁/χ₂ rotamer distributions from protein simulations (see below) narrowed the gap further for the α and α_L backbone conformations. The RMSD values increased with the β conformation due to compromises made to better satisfy the agreement of the other secondary structures and better reproduce sampling in the protein simulations (see below). For most sidechains, the relative energies of the various rotamers are satisfactorily reproduced although the quality of the agreement varied significantly between the different residues (Tables S5, S6, and S7, SI). A significant exception occurred with Glu, which has the highest RMSD, associated, in part, with the charged nature of the residue. While MCSA fitting lead to improvement over the C22/CMAP RMSD, these parameters yielded poor agreement between crystallographic χ₁/χ₂ rotamer distribitutions and results from crystal MD simulations (see below). Accordingly, additional optimization was performed for the χ₂ torsion of Glu via adjustments to the 1-fold torsion term to improve agreement with crystallographic survey distributions. Poor agreement (Firure 2, RMSD > 2.0 kcal/mol) is also seen for Asp and Hsp. This is due to poor reproduction of the local minima required to better reproduce the high-energy regions, a compromise that is due to inherent limitations in the form of the potential energy function that limits the ability to match the entire energy surfaces. Analysis of the RMSD for low-relative energy regions (i.e. > 2 kcal/mol above the energy minima) versus high-relative energy regions (i.e. 2 – 12 kcal/mol above the minima) show the overall improvement for the low energy regions to be minimal with the largest improvements in the higher energy regions (Table S8, SI); such changes indicate that the new model may have a larger impact on sidechain dynamics rather than on sampling of the different χ₁/χ₂ rotamer populations (see below). While alternate fitting protocols may alleviate the lack of significant improvements in the reproduction of the QM data in the low energy regions, as has been shown previously, rigorous reproduction of QM gas phase data does not always assure satisfactory reproduction of condensed phase properties.⁴⁰

Figure 2.

RMS Differences in relative energies between MM and QM potential energy surfaces. RMS Differences were calculated for relative energies less than 12.0 kcal/mol above the global minimum for the three 1D or 2D surfaces. Higher-energy cutoffs of 20.0 kcal/mol for Arg and Lys or 25.0 kcal/mol for Asp, Glu and Hsp were used for the charged amino acids.

Table 3.

Average and RMS differences (RMSD) in kcal/mol between MM and QM calculated energies for all χ₁, χ₂ rotamers over all the amino acids.

	Average Difference				RMSD
	α	β	αL	All	α	β	αL	All
C22/CMAP	1.80	0.74	3.72	2.09	3.55	2.46	4.73	3.69
MCSA-fit	1.68	0.45	3.64	1.92	2.55	1.49	4.64	3.17
C36	1.19	0.22	2.74	1.39	2.47	1.78	3.67	2.75

Target data for further optimization of the χ₁/χ₂ parameters following the initial MCSA fitting was NMR J-coupling data for ubiquitin and GB1 in 8 M urea. Simulations of the two unfolded proteins were undertaken with the results showing that the initial MCSA-based parameter set did not correctly reproduce the experimental χ rotamer distributions as judged by the reproduction of NMR data (Table 4). Therefore, empirical adjustments of the χ dihedral parameters were undertaken to optimize the relative energy of the local minima in order to obtain improved sidechain sampling in the unfolded proteins while maintaining overall fit to QM data. This process primarily involved adjustments of the 1-and 2-fold dihedral terms to shift the relative energies of the minima without significantly impacting the higher energy regions of the χ₁/χ₂ surfaces. Following several iterations of parameter adjustments and simulations, the final parameter set was obtained. The agreement with the NMR target data on the unfolded proteins is significantly improved (Table 4) while the RMSD for the final set of parameters with respect to the QM data was generally only slightly worse than that based on the MCSA fit parameters (Figure 3). The one exception is Glu where significant disagreement with crystal data was observed requiring significant adjustment of the χ₁/χ₂ torsion parameters. The final set of χ dihedral parameters is anticipated to treat the higher energy regions of the sidechain conformations more accurately based on better reproduction of the QM data (Table S8) as well as of the relative sampling of the χ rotamers based on reproduction of the NMR data.

Table 4.

χ² Values for side-chain J-couplings measured in unfolded ubiquitin and GB1, for the MCSA-derived and final sets of side-chain torsion parameters. χ² values calculated using equation 2. Combined χ² values for Ubiquitin and GB1 are obtained as an average over the two proteins, weighted by the number of data points for each. Overall χ² are obtained as an unweighted average of the χ² for the different types of residue. Statistical uncertainty from a block error analysis is given in brackets next to each number⁹².

RES	MCSA-derived Parameters			Final Parameters
	Ubiquitin	GB1	Combined	Ubiquitin	GB1	Combined
Arg	6.1 (0.7)	N.A.	6.1 (0.7)	4.1 (0.6)	N.A.	4.1 (0.6)
Asn	46.7 (3.7)	6.1 (1.3)	16.3 (2.8)	2.7 (1.3)	9.7 (1.1)	8.0 (1.2)
Asp	32.4 (1.7)	32.8 (1.9)	32.7 (1.8)	3.8 (0.9)	5.5 (0.8)	4.8 (0.9)
Cys	N.A.
Gln	11.1 (0.9)	8.3 (1.4)	10.3 (1.2)	5.7 (0.6)	3.4 (0.8)	5.0 (0.7)
Glu	21.9 (2.1)	38.0 (1.8)	29.4 (2.0)	3.4 (0.5)	5.6 (0.7)	4.4 (0.6)
		N.A.			N.A.
His	10.7 (2.3)		10.7 (2.3)	1.1 (1.1)		1.1 (1.1)
Ile	12.6 (2.4)	7.4 (3.6)	11.5 (3.1)	3.6 (1.0)	19.5 (4.9)	7.0 (2.9)
Leu	52.1 (2.4)	64.0 (4.2)	53.6 (3.3)	3.4 (0.5)	3.0 (0.8)	3.4 (0.7)
Lys	8.9 (0.6)	13.0 (1.1)	10.2 (0.8)	3.7 (0.4)	14.7 (0.8)	7.3 (0.6)
Met	N.A.
Phe	19.4 (3.8)	14.3 (2.1)	16.6 (2.9)	3.8 (0.5)	12.9 (2.0)	8.7 (1.3)
Pro	9.5 (0.8)	N.A.	9.5 (0.8)	7.0 (0.7)	N.A.	7.0 (0.7)
Ser	9.9 (2.1)	N.A.	9.9 (2.1)	3.6 (0.9)	N.A.	3.6 (0.9)
Thr	28.5 (2.3)	18.3 (1.9)	22.1 (2.1)	10.0 (1.1)	15.3 (1.2)	13.3 (1.2)
Trp	N.A.	5.0 (3.1)	5.0 (3.1)	N.A.	1.3 (0.5)	1.3 (0.5)
Tyr	53.7 (0.4)	14.3 (2.5)	25.1 (1.5)	4.3 (2.0)	2.7 (0.8)	3.1 (1.5)
Val	9.1 (1.7)	3.6 (0.8)	6.1 (1.1)	0.7 (0.3)	2.2 (0.7)	1.5 (0.5)
Overall	20.8 (2.0)	18.8 (1.9)	17.2 (2.0)	4.1 (0.9)	8.0 (0.9)	5.2 (0.9)

N.A. indicates that no amino acids of that type are available in the respective proteins.

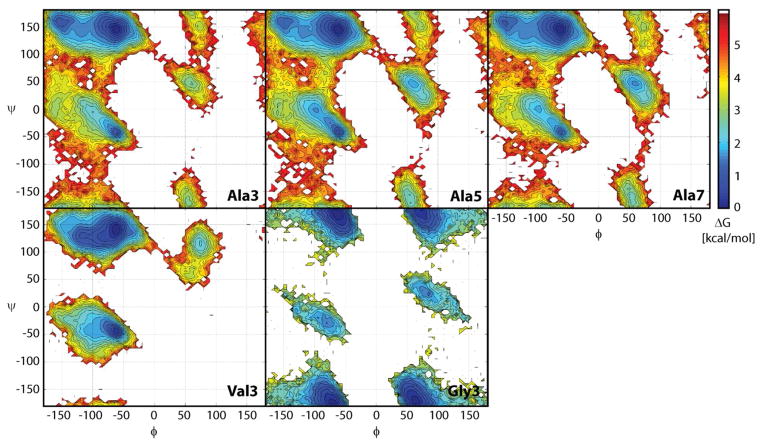
Figure 3.

Sampling of backbone φ/ψ torsion angles in the central residues of Ala₃, Ala₅, Ala₇, Val₃, and Gly₃. Colors indicate relative free energies according to color bar given on the right.

Results: Validation of new parameters

Results for short peptides

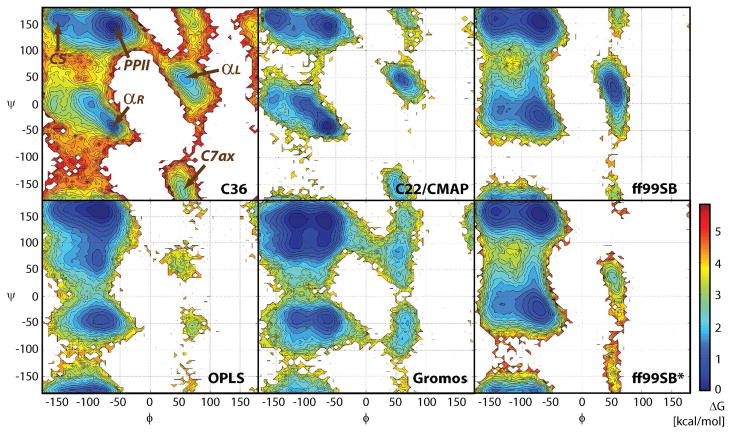
The φ/ψ-sampling for Ala₃, Ala₅, Ala₇, Val₃, and Gly₃ is shown in Figure 3. In alanine- and valine-based peptides, the dominant minimum lies at PPII but additional minima at C5 and α_R are only slightly higher in energy. Additional minima at α_L and C7_ax are about 2–3 kcal/mol higher than the PPII conformation. There is only a small difference between Ala₃, Ala₅, and Ala₇, but the sampling for Val₃ is significantly different because of the presence of the bulkier hydrophobic side chain. Gly₃ exhibits symmetric sampling with similar minima at α_R/α_L and PPII/C7_ax. In Figure 4 the φ/ψ-map with the new parameters is compared against the C22/CMAP map and maps from other popular force fields. It can be seen that the changes with respect to C22/CMAP are relatively subtle with the main differences consisting of a deeper PPII minimum, a higher and more focused α_R minimum, and less sampling of the α_L state. The changes go in the direction of the QM-based map¹⁶, where the PPII minimum is even deeper. Among the other force fields, the Amber ff99SB⁹ map is closest to the new CHARMM force field but significant differences exist. OPLS³⁴ is qualitatively different with a pronounced minimum at C7_eq and the Gromos force field³⁵ has two similarly populated minima in the α_R-basin and a low-energy transition region between α_R and C7_ax that is not present in any of the other force fields.

Figure 4.

Sampling of φ/ψ torsion angles in the central residues of Ala₅ with different force fields: the new force field (C36), the previous C22/CMAP force field (C22)¹⁶, Amber ff99SB⁹, OPLS-AA,³⁴ Gromos 53a6³⁵ and Amber ff99SB*⁷.

The φ/ψ-sampling was further compared with experimental J-coupling constants that are available from NMR experiments. Table 5 summarizes the results with details given in Tables S9 and S10 of the SI. The agreement is very good for the alanine-based peptides and for Gly₃, and reasonable for Val₃. For Ala₅ we also compared with other force fields (Amber ff99SB⁹, OPLS/AA³⁴, Gromos 53a6⁷⁸). The new C36 force field has lower χ² values than all of the force fields and there is, in particular, significant improvement over the previous C22/CMAP force field. This improvement is largely due to decreased sampling of α_R conformations and increased sampling of PPII (Figures 3 and 4). The main reason for the significant improvement over C22/CMAP is the correction of the known bias toward α_R in that force field; the improvement is reflected in the J-couplings probing the ψ backbone torsion angle. However, the main reason for the improvement over other force fields (e.g. ff99SB) is due to the J-couplings probing the ϕ torsion angle (in fact most of the couplings are probing this torsion angle). This improvement largely reflects the balance between the β and ppII regions of the Ramachandran map, which are those contributing the most towards the ensemble-averaged J-couplings in most force fields. Although the χ² value for Val is slightly worse, it should be noted that substituent effects make a significant contribution to the J-coupling and the use of an alternative set of Karplus equation parameters (Table S9 of SI) reduces many of the deviations from experiment. Note that although Gly₃ data was used to derive Gly parameters for the termini (Table S11 of the SI), the internal glycine J-couplings have not been used as target data in the parametrization, with the 2D QM surface used directly to create the Gly φ/ψ CMAP term in the force field. As an independent test of terminal glycine parameters, and of the proline parameters, which were also based directly on the 2D φ/ψ QM surface, we have compared our results with data for the peptide GPGG⁷⁹, obtaining much improved agreement over C22/CMAP, particularly for the C-terminal Gly in GPGG (Table S12 of the SI).

Table 5.

χ² values from comparison of experimental NMR J-coupling constants with simulation results. All values were calculated with flavodoxin-based Karplus parameters⁶⁸. For the new force field, results with DFT-based Karplus parameters (DFT2)⁶⁹ are given in parentheses. For Gly₃ and GPGG only DFT-based⁷⁹ results are given.

	Ala3	Ala5	Ala7	Val3	Gly3	GPGG
C36	0.61 (1.22)	0.74 (1.16)	0.43 (0.68)	2.33 (3.57)	2.33	2.78
C22/CMAP		1.73			3.68	13.37
Amber ff99SB		1.40			3.04	2.39
OPLS-AA		1.35
Gromos 53a6		1.68

19-residue disordered fragment of Hen Lysozyme

In addition to tests on structure-forming peptides, it is important to also consider peptides that form little helix or sheet structure. As a test for such a largely disordered peptide, we chose a 19-residue fragment of hen Lysozyme, for which scalar couplings have been measured by Graf et al.³¹ Extensive sampling of this peptide was obtained by means of replica exchange molecular dynamics, from which the degree of structure formed was assessed by means of backbone scalar couplings. In Table 6, we report scalar couplings for the central alanine residue (full data set in Table S13 of the SI). Overall, the agreement with the couplings is much better than the previous C22/CMAP force field and slightly better than the previously optimized Amber ff99SB* force field. In particular, the agreement with scalar couplings reflecting the ψ torsion angle was the best out of the force fields considered.

Stability of dimeric coiled coil

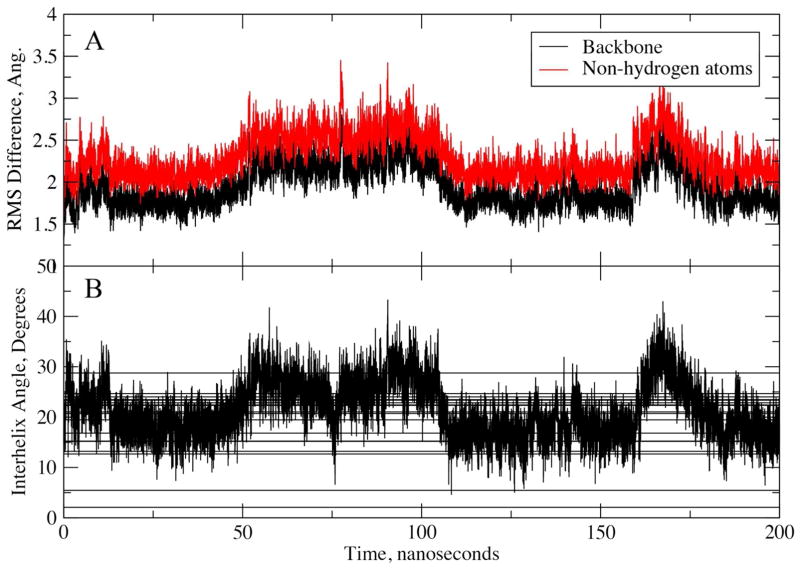
The developed parameters were also tested for their ability to reproduce the structure of a dimeric coiled-coil protein. These structures include two or more individual helices that interact primarily via hydrophobic amino acids protruding along one side of the helices. This class of peptides has been subject to a number of MD simulations, where in some cases obtaining stable native state simulations has been challenging.⁸⁰ One such example is a heterodimeric parallel coiled coil (PDB identifier 1U0I)⁴⁶, which was found to give poor results with a number of force fields, the closest RMS difference from the native being approximately 4 Å. Accordingly, the dimeric peptide represents a good test of the force field in the light of the previous simulation results as well as the overall structure being dominated by hydrophobic interactions between the two helices in the dimer. Figure 5A shows the RMSD as a function of simulation time for a 200 ns simulation initiated with model one from the collection of NMR structures.⁴⁶ The RMSD being in the vicinity of 2 to 2.5 Å, with the C- and N-terminal residues excluded, indicates the overall structure to be stable, representing a significant improvement over previously reported results. The ability of the model to reproduce the experimental structure is futher judged by comparison of the inter-helical angles between the two helices from the simulation with those obtained from the 20 NMR models (Figure 5B). The overlap is excellent, indicating C36 to satisfactorily model the interactions between the two peptides. Additional analysis involved alignment of one of the two helices and calculation of the RMSD for that helix as well as the second helix (Figure S2 of the SI). The RMSD of the backbone atoms of the self-aligned helices are all ~1 Å indicating that the helical structure of the individual peptides was maintained: an important outcome, as the developed FF was designed to yield a lower population of helices and an additional indication that the balance of the FF between sampling of extended and helical conformations is satisfactory. Also shown are the RMSD of the second, non-aligned helix, with the difference being in the range of 2 to 6 Å with the presence of larger fluctuations showing that the helices are moving relative to each other in the simulation indicating that the force field is not overly restraining the dimer in a conformation close to that in the experimental structure. Overall, these results indicate that the FF adequately reproduces the structure of the coiled-coil dimer and thus appropriately models hydrophobic interactions and the helical character of individual helices.

Figure 5.

A) RMS difference from experimental structure and B) Inter-helical angle of the dimeric coiled-coil 1U0I as a function of simulation time. RMS differences are for the backbone (N, C^α, C, O) or non-hydrogen atoms of both helices following least squares alignment of the backbone atoms in both helices. The N- and C-terminal residues were excluded from the analysis. For the inter-helical angles vectors defining the helical axes were calculated using the non-terminal residue C^α atoms using the approach of Chothia et al.⁹⁵. Horizontal lines represent the inter-helical angles from the 20 models generated in the NMR study.

Crystal simulations

To assess the quality of the new parameters on full proteins, simulations were performed on eight proteins of different morphology and size (Table 1) in their crystal environments. By performing these calculations on the full unit cells, the sampling was significantly enhanced, as the unit cells contain two to four monomers of each protein. The analysis emphasizes shifts in the φ/ψ population that may indicate systematic problems in the backbone parameters¹⁶. In addition, analysis of the χ₁/χ₂ distributions was undertaken. Average differences in φ/ψ obtained from the 40-ns simulations are shown in Table 7; average differences were calculated to identify local systematic deviations in the backbone conformations. The overall agreement is good with the MD simulations resulting in minimal deviation from the crystallographic backbone geometries (Table 7). While larger deviations (> 6°) occurred in selected φ/ψ torsions of β-strand regions of Erabutoxin B (PDB id: 3EBX)⁸¹ and crambin (PDB id: 1ejg),⁸² the overall agreement of C36 is similar to that of C22/CMAP. The larger deviations in C36 were not unexpected as the original C22/CMAP was specifically optimized to reproduce the local φ/ψ sampling. Building upon the previous CMAP in the present study appears to lead to the small, yet acceptable, degradation in the local φ/ψ sampling indicating that optimization did not lead to a bias in the sampling of φ and ψ while yielding significant improvements in the treatment of the smaller polypeptides.

Table 7.

Average differences in backbone φ and ψ torsions between MD average and crystallographic values averaged over all residues

C22/CMAP	all				α-helix				β-strands
	φ	SDM	ψ	SDM	φ	SDM	ψ	SDM	φ	SDM	ψ	SDM
135L	−0.67	0.51	0.03	0.64	1.57	0.31	−0.49	0.41	0.03	0.82	3.18	0.72
1BYI	−1.57	0.11	1.08	0.30	−1.17	0.02	0.27	0.05	−0.75	0.13	2.94	0.49
1BZP	−0.59	0.35	1.44	0.54	−0.35	0.11	−0.36	0.18
1EJG	−2.25	0.13	8.02	0.33	−3.91	0.06	8.79	0.05	1.71	0.45	−4.08	0.35
1I27	−0.57	0.40	−3.71	0.70	−0.20	0.21	−0.93	0.25	−0.84	0.62	−3.62	0.56
3EBX	1.90	1.41	1.15	0.85					2.65	3.19	5.59	1.05
3ICB	−3.22	0.29	2.84	0.84	−5.27	0.38	6.79	0.92
5PTI	2.72	0.93	1.53	0.94	−0.89	0.29	0.08	0.54	−3.20	0.57	−0.25	0.45
Avg	−0.05		2.69		−2.04		1.67		1.24		0.85
C36	all				α-helix				β-strands
135L	0.42	0.59	−2.06	0.36	1.19	1.35	−2.12	0.45	1.23	0.13	−2.01	0.35
1BYI	−0.74	0.01	−0.23	0.86	0.33	0.03	−0.85	0.05	−0.47	0.08	0.20	3.73
1BZP	2.31	1.03	2.18	1.00	0.03	0.42	0.24	0.45
1EJG	8.29	0.08	−1.38	0.06	7.42	0.09	6.51	0.05	9.96	0.72	−11.57	0.39
1I27	−0.25	0.65	−2.24	0.97	0.74	0.21	−0.30	0.23	0.85	1.84	−3.33	1.69
3EBX	3.45	3.25	−2.68	2.44					0.99	7.57	−3.93	5.11
3ICB	−1.48	0.11	5.62	0.61	−4.27	0.11	9.41	1.02
5PTI	6.77	2.28	1.11	3.26	0.60	0.34	2.53	0.52	4.29	0.45	−2.90	1.29
Avg	2.35		0.04		0.86		2.20		2.81		−3.92

^*Standard deviation of the mean (SDM) calculated from averages of 5 ns intervals between 5 ns and 40ns of the simulation.

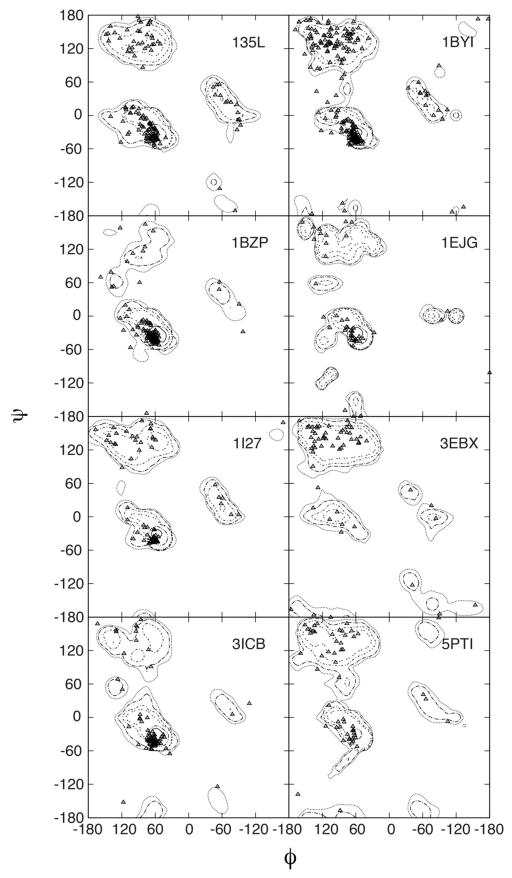
A more detailed analysis of the experimental and calculated backbone φ/ψ distributions is presented in Figure 6. Ramanchandran⁸³ diagrams were constructed by overlaying crystallographic φ/ψ values for each of the simulated proteins with the respective probability distributions calculated from the MD simulations. Overall, φ/ψ sampling yields population distributions centered on crystallographic φ/ψ values. Worth noting is the reproduction of backbone conformations in loop regions as depicted by data points falling outside of the classic Ramachandran secondary structure regions. These results demonstrate the robustness of C36 in maintaining crystal backbone conformations.

Figure 6.

Ramanchandran plot for backbone sampling. Crystallographic φ/ψ values (triangles) are overlaid onto probability distributions obtained from the MD simulation of full unit cells. Probabilities calculated with snapshots between 5ns-40ns at 5ps intervals.

To analyze the conformational properties of the side chains in the crystal simulations χ₁ and χ₂ distributions for each residue type were extracted from the 5ns–40ns portion of the protein crystal simulations and compared to distributions obtained from a crystallographic survey.⁶² The level of agreement was quantified by calculating the overlap coefficients (Eq. 4) between simulation and protein database survey results. Simulation results for the three protonation types of histidine Hsd, Hse, and Hsp were summed and normalized together as appropriate for comparisons with the His distribution from the database survey. The results from this comparison are presented in Table 8. Overall, the crystal simulations with C36 yield excellent agreement with database distributions and demonstrate a small overall improvement over that with C22/CMAP. The χ₁ torsion in Glu and that in Lys were among the torsions that have improved significantly. With Glu, improvement of sampling required sacrificing the quality of agreement with the QM data (Figure 2), as discussed above. For χ₂, Asp benefitted appreciably from the new torsion parameters. However, in a number of cases there are slight degradations in C36 relative to C22/CMAP such that the overall level of agreement for the χ₁/χ₂ distributions is similar for the two models, with both yielding satisfactory agreement with the crystallographic survey data.

Table 8.

Overlap coefficients between χ₁ and χ₁ probability distributions of protein crystal simulations and crystallographic survey data.

Residue	χ1			Residue	χ2
	C22/CMAP	C36	diff		C22/CMAP	C36	diff
Arg	0.97	0.96	−0.01	Arg	0.92	0.93	0.01
Asn	0.90	0.94	0.04	Asn	0.89	0.85	−0.05
Asp	0.92	0.96	0.04	Asp	0.63	0.96	0.33
Cys	0.94	0.94	0.00	Gln	0.93	0.96	0.03
Gln	0.96	0.97	0.01	Glu	0.99	0.96	−0.02
Glu	0.87	0.97	0.10	His	0.86	0.85	−0.01
His	0.87	0.88	0.01	Ile	0.93	0.89	−0.04
Ile	0.89	0.93	0.04	Leu	0.95	0.95	0.00
Leu	0.98	0.97	−0.01	Lys	0.99	0.89	−0.10
Lys	0.87	0.95	0.08	Met	0.93	0.90	−0.04
Met	0.97	0.97	0.00	Phe	0.83	0.88	0.05
Phe	0.91	0.95	0.04	Trp	0.89	0.85	−0.04
Ser	0.84	0.90	0.06	Tyr	0.95	0.97	0.02
Thr	0.89	0.92	0.03
Trp	0.82	0.87	0.05
Tyr	0.93	0.98	0.05
Val	0.82	0.93	0.11
Average	0.90	0.94			0.90	0.91
SD	0.05	0.03			0.09	0.05

Data for His is based on arithmetic average over the OC for Hsd and Hse.

Comparison with NMR data for folded proteins

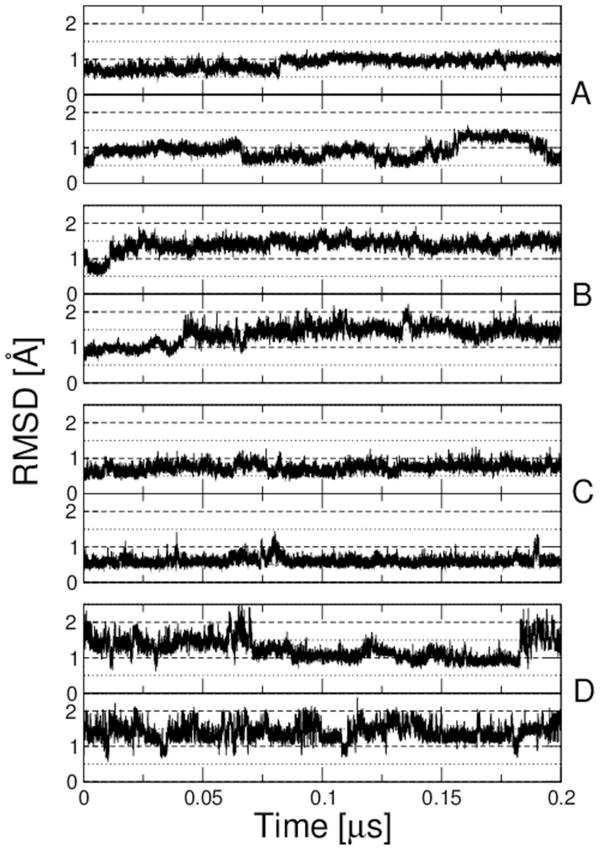
NMR data forms a valuable complement to crystal structure data for validating backbone and side-chain parameters, since it is very sensitive to the full distribution of dihedral angles, particularly the population of multiple rotamers. Accordingly, 200 ns MD simulations were performed on a set of four proteins for which extensive NMR data are available: bovine pancreatic trypsin inhibitor (BPTI), hen lysozyme, GB3 and ubiquitin. A similar data set was recently used by Lindorff-Larsen et al. in their tests of their modified Amber ff99SB force field (ff99SB-ILDN).¹¹ In Figure 7, we show the RMSD of each protein from the experimental reference. In all cases, the backbone RMSD obtained with C36 is comparable or lower than that with C22/CMAP, with deviations generally being ~1.5 Å or less. The larger jumps observed for BPTI have been seen in other force fields and arise from transitions between multiple substates of the native state.⁸⁴

Figure 7.

RMSD from experimental structure for long runs of folded proteins. (A) Ubiquitin, (B) Hen Lysozyme, (C) GB3 and (D) BPTI. Upper plots show results with C22/CMAP, lower plots with C36. Various dotted lines indicated RMSD values of 0.5, 1.0, 1.5 and 2.0 Å.

Two types of NMR data were used for validation. The first were scalar couplings reporting on the side-chain χ₁ torsion angle in folded proteins; this data set was collated from published and unpublished data by Lindorff-Larsen et al. In Table 9, we present the χ² values including the data for all four folded proteins, split by residue type; we also include results for the unfolded proteins used to guide the side-chain optimization. However, we note that the side-chain J-couplings cannot be considered as a true validation, as they were used in the optimization. The χ² values for C36 with respect to this data would therefore be artificially lowered, relative to other force fields. Ideally, a validation would be done for unfolded proteins not included in the present study, which provide a sensitive test of torsion angle distributions. However, the only other data set we are aware of is that reported for Hen Lysozyme by Schwalbe and co-workers⁸⁵ and the size of this system is not amenable to current computational resources. We find that the revised C36 side-chain parameters represent an overall improvement over C22/CMAP, with an overall χ² of 5.2 and 8.5 for unfolded and folded proteins respectively, compared with 9.8 and 9.2 for the original C22/CMAP. The results for C36 are also comparable with the χ² of 9.7 and 8.9 for unfolded and folded proteins obtained with Amber ff99SB-ILDN.

Table 9.

Comparison with side-chain NMR J-coupling data for folded and unfolded proteins. χ² values representing agreement with experimental J-coupling data on unfolded proteins in urea from Vajpal et al.⁹³ and with data for folded proteins collated in Ref¹¹ for three force fields (Amber ff99SB-ILDN, C22/CMAP and C36). Unfolded proteins are ubiquitin and GB1 and folded proteins are ubiquitin, GB3, BPTI and hen lysozyme. The three right-most columns give the number of J-coupling measurements used to calculate each χ² value.

RES	Amber ff99SB-ILDN			C22/CMAP			C36			# DATA
	Unf.c	Fold.a	All	Unf.c	Fold.b	All	Unf.c	Fold.b	All	Unf.	Fold.	All
Arg	2.2	12.7	7.5	7.9	7.0	7.4	4.1	7.7	5.9	22	14	36
Asn	7.8	10.6	9.2	16.1	8.8	12.5	8.0	7.5	7.8	24	56	80
Asp	13.8	12.8	13.3	10.7	17.4	14.0	4.8	12.5	8.7	48	46	94
Cys		9.7	9.7		8.7	8.7		8.6	8.6	0	46	46
Gln	2.4	6.8	4.6	7.1	9.0	8.1	5.0	6.2	5.6	38	18	56
Glu	6.6	13.2	9.9	15.5	11.3	13.4	4.4	11.3	7.9	56	10	66
His	28.1	12.0	20.0	8.7	14.8	11.7	1.1	10.2	5.6	5	6	11
Ile	8.8	7.1	8.0	28.3	4.8	16.6	7.0	5.2	6.1	14	44	58
Leu	2.3	12.3	7.3	7.4	16.3	11.9	3.4	10.9	7.1	50	26	76
Lys	1.9	9.4	5.6	3.9	13.1	8.5	7.3	11.8	9.5	56	30	86
Metd		10.3	10.3		9.1	9.1		4.7	4.7	0	14	14
Phe	5.0	6.1	5.5	2.9	5.0	3.9	8.7	5.4	7.1	22	32	54
Pro	17.4	7.8	12.6	5.8	10.6	8.2	7.0	18.4	12.7	9	4	13
Ser	11.1	8.7	9.9	6.3	9.3	7.7	3.6	12.0	7.8	12	14	26
Thr	8.0	3.5	5.8	10.0	5.1	7.6	13.3	4.5	8.9	43	82	125
Trp	5.3	6.7	6.0	5.6	6.4	6.0	1.3	6.3	3.8	5	10	15
Tyr	9.8	7.8	8.8	10.4	6.6	8.5	3.1	6.8	5.0	22	30	52
Val	24.8	3.6	14.2	10.5	2.8	6.7	1.5	2.2	1.9	22	74	96
ALL	9.7	8.9	9.3	9.8	9.2	9.5	5.2	8.5	6.9	448	278	726

^aData taken from 1.2 μs equilibrium simulations in¹¹.

^bData from 0.2 μs equilibrium simulations in present work.

^cData from solute tempering simulations in present work.

^dNote that the assignments of Met52 H^β protons in BPTI are the reverse of those reported in Ref¹¹ (Kresten Lindorff-Larsen, private communication). Combined χ² values for folded and unfolded are obtained as a simple average over the χ² values for folded and unfolded. Overall χ² are obtained as an unweighted average of the χ² for the different types of residue. An indication of the errors on these values is given in Table 4 for C36, but is omitted here in the interests of clarity.

The second type of data considered were residual dipolar couplings (RDCs) for the folded proteins, which are very sensitive to small structural deviations. The agreement between experiment and simulation has been quantified in this case by the Q parameter conventionally used in structure refinement with RDCs, defined as:

$$Q={\left[\frac{{\displaystyle \sum _i}{(D_{i,\text{calc}}-D_{i,\text{obs}})}^2}{{\displaystyle \sum _i}{D}_{i,\text{obs}}^2}\right]}^{1/2}$$ [5]

where D_i,obs and D_i,calc represent, respectively, the ith residual dipolar coupling from experiment and as back-calculated from the simulation. The results for various alignment media and folded proteins are given in Table 10. Although RDCs have also been measured for the unfolded proteins, because of uncertainties in calculating the alignment tensor in this case, we have not attempted to compute these data from the unfolded state simulations. We find that the backbone RDCs obtained with C36 are generally slightly better than, or comparable to those obtained with C22/CMAP or Amber ff99SB. Relative to C22/CMAP, the improvement in side-chain RDCs is clear for GB3 and HEWL, and the results for ubiquitin are comparable. The results for side-chains are for a significant improvement Amber ff99SB – however, these runs did not include the ILDN side-chain correction.

Table 10.

RDC Q-factors describing agreement between RDC’s computed from simulation and experiment. Smaller values correspond to better agreement with experiment (Equation 5). Errors from a bootstrap analysis are given in brackets⁹⁴.

Data set	Amber ff99SB	C22/CMAP	C36
Backbone:
Ubiquitin, Medium 1	0.29 (0.02)	0.20 (0.01)	0.23 (0.01)
Ubiquitin, Medium 2	0.32 (0.03)	0.20 (0.01)	0.23 (0.01)
GB3, Medium 1	0.14 (0.01)	0.22 (0.02)	0.14 (0.02)
GB3, Medium 2	0.14 (0.01)	0.20 (0.02)	0.15 (0.01)
GB3, Medium 3	0.19 (0.01)	0.22 (0.02)	0.20 (0.02)
GB3, Medium 4	0.18 (0.01)	0.25 (0.04)	0.19 (0.03)
GB3, Medium 5	0.17 (0.02)	0.23 (0.02)	0.16 (0.02)
HEWL, Medium 1	0.30 (0.03)	0.39 (0.04)	0.42 (0.04)
HEWL, Medium 2	0.31 (0.03)	0.42 (0.04)	0.42 (0.04)
Side-chain:
Ubiquitin, Medium 1	0.57 (0.02)	0.38 (0.05)	0.38 (0.04)
Ubiquitin, Medium 2	0.56 (0.03)	0.32 (0.06)	0.28 (0.05)
GB3	0.66 (0.12)	0.59 (0.13)	0.31 (0.06)
HEWL	0.89 (0.15)	0.44 (0.10)	0.37 (0.09)

We have also used the backbone RDCs to assess whether the manual adjustments to the CMAP in order to reduce systematic deviations from canonical secondary structure have any deleterious effects on residues not in elements of canonical secondary structure. For each of the proteins GB3, Ubiquitin and Hen Lysozyme, we have classified the (ϕ,ψ) angles of each residue the Ramachandran map into narrowly defined “α”, “β”, “polyproline II”, “α_L” and “coil”. The definitions (given in the legend of Table 11) are chosen to be mutually exclusive and exhaustive, with “coil” comprising angles not within one of the other regions. For each of these regions, we have calculated a root-mean-square Q-factor Q_k over all alignment media k for all proteins in the following way:

$$Q_{\text{r}.\text{m}.\text{s}.}={\left(\frac{1}{N}\sum _{k=1}^N{Q_k}^2\right)}^{1/2}$$ [6]

Table 11.

Breakdown of RDC Q-factors by Ramachandran angles in the native state (i.e. crystal structure). The following regions of Ramachandran space have been defined: α region: −100°≤ϕ <−30° and −67°≤ψ <−7°; β region: −180°≤ϕ<−100° and 120°≤ψ<180°; ppII region: −100°≤ϕ<−30° and 100°≤ψ<180°; α_L: 30°≤ϕ<100° and 0°≤ψ<80°; coil region: all residues not in other regions. Errors from a bootstrap analysis are given in brackets⁹⁴.

Ramachandran Region	Amber ff99SB	C22/CMAP	C36
α	0.22 (0.02)	0.24 (0.02)	0.20 (0.02)
β	0.18 (0.02)	0.27 (0.05)	0.27 (0.06)
Polyproline II	0.33 (0.06)	0.36 (0.04)	0.22 (0.06)
αL	0.50 (0.03)	0.24 (0.05)	0.22 (0.06)
Coil	0.23 (0.03)	0.24 (0.04)	0.26 (0.04)

The values of Q_r.m.s. for each region and each force field are shown in Table 11. C36 performs well for both the α and β regions, and represents a significant improvement over Amber ff99SB and C22/CMAP for the polyproline II region, as might be anticipated. Interestingly, one area in which both C22/CMAP and C36 are better than Amber ff99SB is the α_L region (which was not manually tweaked in the CMAP). Finally, we note that the Q_r.m.s. for the coil region is not appreciably worse than for Amber ff99SB, suggesting that the tweaks did not lead to detrimental effects on residues outside canonical regions of the Ramachandran map.

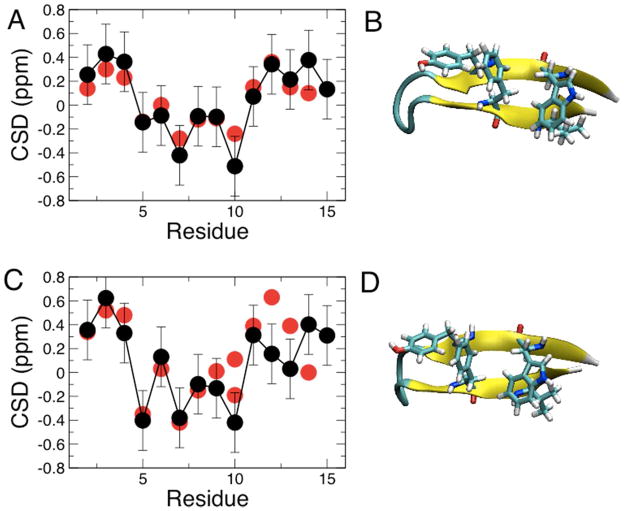
Equilibrium folding simulations of β hairpins

Since most of the backbone optimization focused on helix-forming peptides, we have also determined the folding equilibrium of two β-hairpins using temperature replica exchange. The two hairpins are the original native C-terminal GB1 hairpin, residues 41–56 of protein G^53,54, and the GB1m3 variant ^55,56, which has been optimized for greater stability. Replica exchange runs of both hairpins resulted in well-folded structures. Defining the folded state as being within 1.5 Å backbone RMSD of the hairpin in the protein G crystal structure, a folded fraction of 77 % for GB1 and 99 % for GB1m3 at 300 K is obtained, compared with experimental estimates of 60 % for GB1⁵⁴ and 86 % for GB1m3⁵⁵ (folded structures are shown in Figure 8B and D). However, these estimates are based, in the case of the simulations, on an arbitrary definition of the folded state, and, in the case of the experiment, on fitting a two-state model to a global experimental signal. It is therefore more desirable to compare an ensemble-averaged observable from the simulation with the experiment. Accordingly, ensemble-averaged NMR chemical shift deviations (CSDs) were computed over the trajectory using the SPARTA+ program, with the resulting CSDs for the H^α protons plotted in Figure 8A and C. For both peptides, the agreement with the experimental CSDs is very good, and the more positive CSD values near the termini for GB1m3 (Figure 8C) compared with GB1 (Figure 8A) are consistent with the higher fraction of folded hairpin for the former sequence.

Figure 8.

β-hairpin folding test. H^α chemical shifts from experiment (red symbols) and calculated from simulation using SPARTA+ (black symbols) for: (A) the GB1 hairpin (folded structure from simulation shown in (B)); and (C) the designed GB1m3 hairpin (structure shown in (D)). Error bars on calculated data are the typical RMSD between experiment and H^α shifts predicted by SPARTA+⁶¹. Experimental data at 280 K from Fesinmeyer et al;⁵⁵ simulation data taken from 278 K replica.

Conclusions and Outlook

A revised version of the CHARMM additive protein force field (C36) is reported, the main features of which are a newly optimized backbone CMAP and sidechain torsion potentials. The model is able to correct the propensity of the backbone parameters in the previous C22/CMAP force field to overstabilize helices: as a consequence more reasonable results for the fraction helix in a helix-forming peptide are obtained, with the model still able to fold β-hairpin peptides. For the side chains, the new fit to QM data followed by empirical adjustments results in a significant improvement in agreement with side-chain scalar coupling data for the χ₁ torsion for both folded and unfolded proteins, compared with C22/CMAP. In the future, it would also be interesting to compare with experimental data for the distribution of χ₂, χ₃ and χ₄ for proteins in solution, but at the time of writing no such data is available in the literature. However, comparison with χ₂ crystallographic distributions indicate C36 to satisfactorily treat this degree of freedom.

Our optimization procedure highlighted the importance of considering a range of experimental data measured in the condensed phase, in order to fine-tune the parameters initially obtained from targeting gas-phase QM calculations on model dipeptides. It is anticipated that the lessons learned will be equally useful in optimizing the next generation of polarizable force fields.