Integrating Mitochondrial Energetics, Redox and ROS Metabolic Networks: A Two-Compartment Model

Abstract

To understand the mechanisms involved in the control and regulation of mitochondrial reactive oxygen species (ROS) levels, a two-compartment computational mitochondrial energetic-redox (ME-R) model accounting for energetic, redox, and ROS metabolisms is presented. The ME-R model incorporates four main redox couples (NADH/NAD⁺, NADPH/NADP⁺, GSH/GSSG, Trx(SH)₂/TrxSS). Scavenging systems—glutathione, thioredoxin, superoxide dismutase, catalase—are distributed in mitochondrial matrix and extra-matrix compartments, and transport between compartments of ROS species (superoxide: O₂^⋅−, hydrogen peroxide: H₂O₂), and GSH is also taken into account. Model simulations are compared with experimental data obtained from isolated heart mitochondria. The ME-R model is able to simulate: i), the shape and order of magnitude of H₂O₂ emission and dose-response kinetics observed after treatment with inhibitors of the GSH or Trx scavenging systems and ii), steady and transient behavior of ΔΨ_m and NADH after single or repetitive pulses of substrate- or uncoupler-elicited energetic-redox transitions. The dynamics of the redox environment in both compartments is analyzed with the model following substrate addition. The ME-R model represents a useful computational tool for exploring ROS dynamics, the role of compartmentation in the modulation of the redox environment, and how redox regulation participates in the control of mitochondrial function.

Introduction

At the center of aerobic life, mitochondrial function has been recognized as pivotal to health, disease, and aging. A 70 kg human male at rest will consume 430 liters of O₂ per day (1). This O₂ consumption rate can increase 5- to 10-fold depending on physical activity (2), and is ∼90% channeled into mitochondrial respiration (3). The respiratory chain reduces O₂ efficiently through cytochrome oxidase, but the electron flux can be diverted to produce the free radical superoxide, O₂^⋅−. Muscle mitochondria produce ∼85–90% of O₂^⋅− (4–6), mainly through complex I and III of the respiratory chain (7–9). Sources of O₂^⋅− other than the respiratory chain have been reported, including NADPH oxidases (10) and several other sources (7,11–14). At the organelle level, there are contributors to reactive oxygen species (ROS) generation other than mitochondria, such as the endoplasmic reticulum, Golgi, and the peroxisomes (15,16).

The extent of electron diversion from the respiratory chain to produce O₂^⋅− reportedly ranges from 0.15% to 2% of the O₂ consumption flux (5,17–20). A recent study performed in heart mitochondria demonstrated that, without taking into account ROS scavenging, previous values of ROS production from mitochondria are severely underestimated (21). In isolated mitochondria, the extent of H₂O₂ emission is also highly dependent on energetic status. Substrate choice and concentration, physiological status (states 4 or 3 respiration), and mode of electron transport (forward (FET) or reverse (RET)), are critical factors (19,22,23). FET and RET electron transport occur in the presence of substrates of complex I (e.g., glutamate or pyruvate/malate) or II (e.g., succinate), respectively. At least sixfold lower rates of H₂O₂ emission can be measured under FET as compared with RET (24).

Recognizing that ROS emission is the result of a dynamic balance between production and scavenging (21), as described in the framework of the Redox-optimized ROS Balance hypothesis (17), a number of relevant questions can be raised. What is the role of compartmentation in the control of ROS levels? What is the impact of the redox environment on energetics? How do mitochondria accomplish a reliable energy provision, while keeping ROS within physiological limits compatible with signaling? These key questions have not yet been answered.

In this work, we have formulated a two-compartment mitochondrial energetic-redox (ME-R) model. The ME-R model encompasses four main redox couples and antioxidant systems present in both the matrix and extra-matrix compartments. The ME-R model conserves all the features of its predecessors (25,26) while extending their mechanistic detail. The time-dependent behavior of the model was contrasted with experiments of energetic-redox transitions after substrate addition. The steady-state behavior of the ME-R model was tested with experiments in the presence of substrates, uncouplers of respiration, and inhibitors of the scavenging systems (GSH/Trx). After validation, the ME-R model is used to explore the role of compartmentation in the control of ROS levels, the significance of the different redox couples in the modulation of the redox environment in different compartments, and the functional impact of matrix and extra-matrix redox status on the energetic behavior of mitochondria.

Materials and Experimental and Modeling Methods

Computational model description

A two-compartment computational model of ME-R was formulated (Fig. 1). This model, described by 25 ordinary differential equations (Table S1 in the Supporting Material), is based on our model of mitochondrial energetics that includes pH regulation and ion dynamics (H⁺, Ca²⁺, Na⁺, Pi) (26). Briefly, the previous version of the model by Wei et al. (26) already accounted for respiratory fluxes from complex I and II, tricarboxylic acid cycle (TCA cycle) dynamics, adenine nucleotide exchange (ANT), and ATP synthesis. Previously, a model of ROS metabolism was formulated including the GSH scavenging system, catalase (CAT), and Cu,Zn superoxide dismutase in the extra-matrix space, to understand the mechanism underlying mitochondrial oscillations (25).

Figure 1.

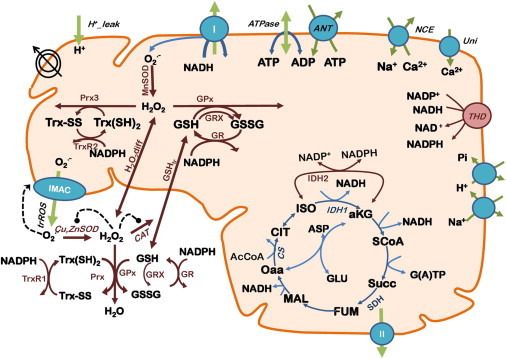
Scheme of the two-compartment ME-R model accounting for mitochondrial energetic and redox processes, their interactions, and transport between compartments. The model takes into account OxPhos and matrix-based processes in mitochondria (26,44) as well as in the extra-matrix compartment. In addition to energy metabolism and ion transport (H⁺, Ca²⁺, Na⁺, Pi) the model accounts for O₂^⋅− being produced in the mitochondrial electron transport chain from both complex I- and complex II-derived electron transport. O₂^⋅− may be dismutated to H₂O₂ by superoxide dismutase (MnSOD) in the matrix or be transported as such to the extra-matrix compartment through the inner membrane anion channel, where it will be scavenged by Cu,ZnSOD generating H₂O₂. In the mitochondrial matrix, H₂O₂ can either diffuse outside or be scavenged by the large capacity GSH and Trx systems. In the extra-matrix compartment H₂O₂ may be additionally scavenged by catalase (CAT). Grx accounts for the recovery of glutathionylated proteins in the matrix. Key to symbols: Concentric circles with an arrow across represent the ΔΨ_m. Dotted arrows indicate regulatory interactions either positive (arrowhead) or negative (●−). (Shunt) indicates the fraction of electrons from respiration diverging toward O₂^⋅−. Not indicated in the scheme is the shunt from complex II respiratory substrates.

The ME-R includes (Fig. 1): i), a complete array of antioxidant defenses in two compartments: mitochondrial matrix and extra-matrix, the latter compartment combining intermembrane space and cytoplasm; ii), NADP⁺-dependent isocitrate dehydrogenase (IDH2) in the TCA cycle, and transhydrogenase (THD), two of the main NADPH sources in mitochondria; iii), the Trx system involving thioredoxin reductase and peroxiredoxin (27), iv), the glutaredoxin system (GRX), which uses GSH as a cofactor and mediates reversal of glutathionylation of proteins (28,29), v), superoxide dismutases (SOD) (MnSOD in matrix, and Cu,ZnSOD extra-matrix), and vi), CAT activity in the extra-matrix compartment. All redox couples considered by the model (NADH/NAD⁺; NADPH/NADP⁺; GSH/GSSG; Trx(SH)₂/TrxSS) are linked through conservation relationships.

The model also accounts for exchange of GSH and H₂O₂ between compartments, the latter by free diffusion. GSH is allowed to move between compartments by passive transport in both directions (GSH_tr in Fig. 1), which is a simplification because it has been reported that its transport is via dicarboxylate and α-ketoglutarate carriers (30). Superoxide moves between compartments through a specific transport pathway, the inner membrane anion channel, as previously described (25).

Kinetic modeling of the antioxidant defenses

Thioredoxin system

Thioredoxin reductase (TrxR1 extra-matrix, and TrxR2 mitochondrial) was modeled as a bisubstrate (NADPH and Trx(SS)) reaction following Michaelis-Menten kinetics with published kinetic parameters (31,32) (see Section S7.4 in the Supporting Material). Peroxiredoxin (Prx3 in the matrix, and Prx extra-matrix; the latter can be Prx1, 2 or 6 (27)) was modeled according to Dalziel kinetics with parameter values as reported (33,34). The Trx system considers reduced/oxidized species of Trx as state variables.

GSH system

The kinetics of the GSH scavenging system components, glutathione peroxidase (GPx) and glutathione reductase (GR) were formulated as described previously (25) (see also Section S7.3 in the Supporting Material). This system includes reduced/oxidized glutathione as state variables.

NADPH-generating systems

The NADPH dynamics in the mitochondrial matrix are described by the activities of the NADP⁺-dependent IDH2 and a proton-coupled THD (see Section S8 in the Supporting Material). IDH2 activity was modeled as a reversible reaction ruled by Michaelis-Menten kinetics with two-substrates according to the mechanism proposed by O’Leary and Limburg (35), and kinetic parameters adjusted to reproduce reported experimental data (35,36) (not shown).

The THD activity was modeled according to the mechanism proposed by Hoek and Rydstrom and Sasanov and Jackson (37,38). Simulation results were able to reproduce the experimental data by Hoek and Rydstrom (37) (not shown).

ME-R model assembly and implementation

Simulations with the ME-R model were run with a code written either in MATLAB (The MathWorks, Natick, MA) or with MatCont v. 2.4 (39), which operates in the MATLAB environment, in both cases ODEs15 was used as the integrator. All model parameters and initial conditions are listed either in Table 1 or in the Supporting Material (Tables S1–S9). The source code of the model is available for download from http://gforge.icm.jhu.edu/gf/projects/mitochondrial_energetics_redox/.

Table 1.

Model parameters

Parameter	Value	Units	Description
${\rho }^{F1}$	5	mM	Concentration of F1F0-ATPase
${\rho }^{res}$	0.2	mM	Concentration of electron carriers (respiratory complexes I-III-IV)
${\rho }^{res\left(SDH\right)}$	0.017	mM	Concentration of electron carriers (respiratory complexes II-III-IV)
[Pi]i	3	mM	Extra-matrix phosphate concentration
[AcCoA]	1	mM	Acetyl CoA concentration
[GLU]	30	mM	Glutamate concentration
gH	2 × 10−6	mM ms−1 mV−1	H+ conductance of inner membrane
$k_{cat}^{CS}$	2.35 × 10−4	ms−1	Catalytic constant of CS
$k_f^{ACO}$	1.17 × 10−4	ms−1	Forward rate constant of ACO
$k_{cat}^{IDH}$	11.9	ms−1	Rate constant of IDH
$k_{cat}^{KDGH}$	1.32 × 10−2	ms−1	Rate constant of KGDH
$k_f^{SL}$	2.80 × 10−2	mM-1ms−1	Forward rate constant of SL
$k_f^{FH}$	8.30 × 10−3	ms−1	Forward rate constant for FH.
$k_{cat}^{MDH}$	1.24 × 10−1	ms−1	Rate constant of MDH
$k_f^{AAT}$	2.14 × 10−2	ms−1	Forward rate constant of AAT
$c_{PiC}$	4.90	mg protein ml−1	PiC concentration
Nai	11	mM	Extra-matrix Na+
$V_{\max }^{uni}$	4.46 × 10−3	mM ms−1	Vmaxuniporter Ca2+ transport
$V_{\max }^{NaCa}$	1.83 × 10−4	mM ms−1	Vmax of Na+/Ca2+ exchanger
VmaxANT	3.15	mM ms−1	Maximal rate of the ANT
${\text{E}}_{\text{MnSOD}}^{\text{T}}$	3 × 10−4	mM	Mitochondrial concentration of MnSOD
${\text{E}}_{\text{MnSOD}}^{\text{T}}$	2.4 × 10−4	mM	Extra-matrix concentration of Cu,ZnSOD
${\text{E}}_T^{Tr\text{xR}2\text{m}}$	3.5 × 10−4	mM	Mitochondrial concentration of TrxR2
${\text{E}}_T^{Tr\text{xR}i}$	3.5 × 10−4	mM	Extra-matrix concentration of TrxR
$E_T^{Prx3m}$	3 × 10−3	mM	Mitochondrial concentration of thioredoxin peroxidase (Prx)
$E_T^{Prx3i}$	1 × 10−1	mM	Extra-matrix concentration of thioredoxin peroxidase (Prx)
$E_T^{GPXm}$	1 × 10−4	mM	Mitochondrial concentration of glutathione peroxidase (GPX)
$E_T^{GPXi}$	5 × 10−5	mM	Extra-matrix concentration of GPX
${\text{E}}_{\text{T}}^{\text{GRm}}$	9 × 10−4	mM	Mitochondrial concentration of GR
${\text{E}}_{\text{T}}^{\text{GRi}}$	9 × 10−4	mM	Extra-matrix concentration of GR
$E_{CAT}^T$	1 × 10−6	mM	Extra-matrix concentration of CAT

Mitochondrial isolation

Procedures for the isolation and handling of heart mitochondria from guinea pig (17,40) were performed as described previously. Respiratory control ratios (state 3/state 4 respirations with 5 mM glutamate + malate or succinate) of 10 and 5 or higher were obtained using these methods.

Assay of mitochondrial respiration

Respiration was assayed in freshly isolated mitochondria with a high throughput automated 96-well extracellular flux analyzer (Seahorse Bioscience XF96, Billerica, MA) as described (24). Briefly, the assay medium contained (in mM): 137 KCl, 2 KH₂PO₄, 0.5 EGTA, 2.5 MgCl₂, 20 HEPES at pH 7.2, and 37°C, in presence of 0.2% fatty-acid-free bovine serum albumin (BSA). Respiration was evaluated with substrates of complex I (glutamate/malate, G/M, 5 mM each). Mitochondrial protein was determined using the bicinchoninic acid method, BCA protein assay kit (Thermo Scientific, Rockford, IL).

Other bioenergetic variables and ROS detection

NAD(P)H, mitochondrial membrane potential (ΔΨ_m) and hydrogen peroxide (H₂O₂) were determined as described previously (21,24,40,41). These variables were monitored simultaneously with a wavelength scanning fluorometer (Quantamaster, Photon Technology International, Birmingham, NJ) using the same medium above for measuring respiration (excluding BSA) and a multidye program for simultaneous online monitoring of different fluorescent probes. NAD(P)H was monitored by exciting mitochondrial suspensions at 340 nm and collecting the emission at 450 nm. ΔΨ_m was recorded using tetramethylrhodamine methyl ester (TMRM; 100 nM) as described (40). H₂O₂ was detected using the Amplex Red kit from Invitrogen (Carlsbad, CA) as described (21).

Results

Experimental validation of the ME-R model

The key feature of the ME-R model (Fig. 1) is that it takes into account the presence of a complete array of antioxidant defenses in two compartments: mitochondrial matrix and extra-matrix, the latter encompassing intermembrane space and cytoplasm.

We performed extensive modular analysis of each new single process considered before assembling the M-ER model (Fig. 1). The model behavior was assessed by comparing simulations with experimental data. A main advantage of this combined experimental-modeling approach is that simulation/experimental protocols can be matched, thus rendering the evaluation process more rigorous. The ability of the ME-R model to reproduce experimentally observed behavior was tested with six different data sets obtained in isolated heart mitochondria from guinea pig. In all cases the same parameter set was used to simulate the experimental data.

Energetic-redox transitions: time-dependent and steady-state behavior

Substrate-induced transitions

Energetic-redox transition experiments triggered by the addition of substrates were performed with isolated mitochondria. The steady-state responses of ΔΨ_m and NADH were monitored as a function of glutamate/malate (G/M) addition. Fig. 2 A shows the gradual buildup of NADH and ΔΨ_m in response to increasing concentrations of G/M. At 1–1.5 mM G/M, both NADH and ΔΨ_m attain maximal values of 100% reduction and ∼170 mV, respectively. Characteristically, ΔΨ_m, as compared with the redox potential, attains saturation at ∼17-fold lower G/M concentrations (Fig. 2 A). The model, in which substrate addition is simulated with acetyl CoA (AcCoA), reproduces to the same order of magnitude ΔΨ_m and NADH, as well as the earlier rise of ΔΨ_m (Fig. 2 B). The increase in AcCoA translates into a very steep rise in the rate of citrate synthase (CS) that under substrate limitation regulates the flux though the TCA cycle until CS becomes saturated (results not shown). A maximal 96% NADH and ΔΨ_m ∼193 mV is reached with AcCoA > 0.025 mM. According to the model, and as expected, the relationship between NADH and ΔΨ_m is linear during the transition from state 4 to state 3 (see Fig. S4).

Figure 2.

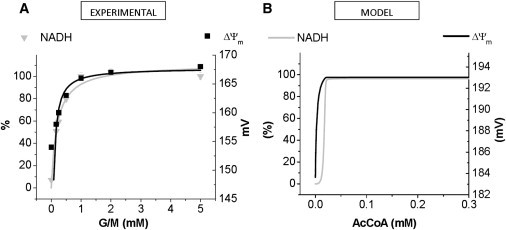
Comparison of experimental results with model simulations of NADH and ΔΨ_m as a function of substrate concentration. (A) Experimentally observed substrate G/M dose-response behavior of NADH (inverted gray triangle) and ΔΨ_m (black solid square) in isolated heart mitochondria. Data points correspond to the mean ± SE (n = 3, three independent experiments). (B) Steady-state behavior of NADH concentration (gray trace) and ΔΨ_m (black trace) in the ME-R model as a function of substrate concentration (represented by AcCoA in the model): from 1 × 10⁻⁶ to 0.3 mM, that emulates the experimental protocol. Model simulations were run with the following parameter values at a fixed value: ADP_i = 0.01 mM (state 4), Shunt = 0.008 and glutamate = 1 × 10⁻⁶ mM.

The experimental and model simulated steady-state behavior of NADH and ΔΨ_m are summarized in Table 2. Additionally, Table 2 compares model simulations with the steady state respiratory fluxes obtained in experiments performed with guinea pig mitochondria. Model values of NADH and ΔΨ_m approximate the experimental data. Simulated respiration and H₂O₂ emission fluxes as a percentage of O₂ consumption under both state 4 and state 3 are on the same order of magnitude as the experimental fluxes. Although the rate of respiration was 2.5 times lower in the model, a threefold increase in the speed of O₂ consumption is observed in the transition from state 4 to state 3 respiration, both in model and experiments (Table 2).

Table 2.

Quantitative comparison between experimental and modeling results of respiration, maximal H₂O₂ emission (after inhibition of GSH/Trx systems), ΔΨ_m and NADH in isolated heart mitochondria from guinea pig

Variable	Experimental∗		Model
	Guinea pig		Simulations
	St 4	St 3	St 4	St 3
Respiration	46 ± 2.6	152 ± 8.5	18.0	56.5
(nmol/mg prot/min)
H2O2 emission	0.56 ± 0.01	0.48 ±0.06	0.32†	0.29†
(nmol/mg prot/min)
% respiratory flux as H2O2 emission	0.74	0.29	1.8	0.8
ΔΨm (mV)	167 ± 7	142 ± 2	200	180
NADH (%)	98 ± 4	78 ± 5	98	65

^∗Aon et al. (24).

^†Total inhibition of glutathione reductase and thioredoxin reductase was achieved by setting the parameters GRm, GR, Trxm, and Trx at a concentration of 10⁻⁹ mM.

Fig. 3 A depicts experimental results of the dynamic response of NADH and ΔΨ_m during substrate-elicited transitions between deenergized mitochondria, state 4, and state 3. Upon G/M addition, mitochondria undergo transition from deenergized to state 4, in which NADH becomes more reduced and ΔΨ_m increases from 140 to 170 mV. As a caveat, the range of ΔΨ_m monitored by TMRM extends from 130–140 mV to ∼220 mV; thus, the value of 140 mV may correspond to an actual lower ΔΨ_m. Following ADP addition, ΔΨ_m depolarizes 20 mV (from 170 to 150 mV). The model was able to reproduce the overall dynamic profile of NADH and ΔΨ_m observed experimentally (Fig. 3). Adding ADP produced ΔΨ_m depolarization of ∼20 mV concomitant with NADH oxidation from 95% to 80%, resembling the shape of the experimental NADH profile (Fig. 3).

Figure 3.

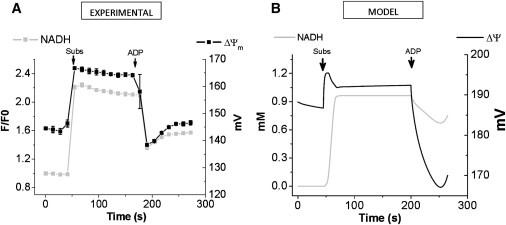
Comparison of experimental results with model simulations of NADH and ΔΨ_m dynamics during transitions between states 4 and 3. (A) Experimental profiles of NADH (gray solid square) and ΔΨ_m (black solid square) after addition of 5 mM G/M (Subs), and 1 mM ADP to guinea pig heart mitochondria, as indicated by arrows. Experimental data at each time point corresponds to the mean ± SE (n = 3). (B) Model simulations were performed by varying the parameters detailed below to emulate the experimental protocol applied in panel A. The addition of substrate was mimicked by a parametric increase in AcCoA and glutamate (Subs) from 1 × 10⁻⁵ to 0.1, and from 1 × 10⁻⁵ to 30, respectively. A basal extra-matrix ADP concentration (ADP_i) of 0.01 mM was used until the state 4→3 transition in which ADP_i = 0.03 mM was applied.

Repetitive pulses of increasing ADP concentrations given to state 4 mitochondria (high ΔΨ_m and NADH) produced cycles of ΔΨ_m depolarization/repolarization of 15–20 mV concomitant to NADH oxidation/reduction of 70–95% following consumption of the ADP added (Fig. 4).

Figure 4.

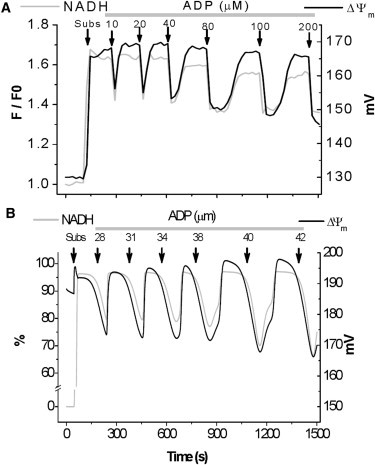
Comparison of experimental results with model simulations of NADH and ΔΨ_m dynamics in response to the addition of consecutive ADP pulses. (A) Depicted are the experimentally determined temporal profiles of NADH (gray trace) and ΔΨ_m (black trace) following the addition of consecutively increasing concentrations of ADP to isolated guinea pig heart mitochondria. Shown is a representative trace from at least three independent experiments. The first arrow indicates addition of substrate (Subs, 5 mM G/M). (B) Model simulation of the experimental time courses shown in panel A. Sequential addition of ADP was simulated by pulses of increasing concentration of cytoplasmic ADP, ADP_i. Arrows point to substrate (Subs) and ADP additions (see also legend Fig. 3).

Uncoupler-elicited transitions

Titration of respiration and redox/energetic behavior of mitochondria with the uncoupler FCCP were also used as an experimental data set for model validation. Fig. 5, A and C, shows the experimental steady-state O₂ consumption fluxes and NADH and ΔΨ_m levels at increasing FCCP concentrations from 10 to 100 nM. In the model, the effect of FCCP addition is mimicked by an increase in H⁺ conductance of the leak current, assumed to be proportional to the proton motive force. The model simulates the hyperbolic increase in the rate of respiration with increasing uncoupling of state 4 mitochondrial respiration. The respiratory fluxes displayed by the model are similar to those determined experimentally (Fig. 5 B). As expected, both NADH and ΔΨ_m decreased with increased uncoupling in experiments (Fig. 5 C) as well as model simulations (Fig. 5 D).

Figure 5.

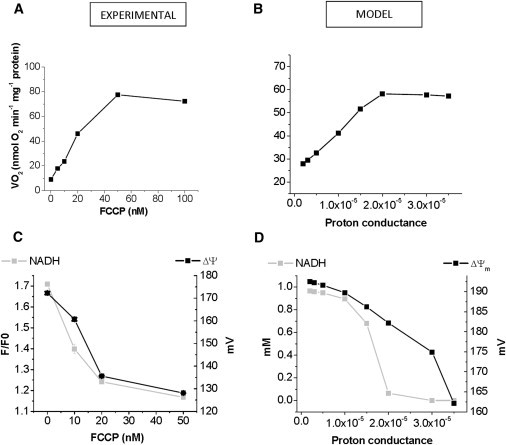
Steady-state behavior of respiration, NADH, and ΔΨ_m as a function of mitochondrial membrane uncoupling. Freshly isolated guinea pig heart mitochondria were subjected up to 100 nM FCCP, an uncoupler of mitochondrial respiration. Respiration (A) and NADH, ΔΨ_m (C) were evaluated as described in the Materials and Methods. To simulate the experimental protocol shown in panel A, the proton conductance (g_h) in the ME-R model was increased from 2 × 10⁻⁶ to 3.5 × 10⁻⁵ mM ms⁻¹ mV⁻¹. Under these conditions, the steady-state values of respiration (V_O2) from both complex I and II (B), and NADH and ΔΨ_m (D) are represented.

ROS and antioxidant systems

Our recently published data highlight the modulatory role exerted by the scavenging systems on H₂O₂ emission from mitochondria. These data suggest that the GSH/Trx systems continuously scavenge ROS produced in the respiratory chain, thereby decreasing the rate of H₂O₂ emission typically observed in isolated mitochondrial studies under conditions of FET (24,41). It is therefore important to unravel the interplay among the biochemical mechanisms responsible for modulating ROS emission from mitochondria. Moreover, the reciprocal interaction between matrix and extra-matrix compartments determining the cytoplasmic and mitochondrial redox environments is incompletely understood.

To investigate these processes, titration experiments were performed on isolated mitochondria with specific inhibitors of the GSH/Trx systems (24,41). Selective inhibition of TrxR with auranofin (AF) (42), or depletion of GSH with 2,4 dinitrochlorobenzene (DNCB), leads to an increase in H₂O₂ emission flux from isolated heart (41) or brain (43) mitochondria. Experimentally, the inhibitor titrations were performed under conditions that affected either the GSH or Trx system independently or in tandem. Computationally, a similar approach was applied; the rates of H₂O₂ release were simulated when GR or TrxR were gradually inhibited independently or in tandem.

Fig. 6 compares dose-response relationships from experimental and computational data for the specific H₂O₂ emission from mitochondria as a function of AF (Fig. 6, A and B), or DNCB (Fig. 6, C and D), concentration. The model is able to reproduce the magnitude of increase in H₂O₂ emission under states 4 and 3 conditions. In the absence of inhibition of the scavenging systems the experimental fluxes were ∼threefold higher than those obtained with the model (Fig. 6). When both inhibitors were applied together, the model was able to approximate the H₂O₂ emission to the same order of magnitude as the experimental values (Table 2). The difference between model simulations and experimental H₂O₂ emission may be attributed to the protein density assumed in the conversion factor adopted to express model results as pmol min⁻¹ mg⁻¹ prot. (0.125 converts nmol mg⁻¹ protein to mitochondrial mM units (44)).

Figure 6.

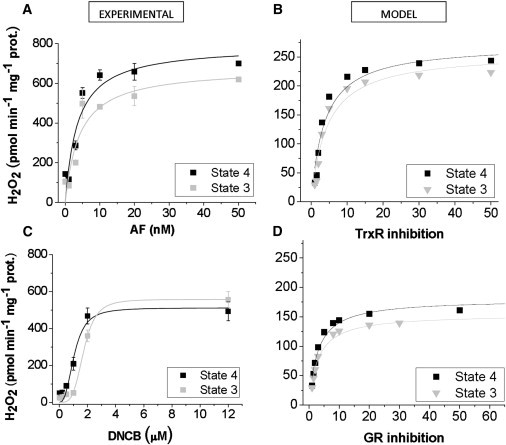
Effect of selective inhibition of Trx or GSH scavenging systems on H₂O₂ emission from heart mitochondria during respiratory states 4 and 3. Freshly isolated mitochondria (∼100 μg mitochondrial protein) from guinea pig hearts were preincubated with the indicated concentrations of AF (A), or DNCB (C) in the presence of G/M (5 mM each). Monitoring of H₂O₂ was performed with the Amplex Red assay during state 4 (black solid square) and 3 (+1 mM ADP, gray solid square) respiration (see Materials and Methods). Shown are the specific fluxes of H₂O₂ emission obtained from two experiments with duplicates in each (24). For simulating AF inhibition with the ME-R model, the concentrations of Trx reductase from mitochondrial (E_trxm) and extra-matrix (E_trx) compartments were simultaneously lowered from a control concentration of 3.5 × 10⁻⁴ mM to 7 × 10⁻⁶ mM. The steady state values of H₂O₂ emission (V_H2O2dif expressed in the same units as the experimental plots) were computed at each inhibitory concentration (B). DNCB inhibition was simulated by simultaneously decreasing mitochondrial (Et_GRm) and extra-matrix (Et_GR) GR from a control concentration of 9 × 10⁻⁴ mM to 3 × 10⁻⁵ mM. In the simulations, the percent inhibition was calculated from dividing the control concentration by Et_GRm and the result multiplied by 100. In experiments and simulations, the kinetic parameters (V_max and K_0.5) that characterize the H₂O₂ emission fluxes as a function of the inhibitor concentrations, were determined by nonlinear regression of the data points with a hyperbolic Michaelis-Menten or Hill type equation (solid lines).

Steady-state behavior of the redox environment

After corroboration of the model’s ability to reproduce qualitatively (shape) and quantitatively (same order of magnitude) experimental data, it was used to analyze the behavior of the redox environment (RE) in matrix and extra-matrix compartments, and their reciprocal influence.

The RE is a thermokinetic metric that accounts for the redox potential and the concentration of reduced species from the redox couples in the various cellular compartments, e.g., cytoplasm, mitochondria. Because the concentration of reduced species is a function of the overall system dynamics, the RE is a dynamically changing metric. It can be calculated by adding the products of the redox potential multiplied by the concentration of the reduced species for each of the linked redox couples, as follows (42) (see also Section S1 in the Supporting Material):

$$Redoxenvironment=\sum _{i=1}^{n\left(couple\right)}{E}_i\times {\left[reducedspecies\right]}_i.$$ (1)

Thermodynamically, the reduction potential, E_i, represents a voltage whose magnitude is determined by the ratio of reduced/oxidized species, which in turn depends on the overall system dynamics producing a certain concentration of the reduced species. The latter embodies an instantaneous reducing capacity or capacitance accounting for the total charge stored (i.e., number of electrons available) (42).

In the matrix compartment of the ME-R model, the RE is determined by the NADH/NAD⁺, NADPH/NADP⁺, GSH/GSSG, and Trx(SH)₂/ TrxSS, redox couples. Fig. 7 displays the redox potential of the four main redox couples as a function of the mitochondrial RE, when either AcCoA (Fig. 7 C) or cytoplasmic ADP (ADPi) (Fig. 7 D) is increased. The model response was investigated by varying AcCoA and extra-matrix ADP as displayed in panels A and B, respectively. The rather narrow concentration range in which AcCoA was varied corresponds with the large model sensitivity to this parameter. Thereby, NADH and ΔΨ_m exhibit the largest changes in response to a narrow range of AcCoA variation, saturating afterward (see Fig. 2 B). Concerning the redox potential, it can be clearly seen that the NADPH/NADP⁺ couple displays the largest (most negative) reductive potential. This underscores the role of NADPH as the main electron donor of cellular/mitochondrial antioxidant systems (Fig. 7, C and D). From NADPH, the reductive potential decreases as follows: NADH/NAD⁺ > Trx(SH)₂/TrxSS > GSH/GSSG (Fig. 7, C and D). In panel 7F, NADH becomes the highest contributor to RE as ADP increases over a threshold level. The most prominent relative contribution of GSH/GSSG and NADH/NAD⁺ to the RE ranges from 50% to 90% or from 5% to 45%, respectively, in the case of AcCoA (Fig. 7 E) or from ∼2% to ∼50% and from ∼45% to ∼90%, respectively, with ADP_i (Fig. 7 F). In our model, the total GSH concentration has been adjusted to the mM range (1–3 mM) in the matrix, according to measurements performed in intact cardiomyocytes, and in isolated mitochondria (41,45). Beyond their quantitative contribution to the redox environment, the role of NADH/NAD⁺ is mainly to fuel energy provision through the respiratory chain, whereas NADPH/NADP⁺ contributes electrons to the antioxidant system. NADH/NAD⁺ may also influence indirectly the antioxidant defenses through its effect on the αKG/ISOC ratio linked to NADPH via IDH. Both redox couples are related through the THD-catalyzed reaction that contributes minimally to NADP⁺ reduction.

Figure 7.

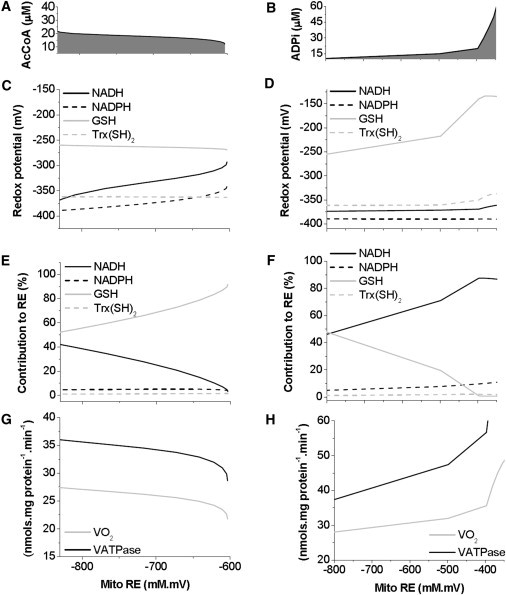
Relationship between redox couples and mitochondrial RE at different concentrations of extra-matrix substrates. Steady-state values were obtained at increasing concentrations of AcCoA: 0.012–0.024 mM (A,C,E,G) or ADP_i: 0.01–0.05 mM (B,D,F,H). (A and D) Redox potential of each mitochondrial redox pair was estimated and represented as a function of the mitochondrial RE (Eq. S3). (E and F) The relative contribution of each mitochondrial redox couple to the RE was estimated (= (E_i^∗[reduced species]_i^∗100)/mitochondrial RE) and represented as a function of the mitochondrial RE. Standard redox potentials used were −320 mV for NADH/NAD⁺; −324 mV for NADPH/NADP⁺ (64) −292 mV for Trx(SH)₂/TrxSS, and −240 mV for 2 GSH/GSSG, −160 mV (41,42). (G and H) Steady-state respiration (VO₂) from complex I and II and rate of ATP synthesis (V_ATPase) are depicted.

Fig. 7, G and H, shows the steady-state behavior of oxidative phosphorylation (OxPhos) fluxes as a function of mitochondrial RE during the metabolic transitions. Increasing concentrations of AcCoA generate a more reduced mitochondrial RE associated with slightly higher VO₂ and V_ATPase (Fig. 7 C), as expected during a transition to state 4 respiration. The low OxPhos fluxes calculated at low AcCoA input correspond to decreased availability of reducing equivalents in the form of NADH to fuel respiration, i.e., at RE > ∼ −700 mM mV (Fig. 7 C). Unlike AcCoA, as ADPi increases the mitochondrial compartment becomes increasingly oxidized due to increased respiratory (VO₂) and ATP synthesis (V_ATPase) fluxes (Fig. 7 H).

Discussion

In this work, we describe a two-compartment computational model of energetic-redox-ROS metabolism. A combined approach of experiments with isolated heart mitochondria and mathematical modeling, in which experimental and simulation protocols were matched, enabled us to use the ME-R model to simulate the following relevant situations: i), the steady-state behavior of ΔΨ_m and NADH during transitions from deenergized to energized states elicited by gradual G/M addition (Fig. 2); ii), the transient ΔΨ_m and NADH dynamics accompanying the state 4 to 3 transition in mitochondrial respiration after a single (Fig. 3) or several pulses of increasing substrate concentration (Fig. 4); iii), the response of mitochondrial respiration and energetic-redox variables (ΔΨ_m, NADH) upon titration with an uncoupler (Fig. 5); and iv), the overall kinetics of H₂O₂ emission rates after titration experiments performed in mitochondrial suspensions with inhibitors of the GSH/Trx scavenging systems (Fig. 6). The ability of the ME-R model to reproduce qualitatively and quantitatively in the same order of magnitude values for a varied set of basic experimental behaviors indicates that the main components participating in ROS and redox metabolisms, their kinetics, and interactions with energetic processes are, to a great extent, accounted for by the present formulation.

Because the ME-R model includes an entirely new set of antioxidant defense mechanisms much lower levels of matrix and extra-matrix ROS than previous models were obtained (25,46). Consequently, a determination of whether oscillatory behavior was still present (25,26) is germane to this new formulation of ROS metabolism. Fig. S2 shows that the model is able to simulate oscillatory dynamics in agreement with the mechanism described previously (25), i.e., ROS imbalance triggered by the interplay between ROS production and ROS scavenging.

Compartmentation, dynamics, and interdependence of redox metabolism

Redox couples are interdependent systems, as illustrated by the existence of common electron donors such as NADPH to main scavenging systems (GSH/Trx), as well as the interconversion of NADH-NADPH pools catalyzed by the THD (Fig. 1) (37). Recent evidence indicates that the GSH and Trx scavenging systems exhibit a well-orchestrated interaction, functionally relieving each other when the antioxidant capacity of either is overwhelmed (24). In this work, we put into evidence the dynamic nature of the RE as a function of the different redox couples, whose relative contribution to determining the RE is given by both their redox potential and the concentration of reduced species (Fig. 7). In this respect, and concerning the relevance of kinetic over thermodynamic control of ROS production in the respiratory chain, we contend that O₂^⋅− generation at electron carriers will be kinetically controlled. As a matter of fact, although the reduction potential of the redox couple O₂^⋅−/O₂ is negative enough to allow different mitochondrial oxidoreductases to become potential sites of ROS generation (Fig. S3) (7), the quick diffusion and scavenging of the resultant O₂^⋅− renders the reverse reaction virtually nonexistent (12, and see 51). This rationale explains why most O₂^⋅− production takes place in the mitochondrial electron transfer chain and is restricted to the complexes that handle the most reduced thermodynamic potentials (complex I and III) (12,20,47).

Compartmentation plays a significant role in the control of ROS levels, the RE, and dynamic behavior, as suggested by our modeling results. Although each compartment exhibits its own dynamics, the interdependence of their RE is mediated by the exchange of redox species (e.g., GSH, ROS). The present ME-R model with antioxidant arrays in both compartments renders O₂^⋅− and H₂O₂ levels in the pM to nM range. ROS concentrations beyond these limits only occur under oxidative stress, when the scavenging capacity of the array of antioxidant defenses is overwhelmed (Figs. 6 and 7). Because GSH/Trx scavenging systems appear to act concertedly and continuously to keep low rates of H₂O₂ emission from mitochondria (24), duplication of antioxidant defense systems in multiple compartments can be viewed as an efficient salvage mechanism in response to oxidative bursts.

In the ME-R model the interplay between SOD activities in both compartments (MnSOD and Cu,ZnSOD) determines the balance between production and scavenging of O₂^⋅−, a decisive trait for the appearance of mitochondrial oscillations. These results also underscore the importance of compartmentation and the role of SODs in determining the RE, which appears crucial for cell (48) and organism survival (49).

Reported experimental evidence supports the notion that scavenging systems play a relevant role in the control of ROS levels in various cellular compartments (24,48,50–52), which in turn exhibit different redox states. In heart and liver mitochondria, the NADH pool is mostly reduced, whereas the cytoplasm is predominantly oxidized (53). Similarly, the bulk of NADP is present as NADPH in liver mitochondria (NADP⁺/NADPH = 0.01) (53,54). The transfer of reducing equivalents across the inner mitochondrial membrane is of fundamental importance for intermediary metabolism, e.g., glycolysis, gluconeogenesis, lipogenesis (53). Our previous work has shown that partial GSH depletion triggers cell-wide mitochondrial oscillations in intact cardiomyocytes, and the onset of oscillation depends upon the extra-matrix redox potential of the GSH/GSSG redox couple, as shown directly in permeabilized cardiomyocytes (48).

The redox environment and energy metabolism

Until recently, there was no integrative view accounting for ROS production, ROS scavenging, the energetic status of mitochondria, and the interactions between these processes (24). The redox-optimized ROS Balance hypothesis proposes that ROS levels (as the net result of production and scavenging) depend on the intracellular and intramitochondrial RE (17). Unlike the mild uncoupling hypothesis, a reduction of ROS levels in the redox-optimized ROS Balance model does not require compromising the efficiency of mitochondrial energy transduction (55). Instead, it postulates that there is a minimum level of ROS emission when mitochondria maximize their energetic output. Under high energy demand, and despite large respiratory rates, ROS emission levels are kept to a minimum by ROS scavenging systems.

As an integrative and highly dynamic metric, the RE characterizes the redox status of the different redox couples while considering the capacity of each, even though they may not be directly in equilibrium with each other. The presence of different metabolic pathways and continuous exchange processes between different subcellular compartments makes the experimental assessment of RE microenvironments in vivo very difficult, hence, the use of experimentally validated mathematical models are crucial for studying the evolution of the RE in each compartment, as well as the interrelationship of the RE with other cellular processes.

The ME-R model shows that, depending on physiological conditions (substrate concentration), the RE and the redox potential as well as the relative contribution of each redox couple can change (Fig. 7). In this respect, the close link between redox and energy metabolisms extends the role of NADH beyond its well-known function as an intermediary between substrate catabolism and ΔΨ_m, because through THD, NADH is also a precursor of mitochondrial NADPH (37). In this context, the RE becomes more reduced when mitochondria are subjected to increasing levels of AcCoA by fueling NAD⁺ reduction, in turn activating the redox and ROS scavenger machinery (Fig. 7). On the other hand, for conditions in which mitochondria are challenged with increasing ADP concentrations (i.e., high work), OxPhos fluxes increase while the RE becomes more oxidized (Figs. 2–4), potentially compromising the antioxidant capacity. As a caveat to this generalization about RE as metric for assessing ROS accumulation, the relative contribution to the RE by each redox couple does not necessarily determine its biological importance. For instance, the functionality of certain proteins that have been oxidized can only be rescued through electrons provided by a specific redox couple, such as the Trx system, which exhibits a higher reductive potential but lower concentration of its components as compared with the GSH system (41,51,53).

Previous modeling and model limitations

Kinetic computational models of radical scavenging have been implemented for Jurkat T cells (56,57). These models only accounted for H₂O₂ scavenging in the cytoplasmic compartment, at different levels of detail, and did not take into account the source of H₂O₂.

The kinetic control of O₂^⋅− generation has being addressed with very detailed models accounting for electron transfer across the different redox centers in respiratory complexes I and III (58,59). Due to the introduction of a large number of state variables for each of the complexes, those models exhibit stiffness that complicates their integration into more global model schemes. On the basis of these arguments, our approach has been to simplify the kinetics of ROS production considering it as a bypass of the electrons involved in energy metabolism. This decision has its limitations, a main one being that, in its present formulation, the ME-R model is unable to simulate the increase in ROS levels when mitochondria evolve into state 4 respiration; further model refinement will be needed to represent this situation.

The differences between the experimental data and model results mainly concern VO₂ and H₂O₂ emission fluxes, and the absolute value of ΔΨ_m and NADH following substrate addition. In the case of respiration, changes in mitochondrial matrix volume accompanying K⁺ movements are not taken into account, and a linear instead of an exponential dependence of the leak current on ΔΨ_m (60,61), postulated by the model, may be responsible. We have started to quantitatively characterize K⁺ fluxes and volume regulation (40). Respiration is well known to be modulated by changes in matrix volume and ΔΨ_m; NADH and ROS emission levels will reflect OxPhos flux changes (62). Quantitative differences between experiment and model results may also arise because the model represents the performance of an average mitochondrion, whereas the experimental system corresponds to the average behavior of a heterogeneous mitochondrial population. Thus, in the experiment we expect to have a range rather than a unique set of kinetic parameter values (63).

The ME-R model does not consider NADH transfer from the cytoplasm into mitochondria or the flow of NADPH from mitochondria that may occur under conditions of utilization of this coenzyme in the cytoplasm (53). NADH is transported from cytoplasmic to mitochondrial compartments through the malate-aspartate (the primary mechanism in cardiac muscle) or α-glycerophosphate shuttles and acyl-CoA elongation/β-oxidation, with practically no backflow of NADH from mitochondria (53). We did not include NADH transport from cytoplasmic to mitochondrial compartments because of its predominantly oxidized status, which would represent a small contribution to the RE (<100 mV mM). Thus, cytoplasmic NADH contribution to mitochondrial redox under our modeling conditions was considered negligible.

Our modeling approach is deterministic, the advantage of which is its relative simplicity with respect to a stochastic approximation. Simplicity is significant for modeling a complex system such as mitochondria with a great deal of mechanistic detail. Our combined experimental-modeling strategy is dependent upon the major number of variables and parameters that can be experimentally assessed. Therefore, assuming that the law of big numbers prevails over stochastic fluctuations is crucial at this phase of model development.

Concluding remarks

Summarizing, the ME-R model presented herein constitutes a valuable tool for addressing the interaction among ionic, energetic, redox, and ROS metabolic networks in mitochondria. This claim is supported by the extensive validation process to which the model was subjected, in a close match between experimental and simulation protocols. By considering four main redox couples, the ME-R model enables a more refined assessment of the RE in different compartments, as well as their interdependence.

Overall, our modeling results support the notion that the RE is highly dynamic, and dependent on compartmentalization as well as the status of distinct redox systems operating under far-from-equilibrium conditions. All redox systems are profoundly interdependent based on sharing of common electron donors of high reductive potential (e.g., NADPH), and the continuous exchange of redox species across compartments.