Abstract
We address the problem of the joint statistical inference of phylogenetic trees and multiple sequence alignments from unaligned molecular sequences. This problem is generally formulated in terms of string-valued evolutionary processes along the branches of a phylogenetic tree. The classic evolutionary process, the TKF91 model [Thorne JL, Kishino H, Felsenstein J (1991) J Mol Evol 33(2):114–124] is a continuous-time Markov chain model composed of insertion, deletion, and substitution events. Unfortunately, this model gives rise to an intractable computational problem: The computation of the marginal likelihood under the TKF91 model is exponential in the number of taxa. In this work, we present a stochastic process, the Poisson Indel Process (PIP), in which the complexity of this computation is reduced to linear. The Poisson Indel Process is closely related to the TKF91 model, differing only in its treatment of insertions, but it has a global characterization as a Poisson process on the phylogeny. Standard results for Poisson processes allow key computations to be decoupled, which yields the favorable computational profile of inference under the PIP model. We present illustrative experiments in which Bayesian inference under the PIP model is compared with separate inference of phylogenies and alignments.
Keywords: phylogenetics, systematics, sequence homology, point process
The field of phylogenetic inference is being transformed by the rapid growth in availability of molecular sequence data. There is an urgent need for inferential procedures that can cope with data from large numbers of taxa and that can provide inferences for ancestral states and evolutionary parameters over increasingly large time spans. Existing procedures are often not scalable along these dimensions and can be a bottleneck in analyses of modern molecular datasets.
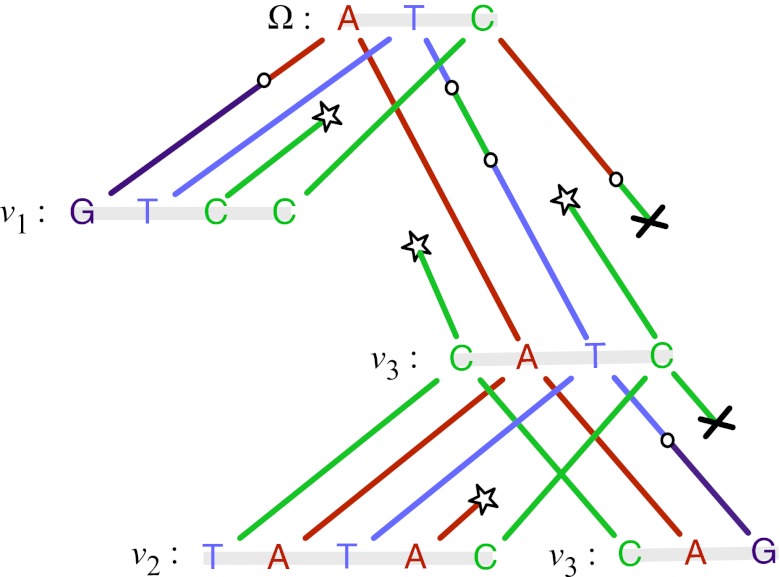
A key issue that renders phylogenetic inference difficult is that sequence data are generally not aligned a priori, having undergone evolutionary processes that involve insertions and deletions. Consider Fig. 1, which depicts an evolutionary tree in which each node is associated with a string of nucleotides, where the string evolves via insertion, deletion, and substitution processes along each branch of the tree. Even if we consider evolutionary models that are stochastically independent along the branches of the tree (conditioning on ancestral states), the inferential problem of inferring evolutionary paths (conditioning on observed data at the leaves of the tree) does not generally decouple into independent computations along the branches of the tree. Rather, alignment decisions made throughout the tree can influence the posterior distribution on alignments along any branch.
Fig. 1.
Depiction of the evolution of a set of strings of nucleotides along the branches of a tree with leaves  and root Ω, where each string is subject to insertion, deletion, and substitution processes. Stars denote nucleotide insertion events, crosses denote deletion events, and circles denote substitution events.
and root Ω, where each string is subject to insertion, deletion, and substitution processes. Stars denote nucleotide insertion events, crosses denote deletion events, and circles denote substitution events.
This issue has come to the fore in a line of research beginning in 1991 with a seminal paper by Thorne et al. (1). In the “TKF91 model,” a simple continuous-time Markov chain (CTMC) provides a string-valued stochastic process along each branch of an evolutionary tree. This makes it possible to define joint probabilities on trees and alignments, and thereby obtain likelihoods and posterior distributions for statistical inference. A further important development has been the realization that the TKF91 model can be represented as a hidden Markov model, and that generalizations to a broader class of string-valued stochastic processes with finite-dimensional marginals are therefore possible (2–9). This has the appeal that statistical inference under these processes (known as transducers) can be based on dynamic programming (10–13). Unfortunately, however, despite some analytical simplification that is feasible in restricted cases (14), the memory needed to represent the state space in these models is generally exponential in the number of leaves in the tree (15). Moreover, even in the simple TKF91 model, there does not appear to be additional structure in the state space that allows for simplification of the dynamic program. Indeed, the running time of the most sophisticated algorithm for computing marginals (16) depends on the number of homology linearizations, which is exponential in sparse alignments (17).
As a consequence of this unfavorable computational complexity, there has been extensive work on approximations, specifically on approximations to the joint marginal probability of a tree and an alignment, obtained by integrating over the derivation (8, 18). A difficulty, however, is that these marginal probabilities play a role in tree inference procedures as the numerators and denominators of acceptance probabilities for Markov chain Monte Carlo (MCMC) algorithms. Loss of accuracy in these values can have large, uncontrolled effects on the overall inference. A second approach is to consider joint models that are not obtained by marginalization of a joint continuous-time, string-valued process. A range of combinatorial (19–24) and probabilistic (25–29) models fall into this category. Although often inspired by continuous-time processes, obtaining a coherent and calibrated estimate of uncertainty in these models is difficult.
A third possible response to the computational complexity of joint inference of trees and alignments is to retreat to methods that treat these problems separately. In particular, as is often done in practice, one can obtain a multiple sequence alignment (MSA) via any method (often based on a heuristically chosen “guide tree”) and then infer a tree based on the fixed alignment. This latter inferential process is generally based on the assumption that the columns of the alignment are independent; in such case, the problem decouples into a simple recursion on the tree [the “Felsenstein” or “sum-product” recursion (30)]. Such an approach can introduce numerous artifacts, however, both in the inferred phylogeny (28, 29, 31), and in the inferred alignment (32, 33).
It is also possible to iterate the solution of the MSA problem and the tree inference problem (34, 35), which can be viewed as a heuristic methodology for attempting to perform joint inference. The drawbacks of these systems include a lack of theoretical understanding, the difficulty of getting calibrated confidence intervals, and overalignment problems (17, 36).
Finally, other methods have focused on analyzing only pairs of sequences at a time (17, 37–39). Although this approach can considerably simplify computation (40, 41), it has the disadvantage that it is not based on an underlying joint posterior probability distribution.
In the current paper, we present a model-based approach to the joint probabilistic inference of trees and alignments. Our approach is based on a model that is closely related to TKF91, altering only the insertion process but leaving the deletion and substitution processes intact. Surprisingly, this relatively small change has a major mathematical consequence: Under our model, evolutionary paths have an equivalent global description as a Poisson process on the phylogenetic tree. We are then able to exploit standard results for Poisson processes (notably, Poisson thinning) to obtain significant computational leverage on the problem of computing the joint probability of a tree and an alignment. Indeed, under our model, this computation decouples in such a way that this joint probability can be obtained in linear time (linear in the number of taxa and the sequence length) rather than in exponential time, as in TKF91.
Our model has two descriptions: the first as a local continuous-time Markov process that is closely related to the TKF91 model and the second as a global Poisson process. We treat the latter as the fundamental description and refer to the newly developed process as the Poisson Indel Process (PIP). The global description not only sheds light on computational issues but opens up new ways to extend evolutionary models, allowing, for example, models that incorporate structural constraints and slipped-strand mispairing phenomena.
Under the Poisson process representation, another interesting perspective on our process is to view it as a string-valued counterpart to stochastic Dollo models (42, 43), which are defined on finite state spaces. In particular, the general idea of the two-step generation process used in Section 2 has antecedents in the literature on probabilistic modeling of morphological or lexical characters, but the literature did not address the string-valued processes that are our focus here.
The remainder of the paper is organized as follows. First, Section 1 provides some basic background on the TKF91 model. Next, in Section 2, we present the PIP model, in both its local and global formulations. Section 3 delves into the computational aspects of inference under the PIP model, describing the linear-time algorithm for computing the exact marginal density of an MSA and a tree. In Section 4, we present an empirical evaluation of the inference algorithm, and, finally, we present our conclusions in Section 5.
1. Background
We begin by giving a brief overview of the TKF91 model. Instead of following the standard treatment based on differential equations, we present a Doob–Gillespie view of the model (44, 45) that will be useful in our subsequent development.
Let us assume that at some point in time t, a sequence has length n. In the TKF91 process, the sequence stays unchanged for a random interval of time Δt, and after this interval, a single random mutation (substitution, insertion, or deletion) alters the sequence. This is achieved by defining a total of 3n + 1 independent exponential random variables, n of which correspond to deletion of a single character, n of which correspond to the mutation of a single character, and n + 1 of which yield insertions after one of the n characters (including one “immortal” position at the leftmost position in the string). These 3n + 1 exponential random variables are simulated in parallel, and the value of the smallest of these random variables determines Δt. The index of the winner determines the nature of the event at time Δt (whether it is a substitution, deletion, or insertion).
The random variables corresponding to a deletion have exponential rate μTKF, whereas those corresponding to an insertion have exponential rate λTKF. If the event is a mutation, a multinomial random variable with parameters obtained from the substitution rate matrix θ is drawn to determine the new value of the character. Finally, if an insertion occurs, a multinomial random variable is drawn to determine the value of the new character, with parameters generally taken from the stationary distribution of θ.
This describes the evolution of a string of characters along a single edge of a phylogenetic tree. The extension to the entire phylogeny is straightforward; we simply visit the tree in preorder and apply the single-edge process to each edge. The distribution of the sequences at the root is generally assumed to be the stationary distribution of the single-edge process (conceptually, the distribution obtained along an infinitely long edge).
Although the TKF91 model is reversible (and the PIP model as well, as we prove in Section 2.3), making the location of the root unidentifiable, it is useful to assume for simplicity that an arbitrary root has been picked, and we will make that assumption throughout. The likelihood is not affected by this arbitrary choice.
2. PIP
In this section, we introduce the PIP. This process has two descriptions: a local description that is closely related to the TKF91 model and a global description as a Poisson process.
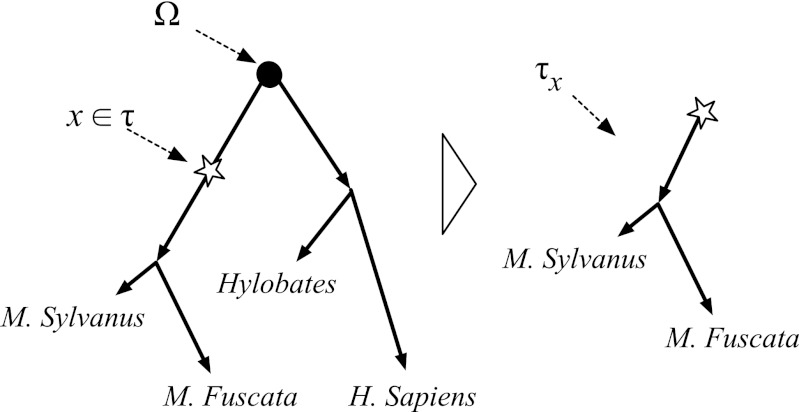
We require some additional notation (Fig. 2). A phylogeny τ will be viewed as a continuous set of points, and its topology will be denoted by 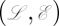 , where
, where  is equal to the finite subset containing the branching points, the leaves
is equal to the finite subset containing the branching points, the leaves 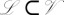 and the root Ω, and where
and the root Ω, and where 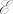 is the set of edges. Parent nodes will be denoted by pa(v), for
is the set of edges. Parent nodes will be denoted by pa(v), for 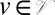 , and the branch lengths will be denoted by b(v), which is the length of the edge from pa(v) to v. For any x ∈ τ (whether x is a branch point in or an intermediate point on an edge), we write τx for the rooted phylogenetic subtree of τ rooted at x (dropping all points in the original tree that are not descendants of x). Finally, the set of characters (nucleotides or amino acids) will be denoted as Σ.
, and the branch lengths will be denoted by b(v), which is the length of the edge from pa(v) to v. For any x ∈ τ (whether x is a branch point in or an intermediate point on an edge), we write τx for the rooted phylogenetic subtree of τ rooted at x (dropping all points in the original tree that are not descendants of x). Finally, the set of characters (nucleotides or amino acids) will be denoted as Σ.
Fig. 2.
Notation used for describing the PIP. Given a phylogenetic tree τ and a point x ∈ τ on that tree, τx is defined as the subtree rooted at x. H. Sapiens, Homo sapiens; M. Fuscata, Macaca fuscata; M. Sylvanus, Macaca sylvanus.
2.1. Local Description.
The stochastic process we propose has a local description that is very similar to the TKF91 process, with the only change being that the insertion rate no longer depends on the sequence length. Therefore, instead of using 3n + 1 competing exponential random variables to determine the next event as in the TKF91 model (n for substitutions, n + 1 for insertions, and n for deletions), we now have 2n + 1 variables (n for substitutions, 1 for insertion, with rate λ, and n for deletion, each of rate μ). When an insertion occurs, its position is selected uniformly at random.* We assume that the process is initialized by sampling a Poisson-distributed number of characters, with parameter λ/μ. Each character is sampled independently and identically according to the stationary distribution of θ.
Note that if λ/λTKF is an integer and the sequence has the length (λ/λTKF) − 1 at some point in time, the distribution over the time and type of the next mutation is the same as in TKF91, using the fact that the minimum of exponential variables with λi is exponential, with a rate equal to the sum of the λi. However, in general, the distributions are different. We discuss some of the biological aspects of these differences in Section 5; for now, we focus on the computational and statistical aspects of the PIP model.
2.2. Poisson Process Representation.
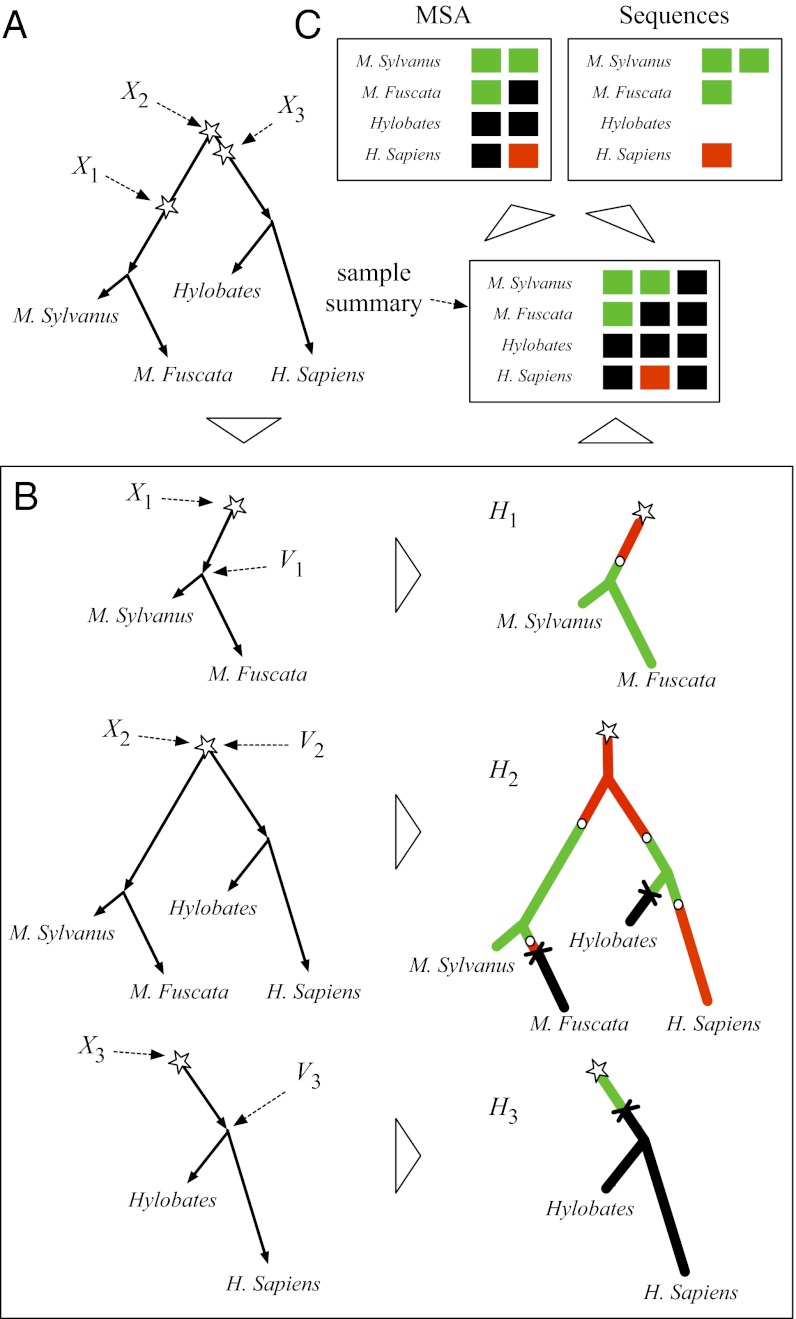
We turn to a seemingly very different process for associating character strings with a phylogeny. This process consists of two steps, with the first involving insertions and the second involving deletions and substitutions.
In the first step, depicted in Fig. 3A, a multiset of insertion points is sampled from a Poisson process defined on the phylogeny τ (46). The rate measure for this Poisson process has an atomic mass at the root of the tree; hence, the need for multisets rather than simple point sets. Except for the root, no other points on the tree have an atomic mass (in particular, and in contrast to population genetics models, the probability that evolutionary events occur at branching points is 0). We denote this multiset of insertion points by X.
Fig. 3.
Example of a PIP sample. Here, Σ has two symbols, represented by red and green squares, and the absorbing deletion symbol ɛ is represented in black. (A) Sample from a Poisson process on τ. (B) Each sampled point corresponds to a rooted tree on which a CTMC path is sampled. (C) Alignments and sequences are obtained as a deterministic function of the first two steps. H. Sapiens, Homo sapiens; M. Fuscata, Macaca fuscata; M. Sylvanus, Macaca sylvanus.
In the second step, we visit the insertion points one at a time. The order of the visits of the insertions is sampled uniformly at random, 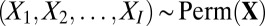 . An insertion visit consists of two substeps. First, we extract the directed subtree rooted at the insertion location Xi. Examples of these subtrees are shown in Fig. 3B (Left). Second, we simulate the fate of the inserted character along
. An insertion visit consists of two substeps. First, we extract the directed subtree rooted at the insertion location Xi. Examples of these subtrees are shown in Fig. 3B (Left). Second, we simulate the fate of the inserted character along 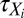 . This is done via a substitution-deletion CTMC whose state space
. This is done via a substitution-deletion CTMC whose state space 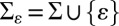 consists of the basic alphabet Σ augmented with an empty string symbol ɛ. As shown in Fig. 3B (Right), the substitution-deletion CTMC yields paths along subtrees in which a single character either mutates or is deleted. The latter event, represented by ɛ, is an absorbing state.
consists of the basic alphabet Σ augmented with an empty string symbol ɛ. As shown in Fig. 3B (Right), the substitution-deletion CTMC yields paths along subtrees in which a single character either mutates or is deleted. The latter event, represented by ɛ, is an absorbing state.
We define a homology path Hi as the single-character history generated by a substitution-deletion CTMC along a phylogeny. If a point x ∈ τ is a descendant of the insertion Xi, Hi(x) is set to the state of the substitution-deletion CTMC at x. If x ∈ τ is not a descendant of Xi, we set Hi(x) to the absorbing symbol ɛ. Thus, formally, a homology path Hi is a random map from any point on τ to Σɛ.
Given a set of homology paths for each inserted character index i, the sequence at any point on the tree, x ∈ τ, is obtained as follows (Fig. 3C, Right). First, we construct a list of all the values taken by Hi(x) at the given point: 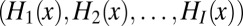 . Second, we remove from the list any characters that are equal to the absorbing symbol ɛ. The string obtained thereby is denoted by Y(x). The set of observed data comprises the values of Y at the leaves of the tree:
. Second, we remove from the list any characters that are equal to the absorbing symbol ɛ. The string obtained thereby is denoted by Y(x). The set of observed data comprises the values of Y at the leaves of the tree: 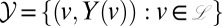 .
.
We can also construct an MSA M from a set of homology paths (Fig. 3C, Left). From each homology path Hi, we extract the characters at the leaves, arranging these characters in a column. Delete any column in which all the characters are the character ɛ. Arrange these columns in the order of the visits to the insertion points. The resulting matrix, whose entries range over the augmented alphabet Σɛ, is the MSA M.
For a given rooted phylogenetic tree τ, we will denote by pτ(m) the marginal probability that this process generates an MSA m, integrating over all homology paths, 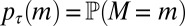 . For joint inference, we make the phylogenetic tree T random, with a distribution specified by a prior with density p(τ).
. For joint inference, we make the phylogenetic tree T random, with a distribution specified by a prior with density p(τ).
2.3. Characterization.
In this section, we show that the local and the global descriptions of the PIP given in the previous two subsections are, in fact, alternative descriptions of the same string-valued stochastic process. In stating our theorem, we let ν denote the rate measure characterizing the insertion process in the global description and Q and π denote the transition matrix and the initial distribution for the substitution-deletion CTMC.
2.3.1. Theorem 1.
Let τ be a phylogenetic tree with an arbitrary rooting, and let us denote the Lebesgue measure on τ by the same symbol. For any insertion rate λ > 0, deletion rate μ > 0, and reversible substitution rate matrix θ, the local and global processes described in Sections 2.1 and 2.2 coincide if we set for all σ, 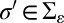 :
:
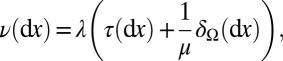 |
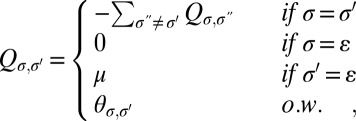 |
and set π to be the quasi-stationary distribution of Q (47).
The proof is given in SI Appendix, Section 1. Note that in the case of interest here, where the rate of deletion does not depend on the character being deleted, πσ is equal to the entry of the stationary distribution of θ corresponding to σ when σ ≠ ɛ, and 0 otherwise. The following result establishes some basic properties of the PIP model. Its proof can be found in SI Appendix, Section 1.
2.3.2. Proposition 2.
For all μ, λ > 0 and reversible rate matrix θ, the PIP model is reversible, with a stationary length distribution given by a Poisson distribution with mean λ/μ.
The Poisson stationary length distribution represents a modeling advantage of PIP over TKF91, which has a geometrically distributed stationary distribution. Based on a study of protein-length distributions for the three domains of life (48), the Poisson distribution has been suggested (49) as a more adequate length distribution.
From proposition 2, we can also obtain an alternative reparameterization of the PIP model, in terms of asymptotic expected length η = λ/μ and insertion-deletion (indel) intensity ζ = λ⋅μ.
3. Computational Aspects
We turn to a consideration of the computational consequences of the Poisson representation of the PIP model. We first consider how the Poisson process characterization allows us to compute the marginal likelihood, pτ(m), in linear time, which is a significant improvement over methods based on the TKF91 model. In SI Appendix, Section 4, we provide a brief discussion of the role that the marginal likelihood plays in inference.
To compute the marginal likelihood, pτ(m), we first condition on the number of homology paths, |X|. Although the number of homology paths is random and unknown, we know that it can be no less than the number of columns |m| in the postulated alignment m. We need to consider an unknown and unbounded number of birth events with no observed offspring in the MSA, but because they are exchangeable, they can be marginalized analytically. This is done as follows:
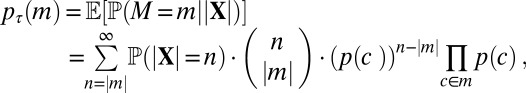 |
where the first factor captures the probability of sampling n homology paths, the second captures the number of ways to pick the |m| observed homology paths (the columns, which contain at least one descendent character at the leaves) out of the n paths, the factor 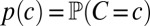 is the likelihood of a single MSA column c, and c is a column with an absorbing deletion symbol at every leaf
is the likelihood of a single MSA column c, and c is a column with an absorbing deletion symbol at every leaf  :
: 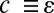 (in this section, we drop subscripts for column-specific random variables, such as C, H, and X, because they are exchangeable). Note that such simplification is not possible in the TKF91 model, because the rate of insertion depends on the length of the internal sequences, and hence of the deletion events.
(in this section, we drop subscripts for column-specific random variables, such as C, H, and X, because they are exchangeable). Note that such simplification is not possible in the TKF91 model, because the rate of insertion depends on the length of the internal sequences, and hence of the deletion events.
This expression can be simplified by introducing the function j defined as follows for all 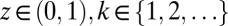 :
:
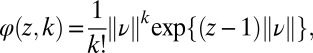 |
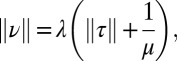 |
where  is the normalization of the measure τ (i.e., the sum of all the branch lengths in the topology). We show in SI Appendix, Section 2 that this yields the simple formula:
is the normalization of the measure τ (i.e., the sum of all the branch lengths in the topology). We show in SI Appendix, Section 2 that this yields the simple formula:
The next step is to compute the likelihood p(c) of each individual alignment column c. We do this by partitioning the computation into subcases depending on the location of the tree at which the insertion point X is located for column c. More precisely, we look at the most recent common ancestor 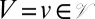 of the characters in c that are not equal to ɛ (Fig. 3B). If v ≠ Ω, this corresponds to the most recent end point of the edge
of the characters in c that are not equal to ɛ (Fig. 3B). If v ≠ Ω, this corresponds to the most recent end point of the edge 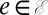 where the insertion occurred.
where the insertion occurred.
Computing the prior probability of the insertion location is greatly simplified by the fact that 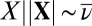 (ref. 50, chap. 2.4), where
(ref. 50, chap. 2.4), where 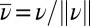 denotes the probability obtained by normalizing the measure ν. We can therefore write:
denotes the probability obtained by normalizing the measure ν. We can therefore write:
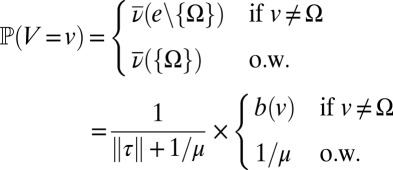 |
Finally, the column probabilities are computed as follows:
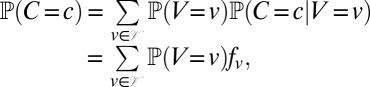 |
where fv is the output of a slight modification of Felsenstein’s peeling recursion (30) applied on the subtree rooted at v (the derivation for fv can be found in SI Appendix, Section 2). Because computing the peeling recursion for one column takes time 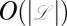 , we get a total running time of
, we get a total running time of 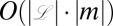 , where
, where 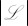 is the number of observed taxa and |m| is the number of columns in the alignment.
is the number of observed taxa and |m| is the number of columns in the alignment.
4. Experiments
We implemented a system based on our model that performs joint Bayesian inference of phylogenies and alignments. We used this system to quantify the relative benefits of joint inference relative to separate inference under the PIP and TKF91 models (i.e., the benefits of inferring trees on accuracy of the inferred MSA and the benefits of inferring MSAs on the accuracy of the inferred tree).
We used synthetic data to assess the quality of the tree reconstructions produced by PIP, compared with the reconstructions of phylogenetic estimation using maximum likelihood (PhyML) 2.4.4, a widely used platform for phylogenetic tree inference (51). We also compared the inferred MSAs with those produced by Clustal 2.0.12 (52), a popular MSA inference system.
Although our implementation evaluated in this section is based on the Bayesian framework, we evaluate it using a frequentist methodology. More precisely, we use Bayes estimators (described in SI Appendix, Section 4) to obtain two point estimates from the posterior: one for the MSA and one for the phylogeny. Each point estimate is compared with the true alignment and tree. It is therefore possible to compare the method with the well-known frequentist methods mentioned above.
In this study, we explored four types of potential improvements: (i) resampling trees and MSAs increasing the quality of inferred MSAs, compared with resampling only MSAs; (ii) resampling trees and MSAs increasing the quality of inferred trees, compared with resampling only trees; (iii) resampling trees increasing the quality of inferred trees, compared with trees inferred by PhyML, and fixing the MSA to the one produced by Clustal; and (iv) resampling MSAs increasing the quality of inferred MSAs, compared with MSAs inferred by Clustal, and fixing the tree to the one produced by PhyML. The results are shown in Table 1. These experiments were based on 100 replicas, with each having seven taxa at the leaves, a topology sampled from the uniform distribution, branch lengths sampled from rate 2 exponential distributions, indels generated from the PIP with parameters η = 100 and ζ = 1, and nucleotides sampled from the Kimura two-parameter model (53).
Table 1.
PIP results on simulated data
| Reconstruction accuracy | ||||
| Tree resampled? | No | Yes | No | Yes |
| MSA resampled? | No | No | Yes | Yes |
| Edge recall (SP) | 0.25 | — | 0.22 | 0.24 |
| Edge Precision | 0.22 | — | 0.56 | 0.58 |
| Edge F1 | 0.23 | — | 0.31 | 0.32 |
| Partition Metric | 0.24 | 0.22 | — | 0.19 |
| Robinson-Foulds | 0.45 | 0.38 | — | 0.33 |
Reconstruction accuracy using five different metrics. The bold font highlights the best-performing combination of resampling for each row.
We measured the quality of MSA reconstructions using the F1 score, defined as the harmonic mean of the reconstructed alignment edge recall [called the sum-of-pairs score or developer’s score in the MSA literature (54)] and alignment edge precision [modeler’s score (55)]. We measured the quality of tree reconstructions using the partition (symmetrical clade difference) metric (56) and the weighted Robinson–Foulds metric (57). Relative improvements were obtained by computing the absolute value of the quality difference (in terms of the F1 for alignments and Robinson–Foulds distance for trees), divided by the initial value of the measure. We report relative improvements averaged over the 100 replicas.
We observed improvements of all four types. Comparing edge F1 relative improvements with Robinson–Foulds relative improvements, the relative additional improvement of type 2 is larger (13%) than that of type 1 (3%). Overall (i.e., comparing the baselines with the joint system), the full improvements of both trees and MSAs are substantial: 43% edge F1 improvement and 27% Robinson–Foulds improvement. A summary of the relative improvements is provided in Fig. 4.
Fig. 4.
Relative improvements for enabling each component of the sampler. Arrows on the left are relative alignment improvements, and arrows on the right are relative tree improvements.
We also tested our system on data generated from the TKF91 model instead of the PIP model. We used the same tree distribution and number of replicas as in the previous experiments and the same generating TKF91 parameters as Holmes and Bruno (2). We again observed improvements over the baseline, both in terms of MSA and tree quality. For MSAs, the relative improvement over the baseline was actually larger on the TKF91-generated data than on the PIP-generated data (47% vs. 43%, as measured by edge F1 improvement over Clustal), and it was lower but still substantial for phylogenetic trees (13% vs. 27%, as measured by Robinson–Foulds improvement over PhyML).
It should be noted that the MCMC kernels used in these experiments (described in the SI Appendix, Section 3) are based on simple Metropolis–Hastings proposals, and can therefore suffer from high rejection rates in large datasets. Fortunately, previous work in the statistical alignment literature has developed sophisticated MCMC kernels, some of which could be applied to inference in our model (e.g., ref. 28). Another potential direction would be to replace the MCMC by a sequential Monte Carlo posterior approximation (58).
It should also be emphasized that point indels are certainly not the exclusive driving force behind sequence evolution. In particular, “long indels” (atomic insertions and deletions of long segments, with a probability higher than the product of their point indels) are also prominent. As a consequence, any system purely based on point indels will have significant biases on biological data. In practice, these biases will introduce three undesirable artifacts: overestimation of the branch lengths; “gappy alignments,” where the reconstructed MSA has many scattered gaps instead of a few long ones; and the related “ragged end” problem, where the prefix and suffix of sequences are poorly aligned because observed sequences are often truncated in practice. In the next section, we propose ways to address these limitations.
5. Discussion
We have presented a string-valued evolutionary model that can be used for joint inference of phylogenies and MSAs. As with its predecessor, the TKF91 model, our model can be used to capture the homology of characters evolving on a phylogenetic tree under insertion, deletion, and substitution events. Its advantage over TKF91 is that it permits a representation as a Poisson process on the tree. This representation has the consequence that the marginal likelihood of a tree and an alignment (marginalizing over ancestral states) can be computed in time linear in the number of taxa rather than exponentially, as in the case of TKF91. Poisson representations have played an important role in pure substitution processes (42, 43, 59), but in this work, we use Poisson representations for indel inference.
Although the insertion process in TKF91 might be argued to be more realistic biologically than that of the PIP model in that it allows the insertion rate to vary as the sequence length varies, in the common setting, in which all the sequences being aligned are of roughly similar lengths, this extra degree of freedom may be of limited value for inference. Indeed, in our experiments, we saw that the PIP model can perform well even when data are generated from the TKF91 model. We might also note that there are biological processes in which insertions originate from a source that is extrinsic to the sequence (e.g., viruses, other genomic regions); in such case, the constant-rate assumption of PIP may actually be preferred.
It is also important to acknowledge, however, that neither TKF91 nor PIP is an accurate representation of biology. Their use in phylogenetic modeling reflects the hope that the statistical inferences they permit, most notably taking into account the effect of indels on the tree topology, will nonetheless be useful as data accrue. This hope is more likely to be realized in larger datasets, motivating our goal of obtaining a method that scales to larger sets of species. However, both models should also be viewed as jumping-off points for further modeling that is more faithful to the biology while retaining the inferential power of the basic models. For example, there has been significant work on extending TKF91 to models that capture the long indels that arise biologically but are not captured by the basic model (7, 60, 61).
In this regard, we wish to note that the Poisson representation of the PIP model provides avenues for extension that are not available within the TKF91 framework. In particular, the superposition property of Poisson processes makes it possible to combine the PIP model with other models that follow a Poisson law. For example, if the location 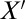 of long indels, slipped-strand mispairing (62), or other nonlocal changes follows a Poisson point process, the union
of long indels, slipped-strand mispairing (62), or other nonlocal changes follows a Poisson point process, the union 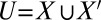 of the nonlocal changes with the point indels X provided by a PIP will also be distributed according to a Poisson process. Moreover, the thinning property of Poisson processes provides a principled approach to inference for such superpositions. Indeed, an MCMC sampler for the superposition model can be constructed as follows. First, we can exploit the decomposition to analytically marginalize X (using the algorithm presented in this paper). Second, the other terms of the superposition and the sequences at these points in time can be represented explicitly as auxiliary variables. Because we have an efficient algorithm for computing the marginal likelihood, the auxiliary variables can be resampled easily. Note that designing an irreducible sampler without marginalizing X would be difficult: Integrating out X creates a bridge of positive probability between any pair of patterns of nonlocal changes.
of the nonlocal changes with the point indels X provided by a PIP will also be distributed according to a Poisson process. Moreover, the thinning property of Poisson processes provides a principled approach to inference for such superpositions. Indeed, an MCMC sampler for the superposition model can be constructed as follows. First, we can exploit the decomposition to analytically marginalize X (using the algorithm presented in this paper). Second, the other terms of the superposition and the sequences at these points in time can be represented explicitly as auxiliary variables. Because we have an efficient algorithm for computing the marginal likelihood, the auxiliary variables can be resampled easily. Note that designing an irreducible sampler without marginalizing X would be difficult: Integrating out X creates a bridge of positive probability between any pair of patterns of nonlocal changes.
Under the parameterization of the process used in this paper, the model assumes both an equal deletion rate for all characters and a uniform probability over inserted characters. It is worth noting that our inference algorithm can be modified to handle models relaxing both assumptions by replacing the calculation of β(v) in SI Appendix, Section 2 by a quasi-stationary distribution calculation (47). It would be interesting to use this idea to investigate what nonuniformities are present in biological indel data.
Finally, another avenue to improve PIP models is to make the insertion rate mean measure more realistic: Instead of being uniform across the tree, it could be modeled using a prior distribution, hence forming a Cox process (63). This would be most useful when the sequences under study have large length or indel intensity variations across sites and branches (64).
Supplementary Material
Acknowledgments
We thank Bastien Boussau, Ian Holmes, Michael Newton, and Marc Suchard for their comments and suggestions. This work was partially supported by a grant from the Office of Naval Research under Contract N00014-11-1-0688, by Grant K22 HG00056 from the National Institutes of Health, and by Grant SciDAC BER KP110201 from the Department of Energy.
Footnotes
The authors declare no conflict of interest.
*More precisely, assume there is a real number 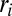 in the interval [0, 1] assigned to each character in the string in increasing order:
in the interval [0, 1] assigned to each character in the string in increasing order: 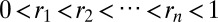 . When an insertion occurs, sample a new real number
. When an insertion occurs, sample a new real number 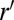 uniformly in the interval [0, 1] and insert the new character at the unique position (with a probability one of 1), such that an increasing sequence of real numbers
uniformly in the interval [0, 1] and insert the new character at the unique position (with a probability one of 1), such that an increasing sequence of real numbers 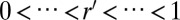 is maintained.
is maintained.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1220450110/-/DCSupplemental.
See Profile on page 1141.
References
- 1.Thorne JL, Kishino H, Felsenstein J. An evolutionary model for maximum likelihood alignment of DNA sequences. J Mol Evol. 1991;33(2):114–124. doi: 10.1007/BF02193625. [DOI] [PubMed] [Google Scholar]
- 2.Holmes I, Bruno WJ. Evolutionary HMMs: A Bayesian approach to multiple alignment. Bioinformatics. 2001;17(9):803–820. doi: 10.1093/bioinformatics/17.9.803. [DOI] [PubMed] [Google Scholar]
- 3.Hein J. An algorithm for statistical alignment of sequences related by a binary tree. Pac Symp Biocomput. 2001;6:179–190. doi: 10.1142/9789814447362_0019. [DOI] [PubMed] [Google Scholar]
- 4.Steel M, Hein J. Applying the Thorne-Kishino-Felsenstein model to sequence evolution on a star-shaped tree. Appl Math Lett. 2001;14(6):679–684. [Google Scholar]
- 5.Metzler D, Fleissner R, Wakolbinger A, von Haeseler A. Assessing variability by joint sampling of alignments and mutation rates. J Mol Evol. 2001;53(6):660–669. doi: 10.1007/s002390010253. [DOI] [PubMed] [Google Scholar]
- 6.Hein J, Jensen JL, Pedersen CN. Recursions for statistical multiple alignment. Proc Natl Acad Sci USA. 2003;100(25):14960–14965. doi: 10.1073/pnas.2036252100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Miklós I, Lunter GA, Holmes I. A “Long Indel” model for evolutionary sequence alignment. Mol Biol Evol. 2004;21(3):529–540. doi: 10.1093/molbev/msh043. [DOI] [PubMed] [Google Scholar]
- 8.Lunter G, Miklós I, Drummond A, Jensen JL, Hein J. Bayesian coestimation of phylogeny and sequence alignment. BMC Bioinformatics. 2005;6:83. doi: 10.1186/1471-2105-6-83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Novák A, Miklós I, Lyngsø R, Hein J. StatAlign: An extendable software package for joint Bayesian estimation of alignments and evolutionary trees. Bioinformatics. 2008;24(20):2403–2404. doi: 10.1093/bioinformatics/btn457. [DOI] [PubMed] [Google Scholar]
- 10.Allison L, Wallace CS, Yee CN. Finite-state models in the alignment of macromolecules. J Mol Evol. 1992;35(1):77–89. doi: 10.1007/BF00160262. [DOI] [PubMed] [Google Scholar]
- 11.Krogh A, Brown M, Mian IS, Sjölander K, Haussler D. Hidden Markov models in computational biology. Applications to protein modeling. J Mol Biol. 1994;235(5):1501–1531. doi: 10.1006/jmbi.1994.1104. [DOI] [PubMed] [Google Scholar]
- 12.Searls DB, Murphy KP. Automata-theoretic models of mutation and alignment. Proc Inf Conf Intell Syst Mol Biol. 1995;3:341–349. [PubMed] [Google Scholar]
- 13.Mohri M. In: Handbook of Weighted Automata, Monographs in Theoretical Computer Science. Droste M, Kuich W, Vogler H, editors. Berlin: Springer; 2009. pp. 213–254. [Google Scholar]
- 14.Song YS. A sufficient condition for reducing recursions in hidden Markov models. Bull Math Biol. 2006;68(2):361–384. doi: 10.1007/s11538-005-9045-9. [DOI] [PubMed] [Google Scholar]
- 15.Dreyer M, Smith JR, Eisner J. Latent-variable modeling of string transductions with finite-state methods. Proceedings of the Conference on Empirical Methods in Natural Language Processing. 2008;13:1080–1089. [Google Scholar]
- 16.Miklós I, Drummond A, Lunter G, Hein J. Algorithms in Bioinformatics. Berlin: Springer; 2003. [Google Scholar]
- 17.Schwartz AS, Pachter L. Multiple alignment by sequence annealing. Bioinformatics. 2007;23(2):e24–e29. doi: 10.1093/bioinformatics/btl311. [DOI] [PubMed] [Google Scholar]
- 18.Westesson O, Lunter G, Paten B, Holmes I. Accurate reconstruction of insertion-deletion histories by statistical phylogenetics. PLoS ONE. 2012;7(4):e34572. doi: 10.1371/journal.pone.0034572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sankoff D. Minimal mutation trees of sequences. SIAM J Appl Math. 1975;28(1):35–42. [Google Scholar]
- 20.Wheeler WC, Gladstein DS. MALIGN: A multiple sequence alignment program. J Hered. 1994;85(5):417–418. [Google Scholar]
- 21.Lancia G, Ravi R. GESTALT: Genomic Steiner alignments. Notes in Computer Science. 1999;1645:101–114. [Google Scholar]
- 22.Varon A, Vinh LS, Wheeler WC. POY version 4: Phylogenetic analysis using dynamic homologies. Cladistics. 2010;26(1):72–85. doi: 10.1111/j.1096-0031.2009.00282.x. [DOI] [PubMed] [Google Scholar]
- 23.Snir S, Pachter L. Tracing the most parsimonious indel history. J Comput Biol. 2011;18(8):967–986. doi: 10.1089/cmb.2010.0325. [DOI] [PubMed] [Google Scholar]
- 24.Löytynoja A, Vilella AJ, Goldman N. Accurate extension of multiple sequence alignments using a phylogeny-aware graph algorithm. Bioinformatics. 2012;28(13):1684–1691. doi: 10.1093/bioinformatics/bts198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hein J. Unified approach to phylogenies and alignments. Methods Enzymol. 1990;183:626–645. doi: 10.1016/0076-6879(90)83041-7. [DOI] [PubMed] [Google Scholar]
- 26.Knudsen B, Miyamoto MM. Sequence alignments and pair hidden Markov models using evolutionary history. J Mol Biol. 2003;333(2):453–460. doi: 10.1016/j.jmb.2003.08.015. [DOI] [PubMed] [Google Scholar]
- 27.Rivas E. Evolutionary models for insertions and deletions in a probabilistic modeling framework. BMC Bioinformatics. 2005;6:63. doi: 10.1186/1471-2105-6-63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Redelings BD, Suchard MA. Joint Bayesian estimation of alignment and phylogeny. Syst Biol. 2005;54(3):401–418. doi: 10.1080/10635150590947041. [DOI] [PubMed] [Google Scholar]
- 29.Redelings BD, Suchard MA. Incorporating indel information into phylogeny estimation for rapidly emerging pathogens. BMC Evol Biol. 2007;7:40. doi: 10.1186/1471-2148-7-40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Felsenstein J. Evolutionary trees from DNA sequences: A maximum likelihood approach. J Mol Evol. 1981;17(6):368–376. doi: 10.1007/BF01734359. [DOI] [PubMed] [Google Scholar]
- 31.Wong KM, Suchard MA, Huelsenbeck JP. Alignment uncertainty and genomic analysis. Science. 2008;319(5862):473–476. doi: 10.1126/science.1151532. [DOI] [PubMed] [Google Scholar]
- 32.Roshan U, Livesay DR, Chikkagoudar S. Improving progressive alignment for phylogeny reconstruction using parsimonious guide-trees. Proc IEEE Int Symp Bioinformatics Bioeng. 2006;6:159–164. [Google Scholar]
- 33.Nelesen S, Liu K, Zhao D, Linder CR, Warnow T. The effect of the guide tree on multiple sequence alignments and subsequent phylogenetic analyses. Pac Symp Biocomput. 2008;13:25–36. doi: 10.1142/9789812776136_0004. [DOI] [PubMed] [Google Scholar]
- 34.Liu K, Raghavan S, Nelesen S, Linder CR, Warnow T. Rapid and accurate large-scale coestimation of sequence alignments and phylogenetic trees. Science. 2009;324(5934):1561–1564. doi: 10.1126/science.1171243. [DOI] [PubMed] [Google Scholar]
- 35.Liu K, et al. SATe-II: Very fast and accurate simultaneous estimation of multiple sequence alignments and phylogenetic trees. Syst Biol. 2012;61(1):90–106. doi: 10.1093/sysbio/syr095. [DOI] [PubMed] [Google Scholar]
- 36.Lunter G, Drummond A, Miklós I, Hein J. In: Statistical Methods in Molecular Evolution, Series in Statistics in Health and Medicine. Nielsen R, editor. New York: Springer; 2004. [Google Scholar]
- 37.Saitou N, Nei M. The neighbor-joining method: A new method for reconstructing phylogenetic trees. Mol Biol Evol. 1987;4(4):406–425. doi: 10.1093/oxfordjournals.molbev.a040454. [DOI] [PubMed] [Google Scholar]
- 38.Roch S. Toward extracting all phylogenetic information from matrices of evolutionary distances. Science. 2010;327(5971):1376–1379. doi: 10.1126/science.1182300. [DOI] [PubMed] [Google Scholar]
- 39.Bradley RK, et al. Fast statistical alignment. PLOS Comput Biol. 2009;5(5):e1000392. doi: 10.1371/journal.pcbi.1000392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Holmes I. A probabilistic model for the evolution of RNA structure. BMC Bioinformatics. 2004;5:166. doi: 10.1186/1471-2105-5-166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Crawford FW, Suchard MA. Transition probabilities for general birth-death processes with applications in ecology, genetics, and evolution. J Math Biol. 2012;65(3):553–580. doi: 10.1007/s00285-011-0471-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Alekseyenko AV, Lee CJ, Suchard MA. Wagner and Dollo: A stochastic duet by composing two parsimonious solos. Syst Biol. 2008;57(5):772–784. doi: 10.1080/10635150802434394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Nicholls G, Gray R. Phylogenetic Methods and the Prehistory Languages. Cambridge, UK: McDonald Institute for Archaeological Research; 2006. pp. 161–172. [Google Scholar]
- 44.Doob JL. Markoff chains: Denumerable case. Trans Am Math Soc. 1945;58(3):455–473. [Google Scholar]
- 45.Gillespie DT. Exact stochastic simulation of coupled chemical reactions. J Phys Chem. 1977;81(25):2340–2361. [Google Scholar]
- 46.Huelsenbeck JP, Nielsen R. Effect of nonindependent substitution on phylogenetic accuracy. Syst Biol. 1999;48(2):317–328. doi: 10.1080/106351599260319. [DOI] [PubMed] [Google Scholar]
- 47.Buiculescu M. Quasi-stationary distributions for continuous-time Markov processes with a denumerable set of states. Revue Roumaine De Mathématiques Pures et Appliqués. 1972;XVII(1):1013–1023. [Google Scholar]
- 48.Zhang J. Protein-length distributions for the three domains of life. Trends Genet. 2000;16(3):107–109. doi: 10.1016/s0168-9525(99)01922-8. [DOI] [PubMed] [Google Scholar]
- 49.Miklós I. Algorithm for statistical alignment of sequences derived from a Poisson sequence length distribution. Discrete Appl Math. 2003;127(1):79–84. [Google Scholar]
- 50.Kingman JFC. Poisson Processes (Oxford Studies in Probabilities, Oxford, UK) 1993. [Google Scholar]
- 51.Guindon S, Gascuel O. A simple, fast, and accurate algorithm to estimate large phylogenies by maximum likelihood. Syst Biol. 2003;52(5):696–704. doi: 10.1080/10635150390235520. [DOI] [PubMed] [Google Scholar]
- 52.Higgins DG, Sharp PM. CLUSTAL: A package for performing multiple sequence alignment on a microcomputer. Gene. 1988;73(1):237–244. doi: 10.1016/0378-1119(88)90330-7. [DOI] [PubMed] [Google Scholar]
- 53.Kimura M. A simple method for estimating evolutionary rates of base substitutions through comparative studies of nucleotide sequences. J Mol Evol. 1980;16(2):111–120. doi: 10.1007/BF01731581. [DOI] [PubMed] [Google Scholar]
- 54.Sauder JM, Arthur JW, Dunbrack RL., Jr Large-scale comparison of protein sequence alignment algorithms with structure alignments. Proteins. 2000;40(1):6–22. doi: 10.1002/(sici)1097-0134(20000701)40:1<6::aid-prot30>3.0.co;2-7. [DOI] [PubMed] [Google Scholar]
- 55.Zachariah MA, Crooks GE, Holbrook SR, Brenner SE. A generalized affine gap model significantly improves protein sequence alignment accuracy. Proteins. 2005;58(2):329–338. doi: 10.1002/prot.20299. [DOI] [PubMed] [Google Scholar]
- 56.Bourque M. 1978. Arbres de Steiner et réseaux dont varie l'emplagement de certains somments. Ph.D. thesis (Université de Montréal, Montreal, QC, Canada)
- 57.Robinson D, Foulds L. Comparison of weighted labelled trees. Lecture Notes in Mathematics. 1979;748:119–126. [Google Scholar]
- 58.Bouchard-Côté A, Sankararaman S, Jordan MI. Phylogenetic inference via sequential Monte Carlo. Syst Biol. 2012;61(4):579–593. doi: 10.1093/sysbio/syr131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Huelsenbeck JP, Larget B, Swofford DL. A compound Poisson process for relaxing the molecular clock. Genetics. 2000;154(4):1879–1892. doi: 10.1093/genetics/154.4.1879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Thorne JL, Kishino H, Felsenstein J. Inching toward reality: An improved likelihood model of sequence evolution. J Mol Evol. 1992;34(1):3–16. doi: 10.1007/BF00163848. [DOI] [PubMed] [Google Scholar]
- 61.Miklós I, Toroczkai Z. An improved model for statistical alignment. Lect Notes Comput Sci. 2001;2149:1–10. [Google Scholar]
- 62.Kelchner SA. The evolution of non-coding chloroplast DNA and its application in plant systematics. Ann Mo Bot Gard. 2000;87(4):482–498. [Google Scholar]
- 63.Cox DR. Some statistical methods connected with series of events. J R Stat Soc Series B Stat Methodol. 1955;17(2):129–164. [Google Scholar]
- 64.Sniret S, Pachter L. Phylogenetic profiling of insertions and deletions in vertebrate genomes. Lect Notes Comput Sci. 2006;3909:265–280. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.