Solvent fluctuations in hydrophobic cavity–ligand binding kinetics

Abstract

Water plays a crucial part in virtually all protein–ligand binding processes in and out of equilibrium. Here, we investigate the role of water in the binding kinetics of a ligand to a prototypical hydrophobic pocket by explicit-water molecular dynamics (MD) simulations and implicit diffusional approaches. The concave pocket in the unbound state exhibits wet/dry hydration oscillations whose magnitude and time scale are significantly amplified by the approaching ligand. In turn, the ligand’s stochastic motion intimately couples to the slow hydration fluctuations, leading to a sixfold-enhanced friction in the vicinity of the pocket entrance. The increased friction considerably decelerates association in the otherwise barrierless system, indicating the importance of molecular-scale hydrodynamic effects in cavity–ligand binding arising due to capillary fluctuations. We derive and analyze the diffusivity profile and show that the mean first passage time distribution from the MD simulation can be accurately reproduced by a standard Brownian dynamics simulation if the appropriate position-dependent friction profile is included. However, long-time decays in the water–ligand (random) force autocorrelation demonstrate violation of the Markovian assumption, challenging standard diffusive approaches for rate prediction. Remarkably, the static friction profile derived from the force correlations strongly resembles the profile derived on the Markovian assumption apart from a simple shift in space, which can be rationalized by a time–space retardation in the ligand’s downhill dynamics toward the pocket. The observed spatiotemporal hydrodynamic coupling may be of biological importance providing the time needed for conformational receptor–ligand adjustments, typical of the induced-fit paradigm.

Molecular recognition and ligand binding are fundamental in various fields of molecular and biological sciences. Water is not just a passive bystander but actively participates in binding events by partially mediating the interactions between the ligand and the receptor site (1, 2). Underlying hydration effects are particularly important in the vicinity of hydrophobic protein patches or in hydrophobic confinement, where dewetting or capillary fluctuation effects significantly contribute to interactions that drive self-assembly and association (3–7).

It has been indeed demonstrated that there is a direct correlation between capillary evaporation and the binding affinity of ligands to hydrophobic protein pockets (8–11). The latter can be empty, filled, or transiently hydrated depending on geometry and local polarity (12–14). Hence, it has been suggested that pockets prone to evaporation represent a general motif for molecular recognition of hydrophobic groups of ligands that are complementary to the pocket geometry and displace unfavorable water molecules (9). Such an expulsion of water from weakly hydrated cavities upon binding was indeed observed in computer simulations of generic hydrophobic pocket–ligand systems (15–18). The hydrophobic association was accompanied with a remarkable enthalpic signature, owing to the highly distorted water network in the pocket (17–20).

Whereas the effect of solvent fluctuations on equilibrium binding affinities has attracted much attention, our knowledge of its influence on binding kinetics and rates is poor, despite its importance for structure-based drug design and the interpretation of kinetic measurements. Theoretically, binding rates are often calculated using implicit approaches, where explicit solvent effects are neglected or only coarsely described (21–24). In the typical view of diffusive encounter of the two reactants, binding kinetics is then governed not only by the free energy (potential of mean force) along the reaction path but also the local diffusivity (or friction) profile (25–29), which, however, is a priori unknown due to missing microscopic insights. In fact, wet/dry hydration fluctuations in the pocket confinement may propagate a new time scale to binding, which can range from a few tens of picoseconds to hundreds of nanoseconds sensitively depending on the size and geometry of the nanocontainer (11, 15, 30–34).

Very recently, Morrone and coworkers demonstrated that solvent fluctuations give rise to important hydrodynamic interactions (HI) in hydrophobic collapse. They investigated the interplay between HI and the free-energy landscape in the pair association kinetics of fullerenes and hydrophobic plates by explicit-water molecular dynamics (MD) simulations and diffusive approaches (35, 36). Local friction was found to increase an order of magnitude due to HI, which slowed the assembly considerably by opposing the overall favorable free energy. However, mean binding times were found to be on the order of the time scale of hydration fluctuations, suggesting a breakdown of the assumption of diffusive (Markovian) behavior (36). A detailed characterization of non-Markovian effects, however, is needed for a better evaluation of the quality of the theoretical tools used for rate prediction. Whether the important findings by Morrone and coworkers are transferable to the biological problem of hydrophobic cavity–ligand binding is still unclear.

In the present paper we investigate whether, and to what magnitude, HI are significant in the molecular association of ligands with hydrophobic pockets. The system is qualitatively different from related previous studies, as it possesses a concave–convex geometry, thus serving as a relevant generic prototype for key–lock-like association events, such as those found for protein–ligand or host–guest systems. To explore the binding kinetics in detail, we calculate the mean first passage time (mfpt) (25) distribution and hydration correlation functions for a ligand binding to a generic model hydrophobic pocket, as shown in Fig. 1, using explicit-water MD simulations. Implicit solvent Brownian dynamics (BD) computer simulations and diffusional Smoluchowski approaches are then used to derive and analyze the spatially dependent friction profiles, predict mfpt distributions, and illuminate non-Markovian effects that are shown to be nonnegligible. Our findings provide useful perspectives for the improvement of theoretical tools for binding rate prediction, or the experimental design of functional ligands, drugs, or synthetic hydrophobic host–guest systems.

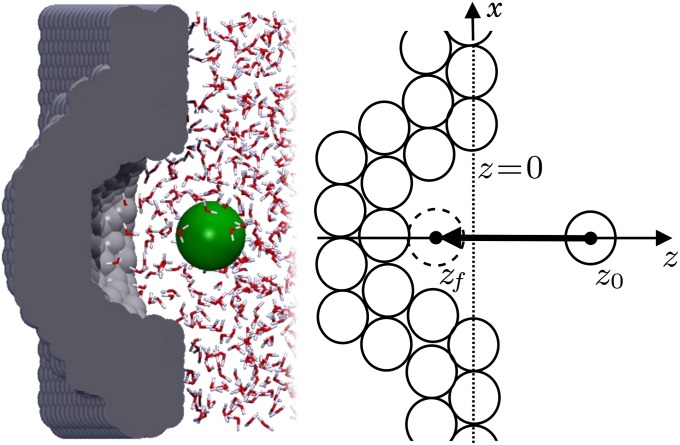
Fig. 1.

Hydrophobic ligand–pocket model. (Left) MD snapshot of pocketed wall and ligand (green sphere) in explicit water. (Right) Coordinate system. A hemispherical, purely nonpolar pocket with a ligand-accessible radius of 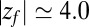Å embedded in a planar wall is in contact with explicit water at normal conditions. The ligand is modeled by a hydrophobic methane sphere and is restrained to the symmetry axis z. In the “umbrella runs” the ligand is additionally constrained to position 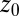by a harmonic potential.

Results and Discussion

Distribution of mfpt for Ligand Binding.

The mfpt defined in this study describes the time scale for binding the ligand as a function of distance from the binding site. The model and coordinate system are illustrated in Fig. 1. The ligand moves one-dimensionally in the z direction, whereas the origin 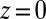is placed right at the pocket mouth. The mfpt distribution 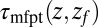for the ligand to start at z and reach the target position deep inside the pocket at 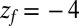Å, calculated from explicit-water MD simulations, is plotted in Fig. 2A up to a maximum distance 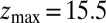Å. The distribution 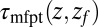monotonically increases from 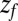to 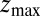because the ligand has to travel farther to the pocket from larger distances. At 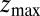we find that it takes the ligand a mean 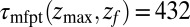ps to bind to the target. For 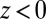the mfpt is vanishingly small, indicating either a very small solvent friction or a highly attractive potential of mean force (pmf), that is, the free energy along z.

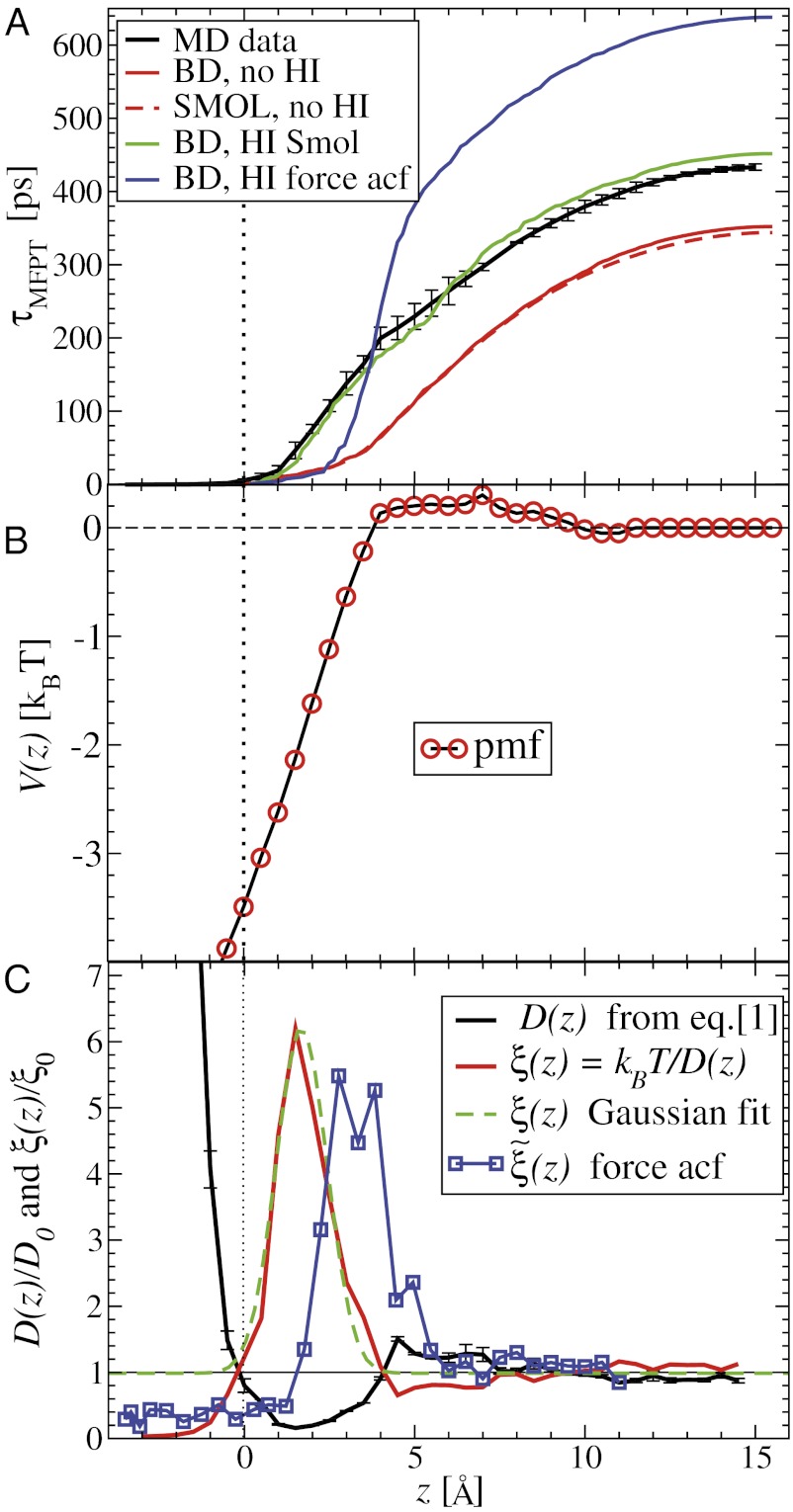
Fig. 2.

(A) Distribution of mfpt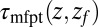 for the ligand to start at z and reach the target 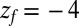Å deep inside the hydrophobic pocket. Results from explicit-water MD simulations (black solid line) are compared with overdamped BD simulations and the Smoluchowski approach (Eq. 1 without HI corrections (no HI, red lines). Also shown are BD results including HI corrections derived from the inversion of the Smoluchowski approach, Eq. 2) (HI Smol, green line) and those from the water–solvent force acf (blue line). (B) Equilibrium pmf 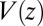. (C) Diffusivity profile 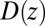from the inversion of the Smoluchowski approach, Eq. 2 (black line), its corresponding friction profile 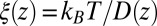(red line), and a Gaussian fit to the latter (green line). Also shown is the friction profile 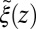calculated from the solvent force acf (blue line) as defined in Eq. 5.

The pmf 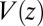along the reaction pathway is plotted in Fig. 2B. Two distinct features are observed: first, a small repulsive barrier of about 0.2 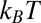between 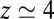and 10 Å; second, a strong linear decay for 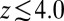with a slope (attractive force) of 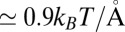. The latter attraction must be attributed to hydrophobic interactions whose interesting thermodynamics was analyzed in detail previously (17).

The question now arises whether the mfpt distribution can be described by a computationally cheap, standard diffusional rate approach, using the ligand’s bulk self-diffusion constant 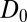and the free-energy landscape 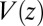as input. According to diffusional passage time theory, the mfpt distribution is given by (25)

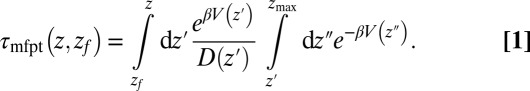We now use 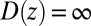for 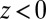to account for the fact that binding is essentially instantaneous once the pocket entrance is passed, and 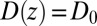for 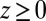. We calculate a bulk self-diffusion constant for the ligand in explicit water of 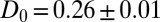Ų/ps. The result for 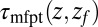is plotted in Fig. 2A, together with the prediction from an overdamped BD simulation using the mean force 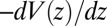and a homogeneous friction constant 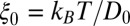. Both diffusional approaches yield equivalent results, whereas the predicted mfpt is too fast by a constant shift 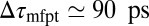compared with the MD results. In the vicinity of the pocket (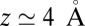) the relative error 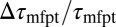is substantial ().

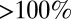Diffusivity Profile Under the Markovian Assumption.

Our results based on the implicit solvent approach were not sufficient to recapitulate the mfpt observed in our MD simulations. This error, we believe, arises due to the models’ assumption of constant diffusivity along the reaction coordinate, which may be inappropriate near the binding site. This failure may be reconciled by introducing a local (z-dependent) diffusivity profile 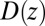or friction profile 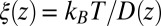. If one assumes the dynamics to be strictly Markovian, Netz and coworkers recently demonstrated that the diffusivity profile D(z) can be obtained from the MD-derived mfpt by differentiating Eq. 1, leading to (28, 29)

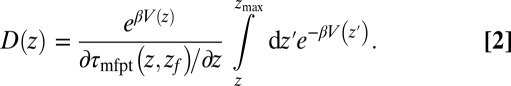The result for 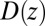, evaluated for the whole range in 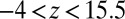Å, is displayed in Fig. 2C. The diffusivity profile is constant and close to 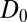for larger distances from the pocket, whereas deviations arise for 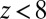Å. Remarkably, for 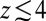Å the diffusivity decreases to a minimum value of 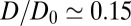at Å, t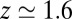hat is, the diffusion is slowed down by a factor of 6 in the vicinity of the pocket entrance. After passing the pocket mouth at 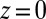the diffusivity significantly increases inside the pocket, pointing to a sharp transition to ballistic motion. The corresponding friction profile 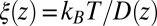is also shown in Fig. 2C and can be fitted to a Gaussian distribution

with the peak at 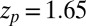Å, 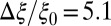, and width 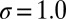Å. The characteristics of the friction profile are qualitatively similar to those calculated between associating fullerenes and hydrophobic plates (35, 36).

By construction, the diffusivity profile 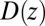derived from Eq. 2 used in Eq. 1 exactly reproduces the MD-derived mfpt distribution in Fig. 2A. The result of the overdamped BD simulation, using the Gaussian-fitted local friction 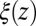in Eq. 3, is also plotted in Fig. 2A and is in very good agreement with the Smoluchowski approach, exemplifying full equivalence of the two implicit methods. Hence, the mfpt distribution is reproducible by a standard BD simulation, provided that the correct friction profile is implemented. The analysis demonstrates that introducing the appropriate diffusivity function 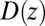could allow a quantitative prediction of the binding kinetics in implicit-solvent applications.

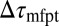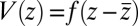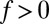To rationalize how the correction is controlled by the shape of the friction profile and the magnitude of the hydrophobic driving force, we can make use of Eq. 1. For this, let us assume that the pmf can be essentially described by a constant force with for 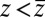, 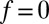otherwise, and we assume that the location of the friction peak 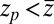. From Eqs. 1 and 3 and setting the target at 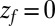, we then obtain for the mfpt shift

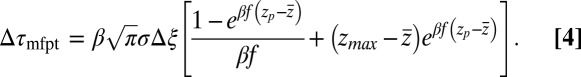For very small forces this expression simplifies to 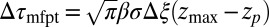. For moderate to high forces and a large attraction range 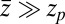, the correction is 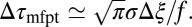Here, we find a correction with a physically sound order of magnitude (40 ps). However, in our system 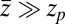is not fully justified; using the full expression Eq. 4 with 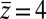Å, we find indeed 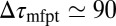ps as found above and displayed in Fig. 2A. Hence, the temporal shift depends not only on magnitude and width of the local friction, but is furthermore inversely proportional to the hydrophobic equilibrium force f. The reflective boundary value plays a role because of the possibility of multiple crossing of the large friction region around 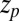and subsequent recurrent reflections at 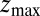. We note that a generalization of Eq. 4 to 3D within the Smoluchowski approach should be feasible, yet it is out of the scope of the current work.

Implicit in our models thus far is the assumption that the system is memoryless; however, the highly dynamic solvent and its possible interplay with the ligand challenge the validity of this Markovian description under these conditions (36). In the following, we investigate more closely the nature of the diffusion kinetics focusing on two questions: What are the governing physical mechanisms behind the locally enhanced friction? Is the ligand kinetics strictly Markovian and describable by standard diffusional methods, i.e., are there simple means to calculate the appropriate diffusivity profile?

Coupling of Ligand Dynamics to Capillary Fluctuations.

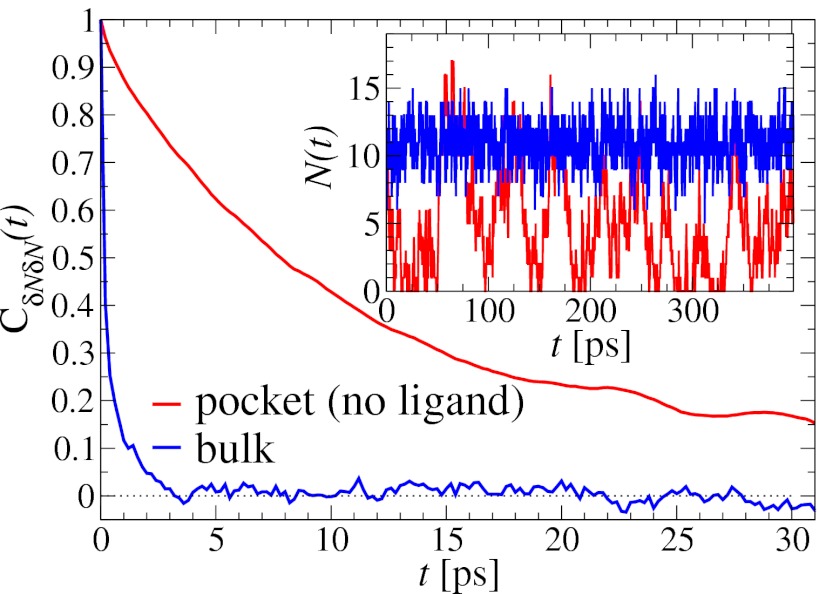
The water occupancy 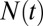within the concave pocket fluctuates between wet and dry states, as shown in the inset to Fig. 3. The physical reason for this bimodal behavior is capillary evaporation with a nucleation barrier between wet and dry states (16, 31). For the latter we find average occupancies 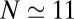and 2, respectively. The mean occupancy fluctuations in the pocket, quantified by a local compressibility 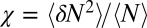, with 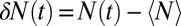, is 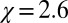, which is 1 order of magnitude larger than compared with the compressibility in the same absolute volume in bulk (compare with Fig. 3 Inset), where 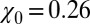. If χ is taken as a hydrophobicity scale, this points to significant hydrophobicity of the concave pocket compared with convex solutes (6). However, more importantly in our kinetic context, the occupancy fluctuations are slower in the pocket than in bulk, as evidenced by the normalized occupancy autocorrelation function (acf), 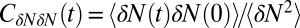(Fig. 3). From single exponential fits we find that the decay time in the pocket is approximately 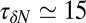ps and thus more than 1 order of magnitude slower than in bulk, where we find 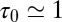ps. The time scale of ≃15 ps compares well with those obtained using a coarse-grained approach to the coupling of ligand dynamics to capillary fluctuations (11).

Fig. 3.

Normalized acf 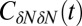of occupancy fluctuations in the pocket with the ligand far away in the bulk (red line) versus the acf of occupancy of bulk water in the same volume (blue line). Pocket fluctuations are 1 order of magnitude slower. (Inset) Pocket occupancy 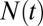versus time t (red) compared with the occupancy of bulk water (blue).

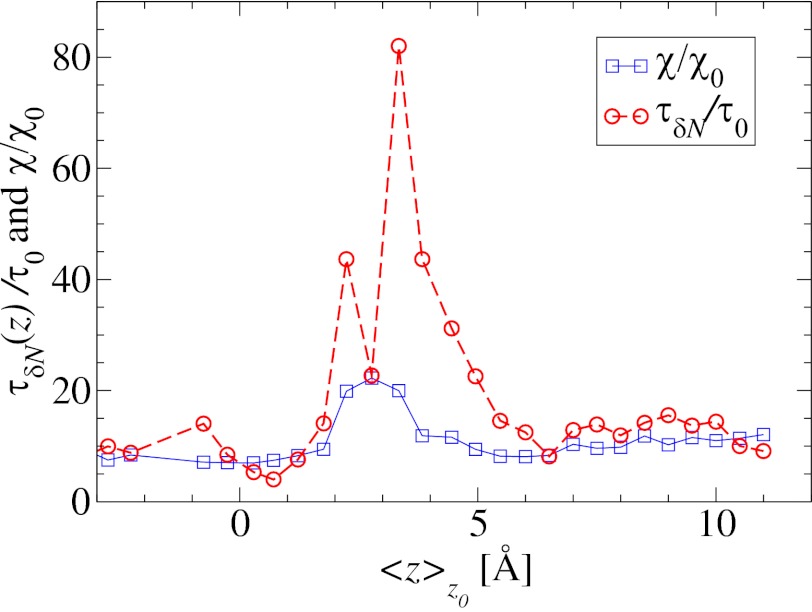
Remarkably, the approaching ligand considerably modifies the fluctuations in the pocket as shown in Fig. 4, where the rescaled fluctuations 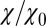and their time scale 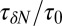are plotted as a function of mean ligand position 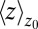(obtained by umbrella sampling at position 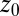; Materials and Methods). For ligand locations close to the pocket in the range 2 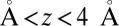, occupancy fluctuations in the pocket are enhanced twofold. More interestingly, in this region the time scale of occupancy fluctuations in the pocket is slowed down manifold with a maximum of 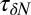at 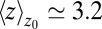Å. Here, the occupancy fluctuations are about 8 times slower compared with when the ligand is in the bulk and thereby 80 times slower than bulk water fluctuations in the same volume. The deceleration of the hydration fluctuations by the ligand very likely has its origin in the increased height of the vapor nucleation barrier at close ligand distances (16). Hydrodynamic deceleration has also been found for an approaching pair of model fullerenes (35).

Fig. 4.

Water occupancy fluctuations inside the pocket 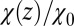(blue squares) versus mean ligand position 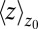and scaled by bulk fluctuations 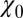. The red circles denote the time scale of the fluctuations 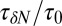with respect to the bulk time scale 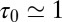ps in the same absolute volume.

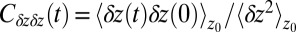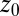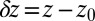In turn, the ligand’s dynamics intimately couples to the local solvent fluctuations as shown in Fig. 5, where we plot the ligand’s normalized position acf, versus the restraining distance , and . Far away from the pocket at 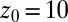Å (that is, bulk-like), the acf decays according to a single exponential with a decay time of about 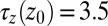ps, comparable to the decay time of bulk water fluctuations. For values smaller than 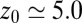Å a second exponential decay occurs, which is about 1 order of magnitude slower than in bulk. The slowest decay overall is found between 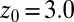and 4.0 Å (corresponding to mean 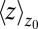values between 2.8 and 3.8 Å). The time scale of about 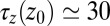ps is comparable to that of the water occupancy fluctuations in the pocket, clearly indicating a direct spatiotemporal coupling between ligand and water dynamics in the vicinity of the binding site. Hence, hydration fluctuations are enhanced by the ligand, in turn leading to a slowing down of the ligand’s positional relaxation time.

Fig. 5.

Normalized position acf 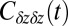of the harmonically restrained ligand for different restraining distances . The decay time is about 15 times slower at 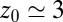Å compared with distances far away from the pocket or close to the pocket mouth.

Memory Effects and Non-Markovian Behavior.

The apparent shortcomings in the Markovian treatment of the system warrant a framework that reflects non-Markovian dynamics. One rigorous route to obtain the diffusivity profile is to calculate the static one-body friction profile 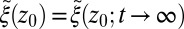by integrating the second fluctuation–dissipation theorem (37)

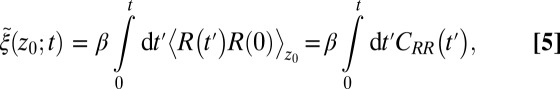in the limit 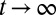. Here, 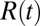is the (random) water force on the restrained ligand only, that is, the constraining force and the equilibrium mean force subtracted from the total force acting on the ligand, whereas the ligand is “clamped” at 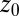(38) (Materials and Methods). By definition 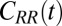represents the memory function in generalized, non-Markovian Langevin approaches to molecular reaction rates (26, 39–43), where the stochastic dynamics are retarded in time:

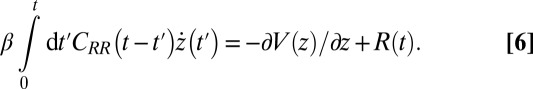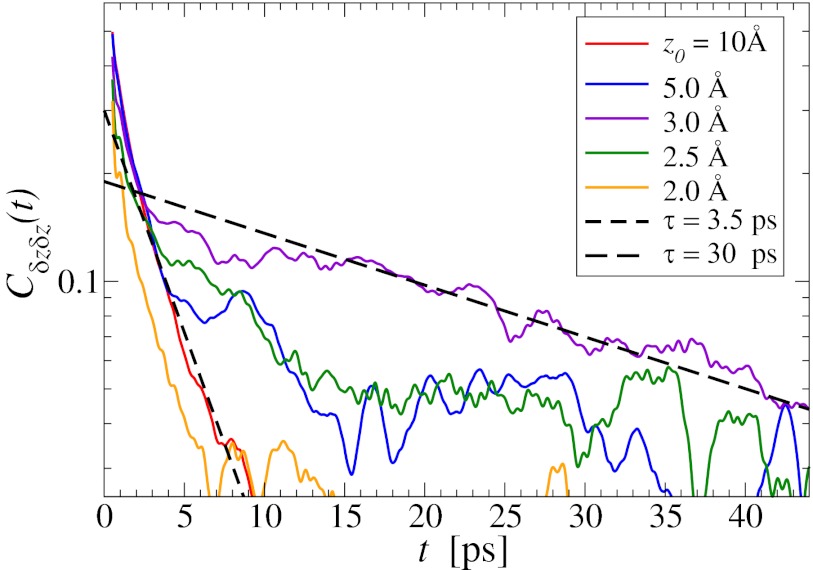
The normalized force acf 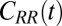is shown in Fig. 6 for selected values of 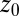. Far away from the pocket (that is, bulk) the force acf is oscillatory on short time scales ( 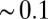ps) and decays quickly (exponentially) in the picosecond range. However, for closer approach of the ligand, a second, much slower decay on the order of tens of picoseconds occurs, as shown in the inset of Fig. 6. The slow decay is most prominent around 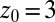and 3.5 Å, where the decay time is 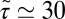ps, consistent with the observed positional fluctuation decay (compare with Fig. 5). This time scale of the random force fluctuations is on the same order of magnitude as the mfpt close to the binding pocket, as well as the characteristic time for the free ligand to diffuse over its Lennard-Jones radius 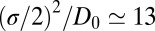ps. This is a clear violation of the Markovian assumption (26, 37, 39).

Fig. 6.

Water–ligand force acf 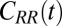for different clamping positions 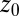. Far away from the pocket ( Å) and at 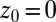the acf decays relatively quickly on a time scale of a few picoseconds. For values around 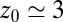Å, where pocket occupancy fluctuations are slow, the force acf decays 1 order of magnitude slower. This behavior is magnified in the Inset.

The static friction 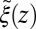(where ) as defined by Eq. 5 is shown in Fig. 2C, together with the profile 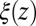obtained from the inversion of Smoluchowski’s diffusive approach, Eq. 2. Strikingly, the profiles are similar in form, magnitude, and width, but are shifted by roughly 1.5–2 Å in space from each other. Input of the profile 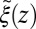into BD simulations yields an mfpt distribution that significantly (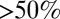) overestimates the MD-calculated mfpt for large z, as shown in Fig. 2A. This can be rationalized by considering Eq. 4, where the distance 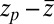between the friction peak at 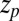and the range of the attractive force 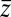quantifies the change in mfpt. We also used an alternative method for calculating the static friction profile 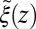based on the position fluctuation time scale and variance under harmonic constraints (29) which corroborates the observed spatial shift of the location of maximum friction (SI Text and Fig. S1).

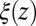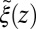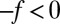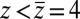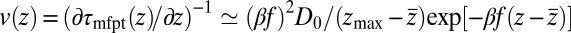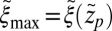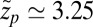The shift between the static friction profiles and along the space coordinate z can be qualitatively understood by the following arguments. Without HI and assuming a constant mean force for Å, the mfpt distribution from Eq. 1 approximately yields an effective net reaction velocity toward the sink of . Evaluated at the location of maximum friction with Å, we find 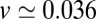Å/ps. Due to the memory effect as expressed in Eq. 6, the ligand feels the friction later, not only in time but in space as well, as it has traveled a mean distance 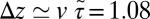Å, where we used the decay time of the force acf 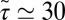ps. Thus, the retardation in time in the process of the “downhill dynamics” to the pocket as a consequence yields a retardation in space, effectively expressed by a spatial shift of the profile 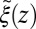versus 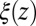, compare with Fig. 2C.

These qualitative arguments may benefit from a quantitative understanding provided in the realm of non-Markovian stochastic approaches to molecular reactions (26, 40–43). The simple shift between 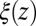and 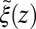points out the possibility of introducing an analytical mapping of the non-Markovian dynamics to a Markovian description for practical applications. In fact, we find that due to the observed separation of time scales, the force acf can be well described by the sum of a position-independent short- and a position-dependent exponential long-time part, viz., 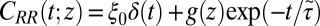, where the spatial dependence is exclusively expressed by 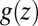. In this case of an exponential memory, time- and position-dependent generalizations of Eq. 6 can indeed be mapped onto Markovian descriptions by introducing an auxiliary variable with an equivalent Fokker–Planck description (44). The coupling of hydration fluctuations and ligand dynamics suggests that the auxiliary variable may be related to the water occupancy in the binding pocket, and a 2D theory could account for the non-Markovian effects, in which translational motion and hydration fluctuations are treated as coupled diffusion processes. Because the solvent fluctuations show relatively sharp transitions between dry and wet (compare with Fig. 3), one could imagine an even simpler description by two-state models, such as stochastic gating models (45, 46), wherein fluctuations might be considered to represent closed and open states of a “solvent gate” with a Markovian rate.

Conclusions

Theoretical and computational ligand binding rate prediction often employs standard diffusive approaches with either no or very approximative treatment of HI. Our study shows that cavity hydration and ligand dynamics are inherently coupled, and the inclusion of the resulting position-dependent friction profile in diffusive approaches is essential for the accurate prediction of binding rates, especially in the systems undergoing a drying transition upon binding. However, that ligand binding kinetics described by a single reaction coordinate is simply Markovian is probably exceptional. Our work demonstrates that, in general, the protein–ligand-hydration dynamics needs to be properly described by approaches similar to Markovian stochastic gating models with a dynamical coupling of variables (45, 46). Future studies shall illuminate whether such a mapping of the system investigated here onto Markovian descriptions exists.

The hydration fluctuation time scale sensitively depends on hydrophobic confinement geometry and specific physicochemical interactions (30–34), and so will the local hydrodynamic coupling to an approaching reaction partner. In contrast, hydration fluctuations may be suppressed in polar pockets (6, 18). Thus, solvent fluctuations may help biomolecules tune their association kinetics and function (7), and solvent configurational ensembles play a more important role than believed so far (2). The observed hydrodynamic coupling and deceleration close to hydrophobic binding sites may be of biological importance to allow for time for conformational receptor–ligand adjustments, such as induced fit. We hope this study will contribute to the establishment of new perspectives for the development of theory and computational tools for molecular recognition and ligand binding.

Materials and Methods

Explicit-Water MD Simulations.

The system simulated in this study is identical to one investigated previously (17, 18). Briefly, it represents a spherical ligand––a united atom methane molecule with OPLS Lennard-Jones (LJ) parameters ε =0.50 k_BT and σ=3.730 Å (47), and a hemispherical pocket of ≃ 8 Å radius embedded in a paraffin-like wall of lateral dimensions 35 × 35 Å (Fig. 1). The wall is composed of LJ particles (ε =9.67 × 10⁻⁴k_BT and σ = 4.152 Å) aligned in a hexagonal close-packed arrangement with a lattice constant of 1.25 Å. The system comprises two identical walls, mirrored along the z axis, with the space between them filled by 1,030 TIP4P water molecules (48). The separation between wall surfaces, 31 Å, is tuned to reproduce bulk water density at T = 298 K and P = 1 bar (998 g/l) at the center of the water box. MD simulations are carried out in the NVT ensemble with a time step of 2 fs and Nosé–Hoover thermostat (49), using the CHARMM package (50). 3D particle mesh Ewald summation is used for electrostatic interactions, with box length along the z axis increased to 100 Å to minimize water–water interaction through the walls, and a vanishing LJ potential at the cutoff distance (12 Å).

The pmf calculations are carried out with the use of umbrella sampling as detailed previously (17, 18). Briefly, a harmonic biasing potential with a spring constant k = 3.37 k_BT/Ų is applied in a series of windows extending from z = −4 Å to z = 11 Å, with 0.5 Å increments, and an additional harmonic potential with a spring constant of 168.63 k_BT is used to keep the ligand at the z axis. Each umbrella window is sampled for 2 ns preceded with 100 ps of equilibration. For each umbrella potential window the random force 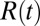time series are estimated based on second numerical derivative of ligand positions, corrected by restraining and pmf forces, respectively:

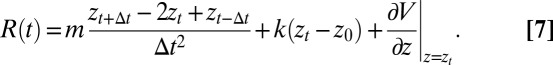Here, m is a ligand mass, 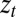is a ligand position at time t, 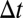is a simulation time step, 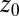and k are umbrella potential center and spring constant, respectively.

Statistics for mfpt are obtained based on a series of new, independent 452 MD runs for the system set up as above, with the exception of the removed biasing umbrella potential acting at the z direction. Each run is started with random initial atomic velocities. After 100 ps of equilibration, the ligand is released at the center of the water box, 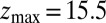Å, and is allowed to move freely along the z axis until it reaches 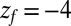Å, at the bottom of either one of the antisymmetric pockets, which is equivalent to one pocket and a reflective boundary at 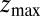. The time to first reach any given distance from 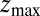is averaged over all runs and then transformed to 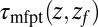––the time to reach 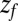while starting from z.

A bulk self-diffusion constant for the ligand, 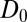, is estimated using the same set of 452 simulations by the standard diffusion relation (Einstein formula), 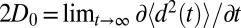, where 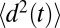is a mean-squared displacement of the ligand along the z axis in time t. Here, the slope of a linear fit to 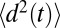is considered for t up to 9.5 ps, ensuring that in none of the simulations does the ligand reach 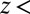6 Å, that is, the region where diversion from the free-diffusion regime is expected.

Implicit-Solvent BD Simulations.

In the BD simulations the overdamped Langevin equation including local friction is solved (21, 51), given by

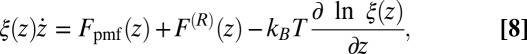where 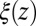is the local friction profile, 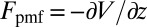is the pocket–ligand mean force, and 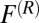is the random force. The latter is assumed to have zero mean 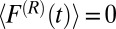and obeys the fluctuation–dissipation theorem via 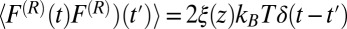. The last term in 8 is needed to compensate for the flux from the local random force (51). The stochastic implicit solvent simulations are performed using a strictly one-dimensional geometry which mimics the symmetric MD setup described above. 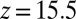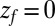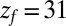The ligand is a point particle starting at Å and is diffusing along the z direction governed by 8 until it reaches the final target position at or Å. The mfpt 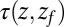it takes to diffuse from a position z to is computed by averaging over 1,000 independent runs. The BD equation is numerically solved as proposed by Ermak and McCammon (21).

Smoluchowski Approach.

In the strictly Markovian Smoluchowski approach we assume that the stochastic evolution of the ligand kinetics is governed by the one-dimensional Fokker–Planck equation (25, 39)

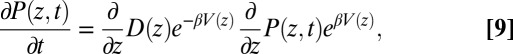where 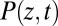is the probability of finding the particle at position z at time t, 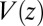is the pmf, and 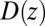is the local diffusion constant, i.e., the diffusivity profile along z. Assuming a steady-state situation, a reflective boundary at 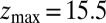Å, and adsorbing boundary conditions at 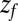, the analytical solution for the mfpt distribution is given by Eq. 1; e.g., ref. 25. The latter can be easily integrated numerically for given arbitrary 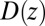and 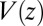. We make the assumption that the Einstein relation holds, i.e., the fluctuation–dissipation equality 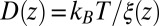. With that assumption, the Langevin approach (Eq. 8) and the Smoluchowski approach (Eq. 9) are equivalent (51).