Synapses with short-term plasticity are optimal estimators of presynaptic membrane potentials

Abstract

The trajectory of the somatic membrane potential of a cortical neuron exactly reflects the computations performed on its afferent inputs. However, the spikes of such a neuron are a very low-dimensional and discrete projection of this continually evolving signal. We explored the possibility that the neuron’s efferent synapses perform the critical computational step of estimating the membrane potential trajectory from the spikes. We found that short-term changes in synaptic efficacy can be interpreted as implementing an optimal estimator of this trajectory. Short-term depression arose when presynaptic spiking was sufficiently intense as to reduce the uncertainty associated with the estimate; short-term facilitation reflected structural features of the statistics of the presynaptic neuron such as up and down states. Our analysis provides a unifying account of a powerful, but puzzling, form of plasticity.

Synaptic efficacies can increase (facilitate) or decrease (depress) several-fold in strength on the time scale of single interspike intervals^1-3. This short-term plasticity (STP), which is well captured by simple, but powerful, mechanistic models^1,3,4, is of a regularity and magnitude that argues against it being treated only as wanton variability⁵. There have thus been various suggestions for the function of STP, including low, high or band-pass filtering of inputs^3,6 (but see ref. 7), rendering postsynaptic responses insensitive to the absolute intensity of presynaptic activity^8,9 decorrelating input spike sequences¹⁰, and maintaining working memories in the prefrontal cortex¹¹.

However, despite the ubiquity of STP in cortical circuits², these suggestions are restricted to select neural subsystems^9,11 or forms of STP^5,8-10 and are often limited to feedforward networks^8-10 or to a firing rate–based description of presynaptic activities⁸, thereby ignoring the fundamentally fast fluctuations in synaptic efficacies as a result of STP. Worse, the vast bulk of models of neural circuit information processing require synaptic efficacies to be constant over the short term of a single computation, changing at most very slowly to average across the statistics of input or changing only in the light of a gating mechanism^12,13. These would seem to be incompatible with substantial STP. Here, we argue that, far from hindering such circuit computations, STP is in fact a near-optimal solution to a central problem neural circuits face that is associated with spike-based communication.

Although, as digital quantities, spikes have the mechanistic advantage of allowing regenerative error correction, they are a substantially impoverished representation of the fast-evolving, analog membrane potentials of the neurons concerned^14-16. These analog quantities are normally considered to lie at the heart of computations,^17,18 and it is common to appeal to averages over space (that is, multiple identical neurons) and/or time (that is, slow currents) to allow them to be represented by spike trains¹⁸. However, both sorts of averages are neurobiologically questionable. In many circumstances, computations need to be executed in the matter of a few interspike intervals^19-21, precluding extensive averaging over time; and, in many circuits, neurons represent independent analog quantities, as in recurrent network models of autoassociative memories^22,23, or partially independent quantities, as in surface attractor models of population codes²⁴. We make the alternative suggestion that the analog membrane potential of a neuron is being estimated in a statistically appropriate manner by its efferent synapses on the basis of the spike trains that the neuron emits and that STP is a signature of this solution.

In particular, the informativeness of an incoming spike about the membrane potential varies greatly depending on the uncertainty left by the preceding spike train. This makes the spike’s effect very context dependent. We found that important elements of this context dependency are realized by synaptic depression and facilitation. Furthermore, as incoming spikes are sparse, the behavior of the optimal estimator critically depends on prior assumptions about presynaptic membrane potential dynamics. Thus, our approach allowed us to make detailed predictions about how the properties of STP, implementing the optimal estimator, should be matched to the statistics of presynaptic membrane potential fluctuations.

RESULTS

Postsynaptic potentials and the optimal estimator

We first defined the optimal estimator of the continuously varying membrane potential u of a presynaptic cell from its past spikes. We found that it depends on these spikes in the same way as a particular measure of its efferent synapses’ contributions to their postsynaptic membrane potentials. Because spikes are discrete, they cannot support recovery of u with absolute certainty and the full solution to the estimation task is a posterior probability distribution^20,25-29 P(u_t | s_0:t) over the possible values that the presynaptic membrane potential at time t, u_t, might take on the basis of all of the spikes observed so far, s_0:t. The mean of this posterior is then the estimator ${\widehat{u}}_t$ that minimizes the squared error²⁵. We interpret the local postsynaptic potential at an excitatory synapse v_t as representing this optimal estimate. This local potential is loosely defined as the sum of all excitatory postsynaptic potentials (EPSPs) at this synapse (Supplementary Note and Supplementary Fig. 1); a filtered version of it is recorded in standard experiments into STP.

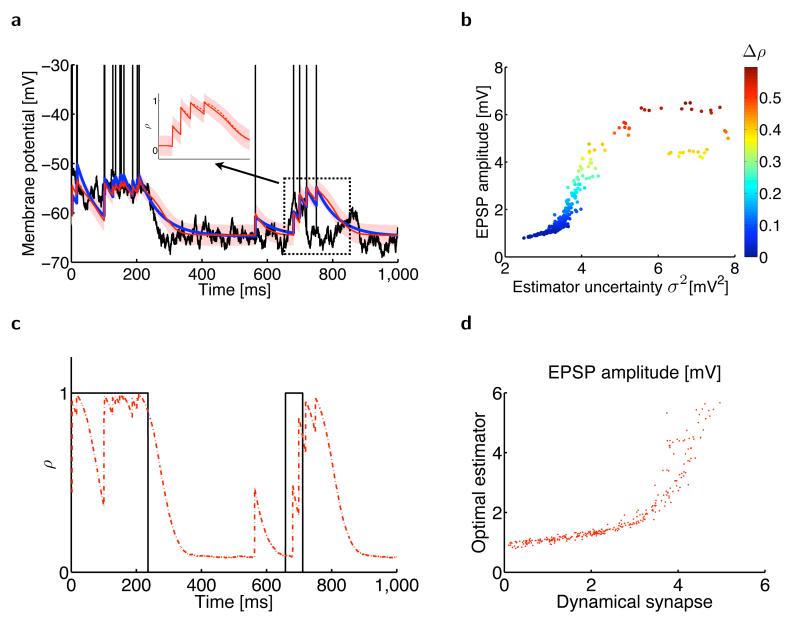
To be correct, the estimator must implicitly incorporate a statistically appropriate model of membrane potential fluctuations and spike generation in the presynaptic neuron²⁵. For the latter, we adopted the common characterization that a spike is created stochastically whenever u_t exceeds a (soft) threshold^30,31 (Fig. 1 and Supplementary Fig. 2). In this case, the occurrence of a spike implies that the membrane potential is likely to be high and the absence of spikes implies that the membrane potential is likely to be low. Thus, ${\widehat{u}}_t$ should increase following a spike and decrease during interspike intervals (Fig. 1a and Online Methods). The decrease should be gradual, as the firing rate of a neuron is limited even at high membrane potential values, and thus the absence of a spike is relatively weak evidence that the membrane potential is low. As required by our interpretation, the local postsynaptic potential, v_t, at an excitatory synapse shows the same qualitative characteristics: it increases suddenly at the times of presynaptic spikes and decayes gradually toward a lower baseline between transmission events (Fig. 1a).

Figure 1.

Estimating the presynaptic membrane potential from spiking information. (a) Sample trace (black) of the presynaptic membrane potential generated by an Ornstein-Uhlenbeck process. When the membrane potential exceeds a soft threshold, action potentials (vertical black lines) are generated. The optimal estimator of the presynaptic membrane potential (red line, mean estimate ${\widehat{u}}_t$; red shading, one s.d. σ_t) closely matches an optimally tuned canonical model of short-term plasticity¹¹ (blue). Inset shows a magnified section. (b) EPSP amplitude of the optimal estimator (red, mean ± s.d.) and of the canonical model of short-term plasticity (blue, mean ± s.d.) as a function of the estimator uncertainty σ². Note that EPSP amplitudes in the biophysical model tend to be smaller than those in the optimal estimator, which is compensating for a somewhat slower decay in the biophysical model (see inset in a). (c) The dynamics of the scaled uncertainty ${\sigma }^2∕{\sigma }_{\max }^2$ (red) closely match the resource variable x_t of the canonical model of STP (blue), σ².

However, this observation is only approximate. As we have mentioned, under STP, the actual size of an EPSP depends on the past history of spiking. Such history dependence is also a hallmark of optimal estimation, as the evidence supplied by a spike needs to be evaluated in the context of the current state of the estimator, that is, the current posterior²⁵. The posterior is computed on-line in a recursive manner, according to standard Bayesian filtering. In this, likelihood information from the current presence or absence of a spike, s_t, P(s_t | u_t), is combined with the posterior computed in the previous time step, P(u_t–δt | s_0:t–δt) (Online Methods):

$$\mathrm{P}(u_t\mid s_{0:t})\propto \mathrm{P}(s_t\mid u_t){\int }_{-\infty }^{\infty }\mathrm{P}(u_t\mid u_{t-\delta t})\mathrm{P}(u_{t-\delta t}\mid s_{0:t-\delta t})d{u}_{t-\delta t}$$ (1)

Thus, the effect of an incoming spike on the mean of the posterior, ${\widehat{u}}_t$, will be context dependent and vary as a function of the posterior propagated from the past.

The precise nature of the context dependence of the changes in ${\widehat{u}}_t$ will depend on the particular statistical model assumed for the dynamics of u_t, P(u_t | u_t–δt ). Below, we consider two increasingly complex models: one in which u_t performs a random walk around a fixed ‘resting’ (or baseline) membrane potential, u^rest (Fig. 1), and one in which $u_t^{\text{rest}}$ itself also changes in time (Fig. 2). This allowed us to explore two fundamental factors contributing to the context dependence of ${\widehat{u}}_t$ that correspond to the effects of synaptic depression and facilitation on v_t.

Figure 2.

Estimating the presynaptic membrane potential when the resting membrane potential randomly switches between two different values. (a) Presynaptic subthreshold membrane potential with action potentials (black), its optimal mean estimate ($\widehat{u}$, red line) with the associated s.d. (σ, red shading), and the postsynaptic membrane potential in a model synapse¹¹ with optimally tuned short-term plasticity (blue line). Inset, the (scaled) optimal estimator (red solid line) strongly depends on the estimated probability ρ of being in the up state (red dashed line). (b) EPSP amplitude in the optimal estimator depends on its uncertainty (horizontal axis, σ²) and the change in the estimated probability that the presynaptic cell is in its up state (color code, Δρ). (c) The estimated probability that the presynaptic cell is in its up state ρ (red) tracks the state of the presynaptic neuron (black) as it randomly switches between its up and down states. (d) EPSP magnitudes in the optimal estimator against EPSP magnitudes in the model synapse.

Synaptic depression and uncertainty

After eliminating the influence of spikes themselves, the simplest approximation to the statistics of the membrane potential u_t of the presynaptic neuron is as an Ornstein-Uhlenbeck process^32,33. For this, the total input to the presynaptic cell is assumed to be Gaussian white noise³³ and is subject to leaky integration, decaying toward its resting value, u^rest (Fig. 1a and Supplementary Fig. 2; Online Methods). In this case, the posterior distribution P(u_t | s_0:t) can be well characterized as a Gaussian with mean ${\widehat{u}}_t$ and variance ${\sigma }_t^2$, which expresses the estimator’s current uncertainty about ${\widehat{u}}_t$. Given the assumption about the way it is generated, observation of a spike provides evidence that u_t is high. However, the quantitative effect on raising ${\widehat{u}}_t$ depends on the uncertainty σ_t. The less the uncertainty, that is, the better known is u_t, the less the estimate should be influenced by a spike (Fig. 1b) and the lower the synapse’s apparent efficacy. The uncertainty is determined by the evidence from past spikes and we should therefore expect the magnitude of the EPSPs to fluctuate according to this history.

Uncertainty in the optimal estimate increases during interspike intervals (Fig. 1c), as the absence of a spike is only weak evidence for a low membrane potential. Therefore, spikes that arrive after a longer period of silence should increase ${\widehat{u}}_t$ by more than spikes arriving in quick succession. This closely resembles, all the way down to fine quantitative details, the effect of synaptic depression in a biophysically motivated canonical STP model^5,34 (Fig. 1). In such a model, depression is mediated by the depletion of a synaptic resource variable x_t, which behaves as the biophysical analog of estimator uncertainty, ${\sigma }_t^2$.

In fact, for a paired-pulse protocol, the dynamical equations describing the time evolution of the optimal estimator and its uncertainty, ${\widehat{u}}_t$ and ${\sigma }_t^2$, are formally equivalent to those of the biophysical STP model describing the time evolution of the postsynaptic membrane potential and synaptic resource variable, v_t and x_t, respectively (Online Methods). As a result, higher presynaptic firing rates lead to diminishing postsynaptic responses in both the optimal estimator and the STP model (Fig. 3a).

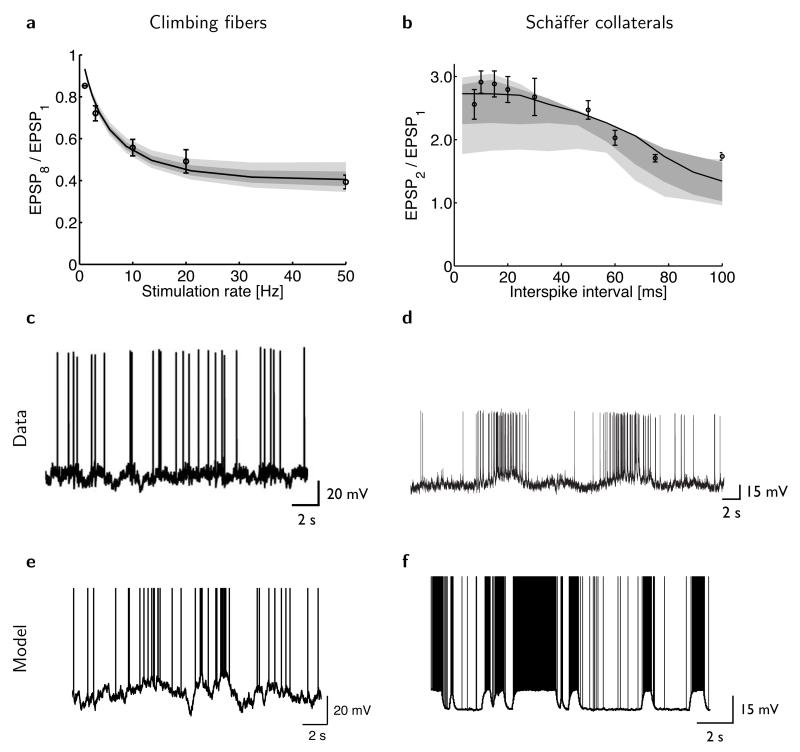
Figure 3.

The optimal estimator reproduces experimentally observed patterns of synaptic depression and facilitation. (a) Synaptic depression in cerebellar climbing fibers (circles: mean ± s.e.m.; redrawn from ref. 6) and in the model (solid line), measured as the ratio of the amplitude of the eighth and first EPSP as a function of the stimulation rate during a train of eight presynaptic spikes. (b) Synaptic facilitation in hippocampal Schäffer collaterals (circles, mean ± s.e.m.; redrawn from ref. 39) and in the model (solid line), measured as the ratio of the amplitude of the second and first EPSP as a function of the interval between a pair of presynaptic spikes. Shading in a and b shows the robustness of the fits (Online Methods): model predictions when best-fit parameters are perturbed by 5% (dark gray) or 10% (light gray). (c–d) Predictions of the model for the dynamics of inferior olive neurons (c) and hippocampal pyramidal neurons (d). Sample traces were generated with parameters fitted to the data about STP in cerebellar climbing fibers (shown in a) and Schäffer collaterals (shown in b). (e–f) In vivo intracellular recordings from inferior olive neurons of the (anesthetized) rat (e, reproduced from ref. 40) and hippocampal pyramidal cells of the behaving rat (f, reproduced from ref. 38).

Synaptic facilitation and ‘up’ state probability

The assumption that the presynaptic membrane potential follows an Ornstein-Uhlenbeck process is often too simplistic³⁵. Fortunately, it is straightforward in our framework to incorporate other statistical properties of membrane potential fluctuations and to study their effects on the features of STP. For example, many cortical cells show phasic activation patterns in which their membrane potential alternates between a resting and a depolarized state, such as ‘up’ and ‘down’ states in the cortex^36,37, or out-of-place field and within-place field activity for hippocampal place cells³⁸. This can be captured by extending the model for the dynamics of u_t to allow the resting membrane potential $u_t^{\text{rest}}$ to switch between two possible values, corresponding to an up and a down state (Fig. 2, Supplementary Note and Supplementary Fig. 2).

In this extended model, the true current value of $u_t^{\text{rest}}$ is unknown to the postsynaptic cell, as with u_t. Thus, the full solution to the estimation problem is a posterior distribution expressing joint uncertainty about these two quantities (Supplementary Note). In this case, the estimated probability that $u_t^{\text{rest}}$ is in its up state also reflects recent spikes and influences ${\widehat{u}}_t$ (ρ_t; Fig. 2a–c). Observing a spike when the current estimate of the membrane potential is compatible with the presynaptic neuron being in its down state increases this probability somewhat. Observing a second spike in a short time window, providing substantial extra evidence for this up state, will thus cause a larger increment in ${\widehat{u}}_t$ (Fig. 2a). EPSPs in the facilitating biophysical STP model and in actual facilitating synapses in a paired-pulse protocol³⁹ (Figs. 2d and 3b) showed the same effect.

Match between STP and the dynamics of the presynaptic cell

Our theory requires the synaptic estimator to be matched to the statistical properties of the presynaptic membrane potential fluctuations that it needs to estimate. Thus, fitting the optimal estimator to experimentally measured STP data (Fig. 3a,b) allowed us to predict, without further parameter fitting, properties of the membrane potential dynamics that the corresponding presynaptic cell type should exhibit. Testing these predictions is challenging because they are about the natural statistics of membrane potential fluctuations and thus require in vivo intracellular recordings, preferably from behaving rather than anaesthetized animals.

Nevertheless, starting from our fits to data about synaptic depression and facilitation for cerebellar climbing fibers (Fig. 3a) and hippocampal Schäffer collateral inputs (Fig. 3b), we predicted membrane potential fluctuations in inferior olive neurons (Fig. 3c) and hippocampal pyramidal cells (Fig. 3d) respectively, that were in broad qualitative agreement with those found in vivo in these cell types^38,40 (Fig. 3e,f). Note that the absence and presence of marked up and down states in these two cell types, respectively, is predicted by our theory directly from the absence and presence of facilitation in their corresponding efferent synapses.

The advantage of STP

To quantify the advantage that STP brings to synapses for tracking the presynaptic membrane potential, we measured how well ${\widehat{u}}_t$ or its biophysical analog v_t performed on the estimation task in terms of the time-averaged squared error between u_t and its estimate (Online Methods). We compared the optimal estimator of the presynaptic membrane potential (Fig. 4a) with the postsynaptic membrane potential occasioned by a synapse undergoing STP. These two traces were very close. Notably, a static synapse without STP, whose fixed efficacy is still optimized for the same estimation task, performed substantially less well.

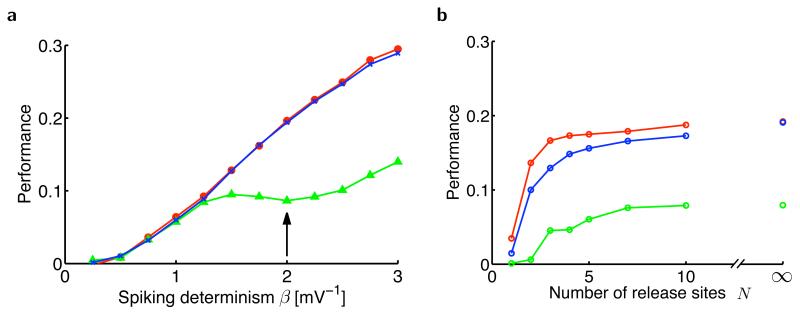
Figure 4.

Estimation performance of the presynaptic membrane potential. (a) Performance as a function of the determinism of presynaptic spiking, β (Online Methods), in the optimal estimator (red), an optimally fitted dynamic synapse (blue) and an optimally fitted static synapse without short-term plasticity (green). When β = 0 (entirely stochastic spiking), spikes are generated independently of the membrane potential and, as a consequence, all models fail to track the membrane potential. As β becomes larger (more deterministic spiking), the dynamic synapse model matches the optimal estimator in performance and substantially outperforms the static synapse. Realistic values for βσ_OU (here σ_OU = 1 mV) have been found to be between 2 and 3 in L5 pyramidal cells of somatosensory cortex⁴⁹. (b) Estimation performance with stochastic vesicle release as a function of the number of synaptic release sites, N. The dynamic synapse (blue) tracked the performance of the optimal estimator (red) well and outperformed the static synapse (green) at all values of N. The performance of all estimators decreases only when the number of independent release sites becomes very low (N = 1 or 2 ). When N is large (N → ∞), synaptic transmission becomes deterministic, even though spike generation itself remains stochastic (with parameter β = 2 shown by the arrow in a).

Our account of synaptic dynamics assumes no transmission failure or, equivalently, a large number of release sites between the pre- and postsynaptic cells. Therefore, we also ran simulations with stochastic synapses⁴ (Online Methods) to test a more realistic regime of synaptic communication (Fig. 4b). The advantage of a dynamic over a static synapse was maintained when the number of release sites was low, even in the face of transmission failures and the added variability of the dynamic synapse entailed by the stochastic restocking of vesicles.

DISCUSSION

We found that STP arranges for the local postsynaptic membrane potential at a synapse, v_t, to behave as an optimal estimator of the presynaptic membrane potential u_t. We argue that this is central for a wide swathe of feedforward and recurrent neural circuits. In particular, it allows network computations based on analog quantities encoded in the somatic membrane potentials of neurons to be realized, even though their spikes offer only a low-dimensional and discrete projection of those potentials.

As a first step, we concentrated on the interaction between a pair of cells and on reproducing as close an estimate as possible to the exact presynaptic membrane potential on the postsynaptic side. Of course, v_t can be changed by many factors other than synaptic currents, such as voltage signals propagating from other dendritic compartments or backpropagating action potentials from the soma. However, under most experimental procedures that have been used to test STP^41,42, the magnitudes of these other factors are minimized, such that the somatic membrane potential recorded reflects, perhaps with some dendritic filtering, the local EPSPs at the stimulated synapse. This allows our theory to be directly applied to data obtained under such conditions (Supplementary Note).

A substantial apparent challenge to our theory, as indeed to many previous functional accounts of STP^8-11, is that different efferent synapses of the same cell can express different forms of STP¹. Two particular classes of factors that can affect v_t may account for this. Both factors have to do with the overall computation performed by the neuron in the network, which need not strictly factorize into individual estimation of each presynaptic membrane potential and combination of these across multiple synapses (Supplementary Fig. 1).

First, computations might be based on estimates of different functions of the presynaptic membrane potentials rather than just their mean value; for example, their rates of change or higher order temporal derivatives. In this case, the different efferent synapses of a single neuron might estimate different functions and therefore be different. It will be an interesting extension of our theory to study how synaptic estimation and single-neuron computation can be blended, rather than being performed as separate algorithmic steps.

Second, the long-run efficacies of synapses in a neural circuit are also important in the computations it performs^18,43, suggesting that presynaptic membrane potentials scaled by these computational factors should be reproduced instead. In this case, the optimal estimator just scales as well. However, if the synapse suffers from saturation or other similar nonlinear constraints, then the form of STP that minimizes the error in the estimate of the scaled presynaptic potential would have to reflect these nonlinearities and change as the long-run weight alters. These changes could take potentially quite complex forms. As different efferent synapses have different long-term weights, they could exhibit different forms of STP. Indeed, metaplasticity of STP as a result of long-term potentiation has been observed experimentally^41,44.

We should also note that differences in STP across efferent synapses have been predominantly shown for inhibitory interneurons^1,45,46. In our theory, estimation of the membrane potential comes in the service of network computations, which are typically posed in terms of the excitatory principal cells rather than inhibitory interneurons. Thus, the theory does not fully extend to cover inhibitory neurons.

Our theory employs a standard account of the relationship between u_t and the presynaptic spikes and is thus a complement of the suggestion⁴⁷ that generation is more complex so that estimation can be straightforward even with a static synapse. The latter account is not easy to reconcile with the fluctuations evident in STP. Others have pursued ideas similar to ours about adaptive gain control mechanisms in neurons generally acting as optimal filters⁴⁸ and dynamic synapses specifically acting as estimators of presynaptic firing rates¹⁵ (B. Cronin, M. Sur & K. Koerding. Soc. Neurosci. Abstr. 663.6, 2007) or interspike intervals¹⁵. Some of these studies do not encompass STP, whereas others address depression, but not facilitation. Finally, these studies have primarily sought to predict a general advantage (if one exists at all⁷) of dynamic synapses over static ones.

Our approach is unique in suggesting that synaptic dynamics are matched to the statistics of presynaptic membrane potential fluctuations that we were able to demonstrate at least qualitatively (Fig. 3c–f). Even such a qualitative match is noteworthy, given that the STP data that we fitted were not extensive, were recorded in vitro under potentially very different stimulation regimes and neuromodulatory milieux for synaptic dynamics than those relevant in vivo, and given our highly simplified statistical model of presynaptic membrane potential dynamics. For example, a common dynamical motif shared by many neurons, including olivary neurons and hippocampal pyramids, and ignored by our model, is the presence of subthreshold membrane potential oscillations^38,40.

The simplicity of our model of presynaptic membrane potential dynamics makes it hard to provide a direct biological interpretation of the optimal parameter values (Online Methods) from the fits to data. Further theoretical work would be necessary to incorporate higher-order statistical regularities of these dynamics into the model. Further empirical studies recording STP under more naturalistic conditions and in vivo membrane potential recordings from the same identified pair of neurons, or at least the same cell type, will also be required. These would jointly license more direct comparisons and interpretations. Such experiments would of course be technically challenging. However, the link to optimal estimation offered by our theory provides them with the potential to test directly an important facet of neural circuit computations.

ONLINE METHODS

The optimal estimator

Our goal was to understand the factors contributing to the mean of the posterior or the estimate

$${\widehat{u}}_t={\int }_{-\infty }^{\infty }{u}_t\mathrm{P}(u_t\mid s_{0:t})d{u}_t$$ (2)

corresponding to the postsynaptic potential under our interpretation and, in particular, to the size of change in this estimate in response to an incoming spike, the analogue of the size of an EPSP.

The Ornstein-Uhlenbeck process

The generative model involves two simplifying assumptions. First, we assume that presynaptic membrane potential dynamics are discrete time and Markovian (Supplementary Fig. 1)

$$\mathrm{P}(u_t\mid u_{0:t-\delta t})=\mathrm{P}(u_t\mid u_{t-\delta t})$$ (3)

In particular, we assume that the presynaptic membrane potential evolves as an Ornstein-Uhlenbeck process, given (in discrete time steps of size δt and thus as a first-order autoregressive process, AR(1)) by

$$\mathrm{P}(u_t\mid u_{t-\delta t})=\mathcal{N}\left[u_t;u_{t-\delta t}+\frac{1}{\tau }\left(u^{\text{rest}}-u_{t-\delta t}\right)\delta t,{\sigma }_{\mathrm{W}}^2\delta t\right]$$ (4)

where u^rest is the resting membrane potential of the presynaptic cell (assumed to be constant here), τ is its membrane time constant and σ_W is the step size for the random walk behavior of its membrane potential. Because both τ and σ_W are assumed to be constant, the marginal variance of the presynaptic membrane potential, ${\sigma }_{\mathrm{OU}}^2={\sigma }_{\mathrm{W}}^2\frac{\tau }{2}$, is stationary.

The second assumption is that spiking activity at any time only depends on the membrane potential at that time

$$\mathrm{P}(s_t\mid u_{0:t})=\mathrm{P}(s_t\mid u_t)$$ (5)

In particular, we assume that the spike-generating mechanism is an inhomogeneous Poisson process. Thus, at time t, the neuron emits a spike (s_t = 1) with probability g(u_t)δt and the spiking probability given the membrane potential can be written as

$$\mathrm{P}(s_t\mid u_t)={[1-g(u_t\left)\delta t\right]}^{1-s_t}{\left[g\right(u_t\left)\delta t\right]}^{s_t}$$ (6)

We further assume that the transfer function is exponential (Supplementary Fig. 1)

$$g\left(u_t\right)=g_0{e}^{\beta u_t}$$ (7)

where g₀ and β are the base rate and determinism of the spike generation process, respectively.

Because equations (3) and (5) define a hidden Markov model, the posterior distribution over u_t can be written in a recursive form as in equation (1)

$$\mathrm{P}(u_t\mid s_{0:t})\propto \mathrm{P}(s_t\mid u_t){\int }_{-\infty }^{\infty }\mathrm{P}(u_t\mid u_{t-\delta t})\mathrm{P}(u_{t-\delta t}\mid s_{0:t-\delta t})d{u}_{t-\delta t}$$ (8)

That is, the posterior at time t, P(u_t | s_0:t), can be computed by combining information from the current time step with the posterior obtained in the previous time step, P(u_t–δt | s_0:t–δt). Note that even though inference can be performed recursively and the hidden dynamics is linear-Gaussian (equation (4)), the standard (extended) Kalman filter cannot be used for inference because the measurement does not involve additive Gaussian noise, but instead comes from the stochasticity of the spiking process (equations (6) and (7)).

Performing recursive inference (filtering), as described by equation (8), under the generative model described by equations (3–7) results in a posterior distribution that is approximately Gaussian⁵ with a mean ${\widehat{u}}_t$ and a variance ${\sigma }_t^2$

$$\begin{array}{cc}\hfill \mathrm{P}(u_t\mid s_{0:t})=& {\left(\frac{g\left(u_t\right)}{{\gamma }_t}\right)}^{s_t}{\left(\frac{1-g\left(u_t\right)\delta t}{1-{\gamma }_t\delta t}\right)}^{1-s_t}.\hfill \\ \hfill & .\mathcal{N}\left[u_t;{\widehat{u}}_{t-\delta t}+\left(u^{\text{rest}}-{\widehat{u}}_{t-\delta t}\right)\frac{\delta t}{\tau },{\sigma }_{\mathrm{W}}^2\delta t+{\left(1-\frac{\delta t}{\tau }\right)}^2{\sigma }_{t-\delta t}^2\right]\hfill \\ \hfill & \simeq \mathcal{N}[u_t;{\widehat{u}}_t,{\sigma }_t^2]\hfill \end{array}$$ (9)

Note that the smaller the bin size δt is, the closer this posterior distribution is to a Gaussian. The expected firing rate γ_t of the presynaptic cell at time t is obtained from the normalization condition ${\langle P(u_t\mid s_{0:t})\rangle }_{u_t\mid s_{0:t}}=1$

$${\gamma }_t={\langle g\left(u_t\right)\rangle }_{u_t\mid s_{0:t}}=g_0\exp \left(\beta {\widehat{u}}_t+\frac{{\beta }^2{\sigma }_t^2}{2}\right)$$ (10)

The mean and variance of the posterior in equation (9) evolve (in continuous time, by taking the limit δt → 0) as⁵

$${\dot{\widehat{u}}}_t=\frac{1}{\tau }[u^{\text{rest}}-{\widehat{u}}_t]+\beta {\sigma }_{t-\epsilon }^2[S_t-{\gamma }_t]$$ (11)

$${\stackrel{.}{\sigma }}_t^2=\frac{2}{\tau }[{\sigma }_{\mathrm{OU}}^2-{\sigma }_t^2]-{\gamma }_t{\beta }^2{\sigma }_t^4$$ (12)

where $S_t={\lim }_{\delta t\to 0}\frac{s_t}{\delta t}$ denotes the spike train of the presynaptic cell represented as a sum of Dirac delta functions, and ε is an arbitrary small positive constant that ensures that at the time of a spike t = t^spike, the update of $\widehat{u}$ is based on the variance just before the spike ${\sigma }_{t^{\text{spike}}-\epsilon }^2$. (A similar, but not identical, derivation can be found in ref. 26.)

Equation (11) indicates that each time a spike is observed, the estimated membrane potential should increase proportionally to the uncertainty (variance) about the current estimate. In turn, this estimation uncertainty then decreases each time a spike is observed (equations (10) and (12)). Conversely, in the absence of spikes, the estimated membrane potential decreases while the variance increases back to its asymptotic value. It can be shown⁵ that the representation of uncertainty about the membrane potential by σ² is self-consistent because it is predictive of the error of the mean estimator, $\widehat{u}$.

The dynamics of the membrane potential estimator in equations (11) and (12) is closely related to the dynamics of short-term depression. This can be shown formally by taking the limit when presynaptic spikes are rare. In this case, equations (11) and (12) can be rewritten⁵ as

$${\dot{\widehat{u}}}_t\simeq \frac{{\widehat{v}}_0-{\widehat{u}}_t}{{\widehat{\tau }}_{\mathrm{m}}}+\widehat{J}\widehat{Y}{\overline{\sigma }}_{t-\epsilon }^2{S}_t$$ (13)

$${\dot{\stackrel{‒}{\sigma }}}_t^2\simeq \frac{1-{\overline{\sigma }}_t^2}{{\widehat{\tau }}_{\mathrm{D}}}-\widehat{Y}{\overline{\sigma }}_{t-\epsilon }^2{S}_t$$ (14)

where ${\overline{\sigma }}^2={\sigma }^2∕{\sigma }_{\infty }^2$ is the normalized variance of the estimator. The other constants involved are ${\widehat{v}}_0={\widehat{u}}_{\infty }$, ${\widehat{\tau }}_{\mathrm{m}}=\tau$, $\widehat{J}=\frac{1}{\tau {\gamma }_{\infty }{\beta }^3{\sigma }_{\infty }^2}$, $\widehat{Y}=\tau {\gamma }_{\infty }{\beta }^4{\sigma }_{\infty }^4$ and ${\widehat{\tau }}_{\mathrm{D}}=\frac{1}{\frac{2}{\tau }+{\gamma }_{\infty }{\beta }^2{\sigma }_{\infty }^2}$, and ${\widehat{u}}_{\infty }$, ${\sigma }_{\infty }^2$ and γ_∞ are the stationary posterior mean, variance and expected firing rate in the optimal estimator (equations (9) and (10)) in the absence of presynaptic spikes. More precisely, from equations (11) and (12), we have

$$0=\frac{1}{\tau }[u^{\text{rest}}-{\widehat{u}}_{\infty }]-\beta {\sigma }_{\infty }^2{\gamma }_{\infty }$$ (15)

$$0=\frac{2}{\tau }[{\sigma }_{\mathrm{OU}}^2-{\sigma }_{\infty }^2]-{\gamma }_{\infty }{\beta }^2{\sigma }_{\infty }^4$$ (16)

where the expected firing rate is ${\gamma }_{\infty }=g_0\exp \left(\beta {\widehat{u}}_{\infty }+\frac{{\beta }^2{\sigma }_{\infty }^2}{2}\right)$. Although it is difficult to get an explicit expression for ${\widehat{u}}_{\infty }$ as a function of the model parameters alone, from equations (15) and (16) we can still express it as a function of the stationary variance ${\sigma }_{\infty }^2$

$${\widehat{u}}_{\infty }=u^{\text{rest}}-\frac{2}{\beta }\left(\frac{{\sigma }_{\mathrm{OU}}^2}{{\sigma }_{\infty }^2}-1\right)$$ (17)

Equations (13) and (14) directly map the posterior mean $\widehat{u}$ and (normalized) variance ${\overline{\sigma }}^2$ onto the postsynaptic membrane potential v and the synaptic resource variable x in a canonical, biophysically motivated model of a synapse undergoing synaptic depression (see equations (20) and (21)).

The switching Ornstein-Uhlenbeck process

We modeled presynaptic membrane potential fluctuations with an Ornstein-Uhlenbeck process around a constant resting membrane potential. We then generalized this process by letting the resting potential itself change. In this switching Ornstein-Uhlenbeck process, the resting membrane potential $u_t^{\text{rest}}$ is not fixed, but randomly switches between two levels, u⁺ and u⁻, corresponding to up and down states (Supplementary Fig. 1)

$$\mathrm{P}(u_t^{\text{rest}}\mid u_{t-\delta t}^{\text{rest}})=\{\begin{array}{c}1-{\eta }^{-}\delta t\text{if}{u}_t^{\text{rest}}=u^{+}\text{and}{u}_{t-\delta t}^{\text{rest}}=u^{+}\hfill \\ {\eta }^{-}\delta t\text{if}{u}_t^{\text{rest}}=u^{-}\text{and}{u}_{t-\delta t}^{\text{rest}}=u^{+}\hfill \\ 1-{\eta }^{+}\delta t\text{if}{u}_t^{\text{rest}}=u^{-}\text{and}{u}_{t-\delta t}^{\text{rest}}=u^{-}\hfill \\ {\eta }^{+}\delta t\text{if}{u}_t^{\text{rest}}=u^{+}\text{and}{u}_{t-\delta t}^{\text{rest}}=u^{-}\hfill \end{array}\phantom{\}}$$ (18)

where η⁻ and η⁺ are the rates of switching to the down and up states, respectively. Similarly to equation (4), the presynaptic membrane potential evolves as an Ornstein-Uhlenbeck process around the resting potential $u_t^{\text{rest}}$ which is now time dependent

$$\mathrm{P}\left(u_t\mid u_{t-\delta t},u_t^{\text{rest}}\right)=\mathcal{N}\left[u_t;u_{t-\delta t}+\frac{1}{\tau }\left(u_t^{\text{rest}}-u_{t-\delta t}\right)\delta t,{\sigma }_{\mathrm{W}}^2\delta t\right]$$ (19)

Spike generation is described by the same rule as before (equations (6) and (7)). Although we were able to develop some analytical insight into the behavior of the optimal estimator in the case of a switching Ornstein-Uhlenbeck process (Supplementary Note), a full analytical treatment remains a challenging task. Thus, the results displayed in Figure 2 were obtained by using standard particle filtering techniques⁵⁰ (see below).

Biophysically motivated STP model

The model we used was taken directly from reference 11 as a canonical model of a synapse undergoing STP. It describes how the postsynaptic potential v_t, the synaptic resource x_t (responsible for depression) and the utilization factor y_t (responsible for facilitation) co-vary in time

$${\stackrel{.}{v}}_t=\frac{v_0-v_t}{{\tau }_{\mathrm{m}}}+J{y}_{t-\epsilon }{x}_{t-\epsilon }{S}_t$$ (20)

$${\stackrel{.}{x}}_t=\frac{1-x_t}{{\tau }_{\mathrm{D}}}-y_{t-\epsilon }{x}_{t-\epsilon }{S}_t$$ (21)

$${\stackrel{.}{y}}_t=\frac{Y-y_t}{{\tau }_{\mathrm{F}}}-Y(1-y_{t-\epsilon })S_t$$ (22)

where v₀ is the postsynaptic resting membrane potential, τ_m is the postsynaptic membrane constant, J is (the static part of) synaptic efficacy, Y is the maximal synaptic utilization (and the rate of increase in y in response to a spike), τ_D is the time constant of synaptic depression and τ_F is the facilitation time constant. Note that if the facilitation time constant is very short (τ_F →0), then y_t can be replaced by Y in equations (20) and (21), resulting in pure depression. Also note that this standard model ignores the finite rise time of EPSPs. However, as rise times are usually about an order of magnitude faster than decay time constants, the effects of this approximation on the estimation performance of a synapse (as shown in Fig. 4) are expected to be negligible and, in any case, affect the static and the dynamic versions of the model equally.

Measuring the performance of estimators

The performance of an estimator, P, was measured as its rescaled root mean squared error (Fig. 4)

$$P=1-\frac{1}{{\sigma }_{\mathrm{OU}}}{\left[\frac{1}{T}{\int }_0^T{({\widehat{u}}_t-u_t)}^{2}dt\right]}^{\frac{1}{2}}$$ (23)

where ${\widehat{u}}_t$ can be substituted with v_t to measure the performance of the biophysical models. Note that this provides a suitably normalized measure of performance as perfect estimation results in P = 1 and an estimator that outputs the expected mean presynaptic membrane potential, thereby completely ignoring presynaptic spikes, has P = 0.

Stochastic release

Figure 4 shows the performance of static and depressing synapses and the optimal estimator for the case of stochastic vesicle release. Here, we provide the details of the calculations involved following reference 4.

Depressing synapses

Let N denote the total number of independent release sites. Each site can release at most one vesicle each time a presynaptic spike occurs. Each released vesicle gives rise to a quantum q = J/N postsynaptic response, where J is the maximal EPSP amplitude. The postsynaptic membrane potential evolves as

$${\stackrel{.}{v}}_t=\frac{v_0-v_t}{{\tau }_{\mathrm{m}}}+q{n}_t^{\mathrm{r}}{S}_t$$ (24)

where τ_m is the membrane time constant, v₀ is the postsynaptic resting potential and S_t is the presynaptic (delta) spike train. The total number of vesicles released at time t in response to a presynaptic spike, $n_t^{\mathrm{r}}$, depends on the number of vesicles that are ready to fuse, $N_t^{\mathrm{r}}$, and the utilization fraction Y. More precisely, at the time of a spike, $n_t^{\mathrm{r}}$ is drawn from a binomial distribution

$$n_t^{\mathrm{r}}~\text{Binomial}(N_t^{\mathrm{r}},Y)$$ (25)

The number of ready-to-fuse vesicles $N_t^{\mathrm{r}}$ decreases by $n_t^{\mathrm{r}}$ each time there is a spike and increases stochastically back to N with a time constant τ_D in the absence of spikes. Formally, the dynamics of $N_t^{\mathrm{r}}$ is given by

$${\stackrel{.}{N}}_t^{\mathrm{r}}=R_t-n_t^{\mathrm{r}}{S}_t$$ (26)

where $R_t={\sum }_{t^{\mathrm{stk}}}{\delta }_{t-t^{\mathrm{stk}}}$ and t^stk denote the stochastic restocking times produced by an inhomogeneous Poisson process with intensity $(N-N_t^{\mathrm{r}})∕{\tau }_D$.

It is easy to show that taking the expectation of equations (24) and (26) over the stochastic release and restocking events, and setting $x_t=\langle N_t^{\mathrm{r}}\rangle ∕N$, we get back the standard model of short-term depression (see equations (20) and (21)).

Static synapses

If we take the limit of a short time constant for depression, that is, τ_D → 0, the restocking of the vesicle described by equation (26) becomes instantaneous and we have $N_t^{\mathrm{r}}\to N$. As a consequence, the number of released vesicles at the time of a spike is given by

$$n_t^{\mathrm{r}}~\text{Binomial}(N,Y)$$ (27)

Optimal estimator

In the case of stochastic vesicle release, the variables of the optimal estimator evolve as

$${\dot{\widehat{u}}}_t=\frac{1}{\tau }[u^{\text{rest}}-{\widehat{u}}_t]+\beta {\sigma }_t^2\left[\frac{n_t^{\mathrm{r}}}{NY}{S}_t-{\gamma }_t\right]$$ (28)

$${\stackrel{.}{\sigma }}_t^2=\frac{2}{\tau }[{\sigma }_{\mathrm{OU}}^2-{\sigma }_t^2]-{\gamma }_t{\beta }^2{\sigma }_t^4$$ (29)

where the number of released vesicles $n_t^{\mathrm{r}}$ is given by equation (27). Note that if we replace $n_t^{\mathrm{r}}$ by its expectation $\langle n_t^{\mathrm{r}}\rangle =NY$, we get back the deterministic optimal estimator derived in equations (11) and (12).

The utilization parameter Y describes the probability of release for a presynaptic spike in all three models. For a fair comparison, it was chosen to be Y = 0.39 for all models, which optimized the performance of the dynamic synapse in the deterministic case for β = 2 (the value we used for the stochastic simulations) and which is consistent with experimentally reported values for the probability of release in cortical pyramidal-to-pyramidal cell connections⁴².

Numerical simulations for the optimal estimator

We evaluated the mean posterior ${\widehat{u}}_t$, the conditional means μ⁺ , μ⁻ and the conditional variances σ⁺ , σ⁻ numerically using a standard particle filtering technique⁵⁰. In practice, we used N^part = 10,000 particles, each of which was two-dimensional $(u_t^{\left(i\right)},u_t^{\text{rest},\left(i\right)})$,i = 1, K, N^part. They evolved according to

$$u_t^{\text{rest},\left(i\right)}~\mathrm{P}\left(u_t^{\text{rest},\left(i\right)}\mid u_{t-\delta t}^{\text{rest},\left(i\right)}\right)$$ (30)

$$u_t^{\left(i\right)}~\mathrm{P}\left(u_t^{\left(i\right)}\mid u_{t-\delta t}^{\left(i\right)},u_t^{\text{rest},\left(i\right)}\right)$$ (31)

where $\mathrm{P}\left(u_t^{\text{rest}}\mid u_{t-\delta t}^{\text{rest}}\right)$ is given by equation (18) and $\mathrm{P}\left(u_t\mid u_{t-\delta t},u_t^{\text{rest}}\right)$ by equation (19).

There was an (importance) weight, $w_t^{\left(i\right)}$, assigned to each particle, which was updated according to

$$w_t^{\left(i\right)}\propto w_{t-\delta t}^{\left(i\right)}\mathrm{P}\left(s_t\mid u_t^{\left(i\right)}\right),i=1,\dots ,N^{\text{part}}$$ (32)

In each step of the simulation, all weights were renormalized such that ${\sum }_{i=1}^N{w}_t^{\left(i\right)}=1$. The particles were resampled when the weights became strongly uneven. Formally, if the number of effective particles at time t, defined as

$$N_t^{\mathrm{eff}}={\left(\sum _{i=1}^N{\left(w_t^{\left(i\right)}\right)}^2\right)}^{-1}$$ (33)

fell below a given threshold N_thresh = 9,000, then all particles were resampled and the weights were all set back to $w_t^{\left(i\right)}=1∕N^{\text{part}}$.

The empirical mean and variance of the posterior membrane potential distribution were determined as

$${\widehat{u}}_t\simeq \sum _{i=1}^N{u}_t^{\left(i\right)}{w}_t^{\left(i\right)}$$ (34)

$${\sigma }_{\mathrm{tot},t}^2\simeq \sum _{i=1}^N{\left(u_t^{\left(i\right)}\right)}^2{w}_t^{\left(i\right)}-{\widehat{u}}_t^2$$ (35)

The numerical evaluation of ${\mu }_t^{+}$ , ${\left({\sigma }_t^{+}\right)}^2$, ${\mu }_t^{-}$ and ${\left({\sigma }_t^{-}\right)}^2$ followed the same procedure except that the summation was restricted to the particles that were in the up (or down) state and the weights were renormalized accordingly.

Model parameters for simulations

Unless otherwise noted, the presynaptic membrane time constant was set to τ = 20 ms. The spiking determinism parameter was β⁻¹ = 3 mV, and g₀ was set such that g(−60 mV)=10 Hz. For Figure 1, the s.d. of the presynaptic membrane potential was σ_OU = 5 mV and the resting membrane potential was u^rest = −60 mV. For Figure 2, the resting values were u⁻ = −65 mV and u⁺ = −55 mV. The transition rates were η⁺ = η⁻ = 2 Hz and σ_OU = 2 mV. For Figure 3a, the fitted parameters were βσ_OU = 1.13, τ = 1000 ms and g(−60 mV)= 10 Hz. Each one of those three parameters were then sequentially perturbed by ± 5% (resp. ±10%). For Figure 3b, the lower baseline potential was fixed at u⁻ = −65 mV. The fitted parameters were σ_OU = 0.28 mV, τ = 85.7 ms, u⁺ = −53.9 mV, η⁻ = 1.09 Hz, η⁺ = 1.13 Hz, β⁻¹ = 3 mV, and g₀ was set such that g(−60 mV ) = 17.8 Hz. Each one of those seven parameters were sequentially perturbed by ± 5% and by ±10%. Note that in this figure, we did not display the experimental data point for the shortest interspike interval (5 ms) because our current spiking model does not include the effects of refractoriness and burstiness that may dominate estimation at such short intervals. For Figure 4, we set u^rest = −60 mV, σ_OU =1 mV and β⁻¹ = 0.5 mV.