Tissue mimicking materials for the detection of prostate cancer using shear wave elastography: A validation study

Abstract

Purpose: Quantification of stiffness changes may provide important diagnostic information and aid in the early detection of cancers. Shear wave elastography is an imaging technique that assesses tissue stiffness using acoustic radiation force as an alternate to manual palpation reported previously with quasistatic elastography. In this study, the elastic properties of tissue mimicking materials, including agar, polyacrylamide (PAA), and silicone, are evaluated with an objective to determine material characteristics which resemble normal and cancerous prostate tissue.

Methods: Acoustic properties and stiffness of tissue mimicking phantoms were measured using compressional mechanical testing and shear wave elastography using supersonic shear imaging. The latter is based on the principles of shear waves generated using acoustic radiation force. The evaluation included tissue mimicking materials (TMMs) within the prostate at different positions and sizes that could mimic cancerous and normal prostate tissue. Patient data on normal and prostate cancer tissues quantified using biopsy histopathology were used to validate the findings. Pathologist reports on histopathology were blinded to mechanical testing and elastographic findings.

Results: Young's modulus values of 86.2 ± 4.5 and 271.5 ± 25.7 kPa were obtained for PAA mixed with 2% Al₂O₃ particles and silicone, respectively. Young's modulus of TMMs from mechanical compression testing showed a clear trend of increasing stiffness with an increasing percentage of agar. The silicone material had higher stiffness values when compared with PAA with Al₂O₃. The mean Young's modulus value in cancerous tissue was 90.5 ± 4.5 kPa as compared to 93.8 ± 4.4 and 86.2 ± 4.5 kPa obtained with PAA with 2% Al₂O₃ phantom at a depth of 52.4 and 36.6 mm, respectively.

Conclusions: PAA mixed with Al₂O₃ provides the most suitable tissue mimicking material for prostate cancer tumor material, while agar could form the surrounding background to simulate normal prostate tissue.

INTRODUCTION

Elastography is a new emerging imaging modality where variations in mechanical properties of tissues have been exploited to serve as clinical diagnostic signs of diseases such as cancer.^{1, 2, 3, 4, 5, 6, 7} For many years, digital palpation using tactile sensation has been used to diagnose changes in elasticity of superficial organs. However, the small size of lesion and location deep in the body may make it difficult to assess pathology just by palpation. In order to meet this challenge, imaging of viscoelastic properties of normal and diseased tissues is expanding and recently it has been clinically applied to a range of disease conditions.^{7, 8, 9, 10, 11, 12, 13, 14} This is carried out either by approaches that estimate displacement and strain or modulus reconstructions in response to a quasistatic deformation^{1, 3, 15, 16, 17, 18} or dynamic approaches for reconstructing the mechanical properties of tissue using external vibration or methods that utilize localized acoustic radiation force to perturb small volumes of tissue.^{4, 10, 19, 20, 21} Krouskop et al.²² first reported the application of Doppler ultrasound for assessing the interaction of a prosthetic socket with an amputee's residual limb and the mechanical properties of soft tissue.

Ultrasound elastography is a rapidly developing technology and several of the approaches discussed above have been implemented in commercial clinical diagnostic systems. This noninvasive technique has since then been reported in clinical trials in different anatomical areas using various perturbation techniques.^{7, 8, 9, 10, 11, 12, 13, 14} Commercial systems include: VirtualTouch (Siemens Medical Solutions USA, Inc., Malvern, Pennsylvania, USA), SonixTablet (ULTRASONIX, British Columbia, Canada), ElastoQ (Toshiba Medical Systems, Otawara, Japan), ShearWave^TM (SWE) elastography (SuperSonic Imagine, Aix-en-Provence, France) etc.

The elastography module on the SonixTablet uses fast algorithms to generate images showing tissue stiffness by measuring strain distributions in tissues in response to external quasistatic compression. Strain ratio measurements are used to quantify the relative stiffness between the lesion and the surrounding tissue. However, Young's modulus value cannot be measured by this relative method, unless modulus reconstructions are performed by solving the inverse problem.

ShearWave^TM elastography^{23, 24} is a quantitative technique based on estimation of the shear wave speed or velocity, which is used to assess true tissue elasticity in real time by displaying a color coded image superimposed on a B-mode image (Fig. 1). The stiffness of tissue, quantified by Young's modulus E (kPa), is related to the shear modulus (μ) by Eq. 1:

$$\mathrm{E}=2\times \mu \left(1+\mathrm{U}\right)\approx 3\mu ,$$ (1)

where U denotes the Poisson's ratio. Under the assumption of tissue incompressibility, i.e., U ≈ 0.495, E ≈ 3μ, the shear modulus is related to the density (ρ) and the shear wave propagation velocity (V) through Eq. 2:

$$\mu =\rho \times V^2.$$ (2)

By measuring the speed of the propagation of the shear wave at every point in the scanned region under the assumption of uniform and constant value of the tissue density, the stiffness of the tissue can be quantified in terms of the shear modulus. In SWE, the elasticity image measured in kilopascals (kPa) is refreshed in real time with the image resolution around 1 mm.²³ However, SWE is an evolving ultrasound technique for the detection of prostate cancer and many parameters need to be standardized.

Figure 1.

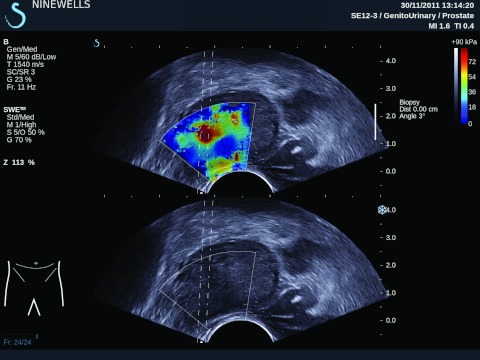
Ultrasound B-mode and Young's modulus image of a human patient's prostate obtained by tracking shear wave propagation based on supersonic shear imaging.

Barr et al.¹¹ reported Young's modulus values of 58 ± 20.7 kPa in prostate cancers. Acoustic radiation force impulse (ARFI) imaging has also been utilized to quantify the stiffness values in the prostate.^{14, 25} Zhai et al.²⁵ reported shear modulus values obtained using ARFI for five types of prostatic tissues, namely, the peripheral zone, central zone, transition zone, benign prostatic hyperplasia (BPH), and prostate cancer (PCa) and atrophy of 4.1 ± 0.8, 9.9 ± 0.9, 4.8 ± 0.6, 10.0 ± 1.0, and 8.0 kPa, respectively.

Tissue mimicking materials (TMMs) and phantoms manufactured from these TMMs play an important role in ultrasound and elastography research by simulating normal and diseased tissues for standardization.^{26, 27, 28, 29} TMM phantoms bridge the gap in translational research without the need of direct experimentation on humans or animals. The phantoms designed with TMMS are essential for assessing different technologies, and for training and research. Various kinds of TMMs have already been used in ultrasound research, such as gelatine, agar, silicone, and polyacrylamide (PAA) gel.^{26, 27, 28, 29} The key parameters in material characterization for ultrasound imaging include the acoustic velocity, the acoustic impedance, and the acoustical attenuation, while Young's modulus is an important parameter for elastography phantoms. Madsen et al.³⁰ have demonstrated the use of TM phantoms for standardization of both ultrasound imaging of the prostate²⁶ and for elastographic imaging^{18, 31} using agar and gelatine materials. Anderson et al.³² have also shown the effect of graphite concentration on shear wave speed in gelatine based phantoms.

Utilization of TMMs for prostate phantoms is based on mechanical measurements of the prostate tissue ex vivo.^{20, 33} Zhang et al.³³ have reported the complex Young's modulus of normal and cancerous prostate of 15.9 ± 5.9 kPa (n = 8) and 40.4 ± 15.7 kPa (n = 9) at 150 Hz using stress relaxation tests. Krouskop et al.²⁰ measured Young's modulus of a larger number of prostate specimens using compression loading at two different precompression levels of 2% and 4% and for three different loading frequencies of 0.1, 1, and 4 Hz, respectively. At a 1 Hz testing frequency and 2% precompression they reported Young's modulus values of 62 ± 17 kPa (n = 32) in the normal anterior and 69 ± 17 kPa (n = 32) in the normal posterior of the prostate. BPH was reported to be softer than the normal prostate at 36 ± 9 kPa (n = 21). Significant differences were observed in Young's modulus of prostate cancers with an increase in the precompression from 2% to 4%, with values increasing by a factor of two from 100 ± 20 kPa (n = 28) to 221 ± 32 kPa, respectively. These reports demonstrate that Young's modulus values can change with the testing frequency and precompression levels for different prostate tissue types.

In this study, we assess different TMMs to

• 1)determine appropriate tissue mimicking phantom material which could be used to simulate prostate cancer foci within the prostate gland and
• 2)design a prostate phantom with different sites and sizes of prostate cancer foci embedded in normal prostate tissue.

MATERIALS AND METHODS

Phantom fabrication

Mimicking the normal prostate and cancerous tumors in the prostate involves determination of an appropriate choice of TMM for these tissue types.^{20, 33} A phantom was designed to characterize the elastic properties of TMMs for shear wave elastography. A phantom container (13.8 × 11.8 × 8.5 cm³) was fabricated using perspex material. Inclusions that mimic the properties of prostate tumors were placed into the phantom container at specific locations and were embedded in normal prostate TMMs, and an opening was prepared for the ultrasound transducer (Fig. 2). Figure 2 includes a schematic diagram showing placement of TMMs in the background (agar) at different levels in relation to imaging transrectal probe. The inclusions to mimic the prostate cancer in different sizes were made using a tumor mould, which consists of two halves with several cavities of different diameters as shown in Fig. 3. In each isolated cavity of the mould, a tiny hole for exhausting air bubbles was drilled. Within the container, materials mimicking prostate cancer were placed at different positions to assess diagnostic accuracy of shear wave velocity and thereby modulus quantification.

Figure 2.

Tissue mimicking prostate phantom (the black circle indicates the opening for ultrasound transrectal probe). Schematic diagram showing placement of TMMs in agar background at different levels in relation to the imaging transrectal probe.

Figure 3.

Tumor mould used to manufacture the spherical TMM inclusions that are embedded in the TM phantom shown in Fig. 2.

Preparation of tissue mimicking materials

Different kinds of materials were used to simulate tumor properties using the tumor mould. The TMMs included silicone, polyacrylamide, agar (at different concentrations), and Al₂O₃ particles mixed material. The size of the samples used in our measurement ranged from 5.0 to 22.9 mm. Square shaped phantoms were used to measure the width and both round and square shaped phantoms were used for elasticity measurement. The surrounding background material is made of low concentration agar, which has lower stiffness close to normal human prostate tissue of around 20 kPa.^{18, 33}

Silicone

The silicone phantom was made of acetoxy cured silicone (Everbuild, Leeds, UK). This material remains stable for months and is nontoxic during fabrication and application. The silicone polymer is antifungal, quick curing, and viscous for fast application, so it is suitable and easy for molding into organ or tumor phantoms.

PAA

PAA based materials present originally in a liquid phase, however, after a chemical reaction, it turns into a partly transparent solid material. The advantages of polyacrylamide based phantoms are that it can form rigid shapes within 15 min at room temperature. The PAA phantom was fabricated using degassed water, acrylamide, N,N^′-methylenebis (acrylamide), ammonium peroxodisulfate, and N,N,N^′,N^′-tetramethylethylenediamine (Sigma-Aldrich, Dorset, UK). The concentration and procedure utilized in this paper were based on the previously reported methods.^{28, 34}

Agar

Solution containing agar powder (Sigma-Aldrich, Dorset, UK) was designed into TM models. Agar powder in solution, after heating and stirring at temperature above 95 °C till it dissolved completely, was poured into the desired mould for cooling down and forming solid inclusions.

Measurement of acoustic properties

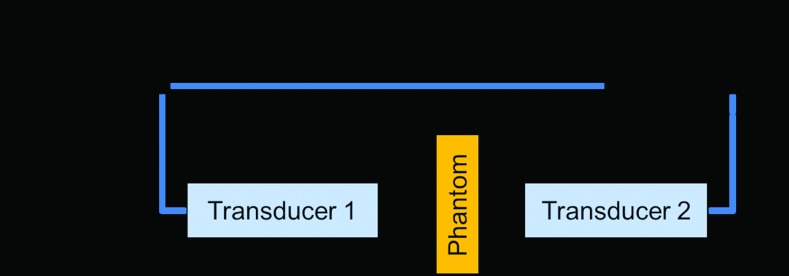
The insertion/substitution technique described by Selfridge³⁵ and Zell et al.³⁶ was applied to measure the acoustic properties in our study. The ultrasound wave propagating from the source to the receiver with and without the sample in a distilled degassed water environment was detected using a matched pair of SLIH5-10 transducers (Sonatest, Milton Keynes, UK). These transducers have the peak frequency at about 4.8 MHz, and function as the ultrasound source and the receiver, respectively, as illustrated in Fig. 4. An arbitrary waveform/function generator (Agilent, Santa Clara, California, USA) was utilized to emit the ultrasound wave (5 bursts) and a digital oscilloscope (Tektronix, Beaverton, Oregon, USA) was used to monitor the sound wave from the receiver transducer.

Figure 4.

Schematic diagram used for the measurement of acoustic properties of tissue mimicking materials.

The longitudinal ultrasound velocity and attenuation are calculated based on Eqs. 3, 4:

$$t_0=\frac{D}{v_w},$$ (3)

$$\frac{h}{v_s}+\frac{D-h}{v_w}=t_1.$$ (4)

We are interested in the difference in the transmission times (Δt) with and without the sample. The acoustic sound speed in the sample is given by

$$v_s=v_w/\left(1-\frac{v_w\Delta t}{D}\right),$$ (5)

where v_w and v_s represent the acoustic velocity in the water and the sample, respectively. t₀ is the ultrasound transmission time in the water between two transducers without the sample. D is the distance of the transmission path, h is the thickness of the sample, and t₁ is the transmission time with the sample in place.

For the measurement of the attenuation coefficient, the amplitude of the wave with the sample out of the beam path and the amplitude of the wave with the sample in place are measured. The attenuation coefficient is given by

$${\alpha }_s\left(dB/\mathrm{cm}\right)=\frac{1}{h\left(\mathrm{cm}\right)}\times 20{\log }_{10}\frac{A_w}{A_s/T_r^2},$$ (6)

where T_r denotes the amplitude transmission coefficient through the sample wall if present. The attenuation through water α_w = 2.5 × 10⁻⁴f² is ignored since it is small, where the frequency f is given in MHz. A_w and A_s are the amplitude of the received ultrasound pulse indices w and s representing water and the sample, respectively.

Shear modulus measurement using the Aixplorer

ShearWave^TM elastography is a quantitative method for imaging the elasticity of biological tissues. The Supersonic Imagine Aixplorer^® (SuperSonic Imagine, Aix-en-Provence, France) was used to estimate the stiffness of the TMMs, as shown in Fig. 5.

Figure 5.

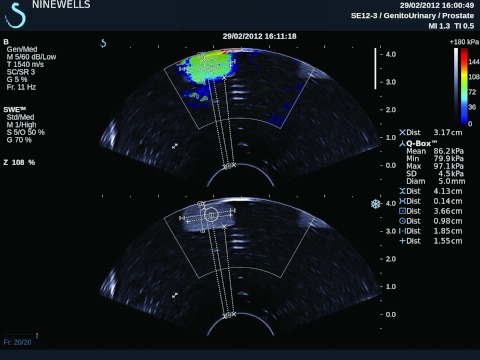
Quantitative estimation of Young's modulus in the TMM phantom using the Supersonic Imagine Aixplorer system.

For the measurements using the Aixplorer, tumor phantoms were prepared in different shapes to indicate different materials used for the TMMs. To display the elasticity result in real time on the system screen, transient shear waves were produced and captured using the supersonic shear imaging method.²³ The shear wave propagation speed was computed at each pixel and shown on the final speed map. The shear wave speed, the size, and the depth of the tumor can be detected simultaneously. Cancer mimicking inclusions were implanted into the background phantom at different depths to investigate the impact of depth on the shear wave velocity results.

Young's modulus measurement

We also used mechanical compression testing to measure Young's modulus of the sample materials. A Tinius Olsen's line of benchtop materials testing machine (Tinius Olsen, Horsham, Pennsylvania, USA) was used to measure Young's modulus of the TMMs directly using a compression test. The measured stress–strain relationship is used to deduce Young's modulus of the samples using a quasistatic measurement.

The Tinius Olsen's line of benchtop materials testing machine with 5000 N load sensor (force accuracy ±0.5% of the indicated load) was used to test the samples. To minimize the effects of the interface friction and the dehydration of the samples, the samples were dipped in water before the compression experiment. Samples were placed between the platens of the testing machine for data collection. The lower plate was fixed while the top one was moved downward at a rate of 0.5 mm/min. Full contact was needed between the top testing plate and the sample surface, and then the compression was applied after a 1–2 N preload. A 2 mm quasistatic displacement was applied, and a plot of force-displacement relationship was obtained, which can be used to calculate the stress–strain relationship using QMat professional software (Tinius Olsen, Horsham, Pennsylvania, USA). With the known constant parameters of the area and the thickness of the samples, Young's modulus was obtained by

$$E=\frac{\sigma }{\varepsilon }=\frac{F/A_0}{\Delta L/L_0},$$ (7)

where E is Young's modulus (modulus of elasticity); σ is the stress; ɛ is the strain; F is the force exerted on an object under tension; A₀ is the original cross-sectional area through which the force is applied; ΔL is the amount by which the length of the object changes; and L₀ is the original length of the sample.

RESULTS

Acoustic parameters discussed in Sec. 2 were measured for the different TMMs. Note that Al₂O₃ was mixed into the TMMs as the source of scattering particles to increase the backscatter in the different TMMs. The acoustic properties of TMMs with different agar percentages along with Al₂O₃, polyacrylamide mixed with Al₂O₃, and silicone are characterized and summarized in Table 1.

Table 1.

Acoustic velocity, density, impedance, and attenuation coefficient of TMMs at 4.8 MHz (at room temperature 20 °C).

Phantom	Acoustic velocity (m/s)	Density (103 kg/m3)	Impedance (Mrayl)	Attenuation coefficient (dB/cm/MHz)
2% agar + 1%Al2O3	1519.19 ± 48.85	1.02 ± 0.02	1.55 ± 0.05	0.78 ± 0.04
3% agar + 1%Al2O3	1522.00 ± 40.18	1.03 ± 0.03	1.57 ± 0.07	0.61 ± 0.04
4% agar + 1%Al2O3	1534.65 ± 42.25	1.05 ± 0.01	1.61 ± 0.03	0.62 ± 0.03
5% agar + 1%Al2O3	1527.68 ± 57.11	1.06 ± 0.02	1.59 ± 0.08	0.50 ± 0.03
PAA	1468.96 ± 19.64	0.96 ± 0.05	1.42 ± 0.06	0.26 ± 0.04
PAA + 2%Al2O3	1471.87 ± 32.03	1.01 ± 0.03	1.49 ± 0.05	0.70 ± 0.04
Silicone	1187.98 ± 38.55	0.98 ± 0.03	1.15 ± 0.08	4.09 ± 0.44

Shear wave elasticity measurements of TMMs and TMM phantoms

Stiffness quantification using shear wave imaging of the TMMs provided estimated Young's modulus values of 86.2 ± 4.5 kPa for PAA mixed with 2% Al₂O₃ particles and 271.5 ± 25.7 kPa for silicone, respectively. All results using the different TMMs are listed in Table 2. The impact of depth on the measurement of Young's modulus using shear wave elastography was studied in phantoms as depicted in Fig. 2. TMMs with an 18.5 mm width cubic shape, for example, PAA with a 2% Al₂O₃ concentration, were utilized to merge into agar background to investigate the impact of depth on the target. Distance of points on the color coded image (Fig. 5 can be measured using “Meas. Tools” of the Aixplorer system. Note that no clear trend was observed with the mean values of the Young's modulus values obtained at different depths. On the other hand, the standard deviations demonstrated an increasing trend with depth. The measured width of the target increased with decreasing depth and smaller depth measurement showed better accuracy (Table 3. At 64.0 mm depth, PAA with 2% Al₂O₃ phantom had higher standard deviation which reached 26.8 kPa and was similar to the SD of silicone at 30.6 mm depth, 25.7 kPa. The standard deviations of the depth within 52.4 mm were all less than 5.8 kPa.

Table 2.

Impact of depth on cancer mimicking phantom elasticity and width measurement.

Phantom	Depth (±0.5 mm)	Young's modulus (kPa)	Measured width (±0.5 mm)
PAA + 2% Al2O3	64.0	84.6 ± 26.8	NA
	52.4	93.8 ± 4.4	11.5
	43.8	78.9 ± 5.8	14.6
	36.6	86.2 ± 4.5	16.5
Silicone	30.6	271.5 ± 25.7	NA

Table 3.

Young's modulus results of TMMs phantoms from mechanical compression test.

Phantom	Young's modulus (kPa)
2% agar + 1% Al2O3	157.8 ± 9.2
3% agar + 1% Al2O3	299.4 ± 7.1
4% agar + 1% Al2O3	331.8 ± 8.8
5% agar + 1% Al2O3	443.0 ± 11.3
PAA + 2% Al2O3	104.3 ± 5.6
Silicone	297.3 ± 6.7

Elasticity of phantoms using mechanical compression testing

Young's modulus results of phantoms materials using mechanical compression testing showed a clear trend of higher elasticity with increasing agar concentrations for the same 1% Al₂O₃ level as shown in Table 3. Silicone TMM had higher elasticity values when compared to PAA with 2% Al₂O₃. Young's modulus of silicone compared favorably with the stiffness value obtained with the 3% agar and 1% Al₂O₃ TMM. PAA with 2% Al₂O₃ TMM had the smallest Young's modulus value of 104.3 ± 5.6 kPa and can be utilized to mimic prostate cancer especially for quasistatic elastography at a 2% precompression level,²⁰ while TMM utilizing an appropriate concentration between 2% and 3% can produce TMMs to mimic tumor at a 4% precompression level.²⁰

A comparison between Young's modulus measurements obtained using shear wave elastography from the Supersonic Imagine Aixplorer^® (Supersonic Imagine, Aix-en-Provence, France) and mechanical compression testing is summarized in Table 4. In general, quasistatic mechanical testing provided higher values of Young's modulus for the same TMM.

Table 4.

Comparison of Young's modulus values obtained by tracking the shear waves using the Supersonic Imagine Aixplorer system and mechanical compression testing.

Phantom	Shear wave elastography (kPa)	Mechanical compression (kPa)
PAA + 2% Al2O3	86.2 ± 4.5	104.3 ± 5.6
Silicone	271.5 ± 25.7	297.3 ± 6.7

Comparison between TMM phantom and patients’ data

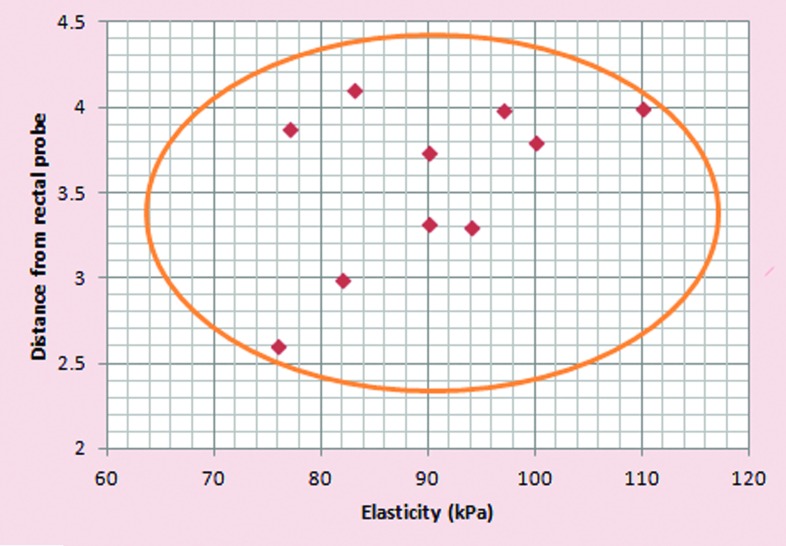
Ten patients suspected of prostate cancer [elevated prostate-specific antigen (PSA) levels andthose with abnormal digital rectal examination] were recruited into the study. The study had local ethical approval (REC Ref 11/AL/0359). The participants had transrectal measurements of shear wave elastography of abnormal areas in prostate using the same Supersonic Imagine clinical ultrasound system as that used in phantoms. These areas were biopsied and subsequently confirmed to be adenocarcinoma of the prostate on histopathology. The mean elasticity measurement in cancerous tissue was 90.5 ± 4.5 kPa as compared to 93.8 ± 4.4 and 86.2 ± 4.5 kPa for PAA with 2% Al₂O₃ phantom at a depth of 52.4 and 36.6 mm, respectively. Figure 6 shows correlation of Young's modulus values (elasticity) of prostate cancer foci diagnosed on histopathology in comparison to the depth from as measured from transrectal probe. All cancer foci diagnosed using shear wave elastography in 10 men were within a distance of 4.5 cm from the rectal probe.

Figure 6.

Correlation of Young's modulus values (elastacity) of prostate cancer foci diagnosed on histopathology in comparison to the depth from as measured from the transrectal probe.

DISCUSSION

TMM phantoms for medical imaging modalities and treatment planning have been reported in the literature^{26, 27, 29, 36} with aim to simulate image generation characteristics of tissues and calculate treatment dose with minimal or no damage to the surrounding tissues. With the introduction of elastographic imaging modalities, there is an increasing need for designing and fabricating phantoms which mimic the diseased and normal biological tissues for research and simulation of treatment parameters.

Acoustic properties and stiffness properties of a variety of TMMs were investigated in this study using a range of materials with an objective to determine appropriate TMM which can mimic prostate cancer. The speed of sound in prostate gland is approximately 1560 m/s, while the attenuation is close to 0.8 dB/cmMHz.³⁷ The acoustic properties of the materials mentioned in this paper are not very different from those of human tissue. The mean Young's modulus of normal prostate tissue was in the 15.0–20.0 kPa range, while the cancerous areas had an average value between 58.0 and 90.5 kPa^{11, 25, 38} based on real patients’ data using shear wave elastography. Cancer mimicking TMMs were merged into agar background to characterize the elasticity using shear wave elastography. Amongst the phantom materials, PAA with 2% Al₂O₃ possessed Young's modulus values closer to human prostate tumors. Silicone used for tumor mimicking materials can be distinguished in elasticity images. The stiffness of silicone is almost three times higher than Young's modulus of prostate cancer. What is more, the ultrasound velocity in silicone is lower than that in prostate which could result in unrealistic refraction at the boundary of a simulated cancer phantom. The standard deviation of Young's modulus measured using the Aixplorer was affected by the target depth. Measurements at larger depths of about 64.0 mm showed low reliability with as high as 26.8 kPa standard deviation. The standard deviation was reduced for depths of 50 mm or less. The errors could be due to tissue attenuation at a higher depth. The cross section of the TM phantom inclusion interrogated by the system could also introduce some errors if surrounding background material is included in the measurements. However, the measurements upto a depth of 5 cm are fairly consistent with lower standard deviations. Measurements were performed using a transrectal transducer, where the ultrasound beams diverge with depth. This may also account for errors in the width measurements for shear wave images. Further research is needed to explore these factors in detail.

In general, shear velocity and modulus measurement using ultrasound imaging of TMM phantoms have been validated using imaging from actual human prostate cancer foci in men suspected of prostate cancer (Fig. 6). Therefore, histopathology based transrectal ultrasound guided biopsies were chosen as the gold standard for ultrasound elastography validation in this study. Overall, the results reported in this paper indicate that TMMs manufactured using PAA with 2% Al₂O₃ particles in the phantom were valid to mimic prostate cancer. This material could be used for prostate cancer simulation studies in the future. Bias was minimized as phantom based measurements and patient’ data were collected by two independent researchers.

Tissue mimicking ultrasound prostate phantoms are available commercially from CIRS (Tissue simulation & Phantom Technology, Norfolk, Virginia, USA) for multi-imaging modality and/or image fusion algorithms.^{39, 40} However, most of these phantoms are meant for ultrasound imaging and other clinical imaging modalities. The validated materials as reported in the present study can be used to mimic prostate cancers at different locations within the gland and can be manufactured in different sizes. We believe that this will pave the way for further research to answer some of the key clinical questions in ultrasound imaging of prostate cancer using both quasistatic and dynamic elastography. Elastography using shear wave technology is still in infancy for prostate cancer imaging and its ability to pick up anteriorily located cancers using the transrectal route remains to be investigated. Tumors at depths of more than 50 mm are also likely to introduce artifacts using shear wave imaging techniques in prostate glands and hence not reliable in diagnosing cancer foci in larger glands and anterior zone cancers. The main limitation of the study is related to the desiccation of elastography phantoms. The mechanical properties of TMMs are time and moisture dependent. The samples were wrapped with cling film and stored in refrigerator to avoid desiccation. They were coated with water or gel to minimize the dehydration during the mechanical compression testing.

The aim of the present study was not to design ultrasound phantoms mimicking normal prostate gland as this has been carried out previously by CIRS (Tissue simulation & Phantom Technology, Norfolk, Virginia, USA) but to study elastographic characteristics of different materials which could mimic prostate cancer tissue-–a disease which has a large spectrum of histological characteristics. A reliable imaging modality is essential not only for diagnosis but also for preoperative planning, in particular, for focal therapies such as focused ultrasound surgery. Prostate phantoms could be used to simulate treatment and tailor therapy based on the size and location of the prostate tumors. The materials and methodology used in the present study could form the basis for designing future TMM phantoms and associated research in this area.

We believe that present work is a step in translational prostate cancer research and envisage growing role of shear wave imaging in prostate cancer imaging. Ultrasound imaging is particularly attractive for volume study and treatment planning such as focal therapy and seed implantation in an outpatient setting. We, however, would like to emphasize protocol based prospective data collection from multiple centers in the evaluation process of this technology in order to guide future clinical practice.

CONCLUSIONS

The acoustic properties and performance of shear wave elastography to estimate quantitative Young's modulus values were compared to mechanical testing and independent acoustic measurements. Based on Young's modulus measurements of TMMs, PAA with 2% Al₂O₃ provides the best fit to mimic prostate tumors. Silicone is another choice for mimicking cancerous prostate tumors due to its convenient preparation and long term stability of these materials, although it is much stiffer than the values reported for prostate cancers. The low ultrasound propagation speed and higher variations (standard deviation) in the shear modulus measurements of silicone should also be considered. In addition, because of the low ultrasound propagation speed of silicone, unrealistic refractions can occur at the boundary of a simulated cancerous tumor, compromising the tracking of shear wave velocity using ultrasound. In summary, PAA mixed with Al₂O₃ particles was the most suitable material for mimicking prostate cancer tumors, while agar material could be used as the surrounding normal prostate background to simulate a two-component TMM prostate phantom.