Properties of hydrophobic free energy found by gas–liquid transfer

Abstract

The hydrophobic free energy in current use is based on transfer of alkane solutes from liquid alkanes to water, and it has been argued recently that these values are incorrect and should be based instead on gas–liquid transfer data. Hydrophobic free energy is measured here by gas–liquid transfer of hydrocarbon gases from vapor to water. The new definition reduces more than twofold the values of the apparent hydrophobic free energy. Nevertheless, the newly defined hydrophobic free energy is still the dominant factor that drives protein folding as judged by ΔCp, the change in heat capacity, found from the free energy change for heat-induced protein unfolding. The ΔCp for protein unfolding agrees with ΔCp values for solvating hydrocarbon gases and disagrees with ΔCp for breaking peptide hydrogen bonds, which has the opposite sign. The ΔCp values for the enthalpy of liquid–liquid and gas–liquid transfer are similar. The plot of free energy against the apparent solvent-exposed surface area is given for linear alkanes, but only for a single conformation, the extended conformation, of these flexible-chain molecules. The ability of the gas–liquid hydrophobic factor to predict protein stability is tested and reasonable agreement is found, using published data for the dependences on temperature of the unfolding enthalpy of ribonuclease T1 and the solvation enthalpies of the nonpolar and polar groups.

The current method of measuring hydrophobic free energy is based on liquid–liquid transfer of alkane solutes and uses the solubility of liquid alkanes in water. The method was criticized by Ben-Naim and Marcus (1) because the solvation free energy of a nonpolar solute is found from gas–liquid transfer results. The original suggestion of Kauzmann (2) was to quantify hydrophobic free energy with data for the transfer of nonpolar solutes between water and a reference solvent. He drew an analogy between solvent transfer of a nonpolar solute and folding, which transfers nonpolar side chains out of water into the protein interior. It was pointed out recently (3) that, when the liquid–liquid transfer of an alkane solute is divided into two successive gas–liquid transfers, less than half of the overall transfer free energy occurs in the hydrophobic transfer from water into vapor, indicating that liquid–liquid transfer gives seriously incorrect values of hydrophobic free energy. Wolfenden and Lewis (4) showed earlier that the reason for a major free energy change when an alkane solute is transferred from vapor into liquid alkane is the presence of a strong interaction among alkane molecules in a liquid alkane.

The conclusion drawn here is that hydrophobic free energy should be defined and measured by the hydrophobic transfer of alkane solutes from water into vapor. The consequences of making this change are examined. A pressing issue is whether hydrophobic free energy, whose apparent value is reduced more than twofold by changing from liquid–liquid to gas–liquid transfer, is in fact a dominant factor driving protein folding. This question is answered by comparing the ΔCp value for heat-induced protein unfolding with values for solvation of hydrocarbon gases and for breaking peptide hydrogen bonds (H-bonds), which has the opposite sign. A second pressing issue is whether the widely used calibration of apparent hydrophobic free energy from liquid–liquid transfer against ASA, the solvent-accessible surface area, is still appropriate when hydrophobic free energy is taken from gas–liquid transfer, and the question is analyzed with data for linear alkanes Finally, the problem is tackled of testing whether gas–liquid transfer data for solvating nonpolar and polar groups can be used to estimate the dependence of protein stability on temperature.

Earlier Work

Several workers concluded earlier that gas–liquid, not liquid–liquid, transfer data should be used to analyze the hydrophobic factor. The pioneering paper (1976) of Wolfenden and Lewis (4) asked why liquid alkanes are poorly soluble in water and answered the question with gas–liquid transfer data. Two papers by Makhatadze and Privalov (5, 6) on gas–liquid transfer provided the results needed for a study reported here. Wu and Prausnitz (7) used gas–liquid transfer data to examine the concepts behind the pairwise hydrophobic interaction between two nonpolar molecules in water.

A 1991 paper by Lee (8) provided the approach used in the study reported here. Lee (8) and Pollack (9) independently derived the important result:

Eq. 1 shows that the gas–liquid transfer free energy ΔG_GL is the sum of two quite different quantitities, the cavity work (ΔG_c) and the solute–solvent interaction energy (E_a). Lee (8) pointed out that, when values of E_a are available from simulations, then values of ΔG_c (the major factor determining hydrophobic free energy) can be determined directly from ΔG_GL. The values of E_a that Lee used came from a simulation study by Jorgensen and coworkers (10).

Analogy Between Protein Folding and Transfer of an Alkane Solute from Water into a Reference Solvent or into Vapor

Kauzmann’s argument that the hydrophobic factor is an important energetic factor in the protein folding process (2) was based on an analogy (2, 11) between folding (which takes nonpolar side chains out of water and inserts them into the protein interior) and the transfer of a nonpolar solute from water into a reference solvent.

The first half of the analogy is clear: the energetics of removing protein nonpolar side chains from water are like those of removing nonpolar solutes from water, provided account is taken of the polar peptide groups in proteins and the polar group effect (3). However, the second half of the analogy is not clear: the energetics of transferring an alkane solute from vapor into liquid alkane are not like those of transferring nonpolar side chains into the protein interior, for several reasons. First, the polypeptide chain is transferred during folding into the protein interior together with the side chains, and this topological feature has no analogy in the transfer of alkane solutes into liquid alkanes. Secondly, there are polar (and H-bonded) peptide (-NHCO-) groups in the protein interior but not in a liquid alkane, and finally the protein interior is close-packed but a liquid alkane is not.

The unclear part of Kauzmann’s analogy is restricted to its second half. The first half of the analogy is used here to equate hydrophobic free energy (ΔG_h) with the free energy of gas–liquid transfer between vapor and water. The problem of finding a suitable transfer model for the second half of Kauzmann’s folding analogy is not discussed here; it is a separate problem from understanding the gas–liquid hydrophobic factor.

Temperature Dependence of the Unfolding Free Energy Used to Find Its Source

Ever since the fundamental work by Kauzmann (2) and Nozaki and Tanford (11), the apparent hydrophobic free energy calculated from liquid–liquid transfer has been regarded as the dominant factor driving protein folding (12, 13). Recently peptide hydrogen bonds (H-bonds) have been considered seriously as an alternative driving factor, owing particularly to Bolen’s work (14–16) showing that stabilizing osmolytes such as trimethylamine oxide drive protein folding by interacting chiefly with the peptide backbone, not the side chains.

The dominant source of the free energy that drives folding is taken here to be the same (but with opposite sign) as the free energy change measured for heat-induced unfolding, since free energy is a state function. The free energy change found on thermal unfolding can be characterized by its temperature dependence, which is large and yields the value of ΔCp. ΔCp is defined by the partial derivative of ΔH with respect to temperature, where ΔH is the enthalpy of transfer, either for transferring a hydrocarbon from the gas phase into aqueous solution or for transferring the folded form of a protein into its unfolded form.

The value of ΔCp distinguishes between solvation of nonpolar groups and breaking peptide H-bonds as the correct explanation for the dominant free energy contribution because their ΔCp values have opposite signs: positive for solvating nonpolar groups and negative for breaking peptide H-bonds. The unusual properties of ΔCp found for protein unfolding are discussed by Kauzmann (17), who argues that ΔCp has an unusual, large and positive, value because there is reordering of the water structure around nonpolar surfaces: compare the recent analysis of the pairwise hydrophobic interaction by Wu and Prausnitz (7). Richardson and Makhtadze (18) measured ΔCp for breaking peptide H-bonds by differential scanning calorimetry, using the heat-induced unfolding of a particularly suitable peptide helix in water. They found ΔCp = –7.6 cal⋅K⁻¹⋅mol⁻¹.

The value of ΔCp for heat-induced protein unfolding is given by a survey of the thermodynamic properties of 49 unfolding reactions by Robertson and Murphy (19); thermal unfolding was measured by differential scanning calorimetry. They found that ΔCp is accurately proportional to n, the number of protein residues; their value of (ΔCp/n) is 13.9 ± 0.5 cal⋅K⁻¹⋅mol⁻¹. To convert the protein unfolding value of ΔCp per residue to a value per peptide H-bond, the protein value is divided by 0.7, giving 19.9 cal⋅K⁻¹⋅mol⋅(H-bond)^–1 because there is 0.7 peptide network H-bond per protein residue (20). Thus, ΔCp for protein unfolding is considerably larger in size (as well as having the opposite sign) as the value (−7.6 cal⋅K⁻¹⋅mol⁻¹) for breaking peptide H-bonds. This comparison indicates that the dominant mechanism of protein unfolding is not breaking peptide H-bonds.

Values of ΔCp for gas–liquid transfer of hydrocarbon gases are needed for comparison with the protein unfolding value. They are surprisingly similar to ΔCp values for liquid–liquid transfer, as shown by comparative values of (ΔCp/ASA) for dissolving gaseous and liquid forms of linear alkanes. For gases, the (ΔCp/ASA) values are (6) ethane 0.402, propane 0.395, and butane 0.410 cal⋅K⁻¹⋅mol⁻¹⋅Å⁻²; for liquids the (ΔCp/ASA) values are slightly smaller, pentane 0.381 and hexane 0.377 cal⋅K⁻¹⋅mol⁻¹⋅Å^–2. The latter values of ΔCp and ASA are from refs. 21, 22. A relation between ΔCp values for gas–liquid and liquid–liquid transfer is derived below.

The value of (ΔCp/ASA) for protein unfolding is obtained as follows. The value of (ΔCp/n) from (19) is 13.9 ± 0.5 cal⋅K⁻¹⋅mol⁻¹ (see above), and the amount of nonpolar surface per residue exposed by unfolding is 42 Ų (23). The significant uncertainty in the latter number comes chiefly from uncertainty about how best to calculate the solvent-exposed nonpolar ASA in a completely unfolded protein. The result of using 42 Ų is (ΔCp/ASA) = 0.33 cal⋅K⁻¹⋅mol⁻¹⋅Å⁻² for protein unfolding, which is fairly close to the values of ΔCp/ASA given above for gaseous hydrocarbons. This comparison indicates that the dominant factor in protein unfolding is solvating the nonpolar groups exposed by unfolding.

Reconciling Evidence from Osmolyte-Driven Folding with Evidence That Solvating Nonpolar Groups Drives Protein Unfolding

Work by Bolen and coworkers (14–16) indicates that stabilizing osmolytes drive folding by interacting chiefly with the peptide backbone, not the side chains. They tested this conclusion by adding stabilizing osmolytes to polypeptide systems that model denatured proteins and found large changes in the physical properties of these model systems (24, 25), as expected. Thus, their overall results show that osmolytes control folding by acting chiefly on the peptide backbone, not on the side chains. Why then does the ΔCp analysis above show that the hydrophobic factor (which acts on the side chains) is the major source of the free energy change found on heat-induced protein unfolding? A straightforward answer is that the thermal folding/unfolding process is different from osmolyte-controlled folding because the osmolyte participates in the folding/unfolding process.

Relating Hydrophobic Free Energy to Apparent Values of Accessible Surface Area

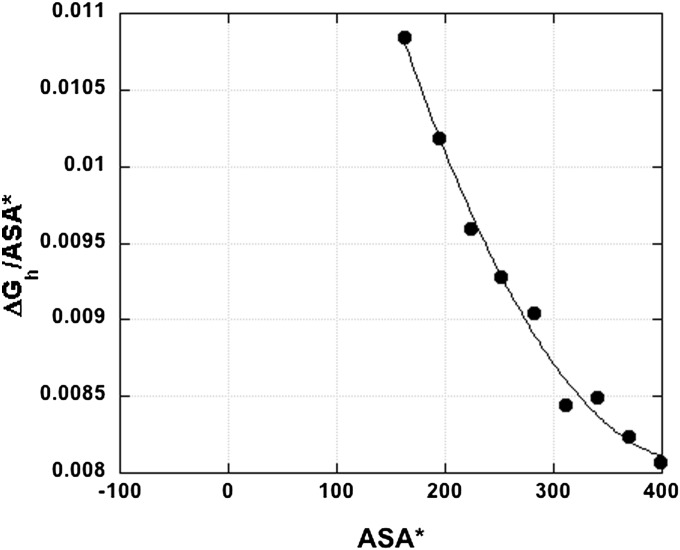
Ever since 1974, when Chothia proposed that hydrophobic free energy should be proportional to ASA (26), his proposal has been widely accepted and used to calculate free energy from ASA values for partly folded protein structures. Fig. 1 shows the dependence of (ΔG_h/ASA*) on ASA*, in the size range of ASA values observed for protein nonpolar side chains. The ASA* values in Fig. 1 are given for a set of linear alkanes, computed for the extended alkane conformation (27). The asterisk in ASA* indicates that these values refer to a single conformation, not to the average ASA values found by exhaustive simulations of all conformations of these flexible-chain molecules. The average ASA values are unfortunately not available.

Fig. 1.

Plot of ΔG_h, the gas–liquid transfer free energy (vapor to water, 25 °C), against apparent accessible surface area (ASA*) for linear alkanes containing 2–10 carbon atoms. The term “apparent accessible surface area” refers to ASA values derived from a single conformation (the extended conformation) of a flexible-chain molecule. The ratio (ΔG_h/ASA*) is shown. ASA* values are from ref. 27. ΔG values for n = 2–8 are from ref, 1 (see also ref. 27) and for n = 9,10 from ref. 27. Units of ASA* are Ų. The line is a polynomial fit, y = a + bx +cx².

Test of Calculated Unfolding Energetics Based on Data from Gas–Liquid Transfer

How reliable are calculations of protein folding energetics based on values of hydrophobic free energy? It is often assumed that the heat-induced unfolding/refolding transitions of proteins are governed chiefly by the temperature dependence of hydrophobic free energy. Makhatadze and Privalov (5) have provided the data needed to answer this question, and the test is made here. The test is to calculate the change with temperature of the enthalpy of protein unfolding from data for the solvation enthalpies of the polar and nonpolar groups as a function of temperature.

Makhatadze and Privalov (5) calculated the solvation enthalpies of the nonpolar and polar groups by using gas–liquid transfer data. They analyzed separately the aliphatic and aromatic side chains because they behave differently. Model compound data were used (28) to estimate the contribution from the polar peptide groups, and the test made here shows that the polar groups do contribute significantly to the temperature dependence of the unfolding enthalpy. Note that the solvation enthalpy of the polar groups has a sign opposite to those of the nonpolar groups.

The results for ribonuclease T1 are shown in Fig. 2 for the temperature range 5–100 °C. The change in the measured unfolding enthalpy (from the 5 °C value) is plotted against the change in the sum of the estimated solvation enthalpies of the nonpolar and polar groups. Quantitative agreement would give a straight line going through 0,0 with a slope of 1.00. The calculated line in Fig. 2 is straight (R = 0.998) and goes through 0,0, but its slope is 1.25. If the polar peptide groups are omitted, the slope increases to 1.87, which indicates that the peptide groups make a significant contribution.

Fig. 2.

Calculation of the temperature dependence of protein stability from data (5) based on gas–liquid transfer. The temperature dependence of the unfolding enthalpy of ribonuclease T1 is calculated from data for the solvation enthalpies of its nonpolar and polar groups (5). The solvation enthalpies of the nonpolar side chains and the polar peptide groups of the unfolded protein are summed and plotted against the enthalpy of protein unfolding after subtracting the values at 5 °C. The five temperatures shown are 5, 25, 50, 75, and 100 °C. A straight line was fitted that includes the point 0,0 (at 5 °C) (see text).

The likely cause of the failure to find quantitative agreement in Fig. 2, which would be a slope of 1.00, is an inability to model correctly the interaction between water and the polar peptide groups. The method of group additivity was used (28), but it is known today that this method is not applicable to the polar peptide groups, basically because of strong dipole–dipole interactions between neighboring—NHCO—groups (29–31). The solvation enthalpy of the polar peptide groups in the unfolded protein was modeled (28) with data for monoamides (such as N-methylacetamide), and the use of monoamide data is known to be a serious source of error (29–31).

Relating Liquid–Liquid and Gas–Liquid ΔH and ΔCp Values

A three-phase model (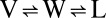) for equilibration of an alkane solute between vapor (V), liquid water (W), and liquid alkane (L) gives a simple relation (6), shown below, that is applicable to various thermodynamic state functions (X). Eq. 2 relates the energetics of alkane transfer from vapor to water (VW) to the transfer energetics from liquid alkane to water (LW) and includes the vaporization equilibrium (LV) of the liquid alkane.

When X = ΔH, Eq. 2 shows that ΔH_LW differs from ΔH_VW by the heat of vaporization of the alkane solute, ΔH_LV. This result explains why the transfer enthalpy passes through 0 near 27 °C for liquid–liquid transfer, based on values for pentane and hexane (21), whereas for gas–liquid transfer the enthalpy change passes through 0 near 95 °C (6).

By setting ΔCp = X in Eq. 2 and also using Eq. 2 with X = ΔH, a relation is obtained between the ΔCp values for gas–liquid (VW) and liquid–liquid (LW) transfer of an alkane solute to water.

Eq. 3 states that the gas–liquid ΔCp value (ΔCp_VW) should differ only slightly from the liquid–liquid value (ΔCp_LW) if the heat of vaporization of a liquid alkane decreases only slightly with increasing temperature, as indicated by results for n-butane and n-pentane in ref. 32. Values of (ΔCp/ASA) given above for linear alkanes are just slightly larger for gas–liquid transfer than for liquid–liquid transfer.