Abstract
Advances in Water Resources has been a prime archival source for implementation of averaging theories in changing the scale at which processes of importance in environmental modeling are described. Thus in celebration of the 35th year of this journal, it seems appropriate to assess what has been learned about these theories and about their utility in describing systems of interest. We review advances in understanding and use of averaging theories to describe porous medium flow and transport at the macroscale, an averaged scale that models spatial variability, and at the megascale, an integral scale that only considers time variation of system properties. We detail physical insights gained from the development and application of averaging theory for flow through porous medium systems and for the behavior of solids at the macroscale. We show the relationship between standard models that are typically applied and more rigorous models that are derived using modern averaging theory. We discuss how the results derived from averaging theory that are available can be built upon and applied broadly within the community. We highlight opportunities and needs that exist for collaborations among theorists, numerical analysts, and experimentalists to advance the new classes of models that have been derived. Lastly, we comment on averaging developments for rivers, estuaries, and watersheds.
Keywords: averaging theory, porous media, environmental modeling, TCAT
1 Introduction
From the first issue of its 35 years of its existence, Advances in Water Resources (AWR) has served as a primary outlet for publication of manuscripts dealing with methods for facilitating a change in scale at which a problem of interest is formulated [14]. In particular, a significant body of literature has been published that deals with an initial formulation of a problem at a small scale, application of an averaging method that transforms that initial formulation to a larger scale, and development of procedures for closing the resultant equations to obtain a problem description. Reports of research results in this area of inquiry are not limited to AWR, as advances dealing with this topic have been published in many other journals. Additionally, some of the work that has appeared in the literature, although an “advance” at the time of publication, has since been superseded by subsequent developments. Such a situation is typical of all fields of scientific inquiry that are subjected to thought, testing, validation, application to ever more complicated scenarios, and development of ancillary experimental, theoretical, and computational investigative tools. Unfortunately, another typical characteristic is a reluctance to leave behind what is comfortably understood as “common knowledge” in favor of an improved understanding with its concomitant challenges and data requirements.
In discussing the use of averaging theory, we will make reference to three different length scales. The smallest is the microscale, which is a continuum scale at which flow variability within the pore space can be described. The microscale is also referred to as the pore scale. The next larger scale is the macroscale with a characteristic length much larger than the microscale, on the order of tens to hundreds of pore diameters, or larger. At the macroscale, spatial variability of functions is modeled, but high frequency variations, on the order of fractions of a pore diameter are filtered out. It may be helpful to recognize that at the microscale, a porous medium system is modeled as composed of juxtaposed phases with well-defined boundaries while at the macroscale, the phases are modeled as overlapping continua that each occupy fractions of space. The largest scale considered is referred to as the megascale. This is the system scale. Models at the system scale do not account for variations of functional values over space but rather make use of averages over the system length scale. A more detailed exposition of the properties of these three scales can be found in [113].
The purpose of this contribution is to serve as a basis from which future understanding of averaging theory and its applications can develop. We will focus primarily on the use of averaging theory applied to conservation and thermodynamic equations, supplemented by an entropy inequality, as a basis for obtaining closed models. This method is called the thermodynamically constrained averaging theory (TCAT). It differs from older methods in that averaging is applied to microscale thermodynamic expressions, and mathematical theorems are used to derive evolution equations needed for closure in some systems. We will highlight the insights gained from this method and point out how this method can be applied further to enhance understanding. We note that the theoretical developments are on the cusp of being implemented for analysis of practical and realistic problems such that abundant opportunities for collaborative advancement exist. We also note that recent theoretical advances in averaging theory resolve several deficiencies present in previous theories and thus form a firm foundation for future advancement. It is our hope that this manuscript will serve as a helpful contribution to those who will be leading the way in developing models that will be important scientific contributions to the community through publication in AWR, and elsewhere, over the next 35 years.
2 Background
Modeling of water resources problems is typically based upon mechanistic representations of the system of concern. These mechanistic representations are often related to conservation principles of conserved quantities, such as mass, momentum, angular momentum, and energy. While such mechanistic representations are well established for single-phase systems based upon conservation over volumes at the microscale where an individual point represents an average over a large number of molecules, the appropriate mechanistic representations are less obvious at the macroscale where an individual point represents some average behavior over a region that includes multiple phases. Averaging theory can be used to derive such mechanistic representations, although traditional, accepted models are often posed directly at the macroscale with forms inspired by experimental observations.
As an example, consider a seemingly simple classical example: the problem of describing single-fluid-phase flow through a porous medium. The initiation of efforts to describe flow quantitatively had its origin in a correlation between flow and head loss over a homogeneously packed column based on the experimental work of Henry Darcy in 1856 [22, 39, 40, 152]. The head loss measured by Darcy was the drop over the full length of the column with no measurements taken within the column. From this data, the form of Darcy’s law obtained is an algebraic relation with the flow rate found to be linearly proportional to the head difference in the form
| (1) |
where q is the volumetric flow per cross-sectional area, K̂ is a proportionality constant, and h2 − h1 is the head loss over the column of length L. The form of this equation suggests that one might consider its implications as the column becomes shorter or longer. This led to postulation that in the limit of a very short column segment, the flow rate is proportional to the gradient in head. Integration of this expression over the column length returns the algebraic form of Darcy’s law over the entire column and a linear variation of head through the column. It is interesting that within the column, in the midst of the porous material, head and flow measurements are not taken. Despite this absence of data, minimal faith is required to conclude that the mathematical result indicating a linear variation in head along the column axis is reasonable for the conditions of Darcy’s experiment. However, if one is interested in heterogeneous columns, columns in which the volume fractions are not constant, or flow of multiple fluids, the leap of faith required to accept applicability of the usual differential form of Darcy’s law is much greater [78, 149]. Nevertheless, this is the usual approach to applying a flow equation for porous media. Any deviation from a linear proportionality between the flow and the head gradient is buried in a non-constant proportionality coefficient. An interest in putting the formulation of flow equations for porous media on a firmer theoretical ground led to efforts to derive Darcy’s law from conservation of momentum principles [e.g., 13, 64, 122, 148, 163, 164].
One of the shortcomings of these efforts is that Darcy’s law is considered to be a “given” correct expression that is a targeted result sought from the alternative approaches considered. In these instances, the analyses do not provide much additional insight but rather are considered valid because they produce the expected answer. A better approach is to develop a method that will provide flow equations at the scale of interest, equations that are not the target of the procedure but rather are the result of the analysis. Then situations can be identified where the Darcy formulation is appropriate and situations where more complex results of the analysis must be employed. Hubbert [82] commented on the fact that Eq. (1) became known as Darcy’s law. He then stated: “Subsequently many separate attempts have been made to give Darcy’s empirical expression a more general physical formulation, with the result that so many mutually inconsistent expressions of what is purported to be Darcy’s law have appeared in published literature that sight has often been lost of Darcy’s own work and of its significance.” In the 55 intervening years since Hubbert’s observation, the efforts to provide a general physical formulation have expanded beyond flow to include transport of heat and mass. It is fair to say that the pool of inconsistent expressions has increased. Ferreting out these inconsistencies is hindered by the need to fight through complex mathematical analyses, consider physics involved, and to determine if results that may look acceptable are actually grounded in a consistent physical problem description. Thus it seems appropriate to consider what we have learned in both the 35 years of AWR and the 155 years since Darcy’s landmark experiment.
The scope of this article is the use of theories that involve averaging of small scale equations to obtain equations at a larger scale. These methods share the feature that they typically assume a separation of length scales and make use of averaging theorems for phases [4, 108, 155, 162]. From this common basis, the methods diverge.
One of the scale change procedures is commonly known as the method of volume averaging (MVA). This procedure has been advanced primarily by Whitaker and co-workers [e.g., 136, 139, 164–166]. The objectives of this method are to obtain spatially smoothed equations, to derive closure problems for the differences between microscale and macroscale quantities, and to compare theory with experiment [e.g. 19, 166]. Features of the method include the fact that the microscale equations are closed before they are averaged; a closure problem is often formulated for a periodic unit cell, which is a model microscale description of a representative region of the porous medium with a spatially periodic structure, that enables macroscale closure parameters to be derived conveniently [e.g., 34, 138, 139, 166]; the solid phase is typically fixed; hierarchies of averages can be employed [136, 166]; interface dynamics associated with common curve movement in multiple fluid phase systems are typically neglected [165]; and a focus on comparisons to experimental observations has been considered an important part of the method [166]. It should be noted that a periodic unit cell is not strictly required by MVA, and recent work has focused on developing MVA models based upon local and non-local microscale structures, including those based upon statistical measures of the subscale media [169].
The strength of MVA is the production of a closed macroscale model that can be compared to experimental observations and macroscale parameters that can be predicted based upon a representation of the microscale structure. When macroscale closure relations are developed with MVA and a suitable unit cell, no adjustable parameters, beyond those that enter in the microscopic closure, arise with the change in scale. Under such conditions, MVA models can be predictive in nature [166]. These predictions will be reliable if the unit cell is a sufficiently accurate representation of the underlying structure, compared to the sensitivity of the results to the differences that exist between the assumed structure and the real structure of the medium of concern.
While extremely convenient when applicable, the reliance on a periodic unit cell for the derivation of MVA-based models imposes at least three important limitations. First, the real system of concern in a macroscale model must be describable by a periodic structure of the porous medium at the microscale. This means that the microscale distribution of phases in a system one wishes to model at the macroscale must be understood in sufficient detail to determine if a periodic unit cell description is a reasonable representation. Second, when analyzing systems, imposition of a periodic structure on the analysis precludes discovery of physical behavior that could be manifest in non-periodic systems. An example of such a case is the derivation of a pressure form of Darcy’s law using MVA [164, 166], which, as we will show, is incomplete in some situations. Third, not only is the reliance upon a periodic unit cell that is fixed in time convenient for analysis when using MVA, such a cell is generally essential if one is to produce a solution that uncouples the scales and allows macroscale simulation without the solution of a coupled microscale problem.
Many systems do not admit such temporally fixed unit cells, including multiple fluid phase flow problems that involve displacement phenomena and hence dynamic common curves. Such multiphase flow problems are of high complexity. The interfaces and common curves evolve with time, are non-periodic in nature, and their essential physics must be described well to model the system rigorously. Efforts to derive macroscale models of multiphase systems have yielded formulations that are essentially identical with the classical two-phase flow models [137, 164]. These models do not account for the evolution of interfacial areas and common curves, and they do not resolve the known dynamics with attainment of capillary pressure equilibrium. The equations obtained from MVA are also dependent on assumptions made regarding the forms selected for deviations, the actual form of the closed microscale equations that are averaged, and the development of deviation equations. Depending on how these three items are handled, the results of MVA can be different [12].
A second method that has been used frequently is averaging of conservation equations with rational thermodynamics (ACRT). This method averages conservation equations for phases, as well as for interfaces between phases before they have been closed. Thus the closure procedure occurs only at the scale of modeling. Guidance for the closure procedure is provided by the second law of thermodynamics, which states that dissipative processes will produce entropy. Inherent in ACRT is the need to make use of a thermodynamic framework that provides constraints on system behavior and incorporates intensive variables into the modeling system. The ACRT approach was first applied to single-fluid-phase flow [72–74]. Subsequently, averaging theorems for interfaces [52] and common curves [67] were developed so that the dynamic conservation equations for these entities could be incorporated into a model.
The drawback of the ACRT approach is that the thermodynamics are postulated at the macroscale such that the connection between smaller scale and larger scale properties is lost [e.g., as in 18, 74, 75, 120]. This disconnect between classically defined thermodynamic variables—such as pressure, temperature, entropy, and chemical potential [7, 27]—and their independently defined macroscale counterparts provides mathematical equations that resemble what might be expected; but the variables that are symbolized in those equations are not related well to physical variables that can be measured either directly or by some sort of averaging of small scale variables. The consequence of this shortcoming is that multiphase ACRT models are mathematical equation sets with limitations in application because the symbols in the equations do not relate directly to physical quantities. Among the erroneous elements that are inherent in ACRT models are a 50% overestimation of the trace of the fluid-fluid surface stress tensor (see correct forms based on microscale considerations [93] and TCAT approach for isotropic and anisotropic systems [56, 85] vs. overestimated surface stress tensor based on ACRT that cannot account for average directional properties of interfaces [e.g., in 75, 123, 127]); the quantity defined to be the capillary pressure is not actually related to the essence of capillarity interfacial tension and curvature; the stress exerted on the solid phase surface by fluid pressures is incorrectly found to be a weighted sum of pressures averaged over the phases; and temperature is ill-defined. Additional conceptual confusion exists in distinguishing between the movement of material in an interface and the movement of the interface itself as well as in obtaining equations that describe the evolution of interfaces between phases. Despite these undesirable features, which range in severity from “drawbacks” to “insurmountable errors,” ACRT served as a worthy effort to capture multiphase porous media flow physics at the macroscale. What it lacks is a systematic thermodynamic framework that not only seems consistent at the larger scale but also is related to microscale thermodynamics and to classical definitions of thermodynamic variables.
As a needed growth step in the employment of averaging methods to derive models of flow and transport phenomena in porous medium systems, the TCAT approach has been employed. This method has a set of characteristics that make it especially well suited as basis for model formulation including flexibility in selecting the details of modeling and in incorporating various thermodynamic frameworks that are consistent across scales. We will thus elucidate aspects of this method prior to providing some of the results obtained from this theory in comparison to those from alternative averaging approaches.
3 Features of the TCAT Approach
The TCAT approach has a number of attractive attributes that do not exist in other methods employed for changing the scale of conservation and thermodynamic equations. One off-putting aspect of the TCAT method is that the mathematics can appear complex. These mathematical details are intrinsic to the objective of developing a mechanistically rigorous macroscale or megascale model. In an effort to cut through the notation and manipulations, in this section we will focus on a conceptual description of the components of the approach rather than the mathematical details that are available in the literature [54–61, 85, 113, 114].
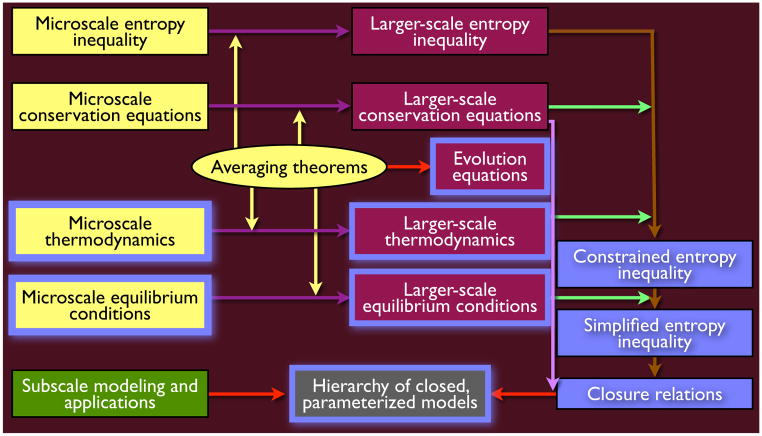
Fig. 1 depicts schematically the components of TCAT models. Essentially, this figure is composed of five different types of elements, as indicated by the five different colors in the boxes. Although some elements of all the boxes are unique to the TCAT approach, blue is used either within a box or outlining a box to indicate those essential and unique features of the TCAT approach that particularly distinguish it from other methods developed to date.
Fig. 1.
Elements of the TCAT approach.
The yellow boxes represent the starting point of the analysis. Standard microscale conservation equations of mass, momentum, and energy are postulated for the entities of interest. These entities include fluid and solid phases, the interfaces between these phases, common curves where three phases meet, and common points where four phases meet. Additionally, microscale thermodynamic equations for each of these entities must be formulated. Any consistent formulation of microscale thermodynamics can be selected, such as classical irreversible thermodynamics (CIT) [41], extended irreversible thermodynamics (EIT) [89, 90, 102], or the theory of internal variables (TIV) [104]. Although microscale rational thermodynamics (RT) could be employed in the formalism, it is not recommended because it is primarily a mathematical framework that lacks physical background and loses touch with experimental observations [101, 103, 110, 161, 170, 171].
For TCAT work performed to date, the simplest thermodynamic formulation of CIT for fluids, solids, interfaces, and common curves has proven to be of utility. Microscale thermal and mechanical equilibrium conditions consistent with the thermodynamic framework employed are generated using variational techniques [24, 26]. By obtaining microscale equilibrium conditions, we have precursors that ensure macroscopic groupings obtained as averages of these conditions will also provide equilibrium conditions. The microscale description of the problem, including conservation equations and thermodynamic relations, is then averaged using a well-defined set of averaging theorems [67, 113], a subset of which also have been previously employed in other averaging approaches [e.g., 6, 15, 52, 53, 72, 108, 109, 155, 162]. These theorems facilitate a change in scale from the microscale to either a macroscale form or directly to a megascale, or entire system, form. The larger scale conservation equations that result describe phase behavior that is similar to a mixture but actually is built on well-described variables and parameters. Most importantly, the precise definition of larger scale variables as averages of microscale variables is explicit, such that ambiguity about the physical meaning of a mathematical symbol is avoided.
The result of the use of the averaging theorems is five types of larger scale equations in the maroon boxes. The first type is the conservation equations. These are expressions for conservation of mass, momentum, and energy within phases, interfaces, common curves, and common points. The equations may be species based, such as the common practice of using an equation of conservation of chemical constituent to describe mass transport, or entity based, such as the common practice to describe momentum and energy transport for the aggregated species that comprise the entity. A more general development leading to species-based momentum equations within all entities has been presented [58]. Additionally, a larger scale entropy inequality is obtained as a sum of the averaged equations for each of the entities. Summation over the entities eliminates inter-entity entropy exchange terms and provides an expression that can be used to assist in the development of closure relations.
The remaining maroon boxes outlined in blue deserve particular attention as they are crucial to the TCAT character and process. When the scale of the conservation equations is increased in a multiphase system, new quantities appear that account for a changed description of the system configuration. At the microscale, phases are juxtaposed and separated by interfaces. The locations of the interfaces must be specified as boundary conditions for the phase equations, which are applied at those interfaces such that phase behavior can be modeled. At the averaged scale, phases are modeled as being co-located with each phase occupying a fraction of the space. These fractions are specified using measures such as porosity, volume fraction, and saturation, all of which are indicators of volumetric densities. Additionally, the amount of area (common curve length) per volume enters the formulation in the larger scale equations for conservation of area (common curve) properties. These properties are functions of time as one phase displaces another phase and interfacial areas between phases evolve. Because these properties do not exist from a microscale perspective, their appearance in the conservation equations creates an equation deficit. This deficit can most flexibly be overcome by developing equations or expressions for evolution of the geometric densities that are based on differential geometry. The need for evolution equations as independent expressions describing the geometric densities was recognized prior to the TCAT formalism [3, 68, 93, 117]. An approach for approximating these equations from averaging theorems for both interfacial areas and common curves has been presented [61].
The larger-scale conservation equations are supplemented by larger-scale thermodynamic and equilibrium equations developed in TCAT by applying averaging theorems to microscopic thermodynamic expressions. This approach to integrating thermodynamics into the modeling formalism is unique to TCAT and is an essential component needed to ensure that quantities are well defined and models are consistent across scales. These larger scale thermodynamic equations provide a connection between terms arising in the entropy balance and conservation of mass, momentum, and energy equations.
The final maroon element is the larger-scale equilibrium conditions. These are obtained as averages of microscale equilibrium conditions and therefore are completely consistent with the microscale perspective. By averaging microscale forms, TCAT ensures that the information in the equations that result is consistent between equations and across scales. This eliminates the procedure of introducing ad hoc definitions of quantities [98, 129] that, while seemingly offering some advantage for the study of one aspect of a problem, actually introduce inconsistencies elsewhere. Knowledge of larger scale equilibrium conditions also serves as an aid in rearranging entropy producing terms in an entropy inequality into force-flux pairs.
At the point where all the expressions in the burgundy colored boxes are derived, one has a full problem description based on the entities comprising the system of interest and the processes occurring in those entities. However, the averaging process exacerbates the standard problem of continuum mechanics in that the number of physical equations is many fewer than the number of unknowns that appear in the upscaled equations. Even with the derived evolution equations for geometric densities, the number of unknowns grows because inter-entity transfer terms now appear as intrinsic parts of the conservation equations rather than as boundary conditions. The excess in variables must be overcome by postulating relations among the variables that appear in the equations; this is the closure problem. Regardless of averaging procedure used to derive a model, this problem always arises. With the TCAT approach [see overview in 55], insight into the variables that need to be postulated and the dependence of those variables on other problem variables is gleaned from, and constrained by, the second law of thermodynamics.
The important model-building components that result directly from the TCAT approach that contribute to completing the closure of a problem of interest are indicated as the blue boxes. One makes use of the full set of conservation equations and thermodynamic equalities as constraints on the entropy inequality. This formal stipulation employs Lagrange multipliers to provide an exact equation referred to as the constrained entropy inequality (CEI). Manipulations are performed to simplify the CEI toward a force-flux form as guided by the equilibrium conditions; however some non-force-flux terms remain. The CEI is an important equation because of its exact nature. While a significant amount of manipulation is involved with deriving a CEI, once such an expression is derived for a particular class of model it can be used to derive a hierarchy of closed models for specific instances that are some subset of the original formulation. This makes the CEI an important equation for archival purposes and provides an entry point for model developers and those wishing to apply TCAT without the burden of performing a relatively complex ab initio development. CEI expressions have been derived for single-fluid-phase flow [56], single-fluid-phase flow and transport of non-dilute solutes [58], two-fluid-phase flow [85], and megascale transition regions involving two-fluid-phase flow and species transport [86]. These available expressions provide a foundation upon which models for a wide variety of specific porous medium systems and applications can be built.
Because the CEI is not uniformly in a force-flux form, further manipulations are needed and some assumptions are introduced to obtain this essential form, referred to as a simplified entropy inequality (SEI). The manipulations needed to derive an SEI are based upon a combination of restrictions to the original more general CEI (such as specification of the entity properties that are to be modeled) and approximations needed (commonly in regard to evaluation of averages of products of microscale properties) to bring non-conforming terms into force-flux form. TCAT requires that these restrictions and approximations be annotated so that they can later either be verified as reasonable or modified if found to be inappropriate. These approximations are based on expected behavior of the system as inferred from microscale or larger scale experimental observations or order of magnitude arguments. Because the SEI obtained will depend on the approximations employed, the path to an SEI as well as the final form are not unique. Put another way an exact CEI can be used as a basis to derive several different SEI’s depending upon the simplifying restrictions and approximations applied. If few restrictions are made and good approximations are used to derive an SEI, the resultant expression will be general and of use for a range of specific applications. For this reason, the SEI derived for a given system can have significant archival value and be of use for deriving a hierarchy of closed models for any system that is a subset of the restricted form upon which the SEI is based. Because some manipulations are required to derive an SEI from a CEI, this archival use is important and allows an entry point for deriving and applying TCAT models that precludes repetition of the vast majority of the manipulations needed to derive a TCAT model from scratch. TCAT-based SEI’s have been derived for a similarly broad set of systems as the CEI’s previously noted [56, 58, 59, 85, 86].
Once an SEI has been formulated, the final piece of the analysis is to develop relations between forces and fluxes (e.g., potential gradients driving flow, thermal gradients driving heat conduction) in light of the known equilibrium conditions and the constraint of the second law of thermodynamics. These relations are the closure relations, or constitutive relations, that parameterize terms in the conservation equations to produce a closed, solvable model. These closure relations are not unique. Rather the SEI provides a basis for deriving sets of closure relations that are consistent with known properties of the system at equilibrium and the second law of thermodynamics. Choices exist regarding the coupling of individual fluxes by selection of the set of forces producing the flux, and the order of the approximation employed. Because of this, a particular SEI can be used as a basis to derive a hierarchy of closed models depending upon the specific closure relations developed from the SEI.
The resultant hierarchy of closed, parameterized models, indicated in the grey box, is the objective of the TCAT procedure. The specific forms and system-dependent values of the parameters that result from TCAT analysis must be quantified. This can be accomplished with the assistance of subscale modeling and experimental observations, accounted for in the green box in Fig. 1, such as lattice Boltzmann [80, 112, 133], high resolution microtomographic imaging of media [35, 36, 111, 118, 119, 132, 134, 135, 159, 167, 168], pore network models [9, 21, 38, 43, 46, 79, 88, 95, 130, 140], and fabrication and analysis of micromodels [29, 30, 156]. However, we emphasize that if information collected at one scale is to be employed to support models at another scale, there must be an explicit relation between variables at the two scales. Furthermore, it is essential when working at a single scale that the variables designated be the same physical quantities as employed in the model equations. TCAT ensures that both of these conditions are met.
In the sections that follow we consider insights gained from the use of TCAT, compare the TCAT results derived to results obtained with alternative approaches, and discuss how TCAT results can be further developed most efficiently.
4 Insights Gained from TCAT for Porous Media Flow
The TCAT method has been applied to a variety of environmental problems at both the macroscale and the megascale. Results obtained in some instances represent extensions in understanding gained from earlier methods. Making use of those extensions in proceeding forward can circumvent problems encountered when working with or trying to parameterize a faulty theoretical model. Here we will present some of these results, which have been derived elsewhere, and indicate why they should be a part of a consistent approach to modeling particular systems of interest.
4.1 Darcy’s Law for Single-phase Flow
In its original form as given in Eq. (1), Darcy’s law is a one-dimensional megascopic expression. Thus, it does not provide information on the variability within a system. Rather it provides a flow rate through a packed column saturated with a single fluid as it relates to the change in head between the two ends of the column. Derivation of an equation of this sort is properly accomplished by integrating directly from the microscale, the scale of intergranular flow, to the megascale, the scale of the system. No macroscale version of the equation is needed. If a macroscale approach were used, it would require information about macroscale parameter variability within the system. The change in scale of the conservation and thermodynamic equations is accomplished using theorems from the [n, (0, 0), 3] family [67] where n is a dimensionality of the entity at the microscale equal to 3 for a phase, 2 for an interface, and 1 for a common curve. For a system consistent with Darcy’s apparatus, a straight column with uniform openings at both ends, and experimental conditions of slow flow, the megascale single-phase flow equation derived in [60] simplifies to a form identical to Eq. (1) where the flow rate q is defined explicitly as [63]
| (2) |
where vw is the microscale velocity of the fluid, ρw is the microscale fluid density, and Λ is the unit vector tangent to the column axis coordinate. The volumetric flow rate per unit area, q, is thus the density weighted velocity averaged over the entire pore space in the column multiplied by the fraction of column volume occupied by the fluid. The averaging operator in Eq. (2) is described briefly in the notation section and in more detail elsewhere [113]. The head on each end of the column is defined as
| (3) |
such that hi, the head at end i, with i =1 or 2, is equal to the density weighted average of the microscale chemical potential, μw, plus the microscale gravitational potential, ψw where the averages are taken over the inlet and outlet of the column occupied by the fluid phase; and g is the scalar acceleration of gravity. Eq. (1) then is written in the form
| (4) |
where the superscript indicates a density weighted average of the w phase potentials at end i of the column. The proportionality constant, K̂, accounts for the permeability of the column as a whole to flow and does not require homogeneity of the column packing.
Although some sources state that Darcy’s law is based on a linear relation between flow and a pressure difference or gradient [e.g., 8, 44], TCAT analysis shows that the most general driving force involves the chemical plus gravitational potential [63]. For the conditions of Darcy’s experiment including a homogeneous solid-phase distribution, isotropy, and constant fluid density, one can obtain an algebraic form in terms of pressure as
| (5) |
where pwei is the average pressure of the fluid over end i defined explicitly as
| (6) |
and ez is a macroscale vector aligned with the vertical direction.
Eq. (4) suggests that an extension to a three-dimensional macroscale form for an isotropic system would be
| (7) |
where K̂w has spatial dependence and μw̄ and ψw̄ are the density-weighted volume averages. By use of the TCAT procedure and with the usual assumption of slow flow, this equation has been derived from basic principles [56].
Based on Eq. (5), one might presume that the macroscale form of Darcy’s law for an isotropic system with constant density in terms of pressure would be
| (8) |
where pw is the volume average pressure over an averaging volume. However consideration of systems where the volume fraction is not constant [54] and derivation based on the TCAT approach [56] indicates that the actual form that results which is consistent with averaged microscale thermodynamics is [62]
| (9) |
The additional term in this expression in comparison to Eq. (8) primarily accounts for the facts that the microscale pressure need not vary linearly in the phase and that a gradient in volume fraction will cause a deviation from the usual expression of the hydrostatic pressure condition at the macroscale. At the microscale, the hydrostatic condition is ∇pw − ρwg = 0. Based on this, one might try to identify some macroscale measure of pressure, denoted as , that allows the hydrostatic condition in terms of macroscale variables to be expressed as
| (10) |
It should be obvious that for the case considered here, at least, with reference to Eq. (9) where ρwg is constant, Eq. (10) will be satisfied if we can define
| (11) |
which may be simplified to
| (12) |
Note that in theory since pw exists, the right side of Eq. (12) can be calculated. Then, with an appropriate boundary condition, the macroscale equation can be solved for . However, a route to direct calculation of as an average of some collection of microscale properties is not provided. Thus, although the mathematics is consistent, one cannot see that the function , implemented on the basis of the aesthetics of the macroscale hydrostatic condition, is a thermodynamic quantity that is useful in describing material properties in a way that is independent of the system being studied. Thus the actual use of to designate pressure, while providing an appearance that is “comforting” to those with a preconceived notion of what the hydrostatic condition looks like, is theoretically problematic. Indeed, a definition of as in Eq. (11) provides Eq. (10) as an expected result and simplifies Eq. (9) so that it resembles Eq. (8) with pw replace by . When 〈∇(pw − pw)〉Ωw, Ωw is negligible compared to ∇pw, the extra term in Eq. (9) can be neglected, and the usual form of Eq. (8) is recovered.
An alternative approach, that we introduce here, is to propose that the extra term arising in the TCAT approach be a function of some system variables. In an effort to gain insight, we note that from the averaging theorems, the identity may be obtained that
| (13) |
This expression converts an integral over the w phase to an integral over the surface bounding the w phase. Consideration of these alternative expressions suggests that when the pressure is constant, this term will be zero. Also, when the pressure is linear, this expression will be zero if the gradient of volume fraction of the w phase, ∇εw, is zero. The magnitude of this correction will also be related to the size of the averaging volume. Therefore, we can propose a functional dependence of this term as, for example
| (14) |
where l is an averaging length scale. Then dimensional analysis provides
| (15) |
When the vector function H is zero, the extra term in Eq. (9) can be neglected. When the velocity is small, as with the majority of porous media flows, the quantity involving qq will be small and can be neglected. Thus the proposed functional form simplifies to
| (16) |
We can speculate, based on the analysis, that when l∇εw approaches zero because the macroscopic length scale is small relative to the length scale of changes in porosity, H2 approaches zero. For example, if the system scale is denoted as L and if over this length εw varies slowly and monotonically, |∇εw| = O(1/L). In this case, |l∇εw| = O(l/L), which becomes vanishingly small when l ≪ L, as is often the case. A linearized approximation of Eq. (16) is
| (17) |
where k̂ε is a second order tensor. In this instance, a generalized form of Darcy’s equation in terms of averaged pressure will be
| (18) |
When the last term is negligible, the usual form of Darcy’s law in terms of volume averaged pressure is recovered.
Darcy’s experiments were carried out under very restrictive conditions of single phase flow in a homogeneous porous medium. The form of the equation has become virtually ubiquitous for description of a much broader range of porous media flows. Indeed a desire to make use of an equation that looks the same as Eq. (8), even for conditions outside the conditions Darcy employed, has motivated some investigators to propose arbitrary, rather than thermodynamic, definitions of “pressure” [e.g. 128]. Indeed, it has been even claimed that there is a single “correct” definition of macroscale pressure [98]. This claim is based on the desire to have some form of a microscale condition of equilibrium be mimicked at the macroscale. However, the result is a definition of pressure that is not thermodynamically based but is tailored to reproduce one expected equation form at the expense of consistency. The fact is that methods of averaging intensive thermodynamic variables are not unique [45, 97, 121]. However, any proposed method for averaging intensive thermodynamic variables such as temperature and pressure indeed leads to average values; but the interpretation of the physical meaning of these average when the intensive variable being averaged is not constant is difficult.
Consider the microscale enthalpy per volume, Hw, and the microscale internal energy per volume, Ew, of a w phase. These are related by the standard thermodynamic relation
| (19) |
If we average these over a representative volume of the w phase, we obtain the macroscale relation
| (20) |
Thus it is shown directly that the macroscale volume average pressure is the difference between macroscale enthalpy per volume and macroscale internal energy per volume. Based on this result, it is seen that the volume average pressure is very convenient when considering this energy relation but, as was shown in the last paragraph, may be less convenient, or perhaps less expected to appear, when considering momentum transport. The important issues are to know what the relations are between microscale and macroscale variables and to ensure that the macroscale forms employed ensure that equalities are maintained for the equations in which they appear.
It has been pointed out in discussing temperature, but equally applicable to pressure and other intensive thermodynamic variables, the fact that there is an infinite number of mathematically legitimate options for averaging [45, 71]. The challenge in averaging is to make sure that consistency is maintained between microscale variables and their averages, however they are calculated. This consistency must span thermodynamics and all the conservation equations employed and must provide a procedure to measure experimentally or to compute values of quantities that can be used as measures of those variables. Arbitrary alteration of definitions is a strategy that will certainly lead to frustration and then failure in parameterization of the resultant equations. Thus, even for simple applications, such as modeling of single-phase flow in porous media, it is important to derive equations that preserve the needed consistency and lead to larger scale equations that describe the processes of interest. It is foolhardy to alternatively designate some classical or desired form of an equation as “the” form that must arise from rigorous theoretical analysis and then contort a systematic procedure into arbitrariness that nonetheless provides that result. Darcy’s law was developed based on careful and appropriate examination of data produced by some excellent experimental work on particular systems. Extension of the form of this law beyond the range of conditions employed when it was developed is speculative business, and one should not necessarily expect the same equation form to properly capture the system physics.
4.2 Two-fluid Flow in Porous Media: Classical Description
Macroscale modeling of two-fluid-phase flow in a porous medium is typically based on Darcy-like equations for flow of each phase solved in conjunction with mass conservation equations. Our goal here is to highlight some important features of this approach as part of a discussion of a simplified model. When the fluids are considered immiscible and the solid motion can be neglected, the mass conservation and flow equations to be solved are, respectively [e.g., 85]
| (21) |
and
| (22) |
where the parameters K̂α and k̂εα must be specified for each phase. The last term in Eq. (22) does not appear in standard formulations and can be neglected here if the purely classical form in terms of pressure is desired. However it was shown in the previous section to be a possible extension when the momentum equation is expressed at the macroscale in terms of a gradient in the fluid pressure. Since Eq. (22) is a vector equation with three components, the pair of equations listed provides eight equalities for the two phases. The sixteen variables appearing in these equations are
| (23) |
In this listing, εα, α ∈ {w, n}, is not included since εα is related directly to variables that are listed with εα = sαε. Because there are only eight conservation equations, a deficit of eight equations exists. Four of these are managed by specifying the porosity, ε, and the three components of the gravitational vector, g. Additionally, the condition that the sum of the saturations must equal one, sw + sn = 1, eliminates one of the saturations as an independent variable. The two densities are typically expressed by equations of state that relate density to pressure, ρα = ρα (pα), for isothermal cases in which changes in composition are not important. Thus a total of seven auxiliary conditions are employed, which leaves a deficit of one equation. The final condition imposed is a heuristic relation that stipulates the difference in pressures can be expressed as a function of saturation in the form
| (24) |
Typically, the function f is claimed to be the capillary pressure. However, this view of the problem is incomplete. In fact, if one performs a careful analysis based on TCAT making use of only phase equations and thereby implicitly considering the properties of interfaces to be negligible, the result derived is that f (sw) must equal zero. This is a reasonable result when interface properties are negligible. This result also confirms the fact that a correct description of the physics of multiphase flow requires proper accounting for the properties of interfaces [see 57, for further discussion of this point]. To produce a model of some utility, traditional approaches define many-valued relations in which the saturation depends upon the temporal history of the fluid pressures [e.g., 115]. These hysteretic relations are a tell-tale sign that the physics of the situation have not been described adequately.
4.3 Two-fluid Flow in Porous Media: TCAT Description
Of particular importance for gaining understanding of proper incorporation of capillary pressure into the description of multiphase flow is the fact that capillary pressure is defined at the microscale, not directly as a pressure difference, but as
| (25) |
where γwn is the interfacial tension of the interface between the fluid phases and Jw is the curvature of the interface. It is crucial to note that in performing the analysis leading to this definition [25, 57], it is necessary to explicitly include conservation (for the dynamic case) and thermodynamic equations accounting for properties of the interface as part of the formulation. Additionally, if the system is at equilibrium, microscale capillary pressure defined as in Eq. (25) is related to the phase pressures according to
| (26) |
One item of particular importance is the fact that the pressures in Eq. (26) are evaluated at the interface. Thus, the difference in the pressures at a point on the interface is related to the capillary pressure at that point at equilibrium. An additional feature of equilibrium Eq. (26) is the presence of a gravitational term. This term accounts for a contribution to a discontinuity in phase pressures across the interface when the interfacial mass density is non-zero and the normal to the interface is not orthogonal to gravity.
A general formulation of the macroscale problem requires use of thermodynamic and conservation equations for the fluid and solid phases as well as the interface between those phases. We can take a simplified look at this situation by neglecting the properties of solid surface interfaces with the fluids and also neglecting any solid-phase motion. Additionally it is assumed that mass transfer to the fluid-fluid interface will be accounted for by some constitutive relation. Thus, we will supplement the fluid-phase mass and momentum conservation equations with corresponding equations for the wn interface. Thus for the three entities being considered, a total of twelve conservation equations is employed. In including the macroscale forms of these interface equations, we will also add the following six variables to the sixteen in Eq. (23)
| (27) |
The total of twenty-two variables are described by twelve conservation equations, the seven auxiliary conditions noted following Eq. (23), and an equation of state for the interface of the form ρwn = ρwn (γwn). Thus, a deficit of two equations remains.
One supplementary condition can be developed for the evolution of the interfacial area between the fluids, εwn, as a function of time. A form for this condition has been obtained based on the averaging theorems and consideration of differential geometry principles [61]. Recognition of the need for an expression for interfacial area evolution can be found in a porous medium context [3, 49, 68, 93] and in bubbly flows without the presence of a solid phase [83, 84, 94]. It is important to emphasize that the evolution equation for the interfacial area is an equation independent of the mass conservation equation for the interface, an equation which has already been considered in assuring equality of equations and unknowns. This fact has been neglected in some formulations that describe area evolution based on mass conservation [2, 87, 123–126], which overlooks the difference between flow in the interface and movement of the interface and which is also unable to account for massless interfaces or interfaces whose mass density changes with time and space.
The second supplementary condition is obtained from the entropy inequality in the TCAT formulation [62]. This equation is a dynamic condition on capillary pressure. For the case where the solid does not deform or move, the resultant equation is
| (28) |
where and are microscale pressure averaged over the wn interface, is the interface density weighted average unit normal outward from the w phase at the interface, and is the equilibrium interfacial area per unit volume. Eq. (28) has a number of interesting features that require discussion.
First is the fact that in proposing Eq. (28) to close the equation set based on the TCAT SEI, we have encountered five new independent variables, , and that must be accounted for. Although this might seem to be burdensome, the fact that explicit accounting for the variables is employed actually sheds light on how capillary pressure is correctly incorporated into the model. In fact, the term on the right side of Eq. (28) is the actual average of the microscale condition for capillary pressure equilibrium. Nevertheless, we do need to make some reasonable approximations that can be evaluated by subsequent analysis.
The quantity can be considered negligible because the average of the vertical component of nw within an averaging volume will be small and the interfacial density is small in most cases. Thus, this term is neglected. It seems reasonable that in many cases the average of the pressures over the interfaces will be approximately equal to their volume averages. This is not the case in regions of high gradients of saturation, but is a first approximation that can be employed. Thus, let us consider a simplified form of Eq. (28)
| (29) |
With reference to Eq. (25), it can be seen that is the macroscale average of the microscale capillary pressure. By the standard approximation, this quantity is proposed to be a function of saturation. However, from the TCAT analysis, we see that what we need is some approximate measure of the average of interfacial curvature as a function of macroscale parameters. We note that making this expression a function of sw only is typically inadequate as it fails to account for the way the fluid is distributed within the averaging volume [e.g. 100]. In other words, for a fixed saturation, there can be a range of values of average interfacial curvature. Admitting that some information is lost in going from the microscale to the macroscale, we nevertheless suggest that inclusion of εwn as an additional independent variable improves the chance of having a good macroscale surrogate for the macroscale interfacial curvature. Thus we propose
| (30) |
Experiments [28, 35, 133, 134] have shown that the inclusion of interfacial area in the proposed functional form for macroscale capillary pressure significantly reduces hysteresis. A functional form is also needed for the equilibrium interfacial area. At equilibrium, pc = pn − pw so we propose that
| (31) |
Note that the form of Eq. (31) can be obtained as an inversion of Eq. (30).
As a last point concerning Eq. (29), it is important to recognize the second term in brackets on the left side. This additional term accounts for the fact that even for a process occurring at constant saturation, a reshaping of the interface due to fluid redistribution must be evidenced in disequilibrium between pw − pn and pc. This effect is not accounted for when the disequilibrium is taken to be proportional only to the rate of change of saturation [10, 157]. This extra redistribution term is also not obtained when the ACRT approach is employed and saturation is arbitrarily added as an independent variable in expressing the functional dependence of macroscale energy per mass [75].
Although disequilibrium due to the rate of change of saturation is part of the story, the TCAT approach also provides the additional important dynamic feature of relaxation of interfaces to a final configuration after a saturation change has been accomplished. The incompleteness of Eq. (29) with is suggested by the fact that efforts to parameterize τ̂A have shown a wide range of variability and produced unsatisfying results [42, 76, 116, 147, 160].
5 Geomechanics Considerations from the TCAT Approach
In geomechanics in general, and in soil mechanics in particular, the solid can be treated under static loading or steady state conditions as a single-phase material because the behavior of the solid skeleton and the interstitial fluid(s) are decoupled. However under consolidation or dynamic situations, there is strong coupling between the solid and the fluid phases that cannot be ignored if the system behavior is to be modeled correctly. Indeed, the phenomena of weakening and of “liquefaction” in solids subjected to cyclical loading, such as occurs in earthquakes, can only be explained by considering the action of the fluid phases and the solids simultaneously. Quantitative analysis and prediction of real behavior can only be achieved by sophisticated computation [173]. However, if the computational effort is to be worthwhile, it is essential that the equations describing the system physics properly describe the phase interactions, especially the inter- and intra-phase phenomena. The coupling of phases is introduced in the momentum balance equations through the concept of effective stress and in the mass balance equation of the fluid(s) through the rate of the volumetric strain in the accumulation term. There are further situations, such as drying of geomaterials [48], where the effective stress concept is important for a correct simulation of the phenomenon. Hence the so-called effective stress principle plays a major role in multiphase geomaterial mechanics. Derivation of the effective stress principle in the context of TCAT provides improved representation of this stress in comparison to other methods.
The effective stress principle is based on some form of the split of the total stress tensor acting on the multiphase system [20, 47, 69]. It is traditionally defined in the case of a ternary mixture composed of a solid phase s, a wetting phase w and a non-wetting phase n as the weighted sum of the partial stress tensors of the phases only
| (32) |
This tensor is usually split to the form
| (33) |
where is the effective stress tensor, is some measure of the pressure acting on the system, α̂ is a weighting coefficient usually called the Biot coefficient, and I is the identity tensor. The solid-phase stress tensor that appears in Eq. (32) is given
| (34) |
where expresses a macroscale measure of the pressure acting on the solid phase, which is not necessarily the same as . A thermostatic approach in the context of ACRT was employed [50, 65] to obtain an explicit form of as
| (35) |
where is the fraction of solid surface in contact with water, known as the Bishop parameter, and are the macroscale RT measures of interfacial tensions between the wetting phase and the solid and the non-wetting phase and the solid, respectively, and and are the macroscale average curvatures of the solid surface obtained by integration of the microscale curvature over the ws and ns interfaces, respectively. Unfortunately, because this expression is based on an ACRT approach, the relation of the macroscale pressures to microscale pressures was not obtained and some extended fundamental dependence of thermodynamic energy functions on independent variables had to be assumed. The lack of interscale consistency between macroscale variables in Eq. (35) and microscale variables makes it difficult to determine what should be or is being measured or simulated if this equation is employed.
In the literature there are several forms of the split between effective stress and a pressure term to account for the total stress [69]. TCAT has permitted some of the aspects connected with this split to be clarified. In particular consistent, well-defined forms for and have been derived. These forms incorporate the contribution of the interfaces, definitions for the fluid pressures and interfacial tensions as averages of microscale variables, explicit definition of the elements of the solid stress tensor , and a mathematical expression of the Biot coefficient α̂. Additionally, a more complete form of the stress measure in Eq. (32) is obtained that also properly accounts for the contribution of the interfacial and common curve stresses to the total stress.
The TCAT formalism has led to the conclusion that the total stress acting on the solid must generally include contributions due to the curvature of the solid surface. Thus the total stress tensor is written with surface and common curve contributions as [66]
| (36) |
The split of this general form between effective stress and a pressure term is expressed similarly to Eq. (33) as
| (37) |
Note, however, that in posing this split of total stress, TCAT provides not only the definitions of the stress tensors and effective stress but also the definition of the Biot coefficient and . The proposed split of Eq. (37) is traditionally known as the Skempton stress [154] when is taken to be some weighted average of the fluid pressures. The TCAT formalism provides the requirements when this split will be thermodynamically correct. Prior to the development of the TCAT approach for geomechanical applications, it had been stated that no continuum theory of thermodynamics had shown the validity of the Skempton effective stress [23]. The stress equations provided by TCAT for use in computation of fluid-solid interactions provide thermodynamic consistency that cannot be achieved by positing the macroscale thermodynamics directly at the macroscale as in the ACRT approach [151].
The application of TCAT has produced the definition of the Biot coefficient α̂ as [69]
| (38) |
where K̂T is the bulk modulus of the solid phase; es is the macroscale average strain tensor (infinitesimal strains); and 〈ns·ts·ns〉Ωss, Ωss is the averaged normal stress at the surface of the solid grains. It has also been shown [69] that
| (39) |
When the terms accounting for interfacial and common curve contributions to the solid surface stress are neglected, evaluation of the averaging operator on the right side of Eq. (39) yields
| (40) |
Eq. (40) shows that the thermodynamically consistent form makes use of the fluid pressures averaged over the appropriate solid surface with weighting parameters equal to the fractions of the surface area in contact with each fluid. This is in contrast to the use of volume averaged pressures weighted by their respective saturations that might be heuristically proposed. Incorporation of Eq. (40) into Eq. (37), with α̂ = 1 allows formal recovery of the Bishop stress [20]. Substitution of the equality produced by eliminating between Eqs. (39) and (40) into Eq. (38) gives the expression for the Biot coefficient. Use of α̂ and given by Eq. (38) in Eq. (37) gives the Skempton stress. The TCAT derivation makes it clear that the pressures that should appear in the expressions for the Bishop and Skempton stresses are actually surface averages rather than volume averages. This is the main change from the traditional forms. Terms that arise from the surface curvature that contribute to the stress have also been identified above and can be retained, if desired or if they are found to be important, so that a more complete expression for the stress is obtained.
The TCAT procedure shows that the solid pressure in Eq. (34) is given by the form [69]
| (41) |
The solid stress tensor has its classical form, obtained as an average of the microscale solid stress tensor and is related to the second Piola-Kirchhoff stress tensor
| (42) |
where js is the microscale solid phase jacobian. This evaluation of the macroscale stress-strain pair has been shown to be consistent with the Hill-Mandel condition [69], i.e. the total work done in the system based on microscale quantities is the same as the total work based on macroscale conditions [77, 107]. The resulting expressions of the solid stress tensor obtained using TCAT are more complex than those appearing typically in the literature because the distinction between averages of pressure over surfaces and phase regions is incorporated into the model. Additionally, the relation between microscale and macroscale pressures is explicit. The Bishop-like parameters are not assumed but dependences on both volume fractions and solid surface fractional areas are retained, and the influence of the interfacial tensions on system behavior is included in the model.
TCAT analysis has facilitated an improvement in standard analyses of work input for unsaturated porous media [81, 172]. This is useful for the choice of the appropriate stress variables in the investigation of the mechanical and hydric behavior of multiphase porous media. It is also useful for the identification of the strains that are work conjugate to the chosen stresses. For a three phase medium the work input has been derived in the form [70]
| (43) |
where the following restrictions have been imposed: the interfaces and common curve have negligible mass; the common curve lineal tension is negligible such that ; mass exchange between entities is negligible; the solid deformations are considered infinitesimal; and the gradient in the areas per volume is negligible.
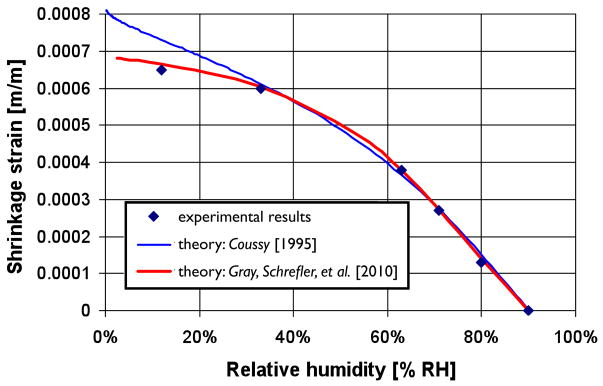
We show now a practical advantage in adopting the split employed in the Skempton stress (Eqs. (37) and (38)) based on the TCAT definition of the terms and the expression for work input. In geomaterials changes of the relative humidity produce a load on the solid phase related to the evolution of the capillary pressure. This additional load produces a macroscopic deformation of the skeleton and may cause shrinkage or swelling. The phenomenon can be properly described through the effective stress principle and appropriate stress-strain relationships. As an example shown in Fig 2, a concrete sample has been exposed to a drying process down to very low degrees of relative humidity; and the ensuing volumetric strains (shrinkage) have been measured. The process has then been simulated with two different effective stress formulations. One form is that proposed by Coussy [32, 33], which makes use of a differential expression such that
Fig. 2.
Comparison of results for shrinkage strain obtained by assuming respectively the Skempton effective stress and the Coussy effective stress, with experimental data from Baroghel-Bouny et al. [11]. Redrawn from [151].
| (44) |
Implementation of this form in a code requires that the differential form be properly evaluated [150]. The Coussy form is based on RT ideas and proposes that the Helmholtz free energy of the solid phase depends only on sw, temperature, and the Lagrangian strain tensor [151]. A second form employed is the TCAT representation of the Skempton stress where the capillary pressure is generalized to account for disjoining pressure. These two expressions were used to simulate the behavior of concrete that is being dried down to a very low degree of humidity. As demonstrated in Fig 2, both formulations model the shrinkage strain well down to a humidity of about 30%. However, the data point at about 12% humidity is modeled much more effectively by the TCAT model of system variables and parameters. This is so because the Coussy form includes an incomplete differential form of the Helmholtz free energy and thus the resulting stress form is incomplete. This difference is of primary importance at low relative humidity, which is consistent with the data shown in the figure.
6 Megascale Modeling Based on Averaging
Averaging procedures can also be employed to facilitate transformation of equations and problem descriptions to scales larger than the macroscale. In some cases, for example, it may be useful to construct a model that ignores spatial variation in one or more dimensions. Thus, in those dimensions averaging is performed over the system or a portion of the system. Such an approach is common, for example, in developing shallow water equations for surface water flow [96, 99, 105], in deriving equations for flow in groundwater aquifers when the Dupuit assumption that flow is essentially horizontal applies [15, 131, 146], in deriving the Saint Venant equations for river flow [1, 37, 92], and in vertically averaged models for land subsidence due to sub-surface pumping [16, 17, 153]. The averaging need not be performed over the entire megascale of a system but can include only a portion of the region, as long as variation in the variables over that region in the direction of averaging is not required [e.g., a multilayer flow model as in 5, 106, 158].
The most significant effort to apply averaging theory in conjunction with a thermodynamic closure theory in the context of megascale systems is the work of Reggiani and co-workers [141–145]. The idea of this work is to identify each element of a watershed (e.g., river channel, aquifer, hillslope) as a megascale element. Then these elements are hooked together by accounting for the fluxes between elements. This work was conducted using RT as the thermodynamic formalism [142]. Use of RT in this context suffers from the issues mentioned previously, but the shortcomings are even more problematic for large systems where representative values are needed for variables that have significant microscale variability. Since the average values of quantities such as pressure and temperature provide potentials for flow between elements, it is important that these be developed in an appropriate form. Because of problems with the pressures obtained being used to drive flow, a patching of the equations was performed to include the gravitational potential [143]. This serves to make the appearance of the RT formalism seem satisfactory, but problems persist about the physical interpretation of some of the symbols that arise and of the validity of the closure relations. Work required to incorporate a better thermodynamic formalism into the study of watersheds at the megascale is significant and has not been published.
The TCAT approach to megascale modeling has been advanced recently but is in its infancy. One effort examined stream channel flow to determine the entropy production rate in uniform flow and the minimum entropy production rate for gradually varied flow [51]. A general procedure for employing TCAT in the megascale context with regard to porous media has been presented and applied to single-fluid-phase-flow [60]. Results obtained using this method have been applied to column flow for the purpose of confirming Darcy’s experimentally based law and studying the validity of its extension to the macroscale situation [63].
7 Discussion
During the years of existence of Advances in Water Resources a significant effort has been made to put the formulation of larger scale models of environmental systems, particularly porous media, on firm theoretical grounds. Averaging of the conservation equations has been applied to equations describing interfaces between phases and common curves where interfaces come together as well as to fluid and solid phases. Although the averaging of these equations can be accomplished relatively easily using appropriate mathematical theorems, the problem arises as to how to close these resultant equations. Because conservation equations must not violate principles of thermodynamics, an implementation of the method to exploit the entropy inequality [31] has been found useful.
One of the challenges in using this method has been the identification of a suitable thermodynamic formalism. This problem arises even when one is performing microscale closure analyses, and its resolution has led to the proposition of thermodynamic structures that go beyond classical irreversible thermodynamics. The rational thermodynamic approach, which allows for a memory effect and expands the set of independent variables on which energy depends, has been used with some success at the microscale despite the fact that it can be criticized because it does not retain the classical definitions of variables such as temperature and entropy [103, 110]. RT is a mathematical, rather than a physical, formalism. The physical disconnect between variables that arise at the macroscale or megascale increases with length scale when the thermodynamics are proposed, using an RT formalism, directly at that larger scale of interest. Because the phases and their properties are distributed within the averaging region in ways that typically are non-uniform, the representation of these properties, particularly intensive properties, is challenging. It is particularly important to ensure that consistency exists across scales so that computations and/or measurements made at a small scale can be systematically transformed to a larger scale in a way that is consistent with their appearance in governing equations. Otherwise, there can be no rigorous multiscale verification of models.
As a tool for overcoming the inadequacies of neglecting thermodynamic implications altogether or of creating a disconnect between the microscale and the larger scale, the TCAT approach has proven to be valuable. The most important characteristic of this method is that a precise relationship is obtained between larger scale variables and their smaller scale antecedents. This feature allows for the use of experimental and computational studies to be employed to study the relations obtained. The important feature of TCAT that provides its robustness are the incorporation of microscale equilibrium and thermodynamic relations directly into the formalism.
The TCAT approach has not only led to macroscale and megascale formulations that have not been obtained previously, it has enabled shortcomings of the ACRT approach to be identified. These include imprecise definitions of intensive variables, a lack of independent equations, and incorrect formulations of the stress tensors, particularly in evaluating the stress on a surface. The TCAT formalism adds a layer of complexity, partly seen in the definitions of variables that arise (e.g., large scale pressures are obtained both as averages over surfaces and averages over phases); but the ability of TCAT to differentiate among these different averages and allow identification of the meaning of the larger scale variables makes it robust.
As Advances in Water Resources looks forward to its next 35 years, much work remains in allowing the methods for rigorous change in scale to reach their potential. The equations obtained must become the forms which underlie stochastic analyses; the values and importance of parameters that enter the equations must be obtained through interdisciplinary work; the forms obtained must be incorporated into existing codes. TCAT has confirmed the observation that “insofar as science is a body of knowledge, that body is provisional: much of what we thought we knew in the past has turned out to be incomplete, or plain wrong.” [91]. With an open-minded approach to what we think we know about modeling systems at a larger scale, a willingness to question and confirm results, the flexibility to change course when needed, and the humility to admit that some favored approaches have not panned out, we can ensure a more effective future.
Highlights.
use of thermodynamically constrained averaging theory (TCAT) in upscaling.
discusses advantages of TCAT relative to other averaging approaches.
Indicates key features of the TCAT approach in modeling multiphase systems.
Clarifies misconceptions about developing meaningful physical upscaled variables.
Defines capillary pressure for multiphase flow and stress tensor in geomechanics.
Acknowledgments
This work was supported by National Science Foundation grant ATM-0941235, Department of Energy grant DE-SC0002163, National Institute of Environmental Health Sciences grant P42 ES05948, and University of Padua Strategic Project STPD08JA32. We thank Brian Wood for helpful discussions related to MVA.
Notation
Roman letters
- d
rate of strain tensor
- d
differential
- Ew
internal energy per volume of the w phase
- e
infinitesimal strain tensor
- ez
unit vector along the axis of a channel positive in the direction from end 1 to end 2
- f
constitutive function equal to pn − pw
- g
gravitational vector
- g
magnitude of the gravitational vector
- H
vector function equal to the difference between the average of the gradient of the microscopic pressure and the gradient of volume averaged pressure
- H
enthalpy per volume
- h
hydraulic head
- I
identity tensor
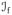
index set of fluid phases, {w, n}
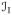
index set of interfaces, {wn, ws, ns}
- Jw
surface curvature of the boundary of phase w defined as the surface divergence of the outward normal from entity w
- js
microscale solid phase jacobian
- K̂
proportionality constant
- K̂T
bulk modulus
- k̂ε
tensor coefficient
modified generation rate coefficient for wn interfacial area
- L
column length
- l
averaging length scale
- M
an arbitrary weighting function used in defining larger-scale averages
- nα
unit vector positive outward from phase α on its boundary
a measure of total system pressure
- p
pressure
macroscale measure of the pressure of the α phase, α ∈ {w, n, s}, whose definition must be provided or derived
pressure of the α phase averaged over the αβ interface that forms a portion of the boundary of the α phase
- q
volumetric flow rate per cross-sectional area in one-dimensional flow
- q
volumetric flow rate per unit volume vector
- sα
saturation of fluid phase α where α ∈ {w, n}
- t
stress tensor
- t
time
- Vm
a vector consisting of m scalar variables
- v
velocity
- W
work input
- X
reference configuration of the solid phase
- x
position vector in the solid phase
Greek letters
- α
qualifier used to indicate a phase, interface, or common curve such that here α may be specified to take on the values w, n, s, wn, ws, ns, or wns
- α̂
Biot coefficient
- αβ
qualifier typically referring to an interface between phases, αβ ∈ wn, ws, ns
- β
qualifier, or part of a qualifier, typically taking on values referring to a phase, β ∈ {w, n, s}
- γ
interfacial tension
- ε
porosity, = 1 − εs
- εα
volume fraction of phase α when α ∈ {w, n, s}
- εαβ
area of αβ interface per unit volume where αβ ∈ {wn, ws, ns }
- εwns
common curve length of wns common curve per unit volume
- Λ
unit vector tangent to the axis of a cylindrical column
- μ
chemical potential
- ρ
mass density
- σ
solid-phase Lagrangian stress tensor
effective stress tensor divided by the solid phase volume fraction
- τ̂A
coefficient in linearized force-flux relation for capillary pressure dynamics
fraction of the solid surface in contact with the α phase forming an αs interface where α ∈ {w, n}
- ψ
gravitational potential
- Ω
spatial domain
Subscripts (for microscale) and superscripts (for macroscale)
- c
capillary pressure
- eq
equilibrium value
- i
designates ends i = 1 and i = 2 of a column
- n
non-wetting-phase qualifier
- ns
qualifier for interface formed between non-wetting and solid phases
- s
solid-phase qualifier
- ss
solid surface qualifier
- Total
total stress tensor
- trad
traditional form of the total stress tensor
- w
wetting-phase qualifier
- wei
wetting phase at end i of a column
- wn
qualifier for interface formed between wetting and non-wetting phases
- wns
qualifier for common curve formed where the wetting, non-wetting, and solid phases meet
- ws
qualifier for interface formed between wetting and solid phases
- ww
qualifier indicating the total surface bounding the w phase
- α
entity qualifier
- αβ
entity qualifier indicating an αβ interface
Symbols
- ∇
gradient operator
- ∇′
surface gradient operator
- –
above a superscript refers to a density weighted macroscale average
- =
above a superscript refers to a larger scale quantity whose relation to a microscale quantity is unknown in RT or is a uniquely defined larger scale quantity in terms of averages of microscale quantities using TCAT
- 〈Fα〉Ωβ,Ωγ,M
, general average of microscale property F of entity α obtained as a weighted average over domain Ωβ where M is the weighting function, normalized by the weighting function integrated over domain Ωγ. When M = 1 it may be omitted in the expression.
- 〈Fα〉Ωα,Ωα,ρα
, density weighted average of a microscale property F of an entity over that entity
- 〈Fα〉Ωα,Ωα
, volume average of a microscale α phase (interface) property F over the phase (interface)
〈Fα〉Ωαβ,Ωαβ, average of a microscale property F of phase α over the αβ interface
Abbreviations and Acronyms
- ACRT
averaging of conservation equations with rational thermodynamics
- AWR
Advances in Water Resources
- CEI
constrained entropy inequality
- CIT
classical irreversible thermodynamics
- EIT
extended irreversible thermodynamics
- MVA
method of volume averaging
- RT
rational thermodynamics
- SEI
simplified entropy inequality
- TCAT
thermodynamically constrained averaging theory
- TIV
theory of internal variables
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
William G. Gray, Email: GrayWG@unc.edu, Department of Environmental Sciences and Engineering, University of North Carolina, Chapel Hill, North Carolina 27599-7431, USA.
Cass T. Miller, Email: miller@unc.edu, Department of Environmental Sciences and Engineering, University of North Carolina, Chapel Hill, North Carolina 27599-7431, USA.
Bernhard A. Schrefler, Email: bas@dic.unipd.it, Dipartimento di Costruzioni e Trasporti Facolta’ di Ingegneria, Universita’ degli Studi di Padova, via F. Marzolo, 9, 35131, Padova, Italy.
References
- 1.Abbott MB. Computational Hydraulics, Elements of the Theory of Free-Surface Flows. Pitman; London: 1979. [Google Scholar]
- 2.Ahrenholz B, Niessner J, Helmig R, Krafczyk M. Pore-scale determination of parameters for macroscale modeling of evaporation processes in porous media. Water Resources Research. 2011;47(W07543) doi: 10.1029/2010WR009519. [DOI] [Google Scholar]
- 3.Alts T, Hutter K. Continuum description of the dynamics and thermodynamics of phase boundaries between ice and water. Part I: Surface balance laws and their interpretation in terms of three-dimensional balance laws averaged over the phase change boundary layer. Journal of Non-Equilibrium Thermodynamics. 1988;13:221–257. [Google Scholar]
- 4.Anderson TB, Jackson R. A fluid mechanical description of fluidized beds. Industrial and Engineering Chemistry Fundamentals. 1967;6:527–539. [Google Scholar]
- 5.Aral MM. Ground Water Modeling in Multilayer Aquifers: Steady Flow. Lewis Publishers, Inc; 1990. [Google Scholar]
- 6.Bachmat Y. Spatial macroscopization of processes in heterogeneous systems. Israel Journal of Technology. 1972;10:391–403. [Google Scholar]
- 7.Bailyn M. A Survey of Thermodynamics. American Institute of Physics Press; New York: 1994. [Google Scholar]
- 8.Balasubramanian K, Hayot F, Saam WF. Darcy’s law from lattice-gas hydrodynamics. Physical Review A. 1987;36:2248–2253. doi: 10.1103/physreva.36.2248. [DOI] [PubMed] [Google Scholar]
- 9.Balhoff MT, Thompson KE, Hjorts M. Coupling pore-scale networks to continuum-scale models of porous media. Computers and Geosciences. 2007;33(3):393–410. [Google Scholar]
- 10.Barenblatt GI. Flow of two immiscible fluids in homogeneous porous medium (in Russian) Izv AN SSSR, Mekh Zhidk i Gaza. 1971;5:144–151. [Google Scholar]
- 11.Baroghel-Bouny V, Mainguy M, Lassabatere T, Coussy O. Characterization and identification of equilibrium and transfr moisture properties for ordinary and high-performance cementitious materials. Cement and Concrete Research. 1999;29:1225–1238. [Google Scholar]
- 12.Baveye P. Comment on “The role of scaling laws in upscaling” by B. D. Wood. Advances in Water Resources. 2010;33(1):123–124. [Google Scholar]
- 13.Bear J. Dynamics of Fluids in Porous Media. Elsevier; New York: 1972. [Google Scholar]
- 14.Bear J. On the aquifer’s integrated balance equations. Advances in Water Resources. 1977;1(1):15–23. [Google Scholar]
- 15.Bear J. Hydraulics of Groundwater. McGraw-Hill; New York: 1979. [Google Scholar]
- 16.Bear J, Corapcioglu MY. Mathematical model for regional land subsidence due to pumping: 1. Integrated aquifer subsidence equations based on vertical displacement only. Water Resources Research. 1981;17(4):937–946. doi: 10.1029/WR017i004p00937.. [DOI] [Google Scholar]
- 17.Bear J, Corapcioglu MY. Mathematical model for regional land subsidence due to pumping: 2. Integrated aquifer subsidence equations for vertical and horizontal displacements. Water Resources Research. 1981;17(4):947–958. doi: 10.1029/WR017i004p00947. [DOI] [Google Scholar]
- 18.Bennethum LS, Murad MA, Cushman JH. Macroscale thermodynamics and the chemical potential for swelling porous media. Transport in Porous Media. 2000;39:187–225. [Google Scholar]
- 19.Bertin H, Quintard M, Corpel V. Two-phase flow in heterogeneous porous media III: Laboratory experiments for flow parallel to a stratified system. Transport in Porous Media. 1990;5(6):543–590. [Google Scholar]
- 20.Bishop AW. The principle of effective stress. Teksnik Ukeblad. 1959;39:859–863. [Google Scholar]
- 21.Blunt M, King P. Relative permeabilities from two- and three-dimensional pore scale network modeling. Transport in Porous Media. 1991;6(4):407–434. [Google Scholar]
- 22.Bobeck P. Geotechnical Translations. Austin, TX: 2004. The Public Fountains of the City of Dijon (translation of Les Fontaines Publiques de la Ville de Dijon by Henry Darcy, 1856) [Google Scholar]
- 23.Borja RI. Cam-Clay plasticity. Part V: A mathematical framework for three-phase deformation and strain localization analyses of partially saturated porous media. Computer Methods in Applied Mechanics and Engineeering. 2004;193:5301–5338. [Google Scholar]
- 24.Boruvka L. PhD thesis. University of Toronto; Toronto: 1975. An Extension to Classical Theory of Capillarity. [Google Scholar]
- 25.Boruvka L, Neumann AW. Generalization of the classical theory of capillarity. Journal of Chemical Physics. 1977;66(12):5464–5476. [Google Scholar]
- 26.Boruvka L, Rotenberg Y, Neumann AW. Free energy formulation of the theory of capillarity. Langmuir. 1985;1(1):40–44. [Google Scholar]
- 27.Callen HB. Thermodynamics and an Introduction to Thermostatistics. Wiley; New York: 1985. [Google Scholar]
- 28.Chen D, Pyrak-Nolte LJ, Griffin J, Giordano NJ. Measurement of interfacial area per volume for drainage and imbibition. Water Resources Research. 2007;43 [Google Scholar]
- 29.Cheng JT, Pyrak-Nolte LJ, Giordano N. Proceedings of the North American Rock Mechanics Symposium. Tunneling Association of Canada; 2002. Micro-model studies of multiphase flow in porous media. [Google Scholar]
- 30.Cheng JT, Pyrak-Nolte LJ, Nolte DD, Giordano NJ. Linking pressure and saturation through interfacial areas in porous media. Geophysical Research Letters. 2004;31(8) [Google Scholar]
- 31.Coleman BD, Noll W. The thermodynamics of elastic materials with heat conduction and viscosity. Archives of Rational Mechanical Analysis. 1963;13:167–178. [Google Scholar]
- 32.Coussy O. Mechanics of Porous Continua. Wiley; Chichester: 1995. [Google Scholar]
- 33.Coussy O. PoroMechanics. Wiley; Chichester: 2004. [Google Scholar]
- 34.Crapiste GH, Rotstein E, Whitaker S. A general closure scheme for the method of volume averaging. Chemical Engineering Science. 1986;41:227–235. [Google Scholar]
- 35.Culligan KA, Wildenschild D, Christensen BSB, Gray WG, Rivers ML, Tompson AFB. Interfacial area measurements for unsaturated flow through a porous medium. Water Resources Research. 2004;40(12) doi: 10.1029/2004WR003278. [DOI] [Google Scholar]
- 36.Culligan KA, Wildenschild D, Christensen BSB, Gray WG, Rivers ML. Pore-scale characteristics of multiphase flow in porous media: A comparison of air-water and oil-water experiments. Advances in Water Resources. 2006;29(2):227–238. [Google Scholar]
- 37.Cunge JA, Holly FM, Verwey A. Practical Aspects of Computational River Hydraulics. Pitman; London: 1980. [Google Scholar]
- 38.Dahle HK, Celia MA. A dynamic network model for two-phase immiscible flow. Computational Geosciences. 1999;3(1):1–22. [Google Scholar]
- 39.Darcy H. Les Fontaines Publiques de la Ville de Dijon. Dalmont; Paris: 1856. [Google Scholar]
- 40.Darcy H. Determination of the laws of flow of water through sand. In: Freeze RA, Back W, editors. Physical Hydrology. Hutchinson Ross; Stroudsburg, PA: 1983. [Google Scholar]
- 41.De Groot SR, Mazur P. Non-equilibrium Thermodynamics. Dover; New York: 1984. [Google Scholar]
- 42.DiCarlo DA. Can continuum extensions to multiphase flow models describe preferential flow? Vadose Zone Journal. 2010;9:268–277. doi: 10.2136/vzj2009.0099. [DOI] [Google Scholar]
- 43.Dillard LA, Blunt MJ. Development of a pore network simulation model to study nonaqueous phase liquid dissolution. Water Resources Research. 2000;36(2):439–454. [Google Scholar]
- 44.Eringen AC. Note on Darcy’s Law. Journal of Applied Physics. 2003;94(3):1282. [Google Scholar]
- 45.Essex C, McKitrick R, Andresen B. Does a global temperature exist? Journal of Non-Equilibrium Thermodynamics. 2007;32:1–27. [Google Scholar]
- 46.Fischer U, Celia MA. Prediction of relative and absolute permeabilities for gas and water from soil water retention curves using a pore-scale network model. Water Resources Research. 1999;35(4):1089–1100. [Google Scholar]
- 47.Fredlund DG, Rahardjo H. Soil Mechanics for Unsaturated Soils. Wiley; New York: 1993. [Google Scholar]
- 48.Gawin D, Pesavento F, Schrefler BA. Modelling creep and shrinkage of concrete by means of effective stress. Materials and Structures. 2007;40:579–591. [Google Scholar]
- 49.Gray WG. Thermodynamics and constitutive theory for multiphase porous-media flow considering internal geometric constraints. Advances in Water Resources. 1999;22(5):521–547. [Google Scholar]
- 50.Gray WG. Macroscale equilibrium conditions for two-phase flow in porous media. International Journal of Multiphase Flow. 2000;26(3):467–501. [Google Scholar]
- 51.Gray WG, Ghidaoui MS. Thermodynamic analysis of stream flow hydrodynamics. Journal of Hydraulic Research. 2009;47(4):403–417. doi: 10.3826/jhr.2009.3331. [DOI] [Google Scholar]
- 52.Gray WG, Hassanizadeh SM. Averaging theorems and averaged equations for transport of interface properties in multiphase systems. International Journal of Multiphase Flow. 1989;15(1):81–95. [Google Scholar]
- 53.Gray WG, Lee PCY. On the theorems for local volume averaging of multiphase systems. International Journal of Multiphase Flow. 1977;3:333–340. [Google Scholar]
- 54.Gray WG, Miller CT. Examination of Darcy’s law for flow in porous media with variable porosity. Environmental Science & Technology. 2004;38(22):5895–5901. doi: 10.1021/Es049728w. [DOI] [PubMed] [Google Scholar]
- 55.Gray WG, Miller CT. Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 1. Motivation and overview. Advances in Water Resources. 2005;28(2):161–180. doi: 10.1016/j.advwatres.2007.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Gray WG, Miller CT. Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 3. Single-fluid-phase flow. Advances in Water Resources. 2006;29(11):1745–1765. doi: 10.1016/j.advwatres.2008.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Gray WG, Miller CT. Consistent thermodynamic formulations for multiscale hydrologic systems: Fluid pressures. Water Resources Research. 2007;43(9) doi: 10.1029/2006WR005811. [DOI] [Google Scholar]
- 58.Gray WG, Miller CT. Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 5. Single-fluid-phase transport. Advances in Water Resources. 2009;32(5):681–711. doi: 10.1016/j.advwatres.2008.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Gray WG, Miller CT. Thermodynamically constrained averaging theory approach for heat transport in single-fluid-phase porous media systems. Journal of Heat Transfer. 2009;131(10):101002. doi: 10.1115/1.3160539. [DOI] [Google Scholar]
- 60.Gray WG, Miller CT. Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 7. Single-phase megascale flow models. Advances in Water Resources. 2009;32(8):1121–1142. doi: 10.1016/j.advwatres.2009.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Gray WG, Miller CT. Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 8. Interface and common curve dynamics. Advances in Water Resources. 2010;33(12):1427–1443. doi: 10.1016/j.advwatres.2010.01.010.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Gray WG, Miller CT. TCAT analysis of capillary pressure in non-equilibrium, two-fluid-phase, porous medium systems. Advances in Water Research. 2011;34(6):770–778. doi: 10.1016/j.advwatres.2011.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Gray WG, Miller CT. On the algebraic and differential forms of Darcy’s equation. Journal of Porous Media. 2011;14(1):33–50. [Google Scholar]
- 64.Gray WG, O’Neill K. On the development of Darcy’s law for the general equations for flow in porous media. Water Resources Research. 1976;12(2):148–154. [Google Scholar]
- 65.Gray WG, Schrefler BA. Thermodynamic approach to effective stress in partially saturated porous media. European Journal of Mechanics A–Solids. 2001;20(4):521–538. [Google Scholar]
- 66.Gray WG, Schrefler BA. Analysis of the solid phase stress tensor in multiphase porous media. International Journal for Numerical and Analytical Methods in Geomechanics. 2007;31(4):541–581. doi: 10.1002/Nag.541. [DOI] [Google Scholar]
- 67.Gray WG, Leijnse A, Kolar RL, Blain CA. Mathematical Tools for Changing Spatial Scales in the Analysis of Physical Systems. CRC Press; Boca Raton: 1993. [Google Scholar]
- 68.Gray WG, Tompson AFB, Soll WE. Closure conditions for two-fluid flow in porous media. Transport in Porous Media. 2002;47(1):29–65. [Google Scholar]
- 69.Gray WG, Schrefler BA, Pesavento F. Work input for unsaturated elastic porous media. In review, Journal of the Mechanics and Physics of Solids. 2009 [Google Scholar]
- 70.Gray WG, Schrefler BA, Pesavento F. Work input for unsaturated elastic porous media. Journal of the Mechanics and Physics of Solids. 2010;58(5):752–765. doi: 10.1016/j.jmps.2010.02.005. [DOI] [Google Scholar]
- 71.Hager J, Whitaker S. The thermodynamic significance of the local volume averaged temperature. Transport in Porous Media. 2002;46:19–35. [Google Scholar]
- 72.Hassanizadeh SM, Gray WG. General conservation equations for multi-phase systems: 1. Averaging procedure. Advances in Water Resources. 1979;2(3):131–144. [Google Scholar]
- 73.Hassanizadeh SM, Gray WG. General conservation equations for multi-phase systems: 2. Mass, momenta, energy, and entropy equations. Advances in Water Resources. 1979;2(4):191–203. [Google Scholar]
- 74.Hassanizadeh SM, Gray WG. General conservation equations for multi-phase systems: 3. Constitutive theory for porous media flow. Advances in Water Resources. 1980;3(1):25–40. [Google Scholar]
- 75.Hassanizadeh SM, Gray WG. Mechanics and thermodynamics of multiphase flow in porous media including interphase boundaries. Advances in Water Resources. 1990;13(4):169–186. [Google Scholar]
- 76.Hassanizadeh SM, Celia MA, Dahle HK. Dynamic effect in the capillary pressure-saturation relationship and its impact on unsaturated flow. Vadose Zone Journal. 2002;1:38–57. [Google Scholar]
- 77.Hill R. The essential structure of constitutive laws for metal composites and polycrystals. Journal of the Mechanics and Physics of Solids. 1967;15:79–95. [Google Scholar]
- 78.Hillel D. Soil and Water. Academic Press; New York: 1971. [Google Scholar]
- 79.Hilpert M, Glantz R, Miller CT. Calibration of a pore-network model by a pore-morphological analysis. Transport in Porous Media. 2003;51(3):267–285. [Google Scholar]
- 80.Hou SL, Shan XW, Zuo QS, Doolen GD, Soll WE. Evaluation of two lattice Boltzmann models for multiphase flows. Journal of Computational Physics. 1997;138(2):695–713. [Google Scholar]
- 81.Houlsby GT. The work input to an unsaturated granular material. Géotechnique. 1997;47(1):193–196. [Google Scholar]
- 82.Hubbert MK. Darcy’s law and the field equations of the flow of underground fluids. Transactions of the American Institute of Mining Engineers. 1956;207:222–239. [Google Scholar]
- 83.Ishii M, Kim S. Development of one-group and two-group interfacial area transport equation. Nuclear Science and Engineering. 2004;146:1–17. [Google Scholar]
- 84.Ishii M, Kim S, Kelly J. Development of interfacial area transport equation. Nuclear Engineering and Technology. 2005;37(6):525–536. [Google Scholar]
- 85.Jackson ABS, Miller CT, Gray WG. Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 6. Two-fluid-phase flow. Advances in Water Resources. 2009;32(6):779–795. doi: 10.1016/j.advwatres.2008.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Jackson AS, Rybak I, Helmig R, Gray WG, Miller CT. Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 9. Transition region models. In review: Advances in Water Resources. 2011 [Google Scholar]
- 87.Joekar-Niasar V, Hassanizadeh SM. Specific interfacial area: The missing state variable in two-phase flow equation. Water Resources Research. 47(W05513):2011. doi: 10.1029/2010WR009291. [DOI] [Google Scholar]
- 88.Joekar-Niasar V, Prodanovíc M, Wildenschild D, Hassanizadeh SM. Network model investigation of interfacial area, capillary pressure and saturation relationships in granular porous media. Water Resources Research. 2010;46(W06526) doi: 10.1029/2009WR008585.. [DOI] [Google Scholar]
- 89.Jou D, Casas-Vazquez J. Extended irreversible thermodynamics and its relation with other continuum approaches. Journal of Non-Newtonian Fluid Mechanics. 2001;96(1–2):77–104. [Google Scholar]
- 90.Jou D, Casas-Vazquez J, Lebon G. Extended Irreversible Thermodynamics. Springer-Verlag; Berlin: 2001. [Google Scholar]
- 91.Judson O. License to wonder. 2009 URL http://opinionator.blogs.nytimes.com/2009/11/03/license-to-wonder/?pa.
- 92.Julien PY. River Mechanics. Cambridge University Press; Cambridge: 2002. [Google Scholar]
- 93.Kalaydjian F. A macroscopic description of multiphase flow in porous media involving spacetime evolution of fluid/fluid interface. Transport in Porous Media. 1987;2:537–552. [Google Scholar]
- 94.Kim S. PhD thesis. Purdue University; West Lafayette, Indiana: 1999. Interfacial Area Transport Equation and Measurement of Local Interfacial Characteristics. [Google Scholar]
- 95.Knackstedt MA, Sheppard AP, Sahimi M. Pore network modelling of two-phase flow in porous rock: The effect of correlated heterogeneity. Advances in Water Resources. 2001;24:257–277. [Google Scholar]
- 96.Kolar RL, Gray WG, Westerink JJ, Luettich RAJ. Shallow water modeling in spherical coordinates: Equation formulation, numerical implementation, and application. Journal of Hydraulic Research. 1994;32(1):3–24. [Google Scholar]
- 97.Kondepudi D, Prigogine I. Modern Thermodynamics. Wiley; Chichester: 1998. [Google Scholar]
- 98.Korteland S, Bottero S, Hassanizadeh SM, Berentsen CWJ. What is the correct definition of average pressure? Transport in Porous Media. 2010;84:153–175. doi: 10.1007/s11242-009-9490-2.. [DOI] [Google Scholar]
- 99.Lamb H. Hydrodynamics. Dover Publications; 1993. [Google Scholar]
- 100.Landry CJ, Karpyn ZT, Piri M. Pore-scale analysis of trapped immiscible fluid structures and fluid interfacial areas in oil-wet and water-wet bead packs. Geofluids. 2011;11(2):209–227. [Google Scholar]
- 101.Lavenda B. Thermodynamics of Irreversible Processes. McMillan; London: 1979. [Google Scholar]
- 102.Lebon G, Grmela M, Lhuillier D. A comparative study of the coupling of flow with non-Fickean thermodiffusion. Part I: Extended Irreversible Thermodynamics. Journal of Non-Equilibrium Thermodynamics. 2003;28(1):1–22. [Google Scholar]
- 103.Lebon G, Jou D, Casas-Vázquez J. Understanding Nonequilibrium Thermodynamics. Springer; Berlin: 2008. [Google Scholar]
- 104.Lhuillier D, Grmela M, Lebon G. A comparative study of the coupling of flow with non-Fickean thermodiffusion. Part III: Internal variables. Journal of Non-Equilibrium Thermodynamics. 2003;28(1):51–68. [Google Scholar]
- 105.Lynch DR. Basic hydrodynamic equations for lakes. In: Gray WG, editor. Physics-Based Modeling of Lakes, Reservoirs, and Impoundments. American Society of Civil Engineers; 1986. [Google Scholar]
- 106.Lynett PJ, Liu PL-F. Linear analysis of the multi-layer model. Coastal Engineering. 2004;51:439–454. [Google Scholar]
- 107.Mandel J. Plasticit Classique et Viscoplasticit. International Center for Mechanical Sciences (CISM), Springer-Verlag; Udine: 1971. [Google Scholar]
- 108.Marle C. Ècoulements monophasiques en milieu poreux. Revue de L’Institut Français du Pétrole. 1967;22(10):1471–1509. [Google Scholar]
- 109.Marle CM. On macroscopic equations governing multiphase flow with diffusion and chemical reactions in porous media. International Journal of Engineering Science. 1982;20(5):643–662. [Google Scholar]
- 110.Maugin GA. The Thermomechanics of Nonlinear Irreversible Behaviors: An Introduction. World Scientific Press; Singapore: 1999. [Google Scholar]
- 111.McClure JE, Adalsteinsson D, Wildenschild D, Gray WG, Miller CT. Computation of interfacial areas, common curve lengths, and interfacial curvatures from experimentally derived data. Proceedings of the 16th International Conference on Computational Methods in Water Resources (CMWR XVI); Copenhagen, Denmark. 19–22 June 2006; 2006. URL http://proceedings.cmwr-xvi.org, Paper 224. [Google Scholar]
- 112.McClure JE, Adalsteinsson D, Pan C, Gray WG, Miller CT. Approximation of interfacial properties in multiphase porous medium systems. Advances in Water Resources. 2007;30(3):354–365. doi: 10.1016/j.advwatres.2006.06.010.. [DOI] [Google Scholar]
- 113.Miller CT, Gray WG. Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 2. Foundation. Advances in Water Resources. 2005;28(2):181–202. doi: 10.1016/j.advwatres.2007.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Miller CT, Gray WG. Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 4. Species transport fundamentals. Advances in Water Resources. 2008;31(3):577–597. doi: 10.1016/j.advwatres.2007.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Miller CT, Christakos G, Imhoff PT, McBride JF, Pedit JA, Trangenstein JA. Multiphase flow and transport modeling in heterogeneous porous media: Challenges and approaches. Advances in Water Resources. 1998;21(2):77–120. [Google Scholar]
- 116.Mirzaei M, Das DB. Dynamic effects in capillary pressure-saturations relationships for two-phase flow in 3D porous media: Implications of micro-heterogeneities. Chemical Engineering Science. 2007;62(7):1927–1947. [Google Scholar]
- 117.Moeckel GP. Thermodynamics of an interface. Archive for Rational Mechanics and Analysis. 1975;57:255–280. [Google Scholar]
- 118.Montemagno CD, Gray WG. Photoluminescent volumetric imaging—A technique for the exploration of multiphase flow and transport in porous media. Geophysical Research Letters. 1995;22(4):425–428. [Google Scholar]
- 119.Montemagno CD, Gray WG. Photoluminescent volumetric imaging - a technique for the exploration of multiphase flow and transport in porous-media. Geophysical Research Letters. 1995;22(4):425–428. [Google Scholar]
- 120.Murad MA, Bennethum LS, Cushman JH. A multi-scale theory of swelling porous media: I. Application to one-dimensional consolidation. Transport in Porous Media. 1995;19:93–122. [Google Scholar]
- 121.Narasimhan TN. A note on volume-averaging. Advances in Water Resources. 1980 Sep;3:135–139. [Google Scholar]
- 122.Neuman SP. Theoretical derivation of Darcy’s Law. Acta Mechanica. 1977;25:153–170. [Google Scholar]
- 123.Niessner J, Hassanizadeh SM. A model for two-phase flow in porous media including fluid-fluid interfacial area. Water Resources Research. 2008;44(W08439) doi: 10.1029/2007WR006721. [DOI] [Google Scholar]
- 124.Niessner J, Hassanizadeh SM. Non-equilibrium interphase heat and mass transfer during two-phase flow in porous media - theoretical considerations and modeling. Journal of Contaminant Hydrology. 2009;32:1756–1766. [Google Scholar]
- 125.Niessner J, Hassanizadeh SM. Two-phase flow and transport in porous media including fluid-fluid interfacial area. In: Martin S, Williams JR, editors. Multiphase Flow Research. Nova Science Publishers; 2009. pp. 709–729. [Google Scholar]
- 126.Niessner J, Hassanizadeh SM. Modeling kinetic interphase mass transfer for two-phase flow in porous media including fluid-fluid interfacial area. Transport in Porous Media. 2009;80:329–344. [Google Scholar]
- 127.Niessner J, Berg S, Hassanizadeh SM. Comparison of two-phase Darcy’s Law with a thermodynamically consistent approach. Transport in Porous Media. 2011;88:133–148. doi: 10.1007/s11242-011-9730-0. [DOI] [Google Scholar]
- 128.Nordbotten JM, Celia MA, Dahle HK, Hassanizadeh SM. Interpretation of macroscale variables in Darcy’s law. Water Resources Research. 2007;43 doi: 10.1029/2006WR005018. [DOI] [Google Scholar]
- 129.Nordbotten JM, Nogués JP, Celia MA. Appropriate choice of average pressure for upscaling relative permeability in dynamic flow conditions. Society of Petroleum Engineers Journal. 2010 Mar;:228–237. [Google Scholar]
- 130.Nordhaug HF, Celia M, Dahle HK. A pore network model for calculation of interfacial velocities. Advances in Water Resources. 2003;26(10):1061–1074. [Google Scholar]
- 131.Pinder GF, Gray WG. Essentials of Multiphase Flow and Transport in Porous Media. John Wiley & Sons, Inc; Hoboken, NJ: 2008. [Google Scholar]
- 132.Porter ML, Wildenschild D. Validation of an image analysis method for computed microtomography image data of multiphase flow in porous systems. Journal of Computational Geosciences. 2009 doi: 10.1007/s10596-009-9130-5.. [DOI] [Google Scholar]
- 133.Porter ML, Schaap MG, Wildenschild D. Lattice-Boltzmann simulations of the capillary pressure-saturation-interfacial area relationship for porous media. Advances in Water Resources. 2009;32(11):1632–1640. [Google Scholar]
- 134.Porter ML, Wildenschild D, Grant G, Gerhard JI. Measurement and prediction of the relationship between capillary pressure, saturation, and interfacial area in a NAPL-water-glass bead system. Water Resources Research. 2010;46(W08512) doi: 10.1029/2009WR007786. [DOI] [Google Scholar]
- 135.Prodanovíc M, Lindquist WB, Seright RS. Porous structure and fluid partitioning in polyethylene cores from 3D X-ray microtomographic imaging. Journal of Colloid and Interface Science. 2006;298:282–297. doi: 10.1016/j.jcis.2005.11.053. [DOI] [PubMed] [Google Scholar]
- 136.Quintard M, Whitaker S. Two-phase flow in heterogeneous porous media: The method of large-scale averaging. Transport in Porous Media. 1988;3(4):357–413. [Google Scholar]
- 137.Quintard M, Whitaker S. Two-phase flow in heterogeneous porous media I: The influence of large spatial and temporal gradients. Transport in Porous Media. 1990;5(4):341–379. [Google Scholar]
- 138.Quintard M, Whitaker S. Convection, dispersion, and interfacial transport of contaminants: Homogeneous porous media. Advances in Water Resources. 1994;17(4):221–239. [Google Scholar]
- 139.Quintard M, Whitaker S. Transport in chemically and mechanically heterogeneous porous media. I: Theoretical development of region-averaged equations for slightly compressible single-phase flow. Advances in Water Resources. 1996;19(1):29–47. [Google Scholar]
- 140.Reeves PC, Celia MA. A functional relationship between capillary pressure, saturation, and interfacial area as revealed by a pore-scale network model. Water Resources Research. 1996;32(8):2345–2358. [Google Scholar]
- 141.Reggiani P, Rientjes THM. Flux parameterization in the representative elementary watershed approach: Application to a natural basin. Water Resources Research. 2005;41(W04013) doi: 10.1029/2004WR003693. [DOI] [Google Scholar]
- 142.Reggiani P, Sivapalan M, Hassanizadeh SM. A unifying framework for watershed thermodynamics: Balance equations for mass, momentum, energy and entropy, and the second law of thermodynamics. Advances in Water Resources. 1998;22(4):367–398. [Google Scholar]
- 143.Reggiani P, Hassanizadeh SM, Sivapalan M, Gray WG. A unifying framework for watershed thermodynamics: Constitutive relationships. Advances in Water Resources. 1999;23(1):15–39. [Google Scholar]
- 144.Reggiani P, Sivapalan M, Hassanizadeh SM. Conservation equations governing hillslope responses: Exploring the physical basis of water balance. Water Resources Research. 2000;36(7):1845–1863. [Google Scholar]
- 145.Reggiani P, Sivapalan M, Hassanizadeh SM, Gray WG. Coupled equations for mass and momentum balance in a stream network: Theoretical derivation and computational experiments. Proceedings of the Royal Society of London Series a-Mathematical Physical and Engineering Sciences. 2001;457(2005):157–189. [Google Scholar]
- 146.Reisenauer AE. Technical report. Pacific Northwest Laboratory; Richland, Washington: 1979. Variable thickness transient ground-water flow model Volume 1. Formulation; p. 99352. [Google Scholar]
- 147.Sakaki T, O’Carroll DM, Illangasekare TH. Direct quantification of dynamic effects in capillary pressure for drainage-wetting cycles. Vadose Zone Journal. 2010;9:424–437. [Google Scholar]
- 148.Santos JE, Sheen D. Derivation of a Darcy’s law for a porous medium composed of two solid phases saturated by a single-phase fluid: A homogenization approach. Transport in Porous Media. 2008;74(3):349–368. [Google Scholar]
- 149.Scheidegger AE. The Physics of Flow through Porous Media. University of Toronto Press; Toronto: 1974. [Google Scholar]
- 150.Schrefler BA, Gawin D. The effective stress principle: Incremental or finite form. International Journal for Numerical and Analytical Methods in Geomechanics. 1996;20(11):785–814. [Google Scholar]
- 151.Schrefler BA, Boso DP, Pesavento F, Gawin D, Lefik M. Mathematical and numerical multiscale modelling. 2011 URL http://www.cmm.il.pw.edu.pl/cd/pdf/302.pdf.
- 152.Simmons CT. Henry Darcy (1803–1858): Immortalised by his scientific legacy. Hydrogeology Journal. 2008;16:1023–1038. [Google Scholar]
- 153.Simoni L, SchreflerFE BA. solution of a vertically averaged model for regional land subsidence. International Journal for Numerical Methods in Engineering. 1989;27:215–230. [Google Scholar]
- 154.Skempton AW. Effective stress in soils, concrete and rock. Pore Pressure and Suction in Soils. 1961:4–16. [Google Scholar]
- 155.Slattery JC. Flow of viscoelastic fluids through porous media. American Institute of Chemical Engineers Journal. 1967;13(6):1066–1071. [Google Scholar]
- 156.Soll WE, Celia MA, Wilson JL. Micromodel studies of three-fluid porous media systems: Pore-scale processes relating to capillary pressure-saturation relationships. Water Resources Research. 1993;29(9):2963–2974. [Google Scholar]
- 157.Stauffer F. Time dependence of the relations between capillary pressure, water content and conductivity during drainage of porous media. International IAHR Symposium on Scale Effects in Porous Media; Thessaloniki, Greece. 1978. [Google Scholar]
- 158.Stewart AL, Dellar PJ. Multilayer shallow water equations with complete Coriolis force. Part I: Derivation on a non-traditional beta-plane. Journal of Fluid Mechanics. 2010;651:387–413. [Google Scholar]
- 159.Thompson KE, Wilson CS, White CD, Nyman S, Bhattacharya JP, Reed AH. Application of a new grain-based algorithm to microtomography images for quantitative characterization and flow modeling. Journal of the Society of Petroleum Engineers. 2008;13(2):164–176. [Google Scholar]
- 160.Tsakiroglou CD, Theodoropoulou MA, Karoutsos V. Nonequilibrium capillary pressure and relative permeability curves of porous media. AIChE Journal. 2003;49(10):2472–2486. [Google Scholar]
- 161.Vavruch I. Conceptual problems of modern irreversible thermodynamics. Chemicke Listy. 2002;96(5):271–275. [Google Scholar]
- 162.Whitaker S. Diffusion and dispersion in porous media. American Institute of Chemical Engineers Journal. 1967;13(3):420–427. [Google Scholar]
- 163.Whitaker S. Advances in theory of fluid motion in porous media. Industrial and Engineering Chemistry. 1969;61(12):14–28. [Google Scholar]
- 164.Whitaker S. Flow in porous media I: A theoretical derivation of Darcy’s law. Transport in Porous Media. 1986;1:3–25. [Google Scholar]
- 165.Whitaker S. Flow in porous media II: The governing equations for immiscible, two-phase flow. Transport in Porous Media. 1986;1:105–125. [Google Scholar]
- 166.Whitaker S. The Method of Volume Averaging. Kluwer Academic Publishers; Dordrecht: 1999. [Google Scholar]
- 167.Wildenschild D, Hopmans JW, Vaz CMP, Rivers ML. Using X-ray microtomography to determine gas and liquid phase distributions in porous media. Advanced Photon Source, Argonne National Laboratory; Argonne, IL: 2000. Advanced photon source activity report 2000. page available at http://www.aps.anl.gov/apsar2000/wildenschild1.pdf. [Google Scholar]
- 168.Wildenschild D, Hopmans JW, Vaz CMP, Rivers ML, Rikard D, Christensen BSB. Using X-ray computed tomography in hydrology: Systems, resolutions, and limitations. Journal of Hydrology. 2002;267(3–4):285–297. [Google Scholar]
- 169.Wood BD, Valdés-Parada FJ. Volume averaging parabolic balance equations: Local and nonlocal closures using a Green’s function approach. In review. 2011 [Google Scholar]
- 170.Woods L. The bogus axioms of continuum mechanics. Bulletin of the Institute of Mathematics and Its Applications. 1981;17:98–102. [Google Scholar]
- 171.Woods L. More on the bogus axioms of continuum mechanics. Bulletin of the Institute of Mathematics and Its Applications. 1982;18:64–67. [Google Scholar]
- 172.Zhao CG, Liu Y, Gao FP. Work and energy equations and the principle of generalized effective stress for unsaturated soils. International Journal for Numerical and Analytical Methods in Geomechanics. 2010;34:920–936. doi: 10.1002/nag.839. [DOI] [Google Scholar]
- 173.Zienkiewicz OC, Chan A, Pastor M, Schrefler BA, Shiomi T. Computational Geomechanics with Special Reference to Earthquake Engineering. Wiley; Chichester: 1999. [Google Scholar]